Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2023 Jul 17;8(29):26079–26087. doi: 10.1021/acsomega.3c02252

Price Estimation of Coal Seam and Its Application in the Optimization of the Mining Sequence: A Case Study

Feiyue Liu †, Ke Yang ‡,†,*, Lingyue Yang †, Wei Hou §, Kai Fu †
PMCID: PMC10373216  PMID: 37521600

Abstract

graphic file with name ao3c02252_0010.jpg

Coal price may vary significantly within a given coal seam, and the accurate characterization of coal price plays an important role in the rational development and utilization of coal resources. A geostatistics-block-based method is proposed to obtain the spatial correlation of borehole survey data and map the heterogenous distribution of coal seam thickness and coal quality (including calorific value, volatile content, ash content, and sulfur content). A block model of thermal coal price is next established considering the spatial distribution of coal quality parameters. Taking an undisclosed coal mine as an example, the estimation process of coal price block model is described in detail, and the mining sequence among several panels is optimized considering the heterogenous coal price. The coal price ranges from 814 to 1671 Chinese Yuan/t within the research area, and the net present value is increased by 1.53% after the optimization of the mining sequence. The result indicated that the coal price is generally heterogenous in a coal seam, and it has a significant influence on the mining sequence. The accurate modeling of coal seam properties has wide applications in mining engineering.

1. Introduction

Due to the differences of geological conditions during deposition and coalification, coal seam properties exhibit heterogeneity in terms of thickness and quality.1,2 Commercially, the coal price is determined by key quality parameters such as calorific value, volatile content, ash content, and sulfur content. Raw coal with a higher calorific value and volatile content, as well as lower ash content and sulfur content, is considered a more valuable product. The heterogenous nature of coal quality directly affects the spatial distribution of coal price within a given coal seam. It is of great importance to characterize the coal price prior to mining, and taking reasonable mining planning to maximum the economic benefits.3 Furthermore, the relationship between coal quantity, cash flow, and the excavated footage is crucial for coal production and sales in the mining activity. Therefore, accurate modeling of coal seam thickness, coal quality, and coal price is essential.

Previous research has indicated that coal quality parameters and coal seam thickness are both heterogenous and continuous in a coal seam, exhibiting both structural and random characteristics. These regionalized variables are best modeled using the geostatistical method.4,5 The coal quality is mainly controlled by the source materials, depositional environment, tectonic setting, and other factors. The final mineral compositions of a given coal seam are a unique genetic code.6 Saikia and Sarkar7 have mapped the coal quality parameters and coal seam thickness using the geostatistical method and identified areas of high uncertainty which helps further sampling to improve the accuracy of estimation. The borehole geophysical log data, seismic investigation data, and other supplementary physical measurements are integrated into the modeling of coal quality parameters and coal seam thickness.8−11 Precious modeling of coal seam properties especially the coal seam thickness and floor contour can provide the geological guarantee for intelligent mining.12 In addition, the coal porosity, effective permeability, and gas content are applicable for geostatistical analysis.13−15 The combination of spatial interpolation methods (such as Kriging, inverse distance weighting, sequential Gaussian, and Bayesian) and geostatistical modeling software (such as SGeMS, Surfer, Maptek Vulcan, and Datamine) enables the spatial analysis and display of coal seam properties, which has been widely applied in the geological modeling of coal seams.10,16,17

In the mining activity, the long-term production schedule planning is the decision of the mining sequence that is the order in which parts of the coal seam should be mined given a specified number of operating units, i.e., panels in longwall coal mine.18 Giving a specified reserve, such as a coal seam, the mining sequence optimization problem is formulated as a maximization of the net present value (NPV).19 Following the logic of the formulation, panels with higher coal price should be extracted in earlier extraction periods to maximize the NPV due to the discounting. For a large coal mine, optimization of the mining sequence can yield significant economic benefits.20 Accurate modeling of the spatial distribution of coal prices is essential for successful optimization. Unfortunately, current research studies reckon without the spatial mapping of coal price within a given coal seam.

In this paper, measured data collected from 161 surrey boreholes of an undisclosed coal mine are taken as an example. The geostatistical method is utilized to obtain the experimental semivariogram of coal seam thickness and coal quality parameters. The spatial mapping of coal seam thickness and coal quality parameters is performed using ordinary Kriging and inverse distance weighting methods, respectively. A coal price block model is established using the thermal coal pricing equation, and the mining sequence among serval panels is optimized to maximize the NPV. This paper can provide ideas and solutions for the geostatistics-block-based modeling of coal price as well as the optimization of mining sequence of coal seam.

2. Modeling of Coal Seam Thickness, Coal Quality, and Coal Price

2.1. Engineering Geological Background

Since much confidential information is presented in this paper, the name of the studied coal mine cannot be disclosed. Nevertheless, the undisclosed coal mine is located in the Yuheng Coal District, North Shaanxi Provence, which is an important energy base of China. The undisclosed coal mine covers an area of 251.75 km2 and contains nine mineable coal seams, namely, Nos. 2, 2–1, 3, 3–1, 4–1. 4–2, 5, 7, and 9 coal seam, in which the No. 2 coal seam is mineable throughout the mine field and was mined first in the undisclosed coal mine. The stratum of No. 2 coal seam is Section 4 of Yan’an Formation in Mid-Jurassic (J2y4), which was deposited in a relatively stable tectonic environment.21 The stratum showed balanced subsidence during the deposition period of Yan’an Formation. The coal seam is mainly controlled by the ancient landform, and there is no obvious tectonic tectonism. The No. 2 coal seam is generally flat with a dip angle less than 1°, and there is no large fault, collapse column, or magmatic rock distributed in the mine field. According to the “Specification for coal exploration” in China, the geological condition is considered “simple,” which makes it suitable for geostatistical analysis. In this paper, the No. 2 coal seam is taken as an example for the modeling of coal seam thickness, coal quality, and coal price.

As shown in Figure 1, there are 161 surface geological survey boreholes distributed along 14 exploration lines in the undisclosed coal mine. Most of the boreholes are distributed in the eastern part of the mine field, and a research area is delineated by a magenta line in Figure 1. The average distance between exploration lines is 800 m, and the coal reserve is “proved” in the research area according to the “Specification for coal exploration.” The minimum and maximum measured thickness of No. 2 coal seam is 0.68 and 8.64 m, with a mean value of 3.41 m. Figure 1 indicated that the measured thickness is both heterogenous and continues in No. 2 coal seam, and the coefficient of variation is 50.4%, indicating a good spatial correlation of measured coal seam thickness. The coal quality parameters, including the calorific value (Qnet,ar), volatile content (Vdaf), ash content (Ad), and sulfur content (St,d), were measured on samples taken from 161 surface geological survey boreholes. The statistical parameters of No. 2 coal seam properties are listed in Table 1.

Figure 1.

Figure 1

Open in a new tab

Surface borehole survey of the No. 2 coal seam.

Table 1. Statistics Parameters of No. 2 Coal Seam Properties.

coal seam properties minimum maximum mean variance coefficient of variation
coal seam thickness 0.68 m 8.64 m 3.40 m 2.93 50.41%
calorific value 22.97 MJ/kg 32.84 MJ/kg 29.79 MJ/kg 4.40 7.04%
volatile content 31.39% 40.89% 36.45% 2.83 4.62%
ash content 3.94% 39.40% 9.33% 19.38 47.20%
sulfur content 0.23% 4.40% 1.38% 0.60 56.25%
Open in a new tab

2.2. Block Model of Coal Seam Thickness and Coal Quality

Coal seam properties including thickness, colorific value, ash content, volatile content, and sulfur content are regionalized variables.22 The special geological structures, particularly faults, may have a significant impact on the geostatistical analysis, as they can abrupt changes in the geological structure and affect the spatial continuity of coal seam properties. In geostatistical analysis, the assumption of spatial continuity is essential, since it is the foundation for estimating values at unmeasured locations and making predictions. To mitigate the impact of faults on geostatistical analysis, it is necessary to account for them explicitly in the modeling process. The research area can be divided into several zones using the faults as the boundary to ensure that the coal seam properties continue in each zone. The geostatistical analysis and spatial interpolation are performed in each zone separately. Since there is no large fault distributed in the No. 2 coal seam, the research area is treated as a single region.

In the geostatistical analysis, a geological region is typically discretized into small units, and each unit processes distinct and definite properties, known as block model. The block model method can simplify the topology relationship and reduce the computer memory usage, which assists the implementation of geological mapping for coal seam properties. Since the No. 2 coal seam is generally horizontal with an average dip angle less than 1°, a two-dimensional block model is established. Many studies have indicated that the shape and size of block units can influence the accuracy of geostatistical evaluation.23 In this paper, the block unit is shaped as a square to ensure uniform modeling resolution for coal seam properties. The size of the block unit corresponds to the borehole sampling density and is generally set as 1/5–1/10 of the average distance between exploration lines. Given a relatively simple boundary of research area (see the magenta square in Figure 1), the size of the block unit is set as 100 m in this paper. A total of 9900 block units are meshed within the research area using the software 3DMine, and the spatial interpolation is carried out at the center of each block unit.

Generally, the experimental semivariogram is used to describe the spatial correlation of measured data:24,25

2.2. 1

where γ(h) is the experimental semivariogram; C(zi) is the value of coal seam property measured in the point zi, and zi + h is the measured point located at a distance h from point zi; n(h) is the number of pairs [C(zi) – C(zi + h)] available for a distance h that is a multiple of the sampling interval, and the distance h is referred as lag. Set the lag h as x-axis, and the experimental semivariogram γ(h) as y-axis, an experimental semivariogram scatter consists of a set of discrete points is plotted, and the scatter can be fitted as a continuous mathematical model for further analysis. The experimental semivariogram of No. 2 coal seam properties is presented in Figure 2 based on the measured data collected from 161 geological boreholes.

Figure 2.

Figure 2

Open in a new tab

Experimental semivariogram of thickness and coal quality of No. 2 coal seam. (a) Coal seam thickness. (b) Colorific value. (c) Volatile content. (d) Ash content. (e) Sulfur content.

The ordinary Kriging (OK) method and inverse distance weighting (IDW) method are commonly used to estimate values of regionalized variable at unmeasured locations within the study area. Compared with the IDW method, the OK method has the advantages of filtering effect and clustering effect, which can improve the spatial estimation result while many measured points are located in the same orientation or clustered together. However, the IDW method is simpler to program and does not require premodeling or subjective assumptions in selecting a semivariogram model. The IDW method is applicable for a small size dataset while the experimental semivariogram is difficult to fit. Generally, the OK method is generally preferred for spatial interpolation under the same conditions, and the IDW method is used while the mathematical function of the experimental semivariogram is difficult to establish within the range.23,26

As shown in Figure 2a, the experimental semivariogram of coal seam thickness increases with the distance and then remains stable. A Gaussian model27 is used to fit the experimental semivariogram:

2.2. 2

where C is the sill equal to 5.4, and Inline graphic is the range equal to 11,000 m, which means that the spatial correlation between two measured coal seam thickness points is nearly disappearing when the distance reaches 11,000 m. The Gaussian model has a parabolic behavior near the origin of coordinates. The slope of this model is initially zero and gradually increases up to the turning point and then quickly climbs to the sill, which indicates that the measured coal seam thickness has a high continuity degree.

The OK method, an unbiased, optimality, and linear interpolation technique, is used for the spatial evaluation of No. 2 coal seam thickness. Unbiased interpolation means that the mathematical expectation of the deviation between the estimated value ẑV and the true value zV remains zero, i.e., E[ẑV – zV] = 0. The optimality interpolation means that the mathematical expectation of the square of the deviation between the estimated value ẑV and the true value zV is minimized, i.e., the Kriging evaluation variance [(ẑV – zV)2] = min. Linear interpolation means that the estimated value ẑV is a linear combination of several measured values:

2.2. 3

where bi is the weight coefficient, and the sum of bi equal to 1, i.e., 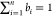Inline graphic. The weight coefficient bi is calculated using the following equation:

2.2. 4

where γij is the experimental semivariogram between the measured data on the location of zi and zj, and 2λ is the Lagrange multiplier. Figure 3 shows the spatial distribution of No. 2 coal seam thickness, which indicated that the coal seam thickness is relatively large in the northwest and small in the southeast.

Figure 3.

Figure 3

Open in a new tab

Block model of coal seam thickness.

In contrast with coal seam thickness, the experimental semivariogram of coal quality parameters, including the calorific value, volatile content, ash content, and sulfur content, is complex and cannot be accurately fitted using specific mathematical functions, as shown in Figure 2b–e. Therefore, the IDW method is employed for the spatial interpolation. Similar to the OK method, the estimated value ẑV is the linear combination of several measured values, and the sum of weight coefficient equal to 1 in the IDW method. The difference is that the weight coefficient bi is determined by the inverse of the N-power of the distance from the measured point to the estimated point:

2.2. 5

where hi is the distance between the estimated point and the i-th measured point, and N is the exponent in the IDW method. A higher exponent indicates that the weight coefficient is accelerated decreasing with the distance.

The cross-validation method is used to obtain an optimized exponent with minimum estimation error. Giving a series of potential exponent Ni, the cross-validation method removes one measured point, and interpolation is performed in the location of the removed point using the remaining samples. The estimation error is defined as the difference between measured value and interpolated value on the removed point. This process is repeated at each measured point, and the overall performance is evaluated by the root-mean of squared residuals, and the exponent with minimum root-mean of squared residuals is the optimized exponent.

2.2. 6

Giving a potential exponent range from 0.0 to 6.0 with an interval of 0.2, the root-mean of squared residuals is decreasing and then increasing with the exponent for all the coal quality parameters, shown in Figure 4. The optimized exponent is 2.6, 3.2, 2.2, and 2.8 for calorific value, volatile content, ash content, and sulfur content, respectively. As shown in Figure 5, the block model of four coal quality parameters is established using the IDW method. Compared with the coal seam thickness, the coal quality parameters exhibit stronger heterogeneity. In particular, measured points with extreme value have disrupted the overall spatial continuity of coal quality parameters. The accuracy of geostatistical analysis and spatial interpolation are strong dependent on the amount of measured data. The results are more realistic when more measured data are available.28 The accuracy of the block model can be further improved by collecting more measured data during the mining period.

Figure 4.

Figure 4

Open in a new tab

Optimization of exponent using the cross-validation method.

Figure 5.

Figure 5

Open in a new tab

Block model of coal quality parameters. (a) Calorific value. (b) Volatile content. (c) Ash content. (d) Sulfur content.

2.3. Establishment of the Coal Price Block Model

Coal type of the undisclosed coal mine consists of noncaking coal and long-flame coal, which are mainly used as fuel in coal fired power plant in China, known as thermal coal. The price of thermal coal depends on its quality,29 which may vary significantly in a coal seam. In China, a widely accepted thermal coal price equation is calculated based on certain coal quality parameters including the calorific value, volatile content, ash content, and sulfur content:30,31

2.3. 7

where C is the thermal coal price; Q is the calorific value; Kc is the price parity of calorific value; Kv is the price parity of volatile content; Ka is the price parity of ash content, Ks is the price parity of sulfur content; Kp is the price parity of coal type; Kx is the price parity of coal size. In particular, a is a constant that fluctuates with the coal market.

As shown in Table 2, the calorific value of thermal coal is divided into 30 levels ranging from 18.0 to 33.5 MJ/kg, and the price parity is set as 100% when the calorific value ranges from 20.5 to 21.0 MJ/kg. The price parity is increasing by 1.2% or decreasing by 0.6% when the calorific value increases or decreases by 0.5 MJ/kg, respectively. Similarly, the referenced price parity of coal volatile content, ash content, and sulfur content is listed in Table 3, Table 4, and Table 5. The coal type is distinguished by the coal size and washing state, and the referenced price parity of coal type is listed in Table 6. The limit rate of lump coal, defined as the rate of coal dimension less than 25 mm, is used to evaluate the coal size. The price parity of coal size is divided into 10 levels according to the limit rate of lump coal, shown in Table 7.

Table 2. Price Parity of Calorific Value.

Qnet,ar (MJ/kg) Kc (%) Qnet,ar (MJ/kg) Kc (%) Qnet,ar (MJ/kg) Kc (%) Qnet,ar (MJ/kg) Kc (%) Qnet,ar (MJ/kg) Kc (%)
33.0–33.5 134.8 29.5–30.0 121.6 26.5–27.0 114.4 23.5–24.0 107.2 20.5–21.0 100.0
32.5–33.0 133.6 29.0–29.5 120.4 26.0–26.5 113.2 23.0–23.5 106.0 20.0–20.5 99.4
31.5–32.0 132.4 28.5–29.0 119.2 25.5–26.0 112.0 22.5–23.0 104.8 19.5–20.0 98.8
31.0–31.5 131.2 28.0–28.5 118.0 25.0–25.5 110.8 22.0–22.5 103.6 19.0–19.5 98.2
30.5–31.0 130.0 27.5–28.0 116.8 24.5–25.0 109.6 21.5–22.0 102.4 18.5–19.0 97.6
30.0–30.5 122.8 27.0–27.5 115.6 24.0–24.5 108.4 21.0–21.5 101.2 18.0–18.5 97.0
Open in a new tab

Table 3. Price Parity of Volatile Content.

Vdaf (%) ≤20 20–28 28–37 >37 lignite
Kv (%) 90 100 110 120 125
Open in a new tab

Table 4. Price Parity of Ash Content.

Ad (%) ≤5.0 5.0–10.0 10.0–15.0 15.0–20.0 20.0–25.0 25.0–30.0 30.0–35.0 35.0–40.0 >40.0
Ka (%) 100 99 97 95 93 92 91 90 89
Open in a new tab

Table 5. Price Parity of Sulfur Content.

St,d (%) ≤0.5 0.5–1.0 1.0–2.0 2.0–3.0 3.0–4.0 4.0–5.0 5.0–6.0 >6.0
Ks (%) 104.5 103 101.5 100 98.5 97 95.5 94
Open in a new tab

Table 6. Price Parity of Coal Type.

coal type size (mm) Kp (%) coal type size (mm) Kp (%)
raw coal   100 washing raw coal   108
extra-large block >100 129 washing extra-large block >100 132
large block 50–100 129 washing large block 50–100 139
mixed block >25 134 washing mixed block >25 139
middle block 25–50 140 washing middle block 25–50 150
mixed middle block 13–100 137 washing mixed middle block 13–100 143
small block 13–25 130 washing small block 13–25 136
granular coal 6–13 125 washing granular coal 6–13 132
mixed coal 0–50 105 washing mixed coal 0–50 107
fine coal 0–13 103 washing fine coal 0–13 109
pulverized coal 0–6 103 washing pulverized coal 0–6 107
coal slime 0–1 60 washing coal slime   60
Open in a new tab

Table 7. Price Parity of Coal Size.

limit rate of lump coal (%) ≤3 3–6 6–9 9–12 12–15
Kx (%) 107.5 106.0 104.5 103.0 101.5
limit rate of lump coal (%) 15–18 18–21 21–24 24–27 27–30
Kx (%) 100.0 98.5 97.0 95.5 94.0
Open in a new tab

In the undisclosed coal mine, raw coal that has not been washed and processed is sold to the power plant directly. Therefore, the price parity of coal type Kp is set as 100% according to Table 6. The fully mechanized longwall mining technique is used in the undisclosed coal mine, resulting in a price parity of coal size of 101.5%. The average local thermal coal price is 780 Chinese Yuan/t in China when the calorific value is 5500 kcal (23.02 MJ/kg, the price parity of calorific value is 106%) in the year of 2022. The constant a in eq 7 is calculated as 31.97 Chinese Yuan/MJ. The price parity of all the coal quality parameters is obtained and the coal price is calculated in each block unit using eq 7. As shown in Figure 6, the coal price ranges from 814 to 1671 Chinese Yuan/t with an average value of 1347 Chinses Yuan/t. The coal price exhibits a strong heterogeneity in the No. 2 coal seam. Overall, the coal price is relatively high in the south (coal seam between exploration line 16 and exploration line 20) and low in the north (coal seam between exploration line 13 and exploration line 16). This heterogeneity can significantly influence the economic benefit of mining activities, and an optimization of mining sequence is necessary to maximize the NPV for the mining company.

Figure 6.

Figure 6

Open in a new tab

Block model of coal price.

3. Optimization of the Mining Sequence Using the Coal Price Block Model

As shown in Figure 7, the inclined shaft development and fully mechanized longwall mining technique are used in the undisclosed coal mine, and five roadways are excavated to access the longwall panels. The research area is divided into two zones by the inclined shafts, namely district 11, and district 12. In most modern coal mine, the dimension of longwall panels is designed as large as possible to reduce the development ratio. The designed width and length of the longwall panels are 350 and 3500 m, respectively, and the interval pillar is 30 m in width. District 11 comprises 24 panels numbered panel 11201 to panel 11224, while district 12 has 24 panels numbered panel 12201 to panel 12224.

Figure 7.

Figure 7

Open in a new tab

Panel layout in the No. 2 coal seam.

A reasonable mining sequence among several districts should meet the need of production capacity, efficiency, and economic benefits. In addition, the roadway excavation, equipment installation, transportation, and ventilation may influence the optimization of mining sequence.32 In particular, the mining sequence is synergistically influenced by safety indicators, including the protrusion hazard, stress distribution, water inrush, gas disaster, etc. Since the research area is the first mined zone in the undisclosed coal mine, the advancing mining among panels with in a district is adopted to ensure the driving of five roadways can synchronized with the mining activities. Therefore, two potential mining planning is proposed based on the production conditions. Plan A excavates the district 11 first, followed by the district 12. The mining sequence of panels is from panel 11201 to panel 11224, then panel 12201 to panel 12224. In contrast, plan B excavates the district 12 first, followed by the district 11, with the mining sequence is from the panel 12201 to panel 12224, then panel 11201 to panel 11224.

The average density of No. 2 coal seam is 1.32 t/m3, and the reserve of all the 48 panels in the research area is calculated to be 273.3 Mt. using the coal seam thickness block model shown in Figure 3. The undisclosed coal mine has a design production capacity of 10 Mt./a, and the service life of the research area is 27 years. The cash flow (i.e., the sales amount of coal) of each year in the service life of two potential mining plans is calculated and presented in Figure 8. The NPV is calculated using the following equation:

3. 8

where Ci is the cash flow of the ith year; r is the discount rate, and r is set as 8% in this case; n is the service life and equal to 27 in the research area. As shown in Figure 8, compared with mining plan B, the plan A can get a higher cash flow in the first several years (from the 1st year to 11th year), and a lower cash flow in the subsequent years (from 12th year to 20th year), which means panels with higher coal price are mined in earlier period in the plan A. The NPV of potential mining plan A and plan B is 14.99 billion Chinese Yuan and 14.76 billion Chinese Yuan, respectively. Compared with mining plan B, the plan A can benefit 225.17 million Chinese Yuan (about increase 1.53%) under the same coal resources and production capacity but different mining sequences. Finally, the mining sequence of plan A in adopted for a better economic performance. The district 11 is mined first, followed by the district 12 in the research area.

Figure 8.

Figure 8

Open in a new tab

Comparison of cash flow between two potential mining sequences.

4. Conclusions

This paper proposed a geostatistics-block-based method for the accurate modeling of coal seam properties including coal seam thickness, coal quality, and coal price. The block model of coal price is next used for the optimization of the mining sequence to achieve a best NPV. A case study is presented to elaborate the detailed process of the proposed method.

  • (1)

    By collecting the coal seam thickness and coal quality information measured from geological survey boreholes, the geostatistics-block-based method can obtain the spatial correlation of measured data, thus providing a relatively reasonable estimation in areas without measured information.

  • (2)

    The thermal coal price is controlled by the coal quality including calorific value, volatile content, ash content, and sulfur content. The coal price ranges from 814 to 1671 Chinese Yuan/t in the No. 2 coal seam of the undisclosed coal mine, which has shown a strong heterogeneity in the spatial distribution.

  • (3)

    The NPV of the sale amount is increased by 1.53%, equivalent to 225.17 million Chinese Yuan, after the optimization of mining sequence in the undisclosed coal mine. The case study indicated that the optimization of mining sequence considering the heterogeneous coal price can increase the economic benefit while mining the same coal resources.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (52204080), the Natural Science Research Project of Anhui Educational Committee (KJ2021A0458), the Institute of Energy, Hefei Comprehensive National Science Center (21KZS215), and the University Synergy Innovation Program of Anhui Province (21KZZ505). We would like to thank Dr. Dylan Liu from McMaster University for his help in English writing.

Data Availability Statement

The original data presented in the study are included in the article, and further inquiries can be directed to the first/corresponding author.

The authors declare no competing financial interest.

References

  1. Heriawan M. N.; Koike K. Identifying spatial heterogeneity of coal resource quality in a multilayer coal deposit by multivariate geostatistics. Int. J. Coal Geol. 2008, 73, 307–330. 10.1016/j.coal.2007.07.005. [DOI] [Google Scholar]
  2. Tang Y. G.; Li R. Q.; Wang S. Q. Research progress and prospects of coal petrology and coal quality in China. Int. J. Coal Sci. Technol. 2020, 7, 273–287. 10.1007/s40789-020-00322-3. [DOI] [Google Scholar]
  3. Rocchi L.; Carter P.; Stone P. Sequence optimization in longwall coal mining. J. Miner. Sci. 2011, 47, 151–157. 10.1134/S106273914702002X. [DOI] [Google Scholar]
  4. Olea R. A.; Luppens J. A. Mapping of coal quality using stochastic simulation and isometric logratio transformation with an application to a Texas lignite. Int. J. Coal Geol. 2015, 152, 80–93. 10.1016/j.coal.2015.10.003. [DOI] [Google Scholar]
  5. Olea R. A.; Luppens J. A.; Egozcue J. J.; Pawlowsky-Glahn V. Calorific value and compositional ultimate analysis with a case study of a Texas lignite. Int. J. Coal Geol. 2016, 162, 27–33. 10.1016/j.coal.2016.05.005. [DOI] [Google Scholar]
  6. Sun R. Y.; Liu G. J.; Zhen L. G.; Chou C. L. Characteristics of coal quality and their relationship with coal-forming environment: a case study from the Zhuji exploration area, Huainan coalfield, Anhui, China. Energy 2010, 35, 423–435. 10.1016/j.energy.2009.10.009. [DOI] [Google Scholar]
  7. Saikia K.; Sarkar B. C. Coal exploration modelling using geostatistics in Jharia coalfield India. Int. J. Coal Geol. 2013, 112, 36–52. 10.1016/j.coal.2012.11.012. [DOI] [Google Scholar]
  8. Zawadzki J.; Fabijańczyk P.; Badura H. Estimation of methane content in coal mines using supplementary physical measurements and multivariable geostatistics. Int. J. Coal Geol. 2013, 118, 33–44. 10.1016/j.coal.2013.08.005. [DOI] [Google Scholar]
  9. Zhou B. Z.; O’Brien G. Improving coal quality estimation through multiple geophysical log analysis. Int. J. Coal Geol. 2016, 167, 75–92. 10.1016/j.coal.2016.09.013. [DOI] [Google Scholar]
  10. Zhu M. B.; Cheng J. Y.; Cui W. X.; Yue H. Comprehensive prediction of coal seam thickness by using in-seam seismic surveys and Bayesian kriging. Acta Geophys. 2019, 67, 825–836. 10.1007/s11600-019-00298-y. [DOI] [Google Scholar]
  11. Jeuken R.; Xu C. S.; Dowd P. Improving coal quality estimations with geostatistics and geophysical logs. Nat. Resour. Res. 2020, 29, 2529–2546. 10.1007/s11053-019-09609-y. [DOI] [Google Scholar]
  12. Mao S. J. Development of coal geological information technologies in China. Int. J. Coal Sci. Technol. 2020, 7, 320–328. 10.1007/s40789-020-00340-1. [DOI] [Google Scholar]
  13. Li X. J.; Li P. N.; Zhu H. H. Coal seam surface modeling and updating with multi-source data integration using Bayesian geostatistics. Eng. Geol. 2013, 164, 208–221. 10.1016/j.enggeo.2013.07.009. [DOI] [Google Scholar]
  14. Karacan C.; Drobniak A.; Mastalerz M. Coal bed reservoir simulation with geostatistical property realizations for simultaneous multi-well production history matching: a case study from Illinois Basin, Indiana, USA. Int. J. Coal Geol. 2014, 131, 71–89. 10.1016/j.coal.2014.06.002. [DOI] [Google Scholar]
  15. Barbosa S.; Almeida J.; Chambel A. A geostatistical methodology to simulate the transmissivity in a highly heterogeneous rock body based on borehole data and pumping tests. Hydrogeol. J. 2019, 27, 1969–1998. 10.1007/s10040-019-01980-7. [DOI] [Google Scholar]
  16. Srivastava R. M. Geostatistics: A toolkit for data analysis, spatial prediction and risk management in the coal industry. Int. J. Coal Geol. 2013, 112, 2–13. 10.1016/j.coal.2013.01.011. [DOI] [Google Scholar]
  17. Karacan C. O.; Olea R. A. Mapping of compositional properties of coal using isometric log-ratio transformation and sequential Gaussian simulation - a comparative study for spatial ultimate analyses data. J. Geochem. Explor. 2018, 186, 24–35. 10.1016/j.gexplo.2017.11.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Al-Juhani M. S. M.Long-term underground mining sequence planning using dynamic programming; West Virginia University, 1994. [Google Scholar]
  19. Kumral M.; Sari Y. A. Simulation-based mine extraction sequencing with chance constrained risk tolerance. Simulation 2017, 93, 527–539. 10.1177/0037549717692415. [DOI] [Google Scholar]
  20. Roy S.; Mohanty R. P. Optimising a production plan for underground coal mining: a genetic algorithm application. Int. J. Oper. Res. 2021, 41, 423–445. 10.1504/IJOR.2021.116264. [DOI] [Google Scholar]
  21. Huang G.; Zhou X. Q.; Wang Z. Q. Provenance analysis of the Yan’an formation in Mid-Jurassic at the southeast area of Ordos basin. Bull. Mineral. Petrol. Geochem. 2009, 28, 252–258. [Google Scholar]
  22. Hower J. C.; Finkelman R. B.; Eble C. F.; Arnold B. J. Understanding coal quality and the critical importance of comprehensive coal analyses. Int. J. Coal Geol. 2022, 263, 104120 10.1016/j.coal.2022.104120. [DOI] [Google Scholar]
  23. Caers J.Petroleum geostatistics; Society of petroleum engineers: Richardson, 2005. [Google Scholar]
  24. Yünsel T. Y. In-situ coal quality variability analysis by combining Gaussian co-simulation and a JavaScript. Energy Source, Part A 2019, 41, 2631–2649. 10.1080/15567036.2019.1568636. [DOI] [Google Scholar]
  25. Pardo-Igúzquiza E.; Dowd P. A.; Baltuille J. M.; Chica-Olmo M. Geostatistical modelling of a coal seam for resource risk assessment. Int. J. Coal Geol. 2013, 112, 134–140. 10.1016/j.coal.2012.11.004. [DOI] [Google Scholar]
  26. Liu F. Y.; Yang T. H.; Deng W. X.; Zhou J. R.; Li J. D. Geostatistics-block-based characterization of heterogeneous rock mass and its application on ultimate pit limit optimization: a case study. Bull. Eng. Geol. Environ. 2021, 80, 1683–1700. 10.1007/s10064-020-02023-2. [DOI] [Google Scholar]
  27. Oliver M. A.; Webster R. A tutorial guide to geostatistics: Computing and modelling variograms and kriging. Catena 2014, 113, 56–69. 10.1016/j.catena.2013.09.006. [DOI] [Google Scholar]
  28. Antony L.; Michael H. The geostatistical evaluation of coal parameters in Seam H, Malinau area, Indonesia. Int. J. Oil Gas Coal Technol. 2013, 6, 703–719. 10.1504/IJOGCT.2013.056706. [DOI] [Google Scholar]
  29. Gupta S.; Pahwa M. S.; Gupta M. A. Innovative price adjustments technique for thermal coal: a study of operation function under changing techno environment. Glob. J. Manage Bus. Res. Fin. 2013, 13, 1–5. [Google Scholar]
  30. Cui E. S.; Zhang Y. C. Calculate the price of thermal coal based on calorific value. Cement 1996, 11, 39–42. [Google Scholar]
  31. Nie Q.The study on power coal quality standard in China; China University of Mining and Technology: Beijing, 2016. [Google Scholar]
  32. Peng S. S.Longwall mining; CRC Press: Netherlands, 2019. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

The original data presented in the study are included in the article, and further inquiries can be directed to the first/corresponding author.

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES