Abstract
Laser-induced breakdown spectroscopy (LIBS) is a remarkable elemental identification and quantification technique used in multiple sectors, including science, engineering, and medicine. Machine learning techniques have recently sparked widespread interest in the development of calibration-free LIBS due to their ability to generate a defined pattern for complex systems. In geotechnical engineering, understanding soil mechanics in relation to the applications is of paramount importance. The knowledge of soil unconfined compressive strength (UCS) enables engineers to identify the behaviors of a particular soil and propose effective solutions to given geotechnical problems. However, the experimental techniques involved in the measurements of soil UCS are incredibly expensive and time-consuming. In this work, we develop a pioneering technique to estimate the soil unconfined compressive strength using artificial intelligent methods based on the spectra obtained from the LIBS system. Decision tree regression (DTR) and support vector regression learners were initially employed, and consequently, the adaptive boosting method was applied to improve the performance of the two single learners. The prediction power of the established models was determined using the standard performance evaluation metrics such as the root-mean-square error, CC between the predicted and actual soil UCS values, mean absolute error, and R2 score. Our results revealed that the boosted DTR exhibited the highest coefficient of correlation of 99.52% and an R2 value of 99.03% during the testing phase. To validate the models, the UCS values of soils stabilized with lime and cement were predicted with an optimum degree of accuracy, confirming the models’ suitability and generalization strength for soil UCS investigations.
1. Introduction
Laser-induced breakdown spectroscopy is a robust elemental identification and quantification technique employed in various sectors, including science, engineering, medicine, and industry.1 The technique has been widely adopted to investigate materials composition and the proportion of different elemental contents. For example, the food processing industries have used the method to investigate the presence of radioactive elements in food items.2 Also, the technique has been used to detect and quantify elements in cancerous specimens to develop an effective correlation between the constituent elements and the disease.3 In construction industries, the technique has been employed to investigate different types of cementitious, soil, and concrete samples to identify the role of the constituent elements on the materials’ properties, such as compressive strength, corrosion rate, and moisture absorption capacity.4
The material to be investigated under LIBS could be in any state, i.e., the solid, liquid, or gaseous form. The method involves concentrating high-energy laser pulses on the surface of the uniformly prepared sample. The laser–material interactions create a plasma plume constituting the atomic emission information of the constituent elements. The emission signatures are captured in a spectrometer in the form of light with varying intensities and wavelengths.5 Principally, the LIBS operation requires matching the elements to their emission lines. However, the elements do not have a unique emission line since more than one electron can be excited within the same or varying energy states during plasma generation.
Soil science is an outstanding field that constitutes the fundamentals of soil chemistry, physics, and biology.6 The soil UCS is a fundamental structural parameter that finds many applications in the audit and design of many environmental and geotechnical structures such as earth dams, bridges, railways, tunnels, buildings, pavements, and road foundations.7 Soil unconfined compressive strength is one of the essential properties of soil that determines its behavior under loading conditions. Estimating soil UCS is a crucial task in soil mechanics and geotechnical engineering, and it is essential to ensure the stability and safety of civil engineering structures built on the soil. The UCS can be harnessed to determine the soil compaction ability. The common way to estimate such a quantity is through a physical property measurement setup in the laboratory. However, this method is relatively expensive and consumes a lot of time, which might add up to the overall construction expenses. Furthermore, several parameters, such as equipment quality and the technical expertise of the experimenter, significantly affect the accuracy of the measurements. Therefore, finding alternative means of determining the soil UCS is imperative.
The field of soil mechanics has recently witnessed a remarkable development, especially regarding testing techniques.8 Many laboratory tests and in situ mechanisms were adopted and enhanced, leading to an overwhelming advancement in the geotechnical research of soils. The testing mechanisms provide quantitative results of soil properties used for design and condition assessment. However, most of these testing techniques are time-consuming and expensive and require laborious experimental work. For example, Hakan et al. demonstrated how the length-to-diameter ratio can affect the unconfined compressive strength of materials.9
Owing to the shortcomings of the existing methods and the importance of calculating soil properties, several works were reported in which soil properties were obtained using empirical techniques.10,11 These methods, often based on statistical relationships between soil properties, are commonly used to estimate the soil unconfined compressive strength of materials. However, these equations are often limited by oversimplification, assumptions, and dependencies on specific soil types or conditions.12 It is important to note the difficulty of employing numerical and empirical methods to model the indirect relationship between the chemical properties of the soil and the UCS, which is a physical property. These methods may not produce the desired target with a reasonable degree of accuracy.10 On the other hand, chemometric techniques, such as multivariate regression, have been applied to analyze spectroscopic data for predicting soil properties.13 While these methods have shown promise, they often rely on assumptions about linearity and may struggle to capture complex nonlinear relationships present in the soil data. Additionally, their interpretability is limited, making it challenging to gain insights into the underlying soil composition and its impact on unconfined compressive strength. This calls for implementing more sophisticated and intelligent techniques that can predict the soil UCS based on the easily obtainable elemental intensities from the LIBS system.
Recently, there has been increased interest in the use of machine learning techniques in geotechnical engineering applications. Machine learning is an advanced method used in predicting unknown quantities from known datasets. The algorithms are trained based on the available data of the input and target variables.14 The input features, otherwise called descriptors, generally represent some inherent features of the desired variable and therefore exhibit a certain degree of correlation with the target variable.15 The ability of such techniques to map the input features of a complex problem to the desired quantity, using a high-dimensional feature space without necessarily utilizing the initial explicit relationship between them, makes it an outstanding tool for contemporary research works. Multiple studies have demonstrated the effectiveness of machine learning techniques in various geotechnical applications. For instance, hybrid artificial neural network (ANN)-based techniques have been successfully employed to predict the cohesion of sandy soil combined with fiber.16 Another study introduced a novel approach for soil classification based on laboratory tests using Adaboost and ANN modeling.17 Furthermore, an efficient optimal neural network based on the gravitational search algorithm was proposed for predicting the deformation of geogrid-reinforced soil structures.18 Genetic algorithms and gray wolf optimizer were utilized to optimize random forest models for evaluating soil liquefaction potential.19 Additionally, evolutionary polynomial regression was applied to develop predictive models of the collapse settlement and the coefficient of stress release of sandy-gravel soil.20
Additionally, machine learning has been employed to solve problems in engineering, sciences, energy, construction, business, and medicine, to mention a few.14,21−24 A couple of works exist where machine learning techniques were used to conduct a calibration-free LIBS study.25,26 This was supported by the ability of the laser-induced spectroscopy device to produce sufficient input datasets and the capacity of machine learning algorithms to process them.27−31 Studying the physical properties of soils under LIBS is utterly cumbersome. However, considering the built-in capability of machine learning techniques to map complex patterns, it can be trained using the acquired chemical properties to predict the physical properties, such as soil UCS, as conducted in the current work.
Herein, several soil samples were extracted from multiple locations within the Kingdom of Saudi Arabia and investigated using the LIBS system. The spectral emission intensities of the constituent elements, together with the measured soil moisture content and bulk density, were employed to develop robust artificial intelligence algorithms that can estimate the soil UCS with a high degree of accuracy. The samples were also stabilized with lime and cement materials and studied under the LIBS system to validate the models. The strength of the developed method in predicting the unconfined compressive strength of the cement and lime-treated samples justifies the generalization strength and prediction accuracy of the models.
The rest of the sections are organized as follows: Section 2 presents the model descriptions together with brief mathematical expressions describing the algorithms. Section 3 presents the parameter optimization strategies employed in this work as well as the description and statistical analysis of the input dataset. The prediction results, model performance evaluations, and model validations and applications are concisely presented in the upcoming sections.
2. Overview of the Developed Algorithms
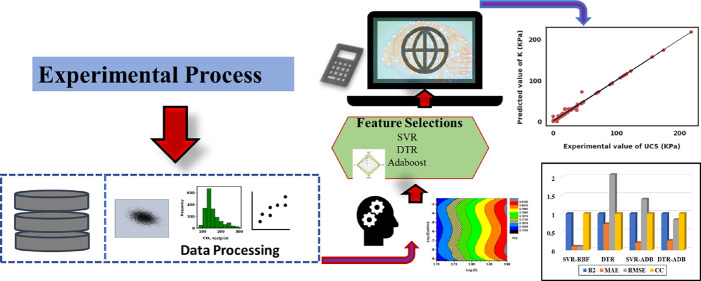
This section summarizes the description of the DTR and SVR models with their mathematical framework. The scikit-learn library was used in model implementation.32 The flow of the research work carried out in this paper from the experimental process to the results analysis is schematically presented in Figure 1.
Figure 1.
Schematic figure depicting the modeling schema.
2.1. Decision Tree Regression
As the name suggests, this is a representation of data in a tree-structured form that is largely utilized to solve machine learning problems for regression and classification. The tree consists of branches, leaves, and multiple internal nodes based on the available dataset. Existing classes are used to divide occurrences and features by the DT algorithm equally. The application of DT as a tool is mostly seen in medical diagnosis, where clinicians get information on the best time to administer treatment to patients with prevailing diseases.33
The given occurrences are created by stimulating the DT, and when the fitness function is minimized, it produces the optimal decision tree. Parameters such as the feature number, split sample, leaf sample, fitness function, number of features, and depth of the tree affect the accuracy of the DT models.34 The number of required presents at a leaf node is referred to as a leaf sample. The lowest number of needed samples to split an internal node is depicted by the split sample. The depth of the tree is described by how deep it can go, and as the depth increases, the tree acquires information on the data. Meanwhile, the fitness error reduces the error between the experimental and predicted results.
2.2. Support Vector Regression
Support vector regression is a robust ML technique used in modeling and prediction in a continuous space that depends on the projected pattern between the target variable and the descriptors.35 The method separates the data class by utilizing the ε-insensitive loss function to influence the hyperplane, which ignores the difference between the predicted values from the actual values at a certain distance. The main idea is to construct a hyperplane that optimizes the margin and decreases the error. SVR can make predictions based on a small training set, making it attractive and computationally less expensive.36 Support vector machine (SVM) and SVR utilize the same principle of Vapnik’s support vectors. However, the latter does not use the regular empirical risk minimization of artificial neural networks but rather the basics of structural risk minimization. Meanwhile, the former is used as a classification tool, and its margin of tolerance ε is not explicit but rather extracted from the problem.15
In SVR, the input features are mapped out into a high-dimensional feature space using a nonlinear transformation function, making it possible to rightly apply a linear regression function in the new feature space.37 An insensitive loss function that has the property ε > 0 is considered when applying the support vector regression algorithm, and also, errors below ε are not taken into consideration by the model.
2.3. Adaptive Boosting of Weak Regressors
The adaptive boosting technique is one of the versatile ML algorithms used for its high prediction efficiency.38 It is otherwise called Adaboost. It can be applied to both classification and regression problems. Adaboost is an ensemble-based learning strategy where the algorithm starts the training by creating a weak learner and figuring out how accurate their predictions are. The samples with poor predicting performance are given greater weight in the succeeding runs. A strong learner, or the boosted ensemble, is created by repeating this process until numerous weak learners with different weights are generated. Below are the learners’ brief mathematical descriptions:38,39
Let eq 1 represent a general problem within a training dataset
| 1 |
where Xi and Yi respectively represent the input data vectors and output value; the total number of the samples and the ith sample in the training dataset are denoted by m and (XiYi) (i = 1, ...;m), respectively. Subsequently, the regression tool is applied to train a weak learner (base learner) G(X) using the accepted base learning algorithm, thereby approximating the relative estimation error using eq 2. L() is a loss function that cannot be a linear, exponential, or square loss function.
| 2 |
A single base learner may not perform well enough to achieve the requisite prediction efficiency. Because of this, the purpose of employing Adaboost is to develop a framework where a series of weak learners may be joined to generate a powerful ensemble learner H(x) by utilizing some tactics. A regression problem’s combination strategy is
| 3 |
where k = 1,2, ...;, N; v ∈ (0,1] is the regularization parameter, δk is the allocated weight of the base learner G(Xi), and g(X) is the median of all the δkδGk(X).
Since no specific algorithm is indicated in eq 4 and, instead, a dummy variable G(x) is provided, which might represent any base learning regression algorithm, it is crucial to note the generality of the adaptive boosting technique.40 The Adaboost ensemble approach is a reliable method that offers a framework for combining a variety of base learning algorithms to accurately forecast the goal quantity. Support vector machines, decision trees, linear regression, and artificial neural networks are some well-known base learning methods.41 Thus, we employed the SVR and DTR base learning algorithms for this study.
In summary, the Adaboost technique consists of four key steps: (1) data collection, (2) creation of strong learners from base learners, (3) testing and validation of the boosted algorithms, and (4) application of the strong learners to real-world issues. The main levels involved in the boosting process are the integration of weak learners into strong learners and the instruction of weak learners using training data.42 The base learner parameters and those of the Adaboost framework make up the main Adaboost parameters. While the latter considers the number of estimators and the learning rate, the former depends on the employed base learners.
2.4. Empirical Study and Computational Methodologies
This section presents the empirical studies and computational methodologies used to estimate the soil unconfined compressive strength. The statistical analysis of the utilized dataset and the justification of the chosen descriptors were also discussed. The models’ hyperparameter optimization strategy has also been highlighted. The used dataset comprises elemental intensities generated using the LIBS system. The scikit-learn library was used for the computation, which is a powerful and widely used machine learning library in Python.
To ensure that the model was not overfitting, 10-fold cross-validation was used to optimize the model’s hyperparameters. In 10-fold cross-validation, the data are divided into 10 parts, and each part is used as a test set, while the remaining nine parts are used as training sets. This process is repeated 10 times, with each part being used as the test set once. GridSearchCV function from scikit-learn was used to search for the optimal hyperparameters. GridSearchCV tests all possible combinations of hyperparameters and selects the one that gives the best performance. By doing this, the model’s performance on unseen data could be assessed and ensure that the model was not overfitting. Different combinations of hyperparameters, such as the number of estimators, the learning rate, and the maximum depth of the decision trees, have been tested.
To select the optimal descriptors to estimate the soil unconfined compressive strength, the statistical analysis of the dataset was used. The correlation between the elemental intensities and the soil unconfined compressive strength was analyzed using a correlation matrix depicted by the heat map in Figure 5.
Figure 5.

Correlation strength between the input features and the soil UCS represented by a heat map.
2.5. Statistics and Characteristics of the Employed Dataset
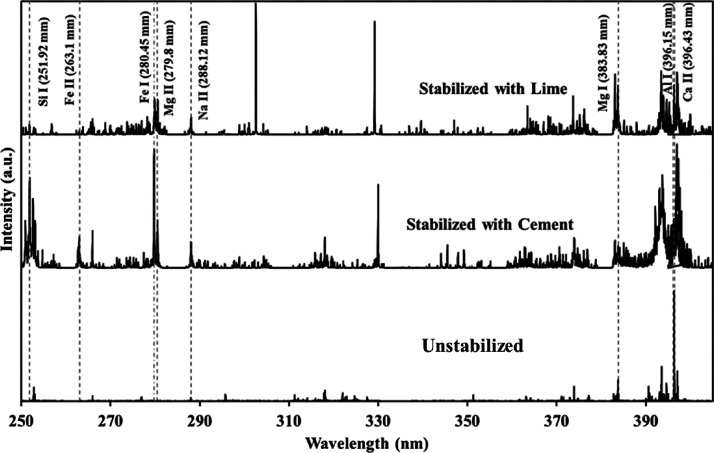
The data used in this work can be categorized into two parts: physical and chemical features. The chemical features, i.e., the emission signatures of the constituent elements were extracted from the LIBS system, while the physical quantities were measured in the laboratory. Figure 2 presents the LIBS spectra showing the constituent elements within the given wavelength range for both the stabilized and unstabilized representative samples. Specifically, the dataset constitutes the persistent lines of Si, Fe, Mg, Ca, Na, Al, Zn, In, Ti, O, and K, as well as two physical quantities, i.e., the water content of the soil sample and bulk density. To ensure the generalization of the model, several soil samples collected from different locations were considered during the input data processing phase. The statistical description of the data is presented in Tables 1a and 1b. Overall, the models were built based on 450 data points. To understand the distribution of the descriptors over the full spectrum, Figures 3 and 4 present histograms showing the relative frequencies of the input features and the target variable.
Figure 2.
Representative laser-induced breakdown spectra highlighting the elements present in the soil samples within certain wavelengths.
Table 1a. The Statistics of the Used Data.
| Si-I (a.u.) | Fe-I (a.u.) | Mg-I (a.u.) | Ca-I (a.u.) | Na-I (a.u.) | Al-I (a.u.) | Zn-II (a.u.) | |
|---|---|---|---|---|---|---|---|
| count | 450 | 450 | 450 | 450 | 450 | 450 | 450 |
| mean | 2011.53 | 3472.19 | 2545.34 | 4348.18 | 3052.15 | 2357.13 | 2302.82 |
| std | 2310.70 | 4008.73 | 2459.58 | 3686.11 | 3349.30 | 2027.71 | 2522. |
| minimum | 7.120 | 7.340 | 7.260 | 30.510 | 54.210 | 8.940 | 97.380 |
| maximum | 13,569.2 | 38,302.4 | 20,496.9 | 23,850.1 | 22,487.0 | 12,691.9 | 13,182.7 |
Table 1b. The Statistics of the Employed Data (Cont.).
| In-II (a.u.) | Ti-I (a.u.) | O-I (a.u.) | K-I (a.u.) | bulk density (g/cm3) | water con. (%) | UCS (kPa) | |
|---|---|---|---|---|---|---|---|
| count | 450 | 450 | 450 | 450 | 450 | 450 | 450 |
| mean | 2011.53 | 3472.19 | 2545.34 | 4348.18 | 3052.15 | 2357.13 | 2302.82 |
| std | 2310.70 | 4008.73 | 2459.58 | 3686.11 | 3349.30 | 2027.71 | 2522. |
| minimum | 7.120 | 7.340 | 7.260 | 30.510 | 54.210 | 8.940 | 97.380 |
| maximum | 13,569.2 | 38,302.4 | 20,496.9 | 23,850.1 | 22,487.0 | 12,691.9 | 13,182.7 |
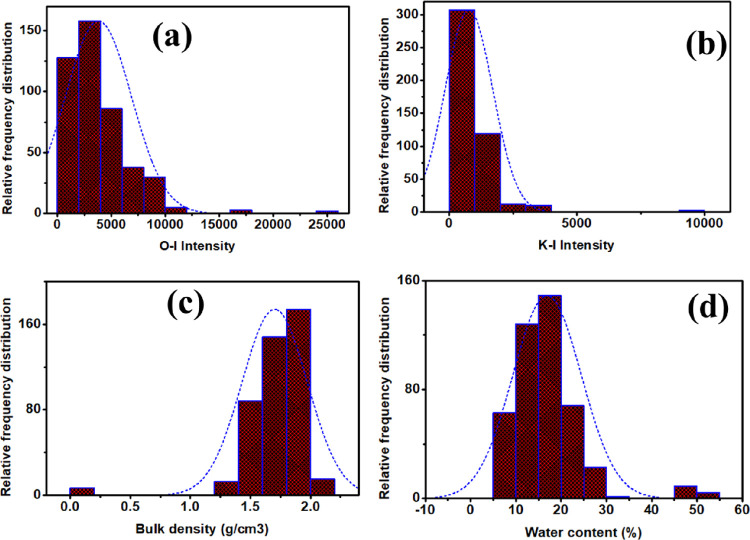
Figure 3.
Histogram representation of the extracted dataset depicting the statistical distribution of the model descriptors for (a) Mg, (b) Fe, (c) Na, (d) Ca, (e) Al, (f) Zn, (g) In, (h) Ti, and (i) Si.
Figure 4.
Histogram representation of the remaining elements depicting the statistical distribution of the model descriptors for (a) O and (b) K, (c) bulk density, and (d) water content.
The choice of the input parameters, otherwise called domain variables, is a crucial step in obtaining efficient machine learning models.43 Here, we analyzed the Pearson correlation coefficients between each domain variable and the soil UCS to determine the strongly correlated features. Figure 5 presents a heat map illustrating the correlation coefficients between the descriptors and the unconfined soil strength. It also highlights the dependence of the model descriptors among themselves and how they affect the target variable. Meanwhile, the choice of the elemental intensities, which subtly indicates that the elemental concentration is a wise selection since the soil UCS will be inherently affected by the material’s constitution.8 Furthermore, it is obvious that the amount of water content and bulk density of the soil samples would dictate their UCS. Therefore, based on this assertion and the calculated correlation coefficients, the choice of the domain variables is in order. Notably, some of the input features, such as Na, Zn, and K, are negatively correlated with the UCS, implying that their presence reduces the absolute soil UCS value. On the other hand, a positive correlation indicates that an increase in the input features would be in favor of the soil UCS. In short, the higher the absolute correlation coefficient between the input features and the soil UCS, the better the performance of the models.
2.6. Optimizing Model Performance through Hyperparameter Tuning
The parameter optimization step is a crucial phase in the establishment of an efficient machine learning model. The optimization step allows the model to fit in the input features with the soil UCS accurately and ensures the generalization strength of the developed model.44 For SVR, the selection of these parameters: epsilon, Kernel, gamma effects, and the regularization parameter C affects the prediction performance of the model.45 These parameters affect how well the model performs in the following ways: The number of support vectors and the margin of tolerance are determined by epsilon. The application of linear regression methods is made possible using a kernel to map a nonlinear function into a high-dimensional feature space. The model may overfit when the regularization parameter is large; thus, it should not be either excessively large or small. On the contrary, a very small regularization parameter does not sufficiently penalize the training data. A trade-off between minimizing the model’s intricacy and reducing the training error is ensured by the regularization parameter. The simultaneous effect of varying epsilon and the regularization parameter during the optimization process on the R2 value of the UCS is presented as a contour plot in Figure 6 for both the single and boosted SVR models.
Figure 6.
Variation of the R2 values with support vector regression hyperparameters epsilon and C represented by a contour map for (a) SVR testing, (b) SVR training, (c) SVR-ADB testing, and (d) SVR-ADB training.
For decision tree models, the tree’s depth is the most significant component because it defines how much the tree may subcategorize data according to the distinctive features of the dataset. However, for the boosted SVR and DTR models, the learning rates and the number of weak estimators are equally important in building efficient models.46 This work employed the test-set-cross-validation technique as the optimization strategy. The method entails tracking each model parameter separately and figuring out the RMSE in every situation. The ideal values of the hyperparameters are the configurations with a high correlation coefficient between the actual and predicted values and the lowest RMSE values. The hyperparameters used in the UCS prediction are given in Table 2. In each case, the hyperparameters are the results of the cross-validation process employed to determine the most suitable set of values.
Table 2. Optimized Parameters for the Models.
| SVR | SVR-ADB | DTR | DTR-ADB | |
|---|---|---|---|---|
| C | 1000 | 1000 | ||
| epsilon | 0.1 | 0.1 | ||
| gamma | 0.01 | 0.01 | ||
| kernel | RBF | RBF | ||
| max depth | 10 | 10 | ||
| learning rate | 0.1 | 1 | ||
| estimators | 25 | 50 |
3. Results and Discussion
The results of the predicted soil UCS estimated using the two weak learners and two strong learners are presented in this section. The unconfined compressive strength of soils is an important parameter used to determine the stability of earth structures such as slopes, foundations, and retaining walls. Machine learning and laser-induced breakdown spectroscopy were simultaneously utilized to estimate the UCS of soils. Specifically, two weak learners (SVR with a radial basis function and DTR) and two strong learners (SVR-ADB and DTR-ADB) were employed to develop the predictive models. The prediction efficiency of the models was assessed using the correlation coefficient, mean absolute error, mean squared error, and coefficient of determination. Table 4 summarizes the performance metrics of the models. The results indicate that the DTR-ADB model outperformed the other models, yielding the lowest values of MAE (1.2834) and RMSE (3.98072) and the highest R2 (0.9903). This suggests that the DTR-ADB model has learned the pattern between the input descriptors and the target variable, making it suitable for estimating UCS in the given soil samples.
Table 4. Model Performance Evaluators during Training.
| SVR | SVR-ADB | DTR | DTR-ADB | |
|---|---|---|---|---|
| R2 | 0.999994 | 0.9989712 | 0.997748 | 0.999634 |
| MAE | 0.09944 | 0.1997737 | 0.713849 | 0.261605 |
| RMSE | 0.099709 | 1.3961107 | 2.065309 | 0.832292 |
| CC | 0.999999 | 0.99949 | 0.99887 | 0.999819 |
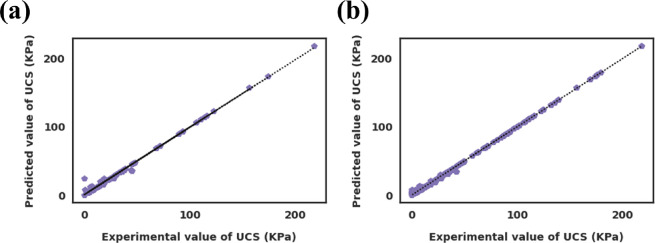
The influence of the model parameters on the overall model performance was also investigated. The parameters considered were the kernel type, epsilon, and regularization parameter for the SVR-RBF models and the number of trees for the DTR models as presented in Table 2. To validate the generalization strength of the developed models, they were used to predict the UCS of soils treated with cement and lime. The results showed that the models were effective in predicting the UCS of the treated soils, as evidenced by the low MAE and MSE values, as presented in detail in the validation section of this paper. The cross-plots between the actual and predicted UCS derived from the SVR-RBF and decision tree models are shown in Figures 7 and 8, respectively. The plots show good agreement between the predicted and actual UCS values, with most of the points lying close to the 45-degree line. This further confirms the accuracy and reliability of the developed models.
Figure 7.
Comparison of the soil UCS values predicted by the SVR-RBF model and experimentally measured values for (a) the testing part and (b) the training part.
Figure 8.
Comparison of the soil UCS values predicted by the DTR model and experimentally measured values for (a) the testing part and (b) the training part.
The two models show excellent agreement between the actual UCS value and the predicted ones, as confirmed by the metric performance indicators presented in the subsequent sections. Furthermore, applying the concept of adaptive boosting enhanced the performance of the DTR model as shown in Figure 9. However, no significant improvement was observed when the adaptive boosting method was applied to SVR, as presented in Figure 10 and substantiated by the metric performance indicators discussed in the subsequent sections.
Figure 9.
Comparison of the soil UCS values predicted by the DTR-Adaboost model and experimentally measured values for (a) the testing part and (b) the training part.
Figure 10.
Comparison of the soil UCS values predicted by the SVR-Adaboost model and experimentally measured values for (a) the testing part and (b) the training part.
The prediction accuracy and the generalization strength of the four models developed in this paper were determined based on acceptable metric performance indicators such as mean absolute error, root-mean-square error, the correlation coefficient between the predicted and experimental UCS, and the R2 value.
Equations 4–6 summarize the mathematical description of such metric quantities:38
| 4 |
| 5 |
| 6 |
where
| 7 |
| 8 |
N is the total number of data points, Yact represents the actual value of the unconfined compressive strength, and Ypred represents the predicted unconfined compressive strength.
The performance indicators (MAE, R2, CC, and RMSE) of the four designed models are given in Table 3 for the testing phase. It is worth noting that the boosted DTR model outperformed the rest of the models in terms of the R2 value and the correlation coefficient between the predicted and actual UCS values. It also exhibited the lowest mean absolute error and root-mean-square error values. This confirms its suitability for the estimation of such a physical quantity owing to its ability to efficiently model the complex relationship between the elemental emission intensities (chemical property) and the UCS. However, the performance of the boosted support vector regression model is marginally less than that of the weak learners, with R2 values of 0.9522 and 0.9528 for the SVR-ADB and SVR, respectively. This simply shows that the inherent complex relationships between the input features and the soil UCS were adequately captured by the weak learner, thus the marginal difference in performance and, therefore, needless to implore the ensemble approach to save computational cost. Both the SVR and DTR have performed excellently in determining the unconfined compressive strength of the soil based on the correlation between the experimental and predicted data. Interestingly, all the metric performance indicators follow a given pattern. For example, the DTR-ADB exhibited the highest values of R2 and correlation coefficient with the lowest values of mean absolute error and root-mean-square error as expected. On the contrary, the boosted SVR was characterized by the lowest R2 and correlation coefficient with the highest MAE and RMSE, as depicted in Figure 11.
Table 3. Model Performance Evaluators during Testing.
| SVR | SVR-ADB | DTR | DTR-ADB | |
|---|---|---|---|---|
| R2 | 0.9528 | 0.95228 | 0.98975 | 0.990396 |
| MAE | 2.4476 | 2.45238 | 1.5355 | 1.2834 |
| RMSE | 8.8229 | 8.87298 | 4.12494 | 3.98072 |
| CC | 0.97754 | 0.9773 | 0.99494 | 0.99519 |
Figure 11.
Bar chart showing the measures of performance of the models during testing (a) and training (b).
The metric performance indicators for the training phase are presented in Table 4. Interestingly, the weak support vector regression learners exhibited the highest R2 value and coefficient of correlation between the actual and estimated UCS values during the training phase followed by the boosted SVR. Although the DTR and DTR-ADB models performed less than the SVR models during the training phase, their ability to outperform the SVR models during the testing and validation phases clearly demonstrates their generalization strength in predicting the UCS of the unseen input dataset.47 The trend of the model performance indicators at the training phase was similar to the testing phase, with the SVR model exhibiting the highest R2 value and CC with the lowest MAE and RMSE, while on the other hand, the DTR model showed the lowest R2 value and CC with the highest MAE and RMSE.
3.1. Validation and Applications of the Proposed Models
In the previous sections, we discussed the development of machine learning models using a dataset that was divided into a ratio of 80:20. The larger portion of the partitioned data was used to train the models, while the smaller portion was used to test the models’ performance. To further evaluate the developed models’ accuracy and generalization strength, we applied the model to external soil samples that were not previously consumed by the model. Specifically, we used some cement-treated and lime-treated soil samples whose LIBS emission intensities were not included in the training or testing dataset. The application of the developed models to estimate the UCS of the modified soil samples using the LIBS emission intensities provided insights into the model’s generalization strength. The models’ ability to accurately estimate the UCS of treated specimens confirms their suitability to be employed in estimating the UCS of any soil-related sample whose emission intensities can be obtained under the LIBS system.
The results obtained from the external sample testing indicated that the developed models could provide reliable predictions of the UCS of treated soil samples. The models’ extrapolation ability beyond the training and testing dataset confirmed their practical utility in soil mechanics and geotechnical engineering applications.48 It is worth noting that the external sample testing provided an opportunity to validate the model’s performance under different soil conditions. The use of cement and lime as stabilizers alters the soil’s characteristics and behavior, making the estimation of UCS a challenging task. Therefore, the ability of the developed models to estimate the UCS of modified soil samples confirms their robustness and reliability in estimating UCS under different soil conditions.
Furthermore, the external sample testing provided insights into the factors that influence the models’ performance. The analysis of the LIBS emission intensities of the treated soil samples revealed that some emission lines were more informative than others in estimating the UCS. The identification of the most informative emission lines can aid in the selection of the appropriate spectral features to improve the models’ performance. The developed models’ accuracy in estimating the UCS of treated soil samples, as demonstrated in the external sample testing, confirms their generalization strength and suitability for use in estimating UCS under different soil conditions. This work highlights the potential of LIBS emission intensities as a source of information for predicting soil properties and provides a basis for further research in this area.
3.1.1. Investigating the Role of Cement as a Stabilizing Agent
To study the impacts of soil stabilization with cement on the model’s prediction capacity, some soil specimens were treated with cement and passed to the LIBS system for elemental spectral emission measurements. Like the untreated samples, the soil UCS was measured in the laboratory using the standard procedure. On the other hand, the emission intensities of the relevant elements, water content, and bulk density were considered as input parameters to estimate the already laboratory-measured UCS to validate the model. Figure 12b,d shows the cross-plot between the estimated and actual UCS values of cement-treated soil samples using SVR and SVR-ADB models. Moreover, the cross-plots between the predicted and experimental UCS values of cement-treated soil samples obtained using DTR and DTR-ADB models are presented in Figure 13b,d. It is interesting to note that all the models were able to predict the unknown UCS values to an appreciable degree of accuracy of more than 95% based on the correlation coefficient between the predicted and experimental values. This further demonstrates the suitability of the developed models in predicting the soil unconfined compressive strength.
Figure 12.
Validation plot comparing the soil UCS predicted by SVR (a,b) and SVR-ADB (c,d) models with the experimental values for different concentrations of stabilizing agents.
Figure 13.
Validation plot comparing the soil UCS predicted by DTR (a,b) and DTR-ADB (c,d) models with the experimental values for different concentrations of stabilizing agents.
3.1.2. Investigating the Role of Lime as a Stabilizing Agent
Investigating the physical properties of lime-treated soils using artificial intelligence techniques is indeed crucial. This is because such analysis is required to design and construct critical infrastructures like dams, bridges, and residential buildings. Lime-treated soils demonstrate improved stabilization, impermeability, load-bearing characteristics, and enhanced workability, especially for soils beneath the road and similar works. Lime is often employed at construction sites to dry wet soil to improve the working surface and reduce downtime. It is, therefore, imperative to develop an intelligent method like machine learning to estimate the UCS properties of such materials. Herein, the four developed models were individually applied to predict the soil unconfined compressive strength of the lime-stabilized samples. The input features were extracted from the LIBS-generated elemental emission intensities of lime-treated soil samples. The predicted soil unconfined compressive strength exhibited high correlation coefficients with the actual UCS values as depicted in Figure 12a,c for SVR and SVR-ADB models. The predicted UCS values for the lime-treated soil samples obtained from DTR and DTR-ADB are presented in Figure 13a,c. The four models have shown great promise in predicting the soil unconfined compressive strength of the lime-stabilized soil samples based on the emission intensities obtained from the LIBS system, water content, and bulk density of the soil as input parameters.
3.2. Limitations of the Models
This section discusses some limitations and challenges of the developed models for the prediction of soil unconfined compressive strength based on the LIBS emission spectra. Some of the limitations include the following:
3.2.1. Dependency on Spectroscopy Data
The models rely on laser-induced spectroscopy emission intensities as input features. While spectroscopy data can provide valuable insights into soil composition, it is important to note that the accuracy of our predictions is contingent on the quality and representativeness of the spectroscopy measurements. Variations in the measurement process, such as instrument calibration and data preprocessing, can introduce uncertainties that may impact the model’s performance.
3.2.2. Generalization to New Environments
The model’s effectiveness in predicting soil unconfined compressive strength may be influenced by the specific conditions and characteristics of the training data. Generalizing the model to new environments or soil types that significantly differ from the training dataset might require additional calibration or retraining to ensure accurate predictions. The performance of the model in such scenarios should be carefully validated.
3.2.3. Interpretability
While machine learning models offer powerful predictive capabilities, some models, such as SVR and Adaboost, may sacrifice interpretability for improved performance. Although our models provide accurate predictions, they may not offer straightforward explanations for the underlying relationships between the laser-induced spectroscopy emission intensities and soil unconfined compressive strength. This limitation may hinder the direct interpretation of the model’s output and could be an area for further investigation.
4. Conclusions and Future Scope
In summary, the soil unconfined compressive strength was estimated using the duo of the LIBS system and machine learning techniques. Laser-induced breakdown spectroscopy was employed to investigate the constituent elements present in the multiple soil samples collected from different locations and their respective concentrations. Subsequently, machine learning techniques used the LIBS-generated emission intensities of selected constituent elements, as well as soil water content and bulk density, as the input features. Initially, a decision tree and a support vector regression model with a radial basis function were used to predict the soil UCS. Consequently, the concept of adaptive boosting of weak learners to create strong regressors was used to improve the performance of each of the two models. The R2 values obtained for SVR, SVR-ADB, DTR, and DTR-ADB are 95.28, 95.22, 98.98, and 99.03%, respectively, during the testing phase. This indicates that the DTR-ADB model outperformed the rest of the models in predicting the soil UCS. The models were validated by studying external systems whose data were not involved in the training and testing phases. The specimens were further stabilized with lime and cement to improve their strength. The LIBS emission intensities of such cement- and lime-treated samples were used to predict their UCS to confirm the validity of the models and ensure their generalization strength. The high degree of accuracy achieved in the prediction of soil strength using the developed models highlights their potential for application in geotechnical engineering. For future works, it will be imperative to take into account the concept of feature selection to minimize the number of input descriptors and lower the computational cost.
Acknowledgments
The authors are thankful to the Deanship of Research, Oversight, and Coordination (DROC) and Interdisciplinary Research Center for Construction and Building Materials, King Fahd University of Petroleum & Minerals (KFUPM), Dhahran, Saudi Arabia for supporting this work under the project INCB2310.
Data Availability Statement
The data is available upon reasonable request.
The authors declare no competing financial interest.
References
- Gondal M. A.; Siddiqui M. N.; Nasr M. M. Detection of Trace Metals in Asphaltenes Using an Advanced Laser-Induced Breakdown Spectroscopy (LIBS) Technique. Energy Fuels 2010, 24, 1099–1105. 10.1021/ef900973s. [DOI] [Google Scholar]
- Gondal M. A.; Habibullah Y. B.; Baig U.; Oloore L. E. Direct Spectral Analysis of Tea Samples Using 266 Nm UV Pulsed Laser-Induced Breakdown Spectroscopy and Cross Validation of LIBS Results with ICP-MS. Talanta 2016, 152, 341–352. 10.1016/J.TALANTA.2016.02.030. [DOI] [PubMed] [Google Scholar]
- Gondal M. A.; Aldakheel R. K.; Almessiere M. A.; Nasr M. M.; Almusairii J. A.; Gondal B. Determination of Heavy Metals in Cancerous and Healthy Colon Tissues Using Laser Induced Breakdown Spectroscopy and Its Cross-Validation with ICP-AES Method. J. Pharm. Biomed. Anal. 2020, 183, 113153. 10.1016/J.JPBA.2020.113153. [DOI] [PubMed] [Google Scholar]
- Gondal M. A.; Dastageer A.; Maslehuddin M.; Alnehmi A. J.; Al-Amoudi O. S. B. Detection of Sulfur in the Reinforced Concrete Structures Using a Dual Pulsed LIBS System. Opt. Laser Technol. 2012, 44, 566–571. 10.1016/J.OPTLASTEC.2011.09.001. [DOI] [Google Scholar]
- Gondal M. A.; Hussain T.; Yamani Z. H.; Baig M. A. On-Line Monitoring of Remediation Process of Chromium Polluted Soil Using LIBS. J. Hazard. Mater. 2009, 163, 1265–1271. 10.1016/J.JHAZMAT.2008.07.127. [DOI] [PubMed] [Google Scholar]
- Dobriyal P.; Qureshi A.; Badola R.; Hussain S. A. A Review of the Methods Available for Estimating Soil Moisture and Its Implications for Water Resource Management. J. Hydrol. 2012, 458-459, 110–117. 10.1016/J.JHYDROL.2012.06.021. [DOI] [Google Scholar]
- Park S. S. Unconfined Compressive Strength and Ductility of Fiber-Reinforced Cemented Sand. Constr. Build. Mater. 2011, 25, 1134–1138. 10.1016/J.CONBUILDMAT.2010.07.017. [DOI] [Google Scholar]
- Degirmenci N.; Okucu A.; Turabi A. Application of Phosphogypsum in Soil Stabilization. Build. Environ. 2007, 42, 3393–3398. 10.1016/J.BUILDENV.2006.08.010. [DOI] [Google Scholar]
- Güneyli H.; Rüşen T. Effect of Length-to-Diameter Ratio on the Unconfined Compressive Strength of Cohesive Soil Specimens. Bull. Eng. Geol. Environ. 2016, 75, 793–806. 10.1007/S10064-015-0835-5/FIGURES/14. [DOI] [Google Scholar]
- Xu X.; Ma F.; Zhou J.; Du C. Applying Convolutional Neural Networks (CNN) for End-to-End Soil Analysis Based on Laser-Induced Breakdown Spectroscopy (LIBS) with Less Spectral Preprocessing. Comput. Electron. Agric. 2022, 199, 107171. 10.1016/j.compag.2022.107171. [DOI] [Google Scholar]
- Akinpelu A. A.; Ali M. E.; Owolabi T. O.; Johan M. R.; Saidur R.; Olatunji S. O.; Chowdbury Z. A Support Vector Regression Model for the Prediction of Total Polyaromatic Hydrocarbons in Soil: An Artificial Intelligent System for Mapping Environmental Pollution. Neural Comput. Appl. 2020, 32, 14899–14908. 10.1007/S00521-020-04845-3. [DOI] [Google Scholar]
- Yilmaz I. A New Testing Method for Indirect Determination of the Unconfined Compressive Strength of Rocks. Int. J. Rock Mech. Min. Sci. 2009, 46, 1349–1357. 10.1016/J.IJRMMS.2009.04.009. [DOI] [Google Scholar]
- Barra I.; Haefele S. M.; Sakrabani R.; Kebede F. Soil Spectroscopy with the Use of Chemometrics, Machine Learning and Pre-Processing Techniques in Soil Diagnosis: Recent Advances–A Review. TrAC, Trends Anal. Chem. 2021, 135, 116166. 10.1016/J.TRAC.2020.116166. [DOI] [Google Scholar]
- Olatunji S. O.; Owolabi T. O. Modeling Superconducting Transition Temperature of Doped MgB2 Superconductor from Structural Distortion and Ambient Temperature Resistivity Measurement Using Hybrid Intelligent Approach. Comput. Mater. Sci. 2021, 192, 110392. 10.1016/J.COMMATSCI.2021.110392. [DOI] [Google Scholar]
- Alrebdi T. A.; Wudil Y. S.; Ahmad U. F.; Yakasai F. A.; Mohammed J.; Kallas F. H. Predicting the Thermal Conductivity of Bi2Te3-Based Thermoelectric Energy Materials: A Machine Learning Approach. Int. J. Therm. Sci. 2022, 181, 107784. 10.1016/J.IJTHERMALSCI.2022.107784. [DOI] [Google Scholar]
- Armaghani D. J.; Mirzaei F.; Nguyen-Thoi T. Hybrid ANN-Based Techniques in Predicting Cohesion of Sandy-Soil Combined with Fiber. Geomech. Eng. 2020, 20, 191–205. 10.12989/gae.2020.20.3.191. [DOI] [Google Scholar]
- Pham B. T.; Nguyen M. D.; Nguyen-Thoi T.; Ho L. S.; Koopialipoor M.; Quoc N. K.; Armaghani D. J.; Van Le H. A Novel Approach for Classification of Soils Based on Laboratory Tests Using Adaboost, Tree and ANN Modeling. Transp. Geotech. 2021, 27, 100508. 10.1016/J.TRGEO.2020.100508. [DOI] [Google Scholar]
- Momeni E.; Yarivand A.; Dowlatshahi M. B.; Armaghani D. J. An Efficient Optimal Neural Network Based on Gravitational Search Algorithm in Predicting the Deformation of Geogrid-Reinforced Soil Structures. Transp. Geotech. 2021, 26, 100446. 10.1016/J.TRGEO.2020.100446. [DOI] [Google Scholar]
- Zhou J.; Huang S.; Zhou T.; Armaghani D. J.; Qiu Y. Employing a Genetic Algorithm and Grey Wolf Optimizer for Optimizing RF Models to Evaluate Soil Liquefaction Potential. Artif. Intell. Rev. 2022, 55, 5673–5705. 10.1007/S10462-022-10140-5. [DOI] [Google Scholar]
- Ghanizadeh A. R.; Delaram A.; Fakharian P.; Armaghani D. J. Developing Predictive Models of Collapse Settlement and Coefficient of Stress Release of Sandy-Gravel Soil via Evolutionary Polynomial Regression. Appl. Sci. 2022, 12, 9986. 10.3390/APP12199986. [DOI] [Google Scholar]
- Olatunji S. O. Modeling Optical Energy Gap of Strontium Titanate Multifunctional Semiconductor Using Stepwise Regression and Genetic Algorithm Based Support Vector Regression. Comput. Mater. Sci. 2021, 200, 110797 10.1016/J.COMMATSCI.2021.110797. [DOI] [Google Scholar]
- Song H.; Ahmad A.; Farooq F.; Ostrowski K. A.; Maślak M.; Czarnecki S.; Aslam F. Predicting the Compressive Strength of Concrete with Fly Ash Admixture Using Machine Learning Algorithms. Constr. Build. Mater. 2021, 308, 125021. 10.1016/J.CONBUILDMAT.2021.125021. [DOI] [Google Scholar]
- Tso G. K. F.; Yau K. K. W. Predicting Electricity Energy Consumption: A Comparison of Regression Analysis, Decision Tree and Neural Networks. Energy 2007, 32, 1761–1768. 10.1016/J.ENERGY.2006.11.010. [DOI] [Google Scholar]
- Hammann F.; Gutmann H.; Vogt N.; Helma C.; Drewe J. Prediction of Adverse Drug Reactions Using Decision Tree Modeling. Clin. Pharmacol. Ther. 2010, 88, 52–59. 10.1038/CLPT.2009.248. [DOI] [PubMed] [Google Scholar]
- Boucher T. F.; Ozanne M. V.; Carmosino M. L.; Dyar M. D.; Mahadevan S.; Breves E. A.; Lepore K. H.; Clegg S. M. A Study of Machine Learning Regression Methods for Major Elemental Analysis of Rocks Using Laser-Induced Breakdown Spectroscopy. Spectrochim. Acta, Part B 2015, 107, 1–10. 10.1016/J.SAB.2015.02.003. [DOI] [Google Scholar]
- Tavares T. R.; Mouazen A. M.; Nunes L. C.; dos Santos F. R.; Melquiades F. L.; da Silva T. R.; Krug F. J.; Molin J. P. Laser-Induced Breakdown Spectroscopy (LIBS) for Tropical Soil Fertility Analysis. Soil Tillage Res. 2022, 216, 105250. 10.1016/J.STILL.2021.105250. [DOI] [Google Scholar]
- Wudil Y. S. S.; Gondal M. A. A.; Rao S. G. G.; Kunwar S. Thermal Conductivity of PLD-Grown Thermoelectric Bi2Te2.7Se0.3 Films Using Temperature-Dependent Raman Spectroscopy Technique. Ceram. Int. 2020, 46, 7253–7258. 10.1016/j.ceramint.2019.11.219. [DOI] [Google Scholar]
- Wudil Y. S.; Gondal M. A.; Rao S. G.; Kunwar S.; Alsayoud A. Q. Improved Thermoelectric Performance of Ternary Cu/Ni/Bi2Te2.7Se0.3 Nanocomposite Prepared by Pulsed Laser Deposition. Mater. Chem. Phys. 2020, 253, 123321 10.1016/J.MATCHEMPHYS.2020.123321. [DOI] [Google Scholar]
- Wudil Y. S.; Gondal M. A.; Almessiere M. A.; Alsayoud A. Q. The Multi-Dimensional Approach to Synergistically Improve the Performance of Inorganic Thermoelectric Materials: A Critical Review. Arabian J. Chem. 2021, 14, 103103. 10.1016/j.arabjc.2021.103103. [DOI] [Google Scholar]
- Wudil Y. S.; Gondal M. A.; Rao S. G.; Kunwar S.; Alsayoud A. Q. Substrate Temperature-Dependent Thermoelectric Figure of Merit of Nanocrystalline Bi2Te3 and Bi2Te2.7Se0.3 Prepared Using Pulsed Laser Deposition Supported by DFT Study. Ceram. Int. 2020, 46, 24162–24172. 10.1016/j.ceramint.2020.06.196. [DOI] [Google Scholar]
- Al-Najjar O. A.; Wudil Y. S.; Ahmad U. F.; Baghabra Al-Amoudi O. S.; Al-Osta M. A.; Gondal M. A. Applications of Laser Induced Breakdown Spectroscopy in Geotechnical Engineering: A Critical Review of Recent Developments. Appl. Spectrosc. 2022, 1–37. 10.1080/05704928.2022.2136192. [DOI] [Google Scholar]
- Pedregosa F.; Varoquaux G.; Gramfort A.; Michel V.; Thirion B.; Grisel O.; Blondel M.; Prettenhofer P.; Weiss R.; Dubourg V.; Vanderplas J. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Pekel E. Estimation of Soil Moisture Using Decision Tree Regression. Theor. Appl. Climatol. 2019, 139, 1111–1119. 10.1007/S00704-019-03048-8. [DOI] [Google Scholar]
- Balogun A. L.; Tella A. Modelling and Investigating the Impacts of Climatic Variables on Ozone Concentration in Malaysia Using Correlation Analysis with Random Forest, Decision Tree Regression, Linear Regression, and Support Vector Regression. Chemosphere 2022, 299, 134250. 10.1016/J.CHEMOSPHERE.2022.134250. [DOI] [PubMed] [Google Scholar]
- Owolabi T. O.; Akande K. O.; Olatunji S. O. Estimation of Surface Energies of Hexagonal Close Packed Metals Using Computational Intelligence Technique. Appl. Soft Comput. 2015, 31, 360–368. 10.1016/j.asoc.2015.03.009. [DOI] [Google Scholar]
- Alade I. O.; Abd Rahman M. A.; Saleh T. A. Modeling and Prediction of the Specific Heat Capacity of Al2O3/Water Nanofluids Using Hybrid Genetic Algorithm/Support Vector Regression Model. Nano-Struct. Nano-Objects 2019, 17, 103–111. 10.1016/j.nanoso.2018.12.001. [DOI] [Google Scholar]
- Guo G.; Niu G.; Shi Q.; Lin Q.; Tian D.; Duan Y. Multi-Element Quantitative Analysis of Soils by Laser Induced Breakdown Spectroscopy (LIBS) Coupled with Univariate and Multivariate Regression Methods. Anal. Methods 2019, 11, 3006–3013. 10.1039/C9AY00890J. [DOI] [Google Scholar]
- Mishra S.; Mishra D.; Santra G. H. Adaptive Boosting of Weak Regressors for Forecasting of Crop Production Considering Climatic Variability: An Empirical Assessment. J. King Saud Univ., Comput. Inf. Sci. 2020, 32, 949–964. 10.1016/J.JKSUCI.2017.12.004. [DOI] [Google Scholar]
- Sun W.; Gao Q. Exploration of Energy Saving Potential in China Power Industry Based on Adaboost Back Propagation Neural Network. J. Cleaner Prod. 2019, 217, 257–266. [Google Scholar]
- Hrahsheh F.; Sani Wudil Y.; Wilemski G. Confined Phase Separation of Aqueous–Organic Nanodroplets. Phys. Chem. Chem. Phys. 2017, 19, 26839–26845. 10.1039/C7CP04531J. [DOI] [PubMed] [Google Scholar]
- Lin N.; Jiang R.; Li G.; Yang Q.; Li D.; Yang X. Estimating the Heavy Metal Contents in Farmland Soil from Hyperspectral Images Based on Stacked AdaBoost Ensemble Learning. Ecol. Indic. 2022, 143, 109330. 10.1016/J.ECOLIND.2022.109330. [DOI] [Google Scholar]
- He M.; Tang L.; Li C.; Ren J.; Zhang L.; Li X. Dynamics of Soil Organic Carbon and Nitrogen and Their Relations to Hydrothermal Variability in Dryland. J. Environ. Manage. 2022, 319, 115751. 10.1016/J.JENVMAN.2022.115751. [DOI] [PubMed] [Google Scholar]
- Almansour N. A.; Syed H. F.; Khayat N. R.; Altheeb R. K.; Juri R. E.; Alhiyafi J.; Alrashed S.; Olatunji S. O. Neural Network and Support Vector Machine for the Prediction of Chronic Kidney Disease: A Comparative Study. Comput. Biol. Med. 2019, 109, 101–111. 10.1016/J.COMPBIOMED.2019.04.017. [DOI] [PubMed] [Google Scholar]
- Owolabi T. O.; Qahtan T. F.; Abidemi O. R.; Saleh T. A.; Adeyemi O. W. Bismuth Oxychloride Photocatalytic Wide Band Gap Adjustment through Oxygen Vacancy Regulation Using a Hybrid Intelligent Computational Method. Mater. Chem. Phys. 2022, 290, 126524. 10.1016/J.MATCHEMPHYS.2022.126524. [DOI] [Google Scholar]
- Wudil Y. S.; Peng Q.; Alsayoud A. Q.; Gondal M. A. Hydrostatic Pressure-Tuning of Thermoelectric Properties of CsSnI3 Perovskite by First-Principles Calculations. Comput. Mater. Sci. 2022, 201, 110917. 10.1016/J.COMMATSCI.2021.110917. [DOI] [Google Scholar]
- Chen Q.; Li L.; Chong C.; Wang X. AI-Enhanced Soil Management and Smart Farming. Soil Use Manage. 2022, 38, 7–13. 10.1111/SUM.12771. [DOI] [Google Scholar]
- Wudil Y. S.; Imam A.; Gondal M. A.; Ahmad U. F.; Al-Osta M. A. Application of Machine Learning Regressors in Estimating the Thermoelectric Performance of Bi2Te3-Based Materials. Sens. Actuators, A 2023, 351, 114193. 10.1016/J.SNA.2023.114193. [DOI] [Google Scholar]
- Wudil Y. S.; Ahmad U. F.; Gondal M. A.; Al-Osta M. A.; Almohammedi A.; Sa’id R. S.; Hrahsheh F.; Haruna K.; Mohamed M. J. S. Tuning of Graphitic Carbon Nitride (g-C3N4) for Photocatalysis: A Critical Review. Arabian J. Chem. 2023, 16, 104542 10.1016/J.ARABJC.2023.104542. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data is available upon reasonable request.