Abstract

Due to their intrinsic stability and reduced toxicity, lead-free halide double perovskite semiconductors have become potential alternatives to lead-based perovskites. In the present study, we used density functional theory simulations to investigate the mechanical stability and band gap evolution of double perovskites Cs2AgBiX6 (X = Cl and Br) under an applied pressure. To investigate the pressure-dependent properties, the hydrostatic pressure induced was in the range of 0–100 GPa. The mechanical behaviors indicated that the materials under study are both ductile and mechanically stable and that the induced pressure enhances the ductility. As a result of the induced pressure, the covalent bonds transformed into metallic bonds with a reduction in bond lengths. Electronic properties, energy bands, and electronic density of states were obtained with the hybrid HSE06 functional, including spin–orbit coupling (HSE06 + SOC) calculations. The electronic structure study revealed that Cs2AgBiX6 samples behave as X−Γ indirect gap semiconductors, and the gap reduces with the applied pressure. The pressure-driven samples ultimately transform from the semiconductor to a metallic phase at the given pressure range. Also, the calculations demonstrated that the applied pressure and spin–orbit coupling of the states pushed VBM and CBM toward the Fermi level which caused the evolution of the band gap. The relationship between the structure and band gap demonstrates the potential for designing lead-free inorganic perovskites for optoelectronic applications, including solar cells as well as X-ray detectors.
1. Introduction
In the recent past, hybrid organic–inorganic lead halide perovskites have garnered tremendous attention from the clean energy sector for future photovoltaic and optoelectronic applications due to their unique intrinsic properties.1−7 In a remarkably short period, the power conversion efficiency (PCE) of perovskite solar cells (PSCs) has increased from 3.8% in a dye-sensitized solar cell architecture to 25.2% NREL-certified in planar heterojunction photovoltaic devices.2,8 The widely studied perovskite for PSCs by far is the CH3NH3PbX3 (X = Cl, Br, and I) perovskite. The allure of halide perovskite materials for application in photovoltaics and LEDs arises due to their composition of inexpensive, earth-abundant elements, and they are synthesized by various methods including solution-processed deposition techniques.9 Yet, the intrinsic instability due to the organic methylammonium cation and toxicity of Pb continue to be two fundamental concerns related to the development of stable perovskite photovoltaic devices. Such concerns have prevented this technology from becoming mainstream solar cell technology. Therefore, the requirement of alternate materials to obtain the desired stability and to contain the environmental effect is indispensable. The first challenge has been partially resolved via the use of cesium ions in place of the organic component to create pure inorganic perovskites with increased stability.10 Second, to reduce or eliminate the toxicity, there has been a desperate hunt for new and nontoxic alternatives to Pb in the CH3NH3PbX3 perovskite.11 This replacement by other divalent cations at the B-site either led to a higher energy band gap (due to alkaline earths), which is not suitable as a photo-absorber, or turned out to be more unstable (as in the case of Sn+2 and Ge+2 introduction).12 The divalent atom Pb has a central role in band gap formation and hence the optoelectronic properties of the chemical compound CH3NH3PbX3. Lead (Pb) is essential to perovskite for achieving an outstanding photovoltaic performance; hence, substitutes for lead must meet strict requirements to maintain efficiency and stability in a perovskite structure.13 Recently, it has been possible to create quaternary halides with a double perovskite structure by using the cation transmutation method, which transforms two divalent Pb2+ ions into one trivalent and one monovalent cation.14 In the main group elements, only the trivalent bismuth (Bi3+) possesses the same electronic configuration as lead. Bi-based Cs2AgBiX6 halide double perovskites have been successfully synthesized and displayed attractive features, including long carrier recombination lifetime and excellent stability, making them promising for photovoltaic and photon detection applications.15 The high Cs2AgBiX6 band gap, however, significantly reduces the device’s performance.16 Therefore, it would be ideal to develop a reliable approach for precisely engineering the band gaps of Cs2AgBiX6 compounds and then gain a thorough understanding of how their structure and properties interact.17
In the recent past, researchers started investigating the pressure-dependent crystal structure and characteristics of halide perovskites.18 The use of pressure to develop novel materials with enhanced characteristics has been reported by several groups.19 Under an induced pressure, halide perovskites show constant changes in their crystal structure and band alignment, revealing their fundamental transformation mechanism.20 Separate groups also systematically investigated the pressure response of hybrid and all-inorganic halide perovskites, and it is observed that the optical energy gaps of semiconducting lead halide perovskites vary.21 This study aimed to search those halide perovskite semiconductors whose characteristics approximate the widely researched CH3NH3PbX3 materials without integrating any toxic metals such as Pb, Cd, Tl, or Hg. The Cs2AgBiX6 (Br and Cl) Bi-based double perovskite semiconductors have been proposed and synthesized with three-dimensional cubic structures having great versatility for compositional variants.22−26 These compounds displayed great potential for a variety of other applications besides solar photovoltaics, such as photodetectors, X-ray detectors, photocatalysts, light-emitting diodes (LEDs), and so forth.27 Also, halide double perovskites were found to exhibit enhanced stability against moisture and temperature and have optical band gaps (in the range 1.83–2.80 eV) which are comparable to their hybrid CH3NH3PbX3 perovskite analogues.22,23,28 Mild pressure can increase the carrier lifetime and tune the band gap to a desired value, leading to the emergence of interesting material characteristics including optical absorption, conductivity, photoresponsivity, and enhanced structural stability. Thus, the next-generation photovoltaics and semiconductor systems can benefit from materials-by-design for tunable, improved, and retainable performance. Therefore, it is essential to comprehend the interplay between pressure-induced electronic and structural changes. In the literature, we come across very few reports on the pressure-dependent photovoltaic properties of halide perovskites that emphasize their structural aspects, and the applied pressure is limited.29 One of the reports describes the first attempt to use hydrostatic pressure up to 38 GPa to control the band gap and photocurrent characteristics of the organometal bromide perovskite, CH3NH3PbBr3 (MAPbBr3).30
In the present study, we report comprehensive theoretical investigations of the structural, elastic, and electronic properties of the halide double perovskites Cs2AgBiX6 (X = Br and Cl) from DFT calculations under high-pressure conditions. Our results indicate that there has been a significant impact on the optical energy gap due to the induced pressure and disorder in the (Ag, Bi) atoms. The halide double perovskite materials under study exhibit some deformation during decompression (release of the hydrostatic pressure) which causes the energy gap to be quenched by a mixture of cubic and tetragonal phases. Our findings show a connection between structural alterations and the photophysical characteristics of Cs2AgBiX6 perovskites at a high pressure. During the experiment, the required pressure can be applied externally, resulting in the disordering of the crystal lattice, or it can be induced by carefully doping metal cations.
2. Computational Method
The first-principles calculations on Cs2AgBiX6 (X = Cl & Br) perovskites were done using Vienna ab initio Simulation Package (VASP)31 with the projector-augmented wave (PAW) method.32 Exchange and correlation energy as an electron–electron interaction was considered by the generalized gradient approximation (GGA) parameterized by the Perdew, Burke, and Ernzerhof (PBE) functional.33 The VESTA tool was used to visualize the crystal structure formation.34 The electronic band gap is usually underestimated by PBE calculations, and the hybrid function that combines the Hartree–Fock and DFT exchange terms is considered to be a practical solution to calculate the energy band gap of the compounds more precisely.35 In order to accurately assess the band gap of Cs2AgBiX6 (X = Br and Cl) perovskites, we adopted the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional.36 The band structure and density of states were calculated while taking into consideration the spin–orbit coupling (SOC) interaction. HSE06 has been demonstrated to create band gaps that are more precise than those produced by conventional LDA/GGA functionals.37 Interaction between the valence electrons and ions was defined via suitable pseudopotentials in the PAW method.38 The conjugate gradient approach was used to optimize the geometry of the cell and the positions of the atoms, with the iterative relaxation of atomic positions being truncated when the forces acting on the atoms were less than 0.01 eV/Å.
Self-consistent calculations were used to optimize the kinetic energy cutoff value. The number of plane waves was limited by the kinetic energy cutoff value, with the total energy adjusted to Ecut = 500 eV for Cs2AgBiX6 in the Fm3̅m structure. After the energy cutoff values were selected, self-consistent calculations for various k-points were implemented using the Monkhorst–Pack method.39 For this phase, the total energy-optimized meshes of k-points were determined to be 12x12x12. The total energies of the crystal structure were determined by increasing and decreasing the equilibrium volume from 1 to 5%, and in these intervals, the kinetic energy cutoff values were optimized for the meshes of k-points. The total energy–volume data obtained from these calculations were fitted to the third-order Birch–Murnaghan equation of state (EoS) to derive the crystal structure properties in terms of bulk modulus, its pressure derivative, and the equilibrium lattice constant.
The cubic phase of the lead-free metal double halide perovskites, Cs2AgBiX6, belongs to the space group Fm3m (no. 225). The Cs atoms are located at the face center of the unit cell structure with a Wyckoff position 8c and coordinates of (1/4 1/4 1/4); at (1/2 1/2 1/2) coordinates, Bi atoms are positioned in the body center with a 4b Wyckoff site; the Ag atoms are positioned at corners (0 0 0) with a Wyckoff site 4a; and halide atoms occupy the face centers with a 24e Wyckoff site.
The elastic stiffness constants Cij were determined by linearly deforming the crystal structures in the current study under a modest strain. To calculate the stiffness constants and total energy of the system, the deformation parameter (δ) was set to change in steps of 0.01 within the −0.03 to 0.03 range. The total energy determined was fit to the third-order polynomial, and the second-order coefficient of this polynomial was equated to the associated energy density equations. A series of equations were obtained which were solved for the elastic constants Cij. For the band gap calculations, two steps are performed. In the first step, a self-consistent computation was done to obtain charge distributions, and using of these charge distributions was required in the next step to simulate the band structure. Energy gap variation with the induced pressure was also simulated and represented in terms of band diagrams. According to calculations, the semiconductor Cs2AgBiBr6 enters the metallic phase at a pressure of 50 GPa, while its chlorine equivalent behaves as a metal at a pressure of 100 GPa.
3. Results and Discussion
3.1. Crystal Structure Optimization
In the AMX3 perovskite structure, the A cation is surrounded by 12 halide (X) anions forming a cuboctahedral geometry, while the metal cation is coordinated to 6 halide anions, making an octahedral cage MX6. The structure for the double perovskites A2MM′X6 remains the same except for alternate MX6 and M′X6 octahedra. In the halide double perovskite matrix, A2MM′X6, A and M are monovalent cations, with the charge state +1, M′ are the elements of oxidation +3, and X belongs to halides (Cl, Br, and I) bearing charge state −1. The equilibrium lattice parameter (a0), bulk modulus B0, and its pressure derivative B′ were obtained from the Birch–Murnaghan EoS when total energies as a function of unit cell volume are fit into the equation. The Birch–Murnaghan equation 1 is given by
| 1 |
Structural parameters such as lattice constants, bulk moduli at zero pressure B0, and its pressure derivative B′ are given in Table 1. As mentioned earlier, the Cs2AgBi (Cl/Br)6 compounds form a perovskite cubic crystal structure with a Cs atom in the middle of the cubic framework, while Ag and Bi are linked with halogen atoms (Cl and Br) to make a rock salt structure, as indicated in Figure 1a. The values of these parameters at different pressures ranging from 0 to 100 GPa, both for bromine and chlorine-based perovskite structures, are summarized in Tables S1 and S2, respectively, in Supporting Information. The results of the total energy–volume optimization calculations are also plotted in Figure 1b,c which include the information relating to the static EoS.
Table 1. Lattice Parameter a(Å), Bulk Modulus B (GPa), Its Pressure Derivative B′, Elastic Constants Cij (GPa), and Elastic Compliances Sij (GPa–1) of Cs2AgBiCl6 and Cs2AgBiBr6.
| Cs2AgBiCl6 |
Cs2AgBiBr6 |
||||||
|---|---|---|---|---|---|---|---|
| phase | this work | experiments | other calculations | this work | experiments | other calculations | |
| Fm3̅m | a | 10.783 | 10.777a | 10.655b, 10.696c, 10.99d, 10.67e | 11.472 | 11.271a | 11.169b, 11.201c, 11.530d, 11.190e |
| B | 23.07 | 23.43d, 32.64e | 20.65 | 20.49d, 28.58e | |||
| B′ | 6.00 | 3.79d | 5.93 | 5.82d | |||
| C11 | 47.13 | 66.70e | 32.34 | 59.02e | |||
| C12 | 20.66 | 15.61e | 15.28 | 13.37e | |||
| C44 | 8.16 | 8.85e | 6.82 | 8.15e | |||
| S11 | 0.02895 | 0.04438 | |||||
| S12 | –0.00882 | –0.01424 | |||||
| S44 | 0.12257 | 0.14652 | |||||
Figure 1.

(a) Crystal structure of the Cs2AgBiX6 (X = Cl and Br) double perovskite unit cells generated using Vesta tool. (b) Energy–volume plot for Cs2AgBiCl6 and (c) energy–volume plot for Cs2AgBiBr6.
The equilibrium lattice constants calculated in our study for the Cs2AgBiCl6 (10.783 Å) and Cs2AgBiBr6 (11.472 Å) perovskites were consistent with the earlier reported experimental data (10.777 and 11.271 Å).23 A small discrepancy in the lattice constant of Cs2AgBiBr6 could be the result of the overestimation of the lattice constant by the GGA exchange–correlation functional, which is well understood and expected while using different structure models. Figure 2 represents the variation of lattice constants under an induced hydrostatic pressure up to 100 GPa.
Figure 2.

Variation of lattice constants with the induced pressure.
The structural parameters calculated in the present study were found in fair agreement with the other theoretical studies and experimentally observed results reported elsewhere.28b,40−42 Under the hydrostatic pressure effect in the range of 0–100 GPa, the lattice constant decreases monotonically for both Cs2AgBiCl6 and Cs2AgBiBr6 perovskites, as indicated in Figure 2. Since Cs2AgBiBr6 has a bigger ionic radius than Cs2AgBiCl6, it also has a larger lattice constant. In comparison to Cs2AgBiCl6, Cs2AgBiBr6 has a smaller bulk modulus and pressure derivative, which suggests that it is less stiff and more compressible.
3.2. Elastic Properties
Understanding the mechanical behavior of crystalline materials requires knowledge of the elastic tensor properties. The three independent elastic moduli Cij of cubic structure crystals, such as pressure-induced Cs2AgBiX6, are C11, C12, and C44. The simulated elastic constants (Cij), bulk moduli (B), and their pressure derivatives (B′) for the double perovskites studied are provided in Table 1. The Born criterion was used to determine whether a crystal’s elastic constants satisfy its mechanical stability. To determine the elastic constants Cij, a strain was applied to the primitive vectors ai0 (i = 1,2,3) of the system. The primitive vectors ai (i = 1,2,3) of the deformed system were calculated by the following equation:
 |
2 |
where I⃡ is the unit matrix, and ε⃡ is the deformation matrix. The total energy of this forced system can be extended to the Taylor series as follows:
| 3 |
Here, σ and ε are the stress and strain tensors, respectively. V and V0 are the volumes of the post-deformation and pre-deformation systems, respectively. E(V, ε) and E0(V0,0) are related to total energies. Cij refers to the second-order elastic constants, and O(δ3) refers to the neglected terms in the series expansion. The second term of the series expansion in eq 3 is zero since in the new equilibrium stress is zero on all atoms. In this case, eq 3 becomes
| 4 |
Elastic constants of the deformed system can be found by using eq 4, which is expressed as energy density. Table 2 summarizes the strain matrix components applied to the cubic Fm3̅m structure and the energy densities corresponding to these strains.
Table 2. Applied Strains (Vi) and the Corresponding Strain Energy Densities (ΔE/V0) for the Cubic Fm3̅m Structure5.
| structure | strain | parameters | ΔE/V0 |
|---|---|---|---|
| Fm3̅m | V1 | ε1 = ε2 = ε3 = δ |
 (C11 + 2C12) δ2 (C11 + 2C12) δ2
|
| V2 | ε1 = δ, ε2 = −δ, ε3 = δ2/(1 – δ2) | (C11 – C12) δ2 + O(δ3) | |
| V3 | ε3 = δ2/(1– δ2), ε6 = δ | 2C44δ2 + O(δ3) |
Single-crystal elastic constants were calculated to understand the mechanical stability of the Cs2AgBiCl6 and Cs2AgBiBr6 materials. For this, three different strains were applied to the unit cell of the cubic structure, and these structures were deformed. The energy density expressions for each strain are also listed in Table 2. The change of the total energy of Cs2AgBiCl6 and Cs2AgBiBr6 materials in the deformed Fm3̅m structure according to the deformation parameter (δ = ±0.03, ±0.02, and ±0.01) is shown in Figures 3 and 4, respectively.
Figure 3.
Total energy of Cs2AgBiCl6 in Fm3̅m phase as a function of the strain parameter δ. (a) Bulk modulus, (b) pure shear elastic constant, C44, and (c) tetragonal shear constant, C11 – C12.
Figure 4.
Display of the total energy of Cs2AgBiBr6 in Fm3̅m phase as a function of strain parameter δ. (a) Bulk modulus, (b) pure shear elastic constant, C44, and (c) tetragonal shear constant, C11–C12.
To determine the elastic constants of the cubic Fm3̅m structures of each material, after volume-conserved strains V1, V2, and V3 were applied to the crystal systems, bulk modulus B and shear moduli Cs and C44 were calculated, respectively. Bulk modulus B = (C11 + 2C12)/3 and tetragonal shear modulus Cs = (C11 – C12)/2 equations were solved together to obtain elastic constants C11 and C12. The results obtained for the bulk modulus B, tetragonal shear modulus Cs, and elastic constants Cij of the Fm3̅m structures of the Cs2AgBiCl6 and Cs2AgBiBr6 materials are given in Table 1. The values of C11, C12, and C44, respectively, are 47.13, 20.66, and 8.16 GPa for Cs2AgBiCl6 and 32.34, 15.28, and 6.82 GPa for Cs2AgBiBr6. These values were comparable to those found in the DFT study elsewhere from the CASTEP code.42 The fact that the elastic constant values of the Cs2AgBiBr6 material are lower than that of the Cs2AgBiCl6 material reveals that the double perovskite Cs2AgBiBr6 has less resistance to deformations. The elastic constants calculated for the Fm3̅m structures of these two materials provide the generalized elastic stability conditions given as C11 – C12 > 0, C11 + 2C12 > 0, and C44 > 0.
The bulk modulus B and the shear modulus G were used instead of the elastic constants Cij to define the elastic behaviors. The shear modulus refers to the resistance to reversible deformations brought on by shear stress, whereas the bulk modulus assesses the material’s reaction to the volume change brought on by the applied pressure. Therefore, this study also aimed to calculate the polycrystalline elastic modulus from the obtained single-crystal properties of Cs2AgBiCl6 and Cs2AgBiBr6 materials. For this, the elastic compliances Sij were calculated by using the single-crystal Cij elastic constants by the following equations:43
| 5 |
| 6 |
| 7 |
Isotropic elastic modules such as bulk modulus B, shear modulus G, Young’s modulus E, and Poisson’s ratio ν for a single-phase polycrystalline material can be obtained using the Voigt–Reuss–Hill (VRH) approach, which includes the average of anisotropic single-crystal elastic properties in all possible directions of the crystal.
According to the Voigt and Reuss approaches in the cubic crystal system, the shear modules GV, GR and the bulk modulus BV, BR (for cubic systems B = BV = BR) are given as follows:43
| 8 |
| 9 |
| 10 |
Using the VRH Voigt–Reuss–Hill (VRH) isotropic elastic modulus approach, the shear and bulk moduli, respectively, are given as follows: G = 1/2(GV + GR) and B = 1/2(BV + BR). By using the isotropic bulk and shear modules calculated according to the VRH approach, Young’s modulus, and Poisson’s ratio, the other polycrystalline elastic properties were calculated, and results are given in Table 3. For the Cs2AgBiCl6 and Cs2AgBiBr6 materials, the results from the Voigt technique and the Reuss approach were comparable, with the difference between the values derived from these two methods being 0.55 and 0.09 GPa, respectively. Pugh44 has suggested that the resistance rate to elastic deformation can be used to describe the brittle or ductile nature of covalent crystals. The critical value for distinguishing a ductile material from a brittle material is 1.75. The B/G values of the Fm3̅m phases of Cs2AgBiCl6 and Cs2AgBiBr6 were calculated to be 2.97 and 2.81, respectively. Therefore, the Cs2AgBiCl6 and Cs2AgBiBr6 compounds in the Fm3̅m phase can be classified as ductile materials. The calculated B/G values were comparable to the values found in the first-principles study.41 Young’s modulus is representative of the resistance of the isotropic material to linear strain and is expressed as E = 9GB/(3B + G). According to the results obtained (Table 3), Cs2AgBiCl6 and Cs2AgBiBr6 perovskites showed less hardness compared to steel (200 GPa) and graphene (1000 GPa). On the other hand, Poisson’s ratio demonstrates the stability of the crystal under shear strain and is expressed as
| 11 |
Table 3. Isotropic Bulk Modulus B (GPa), Shear Modulus G (GPa), Young’s Modulus E (GPa), the Poisson’s Ratio ν, Longitudinal νL (m/s), Transverse νT (m/s), Average Sound Velocity νM (m/s), and Debye Temperature θD (K) for Cs2AgBiCl6 and Cs2AgBiBr6 Polymorphs.
| Cs2AgBiCl6 |
Cs2AgBiBr6 |
||||||
|---|---|---|---|---|---|---|---|
| phase | this work | experiments | other calculations | this work | experiments | other calculations | |
| Fm3̅m | BV | 29.48 | 2.30a | 20.97 | 2.41a | ||
| BR | 29.48 | 20.97 | |||||
| B | 29.48 | 20.97 | |||||
| GV | 10.19 | 7.51 | |||||
| GR | 9.64 | 7.42 | |||||
| G | 9.91 | 7.46 | |||||
| B/G | 2.97 | 2.81 | |||||
| E | 26.75 | 20.01 | |||||
| ν | 0.349 | 0.341 | |||||
| νL | 3183 | 2572 | |||||
| νT | 1534 | 1264 | |||||
| νM | 1724 | 1419 | |||||
| θD | 163 | 126 | |||||
Ref (43).
The bulk modulus B and the pressure dependence of the elastic constants (C11, C12, and C44) for the double perovskites Cs2AgBiX6 (X = Br and Cl) are shown in Figure 5. Although the increase in C44 was less significant, all elastic moduli grow practically linearly with respect to pressure. The value of the bulk modulus obtained from elastic constants was similar to that determined by using the EoS. This implied that our results are considered significantly accurate and precise.
Figure 5.

Effect of induced pressure on the elastic moduli of (a) Cs2AgBiCl6 and (b) Cs2AgBiBr6.
Frantsevich et al.45 earlier reported that it is possible to examine the mechanical behavior of the crystals by considering their Poisson ratio. According to the Frantsevich rule, the borderline ν ∼ 0.33 separates a ductile material from a brittle material. If the Poisson ratio is greater than 0.33, the material will be ductile; otherwise, the material is brittle. According to this rule, Fm3̅m structures of Cs2AgBiCl6 and Cs2AgBiBr6 perovskite materials showing a value greater than 0.33 exhibit a ductile character. Also, our results concerning ductility with the Frantsevich rule are quite consistent with those obtained with the Pugh rule.
After calculating Young’s modulus and Poisson’s ratio, the average sound velocity was calculated from the knowledge of longitudinal and transverse sound velocities. The longitudinal sound velocity ϑl and the transverse sound velocity ϑt were obtained from the material’s isotropic shear module G and bulk module B. The formulas used to obtain sound velocities and Debye temperature are taken from ref (43). The longitudinal νL (m/s), transverse νT (m/s), average sound velocity νM (m/s), and Debye temperature θD (K) for Cs2AgBiCl6 and Cs2AgBiBr6 materials in the Fm3̅m phase were calculated as 3183 m/s, 1534 m/s, 1724 m/s, 163 K and 2572 m/s, 1264 m/s, 1419 m/s, 126 K, respectively (Table 3).
3.3. Electronic Properties
The electronic properties of the two perovskite compounds were studied by simulating the band structure and electronic density of states using HSE06 + SOC. The band structures for each compound predicted at equilibrium as well as at different pressures are displayed in Figures 6 and 7. The energy gap obtained for Cs2AgBiBr6 perovskite at equilibrium was 1.45 eV, whereas for Cs2AgBiCl6, it was 2.48 eV. The valence band maximum (VBM) exhibited at X and the conduction band minimum (CBM) at the high-symmetry Γ-point in the Brillouin zone of the reciprocal lattice for both perovskite compounds. Thus, the k-points corresponding to the CBM and VBM showed different momenta in the E–K plot, implying that the Cs2AgBiX6 (X = Cl and Br) perovskites are indirect band gap semiconductors. The band gap, VBM, and CBM k-points in the band structure concurred with the previously published research listed in Table 4. The band gaps were observed to get reduced subsequently with an applied pressure, and the corresponding values are summarized in Table 5. From the predicted band structures, it was observed that the bottom of the conduction band has two minima within the energy difference of ∼0.2 eV. The minimum of the conduction band can be found at the high-symmetry point Γ or L in the reciprocal space, depending on whether the structure calculations are performed on optimized or experimental structures.15a
Figure 6.

Band structure of Cs2AgBiBr6 at (a) 0 GPa, (b) 10 GPa, (c) 20 GPa, and (d) 30 GPa pressure. Spin–orbit coupling (SOC) was taken into account when calculating the band structure and density of states of the perovskites. The evolution of the small direct bands compared to indirect ones was observed as a result of the applied pressure. However, the fundamental band gap is still indirect.
Figure 7.

Band structure of the Cs2AgBiCl6 halide double perovskite calculated at (a) 0 GPa, (b) 20 GPa, (c) 40 GPa, and (d) 60 GPa pressure. The low-energy direct band transitions and narrowing of the energy gap with the applied induced pressure can be visualized clearly from the plots.
Table 4. Comparison of Band Gap Energy (eV) of the Compounds Investigated with Other Theoretical and Experimental Studies.
Table 5. Pressure-Dependent Direct and Indirect Energy Gaps Obtained for the Two Halide Double Perovskite Structures Using the Hybrid HSE06 Functional with Spin–Orbit Coupling (HSE06 + SOC).
| pressure GPa | Cs2AgBiBr6 |
pressure GPa | Cs2AgBiCl6 |
||
|---|---|---|---|---|---|
| direct Eg (eV) | indirect Eg (eV) | direct Eg (eV) | indirect Eg (eV) | ||
| 10 | 1.897 | 1.047 | 20 | 2.048 | 1.224 |
| 20 | 1.736 | 0.788 | 40 | 1.762 | 0.748 |
| 30 | 1.571 | 0.556 | 50 | 1.623 | 0.544 |
| 40 | 1.424 | 0.361 | 60 | 1.486 | 0.355 |
| 50 | 1.294 | 0.181 | 80 | 1.220 | 0.011 |
In the present study, however, the predicted band calculations were performed on optimized structures, and CBM occurred at the Γ-point of the Brillouin zone. Pressure-dependent band structures, Figures 6 and 7, showed that the band gap energy of the two perovskite systems reduced with the applied pressure, and ultimately the semiconductor phase transformed into a metallic phase, as shown in Figure 8. The computed total density of states (TDOS) for the Cs2AgBiX6 (X = Cl and Br) perovskites are shown in Figures 9 and 10, and the partial density of states (pDOS) graphics are indicated in Figures 11 and 12. The pDOS manifested that the VBM of both perovskites, Cs2AgBiX6 (X = Cl and Br), were mainly contributed from the interactions of Ag-d, Br-p, and Bi-s states (Cl-p in the Cs2AgBiCl6 case). The VBM is localized only on Ag and halide anions; however, the strong directional interaction between Ag-d and halide-p orbitals invites some Bi-s characteristics in the valence band as well, resulting in a high valence band at X-point. This phenomenon is replicated in all members of the Cs2AgBiX6 family, and it seems that the electronic mismatch between Ag and Bi was the reason for the indirect, wide energy gap. Also, it was noted from the DOS study that the frontier orbitals that contributed to CBM contain mostly Ag-s, Bi-p, and halide-p states.
Figure 8.

Band structure displaying the metallic character of the perovskites (a) Cs2AgBiBr6 and (b) Cs2AgBiCl6 at 50 and 100 GPa, respectively.
Figure 9.
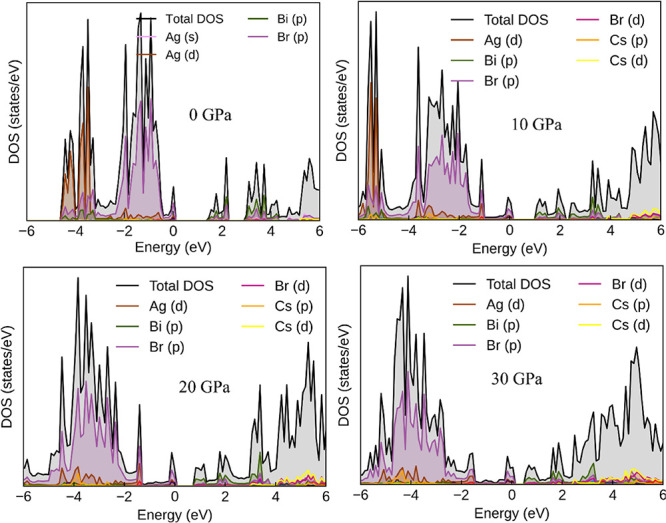
Graph showing the total density of states simulated with SOC along with the contribution from the most dominant orbitals in the band formation of the Cs2AgBiBr6 halide double perovskite at the given applied pressures.
Figure 10.

Graph showing the total density of states simulated with SOC along with the contribution from the most dominant orbitals in the band formation of the Cs2AgBiCl6 halide double perovskite at the given applied pressures.
Figure 11.
pDOS of Cs2AgBiBr6 perovskite in the Fm3̅m phase at 0 GPa. (a) Cs-atom, (b) Ag-atom, (d) Bi-atom, and (d) Br-atom.
Figure 12.
pDOS) of Cs2AgBiCl6 perovskite in the Fm3̅m phase at 0 GPa. (a) Cs-atom, (b) Ag-atom, (c) Bi-atom, and (d) Cl-atom.
Throughout the VBM, the antibonding-hybridized Ag-d and halide-p states predominated, with antibonding Bi-s and halide-p states contributing just marginally. For CBM, it consisted of a mixture of Bi-p orbital, Bi-p and halide-p antibonding, and Ag-s, halide-p bonding states.15a,47 As could be seen from Figure 8, the semiconducting perovskites ultimately achieved a metallic character with the increase in applied pressure. From the pressure-dependent band structure, it was observed that the energy was shifted toward the lower region which was attributed to Bi and Ag ions creating defect energies of halide-p and Bi-s orbitals. Also, with the applied pressure, the contraction and distortion of [AgX6]5– and [BiX6]3– octahedra dominate the energy gap evolution. The molecular orbital diagram was built using the atom-projected density of states to explain some distinctive aspects of the band structures. In the literature, it has been reported from experimental measurements that the deformation occurred due to the applied pressure retained in the structure upon releasing the pressure, resulting in the transformation of the perovskite to a desired band gap compound.46
The halide double perovskite structure Cs2B+B3+X6 (X = Cl, Br, and I) was found to be more stable compared to the hybrid organic–inorganic halide perovskites except that it exhibited a higher band gap which is also indirect. It has been proposed that a small amount of Pb2+-doping, both at B+ and B3+ sites, would bring the optical energy gap down to a spectrally important region, and the nature of the band gap would be direct.47
The molecular orbital band diagrams of the investigated halide double perovskites are given in Figure 13. This diagram served as a schematic representation of bonding and antibonding states in valence and conduction bands. As mentioned, due to the spin–orbit splitting of the Bi-p1/2 and Bi-p3/2 states in both compounds, the conduction band arises and has a predominantly antibonding character. Additionally, a minor contribution from the Bi-s/X-p antibonding state may be found at the VBM. In both compounds, mixed Ag-d/X-p states predominate throughout the VBM, pushing Ag-s states into the conduction band, which is consistent with the noble metal’s + 1 oxidation nature in this chemical environment.
Figure 13.
Molecular orbital diagrams of the two investigated perovskites. Thick black lines indicate the atomic single-electron energies, while blue and green rectangles, respectively, illustrate the Bi-halide and Ag-halide hybrid bands. The orange color rectangles display the bands produced in Cs2BiAgCl6 and Cs2BiAgBr6 perovskites. Rectangles that are filled or left unfilled show the valence and conduction bands, respectively. All the bands were aligned with the Bi-5d1/2 energy level.
The DOS study further revealed that the Cs-cation does not affect the development of frontier band edges, while the halide ions (Cl and Br) control the size of the energy gap but have no bearing on the orbital characteristics or the direct/indirect nature of the energy gap. Thus, the efficiency of halide perovskite photovoltaics and LEDs can be tuned by smart choices of B+ and B3+ cations. In the present case, Ag+ and Bi3+ have been chosen to be at B+ and B3+ sites, respectively, to form the two halide double perovskites Cs2AgBiBr6 and Cs2AgBiCl6. Figures 11 and 12 display the p-DOS of this sequence of structures as determined using the hybrid HSE06 functional with spin–orbit coupling (HSE06 + SOC). The pressure-dependent charge density plots (Figures S5 and S6) are incorporated in the Supporting Information. Bond lengths are shown to decrease monotonically with an increasing stress (Figures S5 and S6 of the Supporting Information), as opposed to the sudden change with the evident phase transition under pressure.50 It implies that under the specified pressure range, lead halide double perovskites do not undergo a structural phase change.
The predicted direct and indirect energy gaps as a function of pressure for Cs2AgBiCl6 and Cs2AgBiBr6 perovskites have been displayed in Figure 14. From the band gap versus pressure graph, one could find that both the direct and indirect gaps vary nonlinearly with the pressure. However, the fundamental gap at equilibrium is indirect (X-Γ) for both perovskite compounds. Also, it was one of the objectives to figure out the value of applied pressure where the compounds exhibit metallic character; as a result, it was noted that the Cs2AgBiBr6 perovskite transformed from the semiconductor to the metal phase at 50 Gpa, while Cs2AgBiCl6 perovskite displayed the same character beyond 80 GPa. To reduce the computational effort while calculating the bands and electronic density of states, different pressure intervals (10 and 20 GPa) were chosen for the two compounds. Since the Cl-based perovskite indicated metallic behavior at 80 GPa, its pressure interval was chosen as 20 GPa.
Figure 14.
Band gap evolution in Cs2AgBiBr6 and Cs2AgBiCl6 perovskite structures with pressure.
4. Conclusions
In the present study, pressure-induced mechanical, electronic, and structural properties of Cs-based Ag and Bi halide perovskites were investigated using DFT calculations. The computed values for the lattice parameters, elastic constants, and band gap were in tune with the available theoretical and experimental studies. Under equilibrium, the obtained band gap values of 1.45 eV for Cs2AgBiBr6 and 1.96 eV for Cs2AgBiCl6 were indirect (X−Γ). Our calculations show that the band gaps were significantly affected by the disordered Ag and Bi atoms; as a result, the energy gap was reduced, and few direct transitions were seen from the pressure-dependent band structures of the two perovskites. The pressure-driven semiconductor perovskites Cs2AgBiBr6 and Cs2AgBiCl6 ultimately transformed into the metallic phases at 50 and 80 GPa, respectively. The covalent bond changes into a metallic bond, and the bond lengths are shortened under the influence of the generated hydrostatic pressure. Meanwhile, the enhanced symmetry breaking in [AgX6]−5 and [BiX6]−3 octahedra under high pressure caused a reduction in DOS on the Fermi surface that resulted in the lowering of the total energy. Our elastic calculations demonstrated that the materials under study were ductile and mechanically stable and that the induced pressure enhanced their ductility.
Acknowledgments
This research was conducted in Turkey as a part of the 2236 Co-Funded Brain Circulation Scheme2 (CoCirculation2) research project funded by TUBITAK (Project No. 121C412). Calculations were performed at TUBITAK ULAKBIM, High Performance and Grid Computing Center (TR-Grid-e-Infrastructure). One of the authors, F.B. extends sincere thanks to TUBITAK-BIDEB-2211 Program for providing the facilities and financial support.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.3c03469.
Detailed description of the computational data of the elastic constants at different pressures, with the pressure range of 0–100 GPa for both the halide double perovskite members, and band structure plots and DOS plots at intermediate pressure ranges (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- McGehee M. D. Perovskite Solar Cells: Continuing to Soar. Nat. Mater. 2014, 13, 845–846. 10.1038/nmat4050. [DOI] [PubMed] [Google Scholar]
- Kojima A.; Teshima K.; Shirai Y.; Miyasaka T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. 10.1021/ja809598r. [DOI] [PubMed] [Google Scholar]
- Stoumpos C. C.; Malliakas C. D.; Kanatzidis M. G. Semiconducting Tin and Lead Iodide Perovskites with Organic Cations: Phase Transitions, High Mobilities, and Near-Infrared Photoluminescent Properties. Inorg. Chem. 2013, 52, 9019–9038. 10.1021/ic401215x. [DOI] [PubMed] [Google Scholar]
- Wehrenfennig C.; Eperon G. E.; Johnston M. B.; Snaith H. J.; Herz L. M. High Charge Carrier Mobilities and Lifetimes in Organolead Trihalide Perovskites. Adv. Mater. 2014, 26, 1584–1589. 10.1002/adma.201305172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pazos-Outon L. M.; Szumilo M.; Lamboll R.; Richter J. M.; Crespo-Quesada M.; Abdi-Jalebi M.; Beeson H. J.; Vrućinić M.; Ansari M.; Snaith H. J.; Ehrler B. Photon Recycling in Lead Iodide Perovskite Solar Cells. Science 2016, 351, 1430–1433. 10.1126/science.aaf1168. [DOI] [PubMed] [Google Scholar]
- Saliba M.; Zhang W.; Burlakov V. M.; Stranks S. D.; Sun Y.; Ball J. M.; Johnston M. B.; Goriely A.; Wiesner U.; Snaith H. J. Plasmonic-Induced Photon Recycling in Metal Halide Perovskite Solar Cells. Adv. Funct. Mater. 2015, 25, 5038–5046. 10.1002/adfm.201500669. [DOI] [Google Scholar]
- Parrey K. A.; Aziz A.; Ansari S. G.; Mir S. H.; Khosla A.; Niazi A. Synthesis and characterization of an efficient hole-conductor free halide Perovskite CH3NH3PbI3 semiconductor absorber-based photovoltaic device for IoT. J. Electrochem. Soc. 2018, 165, B3023–B3029. 10.1149/2.0051808jes. [DOI] [Google Scholar]
- National Renewable Energy Labs (NREL) efficiency chart, 2021. http://www.nrel.gov/ncpv/images/efficiency_chart.jpg (accessed December 2021).
- Stranks S. D.; Snaith H. J. Metal-halide perovskites for photovoltaic and light-emitting devices. Nat. Nanotechnol. 2015, 10, 391–402. 10.1038/nnano.2015.90. [DOI] [PubMed] [Google Scholar]
- Swarnkar A.; Marshall A. R.; Sanehira E. M.; Chernomordik B. D.; Moore D. T.; Christians J. A.; Chakrabarti T.; Luther J. M. Quantum dot–induced phase stabilization of α-CsPbI3 perovskite for high-efficiency photovoltaics. Science 2016, 354, 92–95. 10.1126/science.aag2700. [DOI] [PubMed] [Google Scholar]
- Frolova L. A.; Anokhin D. V.; Gerasimov K. L.; Dremova N. N.; Troshin P. A. Exploring the effects of the Pb2+ substitution in MAPbI3 on the photovoltaic performance of the hybrid perovskite solar cells. J. Phys. Chem. Lett. 2016, 7, 4353–4357. 10.1021/acs.jpclett.6b02122. [DOI] [PubMed] [Google Scholar]
- a Kumar A.; Balasubramaniam K. R.; Kangsabanik J.; Alam A. Crystal structure, stability, and optoelectronic properties of the organic-inorganic wide-band-gap perovskite CH3NH3BaI3: candidate for transparent conductor applications. Phys. Rev. B 2016, 94, 180105 10.1103/PhysRevB.94.180105. [DOI] [Google Scholar]; b Noel N. K.; Stranks S. D.; Abate A.; Wehrenfennig C.; Guarnera S.; Haghighirad A. A.; Snaith H. J. Lead-free organic–inorganic tin halide perovskites for photovoltaic applications. Energy Environ. Sci. 2014, 7, 3061–3068. 10.1039/C4EE01076K. [DOI] [Google Scholar]; c Yokoyama T.; Cao D. H.; Stoumpos C. C.; Song T. B.; Sato Y.; Aramaki S.; Kanatzidis M. G. Overcoming short-circuit in lead-free CH3NH3SnI3 perovskite solar cells via kinetically controlled gas–solid reaction film fabrication process. J. Phys. Chem. Lett. 2016, 7, 776–782. 10.1021/acs.jpclett.6b00118. [DOI] [PubMed] [Google Scholar]
- Giustino F.; Snaith H. J. Toward lead-free perovskite solar cells. ACS Energy Lett. 2016, 1, 1233–1240. 10.1021/acsenergylett.6b00499. [DOI] [Google Scholar]
- Zhao X. G.; Yang J. H.; Fu Y.; Yang D.; Xu Q.; Yu L.; Wei S. H.; Zhang L. Design of lead-free inorganic halide perovskites for solar cells via cation-transmutation. J. Am. Chem. Soc. 2017, 139, 2630–2638. 10.1021/jacs.6b09645. [DOI] [PubMed] [Google Scholar]
- a Filip M. R.; Hillman S.; Haghighirad A. A.; Snaith H. J.; Giustino F. Band gaps of the lead-free halide double perovskites Cs2BiAgCl6 and Cs2BiAgBr6 from theory and experiment. J. Phys. Chem. Lett. 2016, 7, 2579–2585. 10.1021/acs.jpclett.6b01041. [DOI] [PubMed] [Google Scholar]; b Pan W.; Wu H.; Luo J.; Deng Z.; Ge C.; Chen C.; Jiang X.; Yin W. J.; Niu G.; Zhu L.; Yin L.; Zhou Y.; Xie Q.; Ke X.; Sui M.; Tang J. Cs2AgBiBr6 single-crystal X-ray detectors with a low detection limit. Nat. Photonics 2017, 11, 726–732. 10.1038/s41566-017-0012-4. [DOI] [Google Scholar]
- a Shockley W.; Queisser H. J. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 1961, 32, 510–519. 10.1063/1.1736034. [DOI] [Google Scholar]; b Li Q.; Wang Y.; Pan W.; Yang W.; Zou B.; Tang J.; Quan Z. High-Pressure Band-Gap Engineering in Lead-Free Cs2AgBiBr6 Double Perovskite. Angew. Chem. Int. Ed. 2017, 56, 15969–15973. 10.1002/anie.201708684. [DOI] [PubMed] [Google Scholar]
- Huang X.; Huang S.; Biswas P.; Mishra R. Band gap insensitivity to large chemical pressures in ternary bismuth iodides for photovoltaic applications. J. Phys. Chem. C 2016, 120, 28924–28932. 10.1021/acs.jpcc.6b09567. [DOI] [Google Scholar]
- a Szafranski M.; Katrusiak A. Mechanism of pressure-induced phase transitions, amorphization, and absorption-edge shift in photovoltaic methylammonium lead iodide. J. Phys. Chem. Lett. 2016, 7, 3458–3466. 10.1021/acs.jpclett.6b01648. [DOI] [PubMed] [Google Scholar]; b Yin T.; Fang Y.; Chong W. K.; Ming K. T.; Jiang S.; Li X.; Kuo J. L.; Fang J.; Sum T. C.; White T. J.; Yan J.; Shen Z. X. High-Pressure-Induced Comminution and Recrystallization of CH3NH3PbBr3 Nanocrystals as Large Thin Nanoplates. Adv. Mater. 2018, 30, 1705017 10.1002/adma.201705017. [DOI] [PubMed] [Google Scholar]
- a Li B.; Wen X.; Li R.; Wang Z.; Clem P. G.; Fan H. Stress-induced phase transformation and optical coupling of silver nanoparticle superlattices into mechanically stable nanowires. Nat. Commun. 2014, 5, 4179. 10.1038/ncomms5179. [DOI] [PubMed] [Google Scholar]; b Li B.; Bian K.; Lane J. M. D.; Salerno K. M.; Grest G. S.; Ao T.; Hickman R.; Wise J.; Wang Z.; Fan H. Superfast assembly and synthesis of gold nanostructures using nanosecond low-temperature compression via magnetic pulsed power. Nat. Commun. 2017, 8, 14778. 10.1038/ncomms14778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- a Zhu J.; Quan Z.; Lin Y. S.; Jiang Y. B.; Wang Z.; Zhang J.; Jin C.; Zhao Y.; Liu Z.; Brinker C. J.; Xu H. Porous ice phases with VI and distorted VII structures constrained in nanoporous silica. Nano Lett. 2014, 14, 6554–6558. 10.1021/nl503165n. [DOI] [PubMed] [Google Scholar]; b Chen Y.; Fu R.; Wang L.; Ma Z.; Xiao G.; Wang K.; Zou B. Emission enhancement and bandgap retention of a two-dimensional mixed cation lead halide perovskite under high pressure. J. Mater. Chem. A 2019, 7, 6357–6362. 10.1039/C8TA11992A. [DOI] [Google Scholar]
- a Jaffe A.; Lin Y.; Mao W. L.; Karunadasa H. I. Pressure-induced metallization of the halide perovskite (CH3NH3) PbI3. J. Am. Chem. Soc. 2017, 139, 4330–4333. 10.1021/jacs.7b01162. [DOI] [PubMed] [Google Scholar]; b Lü X.; Wang Y.; Stoumpos C. C.; Hu Q.; Guo X.; Chen H.; Yang L.; Smith J. S.; Yang W.; Zhao Y.; Xu H.; Kanatzidis M. G.; Jia Q. Enhanced structural stability and photo responsiveness of CH3NH3SnI3 perovskite via pressure-induced amorphization and recrystallization. Adv. Mater. 2016, 28, 8663–8668. 10.1002/adma.201600771. [DOI] [PubMed] [Google Scholar]
- Slavery A. H.; Hu T.; Lindenberg A. M.; Karunadasa H. I. A Bismuth-Halide Double Perovskite with Long Carrier Recombination Lifetime for Photovoltaic Applications. J. Am. Chem. Soc. 2016, 138, 2138–2141. 10.1021/jacs.5b13294. [DOI] [PubMed] [Google Scholar]
- McClure E. T.; Ball M. R.; Windl W.; Woodward P. M. Cs2AgBiX6 (X = Br, Cl): New Visible Light Absorbing, Lead-Free Halide Perovskite Semiconductors. Chem. Mater. 2016, 28, 1348–1354. 10.1021/acs.chemmater.5b04231. [DOI] [Google Scholar]
- Yang B.; Chen J.; Yang S.; Hong F.; Sun L.; Han P.; Pullerits T.; Deng W.; Han K. Lead-Free Silver-Bismuth Halide Double Perovskite Nanocrystals. Angew. Chem., Int. Ed. 2018, 57, 5359–5363. 10.1002/anie.201800660. [DOI] [PubMed] [Google Scholar]
- Yang B.; Mao X.; Hong F.; Meng W.; Tang Y.; Xia X.; Yang S.; Deng W.; Han K. Lead-Free Direct Bandgap Double Perovskite Nanocrystals with Bright Dual-Color Emission. J. Am. Chem. Soc. 2018, 140, 17001–17006. 10.1021/jacs.8b07424. [DOI] [PubMed] [Google Scholar]
- Du K. Z.; Meng W.; Wang X.; Yan Y.; Mitzi D. B. Bandgap Engineering of Lead-Free Double Perovskite Cs2AgBiBr6 through divalent Metal Alloying. Angew. Chem., Int. Ed. 2017, 56, 8158–8162. 10.1002/anie.201703970. [DOI] [PubMed] [Google Scholar]
- a Steele J. A.; Pan W.; Martin C.; Keshavarz M.; Debroye E.; Yuan H.; Banerjee S.; Fron E.; Jonckheere D.; Kim C. W.; Baekelant W.; Niu G.; Tang J.; Vanacken J.; van der Auweraer M.; Hofkens J.; Roeffaers M. B. J. Photophysical Pathways in Highly Sensitive Cs2AgBiBr6 Double-Perovskite Single-Crystal X-Ray Detectors. Adv. Mater. 2018, 30, e1804450 10.1002/adma.201804450. [DOI] [PubMed] [Google Scholar]; b Pan W.; Wu H.; Luo J.; Deng Z.; Ge C.; Chen C.; Jiang X.; Yin W.-J.; Niu G.; Zhu L.; Yin L.; Zhou Y.; Xie Q.; Ke X.; Sui M.; Tang J. Cs2AgBiBr6 Single-Crystal X-RayDetectors with a Low Detection Limit. Nat. Photonics 2017, 11, 726–732. 10.1038/s41566-017-0012-4. [DOI] [Google Scholar]; c Luo J.; Wang X.; Li S.; Liu J.; Guo Y.; Niu G.; Yao L.; Fu Y.; Gao L.; Dong Q.; et al. Efficient and Stable Emission of Warm-White Light from Lead-Free Halide Double Perovskites. Nature 2018, 563, 541–545. 10.1038/s41586-018-0691-0. [DOI] [PubMed] [Google Scholar]; d Zhou L.; Xu Y. F.; Chen B. X.; Kuang D. B.; Su C. Y. Synthesis and Photocatalytic Application of Stable Lead-Free Cs2AgBiBr6 Perovskite Nanocrystals. Small 2018, 14, e1703762 10.1002/smll.201703762. [DOI] [PubMed] [Google Scholar]
- a Volonakis G.; Filip M. R.; Haghighirad A. A.; Sakai N.; Wenger B.; Snaith H. J.; Giustino F. J. Phys. Chem. Lett. 2016, 7, 1254–1259. 10.1021/acs.jpclett.6b00376. [DOI] [PubMed] [Google Scholar]; b Savory C. N.; Walsh A.; Scanlon D. O. Can Pb-free halide double perovskites support high-efficiency solar cells?. ACS Energy Lett. 2016, 1, 949–955. 10.1021/acsenergylett.6b00471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- a Swainson I. P.; Tucker M. G.; Wilson D. J.; Winkler B.; Milman V. Pressure response of an organic– inorganic perovskite: methylammonium lead bromide. Chem. Mater. 2007, 19, 2401–2405. 10.1021/cm0621601. [DOI] [Google Scholar]; b Gesi K. Effect of hydrostatic pressure on the structural phase transitions in CH3NH3PbX3 (X= Cl, Br, I). Ferroelectrics 1997, 203, 249–268. 10.1080/00150199708012851. [DOI] [Google Scholar]
- Wang Y.; Lü X.; Yang W.; Wen T.; Yang L.; Ren X.; Wang L.; Lin Z.; Zhao Y. Pressure-induced phase transformation, reversible amorphization, and anomalous visible light response in organolead bromide perovskite. J. Am. Chem. Soc. 2015, 137, 11144–11149. 10.1021/jacs.5b06346. [DOI] [PubMed] [Google Scholar]
- a Kresse G.; Furthmüller J. Efficiency of ab-initio total-energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]; b Kresse G.; Hafner J. Ab-initio molecular-dynamics for liquid-metals. Phys. Rev. B 1993, 47, 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Momma K.; Izumi F. VESTA: a three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. 10.1107/S0021889808012016. [DOI] [Google Scholar]
- Muscat J.; Wander A.; Harrison N. M. On the prediction of band gaps from hybrid functional theory. Chem. Phys. Lett. 2001, 342, 397–401. 10.1016/S0009-2614(01)00616-9. [DOI] [Google Scholar]
- Paier J.; Marsman M.; Hummer K.; Kresse G.; Gerber I. C.; Ángyán J. G. Screened hybrid density functionals applied to solids. J. Chem. Phys. 2006, 124, 154709 10.1063/1.2187006. [DOI] [PubMed] [Google Scholar]
- Singh D. J. Electronic structure calculations with the Tran-Blaha modified Becke-Johnson density functional. Phys. Rev. B 2010, 82, 205102 10.1103/PhysRevB.82.205102. [DOI] [Google Scholar]
- Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
- Monkhorst H. J.; Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
- Feng H.-J.; Deng W.; Yang K.; Huang J.; Zeng X. C. Double Perovskite Cs2BBiX6 (B = Ag, Cu; X = Br, Cl)/TiO2 Heterojunction: An Efficient Pb-Free Perovskite Interface for Charge Extraction. J. Phys. Chem. C 2017, 121, 4471–4480. 10.1021/acs.jpcc.7b00138. [DOI] [Google Scholar]
- Kumar N. R.; Radhakrishnan R. Electronic, Optical and Mechanical Properties of Lead-Free Halide Double Perovskites using First-Principles Density Functional Theory. Mater. Lett. 2018, 227, 289–291. 10.1016/j.matlet.2018.05.082. [DOI] [Google Scholar]
- Dong L.; Sun S.; Deng Z.; Li W.; Wei F.; Qi Y.; Li Y.; Li X.; Lu P.; Ramamurty U. Elastic properties and thermal expansion of lead-free halide double perovskite Cs2AgBiBr6. Comput. Mater. Sci. 2018, 141, 49–58. 10.1016/j.commatsci.2017.09.014. [DOI] [Google Scholar]
- Kart S. O.; Cagın T. Elastic properties of Ni2MnGa from first-principles calculations. J. Alloys Compd. 2010, 508, 177–183. 10.1016/j.jallcom.2010.08.039. [DOI] [Google Scholar]
- Pugh S. F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823–843. 10.1080/14786440808520496. [DOI] [Google Scholar]
- Frantsevich I. N.; Voronov F. F.; Bakuta S. A.. Handbook on Elastic Constants and Moduli of Elasticity for Metals and Nonmetals; Naukova Dumka: Kiev, 1982. [Google Scholar]
- Fu R.; Chen Y.; Yong X.; Ma Z.; Wang L.; Lv P.; Lu S.; Xiao G.; Zou B. Pressure-induced structural transition and band gap evolution of double perovskite Cs2 AgBiBr6 nanocrystals. Nanoscale 2019, 11, 17004–17009. 10.1039/C9NR07030C. [DOI] [PubMed] [Google Scholar]
- Kangsabanik J.; Sugathan V.; Yadav A.; Yella A.; Alam A. Double perovskites overtaking the single perovskites: A set of new solar harvesting materials with much higher stability and efficiency. Phys. Rev. Mater. 2018, 2, 055401 10.1103/PhysRevMaterials.2.055401. [DOI] [Google Scholar]
- Ghebouli M. A.; Chihi T.; Ghebouli B.; Fatmi M. Study of the structural, elastic, electronic and optical properties of lead-free halide double perovskites Cs2AgBiX6 (X= Br, Cl). Chinese J. Phys. 2018, 56, 323–330. 10.1016/j.cjph.2018.01.004. [DOI] [Google Scholar]
- Tripathi M. N.; Saha A.; Singh S. Structural, elastic, electronic and optical properties of lead-free halide double perovskite Cs2AgBiX6 (X= Cl, Br, and I). Mater. Res. Express 2019, 6, 115517. 10.1088/2053-1591/ab48ba. [DOI] [Google Scholar]
- a Ma Z.; Li F.; Qi G.; Wang L.; Liu C.; Wang K.; Xiao G.; Zou B. Structural stability and optical properties of two-dimensional perovskite-like CsPb2 Br5 microplates in response to pressure. Nanoscale 2019, 11, 820–825. 10.1039/c8nr05684f. [DOI] [PubMed] [Google Scholar]; b Ying Y.; Luo X.; Huang H. Pressure-induced topological nontrivial phase and tunable optical properties in all-inorganic halide perovskites. J. Phys. Chem. C 2018, 122, 17718–17725. 10.1021/acs.jpcc.8b06712. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.








