Abstract
Cryptic pockets, or pockets absent in ligand-free, experimentally determined structures, hold great potential as drug targets. However, cryptic pocket openings are often beyond the reach of conventional biomolecular simulations because certain cryptic pocket openings involve slow motions. Here, we investigate whether AlphaFold can be used to accelerate cryptic pocket discovery either by generating structures with open pockets directly or generating structures with partially open pockets that can be used as starting points for simulations. We use AlphaFold to generate ensembles for 10 known cryptic pocket examples, including five that were deposited after AlphaFold’s training data were extracted from the PDB. We find that in 6 out of 10 cases AlphaFold samples the open state. For plasmepsin II, an aspartic protease from the causative agent of malaria, AlphaFold only captures a partial pocket opening. As a result, we ran simulations from an ensemble of AlphaFold-generated structures and show that this strategy samples cryptic pocket opening, even though an equivalent amount of simulations launched from a ligand-free experimental structure fails to do so. Markov state models (MSMs) constructed from the AlphaFold-seeded simulations quickly yield a free energy landscape of cryptic pocket opening that is in good agreement with the same landscape generated with well-tempered metadynamics. Taken together, our results demonstrate that AlphaFold has a useful role to play in cryptic pocket discovery but that many cryptic pockets may remain difficult to sample using AlphaFold alone.
Introduction
Cryptic pockets, or pockets absent in ligand-free experimental structures, are a promising means to expand the scope of drug discovery. By one estimate, almost half of all structured domains lack obvious pockets in their experimental structures.1 These proteins have often been considered “undruggable”. However, as proteins fluctuate in solution, they may adopt excited structural states that contain cryptic pockets. Thus, cryptic pockets may provide a means to target these “undruggable” proteins.2 Furthermore, many cryptic pockets are distant from active sites, suggesting that targeting them may lead to the discovery of allosteric activators3 or more specific modulators given the high sequence conservation of many active sites.4
The discovery of cryptic pockets using experimental and computational methods remains difficult in many cases. Most cryptic pockets are discovered serendipitously when experimental structures of a ligand bound to a protein reveal a novel binding site that is closed in ligand-free structures of the same protein.5 While this process has revealed cryptic pockets, it requires knowledge of a ligand a priori. Molecular dynamics simulations can reveal excited states with cryptic pockets that can then be used for structure-based drug design.2,6 However, in certain cases, cryptic pockets may not be discovered by simulations because cryptic pocket opening motions may be slow (e.g., Niemann-Pick C2 Protein in Meller et al.1). Two classes of slow motions include side chain ring flipping7 events and secondary structure rearrangements8 which can both occur on microsecond and slower time scales.
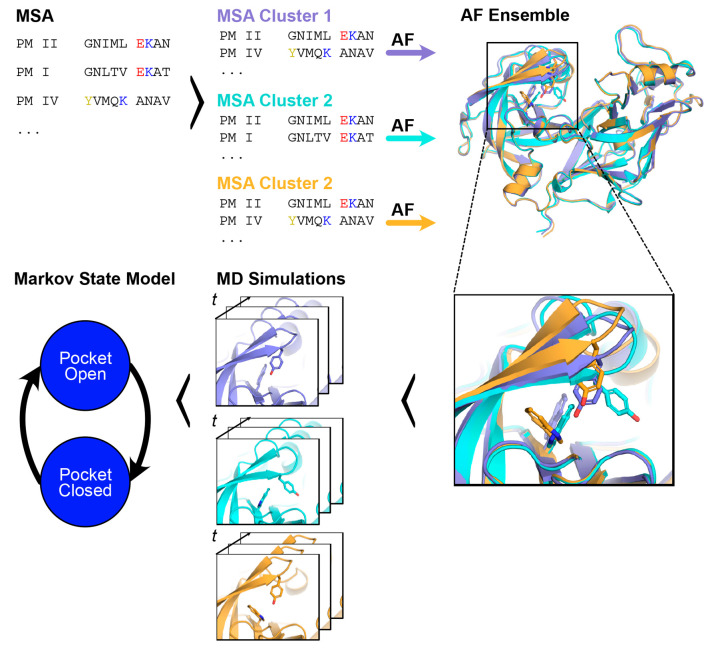
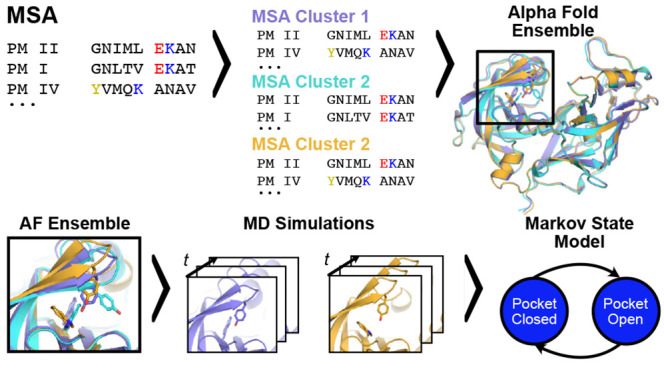
Here, we explore the possibility of using AlphaFold9 to accelerate cryptic pocket discovery. Previous work has shown that stochastic sampling of AlphaFolds’s input multiple sequence alignment can generate diverse conformations of membrane and globular proteins.10,11 We hypothesized that a similar strategy can be applied to discover cryptic pockets. Even if AlphaFold can only capture partial openings, we reasoned that starting molecular dynamics simulations from these structures may capture full openings far more quickly than starting simulations from completely closed structures (Figure 1).
Figure 1.
To efficiently sample cryptic pocket openings, we propose launching molecular dynamics simulations from diverse AlphaFold-generated starting conformations. Starting with an multiple sequence alignment (MSA) of a query sequence (top left), the MSA can be stochastically clustered to create input MSAs of lower depth that are then fed to AlphaFold. Through this procedure, we can generate an ensemble of structures of the same protein (top right shows snapshots of Plasmodium falciparum’s plasmepsin II). These structures may adopt different conformations at known cryptic pockets (bottom right inset highlights different conformations of the plasmepsin II cryptic pocket). To generate free energy landscapes of cryptic pocket opening, we can launch molecular dynamics simulations from these different conformations and then stitch these simulations together with a Markov state model.
We test our strategy of launching simulations from AlphaFold-generated starting structures with plasmepsin II (PM II), a well-studied protease from the causative agent of malaria.12−14 PM II is one of many aspartic proteases that play an important role in the lifecycle of Plasmodium falciparum. It is found in digestive vacuoles where it is used by the parasite to digest hemoglobin. Though functional redundancy in digestive vacuoles may limit the utility of narrow PM II inhibitors, PM II may play a role in antimalarial drug resistance15 and provide insight into developing inhibitors of other aspartic proteases that are essential in the Plasmodium lifecycle. Notably, PM II contains a cryptic pocket adjacent to its active site, which was revealed in several experimental structures capturing PM II bound to different classes of inhibitors. Given that previous simulation studies of PM II have failed to sample cryptic pocket opening,13 here we explore if increasing aggregate simulation time is sufficient to open this pocket or if AlphaFold can accelerate cryptic pocket discovery.
Methods
Ensemble Generation Using AlphaFold
To generate ensembles of structures from a sequence rather than a single structure, we use two modifications to the original AlphaFold implementation. First, we stochastically subsample the multiple sequence alignment (MSA) to a maximum of 32 cluster centers and 64 extra sequences. Each time we generate a structure prediction, a different random seed is used for sequence clustering, so that the input MSA passed to AlphaFold is slightly modified. Second, we also enable dropout during the forward pass through the model.
We generated ensembles for each of the proteins studied using ColabFold,16 a fast and user-friendly implementation of the AlphaFold algorithm. Specifically, we used the Google Collaboratory notebook. We generated initial MSAs using the jackhammer method with prefiltering that enforced a minimum 50% coverage and 20% sequence identity with the query. We then limited the depth of the input MSA by setting the max_msa_clusters variable to 32 and max_extra_msa to 64. We generated an ensemble of 32 or 160 structures by setting num_models to 1 or 5, respectively, and num_samples to 32. We enabled dropout by setting is_training to True. We also enabled use_ptm, set num_ensembles to 1, set tol to 0, and set max_recycles to 3.
The link to the Google Collaboratory notebook is here (https://colab.research.google.com/github/sokrypton/ColabFold/blob/main/beta/AlphaFold2_advanced.ipynb).
Molecular Dynamics Simulations
We prepared molecular dynamics simulations using the tleap module integrated with Amber 202017 with the workflow described here. Proteins were parametrized using the AMBER FF14SB18 force field and solvated in a truncated octahedron box with TIP3P19 waters. Each system was neutralized by 17 Na+ ions. For each system, the box was extended 1.0 nm from protein atoms in all directions. Minimization was performed in two steps: (a) initial minimization where the protein was constrained with a restrained potential of 100 kcal/mol–1 Å2 to minimize only the water and ions (200 steps of steepest descent followed by 200 steps of conjugate gradients) followed by (b) 500 steps of unrestrained minimization of the whole system.
We equilibrated protein systems and performed production runs using Gromacs 2021.20 Following minimization in Amber, we converted Amber topologies to Gromacs format using Acpype.21 Initially, we heated each system (from 0 to 300 K) using the NVT ensemble for 500 ps with harmonic restraints of 500 kJ mol–1nm–2 applied to backbone heavy atoms. Next, each system was equilibrated at 300 K in an NPT ensemble for 200 ps without any restraints using the Parrinello–Rahman barostat22 to maintain the pressure at 1 bar and the v-rescale thermostat for temperature control. Production runs were carried out in the NPT ensemble at 300 K and 1 bar using the leapfrog integrator and Parrinello–Rahman thermostat with a 2 fs time step. Nonbonded interactions were cut off at 1.0 nm, and long-range electrostatic potentials were treated using the Particle Mesh Ewald (PME) method23 with a grid spacing of 0.16 nm. The LINCS algorithm24 was used to constrain H-bonds during MD simulations.
We performed 640 independent MD simulations in total to generate apo-seeded and AF-seeded ensembles each with 32 μs of sampling. We used 32 different AlphaFold-generated starting structures for plasmepsin II with 10 independent (i.e., starting from different initial velocities) simulations launched for each structure. Each simulation was 100 ns in length. For the apo-seeded ensemble, we ran 320 independent simulations 100 ns in length starting from a single starting structure from the PDB (1LF425). We note that while we used an ensemble of 160 structures to evaluate the conformational diversity of structures produced by AF (Figure 2A), we generated an ensemble of 32 structures of plasmpesin II for simulations separately.
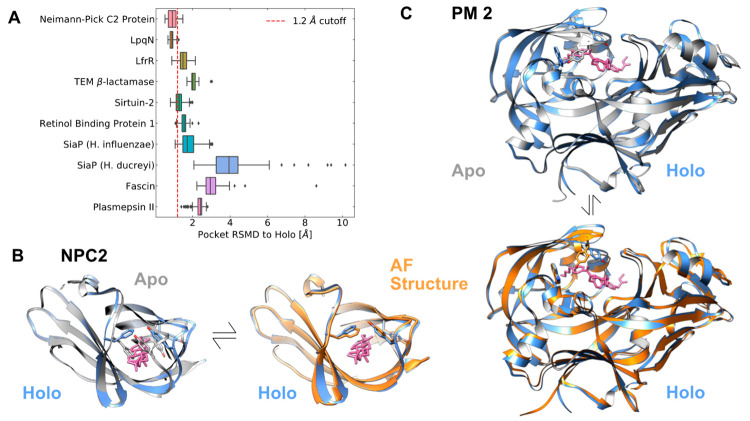
Figure 2.
Stochastic clustering of its input multiple sequence alignment allows AlphaFold to generate structures with open or partially open cryptic pockets across multiple systems. (A) In 6 out of 10 examples, AlphaFold samples the open state of a known cryptic pocket. The box-and-whisker plots show cryptic pocket root-mean-square deviations (RMSD) to a holo crystal structure (defined by heavy atoms within 5 Å of the ligand that binds at the cryptic pocket). For the top five examples, the holo structure was part of the training data set for AlphaFold, but the bottom five examples had their holo crystal structures deposited after AlphaFold was trained. The red line indicates 1.2 Å RMSD, a proposed cutoff for sampling the open state. (B) Structural overlay of an AlphaFold-generated structure with the holo structure of Neimann-Pick C2 Protein (NPC2) shows that AlphaFold samples the open state. The ligand which binds in the cryptic pocket is shown in magenta, the apo structure in gray, the holo structure in blue, and the AF structure in orange. Residues that change rotamer state between apo and holo experimental structures are shown in sticks. (C) Structural overlay of an AlphaFold-generated structure of plasmepsin II with a holo structure containing a cryptic pocket shows that AlphaFold partially samples cryptic pocket openings. Select residues that change rotamer state between apo and holo experimental structures show that AlphaFold samples holo-like tryptophan orientations in the plasmepsin II cryptic pocket. As in B, the ligand which binds in the cryptic pocket is shown in magenta, the apo structure in gray, the holo structure in blue, and the AF structure in orange.
Markov State Modeling
To construct MSMs,26−28 we first defined a subset of features that were relevant to PM II cryptic pocket opening. We focused on the set of residues that were within 0.5 nm of the cryptic extension of the A1T ligand in the holo crystal structure (PDB: 2IGX(29)). Specifically, we located all residues that were within 0.5 nm of the following A1T atoms: C48, C46, C43, C40, C38, C36, C33, C34, C30, N29, and C26. We then used backbone (phi, psi) and side chain dihedrals for those residues to define an initial feature set relevant for cryptic pocket opening. We removed any χ-2 angles that included symmetrically equivalent atoms (e.g., χ-2 for tyrosine residues).
To perform clustering in a kinetically relevant space, we applied time–structure independent component analysis30 (tICA) to these features. Specifically, we used a tICA lag time of 10 ns and retained the top n tICs that accounted for 90% of kinetic variance using commute mapping. We found that the choice of tICA lag time (between 5 and 20 ns) did not affect which slow collective motions were identified by tICA.
To determine the appropriate number of microstates for clustering, we used a cross-validation scheme where trajectories were partitioned into training and test sets. Clustering into k microstates was performed using only the training set, and the test set trajectories were assigned to these k microstates based on their Euclidean proximity in tICA space to each microstate’s centroid. Using the test set only, an MSM was fit using maximum likelihood estimation (MLE), and the quality of the MSM was assessed with the rank-10 VAMP-2 score of the transition matrix. We found that 25 microstates had the highest VAMP-2 score on average across 10 trials on the test set for the AF-seeded ensemble (Figure S17). For consistency, we used the same number of microstates for the apo-seeded MSM.
Finally, MSMs of the PM II cryptic pocket were fit for the apo-seeded and AF-seeded ensembles separately using MLE. Lag times were chosen by the logarithmic convergence of the implied time scales test (Figures S18, S19). Lag times of 12.5 ns were used for both the apo-seeded and AF-seeded MSMs.
MSM construction was performed using the PyEMMA31 software package.
Metadynamics
We performed well-tempered metadynamics32,33 (WTMeta) simulations to sample the conformational landscape associated with Trp41 ring flipping, one of the motions necessary for plasmepsin II cryptic pocket opening. For each residue, we performed two-dimensional WTMeta at 300 K using χ-1 and χ-2 angles as collective variables. Gaussians were deposited every 500 time steps with a width and height of 0.05 radians and 1.2 kJ/mol, respectively, and a bias factor of 20. Unbiased free energy surfaces along different collective variables were extracted from WTMeta using the reweighting protocol described by Tiwary and Parrinello.34
We also used WTMeta simulations to study unbinding of small molecules from two holo conformations (PBD: 2BJU,354AY836). Small molecules were parametrized using the General Amber Force Field37 (GAFF), and the protein was parametrized using the Amber14SB force field. The complexes were neutralized using sodium ions and immersed into a truncated octahedral box such that the distance from protein to the edge of the box was at least 1 nm. Equilibration and production runs were performed using the protocol described in Bhakat and Söderhjelm.13 To estimate the apparent free energy profile of ligand unbinding, we performed multiple independent WTMeta simulations using the distance between the center of mass of the active side residues and the ligand as collective variables. All unbinding WTMeta simulations were performed at 300 K with a bias factor of 10 using a Gaussian width and height of 0.011 nm and 1.2 kJ/mol, respectively.
Results
AlphaFold Predicts Some but Not All Known Cryptic Pocket Openings
We reasoned that AlphaFold (AF) could produce conformations with open cryptic pockets through stochastic sampling of its input multiple sequence alignment. Previous studies have shown that AlphaFold samples diverse conformations of transporters and receptors when its input MSA is stochastically subsampled to only include 16 sequences.10,11 Additionally, AF ensembles of a set of proteins where ligand binding is associated with conformational rearrangements (though not necessarily at the ligand binding site) often included holo-like conformations.38 However, it was not known if AlphaFold samples open structures for proteins known to form cryptic pockets when bound to drug-like molecules (e.g., not ions).
We generated AlphaFold ensembles for 10 known cryptic pocket examples, including a subset that was deposited to the PDB after AlphaFold was trained. These examples include several different types of conformational rearrangements: loop motions, secondary structure motions, and interdomain motions. To ensure that the network was not “memorizing” particular conformations in its training data set, we also focused on five cryptic pocket examples that were deposited to the PDB after April 2018, the date when the AlphaFold training set was pulled. We used ColabFold’s implementation of AlphaFold to generate 160 conformers for each input sequence because it offered a massive speed up and supported stochastic clustering of the input MSA (see Methods). We also used dropout in the forward pass through the network to amplify structural diversity.
We find that AlphaFold samples many but not all cryptic pocket openings (Figure 2). Among proteins that were in the training data set, AlphaFold recapitulates known cryptic pockets in three out of five examples. In those cases, AF predicts a structure with less than 1.2 Å root-mean-square deviation (RMSD) to the holo structure in the cryptic site (i.e., using all heavy atoms within 5 Å of where the cryptic ligand binds for the RMSD calculation). Interestingly, AlphaFold generates open states of the Niemann-Pick C2 Protein that were not discovered in 2 μs of adaptive sampling simulations (Figure 2B).1 However, AlphaFold’s ensemble of TEM β-lactamase structures does not include any open states where the Horn39 or omega6 pockets are open (Figure S1). Among proteins that were not in the training data set, AlphaFold recapitulates three of the five cryptic pockets (i.e., using pocket RMSD of 1.2 Å as the cutoff again). There appears to be a correlation between the size of the rearrangement (i.e., RMSD between apo and holo structures) and the ability of AF to sample cryptic pockets (Figures S2–S12). For example, a cryptic pocket opening in fascin requires a large interdomain motion (0.47 pocket RMSD between apo and holo) and is not captured in the AF ensemble.
Interestingly, for plasmepsin II (PM II), AlphaFold only samples partial cryptic pocket opening, capturing a ring flip that is necessary but not sufficient for pocket opening. In an AF-generated ensemble of 32 structures, there are several different Trp41 orientations (Figure S13A). Notably, ligand-free PM II structures have only ever been observed in a single Trp41 orientation that blocks access to the cryptic site (Figure S14). In contrast, the AF ensemble contains a Trp41 orientation that has only been experimentally observed in holo PM II structures with an open cryptic pocket (Figure 2C, PDB: 2BJU,352IGX, 2IGY(29)). Similarly, AF-generated structures sample the Tyr77 conformation seen in holo PM II structures (Figure S15). Despite this progress toward observing pocket opening, there are still significant differences in the position of the flap domain in the AF ensemble as compared to the holo crystal structures. In the AF ensemble, the flap domain has not moved away from the active site, sterically blocking known cryptic pocket binders. We wondered if simulations launched from the AF ensemble would sample cryptic pocket openings.
PM II’s Cryptic Pocket Opening Is Not Captured with Conventional MD Simulations
We wanted to set a baseline to determine if AlphaFold accelerates cryptic pocket openings. Given recent success in using molecular dynamics to reveal cryptic pockets,40−44 we wondered if simulations launched from a ligand-free PM II structure would sample cryptic pocket openings. Out of the 10 known cryptic pocket examples we tested with AF, we decided to focus on PM II because it was the only one where AF sampled partial cryptic pocket openings (i.e., its ensemble included several structures with pocket RMSD to holo between 1.2 and 2 Å but no structures below 1.2 Å RMSD). Additionally, a previous simulation study of PM II did not observe cryptic pocket opening in ∼2 μs of sampling.13 We hypothesized that increasing the aggregate simulation time might be sufficient to observe cryptic pocket openings. Hence, we launched 320 100 ns-long independent simulations from an apo crystal structure of PM II (PDB: 1LF4(25)).
To our surprise, we find that 32 μs of MD simulations do not reveal cryptic pocket opening in PM II. For the PM II cryptic pocket to open, three separate events must occur: Trp41 must change its side chain orientation, Tyr77 must flip along χ-1, and the “flap” domain must move away from the active site. Our apo-seeded simulations sample both Tyr77 flipping and flap domain movement. However, we do not sample the change in Trp41 side chain orientation (the distance between Trp41’s side chain and the C-alpha of K72 remains large as seen in Figure 3C). Hence, we conclude that PM II’s cryptic pocket opening is not captured with conventional MD simulations, though it is possible that large increases in the amount of sampling could enable us to observe Trp41 ring flipping that is necessary for cryptic pocket opening.
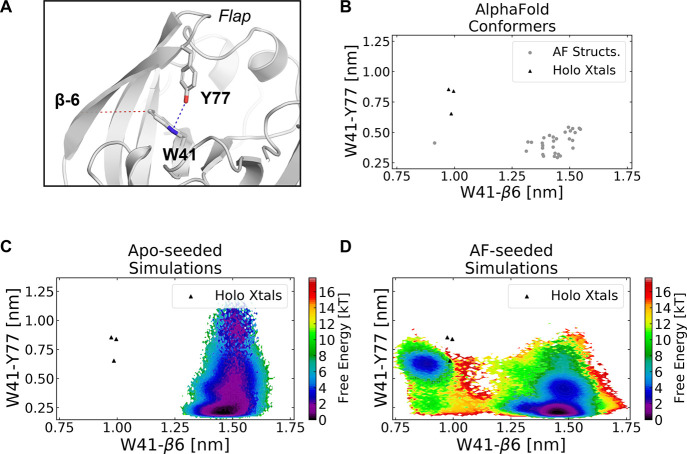
Figure 3.
Launching simulations from AlphaFold-generated structures improves sampling of cryptic pocket opening in plasmepsin II. (A) Structure of PM II’s flap domain showing key residues involved in PM II’s cryptic pocket. Trp41 and Tyr77, part of the flap domain, are shown in sticks. We use the distances indicated in dotted lines to capture pocket opening. Specifically, the cryptic pocket is open when the minimum distance between Y77 and W41 is large (indicated with blue line), and the distance between the W41 side chain (either atom CZ3 or CH2 depending on which is closer) and a reference residue in the 6th β-strand (K72) is small (indicated with red line). (B) Pocket distances for a set of 32 AlphaFold-generated conformers (gray dots) and holo crystal structures (black triangles) show that the AlphaFold ensemble includes partially open states for PM II. Trp41 is in its holo orientation in one of the AlphaFold structures, but the distance between Trp41 and Tyr77 is smaller than it is in holo crystal structures. (C) A free energy surface from a Markov state model from apo-seeded simulations shows that these simulations do not sample cryptic pocket openings. Though the flap dissociates as indicated by large Trp41–Tyr77 distances, Trp41 does not adopt the holo orientation, despite 32 μs of sampling. (D) A free energy surface from a Markov state model generated from AlphaFold-seeded simulations shows robust sampling of the open state. Both requirements for cryptic pocket opening are fulfilled as indicated by the overlay of holo crystal structures (black triangles) on the free energy surface.
Seeding with AlphaFold Accelerates Exploration of the Free Energy Landscape of PM II’s Cryptic Pocket
Given that the AF ensemble of PM II included diverse partially open structures (Figure 3B), we wondered if launching simulations from these structures would accelerate sampling of full cryptic pocket opening. The AF ensemble contains structures with different Trp41 orientations, including one with the Trp41 in the same orientation as holo crystal structures (Figure S13A). Given that flap domain movement was sampled in the simulations initiated from the crystal structure, we hypothesized that we would observe open states in our simulations. We launched 10 independent simulations of 100 ns in length for each of the 32 AlphaFold-generated starting structures (32 μs of aggregate simulation time). We also performed metadynamics simulations to generate a free energy landscape of Trp41 side chain orientations using an orthogonal technique that could be compared against our unperturbed simulations.
We find that simulations launched from the AF ensemble sample cryptic pocket opening. Unlike in single-seeded simulations, we sample all three events required for cryptic pocket opening when simulations are launched from the AF ensemble (Figure 3D). The Trp41 adopts a holo-like orientation while the distance between Trp41 and Tyr77 is large, creating a cavity for ligands to bind. Furthermore, we can build Markov state models26,41,45 (MSMs) of the cryptic pocket ensemble to measure the probability of cryptic pocket opening. MSMs are network models of free energy landscapes composed of many conformational states and the probabilities of transitioning between these states. Specifically, we constructed a MSM using a time–structure independent component analysis (tICA) projection of the backbone and χ-1 dihedrals within the cryptic pocket (see Methods). Despite starting from different starting structures, we find that our model is fully connected in this feature space, and we predict that the probability of cryptic pocket opening is 0.07, indicating that open states are a rare but non-negligible part of the ensemble.
Additionally, reasonable agreement between multiple simulation techniques suggests we have converged to the correct thermodynamics for the force field (Figure 4). We use our MSM to construct a free energy landscape in the space of Trp41 χ-1 and χ-2 dihedral angles and compare against the free energy landscape generated by well-tempered metadynamics (see Methods). Overall, the two free energy landscapes identify similar free energy minima (Figure 4). The deepest well in both landscapes corresponds to the Trp41 side chain orientation seen in ligand-free structures (Figure 4, Figure S13B). There are minor differences in the two free energy landscapes with metadynamics predicting that the well centered on (−1, −2) is more probable than the MSM does. Furthermore, in metadynamics simulations, the probability of the holo Trp41 orientation is 0.30, while in the MSM it is 0.08. Nonetheless, both methods predict that the flipped state necessary for pocket opening is a minor part of the ensemble.
Figure 4.
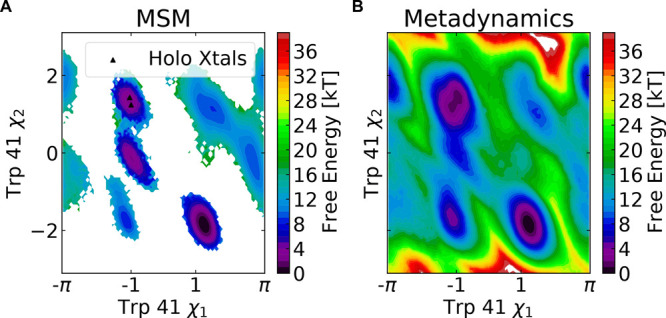
A Markov state model built from AlphaFold-seeded simulations and metadynamics simulations yield a similar free energy landscapes for plasmepsin II cryptic pocket opening. (A) Free energy surface for Trp41 side chain orientations derived from a Markov state model constructed using dihedrals in the PM II cryptic pocket. Holo crystal structures are indicated with black triangles (three points are plotted though only two are visible). Apo crystal structures sample the well centered near (1, −2). (B) Free energy surface from well-tempered metadynamics simulations using Trp41 χ-1and χ-2 angles as collective variables.
Discussion
Certain cryptic pocket opening events remain difficult to sample with classical molecular dynamics simulations. As in previous work,12,13 MD simulations launched from an apo PM-II structure failed to sample full cryptic pocket opening, even with an aggregate simulation time of 32 μs. This result makes PM-II an exception to a general trend. We have found that many cryptic pockets can be discovered with a handful of simulations of intermediate length (i.e., 40 ns).1 Furthermore, significant progress has been made in developing algorithms for cryptic pocket discovery, including Markov state models,6,41 enhanced sampling strategies like SWISH,47 or adaptive sampling approaches like FAST.48 However, we have previously seen that even adaptive sampling strategies can fail to sample known cryptic pockets. This likely stems from the difficulty of sampling rare events in classical molecular dynamics simulations.
The sampling strategy proposed here expands the available computational toolkit for cryptic pocket discovery and characterization without perturbing the underlying energy landscape (Figure 1). Specifically, when assessing a protein as a drug target, we suggest generating diverse conformers of that protein by iteratively passing a stochastically subsampled multiple sequence alignment to AlphaFold. Next, we propose using pocket detection tools, such as LIGSITE,49 fpocket,50 or P2rank,51 to identify pockets that may be absent in both apo experimental structures and the AlphaFold-predicted structure using a complete MSA. In some cases, this will be sufficient to uncover novel cryptic pockets (Figure 2A). However, if this approach yields a partial opening or one is interested in assessing the equilibrium probability of a cryptic pocket opening, we propose using molecular dynamics simulations followed by Markov state model construction. As demonstrated here with PM II, this strategy can greatly accelerate the discovery and characterization of cryptic pockets.
Drug discovery efforts directed toward plasmepsins illustrate that targeting cryptic pockets is a generally promising strategy for discovering selective and potent inhibitors. Ligands that bind at the PM II cryptic site have enhanced potency and selectivity toward PM II compared with other plasmepsins from Plasmodium falciparum (Figure S16A, B). Furthermore, ligands that bind in the cryptic pockets do not inhibit human pepsin-like aspartic proteases (e.g., pepsin, cathepsin D and E).29 To further illustrate the utility of targeting the PM II cryptic site, we used metadynamics to compare the unbinding of an inhibitor from the cryptic site with the unbinding of a ligand from the active site (Figure S16). We find that the ligand which binds at the cryptic pocket has an approximately 25 kJ/mol higher free energy barrier to unbinding because the tyrosine in the cryptic pocket acts as a lid over the ligand (Figure S16C). Slower unbinding kinetics may explain why ligands that bind in the PM II cryptic pocket are more potent and selective. We expect these same principles will apply in other systems.
Finally, AlphaFold-based sampling offers important advantages over existing methods for generating initial structures for simulations, despite AF’s limitations. One approach for generating initial conformations for MD simulations is coarse-grained simulations. Coarse-grained simulations can sample a conformational landscape more rapidly than all-atom simulations, and structures generated by such simulations can be used to reconstruct all-atom structures.52,53 However, coarse-grained simulations may still need to run for prolonged time scales to sample the landscape broadly. In contrast, AF-based sampling is much faster and can be run in a web browser without having to install any specialized software. Furthermore, we have shown here that AF-based structures are in good agreement with experimental structures. It should be acknowledged, however, that some AF-predicted structures may have regions, or even entire domains, with low prediction confidence (i.e., a low predicted local distance difference test). These structures may occupy high-energy regions of conformational space or contain highly flexible domains. A user may manually choose to omit certain structures from simulations or decide to not simulate highly disordered loops if their dynamics are unlikely to affect functionally relevant regions. Another limitation of AF-based sampling is that AF does not provide information for how to weight the ensemble of structures that are generated. Fortunately, MD simulations followed by MSM construction may alleviate some of these limitations of AF-based sampling as simulations are likely to relax away from high-energy conformations, and MSMs can be used to weight an ensemble of structures. Thus, the sampling strategy proposed here should be useful in sampling diverse conformational changes, not just cryptic pocket openings.
Conclusions
We have demonstrated that AlphaFold can be used to accelerate the discovery and characterization of cryptic pockets. When its input multiple sequence alignment is stochastically subsampled, AlphaFold generates diverse conformers of proteins known to form cryptic pockets. In 6 out of 10 examples of proteins known to form cryptic pockets, AlphaFold samples the open state (Figure 2A). Impressively, AlphaFold also makes predictions of the open state even when the holo structure was deposited after AlphaFold was trained. In other cases, like with plasmepsin II, AlphaFold samples partially open states (Figure 2C). For plasmepsin II, the ensemble of AF structures includes structures with a tryptophan side chain in its holo orientation, even though 32 μs of MD simulations launched form an apo crystal structure do not sample tryptophan flipping. We find that launching simulations from this ensemble accelerates sampling of the open state (Figure 3). Furthermore, because we observe both pocket opening and closing events, we can use a Markov state model to generate a free energy landscape of pocket conformations that is in reasonable agreement with a similar landscape generated from metadynamics. Thus, we propose an efficient strategy to discover cryptic pockets that we hope becomes indispensable to future structure-based drug design efforts.
Acknowledgments
This work was funded by NSF MCB 2218156, NIH NIA RF1AG067194, and NIH NIGMS R01GM124007. G.R.B. holds a Packard Fellowship from the David and Lucile Packard Foundation. A.M. was supported by the National Institutes of Health F30 Fellowship (1F30HL162431-01A1).
Data Availability Statement
All input files and analysis scripts corresponding to this study can be accessed here: https://github.com/sbhakat/AF-cryptic-pocket. Additionally, we have deposited analysis notebooks, Markov state models, and AlphaFold ensembles in a OSF repository that can be accessed here: https://osf.io/cb8m7/.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.2c01189.
Comparisons of AlphaFold ensembles to apo and holo structures for all the examples considered in this work, a scatter plot comparing apo–holo experimental RMSDs with the RMSDs of AF structures and apo/holo experimental structures, detailed comparisons of the 32 plasmepsin II structures generated by AF, results from well-tempered metadynamics simulations of ligand dissociation from the cryptic pocket, VAMP-2 score evaluations used to select an optimal number of microstates in the plasmepsin II MSM, implied time scales plots, and correlation plots between input features and time–structure independent components (i.e., tICs). (PDF)
The authors declare the following competing financial interest(s): G.R.B. is a co-founder and equity holder in Decrypt Biomedicine. The remaining authors declare no competing interests.
Supplementary Material
References
- Meller A.; Ward M.; Borowsky J.; Lotthammer J. M.; Kshirsagar M.; Oviedo F.; Ferres J. L.; Bowman G. R. Predicting the Locations of Cryptic Pockets from Single Protein Structures Using the PocketMiner Graph Neural Network. Nat. Comm. 2023, 14, 1177. 10.1038/s41467-023-36699-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuzmanic A.; Bowman G. R.; Juarez-Jimenez J.; Michel J.; Gervasio F. L. Investigating Cryptic Binding Sites by Molecular Dynamics Simulations. Acc. Chem. Res. 2020, 53 (3), 654–661. 10.1021/acs.accounts.9b00613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hart K. M.; Moeder K. E.; Ho C. M. W.; Zimmerman M. I.; Frederick T. E.; Bowman G. R. Designing Small Molecules to Target Cryptic Pockets Yields Both Positive and Negative Allosteric Modulators. PLoS One 2017, 12 (6), e0178678 10.1371/journal.pone.0178678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Longo L. M; Jabłonska J.; Vyas P.; Kanade M.; Kolodny R.; Ben-Tal N.; Tawfik D. S On the Emergence of P-Loop Ntpase and Rossmann Enzymes from a Beta-Alpha-Beta Ancestral Fragment. Elife 2020, 9, 1–16. 10.7554/eLife.64415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horn J. R.; Shoichet B. K. Allosteric Inhibition Through Core Disruption. J. Mol. Biol. 2004, 336 (5), 1283–1291. 10.1016/j.jmb.2003.12.068. [DOI] [PubMed] [Google Scholar]
- Knoverek C. R.; Mallimadugula U. L.; Singh S.; Rennella E.; Frederick T. E.; Yuwen T.; Raavicharla S.; Kay L. E.; Bowman G. R. Opening of a Cryptic Pocket in β-Lactamase Increases Penicillinase Activity. Proc. Natl. Acad. Sci. U. S. A. 2021, 118 (47), e2106473118 10.1073/pnas.2106473118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weininger U.; Modig K.; Akke M. Ring Flips Revisited: 13C Relaxation Dispersion Measurements of Aromatic Side Chain Dynamics and Activation Barriers in Basic Pancreatic Trypsin Inhibitor. Biochemistry 2014, 53 (28), 4519–4525. 10.1021/bi500462k. [DOI] [PubMed] [Google Scholar]
- Amaral M.; Kokh D. B.; Bomke J.; Wegener A.; Buchstaller H. P.; Eggenweiler H. M.; Matias P.; Sirrenberg C.; Wade R. C.; Frech M. Protein Conformational Flexibility Modulates Kinetics and Thermodynamics of Drug Binding. Nature Communications 2017 8:1 2017, 8 (1), 1–14. 10.1038/s41467-017-02258-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jumper J.; Evans R.; Pritzel A.; Green T.; Figurnov M.; Ronneberger O.; Tunyasuvunakool K.; Bates R.; Žídek A.; Potapenko A.; Bridgland A.; Meyer C.; Kohl S. A. A.; Ballard A. J.; Cowie A.; Romera-Paredes B.; Nikolov S.; Jain R.; Adler J.; Back T.; Petersen S.; Reiman D.; Clancy E.; Zielinski M.; Steinegger M.; Pacholska M.; Berghammer T.; Bodenstein S.; Silver D.; Vinyals O.; Senior A. W.; Kavukcuoglu K.; Kohli P.; Hassabis D. Highly Accurate Protein Structure Prediction with AlphaFold. Nature 2021, 596 (7873), 583–589. 10.1038/s41586-021-03819-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- del Alamo D.; Sala D.; Mchaourab H. S.; Meiler J. Sampling Alternative Conformational States of Transporters and Receptors with AlphaFold2. Elife 2022, 11, e75751 10.7554/eLife.75751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein R. A.; Mchaourab H. S. SPEACH_AF: Sampling Protein Ensembles and Conformational Heterogeneity with Alphafold2. PLoS Comput. Biol. 2022, 18 (8), e1010483 10.1371/journal.pcbi.1010483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhakat S. Pepsin-like Aspartic Proteases (PAPs) as Model Systems for Combining Biomolecular Simulation with Biophysical Experiments. RSC Adv. 2021, 11 (18), 11026–11047. 10.1039/D0RA10359D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhakat S.; Söderhjelm P. Flap Dynamics in Pepsin-Like Aspartic Proteases: A Computational Perspective Using Plasmepsin-II and BACE-1 as Model Systems. J. Chem. Inf Model 2022, 62 (4), 914–926. 10.1021/acs.jcim.1c00840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahanti M.; Bhakat S.; Nilsson U. J.; Söderhjelm P. Flap Dynamics in Aspartic Proteases: A Computational Perspective. Chem. Biol. Drug Des 2016, 88 (2), 159–177. 10.1111/cbdd.12745. [DOI] [PubMed] [Google Scholar]
- Nasamu A. S.; Polino A. J.; Istvan E. S.; Goldberg D. E. Malaria Parasite Plasmepsins: More than Just Plain Old Degradative Pepsins. J. Biol. Chem. 2020, 295 (25), 8425–8441. 10.1074/jbc.REV120.009309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirdita M.; Schütze K.; Moriwaki Y.; Heo L.; Ovchinnikov S.; Steinegger M. ColabFold: Making Protein Folding Accessible to All. Nat. Methods 2022, 19 (6), 679–682. 10.1038/s41592-022-01488-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salomon-Ferrer R.; Case D. A.; Walker R. C. An Overview of the Amber Biomolecular Simulation Package. WIREs Computational Molecular Science 2013, 3 (2), 198–210. 10.1002/wcms.1121. [DOI] [Google Scholar]
- Maier J. A.; Martinez C.; Kasavajhala K.; Wickstrom L.; Hauser K. E.; Simmerling C. Ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from Ff99SB. J. Chem. Theory Comput 2015, 11 (8), 3696–3713. 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79 (2), 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- Sousa da Silva A. W.; Vranken W. F. ACPYPE - AnteChamber PYthon Parser InterfacE. BMC Res. Notes 2012, 5 (1), 367. 10.1186/1756-0500-5-367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parrinello M.; Rahman A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52 (12), 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
- Darden T.; York D.; Pedersen L. Particle Mesh Ewald: An N·log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98 (12), 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- Hess B.; Bekker H.; Berendsen H. J. C.; Fraaije J. G. E. M. LINCS: A Linear Constraint Solver for Molecular Simulations. J. Comput. Chem. 1997, 18 (12), 1463–1472. . [DOI] [Google Scholar]
- Asojo O. A.; Gulnik S. v; Afonina E.; Yu B.; Ellman J. A.; Haque T. S.; Silva A. M. Novel Uncomplexed and Complexed Structures of Plasmepsin II, an Aspartic Protease from Plasmodium Falciparum. J. Mol. Biol. 2003, 327 (1), 173–181. 10.1016/S0022-2836(03)00036-6. [DOI] [PubMed] [Google Scholar]
- Husic B. E.; Pande V. S. Markov State Models: From an Art to a Science. J. Am. Chem. Soc. 2018, 140 (7), 2386–2396. 10.1021/jacs.7b12191. [DOI] [PubMed] [Google Scholar]
- Pande V. S.; Beauchamp K.; Bowman G. R. Everything You Wanted to Know about Markov State Models but Were Afraid to Ask. Methods 2010, 52 (1), 99–105. 10.1016/j.ymeth.2010.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowman G. R.; Ensign D. L.; Pande V. S. Enhanced Modeling via Network Theory: Adaptive Sampling of Markov State Models. J. Chem. Theory Comput 2010, 6 (3), 787–794. 10.1021/ct900620b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boss C.; Corminboeuf O.; Grisostomi C.; Meyer S.; Jones A. F.; Prade L.; Binkert C.; Fischli W.; Weller T.; Bur D. Achiral, Cheap, and Potent Inhibitors of Plasmepsins I, II, and IV. ChemMedChem. 2006, 1 (12), 1341–1345. 10.1002/cmdc.200600223. [DOI] [PubMed] [Google Scholar]
- Pérez-Hernández G.; Paul F.; Giorgino T.; de Fabritiis G.; Noé F. Identification of Slow Molecular Order Parameters for Markov Model Construction. J. Chem. Phys. 2013, 139 (1), 015102. 10.1063/1.4811489. [DOI] [PubMed] [Google Scholar]
- Scherer M. K.; Trendelkamp-Schroer B.; Paul F.; Pérez-Hernández G.; Hoffmann M.; Plattner N.; Wehmeyer C.; Prinz J.-H.; Noé F. PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models. J. Chem. Theory Comput 2015, 11 (11), 5525–5542. 10.1021/acs.jctc.5b00743. [DOI] [PubMed] [Google Scholar]
- Barducci A.; Bussi G.; Parrinello M. Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method. Phys. Rev. Lett. 2008, 100 (2), 20603. 10.1103/PhysRevLett.100.020603. [DOI] [PubMed] [Google Scholar]
- Valsson O.; Tiwary P.; Parrinello M. Enhancing Important Fluctuations: Rare Events and Metadynamics from a Conceptual Viewpoint. Annu. Rev. Phys. Chem. 2016, 67 (1), 159–184. 10.1146/annurev-physchem-040215-112229. [DOI] [PubMed] [Google Scholar]
- Tiwary P.; Parrinello M. From Metadynamics to Dynamics. Phys. Rev. Lett. 2013, 111 (23), 230602. 10.1103/PhysRevLett.111.230602. [DOI] [PubMed] [Google Scholar]
- Prade L.; Jones A. F.; Boss C.; Richard-Bildstein S.; Meyer S.; Binkert C.; Bur D. X-Ray Structure of Plasmepsin II Complexed with a Potent Achiral Inhibitor *. J. Biol. Chem. 2005, 280 (25), 23837–23843. 10.1074/jbc.M501519200. [DOI] [PubMed] [Google Scholar]
- Recacha R.; Leitans J.; Akopjana I.; Aprupe L.; Trapencieris P.; Jaudzems K.; Jirgensons A.; Tars K. Structures of Plasmepsin II from Plasmodium Falciparum in Complex with Two Hydroxyethylamine-Based Inhibitors. Acta Crystallographica Section F 2015, 71 (12), 1531–1539. 10.1107/S2053230X15022049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25 (9), 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Saldaño T.; Escobedo N.; Marchetti J.; Zea D. J.; mac Donagh J.; Velez Rueda A. J.; Gonik E.; García Melani A.; Novomisky Nechcoff J.; Salas M. N.; Peters T.; Demitroff N.; Fernandez Alberti S.; Palopoli N.; Fornasari M. S.; Parisi G. Impact of Protein Conformational Diversity on AlphaFold Predictions. Bioinformatics 2022, 38 (10), 2742–2748. 10.1093/bioinformatics/btac202. [DOI] [PubMed] [Google Scholar]
- Horn J. R.; Shoichet B. K. Allosteric Inhibition Through Core Disruption. J. Mol. Biol. 2004, 336 (5), 1283–1291. 10.1016/j.jmb.2003.12.068. [DOI] [PubMed] [Google Scholar]
- Meller A.; Lotthammer J. M.; Smith L. G.; Novak B.; Lee L. A.; Kuhn C. C.; Greenberg L.; Leinwand L. A.; Greenberg M. J.; Bowman G. R. Drug Specificity and Affinity Are Encoded in the Probability of Cryptic Pocket Opening in Myosin Motor Domains. Elife 2023, 12, e83602. 10.7554/eLife.83602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cruz M. A.; Frederick T. E.; Mallimadugula U. L.; Singh S.; Vithani N.; Zimmerman M. I.; Porter J. R.; Moeder K. E.; Amarasinghe G. K.; Bowman G. R. A Cryptic Pocket in Ebola VP35 Allosterically Controls RNA Binding. Nature Communications 2022 13:1 2022, 13 (1), 1–10. 10.1038/s41467-022-29927-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmerman M. I.; Porter J. R.; Ward M. D.; Singh S.; Vithani N.; Meller A.; Mallimadugula U. L.; Kuhn C. E.; Borowsky J. H.; Wiewiora R. P.; et al. SARS-CoV-2 simulations go exascale to predict dramatic spike opening and cryptic pockets across the proteome. Nat. Chem. 2021, 13, 651–659. 10.1038/s41557-021-00707-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sztain T.; Amaro R.; McCammon J. A. Elucidation of Cryptic and Allosteric Pockets within the SARS-CoV-2 Main Protease. J. Chem. Inf Model 2021, 61, 3495. 10.1021/acs.jcim.1c00140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hollingsworth S. A.; Kelly B.; Valant C.; Michaelis J. A.; Mastromihalis O.; Thompson G.; Venkatakrishnan A. J.; Hertig S.; Scammells P. J.; Sexton P. M.; Felder C. C.; Christopoulos A.; Dror R. O. Cryptic Pocket Formation Underlies Allosteric Modulator Selectivity at Muscarinic GPCRs. Nat. Commun. 2019, 10 (1), 1–9. 10.1038/s41467-019-11062-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konovalov K. A.; Unarta I. C.; Cao S.; Goonetilleke E. C.; Huang X. Markov State Models to Study the Functional Dynamics of Proteins in the Wake of Machine Learning. JACS Au 2021, 1 (9), 1330–1341. 10.1021/jacsau.1c00254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comitani F.; Gervasio F. L. Exploring Cryptic Pockets Formation in Targets of Pharmaceutical Interest with SWISH. J. Chem. Theory Comput 2018, 14 (6), 3321–3331. 10.1021/acs.jctc.8b00263. [DOI] [PubMed] [Google Scholar]
- Zimmerman M. I.; Bowman G. R. FAST Conformational Searches by Balancing Exploration/Exploitation Trade-Offs. J. Chem. Theory Comput 2015, 11 (12), 5747–5757. 10.1021/acs.jctc.5b00737. [DOI] [PubMed] [Google Scholar]
- Hendlich M.; Rippmann F.; Barnickel G. LIGSITE: Automatic and Efficient Detection of Potential Small Molecule-Binding Sites in Proteins. J. Mol. Graph Model 1997, 15 (6), 359–363. 10.1016/S1093-3263(98)00002-3. [DOI] [PubMed] [Google Scholar]
- le Guilloux V.; Schmidtke P.; Tuffery P. Fpocket: An Open Source Platform for Ligand Pocket Detection. BMC Bioinformatics 2009, 10 (1), 168. 10.1186/1471-2105-10-168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krivák R.; Hoksza D. P2Rank: Machine Learning Based Tool for Rapid and Accurate Prediction of Ligand Binding Sites from Protein Structure. J. Cheminform 2018, 10 (1), 39. 10.1186/s13321-018-0285-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Jong D. H.; Singh G.; Bennett W. F. D.; Arnarez C.; Wassenaar T. A.; Schäfer L. v.; Periole X.; Tieleman D. P.; Marrink S. J. Improved Parameters for the Martini Coarse-Grained Protein Force Field. J. Chem. Theory Comput 2013, 9 (1), 687–697. 10.1021/ct300646g. [DOI] [PubMed] [Google Scholar]
- Kmiecik S.; Gront D.; Kolinski M.; Wieteska L.; Dawid A. E.; Kolinski A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116 (14), 7898–7936. 10.1021/acs.chemrev.6b00163. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All input files and analysis scripts corresponding to this study can be accessed here: https://github.com/sbhakat/AF-cryptic-pocket. Additionally, we have deposited analysis notebooks, Markov state models, and AlphaFold ensembles in a OSF repository that can be accessed here: https://osf.io/cb8m7/.