A Full Quantum Mechanical Approach Assessing the Chemical and Electromagnetic Effect in TERS

Abstract

Tip-enhanced Raman spectroscopy (TERS) is a valuable method for surface analysis with nanometer to angstrom-scale resolution; however, the accurate simulation of particular TERS signals remains a computational challenge. We approach this challenge by combining the two main contributors to plasmon-enhanced Raman spectroscopy and to the high resolution in TERS, in particular, the electromagnetic and the chemical effect, into one quantum mechanical simulation. The electromagnetic effect describes the sample’s interaction with the strong, highly localized, and inhomogeneous electric fields associated with the plasmonic tip and is typically the thematic focus for most mechanistic studies. On the other hand, the chemical effect covers the different responses to the extremely close-range and highly position-sensitive chemical interaction between the apex tip atom(s) and the sample, and, as we could show in previous works, plays an often underestimated role. Starting from a (time-dependent) density functional theory description of the chemical model system, comprised of a tin(II) phthalocyanine sample molecule and a single silver atom as the tip, we introduce the electromagnetic effect through a series of static point charges that recreate the electric field in the vicinity of the plasmonic Ag nanoparticle. By scanning the tip over the molecule along a 3D grid, we can investigate the system’s Raman response on each position for nonresonant and resonant illumination. Simulating both effects on their own already hints at the achievable signal enhancement and resolution, but the combination of both creates even stronger evidence that TERS is capable of resolving submolecular features.

Since its first experimental demonstration in the year 2000, tip-enhanced Raman spectroscopy¹⁻³ has become an immensely useful tool for the study of surface-bound molecules. Under certain conditions, even submolecular features can be resolved,⁴⁻¹¹ which raised the question as to what the fundamental limits of resolutions are, as this is well beyond the limit of conventional light microscopy. The exact nature of the underlying mechanisms that enable such a high resolution are still under investigation, but are broadly categorized into two contributions.¹² The first of these is the electromagnetic effect,¹³⁻¹⁹ describing how the spatially inhomogeneous electromagnetic fields in the vicinity of the plasmonic tip interact with the sample and enhance the Raman response, especially as a picocavity between the plasmonic tip and a possible metal substrate may form.²⁰⁻²⁶ The other one is the chemical effect,^18,27−32 describing how the molecule’s electronic structure changes while in proximity to the plasmonic particle. In TERS, this is especially relevant since the scanning tip can be moved very precisely with subnanometer precision to different areas of the sample molecule, exhibiting site-specific responses, thereby changing the chemical environment and, thus, the electronic structure of the newly formed molecular-plasmonic hybrid system.

Roughly based on this division into electromagnetic and chemical effects, different approaches to simulating a typical TERS experiment can be distinguished. The group of Schatz,³³⁻³⁷ for example, put emphasis on accurate simulations of plasmonic nanoparticles, allowing the identification of sites with extremely high field strengths and gradients. Aizpurua et al.^21,38−41 generally focused on a theoretical treatment, employing model molecules, while still concentrating on a high-level description of the plasmonic particle. Finally, the discrete interaction model/quantum mechanics (DIM/QM) method⁴²⁻⁴⁶ by Jensen et al. combined an atomistic model for the nanoparticle with a quantum chemical simulation of the sample molecule. While some tip–sample interactions are covered, this model can still not capture the full chemical effect, as it does not contain any explicit metal atoms (from the nanoparticle) in its QM calculations. In particular, charge-transfer processes between the tip and sample are not well described in favor of a more accurate representation of the nanoparticle, as elaborated below. Similar to the joint studies of Rosta, Baumberg et al.,^47,48 that have a few explicit metal atoms bound to a sample molecule, with the field of an artificial dipole in close proximity, it is our goal to investigate the close-range regime of <1 nm tip–sample distance. Here, we assume that the electromagnetic effect is already well-described with classical electrodynamics⁴⁹ and build a model system from the chemical point of view. In contrast to many approaches, this accounts for charge-transfer states of the combined plasmonic-molecular system, which become important when the tip reaches such close distances, as often occurs in the so-called tip–sample interaction region, as well as STM TERS studies.

Our quantum mechanical approach starts from a high-level simulation of the sample molecule and incorporates the plasmonic tip into those simulations as accurately as possible. To properly account for the chemical effect, a small part of the nanoparticle is fully incorporated into the quantum chemical simulations, in the form of the apex atom. Extending our previously established⁵⁰⁻⁵³ model, we here include additionally the electric field in vicinity to the plasmonic nanoparticle mimicked by point charges, which are parametrized such that the electrostatic field caused by the point charges agrees almost quantitatively with a separate field simulation based on the finite element method (FEM), only considering the electromagnetic contribution. This tip model (apex atom and field-creating point charges) is then scanned over the immobilized sample molecule, tin(II) phthalocyanine (SnPc), and allows the study of short-range chemical interaction between the tip and molecule, as well as the influence of the spatially inhomogeneous near-field on the whole system. Additionally, since both parts of the tip model are separable, we can evaluate and quantify the system’s behavior if only one of the two effects is present. However, this approach currently only allows us to use static point charges and therefore static electric fields. We remedy this by running each simulation twice, with an opposing sign for the electric field. The results can then be understood as temporal “snapshots” at the extreme points of a full optical cycle, while the net results can be expressed by means of averaging over the two snapshots of opposite field direction.

The results of this purely quantum mechanical approach, incorporating both the chemical contributions caused by the close proximity of metal atoms to the sample system and giving rise, e.g., to charge-transfer states, and the additional contribution imprinted by the spatially inhomogeneous electromagnetic near-field in form of static point charges are presented in the following contribution. In the first part, the wavelength of the incident radiation is assumed to be far from electronic resonances of the sample molecule. For this case, the chemical effect (no external point charges) and the electromagnetic effect (no explicit tip atom) are first investigated separately and then jointly. The second part focuses on resonant conditions. While the same quantum chemical system (SnPc-Ag) has been investigated before⁵¹ (considering solely the chemical contribution), the addition of the external electric fields is an important extension of the model and provides further insight into the mechanism governing TERS.

Results

In this section, we present the simulated TERS response of the full SnPc-Ag ± E system and compare it to the responses of both subsystems (SnPc-Ag and SnPc ± E) as well as to the free SnPc molecule. This allows us to separate the chemical (subsystem SnPc-Ag; see also ref (51)) from the electromagnetic effect (SnPc ± E), as modeled by the applied electric fields, and evaluate the combined effect. The results for both positive and negative field directions are averaged to yield the net result over a full optical cycle. First, the nonresonant response is evaluated with incident radiation at 1064 nm, far away from any electronic excitations. In the second part, the resonant response to the incident light is investigated, with its wavelength chosen to be in resonance with the calculated electronic excitations.

Nonresonant Tip-Enhanced Raman Scattering

We separately account for the field contribution (Figure 1a,e) and the chemical contribution (Figure 1d), in comparison to the isolated molecule (Figure 1c). In addition, we evaluate the combined effects, when the EM field and chemical modification are considered (Figure 1b,f). Finally, as a net result from a full optical cycle through a maximum and minimum of electric field strength, we present the average maps of both field directions in Figure 1g,h.

Figure 1.

TERS intensity maps (in arbitrary units) for the nonresonant case. Left column (a), (c), (e), (g): EM field contribution only. Right column (b), (d), (f), (h): contribution by adding an explicit Ag atom. The second row is for “zero” field, thus serving as a reference while the first and third rows present the corresponding results for + and – fields, respectively. The last row, (g) and (h), shows the average of rows 1 and 3. (i) Mulliken charges, normalized to the “middle” position with the respective field, relative to the respective field-free case.

The contribution of a spatially inhomogeneous near-field (point charges only) barely affects the molecule’s TERS response (see Figure 1a,e). The only observable effect is a slightly increased signal intensity for the negative field direction while the positive direction slightly decreases the intensity. In both cases, the variation in intensity over the whole map is extremely small with the central area of the molecule being brighter for the positive field direction and darker for the negative direction with respect to the map’s edges. No submolecular features are visible; the effects from both field directions cancel each other out in the average map. The variations shown in the map are 3 orders of magnitude smaller (10^–11 vs 10^–8 arbitrary units) than the underlying signal, as the color bar shows. The differences in the molecule without any kind of tip model (neither field nor Ag atom; Figure 1c) are miniscule. Therefore, neither an increase in signal intensity nor a resolution of molecular features is explainable just through introduction of strongly inhomogeneous fields alone.

For the other subsystem (Figure 1d), with only the tip atom and no EM field, the response is very different. The overall intensity increases by about 1 order of magnitude, showing pronounced bright, submolecular features. Those features correspond to three distinct regions over the molecule: the center directly around the Sn atom, the middle “ring” on top of the alternating C–N atoms, and the edge above the C–H bonds.

Combining both subsystems to form the full system with the Ag atom at the tip apex and the electric field (Figure 1b,f), the signal intensity generally rises, and some of the distinct submolecular structures from Figure 1d are visible. In the case of the positive field direction (Figure 1b), this increase in intensity is 1 order of magnitude compared to the chemical subsystem and 2 orders of magnitude with regard to the electrostatic subsystem. All three features from the field-free chemical subsystem are still present in the map, but the edge and middle areas are less intense than the bright center structure. This corresponds well with the field-only case (Figure 1a), where the intensity in the center of the map is slightly higher. For the negative field direction, only the edge structure remains bright, while middle and center vanish into the background. The maximum intensity of the combined system increases barely by an additional factor of 2. Similar to the positive case, this fits the result from the respective Ag-free subsystem, where the center of the map exhibits a slightly lower intensity. In both cases, the resulting maps for the whole system reveal that the chemical effect is the main contributor to resolution and boosts the intensity while the electromagnetic contribution further enhances (or suppresses, depending on field direction) certain features. The positive field direction leads to a higher overall intensity (compare color scale of Figure 1b vs Figure 1f) and therefore dominates the average map (Figure 1h). This results in a net picture that resembles the one without external fields with slightly higher intensity in the molecule’s center. The already submolecular resolution and signal amplification that was achieved just through the introduction of the Ag tip mimic is further enhanced by inclusion of the static external electric field.

The different behavior of the three features under opposite field directions can be explained by looking at the field-induced partial charge on the Ag atom. For better visualization, the charges shown are relative to the charge at the middle position in the respective subsystem, as the charge at this position is the least influenced by changing electric fields. Additionally, the charges are normalized to the respective position’s charge with no external electric field (see Figure 1i). It is evident that the center structure is far more sensitive to the positive field than the negative field, reflecting the bright and dark center in the respective map. Especially in the case of a negative field direction, the charge and intensity are barely influenced. On the edge position, the behavior is reversed: the charge is strongly affected by the negative field, resulting in a high intensity there. The positive field does not have an equally strong effect on the tip, and the map shows a less pronounced intensity at this position.

After having understood the underlying chemical and electromagnetic contributions to the TERS maps, we now consider selected TERS spectra at the positions discussed before. The TERS spectra (Figure 2) for the three selected positions and possible external electric fields show that in case of the middle position (Figure 2b,e,h), the field’s influence is relatively weak, as the intensity pattern does not change notably. The peak with the highest intensity at about 1040 cm^–1 can be associated with the same C–H bending mode in all cases, and its intensity stays roughly the same, regardless of the external field. Only small variations in the spectra are visible, such as the second-highest peak at 850 cm^–1 slightly losing intensity in SnPc+E and gaining it in SnPc–E.

Figure 2.

Nonresonant TERS spectra (in arbitrary units) for different positions (columns) and field strengths (rows).

For the center and edge positions, the changes are much more pronounced. In the center, without field, three peaks are prominent in the TERS spectra (Figure 2d)). For the SnPc-Ag+E case (Figure 2a), those three peaks stay dominant, though their relative intensities change. Furthermore, the overall intensity of the spectrum increases by more than 1 order of magnitude. In contrast, for the reversed field direction, SnPc-Ag–E (Figure 2g), two of the three prominent peaks are strongly reduced in intensity.

At the edge position (Figure 2c,f,i), similar phenomena are observed: For the positive field direction, the overall intensity grows, especially for peaks that were already dominating the spectrum, like the C–N stretching mode at 1540 cm^–1. The negative field direction likewise shows a slight increase in the overall intensity in this case, mostly preserving the intensity pattern across the spectrum compared to the field-free case.

Resonant Tip-Enhanced Raman Scattering

We next turn toward the resonant case, when the wavelength of the incident light is in resonance with a dipole-allowed electronic transition. The resulting Raman signal is dominated by the resonant term, and the nonresonant term becomes negligible. The signal intensity is proportional to the square of the derivative of the transition polarizability (see eq 5). Therefore, according to eq 6, the two major contributors to a strong resonant Raman response are the transition dipole moment μ_ge (in the z direction) of the state(s) in resonance and their respective energetic position (E_ge), which are shown in Figure 3 and discussed in what follows. The current approach of approximating the oscillating electric field in the vicinity of the nanoparticle with a set of static point charges starts to break down here. Dynamic simulations of excited-state behavior under these circumstances are much more involved, however, and are not feasible for the SnPc-Ag system without other harsh approximations. Nevertheless, the results presented in the following offer insight into how the system reacts under resonant conditions.

Figure 3.

Excitation energies E_ge (in eV) and squared transition dipole moments in z direction 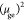(in e Å). The shown π–π* transitions in the upper panels always occur in near-degenerate pairs; for simplicity the displayed energies are averaged between the two while the transition dipole moments are combined. MLCT (LMCT) states are not shown for −E (+E, respectively) as these electronic transitions are outside the considered energy window (<3.2 eV) for resonant irradiation.

Concerning the character of the electronic states of the combined molecule–tip system, we can distinguish different types: local excitations within the SnPc molecule (intramolecular excitation), charge-transfer excitations (in either direction) between the silver tip and the molecule, and local metal-centered excitations within the silver tip (corresponding to plasmons for larger clusters of metallic atoms). The last type of excitation will not be discussed here, as the single-atom model employed for the tip in this work does not provide an accurate description of the plasmonic contribution of a whole Ag nanoparticle.

In line with previous results,^51,52 local excitations on the molecule (mostly of π–π* character here) are relatively insensitive to tip positioning and applied electric fields, in terms of both excitation energy and transition dipole moment (see Figure 3a–l). Typically, these states are also polarized in the molecular plane (xy), which makes them nearly invisible for detection in the z direction. The SnPc molecule is not completely planar; therefore, these π–π* transitions might contribute to signal strength (and therefore submolecular resolution) but are otherwise only of minor importance for signal intensity and resolution.

As explained above, charge-transfer states between the molecule and the tip occur (in the observed energy window) in both directions, i.e. as metal-to-ligand charge-transfer (MLCT) and ligand-to-metal charge-transfer (LMCT, Figure 3o,p,s,t). In contrast to the intramolecular π–π* excited states, these charge-transfer states are very sensitive toward an external electric field: this manifests itself by strong energetic up (down) shifts of up to 0.9 eV, depending on the field direction. The transition dipole moment for charge-transfer states is much greater in the z direction in comparison to the π–π* states, hence a stronger energetic shift is predicted in case of MLCT and LMCT states by virtue of the Stark effect while the direction of the shift is depending on the sign of the transition dipole moment. Moreover, in contrast to the π–π* transitions, the excitation energies are highly dependent on the tip position, regardless of the applied electric field. Thus, in the case of resonant excitation, the applied external field causes an additional, strong contribution to the resolution, due to the strong energetic variations imprinted by the various relative Ag–molecule positions. The field therefore influences the resolution via energetic shifts in certain regions, which, for a given excitation wavelength, may push certain regions of the molecule energetically out of resonance, thereby lowering their contribution to the Raman signal. However, the pattern in the transition dipole moment maps is independent of the applied electric field and even somewhat of the direction of the charge transfer while only the magnitude changes with field strength. Therefore, the electric fields only play a role in enhancing the signal strength and do not affect the resolution.

The behavior of excited states can be observed in the UV/vis spectra (Figure 4). The provided charge density differences show electron density shifts from red to blue upon excitation. In all four cases, electron density is moved from an occupied π orbital of the molecule, moved to an unoccupied π* orbital, or both, hence similar structures are visible around SnPc. For the UV/vis spectra of the middle position (Figure 4b,e,h), predominantly only the π–π* states are accessible in the visible region. As they are mostly xy-polarized, and the transition dipole moment vector has only a small component in the z direction, the molecule-centered π–π* states are relatively unaffected by the external fields (Figure 4b,h), in terms of both oscillator strength and excitation energy. At this position, charge-transfer states are mostly dark (f_z ≈ 0) and here not visible.

Figure 4.

z-polarized oscillator strengths, broadened to simulate UV/vis spectra for different positions (columns) and field strengths (rows). Note the different axis labels of the oscillator strength. The electronic character is labeled and indicated exemplarily for the central position in the absence of an electric field.

At the center and edge positions, the π–π* states are likewise unaffected; however, they are overshadowed by charge-transfer (CT) states, that dominate the resonant regime. Already without any external fields, the excitation energy and oscillator strength of these states are highly dependent on the tip’s position. With additional external fields, the CT states’ oscillator strengths (and squared transition dipole moments, see Figure 3) are increased. Additionally, the excitation energies are shifted according to field and charge-transfer direction (MLCT vs LMCT). The highest peaks in the field-free case (see Figure 4d,f) are states with electron transfer from the Ag tip to the molecule and are therefore stabilized in SnPc-Ag+E (negative charge above Ag), as the respective peaks are shifted to lower energies in Figure 4a,c. Similarly, in the case of SnPc-Ag-E, this charge-transfer state is shifted to higher excitation energy in Figure 4g and replaced by another state with opposite charge transfer character (i.e., from molecule to tip) in Figure 4i. Due to the enormous sensitivity of the resonance Raman signal on the tip position, the applied field (direction), and excitation energy, there is not much additional value to discuss the resulting Raman spectra, as underlying electronic states, with regard to their character, energetic position, and transition dipole moment, are strongly affected. In other words, when fixing the laser wavelength, depending on whether the oscillating electric field is temporarily positive or negative, another electronic state is addressed, and the resulting resonance Raman spectra carry the information on the particular state. Thus, we do not show the Raman spectra here.

Conclusion

In this work, we present a comprehensive analysis of tip-enhanced Raman spectroscopy accounting for the site-specific chemical effects as well as the contribution of the spatially inhomogeneous electric near-field of the tip, mimicked by point charges in a static approximation. This simple setup allows us not only to attribute both contributions individually but also to investigate their combined imprints onto the system of investigation. The system’s response is compared to the same setup without either the silver atom, only showing the effect of the electromagnetic near-field, or the SnPc-Ag system, addressing the site-specific chemical contribution, without any field contributions. This allows us to understand both effects independently and their interaction, in particular regarding signal intensity and resolution. We investigate both nonresonant and resonant Raman scattering.

In case of nonresonant conditions, we observed only a slight increase in signal intensity by introducing the electric fields only to the SnPc molecule, with relatively uniform changes over different tip positions. However, the explicit consideration of the silver atom at the tip’s apex (chemical contribution) introduces strong site-specific submolecular features and raises the overall signal intensity. The combined systems exhibit a convolution of the two individual contributions. We rationalize this through changing partial charges at the tip atom, reacting to the different chemical environments imprinted by the Ag atom’s different relative positions over different parts of the molecule.

The situation strongly changes for the resonant case: here, besides intramolecular excitations, charge-transfer states between the molecule and the Ag tip arise. These charge-transfer states are very sensitive to minute changes of the tip and the field, thus giving rise to strongly increased lateral resolution. As for the nonresonant case, the high, submolecular spatial resolution, accompanied by a strong increase in Raman intensity, is defined by these chemical contributions and explicitly accounting for the near-field increases the overall signal intensity.

Both nonresonant and resonant cases strongly suggest that the chemical interaction between the molecule and the tip atom defines the resolution while the enhanced, spatially inhomogeneous electromagnetic near-fields predominantly increases signal intensity.

Several additional factors could not be included in this model so far, including any chemical interaction with the substrate, as well as dynamic electric fields from the plasmon, and any sort of “backward” interaction from the molecule to the plasmon.

Methods

Electromagnetic Contribution (EM)—Finite Element Simulations

The RF module of Comsol Multiphysics 5.0⁵⁴ was used to solve Maxwell’s equations in a finite element (FEM) setup in order to obtain the field distribution in the vicinity of the silver tip. The underlying equation that governs the electric field is

1

with the permittivity ε_rc and the relative permeability μ_r set to 1 and the wavenumber of the free space k₀ depending on the speed of light c₀:

2

The following computational setup is based on the procedure introduced by Trautmann et al.²² The simulations were performed in a cubic system of size 700 × 700 × 700 nm³ with periodic boundary conditions (Floquet periodicity) in the x and y directions, and top and bottom walls (z direction) defined as periodic port boundaries. To model the field distribution near the tip, a spherical nanostructure (radius 100 Å) above a flat surface, acting as the substrate (glass, n_glass = 1.520), was assumed. In ref (22) it has been shown that single atomic-roughness, e.g., in the form of protrusions to account for the nanoparticle’s crystallinity (edges/corners), is one key ingredient to explain the results. Numerically, this was accounted for by adding a small Gaussian-shaped protrusion to the otherwise spherical nanoparticle and simulating the electromagnetic field of this thus-structured nanoparticle. We follow this procedure here: shortly, a substructure was modeled as solid of revolution from a Gaussian profile resembling a single atom that protrudes from the otherwise smooth surface, creating an atomic-scale substructure. For numerical reasons, for the atomic protrusion, a Gaussian profile was assumed, which was parametrized as

3

with χ = 2.11 Å determining the width of the Gaussian profile and ζ = 8.5 Å resembling the protrusion for a silver atom with an atomic radius of 1.65 Å. The gap between the substrate and the lowest point of the nanoparticle was set to z_g = 10 Å. Material settings for the silver nanoparticle were taken from ref (55).

The incident field, with an electric field strength of 5.142 × 10⁸ V m^–1 (10^–3 au),⁵⁶ entered the system from the bottom port with an angle of θ = 60°, where the incident power was obtained as

4

with ε₀ and n_air = 1 being the vacuum permittivity and air refractive index, respectively. The minimal tetrahedral mesh size was set to 0.9 Å in a 100 nm sphere around the nanoparticle and 5 nm otherwise to reduce the computational cost.

The electric field distribution obtained by the FEM calculations was then mimicked by ten distinct point charges—five above and five below the glass substrate at z = ±2, ±3, ±4, ±5, and ±6 nm, respectively (see Figure 5a, white dots). Two sets of these ten point charges were obtained to model the oscillating electric field at opposing field orientations: the positive (crest) and negative (trough) extreme values. Each set of point charges was introduced in the subsequent quantum chemical calculations, mimicking the field distribution in the vicinity of SnPc-Ag, i.e., at four layers of calibration points covering the investigated molecule and located 2 (90 grid points), 3 (129 grid points), 4 (140 grid points), and 5 Å (151 grid points) above the glass substrate (see Figure 5a, green dots). The electric field at these calibration points, modeled by these point charges, differs from the electric field obtained by the preliminary finite element simulations merely by 1.5% (mean absolute deviation) with a maximum deviation of less than 4% being obtained at the edge of the calibration layers (at x, y ≈ 15 Å). The magnitude of the charges is scaled so that the electric field strength at the molecule’s position is about 3 GV m^–1, to promote strong signals (and signal amplifications) but not lead to a change in the electronic ground state of the system (i.e., no charge separation leading to a SnPc⁺-Ag^– system or vice versa). Lately, Sakko et al.⁵⁶ utilized a similar field strength (∼0.5 GV m^–1) together with a modest field enhancement by a plasmonic nanoparticle. Obtaining experimental evidence of such high field strengths is far from trivial, but Chen et al.⁵⁷ recently determined the field in the xy plane to be around 2 GV m^–1 in their setup.

Figure 5.

Overview over the simulation setup. (a) Electromagnetic contribution with field-creating point charges (white) and calibration points (green) (color bar: field enhancement in arbitrary units). (b, c): Coordinate system for the quantum chemical simulations. For symmetry reasons, only the relative tip positions marked by blue dots are calculated. Exemplarily discussed positions center (C), middle (M), and edge (E) are marked.

Quantum Chemical Simulations

The simulation of the full TERS experiment follows our previously introduced⁵⁰⁻⁵² (TD)DFT-based protocol, with the inclusion of the aforementioned point charges to complement the electromagnetic contribution to the tip model. All quantum chemical calculations were carried out with Gaussian16⁵⁸ on the DFT or TDDFT level of theory, respectively, using the range-separated CAM-B3LYP⁵⁹ functional and 6-311+G**^60,61 triple-ζ basis set. For the heavy atoms (Sn, Ag), the electronic core potentials MWB46 and MWB28 and their respective basis sets⁶² were used. The D3 dispersion correction with Becke–Johnson damping was employed for all calculations.⁶³

The SnPc molecule was optimized with DFT in a vacuum and placed on a coordinate system such that the Sn atom was at the origin and the rest of the molecule above the xy plane. A single silver atom, along with the aforementioned field-creating point charges, was then moved to different x, y positions over the molecule, with the z coordinate of the Ag atom chosen so that the van der Waals spheres of Ag and SnPc touch, as indicated in Figure 5b,c. Ag and SnPc are not relaxed further in these geometries. Previously, we investigated the impact of the tip model with respect to energetic and TERS signals by virtue of a simple one silver atom tip mimic vs a tetrahedral Ag₂₀ cluster.⁵⁰ Both models provide qualitatively very similar energy and TERS maps and point to a subnanometer resolution of TERS while the absolute signal intensity and amplification of specific vibrational modes were found to depend on the tip mimic.

The single-atom tip model allows us to keep the computational cost to a minimum, as it makes use of the sample molecule’s initial symmetry. With this in mind, we only need to scan about one-eighth of the molecule and can still create a full TERS map (see Figure 5). Additionally, we do not need to make further assumptions regarding the exact shape of the cluster of atoms at the tip apex. However, the neighboring atoms of our tip model would still modify the results,^50,52 and more accurate models should be chosen if possible.

To elucidate the interplay of the chemical and the electromagnetic effect in the full SnPc-Ag±E system (comprised of SnPc molecule, Ag tip, and electric field in both directions), two subsystems were investigated as well: one without the field-creating point charges, SnPc-Ag, where only the chemical interaction between the Ag atom and the sample molecule are observed, and one without the Ag atom, SnPc±E, that only shows the molecule’s response to the electric fields. The SnPc-Ag system, and with it the chemical effect, was discussed in depth previously.⁵¹

In line with previous studies, the detection of the Raman signal is assumed to be predominantly in the z direction. Therefore, the intensity of each mode depends on the zz component of the respective derivative of the (transition) polarizability tensor

5

For the nonresonant case, the polarizability derivatives are calculated directly by Gaussian. In the resonant case, transition polarizability derivatives are required and are calculated using the independent-mode displaced harmonic oscillator model (IMDHOM)⁶⁴

6

Here, Δ_e,l is the dimensionless displacement of harmonic oscillators of ground and excited electronic states, E_e,g is the vertical excitation energy from the ground state g to excited state e, Γ is a damping factor accounting for homogeneous broadening (chosen as 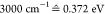), and E_L represents the energy of quanta of the irradiating laser. The function Φ_e, neglecting Franck–Condon factors, is given by

7

A previous version of this manuscript has been published on arXiv.org under the same title.⁶⁵

The authors declare no competing financial interest.