Federated generalized linear mixed models for collaborative genome-wide association studies

Summary

Federated association testing is a powerful approach to conduct large-scale association studies where sites share intermediate statistics through a central server. There are, however, several standing challenges. Confounding factors like population stratification should be carefully modeled across sites. In addition, it is crucial to consider disease etiology using flexible models to prevent biases. Privacy protections for participants pose another significant challenge. Here, we propose distributed Mixed Effects Genome-wide Association study (dMEGA), a method that enables federated generalized linear mixed model-based association testing across multiple sites without explicitly sharing genotype and phenotype data. dMEGA employs a reference projection to correct for population-stratification and utilizes efficient local-gradient updates among sites, incorporating both fixed and random effects. The accuracy and efficiency of dMEGA are demonstrated through simulated and real datasets. dMEGA is publicly available at https://github.com/Li-Wentao/dMEGA.

Graphical abstract

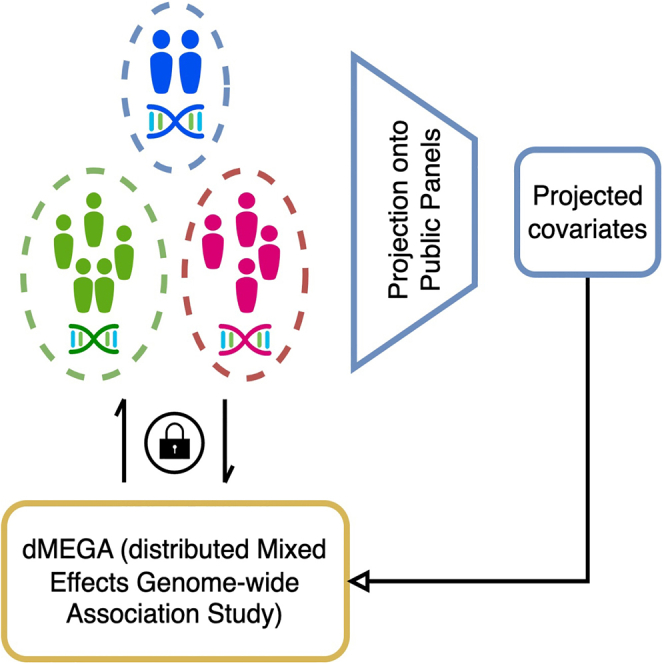
Highlights

• •We developed a federated learning method for genome-wide association studies
• •We use a reference projection method that can be effective for correcting confounders
• •We tackled the data heterogeneity problem with a federated mixed-effect model

Health sciences; Clinical genetics; Human genetics; Genomics

Introduction

Genome-wide association studies (GWASs) are standard methods for discovering genetic variants that explain the genetic component of phenotypic variance. As the sequencing costs are decreasing, there is great incentive to perform large-scale association studies to increase the power of the studies.^1,2 Currently, population-scale joint genotyping and phenotyping efforts such as AllofUs and UK Biobank generate very large resources that provide great opportunities for extensive analysis of genotype-phenotype relationships.^3,4,5 In addition, there are other efforts that aim at focusing on certain phenotypes such as TOPMed,⁶ ADSP,⁷ TCGA,⁸ and GTEx.⁹

There are a number of standing challenges around performing large scale GWAS in existing datasets. Association tests are confounded by numerous factors such as population stratification, which can be especially important in multi-ancestral studies and in admixed populations.¹⁰ Most of the multi-ancestral studies are performed as meta-analyses^11,12 and may make it more challenging to correct biases compared to a pooled individual-level data analysis among sites in a collaborative GWAS setting.^13,14 Furthermore, binary and continuous traits should be modeled using appropriate models to avoid biases in the significance of the genetic effect. It has been shown previously that binary traits are more appropriately analyzed using generalized linear models (GLM) compared to linear models because generalized models can naturally represent the categorical/binary nature of case/control study designs.^15,16 In addition, there can be complex relationships among samples (such as cryptic relatedness), which makes it necessary to account for random polygenic effects that may otherwise bias association signals. Furthermore, increasing sample sizes requires extensive collaboration among large institutions, but data sharing (among institutions) may be restricted under diverse regulations such as HIPAA¹⁷ and GDPR.¹⁸ Consequently, a rising concern for performing large-scale collaborative association studies is the consideration of privacy and related ethical concerns of unauthorized re-identification of the study participants and their relatives in publicly available genealogy services, stigmatization of individuals and groups as a results of phenotype and disease risk predictions, group-level sensitive information prediction (such as inbreeding in Havasupai Tribe), and marginalization of these historically isolated groups^19,20 (Supplementary Information).

Although there are increased incentives around sharing data and making discoveries, regulations are enacted on legislative level for stricter protection of personal genetic data from open sharing. This creates a major hurdle for international collaborations. The most basic data protection is performed by lengthy data transfer agreements that authorize users’ access to data repositories (e.g., dbGAP²¹ and European EGA²²). The agreements only establish accountability and do not meaningfully protect data, because data are still stored and analyzed in plaintext. On technical domain, differential privacy,²³ homomorphic encryption (HE),²⁴ and secure multiparty computation²⁵ enable provably privacy-aware data analysis. Differentially private methods^26,27 are based on noisy data release mechanisms and substantially degrade genetic data utility. HE^28,29,30,31-based approaches enable analysis of encrypted data without decrypting it. Although HE-based methods have made orders of magnitude improvement in terms of performance in the last decade, they still require large computational resources. Similarly, secure multiparty computation (SMC) methods³² rely on the separation of data among multiple entities such that it cannot be recovered by any of the non-colluding entities. SMC-based methods have high data transfer requirements and may not be practically feasible.

Federated association testing (rooted from Federated Learning approaches^33,34) among different sites present a viable solution for increasing sample sizes while underlying genotype and phenotype data are not explicitly shared. In federated association testing methods, the association testing is reformulated as an iterative algorithm. At each iteration, each collaborating site computes intermediary statistics using local genotype and phenotype data and the statistics from other sites. Next, the intermediary statistics are shared among the sites with a central server that is aggregated and re-shared to all sites. Federated testing is advantageous from a privacy perspective because the genotype and phenotype data never leave local sites. This way, all sites make use of the pooled individual-level data that would be otherwise isolated in distributed repositories across institutions.

Here, we present dMEGA (distributed Mixed Effects Genome-wide Association study), a federated generalized linear mixed model that enables federated genetic association testing among collaborating sites. First, each site utilizes a reference projection-based approach, wherein the genotype data at the site is projected on an existing public genotype panel (e.g., The 1000 Genomes Project) and population-based covariates are computed based on the projected coordinates. Usage of projection is advantageous because it decreases computational requirements by circumventing computation of principal component analysis (PCA) among the sites and minimally impacts accuracy. In addition, the computation of population-level covariates does not require data to be pooled and does not incur privacy risks. Next, dMEGA performs federated association testing using the fixed (such as population covariates) and random effects. In this step, the sites locally calculate intermediate statistics that are sent to a central server, which aggregates the statistics from all sites and shares them with all sites. After a number of iterations, the algorithm converges and final results are calculated. We demonstrate the accuracy and efficiency of dMEGA using simulated and real datasets.

Results

Overview of dMEGA

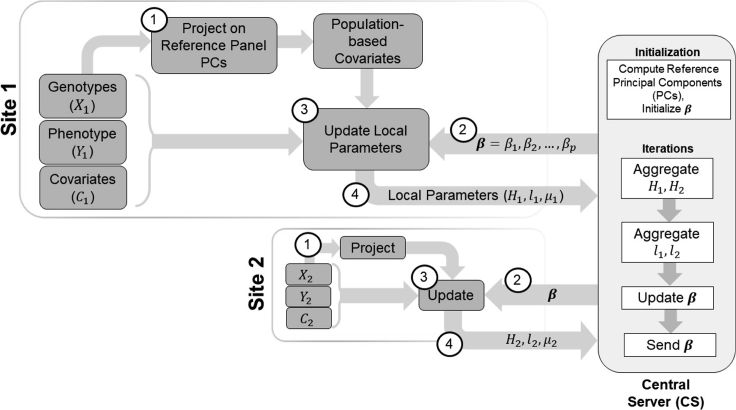
Figure 1 shows the steps of federated association testing workflow. First, the sites project their genotype data on the principal components (PCs) computed from a reference panel. The reference panel dataset represents a comprehensive population-based information pool. The projected coordinates are used as population-based covariates (fixed effect). Next, each site computes the local testing statistics (gradients, effect sizes, Hessian matrices) and send them to the Central Server (CS). At each site, the likelihood is approximated by Laplace approximation and gradients are calculated using the local data and the current parameters (Methods). The Central Server collects intermediate model statistics during the federated learning process, aggregates the site-specific parameters to compute the global model parameters, and sends the parameters to the sites for the next iteration. The individual-level data (genotypes, phenotypes, and covariates) is not shared with other sites or the central server in the inference.

Figure 1.

Illustration of federated association testing workflow for two sites named Site-1 and Site-2

Each site holds genotype, phenotype, and covariate datasets. Each site first downloads the reference panel principal components (PCs) and projects the genotypes to generate the population-based covariates (Step 1). Next, the initial parameters are downloaded from the central server (CS) (Step 2). Using the local genotype, phenotype, and merged covariate data, each site updates the local parameters (Step 3) and sends them to CS (Step 4). After receiving the local parameters from both sites, CS aggregates the parameters and sends the updates parameters to all sites. Steps 2, 3, and 4 are performed until the model converges. Step 1 is performed only once at the before iterations.

Experimental setting and accuracy metrics

We separated the experimental tests into two parts. We first use simulated data and real dataset to present the utility of the projection-based population covariate calculation to be used in GWAS. We explore different scenarios to highlight the importance of reference panel selection.

We next move to usage of the projected covariates in the dMEGA’s GWAS using a real-world dataset obtained from dbGAP (Data Availability). We explore two settings of covariate selection and compare the results from dMEGA with results from a centralized GWAS study using lme4 that is calculated using the covariates obtained from the dbGAP dataset. To decrease computational requirements, we ran plink2 to estimate association of the variants with the binary phenotype (using the dbGAP reported covariates) and we focused on the 10,000 variants that were the most significantly associated with the phenotype.

Performance Metrics. We evaluate the results by comparing (1) the p value concordance between the centralized and federated estimates, (2) the concordance of effect sizes estimated from the centralized and federated estimates, (3) the concordance of the ranking of the most significant SNPs identified by centralized and federated calculations, (4) time requirements of federated algorithm, (5) comparison of the top variants (with changing p value cutoffs) and qualitatively evaluate the results using Manhattan plots, and (6) qualitative comparison of the scatterplots using the first two PCs calculated by the projection-based approach and the full-PCA for simulated case studies and the dbGAP reported covariates for the real dataset.

Projection-based population stratification

We first tested whether dMEGA’s the projection-based population stratification can be used for performing population structure correction in the context of a simple linear model. The justification of a projection-based approach is to make use of the genetic diversity represented within the reference panel and identify the variation of the study participants along the PCs of this panel. Assuming that the reference panel is representative of this genetic diversity, the covariates from the projection should be useful to correct for the population stratification in the linear GWAS model. It should be noted that the covariates represent nuisance parameters, i.e., their exact values are not of essential importance as long as they correct for the population stratification effects within the study cohort^35,36,37 (Supplementary Information). This approach enables a large decrease in computation cost by circumventing the need for a full PCA of the genotype data pooled from all sites^28,32,38,39 and relying on much simpler computation of projections in population-based covariate computation that is used for population-stratification.

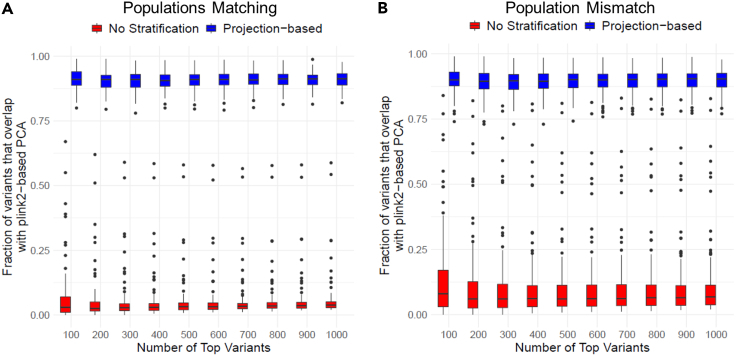
We first simulated 100 GWAS studies where 20 variants with allele frequency below 0.1 were randomly selected as causal with effect on phenotype. We also assigned population and gender-specific biases on the phenotype to introduce population and gender-specific effect. For each simulated study, we simulated genotypes for 3,000 individuals with a corresponding quantitative phenotype that is computed regarding genotypes and covariates. We finally ran plink2 in three configurations to perform GWAS with and without population stratification: (1) We ran plink2 with its default PCA to generate population-based covariates. (2) We ran plink2 with covariates generated by projection-based covariate computation using top 6 PCs. (3) We ran plink2 without population stratification as a control to ensure that population stratification is indeed necessary in GWAS. As a first test scenario, we used CEU, MXL, YRI populations from the 1000 Genomes Project for simulating genotypes and used the same populations as reference to compute the projection-based population covariates, i.e., the projection and simulation ancestries are exactly matched. Overall, p values and effect sizes from GWAS with projection-based population correction match fairly well to default PCA-based population stratification in plink2 (Figures 2, S1A, and S1B). In comparison, the GWAS without population correction gives fairly discordant and biased results (Figures S1C and S1D). We next used the GIH, CHB, PEL populations as the reference panel populations to test for mismatches in the simulated and reference populations. We observed that similar results held where projection-based population correction yields good concordance with plink2’s default PCA-based population correction (Figures S1E and S1F). GWAS p values and effect sizes without population correction yields fairly discordant results when compared to default correction (Figures S1G and S1H). We also observed that top variants detected from projection-based correction matches accurately to default correction (Figures S1A and S1B). Overall, these results show that projection-based population stratification can be effective for correction of population-specific biases to a large extent. Most importantly, this approach can be implemented efficiently in a secure domain with much better overall performance compared to a full PCA-based population correction. We utilize projection-based population stratification to estimate the population covariates in the GWAS analysis.

Figure 2.

Comparison of most significant variant concordance between projection-based population stratification and PCA-based stratification among 100 simulated GWAS

(A) The comparison of significant variant concordance for matching population panels. X axis shows the number of top variants. Y axis shows the concordance fraction. Blue boxplots depict the concordance between projection-based stratification and PCA-based stratification. Red boxplots show the concordance between GWAS with no population stratification and GWAS with PCA-based stratification.

(B) Concordance of most significant variants when projection is performed with a mismatching set of reference populations.

We next tested the impact of mismatch between reference populations used in projection analysis and the study cohort. We first focused on the simulated case study and generated a study cohort consisting CEU, MXL, and YRI samples. We next performed projections where reference was constrained as single populations. When we used a homogeneous European population (TSI), we observed that the projected coordinates did not reflect the genetic ancestry of the study participants. In addition, we observed fairly low concordance between the top associated variants obtained from a full-scale PCA of the study sample (Figure S2A). Of interest, when we use a single admixed population (GIH), we observed better separation of the study subjects albeit with low variant concordance (Figure S2B). When we used another admixed population (PUR), the separation was slightly improved (Figure S2C). When we used a reference population that contained mixture of the European, African, and American samples, we observed a fine separation among the study subjects and much higher concordance between the associated variants (Figure S2D). Overall, these results show that projection-based approach must be carefully applied to ensure that the reference population includes a representative genetic diversity that can encompass that of the study participants.

We next studied our real study sample that is obtained from the dbGAP, for which we did not have a-priori knowledge about the ancestry. For this case, we performed projection using EUR, AMR, and AFR super-populations from the 1000 Genomes Project. Overall, the projection using single super-populations did not reveal the full complexity of the genetic ancestry of the study subjects. For example, EUR reference (Figure S3A) did not appropriately separate the subjects and AMR (Figure S3B) and AFR provided marginal separation of the subjects (Figure S3C). When we use the whole 1000 Genomes populations (Figure S3D), we observed a much better concordance to the principal components that are reported by the dbGAP (Figures S3D and S3E). Particularly, the subjects tended to separate along the Europe-Asian-African Triangle from the two methods. It should again be noted that we do not require the covariates to match exactly because the PCs are treated as nuisance variables in the GWAS analysis, i.e., it is only necessary to capture the population structure. These results again denote that care must be taken to ensure that the reference panel is inclusive of the genetic ancestry of the study cohort.

Accuracy comparison with centralized association tests

First, we compared the accuracy of dMEGA in collaborative setting by comparing the association results with the centralized model as computed by lme4.⁴⁰ We used the genotypes and phenotypes data from the database of genotypes and phenotypes (dbGaP) with accession number phg000049 that comprises 3,007 individuals (1,266 case, 1,279 controls, 462 unknown). This dataset also contains the four covariates that are to be used for population stratification of the study subjects in downstream analyses. We ran dMEGA after partitioning data into three sites based on the k-means algorithm on the genotypes data and used the projection-based covariates for population stratification. The sites were treated as the additive random intercept effect, and this can be more efficient than treating them as fixed-effects when the number of sites is exploding. This assertion is justified since each term needs to be included at each site as a separate fixed effect term and may cause convergence or numerical stability problems. In the comparisons, we focused on the top 10,000 SNPs that were reported by plink⁴¹ version 2 as most significantly associated with the disease status. This variant selection is done to decrease computational requirements. We ensured that the top 10,000 SNPs include the variants that have the highest association with the phenotype (AD-status) and contains large number of variants with no significant association, i.e., it is a representative set of variants for comparing the methods. We also evaluated the utility of projection-based population stratification and correction by estimating the population-based covariates using the 2,504 individuals in the 1000 Genomes Project (Methods).

We first compared the top SNPs at different significance levels using two stratification approaches to evaluate their effect, which are shown in Table 1 using projections on top 4 and 6 components as covariates in population stratification. The choice of 4 projected covariates is for comparing the results when the number of projected covariates matches the dbGAP reported covariates. We also tested usage of 6 projected covariates to demonstrate that projection may require larger number of covariates to capture the genetic diversity in the study cohort. Overall, both methods exhibit high concordance with the centralized model (lme4).

Table 1.

Performance of predicting significant SNPs under various significant level α

α	precision	recall	F1-score	Significant SNPs
Comparison 1: dMEGA on projected 4 PCs versus ‘lme4’ on 4 dbGAP Reported PCs
${10}^{-5}$	0.580645	0.818182	0.679245	22
${10}^{-6}$	0.875	0.875	0.875	8
${10}^{-7}$	1	1	1	6
Comparison 2: dMEGA on projected 6 PCs versus ‘lme4’ on dbGAP Reported 4 PCs
${10}^{-5}$	0.68	1	0.81	19
${10}^{-6}$	1	0.88	0.93	8
${10}^{-7}$	1	1	1	6

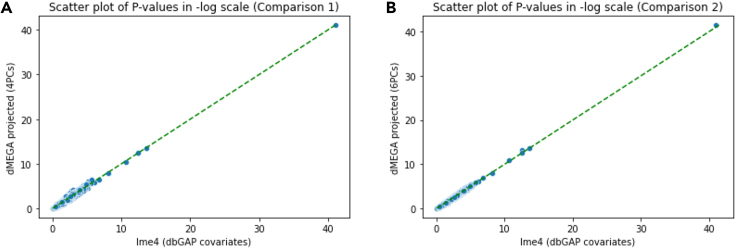
We next pooled all of the SNPs and plotted the assigned p values, which is shown in Figure 3. Consistent with previous result, we observed that using 6 components exhibit a higher concordance of significance levels (Spearman correlation $\rho =0.99$ for 6-components vs. 0.97 for 4-components.) (Table 2)

Figure 3.

Scatterplots of p values from two comparisons

(A) Scatterplot of p values from comparison 1.

(B) Scatterplot of p values from comparison 2. The lme4 baseline models experimented with 4PCs dbGAP reported covariates.

Table 2.

Correlation statistics in two comparisons

	Comparison 1	Comparison 2
Spearman correlation	0.9734	0.9909
Pearson correlation	0.9509	0.9845

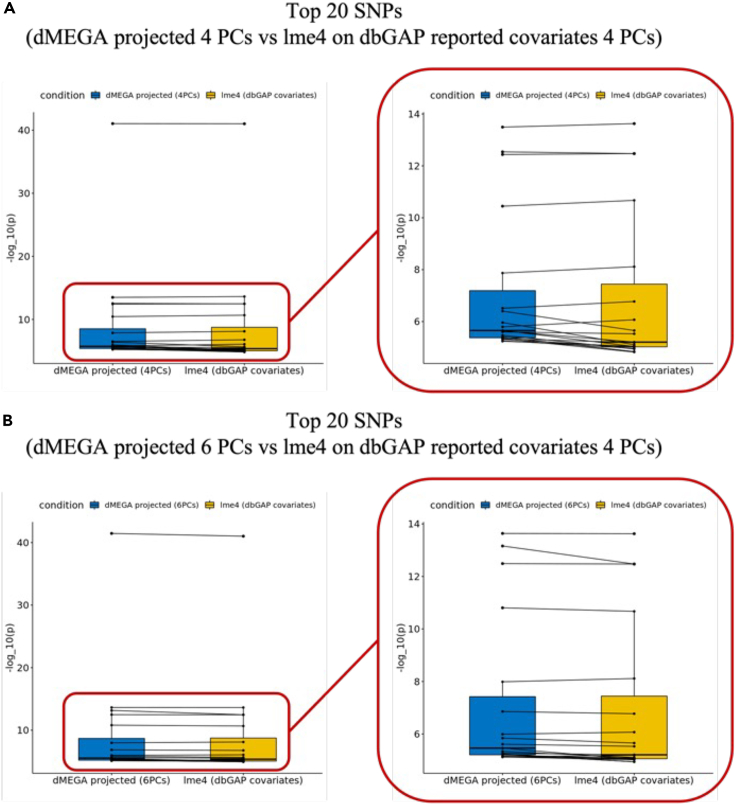
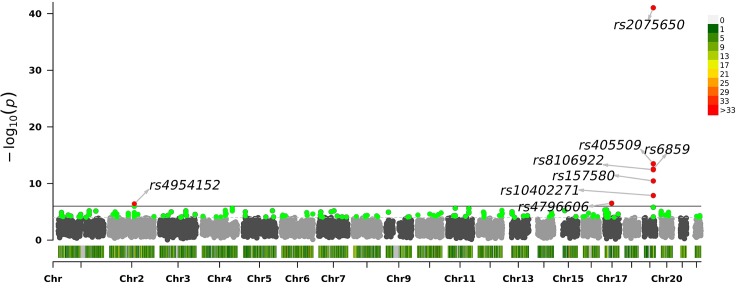
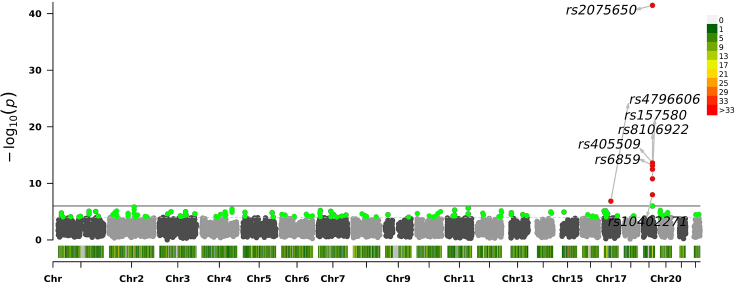
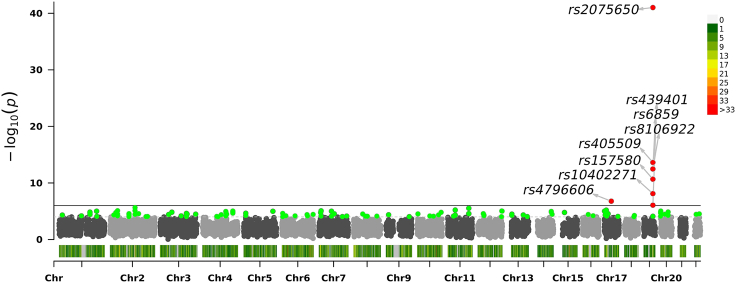
We next compared the ranks assigned to most significant SNPs by the two approaches when they are compared to the centralized model (Figures 4 and S4–S6). This is an important comparison to make sure that the most significant SNPs (from the original set of 10,000 variants), which would be functionally validated by the collaborating sites. Overall, there is fairly high concordance in the top SNPs and their rankings. Qualitatively, we observed ranking consistency to the centralized model is higher for population correction using 6-component projection compared to 4-component projections. Table 3 We finally visually evaluated the genome-wide distribution of the SNP significance, assigned by the 2 projection approaches and the centralized model Figures 5, 6, and 7. As expected, all methods find the most significant associations on chromosome 19 with high concordance, which is known to be associated with AD.

Figure 4.

SNP ranking concordance between lme4 and dMEGA

(A) Paired boxplot of comparison 1.

(B) Paired boxplot of comparison 2. The lme4 baseline models experimented with 4PCs dbGAP reported covariates.

Table 3.

20 Selected SNPs with high significance

SNP	CHR	dMEGA projected 6PCs	dMEGA projected 4PCs	lme4 dbGAP Reported 4PCs
rs2075650	19	3.48E-42	9.14E-42	9.64E-42
rs405509	19	2.30E-14	3.22E-14	2.36E-14
rs8106922	19	3.24E-13	3.65E-13	3.37E-13
rs6859	19	6.93E-14	2.89E-13	3.37E-13
rs157580	19	1.57E-11	3.58E-11	2.13E-11
rs10402271	19	1.03E-08	1.35E-08	7.70E-09
rs4796606	17	1.39E-07	3.07E-07	1.69E-07
rs439401	19	1.02E-06	1.60E-06	8.50E-07
rs4954152	2	1.43E-06	3.95E-07	2.21E-06
rs2507880	11	2.45E-06	2.51E-06	2.96E-06
rs2939753	11	5.38E-06	2.30E-06	6.19E-06
rs11649731	17	7.32E-06	4.55E-06	6.47E-06
rs2924943	2	4.59E-06	1.09E-06	7.84E-06
rs7592667	2	7.55E-06	2.38E-05	8.10E-06
rs1526528	7	6.34E-06	1.05E-05	8.54E-06
rs1798296	12	7.03E-06	5.74E-06	9.01E-06
rs1471263	4	3.47E-06	2.20E-06	9.18E-06
rs6078239	20	8.82E-06	9.74E-06	9.26E-06
rs12320530	12	1.29E-05	1.97E-05	9.54E-06
rs7222487	17	7.52E-06	4.82E-06	9.63E-06

Figure 5.

Association significance of SNPs scored by dMEGA with projected datasets on 4 PCs

Manhattan plot shows the chromosomes on x axis and $lo{g}_{1}0\left(p-value\right)$ on the y axis. Each dot corresponds to an SNP.

Figure 6.

Association significance of SNPs scored by dMEGA with projected datasets on 6 PCs

Manhattan plot shows the chromosomes on x axis and $lo{g}_{1}0\left(p-value\right)$ on the y axis. Each dot corresponds to an SNP.

Figure 7.

Association significance of SNPs scored by lme4 with 4 dbGAP reported PCs

Manhattan plot shows the chromosomes on x axis and $lo{g}_{1}0\left(p-value\right)$ on the y axis. Each dot corresponds to an SNP.

Comparison with cGLMM

We next compared dMEGA with cGLMM⁴² algorithm from the open source GitHub repository https://github.com/huthvincent/cGLMM, and used the provided synthetic data, which comprised of 150 SNPs for 3000 samples also obtained from the same GitHub repository. cGLMM utilizes an MCMC-based optimization for estimating the effect sizes for the covariates in the dataset in the federated GLMM setting. We simulated federated learning conditions by loading the data into two separate clients, each having sample sizes of 1498 and 1502, respectively, while maintaining a central server that managed the communication and aggregation of the intermediate statistics. We ran the cGLMM algorithm 20 times and observed that we could only reproduce the results for 7 runs (Table S1), which we attributed to numerical issues arising from either (1) parameter initialization or (2) Hessian matrix calculations (Personal communication with authors). On further investigation, we found that the intermediate Hessian matrix converged to a matrix of all zeros, which prevented the algorithm from updating beta (Equation 8 in Zhu et al. cGLMM paper).

To test the robustness of dMEGA, we randomly selected 10 SNPs from the 10,000 variant set and ran dMEGA 20 times independently on each SNP and estimated robustness of the statistics. Overall, dMEGA successfully completed all runs on all of the 10 SNPs. In addition, the standard deviation of p value estimated for each SNP among the independent runs is much smaller than the mean of the p value, indicating robust estimate of the p value. We observed a similar robustness for the estimated effect sizes (Table S2).

We also observed important conceptual differences in cGLMM’s design and reported statistics. In particular, cGLMM algorithm aims to fit a single model for a given set of variants or covariates, providing only the effect size for each variant, without a statistical significance (i.e., p values for each covariate) of the effect sizes. This may pose a major limitation for application to GWAS because it is necessary to evaluate significance of the tested variants so as to filter out variants with no association. Thus, we believe cGLMM may not be directly applicable in GWAS settings.

Conversely, dMEGA fits a model for each variant individually and reports both the effect size and statistical significance for each predicted effect size. In summary, our comparisons indicate that the cGLMM algorithm and dMEGA differ in their conceptual design and practical applicability.

Timing, memory, and data transfer

Our experiment was done in a computation environment of 96 threads (24 Cores) Intel(R) Xeon(R) Platinum 8168 CPU @ 2.70 GHz, 1.5 TB memory, Ubuntu 16.04.7 LTS, Python 3.10.4. In the tests, 1 thread was used for estimating the runtime. We observed a small difference between running 6PCs and 4PCs in dMEGA. Federated computation for each SNP took 20 s and 200 MB memory on average to complete. The total communication cost of 4 PCs and 6 PCs federated model are 80 kB and 125 kB on average. This cost includes, for each iteration, each site transmit 88 Bytes of random effect coefficient, 144 Bytes of computational intermediates, and 72 Bytes of fixed effects coefficients (Table 4). Overall, these results indicate low network transfer requirements for dMEGA’s framework (Figure 8). The algorithm can benefit from software optimizations by parallelization of the calculations by multithreading.

Table 4.

Communication summary

$P_i$ to $CS$	$CS$ to $P_i$
Number of PCs p: scalar	Current working SNP’s name S: character
A list of SNPs’ name S: list	Global gradient l: $p+1$vector
Sample size $n_i$: scalar	Global Hessian H: $\left(p+1\right)\times \left(p+1\right)$matrix
Local gradient $l_i^{\prime }$: $p+1$vector	Global parameter θ: $p+1$vector
Local Hessian $H_i$: $\left(p+1\right)\times \left(p+1\right)$matrix	Inference statistics: $p+1$vector
Local mixed effect ${\mu }_i$: scalar
Local Standard Error $S{E}_i$: $p+1$vector

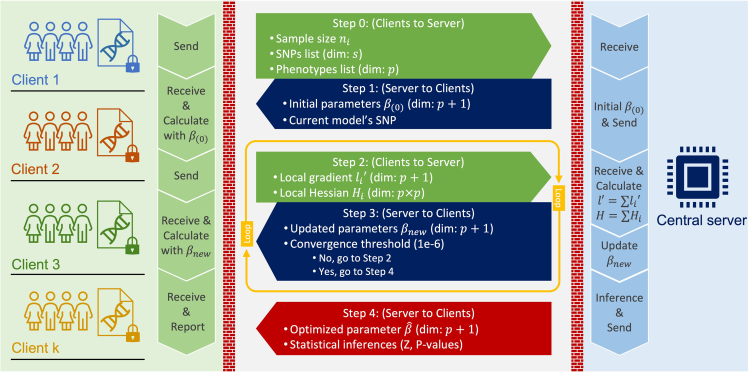
Figure 8.

Diagram of federated GLMM inference in dMEGA

As we are aware that dMEGA requires significant computational resources for large-scale studies involving millions of variants (e.g., estimation for 10,000 SNPs takes 200,000 s on a single thread), we recommend that its application be focused on specific scenarios. For instance, it can be useful in small-scale validation studies or targeted association testing, where sites may focus on small regions deemed significant at each site separately and validate using new samples collaboratively. Alternatively, sites may wish to collaborate on samples genotyped using targeted technologies like exome sequencing and targeted gene panels. These approaches can provide valuable insights into the genetic basis of complex traits while mitigating the computational burden.

Discussion

We presented dMEGA for federated generalized linear mixed modeling. dMEGA is readily applicable to collaborations where data sharing at the summary statistic level can be deployed. Unlike previous methods that rely on a computationally intensive federated PCA for performing population stratification and correction, dMEGA makes use of projection on existing reference panels and to correct for population biases. As the size and diversity of existing panels increase, we foresee that projection-based bias correction can prove more accurate. The projection has very small computational requirements and can be performed at each site before federated analysis.

Another similar method distributed Penalized Quasi-Likelihood (dPQL)⁴³ used penalized quasi-likelihood to approximate the objective function of GLMM. dPQL simplifies the maximization of the log likelihood function of GLMM to fitting a linear mixed model. However, dPQL has inherited drawbacks. For example, dPQL depends strongly on the estimated variance components,⁴⁴ but the inference of variance parameters in dPQL may be biased⁴⁵ because of its linearity assumption. dMEGA approximates the marginal distributions, and it provides more robust estimation since dMEGA considers the marginal predicted ratios associated with each local site, not just identifying samples with particularly high predicted ratios.⁴⁴ Another method that was recently proposed by Zhu et al.,⁴² which utilizes Expectation Maximization by integrating Metropolis-Hastings algorithm with Newton-Raphson as the maximization steps for performing generalized linear mixed model in a collaborative fashion. Although this method is expected to provide matching results with a centralized algorithm, EM requires large sample sizes for robust parameter estimation and may likely get stuck in local optima in the parameter estimation. Our comparison results demonstrate some possible source of stability issues, e.g., convergence to a zero Hessian matrix. More importantly, cGLMM is designed to estimate only the covariate effect sizes and does not provide statistical significance for the effect sizes. This is an important consideration for application in GWAS since significance of the variants are central to filtering them out in these studies. We therefore believe dMEGA and cGLMM differ in conceptual and practical terms and in their application domains.

As the current implementation stands, dMEGA can be used for correcting for site-specific random risk factors (such as environmental factors). In addition, we formulated an approach that can be implemented into dMEGA to include site-level correlations among the random effects. This approach can be integrated into dMEGA’s federated implementation and be used to model more complex random risk effects among sites (e.g., sites close to each other geographically). A related work is lme4qtl,⁴⁶ which can incorporate individual-level random effects using a covariance matrix, e.g., kinship matrix. In its current implementation dMEGA is not able to handle the individual-level covarying random effects. We leave this as a future extension of the dMEGA’s federated GWAS framework.

Limitations of the study

dMEGA has several limitations that warrant further research. While our federated testing approach has small network traffic requirements, each local site is required to handle high computational load. This is a general challenge among federated learning methods. Considering that the gene association tests may involve millions of variants along with large number of phenotypes, the center server aggregation layer can be outsourced to cloud whereby, while the data are kept locally. Another limitation of dMEGA is selection of the reference panels that are used in projection step. As our results indicate, a reference panel that is not reflective of the genetic diversity of the study participants may inadvertently bias the results. Projection-based analysis has been employed previously in ancestry estimation³⁷ and kinship estimation methods⁴⁷ and the main justification for using the projection approaches is to decrease the computational requirements of a full federated PCA that entails large computational load on the sites. The future work in this arena include tuning the projected covariates to match the genetic ancestry of the study participants. For example, the sites can iteratively update the projected covariates to increase the genotypic variance explained by the covariates. We also propose the usage of "worldwide panel PCs³⁷" that encompass the genetic diversity of a large set of populations. It is worth noting that the projection requires the principal components and not the individual level genotype data. Thus, it does not directly increase the individual-level privacy risks. In turn, the worldwide panel PCs can be released even from restricted panels such as TOPMed.

From privacy perspective, dMEGA shares only summary statistics between the central server and the sites. In that regard, it is necessary that the central server is a trusted entity (such as NIH) and that all sites are expected to execute dMEGA in an honest manner. As summary statistics may leak information, honest-but-curious entities can perform re-identification attacks. This is, however, a general concern in federated learning frameworks and not specific to dMEGA. Our approach does not pose a direct risk to the reference panel because projection requires only the principal components. Thus, restricted reference panels from underrepresented populations can be utilized in these computations. It is still worth noting that the principal components are types of summary statistics and can leak information that may be used to re-identify participation using previously described attacks.⁴⁸ Furthermore, the intermediate statistics ($H,I,\mu$) are also vulnerable to certain attacks on federated learning systems such as variants of gradient inversion attacks.⁴⁹ Thus, it is important to protect these model information during the federated learning process. Different approaches can be used to protect these summary statistics such as multi-key homomorphic encryption⁵⁰ (MKHE), or Differential Privacy (DP). The usage of these formalisms requires further research into efficient re-formulations for MKHE and balancing the Gaussian or Laplace noise level for DP for ensuring utility.

To increase the confidentiality of dMEGA, we can utilize noise addition to hide local intermediate information, denoted as $I_i$ (i.e. local sample size, local gradient, local Hessian, local mixed effects, and local standard error), during communication. This idea has been developed in the HyFed⁵¹ framework, which introduces a server called Compensator to collect the local noise $N_i$ values from each client and send the aggregated noise, i.e., $N={\sum }_i{N}_i$, to the CS. In this process, each client generates local noise $N_i$ from a Gaussian distribution with zero mean and a variance of ${\sigma }^2$. Then, each client will mask the intermediate statistics $I_i$ using the noise $N_i$, to generate $I_i^{\prime }=I_i+N_i$, and send the noisy statistic to CS. Simultaneously, each site sends the noise levels to the Compensator. When all clients finish their communication, CS unmasks the global information of interest $I={\sum }_i{I}_i={\sum }_i{I}_i^{\prime }-N$ via deducting the aggregated noise N provided by Compensator.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Late Onset Alzheimer’s Disease Cohort Dataset	Database of Genotypes and Phenotypes (dbGaP)	phs000168
The 1000 Genomes Project Genotype and Metadata	1000 Genomes Project	https://www.internationalgenome.org/data/
R	https://cran.r-project.org/bin/windows/base/	R
dMEGA	https://github.com/Li-Wentao/dMEGA	dMEGA
Plink2	https://www.cog-genomics.org/plink/2.0	Plink2

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Arif Harmanci (Arif.O.Harmanci@uth.tmc.edu).

Materials availability

This study did not generate new unique reagents.

Method details

The goal of dMEGA is to detect significant SNPs that are associated with specific diseases or phenotypes in a federated manner. In our assumption, genotype and phenotype data are stored cohort-wise throughout several entities (e.g., research institutions or hospitals). Each entity is presumed to be prohibited from sending original data. By constructing a logistic regression model with mixed effects, data holders will update the global model with local information bias considered. Notice that the communication process does not put data at risk due to dMEGA will only ask data holders for model information, such as gradients.

Projection-based calculation of population covariates

dMEGA first centers the genotype matrix for each individual and projects the samples on a reference panel that is shared among the sites. In the context of privacy-aware analysis, this is a reasonable assumption because the sites can make use of numerous publicly available panels. For dMEGA, we use The 1000 Genomes Project panel that comprises 26 diverse sets of populations that are geographically sampled over the world.

The reference panel is first processed at the central server. This is done by performing principal component analysis (PCA) on the reference panel by decomposition of the genotype covariance matrix, i.e., $P·P^T=\mathrm{\Pi }·\mathrm{\Lambda }·{\mathrm{\Pi }}^T$, where ${\mathrm{\Pi }}_{N,S}$ denotes the full set of principal components of reference panel genotype matrix $P_{N,S}$ for N genetic variants and S samples in the reference panel, where $S=\mathrm{2,504}$ for The 1000 Genomes Project population data. We use κ top principal components (columns) of this matrix in our projection step.

After the reference panel is processed by the central server, the principal components are sent to collaborating sites. It should be noted that the reference panel is processed once at the central site at the beginning of the computations. The central server does not share the reference panel genotypes directly with the sites. The components do not represent direct risk to the reference panel individuals. This is advantageous for utilizing the restricted population panels, such as the ToPMED panel.⁶

$${\tilde{G}}_{i,j}=G_{i,j}-\frac{1}{N}·\sum _k{P}_{i,k}$$ (Equation 1)

where $\tilde{G}$ denotes the centered genotype matrix.

$$c_{k,j}=\sum _i{\tilde{G}}_{i,j}·{\mathrm{\Pi }}_{i,k},k<\kappa$$ (Equation 2)

where $c_{k,j}$ denotes the $k^{th}$ covariate for $j^{th}$ individual.

Projection-based covariate computation with the 1000 genomes sample

In our experiments, we used The 1000 Genomes Project’s phase 3 genotypes as the reference panel available at . We used the bi-allelic SNPs and subsampled the variants to utilize 77,531 variants. We generated the top 4 and 6 principal components for the 3,007 individuals in the genotype dataset.

Federated association test

We introduce a federated association test algorithm based on Generalized Linear Mixed Model. Assume that there will be k institutions that hold genotype and phenotype data, and that each institution’s database consists of $n_i$ subjects (Figure 8). Let the total number of patients be denoted by $n={\sum }_i^k{n}_{i=1}$. Here, we consider site-wise mixed-effects, denoting ${\mu }_i$ as the mixed-effect of institution i, as well as shared fixed-effects θ. Notice that the fixed-effects parameter space is split into two parts, $\theta =\left(\beta ,\gamma \right)$. Denote β is of $N-1$ dimension parameter for covariates and γ is 1 dimension for genotype. The genotype dataset at institution i denoted as $X_i$ (Matrix of $N-1$ covariates and 1 genotype on $n_k$ individuals), and phenotypes denoted as $Y_i$ (vector of length $n_k$). Thus, the mixed model of each site can be represented as

$$\mathbb{E}\left[Y_i\mid {\mu }_i,X_i\right]=g^{-1}\left(X_i\theta +{\mu }_i\right)$$

$${\mu }_i\sim \mathcal{N}\left(0,\sigma \right)$$

where $g^{-1}(·)$ is the inverse of the link function (i.e., a logit function for logistic regression/binary traits) that defines the relationship between the linear combination of the predictors (genotypes, covariates, and random effects) to the mean of the phenotype. Here, we focus on the random intercept effect at site i, ${\mu }_i$, which follows a normal distribution with mean 0 and variance σ. In this scenario, ${\mu }_i$ is constant for individuals on the same site. Across the sites, ${\mu }_i$ is normally distributed across sites.

For a binary trait (i.e. case/control study), the conditional probability distribution of the phenotype given the variant genotypes and covariates can be written as

$$P\left(Y_{ij}=1\mid X_{ij}\right)=\underset{{\mu }_i}{\int }{g}^{-1}\left(X_i\theta +{\mu }_i\right)\phi \left({\mu }_i\right)d{\mu }_i$$

where φ denotes the probability density function for normal distribution with mean 0 and hyper-parameter variance σ. Thus, the likelihood function of the joint distribution can be formulated as

$$\mathcal{L}\left(\theta ,\sigma \right)=\prod _{i=1}^k{\int }_{-\infty }^{+\infty }\prod _{j=1}^{n_i}P\left(\theta ,{\mu }_i\mid X_{ij},Y_{ij}\right)P\left({\mu }_i\mid \sigma \right)d{\mu }_i$$

The optimization of the likelihood function is a non-tractable problem because the integral over the random effects does not have a closed form representation. To solve the intractable problem, we utilize Laplace approximation for the likelihood function:

$$\mathcal{L}\left(\theta ,\sigma \right)=\prod _{i=1}^k{\int }_{-\infty }^{+\infty }{e}^{\log \left({\prod }_{j=1}^{n_i}P\left(\theta ,{\mu }_i\mid X_{ij},y_{ij}\right)P\left({\mu }_i\mid \sigma \right)\right)}d{\mu }_i\triangleq \prod _{i=1}^k{\int }_{-\infty }^{+\infty }{e}^{f\left(\theta ,{\mu }_i\left(\sigma \right)\right)}d{\mu }_i\approx \prod _{i=1}^k{e}^{f\left(\theta ,{\hat{\mu }}_i\right)}{\left[-\frac{2\pi }{f_{{\mu }_i{\mu }_i}^{″}\left({\hat{\mu }}_i\right)}\right]}^{n_i/2}\triangleq \prod _{i=1}^k{\mathcal{L}}_i\left(\theta ,{\hat{\mu }}_i\right)$$

where ${\hat{\mu }}_i={\mu }_i\left(\hat{\sigma }\right)=argma{x}_{\sigma }{\mathcal{L}}_i\left(\theta ,{\mu }_i\left(\sigma \right)\right),\forall \theta$. And for computational convenience, we take log-likelihood as our objective function, that is

$$l\left(\theta ,\sigma \right)\triangleq \log \mathcal{L}\left(\theta ,\sigma \right)=\sum _{i=1}^k\log {\mathcal{L}}_i\left(\theta ,{\hat{\mu }}_i\right)\triangleq \sum _{i=1}^k{l}_i\left(\theta ,{\hat{\mu }}_i\right)$$

Hence, the goal is to optimize the approximated objective function above. Compared to the centralized (all data pooled in one repository) inference, the optimization in federated learning settings is based on iterations of (1) Calculation of the intermediate statistics computed using each institution’s local data and (2) aggregation of the statistics by a central server (CS). We describe the steps in more detail below:

Initialization. The federated learning will start with a central server $CS$ that connects to k distributed local data repositories. Initial modeling information requests will send to each participant $P_i$.

• •Number of PCs
• •A list of SNPs’ name S
• •A list of sample size across participants N

Step 1. $CS$ will initiate model parameters ${\theta }_{\left(0\right)}$ for each distributed model with SNP in list S. And each local repository $P_i$ computes model’s intermediates and send back to CS

• •Local gradients on fixed effects '$l_i$.
• •Local Hessian matrix on fixed effects Hi
• •Local site-wise mixed effect coefficient ${\mu }_i$

Step 2. $CS$ updates model’s parameter ${\theta }_{new}$ with aggregated information from global gradients $l^{\prime }\left(\mu \right)={\sum }_i{l}_i^{\prime }\left({\mu }_i\right)$, global hessian $H\mu ={\sum }_i{H}_i\left({\mu }_i\right)$, and previous fixed-effects ${\theta }_{prev}=\left({\theta }_1,\dots ,{\theta }_k\right)$. The update is done by Newton’s method ${\theta }_{new}={\theta }_{prev}-l^{\prime }/H$. Then send ${\theta }_{new}$ to each $P_i$.

Step 3. Each $P_i$ will follow Step 2 until model is converged with criteria $\Delta \theta$ and $\Delta \mu$ below threshold ${10}^{-6}$.

Step 4. The $CS$ will compute the local standard errors $S{E}_i=diag\left({\left(X_i^{\top }\hat{W}{X}_i\right)}^{-1/2}\right)$ from $P_i$, then return inference statistics (e.g. Z score, P-values). Where $\hat{W}={\hat{Y}}_i{\left(1-{\hat{Y}}_i\right)}^{\top }$.

All the information in communication is summarized in table below

Dependent site-wise relationship in dMEGA

Furthermore, we can generalize this problem with the site-level variance-covariance matrix. Here, we don’t assume the dependency among federated sites and denote a site covariance matrix $\mathrm{\Sigma }$. Notice that $\mathrm{\Sigma }$ is a $k\times k$ matrix under our scenario. We assume the site variance-covariance matrix $\mathrm{\Sigma }$ is known. And τ is the cross-site hyperparameter to be estimated.

Hence the distribution of the random effect is a multivariate normal distribution and it is shown as

$$\mu ={\left({\mu }_1,\dots ,{\mu }_k\right)}^{\top }\sim {\mathcal{N}}_k\left(0,\tau \mathrm{\Sigma }\right)$$

where μ is the vector of random effects of each federated site, and τ is the hyperparameter that is to be estimated. Now, the objective function of the dependent sites is

$$\mathcal{L}\left(\theta ,\tau \right)=\prod _{i=1}^k{\int }_{-\infty }^{+\infty }\prod _{j=1}^{n_i}P\left(\theta ,\mu \mid X_{ij},Y_{ij}\right)P\left(\mu \mid \tau \right)d\mu$$

Quantification and statistical analysis

p-values reported in the results are estimated with respect to the aforementioned generalized linear mixed models. P-value cutoffs are selected as described in the reported tables and results.

Data sources and experimental setup

We used genotype-phenotype data obtained from database of Genotypes and Phenotypes (dbGaP) with accession number phs000168 for our experiments available for General Research Use (GRU). This dataset contains $\mathrm{575,003}$ variants genotyped by Illumina Human610-Quad version 1 platform over $\mathrm{3,007}$ individuals. Raw data is processed and formatted with plink2.⁴¹ The alternate alleles reported by the array platform were re-coded using in-house scripts to ensure that they were concordant with The 1000 Genomes Project. Any variant for which we could not resolve by strand were excluded. We next used plink2’s "–glm" option to calculate the baseline association signals. We next filtered the SNPs and identified the SNPs with top $\mathrm{10,000}$ variants with the strongest association signal to the phenotype.

The reference panel is obtained from the 1000 Genomes Project FTP portal at ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/. We processed 1000 Genomes dataset by first excluding the SNPs with minor allele frequency (MAF) smaller than $5\%$. We next overlapped the variants with the re-coded array variants, which yielded $\mathrm{155,076}$ common variants. To decrease computational requirements, we focused on variants on the 22 autosomal chromosomes and further sub-sampled the remaining variants to generate the final $\mathrm{77,315}$ variants. These variants were used to generate the principal components and population-based covariates in the projection step.

To evaluate dMEGA, we compared it with a baseline method using the linear mixed model implemented in R package ‘lme4’.⁵² Our experiments were designed as table below:

We will focus on two comparisons (beow table):

Experiments

	Distributed	Pooled
Projected	dMEGA∗†	R(lme4)†
dbGAP Covariates	–	R(lme4)∗

• 1.(Denoted in †) dMEGA in projected and distributed data and baseline in projected and pooled data.

While the datasets are the same (projected), this comparison aims to show the performance of dMEGA in distributed datasets.

• 2.(Denoted in $\ast$) dMEGA using projected covariates and distributed data and baseline in dbGAP provided covariates and pooled data.

The datasets are of different between dMEGA method (using projected covariates) and baseline method (using dbGAP covariates). This comparison will show the capability of projection combining with federated learning.

Published: June 28, 2023

Data and code availability

• All original code has been deposited to github and is publicly available as of the date of publication. Accession link is listed in the key resources table.

• •The reference panel is obtained from the 1000 Genomes Project FTP portal at ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/.
• •dMEGA is publicly available at https://github.com/Li-Wentao/dMEGA.