A Guide to Cross-Validation for Artificial Intelligence in Medical Imaging

Abstract

Artificial intelligence (AI) is being increasingly used to automate and improve technologies within the field of medical imaging. A critical step in the development of an AI algorithm is estimating its prediction error through cross-validation (CV). The use of CV can help prevent overoptimism in AI algorithms and can mitigate certain biases associated with hyperparameter tuning and algorithm selection. This article introduces the principles of CV and provides a practical guide on the use of CV for AI algorithm development in medical imaging. Different CV techniques are described, as well as their advantages and disadvantages under different scenarios. Common pitfalls in prediction error estimation and guidance on how to avoid them are also discussed.

Keywords: Education, Research Design, Technical Aspects, Statistics, Supervised Learning, Convolutional Neural Network (CNN)

Supplemental material is available for this article.

© RSNA, 2023

Summary

The authors provide a guide, with corresponding example codes, for selecting and implementing an appropriate cross-validation approach when developing artificial intelligence algorithms in medical imaging.

Essentials

• ■ Cross-validation (CV) is a set of data sampling methods used by algorithm developers to avoid overoptimism in overfitted models.

• ■ CV is used to estimate the generalization performance of an algorithm but can also be used for hyperparameter tuning and algorithm selection.

• ■ Common CV approaches include the holdout, k-fold, leave-one-out, nested, random sampling, and bootstrap CV methods.

• ■ The most appropriate CV approach for a given project will depend on the intended task, dataset size, and model size.

Introduction

Artificial intelligence (AI) methods are increasingly investigated in medical imaging applications, including for image processing, diagnosis, and prognosis (1–3). However, the large learning capacity of modern deep neural networks makes them susceptible to overfitting on training samples. Overfitting can result in overoptimistic expectations for how a model will perform on future data (4). This results in a gap between what we expect from a model and what it can actually deliver and has become a common source of disappointment in the clinical translation of AI algorithms (5–7).

This review describes approaches to avoid overoptimism in AI performance estimation by using cross-validation (CV). Despite widespread use of CV in AI algorithm development, implementing an appropriate CV approach for a particular dataset can be challenging, as there are advantages and disadvantages to each of the different CV approaches (8,9). We aim to inform readers, particularly trainees, about common pitfalls that should be avoided during algorithm evaluation and to offer a practical guide on how to implement CV for medical imaging studies.

Overfitting

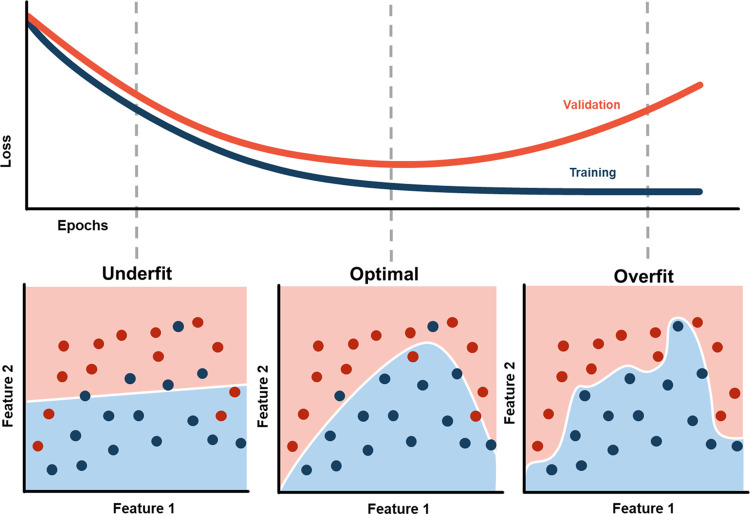
The need for CV arises from the fact that AI algorithms are susceptible to overfitting. Overfitting occurs when an algorithm learns to make predictions based on the presence of image features that are specific to the training dataset and do not generalize to new data (Fig 1). Consequently, the accuracy of a model’s predictions on its training dataset is not a reliable indicator of the model’s future performance (4).

Figure 1:

Graph demonstrates underfitting (left) and overfitting (right) of a model, which can result in poor predictive performance on future unseen data.

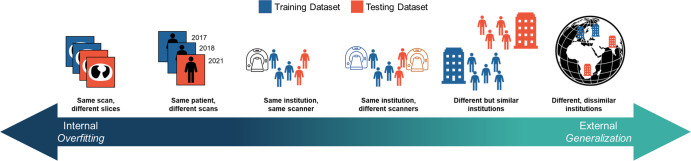
To avoid being misled by an overfitted model, model performance must be measured on data that are independent of the training data. These data are referred to as a holdout test set or external validation (Fig 2). Ideally, a large external holdout test set would always be used to estimate a model’s expected performance, often called its generalization performance. However, during the early stages of development, large external test sets are often not available. In these situations, CV is often used for generalization performance estimation.

Figure 2:

Figure represents the spectrum of data independence. External testing requires patient populations and annotators that are different than those contained in the training dataset. The degree to which the training data are different from the testing data forms a spectrum, with internal evaluation (left) providing no information about the expected generalization performance of the algorithm. Prior to widespread clinical adoption, algorithms require external testing (right).

Cross-Validation

CV is a set of sampling methods for repeatedly partitioning a dataset into independent cohorts for training and testing. Separation of the training and test sets ensures that performance measurements are not biased by direct overfitting of the model to the data. In CV, the dataset is partitioned multiple times, the model is trained and evaluated with each set of partitions, and the prediction error is averaged over the rounds (Fig 3). There are three main reasons for using CV during algorithm development: (a) to estimate an algorithm’s generalization performance, (b) to select the best algorithm from several candidate algorithms, and (c) to tune model hyperparameters (ie, parameters that dictate how a model is configured and trained) (10). We refer to these tasks as performance estimation, algorithm selection, and hyperparameter tuning, respectively. We cover the different CV approaches needed to handle each of these tasks below (11). CV has been used in numerous studies focusing on a variety of medical imaging AI applications, such as for classification of brain MRI studies (12), lesion detection in PET imaging (13), and predicting clinical outcome on the basis of radiographs (14).

Figure 3:

Different methods of cross-validation (CV) that can be used to address different training and evaluation needs. All methods aim to evaluate the model’s performance on independent test datasets. Some CV methods allow for hyperparameter tuning or algorithm selection (one-time split with validation, k-fold with holdout, nested CV, select-shuffle-test, and random sampling CV). Some CV methods are better suited for small datasets (k-fold with folded test set, leave-one-out, nested, and random sampling). Final model training for nested CV is described in Figure 6. (Adapted, with permission, from reference 8.)

Pitfalls

Certain errors and pitfalls that occur during model evaluation can lead to biased or misleading results, but they can be prevented or mitigated by using an appropriate CV approach. Here, we explain how pitfalls can cause biased performance estimation and then discuss approaches to avoid them.

Nonrepresentative Test Sets

If the patients in your test set are insufficiently representative of the patients in the deployment domain, resulting performance estimates can be biased (15). Use of nonrepresentative test sets is a common pitfall, often caused by biased data collection. A related pitfall is dataset shift, also known as a distribution shift, which occurs when your model is applied to data with a different underlying distribution of images or labels relative to your training dataset (7,16,17). For example, a model might work well at one institution but not at a different institution with different scanner technologies.

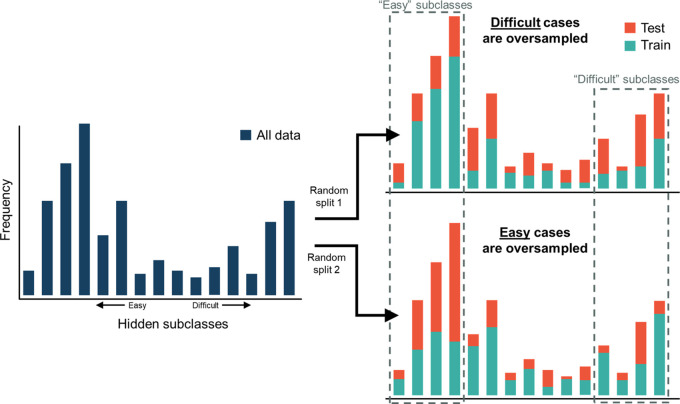
A more subtle cause of nonrepresentative test sets that can occur with small sample sizes or imbalanced datasets is the presence of hidden subclasses. Unlike known subclasses (eg, age groups), hidden subclasses are “unknown” groups within a dataset that share unique characteristics (18). The shared characteristics of a subclass can sometimes make the prediction task more challenging. For example, a subset of patients undergoing PET imaging could have been recently vaccinated, causing elevated tracer uptake in lymph nodes (19). These patients could hypothetically constitute a hidden subclass to PET analysis algorithms. When subclasses are known, the dataset can be partitioned so that each split preserves the overall class distribution–this is called stratified CV (9). However, when subclasses are unknown, random partitioning of the dataset may not preserve the overall class distribution, thus resulting in potential bias (Fig 4). The impact of hidden subclasses decreases with increasing dataset size (15).

Figure 4:

Graphs illustrate susceptibility of one-time splits for small datasets to sampling biases. Some hidden subclasses of data may be easier and/or harder for the model to learn, and those subclasses can be randomly under- or oversampled in the test set with a one-time split of the dataset. This can result in a biased estimate of the model’s generalization performance.

Tuning to the Test Set

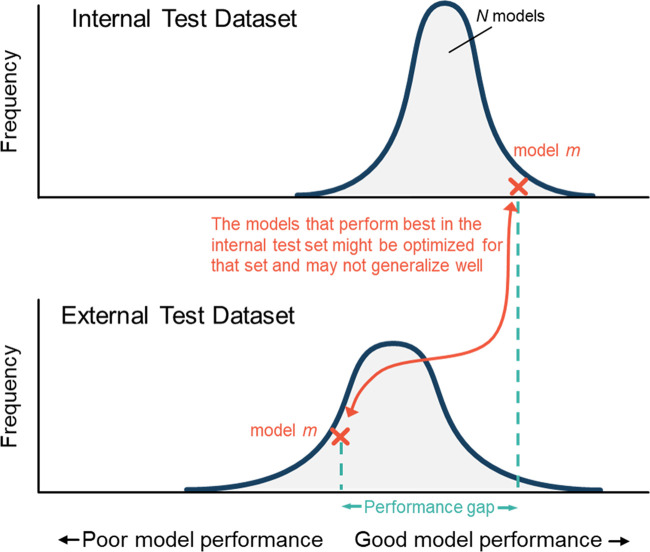
Another pervasive pitfall in AI research is unintentionally tuning the model to the holdout test set (20,21). Even if the model is never trained on samples from the test set, information from the test set can indirectly influence how the model is trained. This often occurs when developers repeatedly modify and retrain their model on the basis of its performance in the holdout test set. By chance alone, certain permutations of a model will perform better on the test set than others, as shown in Figure 5. When developers select the model that performed best in the test set, they have effectively optimized the model to the data in the test set. This leads to overoptimism about how the model will generalize to unseen data. Ideally, the holdout test set should be used only once.

Figure 5:

Graphs illustrate why models suffer performance gaps. Due to randomness (eg, weight initialization), training a model N times with the same training dataset will produce N unique models. When applied to the internal test set (ie, a holdout set split from the developmental dataset), the different models’ performances will produce a distribution (top). Outliers on the high end of the distribution will, by chance alone, perform well in the internal test set. When the models are applied to an external set, the distribution of model performances can shift (dataset shift), and the models that performed best on the internal set often underperform.

Approaches to CV

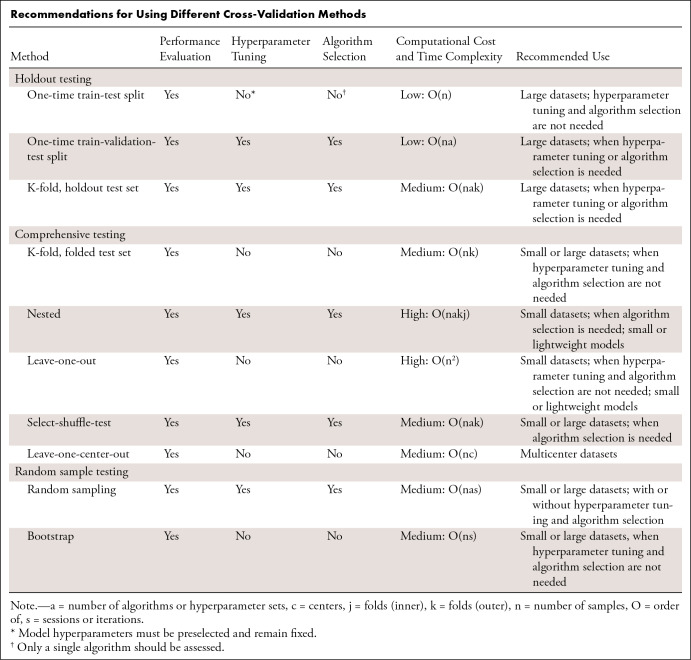
This section discusses the advantages and disadvantages of common CV approaches, including how susceptible each one is to the aforementioned pitfalls and the scenarios under which each approach should be used. The Table compares the different CV methods and groups them into the categories of holdout testing (a designated set of patients withheld for testing), comprehensive testing (each patient is used for testing once), and random sample testing (random selection of testing patients each round). As most AI models are currently developed using libraries in the Python programming language, we have provided instructional Python code in Appendix S1, and our online repository provides ready-to-use examples (https://github.com/zhuemann/Cross-Validation-Guide).

Recommendations for Using Different Cross-Validation Methods

General Principles

There are a few principles that apply to all CV approaches. First, when partitioning datasets, cases in the training, validation, and testing sets should be independent. For example, for datasets containing multiple examinations from the same patient, partitions should not be done at the examination level but rather at the patient level (or higher, if appropriate). Second, for all CV approaches, the final model–the one to be deployed–should be trained using all the data combined. Though the performance of this final model cannot be directly measured because no additional test data are available (ie, the test data have been “burned”), it can be safely assumed that model performance will be at least as good as what was measured using CV (10).

One-Time Splits

A one-time split, often called the holdout method, is a simple data-partitioning approach to model evaluation (it is often not considered as CV). In this approach, the dataset is randomly split into two sets. The model is trained using the training set and evaluated using the test set. Data splits are patientwise, even for two-dimensional and longitudinal images. Sometimes a third set, called the validation set, is also split from the dataset to allow for hyperparameter tuning or algorithm selection (Fig 3). The algorithm or set of hyperparameters that performs best on the validation set is selected as the final model, and its performance is measured on the test set.

The advantage of a one-time split approach is its simplicity. It also produces just a single model, unlike other forms of CV. A weakness of this approach is that the test set is vulnerable to being insufficiently representative of the overall population, especially with small datasets (Fig 4). Furthermore, this approach can be susceptible to the pitfall of tuning the test set, as developers often “peek” at their test set performance during development.

Given these weaknesses, one-time splits are recommended when the dataset is very large, such that the test set can safely be assumed to represent the target population.

K-Fold

In k-fold CV, the dataset is partitioned patientwise into k disjoint sets called folds (Fig 3). First, a single fold is selected to be withheld for testing while the remaining k−1 folds are used for training. Next, a different fold is selected to act as the test set, and the process is repeated. These CV sessions–each session consisting of a model being trained and tested–are repeated k times until k different models have been trained, with each of the k folds acting as the test set once. The optimal value for k is dependent on a number of variables, but generally k = 5 or k = 10 is used (22).

Holdout test set with folded validation set.—For this k-fold CV variant, a test set is split from the overall dataset and withheld from CV (see Fig 3). Then, k-fold CV is performed on the remaining data, and the withheld folds are used for validation (hyperparameter tuning or algorithm selection). A finite number of candidate models are preselected for comparison, which can be different algorithms or sets of hyperparameters; for each session of CV, all candidate models are trained, and their performances are measured on the validation fold. The algorithm or hyperparameter set with the best average performance across all folds is selected to be the final model. This final model is trained using all the training data, and its performance is measured on the holdout test set. A weakness of this approach is that the holdout test set may not be representative of the population.

Folding the test set.—In this k-fold CV variant, each sample in the dataset is used for testing once. The final performance estimate is obtained by averaging the k models’ performances on the k different test sets. This method has the advantage that models cannot be tuned to the test set because the test set changes with each session. It also has the benefit of being able to construct CIs for statistical testing (23). However, the absence of any validation sets precludes hyperparameter tuning and algorithm selection, meaning that this method is useful only for performance evaluation of models with fixed or preselected hyperparameters. For even more precise error estimation, k-fold CV can be repeated using different partitions for each repetition and then averaged (ie, repeated k-fold CV) (22).

Readers should be aware that for any CV approach that folds the test set, the final performance estimate is not the measurement of a single model’s performance. Rather, the expected performance of the “pipeline” used to develop the model is being measured. For k-fold CV, for instance, each session produces a different model because the training data change with each session. Consequently, the final prediction error is an average over k different models. Yet each of those k models was developed using the same pipeline, and it is this pipeline that is being evaluated.

Nested

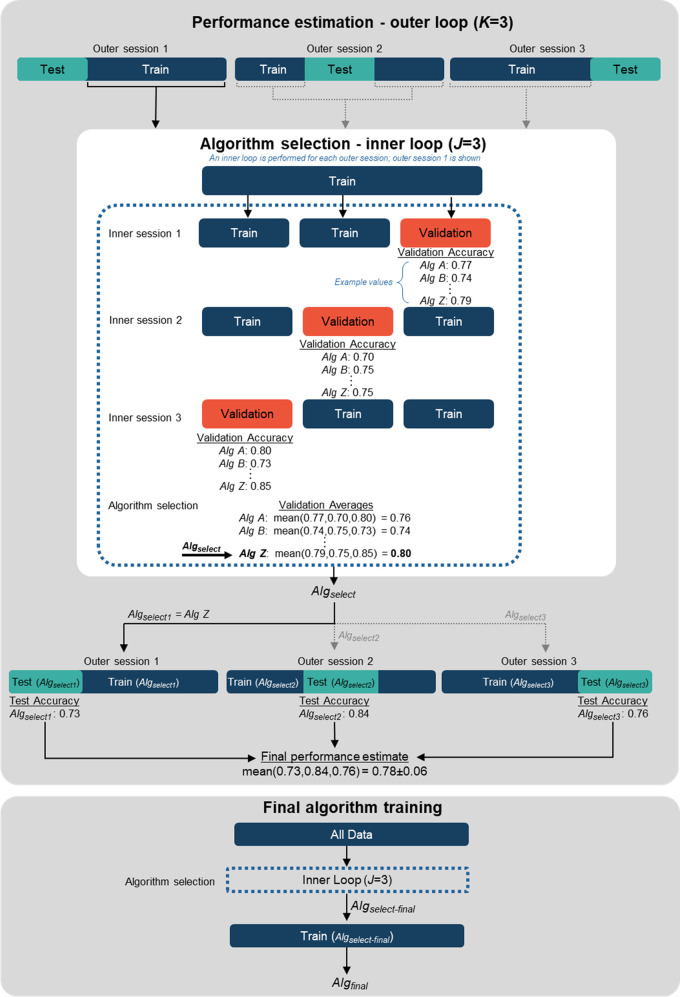
Nested CV allows for both performance estimation and algorithm selection or hyperparameter tuning and is useful for small datasets (24). Nested CV is often used as part of an automated pipeline when model developers are considering many different algorithms or hyperparameter sets and want to estimate the generalization performance of the best model. Various approaches to nested CV have been proposed (11). In nested k-fold CV, there are two loops: an outer loop with k folds and an inner loop with j folds. The inner loop is used to select or tune an algorithm, and the outer loop is used to estimate the performance of the algorithm selected by the inner loop. Nested CV is arguably the most complex CV approach. We have illustrated a common nested CV approach, nested k-fold CV, in Figure 6 and provide Python code in Appendix S1.

Figure 6:

Diagram illustrates nested cross-validation (CV). An example 3 × 3 nested CV procedure is shown for which there are multiple candidate algorithms (Alg A, Alg B, …, Alg Z). For performance estimation (top), each outer session consists of an inner loop that selects the best algorithm (Alg_select). The inner loop shown here is for outer session 1, in which Alg Z is selected as Alg_select. Alg Z is then used in outer session 1 for training and testing. The final performance estimate is the average of the test results for each outer session (note that Alg_select can be different algorithms for each outer session). Final algorithm training (bottom) also includes an inner loop for algorithm selection using all the data, after which the final algorithm, Alg_select-final, is trained using all the data.

It is important to note that the k inner loops may each select a different algorithm (shown as Alg_select in the figure). The final performance estimate would then be an average over the different algorithms. This is not a problem, as the goal of CV is to evaluate the pipeline used to create the algorithm, and in the case of nested CV, the pipeline includes an inner loop that performs algorithm selection. Consequently, if a final algorithm is to be trained or deployed, it must also undergo an algorithm selection step using the same process used in the inner loop (see Figure 6 for details).

Leave-One-Out

In each session of leave-one-out CV (LOOCV), data from a single patient are withheld for testing while the rest are used for training (Fig 3). LOOCV is equivalent to k-fold CV, where k is set to the number of patients available (N). N total models are trained, and the performance is the average across the N performance measurements. The advantage of LOOCV is that, for small datasets, more data can be used for training. Its disadvantages include computational demands, which can impose limitations on model size, and an unclear benefit over k-fold CV (25,26).

Select-Shuffle-Test

We introduce a new CV method to address a drawback of nested CV. In nested CV, the final or deployed algorithm is selected at the end only after the performance of the pipeline has been estimated using the inner and outer loops. However, these independent steps could be reversed: First, the final algorithm is selected and then, that algorithm is tested using CV. Notably, no inner loops are needed with this approach because the final algorithm will have already been selected or tuned up front. Only the outer loop is needed. The result is what we call select-shuffle-test. In select-shuffle-test, k-fold CV is used to select the best algorithm, the data gets randomly shuffled, and then k-fold CV is used again to estimate the performance of the selected algorithm (Fig 3).

Random Sampling

Random sampling CV is known by many names: repeated holdout, Monte Carlo CV, random permutations CV, and shuffle-and-split. In random sampling CV, the samples in the dataset are randomly assigned to training, testing, and, if needed, validation sets according to prespecified proportions. With each iteration, the samples are randomly shuffled so that each set is unique from the previous iteration, even if there is some overlap in the sets from one iteration to the next. This is repeated multiple times, and the performance is averaged over the test sets for all iterations. The advantages of this approach are that it is relatively simple and that it provides CIs. A disadvantage is that some samples may be randomly underrepresented in the test sets over the different iterations.

Bootstrapping

Bootstrap CV is like random sampling CV, except that the training dataset is sampled “with replacement” from the overall dataset. This means that when a sample is randomly selected to be assigned to the training set, it remains in the selection pool. Samples can therefore appear in the training set more than once (Fig 3). Often, the size of the training set is the same size as the overall dataset, but due to random sampling with repeats, only 63.2% of the samples on average will be selected into the training set (27). The remaining 36.8% (sometimes more, sometimes less) serve as the test set for that session (10). Bootstrapping CV does not appear to have meaningful advantages over random sampling CV (28).

Multicenter Evaluation

It is important to consider multicenter evaluation. A primary objective of external validation, which is needed prior to algorithm deployment (8,29), is to measure the sensitivity of the algorithm to dataset shift (Fig 5).

The simplest approach is to withhold data from one or more institutions from training and use them for testing. To quantify the severity of dataset shift, the model’s external accuracy is compared with the model’s internal (CV) accuracy. A weakness of this approach is that the data withheld for external testing may not be representative of other external populations.

An alternative approach is leave-one-institution-out CV (Fig 3), where data from one institution are withheld for external testing while data from the remaining institutions are combined and used for training and hyperparameter tuning (30). This process is repeated until each institution has served as the external test institution. In a study using AI to predict COVID-19 prognosis on the basis of radiographs, leave-one-institution-out CV was compared with k-fold CV and was found to predict poorer generalizability of the models than did k-fold CV (14).

CV for Imbalanced Datasets

Many real-life medical imaging datasets are heavily imbalanced, meaning cases from some classes (eg, disease negative) far outnumber other classes (eg, rare diseases). For CV with imbalanced datasets, special considerations may be needed beyond stratified sampling. As prediction models built from imbalanced datasets can underperform for minority classes (31,32), strategies to cope with imbalanced data have been developed. These include data sampling and algorithmic methods (eg, weighted loss functions) (33). For data-level approaches, undersampling (removing majority examples) or oversampling (replicating minority examples [34]) is often used. For example, Xie et al (35) found that oversampling improved the prediction performance of models in an imbalanced PET radiomics dataset. However, if oversampling is incorrectly combined with CV, it can lead to overoptimism (33). These biases can be avoided by ensuring that oversampling and undersampling are not used to generate the CV validation or test sets.

Recommendations and Discussion

This review and the examples in Appendix S1 are intended to serve as an introduction and guide to readers on implementing CV in medical imaging studies. While we have omitted much of the theory of CV, we recommend to readers additional literature covering these topics (10,36,37).

There is no single CV technique that is recommended for all situations. We recommend that developers first consider their dataset size, their needs for algorithm selection or tuning, and the computational demands of training their model, and then consult the Table to select an appropriate approach. Generally, one of these three CV techniques is often appropriate for medical imaging AI studies: one-time splits when datasets are very large, random-sampling CV when tuning or selection is needed, or k-fold (or repeated k-fold) CV. For further recommendations on selecting the number of folds, iterations, train-test split fractions, or other CV hyperparameters, we recommend additional literature (10,23,38).

Estimating CIs for performance metrics is an important but challenging part of CV. When the performance metric is linear in the data distribution, such as mean-squared error, it is common practice to report the variance of the model’s performance across different rounds of CV, and 95% CIs can be inferred using a normal approximation (10). However, this method does not take into account that because of overlap in the training and, sometimes, testing sets, each round of CV is not independent (39). This approach is even less appropriate for nonlinear performance metrics, such as area under the receiver operating characteristic curve (23). These challenges related to CI estimation, including statistical testing for algorithm comparison, are best addressed in other literature (10,40,41).

A principle deserving of brief discussion is that of bias and variance in the context of CV. Here, bias and variance refer to how well the prediction error estimated with CV matches the true prediction error of the model (ie, if the model were applied to new data drawn from the same population as the training data). Use of certain CV approaches can result in lower bias or lower variance in error estimation compared with other CV approaches (42). Knowledge of these bias-variance trade-offs could guide readers to the most suitable approach. However, it should be recognized that the behavior of CV under various scenarios is complex, and results can depend on the dataset and type of model (22,43,44).

Last, this article focused on CV in the context of AI development, but CV also has applications beyond model performance estimation. For example, CV is used in variable selection for multivariable models (45), which is important for radiomics studies. Additional related principles not covered in this article but described elsewhere include hyperparameter tuning (46), model selection (47), and ensembling (48).

Conclusion

In summary, CV is a powerful tool for developing and evaluating AI models. Appropriate use of CV can help developers avoid pitfalls that can impede the clinical translation of AI algorithms in medical imaging.