Exact inference for disease prevalence based on a test with unknown specificity and sensitivity

Abstract

To make informative public policy decisions in battling the ongoing COVID-19 pandemic, it is important to know the disease prevalence in a population. There are two intertwined difficulties in estimating this prevalence based on testing results from a group of subjects. First, the test is prone to measurement error with unknown sensitivity and specificity. Second, the prevalence tends to be low at the initial stage of the pandemic and we may not be able to determine if a positive test result is a false positive due to the imperfect test specificity. The statistical inference based on a large sample approximation or conventional bootstrap may not be valid in such cases. In this paper, we have proposed a set of confidence intervals, whose validity doesn't depend on the sample size in the unweighted setting. For the weighted setting, the proposed inference is equivalent to hybrid bootstrap methods, whose performance is also more robust than those based on asymptotic approximations. The methods are used to reanalyze data from a study investigating the antibody prevalence in Santa Clara County, California in addition to several other seroprevalence studies. Simulation studies have been conducted to examine the finite-sample performance of the proposed method.

1. Introduction

Determining the proportion of people who have developed antibodies to SARS-CoV-2 due to prior exposure is an important piece of information for guiding the response measures to COVID-19 in different populations. This proportion is also key to understanding the severity of the disease in terms of estimating the infection fatality rate among those infected; for example, see [3,6,13,21], and for an overview of 82 studies, see [14]. One effective way of estimating the proportion of people who have developed antibodies is to conduct a survey in the community of interest: sample a subgroup of people from the target population and measure their antibody status using a test kit. The prevalence of SARS-CoV-2 antibodies can oftentimes be low, in the range of 0–2%, especially at the early stage of viral spread in a population. In these circumstances, the simple proportion of the positive results among all conducted tests can be a poor estimate of the true prevalence due to the simple fact that all tests are not perfect [19]. For example, suppose that the test used in the study has fairly good operational characteristics: sensitivity $=95\mathrm{\%}$ and specificity $=99\mathrm{\%}$. Then, if the true prevalence rate in the study population is 1%, based on a simple calculation, $1\mathrm{\%}\times 95\mathrm{\%}+99\mathrm{\%}\times (1-99\mathrm{\%})=1.9\mathrm{\%}$ of the tests would be positive. The proportion of positive tests, in this case, is almost double the true prevalence.

Therefore, the proportion of the positive tests may not represent the true prevalence and should be adjusted for the sensitivity and specificity of the deployed test. If the sensitivity and specificity of the test are unrealistically assumed to be known, an unbiased estimate of the true prevalence can be obtained easily and its 95% confidence interval can be constructed [18]. However, this is usually not the case, and in practice, the reported sensitivity and specificity of the test are often obtained based on a limited number of experiments and are random estimates subject to errors themselves. In the absence of a gold reference to estimate sensitivity and specificity against, a Bayesian approach is suggested in [7]. Therefore, it is important to develop an inference procedure to account for the randomness from study data as well as from reported sensitivity and specificity. When the prevalence is low and the specificity is around (1-prevalence), statistical inference based on large sample approximation such as delta-method and naive bootstrap may not be reliable. In this paper, we have proposed an exact inference method for the disease prevalence without requiring any large sample approximation if the study participants are randomly sampled from the target population. When biased sampling is used, the weighted inference is needed to correct the bias in estimating the prevalence in the target population. As an extension of the exact method, we have proposed a novel hybrid bootstrap method, which has a more robust finite sample performance than that based on a simple large sample approximation. The method can be useful for statistical inference of the prevalence of antibodies to SARS-CoV-2 in a given population.

2. Method

2.1. Exact inference based on random sampling

Our goal is to construct a reliable confidence interval for disease prevalence in scenarios with true specificity close to 1, where the normality assumption for the reported sensitivity does not necessarily hold. In a typical setting, we observe three separate estimates for the proportion of positive tests $r_0$, sensitivity $p_0$, and specificity $q_0$, denoted by $\hat{r},$ $\hat{p}$ and $\hat{q}$, respectively. Specifically, we assume to observe three independent binomials random variables

$$\begin{array}{rl}& d\sim Bin(D,r_0),\\ & m\sim Bin(M,p_0),\\ & n\sim Bin(N,q_0),\end{array}$$

$\hat{r}=d/D$, $\hat{p}=m/M$ and $\hat{q}=n/N,$ where D is the sample size in the current study; M is the number of positive reference samples used to estimate the sensitivity; and N is the number of negative reference samples used to estimate the specificity. Normally, D is big relative to M and N, whose typical values are in the range of tens or hundreds. Because we assume the experiments to estimate the prevalence, the assay sensitivity, and the assay specificity have no overlap in samples, $\hat{r}$, $\hat{p}$ and $\hat{q}$ are independent.

Based on the relationship

$$r_0={\pi }_0{p}_0+(1-{\pi }_0)(1-q_0),$$

we may solve for the true disease prevalence ${\pi }_0$ in terms of $r_0,p_0,$ and $q_0$ as

$${\pi }_0=f(r_0,p_0,q_0),$$ (1)

where

$$f(r,p,q):=\frac{r+q-1}{p+q-1}.$$

A simple point estimator of the prevalence ${\pi }_0$ adjusted for sensitivity and specificity is thus

$$\hat{\pi }=f(\hat{r},\hat{p},\hat{q}).$$ (2)

As $min(D,M,N)\to \mathrm{\infty }$, under the regularity conditions listed in Theorem A.1 in the appendix, the central limit theorem suggests the weak convergence for each of the binomial random variables. Coupled with the fact that these three estimators are based on independent samples from separate experiments, it suggests asymptotic independence and the joint weak convergence

$$\left[\begin{array}{c}\sqrt{D}(\hat{r}-r_0)\\ \sqrt{M}(\hat{p}-p_0)\\ \sqrt{N}(\hat{q}-q_0)\end{array}\right]⟹dN(\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right],\left[\begin{array}{ccc}{r}_0(1-r_0)& 0& 0\\ 0& p_0(1-p_0)& 0\\ 0& 0& q_0(1-q_0)\end{array}\right]),$$

and $\hat{\pi }-{\pi }_0$ can be approximated by a mean zero Gaussian distribution with variance

$$\frac{r_0(1-r_0)}{D(p_0+q_0-1{)}^2}+\frac{{\pi }_0^2{p}_0(1-p_0)}{M(p_0+q_0-1{)}^2}+\frac{(r_0-p_0{)}^2{q}_0(1-q_0)}{N(p_0+q_0-1{)}^4}.$$

This variance is unknown but can be consistently estimated by

$${\hat{\sigma }}^2=\frac{\hat{r}(1-\hat{r})}{D(\hat{p}+\hat{q}-1{)}^2}+\frac{{\hat{\pi }}^2\hat{p}(1-\hat{p})}{M(\hat{p}+\hat{q}-1{)}^2}+\frac{(\hat{r}-\hat{p}{)}^2\hat{q}(1-\hat{q})}{N(\hat{p}+\hat{q}-1{)}^4}.$$

Therefore, a simple 95% confidence interval for ${\pi }_0$ can be constructed as

$$[\hat{\pi }-1.96\hat{\sigma },\hat{\pi }+1.96\hat{\sigma }].$$ (3)

This confidence interval can be viewed as a product of inverting a Wald test $H_0:{\pi }_0=\pi$ based on the test statistic

$$\hat{T}\left(\pi \right)=\frac{\hat{\pi }-\pi }{\hat{\sigma }}$$

which approximately follows a standard Gaussian distribution with mean zero and unit variance under the null hypothesis $H_0:{\pi }_0=\pi .$ Specifically, the p-value of the test can be calculated as

$$p\left(\pi \right)=P(|Z|>|\hat{T}(\pi \left)|\right)$$

and the 95% confidence interval based on (3) can be expressed as

$$\{\pi \mid p(\pi )>0.05\},$$

i.e. all π, at which we cannot reject the null hypothesis at the 0.05 significance level. Here $Z\sim N(0,1).$

Remark 2.1

The derivation of the asymptotic joint distribution of $\hat{r},\hat{p}$ and $\hat{q}$ above relies on the fact that they are all independent. In a more complex setting, where the test result is obtained by dichotomizing a continuous biomarker level, those estimates can be dependent if the cut-off value itself is estimated empirically, and we would want to account for its randomness when performing inference on $p_0$, $q_0$ and ${\pi }_0$ [1,22].

Remark 2.2

In the extreme case, the confidence interval above may include negative values. To preserve the appropriate range of the prevalence, one may first construct the 95% confidence interval for $\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\left({\pi }_0\right)$ as

$$\left[\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\right(\hat{\pi })-\frac{1.96\hat{\sigma }}{\hat{\pi }(1-\hat{\pi })},\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}(\hat{\pi })+\frac{1.96\hat{\sigma }}{\hat{\pi }(1-\hat{\pi })}]$$

and transform it back via $\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{i}\mathrm{t}(\cdot )$ to a confidence interval for ${\pi }_0.$

When $q_0$ is close to 1 and/or $r_0$ is close to zero, the null distribution of $\hat{T}$ may not be approximated well by the standard normal and the p-value based on asymptotic approximation, i.e. $p\left(\pi \right),$ becomes unreliable. The bootstrap method has also been used to construct the confidence interval of ${\pi }_0.$ There are different variations of the bootstrap method. The simplest version draws

$$\begin{array}{rl}{r}_b^{\ast }& \sim Bin(D,\hat{r})/D,\\ p_b^{\ast }& \sim Bin(M,\hat{p})/M,\\ q_b^{\ast }& \sim Bin(N,\hat{q})/N,\end{array}$$

and calculate ${\pi }_b^{\ast }=f(r_b^{\ast },p_b^{\ast },q_b^{\ast })$ for $b=1,\dots ,B,$ where B is a large integer specified by the user. Then two ends of the 95% confidence interval of ${\pi }_0$ can be constructed as 2.5 and 97.5 percentile of $\{{\pi }_b^{\ast },b=1,\dots ,B\}$. However, the validity of the bootstrap method also relies on a large sample approximation, which may be broken in some settings of interest.

To address this concern, we propose to calculate the exact confidence interval by inverting a test, while accounting for nuisance parameters. Chan and Zhang [4] proposed an exact confidence interval for the difference in two binomial proportions, treating the proportion in the reference group as a nuisance parameter. The exact confidence interval was constructed by inverting a hypothesis test for the difference in proportion, in which the p-value was computed by considering all potential values for the nuisance parameter and thus exact. The author of [9,10,15,20] proposed similar methods for different statistical models such as the beta-binomial model [10] and normal-normal random effects model in meta-analysis [15]. Here, we adopt a similar approach and proceed through the following steps:

1. Construct 99.9% confidence interval for $r_0$, $p_0$ and $q_0$ denoted by $I_r$, $I_p$ and $I_q,$ respectively. The high coverage level of 99.9% is chosen to ensure that the probability of $(r_0,p_0,q_0)\in I_r\times I_p\times I_q$ is much greater than 95%. For example, we can take $I_r$ to consist of all probabilities r such that

   $$min\left\{P\right(Bin(D,r)\ge d),P(Bin(D,r)\le d\left)\right\}\ge 0.1\mathrm{\%}.$$

   Confidence intervals $I_p$ and $I_q$ can be constructed similarly.

2. For a given π, define ${\mathrm{\Omega }}_{\pi }=\left\{\right(r,p,q)\mid f(r,p,q)=\pi ,(r,p,q)\in I_r\times I_p\times I_q\}.$

3. Select a dense net ‘spanning’ ${\mathrm{\Omega }}_{\pi }:$ $\left\{\right(r_k,p_k,q_k)\in {\mathrm{\Omega }}_{\pi },k=1,\dots ,K\}$ such that for any $(r,p,q)\in {\mathrm{\Omega }}_{\pi }$, there exists a $k\in \{1,\dots ,K\}$ such that $|r_k-r|+|p_k-p|+|q_k-q|\le ϵ$ for a small constant $ϵ>0.$

4. For each $(r_k,p_k,q_k)$ from the net, we simulate

   $$\begin{array}{rl}& r_b^{\ast }\sim Bin(D,r_k)/D,\\ & p_b^{\ast }\sim Bin(M,p_k)/M,\\ & q_b^{\ast }\sim Bin(N,q_k)/N,\end{array}$$

   and let

   $$\begin{array}{rl}{\pi }_b^{\ast }& =f(r_b^{\ast },p_b^{\ast },q_b^{\ast }),\\ {{\sigma }_b^{\ast }}^2& =\frac{r_b^{\ast }(1-r_b^{\ast })}{D(p_b^{\ast }+q_b^{\ast }-1{)}^2}+\frac{{{\pi }_b^{\ast }}^2{p}_b^{\ast }(1-p_b^{\ast })}{M(p_b^{\ast }+q_b^{\ast }-1{)}^2}+\frac{(r_b^{\ast }-p_b^{\ast }{)}^2{q}_b^{\ast }(1-q_b^{\ast })}{N(p_b^{\ast }+q_b^{\ast }-1{)}^4}\end{array}$$

   for $b=1,\dots ,B,$ where B is a large number such as $1,000.$ The distribution of $\hat{T}(r_k,p_k,q_k)$ under the simple null hypothesis $H_0:(r_0,p_0,q_0)=(r_k,p_k,q_k)$ can be approximated by the empirical distribution of

   $$\left\{T_b^{\ast }\right(r_k,p_k,q_k),b=1,\dots ,B\},$$

   where

   $$T_b^{\ast }(r_k,p_k,q_k)=\frac{{\pi }_b^{\ast }-\pi }{{\sigma }_b^{\ast }}.$$

   Specifically, the exact p-value for testing $H_0:(r_0,p_0,q_0)=(r_k,p_k,q_k)$ can be estimated by

   $$\hat{p}(r_k,p_k,q_k)=B^{-1}\sum _{b=1}^{B}I\left(|T_b^{\ast }\right(r_k,p_k,q_k)|\ge |\hat{T}(\pi \left)|\right),$$

   where $I(\cdot )$ is the indicator function.
5. Since $H_0:{\pi }_0=\pi$ is a composite null hypothesis, the exact p-value for testing $H_0:{\pi }_0=\pi$ can be approximated by

   $$\hat{p}\left(\pi \right)=\underset{k=1,\dots ,K}{max}\hat{p}(r_k,p_k,q_k).$$

Lastly, the 95% confidence interval for ${\pi }_0$ can be constructed as

$$\{\pi \mid \hat{p}(\pi )\ge 0.05-0.003\},$$

i.e. all π's with an exact p-value is greater than 0.05−0.003 = 0.047. The adjustment of 0.003 in the significance level is needed to account for the joint coverage level of three confidence intervals $I_r,$ $I_p,$ and $I_q$ at step (1), i.e. $P\left(\right(r_0,p_0,q_0)\in I_r\times I_p\times I_q)\ge 1-\mathrm{0.003.}$

Remark 2.3

If ${\mathrm{\Omega }}_{\pi }=\varphi ,$ i.e. there is no $(r,p,q)\in I_r\times I_p\times I_q$ such that $f(r,p,q)=\pi$, then let $\hat{p}\left(\pi \right)=0$.

Remark 2.4

The construction of the grid points in ${\mathrm{\Omega }}_{\pi }$ can be completed by first considering all the points $\left\{\right(p_i,q_j\left)\right\},$ where $\left\{p_i\right\}$ is a set of evenly spaced points over $I_p$ and $\left\{q_j\right\}$ is a set of evenly spaced points over $I_q$. Then for each $(p_i,q_j)$, we may solve the equation $f(r,p_i,q_j)=\pi$ in terms of r. If the solution $r_{ij}\in I_r,$ then the triplet $(p_i,q_j,r_{ij})$ is included in a dense net.

The proposed exact confidence intervals always can cover the true prevalence at the desired level regardless of the sample size, if we ignore the Monte-Carlo error in calculating the p-value $\hat{p}(r_k,p_k,q_k),$ which can be made arbitrarily small by increasing B in the simulation and considering a more dense net spanning the region ${\mathrm{\Omega }}_{\pi }.$

The computation can be slow, since for each hypothesis test, we need to simulate the null distribution of $\hat{T}\left(\pi \right)$ for many triplets $(r_k,p_k,q_k)\in {\mathrm{\Omega }}_{\pi }.$ We can accelerate this computation using hybrid bootstrap [5], where some nuisance parameters are fixed to their point estimates when approximating the distribution of the test statistic. For example, we may assume $p_0=\hat{p}$ and only consider pairs $(r,q)$ such that $f(r,\hat{p},q)=\pi$ to generate the exact p-value of $H_0:{\pi }_0=\pi .$ Specifically, we may let $\{q_j,j=1,\dots ,J\}$ be evenly spaced points over $I_q$ and let $r_j=\pi \hat{p}-(1-\pi )(q_j-1)$. In the end,

$$\hat{p}\left(\pi \right)=\underset{1\le j\le J,r_j\in I_r}{max}\hat{p}(r_j,\hat{p},q_j).$$

Since $p_0$ is fixed at $\hat{p},$ the number of pairs $(r,q)$ to be considered for each fixed level π can be much smaller than the number of triplets $(r,p,q)$. The price for gaining the computation speed is sacrificing the ‘exact’ coverage level in a finite sample due to the fact that the observed point estimator of the nuisance parameters may be quite different from the true parameter. Consequently, the coverage level of the confidence interval based on hybrid bootstrap is not always guaranteed in all settings. However, we expect that it still performs better than the naive confidence interval (3), where all unknown parameters were assumed to be their observed estimates. It can be viewed as a compromise between the computational intensive exact inference and asymptotic inference based on large sample approximations.

2.2. Hybrid bootstrap for weighted inference

When the survey for studying disease prevalence is not conducted using a representative sample, appropriate weighting of the samples is needed to obtain an unbiased estimate of the prevalence. There are two typical settings. (1) There are several strata and the sampling is considered random (and thus representative) within each stratum; In such a case, the strata-specific weighting will be employed. (2) The sampling represents a population different from the target, but a propensity score can be constructed and individual-specific weighting will be needed. In the following, we will address these two cases separately.

2.2.1. Stratum specific weighting

Suppose that the target population consists of S strata with proportions $w_1,\dots ,w_{S-1},$ and $w_S.$ Also suppose that the underlying disease prevalence in each of the S strata is ${\pi }_1,\dots ,{\pi }_{S-1},$ and ${\pi }_S.$ The parameter of interest is the overall disease prevalence in the target population:

$${\pi }_w=\sum _{s=1}^S{w}_s{\pi }_s.$$

Let the number of tests conducted in these strata be $D_1,\dots ,D_{S-1},$ and $D_S,$ respectively. The number of positive tests in stratum s follows a Poisson distribution:

$$d_s\sim Pois\left(D_s{r}_s\right),$$

which can be approximated by $N(D_s{r}_s,D_s{r}_s),$ where $r_s={\pi }_s{p}_0+(1-{\pi }_s)(1-q_0).$ Consequently,

$$d_w=\sum _{s=1}^S{\tilde{w}}_s{d}_s\sim N(D{r}_w,{\lambda }_{0}D{r}_w),$$

where $D=\sum _{s=1}^S{D}_s,$ ${\tilde{w}}_s=w_s/\left(D_s/D\right),$ $r_w=\sum _{s=1}^S{w}_s{r}_s,$ and

$${\lambda }_0=\frac{\sum _{s=1}^S{\tilde{w}}_s{w}_s{r}_s}{r_w}$$

is the variance inflation factor. Noting that ${\pi }_w=f(r_w,p_0,q_0),$ we can estimate ${\pi }_w$ based on $d_w$ by

$${\hat{\pi }}_w=f({\hat{r}}_w,\hat{p},\hat{q}),$$

where ${\hat{r}}_w=d_w/D.$ Define the test statistic

$${\hat{T}}_w\left(\pi \right)=\frac{{\hat{\pi }}_w-{\pi }_w}{{\hat{\sigma }}_w},$$

where

$$\begin{array}{rl}{\hat{\sigma }}_w^2& =\frac{\hat{\lambda }{\hat{r}}_w}{D(\hat{p}+\hat{q}-1{)}^2}+\frac{{\hat{\pi }}_w^2\hat{p}(1-\hat{p})}{M(\hat{p}+\hat{q}-1{)}^2}+\frac{({\hat{r}}_w-\hat{p}{)}^2\hat{q}(1-\hat{q})}{N(\hat{p}+\hat{q}-1{)}^4},\\ \hat{\lambda }& ={\hat{r}}_w^{-1}\left\{\sum _{s=1}^S{\tilde{w}}_s{w}_s{\hat{r}}_s\right\},\end{array}$$

and ${\hat{r}}_s=d_s/D_s.$

To calculate the exact p-value for testing $H_0:{\pi }_w=\pi$, we only need to modify the steps (1), (4) and (5) of the algorithm in Section 2.1.

1. Construct 99.9% confidence intervals for $r_w$ denoted by $I_r$ assuming ${\lambda }_0=\hat{\lambda }.$

2. For each $(r_k,p_k,q_k)$ from the net for ${\mathrm{\Omega }}_{\pi }$, we simulate

   $$r_{wb}^{\ast }\sim N(D{r}_k,\hat{\lambda }D{r}_k)/D$$

   and let ${\pi }_{wb}^{\ast }=f(r_{wb}^{\ast },p_b^{\ast },q_b^{\ast })$ and

   $${\sigma }_{wb}^{\ast 2}=\frac{\hat{\lambda }{r}_{wb}^{\ast }}{D(p_b^{\ast }+q_b^{\ast }-1{)}^2}+\frac{{{\pi }_{wb}^{\ast }}^2{p}_b^{\ast }(1-p_b^{\ast })}{M(p_b^{\ast }+q_b^{\ast }-1{)}^2}+\frac{(r_{wb}^{\ast }-p_b^{\ast }{)}^2{q}_b^{\ast }(1-q_b^{\ast })}{N(p_b^{\ast }+q_b^{\ast }-1{)}^4}$$

   for $b=1,\dots ,B.$ The exact p-value for testing $H_0:(r_w,p_0,q_0)=(r_k,p_k,q_k)$ can be estimated by

   $${\hat{p}}_w(r_k,p_k,q_k)=B^{-1}\sum _{b=1}^{B}I(\left|\frac{{\pi }_{wb}^{\ast }-\pi }{{\sigma }_{wb}^{\ast }}\right|\ge |{\hat{T}}_w(\pi \left)|\right).$$
3. The exact p-value for testing $H_0:{\pi }_w=\pi$ can be approximated by

   $${\hat{p}}_w\left(\pi \right)=\underset{k=1,\dots ,K}{max}{\hat{p}}_w(r_k,p_k,q_k).$$

The 95% confidence interval for ${\pi }_w$ thus consists of all values of π such that the exact p-value for testing $H_0:{\pi }_w=\pi$ is greater than 0.05−0.003. The validity of the resulting confidence interval requires the following assumptions:

• Assumption 1: $d_s\sim Pois\left(D_s{r}_s\right)$, which can be approximated by the Gaussian $N(D_s{r}_s,D_s{r}_s).$ To ensure a good normal approximation to the Poisson distribution, $r_s$ needs to be small and $D_s{r}_s$ needs to be reasonably big, e.g. $\ge$10.

• Assumption 2: $\hat{\lambda }$ is a good approximation for ${\lambda }_0$.

2.2.2. Individual specific weighting

With a slight abuse of notation, now suppose that the ith subject has a test result, denoted by a Bernoulli random variable $d_i\sim Ber\left(r_i\right),$ and a weight $w_i$, where $r_i={\pi }_i{p}_0+(1-{\pi }_i)(1-q_0),$ ${\pi }_i$ is the probability that the subject has the antibody, and $\sum _{i=1}^D{w}_i=D.$ Our goal is again to estimate the weighted prevalence

$${\pi }_w=\frac{1}{D}\sum _{i=1}^D{w}_i{\pi }_i.$$

Since $d_i\sim Ber\left(r_i\right)$, as D grows large, by central limit theorem, we can approximate

$$\frac{1}{D}\sum _{i=1}^D{w}_i{d}_i\sim N(\frac{1}{D}\sum _{i=1}^D{w}_i{r}_i,\frac{1}{D^2}\sum _{i=1}^D{w}_i^2{r}_i(1-r_i\left)\right)=N(r_w,\frac{1}{D^2}\sum _{i=1}^D{w}_i^2{r}_i(1-r_i\left)\right),$$

under the Lindeberg condition that

$$\underset{D\to \mathrm{\infty }}{lim}\frac{1}{s_n^2}\sum _{k=1}^D\mathbf{\text{E}}\left[w_k^2\right(d_k-r_k{)}^{2}I\{w_k|d_k-r_k|>ϵs_n\}]\to 0$$

for any $ϵ>0$, where $r_w=D^{-1}\sum _{i=1}^D{w}_i{r}_i$ and $s_n=\sum _{k=1}^D{w}_k^2{r}_k(1-r_k)$. A sufficient condition for the aforementioned convergence is

$$\underset{D\to +\mathrm{\infty }}{lim}\frac{\underset{1\le j\le D}{max}{w}_j}{\sum _{j=1}^D{w}_j^2{r}_j(1-r_j)}\to 0.$$

This holds, for example, when $w_i$ are uniformly bounded above and below by positive constants and $r_i$ are uniformly bounded away from 0 and 1. Since it is difficult to estimate $\sum _{i=1}^D{w}_i^2{r}_i(1-r_i)$, we make the further approximation

$${\lambda }_0=\frac{\sum _{i=1}^D{w}_i^2{r}_i(1-r_i)}{D{r}_w(1-r_w)}\approx \frac{\sum _{i=1}^D{w}_i^2{r}_i}{D{r}_w}\approx \frac{\sum _{i=1}^D{w}_i^2{d}_i}{\sum _{i=1}^D{w}_i{d}_i}=\hat{\lambda },$$ (4)

and

$$d_w=\sum _{i=1}^D{w}_i{d}_i\sim N(D{r}_w,\hat{\lambda }D{r}_w(1-r_w\left)\right).$$

Then we can repeat the steps above to construct the confidence interval, noting that ${\pi }_w=f(r_w,p_0,q_0)$. We let the test statistic be

$${\hat{T}}_w\left(\pi \right)=\frac{{\hat{\pi }}_w-{\pi }_w}{{\hat{\sigma }}_w},$$

where ${\hat{r}}_w=d_w/D,$ ${\hat{\pi }}_w=f({\hat{r}}_w,\hat{p},\hat{q}),$ and

$${\hat{\sigma }}_w^2=\frac{\hat{\lambda }{\hat{r}}_w(1-{\hat{r}}_w)}{D(\hat{p}+\hat{q}-1{)}^2}+\frac{{\hat{\pi }}_w^2\hat{p}(1-\hat{p})}{M(\hat{p}+\hat{q}-1{)}^2}+\frac{({\hat{r}}_w-\hat{p}{)}^2\hat{q}(1-\hat{q})}{N(\hat{p}+\hat{q}-1{)}^4},$$

To calculate the exact p-value for testing $H_0:{\pi }_w=\pi$, we only need to modify step (4) of the algorithm in Section 2.1.

• (4)
  For each $(r_k,p_k,q_k)$ from the net, we simulate

  $$r_{wb}^{\ast }\sim N(D{r}_k,\hat{\lambda }D{r}_k(1-r_k\left)\right)/D$$

  and let ${\pi }_{wb}^{\ast }=f(r_{wb}^{\ast },p_b^{\ast },q_b^{\ast })$ and

  $${\sigma }_{wb}^{\ast 2}=\frac{\hat{\lambda }{r}_{wb}^{\ast }(1-r_{wb}^{\ast })}{D(p_b^{\ast }+q_b^{\ast }-1{)}^2}+\frac{{{\pi }_{wb}^{\ast }}^2{p}_b^{\ast }(1-p_b^{\ast })}{M(p_b^{\ast }+q_b^{\ast }-1{)}^2}+\frac{(r_{wb}^{\ast }-p_b^{\ast }{)}^2{q}_b^{\ast }(1-q_b^{\ast })}{N(p_b^{\ast }+q_b^{\ast }-1{)}^4}$$

  for $b=1,\dots ,B.$

For the proposed inference to be valid, we require the following assumptions:

• Assumption 1: $\underset{D\to +\mathrm{\infty }}{lim}\frac{\underset{1\le j\le D}{max}{w}_j}{\sum _{j=1}^D{w}_j^2{r}_j(1-r_j)}\to 0$, which is needed for the Central Limit Theorem to hold.

• Assumption 2: $\hat{\lambda }$ is a good approximation for ${\lambda }_0$.

The hybrid bootstrap method, while not exact, is in general more robust than large sample approximation-based methods in finite samples.

3. Simulation

In this section, we have conducted extensive simulation studies to investigate the operational characteristics of the proposed method and compare it with existing methods in finite samples.

3.1. Unweighted inference

In this simulation study, we mimic the Santa-Clara study by considering the following settings:

1. the sensitivity $p_0=83\mathrm{\%};$ sample size $M=157;$

2. the specificity $q_0\in \{97\mathrm{\%},98\mathrm{\%},98.4\mathrm{\%},98.6\mathrm{\%},98.8\mathrm{\%},99\mathrm{\%},99.2\mathrm{\%},99.4\mathrm{\%},99.8\mathrm{\%},99.9\mathrm{\%},100\mathrm{\%}\}$; sample size $N=371;$ and separately for $N=3324;$

3. the true prevalence ${\pi }_0\in \{0.4\mathrm{\%},1.2\mathrm{\%},5\mathrm{\%},10\mathrm{\%}\}$; sample size $D=3330.$

For each setting, we have generated 2000 sets of data and constructed the 95% confidence interval using the proposed exact method, the delta method, nonparametric bootstrap, and hybrid bootstraps where we have fixed the proportion of positive tests $\left(r_0\right)$, sensitivity ( $p_0$), or both. In these simulations, we set B = 1000. Throughout our testing, we have found that setting B>1000 does not significantly change the resulting confidence interval. However, in practice, there is only one set of data and so we can take B to be much larger; the intervals in Section 4 were computed with B = 3000. Table 1 summarizes the average length and the empirical coverage level of constructed 95% confidence intervals for ${\pi }_0=1.2\mathrm{\%}$ and for N = 317 only.

Table 1.

The empirical coverage probability and average length of 95% confidence interval of ${\pi }_0$ based on exact method, delta method, nonparametric bootstrap, and hybrid bootstraps; $\pi =1.2\mathrm{\%},N=371$.

				Hybrid bootstrap
				$p_0=\hat{p}$	$r_0=\hat{r}$	$(p_0,r_0)=(\hat{p},\hat{r})$
$q_0$	Exact method Cov (Length)	Delta method Cov (Length)	Bootstrap Cov (Length)	Cov (Length)	Cov (Length)	Cov (Length)
97.0	0.974 (0.033)	0.939 (0.033)	0.942 (0.047)	0.965 (0.032)	0.957 (0.028)	0.951 (0.030)
98.0	0.973 (0.029)	0.932 (0.029)	0.933 (0.038)	0.973 (0.028)	0.954 (0.024)	0.943 (0.027)
98.4	0.973 (0.027)	0.932 (0.026)	0.935 (0.034)	0.965 (0.026)	0.951 (0.023)	0.949 (0.024)
98.6	0.978 (0.027)	0.924 (0.025)	0.933 (0.032)	0.966 (0.025)	0.949 (0.022)	0.942 (0.023)
98.8	0.976 (0.026)	0.926 (0.024)	0.933 (0.029)	0.970 (0.025)	0.944 (0.021)	0.943 (0.022)
99.0	0.966 (0.025)	0.927 (0.022)	0.924 (0.027)	0.957 (0.024)	0.945 (0.020)	0.946 (0.021)
99.2	0.968 (0.024)	0.920 (0.021)	0.928 (0.024)	0.958 (0.023)	0.943 (0.019)	0.939 (0.019)
99.4	0.975 (0.022)	0.904 (0.019)	0.897 (0.021)	0.963 (0.021)	0.952 (0.017)	0.953 (0.016)
99.6	0.990 (0.021)	0.887 (0.016)	0.869 (0.018)	0.983 (0.019)	0.968 (0.015)	0.939 (0.014)
99.8	0.999 (0.018)	0.933 (0.013)	0.911 (0.014)	0.993 (0.017)	0.918 (0.012)	0.768 (0.011)
99.9	0.994 (0.017)	0.955 (0.011)	0.938 (0.011)	0.991 (0.016)	0.834 (0.011)	0.563 (0.010)
100.0	0.970 (0.015)	0.941 (0.008)	0.947 (0.008)	0.958 (0.014)	0.652 (0.010)	0.367 (0.009)

The exact method always has a coverage of about 95% or above as anticipated. The delta method and nonparametric bootstrap may result in non-trivial under-coverage when the specificity $q_0$ is high. In addition, two hybrid bootstrap methods that fix r also may produce confidence intervals that are too narrow. One explanation of the failure of these hybrid bootstraps is that when fixing $r_0$ at $\hat{r}$, the sensitivity level implied by the true prevalence ${\pi }_0$,

$$\frac{\hat{r}-(1-q)(1-{\pi }_0)}{{\pi }_0}>1,$$

for all qs close to $q_0,$ excluding the true prevalence ${\pi }_0$ from the confidence interval. On the other hand, the hybrid bootstrap that only fixes $p_0=\hat{p}$ has coverage of at least 95% for all values of $q_0$. The same pattern repeats in other simulation settings reported in the supplementary materials as well (see Figures A1 and A2 of the appendix), so moving forward we focus on the exact method and the hybrid bootstrap that fixes $p_0=\hat{p}.$

We also repeated the simulation with N = 3324, the reported sample size in the Santa Clara study after pooling data from multiple sources. The results are summarized in Table 2. In this case, where the sample size used to estimate sensitivity is large, these four methods all give reasonable coverage for tested values of $q_0$. Not that in this case, the exact method is not much more conservative than other methods.

Table 2.

The empirical coverage probability and average length of 95% confidence interval of ${\pi }_0$ based on exact method, delta method, nonparametric bootstrap, and hybrid bootstrap; N = 3324.

					H Bootstrap
					$p_0=\hat{p}$
${\pi }_0$	$q_0$	Exact method CovP (Length)	Delta method CovP (Length)	Bootstrap CovP (Length)	CovP (Length)
1.2	97.0	0.969 (0.022)	0.956 (0.020)	0.953 (0.022)	0.969 (0.021)
1.2	98.0	0.971 (0.020)	0.956 (0.018)	0.955 (0.019)	0.954 (0.019)
1.2	98.4	0.967 (0.018)	0.952 (0.017)	0.952 (0.017)	0.953 (0.017)
1.2	98.6	0.965 (0.017)	0.950 (0.016)	0.948 (0.016)	0.952 (0.017)
1.2	98.8	0.964 (0.017)	0.954 (0.015)	0.952 (0.015)	0.956 (0.016)
1.2	99.0	0.959 (0.016)	0.947 (0.014)	0.945 (0.014)	0.953 (0.015)
1.2	99.2	0.960 (0.015)	0.950 (0.013)	0.948 (0.013)	0.946 (0.014)
1.2	99.4	0.962 (0.013)	0.952 (0.012)	0.951 (0.012)	0.938 (0.013)
1.2	99.6	0.963 (0.012)	0.953 (0.011)	0.951 (0.011)	0.943 (0.011)
1.2	99.8	0.965 (0.011)	0.957 (0.010)	0.955 (0.010)	0.939 (0.010)
1.2	99.9	0.955 (0.010)	0.948 (0.009)	0.952 (0.009)	0.945 (0.009)
1.2	100.0	0.943 (0.009)	0.943 (0.008)	0.945 (0.008)	0.923 (0.008)

Lastly, we've included simulations with reduced numbers of reference materials for estimating the sensitivity and specificity. In this scenario, $M=N=100$. We see from Table 3 that the 95% confidence interval based on the delta method can have very poor coverage. For example, when $q_0=99\mathrm{\%}$, the empirical coverage level is only 62.8%. The bootstrap-based confidence interval also performed poorly with a coverage level of 62.5%. On the other hand, the proposed exact confidence interval has a coverage level of 98.7%. The proposed hybrid bootstrap confidence interval also performs satisfactorily. Even in settings with larger values of M and N, the 95% confidence intervals based on the delta method or bootstrap often have a coverage level below 90%, which may result in misleading conclusions in low prevalence settings.

Table 3.

The empirical coverage probability and average length of 95% confidence interval of ${\pi }_0$ based on exact method, delta method, nonparametric bootstrap, and hybrid bootstraps; $\pi =1.2\mathrm{\%},M=N=100.$

				H Bootstrap
				$p_0=\hat{p}$
$q_0$	Exact method CovP (Length)	Delta method CovP (Length)	Bootstrap CovP (Length)	CovP (Length)
97.0	0.985 (0.050)	0.884 (0.050)	0.924 (0.083)	0.975 (0.047)
98.0	0.981 (0.044)	0.868 (0.040)	0.863 (0.065)	0.981 (0.041)
98.4	0.984 (0.041)	0.807 (0.036)	0.803 (0.057)	0.984 (0.038)
98.6	0.985 (0.040)	0.748 (0.033)	0.744 (0.051)	0.977 (0.035)
98.8	0.989 (0.038)	0.702 (0.030)	0.700 (0.046)	0.984 (0.034)
99.0	0.987 (0.035)	0.628 (0.027)	0.625 (0.041)	0.982 (0.031)
99.2	0.990 (0.032)	0.552 (0.023)	0.544 (0.035)	0.983 (0.029)
99.4	0.991 (0.029)	0.573 (0.020)	0.552 (0.030)	0.986 (0.026)
99.6	0.994 (0.025)	0.716 (0.016)	0.674 (0.024)	0.993 (0.023)
99.8	0.998 (0.021)	0.906 (0.012)	0.878 (0.016)	0.997 (0.020)
99.9	0.994 (0.019)	0.952 (0.010)	0.942 (0.012)	0.988 (0.018)
100.0	0.972 (0.017)	0.944 (0.009)	0.949 (0.009)	0.954 (0.016)

3.2. Stratum-specific weighted inference

In this case, the sensitivity and specificity are chosen as in Section 4.1:

1. the sensitivity is 83%; sample size $M=157;$

2. the specificity $\in \{97\mathrm{\%},98\mathrm{\%},98.4\mathrm{\%},98.6\mathrm{\%},98.8\mathrm{\%},99\mathrm{\%},99.2\mathrm{\%},99.4\mathrm{\%},99.8\mathrm{\%},99.9\mathrm{\%},100\mathrm{\%}\}$; sample size N = 371; and separately for $N=3324.$

The true prevalence is stratum-specific and we have considered six strata summarized in Table 4. The true prevalence for the target population is $\sum _{s=1}^6{w}_s{\pi }_s=1.2\mathrm{\%}.$ For comparison purposes, we constructed the 95% confidence interval using nonparametric bootstrap, delta method, proposed hybrid bootstrap fixing ${\lambda }_0=\hat{\lambda }$, and faster hybrid bootstrap fixing $({\lambda }_0,p_0)=(\hat{\lambda },\hat{p}).$ Table 5 summarizes the simulation results. The empirical coverage level of the nonparametric bootstrap-based confidence intervals was below the required nominal level in general and sometimes substantially so. The delta method is slightly better than the nonparametric bootstrap but still results in undercoverage for $q_0$ very close to 1. On the other hand, the two proposed hybrid bootstrap methods perform satisfactorily. When all four methods yielded confidence intervals with good coverage, the average length of the confidence interval from the proposed hybrid bootstrap method was not much longer and sometimes even shorter than those based on delta method or nonparametric bootstrap, which suggests that there is at most a limited loss in precision in exchange for a higher coverage level.

Table 4.

Simulation setting for stratified inference.

	Strata 1	Strata 2	Strata 3	Strata 4	Strata 5	Strata 6
Weights ( $w_s$)	0.05	0.07	0.08	0.15	0.25	0.40
Prevalence ( ${\pi }_s$)	0.03%	0.70%	0.07%	0.07%	0.77%	2.33%
Number of tests ( $D_s$)	500	700	300	800	230	800

Table 5.

The empirical coverage probability and average length of 95% confidence interval of ${\pi }_0$ based on delta method, nonparametric bootstrap, and hybrid bootstrap for stratum-specific weighted inference.

		Bootstrap	Delta method	H Bootstrap	H Bootstrap
				${\lambda }_0=\hat{\lambda }$	$({\lambda }_0,p_0)=(\hat{\lambda },\hat{p})$
${\pi }_0$	$q_0$	CovP (Length)	CovP (Length)	CovP (Length)	CovP (Length)
1.2	97.0	0.938 (0.046)	0.952 (0.034)	0.964 (0.034)	0.963 (0.033)
1.2	98.0	0.934 (0.038)	0.954 (0.030)	0.962 (0.030)	0.958 (0.030)
1.2	98.4	0.922 (0.034)	0.938 (0.028)	0.964 (0.029)	0.955 (0.029)
1.2	98.6	0.920 (0.031)	0.940 (0.027)	0.968 (0.029)	0.962 (0.028)
1.2	98.8	0.902 (0.029)	0.926 (0.025)	0.962 (0.028)	0.956 (0.027)
1.2	99.0	0.918 (0.027)	0.938 (0.024)	0.978 (0.026)	0.952 (0.026)
1.2	99.2	0.902 (0.024)	0.930 (0.022)	0.972 (0.026)	0.965 (0.025)
1.2	99.4	0.882 (0.021)	0.930 (0.020)	0.970 (0.025)	0.969 (0.024)
1.2	99.6	0.858 (0.017)	0.946 (0.018)	0.986 (0.023)	0.984 (0.022)
1.2	99.8	0.836 (0.013)	0.960 (0.015)	0.996 (0.020)	0.991 (0.019)
1.2	99.9	0.844 (0.012)	0.940 (0.014)	0.984 (0.019)	0.986 (0.018)
1.2	100.0	0.802 (0.008)	0.922 (0.011)	0.970 (0.017)	0.952 (0.016)

3.3. Individual-specific weighted inference

For cases needing individual-specific weighting, we adopted similar simulation settings for sensitivity and specificity in Section 3.2. The same individual weights in [2] were used as weights, whose distribution is shown in Figure 1. The median weight is 0.48 with an inter-quartile range of [0.22, 1.11]. To specify, ${\pi }_i,$ the probability of the ith individual having the disease or antibody, we let

$${\pi }_i=\frac{\exp (-4.40+0.17w_i)}{1+\exp (-4.40+0.17w_i)},i=1,\dots ,D=3330,$$

based on the fitted logistic regression to the observed data in the Santa Clara study, where the intercept is adjusted so that the weighted prevalence $D^{-1}\sum _{i=1}^D{w}_i{\pi }_i=1.2\mathrm{\%}.$ This model suggests a higher individual-specific weight $w_i$ was associated with a higher probability ${\pi }_i$. Again, we compared nonparametric bootstrap, delta method, proposed hybrid bootstrap fixing ${\lambda }_0=\hat{\lambda }$ and faster hybrid bootstrap fixing $({\lambda }_0,p_0)=(\hat{\lambda },\hat{p}).$ The simulation results can be found in Table 6. The nonparametric bootstrap performs poorly for most values of $q_0$. The delta method performs reasonably well until $q_0$ is near 1, where the normality of $\hat{q}$ breaks down and coverage starts to decrease drastically. On the other hand, the performance of the hybrid bootstrap method fixing ${\lambda }_0$ is fairly robust in terms of maintaining the appropriate coverage level except when $q_0=100\mathrm{\%}.$ The hybrid method fixing both ${\lambda }_0$ and $p_0$ performs similarly well. In this case, the average length of the proposed confidence interval could be substantially longer in comparison with the bootstrap and delta methods. For example, when $q_0=98\mathrm{\%}$, the delta-method-based confidence interval had a coverage of 96% and an average length of 0.038. The confidence interval based on hybrid bootstrap fixing ${\lambda }_0$ had a slightly higher coverage, 96.8%, but the corresponding average length increased 24%.

Figure 1.

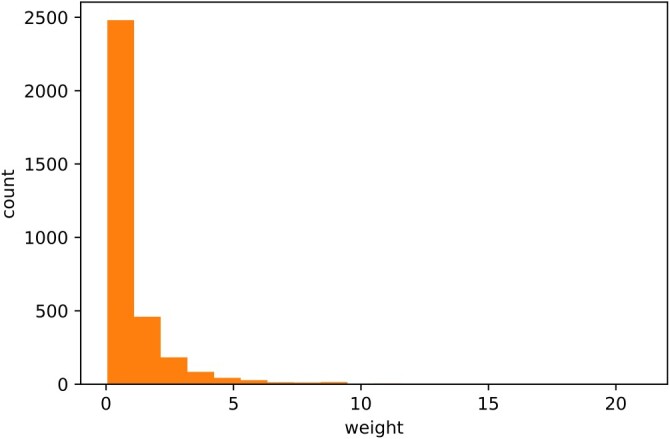
The distribution of individual weights in the Santa Clara study.

Table 6.

The empirical coverage probability and average length of 95% confidence interval of ${\pi }_0$ based on delta method, nonparametric bootstrap, and hybrid bootstrap for individual-specific weighted inference.

		Bootstrap	Delta method	H Bootstrap	H Bootstrap
				${\lambda }_0=\hat{\lambda }$	$({\lambda }_0,p_0)=(\hat{\lambda },\hat{p})$
${\pi }_0$	$q_0$	CovP (Length)	CovP (Length)	CovP (Length)	CovP (Length)
1.2	97.0	0.862 (0.046)	0.964 (0.043)	0.974 (0.049)	0.967 (0.049)
1.2	98.0	0.823 (0.037)	0.960 (0.038)	0.968 (0.047)	0.947 (0.044)
1.2	98.4	0.834 (0.034)	0.956 (0.036)	0.958 (0.043)	0.946 (0.043)
1.2	98.6	0.822 (0.031)	0.970 (0.034)	0.942 (0.042)	0.958 (0.041)
1.2	98.8	0.809 (0.029)	0.954 (0.033)	0.962 (0.043)	0.953 (0.039)
1.2	99.0	0.779 (0.027)	0.955 (0.032)	0.954 (0.039)	0.965 (0.037)
1.2	99.2	0.764 (0.024)	0.949 (0.030)	0.968 (0.038)	0.964 (0.036)
1.2	99.4	0.730 (0.021)	0.940 (0.028)	0.968 (0.036)	0.952 (0.035)
1.2	99.6	0.705 (0.017)	0.911 (0.026)	0.960 (0.034)	0.954 (0.032)
1.2	99.8	0.605 (0.013)	0.894 (0.024)	0.938 (0.031)	0.925 (0.029)
1.2	99.9	0.543 (0.011)	0.854 (0.022)	0.926 (0.029)	0.889 (0.027)
1.2	100.0	0.499 (0.008)	0.780 (0.020)	0.860 (0.027)	0.864 (0.026)

In summary, the proposed methods had substantially more robust performance than traditional approaches in all three settings investigated above. For some specific combinations of the true parameters, the nonparametric bootstrap method or delta method may also produce confidence intervals with sufficient coverage levels. However, their performance was very sensitive to some true parameter values, such as the true test specificity $q_0.$ In most practical applications, there is not enough information to differentiate, for example, between $q_0=98.5$% vs. $q_0=99$%, and thus, it was impossible to know if a confidence interval based on traditional methods had proper coverage, a priori. The simulation results also demonstrated that in contrast to common belief, the nonparametric bootstrap method does not automatically fix the problem in general. The proposed method, on the other hand, achieved a nominal coverage level in almost all cases, and oftentimes without substantially increasing the average length of the resulting confidence interval. Therefore, the proposed exact method and its variations can be viewed as good insurance while incurring relatively little cost.

4. Examples

We first applied our method to analyzing data gathered in [2]. Some of the numbers below are taken from an initial preprint .¹ The objective of this study was to estimate the COVID-19 antibody prevalence in Santa Clara County, California, 2 April 2020. The data included D = 3330 volunteers tested for antibody presence. Among them, there were 50 positive test results. Without considering the measurement error, the crude prevalence is 1.5% with an exact 95% confidence interval of [1.11, 1.97]%. To account for the test performance, the reported sensitivity of 130/157 and specificity of 368/371 based on M = 157 true positive samples and N = 371 true negative samples, respectively, were used to adjust the antibody prevalence estimate in the initial preprint version of the study. In the meantime, far more extensive additional data on test performance were being collected and verified. We present the corresponding result later. For now,

$$\hat{r}=\frac{50}{3330},\hat{p}=\frac{130}{157},\hat{q}=\frac{368}{371},D=3330,M=157,N=371.$$

With the delta method (with the range preserved logit transformation), the resulting 95% confidence interval is [0.20, 3.50]%. The nonparametric bootstrap method yields a similar interval, i.e. [0.00, 1.93]%. Then, we applied our methods with B = 3000 and a dense net consisting of 30 evenly spaced points in each $99.9\mathrm{\%}$ confidence interval for $r_0,p_0$ and $q_0$ to construct the 95% exact confidence interval and the hybrid confidence interval fixing $p_0=\hat{p}$. Figure 2 plots the estimated exact p-value $\hat{p}\left(\pi \right)$, and the corresponding asymptotic p-value based on delta-method, nonparametric bootstrap, and hybrid bootstrap fixing $p_0=\hat{p}.$ It is clear that $\hat{p}\left(\pi \right)$ is higher than its asymptotic counterparts, resulting in a wider confidence interval. The produced confidence intervals can be found in Table 7. All confidence intervals except that from delta method with logit transformation included 0, and we were unable to make strong conclusions about the lower bound of the prevalence with only a sample size of N = 371 for estimating the specificity. Since the resulting study cohort may not be randomly sampled from the Santa-Clara population, weighted analysis with individual-specific weighting to reflect the demographic makeup of the target population was also conducted. The resulting 95% confidence interval was [1.18, 3.78]% and [1.10, 3.69]% based on the delta method and nonparametric bootstrap, respectively. We also constructed the confidence interval based on proposed hybrid bootstrap fixing ${\lambda }_0=\hat{\lambda }$ and $({\lambda }_0,p_0)=(\hat{\lambda },\hat{p}),$ respectively. The lower ends of the hybrid bootstrap confidence intervals were closer to 0 than that from the delta method or nonparametric bootstrap, also suggesting the uncertainty about the lower bound of the prevalence. The basic dilemma was that we cannot reliably differentiate true positives from false positives, since we can't estimate the specificity level with adequate precision.

Figure 2.

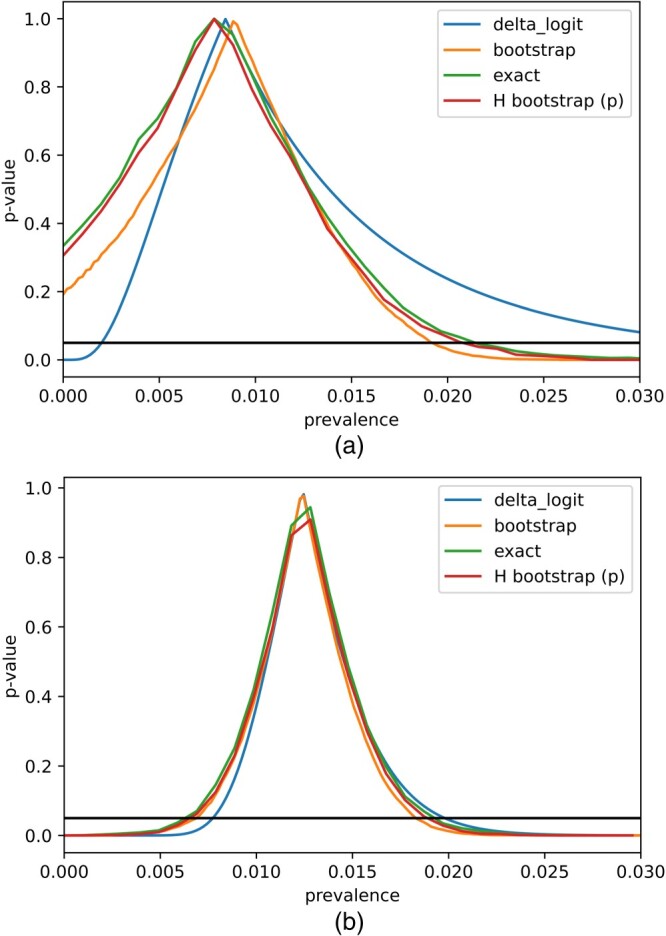
Plot of p-values for various values of π according to different methods. (a) N = 371 and (b) N = 3324.

Table 7.

The point estimators and 95% confidence intervals for the weighted and unweighted prevalence in the Santa Clara study.

N = 371
	${\hat{\pi }}^{\mathrm{a}}$	Delta method ${}^{\mathrm{b}}$	Bootstrap	Exact	H Bootstrap $\left(p_0\right)$
Unweighted (%)	0.85	(0.20, 3.50)	(0.00, 1.93)	(0.00, 2.06)	(0.00, 2.06)
Weighted (%)	2.80	(1.18, 3.78)	(1.10, 3.72)	(0.29, 5.17)	(0.29, 5.07)
N = 3324
Unweighted (%)	1.24	(0.77, 1.98)	(0.66, 1.84)	(0.68, 1.87)	(0.68, 1.77)
Weighted (%)	2.87	(2.10, 3.6)	(2.12, 3.66)	(1.39, 5.28)	(1.49, 5.08)

${}^{\mathrm{a}}$Adjusted for test sensitivity and specificity.

${}^{\mathrm{b}}$Normal logit method.

To address this difficulty, the study team assembled additional results about the specificity based on 2953 more measurements, bringing the total number of true negative samples used to estimate the specificity to N = 3324. We had used different meta-analytic methods to combine data across subsets of control samples accounting for potential between-datasets heterogeneity and the results were reasonably ably robust (not shown here). For illustrative purposes, we ignored the potential heterogeneity and assumed simply pooling data in this application was appropriate. With a larger sample size for estimating specificity ( $\hat{q}=3308/3324$, N = 3324 ), we repeated the construction of 95% confidence intervals for the unweighted and weighted prevalence (Table 7). These resulting estimates were fairly consistent with those presented in [2]. The unweighted results from different methods were very similar, while the weighted results tended to have modestly wider confidence intervals with the ‘exact’ method and hybrid bootstrap. Figure 2 shows that the exact and asymptotic p-values were close to each other based on the increased sample size, implying that the distribution of $\hat{\pi }-\pi$ can be approximated well by $N(0,{\hat{\sigma }}^2)$. The lower bound of the confidence interval based on the delta method and bootstrap for weighted prevalence was slightly higher possibly due to the under-coverage tendency of the bootstrap method at high specificity as our simulation study demonstrated (Section 4).

In order to examine the performance of different methods and the prevailing practices for adjusting for test performances across seroprevalence studies that find low seroprevalence estimates in the tested population, we used a recently published overview of seroprevalence studies [14]. In four studies, crude, unadjusted seroprevalence was reported to not exceed 10% and the authors had tried to adjust for test performance. While three studies from Denmark, the Faroe Islands, and the USA [8,12,17] used the simple bootstrap method to make the statistical inference, the study from Brazil [11] implemented a slightly different resampling method. In all four studies, the adjustment for the test performance changed the seroprevalence point estimate by a small amount reflecting the high precision of the test being used. The analysis results using our proposed methods are summarized in Table 8. The resulting exact 95% confidence intervals were wider than those based on the delta method and bootstrap. When the number of negative samples used to estimate the specificity was small such as the study from the Faroe Islands, the difference became bigger reflecting the effect of unknown specificity. On the other hand, when the sample sizes used to estimate sensitivity and specificity were adequate and the observed prevalence was not low as in the study in New York, the exact confidence intervals were only slightly wider than those based on simple bootstrap. The data based on which the analysis was conducted can be found in the appendix in Table A1 and some of them were reconstructed from the results in the published papers [8,11,12,17].

Table 8.

The point estimators and 95% confidence intervals for the seroprevalence in studies from Brazil, USA, Denmark, and the Faroe Islands.

	$\hat{\pi }$	Delta method	Bootstrap	Exact	H Bootstrap $\left(p_0\right)$
Brazil
Male (%)	0.64	(0.10, 3.52)	(0.00, 1.55)	(0.00, 1.48)	(0.00, 1.38)
Female (%)	0.41	(0.02, 6.30)	(0.00, 1.30)	(0.00, 1.15)	(0.00, 1.15)
USA
Washington Male (%)	1.41	(0.67, 2.95)	(0.33, 2.42)	(0.10, 2.66)	(0.10, 2.56)
Washington Female (%)	1.71	(0.96, 3.03)	(0.70, 2.64)	(0.39, 2.84)	(0.49, 2.74)
New York Male (%)	5.94	(4.50, 7.80)	(4.33, 7.59)	(4.17, 7.74)	(4.27, 7.64)
New York Female (%)	5.66	(4.33, 7.38)	(4.15, 7.23)	(3.98, 7.35)	(4.08, 7.25)
Denmark
Capital (%)	3.23	(2.49, 4.17)	(2.36, 4.06)	(2.13, 4.11)	(2.23, 4.11)
Total (%)	1.87	(1.30, 2.68)	(1.13, 2.48)	(0.78, 2.55)	(0.88, 2.45)
Faroe Islands
Total (%)	0.59	(0.27, 1.31)	(0.19, 1.10)	(0.00, 1.26)	(0.00, 1.16)
Male (%)	0.59	(0.19, 1.82)	(0.00, 1.37)	(0.00, 1.67)	(0.00, 1.57)
Female (%)	0.59	(0.19, 1.82)	(0.00, 1.37)	(0.00, 1.67)	(0.00, 1.57)

In designing a study, one may select the sample size by targeting a desired precision level based on our proposed method. For example, if investigators want to construct 95% confidence intervals of length less than 2%, they can select a combination of $(D,M,N)$, simulate data with assumed prevalence/sensitivity/specificity values, and construct the 95% exact confidence interval using the proposed method to measure the length of the resulting interval. Specifically, if we assume a prevalence of 2.0%, a true sensitivity of 80% and a true specificity of 99%, then based on 250 simulations, the average length of the 95% confidence interval for various $(D,M,N)$ are

• 2.01% for $(D,M,N)=(7000000,500,500)$

• 1.97% for $(D,M,N)=(25000,500,750)$

• 1.98% for $(D,M,N)=(7500,500,1000)$

• 1.95% for $(D,M,N)=(3000,500,2000)$

• 2.07% for $(D,M,N)=(2000,500,5000)$

• 2.08% for $(D,M,N)=(1800,500,10000)$

Therefore, the investigator may sample D = 3000 subjects from the target population and estimate the sensitivity and specificity based on 500 reference positive samples and 2000 reference negative samples, respectively. This combination of D, M and N is not unique. For example, the average length of the confidence interval is also about 2.0% if $(D,M,N)=(7500,500,1000)$, which requires fewer negative samples but substantially larger D. One may consider the availability of reference materials and the cost of enrolling participants from the target population in selecting the final sample sizes.

5. Discussion

In order to estimate the prevalence of a disease using imperfect tests, we developed a method that provides confidence intervals with the appropriate coverage. This is important because in many scenarios there is not enough data for large sample approximations to be accurate, especially when the sensitivity $p_0$ or specificity $q_0$ is very close to 1, which can cause the naive bootstrap confidence intervals to be too narrow. However, our method is computationally more expensive than the bootstrap method by several orders of magnitude, which translates to about half a minute to compute a single confidence interval on a PC with a Ryzen 3900X CPU. In practice, we don't believe this will impose too large a burden, as typically there is no need to compute a confidence interval many times.

In addition, only the proposed method for unweighted inference is truly exact; in two weighted cases, we still make some approximations for the distribution of $r_w$. Such an approximation is unavoidable due to the fact that the variance inflation factor ${\lambda }_0$ is unknown and may not be estimated well empirically. Also, we note that the performance of the simple bootstrap becomes better as the sample size for estimating specificity N rises. Therefore, while the sample size for estimating prevalence D is important, the size of the confidence interval also heavily depends on the sample size for estimating sensitivity and specificity, and especially the latter. Even as D grows, the length of the confidence interval will not shrink to zero, since the uncertainty of the sensitivity and specificity affects the estimation of the true prevalence. For experiments aiming to estimate prevalence in settings where low values are expected, it is worth the effort to accurately estimate the sensitivity and specificity. This prerequisite is no longer a serious issue when the prevalence is sufficiently high.

The proposed exact method has very few model assumptions. One key assumption is that the sensitivity and specificity based on reference materials will not change when the test is applied to the real population. This may not be necessarily true considering the fact that sensitivity and specificity of the test depend on many factors which may not be the same between testing reference materials and actual participants samples. For example, the positive reference sample typically includes people with clear symptoms and/or more severe disease and these people may be more likely to have readily detectable antibody titers than the average person infected in the community. Therefore, the sensitivity in the real population may be lower than what is suggested by the positive reference sample.

Our review of the literature of COVID-19 seroprevalence studies [3,6,13,21] shows that many studies that estimate low crude prevalence do not even try to adjust for test performance. Some of them may try to validate the positive samples using a different laboratory assay [16]. Many others may assume that specificity is perfect. For well-validated assays, this assumption may be approximately correct. For example, in the case of the assay used in the Santa Clara study, the specificity was 99.5 –99.8% depending on how pooling or meta-analysis of control datasets would be performed. Moreover, among the few control samples coined as ‘false positives’, the majority were probably true positives that had been mischaracterized, as these control samples came from data collected during the COVID-19 pandemic, where a negative RT-PCR result cannot rule out the possibility that a person had already been infected in the past. Most of the remaining ‘false positives’ that came from pre-COVID samples were atypical cases (e.g. from people with extremely high titers of rheumatoid factor) that are rarely encountered in the general population. This means the true specificity of the test used in the Santa Clara study may be even higher. However, our simulation study shows that the simple bootstrap or delta method may still yield suboptimal coverage even with a perfect specificity and the method that we propose may have value in such a setting.

Another strategy to alleviate the false positive issue would be via study design: to re-test all patients whose results are positive [19]. An important reason why it is difficult to estimate the prevalence is because that the false positive rate can be relatively high, and the estimated prevalence is very sensitive to the false positive rate. The re-test may or may not have the same sensitivity and specificity as the original test. Testing results from two tests on the same sample may be correlated as well. If one considers a sample being positive if results from the test and re-test are both positive, the specificity of such a test strategy is often substantially higher than that of a single test. If one wants to boost the sensitivity, one may consider a sample being positive if the result from either the original test or re-test is positive. In practice, one always can design a test strategy combining information from multiple tests and estimate the sensitivity and specificity of the strategy by examining testing results from positive reference samples and negative reference samples, respectively.

Appendix.

A.1. Delta method derivation

Theorem A.1

Suppose that as $S_n=D_n+M_n+N_n\to \mathrm{\infty },$ $D_n/S_n\to {\pi }_D\in (0,1),$ $M_n/S_n\to {\pi }_M\in (0,1),$ and $N_n/S_n\to {\pi }_N\in (0,1).$ $d\sim Bin(D_n,r_0),$ $m\sim Bin(M_n,p_0)$ and $n\sim Bin(N_n,q_0)$ are three independent binomial random variables. Then $\hat{\pi }$ and ${\pi }_0$ defined by (2) and (1) satisfies

$$\sqrt{S_n}({\hat{\pi }}_n-{\pi }_0)⟹dN(0,{\sigma }_0^2)$$

in distribution, where

$${\sigma }_0^2=\frac{r_0(1-r_0)}{{\pi }_D(p_0+q_0-1{)}^2}+\frac{{\pi }_0^2{p}_0(1-p_0)}{{\pi }_M(p_0+q_0-1{)}^2}+\frac{(r_0-p_0{)}^2{q}_0(1-q_0)}{{\pi }_N(p_0+q_0-1{)}^4}.$$

Proof.

Note that for $f(r,p,q)=(r+q-1)/(p+q-1),$

$$\begin{array}{rl}\frac{\mathrm{\partial }f}{\mathrm{\partial }r}=& \frac{1}{p+q-1},\\ \frac{\mathrm{\partial }f}{\mathrm{\partial }p}=& -\frac{r+q-1}{(p+q-1{)}^2}=-\frac{\pi }{p+q-1},\\ \frac{\mathrm{\partial }f}{\mathrm{\partial }q}=& \frac{1}{p+q-1}-\frac{r+q-1}{(p+q-1{)}^2}=\frac{p-r}{(p+q-1{)}^2}.\end{array}$$

It follows from the central limit theorem for binomial proportions,

$$\sqrt{S_n}\left[\begin{array}{c}{\hat{r}}_{D_n}-r_0\\ {\hat{p}}_{M_n}-p_0\\ {\hat{q}}_{N_n}-q_0\end{array}\right]⟹dN(\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right],\left[\begin{array}{ccc}\frac{r_0(1-r_0)}{{\pi }_D}& 0& 0\\ 0& \frac{p_0(1-p_0)}{{\pi }_M}& 0\\ 0& 0& \frac{q_0(1-q_0)}{{\pi }_N}\end{array}\right]).$$

We can apply the delta method to see that

$$\sqrt{S_n}({\hat{\pi }}_n-{\pi }_0)=\sqrt{S_n}\left\{f\right({\hat{r}}_{D_n},{\hat{p}}_{M_n},{\hat{q}}_{N_n})-f(r_0,p_0,q_0\left)\right\}$$

converges in distribution to a Gaussian with mean 0 and variance

$$\left[\begin{array}{c}\frac{1}{p+q-1},-\frac{\pi }{p+q-1},\frac{p-r}{(p+q-1{)}^2}\end{array}\right]\left[\begin{array}{ccc}\frac{r_0(1-r_0)}{{\pi }_D}& 0& 0\\ 0& \frac{p_0(1-p_0)}{{\pi }_M}& 0\\ 0& 0& \frac{q_0(1-q_0)}{{\pi }_N}\end{array}\right]\left[\begin{array}{c}\frac{1}{p+q-1}\\ -\frac{\pi }{p+q-1}\\ \frac{p-r}{(p+q-1{)}^2}\end{array}\right],$$

which can be consistently estimated by

$$\frac{\hat{r}(1-\hat{r})S_n}{D_n(\hat{p}+\hat{q}-1{)}^2}+\frac{{\hat{\pi }}^2\hat{p}(1-\hat{p})S_n}{M_n(\hat{p}+\hat{q}-1{)}^2}+\frac{(\hat{r}-\hat{p}{)}^2\hat{q}(1-\hat{q})S_n}{N_n(\hat{p}+\hat{q}-1{)}^4}.$$

A.2. Additional simulation results and data used for the seroprevalence in studies from Brazil, USA, Denmark, and the Faroe Islands

In Figure A1, we plot the empirical coverage levels of various confidence intervals assuming different true prevalence level, i.e. ${\pi }_0\in \{0.4\mathrm{\%},5\mathrm{\%},10\mathrm{\%}\}.$ While most confidence intervals retain appropriate coverage level when ${\pi }_0=10\mathrm{\%},$ only the proposed exact method and hybrid bootstrap fixing $p_0$ at $\hat{p}$ perform satisfactorily when the prevalence ${\pi }_0=0.4\mathrm{\%}.$ Specifically, even when the prevalence is 5%, the 95% confidence interval based on nonparametric bootstrap may still too liberal with a coverage level approximately 90% for some specificity values. Figure A2 plots the average length of the 95% confidence intervals. Note that the average length of the proposal exact confidence interval is not substantially longer than alternatives.

Figure A1.

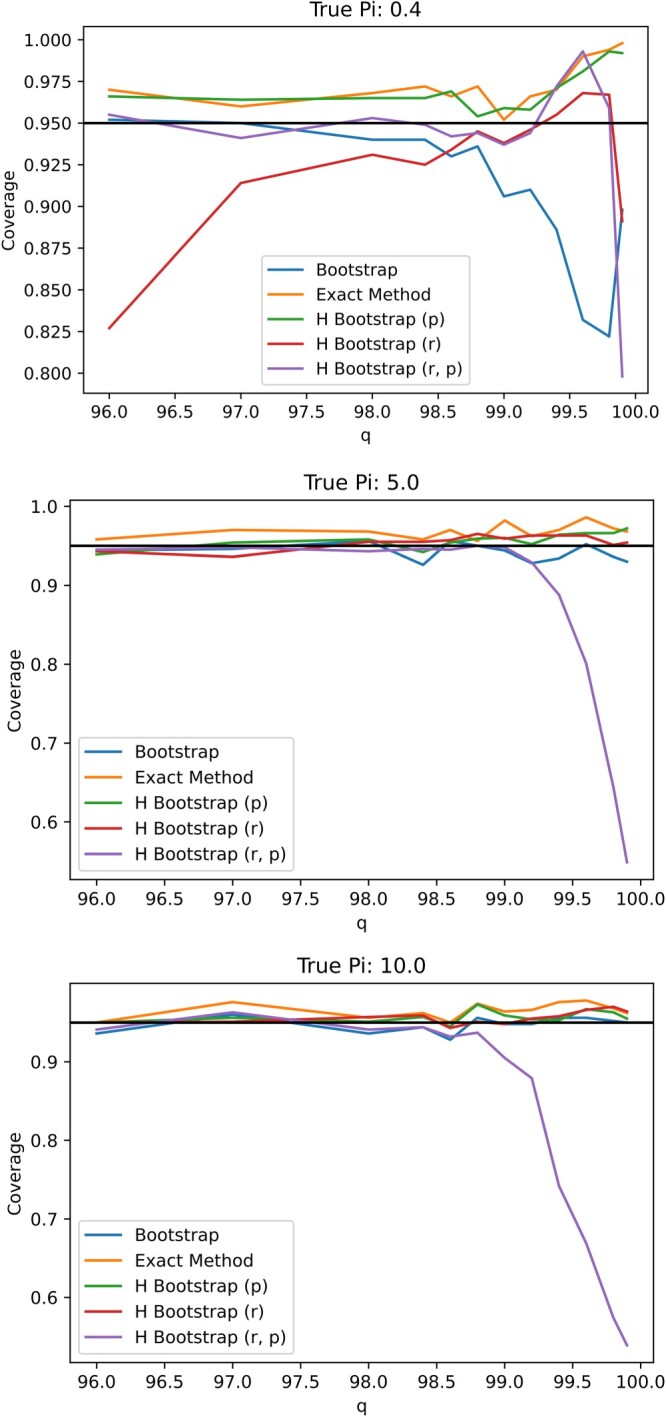
Plot of coverages for varying values of specificity q for N = 371 under $\pi =0.4,5.0,10.0$.

Figure A2.

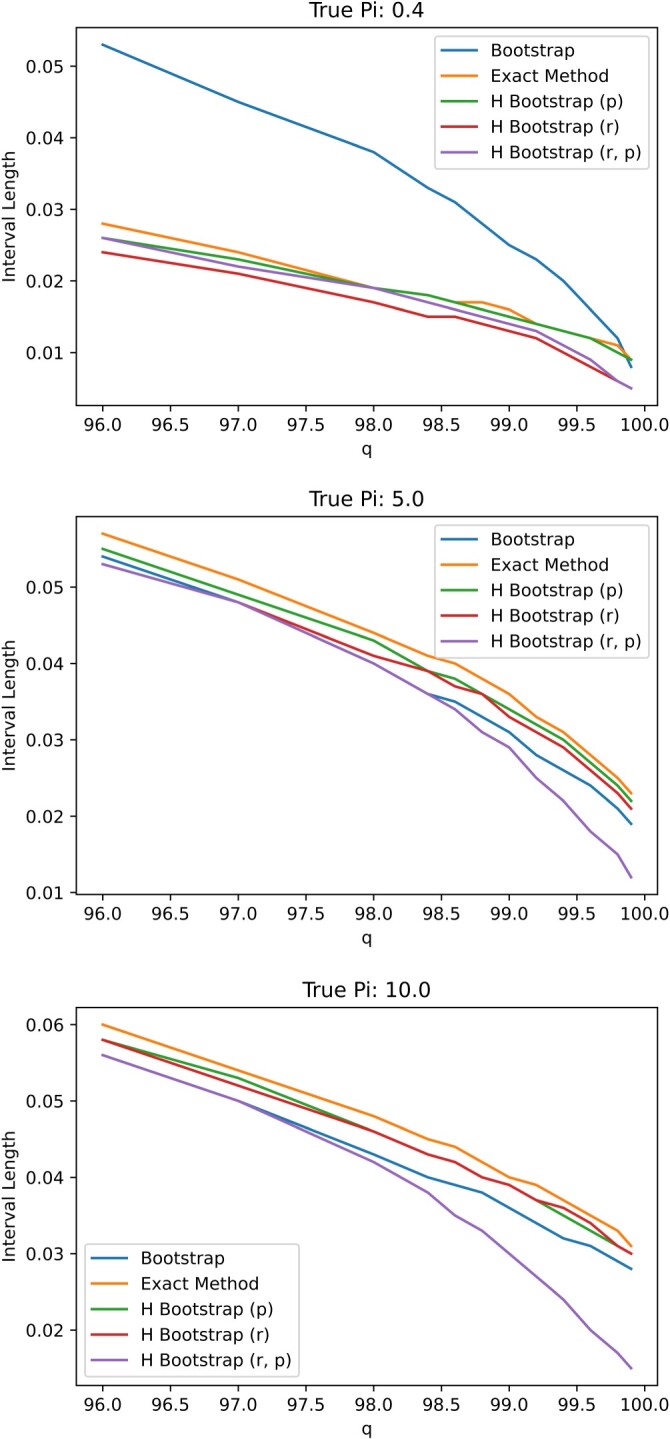
Plot of confidence interval lengths for varying values of specificity q for N = 371 under $\pi =0.4,5.0,10.0$.

Table A1 includes the data used for the analysis of the seroprevalence in studies from Brazil, USA, Denmark and the Faroe Islands. Note that some studies only reported the confidence intervals for the test sensitivity and specificity and the corresponding data were reconstructed based on the confidence interval, which may be slightly different from the actual data.

Table A1.

Data used for the seroprevalence in studies from Brazil, USA, Denmark, and the Faroe Islands.

	r (%)	p (%)	q (%)	d/D	m/M	n/N
Brazil
Male	1.50	84.79	99.03	158/10531	446/526	513/518
Female	1.31	84.79	99.03	189/14464	446/526	513/518
USA
Washington Male	1.95	96.00	99.40	26/1334	96/100	497/500
Washington Female	2.23	96.00	99.40	43/1930	96/100	497/500
New York Male	6.27	96.00	99.40	72/1149	96/100	497/500
New York Female	6.00	96.00	99.40	80/1333	96/100	497/500
Denmark
Capital	3.11	82.58	99.54	203/6528	128/155	648/651
Total	2.00	82.58	99.54	412/20640	128/155	648/651
Faroe Islands
Total	0.56	94.44	100.00	6/1075	238/252	308/308
Male	0.56	94.44	100.00	3/538	238/252	308/308
Female	0.56	94.44	100.00	3/537	238/252	308/308

Funding Statement

The work of Dr Ioannidis is supported by an unrestricted gift from Sue and Bob O'Donnell. The work of Dr Bendavid is support from the Stanford COVID19 Seroprevalence Studies Fund. The work of Dr Tian is partially supported by the National Institutes of Health (NHLBI) [R01HL089778-05].

Disclosure statement

No potential conflict of interest was reported by the author(s).