Abstract
The development of engineered metamaterials has enabled the fabrication of tunable photonic devices capable of manipulating the characteristics of electromagnetic surface waves. Integration of semiconductors in metamaterials is a proven approach for creating thermally tunable metamaterials through temperature control of the semiconductor carrier density. In this paper, an interface consisting of an isotropic dielectric material as a cover and an indium antimonide (InSb) nanowire metamaterial as a substrate, is theoretically introduced to investigate the propagation conditions of Dyakonov surface waves in terahertz (THz) frequencies. Various temperature-dependent properties of Dyakonov surface waves in such a geometry is studied, including allowed THz regions, angular existence domain, dispersion relation, directionality, localization degree and figure of merit. The proposed configuration due to the presence of significant birefringence in InSb nanowire metamaterial, has potential applications in THz sensing, imaging and spectroscopy.
Subject terms: Applied optics; Terahertz optics; Metamaterials; Nanowires; Semiconductors; Surfaces, interfaces and thin films
Introduction
Metamaterials are artificially engineered media that are designed to exhibit extraordinary properties that are not found in naturally existing materials, such as superlensing1,2, invisibility3, negative permittivity and permeability4–6 , waveguiding7 and large birefringence8,9. Semiconductors are gaining attention to be used in metamaterials due to their distinguished features such as the tunability of properties10,11. Small gaps in these types of materials are sensitive to small variations in temperature that leads to significant changes in their optical properties. Furthermore, the frequency range in a semiconductor metamatreial is mostly affected by plasma frequency of the semiconductor, which depends on the free carrier concentration, that is extremely sensitive to the temperature, in contrast to dielectrics and metals. Some semiconductors such as indium antimonide (InSb) have the proper carrier density for their frequency to be located in the terahertz (THz) region, and can therefore be used in place of a metal in conventional metal-dielectric metamaterials12. Moreover, semiconductor films or wires can be easily fabricated by vapor deposition techniques and the carrier density of semiconductors can be controlled by doping, laser light, temperature, and external electric and magnetic fields13–15.
Electromagnetic surface waves which propagate along the interface of two optically dissimilar media and decay in the perpendecular direction to the interface, play an important role in various areas of science and technology, such as sensing16, integrated optics17 and microscopy18. The well-known surface plasmon polariton (SPP) is an example of an electromagnetic surface wave that propagates along the interface of two media with permittivities of opposite signs, e.g. the interaface between a metal and a dielectric. Such surface waves suffer propagation loss due to the presence of metallic absorbtion in typical SPP configurations. In 1988, Dyakonov theoretically proposed a distinguished kind of surface wave that exists at the interface of two transparent dielectric materials in which at least one of them is an anisotropic uniaxial material19. Since the partnering materials in Dyakonov surface waves (DSWs) are lossless dielectrics, they are considered to be lossless surface waves20. In comparison with SPPs, DSWs are weakly localized and extremely directional in such a way that in conventional materials DSWs are only available in a very narrow angular range with respect to the optical axis (OA) of the anisotropic medium21. Due to this high directionality, first experimental observation of DSWs was reported in 2009, almost two dacades after its first theoretical prediction22. After that, more experimental investigations were carried out on DSWs20,23,24. DSWs have been studied theoretically in various materials such as biaxial crystals25,26, magnetic materials27 and metamaterials28–31. The Dyakonov plasmon surface wave (DPSW) is a special case of DSW that exists along the boundary between two media which at least one of them is anisotropic and also one component of the permittivity of either media is negative32–35. DPSWs have the combination of properties of both the DSWs and the SPPs, for instance, they have both the strong localization degree of SPPs and high directionality of DSWs.
In this paper, a configuration consisting of a semiconductor nanowire metamaterial (NWMM) as a substrate and an isotropic dielectric material as a cover is proposed and the frequency and temperature domains of NWMM permittivities for the propagation of DSWs and DPSWs are studied. Then, the temperature-dependent properties of DSWs and DPSWs such as angular domains of propagation, dispersion curves and the penetration depths are investigated. Finally, the figure of merit (FOM) of the propagation of the surface waves is studied in order to show that the dielectric losses are negigible.
Configuration and theory
The ability of semiconductors to tune the carrier density and subsequently the permittivity, makes them effective in tunable metamaterials. Among the semiconductors, it is well-known that indium antimonide (InSb) is a great candidate as a thermally tunable material36–39. The distinct features of InSb such as the small band gap, low effective mass, high electron mobility and highly temperature-dependent carrier density, make its permittivity easily influenced by a small change in temperature. In the THz frequencies, the complex-valued relative permittivity of InSb is obtained by the Drude model40
| 1 |
where is the high frequency dielectric constant, is the resonant frequency, THz is the damping constant and is the plasma frequency, where e is the electron charge, is the effective mass, is the electron mass, is the permittivity of vacuum and N is the carrier density in which depends on temperature, T (in Kelvin) and in InSb is41,42
| 2 |
where is the Boltzmann constant. The variation in T causes the change in N, which subsequently makes the plasma frequency, tunable via changing the temperature. The variation of intrinsic carrier denstiy versus temperature is shown in Fig. 1a. When the temperature increases from 250 K to 360 K, the intrinsic carrier density has a significant enhancement from to . As it is clear, N strongly depends on the temperature, which makes the plasma frequency tunable by changing the environment temperature. Therefore, in the far-infrared part of the THz region, the permittivity of InSb is very sensitive to the temperature, which makes it a remarkable choice to be used in thermally tunable semiconductor metamaterials.
Figure 1.
(a) The functional relationship between the carrier density of InSb in and temperature in K, (b) Schematic of proposed configuration, consisting of an InSb NWMM () with effective permittivities , and an isotropic dielectric () with permittivity . Optical axis (OA) of the NWMM lies along the nanowires (y-z plane), and the surface wave propagates along z direction forming angle with the OA.
Recently nanowire-based composites have attracted significant attention due to their relatively low loss and ease of fabrication43–47. Figure 1b illustrates the proposed interface which includes a polycrystalline quartz as an isotropic cover with permittivity and a semiconductor metamaterial as a substrate. The hyperbolic metamaterial is considered to be nanowires of a semiconductor (InSb) with permittivity , embedded into a dielectric host with permittivity . When the nanowire metamaterial (NWMM) parameters, i.e., the nanowire radius (R) and the distance between two neighboring nanowires (L), are much smaller than the free space wavelength of the incident electromagnetic wave, the system under study can be considered as an effective uniaxial medium with OA parallel to the direction of the nanowires48. The permittivity parallel to the nanowires is the ordinary permittivity , and the permittivity normal to the nanowires is the extraordinary permittivity . On the basis of dynamical Maxwell-Garnett theory, I evaluate the effective permittivities of the NWMM according to49
| 3 |
where is the permittivity of the dielectric host, is the permittivity of the InSb nanowires, and f is the semiconductor (InSb) filling ratio, which is defined as
| 4 |
According to Fig. 1b, R and L defined in the numerator and denominator in Eq. (4) are nanowire area and unit cell area, respectively. The geometry under investigation consists of a semi-infinite layer of isotropic dielectric cover in the region and a semi-infinite layer of a NWMM in the region (see Fig. 1b). Without loss of generality I consider the case where the OA of the NWMM is in the zy-plane.
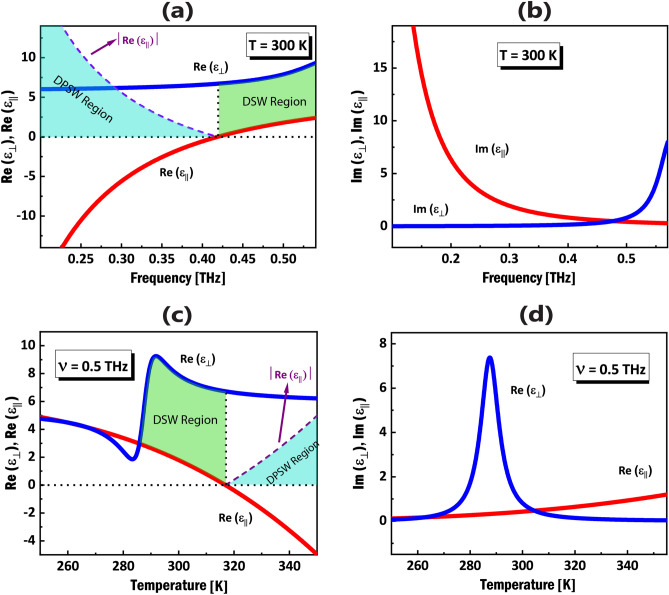
In the proposed configuration, the permittivity values for vitreous silica as the isotropic cover medium and the -quartz as the dielectric host in InSb NWMM in THz, are and , respectively50,51. Also, the filling ratio of InSb in NWMM is considered to be . Variation of the real and imaginary parts of the effective permittivities of the InSb NWMM as a function of frequency at temperature K is depicted in Fig. 2a,b. Note that both and , can be complex numbers due to the presence of the dissipation in the Eq. (1). As can be seen, the real part of , is always positive in the frequency range 0.2 THz to 0.6 THz, while the real part of , can be either positive or negative, depending on the frequency value. Figure 2c,d illustrate the dependence of NWMM effective permittivities on temperature for a single frequency THz. The colored area on the right side of Fig. 2a (DSW region in green color) corresponds to the necessary condition for the permittivity of the cover medium in which the pure DSWs exist (19). In the subsequent calculations for investigating the properties of the DSWs, the frequency THz is chosen from the frequency interval in the Fig. 2a. The left colored side of the plot (DPSW region in turquoise color) shows the necessary condition for the cover permittivity in which the propagation of the DPSWs are allowed (29). Figure 2a shows that the proposed configuration can support two different types of surface waves in THz frequencies.
Figure 2.
Real and imaginary parts of the effective permittivities (red line) and (blue line) of the InSb NWMM in (a), (b) as a function of frequency () at a fixed temperature, K and in (c), (d) as a function of temperature (T) at the fixed THz frequency, THz. In (a), (c), the colored regions indicate the necessary condition for the cover permittivity that supports DSW and DPSW.
The DSWs (and DPSWs) are considered to be hybrid modes which are formed by four evanescent waves with a common wave vector q. In the isotropic cover, the field is a superposition of two independent waves of different polarizations (transverse electric, TE and transverse magnetic, TM) with the same wave vector where . On the other side, in the anisotropic substrate (NWMM), the field is the superposition of the ordinary and extraordinary waves with wave vectors and , respectively, where , . All of the wave vectors are normalized to where c is the speed of light in vacuum. By appling the boundary conditions for the tangential components of the electric and magnetic fields at the interface, the dispersion relation of the different kinds of DSWs is obtained (for details see the refs.34,52) as follows:
| 5 |
Results and discussion
Here I present the results from numerical calculations for the propagation of DSWs and DPSWs in the THz frequencies, at the interface of an isotropic dielectric cover and an InSb NWMM, considering the dispersion relation in Eq. (5). The isotropic cover medium is considered to be vitreous silica with permittivity around 50. Due to the fact that the effective permittivities of the NWMM strongly depends on the environment temperature (see Fig. 2c,d), I expect the characteristics of DSWs and DPSWs resulting from this NWMM, to be tunable by changing the temperature. The colored areas in Fig. 2a show the THz frequency range for a fixed temperature K in which the propagation of the DSWs and DPSWs are allowed, while the colored areas in Fig. 2c illustrate the temperature range for a fixed frequency THz.
One of the most challenging obstacles in practical applications of DSWs is the very narrow angular existence domain (AED) of propagation in natural materials21. The interval of propagation angle of the DSW with respect to the OA of the NWMM, and , is derived by, letting and in the dispersion relation (Eq. 5), respectively19. To study the influence of temperature on the propagation of DSWs, the propagation angles (, ) with respect to the OA upon temperature and AED are demonstrated in Figure 3a,b respectively. One can see that in selected temperature interval, the AEDs in the proposed configuration are in the range of 9 to 18 degrees, which are remarkably large, in comparison to that of natural materials21. By changing the environment temperature, the AED can be tuned to desired values for practical applications.
Figure 3.
(a) Dependence of the propagation angles (, ) on the environment temperature at THz. (b) Angular existence domain (AED) of DSWs upon temperature. (c) Calculated dispersion relation for DSWs in terms of the propagation angle () for different temperature values. (d) Dispersion curves for DPSWs at a fixed propagation angle for different temperature values from to .
Figure 3c demonstrates the dispersion curves of DSWs, considering 5 different temperatures. Using Eqs. (1-4), real parts of the ordinary and extraordinary effective permittivities of the NWMM in are , for , for , for , for and for . The dispersion curves are obtained by numerical solving of the wave vector relations for cover and substrate and the dispersion relation (Eq. 5), simultaneously. It is shown in Fig. 3c that in addition to wide angular domains of propagation in all 5 cases, different angular regions, are thermally tunable via changing the temperature values. The plot shows by increasing the temperature, the angular range of DSW propagation shifts to larger values. The angular directionality is one of the distinct features of DSWs that can lead to steering operations of light at the interface32,53, and also this feature can be manipulated by changing the temperature, the launching frequency and the cover and the substrate optical parameters.
The DPSW is a special case of DSW that in general, can exist at the interface between two materials which at least one of them is anisotropic and also one component of the permittivity of either media is negative32–34. In the present case, the partnering materials have 3 different permittivity values; one for the isotropic cover and two for NWMM, among which the ordinary permittivity of the NWMM is considered to be negative, as was depicted in the colored areas (turquoise color) in Fig. 2a,c. Figure 3d shows the dispersion relation of DPSWs at a fixed propagation angle (with respect to the OA of the NWMM) for different temperatures. The dispersion relation are obtained via implementing the frequency-dependent permittivity of InSb (Eq. (1)) in Eq. (5). It is shown in the plot (Fig. 3d), that DPSWs in different temperatures have different dispersion curves, confirming their tunability upon temperature. Moreover, the specific birefringence of the engineered NWMM for various temperature values, leads to different cut-off frequencies, as is shown in Fig. 3d.
One of the important characteristics of all kinds of surface waves, is the localization degree to the interface. It is well-known that DSWs in natural dielectric materials, are weakly localized to the interface, in comparison to the SPPs that are strongly localized due to the presence of metals. Hence, in Fig. 4a,b I investigate the penetration depths, defined as , , where , and are the wavelength and evanescent wave vector components, respectively28. The subscripts c and e represent the isotropic dielectric cover and the InSb NWMM, respectively. Here, I consider two cases of DSWs with different propagation angles with respect to the OA of the NWMM, that share the same THz frequency THz, for different temperature values. In addition to large confinement factor in both cases, and in cover and substrate, one can see the role of temperature value regarding the magnitude of localization degrees. Figure 4a,b, demonstrate that for both and , the penetration depths can be down to half of the for specific temperature values.
Figure 4.
(a), (b) Penetration depths in the isotropic dielectric cover, (green line) and in the InSb NWMM, (orange line) in terms of the environment temperature for and , respectively. (c) Figure of merit (FOM) in terms of the propagation angle corresponding to DSWs at the boundary between an isotropic dielectric medium and a lossy InSb NWMM in .
It is worth noting, finally, the permittivity of the -quartz as the dielectric host in InSb NWMM was taken from experimental results in ref.51. The same procedure was carried on the vitreous silica as the isotropic cover50. Although, for both materials the absorption coefficients are not zero in THz frequencies, I ignored the loss in permittivities for convenience in calculations. According to refs.54,55 I consider a figure of merit (FOM), defined by FOM = Re(q)/Im(q) to determine the influence of absorption losses on the propagation of DSWs. In other word, calculation of the FOM is a method to measure the propagation length of the surface waves at interfaces consisting of lossy materials. In Fig. 4c, one can see that for 3 different temperatures K, K and K in THz, FOM has extremely high values for specific propagation angles, therefore ignoring the losses in mentioned isotropic materials in my calculations, is totally acceptable.
Conclusion
A geometry of a semiconductor NWMM as a substrate and an isotropic dielectric cover, supporting temperature-dependent DSWs, is proposed and studied theoretically. Due to the presence of InSb in the NWMM, the conditions for the propagation of DSWs in THz frequencies is shown to be extremely temperature-sensitive. The calculated AED in different temperature values, reaches up to 18 degrees, that is significant compared to that of natural media. In addition, tunability of the angular range of propagation upon temperature in THz frequencies, is demonstrated. According to the dispersion relation (Eq. (5)), another kind of Dyakonov-like surface wave, known as DPSWs is also supported in the proposed structure. It is shown that for DPSWs, different temperature values lead to different dispersion curves with distinct cut-off THz frequencies. It is also pointed out that the localization degree of the DSW strongly depends on the environment temperature. Finally, the FOM of the propagating DSW is calculated to ensure that neglecting losses related to dielectrics in the configuration, is valid. From a practical point of view, despite the slowness of thermal tuning, the result of this work is beneficial for the development of various controlling techniques and real applications of such structures to manipulate the properties of DSWs.
Author contributions
M.M. designed the research, performed the numerical calculations, prepared the figures and wrote the manuscript.
Data availability
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Competing interests
The author declares no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Milton GW, Nicorovici N-AP, McPhedran RC, Podolskiy VA. A proof of superlensing in the quasistatic regime, and limitations of superlenses in this regime due to anomalous localized resonance. Proc. Royal Soc. A: Math. Phys. Eng. Sci. 2005;461:3999–4034. doi: 10.1098/rspa.2005.1570. [DOI] [Google Scholar]
- 2.Jacob Z, Alekseyev LV, Narimanov E. Optical hyperlens: Far-field imaging beyond the diffraction limit. Opt. Express. 2006;14:8247–8256. doi: 10.1364/OE.14.008247. [DOI] [PubMed] [Google Scholar]
- 3.Pendry JB, Schurig D, Smith DR. Controlling electromagnetic fields. Science. 2006;312:1780–1782. doi: 10.1126/science.1125907. [DOI] [PubMed] [Google Scholar]
- 4.Smith DR, Padilla WJ, Vier D, Nemat-Nasser SC, Schultz S. Composite medium with simultaneously negative permeability and permittivity. Phys. Rev. Lett. 2000;84:4184. doi: 10.1103/PhysRevLett.84.4184. [DOI] [PubMed] [Google Scholar]
- 5.Smith D, Vier D, Koschny T, Soukoulis C. Electromagnetic parameter retrieval from inhomogeneous metamaterials. Phys. Rev. E. 2005;71:036617. doi: 10.1103/PhysRevE.71.036617. [DOI] [PubMed] [Google Scholar]
- 6.Paniagua-Domínguez R, Abujetas DR, Sánchez-Gil JA. Ultra low-loss, isotropic optical negative-index metamaterial based on hybrid metal-semiconductor nanowires. Sci. Rep. 2013;3:1507. doi: 10.1038/srep01507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Govyadinov AA, Podolskiy VA. Metamaterial photonic funnels for subdiffraction light compression and propagation. Phys. Rev. B. 2006;73:155108. doi: 10.1103/PhysRevB.73.155108. [DOI] [Google Scholar]
- 8.Grann EB, Moharam M, Pommet DA. Artificial uniaxial and biaxial dielectrics with use of two-dimensional subwavelength binary gratings. JOSA A. 1994;11:2695–2703. doi: 10.1364/JOSAA.11.002695. [DOI] [Google Scholar]
- 9.Genereux F, Leonard S, Van Driel H, Birner A, Gösele U. Large birefringence in two-dimensional silicon photonic crystals. Phys. Rev. B. 2001;63:161101. doi: 10.1103/PhysRevB.63.161101. [DOI] [Google Scholar]
- 10.Hoffman AJ, et al. Negative refraction in semiconductor metamaterials. Nat. Mater. 2007;6:946–950. doi: 10.1038/nmat2033. [DOI] [PubMed] [Google Scholar]
- 11.Hoffman AJ, et al. Midinfrared semiconductor optical metamaterials. J. Appl. Phys. 2009;105:122411. doi: 10.1063/1.3124087. [DOI] [Google Scholar]
- 12.Zhang H, Jiao Z, Mcleod E. Tunable terahertz hyperbolic metamaterial slabs and super-resolving hyperlenses. Appl. Opt. 2020;59:G64–G70. doi: 10.1364/AO.391952. [DOI] [PubMed] [Google Scholar]
- 13.Yilmaz M, et al. Micro-/nanostructured highly crystalline organic semiconductor films for surface-enhanced Raman spectroscopy applications. Adv. Func. Mater. 2015;25:5669–5676. doi: 10.1002/adfm.201502151. [DOI] [Google Scholar]
- 14.Biefeld RM. The preparation of InSb and InAs1- x Sbx by metalorganic chemical vapor deposition. J. Cryst. Growth. 1986;75:255–263. doi: 10.1016/0022-0248(86)90035-7. [DOI] [Google Scholar]
- 15.Ge J-P, et al. Halide-transport chemical vapor deposition of luminescent zns: Mn2+ one-dimensional nanostructures. Adv. Func. Mater. 2005;15:303–308. doi: 10.1002/adfm.200400078. [DOI] [Google Scholar]
- 16.Schultz DA. Plasmon resonant particles for biological detection. Curr. Opin. Biotechnol. 2003;14:13–22. doi: 10.1016/S0958-1669(02)00015-0. [DOI] [PubMed] [Google Scholar]
- 17.Ditlbacher H, Krenn JR, Schider G, Leitner A, Aussenegg FR. Two-dimensional optics with surface plasmon polaritons. Appl. Phys. Lett. 2002;81:1762–1764. doi: 10.1063/1.1506018. [DOI] [Google Scholar]
- 18.Specht M, Pedarnig J, Heckl W, Hänsch T. Scanning plasmon near-field microscope. Phys. Rev. Lett. 1992;68:476. doi: 10.1103/PhysRevLett.68.476. [DOI] [PubMed] [Google Scholar]
- 19.D’yakonov M. New type of electromagnetic wave propagating at an interface. Sov. Phys. JETP. 1988;67:714–716. [Google Scholar]
- 20.Takayama O, Artigas D, Torner L. Lossless directional guiding of light in dielectric nanosheets using Dyakonov surface waves. Nat. Nanotechnol. 2014;9:419–424. doi: 10.1038/nnano.2014.90. [DOI] [PubMed] [Google Scholar]
- 21.Takayama O, et al. Dyakonov surface waves: A review. Electromagnetics. 2008;28:126–145. doi: 10.1080/02726340801921403. [DOI] [Google Scholar]
- 22.Takayama O, Crasovan L, Artigas D, Torner L. Observation of Dyakonov surface waves. Phys. Rev. Lett. 2009;102:043903. doi: 10.1103/PhysRevLett.102.043903. [DOI] [PubMed] [Google Scholar]
- 23.Li Y, Sun J, Wen Y, Zhou J. Controllable selective coupling of Dyakonov surface waves at a liquid-crystal-based interface. Phys. Rev. Appl. 2020;13:024024. doi: 10.1103/PhysRevApplied.13.024024. [DOI] [Google Scholar]
- 24.Li Y, Sun J, Wen Y, Zhou J. Spin-dependent visible Dyakonov surface waves in a thin hyperbolic metamaterial film. Nano Lett. 2022;22:801–807. doi: 10.1021/acs.nanolett.1c04418. [DOI] [PubMed] [Google Scholar]
- 25.Walker D, Glytsis E, Gaylord T. Surface mode at isotropic-uniaxial and isotropic-biaxial interfaces. JOSA A. 1998;15:248–260. doi: 10.1364/JOSAA.15.000248. [DOI] [Google Scholar]
- 26.Cojocaru E. Dyakonov hybrid surface waves at the isotropic-biaxial media interface. JOSA A. 2015;32:782–789. doi: 10.1364/JOSAA.32.000782. [DOI] [PubMed] [Google Scholar]
- 27.Crasovan L-C, Artigas D, Mihalache D, Torner L. Optical Dyakonov surface waves at magnetic interfaces. Opt. Lett. 2005;30:3075–3077. doi: 10.1364/OL.30.003075. [DOI] [PubMed] [Google Scholar]
- 28.Artigas D, Torner L. Dyakonov surface waves in photonic metamaterials. Phys. Rev. Lett. 2005;94:013901. doi: 10.1103/PhysRevLett.94.013901. [DOI] [PubMed] [Google Scholar]
- 29.Takayama O, Artigas D, Torner L. Practical Dyakonons. Opt. Lett. 2012;37:4311–4313. doi: 10.1364/OL.37.004311. [DOI] [PubMed] [Google Scholar]
- 30.Zapata-Rodríguez CJ, Miret JJ, Vuković S, Belić MR. Engineered surface waves in hyperbolic metamaterials. Opt. Express. 2013;21:19113–19127. doi: 10.1364/OE.21.019113. [DOI] [PubMed] [Google Scholar]
- 31.Moradi M, Niknam AR. Terahertz Dyakonov surface waves in plasma metamaterials. Opt. Lett. 2018;43:519–522. doi: 10.1364/OL.43.000519. [DOI] [PubMed] [Google Scholar]
- 32.Jacob Z, Narimanov EE. Optical hyperspace for plasmons: Dyakonov states in metamaterials. Appl. Phys. Lett. 2008;93:221109. doi: 10.1063/1.3037208. [DOI] [Google Scholar]
- 33.Takayama O, et al. Midinfrared surface waves on a high aspect ratio nanotrench platform. ACS Photonics. 2017;4:2899–2907. doi: 10.1021/acsphotonics.7b00924. [DOI] [Google Scholar]
- 34.Moradi M, Niknam AR. Terahertz Dyakonov plasmon surface waves supported by a plasma/Tio 2 interface. Phys. Rev. B. 2018;98:085403. doi: 10.1103/PhysRevB.98.085403. [DOI] [Google Scholar]
- 35.Takayama O, et al. Experimental observation of Dyakonov plasmons in the mid-infrared. Semiconductors. 2018;52:442–446. doi: 10.1134/S1063782618040279. [DOI] [Google Scholar]
- 36.Wang X, Belyanin A, Crooker S, Mittleman D, Kono J. Interference-induced terahertz transparency in a semiconductor magneto-plasma. Nat. Phys. 2010;6:126–130. doi: 10.1038/nphys1480. [DOI] [Google Scholar]
- 37.Gül Ö, et al. Towards high mobility InSb nanowire devices. Nanotechnology. 2015;26:215202. doi: 10.1088/0957-4484/26/21/215202. [DOI] [PubMed] [Google Scholar]
- 38.De La Mata M, et al. Twin-induced InSb nanosails: A convenient high mobility quantum system. Nano Lett. 2016;16:825–833. doi: 10.1021/acs.nanolett.5b05125. [DOI] [PubMed] [Google Scholar]
- 39.Yang D, Zhang C, Li X, Lan C. Insb-enhanced thermally tunable terahertz silicon metasurfaces. IEEE Access. 2019;7:95087–95093. doi: 10.1109/ACCESS.2019.2928225. [DOI] [Google Scholar]
- 40.Howells S, Schlie L. Transient terahertz reflection spectroscopy of undoped InSb from 0.1 to 1.1 THz. Appl. Phys. Lett. 1996;69:550–552. doi: 10.1063/1.117783. [DOI] [Google Scholar]
- 41.Halevi P, Ramos-Mendieta F. Tunable photonic crystals with semiconducting constituents. Phys. Rev. Lett. 2000;85:1875. doi: 10.1103/PhysRevLett.85.1875. [DOI] [PubMed] [Google Scholar]
- 42.Cheng BH, Ye Y-S, Lan Y-C, Tsai DP. Temperature tunability of surface plasmon enhanced Smith–Purcell terahertz radiation for semiconductor-based grating. Sci. Rep. 2017;7:6443. doi: 10.1038/s41598-017-06839-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Muskens OL, et al. Epitaxial growth of aligned semiconductor nanowire metamaterials for photonic applications. Adv. Func. Mater. 2008;18:1039–1046. doi: 10.1002/adfm.200701337. [DOI] [Google Scholar]
- 44.Peng K, et al. Three-dimensional cross-nanowire networks recover full terahertz state. Science. 2020;368:510–513. doi: 10.1126/science.abb0924. [DOI] [PubMed] [Google Scholar]
- 45.Kabashin AV, et al. Plasmonic nanorod metamaterials for biosensing. Nat. Mater. 2009;8:867–871. doi: 10.1038/nmat2546. [DOI] [PubMed] [Google Scholar]
- 46.Wurtz GA, et al. Designed ultrafast optical nonlinearity in a plasmonic nanorod metamaterial enhanced by nonlocality. Nat. Nanotechnol. 2011;6:107–111. doi: 10.1038/nnano.2010.278. [DOI] [PubMed] [Google Scholar]
- 47.Barrigón E, Heurlin M, Bi Z, Monemar B, Samuelson L. Synthesis and applications of iii–v nanowires. Chem. Rev. 2019;119:9170–9220. doi: 10.1021/acs.chemrev.9b00075. [DOI] [PubMed] [Google Scholar]
- 48.Elser J, Wangberg R, Podolskiy VA, Narimanov EE. Nanowire metamaterials with extreme optical anisotropy. Appl. Phys. Lett. 2006;89:261102. doi: 10.1063/1.2422893. [DOI] [Google Scholar]
- 49.Sihvola AH. Electromagnetic mixing formulas and applications. IET; 1999. [Google Scholar]
- 50.Naftaly M, Gregory A. Terahertz and microwave optical properties of single-crystal quartz and vitreous silica and the behavior of the boson peak. Appl. Sci. 2021;11:6733. doi: 10.3390/app11156733. [DOI] [Google Scholar]
- 51.Davies CL, Patel JB, Xia CQ, Herz LM, Johnston MB. Temperature-dependent refractive index of quartz at terahertz frequencies. J. Infrared Millim. T. Waves. 2018;39:1236–1248. doi: 10.1007/s10762-018-0538-7. [DOI] [Google Scholar]
- 52.Cojocaru E. Comparative analysis of Dyakonov hybrid surface waves at dielectric-elliptic and dielectric-hyperbolic media interfaces. JOSA B. 2014;31:2558–2564. doi: 10.1364/JOSAB.31.002558. [DOI] [Google Scholar]
- 53.Kildishev AV, Boltasseva A, Shalaev VM. Planar photonics with metasurfaces. Science. 2013;339:1232009. doi: 10.1126/science.1232009. [DOI] [PubMed] [Google Scholar]
- 54.Narimanov EE. Photonic hypercrystals. Phys. Rev. X. 2014;4:041014. [Google Scholar]
- 55.Miret JJ, Zapata-Rodríguez CJ, Jakšić Z, Vuković S, Belić MR. Substantial enlargement of angular existence range for Dyakonov-like surface waves at semi-infinite metal-dielectric superlattice. J. Nanophotonics. 2012;6:063525–063525. doi: 10.1117/1.JNP.6.063525. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.