Edge-assisted quantum protocol for secure multiparty logical AND its applications

Summary

Security and privacy have always been key concerns for individuals in various edge-assisted services. In this paper, we present a feasible quantum solution to an important primitive of secure multiparty computations, i.e., Secure Multiparty Logical AND (SMLA), in which n participants can securely compute logical AND of n private bits. In order to ensure perfect security and achieve good feasibility, we introduce a semi-honest edge server and two non-collusive fog nodes, and design a secure and feasible edge-assisted quantum protocol for SMLA, which cleverly utilizes Secure Multiparty XOR to implement SMLA group by group. Furthermore, we focus on applications of this quantum primitive protocol and design two quantum protocols for Multiple Private Set Intersection and Anonymous One-vote Veto. Compared with classical related protocols, our proposed quantum protocols obtain higher security, which can be guaranteed by the basic principles of quantum mechanics.

Graphical abstract

Highlights

• •A quantum protocol for computing XOR of multiple private bits is proposed
• •A quantum protocol for computing logical AND of multiple private bits is built
• •Two application protocols of proposed quantum AND protocol are designed

Quantum Metrology and Physics

Introduction

With the rapid development of cloud/edge computing, there have appeared various cloud-based and edge-based applications, e.g., cloud-based data storage¹ and edge-based data services (outsourcing services).² Furthermore, in order to control the access to the data stored in the cloud/edge, generally, it needs to encrypt the data before uploading them by using novel cryptographic algorithms, e.g., attribute-based encryption^3,4 and identity-based proxy re-encryption.^5,6 However, it is difficult for most classical cryptographic algorithms to ensure long-term security of the data stored in the remote cloud due to upcoming quantum computers and fast quantum algorithms.^7,8,9 Especially, quantum supremacy (or quantum advantage) has been demonstrated,^10,11 so classical cryptography will certainly face lots of threats and challenges.

Furthermore, as an important branch of modern cryptography, quantum cryptography can ensure information-theoretical security and accordingly provide long-term security, which are guaranteed by the principles of quantum mechanics.¹² Quantum cryptography was formally introduced by C.H. Bennett, et al. in 1984 by first presenting BB84 quantum key distribution (QKD) protocol.¹³ Since that, quantum cryptography has attracted a lot of scientific attention from the cryptography community. Besides QKD, quantum cryptography covers a wide range of research areas, e.g., quantum secret sharing,¹⁴ quantum perfect encryption,¹⁵ quantum signature,¹⁶ quantum secure direct communication,¹⁷ quantum key agreement,¹⁸ and so on.

On the other hand, secure multiparty computation (SMC), which allows a group of mutually distrustful participants to compute a joint function of their respective private inputs without revealing private input of each participant, has various applications in data sharing and privacy-preserving settings, such as electronic voting,¹⁹ electronic auction,²⁰ and federated learning.²¹ Correspondingly, there have appeared many quantum solutions to all kinds of specific SMC problems, e.g., quantum anonymous voting,²² quantum sealed-bid auction,²³ quantum private set intersection,²⁴ quantum secret permutating,²⁵ and so on.

In this paper, to enhance security and privacy, we attempt to construct primitive protocols of SMC by introducing quantum information technologies, i.e., to construct quantum protocols for computing bitwise logical XOR and AND (i.e., product) of multiple private bits, which can be adopted to implement more complicated functions as basic blocks. When designing quantum primitive protocols, we mainly focus on two factors: higher security and better feasibility. In order to achieve these goals, we employ single photons as quantum resources, and accordingly perform single-photon operators and measurements. Finally, we investigate novel applications of these quantum primitive protocols in edge-based environments.

Our main contributions in this paper are summarized as follows.

• (1)We first present a quantum protocol for computing XOR of multiple private bits with single photons and single-photon measurements, i.e., Edge-assisted Secure Multiparty XOR (ESMX) Quantum Protocol, which can guarantee information-theoretical security.
• (2)Based on proposed ESMX quantum protocol, we further present a feasible edge-assisted quantum protocol for computing logical AND (i.e., logical product) of multiple private bits by grouping and computing group by group, i.e., Edge-assisted Quantum Protocol for Secure Multiparty Logical AND (SMLA), which can ensure information-theoretical security.
• (3)We design two application protocols of Edge-assisted Quantum Protocol for SMLA, i.e., Quantum Protocol for Multiparty Private Set Intersection (MPSI) and Quantum Protocol for Anonymous One-vote Veto (AOV), which can achieve perfect security and good feasibility.

Related works

Secure Multiparty Logical AND

Logical AND (i.e., logical product) is an important and fundamental arithmetic operation in evaluating Boolean expressions or Boolean functions. Recently, we defined a new SMC problem in ref.,²⁶ i.e., Secure Multiparty Logical AND (SMLA for short), in which multiple participants can jointly compute bitwise logical AND of their respective private bits. As a primitive of SMC, there are many promising applications of SMLA in distributed cryptographic tasks, e.g., Secret Sharing and Private Set Intersection (PSI)/Union. In ref.,²⁶ we proposed a novel quantum SMLA protocol by using phase-matching quantum conference key agreement and perfect quantum encryption. In this previously proposed quantum SMLA protocol, the most critical process is to adopt three-qubit Toffoli gates to generate $O\left(n\right)$-qubit entangled states. However, it is still difficult to prepare and transmit high-fidelity entangled states in high-dimensional Hilbert space. So, it is of great significance to find a feasible and efficient quantum solution to SMLA.

Multiparty Private Set Intersection

In 2004, M.J. Freedman et al.²⁷ first defined PSI, in which two participants jointly compute the intersection of two private sets without revealing any private set, and presented a PSI protocol by using homomorphic encryption and oblivious polynomial evaluation.

In 2016, Shi et al.²⁸ first designed a cheat-sensitive quantum protocol for PSI based on phase-encoded quantum privacy query, which could output the intersection of two private sets. Furthermore, in order to reveal less privacy information, Shi et al. presented a constant-round quantum protocol for PSI Cardinality (PSI-CA),²⁹ which could output the intersection cardinality of two private sets, instead of any element of the intersection. Compared with the classical related protocols, this quantum PSI-CA protocol has higher security and lower communication complexity. However, it requires additional assumptions for the cardinality of two private sets,²⁹ which might limit its wider applications. Later, in ref.,³⁰ Shi successfully discarded these assumptions and presented a robust quantum PSI-CA protocol without any limitation.

However, these previously proposed quantum protocols still need the complicated oracle operators. Furthermore, in order to enhance the feasibility, Shi et al. introduced a non-collusive third party to assist two legitimate parties to compute the intersection cardinality based on single photons³¹ and Bell states.³² Most recently, Liu et al. designed an improved PSI-CA protocol with single photons by using Bloom filter.³³

In addition, Shi et al.,³⁴ Zhang et al.,³⁵ and Wang et al.³⁶ generalized two-party PSI-CA to multi-party PSI-CA and presented the corresponding multi-party quantum PSI-CA (PUI-CA) protocols. To the best of our knowledge, currently, there is not any quantum protocol for MPSI.

Like QKD, the feasibility of quantum PSI/PSI-CA protocols is the focus of research. However, there are two intractable problems to implement these existing quantum PSI/PSI-CA protocols: one is to find a fully trusted third party in the cyber or virtual world and the other is to implement the complicated (oracle) operators and measurements in high-dimensional Hilbert space.

Please note that an oracle operator is an arbitrary unitary transformation theoretically in arbitrary n-dimension Hilbert space as a “black box”. For example, $O|\psi ⟩={\sum }_{x\in {\left\{\mathrm{0,1}\right\}}^n,y\in {\left\{\mathrm{0,1}\right\}}^m}\alpha \left(x,y\right)|x⟩|y\oplus f\left(x\right)⟩$. Here, the operator $O$ can be viewed as an oracle operator. Generally, for an oracle operator, we focus on what it does and we do not consider how to implement it. Therefore, it has always been our goal to design the practical and feasible quantum PSI/PSI-CA protocols with the present quantum technology.

Anonymous voting

The first electronic voting protocol based on classical cryptography was proposed by David Chaum in 1981.¹⁹ Subsequently, there appeared many electronic voting protocols.^37,38,39,40 Similarly, in order to resist the attack of quantum computers, quantum voting has attracted extensive attention of scholars.

In 2006, Hillery presented two quantum voting models,⁴¹ i.e., traveling ballot model and distributed ballot model. In 2007, Vaccaro et al. defined the basic security properties that quantum voting should meet.⁴² Later, there were lots of well-known quantum voting protocols satisfying different security properties.^43,44,45,46

In 2015, Rahaman et al. presented an anonymous veto protocol without any trusted third party.⁴⁷ In this protocol, suppose that there are a group of jury members, who need to take a unanimous decision, but at the same time want their individual decisions to remain secret, i.e., without disclosing the identity of possible vetoing member. Rahaman’s protocol utilizes generalized multi-qubit Greenberger-Horne-Zeillinger (GHZ) states as quantum resources. However, it is very difficult to implement this multi-qubit GHZ state. In 2021, Wu et al. proposed a novel anonymous veto protocol based on polarized single photons.⁴⁸ Wu’s protocol needs a semi-honest server to assist all voters to complete this cryptographic task, but a dishonest server can reveal partial privacy information.

Results and discussion

Proposed protocols

We first describe the definition of SMLA as follows.

Definition 1²⁶

SMLA: Suppose that there are $n$ ($n>2$) participants: $P_1$, $P_2$, …, $P_n$, each of which owns a private bit $x_i\in \left\{\mathrm{0,1}\right\}$. After executing the SMLA protocol, it outputs ${\bigwedge }_{i=1}^n{x}_i$, where ${\bigwedge }_{i=1}^n{x}_i=x_1\wedge x_2\wedge \dots \wedge x_n$ and $\wedge$ is the logical AND operation. In addition, this protocol should satisfy the following requirements:

Correctness

If all parties honestly execute this protocol, then the final output is equal to ${\bigwedge }_{i=1}^n{x}_i$, i.e., the output is correct.

Privacy

Anyone else but the participant $P_i$ cannot get any private information about $x_i$ except the final output ${\bigwedge }_{i=1}^n{x}_i$.

Fairness

Under no circumstances one participant should have an advantage over another or other parties to get the final output or more private information.

Please note that logical AND is equivalent to logical product, i.e., ${\bigwedge }_{i=1}^n{x}_i={\prod }_{i=1}^n{x}_i\text{.}$ Furthermore, only if all $x_i$ s are equal to 1, then ${\bigwedge }_{i=1}^n{x}_i={\prod }_{i=1}^n{x}_i=1$. Otherwise ${\bigwedge }_{i=1}^n{x}_i={\prod }_{i=1}^n{x}_i=0$.

In addition, it is widely known that perfect secure two-party computations, including classical two-party computation (e.g., bit commitment or oblivious transfer), cannot be implemented in theory by the no-go results.^49,50,51 However, in our defined ESMX Quantum Protocol and Edge-assisted Quantum Protocol for SMLA there are more than two participants, which are not belong to secure two-party computations. As we know, though it is impossible to implement unconditionally secure two-party computations, there are unconditionally secure multi-party computations ($n>2$), e.g., Shamir’s secret sharing and quantum secret sharing. We do not try to evade this type of attack, but our proposed protocols are not bound by the no-go theorem.

System model

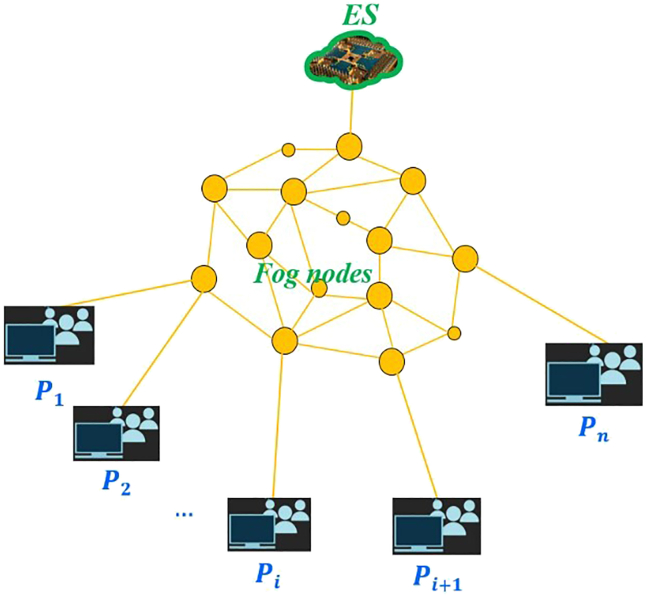
In our system model, suppose that there is an edge server (ES for short), several fog nodes (e.g., ${fog}_1$ and ${fog}_2$), and $n$ participants: $P_1$, $P_2$, …, $P_n$. Here, the ES is taken as a mini cloud and a fog node is defined as a quantum computing and routing device, and further the ES and participants can communicate by the quantum network composed of several fog nodes, as shown in Figure 1.

Figure 1.

System model

In this model, each participant $P_i$ ($i=\mathrm{1,2},\dots ,n$) has a private bit $x_i$ and the ES and the fog nodes will assist $n$ participants to compute the logical AND of all private bits. Furthermore, we assume that all participants (including the ES and the fog nodes) are semi-honest and any two-third parties (i.e., the fog nodes or the ES) are non-collusive. In addition, we assume that there are authenticated quantum channels and authenticated classical channels between any two neighboring parties.

Finally, our security goal is to ensure the privacy of each participant, i.e., the privacy of the input bit $x_i$.

Protocols

Here, we first present an edge-assisted quantum protocol for securely computing XOR of $n$ private bits with single photons and single-photon measurements, which will be utilized later in proposed quantum protocol for computing SMLA.

Edge-assisted Secure Multiparty XOR Quantum Protocol

Step 1. All participants including the ES agree on a small integer $t$, where $t\ge 4$, e.g., $t=4$ or 5.

Step 2. The ES generates $t$ single photons: ${sp}_1$, ${sp}_2$, …, and ${sp}_t$, where each single photon ${sp}_j$ ($j=\mathrm{1,2},\dots ,t$) is randomly in one of four polarized states {|0⟩, |1⟩, |+⟩, |⎯⟩}.

Step 3. After the ES records the initial states of all $t$ single photons, he sends the photon sequence {${sp}_1$, ${sp}_2$, …, ${sp}_t$} to the participant $P_1$ through authenticated quantum channel.

Step 4. After receiving the photon sequence sent from the ES, the participant $P_1$ performs the operator ${U_Y}^{r_1\left[j\right]}{H}^{s_1\left[j\right]}$ on each single photon ${sp}_j$ for $j=\mathrm{1,2},\dots ,t$, where $r_1\left[j\right],s_1\left[j\right]{\in }_R\left\{\mathrm{0,1}\right\}$, and $U_Y$ and $H$ are defined by

$$U_Y=iY=\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]$$ (Equation 1)

$$H=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]\text{.}$$ (Equation 2)

By Equations 1 and 2, we can easily deduce that $U_Y^2=-I$ and $H^2=I$. Please note that both $r_1\left[j\right]$ and $s_1\left[j\right]$ are randomly and privately selected by the participant $P_1$.

Step 5. After performing the corresponding operators, the participant $P_1$ further sends all $t$ single photons to the next participant $P_2$ through authenticated quantum channel.

Step 6. After receiving $t$ single photons sent from the previous participant $P_1$, the participant $P_2$ executes the similar procedure: to first perform the operator ${U_Y}^{r_2\left[j\right]}{H}^{s_2\left[j\right]}$ on the $j$ th single photon ${sp}_j$ for $j=\mathrm{1,2},\dots ,t$ and then send all $t$ single photons to the next participant $P_3$ through authenticated quantum channel.

Step 7. The similar process will be executed $n$ times in total. Finally, the participant $P_n$ performs the corresponding operators and sends all $t$ single photons back to the ES through authenticated quantum channel.

Step 8. After receiving $t$ single photons, i.e., ${sp}_1$, ${sp}_2$, …, and ${sp}_t$, the ES measures each photon ${sp}_j$ in the initial basis for $j=\mathrm{1,2},\dots ,t$. Furthermore, if the measured result of each photon ${sp}_j$ is the same as the initial state, then the ES sets $m\left[j\right]=0$. Otherwise, he sets $m\left[j\right]=1$.

Step 9. The ES informs all participants of selecting successful events among all $t$ events corresponding to $t$ single photons as follows: Each participant $P_i$ ($i=\mathrm{1,2},\dots ,n$) opens their partial secrets, i.e., $s_i\left[j\right]$ for $j=\mathrm{1,2},\dots ,t$, while he keeps the other secrets, i.e., $r_i\left[j\right]$ for $j=\mathrm{1,2},\dots ,t$. Furthermore, all participants select out successful events, satisfying the condition of ${\sum }_{i=1}^n{s}_i\left[j\right]\mathit{mod}2=0$, where $j$ is the sequence number of the successful event.

Step 10. All participants select out a successful event as the encoding event and other successful events as the checking events. Here, we assume that the sequence number of the encoding event is $l$.

Step 11. For all checking events, all participants ask the ES to announce the corresponding $m\left[j\right]$ s. Then, all participants open their corresponding $r_i\left[j\right]$ s for $i=\mathrm{1,2},\dots ,n$. Furthermore, all participants determine whether ${\sum }_{i=1}^n{r}_i\left[j\right]\mathit{mod}2$ is equal to $m\left[j\right]$ for all checking events. If ${\sum }_{i=1}^n{r}_i\left[j\right]\mathit{mod}2\ne m\left[j\right]$ for any checking event, then they will terminate this protocol. Otherwise, they will continue to execute the next step.

Step 12. For the encoding event, each participant $P_i$ ($i=\mathrm{1,2},\dots ,n$) computes ${\tilde{x}}_i=x_i\oplus r_i\left[l\right]$ and sends ${\tilde{x}}_i$ to the ES through authenticated classical channel, where $x_i$ is his private input.

Please note that we assume that each participant and the ES have a common key distributed by QKD protocol in advance, and they encrypt the classical message with the key by the one-time pad method.

Step 13. The ES computes $x={\tilde{x}}_1\oplus {\tilde{x}}_2\oplus \dots \oplus {\tilde{x}}_n\oplus m\left[l\right]$ and outputs $x$ as the final XOR of all private bits.

In the next section, we will focus on how to efficiently solve SMLA with feasible quantum resources, operators, and measurements. On the one hand, in order to ensure the feasible solution of SMLA, we try to divide all participants into different groups, where each group just includes three participants. Furthermore, we compute the logical AND of three private bits group by group. If all AND results of all groups are equal to 1, then the final AND of all $n$ private bits is equal to 1. Otherwise, it is certainly equal to 0. On the other hand, in order to achieve the feasibility, we attempt to compute the logical AND of each group by using different XORs in the corresponding group. For example, we consider a group with three private bits: $x_1$, $x_2$, and $x_3$. Clearly, if we know that $x_1\oplus x_2\oplus x_3=1$, and $x_1\oplus x_2=0$, $x_2\oplus x_3=0$, and $x_1\oplus x_3=0$, then we can easily deduce that $x_1\wedge x_2\wedge x_3=1$ (i.e., $x_1{x}_2{x}_3=1$). Otherwise $x_1\wedge x_2\wedge x_3=x_1{x}_2{x}_3=0$.

Based on the aforementioned proposed XOR protocol, i.e., ESMX Quantum Protocol, we further present Edge-assisted Quantum Protocol for SMLA, which is described in detail as follows.

Edge-assisted Quantum Protocol for SMLA

Step 1 (Grouping). ①All participants publicly agree on the number of groups $w=\lceil n/3\rceil$, where $n$ is the number of all participants, and a small integer $d$, such that $2^d\cong w$. ②Each participant generates a $d$-bit secret $s_i$ as follows: For $j=\mathrm{1,2},\dots ,d$, he prepares a photon in the superposition state $|+⟩=\frac{1}{\sqrt{2}}(|0⟩+|1⟩)$ and then measures it in the computational basis, i.e., {$|0⟩$, $|1⟩$}; If the measured result is in $|0⟩$, then $s_i\left[j\right]=0$, and $s_i\left[j\right]=1$ otherwise. Here $s_i\left[j\right]$ denotes the $j$ th bit of the secret $s_i$. ③According to his/her secret $s_i$, each participant is privately divided into the $s_i$ th group.

Please note that there are $2^d$ groups initially. Since $2^d\cong w$, there are about $w$ groups and each group has about 3 participants due to uniformness and randomness of quantum measurements.

Step 2 (Counting). ① Each participant $P_i$ ($i=\mathrm{1,2},\dots ,n$) generates a 0/1 vector with $2^d$ components, where the $j$ th components is equal to 1 if he/she belongs to the$j$ th group, and all other components are equal to 0. For example, if there are 4 groups in total and he/she belongs to the third group, then his private vector is equal to (0,0,1,0). Furthermore, he/she takes his/her private vector as an 8-nary vector and computes the corresponding integer $S_i$. For example, (0,0,1,0) is corresponding to the integer 8.

Note: In order to avoid the carry, we utilize 8-nary vectors to encode private information, since each group has about 3 participants.

②Each participant $P_i$ ($i=\mathrm{1,2},\dots ,n$) privately generates a polynomial function of degree ($n-1$) over $Z_q$ ($q>8^w$):

$$F_i\left(x\right)=\left(S_i+a_{i,1}x+a_{i,2}{x}^2+\dots +a_{i,n-1}{x}^{n-1}\right)modq\text{,}$$ (Equation 3)

where $F_i\left(0\right)=S_i$ and $a_{i,j}{\in }_R{Z}_q$.

③Each participant $P_i$ ($i=\mathrm{1,2},\dots ,n$) computes the shares of all participants by the polynomial function:

$$S_{i,j}=F_i\left(j\right)modqforj=\mathrm{1,2},\dots ,n\text{.}$$ (Equation 4)

④Each participant $P_i$ ($i=\mathrm{1,2},\dots ,n$) sends the share $S_{i,j}$ to the corresponding participant $P_j$ for $j=\mathrm{1,2},\dots ,n$ ($j\ne i$) through authenticated classical channels.

⑤Each participant $P_i$ ($i=\mathrm{1,2},\dots ,n$) computes the summation of his own shares:

$$S\left(i\right)=\sum _{j=1}^n{S}_{j,i}={\sum }_{j=1}^n{F}_j\left(i\right)modq\text{.}$$ (Equation 5)

Furthermore, he/she sends $S\left(i\right)$ to the ES through authenticated classical channel.

⑥After the ES receiving $n$ shares, he can recover the following secret by using the Lagrange interpolation method:

$$\sum _{i=1}^n{F}_i\left(0\right)=\sum _{i=1}^{n}S\left(i\right)\left(\prod _{j\ne i}^{1\le j\le n}\frac{\left(0-j\right)}{\left(i-j\right)}\right)modq\text{.}$$ (Equation 6)

That is,

$$S=\sum _{i=1}^n{S}_i={\sum }_{i=1}^n{F}_i\left(0\right)modq\text{.}$$ (Equation 7)

As an 8-nary integer, conversely, $S$ is converted by the ES to a $2^d$-component vector ($g_1$, $g_2$, …, $g_{2^d}$), where the $j$ th component $g_j$ represents the number of participants in the $j$ th group (Note. $2^d\cong w$).

Step 3 (Amending). ①If $g_j<3$, then the ES will play the role of a virtual participant whose input bit is equal to 1 and be added into the $j$ th group until $g_j=3$. ②If $g_j>3$, then all participants in the $j$ th group will be subdivided into two subgroups by the similar grouping procedures in Step 1. Accordingly, the number of group (i.e., $w$) will be increased by 1. After amending the number of participants per group, we will assume that each group just has three participants in the next steps and there are $w$ groups in total, i.e., $n=3w$.

Step 4 (Ordering). The ES calls all participants to execute the following procedures: //determining the computing order of each participant in each group.

For $j=\mathrm{1,2},\dots ,w$ do

{①Each participant in the $j$ th group randomly generates a 3-component vector, where only one component is equal to 1, and the other components are equal to 0, e.g., (0,1,0), (1,0,0), or (0,0,1). However, the other participants not in the$j$ th group generate the same 3-component vector: (0,0,0). Here, we assume that each group exactly has 3 participants and there are $n$ participants (i.e., $n=3w$).

②The ES called all participants to parallelly execute ESMX Quantum Protocols to compute the XORs of the corresponding components of $n$ private vectors, as shown in Figure 2.

Figure 2.

An example of computing the XORs to verify the uniqueness of the position indexes

I and II denote the unsuccessful case and the successful case, respectively, where $P_1$, $P_4$, and $P_6$ belong to a group.

③If the XORs are not equal to 111, then it implies that the position indexes of the components which are equal to 1 selected by different participants in the $j$ th group are not unique. For example, three vectors are (0,1,0), (1,0,0), and (0,1,0), respectively, and all other vectors are (0,0,0). Accordingly, the XORs are (1,0,0), not (1,1,1). Furthermore, the ES informs all participants of regenerating their respective vectors of this group to again verify the uniqueness (i.e., go to ①).

④If the XORs are equal to 111, then it means that the position indexes of the components which are equal to 1 selected by different participants in the $j$ th group are unique. Accordingly, the position indexes will be treated as the computing orders in the later computing step.

For example, there are three participants: $P_3$, $P_7$, and $P_{12}$, in the $j$ th group, and they generate three 3-component vectors: (0,1,0), (1,0,0), and (0,0,1), respectively. Obviously, the XORs are equal to 111, so the computing orders of three participants will be corresponding to 2, 1, and 3. Furthermore, the private inputs of three participants in the $j$ th group will be denoted as $x_{j,1}$, $x_{j,2}$, and $x_{j,3}$, respectively. That is, $x_{j,1}=x_7$, $x_{j,2}=x_3$, and $x_{j,3}=x_{12}$. Clearly, each participant in this group only knows his/her computing order, while other participants including the ES cannot know it.

}

Step 5 (Computing). Here, we assume that there are $w$ groups in total and each group has exactly 3 participants. Please note that each participant knows which group he/she belongs to and knows his/her computing order in the group, but others cannot know this private information. The ES calls all participants to execute the following procedures:

For $j=\mathrm{1,2},\dots ,w$ do {//computing group by group

①The ES asks the fog node ${fog}_1$ to assist all participants to securely compute ${\tilde{x}}_1=x_{j,1}\oplus x_{j,2}\oplus x_{j,3}\oplus 0\oplus 0\dots \oplus 0$, i.e., ${\tilde{x}}_1=x_{j,1}\oplus x_{j,2}\oplus x_{j,3}$, where $x_{j,1}$, $x_{j,2}$, and $x_{j,3}$ denote private bits of three participants in the $j$ th group. That is, ${fog}_1$ call all participants to execute ESMX Quantum Protocol, where all participants in the $j$ th group input their real private bits while other participants input 0.

Furthermore, ${fog}_1$ sends ${\tilde{x}}_1$ to the ES through secure classical channel. Similarly, each fog node and the ES have a common key distributed by QKD protocol in advance, and they encrypt the classical message with the key by the one-time pad method.

If ${\tilde{x}}_1=0$, then the ES returns 0 (and ends this protocol). That is, not all of $x_{j,1}$, $x_{j,2}$, and $x_{j,3}$ are equal to 1. So, we can deduce that ${\bigwedge }_{i=1}^n{x}_i={\prod }_{i=1}^n{x}_i=0$. If ${\tilde{x}}_1=1$, then they will continue to execute the next procedures.

② The ES asks the fog node ${fog}_2$ to assist all participants to securely compute ${\tilde{y}}_1=x_{j,1}\oplus x_{j,2}$, ${\tilde{y}}_2=x_{j,1}\oplus x_{j,3}$, and ${\tilde{y}}_3=x_{j,2}\oplus x_{j,3}$, where $x_{j,1}$, $x_{j,2}$, and $x_{j,3}$ denote private bits of three participants in the $j$ th group. That is, ${fog}_2$ call all participants to execute ESMX Quantum Protocol three times, where the participants in the $j$ th group input their real private bits or 0, while other participants input 0. Please note that each participant in this group knows his/her computing order.

Furthermore, ${fog}_2$ computes ${\tilde{x}}_2={\tilde{y}}_1\vee {\tilde{y}}_2\vee {\tilde{y}}_3$ and sends ${\tilde{x}}_2$ to the ES through secure classical channel.

If ${\tilde{x}}_2$ is not equal to 0, then the ES returns 0 (and ends this protocol). That is, ${\bigwedge }_{i=1}^n{x}_i={\prod }_{i=1}^n{x}_i=0$.

}//end for.

Finally, if the ES does not return 0 in the aforementioned For loop, then it implies that the logical AND of each group is equal to 1. So, ${\bigwedge }_{i=1}^n{x}_i={\prod }_{i=1}^n{x}_i=1$. That is, the ES finally outputs 1.

Analysis

In this section, we will analyze the correctness and the security of proposed quantum protocols. We first analyze the correctness and the security of ESMX Quantum Protocol, which are described as Theorem 1 and Theorem 2.

Theorem 1

When all parties honestly executing this protocol, ESMX Quantum Protocol is correct.

Proof. According to this protocol, we can get ${\tilde{x}}_i=x_i\oplus r_i\left[l\right]$ from Step 12 and $x={\tilde{x}}_1\oplus {\tilde{x}}_2\oplus \dots \oplus {\tilde{x}}_n\oplus m\left[l\right]$ from Step 13. So, we can further get

$$x=\left(x_1\oplus r_1\left[l\right]\right)\oplus \left(x_2\oplus r_2\left[l\right]\right)\oplus \dots (x_n\oplus r_n\left[l\right])\oplus m\left[l\right]$$

$$x=\left(x_1\oplus x_2\dots \oplus x_n\right)\oplus \left(r_1\left[l\right]\oplus r_2\left[l\right]\dots \oplus r_n\left[l\right]\right)\oplus m\left[l\right]\text{.}$$ (Equation 8)

Furthermore, we investigate the relation between the initial state of any photon prepared by the ES and the corresponding final state after all $n$ participants performing their respective operators. Without loss of generality, we assume the initial state and the final state of the $j$ th photon are denoted as $|\phi ⟩$ and $|\psi ⟩$, respectively. According to this protocol, we can get

$$|\psi ⟩={U_Y}^{r_n\left[j\right]}{H}^{s_n\left[j\right]}\dots {U_Y}^{r_2\left[j\right]}{H}^{s_2\left[j\right]}{U_Y}^{r_1\left[j\right]}{H}^{s_1\left[j\right]}|\phi ⟩\text{.}$$ (Equation 9)

Given from Equations 1 and 2, we can easily get the following equation

$$U_{Y}H=-H{U}_Y\text{.}$$ (Equation 10)

Accordingly, we can deduce the following equation

$$|\psi ⟩={(-1)}^{\xi }{U_Y}^{{\sum }_{i=1}^n{r}_i\left[j\right]}{H}^{{\sum }_{i=1}^n{s}_i\left[j\right]}|\phi ⟩\text{,}$$ (Equation 11)

where $\xi =0$ if $n$ is odd number, and $\xi =1$ otherwise. Since ${U_Y}^2=H^2=I$, we can get

$$|\psi ⟩={(-1)}^{\xi }{U_Y}^{{\sum }_{i=1}^n{r}_i\left[j\right]\mathit{mod}2}{H}^{{\sum }_{i=1}^n{s}_i\left[j\right]\mathit{mod}2}|\phi ⟩\text{.}$$ (Equation 12)

Later, all participants select out the successful events, which satisfy the condition of ${\sum }_{i=1}^n{s}_i\left[j\right]\mathit{mod}2=0$. That is, for the successful events, it should satisfy

$$|\psi ⟩={(-1)}^{\xi }{U_Y}^{{\sum }_{i=1}^n{r}_i\left[j\right]\mathit{mod}2}|\phi ⟩\text{.}$$ (Equation 13)

In addition, Pauli operator $U_Y$ can also be written as

$$U_Y=|0⟩⟨1|-|1⟩⟨0|\text{.}$$ (Equation 14)

Furthermore, $|\phi ⟩\in${$|0⟩$, $|1⟩$, $|+⟩$, $|⎯⟩$}. Accordingly, we can get

$$U_Y|0⟩=-|1⟩\text{,}$$ (Equation 15)

$$U_Y|1⟩=|0⟩\text{,}$$ (Equation 16)

$$U_Y|+⟩=|-⟩\text{,}$$ (Equation 17)

$$U_Y|-⟩=-|+⟩\text{.}$$ (Equation 18)

So, for the encoding event, we can easily deduce

$${\sum }_{i=1}^n{r}_i\left[l\right]\mathrm{mod}2=m\left[l\right]\text{.}$$ (Equation 19)

Finally, according to Equations 8 and 19, we can get

$$x=\left(x_1\oplus x_2\dots \oplus x_n\right)\text{.}$$ (Equation 20)

Therefore, ESMX Quantum Protocol is correct.

Theorem 2

When all parties honestly execute the protocol, ESMX Quantum Protocol is information-theoretically secure.

Proof.

In our proposed XOR quantum protocol, each participant $P_i$ first performs the operator ${U_Y}^{r_i\left[j\right]}{H}^{s_i\left[j\right]}$ on every receiving photons ${sp}_j$ and then forwards it to the next participant $P_{i+1}$ through authenticated quantum channel. Later, after successful post-selections, each participants hides $x_i$ by using $r_i\left[l\right]$, i.e., he/she sends ${\tilde{x}}_i=x_i\oplus r_i\left[l\right]$ to the ES through secure and authenticated classical channel.

We first prove that proposed protocol can ensure information-theoretical security of the secret $r_i\left[j\right]$ selected randomly by each participant. By Ref. 15, if the output state ${\rho }_{out}$ is a totally mixed state for every input state ${\rho }_{in}$, the quantum protocol is information-theoretically secure, that is, the relation of the input state ${\rho }_{in}$ and the output state ${\rho }_{out}$ should satisfy the following condition:

$${\rho }_{out}=\sum _k{p}_k{U}_k{\rho }_{in}{U_k}^{†}=\frac{1}{2}I\text{,}$$ (Equation 21)

where ${\rho }_{in}$ is the density matrix of every input state of single qubit and $U_k$ is the corresponding unitary operator applied to the input state. Here, the subscript $k$ of the operator $U_k$ is equivalent to the key utilized to encrypt the input state ${\rho }_{in}$.

Furthermore, by our proposed XOR quantum protocol, all possible input states of any single photon prepared by the ES should be in one of four polarized states {$|0⟩$, $|1⟩$, $|+⟩$, $|⎯⟩$}.

If the input state is in $|0⟩$, i.e., ${\rho }_{in}=|0⟩⟨0|$, then we can get

$${\rho }_{out}=\frac{1}{4}{U_Y}^0{H}^0|0⟩⟨0|H^0{U_Y}^0+\frac{1}{4}{U_Y}^0{H}^1|0⟩⟨0|H^1{U_Y}^0+\frac{1}{4}{U_Y}^1{H}^0|0⟩⟨0|H^0{U_Y}^1+\frac{1}{4}{U_Y}^1{H}^1|0⟩⟨0|H^1{U_Y}^1=\frac{1}{4}|0⟩⟨0\left|+\frac{1}{4}\right|+⟩⟨+\left|+\frac{1}{4}\right|1⟩⟨1\left|+\frac{1}{4}\right|-⟩⟨-|=\frac{1}{2}I\text{.}$$ (Equation 22)

If the input state is in $|1⟩$, i.e., ${\rho }_{in}=|1⟩⟨1|$, then we can get

$${\rho }_{out}=\frac{1}{4}{U_Y}^0{H}^0|1⟩⟨1|H^0{U_Y}^0+\frac{1}{4}{U_Y}^0{H}^1|1⟩⟨1|H^1{U_Y}^0+\frac{1}{4}{U_Y}^1{H}^0|1⟩⟨1|H^0{U_Y}^1+\frac{1}{4}{U_Y}^1{H}^1|1⟩⟨1|H^1{U_Y}^1=\frac{1}{4}|1⟩⟨1|+\frac{1}{4}|-⟩⟨-|+\frac{1}{4}|0⟩⟨0|+\frac{1}{4}|+⟩⟨+|=\frac{1}{2}I\text{.}$$ (Equation 23)

If the input state is in $|+⟩$, i.e., ${\rho }_{in}=|+⟩⟨+|$, then we can get

$${\rho }_{out}=\frac{1}{4}{U_Y}^0{H}^0|+⟩⟨+|H^0{U_Y}^0+\frac{1}{4}{U_Y}^0{H}^1|+⟩⟨+|H^1{U_Y}^0+\frac{1}{4}{U_Y}^1{H}^0|+⟩⟨+|H^0{U_Y}^1+\frac{1}{4}{U_Y}^1{H}^1|+⟩⟨+|H^1{U_Y}^1=\frac{1}{4}|+⟩⟨+|+\frac{1}{4}|0⟩⟨0|+\frac{1}{4}|-⟩⟨-|+\frac{1}{4}|1⟩⟨1|=\frac{1}{2}I\text{.}$$ (Equation 24)

If the input state is in $|-⟩$, i.e., ${\rho }_{in}=|-⟩⟨-|$, then we can get

$${\rho }_{out}=\frac{1}{4}{U_Y}^0{H}^0|-⟩⟨-|H^0{U_Y}^0+\frac{1}{4}{U_Y}^0{H}^1|-⟩⟨-|H^1{U_Y}^0+\frac{1}{4}{U_Y}^1{H}^0|-⟩⟨-|H^0{U_Y}^1+\frac{1}{4}{U_Y}^1{H}^1|-⟩⟨-|H^1{U_Y}^1=\frac{1}{4}|-⟩⟨-|+\frac{1}{4}|1⟩⟨1|+\frac{1}{4}|+⟩⟨+|+\frac{1}{4}|0⟩⟨0|=\frac{1}{2}I\text{.}$$ (Equation 25)

From (Equation 22), (Equation 23), (Equation 24), (Equation 25), we can see that the output of the qubit (i.e., after the participant performing private operator) is always a totally mixed state. Therefore, it is equivalent to a perfect quantum encryption, in which it encrypts one qubit by using two bits. Since $r_i\left[j\right]$ is selected privately and randomly by each participant and his/her performing operator on each transmitted photon is equivalent to implementing a perfect quantum encryption, anyone else except himself/herself cannot get any private information about $r_i\left[j\right]$, i.e., $r_i\left[j\right]$ is information-theoretically secure.

Later, each participant sends ${\tilde{x}}_i=x_i\oplus r_i\left[l\right]$ to the ES through secure classical channel. Since the ES or any eavesdropper cannot get any private information about $r_i\left[l\right]$ except for ${\sum }_{i=1}^n{r}_i\left[l\right]\mathit{mod}2$ ($n>2$), so it is also equivalent to encrypt $x_i$ with the key $r_i\left[l\right]$ based on the classical one-time pad method.

In addition, the condition of the successful event must satisfy ${\sum }_{i=1}^n{s}_i\left[j\right]\mathit{mod}2=0$, where $s_i\left[j\right]$ is randomly selected by the $i$-th participant for the $j$-th photon. Clearly, the probability of the successful events among all $t$ events is equal to $1/2$. In order to ensure there exist at least a successful event as the encoding event, so $t\ge 2$. Furthermore, to ensure the security of quantum channels against outsider eavesdroppers, our proposed quantum XOR protocol still needs other successful events as the checking events except the encoding event. For the checking events, all participants ask the ES to open the corresponding measured result $m\left[j\right]$ and further check the honesty of the ES and determine whether there is an outside eavesdropper. Generally, we can set $t\ge 4$. For example, $t=6$. Accordingly, there is about a successfully encoding event and two successfully checking events. If $t$ is too small, then it cannot ensure the security of quantum channels.

Therefore, our proposed XOR quantum protocol can ensure the information-theoretical security of each private input, i.e., $x_i$.

Furthermore, we analyze the correctness and the security of Edge-assisted Quantum Protocol for SMLA, which are described as Theorem 3, Theorem 4, and Theorem 5.

Theorem 3

When all parties honestly executing this protocol, Edge-assisted Quantum Protocol for SMLA is correct.

Proof. This protocol includes five steps: grouping, counting, amending, ordering, and computing. Furthermore, we analyze the correctness of each step in detail.

• (1)Grouping: In this step, each participant $P_i$ can get a $d$-bit secret $s_i$ by performing single-photon measurements $d$ times, where $2^d\cong w$ and $w=\lceil n/3\rceil$. Here, $d$ and $w$ are determined by all parties in advance. Furthermore, each participant $P_i$ will be privately divided into the $s_i$ th group, and accordingly there are $2^d$ groups initially. Please note that single-photon measurements of each participant are independent. What’s more, due to uniformness and randomness of quantum measurements, each group has about 3 participants and there are approximate $w$ groups ($2^d\cong w$), which achieve the desired aims.
• (2)Counting: According to his/her grouping secret $s_i$, each participant $P_i$ can generate a $2^d$-component vector and further compute the corresponding integer of the vector as an 8-nary vector $S_i$. Then, all participants utilize Shamir Secret Sharing to compute the summation, $S={\sum }_{i=1}^n{S}_i$. Furthermore, as an 8-nary integer, in turn, $S$ is converted to a $2^d$-component vector ($g_1$, $g_2$, …, $g_{2^d}$). In fact, we implement the summation of their respective vectors by using the conversion between 8-nary vector and integer. There are about 3 participants per group, while we use 8-nary conversion, so there is no carry when computing the bitwise summation of these vectors. In addition, if the participant belongs to the $j$ th group, then his/her 8-nary vector is (0, …,0,1,0,…0), i.e., only the $j$ th component is equal to 1 and other components are equal to 0. Accordingly, we can easily deduce that the $j$ th component $g_j$ of finally converted vector is equal to the summation of the $j$ th components of all 8-nary vectors because there is no carry. Therefore, the $j$ th component $g_j$ just represents the number of participants in the $j$ th group.
• (3)Amending: After the second step, the ES knows the vector ($g_1$, $g_2$, …, $g_{2^d}$), each of which represents the number of participants in each group. Furthermore, if $g_j<3$, then the ES will be added into the $j$ th group as a virtual participant, whose input is set to 1. As we know, $1\wedge x=x$ for any $x\in \left\{\mathrm{0,1}\right\}$. So, though there is a virtual participant with an input of 1, the final AND remains unchanged. In addition, if $g_j>3$, then all participants in this group will be subdivided into two subgroups by the similar grouping procedures. Accordingly, the number of groups will be increased by 1. Finally, after amending the number of participants per group, each group just has three participants.
• (4)Ordering: The correctness of this step can refer to Figure 2. Given from Figure 2, we can know that if the XORs of the position indexes are equal to 111 (please see Figure 2-II), it implies that the position indexes of 3 participants in a certain group are unique, so their corresponding position indexes can be treated as their computing orders in the next computing step.
• (5)Computing: On the one hand, the logical AND of a certain group is equal to 0, then we can easily deduce the final AND is equal to 0. Furthermore, if all logical ANDs of all groups are equal to 1, then we can know the final AND is equal to 1. On the other hand, for each group, there are exactly 3 participants. We assume their private inputs are $x_1$, $x_2$, and $x_3$, respectively, where $x_i\in \left\{\mathrm{0,1}\right\}$. If “$x_1\oplus x_2\oplus x_3=1$” and “$x_1\oplus x_2=0$, $x_2\oplus x_3=0$, and $x_1\oplus x_3=0$”, then we can easily deduce that $x_1=x_2=x_3=1$. Accordingly, $x_1\wedge x_2\wedge x_3=1$.

To sum up, when all parties honestly executing this protocol, Edge-assisted Quantum Protocol for SMLA is correct.

Theorem 4

Suppose that all parties honestly executing this protocol and any two-third parties, i.e., the fog nodes or the ES, are non-collusive, Edge-assisted Quantum Protocol for SMLA is information-theoretically secure.

Proof. Similarly, we analyze the security of each step as follows.

• (1)Grouping: In this step, each participant performs a measurement on a superposition state $|+⟩=\frac{1}{\sqrt{2}}(|0⟩+|1⟩)$ to generate a random bit, where the superposition state is prepared by himself/herself. Accordingly, there are two kinds of possible results, $|0⟩$ and $|1⟩$, like flipping a coin. Clearly, grouping of each participant is done by himself/herself. So, the measured result is fully unknown to anyone else except himself/herself. Therefore, the grouping information of each participant is perfectly private, i.e., it is information-theoretically secure.
• (2)Counting: In this step, all participants jointly compute the summation by using Shamir Secret Sharing. So, the security of this step is guaranteed by Shamir Secret Sharing, which had been proven to be information-theoretically secure.
• (3)Amending: Adding a virtual participant or subdividing a group cannot reveal any private information about grouping of each participant.
• (4)Ordering: In a certain group, each private 0/1 vector with 3 components is selected privately and randomly by himself/herself. Later, the ES assists three participants in the group to compute the bitwise XORs of all $n$ vectors with 3 components, including 3 real but private vectors and $(n-3)$ zero vectors, by executing ESMX Quantum Protocol three times, which has been proven to be information-theoretically secure. So, the computing order of each participant in the group is perfectly private.
• (5)Computing: In this step, the ES asks two fog nodes to assist all participants to compute “$x_{j,1}\oplus x_{j,2}\oplus x_{j,3}$”, and “$x_{j,1}\oplus x_{j,2}$, $x_{j,2}\oplus x_{j,3}$, and $x_{j,1}\oplus x_{j,3}$” by executing ESMX Quantum Protocol four times. Every time ESMX Quantum Protocol is executed, it always requires that all $n$ participants take part in the computation, where the participants whose private bits are contained in the target formula (task) input real bits, while other participants input 0. That is, all participants exchange information only by using ESMX Quantum Protocol. In addition, the ES only knows that $x_{j,1}\oplus x_{j,2}\oplus x_{j,3}=1or0$ and $\left(x_{j,1}\oplus x_{j,2}\right)\vee \left(x_{j,2}\oplus x_{j,3}\right)\vee \left(x_{j,1}\oplus x_{j,3}\right)=1or0$, but he cannot get $x_{j,1}$, $x_{j,2}$, or $x_{j,3}$. Therefore, ESMX Quantum Protocol ensures the security of this step.

To sum up, when all parties honestly executing this protocol, Edge-assisted Quantum Protocol for SMLA is information-theoretically secure.

Theorem 5

Edge-assisted Quantum Protocol for SMLA is fair.

Proof. On the one hand, there is nothing to connect the initial order of each participant (e.g., $i$ of $P_i$) with the privacy of input bits and the probability of getting the final output, because each participant cannot get any private information of others due to information-theoretical security and he/she can get the correct output at a probability of 100% when all parties honestly execute this protocol. On the other hand, each participant executes the same procedures, e.g., grouping, counting, ordering, and computing. So, each participant in our protocol is perfectly peer entity and he/she has the same probability to get the final output. Therefore, this protocol is fair.

Applications

There are many promising applications of SMLA in novel data services, e.g., privacy-preserving scientific computing in cloud-assisted smart grids and federated learning in blockchain-based Internet of Things. In this section, we mainly focus on its applications in MPSI and AOV.

Multiparty Private Set Intersection

Definition 2 (Multiparty Private Set Intersection)

Suppose that there are $n$ participants: $P_1$, $P_2$, …, $P_n$ ($n>2)$, each of which has a private set $S_i$ over $Z_N$. After executing this protocol, a designated edge server (i.e., ES) outputs $S_1\cap S_2\cdots \cap S_n$. Similarly, it should satisfy the following requirements:

Correctness

If all parties honestly execute this protocol, then the final output is equal to $S_1\cap S_2\cdots \cap S_n$, i.e., the output is correct.

Privacy

Anyone else but the participant $P_i$ cannot get any private information about $S_i$ except the final output $S_1\cap S_2\cdots \cap S_n$.

Fairness

Under no circumstances one participant should have an advantage over another or other parties to get the final output or more private information.

There are important and wide applications of MPSI in modern society, e.g., privacy-preserving smart advertisement and recommendation system, privacy-preserving individual credit information query among many banks, and privacy-preserving data statistics in contact tracing for health authorities to fight the outbreaks of highly contagious diseases.

In the following section, we will present a novel quantum protocol for MPSI based on Edge-assisted Quantum Protocol for SMLA.

Quantum Protocol for MPSI

Step 1. Each participant $P_i$ ($i=\mathrm{1,2},\dots ,n$) secretly encodes his/her private set $S_i$ over $Z_N$ into a 0/1 vector with $N$ components: $(s_i\left[0\right],s_i\left[1\right],\dots ,s_i[N-1])$, where $s_i\left[j\right]=1$ if $j$ belongs to $S_i$ for $j=\mathrm{0,1},\dots ,N-1$, and $s_i\left[j\right]=0$ otherwise.

Step 2. The ES executes the following procedures:

Set $S=\phi$.//$S$ denotes the intersection, which is empty initially.

For $j=0$ to $N-1$ do {

The ES asks for all participants to compute $s\left[j\right]=s_1\left[j\right]\wedge s_2\left[j\right]\wedge \cdots \wedge s_n\left[j\right]$ by using Edge-assisted Quantum Protocol for SMLA, where $s_i\left[j\right]$ is the private input of the participant $P_i$ for $i=\mathrm{1,2},\dots ,n$.

If $s\left[j\right]=1$ then $S=S\cup \left\{j\right\}$. }

Step 3. Finally, the ES outputs the intersection $S$, i.e., $S=S_1\cap S_2\cap \cdots \cap S_n$.

Correctness

If $s\left[j\right]=1$, i.e., $s_1\left[j\right]\wedge s_2\left[j\right]\wedge \cdots \wedge s_n\left[j\right]=1$, then $s_1\left[j\right]=s_2\left[j\right]=\cdots =s_n\left[j\right]=1$. That is, $j\in S_1\wedge j\in S_2\wedge \cdots \wedge j\in S_n$. Accordingly, $j\in S_1\cap S_2\cap \cdots \cap S_n$. Therefore, this protocol is correct.

Security

Clearly, Edge-assisted Quantum Protocol for SMLA ensures perfect privacy of each participant. Furthermore, all participants are equivalent entities, and they can get the final output $S_1\cap S_2\cdots \cap S_n$ with equal opportunities. So, it is also fair.

Anonymous One-vote Veto

Definition 3 (Anonymous One-vote Veto)

Suppose that there are $n$ voters: $V_1$, $V_2$, …, $V_n$ ($n>2$), each of which has a private input $v_i\in \left\{\mathrm{0,1}\right\}$ ($i=\mathrm{1,2},\dots ,n$) corresponding to his voting will. That is, if $v_i=1$, then it means that the voter $V_i$ will vote “for the proposal”; otherwise, he will vote “against the proposal” (i.e., $v_i=0$). After executing this protocol, a designated edge server (i.e., ES) outputs 0 if there is at least one vote of “against the proposal”, and 1 otherwise. In addition, it should satisfy the following requirements:

Correctness

If all parties honestly execute this protocol, then the final output is equal to ${\prod }_{i=1}^n{v}_i$, i.e., if any $v_i=0$ (against the proposal), then ${\prod }_{i=1}^n{v}_i=0$ (failure).

Privacy

Anyone else but the voter $V_i$ cannot get any private information about $v_i$ except the final output ${\prod }_{i=1}^n{v}_i$. Here, perfect privacy implies anonymity, i.e., no one can know who votes the vote $v_i$.

Fairness

Under no circumstances one participant should have an advantage over another or other parties to get the final output or more private information.

Furthermore, as a basic block, we utilize Edge-assisted Quantum Protocol for SMLA to build an efficient quantum AOV protocol, which can achieve the information-theoretical security.

Quantum Protocol for AOV

Step 1. According to his/her voting will, each voter $V_i$ ($i=\mathrm{1,2},\dots ,n$) generates a private bit $v_i$: If he/she want to vote “for the proposal”, then $v_i=1$; Otherwise, $v_i=0$, i.e., he/she wants to vote “against the proposal”.

Step 2. The ES asks for all voters to compute ${\bigwedge }_{i=1}^n{v}_i$ by using Edge-assisted Quantum Protocol for SMLA, where $v_i$ is the private input of the voter $V_i$ for $i=\mathrm{1,2},\dots ,n$.

Step 3. The ES finally outputs ${\bigwedge }_{i=1}^n{v}_i$. If ${\bigwedge }_{i=1}^n{v}_i=1$, it means it is successful; Otherwise, it is unsuccessful (i.e., failure).

Correctness

Clearly, ${\bigwedge }_{i=1}^n{v}_i={\prod }_{i=1}^n{v}_i$ due to $v_i\in \left\{\mathrm{0,1}\right\}$. If ${\prod }_{i=1}^n{v}_i=0$, then it shows that it finally vetos the proposal (i.e., unsuccessful) because at least one voter votes “against the proposal” (i.e., there is at least one $v_i$ which is equal to 0). So, our aforementioned proposed quantum protocol is correct.

Security

Similarly, Edge-assisted Quantum Protocol for SMLA ensures perfect privacy of each voter. Of course, we cannot know who votes the veto or the approval, i.e., it is anonymous. In addition, all voters are equivalent entities, and they can get the final output ${\prod }_{i=1}^n{v}_i$ with equal opportunities. So, it is also fair.

Performance evaluation

Performance analysis

In previous sections, we first propose a quantum primitive protocol for computing XOR, i.e., ESMX Quantum Protocol, and based on the proposed quantum primitive protocol, we further present another quantum primitive protocol for computing AND, i.e., Edge-assisted Quantum Protocol for SMLA. As a basic block, these quantum primitive protocols can be utilized to compute bitwise logical operations (e.g., XOR, AND and OR) of multiple private bits, and further generated to privately compute any (Boolean) function of multiple private inputs.

Here, we first analyze necessary quantum resources, operators and measurements performed by the first quantum primitive protocol, i.e., ESMX Quantum Protocol. Theoretically, it evenly costs 4 single photons to compute 1-bit XOR (i.e., $t=4$), where 2 single photons are corresponding to two successful events and one of two successful events is the encoding event while the other is the checking event. Furthermore, each participant needs to perform 4 operators (e.g., ${U_Y}^{r_i\left[j\right]}{H}^{s_i\left[j\right]}$) on correspondingly transmitted photons and forward them. There are $n$ participants in total. So, the quantum communication complexity is $O\left(n\right)$ qubits (i.e., it achieves the linear communication complexity). Finally, the ES performs 4 single-photon measurements in the basis of {|0⟩, |1⟩} or {|+⟩, |⎯⟩}. In addition, this primitive protocol can be easily generalized to compute multiple-bit XORs in parallel, i.e., it increases the value of the parameter $t$, and remains multiple encoding events.

Second, we analyze necessary quantum resources, operators and measurements required by the second quantum primitive protocol, i.e., Edge-assisted Quantum Protocol for SMLA, which includes five steps: grouping, counting, amending, ordering, and computing. In the step of grouping, each participant prepares $d$ single photons and performs $d$ single-photon measurements, where $d=\log \frac{n}{3}$. In the step of counting, it is a completely classical process due to Shamir Secret Sharing protocols, which needs to transmit $O\left(n^2\right)$ classical messages. In the step of amending, due to good uniformness and randomness of quantum measurements, most of groups do not need to run the amending procedure, while very few groups do it. Furthermore, if the number of the participants in a certain group is less than 3, then it is a fully classical amending process (i.e., no quantum process); if it is greater than 3, then it only needs the participants in this group to regenerate several single photons and perform single-photon measurements. In the step of ordering, the main cost is to execute ESMX Quantum Protocol $O\left(w\right)$ times, where $w\approx \frac{n}{3}$. Please note that it needs to execute this primitive protocol 4.5 (i.e., $\frac{3^3}{3!}=\frac{3\times 3\times 3}{3\times 2}$) times evenly to get a successfully computing order per group and there are $w$ groups in total. In the step of computing, the main cost is also to execute ESMX Quantum Protocol $4w$ times.

In a word, there is no any quantum communication in the first three steps, while it exchanges quantum messages (i.e., qubits) only by using ESMX Quantum Protocol in the last two steps and further it needs to execute this primitive protocol $O\left(w\right)$ times in each step, where $w\approx n/3$. Therefore, the quantum communication complexity of this primitive protocol is $O\left(n^2\right)$ qubits.

In addition, we can deduce that Quantum Protocol for MPSI and Quantum Protocol for AOV need to execute Edge-assisted Quantum Protocol for SMLA $N$ times and once, respectively. Accordingly, the quantum communication complexities of these two protocols are $O\left(n^{2}N\right)$ and $O\left(n^2\right)$ qubits, respectively.

Furthermore, we give a comparison between our proposed quantum protocol for SMLA and previously proposed quantum protocol for SMLA in ref. ²⁶ from quantum resources, quantum operators, quantum measurements, transmitted qubits, and so on, as listed in Table 1.

Table 1.

Comparisons between two quantum protocols for SMLA

Protocols	Quantum resources	Quantum operators	Quantum measurements	Transmitted qubits	TP
Shi et al.26	O(n)-qubit entangled states	O(n) 3-qubit T- gates	O(n) single-qubit measurements	O(n) qubits	QC
Our proposed protocol	O(n)-qubit single photons	O(n) 1-qubit P-gates and H-gates	O(n) single-photon measurements	O(n2) qubits	ES

Note. P-gate, H-gate, and T-gate denote Pauli gate, Hadamard gate, and Toffoli gate, respectively. TP, QC, and ES represent Third Party, Quantum Cloud, and Edge Server, respectively.

Given from Table 1, we can see that the transmitted qubits of the proposed protocol are more than those of ref.,²⁶ i.e., the communication cost of the proposed protocol is higher than that of ref.²⁶ However, it is still difficult to implement the scheme of ref. ²⁶ with the present technologies, due to its necessary quantum resources, quantum operators and quantum measurement. Accordingly, our new proposed quantum protocol for SMLA is more feasible than previously proposed protocol with the present quantum processing technology, since this new protocol only needs single photons and corresponding single-photon operators and measurements, instead of multiple-qubit entangled states and multiple-qubit quantum operators in high-dimensional Hilbert space. At present, it is still difficult to implement 3-qubit Toffoli gate,⁵² which is necessary quantum operators in ref.²⁶ In addition, previously proposed quantum protocol for SMLA in ref. ²⁶ still needs the help of quantum conference key agreement to generate a secure key among all participants in advance. In a word, our new proposed quantum protocol for SMLA achieves better feasibility by sacrificing easy quantum resources (i.e., single photons).

In addition, we give detailed comparisons of related quantum protocols on multi-party/two-party PSI (MPSI/PSI), which outputs the intersection of multiple/two private sets, or multi-party/two-party PSI Cardinality (MPSI-CA/PSI-CA), which outputs the cardinality of the intersection of multiple/two private sets, listed in Table 2. Similarly, the communication complexity of our proposed MPSI quantum protocol is not the best in Table 2, but our protocol has better feasibility than other related protocols, because our protocol only needs single photons as quantum resources, and performs single-photon operators and measurements in 2-dimension Hilbert space, instead of high-dimension Hilbert space.

Table 2.

Comparisons of related quantum protocols for PSI

Protocols	Quantum resources	Quantum operators	Quantum measurements	Transmitted qubits	Output
Shi et al.24	2logN-qubit entangled states	2-qubit CNOT gates	Projective measurements in N-dimension Hilbert space	O(N) qubits	MPSI-CA
Shi et al.26	n-qubit entangled states	3-qubit Toffoli gates	Projective measurements in 2-dimension Hilbert space	O(nN) qubits	MPSI-CA
Shi et al.28	logN-qubit superposition states	logN-qubit Oracle operators	Projective measurements in N-dimension Hilbert space	O(logN) qubits	PSI
Shi et al.29	2logN-qubit entangled states	logN-qubit Oracle operators	Projective measurements in N-dimension Hilbert space	O(logN) qubits	PSI-CA
Our quantum MPSI protocol	single-qubit photons	1-qubit Pauli gates and Hadamard gates	Projective measurements in 2-dimension Hilbert space	O(nN) qubits	MPSI

Simulated experiments

Here, we attempt to do simulated experiments about new proposed quantum primitive protocols in Qiskit of IBM (Qiskit-0.35.0; Python-3.8.13; OS-Linux) to verify the correctness and the feasibility of these protocols.

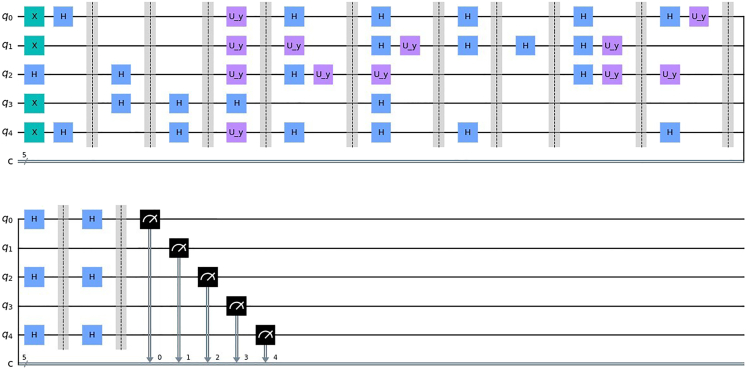
First, we simulate ESMX Quantum Protocol. Figure 3 gives an example to compute XOR of 11 private bits with five qubits, i.e., $t=5$ and $n=11$, where the second qubit and the fourth qubit are corresponding to successful events and further one of two successful events is treated as the encoding event (e.g., $q_3$) while the other is taken as the checking event (e.g., $q_1$). Finally, all simulated results verify the correctness and feasibility of the first quantum primitive protocol, i.e., ESMX Quantum Protocol.

Figure 3.

Quantum circuits of computing XOR among 11 participants

Furthermore, we mainly simulate grouping in Edge-assisted Quantum Protocol for SMLA. In the grouping step, we first prepare lots of single-qubits in $1/\sqrt{2}(|0⟩+|1⟩)$, then we directly measure them in the computational basis. The statistical results of 1000 experiments are listed in Table 3, where there are 12 participants in these experiments. From Table 2, we can see that the probabilities of the measured results of 00, 01, 10, and 11 are 0.256, 0.249, 0.246, and 0.249, respectively. Accordingly, there are 3.072, 2.988, 2.952, and 2.988 participants on average in the first, second, third, and fourth group, respectively. That is, there are about 3 participants per group due to good advantages of quantum measurements, e.g., uniform, independent, and random.

Table 3.

Grouping experiments

Measured results	00 (The 1st group)	01 (The 2ND group)	10 (The 3rd group)	11 (The 4th group)
$p$	0.256	0.249	0.246	0.249
$g$	3.07	2.988	2.952	2.988

Note. $p$ and $g$ denote the probability of the measured result and the average number of the participants in the corresponding group.

Finally, based on the feasibility and the correctness of ESMX Quantum Protocol, we can easily see that Edge-assisted Quantum Protocol for SMLA is also feasible and correct.

In a word, all simulated experiments verify the correctness and the feasibility of our proposed quantum primitive protocols.

Conclusions

In summary, we first presented two quantum primitive protocols, including ESMX Quantum Protocol and Edge-assisted Quantum Protocol for SMLA, which could be adopted widely in privacy-preserving settings with multiple participants as basic blocks. In these quantum primitive protocols, we take single photons as quantum resources and perform single-photon operators and measurements. So, it is feasible and efficient to implement these quantum protocols with the present quantum technologies. Furthermore, based on these quantum primitive protocols, we designed two application protocols, i.e., Quantum Protocol for MPSI and Quantum Protocol for AOV. Compared with classical related protocols, our proposed quantum protocols obtain higher security (i.e., information-theoretical security and long-term security), which can be guaranteed by the basic principles of quantum mechanics.

Our work further shows that quantum cryptography can not only ensure data security (e.g., QKD) but also protect user privacy (e.g., PSI). Especially, like mathematical cryptography, we can construct various kinds of quantum protocols based on quantum mechanics to meet different applications in novel cloud/edge environments.

Limitations of the study

As discussed previously, we only conducted simulated experiments. This work was limited by a real experimental environment. Further, proposed quantum protocols should be performed in real quantum devices to verify their feasibilities.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Other
Photon	Zhong et al.11	N/A
Bell state	Shi et al.25	N/A
Pauli Operator	Shi et al.24	N/A
Toffoli gate	Kim et al.52	N/A
Superposition state	This paper	N/A

Resource availability

Lead contact

Futher information and requests for resouces should be directed to the lead contact Run-hua Shi (rhshi@ncepu.edu.cn).

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

We simulated the key process of proposed quantum protococols in Qiskit of IBM (Qiskit-0.35.0; Python-3.8.13; OS-Linux), which is available at: https://qiskit.org/documentation/getting_started.html.

Published: May 29, 2023

Data and code availability

This study has no data and code available.