Abstract
Ultra-high dose-rate (UHDR) irradiations, known as FLASH radiotherapy (RT), rely on delivery of therapeutic doses at instantaneous dose-rates several orders of magnitude higher than those currently used in conventional radiotherapy. It has been shown that such an extremely short delivery of radiation leads to remarkable reduction of normal tissue toxicity with respect to conventional dose-rate RT. However, dosimetry at UHDRs is complicated and it is essential to understand the effects that will influence detector response. To date, FLASH RT research has been focused on finding pragmatic solutions that allow the use of UHDR beams in the research setting, but there has been limited focus on absolute dosimetry utilizing primary and secondary standard devices. However, very recently, the data on existing standard dosimeters and novel solutions which could serve as secondary standard devices in UHDR dosimetry started emerging. This review provides an overview of the studies that have been conducted employing calorimeters and innovative solutions utilizing ionization chambers.
Introduction
In the last three decades, survival of radiotherapy (RT) patients has greatly improved due to technological advances in delivery of radiation to tumor volumes, such as stereotactic radiosurgery, intensity-modulated RT and the introduction of proton beam radiotherapy. 1–3 However, in spite of improvements in delivery of conformal RT, a significant number of patients still experience severe toxicity from radiation treatment, particularly when the treatment volume overlaps with organs at risk. 4–7
It has been demonstrated that ultra-high dose rate (UHDR) irradiation, known as FLASH RT lead to remarkable reduction of normal tissue toxicity while maintaining tumor control with respect to conventional dose-rate RT. 8–13 These show that FLASH RT could lead to significant improvement of radiation therapy efficacy by increase of the therapeutic window. Even though the literature on demonstration of the FLASH effect is growing very rapidly, the published studies may lead to flawed interpretation of data due to lack of established dosimetry methods for this new radiotherapy modality. Dosimetry at UHDR is complicated and it is essential to understand the effects that impact detector response in this radiotherapy modality. Without a clear understanding of the fundamental dosimetry issues, there is potential for significant dosimetric errors. Accurate dosimetry is crucial for the safe implementation of any radiotherapy technique and ensures best practice and consistency of treatments across different radiotherapy centers.
There are limited data on the functionality of existing standard dosimeters when they are used to measure beams delivered in the UHDR mode. As a result, this paper focuses on review of primary and secondary standard methods, focusing solely on online devices, and discusses the need for further developments.
Calorimetry
Calorimetry is the best approach for establishing absorbed dose standards. The absorbed radiation energy appears as heat, hence the basic principle of calorimetric measurement is based on measurement of a temperature rise. A calorimeter has capability to realize the absorbed dose to a medium Dmed, defined as the quotient of the energy absorbed, E, and matter with mass, mmed, in which the energy is absorbed Dmed = ΔE/Δm. 14 For establishing the absorbed dose to water, a water calorimeter is ideally employed. However, most calorimeters developed for the purposes of radiation dosimetry have been constructed from graphite due to several challenges associated with working with a liquid system. Graphite is the material of choice as it possesses similar radiation absorption characteristics to water but with approximately six times lower specific heat capacity than water. This puts less stringent requirements on the sensitivity of the temperature probe in graphite calorimeters as for the same dose, the temperature rise in graphite will be sixfold the temperature rise in water.
In absorbed dose calorimeters, dose to the sensitive volume is determined from measured temperature rise and the specific heat capacity of the medium, cp,med. 15 The relation below summarizes determination of absorbed dose to water with calorimetry:
| (1) |
where, ΔT is the temperature rise due to the absorbed radiation, cp,med is the specific heat capacity of the absorbing material, is the dose conversion factor between the dose absorbed in a material and water (for water calorimeters is equal to unity) and correction factors, ki , account for non-ideal measurement conditions. For water calorimeter, the equation for absorbed dose to water is given by:
| (2) |
where kht is a general correction factor for heat transfer due to conduction and convection, kp is the radiation field perturbation factor due to the presence of non-water materials in the beam and kdd corrects for a non-uniform dose profile at the point of measurement. khd is a heat defect correction factor that takes into account any radiochemical interactions, which would break the proportionality between the energy absorbed and the temperature rise and kρ accounts for the difference in density between the calorimeter operating temperature and the temperature at which another detector is calibrated. 16,17
Graphite calorimeters realize absorbed dose to graphite, at a specified point. The effects of heat transport in graphite calorimeters are minimized by separating the core, from the surrounding jacket (or jackets), by vacuum gaps. When neglecting heat defect, the equation for energy balance in graphite calorimeters is defined by:
| (3) |
Where , and are energy absorbed from radiation (appearing as heat), electrical heating and heat transfer from the environment, respectively.
In graphite calorimeters, the energy imparted to the core by radiation divided by the mass of the core gives the expression for the mean absorbed dose in the graphite core, :
| (4) |
Functionally, the graphite calorimeters may be operated either adiabatically, 18 quasi-adiabatically, 19 or quasi-isothermally. 20,21 In the full-adiabatic mode, the temperature in all components is allowed to drift, so any energy deposited in the calorimeter by the radiation gives rise to temperature increase of the components. In this mode, there is no electrical heating involved.
In the quasi-adiabatic mode, the temperature of the outer jacket is fixed, but the core and inner jacket are allowed to drift. This mode is particularly useful in situations when the changes in the room temperature are much larger than those induced during irradiation. Operating a calorimeter in the quasi-adiabatic mode provides an environment with greater stability for the inner components. The core temperature in adiabatic and quasi-adiabatic modes is measured over time in the absence of electrical heating, i.e. , hence eq. (4) becomes where the last factor is a correction.
In contrast to the adiabatic mode, in the quasi-isothermal operation all calorimeter bodies are kept at constant equilibrium temperature throughout the measurement. In this mode of operation, the electrical power necessary to maintain an isothermal state is used to determine the rate of energy imparted by the ionizing radiation. 20,22–25 The measurement is done by substitution, with radiation heating power replaced by electrical heating power in a null measurement. The energy from electrical heating of the core is obtained by integrating the core electrical power with respect to time. Subsequently, the equation (4) takes the following form
where the expression in the bracket is a correction.
Once fully characterized, calorimeters are ideal devices for determination of absorbed dose in FLASH radiotherapy. They do not require recalibration or post-irradiation processing and can provide immediate information about temperature rise. Moreover, as shown in Equation 1, there is no parameter directly dependent on the dose rate or dose-per-pulse (DPP) and, therefore, a calorimeter will respond linearly with dose over a wide range of dose rate and DPP values. The kht could introduce dose rate dependence if the heat loss constant was of the same order as the exposure time. However, for the UHDR irradiations this is not possible as the exposure time (well below 1 s) is at least two orders of magnitude shorter than the thermal time constant for modern calorimeters. 16,26 For the graphite calorimeters, the isothermal mode cannot be used for absorbed dose measurement in UHDR beams due to very short exposure times. Also, the sampling rate in the isothermal mode is a limitation, as the software is not able to control thermal equilibrium of the calorimeter’s component in such a short delivery time as those in FLASH RT. However, operation in the full or quasi-adiabatic mode is easy to realize. At ultra-high DPP, where radiation dose is delivered in a short time, the thermal isolation of calorimeters is not such a constraint, and a simpler design can be employed. In the water calorimeters, the heat defect, , which corrects for the radiation-induced chemical changes in the water, could have a potential implication when operating these devices in the UHDR regime. However, in primary standard water calorimeters, the vessel is filled with high-purity water saturated with hydrogen. In the reactions that take place, hydrogen acts as a scavenger for reactive species with a zero enthalpy balance. This effect is not expected to change when the delivery of dose is completed in a very short time. Therefore, the change in between conventional and UHDR exposures is expected to be negligible. The aspect of implementation of calorimeters to dosimetry in FLASH RT is one of the areas of development within the EMPIR’s UHDpulse project, 27 where some of the participating institutes explore applicability of existing calorimeters for UHDR dosimetry.
Calorimeters have been previously used for high dose rate measurements for the dosimetry of radiation processing beams. 28 However, implementation of calorimeters for measurements of therapeutic doses has been published very recently (Table 1).
Table 1.
Studies implementing calorimeters for dosimetry of FLASH beams
| Calorimeter type | Beam & energy | Average dose rate | Dose-per-pulse | Pulse duration | Uncertainty (k = 1) | Reference |
|---|---|---|---|---|---|---|
| Primary standard graphite calorimeter | 250 MeV protons | Approx. 65 Gy/s | N/A | 72.8 MHz RF repetition rate corresponding to 0.2 ns micro-pulses separated by 13.7 ns intervals | 0.9 % | 29,30 |
| Transfer standard graphite calorimeter | 200 MeV electrons | 0.2–50 Gy/s | 0.03–5.3 Gy/pulse | Approx. 100 ns | 1.2% (no uncert. budget) | 31,32 |
| Small portable graphite calorimeter | 15–40 MeV laser-driven protons | 109 Gy/s (one ps pulse delivered) | 1–3 Gy/pulse | Approx. ns | Not stated | 33 |
| Aluminium calorimeter a | 50 MeV electrons | 1–9 Gy/s | 0.2–1.8 Gy/pulse | 2.5 µs | 0.5% (no uncert. budget) | 31 |
| Aerrow graphite calorimeter a | 20 MeV electrons | 3–28 Gy/s | 0.6–5.6 Gy/pulse | 2.5 µs | 1.06 % | 34,35 |
| Al-core secondary standard calorimeter | 6 MeV electrons | 180 Gy/s | Approx. 0.45 Gy/s | 4 µs | 1.25% | 32 |
These studies used average dose rates below the threshold of the FLASH effect. 8
The only work that has been carried out so far with the utilization of the primary standard calorimeter has been published by Lourenco et al. 29 The authors presented absorbed dose measurements at the Cincinnati Children’s Hospital Medical Center for UHDR proton beam with an averaged dose rate of ~63 Gy·s−1. The system used was a ProBeam cyclotron producing 250 MeV proton bunches with 0.2 ns pulse duration at 72.8 MHz RF repetition rate corresponding to 0.2 ns micro-pulses separated by 13.7 ns intervals. 30,33 The absorbed dose measurements have been performed with a primary standard proton calorimeter (PSPC) developed at the National Physical Laboratory (NPL), the UK’s National Measurement Institute. This device consists of disc-shaped graphite components that are arranged in a nested configuration with the core dimensions equivalent to the PTW Roos chamber sensitive air volume 36 (i.e. 2 mm thickness and 16 mm diameter). The volume within the mantle was maintained under vacuum to minimize the heat-transfer between components and the environment. For this investigation, the calorimeter was operated in the quasi-adiabatic mode, where the outer jacket of the calorimeter was kept constant at a temperature few degrees higher than the room temperature. This mode of operation provided a more stable environment to the core as it suppressed any temperature changes in the treatment room. The average absorbed dose to the graphite core was determined by multiplying the measured increase in temperature by the specific heat capacity of the core, which was previously determined. 31 The absorbed dose-to-core was then converted to absorbed dose-to-water by applying the necessary beam-dependent correction factors determined using Monte Carlo (MC) simulations. The absorbed dose-to-water determined by the PSPC was quoted with an uncertainty of 0.9% with a coverage factor of k = 1.
Other work implementing calorimeters in UHDR beam has been published by McManus et al. 37 In this work, the authors used NPL’s transfer standard graphite calorimeter (similar to that described by Duane et al. 38 ) in the quasi-adiabatic mode at CLEAR facility in CERN 34 employing 200 MeV very high energy electron (VHEE) beam at a wide range of dose-per-pulse (up to 5 Gy/pulse). The device used in this work consists of a cylindrical graphite core measuring 7 mm in both height and diameter, housed in a graphite jacket of 1 mm thickness, with a 1 mm vacuum gap between the jacket and the core. The main purpose of the calorimetric measurement in this study was to establish ion recombination correction factor for the PTW Roos ionization chamber when operating it under a wide range of dose-per-pulse. Even though the measurements of absorbed-dose-to-water are mentioned, the study lacks a full uncertainty budget incorporating all quantities influencing the measurement. However, for majority of beam parameters used, an uncertainty of 1.2% with a coverage factor of k = 1 has been quoted. The authors evaluated the graphite-to-water conversion factor ( ) and the vacuum gap correction factor employing MC simulations. 39 The calculated factor showed approximately 1% increase with respect to previously evaluated value 37 and demonstrated that improved calculations of the graphite-to-water conversion factor using MC methods has an impact on the analysis and the interpretation of the ion chamber data presented in this previous work. 37
Graphite calorimetry has been also implemented in the laser-driven environment 40 at the PetaWatt Vulcan Laser of the Central Laser Facility at the Rutherford Appleton Laboratory in the UK, where a proton beam with energy ranging from 15 to 40 MeV at an instantaneous dose rate of 109 Gy·s−1 was used. In this work a small body portable graphite calorimeter (SPGC) developed at NPL has been utilized. 41 The measured doses were reported at a level of 1–3 Gy, however, no uncertainty evaluation has been mentioned.
Bourgouin et al. 42 used an open-to-atmosphere aluminium calorimeter, with design similar to a graphite calorimeter developed at the NPL for industrial processing dose measurement 35 in a 50 MeV electron beam (with dose-per-pulse to 1.8 Gy/pulse) with an average dose rate not exceeding 10 Gy/s. The calorimeter consists of a high purity aluminium core 21.7 mm in diameter and 2.01 mm thick enclosed in a jacket made of the same material, separated by 1 mm air gap. This device was enclosed in an alloy phantom surrounded by a polystyrene box to improve thermal isolation. The approximate conversion factor from aluminium to water ( ) was determined by averaging the mass restricted collisional stopping power ratio over the calculated energy spectrum. The specific heat capacity of aluminium core was assumed to be constant throughout the measurements and the heat defect was considered to be negligible. The device has been operated in the quasi-adiabatic mode. The calorimetric dose measurements were in good agreement with those measured with alanine dosimeters. The authors stated that an achievable overall uncertainty in the determination of absorbed dose to water using this calorimeter design is 0.5% (k = 1), however, a detailed uncertainty budget was not presented.
Bourgouin et al. 43 also employed a probe type graphite calorimeter (Aerrow 32 ) in a 20 MeV electron beam at ultra-high dose per pulse (up to 5.6 Gy/pulse). This device was proposed to be an alternative to ionization chambers for clinical dosimetric use. Aerrow was operated in quasi-adiabatic mode and dose conversion from graphite to water and heat loss correction factors were computed using MC and thermal simulations, respectively. The heat loss correction factor for Aerrow was found to be below 1% with good performance for relative and absolute dose measurement. The uncertainties for determination of absolute doses were reported recently. 44
Bass et al. 45 utilized a simple, low-cost secondary standard level calorimeter (SSC) physically resembling a Roos-type ionization chamber with a single sensing thermistor in the aluminium core. This instrument has been used in a converted clinical electron LINAC to deliver UHDR 6 MeV electron beam with an average dose rate of 180 Gy/s and 0.45 Gy/pulse. The calibration of the Al-core SSC has been performed against the NPL’s primary standard electron graphite calorimeter. Several corrections were applied to the primary standard calorimeter response in 6 MeV reference conditions to obtain dose in the UHDR mode. Additionally, it was assumed for the purposes of this experiment that the same corrections were applicable in these non-reference conditions. Combining the dose output measurement from the primary standard calorimeter with the mean temperature rise of the SSC resulted in a calibration coefficient for the SSC of 1139 Gy/K at 20°C (sdom 0.5 %) with an estimated uncertainty of ±1.25% (k = ).
Ionization chambers
Ionization chambers have been always considered the gold-standard for reference dosimetry in radiation therapy and they are currently recommended by international dosimetry protocols for most of the irradiation modalities. 46 Using ionization chambers with UHDR beams is challenging, as ion recombination effects heavily affect their response. The temporal structure of the involved beams, which is a direct consequence of the type of technology used for particle beam acceleration, is of crucial importance for proper assessment of ion recombination effects. Pulse duration, pulse frequency and dose per pulse are all parameters which must be accurately evaluated when dealing with ionization chambers. 47 The combination of those parameters with the ion collection time, i.e. the time required to completely collect all produced charges at the chamber electrodes, strongly determine the ion collection efficiency and the way in which it is possible to correct for a lack of charge collection due to ion recombination. The charge collected by the chamber can be converted into dose to water (Dw ) by the equation 34 :
| (5) |
where Dw is the absorbed dose to water, ND,w is the calibration coefficient, Mk is the collected charge corrected for pressure and temperature, kq is the correction factor for the different beam quality used in calibration conditions and ksat is the ion recombination correction factor.
Ion collection time and efficiency are strongly influenced by the ion chamber geometrical configuration, the shape (cylindrical vs parallel plate configuration), the sensitive volume, the gas mixture and the applied voltage. Typical collection times range between a few microseconds up to hundreds of microseconds.
For proton cyclotrons, application of ionization chambers for reference dosimetry requires corrections which are still acceptably small, and accurate absorbed dose measurements with commercially available ionization chambers used at UHDRs have been demonstrated. 47,48 Commercially available ionization chambers for reference dosimetry are typically characterized by ion collection times between tens and a few hundreds of microseconds which, compared to a typical pulse structure of an isochronous cyclotron, is a much longer time with respect to the pulse duration and the time interval between cyclotron pulses. Isochronous cyclotrons deliver nanosecond pulses spaced by tens of nanoseconds, i.e. with pulse frequency of the order of tens or hundreds of megahertz. In the context of ion chamber collection time, such beams can be considered as “quasi-continuous” and the “dose-per-pulse” becomes irrelevant. Only the average dose rate is being considered, which, for isochronous cyclotrons operating in the UHDR mode, is typically not larger than hundreds of Gy/s. The same consideration is not applicable for beams generated by synchrocyclotrons or linear accelerators at UHDR regimes, which are characterized by pulse duration of the order of 1–10 μs, with pulses delivered every few milliseconds, and a consequent repetition rate ranging between 100 and 1000 Hz. In these cases, the beams must be considered as pulsed, since the typical ion collection time of an ionization chamber is comparable or larger than the pulse duration of the beam. Moreover, the time interval between pulses is much larger than the ion collection time, therefore the produced (and collected) charge is only related to each single pulse and the corresponding delivered dose per pulse. Therefore, for those two types of accelerators, the relevant quantity to study the ion chamber response is not the average dose rate but the dose-per-pulse, which can reach values from 0.1 to 10 Gy/pulse (corresponding to instantaneous dose rates up to several MGy/s). Hence, for synchrocyclotrons and linear accelerators operating at UHDR regimes, reference dosimetry through ionometric measurements is challenging, due to the high dose per pulse values and instantaneous dose rates giving rise to much larger ion recombination effects. Therefore, alternative approaches, compared to those normally used for conventional dose rates, must be followed. 49 Indeed, as an example, using pulsed beams accelerated by electron linear accelerators exploited in the first experimental investigations of the FLASH effect and characterized by pulse duration of the order of microseconds, ion collection efficiencies lower than 50% were found when using PTW Advanced Markus ionization chambers with dose per pulse larger than 1 Gy. 50 Similar results were found with even more bunched beams, with macro-pulses of the order of 100 ns, using very high energy electron (VHEE) beams at 200 MeV. 42 The authors found collection efficiency lower than 10% for a PTW Roos chamber at dose-per-pulse of 5 Gy. Currently used models for ion recombination corrections 51,52 and, in particular, the commonly used two-voltage method fail at these extreme regimes, as shown by McManus et al. 42 A few attempts of retrieving semi-empirical models have been successfully done, although they are still lacking general validity. 42,50
Dosimetry for FLASH radiotherapy does not represent the first efforts in terms of addressing challenges related to the ion recombination effects. Intraoperative radiation therapy (IORT) posed similar challenges more than 20 years ago, as linear accelerators with highly pulsed beams and consequent large dose per pulses (up to 20 cGy) were produced. Dose-rate independent passive dosimeters were typically implemented, such as Fricke dosimeters, as commercially available ionization chambers could not cope with these regimes. However, as real-time response given by active detectors is always preferable with respect to passive dosimeters, the first attempts to correct for the large ion recombination effects in commonly used ionization chambers for reference dosimetry were carried out. Two solutions were proposed, by Laitano et al. 53 and Di Martino et al., 54 respectively. However, both these approaches relied on an accurate evaluation of the free electron fraction, p, which depends only on the chamber characteristics. p is defined as the fraction of collected charge which comes purely from the collection of free electrons instead of negative ions. In the first approach, an analytical method that calculates p from the free electrons drift velocity and lifetime was proposed. This approach accurately calculates ksat but it is valid only for dose-per-pulse values up 20 cGy. 53 This was acceptable for IORT but would not be sufficient for larger dose-per-pulse values delivered for FLASH radiotherapy with linear accelerators. The second approach relies on the cross-comparison with an alternative dose rate independent detector, i.e. Fricke dosimeters and radiochromic films (RCF). Fitting experimental ksat values obtained with the dose rate independent dosimeters, the p-values for both a PTW Roos and Advanced Markus ionization chambers were found. 54 A third direct method, used to determine p and study the variations as a function of the applied voltage, was successfully tested with plane-parallel as well as Farmer ionization chambers. 52 However, this approach makes use of complex experimental procedures relying on oscillographic recording of the fast component in the current induced in the external circuit by the transit of the free electrons across the chamber and, therefore, is not easy to implement in the clinical routine.
Recently, a new approach was proposed to directly determine p for a PTW Advanced Markus ionization chamber without using alternative dose rate independent dosimeters. With this method, p is directly determined through ionometric measurements only, performing charge measurements at various applied voltages V. 55 This solution was successfully demonstrated through a dedicated experimental campaign with UHDR electron beams up to 0.5 Gy/pulse. It is valid if the perturbative effects on the electric field generated by the applied voltage in the chamber can be considered negligible, i.e. if the electric field generated by the produced charge density in the volume is much smaller than the one created by the applied voltage at the electrodes.
Considering that the recombination of electrons with positive ions and variation of oxygen molecules density due to ionization are both negligible, the authors retrieved an expression of the free electron fraction, p, for plane parallel ionization chambers (extendable also to cylindrical ones) that only depends on the applied voltage V and a parameter, lp , where lp is only characteristic of the user chamber. Therefore, fixing a specific voltage V and knowing lp it is possible to determine p. The novelty of the proposed approach relies on the fact that the lp parameter is directly obtained through ionometric measurements, i.e. fitting the experimental data obtained for qcoll at different applied voltages. Once lp is experimentally obtained, p is directly retrieved. Finally, starting from the original formulation of the Boag theory, 47,48 it is possible to derive ksat as 50 :
| (6) |
where p is the free electron fraction, qcoll is the collected charge, and α is a parameter that depends on a constant related to the gas in the cavity chamber, the effective volume, the distance between the electrodes and the voltage.
The absorbed dose was measured with the ionization chamber corrected for the retrieved ksat , with total estimated uncertainty of 5% (k = 1), and it was found to be in agreement with the dose measured through dose-rate-independent RCF, within the total estimated uncertainties. The authors suggest using such a simple method for UHDR linac commissioning and for periodic validation of the output stability. 55
Apart from the approaches to correct for ion recombination effects in commercially available chambers described above, a few novel ionization chamber prototypes have been proposed for application in UHDR beams. In particular, two ion chamber prototypes have been recently explored, both aiming at drastically reducing ion recombination effects.
The first approach was recently reported by Gomez et al. 56 The authors developed an ultra-thin parallel-plate ionization chamber, with electrode distance separation of 0.25 mm, demonstrating that it is possible to operate this device in UHDR beams at conventionally used voltages with reduced ion recombination factors (Table 3). Preliminary numerical simulations were performed to investigate the behavior of charge transport at UHDRs for different electrode distance separation. Simulation results showed that to achieve charge collection efficiencies not less than 99% for up to 10 Gy dose per pulse and pulse duration of few microseconds, electrode distance of less than 0.3 mm must be considered.
Two prototypes with slightly different electrode distances, with respect to the nominal one, were respectively tested with electron beams at 20 MeV produced by the PTB linear accelerator, with pulse duration of 2.5 µs and dose per pulse up to 5.4 Gy. Additionally, measurements with electron beams produced by the SIT-Sordina ElectronFLASH accelerator at 9 MeV were performed, for dose per pulse ranging from 1 to 12 Gy, with pulse duration spanning between 0.1 and 4 µs, respectively. A capacitor was used to overcome the issues related to the extremely high instantaneous current produced (of the order of few milliamps), which would have exceeded the electrometer specifications. In the PTB experimental campaign, recombination losses of 1.4% at 5.4 Gy per pulse were found, for an applied voltage of 250 V. In the measurements with the SIT accelerator, charge collection efficiencies not less than 99% were obtained at dose per pulse up to 12 Gy and operating voltage of 300 V.
This promising new approach, based on the use of ultra-thin ionization chambers, paves the way for using the ionometric approach, currently recommend by the international codes of practice, also at UHDRs, although technological challenges have to be considered for the chamber realization.
The second approach was recently developed by Di Martino et al. 57 The authors developed a novel prototype of ionization chamber, which was recently patented, 58 that is filled in with a noble gas at a set pressure. The chamber allows the measurement of absorbed dose up to 40 Gy/pulse with a perturbative effect on the electric field due to the charge density into the chamber lower than 1%. The choice of argon specifically allows the elimination of ion recombination issues, given that the electric field is greater than zero in any part of the chamber. If the latter condition is satisfied, the noble gas prevents electron capture by a molecule, as typically happens for electronegative gases, as in air-filled ionization chambers. The only possible recombination could come from direct recombination of electrons with positive ions, which can be considered negligible in the presence of electric field. Under these assumptions, the authors showed that the behavior of the electric field can be described analytically as a function of the dose-per-pulse, the applied voltage, the electrode distance, the gas density and the pulse duration. This study shows that it is possible to vary the chamber parameters in a controlled way in order to maintain negligible ion recombination, while preventing the creation of uncontrolled secondary charged production. Additionally, this device allows the control of the maximum electric field perturbation due to produced charge (equivalent to charge multiplication regime) while maintaining the required accuracy. In particular, it is possible to reach all these goals reducing the pressure of the gas in the chamber. From the operational point of view, the steps summarized in Table 2 must be followed to measure the dose per pulse.
Table 2.
Steps to be followed from the operation point of view to measure the absorbed dose
| Steps | Calculation process |
|---|---|
| Vlim calculation | Calculate the minimum value of voltage Vlim which must be applied at the electrodes in order to obtain an electric field larger than zero to avoid direct electron/positive-ion recombination |
| Vop check | Choose a proper gas pressure so that the applied operational voltage Vop > Vlim |
| Charge multiplication regime check | If Vop is such that the chamber is working in uncontrolled charge multiplication regime, decrease the pressure to be out of this regime, according to the Paschen curve |
| Further pressure optimization | Further optimize the pressure to satisfy the required value, according to the electric field perturbation due to the produced charge |
The chamber prototype was designed according to the theory discussed in Di Martino et al. 57 and a first prototype operating at 200 V and 100 Pa argon pressure has been recently realized. Dedicated tests of the first patented prototype with low energy electron beams are in progress.
Table 3 provides a summary of the ionometric approaches discussed above with the respective experimental studies.
Table 3.
Studies implementing new ionometric approaches for dosimetry of FLASH beams
| Ionometric approach | Beam & energy | Average dose rate | Dose-per-pulse | Pulse duration | Uncertainty (k = 1) | Reference |
|---|---|---|---|---|---|---|
| PTW Advanced Markus (new ksat correction approach) | 7 MeV electron beams | 125 Gy/s | 0.5 Gy | 1–4 µs | 5 % | 55 |
| Ultra-thin chamber | Electron beams at:
|
|
|
|
Not stated | 56 |
| Variable low pressure noble gas chamber* | 7 MeV electron beams | up to 10 kGy/s | up to 40 Gy/pulse | 4 µs | Not stated | 57 |
*Only theoretical studies, tests in progress.
Calorimetry vs ion chamber dosimetry
It is clear that calorimetry methods have several advantages over ionization chambers for the determination of absorbed dose delivered in UHDR regime (Table 4). In calorimeters, energy absorbed in a material rapidly gives rise to a temperature increase that is directly proportional to absorbed dose. Primary standard ionization chambers, on the other hand, can only directly disseminate air kerma, which is not the quantity of interest in modern high energy radiotherapy. The thermal effect in the calorimeters, which is the energy locked up or released in a chemical change or lattice defects, can be minimized by selection of adequate materials in the construction of calorimeters. Unlike ion chambers, calorimeters do not suffer from saturation or ion recombination effects that introduce large errors at high dose rates or high dose-per-pulse. Also, if the thermal defect in calorimeters was to be slightly dependant on the dose rate, it would involve only a second-order correction. However, in such a short delivery time as those used in FLASH RT, it is expected to be negligible. The principal limitation of water calorimetry is low sensitivity; e.g. an absorbed dose of 1 kGy would give rise to a temperature increase of only 0.24°C. However, for short irradiations (such as in FLASH RT) the temperature in the calorimeter rises very suddenly and slow drifts or frequency noise in the measuring system will not be as prominent as in conventional low dose-rate beam exposures. Also, the low sensitivity of calorimeters can be overcome by utilizing devices constructed from solid materials (such as graphite). In fact, all of the published studies employing calorimeters for the UHDR dosimetry have been conducted either with graphite or aluminium calorimeters. Further developments of simple non-expensive calorimeters for routine clinical use would greatly complement the existing technology to improve dosimetry assessment in FLASH RT. It is also important to note that the ICRU Report 24 (1976) 59 recommends that the dose delivered to the planning target volume should be within 5% (k = 1). This includes the uncertainties on dose delivery, dose measurement as well as dose calculation uncertainties. Therefore, in order to satisfy this requirement for clinical implementation, the reference absorbed dose-to-water measurements should be performed with an uncertainty below 1% (k = 1). Consequently, further effort is required to fully evaluate all the correction and conversion factors when employing calorimeters for clinical dosimetry.
Table 4.
Advantages and disadvantages of calorimeters and ionization chambers for dosimetry in FLASH RT
| Advantages | Disadvantages | |
|---|---|---|
| Calorimeters |
|
|
| Ionization chambers |
|
|
RT, radiotherapy.
However, recent developments in ion chamber dosimetry presented in the Ionization chambers section demonstrate promising advances in ionometry for UHDR beams. New solutions, in terms of both new methods of determination of ksat as well as development of new devices, are required to maintain the use of ionization chambers as secondary standard dosimeters in FLASH RT, particularly for high dose-per-pulse beams. The possibility of using ionization chambers still at UHDRs is desirable in order be able to apply the existing protocols for beam dosimetry based on ionometric approaches. Indeed, ionization chambers have been always considered the gold-standard for dosimetry of radiation therapy and their ease of use would further contribute to the clinical translation of FLASH radiotherapy, provided the ion recombination issues are definitively addressed.
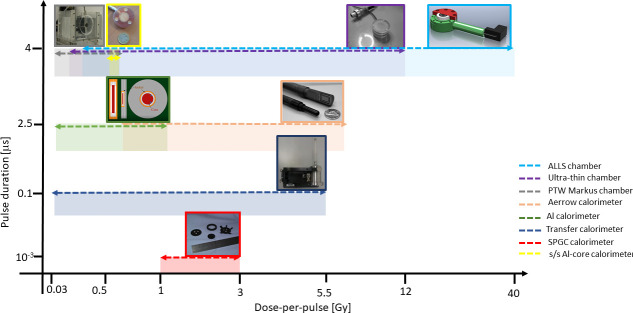
Calorimeters and ionization chambers represent the most reliable approaches so far developed for dosimetry of UHDR beams for FLASH radiotherapy. Depending on the beam parameter conditions, such as dose per pulse, pulse duration and pulse frequency, one technology could be preferred to the other one, as compromise between accuracy, reliability and ease of use must be found in a future clinical routine. In Figure 1, the operational ranges, in terms of dose per pulse and pulse duration at which the response of the above discussed detectors has been studied are shown. The recent efforts focused on further optimization of detectors for absolute dosimetry in UHDR regime will significantly contribute to the clinical translation of FLASH radiotherapy.
Figure 1.
Ion chambers and calorimeters used in UHDR beams (axes not to scale).
Summary
Absolute dosimeters such as calorimeters are the most desirable detectors for application in FLASH RT due to their accuracy. However, their complexity at present (associated particularly with primary standard devices) makes them unsuitable for routine clinical measurements. New advances in the development of simple clinical calorimeters could pave a way for accurate dissemination of dose in clinical FLASH RT. Also, new developments in ionometry will play a very important role in the development of this new radiotherapy modality. Dosimeters such as film, alanine, diodes, scintillators and others will play a very important role in providing verification and confidence in the dosimetry in clinical and pre-clinical FLASH radiotherapy.
Footnotes
Acknowledgments: This project 18HLT04 UHDpulse has received funding from the EMPIR programme co-financed by the Participating States and from the European Union’s Horizon 2020 research and innovation programme. The FRIDA project, funded by the CSN5 of the INFN, has also partially supported this work. We would like to thank Graham Bass for his valuable input.
Funding: EMPIR 18HLT04 UHDpulse and FRIDA INFN CSN5.
Contributor Information
Anna Subiel, Email: anna.subiel@npl.co.uk.
Francesco Romano, Email: francesco.romano@ct.infn.it.
REFERENCES
- 1. Beadle BM, Liao K-P, Elting LS, Buchholz TA, Ang KK, Garden AS, et al. Improved survival using intensity-modulated radiation therapy in head and neck cancers: a seer-medicare analysis. Cancer 2014; 120: 702–10. doi: 10.1002/cncr.28372 [DOI] [PubMed] [Google Scholar]
- 2. Boyer MJ, Williams CD, Harpole DH, Onaitis MW, Kelley MJ, Salama JK. Improved survival of stage I non-small cell lung cancer: A va central cancer registry analysis. J Thorac Oncol 2017; 12: 1814–23. doi: 10.1016/j.jtho.2017.09.1952 [DOI] [PubMed] [Google Scholar]
- 3. Iacobucci G. Cancer survival in England: Rates improve and variation falls. BMJ 2019; l1532. doi: 10.1136/bmj.l1532 [DOI] [PubMed] [Google Scholar]
- 4. Lee N, Chuang C, Quivey JM, Phillips TL, Akazawa P, Verhey LJ, et al. Skin toxicity due to intensity-modulated radiotherapy for head-and-neck carcinoma. Int J Radiat Oncol Biol Phys 2002; 53: 630–37. doi: 10.1016/s0360-3016(02)02756-6 [DOI] [PubMed] [Google Scholar]
- 5. Packer RJ, Zhou T, Holmes E, Vezina G, Gajjar A. Survival and secondary tumors in children with medulloblastoma receiving radiotherapy and adjuvant chemotherapy: Results of children’s oncology group trial a9961. Neuro Oncol 2013; 15: 97–103. doi: 10.1093/neuonc/nos267 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Lindberg K, Bergström P, Brustugun OT, Engelholm S, Grozman V, Hoyer M, et al. OA24.05 the Nordic HILUS-trial-first report of a phase II trial of SBRT of centrally located lung tumors. Journal of Thoracic Oncology 2017; 12: S340. doi: 10.1016/j.jtho.2016.11.369 [DOI] [Google Scholar]
- 7. Salloum R, Chen Y, Yasui Y, Packer R, Leisenring W, Wells E, et al. Late morbidity and mortality among medulloblastoma survivors diagnosed across three decades: A report from the childhood cancer Survivor study. J Clin Oncol 2019; 37: 731–40. doi: 10.1200/JCO.18.00969 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Favaudon V, Caplier L, Monceau V, Pouzoulet F, Sayarath M, Fouillade C, et al. Ultrahigh dose-rate flash irradiation increases the differential response between normal and tumor tissue in mice. Sci Transl Med 2014; 6(): 245ra93. doi: 10.1126/scitranslmed.3008973 [DOI] [PubMed] [Google Scholar]
- 9. Bourhis J, Sozzi WJ, Jorge PG, Gaide O, Bailat C, Duclos F, et al. Treatment of a first patient with FLASH-radiotherapy. Radiother Oncol 2019; 139: 18–22. doi: 10.1016/j.radonc.2019.06.019 [DOI] [PubMed] [Google Scholar]
- 10. Bourhis J, Montay-Gruel P, Gonçalves Jorge P, Bailat C, Petit B, Ollivier J, et al. Clinical translation of flash radiotherapy: Why and how? Radiother Oncol 2019; 139: 11–17. doi: 10.1016/j.radonc.2019.04.008 [DOI] [PubMed] [Google Scholar]
- 11. Vozenin M-C, De Fornel P, Petersson K, Favaudon V, Jaccard M, Germond J-F, et al. The advantage of FLASH radiotherapy confirmed in mini-pig and cat-cancer patients. Clin Cancer Res 2019; 25: 35–42. doi: 10.1158/1078-0432.CCR-17-3375 [DOI] [PubMed] [Google Scholar]
- 12. Natarajan S, Levy K, Wang J, Chow S, Eggold J, Loo P, et al. Abstract 5351: FLASH irradiation enhances the therapeutic index of abdominal radiotherapy in mice. Cancer Res 2020; 80(): 5351. doi: 10.1158/1538-7445.AM2020-5351 [DOI] [Google Scholar]
- 13. Soto LA, Casey KM, Wang J, Blaney A, Manjappa R, Breitkreutz D, et al. FLASH irradiation results in reduced severe skin toxicity compared to conventional-dose-rate irradiation. Radiat Res 2020; 194: 618–24. doi: 10.1667/RADE-20-00090 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Radiation dosimetry: x-rays and gamma rays with maximum energies between 0.6 MeV and 50 MeV. International Commission on Radiation Units and Measurements; 1969. [Google Scholar]
- 15. Osborne NS, Stimson HF, Ginnings DC. Measurements of heat capacity and heat of vaporization of water in the range 0 degrees to 100 degrees C. J RES NATL BUR STAN 1939; 23: 197. doi: 10.6028/jres.023.008 [DOI] [Google Scholar]
- 16. Seuntjens J, Duane S. Photon absorbed dose standards. Metrologia 2009; 46: S39–58. doi: 10.1088/0026-1394/46/2/S04 [DOI] [Google Scholar]
- 17. Renaud J, Palmans H, Sarfehnia A, Seuntjens J. Absorbed dose calorimetry. Phys Med Biol 2020; 65(): 05TR02. doi: 10.1088/1361-6560/ab4f29 [DOI] [PubMed] [Google Scholar]
- 18. Hochanadel CJ, Ghormley JA. A calorimetric calibration of gamma-ray Actinometers. The Journal of Chemical Physics 1953; 21: 880–85. doi: 10.1063/1.1699051 [DOI] [Google Scholar]
- 19. Genna S, Jaeger RG, Sanielevici A, Nagl J. Quasi-adiabatic calorimeter for the direct determination of radiation dose in rads at. Energy Rev 1963; 1: 239. [Google Scholar]
- 20. Witzani J, Duftschmid KE, Strachotinsky C, Leitner A. A graphite absorbed-dose calorimeter in the quast-isothermal mode of operation. Metrologia 1984; 20: 73–79. doi: 10.1088/0026-1394/20/3/001 [DOI] [Google Scholar]
- 21. Daures J, Ostrowsky A. New constant-temperature operating mode for graphite calorimeter at LNE-LNHB. Phys Med Biol 2005; 50: 4035–52. doi: 10.1088/0031-9155/50/17/008 [DOI] [PubMed] [Google Scholar]
- 22. Gunn SR. Radiometric calorimetry: A review. Nuclear Instruments and Methods 1964; 29: 1–24. doi: 10.1016/0029-554X(64)90002-3 [DOI] [Google Scholar]
- 23. Gunn SR. Radiometric calorimetry: A review (1970 supplement). Nuclear Instruments and Methods 1970; 85: 285–312. doi: 10.1016/0029-554X(70)90250-8 [DOI] [Google Scholar]
- 24. Domen S.R., Advances in calorimetry for radiation dosimetry. 1987, United States: Academic Press. [Google Scholar]
- 25. Gunn SR. Radiometric calorimetry: A review. Nuclear Instruments and Methods 1976; 135: 251–65. doi: 10.1016/0029-554X(76)90172-5 [DOI] [Google Scholar]
- 26. McEwen MR, Duane S. A portable calorimeter for measuring absorbed dose in the radiotherapy clinic. Phys Med Biol 2000; 45: 3675–91. doi: 10.1088/0031-9155/45/12/312 [DOI] [PubMed] [Google Scholar]
- 27. UHDpulse 2022; Available from: http://uhdpulse-empir.eu/.
- 28. Miller A, Kovas A. Application of calorimeters for routine and reference dosimetry at 4–10 MeV industrial electron accelerators. International Journal of Radiation Applications and Instrumentation Part C Radiation Physics and Chemistry 1990; 35: 774–78. doi: 10.1016/1359-0197(90)90314-8 [DOI] [Google Scholar]
- 29. Lourenço A, Subiel A, Lee N, Flynn S, Cotterill J, Shipley D, et al. Absolute dosimetry for flash proton pencil beam scanning radiotherapy. Sci Rep 2023; 13(): 2054. doi: 10.1038/s41598-023-28192-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Lee E, Lourenço AM, Speth J, Lee N, Subiel A, Romano F, et al. Ultrahigh dose rate pencil beam scanning proton dosimetry using ion chambers and a calorimeter in support of first in-human flash clinical trial. Med Phys 2022; 49: 6171–82. doi: 10.1002/mp.15844 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Williams AJ, Burns DT, McEwen M. Measurement of the specific heat capacity of the electron-beam graphite calorimeter. National Physical Laboratory: Teddington; 1993. [Google Scholar]
- 32. Renaud J, Sarfehnia A, Bancheri J, Seuntjens J. Aerrow: A probe-format graphite calorimeter for absolute dosimetry of high-energy photon beams in the clinical environment. Med Phys 2018; 45: 414–28. doi: 10.1002/mp.12669 [DOI] [PubMed] [Google Scholar]
- 33. Timmer JH, Röcken H, Stephani T, Baumgarten C, Geisler A. Automated cyclotron tuning using beam phase measurements. nuclear instruments and methods in physics research section A: accelerators, spectrometers. Detectors and Associated Equipment 2006; 568: 532–36. [Google Scholar]
- 34. Gamba D, Corsini R, Curt S, Doebert S, Farabolini W, Mcmonagle G, et al. The clear user facility at CERN. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 2018; 909: 480–83. doi: 10.1016/j.nima.2017.11.080 [DOI] [Google Scholar]
- 35. Ross CK, Seuntjens JP, Klassen NV, Shortt KR. The NRC sealed water calorimeter: Correction factors and performance. In: NPL Workshop on Recent Advances in Calorimetric Absrobed Dose Standards. National PhysicalLaboratory; 2000, pp. 90–102. [Google Scholar]
- 36. PTW 2022; Available from: https://www.ptwdosimetry.com/en/products/roos-electron-chamber/.
- 37. McManus M, Romano F, Lee ND, Farabolini W, Gilardi A, Royle G, et al. The challenge of ionisation chamber dosimetry in ultra-short pulsed high dose-rate very high energy electron beams. Sci Rep 2020; 10(): 9089. doi: 10.1038/s41598-020-65819-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Duane S, Aldehaybes M, Bailey M, Lee ND, Thomas CG, Palmans H. An absorbed dose calorimeter for IMRT dosimetry. Metrologia 2012; 49: S168–73. doi: 10.1088/0026-1394/49/5/S168 [DOI] [Google Scholar]
- 39. McManus M. Dosimetry of Ultra-Short High Dose-Per-Pulse Very High Energy Electrons. In: Medical Physics And Biomedical Engineering. University College London; 2022, pp. 222. [Google Scholar]
- 40. Romano F, Subiel A, McManus M, Lee ND, Palmans H, Thomas R, et al. Challenges in dosimetry of particle beams with ultra-high pulse dose rates. J Phys: Conf Ser 2020; 1662: 012028. doi: 10.1088/1742-6596/1662/1/012028 [DOI] [Google Scholar]
- 41. Palmans H, Thomas R, Simon M, Duane S, Kacperek A, DuSautoy A, et al. A small-body portable graphite calorimeter for dosimetry in low-energy clinical proton beams. Phys Med Biol 2004; 49: 3737–49. doi: 10.1088/0031-9155/49/16/019 [DOI] [PubMed] [Google Scholar]
- 42. Bourgouin A, Schüller A, Hackel T, Kranzer R, Poppinga D, Kapsch R-P, et al. Calorimeter for real-time dosimetry of pulsed ultra-high dose rate electron beams. Front Phys 2020; 8: 8. doi: 10.3389/fphy.2020.567340 [DOI] [Google Scholar]
- 43. Bourgouin A. Performance of a Probe Type Graphite Calorimeter (Aerrow) in Ultra High Dose Per Pulse Electron Beams 2021; Available from: http://uhdpulse-empir.eu/wp-content/uploads/FRPT_Bourgouin_Calorimetry-presentation.pdf.
- 44. Bourgouin A, Keszti F, Schönfeld AA, Hackel T, Kozelka J, Hildreth J, et al. The probe-format graphite calorimeter, aerrow, for absolute dosimetry in ultrahigh pulse dose rate electron beams. Med Phys 2022; 49: 6635–45. doi: 10.1002/mp.15899 [DOI] [PubMed] [Google Scholar]
- 45. Bass GA, Shipley DR, Flynn SF, Thomas RAS. A prototype low-cost secondary standard calorimeter for reference dosimetry with ultra-high pulse dose rates. Br J Radiol 2023; 96(): 20220638. doi: 10.1259/bjr.20220638 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. IAEA TECHNICAL REPORTS SERIES . Absorbed Dose Determination in External Beam Radiotherapy, Technical Reports Series No. 398. Vienna, IAEA: 2000. [Google Scholar]
- 47. Romano F, Bailat C, Jorge PG, Lerch MLF, Darafsheh A. Ultra-high dose rate dosimetry: Challenges and opportunities for flash radiation therapy. Med Phys 2022; 49: 4912–32. doi: 10.1002/mp.15649 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Darafsheh A, Hao Y, Zhao X, Zwart T, et al. Spread-out bragg peak proton FLASH irradiation using a clinical synchrocyclotron: proof of concept and ion chamber characterization. Medical Physics 2021; 48(8): 4472. doi: 10.1002/mp.15021 [DOI] [PubMed] [Google Scholar]
- 49. Di Martino F, Barca P, Barone S, Bortoli E, Borgheresi R, De Stefano S, et al. FLASH radiotherapy with electrons: Issues related to the production, monitoring, and dosimetric characterization of the beam. Front Phys 2020; 8: 8. doi: 10.3389/fphy.2020.570697 [DOI] [Google Scholar]
- 50. Petersson K, Jaccard M, Germond J-F, Buchillier T, Bochud F, Bourhis J, et al. High dose-per-pulse electron beam dosimetry-a model to correct for the ion recombination in the advanced Markus ionization chamber. Med Phys 2017; 44: 1157–67. doi: 10.1002/mp.12111 [DOI] [PubMed] [Google Scholar]
- 51. Boag JW. Ionization measurements at very high intensities—part I. BJR 1950; 23: 601–11. doi: 10.1259/0007-1285-23-274-601 [DOI] [PubMed] [Google Scholar]
- 52. Boag JW, Hochhäuser E, Balk OA. The effect of free-electron collection on the recombination correction to ionization measurements of pulsed radiation. Phys Med Biol 1996; 41: 885–97. doi: 10.1088/0031-9155/41/5/005 [DOI] [PubMed] [Google Scholar]
- 53. Laitano RF, Guerra AS, Pimpinella M, Caporali C, Petrucci A. Charge collection efficiency in ionization chambers exposed to electron beams with high dose per pulse. Phys Med Biol 2006; 51: 6419–36. doi: 10.1088/0031-9155/51/24/009 [DOI] [PubMed] [Google Scholar]
- 54. Di Martino F, Giannelli M, Traino AC, Lazzeri M. Ion recombination correction for very high dose-per-pulse high-energy electron beams. Med Phys 2005; 32: 2204–10. doi: 10.1118/1.1940167 [DOI] [PubMed] [Google Scholar]
- 55. Di Martino F, Del Sarto D, Barone S, Giuseppina Bisogni M, Capaccioli S, Galante F, et al. A new calculation method for the free electron fraction of an ionization chamber in the ultra-high-dose-per-pulse regimen. Phys Med 2022; 103: 175–80. doi: 10.1016/j.ejmp.2022.11.001 [DOI] [PubMed] [Google Scholar]
- 56. Gómez F, Gonzalez-Castaño DM, Fernández N, et al. Development of an ultra-thin parallel plate ionization chamber for dosimetry in FLASH radiotherapy. Med Phys 2022; 49(7): 4705. doi: 10.1002/mp.15668 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Di Martino F, Del Sarto D, Giuseppina Bisogni M, Capaccioli S, Galante F, Gasperini A, et al. A new solution for UHDP and UHDR (flash) measurements: Theory and conceptual design of ALLS chamber. Phys Med 2022; 102: 9–18. doi: 10.1016/j.ejmp.2022.08.010 [DOI] [PubMed] [Google Scholar]
- 58. “ALLS” chamber, Patent N.102021000019520. 2022.
- 59. ICRU . Determination of Absorbed Dose in a Patient Irradiated by Beams of x or Gamma Rays in Radiotherapy Procedures. ICRU Report 24, Bethesda, Maryland and Washington DC: 1976. [Google Scholar]