Keywords: glucose metabolism, identifiability, insulin sensitivity, parameter estimation, prediabetes
Abstract
Assessing free fatty acids (FFAs) kinetics and the role of insulin and glucose on FFA lipolysis and disposal may improve our understanding of the pathogenesis of type 2 diabetes (T2D). Some models have been proposed to describe FFA kinetics during an intravenous glucose tolerance test and only one during an oral glucose tolerance test. Here, we propose a model of FFA kinetics during a meal tolerance test and use it to assess possible differences in postprandial lipolysis in individuals with type 2 diabetes (T2D) and individuals with obesity without type 2 diabetes (ND). We studied 18 obese ND and 16 T2D undergoing three meal tolerance tests (MTT) on three occasions (breakfast, lunch, and dinner). We used plasma glucose, insulin, and FFA concentrations collected at breakfast to test a battery of models and selected the best one based on physiological plausibility, ability to fit the data, precision of parameter estimates, and the Akaike parsimony criterion. The best model assumes that the postprandial suppression of FFA lipolysis is proportional to the above basal insulin, while FFA disposal is proportional to FFA concentration. It was used to compare FFA kinetics in ND and T2D along the day. The maximum lipolysis suppression occurred significantly earlier in ND than T2D (39 ± 6 min vs. 102 ± 13 min, 36 ± 4 min vs. 78 ± 11 min, and 38 ± 6 min vs. 84 ± 13 min, P < 0.01, at breakfast, lunch, and dinner, respectively), making lipolysis significantly lower in ND than T2D. This is mainly attributable to the lower insulin concentration in the second group. This novel FFA model allows to assess lipolysis and insulin antilipolytic effect in postprandial conditions.
NEW & NOTEWORTHY In this study, we propose a new mathematical model able to quantify postprandial FFA kinetics and adipose tissue insulin sensitivity in both subjects with obesity without type 2 diabetes (ND) and subjects with type 2 diabetes (T2D). Results show that the slower postprandial suppression of lipolysis in T2D contributes to the higher free fatty acid (FFA) concentration that, in turn, may contribute to hyperglycemia.
INTRODUCTION
The disposal of plasma free fatty acids (FFAs) and glucose (G) are interrelated. Randle et al. (1) described for the first time the “glucose-fatty acid cycle,” i.e., the concept that FFAs and glucose compete for mitochondrial oxidation in skeletal muscle. In fact, an elevation of FFA concentration and their oxidation inhibits the activities of glycolytic enzymes, which increases glucose 6-phosphate (G6P), causing an impairment in glucose uptake by skeletal muscles (1).
Based on this theory, several hypotheses on the possible mechanisms of FFA-glucose-insulin interaction were developed. In particular, a study reported that FFAs primarily inhibit glucose transport and phosphorylation in human skeletal muscles and interfere with insulin signaling, abolishing the increase in insulin receptor substrate IRS-1-associated phosphatidylinositol 3-kinase (PI3K) in human skeletal muscles (2). Other studies have shown that FFAs induce an elevation of hepatic glucose production (acting on both gluconeogenesis and glycogenolysis; 3–7). Furthermore, in healthy individuals, elevated FFAs stimulate insulin secretion to compensate for the FFA-induced insulin resistance, whereas chronic FFA elevation impaired this mechanism in people predisposed to the development of type 2 diabetes (8, 9). On the other hand, although it is well known that insulin has an antilipolytic effect (10–12), a direct effect of glucose on FFA metabolism is still controversial: Szkudelski et al. (13) and Botion et al. (14) described the lipolytic effect of prolonged hyperglycemia, whereas Sidossis et al. (15) proposed the so-called “glucose-FFA cycle reversed,” in which glucose or insulin reduces FFA oxidation.
Some mathematical models have been published to measure FFA kinetics during an intravenous glucose tolerance test (IVGTT; 16, 17). However, during IVGTT, glucose and insulin concentration pattern levels are known to be nonphysiological given the rapid perturbation due to glucose infusion. To the best of our knowledge, only a mathematical model of FFA kinetics was developed to describe the system dynamic during a more physiological perturbation, like the oral glucose tolerance test (OGTT; 18) but, as stated by the authors, it poorly performed during the meal tolerance test (MTT). Our goal was to test published models and, if necessary, to develop a new model to describe FFA kinetics during a MTT and use it to assess possible differences in FFA kinetics in individuals with obesity without type 2 diabetes (ND) and individuals with type 2 diabetes (T2D) during the day.
MATERIALS AND METHOD
Subjects and Protocol
The study was approved by the University of Virginia (UVA) Institutional Review Board. After written informed consent was received, 18 obese participants without diabetes [8 males, age = 54 ± 12 yr (mean ± SD) and body mass index (BMI) = 29 ± 5 kg/m2] and 16 with type 2 diabetes (10 males, age = 62 ± 11 yr and BMI = 32 ± 5 kg/m2) were studied for 3 days, in which they received three identical caffeine-free meals (8 kcal/kg/meal; 75 g carbohydrates) at breakfast (B) (7:00 AM), lunch (L) (1:00 PM), and dinner (D) (7:00 PM), each of which consisted of 33% of the subject’s total estimated calorie intake, based on Harris–Benedict + 20% calorie requirements, as described in Ref. 19. Blood was sampled periodically for measurement of plasma glucose (G), insulin (I), and free fatty acid (FFA) concentrations.
Analytical Techniques
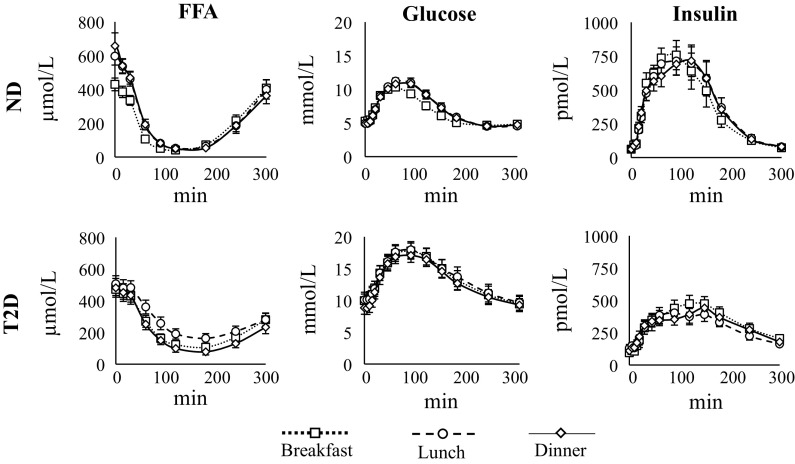
Blood samples were collected in prechilled syringes and dispensed into prechilled tubes. Samples for free fatty acids were collected in tubes containing 50 μL of Paraoxon (diethyl-p-nitrophenyl-phosphate; Sigma Chemicals, St Louis, MO) diluted to 0.04% in diethyl ether to prevent ex vivo lipolysis. Samples were placed in ice, centrifuged at 4°C, and separated. Plasma G was measured using a glucose oxidase method (YSI Inc., Yellow Springs, OH; 19); plasma I was measured using a chemiluminescence assay (Access Assay; Beckman Coulter, Chaska, MN), as described in Ref. 20. Plasma FFA concentration was measured at t = −30, 0, 15, 30, 60, 90, 120, 180, 240, and 300 min using the modified microfluorometric enzymatic method implemented in the Cobas, MIRA analyzer (Roche; 21). The time courses of plasma FFA, G, and I concentration measured at B, L, and D in ND and T2D are reported in Fig. 1.
Figure 1.
Average time course of plasma FFA (left), glucose (middle), and insulin concentrations (right) in ND (top) and T2D (bottom) at breakfast (dotted lined with squares), lunch (dashed line with circles), and dinner (continuous line with diamond). Vertical bars represent ± standard error. FFA, free fatty acid; ND, obese nondiabetic patients; T2D, patients with type 2 diabetes.
Models
The most recent models available in the literature to describe FFA production and clearance during an IVGTT are those proposed by Periwal et al. (16) and Stefanovski et al. (17).
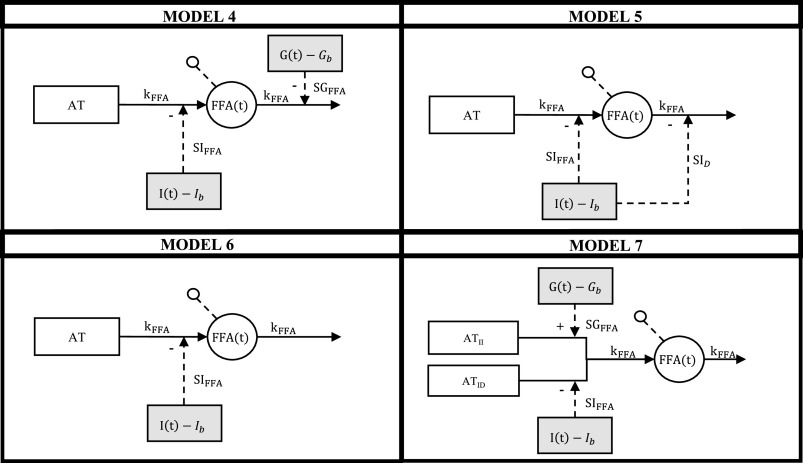
As a first attempt to assess FFA kinetics during a mixed meal test, we tested if such models (Model 1 and Model 2, in the following) were valid also in postprandial conditions, but, unfortunately, as discussed in the results, this was not the case. We also tested the model developed by Boston et al. (18) (Model 3), which was developed to describe FFA kinetics during an IVGTT, OGTT, and MTT. As anticipated by the authors and confirmed by our analysis, its performance during a MTT was not satisfactory. Therefore, we formulated and tested four new models (Models 4–7; Fig. 2).
Figure 2.
Graphical representation of the four new tested models. White circles represent model variables, white boxes represent tissues, and gray boxes represent forcing functions.
Model 1 (Periwal model).
This model was developed to describe FFA kinetics during an IVGTT (16). It assumes that there exist two sources of FFA, one insulin dependent and suppressible by a remote insulin compartment (X(t)) and one insulin independent ():
| (1) |
where is the minimal lipolysis rate, is the maximal lipolysis rate, β is the Hill constant, α is the Hill coefficient. FFA is cleared from the plasma as a first-order process with rate . X is insulin concentration in a remote compartment, which depends on the over-basal plasma insulin. The rate constant at which insulin can enter in the remote compartment is . We also tested the model performance assuming the steady state condition at time 0 min, i.e., by fixing (see discussion).
Model 2 (Stefanovski model).
This model was developed to describe FFA kinetics during an IVGTT (17). It assumes that adipose tissues (AT) are responsible of FFA lipolysis (L), insulin exerts an antilipolytic effect via a remote compartment (XFFA) and glucose (G) stimulates FFA disposal (D) through parameter α, representing how much sensitive FFA disposal is to glucose variation. Model equations are:
| (2) |
where FFA(t) is the plasma free-fatty acid concentration, G(t) plasma glucose concentration, and I(t) plasma insulin concentration (subscript “b” denotes basal, premeal values), SFFA the fractional FFA disposal rate (implicitly assumed to be equal to the fractional lipolysis rate in absence of insulin antilipolytic effect), pXFCR the rate constant of the remote insulin action, XFFA, pXa a scale factor governing its amplitude and α a scaling factor for the effect of plasma glucose on FFA disposal. It is worth noting that, in the original work, the authors did not constrain α to be equal to 1/Gb, therefore steady state condition at time 0 min was not guaranteed.
Model 3 (Boston model).
This model was proposed to describe FFA dynamics during IVGTT, OGTT, and MTT (18). It assumes that FFA lipolysis is controlled by glucose in a remote compartment (R(t)):
| (3) |
where is the maximal rate of lipolysis and is the rate at which FFA leave the plasma compartment. The glucose action on FFA lipolysis emanates from a remote compartment, R, and saturates following a Michaelis–Menten law (Φ represents the value of R at which the rate of lipolysis is halved); is the amount of plasma glucose, G, that can enter the remote compartment through , if it is over a certain threshold ():
| (4) |
In the original work, authors did not constrain model parameters to guarantee the steady state at time 0 min. We also tested model performance when adding the steady state constraints: , , and (see discussion).
Model 4.
According to the theory of the “glucose-FFA cycle reversed” proposed by Sidossis et al. (15), in this model, we assumed that the over-basal glucose reduces, or completely suppresses, FFA disposal. In addition, since during a meal glucose and insulin concentrations vary more gently than during an IVGTT (and consequently, parameters governing the dynamic of the remote insulin action were estimated with poor precision, see results, Model Assessment), we tested the hypothesis that plasma insulin concentration acts directly on the suppression on FFA lipolysis. We also added a nonnegativity constraint on FFA lipolysis and disposal.
The model equation is:
| (5) |
with
| (6) |
| (7) |
where is the fractional FFA disposal rate in absence of glucose stimulus, implicitly assumed to be equal to the fractional lipolysis rate in absence of insulin antilipolytic effect, SGFFA the fractional effectiveness of glucose to suppress FFA disposal and SIFFA the sensitivity to insulin, i.e., the ability of insulin to suppress lipolysis.
Model 5.
Given that, in Sidossis et al. (15), it was not clear if glucose or insulin act to suppress FFA disposal, in Model 5 we assumed that over-basal insulin act to suppress both FFA lipolysis and disposal. FFA dynamics are described by Eq. 5; lipolysis has the same formulation of Eq. 7 but disposal is described by:
| (8) |
where represent the insulin effect on FFA disposal.
Model 6.
Models 3–4 assume that plasma glucose has a direct effect on FFA disposal. However, given that a direct action of glucose on FFA disposal is debated, we chose to incorporate in Model 6 only the well-established insulin-mediated inhibition of lipolysis (10–12), without including any potential glucose effect on FFA disposal. FFA dynamics are described by Eq. 5, lipolysis is that of Eq. 7, whereas FFA disposal is:
| (9) |
where is the fractional FFA disposal rate.
Model 7.
This model incorporates the knowledge that there are two main sources of FFA from adipose tissues (AT). According to Szkudelski et al. (13) and Botion et al. (14), which reported a lipolytic effect of prolonged hyperglycemia, we assumed that the insulin independent FFA production is controlled by the over-basal glucose concentration. Thus, one has that FFA dynamics are described by Eq. 5, FFA disposal is that of Eq. 9 and lipolysis is:
| (10) |
where kFFA and SIFFA are those defined above and SGFFA is the sensitivity to glucose, i.e., the ability of glucose to suppress lipolysis.
Model Identification
A priori identifiability was assessed using Daisy software (22), which implements an algorithm based on differential algebra. Uniquely identifiable parameters were estimated from plasma FFA concentrations using nonlinear weighted least squares (23), implemented in Matlab (R2021a) (24). Measurement error was assumed to be independent, Gaussian, with zero mean and unknown constant standard deviation, estimated a posteriori. Plasma glucose and insulin concentrations were the model forcing functions, assumed to be known without error.
Model Assessment
Breakfast ND and T2D data were used for model development and to select the most parsimonious one. Model performances were compared based on standard criteria, such as the ability to describe the data [weighted residual sum of squares, WRSS, and residual independence, assessed through Wald–Wolfowitz run test (25)], the precision of parameter estimates (expressed as coefficient of variation, CV%) and physiological plausibility of model parameters. Among the models that well fitted the data and provided precise estimate of the parameters, the best one was selected using the Akaike information criterion (AIC; 26).
Assessing the Diurnal Pattern of FFA Kinetics in ND and T2D
The selected model was applied also to the data measured at lunch and dinner in ND and T2D subjects. This allowed to assess the diurnal pattern of model parameters and both lipolysis and FFA disposal in ND and T2D using Eqs. 7 and 9, respectively. To better characterize the curves, from these, we determined the times of the maximum suppression, as the time at which lipolysis (TL) and FFA disposal (TD) reached their nadir, and the percentage of suppression of lipolysis (%SL) and disposal (%SD) at 180 min, as previously reported (27).
Statistical Analysis
The statistical analysis was performed using MATLAB and Minitab. Data are reported as means ± SE for normally distributed variables and median and (25th−75th) percentile for not normally distributed ones. Normality of the variables was assessed using Anderson–Darling test (28) and, when appropriate, variables were log-transformed. Homoscedasticity was evaluated using F test.
The comparisons within groups (ND vs. T2D and B vs. L vs. D) was done using two-way-ANOVA test and Tukey’s test for post hoc analysis, with significance level set to 0.05.
RESULTS
Model Assessment
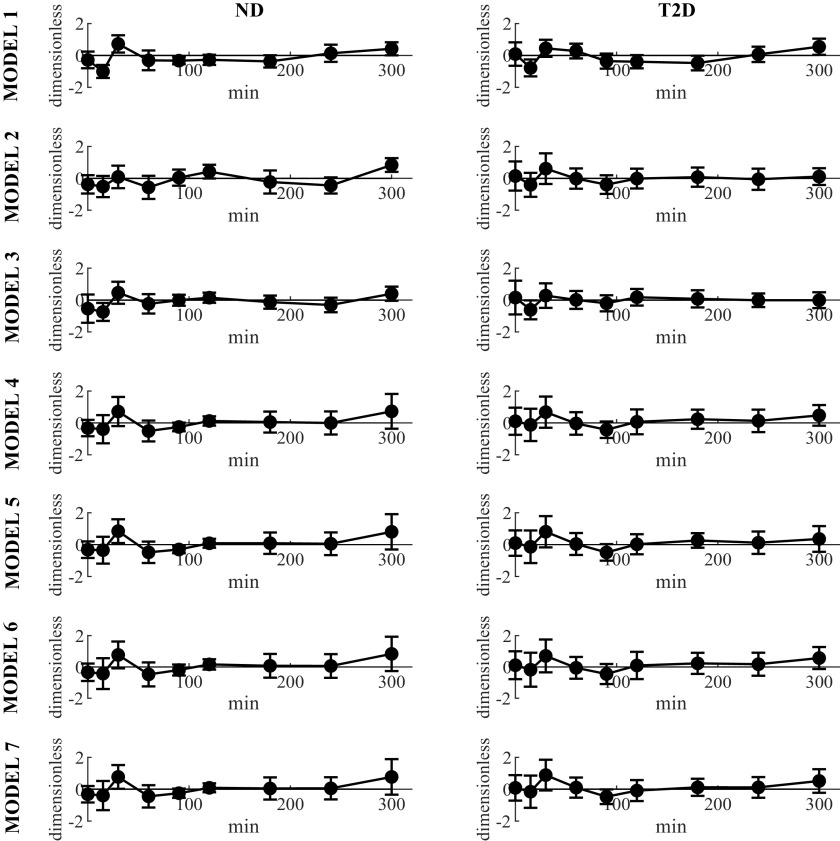
According to Wald–Wolfowitz run test, all the tested models provided independent weighted residuals when fitted to FFA data of ND and T2D subjects at breakfast (Fig. 3, Table 1).
Figure 3.
Average weighted residuals (continuous line with circles) of the seven tested models in ND (left) and T2D (right column). Vertical bars represent ± SD. ND, obese nondiabetic patients; T2D, patients with type 2 diabetes.
Table 1.
Model Selection
| Precision |
|||||
|---|---|---|---|---|---|
| Model | Runs Test | WRSS × 103 | CV% | N cv>100% | AIC |
| ND | |||||
| 1 | Yes | 12.4 ± 1.8 | >100 | 17 | 28.9 ± 0.4 |
| 2 | Yes | 26.6 ± 11.7 | 41 ± 8 | 4 | 26.9 ± 0.5 |
| 3 | Yes | 6.9 ± 1.3 | 99 ± 68 | 11 | 26.9 ± 0.5 |
| 4 | Yes | 36.2 ± 13.2 | >100 | 17 | 25.7 ± 0.5 |
| 5 | Yes | 25.5 ± 5.6 | >100 | 15 | 25.5 ± 0.4 |
| 6 | Yes | 26.8 ± 6.1 | 32 ± 4 | 0 | 23.6 ± 0.4 |
| 7 | Yes | 26.5 ± 6.1 | >100 | 18 | 25.6 ± 0.4 |
| T2D | |||||
| 1 | Yes | 9.3 ± 1.2 | >100 | 14 | 28.0 ± 0.4 |
| 2 | Yes | 7.1 ± 1.0 | 37 ± 5 | 3 | 25.4 ± 0.3 |
| 3 | Yes | 4.1 ± 1.0 | >100 | 12 | 25.6 ± 0.5 |
| 4 | Yes | 12.3 ± 2.0 | >100 | 12 | 24.9 ± 0.3 |
| 5 | Yes | 11.9 ± 2.0 | >100 | 11 | 24.3 ± 0.3 |
| 6 | Yes | 12.6 ± 1.9 | 34 ± 8 | 0 | 22.5 ± 0.3 |
| 7 | Yes | 11.9 ± 2.0 | >100 | 16 | 24.8 ± 0.3 |
Data are reported as means ± SE. Models performance in ND and T2D subjects. NCV > 100% indicates the number of subjects in which at least one parameter is estimated with CV > 100%. The bold values highlight the most parsimonious model. AIC, Akaike information criterion; ND, obese nondiabetic patients; T2D, patients with type 2 diabetes; WRSS, weighted residual sum of squares.
However, Models 1, 2, 3, 4, 5, and 7 did not allow to estimate the parameters with precision in a significant percentage of the subjects. Conversely, Model 6 provided precise estimate of all the parameters. In addition the parsimony AIC index was the lowest one (23.6 ± 0.4, in ND subjects, and 22.5 ± 0.3, in T2D subjects, respectively). Taken together, these results suggest selecting Model 6 as the best one.
Assessing the Diurnal Pattern of FFA Kinetics in ND and T2D
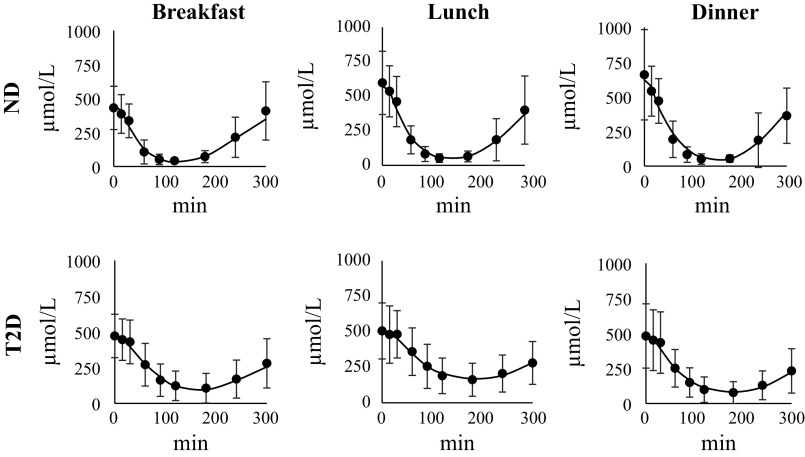
Model 6 well predicted FFA data of ND and of T2D subjects also at lunch and dinner (Fig. 4) and provided precise parameter estimates (not shown). Estimated kFFA and SIFFA are reported in Table 2. kFFA was significantly higher in ND versus T2D at lunch (P = 0.01). In the ND group, kFFA was significantly higher at B than both L and D (P < 0.05) whereas, in the T2D group, kFFA was significantly lower at L than both B and D (P < 0.05). On the other hand, SIFFA was not different in the two groups and did not vary significantly during the day.
Figure 4.
Average model predictions (continuous lines) vs. FFA data (black circles) in ND (top) and T2D subjects (bottom) at breakfast (left), lunch (middle), and dinner (right). Vertical bars represent ± SD. FFA, free fatty acid; ND, obese nondiabetic patients; T2D, patients with type 2 diabetes.
Table 2.
Model Parameters
|
kFFA, min−1 |
SIFFA, min−1 per pmol/L 10−4 |
|||
|---|---|---|---|---|
| ND | T2D | ND | T2D | |
| B | 0.030 | 0.032 | 1.16 | 0.86 |
| (0.023–0.034) | (0.018–0.041) | (0.68–2.19) | (0.63–2.41) | |
| L | 0.022# | 0.015*§ | 0.85 | 0.73 |
| (0.017–0.028) | (0.008–0.021) | (0.56–2.62) | (0.35–1.10) | |
| D | 0.020# | 0.019 | 1.43 | 1.09 |
| (0.016–0.029) | (0.016–0.024) | (0.51–3.46) | (0.60–1.53) | |
Median and (25th–75th) percentile of estimated parameters during breakfast (B), lunch (L), and dinner (D) in ND and T2D subjects (*P < 0.01 vs. ND; #P < 0.05 vs. B; §P < 0.05 vs. B and D). kFFA, FFA fractional disposal rate (min−1); ND, obese nondiabetic patients; SIFFA, adipose tissue insulin sensitivity (min−1 per pmol/L 10−4); T2D, patients with type 2 diabetes.
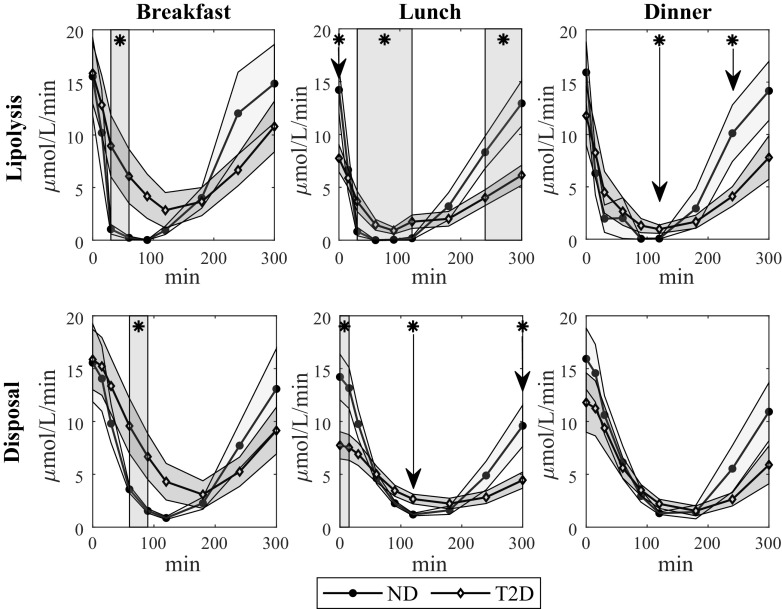
FFA lipolysis and disposal were estimated using Eqs. 7 and 9. Time courses at breakfast, lunch, and dinner are shown in Fig. 5, for ND and T2D. Briefly, lipolysis was significantly lower in ND than T2D between 30 and 60 min at breakfast, between 30 and 120 min at lunch (although it was significantly higher before meal ingestion), and at 120 min at dinner. FFA disposal was significantly lower in ND than T2D between 60 and 90 min at breakfast and at 120 min at lunch (although it was significantly higher before meal ingestion).
Figure 5.
Mean time course of FFA lipolysis (top), and disposal (bottom) during breakfast (left), lunch (middle), and dinner (right) in ND (continuous line with circles) and T2D subjects (continuous line with diamonds). Gray areas represent means ± SE intervals. *P < 0.005 according to Student’s t test. FFA, free fatty acid; ND, obese nondiabetic patients; T2D, patients with type 2 diabetes.
Calculated TL, %SL, TD, and %SD and the results of the statistical comparison are reported in Table 3. In summary, TL was significantly lower and %SL was higher in ND than T2D; %SD was also significantly higher in ND than T2D, whereas TD was not. TL tended to decrease during the day in T2D and, at lunch, it was significantly lower than breakfast, whereas TD tended to increase during the day in ND, with dinner significantly higher than breakfast.
Table 3.
Parameters characterizing lipolysis and disposal daily pattern in ND and T2D
| Lipolysis | TL, Min |
%SL (%) |
||||
|---|---|---|---|---|---|---|
| ND | T2D | P Value | ND | T2D | P Value | |
| B | 39 ± 6 | 102 ± 13 | 0.002 | 83 ± 2% | 69 ± 4% | 0.007 |
| L | 36 ± 4 | 78 ± 11# | 0.001 | 87 ± 2% | 69 ± 5% | 0.002 |
| D | 38 ± 6 | 84 ± 13 | 0.005 | 87 ± 3% | 75 ± 4% | 0.021 |
| Disposal | TD, min |
%SD(%) |
||||
|---|---|---|---|---|---|---|
| ND | T2D | P Value | ND | T2D | P Value | |
| B | 143 ± 11 | 176 ± 14 | 0.07 | 68 ± 2% | 53 ± 3%, | 0.001 |
| L | 159 ± 10 | 184 ± 14 | 0.16 | 64 ± 2% | 40 ± 4%§ | <10−4 |
| D | 173 ± 10# | 192 ± 13 | 0.27 | 63 ± 2% | 52 ± 3% | 0.008 |
Means ± SE of the calculated times of the maximum suppression of lipolysis (TL) and disposal (TD) and percent suppression of lipolysis (%SL) and disposal (%SD) at breakfast (B), lunch (L), and dinner (D) in ND and T2D subjects (#P < 0.05 vs. B, §P < 0.05 vs. B and D). Bold values are used to highlight statistically significant P values (< 0.05). ND, obese nondiabetic patients; %SL, lipolysis percentage of suppression (%); %SD, disposal percentage of suppression (%); TD, time of maximum suppression FFA disposal (min); T2D, patients with type 2 diabetes.
DISCUSSION
Free fatty acids play an essential role in the human metabolism by providing an alternative source of energy in fasting conditions. However, when FFAs levels are excessive, they can impair glucose-insulin regulation, e.g., by affecting glucose production (3–7) and disposal by skeletal muscles (1, 2), and also by interfering with insulin signaling (8, 9), which can lead to insulin resistance and contribute to the development and progression of type 2 diabetes. On the other hand, several hypothesis were formulated on how insulin (10–12) and glucose (13–15) modulate FFA turnover.
A detailed understanding of the FFA kinetics and their interactions with glucose and insulin is crucial for assessing the complex mechanisms underlying glucose-insulin regulation. Given the intricate relationship among FFAs, glucose and insulin, mathematical modeling can provide a powerful tool to quantitatively and comprehensively describe the dynamics of such interactions.
The most recent works on this topic are those by Periwal et al. (16) by Stefanovski et al. (17), which proposed mathematical models to assess the kinetics of FFAs and their relationship with insulin and/or glucose, during an IVGTT. However, the rapid perturbation due to glucose intravenous infusion produces nonphysiological glucose and insulin dynamics. The only mathematical model to assess FFA kinetics during an OGTT was that developed by Boston et al. (18), which included a remote glucose action on FFA disposal. Such hypothesis is controversial in the literature. Moreover, the authors reported that this model had poor performance during a MTT and this was confirmed by our results.
The original contribution of this work was the development of a simple mathematical model to evaluate FFA kinetics after a physiological test, like OGTT or MTT, and its use in ND and T2D individuals to assess possible differences in lipolysis and FFA disposal and their diurnal pattern.
We tested seven models of different complexity, including three of the literature (16–18), as per good modeling practice. They fitted the data satisfactorily, but model parameters were estimated with poor precision in 17 of the 18 ND and 14 of the 16 T2D (Model 1), in 4 of the 18 ND and 3 of the 16 T2D (Model 2), and in 11 of the 18 ND and 12 of the 16 T2D (Model 3). We hypothesized that both Model 1 and 3 had too many degrees of freedom, which led to data overfitting and to an imprecise estimation of the model parameters in many subjects. To overcome this issue, we also tested a version of the models including a steady state constraint at time 0 min (the time of glucose ingestion). Unfortunately, despite doing so we reduced the number of model parameters by one, this did not improve the model ability to precisely estimate the parameters as hoped (not show). Concerning Model 2, we speculated that its inability to provide precise parameter estimates could be due either to the absence of a steady-state constraint in t = 0 or to the assumption that insulin action is delayed with respect to plasma insulin, likely not verified when insulin rise is smoother, like during a MTT, or both. Therefore, we also tested a model introducing the steady-state constraint and a model assuming that insulin acts directly on lipolysis instead of through a remote compartment. However, this did not solve the a posteriori identifiability issues of such model (not shown).
Other models were tested, two implementing the “glucose-FFA cycle reversed” theory proposed by Sidossis et al. (15) (Model 4 and 5), one assuming that insulin immediately suppresses FFA lipolysis and glucose does not affect FFA disposal (Model 6), and one describing the lipolytic effect of hyperglycemia, reported by Szkudelski et al. (13) and Botion et al. (14) (Model 7). The systematic model comparison suggested that Model 6 was the model of choice for both ND and T2D, since it was the most parsimonious one (Table 1). However, this does not imply that FFA and glucose have independent metabolism, but simply that, during a MTT, insulin plays the major role in controlling FFA metabolism and this can hide glucose action.
We then used the selected model to assess if, and to what extent, lipolysis and FFA disposal differed in ND and T2D and if such differences were consistent through the day. Model-based results suggested that, after an overnight fast, FFA production was similar in ND and T2D; however, after breakfast, the suppression of lipolysis was much pronounced and faster in ND than T2D, while, at variance with T2D, in ND lipolysis came back to basal more rapidly. This explained while prelunch lipolysis was lower in T2D than ND. The same different dynamic was found also after lunch and dinner. Given that we did not find any significant difference between SIFFA in ND and T2D, we concluded that the impaired suppression in FFA lipolysis observed in T2D is attributable to the different insulin exposure, which was indeed significantly higher in ND than T2D in the first 3 h after breakfast, lunch, and dinner. As further confirmation of this hypothesis, in our previous study (19), we reported that both beta-cell responsivity to glucose and disposition index were significantly lower in T2D subjects than in ND subjects throughout the day.
Similarly, after an overnight fast, FFA disposal was similar in ND and T2D; however, after breakfast, the fall in FFA disposal was much more pronounced and slightly faster in ND than T2D, while, at variance with T2D, in ND, FFA disposal came back to basal more rapidly. This explained while prelunch disposal was lower in T2D than ND. The same different dynamic was found also after lunch and dinner. Finally, the fractional FFA disposal rate, , was significantly higher in ND than T2D at lunch, but similar at B and D in the two groups. Taken together, these results suggest that the higher FFA concentration in T2D increases FFA disposal, but is likely not enough to compensate the higher lipolysis. If this derangement plays a major role in the onset and progression of T2D remains to be ascertain.
The main limitation of this study is the limited number of samples per subject available. Unfortunately, we could not take more samples because of the maximum blood volume constraint. We acknowledge that a more frequent sampling might have favored a more complex model, including some interesting physiological features (e.g., Model 1 or Model 7). Therefore, it is worth stressing that Model 6 performed best, always providing precise meaningful parameter estimates, in the experimental conditions of our protocol.
Another shortcoming of the study is that it was not primarily designed to assess possible statistical differences in model parameters, e.g., SIFFA. As a matter of fact, the power analysis revealed that one would have had studied 284 subjects to detect a significant difference in this parameter between ND and T2D with a power of 0.8 and an error probability of 0.05.
Another drawback of this study is that the experimental settings precluded us to estimate FFA volume of distribution (to do that, one would need an infusion/injection of lipids in the vein and/or a tracer experiment). To the best of our knowledge, Jensen et al. (29) studied FFA kinetics in dogs and found a volume of distribution of 90 mL/kg, but there are no studies reporting values of such parameters in humans.
Future work will include testing the model on more frequently sampled FFA profiles and possibly validating the model using tracer dilution techniques.
In conclusion, we proposed a novel model to accurately quantify insulin antilipolytic effect in ND and T2D subjects and use it to assess the diurnal pattern of FFA lipolysis and disposal in response to a meal intake. This model can be easily used to assess FFA kinetics by investigators who perform a MTT and measure FFA and insulin concentrations. Given that the model assumes an antilipolytic action of insulin, as by-product, one can use it to quantify SIFFA, which represents the adipose tissue sensitivity insulin.
DATA AVAILABILITY
Data will be made available upon reasonable request.
GRANTS
This study was supported by National Institutes of Diabetes and Digestive and Kidney Diseases DK029953 (to R.B.) and DK085516 (to A.B.).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
A.B., C.C., R.B., and C.D.M. conceived and designed research; Y.Y. and R.B. performed experiments; J.B. analyzed data; J.B., J.M., A.B., C.C., R.B., and C.D.M. interpreted results of experiments; J.B. and C.D.M. prepared figures; J.B. and C.D.M. drafted manuscript; J.M., A.B., C.C., and R.B. edited and revised manuscript; J.B., Y.Y., J.M., A.B., C.C., R.B., and C.D.M. approved final version of manuscript.
REFERENCES
- 1. Randle PJ, Garland PB, Hales CN, Newsholme EA. The glucose fatty-acid cycle. Its role in insulin sensitivity and the metabolic disturbances of diabetes mellitus. Lancet 1: 785–789, 1963. doi: 10.1016/S0140-6736(63)91500-9. [DOI] [PubMed] [Google Scholar]
- 2. Roden M. How free fatty acids inhibit glucose utilization in human skeletal muscle. News Physiol Sci 19: 92–96, 2004. doi: 10.1152/nips.01459.2003. [DOI] [PubMed] [Google Scholar]
- 3. Roden M, Price TB, Perseghin G, Petersen KF, Rothman DL, Cline GW, Shulman GI. Mechanism of free fatty acid-induced insulin resistance in humans. J clin Invest 97: 2859–2865, 1996. doi: 10.1172/JCI118742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Roden M, Stingl H, Chandramouli V, Schumann WC, Hofer A, Landau BR, Nowotny P, Waldhäusl W, Shulman GI. Effects of free fatty acid elevation on postabsorptive endogenous glucose production and gluconeogenesis in humans. Diabetes 49: 701–707, 2000. doi: 10.2337/diabetes.49.5.701. [DOI] [PubMed] [Google Scholar]
- 5. Boden G, Chen X, Capulong E, Mozzoli M. Effects of free fatty acids on gluconeogenesis and autoregulation of glucose production in type 2 diabetes. Diabetes 50: 810–816, 2001. doi: 10.2337/diabetes.50.4.810. [DOI] [PubMed] [Google Scholar]
- 6. Chen X, Iqbal N, Boden G. The effects of free fatty acids on gluconeogenesis and glycogenolysis in normal subjects. J clin Invest 103: 365–372, 1999. doi: 10.1172/JCI5479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Lam TK, Carpentier A, Lewis GF, van de Werve G, Fantus IG, Giacca A. Mechanisms of the free fatty acid-induced increase in hepatic glucose production. Am J Physiol Endocrinol Metab 284: E863–E873, 2003. doi: 10.1152/ajpendo.00033.2003. [DOI] [PubMed] [Google Scholar]
- 8. Itoh Y, Kawamata Y, Harada M, Kobayashi M, Fujii R, Fukusumi S, Ogi K, Hosoya M, Tanaka Y, Uejima H, Tanaka H, Maruyama M, Satoh R, Okubo S, Kizawa H, Komatsu H, Matsumura F, Noguchi Y, Shinohara T, Hinuma S, Fujisawa Y, Fujino M. Free fatty acids regulate insulin secretion from pancreatic beta cells through GPR40. Nature 422: 173–176, 2003. doi: 10.1038/nature01478. [DOI] [PubMed] [Google Scholar]
- 9. Boden G. Free fatty acids and insulin secretion in humans. Curr Diab Rep 5: 167–170, 2005. doi: 10.1007/s11892-005-0004-5. [DOI] [PubMed] [Google Scholar]
- 10. Arner P, Bolinder J, Engfeldt P, Ostman J. The antilipolytic effect of insulin in human adipose tissue in obesity, diabetes mellitus, hyperinsulinemia, and starvation. Metabolism 30: 753–760, 1981. doi: 10.1016/0026-0495(81)90020-2. [DOI] [PubMed] [Google Scholar]
- 11. Zhao J, Wu Y, Rong X, Zheng C, Guo J. Anti-lipolysis induced by insulin in diverse pathophysiologic conditions of adipose tissue. Diabetes Metab Syndr Obes 13: 1575–1585, 2020. doi: 10.2147/DMSO.S250699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Choi SM, Tucker DF, Gross DN, Easton RM, DiPilato LM, Dean AS, Monks BR, Birnbaum MJ. Insulin regulates adipocyte lipolysis via an Akt-independent signaling pathway. Mol Cell Biol 30: 5009–5020, 2010. doi: 10.1128/MCB.00797-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Szkudelski T, Szkudelska K. Glucose as a lipolytic agent: studies on isolated rat adipocytes. Physiol Res 49: 213–217, 2000. [PubMed] [Google Scholar]
- 14. Botion LM, Green A. Long-term regulation of lipolysis and hormone-sensitive lipase by insulin and glucose. Diabetes 48: 1691–1697, 1999. doi: 10.2337/diabetes.48.9.1691. [DOI] [PubMed] [Google Scholar]
- 15. Sidossis LS, Wolfe RR. Glucose and insulin-induced inhibition of fatty acid oxidation: the glucose-fatty acid cycle reversed. Am J Physiol Endocrinol Physiol 270: E733–E738, 1996. doi: 10.1152/ajpendo.1996.270.4.E733. [DOI] [PubMed] [Google Scholar]
- 16. Periwal V, Chow CC, Bergman RN, Ricks M, Vega GL, Sumner AE. Evaluation of quantitative models of the effect of insulin on lipolysis and glucose disposal. Am J Physiol Regul Integr Comp Physiol 295: R1089–R1096, 2008. doi: 10.1152/ajpregu.90426.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Stefanovski D, Punjabi NM, Boston RC, Watanabe RM. Insulin action, glucose homeostasis and free fatty acid metabolism: insights from a novel model. Front Endocrinol (Lausanne) 12: 625701, 2021. [Erratum in Front Endocrinol (Lausanne) 12: 789390, 2021]. doi: 10.3389/fendo.2021.625701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Boston RC, Moate PJ. NEFA minimal model parameters estimated from the oral glucose tolerance test and the meal tolerance test. Am J Physiol Regul Integr Comp Physiol 295: R395–R403, 2008. doi: 10.1152/ajpregu.90317.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Yadav Y, Romeres D, Cobelli C, Dalla Man C, Carter R, Basu A, Basu R. Impaired diurnal pattern of meal tolerance and insulin sensitivity in type 2 diabetes: implications for therapy. Diabetes 72: 223–232, 2023. doi: 10.2337/db22-0238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Basu A, Dalla Man C, Basu R, Toffolo G, Cobelli C, Rizza RA. Effects of type 2 diabetes on insulin secretion, insulin action, glucose effectiveness, and postprandial glucose metabolism. Diabetes Care 32: 866–872, 2009. doi: 10.2337/dc08-1826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Basu R, Shah P, Basu A, Norby B, Dicke B, Chandramouli V, Cohen O, Landau BR, Rizza RA. Comparison of the effects of pioglitazone and metformin on hepatic and extra-hepatic insulin action in people with type 2 diabetes. Diabetes 57: 24–31, 2008. doi: 10.2337/db07-0827. [DOI] [PubMed] [Google Scholar]
- 22. Bellu G, Saccomani MP, Audoly S, D'Angiò L. DAISY: a new software tool to test global identifiability of biological and physiological systems. Comput Methods Programs Biomed 88: 52–61, 2007. doi: 10.1016/j.cmpb.2007.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Cobelli C, Carson ER. Introduction to Modeling in Physiology and Medicine. Cambridge, MA: Academic Press, 2019. [Google Scholar]
- 24.MATLAB. R2021a. Natick, Massachusetts: The Matwork Inc, 2021. [Google Scholar]
- 25. Wald A, Wolfowitz J. On a test whether two samples are from the same population. Ann Math Statist 11: 147–162, 1940. doi: 10.1214/aoms/1177731909. [DOI] [Google Scholar]
- 26. Akaike H. A New Look at the Statistical Model Identification. New York, NY: Springer, 1974. doi: 10.1007/978-1-4612-1694-0_16. [DOI] [Google Scholar]
- 27. Basu R, Di Camillo B, Toffolo G, Basu A, Shah P, Vella A, Rizza R, Cobelli C. Use of a novel triple-tracer approach to assess postprandial glucose metabolism. Am J Physiol Endocrinol Physiol 284: E55–E69, 2003. doi: 10.1152/ajpendo.00190.2001. [DOI] [PubMed] [Google Scholar]
- 28. Anderson TW, Darling DA. A test of goodness-of-fit. J Am Stat Assoc 49: 765–769, 1954. doi: 10.2307/2281537. [DOI] [Google Scholar]
- 29. Jensen MD, Heiling V, Miles JM. Measurement of non-steady-state free fatty acid turnover. Am J Physiol Endocrinol Physiol 258: E103–E108, 1990. doi: 10.1152/ajpendo.1990.258.1.E103. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available upon reasonable request.