Numerical simulation and exergy analysis of a single-stage GM cryocooler

Abstract

Improving the efficiency of the GM cryocoolers is of great importance for energy saving and CO₂ emission reduction due to the large amount of cryocoolers installed in the emerging fields of semiconductor manufacture and High Temperature Superconductors (HTS) cooling. Previous studies mainly focused on the losses analysis and optimization on the part of cold head, but the details of losses distribution in the parts of compressor and rotary valve were seldom carried out. In this paper, a numerical model of a single stage GM cryocooler including compressor, rotary valve and expander is built, and the feasibility of the model is verified by the experimental results. The losses characteristics of the whole cryocooler are studied based on the exergy analysis method with the help of the numerical model. The results indicate that the main losses are occurred in compressor and rotary valve, the value of exergy loss in compressor decrease with the cooling temperature, and accounts for more than 60% at all cooling temperature. The loss in rotary valve accounts for about 20% of the input electric power, and it does not significantly vary at different cooling temperatures. Pressure drop dominates the loss in the compressor and rotary valve. The insufficient heat exchange between the working gas and regenerative material is the main loss in regenerator, and the losses in regenerator increase significantly with the decrease of cooling temperature when the compressor and rotary valve are fixed. This study provides useful guides for the optimization of GM-type cryocoolers.

Highlights

• •A Sage model is established to analyze exergy loss distribution in GM cryocooler.
• •Compressor accounts for more than 60% of losses at all cooling temperature.
• •GM-type cryocooler compressor's output performance contour map is first presented.
• •Rotary valve accounts for about 20% losses and keeps constant with temperature.

Nomenclature

a

Fitting coefficient,

A

Flow area, m²

C_d

Discharge coefficient,

$\dot{E}$

Rate of exergy, W

F

Axial pressure gradient, Pa/m

F_R

Flow area multiplier,

F_min

Minimum flow area multiplier,

g

Specific Gibbs free energy, J/kg

G

Gibbs free energy, J

h

Specific enthalpy, J/kg

$\dot{m}$

Mass flow rate, kg/s

Ntnode

Time node,

P

Pressure, Pa

$\dot{q}$

Heat flux, W/m²

${\dot{Q}}_c$

Cooling power, W

s

Specific entropy, $\mathrm{J}/\left(\mathrm{k}\mathrm{g}\cdot \mathrm{K}\right)$

S

Entropy, $\mathrm{J}/\mathrm{K}$

t

Time, s

T

Temperature, K

u

Velocity, m/s

${\dot{W}}_e$

Input electric power, W

$x_A$

Relative displacement amplitude, m

δ

Width of gas gap, m

η

Compression efficiency

ρ

Density, $\mathrm{k}\mathrm{g}/{\mathrm{m}}^3$

λ

Thermal conductivity, $\mathrm{W}/\left(\mathrm{m}\cdot \mathrm{K}\right)$

Subscripts

h

High-pressure

l

Low-pressure

c

Cold head

o

Orifice

fric

Friction

leak

Leakage

s

Shuttle

com

Compressor

rv

Rotary valve

dv

Discharge valve

sv

Suction valve

1. Introduction

Benefiting from the compact structure, high reliability and low cost, GM type cryocoolers (including GM cryocoolers and GM pulse tube cryocoolers) are widely used in the field of superconducting cooling [1,2], dilution refrigerator (DR) [3], magnetic resonance imaging (MRI), scientific instruments [4] and semiconductor manufacturing [[5], [6], [7]]. Fig. 1 shows the FOM (Figure of Merit) of on-sale GM type cryocoolers produced by Cryomech and SHI (Sumitomo Heavy Industry), as shown in the figure, the efficiency of GM cryocooler is much higher than that of GM pulse tube cryocooler (PTC), especially at high cooling temperature. The comparison indicates that the loss distribution of the two types of GM cryocoolers is different, and the high efficiency and compact structure makes the GM cryocooler more widely used.

Fig. 1.

The comparison of FOM between GM cryocooler and GM PTC at different temperature.

According to the survey of Demko in 2002 [8], a higher than 30% relative Carnot efficiency of the cryocooler at 80 K is essential for the large scale commercial application of HTS. Unfortunately, the efficiency of the current cryocoolers is still below the requirement. Furthermore, cryopumps are necessary to obtain high vacuum condition for the fabrication of semi-conductor devices, more than 2000 cryopumps which adopts GM cryocoolers as cold sink to condensate the residual gas inside the chamber is installed in a 12-inch chip production line, so, improving the efficiency of the GM cryocoolers is of great importance for energy saving and CO₂ emission reduction.

To improve the efficiency of GM cryocoolers, many works have been carried out from the aspects of numerical calculation and experimental test [9]. Wang [10] calculated the cooling performance of the second stage of a two-stage GM cryocooler (RGD 5/100) produced by Leybold. The following conditions were set: The energy equation and continuity equation were used as the governing equations, the warm end and cold end of the second regenerator were fixed at 40 K and 10 K respectively, and the axial heat conduction and the pressure drop in the regenerator were ignored. The calculated results showed that there was a temperature plateau near the cold end of the regenerator, and the mass flow at the warm end accounted for only 58% of that at the cold end. In 2012, Xu et al. [[11], [12], [13]] from SHI proposed a numerical simulation method that could predict the cooling capacity of two-stage GM cryocooler. This method can calculate shuttle loss and radiation loss besides other losses in regenerator like real gas loss, regenerative loss, pump gas loss, heat conduction loss and leakage loss.

In 2015, Xu and T. Morie [14] used the method to simulate the displacement of displacer, and proposed a novel scotch yoke which can enlarge the expansion cycle, while shorten the compression cycle, the experiment indicated that the cooling power of the first stage was increased by 10% with the new scotch yoke. In 2017, Zhi et al. [15] analyzed the performance of a single-stage GM cryocooler made by SHI through CFD simulation. SST k-ε model and PISO principle were used for turbulence calculation and pressure-velocity coupling separately, the pressure boundary conditions were given according to the experimental data. The calculation results showed that large temperature gradient mainly distributed in the middle of the regenerator, and the temperature oscillation in one cycle was up to 128 K, thus the irreversible heat exchange loss in the regenerator was large. The simulation results suggested that regenerative materials with high porosity placed in the warm end of regenerator can reduce the pressure drop. In 2019, Panda et al. [16] introduced the experimental empirical correlation to represent the fluid flow and heat exchange characteristics in the regenerator based on Xu's work [12]. The author further studied the shape of orifice and waiting time in rotary valve, which indicated that smaller waiting time and Gaussian-shaped port can acquire more PV work in the expansion chamber, so as to obtain higher cooling power.

Besides the GM cryocoolers, Liu et al. [17,18] established a Sage numerical model of GM PTC, and investigated the loss distribution of the loss inside the whole cryocooler. As shown in Fig. 1, the loss mechanism in GM cryocooler is much different from that of GM PTC, so it is necessary to further analyze the loss distribution in GM cryocooler. Some other Sage model were also developed to predict the performance GM PTCs [19,20].

From the above literature survey, we can know that the studies of GM cryocoolers were mainly focused on the analysis and optimization of cold head by the means of numerical simulation and experimental test. The loss inside the compression unit (compressor and rotary valve) and the coupling between the compression unit and cold head were seldom carried out. A comprehensive numerical model consists the compression unit and cold head of GM cryocooler also lack due to the difficulty of the dynamic behavior of the displacer and the unknown coupling mechanism of the compression unit and cold head.

In this article, a numerical model of the single stage GM cryocooler using Sage V10 software (copyright by Gedeon Associates) is developed first time to the knowledge of the authors, the components of the compression unit and cold head are included in the model. The feasibility of the model is verified by the experimental results of a GM cryocooler from CSIC Pride Cryogenics. The exergy loss in the whole cryocooler is analyzed in detail based on the numerical model, the results would helpful for the design and optimization of GM-type cryocoolers.

2. Numerical model of the cryocooler

GM cryocooler is mainly composed of compressor, rotary valve and cold head. The compressor provides high-pressure working medium (without oil), and the rotary valve converts the DC flow into low-frequency alternating flow to drive the cold head.

2.1. Model of compressor

The compressor is one of the most important components in GM cryocooler, and the output performance of the compressor (volume flow rate, efficiency et al.) is essential for the development of the numerical model. To get an accurate description of the compressor, a compressor test platform shown in Fig. 2 was established and used to obtain the flow characteristics and input electric power of the compressor. A S603DH compressor produced by Hitachi was tested in this study, the suction and discharge pressures are measured by GE UNIK5000 with an accuracy of 3 kPa. The mass flow is attained by TELEDYNE HASTINGS HFM305 flow-meter with an accuracy of 25 slm.

Fig. 2.

Schematic diagram of compressor test platform.

As the compressed helium is cooled to ambient temperature by oil and water, therefore, both the suction and discharge temperatures of the compressor are equal to room temperature [21]. The volume flow of the compressor under standard condition is only related to the suction pressure. Fig. 3, Fig. 4 show the flow characteristic and the input electric power of S603DH with different suction pressures, respectively. As Fig. 3 shows, the blue broken line is the standard volume flow rate obtained from the specification of S603DH manual [22], and the red scatters show the data obtained by experiment.

Fig. 3.

Comparison of flow characteristic curve.

Fig. 4.

Comparison of input electric power.

The blue broken line in Fig. 3 is the standard input electric power from the manual, and the red scatters is the experimental data. The charge pressure in the experimental system is 1.53 MPa. When the suction pressure increases, the discharge pressure decreases from 2.08 MPa to 1.89 MPa, and the pressure ratio also decreases. From Fig. 3, Fig. 4, we can see that the flow characteristic and input electric power of the experiment are in well agreement with that provided by the technical manual.

The data of the experimental test were used to calculate the exergy loss of the compressor, the flow characteristic and input power (${\dot{W}}_e$) of S603DH can be obtained by linear fit from Fig. 3, Fig. 4:

$$\dot{m}=6.0887\cdot P_l-0.021\left(\mathrm{g}/\mathrm{s}\right)$$ (1)

$${\dot{W}}_e\left(P_h\right)=a_1\cdot {P_l}^2+a_2\cdot P_l+a_3\left(\mathrm{W}\right)$$ (2)

where a₁, a₂, a₃ are constants related to discharge pressure P_h, P_l is the suction pressure. The coefficients (a₁, a₂ and a₃) of the S603DH compressor under different discharge and suction pressures are obtained from the specification provided by Hitachi. The following formula to define rate of exergy ${\dot{E}}_{com}$ produced by compressor [23]:

$${\dot{E}}_{com}=\dot{m}\left\{\left[h\left(P_h,T_0\right)-h\left(P_l,T_0\right)\right]-T_0\left[s\left(P_h,T_0\right)-s\left(P_l,T_0\right)\right]\right\}$$ (3)

where h and s are the enthalpy and entropy at each state, and T₀ is the ambient temperature. Then the compression efficiency is defined by the following equation:

$$\eta ={\dot{E}}_{com}/{\dot{W}}_e$$ (4)

The efficiency and volume flow rate of the S603DH compressor at different discharge pressure and suction pressure is calculated by equations (1), (2), (3) and the results is shown in Fig. 5. The black solid line in the figure refers to the compression efficiency of the compressor defined by equation (4). The compression efficiency varies from 39% to 50% when the suction pressure is 0.3–0.7 MPa and the discharge pressure is 1.7–2.5 MPa. When the discharge pressure is fixed, the higher the suction pressure, the higher the efficiency. The electric input power (the blue solid line) varies between 4.5–7.1 kW under different suction and discharge pressures. During the cool-down process, the input electric power changes greatly with work conditions, and the maximum exergy produced by S603DH (the red solid line) is about 3.4 kW. The input power and exergy are positively correlated with discharge and suction pressures, so the high suction pressure area is the ideal working area of the compressor to obtain high efficiency and exergy.

Fig. 5.

Contour map of the output performance of S603DH compressor.

According to the compressor's efficiency contour map, for an ideal compressor, the working condition of the optimal compression efficiency is consistent with that of the maximum output exergy. Fig. 5 also reveals that a design method which consider the coupling between the high efficiency working zones of compressor with the cold head may be useful for the further improvement of GM cryocoolers' performance. As the topic of this paper is about the operating characteristics of key components and exergy losses distributed in the whole cryocooler, and the coupling method is very complicated [24,25], so the coupling method will be investigated in another paper.

2.2. Model of rotary valve

Rotary valve, changing DC flow into low-frequency alternating flow, is a key component connecting compressor and cold head [26]. This switching function is accomplished by the discharge and suction valves inside the rotary valve. Fig. 6 shows the mass flow and pressure inside the rotary valve during the three periods of intake (Fig. 6(a)), peace (Fig. 6(b)) and exhaust (Fig. 6(c)). Subscripts h, l and c refer to the pressure and mass flow in the high-pressure chamber, low-pressure chamber and cold head, respectively. It is specified that the direction of the red arrow is positive, while the direction of the blue arrow is negative.

Fig. 6.

Flow diagram of rotary valve.

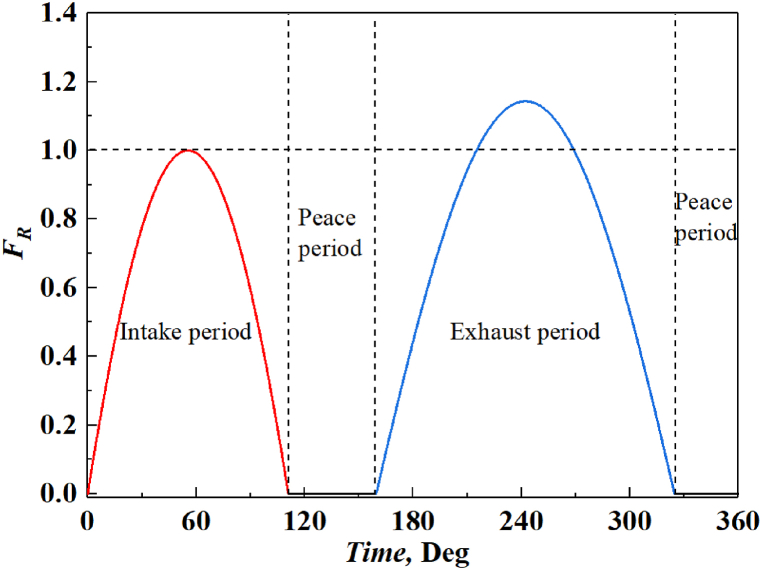
The working helium enters and exits the cold head during the intake and exhaust periods [18], and the sequence of the rotary valve is shown in Fig. 7. F_R is defined as flow area multiplier of the rotary valve, the valve changes from closed to fully open when F_R changes from 0 to 1. During the intake period and the exhaust period, the discharge valve and the suction valve are respectively opened, then the expander is connected with the high-pressure side or low-pressure side of the compressor. During peace period, the two valves are fully closed and the expander is disconnected from the compressor. However, the valves cannot be completely closed due to the existence of dynamic seals, F_min is defined as the minimum flow area multiplier in Sage, with a recommended value of 1%∼3%.

Fig. 7.

The sequence of rotary valve.

The discharge valve and suction valve in the rotary valve can be treated as a sharp-edged orifice. When the fluid flows through the sharp-edged orifice, the relationship between the mass flow and the pressure difference before and after the orifice are nonlinear, which can be expressed [27] as equation (5):

$$\dot{m}=-C_d{A}_o{\rho }_e\Delta P$$ (5)

where C_d is the discharge coefficient, ρ_e is the local density of the working gas. The rotary valve is a time-dependent valve whose flow area multiplier is continuously changing. When the rotary valve is opened, the mass flow in the valve is shown as equation (6):

$$\dot{m}=-F_R{C}_d{A}_o{\rho }_e\Delta P$$ (6)

When the discharge valve or suction valve in the rotary valve is closed, the leakage helium ${\dot{m}}_{leak}$ through the valve is expressed as equation (7):

$${\dot{m}}_{leak}=-F_{\mathit{min}}{C}_d{A}_o{\rho }_e\Delta P$$ (7)

Only the discharge valve is opened during the intake period, the leakage helium through the low-pressure buffer ${\dot{m}}_{leak}$ is deified as equation (8):

$${\dot{m}}_{leak}={\dot{m}}_l={\dot{m}}_h-{\dot{m}}_c,\mathrm{I}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{k}\mathrm{e}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{d}$$ (8)

The suction valve opens while the discharge valve closes during the exhaust period. The leakage helium through the high-pressure buffer is pressed as equation (9):

$${\dot{m}}_{leak}={\dot{m}}_h={\dot{m}}_l-{\dot{m}}_c,\mathrm{E}\mathrm{x}\mathrm{h}\mathrm{a}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{d}$$ (9)

The discharge valve and the suction valve are both closed during the peace period, the leakage helium is approximately shown as equation (10):

$${\dot{m}}_{leak}\approx {\dot{m}}_h={\dot{m}}_l,\mathrm{P}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{d}$$ (10)

Regardless of the working state, the leakage helium in the rotary valve is defined by the following equation (11):

$${\dot{m}}_{leak}=\min \left({\dot{m}}_h,{\dot{m}}_l\right)$$ (11)

Based on equations (8), (9), (10), (11), the leakage flow rate in the rotary valve ${\dot{m}}_{leak}$ during the whole operating period is well defined.

2.3. Numerical model of the single-stage GM cryocooler

With the flow characteristic and the sequence settings introduced by the previous contents, a numerical model of single-stage GM cryocooler is established by Sage software. The parameters of the simulated cryocooler and the interface of the model are shown in Table 1 and Fig. 8, respectively.

Table 1.

The structure and operation parameters of GM cryocooler.

Regenerator	phosphor bronze 150# mesh screen 72.5 × 96.5 mm (D × L)
Displacement	25 mm
Phasor difference between displacer and rotary valve	35.5°
Ambient temperature	300 K
Cooling temperature	22.2 K、29.1 K、37.8 K, 50.0 K、67.8 K
Operation temperature	1 Hz
Charging pressure	1.6 MPa

Fig. 8.

Sage model interface of the GM cryocooler.

3. Experimental verification

3.1. Performance test of single-stage GM cryocooler

A single-stage GM cryocooler used for high temperature superconducting, with a cooling capacity of about 54 W@40 K, is used in this experimental study. The schematic and photo of the cryocooler's performance test system are showed in Fig. 9(a) and (b). Three high-frequency response pressure sensors (M5HB produced by Keller) are applied to monitor the discharge pressure P_h suction pressure P_l and the pressure of cold head P_c. P_c is installed at the hot end of the cold head (Fig. 9(c)). The cooling temperature is measured by silicon diode temperature sensor manufactured by Lakeshore, its test accuracy is about ±32 mK.

Fig. 9.

GM cryocooler's performance test system: (a) schematic diagram of the system, (b) photograph of the system, (c) high frequency response pressure sensor at warm end of the expander.

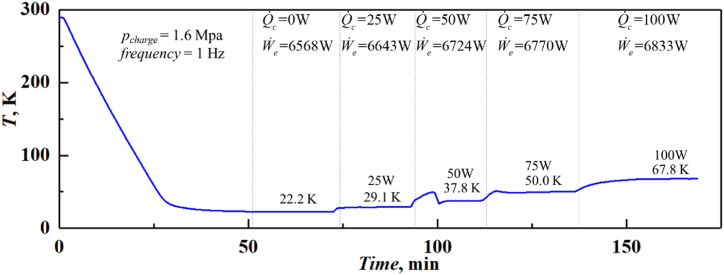
Fig. 10 gives the cool down curve and performance under a charging pressure of 1.6 MPa and an operation frequency of 1 Hz. From the figure, we can see that a no-load cooling temperature of 22.2 K was obtained within 50 min, and the cryocooler can provide a cooling power of 50 W and 100 W at 37.8 K and 67.8 K, respectively. With the increase of cooling temperature, the input power increases slightly.

Fig. 10.

Performance test process of the cryocooler.

3.2. Verification of sage model

The feasibility of the Sage model is verified by the experimental results, and the comparison of the numerical and experimental results is shown in Fig. 11, Fig. 12. Fig. 11 shows the comparison of discharge pressure and suction pressure obtained from theoretical calculation and experimental test at different cooling temperatures. As shown in the figure, the calculated pressure is well consistent with the experimentally tested value. The difference between suction pressure and discharge pressure increases with the cooling temperature, but the helium flow rate decreases, this may be caused by the increase of helium viscosity with temperature.

Fig. 11.

Comparison of operation pressure at different cooling temperatures.

Fig. 12.

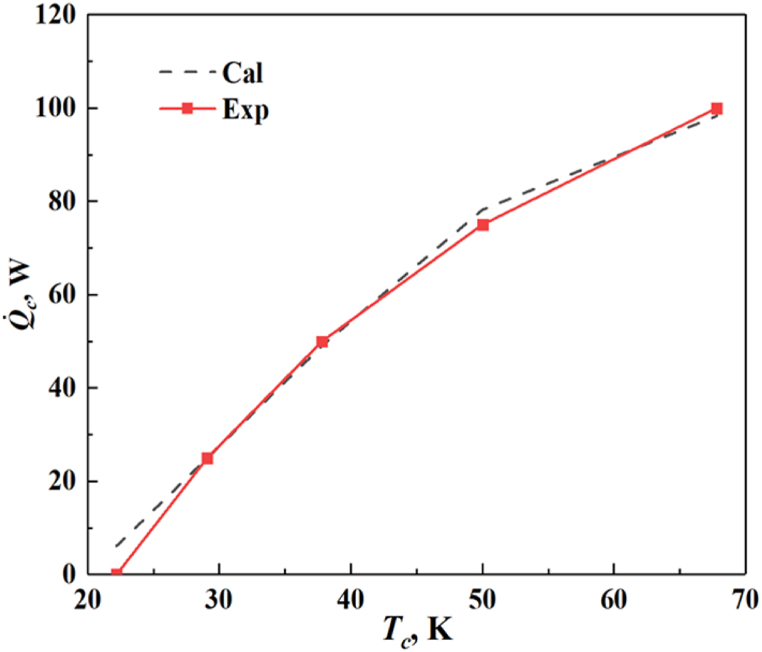
Comparison of cooling power at different cooling temperatures.

The comparison of cooling power obtained by calculating and experimental testing is depicted in Fig. 12. From the figure, we can see that a well agreement is achieved at high cooling temperature. The deviation at low cooling temperature mainly comes from the deviation of high pressure and that no insulation material was wrapped during the experiment.

Fig. 13 shows the comparison of pressure oscillation of P_h, P_l, P_c during two operation periods when the cooling temperature is 37.8 K. The solid line is the pressure oscillation in high-pressure buffer (P_h), low-pressure buffer (P_l) and inlet of the cold head (P_c). The dotted line is the pressure oscillation calculated by the numerical model. From the figure, we can see that the amplitudes of the pressures are in good agreement, and the phases of P_h and P_l are also in good agreement, but there is a small phase lag between the calculated and measured pressure waveform of P_c. Because of the exist of phase lag in displacement sensor of the displacer, the angle can't be eliminated by changing the discharge coefficient, leakage rate and other parameters of the suction and discharge valves.

Fig. 13.

Comparison of pressure wave (T_c = 37.8 K).

Based on the comparison of pressure wave and cooling capacity, the calculation result is in good agreement with the measured data. In the next sections, the numerical model is used to reveal the working mechanism of the GM cryocooler and investigate the loss distributions inside the cryocooler.

4. Exergy analysis and discussion

4.1. Exergy loss in rotary valve

The exergy loss generated in the rotary valve includes leakage loss and viscosity loss:

$${\dot{E}}_{rv}={\dot{E}}_{leak}+{\dot{E}}_{fric}$$ (12)

The exergy loss caused by leakage loss through rotary valve is:

$${\dot{E}}_{leak}=\frac{1}{\tau }\underset{0}{\overset{\tau }{\int }}\Delta Gdt=\frac{1}{Ntnode}\sum _1^{Ntnode}{\dot{m}}_{leak}\cdot \left(g_h-g_l\right)$$ (13)

Where Ntnode refers to time nodes defined in sage model. G is the Gibbs free energy [28], and the subscripts h and l represent the Gibbs free energy on the high-pressure side and low-pressure side of the compressor respectively. Exergy losses caused by non-linear flow resistance of nozzle in discharge valve and suction valve are defined as:

$${\dot{E}}_{fric,dv}=\frac{1}{\tau }\underset{0}{\overset{\tau }{\int }}\Delta Gdt=\frac{1}{Ntnode}\sum _1^{Ntnode}{\dot{m}}_c\left(g_h-g_c\right),\mathrm{i}\mathrm{f}{\dot{m}}_c>0$$ (14)

$${\dot{E}}_{fric,sv}=\frac{1}{\tau }\underset{0}{\overset{\tau }{\int }}\Delta Gdt=\frac{1}{Ntnode}\sum _1^{Ntnode}\left|{\dot{m}}_c\right|\left(g_c-g_l\right),\mathrm{i}\mathrm{f}{\dot{m}}_c<0$$ (15)

Where the subscripts dv and sv represent exergy loss in discharge valve and suction valve. The exergy loss caused by friction in rotary valve is:

$${\dot{E}}_{fric}={\dot{E}}_{fric,dv}+{\dot{E}}_{fric,sv}$$ (16)

Mass flow is necessary for the calculation of equations (12), (13), (14), (15), (16), and the mass flow through the discharge valve and the suction valve is depicted in Fig. 14 when charging pressure is 1.6 MPa, and cooling temperature is 22.2 K. The red dash line, blue dash line and the green dash line are the mass flow through the high-pressure buffer, low-pressure buffer and the warm end of cold head, respectively. From the figure, we can see that there is a small amount of helium leakage in the rotary valve along the operation period.

Fig. 14.

Mass flow in rotary valve during one cycle.

According to equation (12)∼(13), the exergy loss in the rotary valve caused by helium leakage and flow resistance at different cooling temperatures is calculated and showed in Fig. 15, the orifice diameter of the discharge and suction valves is 7 mm, and F_min is 1% in the calculation. In Fig. 15, the orange histogram represents total exergy loss calculated by sage, and the purple and green histograms represent the ${\dot{E}}_{leak}$ and ${\dot{E}}_{fric}$ calculated by the equations respectively. The exergy losses in the rotary valve are about 1.5 kW at differential cooling temperature. According to our simplified calculation, the exergy loss caused by helium leakage accounts for about 20% of the input electric power. The calculated differential pressure is slightly greater than the practical one. Therefore, the total exergy loss of the rotary valve calculated by equations is greater than that obtained by Sage.

Fig. 15.

Exergy loss in rotary valve at different cooling temperature.

As exergy loss is positively related to the mass flow and differential pressure, with the increase of cooling temperature, the pressure difference increases but the mass flow decreases, so the interaction between them leads to a little change of the total exergy loss in the rotary valve, the result is also shown in Fig. 15.

F_min is related to the manufacturing process, which determines the amount of leakage helium, a value of 1% is recommended by Sage software. Fig. 16 introduces the effect of F_min on operation pressure when the cooling temperature is fixed at 22.2 K. The red line and the blue line represent the discharge pressure and suction pressure respectively. With the increase of F_min, the leakage helium through the rotary valve increases, while the pressure difference between P_h and P_l decreases.

Fig. 16.

Effect of F_min on suction and discharge pressure.

As shown in Fig. 17, with the increase of F_min, although the exergy loss (red solid line) in the rotary valve decreases, the ratio of the loss relative to the input electric power (blue solid line) increases from 57% to 62%. Furthermore, the proportion of exergy loss caused by leakage (blue broken line) in the total exergy loss in rotary valve also increased from 16% to 43%. In order to increase the exergy entering the cold head and reduce the loss in the rotary valve, the leakage loss in the rotary valve should be reduced by improving the dynamic sealing process.

Fig. 17.

Effect of F_min on exergy loss in rotary valve.

4.2. Exergy loss in regenerator

The exergy loss in the regenerator is mainly caused by irreversible entropy generation caused by heat exchange, viscous gas, shuttle, real gas effect, etc. [28] As the real gas effect of helium is not obvious when the cooling temperature is above 20 K, so the entropy generation caused by real gas effect was ignored in this study. The entropy generation caused by the temperature difference between the solid (matrix), gas (helium) and the gas-solid can be expressed by the following formula [27]:

$$\Delta S_{\Delta \mathrm{T}}=-{\oint }_{dt}{\int }_{dv}\frac{\dot{q}\cdot \nabla T}{T^2}\text{.}$$ (17)

Where the integrand is the local rate of entropy production $\Delta S_{\Delta \mathrm{T}}$ due to heat flux $\dot{q}$ in a temperature gradient $\nabla T$, T is the local temperature. The entropy generation $\Delta S_{\Delta p}$ caused by pressure drop is related to axial pressure gradient F [27]:

$$\Delta S_{\Delta p}=-{\oint }_{dt}{\int }_{dv}\frac{uAF}{T^2}$$ (18)

where uA is the volume flow through the regenerator. The entropy generated by the shuttle gas is:

$$\Delta S_{\mathrm{s}\mathrm{h}\mathrm{u}\mathrm{t}\mathrm{t}\mathrm{l}\mathrm{e}}=-{\oint }_{dt}{\int }_{dv}\frac{{\dot{q}}_s\cdot \nabla T}{T^2}\text{.}$$ (19)

The heat flux ${\dot{q}}_s$ of gas in the gap is determined by the temperature gradient, axial length x, width of gas gap δ, gas thermal conductivity k and wall thermal conductivity factor λ [27]:

$${\dot{q}}_s={\left(x_A/\delta \right)}^2\frac{1+\lambda }{2\left(1+{\lambda }^2\right)}\left(k\frac{\partial T}{\partial x}\right)\text{.}$$ (20)

Fig. 18 shows the axial temperature distribution in the regenerator at different cooling temperatures, where position 0 refers to the warm end and position 1 refers to the cold end of the regenerator. As Fig. 18 (a) shows, there is a temperature plateau near the cold end of regenerator, the length of which extends as the cooling temperature gets lower. The specific heat capacity of matrix decreases while the specific heat capacity of helium increases with the decrease of temperature, resulting in insufficient cold storage capacity of the matrix. In order to achieve a lower cooling temperature, more matrix material is required. That means at the given length of regenerator, the exergy loss will get higher as the cooling temperature goes lower due to increasing temperature difference.

Fig. 18.

Axial distribution of (a) average temperature and (b) temperature oscillation in regenerator.

The axial distribution of temperature oscillation in regenerator during one operating period is shown in Fig. 18(b). The oscillation amplitude of temperature is larger as the cooling temperature gets lower, and the maximum temperature oscillation near the temperature plateau can reach 68 K when the cooling temperature is 22.2 K.

Fig. 19 shows the pressure oscillation in the regenerator in one cycle at different cooling temperatures, there's almost no attenuation of pressure wave along the axial regenerator at different cooling temperatures. The difference between peak and valley of pressure wave is defined as Δp. As the cooling temperature gets lower, the impedance of cold head decreases, which contributes to decrease of Δp. Fig. 20 shows the pressure drop of Δp along the axial regenerator. The pressure drop is mainly concentrated in the warm end of the regenerator, because the viscosity of helium decreases with the decrease of temperature. As the cooling temperature decreases, the mass flow in the regenerator increases, resulting in an increase of pressure drop.

Fig. 19.

Pressure oscillation during one operating period in regenerator.

Fig. 20.

Pressure drop along the axial regenerator.

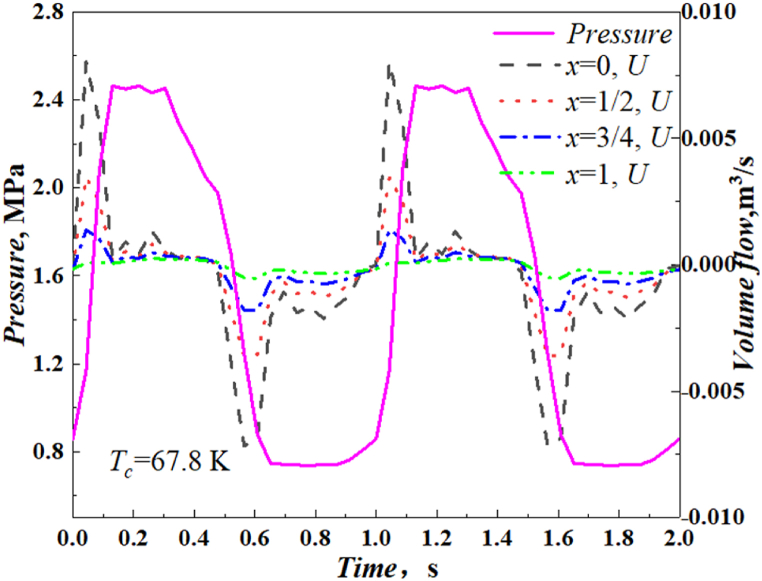
Fig. 21 show the pressure oscillation and volume flow in the regenerator at the cooling temperature of 67.8 K in two operation cycles, respectively. As shown in the figure, with the decrease of temperature in axial, the amplitude of volume flow gets lower, but the phase difference between volume flow and pressure remains constant, which is different with the phase relationship in G-M type PTC [20].

Fig. 21.

The relationship between pressure oscillation and volume flow rate in regenerator.

The main exergy loss in the regenerator at different cooling temperatures calculated by equation (17)∼(20) are shown in Fig. 22. As the figure shows, in the low-frequency regenerative cryocooler, the exergy loss in the regenerator caused by viscous friction accounts for little of the regenerator loss, by contrast, the irreversible exergy loss caused by heat exchange is the main factor leading to the reduction of the regenerator efficiency. With the decrease of cooling temperature, the insufficient heat capacity of the matrix leads to a large temperature oscillation of gas and solid in the regenerator, which further increase heat exchange loss. So regenerative material with high specific heat capacity would be useful for decreasing the loss, and especially at low temperature [29].

Fig. 22.

The exergy distribution in regenerator at different cooling temperature.

4.3. Exergy loss in cryocooler

The exergy loss in the cryocooler is mainly in the compressor, rotary valve and regenerator. Fig. 23 shows the distribution of exergy loss in the whole cryocooler at different cooling temperatures, the available power used for cryocooler only accounts for 1%∼6% of the input electric power. The proportion of exergy loss due to compression process and rotary valve in the cryocooler is up to 68% and 22% respectively. The proportion of exergy loss in compressor and rotary valve is similar to that in GM PTC [18]. In Stirling cryocooler, the efficiency of linear compressor is up to 80%∼90%, which is much higher than that of the compressor used in GM cryocooler [30]. As the cooling temperature decreases, the regenerator loss gradually increases in proportion to the loss of the whole cryocooler. When the cooling temperature is 22.2 K, the regenerator loss accounts for 11% of the input electric power.

Fig. 23.

Exergy distribution in the cryocooler at different cooling temperature.

Compared with high frequency cryocooler, the above analysis indicates that the regenerator efficiency of the G-M cryocooler is high, and the main exergy loss of the cryocooler is centered in compressor and rotary valve. Therefore, for GM cryocoolers, it's prior to improve the efficiency the cryocooler through optimizing the structure of compressor and rotary valve. To improve the performance of the cryocooler should not only focus on the regenerator, but also on the matching of the compressor, valve and cold head. Scholars have done lots of work on Acoustic-Mechanical-Electrical (AcME) coupling between the linear compressor and the Stirling-type cryocoolers [24]. It is necessary to strengthen the work on the whole coupling of low-frequency cryocooler, because there is almost no relevant research now.

5. Conclusion

GM cryocoolers have been widely applied in scientific research, HTS, MRI, etc. In order to analyze the internal loss mechanism and improve the performance of the cryocooler, numerical simulation and experimental study were carried out in this paper, and the main conclusion are drawn as follow.

• (1)A comprehensive numerical model of a single-stage GM cryocooler using Sage software was firstly established based on the model of compressor and rotary valve. The model includes three modules: compressor, rotary valve and cold head. The reliability of the model is verified by the pressure oscillation and cooling capacity obtained from the experiment. The calculated cooling capacity is consistent with the experimental one at the high temperature zone above 30 K. There is a partial deviation between the calculation result and the experiment at liquid hydrogen temperature, which may be due to the real gas effect and insufficient calculation nodes.
• (2)The exergy loss in the cryocooler is systematically analyzed. The exergy losses of compressor, rotary valve and cold head are analyzed quantitatively based on Sage model. The regenerator efficiency of GM cryocooler is much higher than that of Stirling cryocooler due to the low operating frequency which can achieve more sufficient heat exchange between the matrix and working gas, and the exergy loss in GM cryocooler is mainly produced in compressor and rotary valve. Taking the cooling temperature of 22 K as an example, the losses in the compressor and rotary valve account for 60% and 22% respectively, and the available energy entering the cold head is only 18%.
• (3)The results indicate that improving the efficiency of the compression unit is important for the further development of high efficiency GM cryocoolers, and the coupling of compressor, rotary valve and cold head is also critical for improving the performance of the GM cryocoolers. The coupling method is complex and systematic, and more experimental tests are necessary for the verification of the coupling method, so the coupling method will be presented in another article. In fact, it's difficult for compressor to make major changes, the structural optimization of the rotary valve may be useful for improving the performance of GM-type cryocoolers. Specifically, the leakage helium through the rotary valve should be minimized as much as possible, and the flow area of the rotary valve should be adjusted to an appropriate size to reduce flow resistance.

Author contribution statement

Zhao Qinyu: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Wang Bo: Conceived and designed the experiments; Analyzed and interpreted the data; Wrote the paper.

Chao Wei, Cheng Jun, Zhang Yanrui: Performed the experiments; Analyzed and interpreted the data.

Zhang Hua: Conceived and designed the experiments; Wrote the paper.

Gan Zhihua: Conceived and designed the experiments; Performed the experiments; Wrote the paper.

Data availability statement

Data will be made available on request.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.