Fast and low-dose medical imaging generation empowered by hybrid deep-learning and iterative reconstruction

Summary

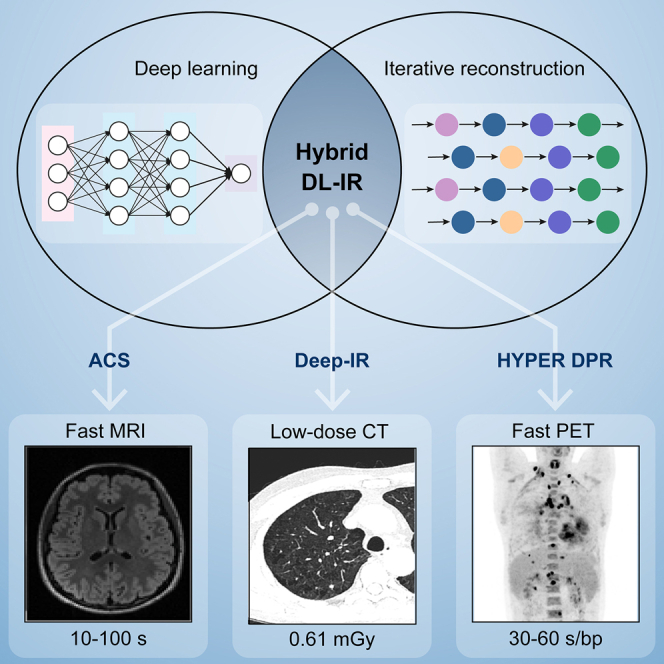
Fast and low-dose reconstructions of medical images are highly desired in clinical routines. We propose a hybrid deep-learning and iterative reconstruction (hybrid DL-IR) framework and apply it for fast magnetic resonance imaging (MRI), fast positron emission tomography (PET), and low-dose computed tomography (CT) image generation tasks. First, in a retrospective MRI study (6,066 cases), we demonstrate its capability of handling 3- to 10-fold under-sampled MR data, enabling organ-level coverage with only 10- to 100-s scan time; second, a low-dose CT study (142 cases) shows that our framework can successfully alleviate the noise and streak artifacts in scans performed with only 10% radiation dose (0.61 mGy); and last, a fast whole-body PET study (131 cases) allows us to faithfully reconstruct tumor-induced lesions, including small ones (<4 mm), from 2- to 4-fold-accelerated PET acquisition (30–60 s/bp). This study offers a promising avenue for accurate and high-quality image reconstruction with broad clinical value.

Graphical abstract

Highlights

• •Hybrid DL-IR is a generalized scheme for medical image reconstruction
• •The model enables 10- to 100-s organ-level scan time in MRI data
• •The model alleviates noises and streak artifacts in CT with 10% radiation dose
• •The model reconstructs PET with 2- to 4-fold acceleration, preserving small lesions

Liao et al. propose a generalized reconstruction scheme (hybrid DL-IR) that simultaneously leverages the capability of deep learning to mitigate noises and artifacts and the strengths of iterative reconstruction to preserve detailed structures. Its clinical utility is demonstrated in fast MRI, low-dose CT, and fast PET scenarios.

Introduction

Medical image reconstruction translates physical data acquired by the imaging equipment into diagnostic images to visualize modality-specific tissue properties in the spatial domain. The translation process is usually performed as the inverse of a forward mapping from spatial-domain tissue map to acquired data, which are theoretically formulated by respective physics models. Therefore, the design of reconstruction algorithms and the quality of reconstructed images are both dependent on the acquisition schemes and can in turn affect the accuracy and consistency of the downstream diagnosis.¹

In clinical scenarios, magnetic resonance imaging (MRI), computed tomography (CT), and positron emission tomography (PET) are the three most widely used non-invasive imaging modalities for diagnosis. The straightforward MR reconstruction uses inverse fast Fourier transform (IFFT), while CT and PET reconstructions apply filtered back projection (FBP) and iterative reconstruction (IR) to the acquired data, respectively. However, radiologists further seek fast (e.g., MRI and PET) and low-dose (e.g., CT) acquisition schemes for improved patient safety, comfort, and throughput.^2,3,4 Such acquisition schemes collect incomplete or unreliable data, making image reconstruction an ill-posed inverse problem. Therefore, a priori knowledge should be incorporated in reconstruction to suppress noises and artifacts related to suboptimal acquisitions.

IR methods have been extensively studied to tackle ill-posed reconstruction tasks. In general, IR methods can significantly improve image quality by simultaneously ensuring data consistency with acquired data and explicitly applying manually defined constraints to reconstructed images (e.g., sparsity, low rankness, and smoothness) or acquired data (e.g., theoretical distribution) for denoising purposes.^5,6 Typical IR methods include compressed-sensing (CS) reconstruction for MRI,⁷ model-based IR (MBIR) for CT,^5,8 and ordered subset expectation maximization (OSEM) for PET.^9,10

Recently, deep-learning (DL)-based data-driven methods are shown to achieve impressive construction results, even outperforming IR methods in suppressing noises and artifacts.^{11,12,13,14,15,16} Most DL-based reconstruction methods map acquired data or straightforwardly reconstructed images (i.e., by IFFT, FBP, or IR) to their fully sampled (MRI) or denoised (CT/PET) counterparts via convolutional neural network (CNN)^17,18,19,20 methods including generalized adversarial networks (GANs) and U-Net.^{21,22,23,24,25,26} Instead of denoising with manually designed constraints, DL-based methods exploit the excellent capability of neural networks to implicitly learn feature representations of inputs and outputs and the mapping function to transfer input features to output features.^27,28 However, since the same data-to-data or image-to-image mapping is applied to all denoising scenarios, DL-based methods can struggle to accommodate large variability in the size and appearance of organs and lesions, leading to over-smoothing and also loss of anatomical details.

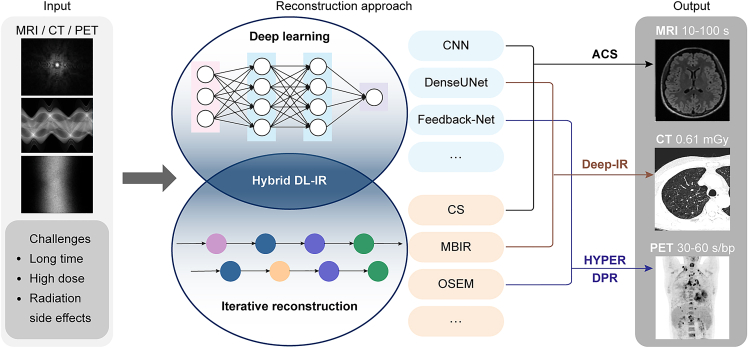
In this article, we propose a generalized hybrid DL-IR scheme to solve ill-conditioned reconstruction problems for fast MRI, low-dose CT, and fast PET acquisitions (Figure 1). Hybrid DL-IR serves as a generalized reconstruction scheme that simultaneously leverages the capability of DL-based methods to mitigate noises and artifacts and the strengths of IR methods to preserve detailed structures. The modality-specific knowledge required by the reconstruction tasks can be flexibly incorporated into this generalized DL-IR scheme for specific applications. For example, (1) for fast MRI, DL-based reconstruction is first performed to alleviate noises and aliasing artifacts in reconstructed images, followed by a CS algorithm to refine the detailed structures; (2) for low-dose CT, a 3D DL-based spatial-domain denoiser is incorporated into the MBIR iterations so that a more effective regularization function can be implicitly learned by the 3D DL denoiser; and (3) for fast PET, both denoising and enhancement networks are incorporated into the iteration process so as to simultaneously improve the image contrast and noise performance. We name the specific applications as artificial intelligence (AI)-assisted CS (ACS) in MRI, deep IR in CT, and HYPER deep progressive reconstruction (DPR) in PET. We then evaluate the performance of the hybrid DL-IR scheme in these applications.

Figure 1.

Schematics of general hybrid deep-learning and iterative reconstruction (hybrid DL-IR)

The acquired data (left), reconstruction methods (middle), and reconstructed images (right) are shown for fast MRI, low-dose CT, and fast PET, respectively.

Results

The rational and clinical utility of hybrid DL-IR is described in the following three applications, i.e., fast MRI, low-dose CT, and fast PET, respectively. Data are collected from varying scanners of three centers, termed institutes A, B, and C (please refer to the STAR Methods for details). The generalizability of the model is also evaluated in experiments including unseen external validation in each of the three tasks.

ACS for fast MRI scans

MR data are acquired in the k-space, which is the frequency domain, and can be connected to the spatial domain via IFFT. Fast MRI accelerates data acquisition by sampling fewer k-space frequency components than required by the Nyquist sampling criterion, leading to increased noises and aliasing artifacts in the reconstructed images. A variety of acquisition and reconstruction schemes have been developed for fast MRI in the past decades, including half Fourier,²⁹ parallel imaging (PI),^30,31 CS,^7,32 and DL-based methods.^{33,34,35,36,37} These methods exploit various prior knowledge to either directly infer the missing k-space data or perform denoising and dealiasing in the reconstructed images. For example, half Fourier imaging assumes conjugate symmetry of k-space data about its origin, PI uses knowledge of coil sensitivity maps to recover and unfold each aliased component, CS assumes sparsity of reconstructed image in the wavelet domain, and DL hypothesizes that the patterns of noises and aliasing artifacts learned in the training data can be generalized to the testing data.^{33,34,35,36,37} With respective priors, the half Fourier method allows an acceleration factor up to 2×, and PI typically allows 2- to 3-fold-accelerated acquisition, while CS and DL-based reconstruction methods enable more than 3-fold-accelerated data acquisition. In the reconstruction of MR images, DL-based methods outperform CS in denoising efficacy and also tolerance to data acquired with a larger acceleration factor, while they suffer from over-smooth effects, lower fidelity, and limited generalizability to various MR imaging contrasts and organs of interest.³⁸

Our hybrid DL-IR scheme employs an ACS reconstruction algorithm for fast MRI (Figure 2). ACS first relies on an AI module to reconstruct an image with a minimal amount of noises and aliasing artifacts. The image inferred by the AI module is then used as a spatial regularizer to guide image reconstruction in a CS module (Figure 2A). Since MR images contain a large variety of contrasts, organs, and image orientations, the design of the ACS algorithm ensures that the CS module can get a good spatial constraint from the AI module to reduce noises and aliasing artifacts, and the generalizability of the CS module is maximally exploited to ensure reasonable reconstruction for all possible imaging settings.

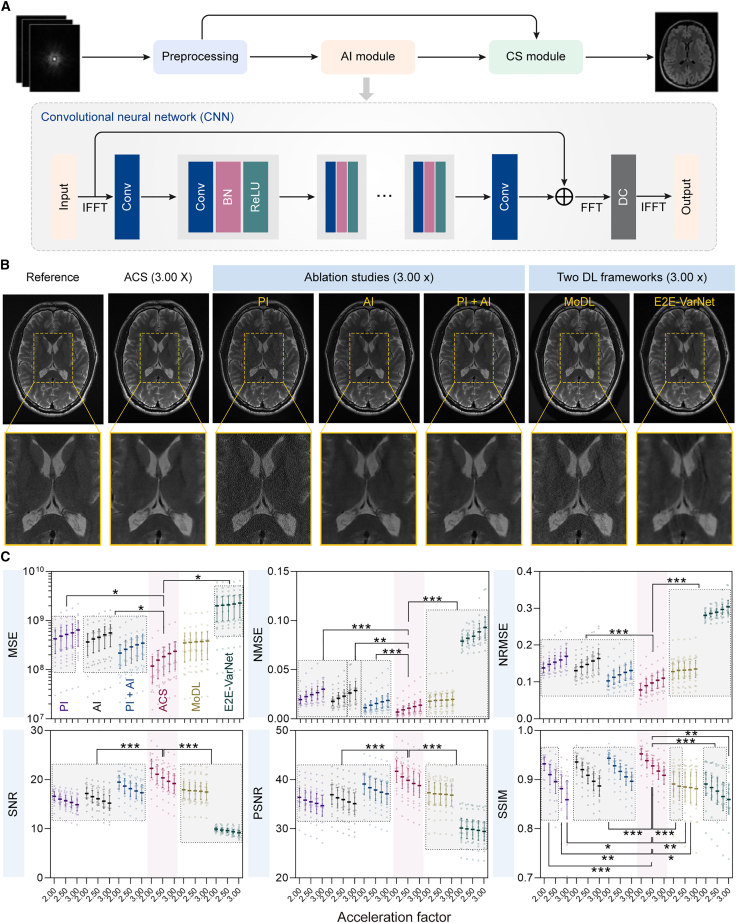
Figure 2.

AI-assisted compressed-sensing (ACS) reconstruction performance under different acceleration factors

(A) The schematics of ACS reconstruction framework.

(B) Representative T2w head images reconstructed from fully sampled k-space data from the testing dataset (left) and from 3× down-sampled k-space data using ACS, PI, AI, PI + AI, MoDL, and E2E-VarNet methods.

(C) Six quantitative metrics (i.e., MSE, NMSE, NRMSE, SNR, PSNR, and SSIM) of reconstructed images from six methods (i.e., ACS, PI, AI, PI + AI, MoDL, and E2E-VarNet) under different acceleration factors for testing data.

See also Tables S2 and S3.

To evaluate the clinical use of ACS, a total of 6,066 cases of fully sampled k-space data are retrospectively acquired from three centers using the 3 T whole-body MR scanner uMR780. Among 6,066 cases of MR data, 5,910 cases from institutes A and B are randomly divided into the training dataset (4,728 cases, 80%) and the testing dataset (1,182 cases, 20%) (Figure S1), and the other 156 cases from institute C are serve as the external validation dataset. We evaluate the ACS and PI methods using the k-space down-sampled MRI data, which are obtained with acceleration factors in the range of 2× to 4× to simulate fast MRI scans. The reconstruction performance is analyzed by quantifying the visibility of errors between the reconstructed and reference images (i.e., mean squared error [MSE], normalized MSE [NMSE], and normalized root MSE [NRMSE]), calculating the signal-to-noise ratio (SNR) and peak SNR (PSNR) reflecting image fidelity, and assessing the degradation of structural information (i.e., structural similarity [SSIM] index).³⁹ The training and testing data are collected from 9 organs, with 2–5 pulse sequences applied to each organ to create various image contrasts (Table S1). The reconstruction performance of ACS is assessed by ablation studies including PI, AI, and PI + AI, and comparison studies of other two DL frameworks named model-based reconstruction using deep-learned priors (MoDL)⁴⁰ and end-to-end variational networks (E2E-VarNets).⁴¹ Here, MoDL combining the power of a physics-derived model-based framework with data-driven learning is proposed for general inverse problems.⁴⁰ The E2E-VarNet is designed for multi-coil MRI reconstruction (i.e., PI and CS) by estimating the sensitivity maps within the network and learning fully end to end.⁴¹ The representative reconstructed images of ACS, ablation studies (i.e., PI, AI, and PI + AI), and comparison studies (i.e., MoDL and E2E-VarNet) in the testing dataset are shown in Figure 2B, where the brain images reconstructed by ACS have good agreement with the reference images. As we can see, PI results exhibit a certain degree of noises, and E2E-VarNet results show aliasing artifacts. With an acceleration factor of 3×, images reconstructed by ACS show reduced artifacts and noises and refine detailed structures compared with those reconstructed by other methods. As shown in Figure 2C and Tables S2 and S3, ACS owns statistically lower error-related metrics (i.e., MSE, NMSE, and NRMSE) and higher consistency-related metrics (i.e., SNR, PSNR, and SSIM) than other methods across most acceleration factors. Especially in the case of high acceleration factors, ACS shows advantages over PI for all combinations of pulse sequences and organs (Figure S2).

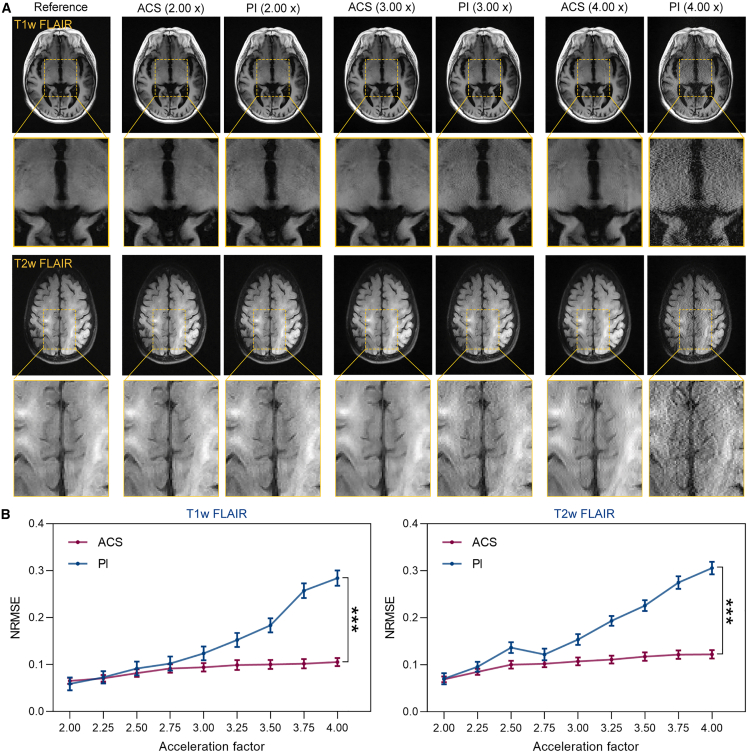
Similar results are also observed in the external validation dataset, which is collected from the head with 2 pulse sequences (i.e., T1-weighted (T1w) fluid attenuated inversion recovery (FLAIR) and T2-weighted (T2w) FLAIR). The reconstruction performance of ACS and PI is also evaluated on the k-space down-sampled MRI data with acceleration factors in the range of 2× to 4×. As shown in Figure 3A, images reconstructed by ACS demonstrate reduced artifacts and noises compared with those reconstructed by PI under high acceleration factors. Quantitative NRMSE values of ACS are statistically lower than those of PI under most acceleration factors, which is consistent with the visualized results (Figure 3B; Table S4).

Figure 3.

ACS reconstruction performance under different acceleration factors in the external validation dataset

(A) Representative T1w FLAIR and T2w FLAIR head images reconstructed from fully sampled k-space data from the external validation dataset and from down-sampled k-space data with acceleration factors of 2, 3, and 4 using ACS and PI methods.

(B) NRMSE of ACS- and PI-reconstructed images under different acceleration factors for external validation dataset. Statistical analyses are performed using paired t tests (n = 78), ∗∗∗p < 0.001. Significant differences are observed in all acceleration factors.

See also Table S4.

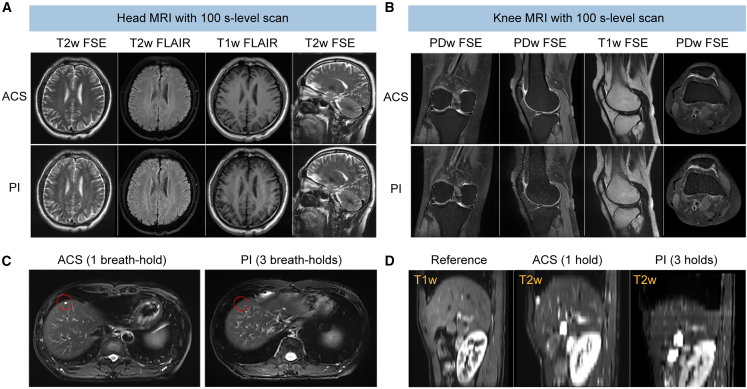
In addition, we demonstrate the excellent capability of the ACS method in reconstructing fast MRI data with varying acquisition protocols by exploring the 100-s-level scan for a static organ (e.g., brain and knee) without compromising the SNR or inducing artifacts in reconstructed images. The results of the 100-s-level fast MRI study are shown in Figures 4A, 4B, and S3. Specifically, ACS enables reasonable image reconstruction from k-space data acquired by transversal T2w fast spin echo (FSE), transversal T2w FLAIR, transversal T1w FLAIR, and sagittal T2w FSE in 19.2, 30.4, 55.0, and 16.6 s, respectively, with the accelerated scanning protocol using subsampled k-space data (Figure 4A). Therefore, the total scan time for brain MRI using these four sequences is 121.2 s, which is only 30%–40% of the time spent when using conventional PI (5–6 min in total). For knee imaging, similarly, ACS allows reconstruction of data acquired by proton density-weighted (PDw) FSE, sagittal PDw FSE, sagittal T1w FSE, and transversal PDw FSE in 30.0, 30.0, 25.2, and 27.0 s, respectively (Figure 4B). The total scan time of these four sequences is 112.2 s with ∼60% time saving compared with that using PI. Meanwhile, ACS reconstruction of the 100-s-level fast MRI scans is shown in Figure S3 for other static organs, including the cervical spine, lumbar spine, hip, and ankle joint. Further, ACS enables high-quality reconstruction from single breath-hold chest MRI, which can address the problem of a spatial mismatch from physiological movement, and can accurately reconstruct small lesions in locomotive organs. As shown in Figure 4C, a focal lesion is missed in the 3-breath-hold T2w FSE acquisition (a net acceleration factor of 1.80×) reconstructed by PI but is successfully captured in the same slice in the single-breath-hold acquisition (a net acceleration factor of 3×) reconstructed by ACS. In addition, the liver in the 3-breath-hold images reconstructed by PI is significantly distorted in the slice direction, while the single-breath-hold images reconstructed by ACS preserve anatomical structures of the liver (Figure 4D).

Figure 4.

ACS reconstruction for 100-s-level MRI scans and single-breath-hold MRI scans

(A and B) Representative images of the head (A) and knee (B) reconstructed by ACS (at a 100-s level) and PI using four pulse sequences.

(C and D) Reconstruction of the chest MR images by ACS with data acquired in a single breath hold and by PI with data acquired in three breath holds at the transversal (C) and sagittal (D) sections. The red circle in (C) labels a focal lesion, which is missed in the three-breath-hold acquisition reconstructed by PI while being successfully captured in the single-breath-hold acquisition reconstructed by ACS. The reference in (D) is acquired with a spoiled gradient echo sequence in a single breath hold. Red circles highlight the focal lesions in the liver.

See also Figure S3.

In this fast MRI reconstruction study, we demonstrate that ACS consistently outperforms PI in terms of acquisition time and image quality. By combining DL’s capability in denoising and IR’s strengths in fidelity and generalizability in the ACS framework, we enable both fast MR scans with a higher acceleration factor and superior quality in reconstructed images.

Deep IR for low-dose CT scans

In the reconstruction of low-dose CT images, both MBIR and DL-based reconstruction have been extensively studied.^{5,8,11,17,19,24} MBIR relies on the regularization function to reduce noises and artifacts in the reconstructed images. Unfortunately, traditional regularization functions in MBIR need to be determined manually and empirically and may result in blurred, plastic, or cartoonish images in low-dose CT scans.⁵ On the other hand, DL-based reconstruction normally operates on the low-dose CT images reconstructed by FBP and estimates the normal-dose image.⁴² However, when ultra-low doses are applied, anatomical structures are often overwhelmed by mottled noises and noise-induced streaking artifacts, especially in the shoulder and pelvis, causing the failure of DL-reconstructed images in meeting diagnostic criteria.

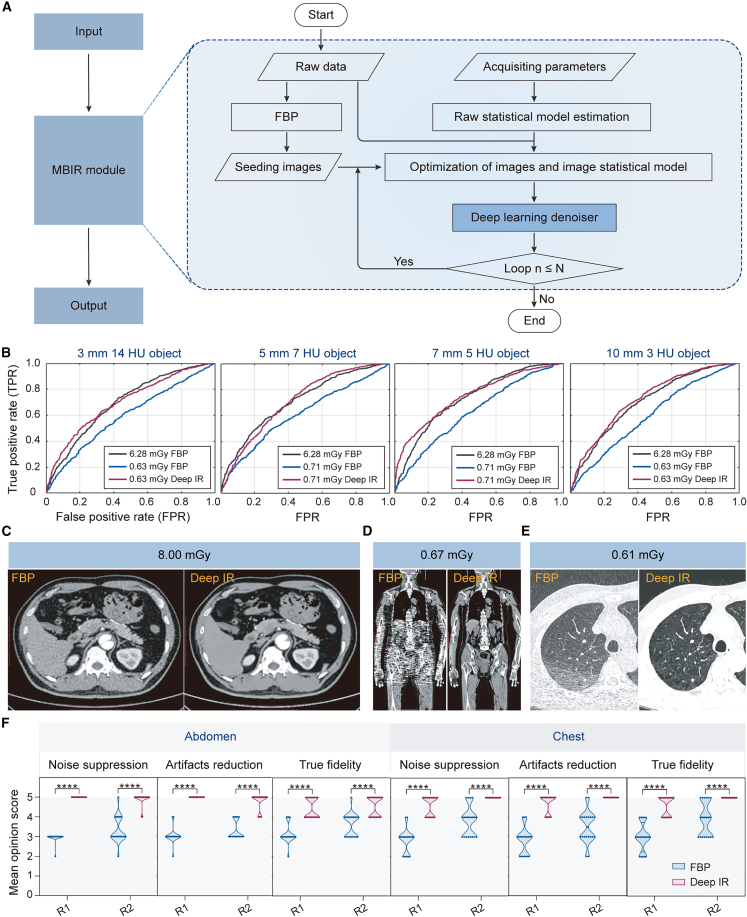
To overcome the above problems, we propose deep IR, a hybrid reconstruction algorithm integrating DL-based reconstruction and MBIR, to reconstruct high-quality images from low-dose CT scans (Figure 5). In this algorithm, reconstruction uses MBIR as the backbone to transform the data acquired in the projection domain into the images in the spatial domain. Deep IR innovatively incorporates a 3D DL denoiser (DenseUNet)⁴³ to replace the traditional regularization function for improved denoising performance (Figure 5A). We hypothesize that such a design would allow deep IR to have superior reconstruction performance in low-dose CT scans, with reduced image noise and streak artifacts, increased spatial resolution, and improved low-contrast detectability (LCD).

Figure 5.

Deep IR reconstruction for low-dose CT scans

(A) The schematics of deep IR reconstruction framework.

(B) The ROC curves of three models, including FBP with reference dose, FBP with a lower dose, and deep IR with a lower dose.

(C–E) Representative images reconstructed by FBP and deep IR at 8.00 mGy (40% of a normal dose) (C) and ultra-low doses of 0.67 (D) and 0.61 mGy (E).

(F) Mean opinion score from two radiologists evaluating the chest and abdomen parts of the images. Statistical analyses are performed between R1 and R2 using Mann-Whitney U tests with ∗∗∗∗p < 0.0001.

To evaluate the clinical value of deep IR for low-dose CT scans, phantom and clinical experiments are performed. For the phantom study, dose reduction is measured based on the model observer LCD evaluation method. Images reconstructed by FBP and deep IR from low-dose CT scans (0.60–0.75 mGy) are obtained and compared with those reconstructed by conventional FBP in reference-dose (6.28 mGy) CT scans. The receiver operator characteristic (ROC) curves are drawn for different doses and contrast objects (Figure 5B). The ROC curves show that deep IR with a dose reduction of 88%–90% can achieve a comparable image quality to the FBP with the reference dose under varied conditions, demonstrating that deep IR can effectively improve LCD.

For the clinical low-dose CT study, a total of 142 cases are collected by CT scanners (uCT 760/780). Among all cases, 98 cases (from institute B) and 44 cases (from institute C) are used for training and testing, respectively. The reference images are reconstructed by the non-regularization IR method with a reference dose, while the low-dose CT images are collected with lower doses and reconstructed by deep IR and FBP seperately. A series of experiments are designed to compare the reconstruction performance of the FBP and deep IR. Qualitative comparisons are shown in Figures 5C–5E. Results show that deep IR allows improved reconstruction at a lower CT dose with higher resolution and fewer noises and artifacts than the FBP reconstruction. It should be noted that deep IR can successfully reconstruct the chest CT images with only 10% radiation dose (0.61 mGy). Also, reconstructed images of the chest and abdomen are independently evaluated by two radiologists (denoted as R1 and R2) (Figure 5F). The mean opinion scores are graded on a scale of 1–5 points considering the following three aspects: noise suppression, streaking artifact reduction, and image structure fidelity. Therefore, higher mean opinion score can be associated with better diagnostic interpretation. By applying multiple Mann-Whitney U tests, we notice that the mean scores of images reconstructed by deep IR are significantly higher than those of FBP reconstruction in all three aspects. Our results indicate that the images reconstructed by deep IR may improve diagnostic decisions.

In conclusion, deep IR achieves promising performance in reconstructing ultra-low-dose CT images with high spatial resolution, reduced noise and artifacts, and also improved LCD, which can fulfill the diagnostic requirement.

HYPER DPR for fast PET scans

For PET imaging, shortening acquisition time is one of the key factors to effectively improve patient comfort and reduce motion artifacts. However, a shorter acquisition time in PET imaging usually leads to reduced image quality and amplified noise. The DL-based reconstruction strategy has attracted significant attention in image denoising for fast PET scans.^44,45 However, it has been reported that the denoising operation performed via CNNs may increase the risk of blurring small lesions, especially in the low SNR images reconstructed from fast PET scans.^17,46,47,48 Therefore, directly learning of the end-to-end mapping from fast PET scans reconstructed images to standard PET scans reconstructed images can be unstable.

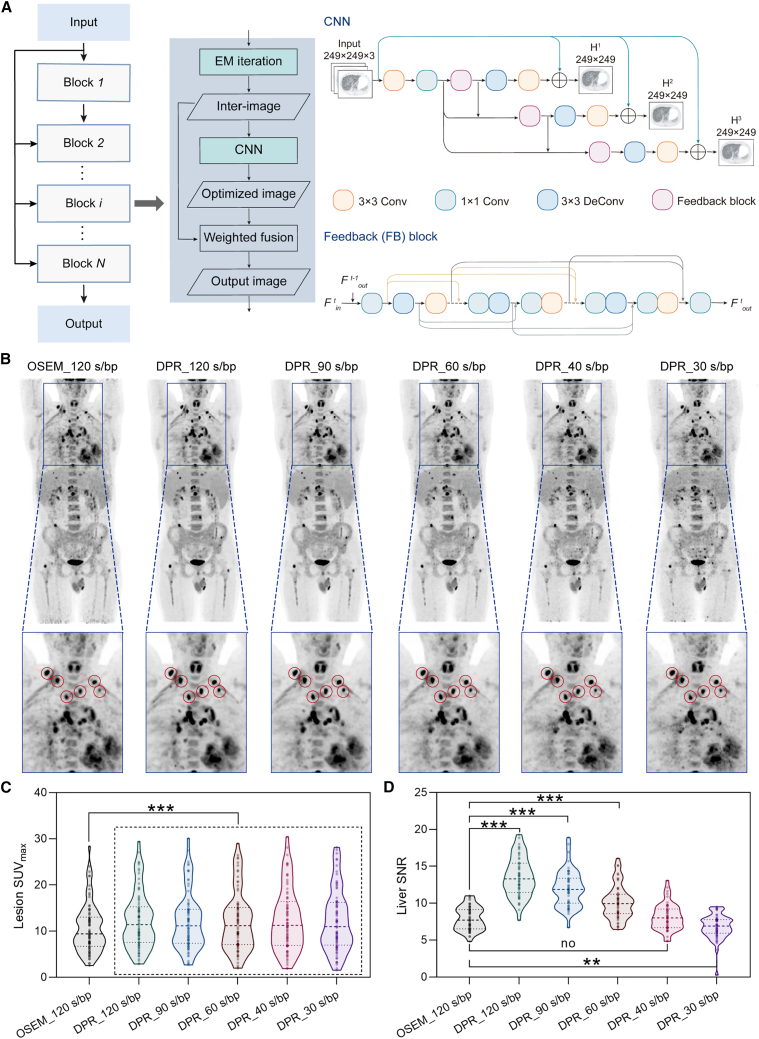
To address the limitation of existing DL-based reconstruction methods, HYPER DPR, a hybrid DL-IR reconstruction strategy integrating the DL-based image reconstruction algorithm and the OSEM algorithm (Figure 6), is presented for fast PET imaging. DPR uses a chain of CNN blocks, where OSEM reconstruction is refined by a CNN-based feedback network (FB-Net),⁴⁹ and then fused with the CNN outputs according to a weighting parameter as an adjustable variable. The optimal numbers of blocks, iterations, and subsets were determined via phantom study, as shown in our previous work.⁵⁰ Specifically, the OSEM algorithm defines subsets as 20 and fixes the iteration number at 2. DPR is implemented with two types of blocks, with the first block using subsets and iteration numbers of 20 and 2, respectively, and the second block using subsets and iteration numbers of 5 and 1, respectively. Only one of the denoising CNNs (CNN-DEs) and enhancement CNNs (CNN-EHs) is applied within each block, and they are alternated between different blocks to perform the tasks of image denoising and image enhancement alternately (Figure 6A). Therefore, in a CNN-DE block, CNN-DE maps the images reconstructed by OSEM to denoised images. In the following enhancement block, OSEM gradually recovers small lesions, while the CNN-EH is used to further enhance detailed structures in the reconstructed images. The enhanced images will be sent to the next denoising block, and so on and so forth, until the reconstruction converges.

Figure 6.

HYPER DPR reconstruction for fast PET scans

(A) Schematics of HYPER DPR.

(B) Representative body images reconstructed by OSEM and DPR with varied acquisition times. The locations of small lesions are highlighted by red circles.

(C and D) The SUV_max of the identified lesions (C) and SNR in the liver (D) for different methods. Statistical analyses on SUV_max are performed using repeated measures one-way ANOVA followed by Turkey’s multiple comparisons tests (n = 78). Statistical analyses on SNR are performed using Friedman tests followed by Dunnett’s multiple comparisons tests (n = 51). Asterisk represents two-tailed adjusted p value, with ∗p < 0.05, ∗∗p < 0.01, and ∗∗∗p < 0.001.

See also Figure S6 and Table S5.

To evaluate the clinical utility of the HYPER DPR for fast PET scans, a total of 131 cases are collected from two hospitals using different PET scanners. Briefly, 80 PET scans are performed in institute B using a total-body digital time-of-flight (TOF) PET/CT scanner (uEXPLORER), serving as the training dataset. The other 51 PET scans are performed in institute C using uMI 780, serving as the testing dataset. For the training dataset, all photon counts acquired from the 900-s scans are used to reconstruct the reference PET images, in which the CNN-DE is trained to remove noises from the input image, with a training target of images acquired 15 min, and the CNN-EH is trained to map low convergent images to high convergent images, with a training target of images with high iterations (>4 iterations). Fast PET scans are simulated by uniformly and retrospectively sampling 10% of the total counts from the list-mode data. For the testing dataset, each patient is scanned with a standard OSEM protocol with 120-s-per-bed position (s/bp). HYPER DPR is applied to reconstruct images from PET data retrospectively rebinned corresponding to acquisition times of 30–120 s/bp. Compared with images reconstructed by OSEM_120 s/bp, images reconstructed by DPR from the 40-s/bp acquisition show comparable contrast and SNR (Figure 6B). Note that although some small lesions seem vague and blurry in the images reconstructed by OSEM (120 s/bp), they become prominent with sharp delineation in the images reconstructed by DPR (90–120 s/bp). Further, to quantitatively evaluate the efficacy of reconstructed images in small-lesion detection, the maximum standardized uptake value (SUV_max) of ¹⁸F-FDG within 78 identified volumes of interest (VOIs) is measured. The median SUV_max of images reconstructed by OSEM_120, DPR_120, DPR_90, DPR_60, DPR_40, and DPR_30 s/bp are 9.42, 11.42, 11.14, 11.17, 11.25, and 10.99, respectively, demonstrating that DPR can statistically improve small-lesion detectability (Figure 6C; Table S5) in all acquisition times. The SUV_max decreases with the acquisition time, with details of statistical analyses shown in Figure S6. The efficacy of HYPER DPR for small-lesion detection has also been investigated by a phantom study in our previous work, which suggested that DPR can enhance SUV_max but not surpass the limit.⁵⁰ Also, the liver SNR is calculated to evaluate the denoising capability of different reconstruction algorithms. The SNR values of OSEM_120, DPR_120, DPR_90, DPR_60, DPR_40, and DPR_30 s/bp are 7.91 ± 1.57, 13.53 ± 2.65, 11.99 ± 2.48, 10.14 ± 2.30, 8.16 ± 1.78, and 6.79 ± 1.65, respectively (Table S3). From Figure 6D, we find that DPR with 60- to 120-s/bp scans significantly improves the SNRs, while there is no statistically significant difference between DPR with 40-s/bp scans and OSEM with a 120-s/bp scan. Therefore, both qualitative and quantitative evaluations confirm that DPR can achieve better or comparable image contrast for small lesions with 2- to 4-fold scan accelerations.

In conclusion, HYPER DPR is an effective reconstruction technique for fast PET imaging. It enables a 2- to 4-fold-accelerated PET scan while preserving SNR in reconstructed images, as well as details and contrasts of small tumor lesions.

Discussion

We demonstrate that the proposed hybrid DL-IR couples DL with domain-specific IR and provides a perspective for accurate and high-quality image reconstruction. We present evidence that the proposed DL-IR reconstruction strategy is general and flexible and can be customized and adapted to different specific reconstruction tasks. (1) In fast MRI, the image is sequentially reconstructed by DL-based reconstruction and an IR process in which IR is used to refine the detailed structures of initial reconstructed images; (2) in low-dose CT, the image is first reconstructed by the IR process and then DL-based reconstruction, in which DL is used to reduce noise effect and remedy details of the reconstructed images; (3) and in fast PET, both denoising and enhancement networks are incorporated into the iteration process so as to simultaneously improve the image contrast and noise performance.

Prior works indicated that DL-based reconstruction may be superior to the IR algorithm in terms of reduced noise, increased spatial resolution, and improved LCD.^{51,52,53,54,55,56} For example, Parakh et al. reported that in a dataset containing 200 abdominal CT images (from 50 patients), sinogram-based DL image reconstruction showed improved image quality, superior to IR both subjectively and objectively.⁵¹ Park et al. compared the reconstruction performance of two methods in lower-extremity CT angiography images (from 37 patients), demonstrating that DL-reconstructed images owned significantly higher SNR values and lower blur metrics.⁵² Meanwhile, the radiation dose of cardiac CT angiography was significantly lower with DL-based reconstruction (6.9 ± 3.2 mGy) than with the IR algorithm (11.5 ± 2.2 mGy).⁵³ In addition, DL-based reconstruction also showed better performance in contrast-enhanced CT images of the upper abdomen with a <50% radiation dose (7.1 ± 1.9 mGy).⁵⁴ It is important to underline the need for reducing the radiation dose. Indeed, with the increasing number of examinations performed, the doses delivered to patients carry a potential risk of radiation-induced cancer, especially in radio-sensitive organs such as breasts, myocardium, and coronaries.^57,58,59

However, the classical DL-based methods, known as the image-to-image mapping scheme or data-to-data mapping scheme, may lead to over-smoothing and loss of anatomical details. Regarding this, our proposed hybrid DL-IR simultaneously integrates the benefits of the robustness from the DL-based reconstruction approach to avoid gross failure reconstruction and the signals’ physical properties from IR to preserve the anatomical details. Similar hybrid concepts have been proposed in other papers and have achieved remarkable superiority over other existing methods in reconstruction performance, manifested in artifact suppression, tissue recovery, and edge preservation.^{60,61,62,63,64} For example, Hata et al. combined DL-based denoising and MBIR to reconstruct ultra-low-dose (0.3 ± 0.0 mGy) CT images of the chest (from 41 patients with 252 nodules), showing that the hybrid method outperformed a single method in terms of image quality and Lung-RADS assessment.⁶⁰ Instead of directly deploying the regularization term on image space, Hu et al. proposed a deep IR framework for limited-angle CT, which combined iterative optimization and DL based on the residual domain, significantly improving the convergence property and generalization ability.⁶¹ Chen et al. also incorporated the benefits from the analytical reconstruction method, the IR method, and deep neural networks into AirNet, which was validated on a CT atlas of 100 prostate scans, yielding good image quality and further optimal treatment planning.⁶² The majority of hybrid reconstruction strategies were designed for CT images and rarely for MRI or PET images.^60,61,62 Moreover, existing hybrid strategies have only been validated on one specific imaging modality, and their extendibility and generality remain to be assessed. Based on the above challenges, we propose the generalized hybrid DL-IR scheme for multiple imaging modalities that can flexibly incorporate the modality-specific knowledge to achieve customized applications. Notably, hybrid DL-IR can be altered by a series of parameters, such as the IR algorithm, the DL algorithm, the relative position and organic connection between two algorithms, DL structure (e.g., CNN layers, loss function), etc. We evaluate the hybrid DL-IR scheme in three of the most widely used imaging modalities in the clinic, and it achieves high scan speeds (in MRI and PET) and low radiation doses (in CT) comparable to state-of-the-art methods.⁶⁵ Hybrid DL-IR has the potential to benefit numerous challenging tasks. One such task is abdominal MRI, which is often accompanied by motion artifacts resulting from involuntary patient movements such as breathing, muscle contractions, or peristalsis. ACS can empower this process by enabling fast MRI, thus reducing motion-associated artifacts.

Limitations of the study

Although hybrid DL-IR demonstrates encouraging improvement in fast and low-dose reconstructions, some issues are still to be addressed. Firstly, although the clinical value of hybrid DL-IR is evaluated in a large-scale MRI study, the study populations for CT and PET are relatively small, with 142 and 51 patients, respectively. Future studies may include a large clinical trial with multiple clinical centers to better validate its clinical value. Secondly, this study only includes limited scanners and imaging protocols, such as specific magnetic field strength and PET imaging tracer. Further work could expand to include a wide range of scanners and imaging protocols to increase its generalizability. Thirdly, there is still a challenge in balancing denoising effects and image details in fast or low-dose imaging scenarios. For example, there may be a loss of details when the acceleration factor significantly increases in ACS or a loss of small lesions in DPR. Moving forward, we would continue to explore effective ways to integrate the IR methods with the state-of-the-art DL approaches for better outcomes. Lastly, the existing dual-modality PET/CT and PET/MR systems could be benefited from the proposed approach, i.e., by integrating the corresponding algorithms in both imaging modalities. Further studies are warranted to explore the possibilities of combing these modalities for better performance. We anticipate that this generalized reconstruction scheme can be applied to broad image reconstruction tasks, such as low-contrast agent imaging. We expect that it can be truly transformed in the clinic to realize the screening and diagnosis of diseases so as to provide reasonable treatment planning.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Analyzed data	This paper	Hybrid DL-IR Data: https://doi.org/10.17632/j7khwb3z3r.1
Software and algorithms
GraphPad Prism 9	GraphPad Software	http://www.graphpad.com/; RRID: SCR_000306
IBM SPSS Statistics 26.0	SPSS Software	https://www.ibm.com/products/spss-statistics; RRID: SCR_019096
Adobe Illustrator CC 2019	Adobe Illustrator Software	https://www.adobe.com/products/illustrator.html; RRID: SCR_010279
ITK-SNAP 3.8.0	ITK-SNAP Software	http://www.itksnap.org/pmwiki/pmwiki.php; RRID: SCR_017341
Original code about deep learning and iterative reconstruction models for image reconstruction	This paper	https://github.com/simonsf/Hybrid-DL-IR
Other
NVIDIA Tesla V100 GPU	NVIDIA TESLA V100 GPU	https://www.nvidia.com/en-gb/data-center/tesla-v100/
NVIDIA TITAN RTX GPU	NVIDIA TITAN RTX GPU	https://www.nvidia.com/en-us/deep-learning-ai/products/titan-rtx/
NVIDIA Quadro RTX 6000 GPU	NVIDIA Quadro RTX 6000 GPU	https://www.nvidia.com/en-us/design-visualization/previous-quadro-desktop-gpus/

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Dinggang Shen (dinggang.shen@gmail.com).

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

Human participants

All data were collected from three centers, as Shanghai United Imaging Healthcare Co., Ltd., Shanghai, China (Institute A), Zhongshan Hospital, Shanghai, China (Institute B), and China-Japan Union Hospital of Jilin University, Changchun, China (Institute C).

For the fast MRI study, a large-scale dataset of 6,066 fully sampled k-space data were retrospectively acquired from three centers. Among 6,066 cases of MR data, 5,910 cases from Institutes A and B were randomly divided into the training dataset (4,728 cases, 80%) and testing dataset (1,182 cases, 20%) (Figure S1), and the rest 156 cases from Institute C were served as the external validation dataset. For the low-dose CT study, a total of 142 cases from two centers were included in this study, in which 98 cases (from Institute B) and 44 cases (from Institute C) were used for training and testing, respectively. For the fast PET study, a total of 131 cases from two centers were included in this study, and divided into the training dataset (80 cases from Institute B) and the testing dataset (51 cases).

Ethics statement

This study was approved by the Research Ethics Committees in the China-Japan Union Hospital of Jilin University, Changchun, China (No. 20201112) and Zhongshan Hospital, Shanghai, China (No. B2020-081R). Informed consent was waived because of the retrospective nature of the study. The related systems of MRI, CT, and PET have been approved by the Chinese National Medical Products Administration (NMPA, with certificate numbers of 20213060250, 20163062251, and 20163332251, respectively), and the United States Food and Drug Administration (FDA, with certificate numbers of K193176, K193073, and K210001, respectively).

Method details

Study design

Three experiments were performed to evaluate the clinical use of Hybrid DL-IR. For each imaging modality, reference images, k-space down-sampled MRI, low-dose CT, and fast-scanned PET images were acquired from corresponding scanners. DL network and IR algorithm were connected to serve as the hybrid model and trained on the training dataset. The reconstruction performance between ACS and PI, between Deep IR and FBP, and between HYPER DPR and OSEM in the testing datasets were compared qualitatively and quantitatively. The Hybrid DL-IR model was repeated five times, and the performances were average as the final results.

Image dataset acquisition and pre-processing

• (1)Fast MRI: All MRI studies were performed on the 3.0 T whole-body MR scanner - uMR780. A total of 6,066 cases of fully sampled k-space data were collected from 9 organs (i.e., ankle, breast, cardiac, cervical spine, head, hip, knee, lumbar spine, pelvis) using 2 to 5 pulse sequences (i.e., T2w FSE, T2w FLAIR, T1w FLAIR, T1w FSE, PDw FSE). Breath-hold chest MR scans were also performed. Detailed imaging protocols were listed in Table S1. Reference images were reconstructed by IFFT of fully sampled k-space data. Down-sampling of k-space data was performed retrospectively to simulate fast MRI scans with acceleration factors of 2.00, 2.25, 2.50, 3.00, 3.25, 3.50, 3.75, and 4.00. Among 6,066 cases of MR data, 4,728 cases (from Institute A), 1,182 cases (Institute B), and 156 cases (Institue C) were used as the training, testing, and external validation datasets, respectively. For robust reconstruction and reliable validation, the training and testing data covered all possible organs, pulse sequences, acceleration factors, and imaging orientations.
• (2)Low-dose CT: A total of 142 cases were collected by CT scanners - uCT 760/780, including non-contrast and contrast scans in different phases. Among all cases, 98 cases of the training dataset (Institute B) were collected with a normal dose of 20 mGy, and the testing 44 cases (Institute C) were collected with lower doses between 0.62 mGy and 20.45 mGy. In the training dataset, reference images were reconstructed by the non-regularization IR method due to its improved capability over FBP in suppressing streak artifacts and noises (Figure S4). In addition, low-dose CT data was simulated by adding noise to the 20-mGy normal-dose data (Figure S5). The noise was modeled considering the Poisson and electronic noise features in the projection raw data. A wide range of dose levels were simulated to ensure the robustness of the Deep IR algorithm.
• (3)Fast PET: A total of 131 cases from two centers with different scanners were included in this study, and divided into the training dataset (80 cases from Institute B using uEXPLORER) and the testing dataset (51 cases from Institute C using uMI 780). For the training dataset, the injected dose of ¹⁸F- FDG was in the range of 3.7–4.4 MBq/kg (3.7 MBq/kg for oncology patients), and the uptake time was about 60 min. Total-body PET imaging was performed in a scan time of 900 s to provide high-quality reference images with a minimal amount of noise and sharp image contrasts. All photon counts acquired from the 900-s scan were used to reconstruct the reference PET images. Fast PET scans were simulated by uniformly and retrospectively sampling 10% of the total counts from the list-mode data. The DL module of the HYPER DPR algorithm was trained on 161,040 slice pairs collected from these 80 cases, which were further augmented via flipping and rotation.

Image preprocessing were performed in different modalities accordingly. For MRI images, they were normalized by subtracting the mean intensity value and dividing by the variance of intensities. For CT images, original images were directly used. For PET images, each image was globally Z score normalized. For all modalities, image resolution kept unchanged.

Deep learning architecture

• (1)ACS: A CNN was adopted to remove noises and aliasing artifacts from reconstructed images (Figure 2A). The CNN took noisy and aliased images reconstructed by IFFT of down-sampled k-space data as the input. First, 3 down-sampling operations with a stride of 2 were performed to expand the receptive field of the network to handle global aliasing artifacts. The network then encompassed multiple “CONV-BN-ReLU” blocks. Each block consisted of a 3 × 3 convolutional layer (CONV), batch normalization (BN), and ReLU activation. Finally, 3 up-sampling operations with a stride of 2 were performed for recovered spatial resolution in the CNN outputs. A skip connection was applied between input images and CNN outputs. Therefore, the noises and aliasing artifacts could be modeled by CNN, and then subtracted from the input images via skip connection. A data consistency (DC) layer was further added to ensure that the k-space data of the denoised images were consistent with the acquired k-space data, improving the fidelity of output images.
• (2)Deep IR: The 3D DL denoiser had two inputs: the noisy image volume and its associated noise deviation map. In the noisy image volume, strong denoising was performed by DL denoiser onto voxels with large deviations, while weak denoising was performed on voxels with small deviations. Therefore, denoised CT images preserving as much detail as possible would be output by the 3D DL denoiser. A variety of networks could be applied in this denoising task, such as U-Net, Dense-Net, variational network, etc. In this study, we used 3D DenseUNet to serve as a denoiser.
• (3)HYPER DPR: The denoising network (i.e., CNN-DE) and the enhancement network (i.e., CNN-EH) were trained separately. For CNN-DE, PET images reconstructed from down-sampled counts were used as the input, and PET images with complete counts were used as the training targets. For CNN-EH, PET images with insufficient iterations were used as input, and PET images with sufficient iterations were used as the training targets. The weighting parameter for PET fusion was pre-determined. We used the same weighting parameter for each block. Surely, it can be individual for each block to meet the clinician’s preference on image smoothness/sharpness. Both CNN-DE and CNN-EH were designed based on the FB-Net. The FB-Net had three branches (Figure 6A) with H¹, H^2, and H³ denoting their respective outputs. Skip connections were applied between the input and the intermediate output of each branch (green lines). Each branch of the FB-Net shared weights, which greatly compressed the network’s size and reduced inference time. The output of the last branch was the final output of the network.

In more detail, each branch of the FB-Net consisted of several convolution layers and a feedback (FB) block.⁴⁹ The FB block in each branch had multiple 1 × 1 convolution layers and duplicated modules with paired inverse convolution and convolution layers. The 1 × 1 convolution layer could reduce the number of feature maps and accelerate the inference process of the network. Dense connections were applied among different modules to enrich the expression of high-level features (gray lines). The FB block took the high-level features ${\mathrm{F}}_{\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{t}-1}$ generated in the (t-1)^th branch as an additional input, which served as FB information to guide the extraction of low-level features ${\mathrm{F}}_{\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{t}}$ from ${\mathrm{F}}_{\mathrm{i}\mathrm{n}}^{\mathrm{t}}$ in the t^th-branch and made the learning and expression ability of the network gradually enhanced.

Notably, the optimal number of blocks, iterations, and subsets were determined via phantom study in our previous work.⁵⁰ For an HYPER DPR implementation of two blocks, in the first block the subsets were 20 and the iteration number was 2, and in the second block the subsets were 5 and the iteration number was 1. Only one of the CNN-EH and CNN-DE was applied within each block and they were alternated between different blocks. Notably, The PET reconstruction was performed with 3D OP-OSEM. And the DPR network employed a 2.5D architecture, which proved to be superior in accuracy compared to the 2D architecture, and more cost-effective than the 3D architecture. To be specific, three adjacent slices of the input PET images corresponded to one slice of the target PET image, utilizing both axial and trans-axial planes to incorporate spatial information in the network.

Training details

• (1)ACS: The training objective of the AI module was to minimize the mean squared error (MSE) between the network outputs and reference MR images. The network training was implemented in the PyTorch DL framework, using an ADAM optimizer with an initial learning rate of 0.0002, betas of (0.9, 0.999), and a batch size of 1. The learning rate decayed by half every 100 epochs. The whole slice was input to the ACS, so the patch size was the original size of the slice, which varied with scanning settings. The regularization parameters of the model were determined via a hyperparameter tuning process that aimed to achieve optimal performance on the validation dataset while avoiding overfitting on the training dataset. The regularization parameters were initially set based on prior knowledge or experience with similar models and datasets. If the initial parameters performed sub-optimally on the validation dataset, Bayesian optimization and grid search were used to further optimize the parameters, taking model complexity and data volume into account. In this study, the network was trained with an NVIDIA Tesla V100 GPU.
• (2)Deep IR: The network was trained to denoise the images reconstructed by the IR module by minimizing the sum of MSE and mean absolute error (MAE) between the network outputs and reference CT images. The network training used an ADAM optimizer with a learning rate of 1e-3, weight decay of 1e-5, a batch size of 144, and a patch size of 64 × 64 × 64. This network was trained with 8 × NVIDIA TITAN RTX GPU.
• (3)HYPER DPR: Both CNN-DE and CNN-EH used the same training settings and were trained separately. The training objective was to minimize MAE between the network outputs and the reference PET images. Network training used an ADAM optimizer with a cyclical learning rate, a batch size of 16, and a patch size of 249 × 249 × 3. The minimum and maximum values for the cyclical learning rate were 1e-5 and 1e-4, respectively. The training was conducted on a computer cluster with 4 × NVIDIA Quadro RTX 6000 GPU.

Iterative reconstruction module

(1) ACS: Let us denote the output of de-aliased images by the AI module as $x_{AI}$, and denote the acquired k-space data as $y$. The final image was reconstructed in a CS module by solving the following optimization problem, as shown in Equation 1:

$$\underset{x}{\mathrm{argmin}}{{\Vert Ex-y\Vert }_2^2+{\lambda }_1\Vert Фx\Vert }_1+{{\lambda }_2\Vert x-x_{AI}\Vert }_1$$ (Equation 1)

Here, $Ф$ denoted the wavelet transformation, and ${\lambda }_1,{\lambda }_2$ were scalar factors to perform trade-offs among the data consistency term (i.e., ${\Vert Ex-y\Vert }_2^2$) and different regularization terms (i.e., ${\Vert Фx\Vert }_1$ and ${\Vert x-x_{AI}\Vert }_1$). The regularization term ${\Vert x-x_{AI}\Vert }_1$ was introduced to incorporate the information obtained by the AI module into the final reconstructed image. Based on the assumption that the predicted image $x_{AI}$ was close to the true image $x$, the subtraction operation $x-x_{AI}$ could be taken as a sparse transform.

(2) Deep IR: Conventional MBIR method could be formulated as the following optimization problem (Equation 2):

$$\underset{U}{\mathrm{argmin}}{\Vert W_S·\left(AU-Y\right)\Vert }_2^2+\beta R\left(U\right)\text{,}$$ (Equation 2)

where $Y$ was the raw acquisition projection data, $A$ was the system matrix, and $U$ was the reconstructed image volume. ${\Vert W_S·\left(AU-Y\right)\Vert }_2^2$ was a weighted data-consistency term with the statistical weighting factors $W_S$ being inversely proportional to the statistical noise estimated in the projection domain, and $·$ representing the element-wise multiplication. Therefore, a lower weight was assigned to the unreliable noisy projection data yielded by X-ray photons passing objects with high attenuation coefficients. In addition, $R\left(U\right)$ was a regularization term to further reduce noises and artifacts in $U$, and $\beta$ was a strength factor for regularization.

In Deep IR, Equation 2 was split into two sub-problems of data consistency in the projection domain and regularization in the image domain, as shown in Equation 3:

$$\{\begin{array}{c}{U}_{k+1}=\underset{U}{\mathrm{argmin}}{\Vert W_S·\left(AU-Y\right)\Vert }^2+\mu {\Vert U-X_k\Vert }^2\text{,}\\ X_{k+1}=\underset{X}{\mathrm{argmin}}\frac{\mu }{2}{\Vert X-U_{k+1}\Vert }^2+\beta R\left(X\right)\text{,}\end{array}$$ (Equation 3)

where the two decoupled items $U$ and $X$ could be solved alternately. Deep IR estimated $X_{k+1}$ using the 3D DL denoiser as described previously. The DL denoiser was trained to remove noise patterns specific to the first sub-problem, and its output $X_{k+1}$ was the denoised image volume and could be served as the initial seed in solving $U_{k+2}$. With the application of DL denoiser, Equation 3 therefore became Equation 4 as follows:

$$\{\begin{array}{c}{U}_{k+1}=\underset{U}{\mathrm{argmin}}{\Vert W_S·\left(AU-Y\right)\Vert }^2,\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{s}\mathrm{e}\mathrm{e}\mathrm{d}{U}^{\left(0\right)}=X_k\text{,}\\ X_{k+1}=3D\_DL\_Denoisor\left(U_{k+1}\right)\text{,}\end{array}$$ (Equation 4)

• (3)HYPER DPR:

The maximum likelihood estimate of the unknown image $\mathit{x}$ could be calculated as

$$\hat{\mathit{x}}=\underset{x}{\arg \max }\left\{L\left(\mathit{y}|\mathit{x}\right)-\frac{\lambda }{2}{\Vert \mathit{x}-\mathcal{z}\Vert }^2\right\}$$ (Equation 5)

where $L\left(\mathit{y}|\mathit{x}\right)$ was the log likelihood function, and $\mathcal{z}=\mathit{f}\left(\mathit{x};\mathit{\theta }\right)$ was a CNN representation of an image $\mathcal{z}$ with input image $\mathit{x}$ and parameters $\mathit{\theta }$. The DPR algorithm suggested that the network $\mathit{f}$ could be decomposed into many sub-networks to make the network training easier. Our current implementation employed two sub-networks, that is, $f=f_{DE}\circ f_{EH}$, where $f_{DE}:\mathit{x}+\mathit{v}\to \mathit{x}$ represented the denoising network (CNN-DE) which could remove the noise $\mathit{v}$ from the input image, and $f_{EH}:{\mathit{x}}^{\left(k\right)}\to {\mathit{x}}^{\left(k+q\right)}$ represented the enhancement network (CNN-EH) which mapped from a low convergent image ${\mathit{x}}^{\left(k\right)}$ to a high convergent image ${\mathit{x}}^{\left(k+q\right)}$.

Experimental settings and evaluation metrics

(1) Fast MRI: First, we compared the overall reconstruction performance of ACS and other methods (i.e., PI, AI, PI + AI, MoDL, and E2E-VarNet) on the testing data down-sampled according to predefined acceleration factors between 2 × and 3 ×. Six metrics were calculated to quantitatively evaluate the error and similarity between the reference and reconstructed images, including mean squared error (MSE), normalized mean squared error (NMSE), normalized root mean squared error (NRMSE), signal-to-noise ratio (SNR), peak signal-to-noise ratio (PSNR), and structural similarity (SSIM) index. Theses metrics were defined as follows (Equations 6, 7, 8, 9, 10, and 11):

$$MSE=\frac{\sum _{i=1}^M\sum _{j=1}^N{\Vert I_{full}\left(P_i,P_j\right)-I_{evaluation}\left(P_i,P_j\right)\Vert }^2}{M\times N}\text{,}$$ (Equation 6)

$$NMSE=\frac{\sum _{i=1}^M\sum _{j=1}^N{\Vert I_{full}\left(P_i,P_j\right)-I_{evaluation}\left(P_i,P_j\right)\Vert }^2}{\sum _{i=1}^M\sum _{j=1}^N{\Vert I_{full}\left(P_i,P_j\right)\Vert }^2}\text{,}$$ (Equation 7)

$$NRMSE=\sqrt{\frac{{\Vert I_{full}-I_{evaluation}\Vert }_2^2}{{\Vert I_{full}\Vert }_2^2}}\times 100\%\text{,}$$ (Equation 8)

$$SNR=10{\log }_{10}\left(\frac{\sum _{i=1}^M\sum _{j=1}^N{\Vert I_{full}\left(P_i,P_j\right)\Vert }^2}{MSE}\right)\text{,}$$ (Equation 9)

$$PSNR=10{\log }_{10}\left(\frac{{{\mathit{MAX}}_I}^2}{MSE}\right)\text{,}$$ (Equation 10)

$$SSIM\left(x,y\right)=\frac{\left(2{\mu }_x{\mu }_y+c_1\right)\left(2{\sigma }_{xy}+c_2\right)}{\left({{\mu }_x}^2+{{\mu }_y}^2+c_1\right)\left({{\sigma }_x}^2+{{\sigma }_y}^2+c_2\right)}\text{,}$$ (Equation 11)

where $I_{full}$ represented reference images reconstructed from fully sampled k-space data, and $I_{evaluation}$ represented the reconstructed image by different algorithms (i.e., ACS, PI, AI, PI + AI, MoDL, or E2E-VarNet) from down-sampled k-space data. Both images owned sizes of $M\times N$. $\mathrm{P}$ was the intensity of the pixels, and $\left(P_i,P_j\right)$ was the position of the pixel in the selected area. ${\mathit{MAX}}_I$ denoted the maximum value of the image point color. $\mu$ and $\sigma$ represented mean and variance, respectively. Box-and-whisker plots of six metrics were used to qualitatively compare the reconstruction performance of ACS with other methods under each acceleration factor. Similarly, we compared the overall reconstruction performance of ACS and PI on the external validation data down-sampled according to predefined acceleration factors between 2 × and 4 ×. The mean and standard deviation of NRMSE under each acceleration factor was plotted.

Next, by down-sampling the same testing dataset with an acceleration factor of 5 ×, we evaluated the feasibility of using ACS or PI to reliably reconstruct images from multiple fast MRI scans performed at the 100-s level for various static organs (e.g., head, cervical spine, lumbar spine, hip, knee), as well as from fast chest MR scan acquired within a single breath hold. Note that PI used uniform k-space under-sampling along the phase encoding direction, and requires additional 24 reference lines in the center k-space to calibrate coil sensitivity maps. In contrast, ACS achieved an identical net acceleration factor with a pre-defined pseudo-random under-sampling pattern in the phase encoding direction. Here, we listed the detailed imaging parameters used by the head and knee scans in the 100-s level fast MRI study. Head scans (Figure 4A): T2w FSE (matrix: 334 × 384), transversal T2w FLAIR (matrix: 250 × 288), transversal T1w FLAIR (matrix: 264 × 304), and sagittal T2w FSE (matrix: 334 × 384). Knee scans (Figure 4B): coronal PDw FSE (matrix: 259 × 288), sagittal PDw FSE (matrix: 259 × 288), sagittal T1w FSE (matrix: 288 × 288), and transversal PDw FSE (matrix: 259 × 288).

(2) Low-dose CT: For in vivo validation, a CCT189 MITA CT IQ low contrast phantom (The Phantom Laboratory, Salem, NY), containing four rods with different diameters and contrasts, was used. Following a helical CT protocol developed for the abdominal scans, the uniform section (only background) and the section containing data rods were repeatedly scanned 10 times with varying dose levels. For each dose level and contrast object, the corresponding region of interest (ROI) pairs were used as the input to a channelized Hotelling observer (CHO) with Gabor filters. SNR (i.e., detectability) was then calculated in the output of CHO and used as the quantitative metric for the LCD comparison between images reconstructed by Deep IR and FBP. Note that FBP used a body sharp kernel, because it could generate a similar spatial resolution to that achieved by the Deep IR method.

For in vivo validation, Deep IR-based reconstruction and FBP-based reconstruction were compared at different radiation doses, including 40% of the normal dose (8.00 mGy), 0.67 mGy, and 0.61 mGy. The reconstructed images in the chest and abdomen area were evaluated by two radiologists. The mean opinion scores were graded on a scale of 1–5 in terms of three aspects, i.e., noise suppression, streaking artifact reduction, and image structure fidelity. The higher the score, the better the diagnostic interpretation.

(3) Fast PET: PET data acquired in list mode for 120 s/bp were rebinned to 90, 60, 40, and 30 s/bp to simulate fast PET scans. The HYPER DPR algorithm was applied to the rebinned PET data, and the reconstructed images were compared to those using the standard OSEM algorithm with a 120 s/bp scan. For all reconstructions, TOF and resolution modeling techniques were used. To ensure the optimal settings for both OSEM and DPR algorithms, the subsets and the number of iterations of the two algorithms are determined independently and differently. Specifically, the OSEM algorithm defined subsets as 20 and fixed the iteration number at 2. In contrast, the DPR implementation involved 2 blocks, with the first block using subsets and iteration number of 20 and 2, respectively, and the second block using subsets and iteration number of 5 and 1, respectively.

For each patient, a volume of interest (VOI) with a diameter of 30 ± 3 mm was manually drawn on a homogeneous area of the right liver lobe, and the liver SNR were calculated as the ratio of VOI's mean value to its standard deviation. We calculated the SUV_max of 78 selected lesions, to quantitatively compare the efficacy of small lesion detection by DPR and OSEM. The median diameter of lesions was 15.0 mm.

Implementation details

The modality-specific reconstruction algorithms, ACS, Deep IR, and HYPER DPR, were implemented on United Imaging (Shanghai United Imaging Healthcare Co., Ltd., Shanghai, China)’s MRI, CT, and PET scanners, respectively. In this study, ACS was integrated into the 3 T MR whole-body scanner uMR780. Deep IR was packaged into uCT760 and uCT780. HYPER DPR was embedded into uEXPLORER and uMI 780.

Quantification and statistical analysis

For continuous variables that were approximately normally distributed, they were represented as mean ± standard deviation. For continuous variables with asymmetrical distributions, they were represented as median (25^th, 75^th percentiles). To quantitatively compare the reconstruction performance of ACS and other five methods (i.e., PI, AI, PI + AI, MoDL, and E2E-VarNet) in the testing dataset, six quantitative metrics (i.e., MSE, NMSE, NRMSE, SNR, PSNR, and SSIM index) were calculated. Statistical analyses are performed using two-way ANOVA followed by Sidak’s multiple comparisons tests. To quantitatively compare the reconstruction performance of ACS and PI in the external validation dataset, statistical analyses were performed on the NRMSE of the two reconstructed images using paired t-tests. To quantitatively compare the reconstruction performance of Deep IR and FBP, statistical analyses were performed on the opinion scores of the two reconstructed images using multiple Mann-Whitney U tests. To quantitatively compare the reconstruction performance of HYPER DPR and OSEM, statistical analyses were performed on SUV_max and SNR between two reconstructed images using the Friedman test, and all p values in this test were corrected by Bonferroni correction. All statistical analyses were implemented using SPSS (version 26.0), with ∗ indicating p < 0.05, ∗∗ indicating p < 0.01, ∗∗∗ indicating p < 0.001, and ∗∗∗∗ indicating p < 0.0001.

Published: July 18, 2023

Data and code availability

Data related to the experiments including MRI, CT, and PET are available publicly: https://doi.org/10.17632/j7khwb3z3r.1.

The custom code for training deep learning and iterative reconstruction models were written in Python with PyTorch. The code is available publicly: https://github.com/simonsf/Hybrid-DL-IR. Any additional information required to reanalyze the data reported in this work is available from the lead contact upon request.