Skip to main content
PMC home page
EPA Author Manuscripts logoLink to EPA Author Manuscripts
. Author manuscript; available in PMC: 2023 Aug 2.
Published in final edited form as: Auk. 2017 Oct 9;134(4):903–916. doi: 10.1642/auk-16-230.1

Demographic analysis demonstrates systematic but independent spatial variation in abiotic and biotic stressors across 59 percent of a global species range

El análisis demográfico demuestra variación espacial sistemática pero independiente en factores de estrés abiótico y biótico a través del 59% del rango global de una especie

Katharine J Ruskin 1,*, Matthew A Etterson 2, Thomas P Hodgman 3, Alyssa C Borowske 4, Jonathan B Cohen 5, Chris S Elphick 4, Christopher R Field 4, Rebecca A Longenecker 6, Erin King 7, Alison R Kocek 5, Adrienne I Kovach 8, Kathleen M O’Brien 9, Nancy Pau 10, W Gregory Shriver 6, Jennifer Walsh 8, Brian J Olsen 1
PMCID: PMC10395324  NIHMSID: NIHMS1877442  PMID: 37534301

Abstract

The balance of abiotic and biotic stressors experienced by a species likely varies across its range, resulting in spatially heterogeneous limitations on the species’ demographic rates. Support for spatial variation in stressors (often latitudinal gradients) has been found in many species, usually with physiological or correlative occupancy data, but it has rarely been estimated directly with demographic data. We collected demographic data from 23 sites spanning the majority of the Saltmarsh Sparrow (Ammodramus caudacutus) breeding range. Using data from 837 nests, we quantified the abiotic and biotic variables most important to nest survival, which is the dominant driver of both fecundity and population growth rate in this species. We separately estimated daily nest failure probability due to nest depredation (biotic stressor) and nest flooding (abiotic stressor), which collectively account for almost all nest failure in the species. Nest depredation decreased with latitude, whereas nest flooding was not related to latitude. Instead, nest flooding was best predicted by a combination of maximum high tide, extremity of rare flooding events, and date. For a single vital rate, we observed predictable variation in competing biotic and abiotic stressors across this species range. We observed that biotic and abiotic stressors were geographically independent, both on a large spatial scale and locally. Our results suggest that stressors on the fecundity of Saltmarsh Sparrow vary systematically across its range, but independently. The observed patterns of biotic and abiotic stress provide information for efforts to conserve the Saltmarsh Sparrow, which is considered threatened. Further, understanding the effects that different stressors, and their interactions, have on demographic rates is necessary to unravel the processes that govern species distributions and to effectively conserve biodiversity in the face of global change.

Keywords: Ammodramus caudacutus, fecundity, latitudinal gradients, nest survival, species range, stress gradients

INTRODUCTION

Factors that affect demographic processes vary over space in multiple taxa, often in conjunction with latitude. Theodosius Dobzhansky (1950) suggested that populations within the same species face systematically different types of stressors across the species range. He hypothesized that abiotic stressors such as climate pose greater challenges at high latitudes, whereas biotic stressors such as competition are more limiting for a species near its low-latitude range edge. In the years since its original publication, Dobzhansky’s hypothesis has been expanded by subsequent ecologists to the idea that the range of a species is limited by abiotic stressors at high latitudes and by biotic stressors at low latitudes (MacArthur 1984, Brown 1995, Brown et al. 1996). The theory has also grown to include at least 2 other gradients of abiotic stress, elevation (Diamond 1973) and water depth (Connell 1961). Normand et al. (2009) called this integrated theory the “asymmetric abiotic stress limitation” (AASL) hypothesis. Broadly, it postulates that a trade-off exists between physiological hardiness, which increases fitness in stressful abiotic conditions, and competitive ability, which increases fitness in areas of low abiotic stress.

The AASL hypothesis has been supported by a wide range of tests in a diverse array of species (for a review, see Parmesan et al. 2005). In many systems, the influence of biotic interactions on a species has been observed to increase with decreasing latitude. For example, rates of predation, herbivory, and parasitism often increase toward low latitudes in a wide variety of taxa (Schemske et al. 2009). In other systems, abiotic variables such as climate have been found to correlate with increased physiological tolerances. For example, Bergmann’s rule describes the pattern observed in many endothermic species, in which body size increases with latitude, a sign of increased physiological tolerance to abiotic stress that allows for increased survival in harsh climates (Bergmann 1847, Meiri and Dayan 2003). Despite physiological and correlative evidence that supports the AASL (Lord 1960, Caughley et al. 1988, Root 1988, Sand et al. 1995, Mehlman 1997, Loehle 1998, Sæther et al. 2008, Gaston 2009, Sexton et al. 2009), the effects of biotic and abiotic stressors and their interaction on species’ demographic rates have rarely been quantified across large spatial scales (for a notable exception, see Brewer and Gaston 2003).

In the present study, we used detailed demographic data collected across the breeding range of the Saltmarsh Sparrow (Ammodramus caudacutus) to quantify the abiotic and biotic variables that influence a key demographic parameter and examine how they vary with latitude. Using a multistate Markov model (Etterson et al. 2007, 2014), we separately estimated the probability of nest failure due to biotic stress (depredation) and abiotic stress (flooding) to explore 2 questions. First, we tested whether biotic and abiotic stress to Saltmarsh Sparrow fecundity varied systematically with latitude across the species range. We expected that, as predicted by the AASL, both nest depredation and flooding would be related to latitude. Specifically, we expected that there was a trade-off between these stressors, whereby nest flooding would increase and nest depredation decrease with latitude. Second, we explored which landscape-scale covariates best predicted biotic and abiotic stress affecting nest survival across a large spatial scale.

METHODS

Study System

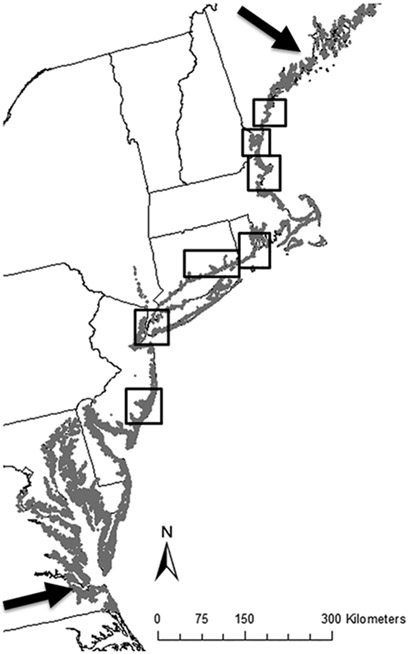
Saltmarsh Sparrows are well suited for investigating spatial gradients in stressors because they provide a simplified system in which we can examine the relative importance of biotic and abiotic variables in affecting demographic rates across the range of a species. First, we can focus on the latitudinal range boundaries because of the configuration of the Saltmarsh Sparrow range. Saltmarsh Sparrows breed exclusively in tidal marshes on the coast of the northeastern United States, from southern Maine to Virginia (Greenlaw and Rising 1994; Figure 1). Thus, the species range is oriented north–south along the U.S. Atlantic coast, with longitudinal boundaries clearly defined by absence of tidal-marsh habitat (Greenlaw and Rising 1994, Hodgman et al. 2002). Second, Saltmarsh Sparrows are specialists in a simple, relatively homogeneous habitat (Greenberg et al. 2006b, Tiner 2013) that allows us to rule out many confounding factors associated with more diverse systems, such as intraspecific competition (Greenlaw and Rising 1994, Bayard and Elphick 2010).

FIGURE 1.

FIGURE 1.

Open in a new tab

Our demographic study plots spanned 7 states within the Saltmarsh Sparrow breeding range (gray). Within each boxed area, we surveyed 1–5 study plots.

Third, nest survival is the dominant driver of both fecundity and population growth rate in this species (Field et al. 2017) and is largely determined by only 2 variables, one biotic (nest depredation) and one abiotic (nest flooding) (Greenlaw and Rising 1994, Gjerdrum et al. 2005, Greenberg et al. 2006a, Shriver et al. 2007). Nest flooding is the dominant abiotic stressor on Saltmarsh Sparrow fecundity because the species range is relatively small and governed by a temperate marine climate. Saltmarsh Sparrows build their nests a few centimeters above the ground in the high-marsh zone (Humphreys et al. 2007), which typically floods during monthly astronomical high tides and some storm events (Tiner 2013). Consequently, nest flooding is a major cause of nest failure for the species and an important driver of its nesting ecology (Greenlaw and Rising 1994, Gjerdrum et al. 2005, 2008, Shriver et al. 2007). Eggs can hatch after submersion in cold saltwater during ≤10 flooding events (Bayard and Elphick 2011) that typically last 1–2 hr (Gjerdrum et al. 2008), nesting females continue incubation following multiple flooding events (Bayard and Elphick 2011), and chicks can temporarily scramble up to the grass to stay above the water level during flooding events (Bayard and Elphick 2011).

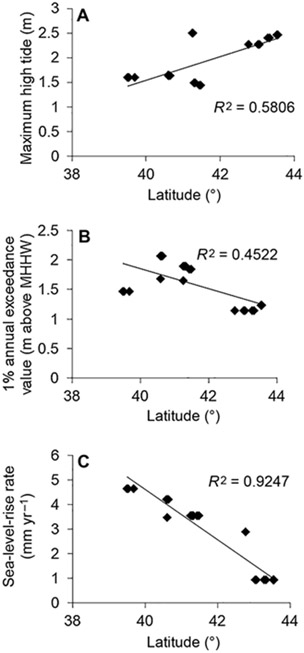
Tidal marshes are shaped by both regular flooding caused by astronomical tides and irregular flooding caused by weather (Teal 1986). In addition, recent anthropogenic sea-level rise has contributed to higher water levels and increased flooding of tidal marshes (Wong et al. 2014). These contributing factors to hydrology vary spatially throughout the Saltmarsh Sparrow range. Regular tidal flooding tends to increase with latitude within the species range, with marshes at the high-latitude edge of the range experiencing astronomical high tides that are ~2 times greater than those experienced in more southerly marshes (Figure 2A). By contrast, the extremity of rare flooding events is spatially heterogeneous across the range (Figure 2B), and rates of sea-level rise tend to decrease with latitude in this region (Figure 2C).

FIGURE 2.

FIGURE 2.

Open in a new tab

(A) Maximum high-tide height, as measured by maximum observed water level, May–August, 2011–2013, by study plot. Maximum high-tide height generally increases with latitude on the northeastern coast of the United States. (B) Extremity of rare flooding events, as measured by 1% annual exceedance value above the typical high-water mark (mean higher high water [MHHW]), by study plot. Areas within the geographic center of the Saltmarsh Sparrow range experience the highest exceedance values. (C) Relative sea-level-rise rate by study plot. Generally, sea-level-rise rate decreases with latitude within this region.

Nest depredation is the other primary cause of nest failure in Saltmarsh Sparrows and is also expected to vary spatially across the species range, due to large differences in predator community. For instance, lower-latitude marshes host nest predators that have no high-latitude analogue (e.g., rice rats [Oryzomys palustris]; Post 1981). Supporting this prediction, a meta-analysis of all avian taxa endemic to North American tidal marshes found that nest predation rates decreased with increasing latitude (Greenberg et al. 2006a).

Data Collection

From 2011 to 2013, we implemented a standardized data-collection protocol at 23 study plots spanning a great-circle distance of ~575 km (Figure 1). Our survey covered 59% of the Saltmarsh Sparrow’s latitudinal breeding range (Wiest et al. 2016). Study plots consisted of 1- to 28-ha areas of tidal marsh in the high-marsh zone, where Saltmarsh Sparrows build their nests. Saltmarsh Sparrow clutch size ranges from 2–5 eggs, with a mean (± SD) clutch size of 3.65 ± 0.74 across this study area from Maine to New Jersey. At each study plot, we searched for nests at least once per week throughout the breeding season (May–August). Once we found a nest, we revisited it every 2–5 days to determine success or failure. If a nest failed, we used multiple lines of evidence at the nest site to determine the cause of failure (for protocol, see Ruskin et al. 2017: appendix A).

We assigned depredation (biotic variable) as the cause of failure for nests found with broken or punctured eggs or with mangled chicks, and for nests that were empty and dry after nights that did not have tides high enough to flood the high marsh. We assigned flooding (abiotic variable) as the cause of failure for nests that were wet after nights with tides high enough to inundate the high marsh, that contained drowned chicks, or that had intact eggs outside the nest (because they floated out). We classified nests as failed for unknown reasons in cases of rare uncertain events (e.g., possible abandonment) or when we found conflicting evidence (e.g., nest bowl was wet and contained punctured eggs). We considered nests successful if, after survival on all previous visits, they were found empty when at least one nestling would have been 10 days old, the age at which chicks are able to leave the nest (Greenlaw and Rising 1994).

First, we tested whether both nest depredation (biotic variable) and nest flooding (abiotic variable) probabilities varied systematically across the Saltmarsh Sparrow range. Specifically, we tested whether nest failure probabilities varied with latitude. We recorded the latitude and longitude of each study plot at its approximate center using ArcGIS 10.1 (ESRI, Redlands, California, USA).

Second, we tested other variables as predictors of nest depredation and flooding probabilities, based on a priori hypotheses, to explore which landscape-scale and climatic variables affect Saltmarsh Sparrow fecundity. In addition to latitude, we expected that nest depredation would be related to serial date, and specifically that depredation would increase with date in the breeding season. This pattern has been found previously in a variety of avian taxa, perhaps due to nest predators increasing their foraging effort to feed their own growing young (Verhulst and Nilsson 2008). We also expected that nest depredation would be related to the age of the nest. Predation risk has been observed to change with nest age in a variety of systems, though results have been mixed regarding which ages of nests are most vulnerable to predation (Grant et al. 2005, Thompson 2007). For each nest, we estimated age as a continuous variable in 3 ways based on how much information was available (for details, see Ruskin et al. 2017: appendix B). For nests observed during egg laying, we assigned first egg date (date the first egg of the clutch was laid) by assuming that one egg was laid per day (Greenlaw and Rising 1994). For nests that were first observed with full clutches and hatched, we counted back to the first egg date using a visual estimation of chick ages and an average incubation interval of 12 days (Ruskin et al. 2017), assuming that incubation began with the last egg laid (Greenlaw and Rising 1994). For nests that were first observed with full clutches and did not hatch, we subtracted an average number of days until discovery, pooled by year and study plot, from the date the nest was first found.

We tested 3 potential predictors of nest flooding probability that reflect distinct inputs to tidal-marsh hydrology: maximum high tide to describe the amplitude of regular monthly flooding, extremity of rare flooding events, and relative sea-level-rise rate. For maximum high tide and extremity of rare flooding events, we obtained water-level data from the National Oceanic and Atmospheric Administration using the observation station that was closest to each study plot (approximately 15–50 km by water; Appendix Table 3). We used 1% annual exceedance probabilities above the mean daily high tide (i.e. mean higher high water [MHHW] datum) to reflect the extremity of rare flooding events at each study plot. Exceedance probabilities describe the likelihood that the water level will surpass a given height; for example, a 1% annual exceedance probability level of 1.23 m above MHHW means that the water level is expected to reach 1.23 m above MHHW only once in a century. This datum is corrected for local relative sea-level rise. We collected linear sea-level-rise estimates based on 1969–2011 water levels from Boon (2012), using the location nearest to each study plot (approximately 15–55 km by water). We expected that nest flooding probability would increase with each of these indices of flooding. Finally, we included serial date as a covariate for flooding risk because monthly high tides typically decrease in height throughout the breeding season, and thus we expected nest flooding probability to decrease with increasing serial date.

Statistical Analyses

We used the program MCestimate (Etterson et al. 2007, 2014) to calculate daily probabilities of nest survival and failure from competing risks. Daily probabilities control for biases introduced by the age at which nests are discovered (Mayfield 1975). MCestimate employs a multistate maximum likelihood approach to estimate daily nest failure probabilities as a Markov process via a generalization of the Mayfield method (Mayfield 1975, Etterson and Bennett 2005). In short, observations of the nest status for each visit and the number of days between visits (exposure days) are used to estimate daily probabilities of nest survival and failure for groups pooled by covariate values within a generalized linear modeling framework. Unlike traditional logistic exposure models (Dinsmore et al. 2002, Rotella et al. 2004, Shaffer 2004), MCestimate separately estimates probabilities of failure due to competing risks, in addition to total daily nest survival probability. We used MCestimate to generate daily nest failure probabilities as logitlinear (linear in the log-odds) functions of nest-level and study-plot-level covariates from nest monitoring data (Shaffer 2004, Etterson and Stanley 2008).

We adopted a 2-stage approach for model selection (Table 1). First, we separately compared candidate models for nest depredation and flooding. We compared models containing all additive combinations of potential covariates of nest depredation probability (latitude, serial date, and nest age) while modeling nest flooding probability as constant, plus an intercept-only null model (9 candidate models in total). Similarly, we modeled nest depredation probability as constant while we compared all additive combinations of the potential covariates of nest flooding probability (latitude, maximum high tide, 1% exceedance value, linear sea-level-rise rate, and serial date). Again, we also included the intercept-only null model (32 candidate models in total). We used second-order Akaike’s Information Criterion (AICc) to compare candidate models in each set while accounting for small sample size. We used a difference of 2 or more in AICc values to identify which models most parsimoniously described nest failure (Akaike 1974, Burnham and Anderson 2002), treating the simplest model within 2 AICc values of the model with the lowest AICc as the best (Arnold 2010). We also compared cumulative variable weights for all candidate variables to identify uninformative variables. For the second stage of model selection, we combined the best models for nest depredation and flooding, and compared the combined model to an intercept-only null model and the best models from the previous stage.

TABLE 1A.

Comparison of predictors of nest depredation probability, in the first stage of model selection.

Predictors of nest depredation Predictors of nest flooding Negative log likelihood ΔAICc a Weight K b
Latitude + nest age Intercept-only 1,508.76 0 0.71 4
Latitude + serial date + nest age Intercept-only 1,508.63 1.75 0.29 5
Nest age Intercept-only 1,522.44 25.39 0 3
Serial date + nest age Intercept-only 1,521.69 25.88 0 4
Latitude + serial date Intercept-only 1,531.05 44.93 0 4
Latitude Intercept-only 1,533.17 47.25 0 3
Intercept-only Intercept-only 1,548.19 75.39 0 2
Serial date Intercept-only 1,548.11 77.22 0 3
Open in a new tab
a

The AICc value of the top model was 3,025.52.

b

K = number of estimated parameters.

To report the daily probabilities of nest failure by study plot, we created models with study plot as the sole fixed-effect covariate to allow for maximum local variation. We created a separate model for each nest depredation probability, nest flooding probability, and total nest survival probability as predicted by study plot. We computed Pearson’s correlation coefficient to test whether daily nest flooding and nest depredation probabilities by study plot were related to each other, which would indicate a potential trade-off between biotic and abiotic stressors on a local scale (R Core Team 2014, package “Hmisc” function “rcorr”).

We also used the study-plot models for nest depredation, flooding, and total nest survival probabilities to assess the fit of our large-scale models using analyses of deviance (ANODEV; Skalski et al. 1993). We compared the study-plot models (which include the maximum variance, akin to observed values) to the latitude models and intercept-only models to quantify the amount of observed variation explained by latitude for each cause of nest failure. Similarly, because our top model for nest flooding probabilities included serial date, we compared models with an additive combination of study plot and serial date to the best large-scale and intercept-only nest-flooding models to quantify the amount of observed variation explained by our top model. We also conducted parametric bootstrapping goodness-of-fit tests, based on White et al. (2001), on our top models.

RESULTS

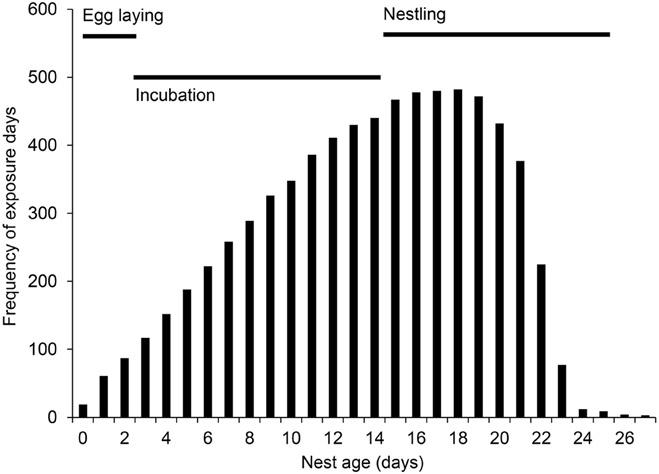
We collected nest monitoring data from 858 nests found over 3 yr of study, ranging between 3 and 138 nests plot−1. We excluded from analyses nests that, after censoring, had only one observation and one study plot where we found only one nest, resulting in a sample size of 837 nests. We included 3,059 nest visits in our analysis, covering a total of 8,859 exposure days. Using a subset of nests for which precise estimation of nest age was possible (nests observed during egg laying or that hatched), observations were relatively evenly distributed between incubation (43%) and nestling stages (54%), with small percentages of observations during egg laying (2%) and when nests were >24 days old (0.4%) (Appendix Figure 5).

We observed daily nest depredation probabilities that ranged from <0.001 to 0.087 and daily nest flooding probabilities that ranged from 0.016 to 0.116 by study plot. Daily nest survival probabilities ranged widely by study plot, from 0.857 to 0.970 (2–48% total nest survival over the 24-day nesting period; Appendix Table 4). Despite local heterogeneity, we observed clear, large-scale patterns in the nest failure probabilities of Saltmarsh Sparrows. ANODEV results confirmed a significant relationship between latitude and nest depredation probabilities (for maximum-variance study-plot model, negative log-likelihood [NLL] = 1,500.65, number of parameters [K] = 23; ANODEV: F1,20 = 9.24, P = 0.006), and parametric bootstrapping tests showed no evidence of lack of fit of this model to the observed data. Conversely, latitude offered almost no explanatory power for nest flooding probability, as judged by ANODEV (for maximum-variance study-plot model, NLL = 1,506.93, K = 23; ANODEV: F1,20 = 0.02, P = 0.88).

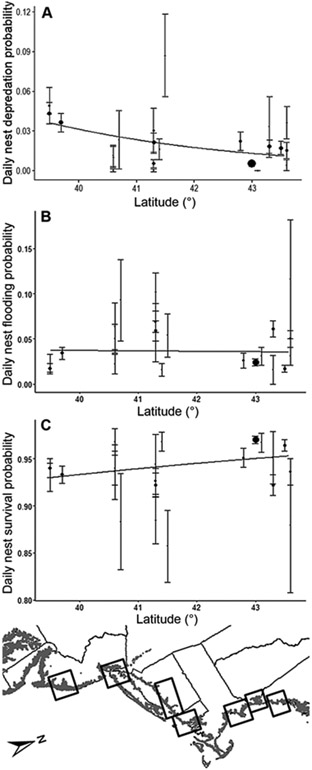
A combination of latitude and nest age best predicted daily nest depredation probability and performed better than the null model (Table 1A; ΔAICc = 74.86). Results from the ANODEV confirmed that the top model significantly explained observed variance in daily nest depredation probabilities (for maximum-variance study-plot model, NLL = 1,500.65, K = 23; ANODEV: F1,20 = 97.24, P < 0.001), and parametric bootstrapping tests showed no evidence of lack of fit of this model to the observed data. The log-odds of nest depredation probability increased linearly moving toward low latitudes (Figure 3) and increased with nest age (Table 2).

FIGURE 3.

FIGURE 3.

Open in a new tab

Daily nest failure and survival probabilities modeled as functions of latitude (lines) and study plot (demonstrates maximum local variance, akin to observed values; dot size is proportional to the sample size [number of nests] at each study plot; bar length is proportional to 1 SE), with date held constant (mean serial date = 188). (A) Nest depredation probability decreased with increasing latitude. (B) Daily nest flooding probability was not related to latitude. (C) Total daily nest survival probability increased slightly with increasing latitude.

TABLE 2.

Multinomial logit scale estimates from the top-ranked model of variables affecting nest survival probabilities of Saltmarsh Sparrows, 2011–2013.

Nest fate Predictor Coefficient a SE Observed
minimum		 Observed
maximum
Depredated Intercept 6.1594 2.2290 1 1
Depredated Latitude (decimal degrees) −0.2859 0.0533 39.5056 43.5655
Depredated Nest age 0.1300 0.0192 0 28
Flooded Intercept −4.5463 0.7573 1 1
Flooded Maximum high tide (m) 0.7823 0.1710 1.4377 2.5021
Flooded 1% exceedance value (m above mean higher high water) 1.1313 0.2133 1.1400 2.0604
Flooded Serial date −0.0107 0.0032 138 244
Open in a new tab
a

The coefficients are not scaled, but we provide the observed minimum and maximum columns to describe the range of values observed for each covariate in these data.

Three models of daily nest flooding probability were within 2.0 AICc values of the model with the lowest AICc. Of these 4, one model contained 5 predictive variables, 2 models contained 4 predictive variables, and one model contained only 3 predictive variables. The simplest model within this set also contained only the predictive variables with high cumulative variable weights (maximum high tide: 0.80; extremity of rare flooding events: 0.99; and serial date: 0.99), whereas the other, less parsimonious models contained predictive variables with low cumulative weights (latitude: 0.46; sea-level rise: 0.45). Further, the simplest model is also the only one in the set of 4 that did not include at least one predictive variable that had a parameter estimate with a 95% confidence interval that overlapped zero. Based on these multiple lines of evidence that the simplest model was the most parsimonious and contained variables with the most explanatory power, we chose the simplest model as our top model. Our top model used an additive combination of maximum high tide, extremity of rare flooding events, and serial date to predict daily nest flooding probability and performed much better than the null model (Table 1B; ΔAICc = 33.28). Results from the ANODEV confirmed that this model significantly explained observed variance in daily nest flooding probabilities (for maximum-variance study-plot + serial-date model, NLL = 1,499.37, K = 24; ANODEV: F1,20 = 13.46, P = 0.002), and parametric bootstrapping tests showed no evidence of lack of fit of this model to the observed data. The log-odds of nest flooding probability increased with maximum high tide, increased with extremity of rare flooding events (Figure 4), and decreased throughout the breeding season (Table 2).

TABLE 1B.

Comparison of predictors of nest flooding probability, in the first stage of model selection.

Predictors of nest
depredation		 Predictors of nest flooding Negative log
likelihood		 ΔAICc a Weight K b
Intercept-only Maximum high tide + sea-level rise + 1% exceedance value + serial date 1,527.22 0 0.29 6
Intercept-only Latitude + maximum high tide + 1% exceedance value + serial date 1,527.24 0.03 0.29 6
Intercept-only Maximum high tide + 1% exceedance value + serial date 1,528.55 0.65 0.21 5
Intercept-only Latitude + maximum high tide + sea-level rise + serial date + 1% exceedance value 1,527.16 1.88 0.11 7
Intercept-only Latitude + 1% exceedance value + serial date 1,530.05 3.66 0.05 5
Intercept-only Sea-level rise + 1% exceedance value + serial date 1,530.65 4.85 0.03 5
Intercept-only Latitude + sea-level rise + 1% exceedance value + serial date 1,530.02 5.60 0.02 6
Intercept-only Maximum high tide + 1% exceedance value 1,535.02 11.59 <0.01 4
Intercept-only Latitude + maximum high tide + 1% exceedance value 1,534.64 12.84 <0.01 5
Intercept-only Maximum high tide + sea-level rise + 1% exceedance value 1,534.69 12.94 <0.01 5
Intercept-only Latitude + maximum high tide + sea-level rise + 1% exceedance value 1,534.64 14.84 <0.01 6
Intercept-only Latitude + 1% exceedance value 1,536.93 15.42 <0.01 4
Intercept-only 1% exceedance value + serial date 1,537.28 16.12 <0.01 4
Intercept-only Sea-level rise + 1% exceedance value 1,537.48 16.52 <0.01 4
Intercept-only Latitude + sea-level rise + 1% exceedance value 1,536.93 17.42 <0.01 5
Intercept-only Maximum high tide + sea-level rise + serial date 1,538.71 20.99 <0.01 5
Intercept-only 1% exceedance value 1,540.9 21.36 <0.01 3
Intercept-only Latitude + maximum high tide + sea-level rise + serial date 1,538.04 21.65 <0.01 6
Intercept-only Latitude + maximum high tide + serial date 1,540.02 23.61 <0.01 5
Intercept-only Maximum high tide + serial date 1,541.26 24.08 <0.01 4
Intercept-only Latitude + sea-level rise + serial date 1,540.81 25.18 <0.01 5
Intercept-only Serial date 1,543.58 26.71 <0.01 3
Intercept-only Latitude + serial date 1,543.36 28.27 <0.01 4
Intercept-only Sea-level rise + serial date 1,543.58 28.71 <0.01 4
Intercept-only Maximum high tide + sea-level rise 1,543.66 28.88 <0.01 4
Intercept-only Latitude + maximum high tide + sea-level rise 1,543.1 29.75 <0.01 5
Intercept-only Latitude + maximum high tide 1,545.27 32.10 <0.01 4
Intercept-only Latitude + sea-level rise 1,545.39 32.34 <0.01 4
Intercept-only Intercept-only 1,548.19 33.93 <0.01 2
Intercept-only Maximum high tide 1,547.44 34.43 <0.01 3
Intercept-only Sea-level rise 1,547.73 35.01 <0.01 3
Intercept-only Latitude 1,548.14 35.84 <0.01 3
Open in a new tab
a

The AICc value of the top model was 3,066.45.

b

K = number of estimated parameters.

FIGURE 4.

FIGURE 4.

Open in a new tab

Daily nest flooding probabilities modeled as functions of landscape-level variables (lines) and study plot (akin to observed values; dot size is proportional to the number of nests at each study plot; bar length is proportional to 1 SE), with date held constant (mean serial date = 188). Daily nest flooding probability of Saltmarsh Sparrows was best predicted by an additive combination of (A) maximum observed high tide during the study period (May–August, 2011–2013); and (B) extremity of rare flooding events, as measured by 1% annual exceedance probability level (MHHW = mean higher high water) and serial date.

The combined model (nest depredation probability predicted by latitude and nest age; nest flooding probability predicted by maximum high tide, exceedance value, and serial date) predicted nest failure probabilities better than the best model for nest depredation probability (Table 1C; ΔAICc = 34.08), the best model for nest flooding probability (ΔAICc = 76.29), and the intercept-only null model (ΔAICc = 109.57). Parametric bootstrapping tests showed no evidence for lack of fit of the top model to the observed data. Daily nest depredation and nest flooding probabilities by study plot were not related (r = −0.17, n = 22, P = 0.46).

TABLE 1C.

Comparison of predictors of nest survival, in the second stage of model selection.

Predictors of nest
depredation		 Predictors of nest flooding Negative log
likelihood		 ΔAICc a Weight K b
Latitude + nest age Maximum high tide + 1% exceedance value + serial date 1,488.40 0 1 7
Latitude + nest age Intercept-only 1,508.76 34.71 0 4
Intercept-only Maximum high tide + 1% exceedance value + serial date 1,528.55 76.29 0 5
Intercept-only Intercept-only 1,548.19 109.57 0 2
Open in a new tab
a

The AICc value of the top model was 2,990.81.

b

K = number of estimated parameters.

DISCUSSION

We observed a variable landscape of competing abiotic and biotic stressors on Saltmarsh Sparrow fecundity across the species range. We observed a latitudinal trend in nest depredation probability. Consistent with the AASL, we observed that nest depredation increased toward low latitudes (Figure 3A). Few data exist on the abundance and diversity of nest predators in tidal marshes. However, the species richness of mammalian, reptilian, and avian predators all increase at lower latitudes (Cook 1969, Currie 1991). Nest flooding probability was not related to latitude, a result that is not consistent with the AASL. Instead, nest flooding probability was high in relation to nest depredation across the species range (Figure 3B) and was best predicted by an additive combination of 3 variables. Our results indicate that both regular monthly flooding from astronomical tides (represented by maximum high tide) and irregular, weather-related flooding (represented by exceedance value) drive spatial patterns of Saltmarsh Sparrow nest flooding. Further, nest depredation and flooding probabilities at each plot were uncorrelated, demonstrating that biotic and abiotic stressors on Saltmarsh Sparrow fecundity are not related at either a local or a large spatial scale. Therefore, in opposition to modern formulations of the AASL hypothesis, our results suggest that in this system, there is not a direct trade-off between physiological tolerance and competitive ability.

The underlying mechanisms structuring nest predator communities in this system appear to be independent of the controls on nest flooding rates at the scales we examined. These results suggest that Saltmarsh Sparrow fecundity is shaped by 2 different gradients of stress that vary independently but act simultaneously. The AASL hypothesis originally cited a single gradient, latitude, which explained both biotic diversity and abiotic stress gradients. Extensions of this hypothesis have similarly used single gradients (e.g., elevation or water depth) to explain the strength of both biotic and abiotic stressors as drivers of the distributions and demographic rates of species (Connell 1961, Diamond 1973). To our knowledge, multiple gradients have not been examined in the same species, though results suggesting 2 abiotic stress gradients have been found previously (Pianka 1970). We found that the stressors of nest flooding and depredation were geographically independent throughout the Saltmarsh Sparrow range. Similar patterns of both abiotic and biotic stress gradients affecting one vital rate of a species might be expected in other systems in which gradients of abiotic stress vary independently in relation to broad latitudinal patterns in biodiversity (e.g., gradients of fire regime, wind damage, or urbanization).

The spatially independent patterns of biotic and abiotic stress on fecundity that we observed may be signs of a stress gradient related to human modification of the landscape. The extremity of rare flooding events was an important predictor of nest flooding in this system, and extreme water levels have increased on a global scale (Wong et al. 2014). Generally, this trend is driven by sea-level rise (Wong et al. 2014). However, New York and Connecticut—which have high nest-flooding probabilities compared to the local maxima of high tides—also host particularly high exceedance values for the region. One explanation could be that these areas have more impermeable surfaces, which result in increased runoff and “flashier” flooding patterns (Hollis 1975). Authors have also noted that increased rates of nutrient pollution associated with runoff have corresponded in time with accelerated rates of marsh loss within these urbanized states (Hartig et al. 2002, Deegan et al. 2012).

Regardless of whether the spatial independence of stressors on saltmarsh fecundity is a historical pattern or a result of anthropogenic change, modern Saltmarsh Sparrow populations are affected by an axis of abiotic stress that is independent of latitude. The patterns of biotic and abiotic stress that we observed provide important information for efforts to conserve the Saltmarsh Sparrow, which is considered threatened (Greenlaw and Rising 1994, Butcher et al. 2007, IUCN 2012). For example, these results suggest that predator control may be an effective management tool at low latitudes of the species range but not at higher latitudes.

Further, understanding the effects that different stressors, and their interactions, have on demographic rates is necessary to unravel the processes that govern species distributions and predict their responses to anthropogenic change. For Saltmarsh Sparrows, we observed that the extremity of rare storms, which is linked to human modification of the landscape, is an important predictor of nest failure. We would thus expect that increased human development along the coast within the Saltmarsh Sparrow range would lead to declines in fecundity. This result highlights the possibility that other species may also be affected by a stress gradient that is correlated with human activity, such as urbanization or fire regime. Thus, understanding the demographic and spatial dynamics of species ranges is not only an important topic in theoretical ecology, but will become increasingly important for conservation in the face of global change.

ACKNOWLEDGMENTS

Thank you to our many collaborators and to the dozens of field technicians who helped collect these data.

Funding statement:

This work was primarily funded by a Competitive State Wildlife Grant (U2-5-R-1) via the U.S. Fish and Wildlife Service (USFWS), Federal Aid in Sportfish and Wildlife Restoration, to the states of Delaware, Maryland, Connecticut, and Maine. We received additional funding from the USFWS (Region 5, Division of Natural Resources, National Wildlife Refuge System), the U.S. Department of Agriculture (State Agricultural Experiment Station Project ME0-H-6-00492-12 and National Institute of Food and Agriculture McIntire-Stennis Project 225575), the National Park Service Gateway Learning Center Fellowship, the New York Department of Environmental Conservation (AM08634), and the National Science Foundation (DEB-1340008). This is Maine Agricultural and Forest Experiment Station Publication Number 3559. Graduate students were also funded in part by the University of Maine, the University of New Hampshire, and the University of Connecticut. The views expressed in this paper are those of the authors and do not necessarily reflect the views or policies of the U.S. Environmental Protection Agency. The findings and conclusions of this article are those of the authors and do not necessarily represent the views of the USFWS.

APPENDIX

Distribution of Observations across Breeding Stages: Methods and Results

To estimate the distribution of observations across different nest ages, we examined the subset of nests with the most precise nest ages, specifically nests that were either observed during egg-laying or hatched (n = 558). This subset excludes nests that were first observed with full clutches and only observed with eggs, because the nest ages are most imprecise for this subset of nests. Using the subset of nests with precise nest ages, observations were primarily distributed between observations during incubation (43%) and nestling stages (54%), with small percentages of observations during egg laying (2%) and when nests were >24 days old (0.4%), which is largely an artifact of the 2- to 5-day nest-check schedule. These percentages exclude nests with imprecise nest ages (n = 279), all of which were observed during incubation. Though we cannot precisely attribute observations to specific ages for these nests, we estimate that including those observations would not substantially change the distribution of observations. The small percentages of observations during egg laying and at >24 days would grow smaller, and we expect that the balance of observations between incubation and nestling stages would shift from 43% and 54% to approximately 57% and 40%, respectively. Finally, we note that the estimates of percentages of observations in different stages are an approximation because nests were not visited daily, and breeding stages can vary among individual nests.

APPENDIX FIGURE 5.

APPENDIX FIGURE 5.

Open in a new tab

Using the subset of nests with precise age estimates (nests that were observed during egg laying or that hatched; n = 571), observations were primarily distributed between incubation (43%) and nestling stages (54%), with few observations during egg laying (2%) or when nests were >24 days old (0.04%). Labeled bars at the top of the figure delineate the breeding stages for a typical nest, though we note that this is an approximation due to the 2- to 5-day visit schedule and individual variation.

APPENDIX TABLE 3.

Study plots and associated covariate information.

Study plot State Latitude
(decimal
degrees)		 Longitude
(decimal
degrees)		 Nearest
observed
water-level
station		 Maximum
high tide,
May–August,
2011–2013 (m)		 Nearest
observed
exceedance-level
station		 1%
exceedance
probability
value (m)		 Nearest
sea-level-rise
location a 		Sea-level-rise
probability,
1969–2011
(mm yr−1)
Oyster Creek NJ 39.5 −74.4 Atlantic City, NJ 1.60 Atlantic City, NJ 1.47 Atlantic City, NJ 4.63
Mullica Wilderness NJ 39.5 −74.4 Atlantic City, NJ 1.60 Atlantic City, NJ 1.47 Atlantic City, NJ 4.63
AT&T NJ 39.7 −74.2 Atlantic City, NJ 1.60 Atlantic City, NJ 1.47 Atlantic City, NJ 4.63
Four Sparrow Marsh b NY 40.6 −73.9 Sandy Hook, NJ 1.64 Sandy Hook, NJ 2.06 Sandy Hook, NJ 4.19
Sawmill Creek b NY 40.6 −74.2 Bergen Point West Reach, NY 1.65 The Battery, NY 1.68 The Battery, NY 3.47
Marine Nature Park b NY 40.6 −73.6 Sandy Hook, NJ 1.64 Sandy Hook, NJ 2.06 Sandy Hook, NJ 4.19
Idlewild b NY 40.7 −73.8 Sandy Hook, NJ 1.64 Sandy Hook, NJ 2.06 Sandy Hook, NJ 4.19
East River CT 41.3 −72.7 New Haven, CT 2.50 Bridgeport, CT 1.65 New London, CT 3.53
Hammonasset CT 41.3 −72.5 New Haven, CT 2.50 New London, CT 1.89 New London, CT 3.53
Pattagansett CT 41.3 −72.2 New London, CT 1.50 New London, CT 1.89 New London, CT 3.53
Waterford CT 41.3 −72.1 New London, CT 1.50 New London, CT 1.89 New London, CT 3.53
Barn Island CT 41.3 −71.9 New London, CT 1.50 New London, CT 1.89 New London, CT 3.53
John H. Chaffee RI 41.4 −71.5 Newport, RI 1.44 Newport, RI 1.84 New London, CT 3.53
Sachuest Point RI 41.5 −71.2 Newport, RI 1.44 Newport, RI 1.84 New London, CT 3.53
Parker River MA 42.8 −70.8 Fort Point, NH 2.27 Seavey Island, ME 1.14 Boston, MA 2.88
Chapman’s Landing NH 43.0 −70.9 Fort Point, NH 2.27 Seavey Island, ME 1.14 Portland, ME 0.94
Lubberland Creek NH 43.1 −70.9 Fort Point, NH 2.27 Seavey Island, ME 1.14 Portland, ME 0.94
Eldridge Road ME 43.3 −70.6 Wells, ME 2.41 Seavey Island, ME 1.14 Portland, ME 0.94
Little River ME 43.3 −70.5 Wells, ME 2.41 Seavey Island, ME 1.14 Portland, ME 0.94
Jones Creek ME 43.5 −70.4 Portland, ME 2.46 Portland, ME 1.23 Portland, ME 0.94
Nonesuch River ME 43.6 −70.3 Portland, ME 2.46 Portland, ME 1.23 Portland, ME 0.94
Libby River ME 43.6 −70.3 Portland, ME 2.46 Portland, ME 1.23 Portland, ME 0.94
Scarborough River ME 43.6 −70.4 Portland, ME 2.46 Portland, ME 1.23 Portland, ME 0.94
Open in a new tab
b

Water-level values were obtained from 2012 and 2013 data only, because this study plot was not surveyed in 2011, when Hurricane Irene resulted in particularly high water levels in this area.

APPENDIX TABLE 4.

Global and local predicted probabilities of nest depredation, nest flooding, and total nest survival (± SE) for Saltmarsh Sparrows by study plot (ordered from low to high latitude), 2011–2013.

Site a State Number
of nests		 Global daily nest
depredation
probability b 		Local daily nest
depredation
probability c 		Global daily nest
flooding
probability b 		Local daily nest
flooding probability c 		Global daily nest
survival
probability b 		Local daily nest
survival
probability c
Oyster Creek NJ 34 0.031 ± 0.004 0.049 ± 0.014 0.026 ± 0.003 0.023 ± 0.010 0.944 ± 0.005 0.930 ± 0.015
Mullica Wilderness NJ 76 0.030 ± 0.004 0.043 ± 0.008 0.026 ± 0.003 0.017 ± 0.006 0.944 ± 0.005 0.940 ± 0.010
AT&T NJ 79 0.029 ± 0.004 0.036 ± 0.007 0.026 ± 0.003 0.034 ± 0.007 0.945 ± 0.005 0.933 ± 0.009
Four Sparrow Marsh NY 15 0.023 ± 0.002 0.011 ± 0.008 0.051 ± 0.007 0.022 ± 0.011 0.928 ± 0.007 0.968 ± 0.014
Sawmill Creek NY 23 0.023 ± 0.002 0.010 ± 0.008 0.034 ± 0.003 0.050 ± 0.016 0.945 ± 0.004 0.940 ± 0.018
Marine Nature Park NY 8 0.023 ± 0.002 0.000 ± 0.001 0.051 ± 0.007 0.064 ± 0.026 0.928 ± 0.007 0.936 ± 0.029
Idlewild NY 6 0.022 ± 0.002 0.023 ± 0.022 0.051 ± 0.007 0.093 ± 0.045 0.929 ± 0.007 0.883 ± 0.051
Hammonasset CT 49 0.019 ± 0.002 0.005 ± 0.003 0.076 ± 0.010 0.069 ± 0.012 0.904 ± 0.010 0.926 ± 0.014
East River CT 59 0.019 ± 0.002 0.021 ± 0.007 0.059 ± 0.006 0.059 ± 0.011 0.921 ± 0.006 0.922 ± 0.013
Pattaganset CT 5 0.019 ± 0.002 0.000 ± 0.001 0.039 ± 0.005 0.057 ± 0.032 0.945 ± 0.005 0.944 ± 0.032
Barn Island CT 30 0.018 ± 0.002 0.030 ± 0.017 0.039 ± 0.005 0.102 ± 0.021 0.945 ± 0.005 0.885 ± 0.025
John H. Chaffee RI 25 0.018 ± 0.002 0.016 ± 0.008 0.035 ± 0.005 0.016 ± 0.007 0.948 ± 0.005 0.968 ± 0.010
Sachuest Point RI 18 0.018 ± 0.002 0.087 ± 0.031 0.035 ± 0.005 0.054 ± 0.024 0.949 ± 0.005 0.857 ± 0.038
Parker River MA 43 0.012 ± 0.002 0.022 ± 0.007 0.030 ± 0.003 0.026 ± 0.008 0.958 ± 0.003 0.951 ± 0.010
Chapman’s Landing NH 138 0.011 ± 0.002 0.005 ± 0.002 0.030 ± 0.003 0.024 ± 0.004 0.959 ± 0.003 0.970 ± 0.004
Lubberland Creek NH 24 0.011 ± 0.002 0.000 ± 0.000 0.030 ± 0.003 0.031 ± 0.010 0.959 ± 0.003 0.967 ± 0.010
Eldridge Road ME 64 0.011 ± 0.002 0.018 ± 0.005 0.032 ± 0.003 0.061 ± 0.009 0.957 ± 0.003 0.922 ± 0.011
Little River ME 5 0.010 ± 0.002 0.033 ± 0.023 0.032 ± 0.003 0.016 ± 0.016 0.957 ± 0.003 0.951 ± 0.028
Jones Creek ME 62 0.010 ± 0.002 0.017 ± 0.005 0.037 ± 0.003 0.017 ± 0.004 0.953 ± 0.003 0.964 ± 0.006
Nonesuch River ME 25 0.010 ± 0.002 0.036 ± 0.012 0.037 ± 0.003 0.031 ± 0.010 0.953 ± 0.003 0.936 ± 0.014
Libby River ME 3 0.010 ± 0.002 0.004 ± 0.004 0.037 ± 0.003 0.116 ± 0.066 0.953 ± 0.003 0.879 ± 0.071
Scarborough Marsh ME 46 0.010 ± 0.002 0.015 ± 0.006 0.037 ± 0.003 0.050 ± 0.009 0.953 ± 0.003 0.936 ± 0.014
Open in a new tab
a

The study plot Waterford in Connecticut was excluded from analyses due to small sample size (n = 1).

b

Global probabilities were calculated using the parameter estimates and SEs from the top-ranked combined model (nest depredation modeled as a function of latitude and nest age, nest flooding as a function of maximum high tide, 1% exceedance value, and serial date) based on the covariate values for each study plot. Date and nest age were held constant at the mean values observed (nest age = 13 days; serial date = 188).

c

Local probabilities were calculated using study plot as the sole predictive variable in models of daily nest depredation, flooding, and survival.

Footnotes

Ethics statement: This research was conducted in compliance with the institutional animal care and use committees of the University of Maine (approval A2011-04-02), University of New Hampshire (approvals 100605 and 130604), State University of New York College of Environmental Science and Forestry (approval 120101), University of Connecticut (approval A11-013), and University of Delaware (approval AUP1157-2015-2).

LITERATURE CITED

  1. Akaike H (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control AC- 19:716–723. [Google Scholar]
  2. Arnold TW (2010). Uninformative parameters and model selection using Akaike’s Information Criterion. Journal of Wildlife Management 74:1175–1178. [Google Scholar]
  3. Bayard TS, and Elphick CS (2010). Using spatial point-pattern assessment to understand the social and environmental mechanisms that drive avian habitat selection. The Auk 127:485–494. [Google Scholar]
  4. Bayard TS, and Elphick CS (2011). Planning for sea-level rise: Quantifying patterns of Saltmarsh Sparrow (Ammodramus caudacutus) nest flooding under current sea-level conditions. The Auk 128:393–403. [Google Scholar]
  5. Bergmann C (1847). Über die Verhältnisse der Wärmeokönomie der Thiere zu ihrer Grösse. Gottinger Studien 3:595–708. [Google Scholar]
  6. Boon JD (2012). Evidence of sea level acceleration at U.S. and Canadian tide stations, Atlantic Coast, North America. Journal of Coastal Research 28:1437–1445. [Google Scholar]
  7. Brewer AM, and Gaston KJ (2003). The geographical range structure of the holly leaf-miner. II. Demographic rates. Journal of Animal Ecology 72:82–93. [Google Scholar]
  8. Brown JH (1995). Macroecology. University of Chicago Press, Chicago, IL, USA. [Google Scholar]
  9. Brown JH, Stevens GC, and Kaufman DM (1996). The geographic range: Size, shape, boundaries, and internal structure. Annual Review of Ecology and Systematics 27:597–623. [Google Scholar]
  10. Burnham KP, and Anderson DR (2002). Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach, second edition. Springer, New York, NY, USA. [Google Scholar]
  11. Butcher GS, Niven DK, Panjabi AO, Pashley DN, and Rosenberg KV (2007). The 2007 WatchList for United States birds. American Birds 61:18–25. [Google Scholar]
  12. Caughley G, Grice D, Barker R, and Brown B (1988). The edge of the range. Journal of Animal Ecology 57:771–785. [Google Scholar]
  13. Connell JH (1961). Effects of competition, predation by Thais lapillus, and other factors on natural populations of the barnacle Balanus balanoides. Ecological Monographs 31:61–104. [Google Scholar]
  14. Cook RE (1969). Variation in species density of North American birds. Systematic Biology 18:63–84. [Google Scholar]
  15. Currie DJ (1991). Energy and large-scale patterns of animal- and plant-species richness. The American Naturalist 137:27–49. [Google Scholar]
  16. Deegan LA, Johnson DS, Warren RS, Peterson BJ, Fleeger JW, Fagherazzi S, and Wollheim WM (2012). Coastal eutrophication as a driver of salt marsh loss. Nature 490:388–392. [DOI] [PubMed] [Google Scholar]
  17. Diamond JM (1973). Distributional ecology of New Guinea birds. Science 179:759–769. [DOI] [PubMed] [Google Scholar]
  18. Dinsmore SJ, White GC, and Knopf FL (2002). Advanced techniques for modeling avian nest survival. Ecology 83:3476–3488. [Google Scholar]
  19. Dobzhansky T (1950). Evolution in the tropics. American Scientist 38:209–221. [Google Scholar]
  20. Etterson MA, and Bennett RS (2005). Including transition probabilities in nest survival estimation: A Mayfield Markov chain. Ecology 86:1414–1421. [Google Scholar]
  21. Etterson MA, and Stanley TR (2008). Incorporating classification uncertainty in competing-risks nest-failure analysis. The Auk 125:687–699. [Google Scholar]
  22. Etterson MA, Greenberg R, and Hollenhorst T (2014). Landscape and regional context differentially affect nest parasitism and nest predation for Wood Thrush in central Virginia, USA. The Condor: Ornithological Applications 116:205–214. [Google Scholar]
  23. Etterson MA, Nagy LR, and Robinson TR (2007). Partitioning risk among different causes of nest failure. The Auk 124:432–443. [Google Scholar]
  24. Field CR, Bayard TS, Gjerdrum C, Hill JM, Meiman S, and Elphick CS (2017). High-resolution tide projections reveal extinction threshold in response to sea-level rise. Global Change Biology 23:2058–2070. [DOI] [PubMed] [Google Scholar]
  25. Gaston KJ (2009). Geographic range limits: Achieving synthesis. Proceedings of the Royal Society B 276:1395–1406. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Gjerdrum C, Elphick CS, and Rubega M (2005). Nest site selection and nesting success in saltmarsh breeding sparrows: The importance of nest habitat, timing, and study site differences. The Condor 107:849–862. [Google Scholar]
  27. Gjerdrum C, Sullivan-Wiley K, King E, Rubega MA, and Elphick CS (2008). Egg and chick fates during tidal flooding of Saltmarsh Sharp-tailed Sparrow nests. The Condor 110:579–584. [Google Scholar]
  28. Grant TA, Shaffer TL, Madden EM, and Pietz PJ (2005). Time-specific variation in passerine nest survival: New insights into old questions. The Auk 122:661–672. [Google Scholar]
  29. Greenberg R, Elphick C, Nordby JC, Gjerdrum C, Spautz H, Shriver G, Schmeling B, Olsen B, Marra P, Nur N, and Winter M (2006a). Flooding and predation: Trade-offs in the nesting ecology of tidal-marsh sparrows. Studies in Avian Biology 32:96–109. [Google Scholar]
  30. Greenberg R, Maldonado JE, Droege S, and McDonald MV (2006b). Tidal marshes: A global perspective on the evolution and conservation of their terrestrial vertebrates. BioScience 56:675–685. [Google Scholar]
  31. Greenlaw JS, and Rising JD (1994). Saltmarsh Sparrow (Ammodramus caudacutus). In Birds of North America Online (Rodewald PG, Editor). Cornell Lab of Ornithology, Ithaca, NY, USA. http://bna.birds.cornell.edu/bna/species/112 [Google Scholar]
  32. Hartig EK, Gornitz V, Kolker A, Mushacke F, and Fallon D (2002). Anthropogenic and climate-change impacts on salt marshes of Jamaica Bay, New York City. Wetlands 22:71–89. [Google Scholar]
  33. Hodgman TP, Shriver WG, and Vickery PD (2002). Redefining range overlap between the sharp-tailed sparrows of coastal New England. The Wilson Bulletin 114:38–43. [Google Scholar]
  34. Hollis GE (1975). The effect of urbanization on floods of different recurrence interval. Water Resources Research 11:431–435. [Google Scholar]
  35. Humphreys S, Elphick CS, Gjerdrum C, and Rubega M (2007). Testing the function of the domed nests of Saltmarsh Sharp-tailed Sparrows. Journal of Field Ornithology 78:152–158. [Google Scholar]
  36. IUCN (2012). Ammodramus caudacutus. The IUCN Red List of Threatened Species. http://www.iucnredlist.org/ [Google Scholar]
  37. Loehle C (1998). Height growth rate tradeoffs determine northern and southern range limits for trees. Journal of Biogeography 25:735–742. [Google Scholar]
  38. Lord RD (1960). Litter size and latitude in North American mammals. American Midland Naturalist 64:488–499. [Google Scholar]
  39. MacArthur RH (1984). Geographical Ecology: Patterns in the Distribution of Species. Princeton University Press, Princeton, NJ, USA. [Google Scholar]
  40. Mayfield HF (1975). Suggestions for calculating nest success. The Wilson Bulletin 87:456–466. [Google Scholar]
  41. Mehlman DW (1997). Change in avian abundance across the geographic range in response to environmental change. Ecological Applications 7:614–624. [Google Scholar]
  42. Meiri S, and Dayan T (2003). On the validity of Bergmann’s rule. Journal of Biogeography 30:331–351. [Google Scholar]
  43. Normand S, Treier UA, Randin C, Vittoz P, Guisan A, and Svenning J-C (2009). Importance of abiotic stress as a range-limit determinant for European plants: Insights from species responses to climatic gradients. Global Ecology and Biogeography 18:437–449. [Google Scholar]
  44. Parmesan C, Gaines S, Gonzalez L, Kaufman DM, Kingsolver J, Peterson AT, and Sagarin R (2005). Empirical perspectives on species borders: From traditional biogeography to global change. Oikos 108:58–75. [Google Scholar]
  45. Pianka ER (1970). Comparative autecology of the lizard Cnemidophorus tigris in different parts of its geographic range. Ecology 51:703–720. [Google Scholar]
  46. Post W (1981). The influence of rice rats Oryzomys palustris on the habitat use of the seaside sparrow Ammospiza maritima. Behavioral Ecology and Sociobiology 9:35–40. [Google Scholar]
  47. R Core Team (2014). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. [Google Scholar]
  48. Root T (1988). Environmental factors associated with avian distributional boundaries. Journal of Biogeography 15:489–505. [Google Scholar]
  49. Rotella JJ, Dinsmore SJ, and Shaffer TL (2004). Modeling nest-survival data: A comparison of recently developed methods that can be implemented in MARK and SAS. Animal Biodiversity and Conservation 27:187–205. [Google Scholar]
  50. Ruskin KJ, Etterson MA, Hodgman TP, Borowske AC, Cohen JB, Elphick CS, Field CR, Kern RA, King E, Kocek AR, Kovach AI, et al. (2017). Seasonal fecundity is not related to geographic position across a species’ global range despite a central peak in abundance. Oecologia 183:291–301. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Sæther B-E, Lillegård M, Grøtan V, Drever MC, Engen S, Nudds TD, and Podruzny KM (2008). Geographical gradients in the population dynamics of North American prairie ducks. Journal of Animal Ecology 77:869–882. [DOI] [PubMed] [Google Scholar]
  52. Sand H, Cederlund G, and Danell K (1995). Geographical and latitudinal variation in growth patterns and adult body size of Swedish moose (Alces alces). Oecologia 102:433–442. [DOI] [PubMed] [Google Scholar]
  53. Schemske DW, Mittelbach GG, Cornell HV, Sobel JM, and Roy K (2009). Is there a latitudinal gradient in the importance of biotic interactions? Annual Review of Ecology, Evolution, and Systematics 40:245–269. [Google Scholar]
  54. Sexton JP, McIntyre PJ, Angert AL, and Rice KJ (2009). Evolution and ecology of species range limits. Annual Review of Ecology, Evolution, and Systematics 40:415–436. [Google Scholar]
  55. Shaffer TL (2004). A unified approach to analyzing nest success. The Auk 121:526–540. [Google Scholar]
  56. Shriver WG, Vickery PD, Hodgman TP, and Gibbs JP (2007). Flood tides affect breeding ecology of two sympatric sharp-tailed sparrows. The Auk 124:552–560. [Google Scholar]
  57. Skalski JR, Hoffman A, and Smith SG (1993). Testing the significance of individual- and cohort-level covariates in animal survival studies. In Marked Individuals in the Study of Bird Populations (Lebreton J-D and North PM, Editors). Birkhäuser, Basel, Switzerland. pp. 39–49. [Google Scholar]
  58. Teal JM (1986). The ecology of regularly flooded salt marshes of New England: A community profile. U.S. Fish and Wildlife Service, Biological Report 85(7.4). [Google Scholar]
  59. Thompson FR III (2007). Factors affecting nest predation on forest songbirds in North America. Ibis 149:98–109. [Google Scholar]
  60. Tiner RW (2013). Tidal Wetlands Primer: An Introduction to Their Ecology, Natural History, Status, and Conservation. University of Massachusetts Press, Amherst, MA, USA. [Google Scholar]
  61. Verhulst S, and Nilsson J-Å (2008). The timing of birds’ breeding seasons: A review of experiments that manipulated timing of breeding. Philosophical Transactions of the Royal Society B 363:399–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. White GC, Burnham KP, and Anderson DR (2001). Advanced features of program MARK. In Wildlife, Land, and People: Priorities for the 21st Century. Proceedings of the Second International Wildlife Management Congress (Field R, Warren RJ, Okarma H, and Sievert PR, Editors). The Wildlife Society, Bethesda, MD, USA. pp. 368–377. [Google Scholar]
  63. Wiest WA, Correll MD, Olsen BJ, Elphick CS, Hodgman TP, Curson DR, and Shriver WG (2016). Population estimates for tidal marsh birds of high conservation concern in the northeastern USA from a design-based survey. The Condor: Ornithological Applicationsrwo 118:274–288. [Google Scholar]
  64. Wong PP, Losada IJ, Gattuso J-P, Hinkel J, Khattabi A, McInnes KL, Saito Y, and Sallenger A (2014). Part A: Global and sectoral aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. New York, NY, USA. pp. 361–409. [Google Scholar]

RESOURCES