Simulation of two electrode reactions coupled by the chemical reaction

Abstract

A model of an ECE mechanism consisting of two reversible electrode reactions coupled by the kinetically controlled, second order, reversible chemical reaction is developed for the staircase cyclic voltammetry on the rotating disk electrode. The relationship between the limiting current of the second wave and the rate constant of chemical reaction is investigated. The concentration of electroinactive component of the forward reaction influences the half-wave potential of the first wave and the limiting current of the second wave. The responses of the mechanisms with reversible and irreversible chemical reactions are compared.

1. Introduction

In organic electrolytes, electrode reactions of many compounds, such as catechols [1] and quinones [2], consist of two successive electron transfers connected by the transfer of protons [3–5]. These reactions are examples of the ECE mechanism [6–12] and the nine-member square scheme [13–15]. They were observed in electroreduction of p-nitrosophenol [16, 17], benzenesulfonyl floride [18, 19] and hexacyanochromate(III) [20] and in electrooxidation of tocopherols [21], methylcatechol [22, 23] and dopamine [24]. The theory of this mechanism is developed for polarography [8, 25–29], cyclic voltammetry [20, 30–33], square wave voltammetry [34–38], rotating disk measurements [39, 40] and the surface reactions in protein film voltammetry [41, 42]. The steady state responses on the rotating disk were calculated for totally irreversible chemical reactions and in this paper the investigation is extended to kinetically controlled, second order, reversible chemical reactions. The role of the electroinactive component of the reaction is analysed.

2. Model

It is assumed that an electrolytic solution contains dissolved reactant of the first electrode reaction and an electroinactive substance Y that cannot react with the mentioned reactant. The first electron transfer is fast and reversible electrooxidation. Its product cannot participate in the second electron transfer, but it can react with the substance Y to produce a compound that is stable at the given potential, but can be electrooxidized at higher potentials. Both chemical reaction and the second electrode reaction are reversible and the latter is fast. This mechanism can be represented by the following chemical equations:

$$\text{A}\leftrightarrow \text{B}+{\text{e}}^{-}$$ (1)

$$\text{B}+\text{Y}\leftrightarrow \text{G}$$ (2)

$$\text{G}\leftrightarrow \text{H}+{\text{e}}^{-}$$ (3)

On the rotating disk electrode, the mass transfer and currents are defined by the following system of differential equations and the initial and boundary conditions:

$$\frac{\partial c_A}{\partial t}=D\frac{{\partial }^2{c}_A}{\partial x^2}-v\frac{\partial c_A}{\partial x}$$ (4)

$$\frac{\partial c_B}{\partial t}=D\frac{{\partial }^2{c}_B}{\partial x^2}-v\frac{\partial c_B}{\partial x}-k_f{c}_B{c}_Y+k_b{c}_G$$ (5)

$$\frac{\partial c_Y}{\partial t}=D\frac{{\partial }^2{c}_Y}{\partial x^2}-v\frac{\partial c_Y}{\partial x}-k_f{c}_B{c}_Y+k_b{c}_G$$ (6)

$$\frac{\partial c_G}{\partial t}=D\frac{{\partial }^2{c}_G}{\partial x^2}-v\frac{\partial c_G}{\partial x}+k_f{c}_B{c}_Y-k_b{c}_G$$ (7)

$$\frac{\partial c_H}{\partial t}=D\frac{{\partial }^2{c}_H}{\partial x^2}-v\frac{\partial c_H}{\partial x}$$ (8)

$$t=0,x\ge 0:c_A=c_A^{*},c_B=0,c_Y=c_Y^{*},c_G=0,c_H=0$$ (9)

$$t>0,x\to \infty :c_A=c_A^{*},c_B\to 0,c_Y=c_Y^{*},c_G\to 0,c_H\to 0$$ (10)

$$x=0:\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{c}_{B,x=0}-c_{A,x=0}\hspace{0.17em}exp\hspace{0.17em}\left(\frac{F}{RT}(E-E_1^0)\right)$$ (11)

$$c_{H,x=0}=c_{G,x=0}\hspace{0.17em}exp\hspace{0.17em}\left(\frac{F}{RT}(E-E_2^0)\right)$$ (12)

$$D\hspace{0.17em}{\left(\frac{\partial c_A}{\partial x}\right)}_{x=0}=\frac{I_1}{FS}$$ (13)

$$D\hspace{0.17em}{\left(\frac{\partial c_B}{\partial x}\right)}_{x=0}=-\frac{I_1}{FS}$$ (14)

$${\left(\frac{\partial c_Y}{\partial x}\right)}_{x=0}=0$$ (15)

$$D\hspace{0.17em}{\left(\frac{\partial c_G}{\partial x}\right)}_{x=0}=\frac{I_2}{FS}$$ (16)

$$D\hspace{0.17em}{\left(\frac{\partial c_H}{\partial x}\right)}_{x=0}=-\frac{I_2}{FS}$$ (17)

$$v=-0.510\hspace{0.17em}{\omega }^{3/2}{\nu }^{-1/2}{x}^2$$ (18)

$$K=\frac{k_f}{k_b}.$$ (19)

The meanings of all symbols are reported in Table. Equations (4)–(8) were solved by the finite difference method [43]. The current was calculated for the staircase cyclic voltammetry. The dimensionless current is defined by the following equations:

Table.

Meanings of symbols.

Symbol	Meaning
c Z	Concentration of species Z
$c_A^{*},c_Y^{*}$	Bulk concentrations of species A and Y
D	Diffusion coefficient
δ	Diffusion layer thickness
ΔE	Potential increment
Δt	Time increment
Δ x	Space increment
E	Potential
$E_1^0,E_2^0$	Standard potentials
F	Faraday constant
I 1 ,I 2	Currents
ν	Kinematic viscosity
kf, kb	Rate constants of chemical reaction
K	Equilibrium constant of chemical reaction
ω	Rotation rate
R	Gas constant
S	Electrode surface area
T	Time
T	Temperature
τ	Step duration
V	Flow rate of solution

$$\mathrm{\Phi }=(I_1+I_2){\delta }_{ss}/FS{c}_A^{*}D$$ (20)

$${\delta }_{ss}=1.61\hspace{0.17em}{D}^{\frac{1}{3}}{\nu }^{\frac{1}{6}}{\omega }^{-\frac{1}{2}}.$$ (21)

The following parameters were not changed: D = 10⁻⁵ cm²/s, v = 10⁻² cm²/s, Δt = 10⁻⁵ s, $\frac{D\mathrm{\Delta }t}{\mathrm{\Delta }{x}^2}=0.2$,ΔE = 1 mV and τ = 10 ms.

3. Results and discussion

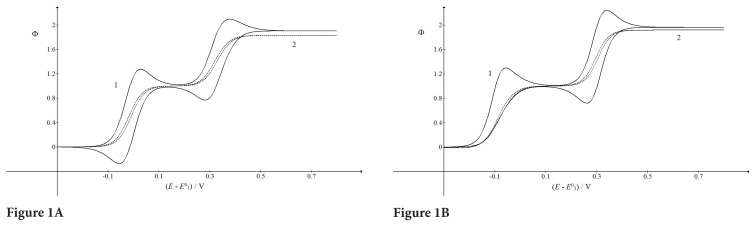
On the rotating disk electrode, the cyclic staircase voltammograms of the ECE mechanism with stable intermediates depend on the scan rate, the electrode rotation rate and the kinetics of chemical reaction. Some examples are shown in Figure 1. They were calculated assuming that the concentration of substance Y can be freely changed and adjusted to the concentration of the reactant A. If the rate constants of chemical reaction are very high and equal ( $K{c}_A^{*}=1$) and the rotation rate is low, the response is characterized by two maxima and two minima at 0.027 V, 0.378 V, 0.281 V, and −0.057 V vs. $E_1^0$, respectively. Considering that $E_2^0-E_1^0=0.3\hspace{0.17em}\text{V}$, the two parts of the response are well separated. The last minimum at −0.057 V is important because it shows that very fast chemical reaction is transforming the second reactant G into the first product B in the reverse branch of voltammograms. This minimum is the evidence that the whole ECE mechanism is close to the equilibrium. The absence of this minimum that can be noted in Figure 1B shows that chemical reaction is irreversible. It is a consequence of very high equilibrium constant and very low backward rate constant that cannot produce the first product B in the reverse branch. The potentials of two maxima and the minimum are: −0.058 V, 0.340 V, and 0.261 V, respectively. The potential of the first maximum is 85 mV lower than in Figure 1A because the chemical reaction is consuming the product of the first electrode reaction and decreasing the formal potential of the first electron transfer [33].

Figure 1.

Dimensionless cyclic staircase voltammograms of the ECE mechanism on the rotating disk electrode under the transient (full line) and near steady-state (broken line) conditions. $E_2^0-E_1^0=0.3\hspace{0.17em}\text{V}$, DeltaE/τ = 0.1 V/s, $c_Y^{*}/c_A^{*}=1,\hspace{0.17em}{k}_f\hspace{0.17em}{c}_A^{*}={10}^4{\text{s}}^{-1},\hspace{0.17em}K{c}_A^{*}=1\hspace{0.17em}(\text{A})$ and 10³ (B) and ω/rad s⁻¹ = 4π (1) and 40π (2)

At higher rotation rates, the maxima and minima disappear and the response acquires the form of polarogram. The dimensionless limiting current of the first wave is equal to unit at 0.15 V vs. $E_1^0$. This is the base line for the measurement of limiting currents of the second wave. In Figure 1A the half-wave potentials are −0.019 V and 0.321 V in the anodic branch and −0.010 V and 0.330 V in the cathodic branch. This is because this response corresponds to the near steady state conditions. Under strict steady state both branches are overlapped. If $K{c}_A^{*}={10}^3$ the first wave appears at −0.082 V because of irreversibility of chemical reaction.

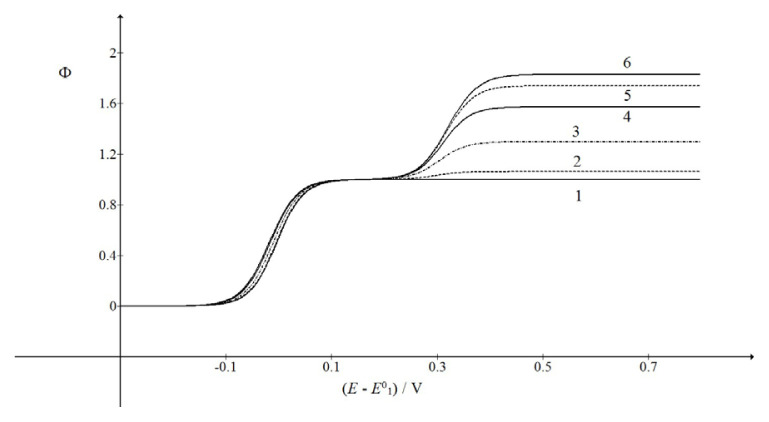
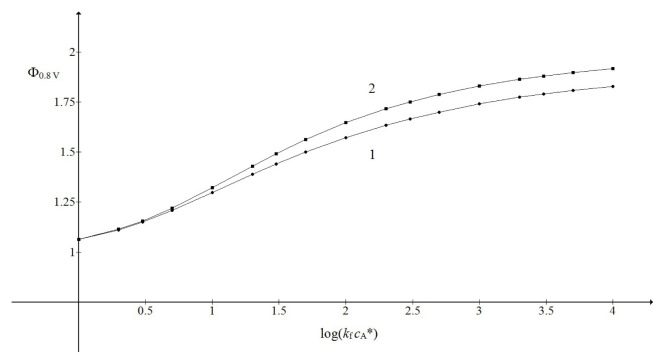
Limiting currents of the second wave depend on the normalized forward rate constant of the chemical reaction. This is shown in Figure 2. The half-wave potentials of the second wave are changing from 0.298 V vs. $E_1^0\hspace{0.17em}(k_f\hspace{0.17em}{c}_A^{*}=1\hspace{0.17em}{\text{s}}^{-1})$ to 0.321 V (curve 6) and those of the first wave from −0.004 V (1) to −0.019 V (6). These opposite trends are caused by the increasing rate of chemical reaction that creates a combination of EC and CE mechanisms. Furthermore, Figure 1A shows that the current at 0.8 V decreases with the increasing rotation rate. This is because the time that the product B spends near the electrode surface is longer if the rotation rate is slower. The limiting currents of the second wave depend on the logarithm of the product $k_f\hspace{0.17em}{c}_A^{*}$ in a sigmoidal manner, as can be seen in Figure 3. This figure also shows that the limiting currents of irreversible chemical reaction are higher than those of reversible one. Obviously, the backward component of the reaction diminishes its net gain. The relationship of this type can be represented by the general function [44]:

Figure 2.

Dependence of the second wave on the product of the forward rate constant of chemical reaction and the bulk concentration of the reactant A. $K{c}_A^{*}=1$, ω = 40π rad/s and $k_f\hspace{0.17em}{c}_A^{*}/{\text{s}}^{-1}=0\hspace{0.17em}(1)$, 1 (2), 10 (3), 100 (4), 1000 (5) and 10000 (6). All other data are as in Figure 1.

Figure 3.

Dependence of the limiting current of the second wave on the logarithm of the product $k_f\hspace{0.17em}{c}_A^{*}$. $K{c}_A^{*}=1$ (1) and 10³ (2). All other data are as in Figure 2.

$$\mathrm{\Phi }=1+{(k_f\hspace{0.17em}{c}_A^{*})}^p/\left[{(k_f\hspace{0.17em}{c}_A^{*})}^p+{(k_f\hspace{0.17em}{c}_A^{*})}_{1/2}^p\right].$$ (22)

Figure 4 shows that this representation is suitable for the limited range of the argument. The parameters p and ${(k_f\hspace{0.17em}{c}_A^{*})}_{1/2}$ can be determined by the logarithmic analysis:

Figure 4.

Dependence of the limiting currents of the second wave (the symbols) on the product $k_f\hspace{0.17em}{c}_A^{*}$. $K{c}_A^{*}=1$ (1) and 10³ (2). The lines 1 and 2 are calculated by Eq. (22) using parameters p = 0.4 and ${(k_f\hspace{0.17em}{c}_A^{*})}_{1/2}=54.54\hspace{0.17em}(1)$ and p = 0.5 and ${(k_f\hspace{0.17em}{c}_A^{*})}_{1/2}=33.34\hspace{0.17em}(2)$. All other data are as in Figure 2.

$$log\mathrm{\Psi }=p\hspace{0.17em}log(k_f\hspace{0.17em}{c}_A^{*})-p\hspace{0.17em}log{(k_f\hspace{0.17em}{c}_A^{*})}_{1/2}$$ (23)

$$\mathrm{\Psi }=(\mathrm{\Phi }-1)/[1-(\mathrm{\Phi }-1)].$$ (24)

Firstly the function Ψ is calculated and then the parameters are measured from the relationship between logΨ and $log(k_f\hspace{0.17em}{c}_A^{*})$. For instance, the limiting currents shown by the curve 2 in Figure 3 when transformed by Eq. (24) gave a set of log values that depended linearly on the corresponding $\text{log}(k_f\hspace{0.17em}{c}_A^{*})$ arguments, with the slope 0.5 and the intercept 5.8 (not shown). The curves 1 and 2 in Figure 4 are defined by the following functions:

$$\mathrm{\Phi }=1+{(k_f\hspace{0.17em}{c}_A^{*})}^{0.4}/\left[{(k_f\hspace{0.17em}{c}_A^{*})}^{0.4}+{54.54}^{0.4}\right]$$ (25)

$$\mathrm{\Phi }=1+\sqrt{k_f\hspace{0.17em}{c}_A^{*}}/[\sqrt{k_f\hspace{0.17em}{c}_A^{*}}+\sqrt{33.34}].$$ (26)

This procedure is useful for the transformation of the set of discrete data into a continuous function. By the variation of concentrations of A and Y, keeping them equal, one can estimate the parameter p from the gradient $\partial log\mathrm{\Psi }/\partial log{c}_A^{*}$. If the limiting current of the second wave is one half of the first limiting current and ω=40π rad/s, then logΨ=0 and $log{k}_f=log44-log{(c_A^{*})}_{1/2}$. The number 44 is an average of ${(k_f\hspace{0.17em}{c}_A^{*})}_{1/2}$ values corresponding to reversible and irreversible chemical reactions. However, this estimation is rough and requires that the concentration of Y can be freely changed, which does not have to be fulfilled.

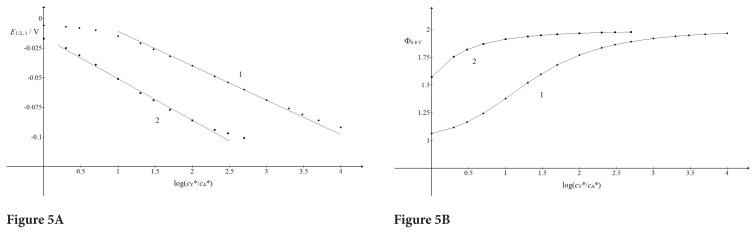
The variation of the bulk concentration of the substance Y influences both waves of the ECE response. The limiting current of the first wave is independent of but the half-wave potential of this wave decreases significantly with the increasing of this concentration. Regarding the second wave, its limiting current is influenced mostly, while E_1/2,2 is less affected. This is shown in Figure 5 for the reversible chemical reaction. The compound Y contributes to the forward rate of chemical reaction and its influence depends on the product $k_f\hspace{0.17em}{c}_A^{*}$. The relationship between E_1/2,1 and $\text{log\hspace{0.17em}}(c_Y^{*}/c_A^{*})$ is sigmoidal and in the vicinity of inflexion points it can be approximated by the straight lines:

Figure 5.

Dependence of the half-wave potential of the first wave (A) and the limiting current of the second wave (B) on the logarithm of the ratio between bulk concentrations of the substance Y and the reactant A; $k_f\hspace{0.17em}{c}_A^{*}/{\text{s}}^{-1}=1\hspace{0.17em}(1)$ and 100 (2). The straight lines 1 and 2 are defined by Eqs. (27) and (28), respectively. All other data are as in Figure 2.

$$E_{1/2,1}-E_1^0=-0.029\hspace{0.17em}\text{log\hspace{0.17em}}(c_Y^{*}/c_A^{*})+0.018\hspace{0.17em}\text{V}$$ (27)

$$E_{1/2,1}-E_1^0=-0.035\hspace{0.17em}\text{log\hspace{0.17em}}(c_Y^{*}/c_A^{*})-0.016\hspace{0.17em}\text{V}\text{.}$$ (28)

If the dimensionless equilibrium constant is 10³ this relationship is very similar and the straight lines are:

$$E_{1/2,1}-E_1^0=-0.028\hspace{0.17em}\text{log\hspace{0.17em}}(c_Y^{*}/c_A^{*})+0.015\hspace{0.17em}\text{V}$$ (29)

$$E_{1/2,1}-E_1^0=-0.024\hspace{0.17em}\text{log\hspace{0.17em}}(c_Y^{*}/c_A^{*})-0.044\hspace{0.17em}\text{V}\text{.}$$ (30)

They apply for $k_f\hspace{0.17em}{c}_A^{*}$ 1 s⁻¹ and 100 s⁻¹, respectively. The limiting currents of the second wave are the sigmoidal function of $\text{log\hspace{0.17em}}(c_Y^{*}/c_A^{*})$ if $k_f\hspace{0.17em}{c}_A^{*}$ 1 s⁻¹, but this relationship is only an upper fraction of the sigmoidal curve if 100 s⁻¹. This is because these two arguments add up giving the joint effect. If $K{c}_A^{*}={10}^3$ the second half-wave potential is independent of $c_Y^{*}$, but if $K{c}_A^{*}=1$ it changes from the values reported in Figure 2 to 0.296 V vs. $E_1^0$, which is the potential that corresponds to the irreversible chemical reaction. This change occurs within the interval $1<c_Y^{*}/c_A^{*}<50$.

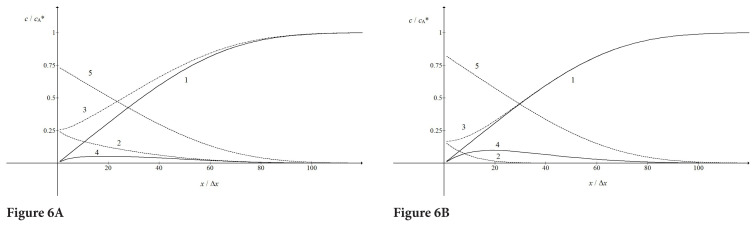
The difference in limiting currents of the second wave between the ECE mechanisms with reversible and irreversible chemical reactions can be explained by the inspection of distribution of chemical species in the diffusion layer that is shown in Figure 6. One can notice that the dimensionless concentrations of B, Y and G are particularly sensitive to the dimensionless equilibrium constant of chemical reaction. If the reaction is reversible the concentration of Y at the electrode surface is 0.26 and the maximum concentration of G is 0.05, but under the influence of irreversible reaction these concentrations change to 0.17 and 0.1, respectively. Consequently, the gradient of H is steeper if the reaction is irreversible and the current is higher.

Figure 6.

Distribution of the reactant A (1), the product B (2), the compound Y (3), the second reactant G (4) and the final product H (5) in the diffusion layer at 0.8 V vs. $E_1^0$; ω= 40 rad/s, $C_Y^{*}/C_A^{*}=1,k_f\hspace{0.17em}{c}_A^{*}{10}^3{\text{s}}^{-1}$ and $K{c}_A^{*}=1\hspace{0.17em}(\text{A})$ and 10³ (B). All other data are as in Figure 1.

The models of ECE mechanism in the voltammetry on stationary macroelectrodes give qualitative descriptions of the responses because the transient currents consist of the diffusion and kinetic components [25, 33, 34, 38]. Under steady-state conditions on microelectrodes [6] and rotating disk electrodes [40] the diffusion component can be controlled and the kinetic contribution can be quantified. In this paper, it is shown that the kinetic current satisfies a general equation (22) and that the rate constant of chemical reaction can be estimated under certain conditions.

4. Conclusion

The difference between ECE mechanisms with the reversible and irreversible chemical reactions originates from the influence of the backward rate constant on the net gain of the reaction. If the reaction is of the second order, its forward rate depends on the component Y and the limiting current of the second wave becomes higher if the concentration of Y is increased. The rate constant can be estimated from the relationship between currents and the concentrations of the reactant of the first electrode reaction.

Data availability

All relevant data are available on demand.