The development of nucleic acids force fields: From an unchallenged past to a competitive future

Abstract

Molecular dynamics simulations have strongly matured as a method to study biomolecular processes. Their validity, however, is determined by the accuracy of the underlying force fields that describe the forces between all atoms. In this article, we review the development of nucleic acids force fields. We describe the early attempts in the 1990s and emphasize their strong influence on recent force fields. State-of-the-art force fields still use the same Lennard-Jones parameters derived 25 years ago in spite of the fact that these parameters were in general not fitted for nucleic acids. In addition, electrostatic parameters also are deprecated, which may explain some of the current force field deficiencies. We compare different force fields for various systems and discuss new tests of the recently developed Tumuc1 force field. The OL-force fields and Tumuc1 are arguably the best force fields to describe the DNA double helix. However, no force field is flawless. In particular, the description of sugar-puckering remains a problem for nucleic acids force fields. Future refinements are required, so we review methods for force field refinement and give an outlook to the future of force fields.

Significance

Molecular dynamics simulations employ force fields as a basis to compute the forces between all atoms in a system. Thus, the reliability of simulations is limited by the force field accuracy. In this article, we summarize the history of force field development for nucleic acids and discuss the performance of recent force fields and methods to refine them.

Main text

DNA and RNA are the two most abundant types of nucleic acids in living systems. It is consensus that their biological function is largely determined by conformational flexibility during folding processes, genome packing, or the specific recognition by proteins (1,2,3). Although the spatial and time resolution of experiments to study these phenomena is often limited, molecular dynamics (MD) simulations provide atomistic resolution and have matured over the past decades as an increasingly valued computational microscope (4,5). This is also impressively mirrored in its growing role for the development of nano-systems, such as a synthetic enzyme to flip lipids in biological membranes or nanopores (6,7). The increase of MD simulations’ popularity is leveraged by methodological improvements and the advances in hardware, which allow us to perform MD simulations routinely on the microsecond timescale. Still, simulations are an approximation to reality, and the reliability stands and falls with the accuracy of force fields.

During MD simulations, the forces between atoms are derived from classical force fields that are expressed as a functional form. For nucleic acids, the path to modern force fields has notably been pioneered by the groups of Karplus (8) and Weiner and Kollman (9,10). State-of-the-art force fields still rely on the functional form already used by them 40 years ago:

$$E=\sum _{bonds}{k}_r{\left(r-r_0\right)}^2+\sum _{angles}{k}_{\theta }{\left(\theta -{\theta }_0\right)}^2+\sum _{dihedrals}\frac{V_n}{2}\left[1+\cos \left(n\phi -\gamma \right)\right]+\sum _{i<j}\left[\frac{A_{ij}}{R_{ij}^{12}}-\frac{B_{ij}}{R_{ij}^6}+\frac{q_i{q}_j}{ϵr_{ij}}\right]$$ (1)

These early force field developments are also the basis for the most frequently employed force fields nowadays for simulations of nucleic acids that belong to the AMBER (Assisted Model Building with Energy Refinement) (11) or CHARMM (Chemistry at Harvard Macromolecular Mechanics) (12) force field families. In the following, we first focus on the AMBER-type nucleic acid force fields. The comprehensive parameterization of the force field functional form by Cornell et al. in 1995 is a milestone in force field development (11). Almost 30 years later, the most prominent, recent DNA and RNA force fields are basically minor modifications and improvements to this work. For the Cornell et al. design, equilibrium parameters $r_0$ and ${\theta }_0$ have been determined from x-ray structures. The force constants $k_r$ and $k_{\theta }$ were derived from interpolation of observed distances and vibrational analysis. Note that a least-squares optimization scheme to interpolate force field parameters against experimental data (specifically excess enthalpies, equilibrium conformations, and vibrational frequencies) has already been elaborated by Warshel and Lifson in 1968 (13). Given the lower computational capacities back then, their iterative optimization is based on expressing differences between computed and experimentally determined observables as a Taylor series of force field parameters. In the Cornell-set, constants describing the dihedral angles (dihedrals) were mostly parameterized empirically by accounting for the population of specific substates and interpolating between the multiplicities of chemical bondings. However, dihedrals around phosphorus-ester bonds, which build the backbone of DNA and RNA, were adjusted with quantum mechanical calculations (MP2/6-31G^∗) for three different substates. Van der Waals (vdW) parameters were introduced as a universal set: all sp3-hybridized carbon atoms share the same atom-type and hence vdW parameters, and the same rule applies for all sp2-hybridized carbon atoms. Hence, all carbon atoms of A, C, G, and U bases are assigned exactly the same vdW parameters (only thymine includes an sp3-hybridized atom due to its methyl group). Originally, vdW parameters for these carbon atoms as well as for aliphatic and aromatic hydrogens were fitted to reproduce densities and enthalpies of vaporization for alkanes and benzenes. Parameters for oxygens, nitrogens, and the phosphorus atom stem from earlier studies in which the parameters were assigned to reproduce liquid properties and fit lattice energies and crystal structures (10,14,15,16). Note that this set of vdW parameters is still used by the present DNA and RNA force fields of AMBER (bsc-series, ol-series, Tumuc1, see below), but it has never been parameterized toward base stacking.

The partial charges on atoms were derived from Hartree-Fock calculations (6-31G^∗) on subsystems of the nucleotides using the RESP method (17). Finally, the Cornell et al. charge model includes a scaling factor for electrostatic 1–4 interactions (atoms separated by three bonds) of 1/1.2, which was calibrated on liquids. VdW 1–4 interactions are scaled by 0.5. This choice dates back to the works by Weiner et al. (10) that introduced this scaling based on phenomenological reasoning and subsequently demonstrated improved results for nucleosides and peptides. Altogether, this set proposed by Cornell et al. represents the basis of all AMBER-type DNA and RNA force fields, which are the most widely used nucleic acids force fields.

In 1998, the Kollman group improved sugar-puckering and glycosidic dihedrals by adjusting dihedral parameters based on quantum mechanical calculations (parm98) (18), but revised the torsional profiles for the sugar rings only 1 year later (parm99) (19). However, it turned out that 50-ns MD simulations using the parm99 force field result in severe distortions of the DNA double helix due to unrealistic transitions in the $\alpha /\gamma$ dihedral angles (20) (Fig. 1). Consequently, the $\alpha$ and $\gamma$ dihedral parameters were revised by Perez et al. based on quantum mechanical scans (using LMP2/6-31G(d) and B3LYP/6-31+G(d) level of theories) resulting in the bsc0 force field (21). Nevertheless, the bsc0 force field still shows structural inaccuracies (e.g., slightly deformed Z-DNA structures, intrinsic slight undertwisting of B-DNA, and too low population of the BII state in B-DNA) (22,23,24). The BI/BII states in B-DNA correspond to a common coupled transition of the backbone dihedral angles $ϵ$ and $\zeta$ (illustrated in Fig. 1). Efforts to further improve the bsc0 force field lead to a branch of two different albeit qualitatively similar attempts. Firstly, the Sponer group developed the ol-series of force fields (22,25,26), from which the ol15 force field became one of the main choices as a DNA force field. Recently, this group has again refined the $\alpha$ and $\gamma$ dihedral parameters (ol21 force field), which results in a higher accuracy for the Z-DNA description, and present results indicate that the accuracy for B-DNA is not downgraded by these modifications. Further testing, however, seems required (27). Secondly, the Orozco group developed the bsc1 force field based on the earlier bsc0 (28). The parameterization strategy is similar to the ol-series, and several dihedral angles have been revised based on QM (MP2) calculations. It is notable that both ol15/21 and bsc1 force field modifications lead to substantial improvements over bsc0. These newer force fields correct the systematic undertwisting of the DNA double helix present in bsc0 and also in a new force field from the Shaw group (see below), for example (23,29,30). Undertwisting of the double helix is particularly problematic for longer DNA double helices that are topologically closed (e.g., minicircles), as it leads to an underestimation of DNA’s total winding number and hence affects the supercoiling density. Besides, pulsed electron-electron double resonance experiments have demonstrated that newer force fields (bsc1, ol15) describe global elasticities clearly better than older ones (bsc0 and parm94) (31), and a recent study by Minhas and co-workers indicates that bsc1 captures global elasticities slightly better than ol15 (32). On the downside, bsc1 does not include any refinement of the $\beta$-dihedral angle parameters and is hence less accurate for Z-DNA. In addition, the bsc1 force field also allows population of a $\beta =70°$ state in B-DNA that can cause local and likely artificial distortions in the DNA double helix (27,33,34). However, both, bsc1 and ol15, still include the nonbonded parameter set from Cornell et al. (11), and a modification of nonbonded parameters would also demand a revision of dihedral angle parameters.

Figure 1.

Structural motifs in double-stranded DNA: (A) BI conformation for a basepair step. (B) BII conformation, which mostly represents a high-twist state. Note that both conformations are in the canonical $\alpha /\gamma$ state, whereas (C) shows a $\alpha /\gamma$-flip that my cause strong structural distortions in the DNA. To see this figure in color, go online.

Recent studies indicate that the nonbonded Cornell parameters are far from optimal for nucleic acids. Basepairing is under- and base stacking significantly overstabilized (35,36,37,38,39,40,41), and binding by proteins and DNA-DNA interactions are too attractive, leading to unrealistic aggregation during MD simulations (42,43).

The Aksimentiev group addressed this issue by calibrating the Lennard-Jones parameters to reproduce osmotic pressure measured experimentally. Their new parameter set (CUFIX) provides an improved description of DNA condensation (38). Note that the diffusion constant for sliding of the PCNA protein along DNA is underestimated by bsc0 and bsc1 force fields by two orders of magnitudes. Strictly speaking, nothing happens in these microsecond-long MD simulations, and the same is expected for ol-force fields. CHARMM force fields underestimate it by one order of magnitude, whereas the CUFIX set reproduces experimental values within the error range (44). This is an impressive improvement one needs to bear in mind when carrying out protein-DNA simulations, despite the fact that only minor differences to bsc1 simulations on amino-acid induced DNA duplex stabilization have been reported recently (45). Furthermore, it has not yet solved the problem of overstabilization of base stacking. Although the CUFIX set is not a final solution, the results demonstrate that the rescaling method successfully tackles some major force field deficiencies. We argue that it will play an important role in future force field developments.

Separate from that, the Shaw group has rescaled Lennard-Jones and a few dihedral parameters for RNA to match quantum mechanical stacking and hydrogen-bonding landscapes (DESRES-set) (46). Simulations on RNA-duplexes, single-strands, and tetraloops overall show a realistic dynamics on the $\sim 100\mu s$ timescale, which is about two orders of magnitudes longer than the tests of most other force fields. Base stacking, however, is still overstabilized, and melting temperatures are overestimated by 5–50 K depending on the sequence. Even more problematic are simulation results reported by Kührova et al., which reveal severe degradation of the ribosomal L1-stalk segment (40). Very recently, the Shaw group has transferred the parameters and reoptimized them for simulations of DNA (DES-Amber 3.0) (29). The revision includes nonbonded (rescaled Lennard-Jones parameters) and dihedral angle parameter adjustments as well. The authors have tested DES-Amber 3.0 on several different systems on timescales of $\sim 100\mu s$. Intriguingly, the authors found slight destabilization in the nearest-neighbor stacking parameters and even detected local strand dissociation in a $50-\mu s$ unrestrained MD simulation for one sequence. Over the broad range of systems, the performance of DES-Amber 3.0 is very decent. In addition, also parameters of the DESRES-RNA force field have been adjusted. The authors demonstrate that the revised RNA force field corrects the deficiencies reported for the ribosomal L1-stalk system. However, specifically for B-DNA, the early results are not fully convincing, as the DNA during simulations is intrinsically undertwisted ($\sim 33°$ average twist) and underpopulates the BII substates. The balance between BI/BII states (see Fig. 1 for comparison) at each nucleotide plays an important role in DNA’s conformational flexibility and also binding by proteins (41,47,48,49,50,51,52). For this reason, other groups have put a strong focus to achieve an accurate BI-BII balance. Bsc1, ol15/21, and Tumuc1 hence indicate realistic BI/BII populations compatible with experimental results. Nevertheless, the development of DES-Amber 3.0 represents an impressive amount of work, and the force field may be close to a good parameter set. The BI/BII misbalance may be corrected by a future refinement of the $ϵ,\zeta$ or $\beta$ dihedral angle parameters. This will most likely automatically fix the issue of undertwisting, as BII states represent high-twist states.

Such modifications can possibly be tackled with new machine learning (ML)-based concepts to improve force fields. The Bussi group has proposed ML methods to refine dihedral angles to better match experimental observables (53,54,55). Training of dihedral parameters is achieved via a correction potential in the typical Fourier series for dihedrals:

$$V_{corr}=k_{B}T\sum _{t\in dihedrals}\sum _{i=1}^{N_t}\sum _{n=1}^3({\lambda }_{1tn}\cos \left(n{\phi }_{ti}\right)+{\lambda }_{2tn}\sin \left(n{\phi }_{ti}\right))$$ (2)

N_t is the number of nucleotides involved in the weights ${\lambda }_{1tn}$ and ${\lambda }_{2tn}$. The weights are trained by minimizing an error function depending on the observables including a regularizer to avoid overfitting:

$$\tilde{E}\left(<O_1>\left(\lambda \right),\dots ,<O_M>\left(\lambda \right)\right)+\alpha {\left|\lambda \right|}^2$$ (3)

Intriguingly, optimization of the dihedral angle parameters on top of the ol3 force field for RNA was not sufficient to accurately capture the native state for RNA tetraloops (53). This finding calls for a revision of nonbonded parameters. The Sponer group has proposed to empirically adjust hydrogen bonding to decrease sugar-phosphate and base-phosphate interactions, and to strengthen basepairing, as well as modifications targeting terminal nucleotides (40,56). MD simulations including these corrections show clear improvement for small RNA motifs, though the agreement with NMR data is still not optimal. Note that such empirical modifications can also be achieved employing a ML routine related to the one described above (57). Inclusion of empirical hydrogen bonding terms can also be seen as a renaissance of the very early AMBER force fields (10,15), which included an explicit hydrogen bonding term in addition to the terms in Eq. 1, but were then omitted by Cornell et al. (11).

Chemistry at Harvard Macromolecular Mechanics (CHARMM) represents another prominent simulation suite initiated by the Karplus group and comes along with its own force fields (8,58). A force field for nucleic acids (CHARMM22) was released at the same time as the AMBER force field by Cornell et al. (12). It has the same functional form (Eq. 1) with the addition of an Urey-Bradley term, which represents harmonic springs between 1,3 atoms in a valence angle. In CHARMM22, bonded parameters were parameterized on both, experimental (crystal structures, spectroscopic data) and quantum mechanical information. Nonbonded parameters were derived to reproduce quantum mechanical (HF/6-31G^∗) interaction energies and geometric arrangements of water molecules around model compounds, and to match experimentally measured gas-phase properties for basepairing (also dipole moments determined by experiments and quantum mechanical calculations). The efforts were continued by the MacKerell group with the release of CHARMM27 in which the CHARMM22 parameters were further refined in an iterative procedure to fit experimental and quantum mechanical data (59,60). The main goal for CHARMM27 was a better description of the sugar-puckering (C3′-endo:A-form, C2′-endo:B-form), and based on simulations of DNA duplexes under various conditions of water activity, a good B to A equilibrium was reported (60,61). However, at the time of force field development the maximum simulation times were only a few nanoseconds. Simulations with CHARMM27 indicate a too low population of BII states (determined by the distribution of $ϵ$ and $\zeta$ dihedral angles), but also sugar-puckering required revision in CHARMM36 (62). Although CHARMM36 describes the BI/BII balance better than its predecessor, local distortions in the DNA duplex and undertwisting were reported for CHARMM36 (23,28,30). CHARMM27 also reproduces global elasticities better than CHARMM36 and even as the AMBER force fields (32), but its BI/BII misbalance remains a serious drawback. In general, CHARMM force fields have not been refined and tested as much as AMBER force fields for nucleic acids over the last years. Nevertheless, the latter are not flawless, especially since they left the nonbonded Cornell parameters unrevised. In particular, the electrostatic description has been questioned in recent studies (43,44,63,64). This is not surprising, as the partial charges were derived from Hartree-Fock calculations on small fragments and a low grid resolution for fitting.

Although this was a high-level approach back in the 1990s, today’s computational resources equip us with much more powerful approaches. For this reason, we have parameterized an entirely new DNA force field (Tumuc1) in a bottom-up approach based on quantum mechanical calculations and the functional form by Cornell et al. (Eq. 1) (33). This also includes bond and angle parameters, which we derived from vibrational frequency calculations. Resulting Cartesian Hessian Matrices were then mapped into internal coordinates with the modified Seminario method (65). We fitted the partial charges to reproduce the quantum mechanical (RI-MP2/def2-TZVP) (66,67) electrostatic potential of model systems larger than a nucleotide (68). Note that the fitting procedure also includes constraints to enforce a unit charge for a nucleotide and restraints to assign the same charges for equivalent atoms. The electrostatic description differs significantly from other force fields. For in-vacuo basepairing, Tumuc1 is also considerably closer to the quantum mechanical reference data than the Cornell-set, which understabilizes hydrogen bonding in agreement with other reports (36,38,39,40). In such a bottom-up approach, parameterization of the dihedral angle parameters is the most crucial and tedious part. In particular, for nucleic acids the parameterization of dihedral angle terms is difficult due to the relatively long sugar-phosphate backbone. A robust description for DNA’s backbone dihedral angles is essential to avoid an immediate collapse of the B-DNA structure, whereas the sensitivity is much smaller for nonbonded parameters. Yet, also a certain flexibility of the backbone is required to accurately describe the BI-BII balance and other topologies such as Z-DNA. As concluded from blunt-end stacking simulations and crystal structures, B-DNA’s right-handed helical structure is not determined by basepair stacking, but by its backbone (69). This conception is supported by comparison of QM landscapes for the backbone dihedrals and distributions obtained from a survey of crystal structures as carried out by MacKerell (70). The strong compatibility between QM energy minima and maxima of the crystallographic distributions reveals a significant mechanical stabilization of DNA’s double helical structure by the phosphate backbone. Intriguingly, this effect also implies a reduction of the entropic cost for double-strand formation, as single-stranded DNA is intrinsically stabilized toward the correct structural arrangement. This highlights the significance of an accurate description of DNA’s backbone dihedrals. In the following, we share a few of our experiences in fitting the dihedral angle parameters. The dihedrals are fitted on quantum mechanical dihedral angle scans of model systems. To this purpose, the model system also needs to be parameterized, and the Fourier series like dihedral potentials $V_{t_i}$ are initially set to zero and fitted to minimize the difference between molecular mechanical and quantum mechanical energies:

$$\sum _{t_i\in dihedrals}^{t_N}\sum _{j\in dat{a}_{t_i}}{\left\{\left[E_{QM}\left(j\right)-E_{MM}\left(j;V_{t_1}=0,..,V_{t_N}=0\right)-\sum _{t_i}{V}_{t_i}\left(j\right)\right]·w\left(j\right)\right\}}^2$$ (4)

In this scheme, we fit the dihedral parameters for one model system simultaneously; i.e., a dihedral $t_k$ is also trained on the scans for dihedral $t_i$. We designed the weight functions w(j) flexibly, and overestimation of molecular mechanical energies in unfavorable regions is penalized by low weights and underestimation by high weights. Moreover, higher weights are used for low-energy regions to achieve better fitting quality in the thermodynamically more relevant subspaces. We have not used an analytic scheme to determine the w(j), as the accuracy of the functional form for the force field (Eq. 1) is noisy. For dihedral fitting, the harmonic approximation of angles and the absence of dihedral angle coupling and other terms in the functional force field form is a problem. We have observed that angles can change substantially (up to $\sim 30°$) when changing the dihedral to high-energy regions. In such cases, the force field overestimates the energies, and simple dihedral fitting would result in very stabilizing dihedral potentials in these areas. During simulations on DNA, however, these areas may not be sterically as unfavorable as in the model system, and the dihedral potential can falsely drive the DNA into these states. In order to suppress such scenarios and to better isolate the contribution by the dihedral, we applied several restraints in our scans acting on dihedral and bond angles.

As a rule of thumb, molecular mechanics force fields overshoot in high-energy areas, for which it should not be compensated for in fitting. In general, force fields are typically fitted with respect to stable substates, i.e., local minima in the energy landscapes, but less to transition regions. Thus, it is questionable how sensible MD-based kinetic studies are, as rates depend on barrier heights to transition states. Given the difficulties in dihedral fitting, it may in the future be worth to try not to fit on the potential energies but on Hellmann-Feynman forces instead: (71)

$$F_x^i=-<\psi \left|\frac{\partial \hat{H}}{\partial x^i}\right|\psi >=-\int {\psi }^{\ast }\psi \frac{\partial U}{\partial x^i}dV\text{,}$$ (5)

where x denotes the spatial component of the nucleus labeled i, and completeness of the basis set is assumed. Finally, there emerge two contributions to the force on a nucleus, one due to the electronic density and one due to the electric fields by all other nuclei. Whether Hellmann-Feynman forces represent an attractive route to parameterize force field terms remains to be tested, but potential advantages may be that one can extract forces more directly from QM calculations in contrast to fitting a scanned potential energy surface that includes orthogonal structural changes. This could help not only for dihedral parameterization but also for the refinement of hydrogen-bonds, which suffer from misbalances in the current AMBER force fields (40). Using electron density as a basis for MD simulations has already been successfully utilized by MD flexible fitting. In this method, two extra terms are added to the conventional force field: one to restrain secondary-structure motifs, and one representing a weighted Coulomb-potential derived from cryo-EM data. This allows not only to perform MD simulations capturing cryo-EM indicated dynamics better, but also for structure determination where impressive results have been achieved for resolving ribosomal complexes (72,73).

As outlined above, fitting of dihedral parameters to reproduce potential quantum mechanical energy landscapes has an empirical flavor. Indeed, a pure quantum mechanical approach may not be optimal. The electronic structure calculations as well as classical MD simulations do not include nuclear quantum effects such as proton tunneling (74,75). In a theoretical study, Fang et al. have shown that nuclear quantum effects stabilize AT/GC basepairing by 0.55/0.39 kcal/mol at room temperature, and hence are not negligible (76). Further path integral MD simulations are of interest to better understand the significance of nuclear quantum effects in nucleic acids dynamics. Otherwise, neglecting these effects speaks in favor of empirical approaches (77). For the fitting of sugar-puckering in Tumuc1, we had to allow overstabilization of the C3′-endo state, and a similar empirical choice was also made for AMOEBA (described below) (78). Overall, Tumuc1 improves the B-DNA backbone description and achieves accurate BI/BII balancing and $\alpha /\gamma$ stability. For Z-DNA, the ol15 force field yields a better dihedral- and mean-structural description, but sugar-puckering and helicity are better reproduced by Tumuc1, and bsc1 falls behind. G-quadruplex structures have remained stable, and potassium ions remained inside the layers during 2$-\mu s$ MD simulation with Tumuc1. Furthermore, correct hairpin folding has also been achieved, and good compatibility with the ff14SB protein force field has been demonstrated for four DNA-protein complexes. Note that Tumuc1 uses the Lennard-Jones parameters by Cornell et al. We seek to extensively test Tumuc1 and track the reports by the scientific community to subsequently refine Lennard-Jones parameters.

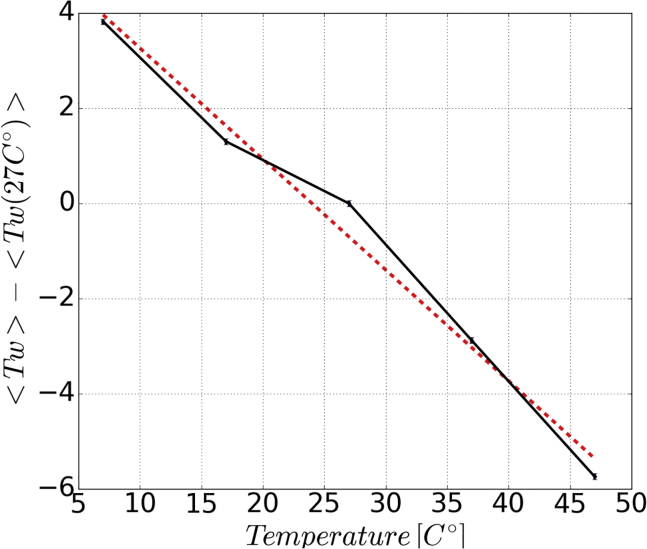
An interesting effect and test for force fields is the temperature dependence of DNA’s helical twist. Upon temperature increase, the winding of DNA decreases. Experimentally a twist-temperature dependence of $\Delta Tw\left(T\right)=\frac{\left(-11.5\pm 1.0\right)°}{°C·kbp}$ was found (79). This relation was obtained in quantitative agreement by ol15, but underestimated by bsc0 (79,80). Quantitative reproduction of such thermodynamic effects is an impressive force field performance, and it shows that newer force fields can provide substantial contribution to the biophysics field and may yield further trust in MD simulations in general. We have performed $1-\mu s$-long MD simulations on the 33-bp-long DNA sequence used in Kriegel et al. (79) at five different temperatures from 280 to 320 K in 10-K steps with Tumuc1. From the recorded mean twist over the central two DNA turns, we have inferred the twist-temperature dependence via linear regression (Fig. 2), and we obtained $\Delta Tw\left(T\right)=\frac{\left(-11.1\pm 0.8\right)°}{°Ckbp}$ in excellent agreement with experiments.

Figure 2.

Temperature-twist relation for double-stranded DNA obtained with Tumuc1. The mean twist values over the central two turns as a function of temperature are plotted in black. The linear interpolation is shown in red. To see this figure in color, go online.

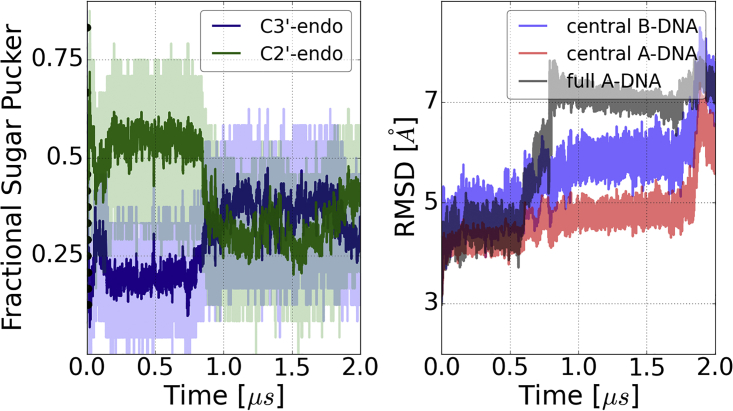
As another test for Tumuc1, we have performed a $2-\mu s$ long MD simulation of the Dickerson-Drew-Dodecamer sequence starting from A-form structure exposed to ethanol/water $\left(85\%/15\%\right)$. Under these solvent conditions, the A-form structure should be stable. However, neither ol15 nor bsc1 accomplish that, as both force fields overstabilize the C2′-endo (B-form) state (81). In the simulation with Tumuc1, the population of C3′-endo states drops rapidly but is not fully destabilized and occurs in a mixed phase with C2′-endo states. In addition, three terminal basepairs melt at around $\sim 0.75\mu s$ (as indicated by increase in the rmsd, right panel Fig. 3, black curve) and after $\sim 1.8\mu s$ melting of two central basepairs also occurs. It may indicate a force field inaccuracy, although it has been observed that increased ethanol concentrations decrease the melting temperature of DNA (82). In spite of the fact that the trajectory remains closer to an A-DNA reference structure compared with B-DNA, the results point to a slight overstabilization of the C2′-endo state by Tumuc1, hence requiring further testing and improvements. Note, sequence-dependent sugar-puckering in Z-DNA and protein-DNA complexes have been captured well by Tumuc1 (33).

Figure 3.

$2-\mu s$ MD simulation of the Dickerson-Drew Dodecamer with Tumuc1 starting from A-form. Sugar-puckering sampled during the simulation is shown in the left panel. Black dots represent C3′-endo population along the first 10 ns and highlight a strong decrease of these states at the beginning of the simulation. RMSD curves (right panel) reveal instabilities for terminal basepairs (black curve) and central basepairs in reference to A- and B-DNA structures (red and blue curve). To see this figure in color, go online.

As outlined above, accurate description of sugar-puckering has been a force field issue discussed already in the 1990s. 25 years later, no convincing progress has been made in this respect. Regarding solvation, the choice of water and ion models for simulation is often debated. Note that we have not parameterized an implicit water model for Tumuc1, as nucleic acids are generally simulated with explicit solvent. Similar to the ol15 and bsc1 force fields, Tumuc1 is fairly independent from the water model. Using the OPC-water model may yield slightly more accurate structural fluctuations compared with TIP3P, but the differences are marginal for simulations of the Dickerson-Drew-Dodecamer (23,33). Besides, an increase in salt concentration increases the helical twist of B-DNA. This behavior is in good agreement with experimental data in all atom simulations with bsc1 and ol15 (83,84). Thus, both, entropy (due to temperature dependence) and chemical potential (due to salt-concentration dependence) must be a function of helical twist. Zhang et al. have given a convincing explanation for these thermodynamic effects (84): twisting DNA is negatively correlated to its diameter, and conformational entropy is a function of diameter (higher flexibility for a larger diameter). As a consequence, increase in temperature must increase DNA’s diameter and hence decrease its twist. In addition, the authors have shown that salt concentration affects DNA’s diameter via phosphate-phosphate repulsion. Higher salt concentration screens the phosphate repulsion allowing the diameter to shrink, which causes an increase in twist. Nevertheless, the salt dependence is very small ($0.3°$ changes in twist per bp from 50 to 1000 mM) (83), and recorded ensembles for different solvent conditions are highly similar (33). We therefore argue that there is no need to be a perfectionist on solvent models, as the accuracy is mainly determined by the nucleic acid force field.

On the other side, classical, additive force fields (based on Eq. 1) must be seen critically in combination with divalent ions. Cassone et al. studied the binding of cations to cyclic nucleotides with ab initio MD, and they demonstrated that an entire unit charge is transferred away from a magnesium ion upon binding (85). Thus, it is unlikely that classical, additive force fields can be tuned to describe divalent ions at sufficient accuracy. Rather a model including polarization is required, and better balancing of interactions between $M{g}^{2+}$ ions and solvent molecules and nucleic acid moieties as well has already been demonstrated by Lemkul and co-workers (86). The importance of polarization effects has also been shown for ion channels. More reliable conformational behavior is achieved for voltage-gated sodium channels, and better agreement with experimental data has been reported for the transport of a Li⁺ ion through a gramicidin A channel when polarization is included (87,88). In a recent study on $F^{-}$ permeation through fluoride channels, strongly improved results have been obtained when using a polarizable instead of an additive force field, and the necessity of polarizable models for such processes was concluded (89).

However, for nucleic acids, classical, additive, force fields are still most widely used and therefore represent the state of the art. In 2014, the group by MacKerell released a polarizable DNA force field (90), which was found to be unstable on the timescale of hundreds of nanoseconds (30) and hence revised in a later version (91,92). In this model, polarization is included via Drude particles, which are virtual particles connected to nonhydrogen atoms. The charge of the Drude particle bound to atom i is assigned to reproduce the polarizability:

$${\alpha }_i=\frac{q_{D,i}^2}{k_D}$$ (6)

$q_{D,i}$ is always negative to mimic electronic degrees of freedom, and $k_D$ is the spring constant between atom and Drude particle and usually set to 1000 $kcal/mol/{\stackrel{\circ }{A}}^2$. This choice is not mandatory but simplifies the fitting process. In addition, interactions of neighboring induced dipoles are also accounted for including a screening function. B-DNA simulations with the recent Drude force field are stable on the low microsecond timescale, but also show space for improvement. For example, sugar-puckering description is imperfect (like in other nonpolarizable force fields), the BII population is too low, and the opening angle between basepairs is shifted to negative values. A consequence of this is that the minor groove is too large and the major groove is too narrow (92). AMOEBA (Atomic Multipole Optimized Energetics for Biomolecular Simulation) is another prominent, polarizable force field (78,93). In contrast to the Drude model, it does not use virtual particles, but its functional form includes a permanent multipole (single-point, dipole, and quadrupole moments) and an inducible dipole term capturing polarization. An electric field E induces a dipole at point p according to

$${\mu }_p={\mathit{\alpha }}_p·\left[{\mathbf{E}}_p-\sum _{q\ne p}{\mathbf{T}}_{pq}{\mu }_q\right]\text{.}$$ (7)

${\mathbf{T}}_{pq}$ is the dipole field tensor, and ${\mathit{\alpha }}_p$ is the atomic polarizability tensor. Atomic polarizabilities are fitted to reproduce molecular polarizabilities (94). An induction of dipoles alters the electric field, so Eq. 7 is solved in a consistent, iterative way, and very short-range polarization interactions are damped to avoid polarization catastrophe (93). Although the AMOEBA force fields for DNA and RNA show decent accuracy, they do not so far outperform the current state of the art additive AMBER force fields. Under standard conditions, the DNA double helix remains stable during $100-ns$-long MD simulations with AMOEBA, though the recorded dihedral distributions for $ϵ$ and $\zeta$ show noticeable underpopulation of the BII state (78). In addition, the authors have also performed MD simulations on DNA duplexes in water/ethanol mixtures starting from both A- and B-form structures at 298 and 328 K, respectively. No topological interconversion occurs at 298 K, and RMSD time traces rather indicate instabilities of both topologies after $\sim 500ns$. At 328 K, B- to A-form transitions have been observed before melting of the DNA duplexes, which is in agreement with experiments (82). Furthermore, a force field study on G-quadruplex structures has reported deficiencies in AMOEBA. Intriguingly, this study shows best though not flawless performance for the Drude force field (compared with bsc0, bsc1, OL15, and AMOEBA) (95).

Altogether, although polarizable force fields have not yet outperformed additive force fields, current development of the Drude and AMOEBA force fields need to be acknowledged as pioneering works offering significant potential for future improvement. Outperforming the additive force fields by introducing new terms in the potential energy function is not straightforward, and we assume the problems to be primarily of a technical nature, as large improvements in stacking interactions, for instance, are balanced out by only slight inaccuracies in the dihedrals. Furthermore, one needs to take into account that most force field tests are conducted as single-molecule studies to address structure and flexibility of biomolecules. Under such conditions, it is fair to assume that polarization effects have a lesser impact than for association or dissociation of molecules, for example. As discussed above, tests on DNA force fields toward binding affinities have indeed brought to light major deficiencies. The limitations of additive, nonpolarizable force fields concerning binding affinities have been pointed out by Piana et al. for proteins (96): Binding affinities for proteins deviate substantially from experimental results, even upon refinement of nonbonded interactions. Although nonpolarizable force fields are state of the art for most biomolecules, their accuracy needs hence to be scrutinized more closely for multimolecule systems, and likely, better results can be obtained upon inclusion of polarization effects.

In the future, such effects may not necessarily be included by explicit polarization terms (as in the Drude model or AMOEBA), but indirectly through many body terms, which may be achieved via AI (artificial intelligence)-based force fields. Here, the power of AI is demonstrated by the ANI neural network potential (97). ANI expresses the total energy as a sum of atomic contributions, and each atomic contribution is evaluated by a neural network, in which modified Behler-Parinello symmetry functions are used as features (98). These functions represent the chemical environment, and by using the same neural network potential for identical atom types, ANI becomes transferable. ANI has been trained on DFT data, and the tests on molecules consisting of up to 53 atoms reveal high predictive power. A detailed comparison of neural network methods for biomolecular simulation is out of scope for this article, but we emphasize that impressive results have also been achieved by SchNet (99), NequIP (100), and other methods (101,102). Besides neural network approaches, Gaussian process regression (GPR) has also turned out as a powerful method to predict molecular properties (103,104). In GPR, predictions are made based on the similarity between atomic environments that are evaluated using a descriptor dependent kernel function. Smooth overlap of atomic positions vectors (power spectrum of atomic densities) are a popular choice as descriptors due to permutational and rotational invariance (103,105). For simulations, GPR has, to the best of our knowledge, been mostly used for materials. In general, AI approaches face two difficulties in the simulation of biomolecules: first, very short-range interactions may not be captured accurately, as there is too little information in the training set. Second, long-range interactions surpassing the descriptors scope are not captured.

Thus, a promising approach for future force field development is the use of an additive force field (includes very short-range and long-range interactions analytically) as a baseline, complemented by an AI model that “knows” about the force field’s deficiencies (103). Intriguingly, this idea has already been realized in coarse graining long ago, where coarse-grained forces are fit to reproduce atomistic forces subtracted by a Coulomb term for the coarse-grained force field (106). Very recently, such a hybrid machine learning/classical force field approach was published by the Piquemal group (107). The authors have developed a hybrid ANI/AMOEBA model and tested it with respect to solvation free energies for several molecules in different solvents. Their hybrid model is overall in very good agreement with solvation free energies obtained from experiments. In addition, this group also provides a platform (Deep-HP) to use neural network potentials for MD simulations. JAX-MD is another new molecular dynamics package that enables the use of neural networks for molecular simulation (108). These initiatives are probably necessary, as software code of the traditional platforms might be too specialized for a straightforward inclusion of AI-based biomolecular potentials.

Challenges for an AI-derived nucleic acids force field are the substantial amount of QM calculations that need to be performed to generate a solid training set, in particular, in consideration of the polymorphic dynamics of the negatively charged phosphate backbone. In addition, nuclear quantum effects might also have to be accounted for. Furthermore, the computational efficiency will also be substantially drained compared with additive force fields. Although AI will not come without cost, it will be nevertheless interesting to follow and participate in this new trend of biomolecular simulation, and in the long-run, the ability to use AI-descriptions in the simulation of biomolecules will give a new twist to the development of force fields.

Summarizing the development of nucleic acid force fields, we find the fundamental works in the 1980s and 1990s. Over the last 30 years, the approaches have mostly been minimally invasive. This can be seen in the fact that recent AMBER force fields for DNA (bsc1, ol15/21), which are the most widely used ones up today, still employ the same vdW and electrostatic parameters as parameterized by Cornell et al. Efforts for force field improvement focused mostly on modifying dihedral angles parameters. However, recently new trends are evolving. Several new groups have entered the field of force field development, and the methodological arsenal has significantly grown. The substantial increase in computational efficiency allows us to gain more information from quantum mechanical computations and to test force fields on much longer timescales than in the early days of force field development. Moreover, AI will not hold back from force fields but in the long run is likely to overtake this domain, as its competitors (the classical, additive force fields) are in general not 21st century approaches. However, the classical, additive force fields will probably still be important as they can serve as baseline models in hybrid potentials. In the future, simulations studies on nucleic acids will be even more fascinating than nowadays. MD simulations employing atomistic force fields can serve as a basis to parameterize multiscale coarse-grained models via force matching or relative entropy minimization (106,109,110). Coarse-grained simulations studies of DNA are of particular interest as they can capture long-range allosteric effects. Global mechanical stress, for instance, can localize at specific sites of the DNA double helix, which is likely implicated in the repair of DNA damages and binding by proteins (41,111,112,113). However, the accuracy of multiscale coarse-grained models also stands on the shoulders of the accuracy of atomistic force fields. Current state-of-the-art force fields overstabilize basepair stacking and protein binding significantly. Thus, not much is happening during MD simulations of double-stranded DNA on the timescale of a few microseconds. Simulations on longer timescales employing force fields with a better description of nonbonded interactions will probably show a higher degree of conformational transitions including stronger local basepair breathing and lower barriers for base flipping and facilitate us to extract more fascinating dynamics of nucleic acids.

Author contributions

Designed research: M.Z. and K.L.; performed research: K.L.; wrote the paper: M.Z. and K.L.

Editor: Meyer Jackson.