Abstract
The actin filament network is in part remodeled by the action of a family of filament severing proteins that are responsible for modulating the ratio between monomeric and filamentous actin. Recent work on the protein actophorin from the amoeba Acanthamoeba castellani identified a series of site-directed mutations that increase the thermal stability of the protein by 22°C. Here, we expand this observation by showing that the mutant protein is also significantly stable to both equilibrium and kinetic chemical denaturation, and employ computer simulations to account for the increase in thermal or chemical stability through an accounting of atomic-level interactions. Specifically, the potential of mean force (PMF) can be obtained from steered molecular dynamics (SMD) simulations in which a protein is unfolded. However, SMD can be inefficient for large proteins as they require large solvent boxes, and computationally expensive as they require increasingly many SMD trajectories to converge the PMF. Adaptive steered molecular dynamics (ASMD) overcomes the second of these limitations by steering the particle in stages, which allows for convergence of the PMF using fewer trajectories compared with SMD. Use of the telescoping water scheme within ASMD partially overcomes the first of these limitations by reducing the number of waters at each stage to only those needed to solvate the structure within a given stage. In the PMFs obtained from ASMD, the work of unfolding Acto-2 was found to be higher than the Acto-WT by approximately 120 and reflects the increased stability seen in the chemical denaturation experiments. The evolution of the average number of hydrogen bonds and number of salt bridges during the pulling process provides a mechanistic view of the structural changes of the actophorin protein as it is unfolded, and how it is affected by the mutation in concert with the energetics reported through the PMF.
Significance
We have combined chemical denaturation studies and full atomistic computer simulations to explain the increase in thermal or chemical stability of the actophorin Acto-2 mutant. Using ASMD with telescoping solvent boxes, we determined the PMF, the instantaneous number of native contacts, the average number of hydrogen bonds, and the number of salt bridges as the protein is unfolded. Our findings revealed the interactions responsible for the improved stability of the identified mutant.
Introduction
Many cellular processes—including cytokinesis, invasiveness, and membrane protrusion—rely on the underlying control of actin filament networks (1,2). The actin depolymerizing factor/cofilin (ADF/C) protein family is responsible for remodeling the actin filament network by severing filaments (3,4). Actophorin is a member of the ADF/C family isolated from the amoeba Acanthamoeba castellani (5). The protein is concentrated at the leading edge of the amoeba, thus participating in the process of cellular locomotion, and is particularly associated with the amoebastome, a structure associated with feeding (6). The protein is monomeric, has a weight of 15.5 kDa, and is composed of 138 amino acids. Several x-ray crystal structures of actophorin are available (7,8,9,10).
The actophorin-induced F-actin severing mechanism has been extensively characterized (11,12,13). The protein has a higher affinity for muscle actin (Kd = 0.5 M) versus amoeba F-actin (Kd = 5.0 M) and binds slowly to amoeba F-actin with dissociation that is described by a bimolecular reaction, versus observed binding cooperativity when muscle F-actin is the substrate (13). Actophorin severs actin filaments both at steady state and during spontaneous polymerization. This was observed both visually with rhodamine phalloidin-labeled actin and by the measured reduction in the low shear viscosity of actin filaments. The action of actophorin is similar to other members of the ADF/C family, notably cofilin (14,15). In essence, ADF/C binding to F-actin creates discontinuities in mechanics and topology along the actin filament that generates localized stress, which in turn promotes actin filament severing at actin monomer junctions between sites with and without bound ADF/C (16). This hypothesis is supported by the observation (17) that ADF/C binding weakens lateral contacts between adjacent actin monomers in the actin filament due to a 5° rotation per bound actin monomer. This induced stress drives filament depolymerization and turnover.
Molecular dynamics simulation has supported the role that ADF/C plays in modulating F-actin topology and mechanical properties of the filament (18). Recent analysis of cryo-EM structures of cofilin-bound F-actin (19) reveals that actin filament deformation is localized to sites of cofilin binding, and that multiple cofilin binding events result in higher severing activity. Filament mechanical properties have been characterized through simulation (20), and revealed the role that filament bending, twisting, and buckling play in ADF/C binding (21). Most striking is the repartitioning of filament elastic energy by cofilin binding in a manner that accelerates depolymerization.
Members of the ADF/C family differ in size, primary sequence, and quaternary structure, but exhibit a remarkably conserved tertiary fold. A hallmark of this fold is the actin depolymerizing factor homology (ADF-H) domain that is extant in several different F-actin metabolizing protein families (22). The ADF-H domain dictates interactions with both F-actin and G-actin, as well as with the Arp2/3 complex (23). This region is seen to make significant contact with actin in a cocrystal structure of actin and the C-terminal region of the actin monomer sequestering protein twinfilin (24). ADF-H interacts with actin sub domains 1 and 3 and buries nearly 1200 Å2 of surface area. The actophorin ADF-H domain consists of the extreme N-terminal region (amino acid residues 1–3, which are not extant in either actophorin structure), portions of helix-3 (residues 93–95 and 102–107), and the end of the terminal helix-4 (residues 131–135).
Chemical denaturation studies are pivotal for understanding the basis of protein stability, as well as in comparing stability differences between mutant forms of the protein. Both thermodynamic (primarily the free energy of unfolding) and kinetic (the unfolding rate constant) terms can be determined by chemical denaturation. An even more detailed understanding of protein denaturation behavior can be achieved by contrasting the combination of chemical and thermal denaturation experiments (25) with the behavior of protein denaturation under force (26). Both types of experiment have been shown to produce similar denaturation pathways and rates (27,28). Computational simulations can add atomistic details (29) when combined with chemical/thermal denaturation studies.
Steered molecular dynamics (SMD) is an in silico technique for driving the unfolding of a protein or peptide under force, which, when combined with experimental denaturation, helps correlate thermodynamic and kinetic properties with statistically rigorous atomistic details. The adaptive steered molecular dynamics (ASMD) technique involves performing a sequential stage-wise force extension of the protein (30,31). In essence, it involves running multiple SMD simulations in stages consisting of a fixed small-distance pull followed by a contraction of the nonequilibrium distribution. The key to this contraction, as reported in (32), is that it selects structures from the nonequilibrium distribution, that are in turn representative of the equilibrium distribution. Relaxation of the entire system, while holding the protein ends fixed, can achieve this contraction but it is expensive because it involves additional propagation. Naive ASMD is the most aggressive form of the contraction because it leads to only one representative structure, namely the one those work value is closes to the Jarzynski average (JA). It is the most efficient, as it requires no additional propagation, but can lead to errors in the energetics and observables if the protein does not follow a single dominant unfolding pathway. Nevertheless, we use naive ASMD in the present work because of its relative efficiency, and our finding—in the observed convergence and agreement with experimental trends—that the present pair of proteins appear to satisfy the criteria for its use. The cycle of pulling stages and contraction in ASMD is then repeated until the protein is completely unfolded.
The primary quantity of interest that is measured from ASMD simulations is the equilibrium work of unfolding known as the potential of mean force (PMF). The PMF effectively captures the energetics of the process along the reaction coordinate and provides an effective tool for revealing and contrasting the stability of multiple protein systems (31,33). The PMF is an equilibrium quantity while SMD simulations are performed out-of-equilibrium owing to the large pulling velocities employed during the process. The Jarzynski equality (JE) establishes a relationship between the nonequilibrium pulling and the free energy of unfolding (34). It involves taking an exponential average of the unfolding work of multiple SMD trajectories. Schulten and co-workers (35,36) compared the exponential averaging scheme in JE versus various orders of cumulant expansion and confirmed that, for large ensemble sizes, JE yields accurate PMF values. The advantage of the ASMD technique is that its use of relatively short SMD trajectories within each stage, which allows for faster convergence of the PMF without suffering much loss in accuracy (30).
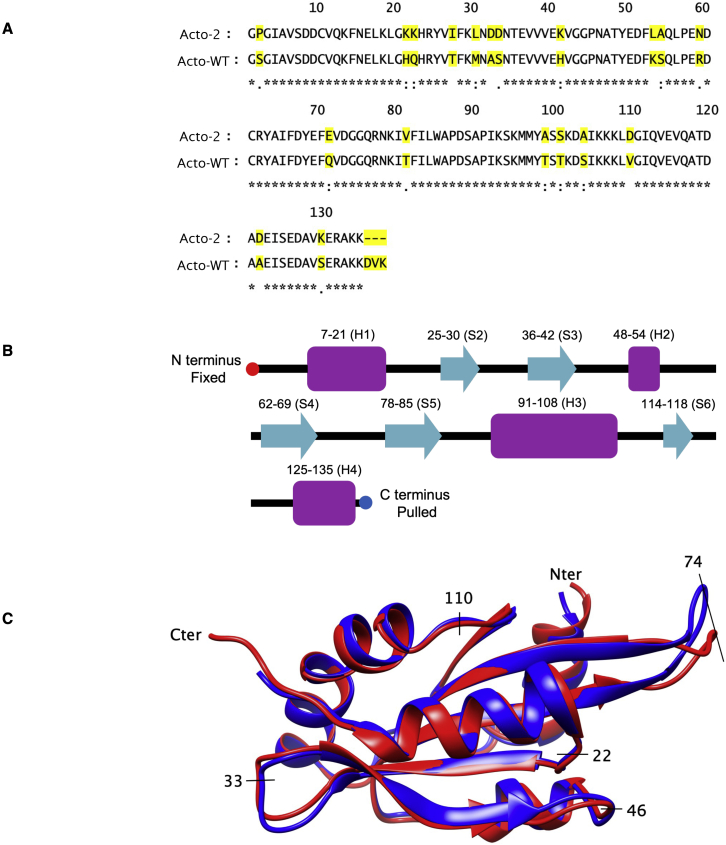
Site-specific mutations in actophorin at 19 locations (refer to Fig. 1) were found to increase the chemical and thermostability of the resulting mutant (Acto-2) compared with wild-type (Acto-WT) (9,10). Of the 19 mutations, 9 are conservative, 5 are moderately conserved, and 5 are nonconserved. In addition, Acto-2 contains a three-residue C-ter truncation. Superposition of the x-ray crystal structures of both proteins align within 1.1 Å root mean-square deviation (RMSD), with an exception of the flexible beta turn region between amino acid residues 70 and 75. Some of the mutations are found to introduce new charges within and on the surface of the protein, resulting in the formation of new salt bridges while others improve internal packing and increase number of hydrophobic surfaces patches (10). Evolution of the number of hydrogen bonds and salt bridges as the protein is unfolded provide details of the interactions that are formed and broken during the unfolding process. Below, we report the energetics of Acto-WT and its mutants as seen through the PMFs obtained using ASMD. We found agreement in the trends in the relative stability of all of these structures between experiment and simulation.
Figure 1.
(A) Primary sequence comparison of Acto-WT and Acto-2. Sequence differences are highlighted. Identical amino acids are denoted by asterisks, conserved amino acids are denoted by colon, less conserved by period and nonconserved by blank. (B) Secondary structure sequence in Acto-2. Strands are indicated by cyan arrows. Helices are indicated by purple rectangle. Individual helices and strands are identified and referred to in text by the identifier shown in the parentheses above the purple rectangles and cyan arrows, respectively. (C) Three-dimensional superpositions of Acto-WT (PDB: 1AHQ; red) and Acto-2 (PDB: 7SOG; blue). To see this figure in color, go online.
Methods
Biochemical experimental methods
Protein denaturation studies
Actophorin was purified to homogeneity as described in Quirk and Lieberman (9). Acto-WT and Acto-2 were chemically denatured in guanidinium hydrochloride (Sigma Chemical, St. Louis, MO, USA) at a concentration of 20 M in 10 mM Tris-HCl (pH 8.0). After mixing, the tubes were incubated for 12 h at room temperature to make sure the denaturation reactions were at equilibrium. Fluorescence emission intensity was measured (280 nm excitation wavelength with a 2 nm slit width) on a Chirascan V100 spectropolarimeter (Applied Photophysics, Inc. Beverly, MA, USA) equipped with a CCD fluorometer detector. Emission spectra were analyzed in the region 300–450 nm. Thermodynamic parameters were calculated from the emission intensity maximum assuming a two-state model. The fraction of unfolded protein at any point along the denaturation pathway is
| (1) |
where represents the fraction of unfolded proteins, and are the fluorescence emission baseline values for fully folded and unfolded proteins, respectively, and is the observed fluorescence emission intensity at a given denaturant point . The equilibrium constant and free energy change of unfolding are
| (2a) |
| (2b) |
where is the gas constant 1.987 , is the absolute temperature (K), and is measured near the midpoint of the unfolding transition to minimize error (37). To determine the free energy in the absence of denaturant, a linear fit was performed on the data pairs, , and the concentration of GdHCl according to
| (3) |
where represents the slope of the line and is a measure of the dependence of free energy on the concentration of denaturant (38). A comparison of stability between the two proteins using only is subject to error caused by the possibility that the uncertainty in the slope can be magnified in the extrapolation required in Eq. 3. We avoid this by implementing the method reported in Fersht and co-workers (39) wherein the difference in free energy of unfolding is calculated at the midpoint of the unfolding transition as follows:
| (4) |
The kinetics of the chemical denaturation were measured using an SF3 stopped flow device coupled to the Chirascan V100 spectropolarimeter (Applied Photophysics). Protein at 20 M in 10 mM Tris-HCl (pH 8.0) was rapidly (deadtime of 2 ms) mixed with 3.0 M GdHCl (Acto-WT) or 5.0 M GdHCl (Acto-2), giving final denaturant concentrations of 2.7 and 4.5 M, respectively. Twenty injections—viz replicates—were averaged. Fluorescence emission intensity at 330 nm was monitored with a 280 nm excitation wavelength. The unfolding rate constant was calculated as a single exponential as described in Gruber and Balbach (40),
| (5) |
where is the fluorescence emission signal at time , and is the amplitude of the corresponding kinetic phase. Data were fit using the fitting function in QtiPlot.
Actin filament severing
Actin filament networks were formed by polymerizing monomeric rabbit skeletal actin (Cytoskeleton) to a final concentration of 100 M in 5 mM Tris-HCl (pH 8.0), 0.2 mM CaCl2, 50 mM KCl, 2.0 mM MgCl2, and 1.0 mM ATP. Filaments were formed at 25°C for 1 h after which the reaction was centrifuged at 14,000 × g for 15 min and the supernatant was decanted. The mixture was placed into a Viscolab-4000 microviscometer (Cambridge Viscometry, Boston, MA, USA) that was equipped with a 1–20 cP piston. After reading a baseline viscosity value, Acto-WT or Acto-2 were added to the solution at a final concentration of 10 M. Viscosity values were recorded for 80 min at room temperature.
Computational methods
ASMD
When performing mechanical unfolding of proteins, an atom from one of the ends of the protein—e.g., a carbon or nitrogen atom from a terminating residue—is typically held fixed by applying a constraint. This is called the fixed atom. Similarly an atom at the other end of the protein is pulled by an application of a constant force or constant velocity. This is the steered atom (called SMD atom). In the case of constant velocity pulling, the steered atom is attached to a dummy atom via a spring and the dummy atom moves with constant velocity while the steered atom moves according to the net force from its bonded and unbonded interactions, and the spring from the dummy atom. The force imparted on the steered atom by the dummy atom is the product of the distance between the steered and dummy atoms, and the spring constant. The instantaneous energy and force can be written as:
| (6) |
| (7) |
where is the spring constant, is the pulling velocity, is the actual position of SMD atom, is Initial position of SMD atom, and is direction of pulling. For simplicity, ASMD is performed in an axis frame in which the vector from the fixed to dummy atoms is parallel to the direction of the constant velocity pulling. From the force extension measurements, the work of each SMD unfolding trajectory is calculated and inserted into the JE
| (8) |
to obtain the PMF, (35). In Eq. 8, the larger the unfolding work value of an SMD trajectory, the smaller is its contribution when taking the exponential average. Hence, only low unfolding work values tend to contribute to the PMF. Meanwhile, large pulling velocities can cause the SMD trajectories to move far from the near-equilibrium trajectories that contribute the most to the average, leading them to be sampled infrequently. A large number of SMD simulations must thus be run to successfully converge the PMF, particularly as the extension of the pull increases allowing for the trajectories to wander even farther away from equilibrium. In ASMD, we perform the pulling process in several stages so as to reduce this effect. In between stages, the space accessed by the system is contracted, without doing work on the system, to states closer to the dominant equilibrium trajectories (30).
There are several ways to contract the space in between stages of ASMD, such as full-relaxation ASMD (FR-ASMD) (41,42), partial-relaxation ASMD (PR-ASMD) (32), and multiple-branched ASMD (MB-ASMD) (43). In FR-ASMD and PR-ASMD the entire ensemble of trajectories has to be equilibrated after each stage and in MB-ASMD multiple trajectories close to the mean work value are selected for the next stage. The simplest method involves contracting the entire ensemble of structures at the end of a stage to a single representative structure. The structure that is selected at the end of the stage is the one that has its unfolding work closest to that calculated from JE (44). This structure is then selected as the initial configuration for the next stage of nonequilibrium pulling and the process is repeated. This method, called naive ASMD, is efficient when obtaining the PMF of unfolding for large proteins due to the lower computational costs (32).
It was earlier seen that pulling deca-alanine at 100 Å/ns and using 100 trajectories per stage converges the PMF much faster than compared with using the SMD method which requires using 10,000 trajectories for convergence (32). ASMD has also been applied previously to characterize the structural dynamics of Neuropeptide Y (30,31), deca-alanine stretching in water (44) and vacuum (41), alanine-rich helices (45), energetics of small β sheets (46), and stability of trpzip1 and its mutants (33).
ASMD with telescoping water box
Proteins are generally solvated in an aqueous environment within cells, and thus water plays an important role in their structure and function (47,48,49). To determine the unfolding energetics of proteins computationally, such conditions can be simulated using all-atom water distributed in a periodic box (44). It satisfies charge neutrality through the addition of counterions balancing the charges on the protein. SMD trajectories are generated on an unsegmented unfolding coordinate in a single stretch and, hence, the water box must be large enough from the start to contain the fully unfolded protein at the end of the pulling process. This requires the length of the box along the pulling direction to be long enough to contain the extended protein and solvent to avoid self-interactions. The lengths along the other two directions, can be shorter and equal to the length that would be required to contain the initial solvated protein. As a consequence, the periodic box typically contains hundreds of thousands of water molecules, and their propagation adds significantly to the cost of the computation.
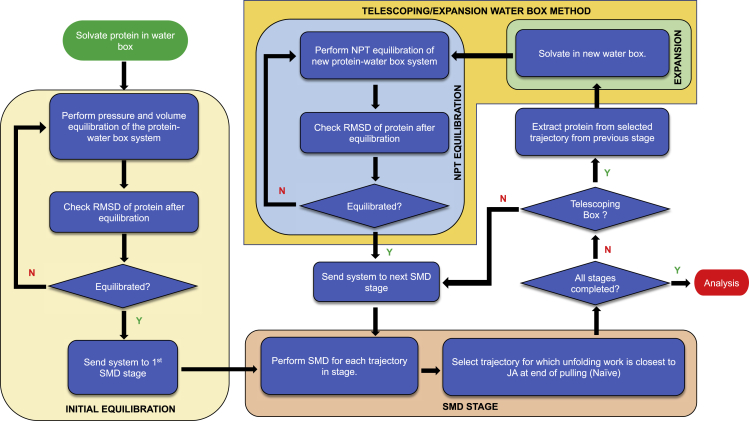
In ASMD, the system is staged, but the periodic water box typically remains fixed and suffers from the same numerical integration challenge of SMD. Recently, we found that we can implement so-called telescoping water boxes in which the periodic boxes are resized between stages, allowing for a significant reduction in the computation time and required memory usage (50). For instance, if in each stage the protein is pulled 20 Å, then the length of the periodic box can be increased by 20 Å along the axis of pulling to accommodate the lengthening protein. At each stage, water molecules must now be inserted or removed to fill the new periodic box relative to the old periodic box. In practice, this can be achieved easily by removing all of the water from the previous periodic box, and filling the new box with water under the appropriate constraints (as detailed below). A gentler approach would retain the waters contained in the intersection of the two boxes, remove those not in the new box, and add water in the new unoccupied space under similar constraints. As some of us recently found that the results did not vary much using this procedure (50), we did not implement it here. Nevertheless, it is possible that water molecules close to the protein may be quite sensitive to this procedure, and this could be a source of error that should be confirmed in future studies. Under the constant cross-section constraint implemented here, the dimensions along the two axes perpendicular to the pulling direction are kept constant throughout the pulling process. A visual representation of the Acto-2 protein lying inside of the telescoping boxes at the end of each stage is available in Figs. S1–S3. The constant volume constraint—in which the cross section is reduced to compensate for the increased length—would provide even more savings, but it was not implemented here. Nevertheless, present implementation of the telescoping box technique significantly cuts down the number of atoms for which force calculations are to be performed during most of the steering.
The telescoping water box workflow is shown in Fig. 2. The first step involves selecting an appropriately sized water box to completely solvate the protein system. The protein water box system is then equilibrated at constant (at 300 K and 1.01325 bar) while maintaining the terminal ends of the protein fixed. Next, the system is equilibrated at constant while keeping the backbone and ends of the protein fixed using harmonic energy constraints. The latter are released slowly through the following sequence: 100,000 timesteps with a constraint scaling factor of 10, 100,000 timesteps with a constraint scaling factor of 5, 100,000 timesteps with constraint scaling factor of 1, and finally 2,200,000 timesteps with no constraint. A final constant- equilibration of the system is performed, during which the RMSD of the protein is checked to confirm the stabilization—viz equilibration—of the structural deviations. If the RMSD of the structure has not been equilibrated, then additional constant- equilibrations are performed until the RMSDs are stabilized. The resulting equilibrated structure is then used to initiate the first ASMD stage. During each ASMD stage, naive ASMD is applied and the configuration that has the work value closest to the JA is chosen as the structure to initiate the next resizing stage. The partially unfolded protein present therein is removed from the old water box and solvated, ionized, and equilibrated in the resized water box while the protein ends are constrained. equilibration is performed and repeated until the RMSD indicates that it has equilibrated, and the new protein-water box system is then sent to the next pulling stage of ASMD.
Figure 2.
Adaptive steered molecular dynamics with telescoping water box workflow. To see this figure in color, go online.
Another type of dynamic water box is the elongating water sphere. This was employed when unfolding titin (51). While the elongating water sphere model allows for the determination of the unfolding intermediates during the early stages of pulling, for large extensions of the protein it suffers from extreme deformations and requires additional artificial forces to maintain the shape (52). It was also not coupled with the determination of the free energy as done here.
There are additional precedents for the use of expanding water boxes in the literature. Best et al. (53) have resolvated and reequilibrated their protein water systems twice in the course of performing SMD Bryer et al. (54) have performed a similar resolvation, reionization, and reminimization step twice in their simulations of HIV-1 vesicle systems. They observed certain anomalies with their bilayer structure after 1.5 s of equilibration. After rectification of the anomalies, they performed a resolvation of the vesicle water system with a spherical water shell and minimized the system using steepest gradient descent, but did not implement the technique within SMD.
A simpler implementation of the expanding water box method was implemented by Gilquin et al. (55) when studying the unfolding of hen egg lysozyme using a procedure similar to SMD called path exploration with distance constraints. They initially solvated the protein in a smaller water box and then, half-way through a 1.2 ns simulation, they immerse the smaller water box in a larger preequilibrated water box and remove the overlapping water molecules. (This latter approach is formally also available here, but we found earlier in (50) that its use in the resolvation stages of the telescoping boxes gave rise to only a modest improvement in the results.) Ma and Nussinov (56) also follow the same technique as in (55) when performing thermal unfolding with microglobulin. To the best of our knowledge, our telescoping water box method combined with naive ASMD was an advance (50) to these approaches because it allows for the determination of the free energy (and forces) along the steered direction. In this work, we demonstrate its utility in resolving the energetics of actophorin.
Observables
The average number of hydrogen bonds at a time of steering between the residues of any two subsets and of the protein is an ensemble average over trajectories (45),
| (9) |
of the instantaneous number of hydrogen bonds . Here, is the work obtained for each of the trajectories, —indexed by —during the stage corresponding to the time such that , where is the time at the end of the stage. For example, when calculating all of the hydrogen bonds within a single protein and are both equal to the set of all the residues in the protein. In practice, the instantaneous number of hydrogen bonds is sampled for frames at discrete (and regular times) along the trajectories. The intramolecular hydrogen bonds are assigned using MDAnalysis (57,58,59,60). Specifically, a hydrogen bond is assigned between any two possible atoms that are capable of hydrogen bonding that satisfy the conditions that the atoms are within a cutoff of 4 Å and with respect to which the hydrogen makes an angle of 140°.
In some cases, we will restrict the sum in to include only selected pairs of residues from the two subsets and we adjust the notation accordingly. For example, to report the number of hydrogen bonds between residues that are three, four, or five residues apart as in , and helices, we use the notation, , , and , respectively.
A native contact is a contact between the side chains of two residues that are not neighbors along the amino acid sequence. Generally, native contacts are calculated for side chains that are at least three residues apart, and assigned when the distances between nonbonded atoms from the respective residues are less than 4.5 Å. The fraction of native contacts can be determined according to (61) as
| (10) |
where represents the conformation, is the distance between atoms and in the conformation , is the distance between the heavy atoms and in the native state, is a set of all heavy combinations that obey the cutoff rules specified above, and denotes the size of the set. The ad hoc parameters and are selected to smoothen the contribution of a native contact, and to account for fluctuations in the contact length, respectively. Following Best et al. (61), they are fixed at and . Similar to the calculation performed for hydrogen bonding, one can obtain the average fraction of native contacts by averaging over the ensemble structures in the trajectories at time , i.e.,
| (11) |
In practice, however, we have seen that this average is dominated by the structures along the dominant JA trajectory , which is pieced together from the each of the stages according to the contraction that picks the trajectory whose work is closest to the JE. Thus, below we report
| (12) |
and determine the native contacts for the representative structure at each time using the mdtraj implementation (62).
Meanwhile, salt bridges are also inferred from structures along the dominant JA trajectory in analogy to Eq. 12. A salt bridge is inferred when an oxygen atom of an acidic residue—viz an aspartic acid or glutamic acid—and a nitrogen atom of a basic residue—viz arginine or lysine—that are within a cutoff distance. Following the usual default in VMD, we set the cutoff distance at 3.2 Å. The number of salt bridges for a given structure was calculated using the python package MDAnalysis (57,58,59,60).
Simulation parameters and methods
The ASMD simulations reported here were run using NAMD 2.14. It supports the SMD module as well as CUDA acceleration (63). Each ASMD stage was run using 1 GPU node on the ARCH resource called Rockfish, which comprises 44 Intel Xeon Gold Cascade Lake 6248R processors and 4 Nvidia A100 GPUs. For example, on Rockfish, the compute time for stage 1, which has the smallest water box is 22.27 min per trajectory while the compute time for stage 19, which has the largest water box, is 73.02 min per trajectory. The accuracy and convergence of the PMF obtained from ASMD depends primarily on three factors: 1) the pulling velocity, 2) the number of trajectories sampled per stage, and 3) the distance the protein is pulled per stage. The slower the protein is pulled, the closer the pulling process is toward an equilibrium pulling process. Increasing the number of trajectories increases the ensemble size allowing for sampling of more low work value trajectories, which helps converge the PMF. Decreasing the distance pulled per stage will limit the spread in the work values of the trajectories in the ensemble, thereby allowing more of them to contribute to the exponentially weighted sum in the JA calculation.
We carry out our simulations with an ensemble of 100 trajectories per stage at a pulling velocity of 10 , as this was found earlier to achieve convergence when performing ASMD with deca-alanine in explicit water (45). Each of their stages had a pulling distance of 2 Å. In the present case of actophorin, the protein has 135 residues, and should be approximately 390 Å long when fully unfolded. We arrive at this latter estimate by summing the C-N distance ( Å) and C-C bond distance ( Å) of a typical peptide (64), and then multiplying it by the number of residues in actophorin. To avoid the accounting that would be required to track 200 stages of 2 Å each for 400 Å pulls, we implemented longer pulling stages. We found, and report below, that twenty 20 Å pulling stages led to reasonable convergence, allowing for the relative comparisons that we report below. A detailed plot showing the Jarzynski weighted cumulative error at the end of the stages is shown in Fig. S4, and it suggests that the extra error introduced by the longer pulling stages is within the required tolerance.
Pulling within the stages of ASMD is performed with the at the N-terminus of the protein held fixed, and the at the C-terminus being pulled by the moving dummy particle along the axis. They are attached by a stiff harmonic spring with a spring constant value equal to 10 . This choice of spring constant was previously used in modeling the unfolding of the immunoglobulin domain in titin (51). Notably, they constrained the atoms and measured the spatio-thermal fluctuations of the Ig domain at 300 K to be 0.32 Å.
Water molecules are represented through the TIP3P model, and the system was neutralized by introducing Na+ ions through the NAMD protocol for ionization. Acto-WT actophorin required three Na+ ions for neutralization while Acto-2 required five Na+ ions for neutralization. Both proteins were initially solvated and ionized in a square cuboid water box with two equal sides of lengths, , and a third side of length . Periodic boundary conditions were maintained for all equilibration and production simulations.
The CHARMM36 force field was used to model the interaction forces because they have been seen to provide significant improvement in the prediction of the and dihedral interaction energies through the CMAP correction terms generally (65,66), and in ASMD in particular (67). A 2 fs timestep was chosen assuming that the vibration of hydrogen atoms can be ignored without affecting the PMF calculation. The van der Waals interaction cutoff distance is 12 Å, and the smooth switching function distance is 10 Å. Particle mesh Ewald was used to compute the electrostatic interactions within the system. Constant temperature control and constant pressure control were maintained using the Langevin method at 300 K and 1.01325 bar, respectively. The damping coefficient was set at 5 ps−1 with a decay period of 100 fs and a damping time constant of 50 fs.
Results
Actin filament severing
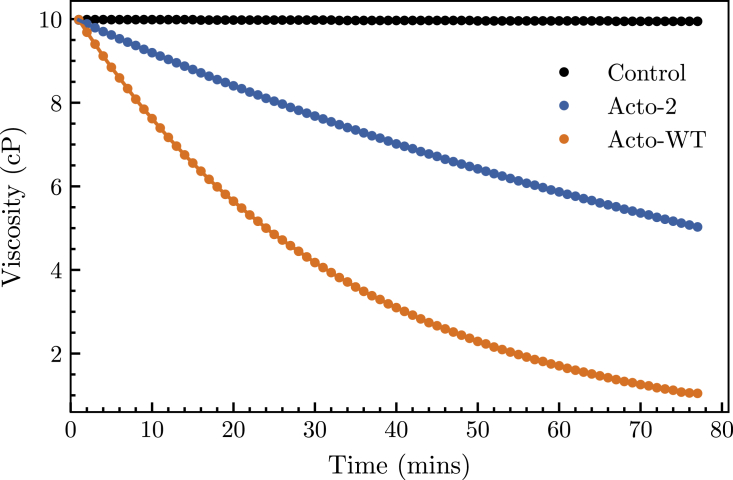
Both the Acto-WT and Acto-2 proteins have been seen to reduce the viscosity of actin filament networks. This results from a severing reaction, which is a hallmark of proteins in the ADF/C family. The extent of the severing reaction can consequently be easily monitored by measuring the reduction in the viscosity of a solution of actin filaments. Actin filaments at 100 M have on average a viscosity of 10.0 ± 0.2 cP. The addition of actophorin in a 1:10 ratio (actophorin:F-actin) results in an immediate viscosity reduction. Acto-WT reduces viscosity at a rate of 0.2 while Acto-2 is 2.5-fold less active and reduces viscosity at a rate of 0.08 . The activities of the two proteins in the F-actin severing reaction is shown in Fig. 3. The standard deviation for the three independent trials of the reaction was within 0.5% of the measured value.
Figure 3.
Viscosity reduction in F-actin network in presence of 10 M Acto-WT (orange) and Acto-2 (blue). Actin was polymerized at 100 M. F-Actin alone control (black). Plot represents average of three trials. To see this figure in color, go online.
Chemical denaturation assays
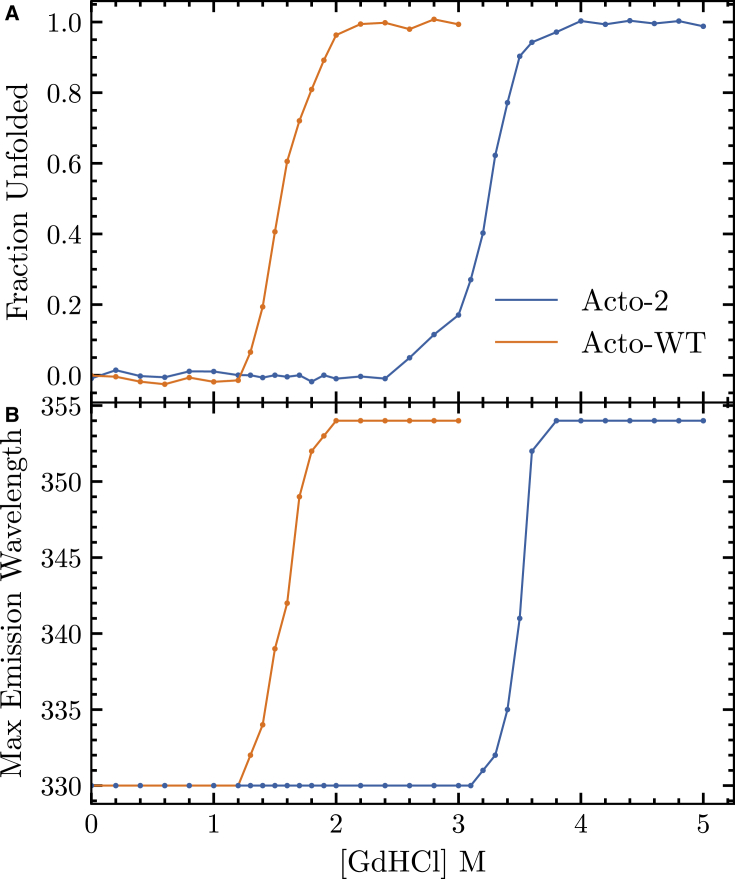
Chemical denaturation studies of the two proteins using guanidine hydrochloride reveal that the Acto-2 is significantly more resistant to denaturation compared with the Acto-WT. Both proteins unfold in a highly cooperative manner that is fully reversible and is consistent with a two-state unfolding mechanism, as can be seen from the single transition state in the unfolding curve in Fig. 4. Intrinsic fluorescence provides a strong signal when a 280 nm excitation wavelength is employed, emanating from the five tyrosine residues (with a minor contribution from the single tryptophan residue). Acto-WT begins to unfold in 1.25 M GdHCl and the unfolding reaction is complete at 2.1 M GdHCl with a transition midpoint at 1.6 M denaturant. Acto-2 begins to unfold at 2.5 M GdHCl and the unfolding reaction is complete at 3.8 M GdHCl with a transition midpoint at 3.3 M GdHCl. The wavelength of maximum fluorescence emission intensity follows a steep transition about the GdHCl midpoints from 300 to 354 nm for both proteins, as can be seen in Fig. 4.
Figure 4.
(A) Fraction of unfolded of Acto-WT (orange) and Acto-2 (blue) as a function of GdHCl concentration. (B) The maximum emission wavelength for Acto-WT (orange) and Acto-2 (blue) versus GdHCl concentration. The reported values are the average of three independent experiments. To see this figure in color, go online.
The free energy of unfolding of the two proteins in the absence of denaturant is determined using Eq. 3. Acto-2 can be seen to be more stable than Acto-WT by 3.6 . Analysis of the “” values—which is a measure of unfolding cooperativity—suggests that the Acto-WT unfolding is more cooperative than the Acto-2 by 1.0 . Calculating the free energy difference at the transition midpoint using Eq. 4 shows that the Acto-2 is more stable by 6.97 . These calculations show that Acto-2 is a more stable variant than the Acto-WT. Table 1 summarizes the results obtained from the chemical denaturation experiments. The difference between the values of and illustrates the inherent difficulties with extrapolation back to the absence of denaturant (68), but the data are consistent with the hypothesis that Acto-2 is more stable than Acto-WT.
Table 1.
Chemical denaturation of Acto-WT and Acto-2
| Protein | a | m b | [M]c | d |
|---|---|---|---|---|
| Acto-WT | 7.39 (0.2)e | 4.6 (0.1) | 1.6 (0.05) | 0.0 |
| Acto-2 | 11 (0.3) | 3.6 (0.1) | 3.3 (0.04) | 6.97 |
Free energy of the protein in the absence of denaturant.
Slope of the unfolding free energy plot versus .
at the midpoint of the unfolding transition.
Unfolding free energy difference at the transition midpoint.
The standard deviation from three independent trails are noted in parentheses.
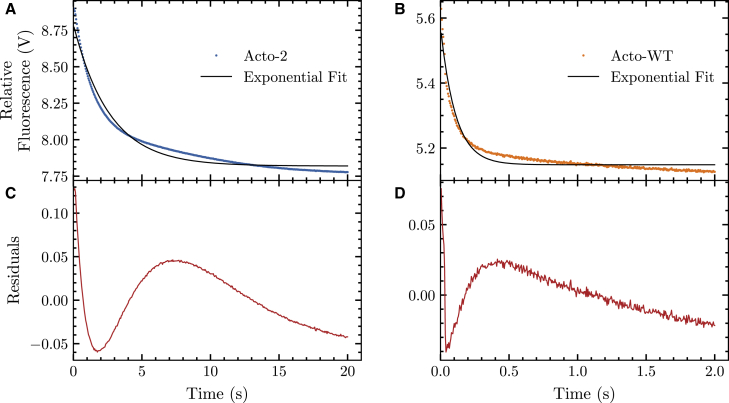
Stopped flow fluorescence can be used to determine the kinetic rate constants of the unfolding reaction shown in the top panels of Fig. 5. In single-mixing experiments, both Acto-WT and Acto-2 were rapidly unfolded using a GdHCl concentration that was just beyond the unfolding transition midpoint concentration of each protein. Fluorescence emission intensity at 330 nm (280 nm excitation wavelength) was used to monitor the unfolding reaction. Data were best fit to a single exponential equation. The first-order rate constant for the unfolding of Acto-WT (for transition from 0 to 3 M GdHCl) is 9.14 s−1, whereas it is 0.38 s−1 (for the transition from 0 to 5 M GdHCl) for Acto-2. Hence, Acto-2 unfolds more slowly than the Acto-WT by a factor of 24-fold. The lower panels of Fig. 5 show residuals for each fit and the experimental curve is the average of 20 separate traces. Although the magnitude of the residuals is small, there is some degree of nonrandomness to the residuals. This is particularly pronounced in the part of the curves where the signal begins to plateau. The precise reason for this is unknown, but is consistently observed in such measurements.
Figure 5.
(A) Fluorescence detected unfolding of Acto-2 by the rapid addition of 5 M GdHCl to a final concentration of 4.5 M. Data were fit to a single exponential function according to Eq. 5 in methods. (B) Fluorescence detected unfolding of Acto-WT by the rapid addition of 3 M GdHCl to a final concentration of 2.7 M. Data were fit to a single exponential function according to Eq. 5 in methods. Lower panels (C) and (D) show residuals for each fit. Each experimental curve is the average of 20 separate traces. To see this figure in color, go online.
PMF of unfolding
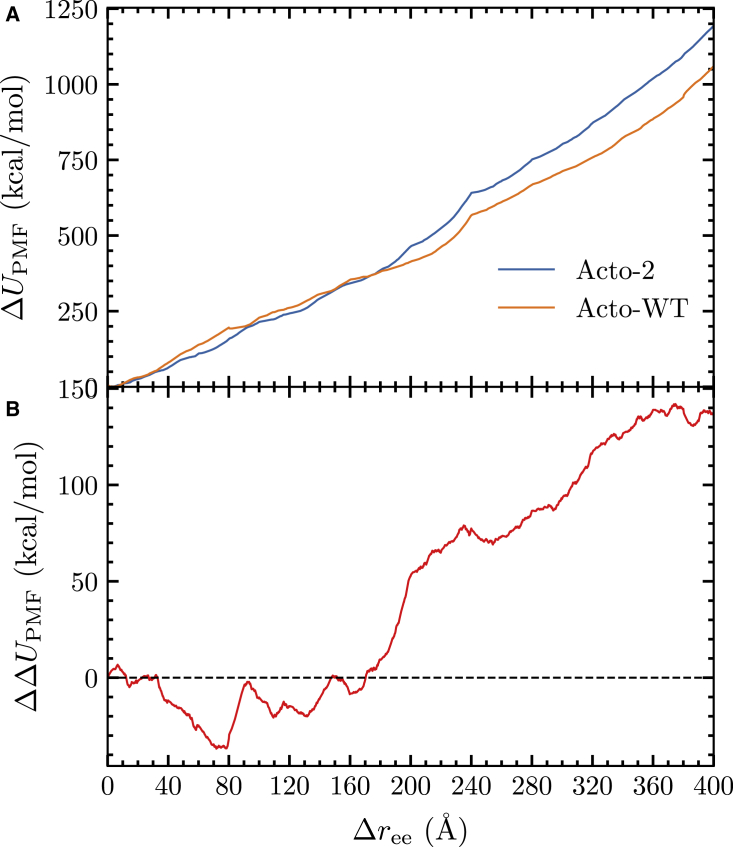
The PMF of unfolding of the Acto-2 and Acto-WT, along with the change in the end-to-end distance of the protein, is shown in Fig. 6. A more detailed rendering of the construction or the PMFs is also available in Fig. S4, illustrating the spread of the work values along the ASMD stages. The accumulated error is small—also available in Table S1—in comparison with the magnitude of the PMFs. The trend with increasing in the rise of the PMFs of Fig. 6 for both proteins correlates with our expectation that the mutations do not create any conformational change in Acto-2. Both structures align within 1.1 Å RMSD. The top panel indicates that the cumulative work of unfolding of Acto-2 exceeds that of Acto-WT, and this correlates well with experimental observations, indicating that Acto-2 has more resistance to unfolding. The difference in the work of unfolding of Acto-2 compared with Acto-WT is approximately 120 .
Figure 6.
(A) PMFs of Acto-2 (blue) and Acto-WT (orange). (B) The difference in the PMFs of Acto-2 minus Acto-WT. To see this figure in color, go online.
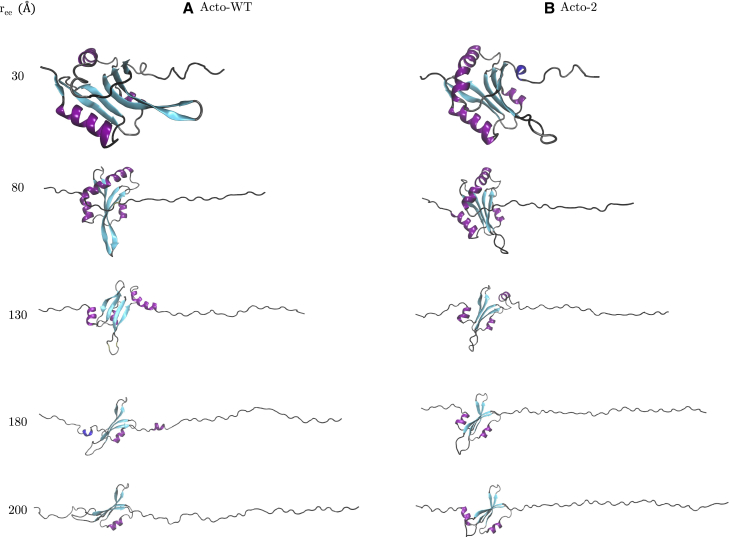
The bottom panel in Fig. 6 tracks the energy difference between Acto-WT and Acto-2 as a function of . In the first 30 Å of unfolding, as the helix (H4) and strand (S6) at the C-terminus end are unfolded, the difference in the PMF values remains low (refer to Fig. 1 for nomenclature). The corresponding unfolded structures at = 30 Å can be observed in Fig. 7. At = 150 Å, the work required to unfold Acto-2 relative to Acto-WT hits a minimum and reaches net zero (when the curves cross) at around = 200 Å. Representative snapshots of the structures present at = 180 Å can be seen in Fig. 7, and reveal that helices H4 and H3 and the strand S6 have been unfolded and helix H1 is starting to unfold. In the Acto-WT, the interactions between H1 (colored in blue) and the -sheets are broken and H1 completely unfolds by 200 Å. Meanwhile in Acto-2, the H1 (shown in purple) remains in the folded state.
Figure 7.
(A) Structure of Acto-WT and (B) structure of Acto-2 at of 30, 80, 130, 180, and 200 Å. Helices are colored purple, 310 helix blue, sheets cyan, coils black, and turns gray. To see this figure in color, go online.
Native contacts, intramolecular hydrogen bonds, and salt bridges
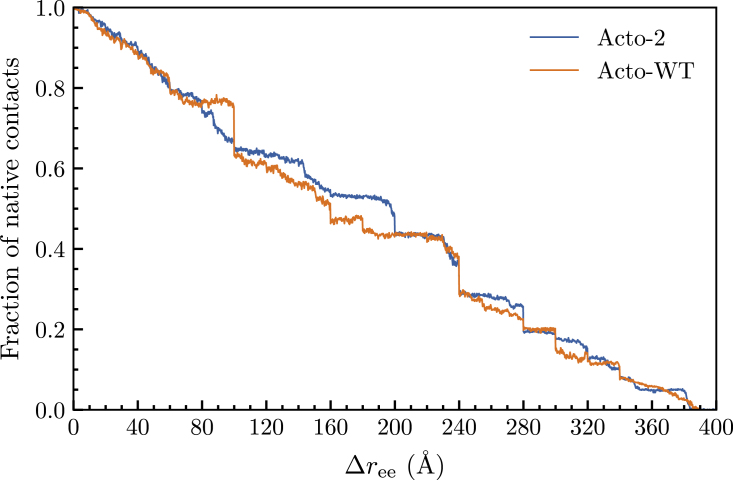
The mutations in Acto-2 give rise to a greater effective number of native contacts in Acto-2 than those calculated for Acto-WT. Using Eq. 10, we obtain the number of native contacts in the initial undenatured Acto-2 and Acto-WT structures to be 1663 and 1587, respectively. Some of the mutations have indirectly increased the effective number of native contacts by improving the overall packing of secondary structures within the protein while others have formed new contacts with non-neighboring residues—viz residues greater than 3 units apart.
We report the fraction of native contacts as a function of in Fig. 8) using the approximate formula of Eq. 12. The transitions between stages in the naive ASMD we implement here give rise to a step-like behavior in the observables, which on one hand can retain the structure in a local minimum longer than it should, and on the other hand can lead to a sudden correction. Thus, the interpretation of the reported values in Fig. 8 need to carefully account for this confounding factor. Nevertheless, we see a similar trend in the fraction of native contacts that remains in both structures in the first of 100 Å of the pull. For the next 100 Å, we then observe a notable drop in the fraction of native contacts in Acto-WT relative to Acto-2. This coincides with the relative increase in the PMF for Acto-2 seen in Fig. 6. It suggests that the new contacts in the initial structure of Acto-2 that have now been broken were due to a greater number of ionic interactions. This hypothesis is also in agreement with the evolution of the number of salt bridges and average number of hydrogen bonds as the protein unfolds that we report below.
Figure 8.
Average number of fraction of native contacts for Acto-2 (blue) and Acto-WT (orange) as a function of pulling distance. To see this figure in color, go online.
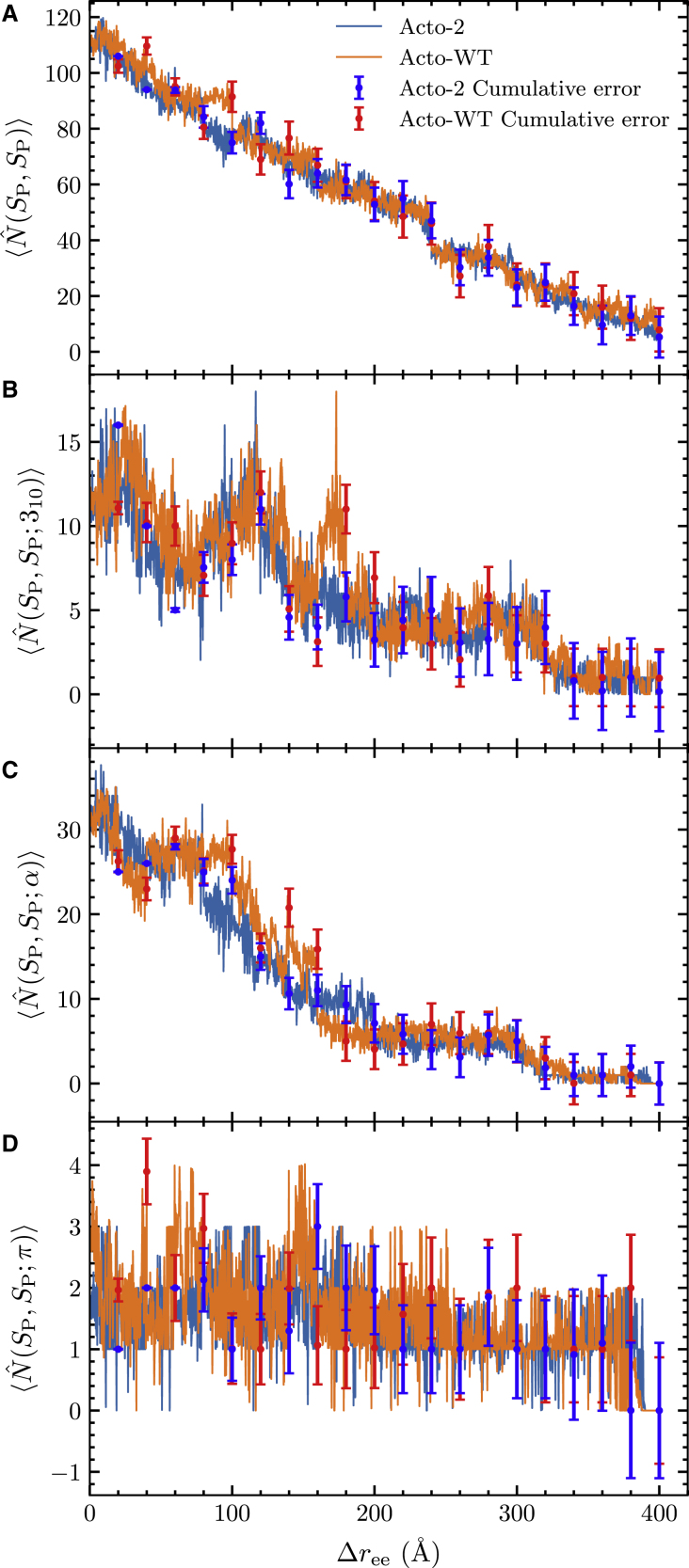
The hydrogen bonding profiles of a protein along the steered coordinate can be tracked using the weighted average in Eq. 9. The evolution of the hydrogen bonds between all of its residues—viz the set —along the pulling distance is shown in the top panel of Fig. 9. We can also restrict the hydrogen bond count according to which pairs of residues are hydrogen bonded. Specifically, , , and contacts correspond to those pairs of residues in , - and -helical structures, respectively. The evolution of the hydrogen bonds restricted to these structures are reported in Fig. 9, B–D. As should be expected for -helical proteins, the -helical structure is the dominant structure in the Acto-WT and Acto-2 proteins and it gives rise to the largest number of hydrogen bonds. We find that, beyond of 200 Å, very few helical contacts remain in either Acto-WT or Acto-2. It is notable that an hydrogen bond does not necessarily guarantee that the local structure is -helical. In Fig. S5, we report the helical structure along the dominant JA trajectory, and find the same general trend between the -helical fraction and . We also plot the fraction of residues retained in the different helical structure and sheets as a function of in Fig. S5. The rise of the coil fraction also anticorrelates with the loss hydrogen bonds in .
Figure 9.
Average number of (A) total, (B) 310, (C) , and (D) helix hydrogen bonds for Acto-2 (blue) and Acto-WT (orange) as a function of the pulling distance, .The error bars for the WT (red) and mutant (blue) represent the Jarzynski weighted cumulative error over the ensemble of 100 nonequilibrium trajectories determined at the end of each stage. To see this figure in color, go online.
The change in structure along the JA trajectory is also revealed in the representative snapshots of Fig. 7. Therein, the H1 helix can be seen to change from an -helical structure to a -helical structure as indicated by the blue H1 helix in Acto-WT. This transition is also captured in the average number of and hydrogen bond plots (Fig. 9, B and C). The orange Acto-WT curve exhibits a spike in the average number of hydrogen bonds just before = 200 Å, and a corresponding decrease in the average number of hydrogen bonds. From the average number of hydrogen bonds plot (Fig. 9 A) we can observe a larger number of intramolecular hydrogen bonds for Acto-WT up until when 200 Å. Thereafter, a slightly larger number of hydrogen bonds remain within Acto-2 compared with Acto-WT. Not surprisingly, this range in the end-to-end extensions matches the region before the crossover in the PMF plot (Fig. 6). This agreement is due to the preferential loss of bonds of the Acto-WT, which also leads to an increase in .
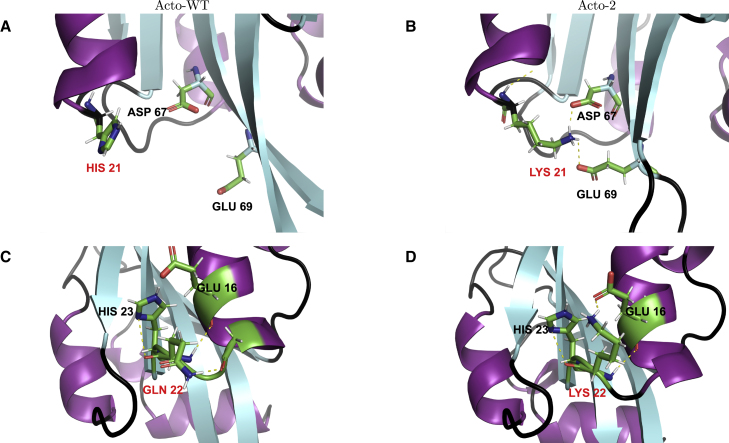
Thermophilic proteins with biological activity at higher temperatures are known to have a greater number of salt bridges compared with proteins that operate at lower temperatures (69). Indeed, we find salt bridges in the initial structures anchoring H1 to the neighboring helices and sheets. The N atom of lysine 21 also forms salt bridges with O atoms of aspartic acid and glutamic acid located at residues 67 and 69, respectively (Fig. 10). A conserved lysine mutation at residue 22 forms a salt bridge with glutamic acid located at residue 16. The alanine mutation at residue 104 improves the hydrophobic packing between H1 and H3.
Figure 10.
Comparison of structures between Acto-WT (A and C) and Acto-2 (B and D) near site 21 (A and B) and site 22 (C and D). Mutated residues indicated in red. To see this figure in color, go online.
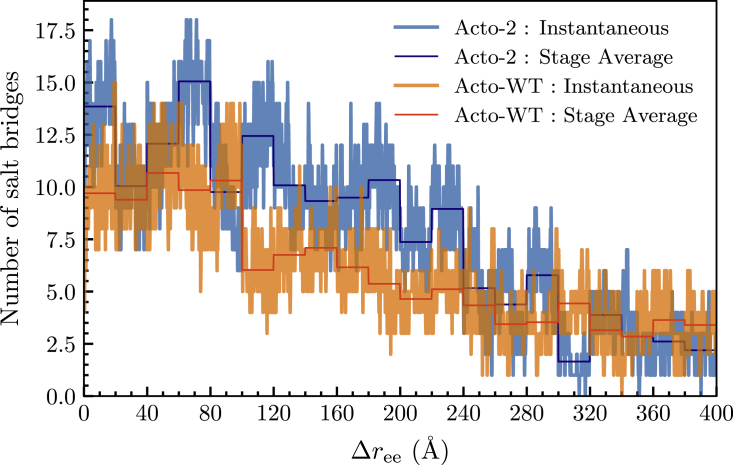
The evolution of the salt bridges is indicated in Fig. 11 along the dominant JA trajectory. Acto-2 displays a greater number of salt bridges throughout the pulling process. We can also see that, for values of between 100 and 240 Å, Acto-2 displays a significantly greater number of salt bridges, which verifies that observed in the individual analysis of the interactions of mutations. Fig. S6 shows the nonbonded interactions at sites 21 and 22 for Acto-WT and Acto-2 at equal to 0, 30, 80, 130, and 180 Å, and illustrate the same general trends seen in Fig. 11.
Figure 11.
Number of salt bridges in Acto-WT and Acto-2 verses for the trajectory closest to JE. The dark blue and dark orange lines represent the average number of salt bridges in each stage while the lighter blue and orange lines show the instantaneous fluctuations in the number of salt bridges during a stage. To see this figure in color, go online.
Discussion
The physiological role of actophorin is to bind actin filaments at monomer junctions where actin-bound ATP has hydrolyzed to ADP-Pi (12,13). This binding alters the topology and dynamics of the filament and promotes filament severing (16). Continuum mechanics calculations show that elastic energy is built up at boundaries between segments that contain and do not contain bound ADF/C. This creates nonuniform elasticity across the filament, which accelerates severing (20). The fact that F-actin severing is solely a mechanical process (versus enzymatic) is why the study of actophorin thermostability is germane to better understanding the physical reaction.
The Acto-2 protein was designed to take advantage of the benefits of microgravity crystallization (9) by improving crystal lattice formation via a more rigid/stable protein variant of actophorin. The three-dimensional structure of the protein was determined to 1.7 Å resolution (10), and one of the chains from the asymmetric unit was used for the ASMD simulations. Biochemically and biophysically, the WT and mutated actophorin proteins are clearly differentiable. Nevertheless, both can sever preformed actin filaments as measured by the reduction of filament network viscosity.
There are two regions of actophorin that are important to the efficiency of the severing reaction. The first is a small -turn. Crystal structures of actophorin under numerous conditions (7,8,9,10) show that protein main-chain atomic positions are nearly identical (RMSD = 0.1 Å) except for a single -turn region between residues 68 and 78 (9,10). This region shows a higher degree of structural plasticity with main-chain RMSD of 2.0 Å (9). Normal mode analysis (10) indicates that Acto-2 is less flexible than Acto-WT, as evidenced by larger fluctuations, larger atomic displacements, and lower average deformation energies in Acto-WT compared with Acto-2, except for this turn region, where the magnitude of the displacements is equal. This analysis may indicate that the effect of the increased thermal stability in Acto-2 is to dampen flexibility throughout the protein, except for the -turn region.
The second critical area for actophorin function is Ser-2. In Acto-WT, Ser-2 makes a bidentate hydrogen bond to actin Gln-354 (NH2) and Met-355 (backbone N). Phosphorylation of the serine significantly reduces the rate of F-actin severing (8). Mutating this residue to proline has a similar effect on the kinetics of filament turnover, but positively affects thermostability (10). When Pro-2 in Acto-2 is reverted to serine, the mutant servers F-actin 1.3-fold faster than Acto-WT (10). Acto-2/P2S is 1.8°C less stable than Acto-2 (10).
Taken together, our results and those of Quirk and Lieberman (9,10) indicate that increased thermodynamic and thermal stability work to increase the ability of actophorin to sever preformed actin filament networks by dampening main-chain flexibility except for the two regions that drive actophorin-actin filament binding interactions.
Chemical denaturation was used here to obtain results for comparison with the ASMD mechanical unfolding numerical experiments. Acto-2 is significantly more resistant to chemical denaturation than Acto-WT with a midpoint GdHCl concentration 1.7 M higher than the Acto-WT midpoint concentration, although both proteins exhibit similar slopes during the unfolding transition and a similar width of the transition. Acto-2 unfolding is characterized by a value of 6.9 . Chemical denaturation is not as directly comparable with the ASMD calculations because in solution both ends of the protein are free, whereas their relative distance is held fixed in the simulations. A more direct mechanical-mechanical comparison would be to perform atomic force microscope unfolding in solution (e.g., (70)); however, it is still instructive to compare mechanical and solution chemical denaturation profiles.
Many thermophilic proteins unfold more slowly, that is have a decrease in the unfolding rate constant relative to less thermostable or mesophilic proteins (71,72,73,74). Yet thermostable proteins fold at nearly the same rate compared with their mesophilic or psychrophilic homologs due to a lowering in the (75). In fact, slow unfolding may be a generalized mechanism for protein adaptation to higher temperatures (76) and is driven by core hydrophobic interactions as the unfolding rate difference persists for thermophile–mesophile homologs at low pH, where electrostatic contributions are minimal (77). Acto-WT and Acto-2 actophorin are essentially a model of a thermophilic and mesophilic homolog set and the 10-fold slower rate of GdHCl-induced unfolding is typical of thermophile–mesophile homologs. Slow unfolding kinetics are related to a high activation free energy barrier of unfolding (78). Mutations were designed to better pack internal hydrophobic cores, to optimize surface hydrophobic patches, and to increase sidechain–sidechain interactions. A major stabilizing mutation was the three residue C-ter deletion (10), a stabilization feature that has been observed in other protein systems (79). All the features of the mutations in Acto-WT are hallmarks that drive thermostability (80).
Conclusions
The function of a protein is invariably dictated by its structure. SMD simulations of protein unfolding provide atomic level detail of the interactions between residues that give the protein its structure and define its function. The PMF is a useful and concise tool to extract important molecularly resolved information from biological systems. It has been used to relate the function of titin in muscle cells with the mechanism by which its immunoglobin domains undergo unfolding (51). While the PMF is an important measurable, it is generally costly to compute as it requires running many protein unfolding trajectories. In addition, the cost also scales in proportion to the size of the protein system that is studied. As remarked in the introduction, in earlier work we had developed ASMD to reduce the cost of computation and time required for generating the PMF (30,41). We demonstrated the effectiveness of this technique by studying structural dynamics of multiple protein systems, as summarized in the methods section. To facilitate and expand the application of ASMD for studying the dynamics of unfolding of large proteins, we also developed a telescoping water box workflow integrated with ASMD (50). The workflow takes advantage of the stage-wise unfolding of the protein to dynamically increase the size of the water box after each stage.
We have shown that the ASMD telescoping water box method can effectively and accurately model the dynamics of protein unfolding and the results can be used in combination with experimental observations from chemical denaturation to answer questions related to stability and function of actophorin. Specifically, we found that the relative stability of the mutant Acto-2 relative to the wild-type stems from differences in the relative number of hydrogen bonds and salt bridges that the mutant can accommodate when they are partially unfolded. Such insights from the atomic interactions observed between the Acto-2 and Acto-WT about the relative importance of the structure along the unfolding pathway can be further used to develop new Acto-mutants with more interesting properties.
Author contributions
N.T. performed research, developed methods, analyzed data, and wrote the manuscript. S.Q. designed research, conducted experiments, developed methods, analyzed results, and wrote the manuscript. Y.Z. developed methods and analyzed data. E.R.S. conducted numerical simulations. R.L.L. designed and conducted experiments. R.H. designed research, developed methods, analyzed results, and wrote the manuscript. All authors participated in editing the manuscript.
Acknowledgments
This work has been partially supported by the National Science Foundation through grant no. CHE 2102455. The computing resources necessary for this work were provided in part by the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant no. ACI-1548562 through allocation CTS090079, and the Advanced Research Computing at Hopkins (ARCH) high-performance computing (HPC) facilities supported by NSF grant no. OAC-1920103. We also acknowledge Eli Hershkovits for useful discussions and early collaboration on the idea of a telescoping box in the context of general methods for pulling proteins.
Declaration of interests
The authors declare no competing interests.
Editor: Chris Chipot.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2022.11.2941.
Supporting material
References
- 1.Van Troys M., Huyck L., et al. Ampe C. Ins and outs of ADF/cofilin activity and regulation. Eur. J. Cell Biol. 2008;87:649–667. doi: 10.1016/j.ejcb.2008.04.001. [DOI] [PubMed] [Google Scholar]
- 2.Kanellos G., Frame M.C. Cellular functions of the ADF/cofilin family at a glance. J. Cell Sci. 2016;129:3211–3218. doi: 10.1242/jcs.187849. [DOI] [PubMed] [Google Scholar]
- 3.McGough A., Pope B., Weeds A. Springer Berlin Heidelberg; 2001. The ADF/Cofilin Family: Accelerators of Actin Reorganization; pp. 135–154. [DOI] [PubMed] [Google Scholar]
- 4.Maciver S.K., Hussey P.J. The ADF/cofilin family: actin-remodeling proteins. Genome Biol. 2002;3 doi: 10.1186/gb-2002-3-5-reviews3007. reviews3007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cooper J.A., Blum J.D., et al. Pollard T.D. Purification and characterization of actophorin, a new 15, 000-Dalton actin-binding protein from acanthamoeba castellanii. J. Biol. Chem. 1986;261:477–485. [PubMed] [Google Scholar]
- 6.Quirk S., Maciver S.K., et al. Pollard T.D. Primary structure of and studies on acanthamoeba actophorin. Biochemistry. 1993;32:8525–8533. doi: 10.1021/bi00084a019. [DOI] [PubMed] [Google Scholar]
- 7.Leonard S.A., Gittis A.G., et al. Lattman E.E. Crystal structure of the actin-binding protein actophorin from acanthamoeba. Nat. Struct. Biol. 1997;4:369–373. doi: 10.1038/nsb0597-369. [DOI] [PubMed] [Google Scholar]
- 8.Blanchoin L., Robinson R.C., et al. Pollard T.D. Phosphorylation of acanthamoeba actophorin (ADF/cofilin) blocks interaction with actin without a change in atomic structure. J. Mol. Biol. 2000;295:203–211. doi: 10.1006/jmbi.1999.3336. [DOI] [PubMed] [Google Scholar]
- 9.Quirk S., Lieberman R.L. Improved resolution crystal structure of acanthamoeba actophorin reveals structural plasticity not induced by microgravity. Acta Crystallogr. F Struct. Biol. Commun. 2021;77:452–458. doi: 10.1107/S2053230X21011419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Quirk S., Lieberman R.L. Structure and activity of a thermally stable mutant of Acanthamoeba actophorin. Acta Crystallogr. F Struct. Biol. Commun. 2022;78:150–160. doi: 10.1107/S2053230X22002448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Maciver S.K., Zot H.G., Pollard T.D. Characterization of actin filament severing by actophorin from acanthamoeba castellanii. J. Cell Biol. 1991;115:1611–1620. doi: 10.1083/jcb.115.6.1611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Maciver S.K., Wachsstock D.H., et al. Pollard T.D. The actin filament severing protein actophorin promotes the formation of rigid bundles of actin filaments crosslinked with alpha-actinin. J. Cell Biol. 1991;115:1621–1628. doi: 10.1083/jcb.115.6.1621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Blanchoin L., Pollard T.D. Mechanism of interaction of acanthamoeba actophorin (ADF/cofilin) with actin filaments. J. Biol. Chem. 1999;274:15538–15546. doi: 10.1074/jbc.274.22.15538. [DOI] [PubMed] [Google Scholar]
- 14.Ono S. Mechanism of depolymerization and severing of actin filaments and its significance in cytoskeletal dynamics. Int. Rev. Cytol. 2007;258:1–82. doi: 10.1016/S0074-7696(07)58001-0. [DOI] [PubMed] [Google Scholar]
- 15.De La Cruz E.M. How cofilin severs an actin filament. Biophys. Rev. 2009;1:51–59. doi: 10.1007/s12551-009-0008-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Elam W.A., Kang H., De la Cruz E.M. Biophysics of actin filament severing by cofilin. FEBS Lett. 2013;587:1215–1219. doi: 10.1016/j.febslet.2013.01.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.McGough A., Chiu W. ADF/cofilin weakens lateral contacts in the actin filament. J. Mol. Biol. 1999;291:513–519. doi: 10.1006/jmbi.1999.2968. [DOI] [PubMed] [Google Scholar]
- 18.Pfaendtner J., De La Cruz E.M., Voth G.A. Actin filament remodeling by actin depolymerization factor/cofilin. Proc. Natl. Acad. Sci. USA. 2010;107:7299–7304. doi: 10.1073/pnas.0911675107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Huehn A.R., Bibeau J.P., et al. Sindelar C.V. Structures of cofilin-induced structural changes reveal local and asymmetric perturbations of actin filaments. Proc. Natl. Acad. Sci. USA. 2020;117:1478–1484. doi: 10.1073/pnas.1915987117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Schramm A.C., Hocky G.M., et al. De La Cruz E.M. Actin filament strain promotes severing and cofilin dissociation. Biophys. J. 2017;112:2624–2633. doi: 10.1016/j.bpj.2017.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.De La Cruz E.M., Gardel M.L. Actin mechanics and fragmentation. J. Biol. Chem. 2015;290:17137–17144. doi: 10.1074/jbc.R115.636472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lappalainen P., Kessels M.M., et al. Drubin D.G. The ADF homology (ADF-H) domain: a highly exploited actin-binding module. Mol. Biol. Cell. 1998;9:1951–1959. doi: 10.1091/mbc.9.8.1951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Poukkula M., Kremneva E., et al. Lappalainen P. Actin-depolymerizing factor homology domain: a conserved fold performing diverse roles in cytoskeletal dynamics. Cytoskeleton. 2011;68:471–490. doi: 10.1002/cm.20530. [DOI] [PubMed] [Google Scholar]
- 24.Paavilainen V.O., Oksanen E., et al. Lappalainen P. Structure of the actin-depolymerizing factor homology domain in complex with actin. J. Cell Biol. 2008;182:51–59. doi: 10.1083/jcb.200803100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mahapa A., Mandal S., et al. Sau K. Chemical and thermal unfolding of a global staphylococcal virulence regulator with a flexible C-terminal end. PLoS One. 2015;10 doi: 10.1371/journal.pone.0122168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jagannathan B., Marqusee S. Protein folding and unfolding under force. Biopolymers. 2013;99:860–869. doi: 10.1002/bip.22321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Botello E., Harris N.C., et al. Kiang C.-H. Temperature and chemical denaturant dependence of forced unfolding of titin I27. J. Phys. Chem. B. 2009;113:10845–10848. doi: 10.1021/jp9002356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kelly C., Gage M.J. Protein unfolding: denaturant vs. force. Biomedicines. 2021;9:1395. doi: 10.3390/biomedicines9101395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Candotti M., Esteban-Martín S., et al. Orozco M. Toward an atomistic description of the urea-denatured state of proteins. Proc. Natl. Acad. Sci. USA. 2013;110:5933–5938. doi: 10.1073/pnas.1216589110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ozer G., Valeev E.F., et al. Hernandez R. Adaptive steered molecular dynamics of the long-distance unfolding of neuropeptide y. J. Chem. Theory Comput. 2010;6:3026–3038. doi: 10.1021/ct100320g. [DOI] [PubMed] [Google Scholar]
- 31.Quirk S., Hopkins M.M., et al. Bain D.L. Mutational analysis of neuropeptide y reveals unusual thermal stability linked to higher-order self-association. ACS Omega. 2018;3:2141–2154. doi: 10.1021/acsomega.7b01949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zhuang Y., Bureau H.R., et al. Hernandez R. Adaptive steered molecular dynamics of biomolecules. Mol. Simul. 2021;47:408–419. [Google Scholar]
- 33.Bureau H.R., Quirk S., Hernandez R. The relative stability of trpzip1 and its mutants determined by computation and experiment. RSC Adv. 2020;10:6520–6535. doi: 10.1039/d0ra00920b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jarzynski C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997;78:2690–2693. [Google Scholar]
- 35.Park S., Khalili-Araghi F., et al. Schulten K. Free energy calculation from steered molecular dynamics simulations using Jarzynski’s equality. J. Chem. Phys. 2003;119:3559–3566. [Google Scholar]
- 36.Park S., Schulten K. Calculating potentials of mean force from steered molecular dynamics simulations. J. Chem. Phys. 2004;120:5946–5961. doi: 10.1063/1.1651473. [DOI] [PubMed] [Google Scholar]
- 37.Monera O.D., Kay C.M., Hodges R.S. Protein denaturation with guanidine hydrochloride or urea provides a different estimate of stability depending on the contributions of electrostatic interactions. Protein Sci. 1994;3:1984–1991. doi: 10.1002/pro.5560031110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Courtemanche N., Barrick D. Folding thermodynamics and kinetics of the leucine-rich repeat domain of the virulence factor internalin b. Protein Sci. 2008;17:43–53. doi: 10.1110/ps.073166608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sali D., Bycroft M., Fersht A.R. Surface electrostatic interactions contribute little to stability of barnase. J. Mol. Biol. 1991;220:779–788. doi: 10.1016/0022-2836(91)90117-o. [DOI] [PubMed] [Google Scholar]
- 40.Gruber T., Balbach J. Protein folding mechanism of the dimeric amphiphysinII/Bin1 N-bar domain. PLoS One. 2015;10:e0136922. doi: 10.1371/journal.pone.0136922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ozer G., Quirk S., Hernandez R. Adaptive steered molecular dynamics: validiation of the selection criterion and benchmarking energetics in vacuum. J. Chem. Phys. 2012;136 doi: 10.1063/1.4725183. [DOI] [PubMed] [Google Scholar]
- 42.Bureau H.R., Merz D.R., Jr., et al. Hernandez R. Constrained unfolding of a helical peptide: implicit versus explicit solvents. PLoS One. 2015;10 doi: 10.1371/journal.pone.0127034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ozer G., Keyes T., et al. Hernandez R. Multiple branched adaptive steered molecular dynamics. J. Chem. Phys. 2014;141 doi: 10.1063/1.4891807. [DOI] [PubMed] [Google Scholar]
- 44.Ozer G., Quirk S., Hernandez R. Thermodynamics of decaalanine stretching in water obtained by adaptive steered molecular dynamics simulations. J. Chem. Theory Comput. 2012;8:4837–4844. doi: 10.1021/ct300709u. [DOI] [PubMed] [Google Scholar]
- 45.Zhuang Y., Bureau H.R., et al. Hernandez R. Energetics and structure of alanine-rich α-helices via adaptive steered molecular dynamics (ASMD) Biophys. J. 2021;120:2009–2018. doi: 10.1016/j.bpj.2021.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Bureau H.R., Hershkovits E., et al. Hernandez R. Determining the energetics of small beta sheet peptides using adaptive steered molecular dynamics. J. Chem. Theory Comput. 2016;12:2028–2037. doi: 10.1021/acs.jctc.5b01110. [DOI] [PubMed] [Google Scholar]
- 47.Levy Y., Onuchic J.N. Water mediation in protein folding and molecular recognition. Annu. Rev. Biophys. Biomol. Struct. 2006;35:389–415. doi: 10.1146/annurev.biophys.35.040405.102134. [DOI] [PubMed] [Google Scholar]
- 48.Li J., Fernandez J.M., Berne B.J. Water’s role in the force-induced unfolding of ubiquitin. Proc. Natl. Acad. Sci. USA. 2010;107:19284–19289. doi: 10.1073/pnas.1013159107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Jungwirth P. Biological water or rather water in biology? J. Phys. Chem. Lett. 2015;6:2449–2451. doi: 10.1021/acs.jpclett.5b01143. [DOI] [PubMed] [Google Scholar]
- 50.Zhuang Y., Thota N., et al. Hernandez R. Implementation of telescoping boxes in adaptive steered molecular dynamics (ASMD) J. Chem. Theory Comput. 2022;18:4649–4659. doi: 10.1021/acs.jctc.2c00498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Lu H., Isralewitz B., et al. Schulten K. Unfolding of titin immunoglobulin domains by steered molecular dynamics simulation. Biophys. J. 1998;75:662–671. doi: 10.1016/S0006-3495(98)77556-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Gao M., Craig D., et al. Schulten K. Identifying unfolding intermediates of FN-III10 by steered molecular dynamics. J. Mol. Biol. 2002;323:939–950. doi: 10.1016/s0022-2836(02)01001-x. [DOI] [PubMed] [Google Scholar]
- 53.Best R.B., Li B., et al. Clarke J. Can non-mechanical proteins withstand force? stretching barnase by atomic force microscopy and molecular dynamics simulation. Biophys. J. 2001;81:2344–2356. doi: 10.1016/S0006-3495(01)75881-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Bryer A.J., Reddy T., et al. Perilla J.R. Full scale structural, mechanical and dynamical properties of HIV-1 liposomes. PLoS Comput. Biol. 2022;18 doi: 10.1371/journal.pcbi.1009781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Gilquin B., Guilbert C., Perahia D. Unfolding of hen egg lysozyme by molecular dynamics simulations at 300K: insight into the role of the interdomain interface. Proteins. 2000;41:58–74. [PubMed] [Google Scholar]
- 56.Ma B., Nussinov R. Molecular dynamics simulations of the unfolding of 2-microglobulin and its variants. Protein Eng. 2003;16:561–575. doi: 10.1093/protein/gzg079. [DOI] [PubMed] [Google Scholar]
- 57.Michaud-Agrawal N., Denning E.J., et al. Beckstein O. MDAnalysis: a toolkit for the analysis of molecular dynamics simulations. J. Comput. Chem. 2011;32:2319–2327. doi: 10.1002/jcc.21787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Gowers R., Linke M., et al. Beckstein O. SciPy. 2016. MDAnalysis: a Python package for the rapid analysis of molecular dynamics simulations; pp. 98–105. [Google Scholar]
- 59.Gowers R.J., Carbone P. A multiscale approach to model hydrogen bonding: the case of polyamide. J. Chem. Phys. 2015;142 doi: 10.1063/1.4922445. [DOI] [PubMed] [Google Scholar]
- 60.Smith P., Ziolek R.M., et al. Lorenz C.D. On the interaction of hyaluronic acid with synovial fluid lipid membranes. Phys. Chem. Chem. Phys. 2019;21:9845–9857. doi: 10.1039/c9cp01532a. [DOI] [PubMed] [Google Scholar]
- 61.Best R.B., Hummer G., Eaton W.A. Native contacts determine protein folding mechanisms in atomistic simulations. Proc. Natl. Acad. Sci. USA. 2013;110:17874–17879. doi: 10.1073/pnas.1311599110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.McGibbon R.T., Beauchamp K.A., et al. Pande V.S. MDtraj: a modern open library for the analysis of molecular dynamics trajectories. Biophys. J. 2015;109:1528–1532. doi: 10.1016/j.bpj.2015.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Kalé L., Skeel R., et al. Schulten K. NAMD2: greater scalability for parallel molecular dynamics. J. Comput. Phys. 1999;151:283–312. [Google Scholar]
- 64.Corey R., Pauling L. Fundamental dimensions of polypeptide chains. Proc. R. Soc. Lond. B Biol. Sci. 1953;141:10–20. doi: 10.1098/rspb.1953.0011. [DOI] [PubMed] [Google Scholar]
- 65.Best R.B., Mittal J., et al. MacKerell A.D., Jr. Inclusion of many-body effects in the additive CHARMM protein CMAP potential results in enhanced cooperativity of alpha-helix and beta-hairpin formation. Biophys. J. 2012;103:1045–1051. doi: 10.1016/j.bpj.2012.07.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Buck M., Bouguet-Bonnet S., et al. MacKerell A.D., Jr. Importance of the CMAP correction to the CHARMM22 protein force field: dynamics of hen lysozyme. Biophys. J. 2006;90:L36–L38. doi: 10.1529/biophysj.105.078154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Allen C., Bureau H.R., et al. Hernandez R. Benchmarking adaptive steered molecular dynamics (ASMD) on charmm force fields. ChemPhysChem. 2022;23 doi: 10.1002/cphc.202200175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Green S.M., Meeker A.K., Shortle D. Contributions of the polar, uncharged amino acids to the stability of staphylococcal nuclease: evidence for mutational effects on the free energy of the denatured state. Biochemistry. 1992;31:5717–5728. doi: 10.1021/bi00140a005. [DOI] [PubMed] [Google Scholar]
- 69.Bosshard H.R., Marti D.N., Jelesarov I. Protein stabilization by salt bridges: concepts, experimental approaches and clarification of some misunderstandings. J. Mol. Recognit. 2004;17:1–16. doi: 10.1002/jmr.657. [DOI] [PubMed] [Google Scholar]
- 70.Afrin R., Takahashi I., et al. Ikai A. Tensile mechanics of alanine-based helical polypeptide: force spectroscopy versus computer simulations. Biophys. J. 2009;96:1105–1114. doi: 10.1016/j.bpj.2008.10.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Perl D., Welker C., et al. Schmid F.X. Conservation of rapid two-state folding in mesophilic, thermophilic and hyperthermophilic cold shock proteins. Nat. Struct. Biol. 1998;5:229–235. doi: 10.1038/nsb0398-229. [DOI] [PubMed] [Google Scholar]
- 72.Cavagnero S., Debe D.A., et al. Chan S.I. Kinetic role of electrostatic interactions in the unfolding of hyperthermophilic and mesophilic rubredoxins. Biochemistry. 1998;37:3369–3376. doi: 10.1021/bi9721795. [DOI] [PubMed] [Google Scholar]
- 73.Dams T., Jaenicke R. Stability and folding of dihydrofolate reductase from the hyperthermophilic bacterium thermotoga maritima. Biochemistry. 1999;38:9169–9178. doi: 10.1021/bi990635e. [DOI] [PubMed] [Google Scholar]
- 74.Gráczer E., Varga A., et al. Vas M. Rates of unfolding, rather than refolding, determine thermal stabilities of thermophilic, mesophilic, and psychrotrophic 3-isopropylmalate dehydrogenases. Biochemistry. 2007;46:11536–11549. doi: 10.1021/bi700754q. [DOI] [PubMed] [Google Scholar]
- 75.Ratcliff K., Corn J., Marqusee S. Structure, stability, and folding of ribonuclease H1 from the moderately thermophilic chlorobium tepidum: comparison with thermophilic and mesophilic homologues. Biochemistry. 2009;48:5890–5898. doi: 10.1021/bi900305p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Mukaiyama A., Takano K. Slow unfolding of monomeric proteins from hyperthermophiles with reversible unfolding. Int. J. Mol. Sci. 2009;10:1369–1385. doi: 10.3390/ijms10031369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Wittung-Stafshede P. Slow unfolding explains high stability of thermostable ferredoxins: common mechanism governing thermostability? Biochim. Biophys. Acta. 2004;1700:1–4. doi: 10.1016/j.bbapap.2004.04.002. [DOI] [PubMed] [Google Scholar]
- 78.Karshikoff A., Nilsson L., Ladenstein R. Rigidity versus flexibility: the dilemma of understanding protein thermal stability. FEBS J. 2015;282:3899–3917. doi: 10.1111/febs.13343. [DOI] [PubMed] [Google Scholar]
- 79.Ban X., Liu Y., et al. Li Z. Thermostabilization of a thermophilic 1, 4-α-glucan branching enzyme through C-terminal truncation. Int. J. Biol. Macromol. 2018;107:1510–1518. doi: 10.1016/j.ijbiomac.2017.10.020. [DOI] [PubMed] [Google Scholar]
- 80.Li W.F., Zhou X.X., Lu P. Structural features of thermozymes. Biotechnol. Adv. 2005;23:271–281. doi: 10.1016/j.biotechadv.2005.01.002. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.