An implementation of the Martini coarse-grained force field in OpenMM

Abstract

We describe a complete implementation of Martini 2 and Martini 3 in the OpenMM molecular dynamics software package. Martini is a widely used coarse-grained force field with applications in biomolecular simulation, materials, and broader areas of chemistry. It is implemented as a force field but makes extensive use of facilities unique to the GROMACS software, including virtual sites and bonded terms that are not commonly used in standard atomistic force fields. OpenMM is a flexible molecular dynamics package widely used for methods development and is competitive in speed on GPUs with other commonly used packages. OpenMM has facilities to easily implement new force field terms, external forces and fields, and other nonstandard features, which we use to implement all force field terms used in Martini 2 and Martini 3. This allows Martini simulations, starting with GROMACS topology files that are processed by custom scripts, with all the added flexibility of OpenMM. We provide a GitHub repository with test cases, compare accuracy and performance between GROMACS and OpenMM, and discuss the limitations of our implementation in terms of direct comparison with GROMACS. We describe a use case that implements the Modeling Employing Limited Data method to apply experimental constraints in a Martini simulation to efficiently determine the structure of a protein complex. We also discuss issues and a potential solution with the Martini 2 topology for cholesterol.

Significance

We implemented the widely used Martini force field for coarse-grained simulations in the flexible molecular dynamics package OpenMM. This allows combining the use of Martini 2, including polarizable Martini, and Martini 3 with the capabilities and extendibility of OpenMM. We also provide a set of test systems that incorporates all potential terms and simulation features used in Martini 2 and 3, which should be useful for implementation of Martini in other software packages.

Introduction

Martini is a widely used coarse-grained force field (1,2). Its origins are in simulations of lipids (3,4), but over time it has been extended to include other biomolecules (5), polymers, and more recently, increasingly other chemical systems (1,2). In essence, Martini is a force field that can be implemented in various molecular dynamics (MD) engines and uses many standard potential function terms. However, Martini was developed within the context of the GROMACS software (6) and uses several features of GROMACS that are not readily available in other packages. These include virtual sites to improve stability and enable larger time steps and features specific to the coarse-grained nature of Martini, like the force field terms that explicitly prevent singularities in dihedral potentials for beads that are not prevented from being co-linear by the chemistry that does so for atomistic geometries (7). Although Martini implementations in other packages (8,9,10,11,12,13) exist, these typically lack some features or implement older versions of Martini.

Here we describe an implementation of Martini 2 and Martini 3 in the flexible OpenMM package (14). The implementation includes all potential function terms used in Martini 2 and Martini 3 (Table S1). Virtual sites are reconstructed using the virtual sites framework in OpenMM with equivalent results. We show that single-step energies and forces are reproduced within expected numerical accuracy. We calculate ensemble averages of properties for several test cases spanning Martini 2 (15), polarizable Martini 2.3P (16), and Martini 3 (17).

There are particular advantages to having an accurate Martini implementation in OpenMM. OpenMM is uniquely flexible among major MD packages while still being competitive in speed for systems that can be simulated on single GPUs. OpenMM allows easy access to forces and energies. This makes it easier to implement missing potential energy terms, like the coupled bond-angle potential, but it also makes it easy to simulate custom situations where standard MD forces need to be augmented by arbitrary external forces. Here we describe an example using the Modeling Employing Limited Data (MELD) algorithm (18), which dramatically improves sampling for folding proteins or finding complex structures by adding constraints derived from low-accuracy experimental data to a standard force field. A typical scenario for this uses an all-atom approach with AMBER force fields (19) in implicit solvent, but here we show that the same approach is quite efficient with Martini and explicit Martini solvent.

In a broader context, we expect our implementation to be useful for parameter development for future incarnations of Martini, as OpenMM enables easy implementation of new bonded and nonbonded potentials (even if there are workarounds in the form of table lookups in GROMACS). These could move in the direction of approaches to implement protein internal dynamics or experiment more accurately with basic nonbonded potentials that have different forms from the 12-6 Lennard-Jones potential currently used (20,21). OpenMM also has an advantage in methods that combine MD with Monte-Carlo or other methods that do not yield continuous forces for integration, including fragment-based docking like SILCS (22), lipid alchemy for switching lipids (23), or coupling simulations to experimentally derived data (18,24,25). Lastly, compared with other software packages, it may be easier to use OpenMM for simulations that include external forces, including electric fields, shock waves, velocity gradients, and others. Our suite of test cases should also prove useful for implementing Martini in other software packages. The code and a tutorial are available at https://github.com/maccallumlab/martini_openmm.

Materials and methods

Implementation

Automated testing

To ensure that our implementation faithfully reproduces the canonical GROMACS implementation of Martini, we implemented a series of automated tests (see below). These tests can be run on demand and are automatically triggered whenever changes are pushed to the project GitHub repository using GitHub Actions.

OpenMM architecture

OpenMM uses a modular architecture that allows for easy extensions. The central object in OpenMM is the “System,” which describes the system to be simulated, including the number of atoms and their masses. For each type of interaction, e.g., a harmonic bond, a “Force” object of the appropriate type and associated parameters are added to the “System.” Nonbonded Lennard-Jones and electrostatic interactions are added similarly.

Parsing

OpenMM includes a parser for GROMACS topology files in the standard “.top” and “.itp” formats. The parser is a python routine that reads in the GROMACS topology and constructs the appropriate OpenMM “System” and “Force” objects. For our implementation of Martini, we extended the parser to include all the interaction types used in Martini (Table S1).

Custom forces

Martini uses several interaction types not included among the standard functional forms supported by OpenMM. However, OpenMM has the unique capability to easily define custom forces by supplying a mathematical expression for the energy of the interaction. OpenMM parses this expression, symbolically differentiates it, and automatically compiles platform-optimized code for evaluating the energies and forces. Using this custom force capability, we implemented all the functional forms used in Martini, including several nonstandard bond, angle, and dihedral interaction types (Table S1). Similarly, we produced custom nonbonded forces that reproduce Martini’s Lennard-Jones and electrostatic interactions using a reaction field, including the treatment of forces and energies at the nonbonded cutoff that is implemented in GROMACS. The implementation currently does not support PME.

Virtual sites

Martini makes extensive use of virtual sites to improve stability and enforce geometrical features like planarity (26). OpenMM has extensive support for virtual sites, so it was generally straightforward to translate the specification in the GROMACS topology files into the appropriate OpenMM virtual site construction. One difficulty we encountered, however, was that whereas GROMACS allows specific constructions where one virtual site depends on another, OpenMM builds all virtual sites in parallel and does not allow such dependencies. A linear virtual site is one where the constructed position is a linear combination of the positions of its base particles. Suppose a linear virtual site depends on another linear virtual site. In that case, we can always remove this dependency by expressing the position as a linear combination of nonvirtual site particles. We implemented this dependency elimination as part of our parser. This elimination is impossible for nonlinear constructions, so our parser will raise an error in this case. All existing virtual site dependencies in Martini are of the linear type. Dependencies involving nonlinear virtual sites in future developments in Martini should be avoided to maintain future compatibility and can generally be avoided without loss of functionality.

Constraints

GROMACS and OpenMM use different constraint algorithms—LINCS (27) and Constant Constraint Matrix Approximation (CCMA) (28), respectively—that make fundamentally different assumptions. CCMA uses the topology’s bond, angle, and constraint information to construct a matrix that describes the coupling between constraints. There are two requirements for stability. First, for any pair of constraints sharing an atom, one must have an angle, bond, or third constraint that defines a triangle determining the coupling between the constraints. Second, the bond or angle determining the coupling must be sufficiently stiff. The couplings in the constraint matrix are determined from the topology’s equilibrium bond lengths and angles. If these are too flexible, the constraint matrix may not accurately reflect the actual geometry, leading to instability. Aside from cholesterol (see below), we did not encounter any problematic molecules in our tests. Future development of Martini should ensure that topologies satisfy the two criteria above, ensuring compatibility with both constraint algorithms.

Cholesterol

The standard cholesterol topology in Martini 2 uses a constraint network with two triangles fused along one edge (Fig. S1 a). This construction causes instability with CCMA because there are no angles (1-3-7 and 1-4-7), bonds (1–7), or constraints (1–7) that describe the coupling between pairs of constraints (1–3 and 3–7, and 1–4, 4–7). To ameliorate this issue, we developed a modified topology using virtual sites (Fig. S1 b), which eliminates the problematic constraint network. See Supporting material for details. The Martini 2 topology for cholesterol is problematic, as two recent papers have pointed out (29,30). Its constraint network is difficult to solve accurately and computationally expensive high LINCS orders are required to solve it (29). At standard LINCS orders, temperature gradients develop, and even at high LINCS orders, flexibility is too large for CCMA to satisfy the constraints the resulting structures still lead to instability when transferred to OpenMM. The topology needs to be replaced to run Martini 2 systems with cholesterol in OpenMM. See “Development of a modified cholesterol topology for OpenMM” in the Supporting material for more details.

Testing

Single-point calculations

Test systems were created to test the OpenMM implementation of the potentials in use in Martini 3 (17) and Martini 2 (4,5,15). For each system, the last frame of the setup and equilibration protocols described in the Supporting material was used for single-point calculations to compare energies and forces extracted from simulations carried out with GROMACS and OpenMM.

For energies, we compared the total potential energy by extracting this quantity from the respective GROMACS and OpenMM simulation. The two systems are considered to be in agreement if the absolute error is less than 10⁻³ kJ/mol and the relative error is less than 10⁻⁵. These are somewhat arbitrary criteria as we are unaware of a formal discussion in the literature of what degree of agreement is acceptable. We note that this is within the range of differences between implementations of the same CHARMM force field in CHARMM, NAMD, and GROMACS (31,32).

Forces are compared by extracting the forces on each atom. As OpenMM and GROMACS differ in how the forces on virtual sites are reported (in GROMACS these are set to zero, whereas in OpenMM they are not), OpenMM forces on virtual sites are set to zero before comparison. The positions of virtual sites are not integrated but reconstructed every step, so this difference has no impact on dynamics. The forces are considered to be in agreement if all absolute errors are within 10⁻⁴ kJ/mol/nm and all relative errors are less than 10⁻⁵.

To test the correct implementation of constraints and virtual sites, we applied constraints and rebuilt virtual sites for each test structure in OpenMM. The implementation is considered to be correct if no particle moves by more than 10⁻³ nm.

Unless otherwise specified, simulation parameters were chosen according to de Jong et al. (33), and single-point calculations were obtained using GROMACS version 2021.2 compiled in double precision (6) and OpenMM version 7.5 in double precision mode with the “Reference” platform (14). The code related to the single-point calculations can be found at https://github.com/maccallumlab/martini_openmm/tests/test_martini.py.

MD simulations

To verify the convergence of average properties obtained from Martini 2 and Martini 3 simulations carried out in GROMACS and OpenMM, several MD simulation systems were simulated in the NPT, NVT, and NVE ensemble, primarily to identify issues arising from differences in pressure and temperature control algorithms. For each ensemble, simulations were performed at four different time steps, namely 20, 10, 5, and 2 fs, in both double and mixed precision, unless otherwise specified. The standard Martini time step is 20 fs, and 2 fs should be considered very conservative given the large masses of Martini particles compared with actual atoms. The duration of each simulation is 10 ns. See Supporting material for more details on system setup and simulation details.

Average properties including volume, density, potential energy, and temperature were obtained from the simulations using gmx energy in GROMACS and by parsing the output log file of OpenMM. As the simulations were performed using different time steps, the sampling frequency was adapted to obtain the same number of data points for all simulations. For each calculated property, the average value and standard deviation were computed from a series of 2500 data points over 10 ns. The Data S1 includes the average values and corresponding standard deviations obtained from GROMACS and OpenMM. To compare the values obtained from GROMACS and OpenMM, we calculated the percentage of change defined as in Eq. 1 below:

$$Percentageofchange=Abs\left(\frac{{Avg}_{OpenMM}-{Avg}_{Gromacs}}{{Avg}_{Gromacs}}\right)\times 100$$ (1)

Additional analyses were done using GROMACS programs, and the area per lipid was calculated with FATSLiM (34), selecting the PO4 beads to describe the lipid headgroup.

Results and discussion

We tested our implementation by comparing many systems between OpenMM and GROMACS, using both single-point calculations for energies and forces and average properties to investigate the possible effects due to differences in integrators and, where applicable, thermostats and barostats. These systems span all potential energy function terms and other features used in Martini 2 and Martini 3, including the Gō model and elastic network approaches to maintaining protein structure, different bead sizes in Martini 3, the use of virtual sites, and the polarizable Martini 2.3P force field. Currently, there is no final polarizable Martini 3 force field. The results are summarized in the Supporting material document, the Data S1, and Table 1. Table S1 is a summary of all the Martini potential tested, and Tables S2 and S3 summarize all systems, which span basic model systems, including water, alkanes, and small molecules, and most areas of biomolecular simulation, including different soluble proteins and a peptide, complex lipid bilayer systems with membrane proteins, and nucleobases. In general, all single-point calculations show close agreement between the two software packages, as should be expected.

Table 1.

Average properties calculated from GROMACS and OpenMM simulations performed with a time step of 20 fs, in the NPT and NVT ensemble, as common simulations settings for Martini

Property	Test System Name									Ensemble
	Water (dp)	1UBQ (dp)	1UBQ (mp)	Dodecane (dp)	Dodecane (mp)	POPC (dp)	POPC (mp)	WLRLL (dp)	WLRLL (mp)
Potential energy	0.28%	0.35%	0.33%	0.42%	0.39%	0.49%	0.29%	0.93%	0.92%	NPT
Volume	0.18%	0.25%	0.22%	0.20%	0.19%	0.22%	0.16%	0.40%	0.40%
Temperature	0.05%	0.00%	0.03%	0.13%	0.05%	0.04%	0.04%	0.26%	0.24%
Density	0.18%	0.25%	0.22%	0.20%	0.18%	0.22%	0.16%	0.40%	0.40%
Potential energy	0.12%	0.16%	0.14%	0.18%	0.26%	0.28%	0.07%	0.58%	0.58%	NVT
Temperature	0.21%	0.00%	0.00%	0.18%	0.12%	0.02%	0.03%	0.25%	0.26%

The data is expressed as percentage of change between average values extracted from both the GROMACS and OpenMM simulations, in double or mixed precision (dp and mp, respectively). See Data S1 for the corresponding values from GROMACS and OpenMM, for data obtained from simulations at different time steps, and for the NVE ensemble. A description of each test system can be found in Table S3.

For average properties (Data S1), the results do not only depend on the implementation of the potential function but also on specific algorithms. There is no one-to-one correspondence between OpenMM and GROMACS for many key algorithms. The thermostats, barostats, and constraint algorithms differ between the packages. The results also become somewhat time step dependent, as expected for the generally relatively large time steps Martini uses, representing a trade-off between sampling and integration accuracy (35). However, the average properties generally agree to within a very small tolerance in the NPT and NVT ensemble at the commonly used time step of 20 fs (Table 1). In addition, no significant differences between the two software were retrieved in the area per lipid of the POPC simulation system (Table S4).

There are two anomalies, probably both related to the LINCS constraint algorithm (27) in GROMACS. Although we could implement all of Martini 2 and Martini 3 in OpenMM, the commonly used Martini 2 topology for cholesterol is unstable in OpenMM. We traced this back to the definition of constraints in the virtual sites used in cholesterol. These constraints are deemed solved with LINCS, although the solution is inaccurate, and the OpenMM algorithm cannot satisfy the constraints. We developed a modified cholesterol topology for Martini 2 (Fig. S1 and Supporting material: “Development of a modified cholesterol topology for OpenMM”) that uses a different set of constraints and a total of four virtual sites, which improves the geometry and satisfies the OpenMM algorithm. This is easily substituted into the OpenMM simulations by a simple modification to the input files. We verified that the modified topology reproduces in GROMACS the internal geometry of cholesterol and solvent accessible surface area obtained from the current Martini 2 cholesterol topology (Figs. S2 and S3). In addition, we tested this modified topology in GROMACS and OpenMM simulations of a DPPC:cholesterol bilayer, obtaining comparable results in terms of cholesterol distribution in the membrane, calculated as number of lipid neighbors for each lipid species (Fig. S4; see Supporting material: “Development of a modified cholesterol topology for OpenMM”).

A second, minor anomaly is the instability of NVE simulations at large time steps of polarizable Martini 2.3P in GROMACS. This is known from user experience, and the solution is to use a time step smaller than 10 fs. Still, it is interesting to note that OpenMM allows reasonable energy conservation at 10-fs and 20-fs time steps, suggesting LINCS is an issue. Since NVE simulations are not practically useful for this type of setup and our implementation in OpenMM is actually more stable than in GROMACS, for the current paper, we did not pursue this matter further.

Application: Modeling employing limited data

The performance of OpenMM on single GPU is competitive compared with GROMACS (we obtained an average of 6.30 $\pm$ 0.23 μs/day for OpenMM and 6.00 $\pm$ 0.13 μs/day for GROMACS using a DPPC:cholesterol bilayer as a test system; see Supporting material for more details) and enables simulations of systems that expand beyond the test systems described above.

To illustrate the power of the implementation of Martini 3 in OpenMM, we showcase an example where we predict the structure of a large protein complex guided by cross-linking mass spectrometry (XL-MS) data. In this example, we pair our implementation of Martini with the MELD (18,36) framework, which builds upon OpenMM by combining physical models with experimental data. This application is a good example of the power of OpenMM, as MELD translates experimental constraints into nonstandard potential function terms that are readily implemented in OpenMM but complicated to implement in GROMACS. Furthermore, XL-MS data is generally sparse, noisy, and ambiguous, which makes its use for structure determination challenging (37,38,39). MELD guides sampling by deciphering the correct interpretation of ambiguous data points while also ignoring the noise.

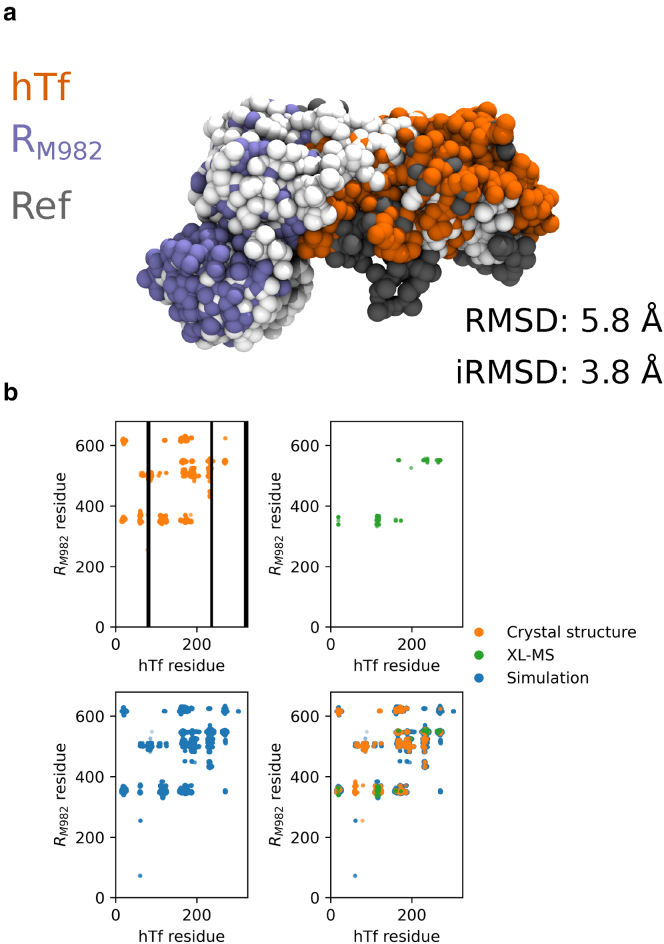
To determine the structure of human transferrin (hTf)/Neisseria meningitidis strain M982 transferrin-binding protein (R_M982) complex, we perform Martini 3 Hamiltonian replica exchange simulations (56 replicas, 600 ns per replica) within MELD/OpenMM. These simulations are guided by XL-MS-derived restraints (40), where the strength of the restraints is weakest at the top of the replica ladder and strongest at the bottom replica (see Supporting material for complete simulation details). From our clustered simulation, the average RMSD to the reference crystal structure (PDB ID: 3VE2) (41) from the most populated cluster is approximately 5.8 Å, with several sampled structures having RMSD values as low as approximately 3.0 Å (Fig. 1). The moderate RMSD arises due to the complex’s large size, where the monomers' slight tilt can substantially affect the RMSD. Nevertheless, the simulation reproduces the hTf − R_M982 interface with reasonable accuracy (interfacial RMSD = 3.8 Å, Fig. 1 a). Indeed, the simulation predicts many correct contacts between the two proteins despite the lack of experimental data guiding the formation of those interactions on many occasions (Fig. 1 b). Our simulations generally utilize the useful crosslinks while ignoring the spurious or overlength crosslinks (Fig. S5).

Figure 1.

Martini 3/OpenMM simulations are able to predict the correct interface between hTf and R_M982. (a) Overlay of hTf (orange) and R_M982 (purple) onto the reference crystal structure (PDB ID: 3VE2, white/gray) (41). RMSD (backbone) is calculated on all residues resolved in the X-ray crystal structure, and iRMSD includes residues that are less than 10 Å from the other protein. Unresolved residues in the reference crystal structure are shown in gray and excluded from RMSD calculations. (b) Scatter plots of hTf and R_M982 contacts from the reference, cross-linking mass spectrometry data, and simulation. Contacts are defined when two residues on separate monomers are within 10 Å. Black bars indicate regions that are unresolved in the reference crystal structure. XL-MS, cross-linking mass spectrometry. To see this figure in color, go online.

This example illustrates that Martini 3 models with limited experimental data can attain relatively high accuracy structures. Furthermore, this showcases the utility of an OpenMM-based method, MELD, to actively discern the correct interpretation of each experimental peak and the ability to ignore peaks that are incompatible with the physical models.

Conclusions

We present a complete implementation of Martini 2 and Martini 3 in OpenMM, including a comprehensive suite of automated tests, and we demonstrate the usefulness of the combination of the flexibility of OpenMM and the power of Martini on the structure prediction of a protein complex. In general, single-step force and energy calculations show excellent agreement between OpenMM and GROMACS. As can be expected, small differences arise in ensemble averages. In addition, simulations with different time steps show minor variations between the two packages, pointing at implementation differences in integration, constraint, thermostat and barostat, and perhaps other algorithms like neighbor searching and neighbor lists. Martini makes excellent use of the extensive capabilities and features of GROMACS, but the reliance on virtual sites and constraints requires some restraint in future development of Martini to facilitate the implementation of the force field in other software. We recommend not building virtual sites based on other virtual sites, and carefully designing constraint networks that do not rely on the plasticity of LINCS to be integrated accurately.

Author contributions

J.L.M. and D.P.T. designed and coordinated the project. J.L.M. wrote the OpenMM code. S.H., V.C., and J.L.M. implemented and carried out the tests, with the help of P.C.T.S. S.H. and P.C.T.S. wrote the Martini-OpenMM tutorial included in GitHub. S.L. and J.L.M. carried out the MELD application. D.P.T. drafted the initial version of the manuscript. All authors contributed to the final manuscript.

Editor: Abhishek Singharoy.

Supporting citations

References (42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67) appear in the Supporting material.