RDRGSE: A Framework for Noncoding RNA-Drug Resistance Discovery by Incorporating Graph Skeleton Extraction and Attentional Feature Fusion

Abstract

Identifying noncoding RNAs (ncRNAs)-drug resistance association computationally would have a marked effect on understanding ncRNA molecular function and drug target mechanisms and alleviating the screening cost of corresponding biological wet experiments. Although graph neural network-based methods have been developed and facilitated the detection of ncRNAs related to drug resistance, it remains a challenge to explore a highly trusty ncRNA-drug resistance association prediction framework, due to inevitable noise edges originating from the batch effect and experimental errors. Herein, we proposed a framework, referred to as RDRGSE (RDR association prediction by using graph skeleton extraction and attentional feature fusion), for detecting ncRNA-drug resistance association. Specifically, starting with the construction of the original ncRNA-drug resistance association as a bipartite graph, RDRGSE took advantage of a bi-view skeleton extraction strategy to obtain two types of skeleton views, followed by a graph neural network-based estimator for iteratively optimizing skeleton views aimed at learning high-quality ncRNA-drug resistance edge embedding and optimal graph skeleton structure, jointly. Then, RDRGSE adopted adaptive attentional feature fusion to obtain final edge embedding and identified potential RDRAs under an end-to-end pattern. Comprehensive experiments were conducted, and experimental results indicated the significant advantage of a skeleton structure for ncRNA-drug resistance association discovery. Compared with state-of-the-art approaches, RDRGSE improved the prediction performance by 6.7% in terms of AUC and 6.1% in terms of AUPR. Also, ablation-like analysis and independent case studies corroborated RDRGSE generalization ability and robustness. Overall, RDRGSE provides a powerful computational method for ncRNA-drug resistance association prediction, which can also serve as a screening tool for drug resistance biomarkers.

Introduction

Noncoding RNAs (ncRNAs), including lncRNAs, circRNAs, miRNAs, and snoRNAs, as human transcripts, are differentially expressed in various drug resistance events.¹ Recent studies have shown that ncRNAs are involved in many aspects of drug resistance in tumor cells, including epithelial-to-mesenchymal transition, DNA repair, drug efflux and metabolism, and cell cycle progression, which elucidated ncRNAs’ potential pharmacotherapy implications.^2,3 The past decade has witnessed the remarkable progress of pharmacological experiments in ncRNA with drug resistance, revealing diverse individuals’ drug responses when corresponding pathways are perturbated.⁴⁻⁶ Due to their critical role during personalized treatment, detecting ncRNA-drug resistance association (RDRA) is crucial for revealing the ncRNA molecular mechanisms and boosting the diagnosis and treatment of drug resistance in cancers. Conventional pharmacological wet experiments for uncovering RDRA are often costly and time-consuming. Hence, it would be essential to construct efficient and accurate models for identifying potential RDRA via computational methods.

Over the past few years, advances in graph representation learning-based methods,^7,8 especially representation learning for a heterogeneous bipartite graph (HBG) consisting of an ncRNA/drug subgraph and an adjacent RDRA subgraph, enabled the RDRA prediction under the computational paradigm.⁹ A graph characterizes the topological resistance relationship between an ncRNA and its target drug, natural and expressive to the modeling of RDRA and discovery of novel RDRAs. By graph representation learning, RDRA prediction can be regarded as a link prediction issue by aggregating neighbor information to learn node/edge representation. Increasingly rich RDRA information resources and data, on the other hand, are available, making drug resistance analysis with the use of copious data under the graph deep learning paradigm possible.

Currently, applying a graph convolutional network (GCN)¹⁰ to the ncRNA-drug resistance association bipartite graph to view RDRA prediction as a collaborative filtering issue in the recommended system has become a common practice. For example, GSLRDA¹¹ makes RDRA prediction with the aid of LightGCN,¹² which aimed to simplify the design of GCN to make it simpler and more suitable for RDRA prediction following the recommendation system pattern. LRGCPND¹³ constructed a bipartite graph and then proposed a linear residual graph convolution algorithm to conduct the recommendation between ncRNAs and drug resistance under the condition of not requiring additional data. Similar research fields to RDRA prediction, such as miRNA-drug sensitivity prediction, miRNA-drug resistance prediction, and circRNA-drug sensitivity prediction, also adopted similar research strategies. For instance, PDSM-LGCN¹⁴ continues to simplify standard GCN and only maintains its neighborhood information aggregation (fusion) module as a simple aggregator to update the current node and then to make miRNA-drug sensitivity prediction. Some models tried to introduce more diversified ncRNA/drug feature information, such as similarity metric or gene/ncRNA expression profile data, to conduct link prediction tasks on the RDRA bipartite graph. GCMDR¹⁵ is one of the representatives that integrate multiple information into miRNA-drug resistance prediction. GATECDA¹⁶ leveraged multiple databases (i.e., the sequences of host genes of circRNAs and the structure of drugs) and extracted the low-dimensional representation of nodes via a graph attention auto-encoder to conduct circRNA-drug sensitivity prediction. MNGACDA¹⁷ adopted a circRNA similarity network, a drug similarity network, and a known circRNA-drug sensitivity network to separately extract node features and then concatenate them to make circRNA-drug sensitivity prediction. Despite its rationality from a pure computational perspective, it may be controversial and has not stood up to the biological significance due to the assumption that the drug sensitivity in the same ncRNA sets is similar. Sometimes, a single nucleotide difference can completely change the nature of an ncRNA. Admittedly, coarse-grained feasibility enables drug resistance or sensitivity prediction to a certain extent for researchers, but the false positive problems at the same time cannot be neglected. Besides, these models all view bipartite graphs as the ground truth edges to provide adjacency information for the downstream link prediction tasks.

However, one subtle, hidden trouble of graph deep learning-based RDRA models is that they habitually treat known observed RDRA associations as ground truth edges to construct the graph. This practice is not robust as an RDRA prediction model because of inevitable noises from the batch effect and experimental errors. In addition, despite decent aforehand denoising operation, the original graph structure may still contain task-irrelevant information undesired for the downstream link prediction task or even counteractive links that may come from false-negative edges.¹⁸ In practical application, some edges in the RDRA graph often need to be discarded or weakened to capture the most valuable edges and alleviate over-smoothing. In contrast, the model must emphasize some functional edges depending on the downstream link prediction task.

In parallel, existing methods detecting the resistance association between ncRNAs and drugs have emerged, and they commonly depend on ncRNA/drug subgraph information besides indispensable adjacent RDRA subgraph information, which assumes that entities (ncRNA/drug) with similar targets may interact following co-expression/co-regulation/co-targeted patterns on top of the HBG.¹⁹ Despite its plausibility, it is still debated, and model performance may fluctuate due to either the ncRNA/drug subgraph sparsity/density or the similarity metric indistinguishability. In this regard, whether and how the ncRNA/drug subgraph of RDRA should be adopted when we conduct RDRA identification is yet to be fully explored. Moreover, from the perspective of regulatory relationship integration, screening the most beneficial relationships between ncRNAs only from isolated ncRNA subgraphs is also improper. It follows then that synergetic exploration of the effect between the ncRNA/drug subgraph and the adjacent RDRA subgraph is imperative, intending to uncover precisely the significative skeleton structures of the HGB in the context of RDRA prediction. Therefore, it is vital to jointly verify and learn the adjacent RDRA subgraph structure and ncRNA/drug subgraph within the HGB toward the downstream link prediction task (i.e., RDRA prediction).

In this paper, we proposed a framework, RDRGSE, which extracted and evaluated two structure views by an estimator based on GCN and attentional feature fusion (AFF) to learn final edge embedding and significative skeleton structures jointly lurked in the RDRA-HBG. Specifically, we first constructed the ncRNA and drug subgraph separately by projecting the known RDRAs as links into subgraph space. Together with the known RDRA, RDRA-HBG is a heterogeneous graph/network that includes an ncRNA subgraph to manifest the relationship among ncRNAs, a drug subgraph to reflect drug–drug information, and an RDRA subgraph to depict the association between ncRNAs and drug resistance. Then, we designed a structure evaluation-based bi-view skeleton structure learning strategy to optimize and filter the original graph structure by the estimator to obtain a high-quality skeleton structure. Furthermore, we integrated two types of embeddings formed by bi-view to get final edge embedding after taking full advantage of the AFF mechanism. Thus, accurate aforehand uncovering of significative skeleton structures, end-to-end training, and optimizing link representation under the auspices of AFF were organically integrated as the RDRGSE framework. To evaluate the performance of RDRGSE, extensive in silico experiments were performed. RDRGSE achieved competitive performance under 5-fold cross-validation (5-CV), outperforming existing state-of-the-art methods. Case studies further confirmed the efficacy of RDRGSE on RDRA prediction.

Materials and Methods

Datasets and Preprocessing

The manually curated ncRNA-drug resistance association datasets were collected from publicly available NoncoRNA²⁰ and ncDR²¹ as the benchmark dataset used in our framework. Here, we only chose those experimentally verified RDRA pairs. Concretely, NoncoRNA (the Feb 2020 version) collected 5568 ncRNAs, 154 drugs, and experimentally supported ncRNA-drug resistance associations in 134 cancers. For ncDR (the June 2016 version), it contains 5864 resistance associations between 1039 ncRNAs (162 lncRNAs and 877 miRNAs) and 145 drugs (compounds) collected by nearly 900 pieces of the published literature. Finally, after performing the inclusion of identifier unification, de-redundancy, and deletion of the irrelevant items from the two databases (i.e., NoncoRNA and ncDR), we got the benchmark dataset including 2693 pairs of known resistance associations between 625 ncRNAs and 121 drugs.

Method Overview

Synchronously learning embeddings for edges and extracting the skeleton structure for RDRA-HBG is a crucial strategy for our framework. Based on this, the rationale of our method is to iteratively estimate appropriate bi-view guided by label information and simultaneously optimize the RDRA-HBG graph structure as a skeleton structure to provide the essential but sufficient information fully capable of RDRA prediction. Furthermore, the final edge embedding can be obtained by exerting the AFF algorithm, and we thus can carry out the RDRA prediction via an end-to-end pattern. The framework of RDRGSE is shown in Figure 1. Specifically, RDRGSE contains three processes marked by the purple, blue, and yellow dotted lines, respectively. First, there is a bi-view construction consisting of V^KNN and V^Diffusion based on k nearest neighbors (KNN) and graph diffusion algorithm. Then, the purple process was designed to initially estimate two types of skeleton views (V_skeleton^k and V_skeleton), and the corresponding edge embedding can be obtained by the estimator (i.e., GNN with two layers). Second, an AFF algorithm was applied for final edge embedding to assign a learnable weight on both edge embedding from V_skeleton^k and edge embedding from V_skeleton. Third, we scored candidate RDRAs by a multilayer perceptron (MLP) with three layers and calculated the classification loss, thus completing the first training epoch. Next, the blue process was iteratively implemented to train generalization errors, thus making the classification loss convergent. Finally, we assessed the loss difference between embedding from the graph skeleton and final embedding to restart the new subgraph view construction by the yellow process. The latest round of the purple process and blue process was also launched.

Figure 1.

Framework of RDRGSE. RDRGSE contains three processes marked by purple, blue, and yellow dotted lines, respectively.

With the three processes, in conclusion, we follow a different graph skeleton extraction route with the aim of iteratively estimating feature-based KNN and topology-based diffusion view fusion effects among nodes while simultaneously training the parameters of the graph neural network (GNN). Intuitively, GNNs act both as an edge representation learner and a skeleton estimator until RDRA prediction performance reaches the predetermined level and thus the final graph skeleton can be obtained. We propose to learn a generative skeleton extraction framework from the constructed graph and original graph, respectively. Meanwhile, edges contained in the two types of graphs are sampled or modeled with differentiated views whose parameters under the estimator are treated as the optimization objective in three learning processes. We iteratively sample the structures (edges) as view skeletons while minimizing a link classification loss and get the final skeleton structure by minimizing a gap between the optimized skeleton and the ultimately convergent one. See the (i)–(iii) subsections in the “Bi-View Graph Skeleton Structure Extraction” section for details about the three processes.

Composition of the RDRA Heterogeneous Bipartite Graph

Based on graph theory, we can treat the detection of potential RDRAs as a link prediction task in a graph. Thus, an HBG consisting of the ncRNA subgraph, drug resistance subgraph, and known ncRNA-drug resistance subgraph is established. Specifically, we integrated the three subgraphs into a heterogeneous graph G. After aligning nodes of different subgraphs according to the node map, the adjacency matrix A_RD of G is defined as follows:

1

where N is the number of ncRNAs, and M is the number of drug resistance. S_R denotes the projection matrix of ncRNA and S_D denotes the corresponding drug resistance projection matrix. A denotes the known RDRA matrix and A^T denotes its transposition.

Besides, suppose we remove the two subgraphs (i.e., S_R and S_D) from A_RD after aligning the node location according to a symmetric matrix, in that case, the adjacency matrix without subgraph A_nRD of G is defined as follows:

2

where N is the number of ncRNAs and M is the number of drug resistance, for which they are used to occupy corresponding positions to meet the symmetry of the adjacency matrix. o denotes the element with zero value in the original S_R/S_D. A denotes the known RDRA matrix and A^T denotes its transposition.

ncRNA/Drug Resistance Subgraph Construction

In this study, we adopted the projection of a bipartite graph^22,23 to construct the ncRNA subgraph and drug resistance subgraph individually. We assume that R = {R₁, R₂,..., R_n} is the set of ncRNA nodes and D = {D₁, D₂,..., D_m} is the set of drug resistance nodes. Given an ncRNA-drug resistance bipartite graph B_RDR = (R, D, ω), where ω ⊆ R × D is the ncRNA-drug resistance edge set. Thus, we can construct the ncRNA subgraph G_R, G_R = (R, ώ), where all ncRNAs within R and {R_i, R_j} ∈ ώ if and only if two ncRNAs associated with at least one same drug resistance. The same procedure applies to drug resistance subgraph construction.

Node Primary Feature Construction

Initial features for ncRNA or drug resistance node, as the primary node representation complementary to topological structure information, are crucial to extracting the skeleton structure from the RDRA heterogeneous graph based on graph structure learning (GSL). Considering the particularity of the RDRA prediction issue to felicitously depict the specific characteristics of the ncRNA/drug resistance node, we used the node2vec algorithm²⁴ to generate the initial node feature and as a pre-embedding process to enhance node diversity and signal smoothness. In doing so, X = [x₁, x₂,..., x_N] 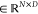for the ncRNA node and Y = [y₁, y₂,..., y_M] 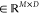for the drug resistance node can be obtained, where x_i or y_j means the D dimensional feature vector of ncRNA node i or drug resistance node j, respectively.

Bi-View Graph Skeleton Structure Extraction

Graph skeleton structure extraction is inspired by GSL,^18,25 which conducts joint optimization between the graph structure of the original graph and GNN²⁶ parameters to improve downstream tasks. According to the GSL pipeline, the core of bi-view graph skeleton structure extraction can be followed in three stages: (i) bi-view graph skeleton construction, (ii) graph skeleton estimator, and (iii) attention graph skeleton fusion.

Graph Convolutional Network

We utilized the GCN²⁷ with two convolution layers as the GNN backbone encoder. Specifically, the given graph adjacency matrix A, the feature matrix H with the trainable weight vector W, and the non-linear activation function σ were used to define the neural network f (·) as follows:

3

where G = D^(− 1/2)A^′D^(− 1/2) with A^′ = A + I and D is the diagonal degree matrix of A^′, and ReLU is adopted as σ.

I. Bi-View Graph Skeleton Construction

To learn an optimizable and preliminary graph structure as the starting point of the skeleton structure from the original RDRA heterogeneous graph, we thus adopted a metric-based bi-view strategy consisting of KNN and diffusion matrix view.

Here, to take full advantage of the local similarity in node primary feature space, we utilized the primary node feature (details can be found in the Node Primary Feature Construction section) to calculate cosine similarity between each node pair, then reserving top-k similar nodes for each node to thus form the KNN view V_K. Synchronously, to capture a global view of the original RDRA heterogeneous graph, we employed Personalized PageRank (PPR)²⁸ with the closed-form solution S = γ(I – (1 – γ)D^–1/2AD^–1/2) ^–1 (here, γ ∈ (0,1] is the transition probability in a random walk, I denotes an identity matrix, and D represents the degree matrix of A) to conduct diffusion operation from one node to other nodes and finally construct the diffusion matrix view V_D. Thus, a bi-view graph skeleton can be obtained reflecting both local and global perspectives of the original RDRA HBG.

ii. Graph Skeleton Estimator

We further optimized two views, V_K and V_D, to obtain the final skeleton structure. Concretely, for view V_K, we first conduct a GCN layer to get the representation Z^k = σ(GCN(V_K, X)), where f_e denotes the dimension value of Z^k and σ indicates the non-linear activation. Next, we reappraised the probability of an edge between each node pair within V_K. For any node pair (i, j), we thus can obtain the weight ω_ij^k between i and j by an MLP layer as follows:

4

where 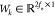denotes the mapping vector and 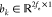denotes the bias vector. Then, we normalized ω_ij^k to get the probability ρ_ij as follows:

5

where s^k denotes the estimation or inspection scope (here, we adopted the k-hop neighbors for V_K as _S^k and the top h neighbors according to PPR values for V_D as its corresponding _S^D), while h and k are hyper-parameters; combined with the original RDRA-HBG structure, the estimated skeleton is as follows:

6

where μ^k∈ (0,1) denotes the combination coefficient. Analogously, V_skeleton^D can also be obtained by following the same process with a different set of parameters. Then, we can get the following:

7

8

where Z_ncRNA^k and Z_ncRNA denote the node representation corresponding to V_skeleton^k and V_skeleton and A_skeleton^k/A_skeleton denotes the corresponding adjacency matrix of V_skeleton^k/V_skeleton. Similarly, Z_drug^k/Z_drug can be obtained using the same process.

Finally, we can obtain two types of edge representations via V_skeleton^k and V_skeleton as follows:

9

where Z_RD^k(D) is the RDRA representation formed by V_skeleton and∥ denotes the concatenation.

iii. Attention Graph Skeleton Fusion

Given two skeletons, V_skeleton^k and V_skeleton, we need to fuse them further to obtain the optimal skeleton structure as the final RDRA-HBG to make RDRA prediction. Here, we used two edge representations Z_RD^k and Z_RD to calculate the weight for the final skeleton structure through edge attention scores by the AFF algorithm:²⁹

10

where denotes the attentional weights and ⊗ denotes the element-wise multiplication. Finally, we generated the final embedding Z_f based on the above weights:

11

Thus, we can get the predictions ŷ_i of RDRA based on Z_f:

12

Iteratively, to make loss(ŷ_i,y_L) converge to the range of objective performance → re-optimize V_skeleton^k and V_skeleton → re-optimize Z_RD^k/Z_RD → AFF → Z_f → ŷ_i → new loss(ŷ_i,y_L) until loss(ŷ_i,y_L) meet desired model performance. Hence, we generate the skeleton structure V_skeleton by ⊕ fusion operator based on V_skeleton^k and V_skeleton:

13

where ⊕ denotes the view fusion operator. Then, we can get skeleton embedding Z_skeleton and the corresponding predictive score ŷ_i^′:

14

15

Finally, if loss(ŷ_i^′, y_L) > loss(ŷ_i, y_L), then go to (i). Overall, the optimized graph structure (skeleton structure) can also be synchronously learned while learning edge representation.

Loss Function

For RARDA prediction, we used the cross-entropy loss function with regularization to obtain the optimal classifications. The loss function is defined as follows:

16

where and 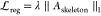, with λ being a hyper-parameter. The Θ is the learnable parameter and Φ denotes the edge set of the skeleton structure.

Results

Experiment Design

Comprehensive experiments were designed to evaluate the overall performance and validate our framework’s structure efficacy. First, 5-CV was conducted to assess the overall performance of RDRGSE. Then, prediction performances were compared among RDRGSE and state-of-the-art methods. To observe the effect of AFF, heatmap visualization of edge embedding from two types of views and final edge embedding after AFF were drawn and compared. Subsequently, we presented the following ablation-like experiments: with graph skeleton extraction versus without graph skeleton extraction; with the ncRNA/drug subgraph versus without the ncRNA/drug subgraph; and with AFF versus without AFF; case studies about 5-fluorouracil, cisplatin, and paclitaxel were made to evaluate the generalizability of RDRGSE and the adaptability in practical RDRA screening scenarios.

The prediction performance of RDRGSE was evaluated mainly using the area under the receiver operating characteristic curve (AUC) and the area under the precision-recall curve (AUPR). Relevant evaluation metrics include Accuracy (Acc.), Precision (Prec.), Recall, F1-Score, Precision@k, and Recall@k and their definitions as follows.

17

18

19

20

21

where TP, FP, TN, and FN, respectively, represent the number of true positives, false positives, true negatives, and false negatives. K denotes the first k results.

For RDRGSE, the parameter epoch was set to 500 for optimization loss. The learning rate was set to 0.002, and the dropout rate was set to 0.2.

Performance of RDRGSE and Comparison with State-of-the-Art Methods

We conducted 5-CV to assess the overall model performance. Following the previous methods’ setup, we took 2693 RDRAs as positive samples and randomly selected the same number of unlabeled RDRAs as negative ones. For each fold, randomly divided subsets containing positive and equal-size negative samples were held out as training data, and the rest were used as test data.

As shown in Figure 2A–C, RDRGSE shows satisfactory performances and obtains a mean AUC of 0.9768 and a mean AUPR of 0.9736 on the benchmark dataset, which validates the strategies of RDRGSE for detecting potential RDRAs. It is worth noting that although the AUC and AUPR in the 3rd fold are slightly lower than the other fold, the average evaluation metric keeps at a similar and stable level, suggesting that RDRGSE offered both high sensitivity and high specificity advantages under a balanced positive-to-negative sample ratio.

Figure 2.

Performance of RDRGSE and comparison with state-of-the-art methods. (A) Performance of RDRGSE on the benchmark dataset under 5-CV including Accuracy, Precision, Recall, and F1-Score; (B) AUC metric of RDRGSE on the benchmark dataset under 5-CV; (C) AUPR metric of RDRGSE on the benchmark dataset under 5-CV; (D) performance comparison of RDRGSE with state-of-the-art methods on AUC metric; (E) performance comparison of RDRGSE with state-of-the-art methods on AUPR metric; and (F) net visualization for potential RDRAs predicted by RDRGSE.

Then, we compared our model with existing state-of-the-art methods, i.e., LRGCPND and GSLRDA. For practical RDRA prediction scenarios, observing the resistance association between the ncRNA as a whole and the drug is a special attention perspective. LRGCPND and GSLRDA were designed for this and work well at this point. The main aim of our study is to focus on the resistance associations between the composite ncRNA entity and the drug entity by an optimized ncRNA-drug bipartite graph structure using bi-view structure evaluation. To fairly compare the performance of RDRGSE with the state-of-the-art methods, we adopted the same dataset and used the same evaluation metrics.

As shown in Figure 2D,E, our model has the best prediction performance in AUC and AUPR evaluation metrics under the same dataset. Compared with LRGCPND and GSLRDA, the performance of RDRGSE outdoes them with a complete advantage. Its evaluation metrics, both in AUC and AUPR, were much better than the corresponding items of the two baselines. Compared with them, RDRGSE improved the prediction performance by 6.7% in terms of AUC and 6.1% in terms of AUPR. For LRGCPND, despite its success in RDRA identification, the model aggregated the features of neighboring nodes using a spectral rule and adopted a residual block to fuse features. Original RDRA bipartite graphs are naturally suboptimal in structural, topological connection for the downstream link prediction task. The bi-view structure optimization strategy in our proposed RDRGSE framework learned a high-quality skeleton structure as the final graph structure to aggregate and represent node features and gave better predictions than the LRGCPND would do. Besides, although GSLRDA was designed using graph contrast learning and shows the next highest AUC and AUPR, it does not get the same-level metrics as RDRGSE, which the inherent defect in contrast learning may cause because of edge information random deletion. For the two state-of-the-art methods, our framework shows significant improvements. Together, the consistent best prediction performances of RDRGSE also support the robustness of our framework. Furthermore, to comprehend the learning abilities of RDRGSE, we charted the potential RDRAs by our framework. As shown in Figure 2F, the predicted RDRAs in which some can be confirmed in the corresponding biological literature studies. For instance, as shown in the small window, the LIN28B-long isoform-expressing cells exhibited increased drug resistance to fluorouracil (5-FU, 5-fluorouracil) in a let-7-dependent manner.³⁰ MiRNA-155 promotes glioma progression and temozolomide resistance by targeting the Six1 signal pathway,³¹ while miR-26b reverses temozolomide resistance via targeting Wee1 in glioma cells.³² These predicted RDRAs enable preclinical biomarker detection and bio-experiment preliminary screening under scientific drug discovery.

To validate the generalization performance, we have added an external dataset (i.e., circRNA-drug sensitivity association) to evaluate our model. Specifically, we extracted the known circRNA-drug sensitivity association (CDS) from the Genomics of Drug Sensitivity in Cancer (GDSC)³³ and circRic³⁴ database to construct the external dataset, which contained significant associations with a false discovery rate of less than 0.05. As shown in Table 1, RDRGSE achieved an AUC of 0.9249 and an AUPR of 0.9183. Both the benchmark dataset and the independent dataset exhibit a consistent level of predictive performance. This indicates that RDRGSE has satisfactory generalization ability.

Table 1. Performance of RDRGSE on the CDS Dataset under 5-CV.

fold	accuracy	precision	recall	F1-score	AUC	AUPR
1	0.8664	0.8526	0.8847	0.8684	0.9383	0.9326
2	0.8337	0.8225	0.8438	0.8330	0.9126	0.8964
3	0.8525	0.8377	0.8761	0.8565	0.9265	0.9238
4	0.8603	0.8282	0.9173	0.8704	0.9308	0.9260
5	0.8445	0.8396	0.8488	0.8441	0.9162	0.9128
mean	0.8515	0.8361	0.8741	0.8545	0.9249	0.9183

Furthermore, to comprehend the learning abilities of AFF for RDRA prediction, we plotted the heatmap of three edge embeddings from the KNN view (e1), diffusion view (e2), and AFF (Figure 3A), respectively. To watch the learned changes among them, as shown in Figure 3B, we randomly selected the edge embedding dimension range from 129 to134 (corresponding to 10 ncRNA-drug resistance associations) and plotted the heatmap with embedding values from which we can observe the differentiated embedding values within the same range, and this suggests distinct learning ability by e1, e2, and AFF. Meanwhile, as shown in Figure 3C,D, the attention-weight heatmap matrix and its local matrix learned by AFF were provided. By AFF, edge embeddings (e1 and e2) with different coefficients or proportions are fused to form the final edge embedding. AFF incorporates the differentiated semantic and scale feature reflected in e1 and e2, obtaining the final optimized embedding.

Figure 3.

Heatmap visualization for three types of edge embeddings and weight matrix with AFF. (A) Heatmap of edge embedding from KNN (e1), diffusion (e2), and AFF view; (B) heatmap of the edge embedding dimension range from 129 to 134; and (C) attention-weight heatmap matrix and its local matrix (D) learned by AFF.

Impact of Optimization for the Skeleton Structure on Model Performance

Following the GSL paradigm, that is, using a skeleton structure to replace the original graph structure, we explored the influence of the two model structures: original graph structure without skeleton structure extraction (RDRGSE_-noSK) and graph structure with skeleton structure extraction (RDRGSE). To hold the consistent node characteristics for two graph structure types, we first initialized node features for each node (ncRNA or drug), respectively, and then compared to evaluate the impact of operation with or without the skeleton structure pruning under 5-CV. Besides, because we have already utilized the similarity to extract the first view, we reset the feature for each node. Here, we can take node2vec as node pre-representation. Node2vec has a proper representation effect and works well in unsupervised graph embedding.³⁵

Figure 4A displays the performance comparisons between the original and manicured graph structure in six metrics. We observed that using the original graph structure to conduct RDRA prediction performs poorly. Notably, RDRGSE_-noSK has an AUC of 0.76 and an AUPR of 0.75. For RDRGSE, considering the impact of other framework components, after conducting the same component operations, the model prediction results show that pruning of graphs dramatically changes the model performance. As expected, it increased the prediction performance by 21% on AUC and 20% on AUPR. The improvement validates the advantage of the skeleton structure pruning strategy.

Figure 4.

Performance comparison of three types of ablation-like analysis. (A) Performance without skeleton extraction. (B) Performance without the ncRNA and drug subgraph. (C) Performance without AFF.

Impact of the Projection Subgraph on Model Performance

In order to investigate the necessity existing of the projection subgraph (ncRNA/drug subgraph), we designed the ablation-like scheme. We construct a bipartite graph with and without a projection subgraph for the manicured graph structure. To evaluate the impact of the projection subgraph, we held and fixed other model components with or without the projection subgraph. Here, the rationale of the ablation-like scheme is to examine the influence of perturbations with/without the ncRNA and drug subgraph on model performance after optimizing the graph structure.

As shown in Figure 4B, without the ncRNA and drug subgraph, the model performs as well as the scheme with a subgraph. By contrast, we can observe that two performance lines are superimposed on a radar map where each other is completely covered. The AUC and AUPR of the scheme without the subgraph keep at the same level as the scheme with the subgraph and continue to be outperformed by the existing state-of-the-art methods. For Accuracy (Acc.), Precision (Prec.), and F1, their value even rises slightly. We can find that it is the ncRNA/drug subgraph that has a lesser influence on our model level of performance, suggesting a weak dependency of model performance on the subgraph.

Experiment results indicated that the contribution from the ncRNA and drug subgraph is limited for detecting potential RDRAs. Even after adding the ncRNA/drug subgraph on the RDRA bipartite graph, the prediction performance increased slightly, and only the fourth decimal place improved for AUC and AUPR. Such a slight improvement could be negligible. It suggests that the model is insensitive to subgraph information even if subgraphs are changed or removed, thus substantiating the limited roles of projection subgraphs in recognizing possible ncRNA-drug resistance links. Together, the experiments showed that for the ncRNA and drug projection subgraph, removing them will not seriously hinder the performance of prediction. It has also been proved that most of the model prediction performances can be supported and contributed directly through the skeleton structure of the RDRA graph. Thus, the ncRNA and drug projection subgraph is optional in our ncRNA-drug resistance bipartite graph. Admittedly, integrating them into our bipartite graph can enhance the RDRA prediction within certain limits, but they are unnecessary in our issue.

Impact of AFF on Model Performance

For AFF that can efficaciously integrate link feature representation, it is crucial to evaluate its effect on model performance. We built the model ablation scheme without AFF. Then, we trained and tested our model on the scheme under 5-CV. As shown in Figure 4C, the scheme has suboptimal performance when fixing other model components. As expected, AUC and AUPR decreased with the removal of AFF. The lower performance (0.5438 on AUC and 0.6047 on AUPR) remains at a scanty and practically unsatisfactory level. It suggests that the model is sensitive to AFF when changed or removed. Our method performs poorly in model performance without AFF.

Case Studies

Case studies on 5-fluorouracil, cisplatin, and paclitaxel were conducted to identify the potential ncRNAs associated with the drug resistances, respectively. For fairness of comparison, we applied RDRGSE to an independent RDRA dataset in which we ensured that the node information of collected 5-fluorouracil/cisplatin/paclitaxel drug resistance data was included in our training dataset without corresponding edge information. The top 30 predicted 5-fluorouracil resistance-related ncRNAs, the top 20 predicted cisplatin resistance-related ncRNAs, and the top 10 predicted paclitaxel resistance-related ncRNAs were used to assess the applicability of RDRGSE. For the three types of drugs, to show the prediction results, as shown in Figure 5A, the resistance scores of predicted ncRNAs are marked by the red block for probability scoring >0.5 and the blue block for probability scoring <0.5. To present the prediction performance on 5-fluorouracil, cisplatin, and paclitaxel, we adopted the Recall@k metric to assess top k ncRNAs related to three types of drug resistances predicted by RDRGSE when strict probability scoring >0.70. As shown in Table 2, RDRGSE exhibits objective and reasonable performance for three types of drug resistances in the condition of top30, top20, and top10, respectively. Furthermore, these ncRNAs are confirmed by the NoncoRNA and ncDR database, and we also presented a score heatmap (Figure 5B) of three types of drugs to illustrate their prediction confidence. Together, the case studies further substantiate the superior performance of RDRGSE in predicting new RDRAs.

Figure 5.

Probability scoring of 5-fluorouracil/cisplatin/paclitaxel drug resistance (A) and the corresponding score heatmap (B).

Table 2. Performance under Recall@k for Top k ncRNAs Related to Three Types of Drug Resistances Predicted by RDRGSE When Probability Scoring >0.70.

k	drug	recall@k
top30	5-fluorouracil	0.93
top20	cisplatin	0.55
top10	paclitaxel	0.60

As shown in Tables 3–5, we also listed the top 10/20/30 predicted ncRNAs for three types of drugs and then checked whether these ncRNAs can be confirmed in the biology literature. If they can be confirmed in the corresponding biology literature, it means that they also were verified in biology wet experiments. Meanwhile, it also can indicate the consistency between our model and biology wet experiments. Typically, for ncRNA-drug resistance association (RDRA) databases (such as NoncoRNA and ncDR), these databases usually collected experimentally supported RDRA data from the biology literature. If some potential ncRNAs without PMID that our model predicted can be found in relevant independent databases, we can still think of it as evidence. Thus, “Evidence” means these ncRNAs can be found and confirmed in relevant independent databases such that we can demonstrate the ability to discover new associations by our model to some extent.

Table 3. Top 10 ncRNAs Related to Paclitaxel Resistance Predicted by RDRGSE^a.

rank	ncRNAs	evidence
1	miR-4716	NoncoRNA & ncDR
2	miR-1914*	NoncoRNA & ncDR
3	miR-4783	NoncoRNA & ncDR
4	miR-302a	NoncoRNA & ncDR
5	miR-503	NoncoRNA & ncDR
6	miR-762	NoncoRNA & ncDR
7	lnc-VLDLR	NoncoRNA & ncDR
8	miR-1256	NoncoRNA & ncDR
9	miR-216a	NoncoRNA & ncDR
10	let-7a	NoncoRNA & ncDR

^a* indicates part of the miRNA name.

Table 5. Top 30 ncRNAs Related to 5-Fluorouracil Resistance Predicted by RDRGSE^a.

rank	ncRNAs	evidence
1	miR-874	NoncoRNA & ncDR
2	miR-4532	NoncoRNA & ncDR
3	miR-4288	NoncoRNA & ncDR
4	miR-369	NoncoRNA & ncDR
5	miR-7-1*	NoncoRNA & ncDR
6	miR-1229-5p	NoncoRNA & ncDR
7	SLC25A25-AS1	NoncoRNA & ncDR
8	miR-633	NoncoRNA & ncDR
9	miR-1825	NoncoRNA & ncDR
10	miR-338	NoncoRNA & ncDR
11	miR-522	NoncoRNA & ncDR
12	miR-6087	NoncoRNA & ncDR
13	miR-106-25	NoncoRNA & ncDR
14	miR-1183	NoncoRNA & ncDR
15	miR-382	NoncoRNA & ncDR
16	miR-125b-5p	NoncoRNA & ncDR
17	miR-455	NoncoRNA & ncDR
18	miR-519	NoncoRNA & ncDR
19	let-7b	NoncoRNA & ncDR
20	miR-378a	NoncoRNA & ncDR
21	miR-17-5p	NoncoRNA & ncDR
22	miR-30d	NoncoRNA & ncDR
23	miR-335	NoncoRNA & ncDR
24	XIST	NoncoRNA & ncDR
25	miR-223	NoncoRNA & ncDR
26	miR-1233	NoncoRNA & ncDR
27	miR-543	NoncoRNA & ncDR
28	miR-125b	NoncoRNA & ncDR
29	miR-146a	unconfirmed
30	GAS5	unconfirmed

^a* indicates part of the miRNA name.

Table 4. Top 20 ncRNAs Related to Cisplatin Resistance Predicted by RDRGSE^a.

rank	ncRNAs	evidence
1	miR-187*	NoncoRNA & ncDR
2	miR-4516	NoncoRNA & ncDR
3	miR-4665	NoncoRNA & ncDR
4	miR-3619	NoncoRNA & ncDR
5	miR-4484	NoncoRNA & ncDR
6	miR-3647	NoncoRNA & ncDR
7	miR-4465	NoncoRNA & ncDR
8	miR-4466	NoncoRNA & ncDR
9	miR-1260	NoncoRNA & ncDR
10	miR-30a*	NoncoRNA & ncDR
11	miR-369	NoncoRNA & ncDR
12	miR-601	NoncoRNA & ncDR
13	HULC	NoncoRNA & ncDR
14	miR-505	NoncoRNA & ncDR
15	miR-187	NoncoRNA & ncDR
16	miR-485	NoncoRNA & ncDR
17	miR-224	NoncoRNA & ncDR
18	miR-17-5P	unconfirmed
19	miR-486	unconfirmed
20	miR-27b	unconfirmed

^a* indicates part of the miRNA name.

Discussion

The RDRGSE introduced a learning strategy at the edge perspective to optimize the insufficiency of the original graph structure by the higher level of skeleton structure extraction. Learning a downstream link task-oriented skeleton structure can effectively detect the associations between ncRNAs and drug resistances in link prediction contexts. To efficaciously extract the significative drug resistance associations available from the original RDRA bipartite graph, we proposed RDRGSE to obtain the supervised representation of links on the RDRA graph.

Based on the performance evaluation and experiments conducted, the advantages of RDRGSE are summarized as follows. First, it introduced a bi-view optimization strategy for a sufficient structure to capture the most valuable links between ncRNAs and drug resistances. This treatment is distinct from the commonly used edge sampling approaches. The outstanding performance suggests the potential of applying the strategy to RDRA identification. Second, an AFF mechanism was leveraged to adaptively fuse the bi-view link representation into the final link representation. As a significant exploration, projection subgraphs of ncRNAs and drug resistances are optional in our task scenario, which dialectically mines their necessity according to various issue contexts.

Although known original graph data have been directly utilized to model and conduct biomedical entity association prediction tasks for a long time,³⁶⁻³⁸ it is a debate to mine the confident interplay relation composed from a bipartite graph-based heterogeneous network.

For our RDRA prediction scene, similarly, imperceptible pseudo-edges formed by the batch effect of biological wet experiments have been ignored habitually. The undesirable impact of these edges is often not verified entirely when directly treating them as accurate RDRA-HBG edges. This ubiquitous structural redundancy or deviation and corresponding consequences are not only very tricky in predictive performance promotion but, in all likelihood, degrading the model’s representation power. Therefore, a reliable and accurate skeleton structure is vital to learn high-quality edge embedding. This has been verified and efficaciously improved in our experiments, suggesting that RDRGSE can jointly learn edge embedding and graph skeleton structure and work better in RDRA prediction. Besides, recently, various single ncRNA-drug resistance association prediction methods, such as miRNA-drug resistance/sensitivity association prediction^15,16 and circRNA-drug resistance/sensitivity association prediction,^14,17 have been provided. Our framework can migrate to these issues well. Essentially speaking, their modeling pattern and optimization objective are consistent with each other.

Although this study targeted RDRA prediction, the method involved design tactics (i.e., taking full advantage of joint learning between edge embedding and graph skeleton structure) and can also be easily extended to other biomedical entity association prediction scenarios due to the consistency of the link prediction task principle.

Conclusions

In this paper, we proposed RDRGSE, a computational method for potential RDRA identification, where high-quality edge embedding and graph skeleton structure extraction can complement each other well. Its prediction performance was evaluated by various comparative experiments extensively. Compared with the existing methods, RDRGSE shows outstanding performance on RDRA prediction. Moreover, competitive AUC and AUPR of RDRGSE support the advantages of RDRGSE as a screening tool in practice.

Data Availability Statement

The datasets and codes presented in this study can be found in online repositories (https://github.com/pzhangBIO/RDRGSE).

Author Contributions

P.Z., L.W., and L.L. designed the methods and arranged the datasets. P.Z., Z.W., W.S., and J.X. implemented the methods and performed the analyses. W.S., W.Z., K.W., and J.X. tested the methods. P.Z. wrote the manuscripts. L.W. and L.L. provided financial support and gave suggestions for improvement of the methods. All authors read and approved the final manuscript. P.Z. and Z.W. contributed equally.

This work was supported in part by STI 2030-Major Projects, under grant no. 2021ZD0200403, in part by the Guangxi Postdoctoral Special Funding Project, the Natural Science Foundation of Guangxi, under grant no. 2022JJD170019, the National Natural Science Foundation of China, under grant no. 62172355, and the Guangxi Science and Technology Base and Talent Special Project under grant nos. 2021AC19394 and 2021AC19354.

The authors declare no competing financial interest.