Hybrid Smart Strategies to Predict Amine Thermal Degradation in Industrial CO₂ Capture Processes

Abstract

CO₂ emission reduction is an essential step to achieve the climate change targets. Solvent-based post-combustion CO₂ capture (PCC) processes are efficient to be retrofitted to the existing industrial operations/installations. Solvent degradation (and/or loss) is one of the main concerns in the PCC processes. In this study, the thermal degradation of monoethanolamine (MEA) is investigated through the utilization of hybrid connectionist strategies, including an artificial neural network-particle swarm optimization (ANN-PSO), a coupled simulated annealing-least squares support vector machine (CSA-LSSVM), and an adaptive neuro-fuzzy inference system (ANFIS). Moreover, gene expression programming (GEP) is employed to generate a correlation that relates the solvent concentration to the operating variables involved in the adverse phenomenon of solvent thermal degradation. The input variables are the MEA initial concentration, CO₂ loading, temperature, and time, and the output variable is the remaining/final MEA concentration after the degradation phenomenon. According to the training and testing phases, the most accurate model is ANFIS, and the reliability/performance of its optimal network is assessed by the coefficient of determination (R²), mean squared error, and average absolute relative error percentage, which are 0.992, 0.066, and 2.745, respectively. This study reveals that the solvent initial concentration has the most significant impact, and temperature plays the second most influential effect on solvent degradation. The developed models can be used to predict the thermal degradation of any solvent in a solvent-based PCC process regardless of the complicated reactions involved in the degradation phenomenon. The models introduced in this study can be employed for the development of more accurate hybrid models to optimize the proposed systems in terms of cost, energy, and environmental prospects.

1. Introduction

Carbon capture and storage (CCS) is considered a promising approach to decrease the climate change progress and to accomplish the Paris Agreement expectations.¹ It is estimated that CCS contributes to a 14% decrease in the world CO₂ emissions under the 2 °C scenario (i.e., to limit the global temperature increase below 2 °C) and a further 32% under the beyond 2 °C scenario.² The concentration of CO₂ in the atmosphere is constantly increasing. Figure 1 shows the trend of CO₂ concentration with time reported by the Global Monitoring Laboratory of the National Oceanic and Atmospheric Administration (NOAA). The concentration of CO₂ was 412.18 ppm in March of 2019, and its current concentration (March of 2023) is 421.00 ppm.³

Figure 1.

Monthly average concentration of CO₂ reported by Mauna Loa Observatory in Hawaii.³ [Data taken from ref (3) (https://gml.noaa.gov/ccgg/trends/data.html).]

One of the most concerning issues in the amine-based post-combustion CO₂ capture (PCC) process is solvent degradation, which takes place through the transformation of amines into other chemical components due to the chemical reactions. This adverse phenomenon occurs through thermal degradation and oxidative degradation. In thermal degradation, the amines react with CO₂ to form compounds (e.g., cyclic amines) having a high molecular weight. In oxidative degradation, the amines react with oxygen to generate various components (e.g., carboxylic acids) having a low molecular weight.⁴ It was also found that high-stable salts are formed due to the reaction between the carboxylic acids and the amines. These high-stable salts put a high burden on the regeneration process and increase the risk of corrosion in the process equipment/materials, highlighting the significant importance of avoiding their synthesis. It has been confirmed that higher temperatures lead to a higher reaction rate.⁴

Monoethanolamine (MEA) is the most common solvent, which is regarded as a benchmark solvent in the solvent-based PCC processes. MEA is lost in the solvent-based PCC process through thermal degradation, oxidative degradation, and volatility losses. Thermal degradation takes place by the polymerization of carbamate, leading to high-molecular-weight byproducts. Oxidative degradation occurs in the stripper, resulting in producing high-stable salts; this is not usually a concern in the applications of the amine absorption/stripping processes (e.g., treatment of natural gas and H₂ production) as O₂ is not in the system. Volatility losses in the absorber and stripper can be reduced by employing a sophisticated control system.⁵

PCC operating conditions (e.g., CO₂ concentration) have a significant impact on solvent degradation.⁶ Changes in the operating conditions of CO₂ loading and the physical properties of heat-stable salts can alter the solution properties (e.g., viscosity and specific heat capacity), affecting the overall consumption of energy.⁷ The acidic impurities in the flue gas do not have a substantial influence on the MEA degradation in a CO₂ capture process.⁸ Quantification of the solvent degradation is a key factor in a close analysis of the process. There is a ten-fold increase in the oxidation rate of MEA in a CO₂ capture process while using dissolved Fe, Mg, and Cu as potential catalysts.⁹ Quantification of the products of the oxidative and thermal degradation of MEA verified that differences in the type of degradation products between samples of lean and rich amine indicate the chemical reaction of the products. Rich amine was more susceptible to thermal degradation than oxidative degradation.¹⁰ Operation time plays a major role in the solvent degradation. MEA concentration decreases by 95% due to the thermal degradation at 160 °C for 8 weeks; however, the remaining solvent maintains its capacity at 22% to remove CO₂, possibly owing to the capacity of some of the degradation product to remove CO₂.¹¹ The gas contaminants have different degrees of impact on the thermal degradation. At the same molar concentration of MEA, the degradation rate in the presence of nitrile (5000 ppm) is much higher than that of MEA alone. Sodium sulfate, fly ash, and sodium thiosulfate do not have any impact on the thermal degradation rate of MEA.¹² The utilization of oxidative degradation inhibitors should be seriously considered in the solvent solution design, including additives for the CO₂ capture applications. There is a 58% increase in the MEA oxidative degradation influenced by the metal ions, which are resulted from the solvent impurities and wall leaching.¹³ A mixture of different solvents can be used in the process. However, it is significantly affected by the operating conditions. For example, thermal degradation of the piperazine/diethanolamine (PZ/DEA) blend was studied with a CO₂ loading range of 0–0.4 mol CO₂/mol alkalinity at 135 °C. At high CO₂ loading, there were more amounts of degradation products, and the formation of triethanolamine and 1,4-bis(2-hydroxyethyl) piperazine increased.¹⁴ It is to be noted that different solvents have various levels of degradation. MEA is less thermally stable than morpholine (MOR). Moreover, N-(2-hydroxyethyl) ethylenediamine (HEEDA) and N-(2-hydroxyethyl)imidazolidine-2-one (HEIA) are the products of MEA thermal degradation, and these products are not produced from MOR thermal degradation after two and four weeks.¹⁵

Reactive constituents in flue gas (e.g., O₂, NO_x, SO₂, and inorganic oxide fly ash) react with amines, resulting in the irreversible degradation of amines into different products of degradation. This degradation leads to a reduction in absorption efficiency and corrosion problems.¹⁶ Reduced solvent capacity, solvent loss, degradation products formation, ammonia emissions, and aerosol emissions are the critical problems that require an adequate understanding of solvent degradation and deeper insight into the mentioned concerns.¹⁷ Therefore, the stability of the solvent in the CO₂ capture process is one of the most important matters that requires to be closely monitored to control the desired efficiency of the solvent’s performance as well as CO₂ capture absorption’s optimal operation. Detailed knowledge on the mechanisms of degradation and the impact of the operating conditions on the governing mechanisms help design more efficient mitigation strategies. The literature review reveals that no research investigation has been performed on the analysis of thermal degradation of solvent in a solvent-based PCC process through employing smart techniques (artificial intelligence/machine learning tools). This study aims to fill this knowledge gap. The developed hybrid models can provide a suitable platform for the analysis of solvent degradation in the targeted process. The models can also be used for the modeling and optimization of solvent-based PCC processes. Incorporating the thermal degradation into the modeling and/or optimization of the process can lead to more reliable results and eventually cause further improvement in the system performance and the process design.

2. Theory and Background

This section includes a literature review on solvent degradation and the CO₂ capture process description. In the literature review part, the experimental and modeling studies regarding solvent degradation are described. In the process description, a conventional CO₂ capture process is explained along with the fundamental knowledge of the chemical reactions involved in the MEA absorption process.

2.1. Literature Review

There have been many research studies on the degradation of the solvents used in the carbon capture process. For instance, Davis and Rochelle¹⁸ quantified the thermal degradation of MEA as a function of CO₂ loading, initial MEA concentration, and temperature during the normal operating conditions of the stripper. They concluded that the MEA loss leads to the formation of N,N′-bis-(2-hydroxyethyl)urea, HEIA, and HEEDA. Using the speciation data (chemical species) from the Aspen model of a stripper confirmed that a significant solvent loss occurred in the packing; however, its major loss took place in the reboiler and the reboiler sump. In addition, thermal degradation in the stripper was low when the temperature of the reboiler was controlled below 110 °C. This loss became substantial when the stripper pressure increased.¹⁸ The performance of various solvents [i.e., MEA, diethanolamine (DEA), and 2-amino-2-methyl-1-propanol (AMP)] in a 90% CO₂ capture process from a 550 MW coal-fired power plant was evaluated using Aspen Plus software. The best operating conditions of the process were determined using an electrolyte-NRTL thermodynamic model and multi-objective optimization by employing a genetic algorithm (GA). The results indicated a higher working capacity of DEA compared to that of MEA at optimal operating conditions, leading to a lower heat duty of the reboiler. Moreover, the selection of the thermodynamic model was very decisive; therefore, consideration of proper/reliable thermodynamic models for the solvents is of significant importance in the performance analysis of the proposed system.¹⁹ The common causes of thermal stability of sodium salts of sarcosine, glycine, alanine, and β-alanine were scrutinized through thermal degradation at the temperatures of 125, 135, and 145 °C. The salts improved the rates of thermal degradation compared to those of MEA as the reference solvent. The results also revealed that the amine group steric hindrance has a positive impact on amino acid protection against degradation. The thermal stability was increased in the order β-alanine > alaninate > sarcosinate > MEA.²⁰ Léonard et al.²¹ developed a kinetic model for the degradation of MEA in the CO₂ capture process. It was found that oxidative degradation is enhanced by the O₂ concentration in the gas feed. However, the gas feed CO₂ concentration had no considerable impact on the degradation. A significant thermal degradation was observed at high temperatures (i.e., 140 °C) and in the presence of CO₂.²¹ The stability of five amine solutions (e.g., MEA, AMP, and PZ) to oxidative and thermal degradation was investigated in the presence and absence of CO₂. The analysis performed by HPLC revealed that the presence of CO₂ and O₂ significantly affects the thermal degradation rate.²² A CO₂ capture process model was developed, including the degradation of MEA based on the experimental data, where the impact of the operating conditions on the process solvent loss was assessed. It was concluded that the main cause of solvent loss was oxidative degradation in the absorber, while thermal degradation was not a serious concern.²³ A research investigation was done about the thermal degradation of N,N-diethylethanolamine (DEEA) as a function of CO₂ loading, temperature, and DEEA concentration in an autoclave. Thermal degradation of DEEA in the absence of CO₂ was insignificant, and there was a decrease in the DEEA remaining fraction while increasing CO₂ loading, temperature, and DEEA concentration.²⁴ Thermal degradation rates of AMP and 4,4-dimethyl-1,3-oxazolidin-2-one (DMOZD) were determined by employing the experimental data obtained at the temperatures of 120, 135, and 150 °C as a function of the concentrations of amine and CO₂. The thermal degradation of AMP had a smaller degradation rate constant than that of MEA. Moreover, the rate of DMOZD formation had a lower dependency on CO₂ concentration and a higher dependency on AMP concentration.²⁵ In another study, a thermodesorption-gas chromatography-mass spectrometry method was developed for the quantitative analysis of the products (e.g., pyrrole, dimethylformamide, and pyrazine) of the MEA thermal degradation in the gas effluent of the CO₂ capture process. The researchers claimed that the developed method could be used for the simultaneous quantification of numerous products of thermal degradation.²⁶ A gas chromatography-flame ionization detector was employed to investigate the stability of thermal degradation of methyldiethanolamine (MDEA) and its mixture with glycine in the presence and absence of CO₂. The results indicated that the CO₂ presence significantly affects the solution’s thermal degradation. Moreover, there was a reduction in MDEA thermal degradation when glycine was added to the MDEA solution.²⁷ Molecular mechanisms describing the MEA thermal degradation were analyzed using molecular dynamics simulation along with metadynamics sampling. It was concluded that the formation of 2-oxazolidinone (OZD) as an intermediate and the main products of HEEDA and HEIA are thermodynamically favorable.²⁸ In a study, density functional theory was implemented to further understand the plausible chemical pathways that led to the formation of the products of the thermal and oxidative degradations of MEA. It was concluded that MEA could bear the oxidative degradation to create hydroperoxides and imines. The authors claimed that by employing proper activation energies and Arrhenius data along with the aid of chemical kinetic mechanisms, it would be possible to synthesize new amine molecules/chemicals which could be more tolerant against the adverse phenomenon of degradation.²⁹ The stability of MOR was investigated under the operating conditions of the stripper in the carbon capture process. The degradation kinetics of MOR was scrutinized under the fluctuations of temperature and CO₂ loading. It was concluded that a significant degradation rate was observed at temperatures above 175 °C, and the rate of degradation increased upon an increase in the CO₂ loading. Moreover, the thermal stability of MOR was higher than that of MEA, DEA, MDEA, and PZ.³⁰ In a recent study, Braakhuis et al.³¹ developed a kinetic model to predict MEA thermal degradation in a carbon capture process. The rates of thermal degradation and the degradation products were analyzed as a function of temperature, time, and loading. The developed model employing the literature data had an error of 17.5% due to its limited reproducibility and high experimental uncertainty. The results indicated that the thermal and oxidative degradation mechanisms interacted, and the concentrations of thermal degradation products were influenced by this interaction.³¹

2.2. Process Description

Carbon dioxide emission significantly leads to the greenhouse effect and, therefore, to global warming.³² Hence, its concentration reduction in the atmosphere is a crucial matter for different environmental and industrial sectors.³³ Several commercial projects have been developed in view of the importance of CCS, such as the Petra Nova in Texas (US) and the Boundary Dam in Saskatchewan (Canada). Both projects utilize amine-based PCC technologies to capture CO₂ from the flue gas streams. The thermally regenerative amine-based PCC is a conventional technology which includes an absorber to capture CO₂ from the flue gas and a desorber to strip CO₂ from the CO₂-rich solvent with heat, which is usually provided by the steam cycle of the power plant. Figure 2 depicts a typical solvent-based CO₂ capture process.³⁴ Although there have been considerable improvements in the industrial applications of amine technology, there are still some limitations, such as the high energy requirement, significant capital cost, and amine degradation in this technology. The high energy need of an amine-based PCC process is generally due to the requirement of high thermal heat (i.e., 120–150 °C) for the amine regeneration. There have been many investigations with a special focus on technology development to increase the energy efficiency of the capture process and to minimize the absorbent regeneration heat requirement.²

Figure 2.

Conventional solvent-based PCC process. Copyright 2013 American Chemical Society. Adapted with permission from ref (34).

To absorb one molecule of CO₂, two molecules of MEA are required, producing the ion pair of MEACOO^– (carbamate) and MEAH⁺ (protonated MEA). CO₂ absorption with MEA can be carried out primarily through a two-step mechanism, as follows³⁵

1

2

The zwitterion, MEA⁺COO^–, formed from the reaction of MEA and solvated CO₂ is considered the rate-limiting step of the CO₂ capture.³⁶ Aqueous MEA experiences thermal degradation in the stripper at temperatures above 110 °C in the presence of CO₂. It is proven that MEA thermal degradation materializes through the synthesis of oxazolidinone from the dehydration of carbamic acid (MEACOOH). Oxazolidinone might eventually react with MEA, leading to more stable products, implying that MEACOOH is another crucial intermediate in the CO₂ absorption/stripping process.³⁵

In the CO₂ capture process, thermal degradation usually takes place in the stripper. Most previous studies have reported that high temperature in the presence of CO₂ is the reason for degradation.³⁷ According to some research works, the thermal degradation is due to the high temperature in the absence of CO₂, highlighting the important role of heat.³⁷ This kind of degradation results in dimerization, dealkylation, and cyclization. The main products of the MEA thermal degradation are oxazolidine-2-one (OZD), HEEDA, HEIA, and N,N′-bis-(2-hydroxyethyl)urea. Oxidative degradation usually occurs in the absorber, and the main reactions occurring in this equipment are addition, dealkylation, and piperazinones. The main products of the MEA oxidative degradation are ammonia, formaldehyde, methylamine, acetaldehyde, formamide, formic acid, glyoxal, and acetic acid.³⁷

3. Theory of Smart Techniques

Models are developed/utilized to reflect the performance of a process of interest.³⁸ There are various challenges in the analysis of the chemical and process engineering systems due to the high dimensionality and complicated dependencies between various parameters of the process, whose modeling is required for the ensuing efficient process design, control, optimization, and fault detection. A part of the challenge is commonly addressed by the time-consuming and costly endeavors of experimentation and simulation. Utilization of artificial intelligence (AI)/machine learning (ML) techniques in the modeling attempts is a promising solution to most of the mentioned problems.³⁹ The intelligent methods or/and ML tools such as artificial neural network (ANN), genetic algorithm (GA), functional network (FN), least square support vector machine (LSSVM), fuzzy decision tree (FDT), imperialist competitive algorithm (ICA), particle swarm optimization (PSO), fuzzy logic (FL), recurrent neural network (RNN), and adaptive neuro-fuzzy inference system (ANFIS) have been broadly utilized for industrial and theoretical applications to estimate target parameters, find best patterns, and obtain nonlinear data.⁴⁰ The utilization of the classical AI in the field of chemical engineering was suggested in the 1980s with the development of expert systems (e.g., catalyst design and thermophysical properties) for the first time.⁴¹ Nowadays, AI and ML are employed in the analysis of different problems/processes, such as oil and gas industry (e.g., deposition of wax in surface and subsurface pipes⁴² and hydrate formation in production facilities^43,44) and medicine (e.g., breast cancer diagnosis⁴⁵). Indeed, ML is in the category of AI and originated from computer science and mathematics. It provides the computers with the ability to learn from data without being explicitly programmed. It is generally categorized into supervised learning and unsupervised learning approaches.⁴¹ ML methods can overcome the limitations of mechanistic modeling due to their capability of learning complicated behaviors of systems/processes, the cheaper development of the proposed system model, and a more convenient and easier way of system optimization.³⁹ Physical properties play a critical role in the design of chemical processes and products. AI techniques can be employed to predict the physical characteristics of various chemicals/components.⁴⁶

3.1. Artificial Neural Network—Particle Swarm Optimization

An ANN model is a powerful tool that is utilized for a wide range of problems (e.g., forecasting, recognition, and regression).⁴⁷ ANNs are capable of estimating non-linear functions. Training algorithms play the most significant role when dealing with applications with high non-linearity nature.³⁸ A classical ANN is composed of three types of layers: an input layer, followed by a number of hidden layers and an output layer. All layers are interconnected by synaptic links with the corresponding connection weights.⁴⁸ The ANN is trained by adjusting the weights, attempting to minimize the error between the calculated values/outputs and the expected/target values.⁴⁹ A training or learning algorithm is considered a procedure to adjust the coefficients (weights and bias) of ANN outputs for the proposed/given inputs and correct the known outputs (target values).⁵⁰ Different training algorithms have been developed in the past few years. However, they might not be suitable/efficient in some specific cases, and they might not lead to optimum solutions. Therefore, some other techniques, such as bio-inspired algorithms (BIAs), are needed to train an ANN. These algorithms are powerful optimization tools, which are able to solve very complicated optimization problems. BIAs work on the principle of nature’s behavior known as swarm intelligence, which is defined as a property of systems consisting of unintelligent agents with an intelligent collective behavior but limited individual capabilities.⁴⁷ Parameter optimization of multivariable systems is a common concern in computational biology. One of the methods, which were developed for parameter optimization, is PSO, first introduced by Kennedy and Eberhart in 1995.⁵¹ PSO is a meta-heuristic algorithm, which is mostly employed in continuous, discrete, and combinational optimization problems.⁵² The PSO algorithm is based on a stochastic search in multimodal search space, developed from the dynamic system simulations, such as bird flocks and fish swarms.⁵³ The PSO idea comes from a swarm of particles flying throughout a multi-dimensional search space, searching for the global optimum. The particles can impact each other’s movements by exchanging information. Each particle keeps an individual (or cognitive) memory of the best position that it has visited/searched, along with the global (social) memory of the best position visited/searched by all particles in the swarm. The next position of a particle is calculated by considering its last movement vector, a random component, and the global and individual memories.⁵¹ The advantages of the PSO method are reasonably well handling of the optimization problems with multiple local optima and its simple implementation.⁵¹ In the idea of PSO, a single solution is called a particle, and the collection of all solutions is called a swarm. The key idea of PSO is that each particle is only aware of its current velocity, its own best configuration accomplished in the past (pBest), and which particle is the current global best in the swarm (gBest). At each iteration, each particle corrects its velocity so that its new position will be closer to its pBest and gBest simultaneously. The following equation determines each particle’s velocity update⁵²

3

where v_i,j symbolizes the ith particle velocity in the jth dimension; x denotes the particle’s current position; w signifies a constant (momentum), correcting/adjusting the degree of influence of the velocity from the previous time step on the velocity from the current time step; c_p and c_g are constants; and r_p and r_g are the random numbers within [0,1]. The algorithm capability for exploitation and exploration can be adjusted by modifying the constants c_g and c_p, respectively.⁵²

Finally, the following equation is employed to update the position of the ith particle in the jth dimension⁵²

4

Historically, the first application of PSO was to accelerate the assessment of the transfer functions in the ANNs.⁵⁴ An ANN training process results in a minimization problem that can be tackled by a conventional or meta-heuristic algorithm. In a hybrid ANN-PSO model, PSO deals with the error minimization of the ANN by assigning the optimum values for the weights and biases of the model. Therefore, the feasible space of the problem is dependent on the interval at which the weights and biases vary.⁵⁵Figure 3 illustrates the schematic algorithm of an ANN-PSO model.⁵⁶

Figure 3.

Layout of the ANN-PSO model algorithm. Adapted from ref (56).

3.2. Coupled Simulated Annealing-Least Squares Support Vector Machine

The support vector machine (SVM) is a commonly accepted mathematical approach to achieve a proper interrelation between the variables of a defined mathematical problem.⁵⁷ The SVM learning method, which is based on the principle of statistical machine structure risk minimization, can decrease the confidence range; therefore, it leads to a small real risk, having better generalization ability of unknown samples. The main idea of this approach is that solving the dual problem is achieved by solving the linear programming problem based on the maximum distance between the sample points and segmentation for modeling.⁵⁸ The generalization theory provides an effective strategy to control capacity and, therefore, hinders controlling the hyperplane margin measures. Optimization theory gives the mathematical methods which are required to find hyperplanes optimizing these measures.⁵⁹ The SVM methodology has been usually utilized in two areas of classification and function estimation.^60,61 SVM has several applications, such as text categorization, biosequence analysis, biological data mining, image classification, and hand-written character recognition.⁵⁹ The concepts in structural risk minimization and statistical learning theory are the fundamentals of SVM.⁶² The LSSVM is an improved version of the standard SVM algorithm.⁶³ It is capable of transforming quadratic program problems into linear problems via least squares value functions and equality constraints. It trains faster and converges more precisely.^64,65 LSSVM converts the SVM linear programming problem into constraint conditions and changes the loss function structure, leading to a huge reduction in the computational effort.⁶⁶ LSSVM employs this hyperplane to fit the location of sample points.⁵⁸

We consider a set of nonlinear sample points as follows

5

where x_i is the input vector; y_i symbolizes the output vector; l indicates the number of training samples; ⌀:x_i ∈ Rⁿ → φ(x_i) ∈ H; and the input vector x_i is mapped into the high-dimensional feature space. Mapping is used to linearize these sample points. The LSSVM regression function is expressed by the following equation⁵⁸

6

where φ(x) is a nonlinear function (mapping function) that can have different forms (e.g., linear, polynomial, and radial basis function); and ω and b (offset value/bias) represent the weights and determine constant coefficients in the training process. The Kernel function transforms the nonlinear estimation function into a linear one in H space.⁵⁸

LSSVM optimization can be defined as follows⁵⁸

7

where γ is the regularization parameter, and ξ denotes the slack variable or random error.^67,68

The bound conditions are as follows⁵⁸

8

In LSSVM, constraint conditions are signified by equations, which are different from SVM optimization. The Lagrange function is as follows⁵⁸

9

where α_i is the multiplier of Lagrange.⁵⁸

The constraints are in accordance with the Karush–Kuhn–Tucker condition, as given below⁵⁸

10

After eliminating ω and ξ, the linear system of equations is written below

11

where y = [y₁, y₂, ..., y_N], 1⃗ = [1, 1, ..., 1]; α = [α₁, α₂, ..., α_N]; and I is the unit matrix.⁵⁸

The Kernel function can be defined in accordance with the Mercer’s condition as follows

12

In eq 12, K(x_i,x_j) is the Kernel function of SVM, which meets the conditions of the Mercer theorem. Since eq 11 is a non-singular equation, the values of α and b can be determined.⁵⁸ These parameters can be calculated using the least squares method.⁶⁹ It means that eq 6 can be represented by the following equation (the LSSVM regression model)⁵⁸

13

String Kernels are usually employed for the case of character training samples. The Gauss Kernel functions and polynomial Kernel functions are usually utilized for numerical training samples. For numerical training samples, polynomial Kernel functions have a poor learning ability compared to the Gauss Kernel function.⁵⁸ The Gauss Kernel function is commonly employed as the Kernel function as follows

14

where σ is the width function of the Gauss Kernel, and its size indicates the degree of sensitivity of the LSSVM model to the input data. In other words, smaller σ signifies the model’s higher sensitivity to the input data changes, and larger σ implies higher unresponsiveness to the data changes.⁵⁸

Simulated annealing (SA) is the first proposed algorithm to broaden the local search methods. Prevention from the local optima is the key aspect of this method.⁷⁰ SA was proposed by Metropolis et al.⁷¹ and then popularized by Kirkpatrick et al.⁷² SA is a stochastic optimization algorithm employed for finding the global solution in combinatorial optimization problems.⁷³ Coupled-simulated annealing (CSA), which was proposed by Suykens et al.,⁷⁴ is an improved version of simple SA, incorporating a series of parallel SA with greater accuracy and convergence speed. The key drawbacks of SA are moving toward solutions with worse quality and preventing the local optima, which were improved in the CSA method. Therefore, CSA can avoid the local optimum in non-convex problems and perform with higher accuracy and acceptance probability while sustaining the speed of convergence during the problem optimization.⁷⁵⁻⁷⁷ The CSA algorithm is employed to calculate the tuning parameters of γ and σ² (regularization parameter and the width function). Figure 4 displays the algorithm of a CSA-LSSVM hybrid model.⁷⁸

Figure 4.

Typical structure of the CSA-LSSVM model. Adapted with permission from ref (78). Copyright 2014. Published by Elsevier Ltd.

3.3. Adaptive Neuro-Fuzzy Inference System

ANFIS, which was developed by Jang,⁷⁹ is established/structured based on the combination of the capabilities of the fuzzy inference system (FIS) and ANN.⁸⁰⁻⁸² The Sugeno fuzzy inference approach was employed in the modeling of the neuro-fuzzy systems.^81,83 The FIS can create complicated mapping relations based on fuzzy rules, making it suitable for representing fuzzy knowledge and experiences.⁸⁴ The role of the fuzzy part is to group the input data into sets determined by the membership degree, which can be any value between zero and one.⁸¹ If-Then fuzzy rules from fuzzy sets are created by the FIS with a suitable membership function (MF) to reflect the human thinking nature/process; however, it is limited to adaptive learning capabilities.⁸⁰ The relationships between inputs and outputs in a traditional ANN procedure are established through data training and learning; however, the ANN is not able to simulate the thinking process of the human mind.⁸⁴ In other words, even though the ANN has the capability of adaptive learning, it is not able to explain how the decision is made. Therefore, the ANFIS model can extract the logical rules hidden in the data by itself.⁸⁴ Applying the ANN adaptive learning capabilities to the If-Then rules in the FIS structure makes it a powerful tool/technique for the solution of the complicated engineering and non-engineering problems.⁸⁰ ANFIS utilizes two algorithms of post-error propagation and the hybrid method, which is a combination of error quadratic and descending gradient methods, to train the network, leading to the reduction of algorithm complexity and an improvement of network learning time.⁸¹Figure 5 shows the schematic structure of the ANFIS with two inputs and one output.⁸⁵

Figure 5.

Typical architecture of an ANFIS model. Adapted with permission from ref (85). Copyright 2018. Published by Elsevier Ltd.

The ANFIS basic rule with two inputs of x₁ and x₂ and one output of y is defined as follows:⁸⁶

Rule #1: if x₁ is A₁ and x₂ is B₁, then y₁ = p₁x₁ + q₁x₂ + r₁

Rule #2: if x₁ is A₂ and x₂ is B₂, then y₂ = p₂x₁ + q₂x₂ + r₂

A_i and B_i are the fuzzy set parameters of each input in the premise part (part-if) and p_i, q_i, and r_i are the linear parameters in the consequent part (part-then).

ANFIS is composed of five layers, and each layer is formed by some nodes.⁸⁷

Layer #1 (Fuzzification): Each node i is an adaptive node, where the output is described as follows^81,85,86

15

16

Here, O_i¹ is a function of the membership of A_i and μA_i and μB_i introduce the membership degrees for the fuzzy set parameters.

Layer #2 (Implication): The nodes are fixed ones, which are labeled as Π, and they perform as a simple multiplier. The output of each node is w_i, which is the firing strength of a rule created by incoming signals as defined below

17

Layer #3 (Normalization): In this layer, each node is a fixed one, which is labeled as N. is the output signal of the ith node, which is computed by the ratio of the firing strength of rule i to the sum of the firing strength for all rules as defined below

18

Layer #4 (Defuzzification): Each node (i) is an adaptive one with a node function encompassing the resultant/conclusion parameters of p_i, q_i, and r_i; and refers to a normalized firing strength from Layer #3 as follows

19

Layer #5 (Sum/Combination): It includes a single fixed node, which is labeled as Σ, implying it adds all the input signals to compute the final output as described below

20

3.4. Gene Expression Programming

A powerful deterministic approach, called gene expression programming (GEP), is developed in accordance with the idea of iterative improvement of a population of potential solutions employing an evolutionary process, which is based on the concept of survival of the fittest.⁸⁸ GEP is employed to determine the relationship between independent variables according to experimental data. The fundamental of GEP is similar to the principle of the human chromosome, wherein the predicted and actual/experimental data exemplify the chromosomes.⁸⁹ GEP is formed by the combination of GA and genetic programming (GP).^90,91 GEP is one of the most recently introduced methods to find the best solution for nonlinear problems, eliminating the drawbacks of GA and GP by employing advanced regression techniques.^92,93 GEP is a genetic algorithm since it employs the individuals’ populations, selects them in accordance with fitness, and suggests genetic variation by utilizing one or more genetic operators. GEP is like GP and GA; however, their major difference is in the nature of the individuals. In GP, the individuals have a nonlinear nature having various shapes and sizes (parse trees); in GA, the individuals are linear strings of fixed length (chromosomes); and in GEP, they are encoded as linear strings of fixed length (the chromosomes and genome), which are thereafter structured as nonlinear entities of various shapes and sizes.⁹⁴ The key players in GEP are the chromosomes and the expression trees (ETs). The ETs consist of the genetic information expression encoded in the chromosomes.⁹⁵ The human gene incorporates a head (an encoded function) and a tail (a non-encoded function). The tail typifies the variables and constants, and the head presents the function, variables, and constants. The GEP output is indicated in the form of a mathematical formula in the software language (e.g., Python) and ETs. The accuracy of the mathematical formula is dependent on the number of genes employed in the simulation. The genetic codes utilized in GEP are chosen on the basis of the nature of the simulation.⁸⁹ In this method, different phenomena are modeled employing a series of functions and terminals. The functions commonly incorporate the main arithmetic operators (i.e., addition, subtraction, multiplication, and division), trigonometric functions, mathematical functions (e.g., exp, log, and sin), or functions defined by the user, who believes that they could be most suitable to efficiently represent the model. The set of terminals consists of independent variables and constant values of the problem. In the GEP algorithm, the head component of the gene can hold functions and terminals, and the tail component of the gene can only control terminals. The codes relevant to each gene lead to the construction of a sub-ET. The sub-ETs communicate with each other to create a more complex and larger ET (i.e., they are connected together by a function known as the linking function to form the complex structure).⁹⁶

In the GEP, the linear chromosomes of fixed length consist of genes structured in a head and tail (i.e., function as genotype) and the parse trees (ETs) (i.e., function as phenotype), establishing a genotype-phenotype system. The computer programs produced by GEP incorporate multiple ETs because of the multigenic entity of the genotype-phenotype system, allowing the evolution of more complicated programs composed of several subprograms. The GEP model has two languages: genetic and ET. This bilingual notation is known as Karva. Figure 6 displays the expression trees of the phenotype for the following equation, and Figure 7 depicts the algorithm of a GEP system.⁹⁷

21

Figure 6.

Algebraic expression tree of the phenotype for eq 21 [root node = 0; function node (branch point) = 1, 2, 3; terminal (leaf) node = 4, 5, 6, 7] (selection acts on phenotype according to the fitness). Adapted with permission from ref (97). Copyright 2017. Published by Elsevier Ltd.

Figure 7.

Algorithm of a GEP model. Adapted with permission from ref (97). Copyright 2017. Published by Elsevier Ltd.

4. Methodology

In this study, four different smart techniques/approaches, which were explained in the previous section, are used to analyze the degradation of MEA under the industrial operating conditions of the CO₂ capture process. The validation of the models is carried out by employing the experimental data.⁵ The models are compared to each other based on their accuracy of prediction. Furthermore, the parametric sensitivity analysis is performed using the most accurate model.

4.1. Data Processing

The prediction performance of the proposed solvent degradation requires an adequate number of data points. The data is collected from a Ph.D. thesis completed on the degradation of MEA. The basic step in developing a smart model is to identify the input and output parameters of the model. In this research, MEA initial concentration, CO₂ loading, time, and temperature are considered the input variables, and the MEA concentration left in the system after a certain period of time is denoted as the output parameter. Thermal degradation is strongly dependent on the temperature of the system, and it takes place at higher extent of temperature. CO₂ loading stimulates thermal degradation, and a larger loading of CO₂ was proven to increase thermal degradation either by increasing the proton donor availability through catalyzing the dehydration or through the formation of more carbamate.³¹ Regarding the impact of time, thermal degradation products usually increase with time.¹⁰ Obviously, the concentration of the solvent in the system plays a significant role in the thermal degradation of the solvent. For instance, increasing MEA concentration unexpectedly decreases the rate of thermal degradation.⁵ Considering the impact of vital parameters on the MEA thermal degradation, the remaining MEA concentration in the system can be presented by the following equation

22

In this equation, C_f indicates the final concentration of MEA in m (molality); C_i denotes the initial concentration of MEA in m; L represents the CO₂ loading in a (moles of CO₂/moles of MEA); t symbolizes the time in d; and T is the system temperature in °C. There are many studies on the amine’s thermal degradation in the literature. The studies employed different parameters impacting the amine’s thermal degradation. Moreover, the presented operating conditions are in very different ranges, which could not be used for the development of a unique smart model. The data used in this research is collected from a Ph.D. thesis as the most extensive work done on MEA thermal degradation. The number of data points is fairly enough (159 data points) to develop smart techniques/models for the prediction of the amine’s thermal degradation. Table 1 includes the data used in this study.⁵

Table 1. Data Used to Develop the Connectionist Models (Data Taken from ref (5))^a.

T = 100°C				T = 120°C				T = 135°C
Ci (m)	a	d	Cf (m)	Ci (m)	a	d	Cf (m)	Ci (m)	a	d	Cf (m)
3.5	0.2	7	3.51	3.5	0.2	7	3.94	3.5	0.2	7	3.39
3.5	0.2	14	3.5	3.5	0.2	14	3.3	3.5	0.2	14	3.29
3.5	0.2	28	3.44	3.5	0.2	28	3.19	3.5	0.2	28	3.13
3.5	0.2	42	3.48	3.5	0.2	42	3.15	3.5	0.2	42	3.09
3.5	0.2	56	3.34	3.5	0.2	56	3.18	3.5	0.2	56	2.81
3.5	0.4	7	3.49	3.5	0.4	7	3.85	3.5	0.4	7	3.3
3.5	0.4	14	3.39	3.5	0.4	14	3.22	3.5	0.4	14	2.95
3.5	0.4	28	3.46	3.5	0.4	28	3.13	3.5	0.4	28	2.71
3.5	0.4	42	3.54	3.5	0.4	42	3.01	3.5	0.4	42	2.5
3.5	0.4	56	3.45	3.5	0.4	56	3.43	3.5	0.4	56	2.3
3.5	0.5	7	3.5	3.5	0.5	7	3.91	3.5	0.5	7	3.08
3.5	0.5	14	3.45	3.5	0.5	14	3.26	3.5	0.5	14	3.75
3.5	0.5	28	3.4	3.5	0.5	28	2.82	3.5	0.5	28	2.43
3.5	0.5	42	3.52	3.5	0.5	42	2.81	3.5	0.5	42	2.34
3.5	0.5	56	3.7	3.5	0.5	56	2.9	3.5	0.5	56	1.81
7	0.2	7	6.96	7	0.2	7	7.3	7	0.2	7	6.25
7	0.2	14	7.02	7	0.2	14	6.52	7	0.2	14	6.29
7	0.2	28	7.06	7	0.2	28	6.56	7	0.2	28	6.09
7	0.2	42	6.99	7	0.2	42	6.26	7	0.2	42	5.5
7	0.2	56	7	7	0.2	56	6.29	7	0.2	56	4.99
7	0.4	7	6.99	7	0.4	7	6.88	7	0.4	7	6.16
7	0.4	14	6.66	7	0.4	14	6.43	7	0.4	14	6.11
7	0.4	28	6.99	7	0.4	28	6.13	7	0.4	28	4.88
7	0.4	42	6.94	7	0.4	42	6.07	7	0.4	42	4.83
7	0.4	56	7.03	7	0.4	56	6.15	7	0.4	56	3.39
7	0.5	7	7.09	7	0.5	7	6.56	7	0.5	7	5.78
7	0.5	14	7.05	7	0.5	14	6.03	7	0.5	14	4.95
7	0.5	28	6.87	7	0.5	28	5.71	7	0.5	28	3.83
7	0.5	42	6.98	7	0.5	42	5.25	7	0.5	42	3.45
7	0.5	56	6.99	7	0.5	56	5	7	0.5	56	2.46
11	0.2	7	10.63	11	0.2	7	10.23	11	0.2	7	10.73
11	0.2	14	10.86	11	0.2	14	10.59	11	0.2	14	9.9
11	0.2	28	11.14	11	0.2	28	9.8	11	0.2	28	9.38
11	0.2	42	11.86	11	0.2	42	10.42	11	0.2	42	8.67
11	0.2	56	11.26	11	0.2	56	9.66	11	0.2	56	7.86
11	0.4	7	10.81	11	0.4	7	10.39	11	0.4	7	9.7
11	0.4	14	11.07	11	0.4	14	9.86	11	0.4	14	7.41
11	0.4	28	11.24	11	0.4	28	9.33	11	0.4	28	7.13
11	0.4	42	10.9	11	0.4	42	8.59	11	0.4	42	5.46
11	0.4	56	11.04	11	0.4	56	8.14	11	0.4	56	4.59
11	0.5	7	9.12	11	0.5	7	10.36	11	0.5	7	8.36
11	0.5	14	10.18	11	0.5	14	9.63	11	0.5	14	6.84
11	0.5	28	10.69	11	0.5	28	10.2	11	0.5	28	4.94
11	0.5	42	11.18	11	0.5	42	6.98	11	0.5	42	4.15
11	0.5	56	11.07	11	0.5	56	6.6	11	0.5	56	3.09

^aC_f: final concentration of MEA in m (molality); C_i: initial concentration of MEA in m; a: CO₂ loading (moles of CO₂/moles of MEA); d: time in days; and T: temperature in °C.

To structure the models, 85% of the data is used in the training phase, and the remaining data is employed to test the models (i.e., to assess the performance of the trained models). The closeness of the R-squared value to unity and the closeness of the error values to zero are considered the termination criteria of the model runs.

4.2. Programming

MATLAB software is used to develop the models of ANN-PSO, CSA-LSSVM, and ANFIS. Different configurations of each model are employed to obtain the most optimal results. The GEP model is constructed in the environment of GeneXproTool5 5.0. In all models, the MEA degradation is examined using the collected data and the defined inputs.⁵ For the models of ANN-PSO, CSA-LSSVM, and ANFIS, all data are normalized within the range of [−1 1] in order to avoid numerical overflow in the program runs and reach the desired convergence. The following equation is used to normalize the data

23

where x̂ denotes the normalized value of x_i, and x_min and x_max indicate the minimum and maximum values of the experimental data.

4.3. Model Performance Evaluation

The statistical parameters such as the average absolute relative error percentage (AARE%), mean squared error (MSE), and coefficient of determination (R²) are employed to evaluate the accuracy and performance of the models developed in this study. The following equations represent the abovementioned statistical parameters⁹⁸⁻¹⁰⁰

24

25

26

where x_dⁱ and x_m are the values of the experimental data and the prediction; x̅ is the average value of the experimental data; and n denotes the number of data.

5. Results and Discussion

In this section, the results of each smart model are presented, and the performance of each model is discussed through different figures and tables. In all models, the input variables are the MEA initial concentration, CO₂ loading, time, and temperature, and the target output is the remaining concentration of MEA after circulation in the system. The programs/codes for all models are written in MATLAB 2021b. An ML model should be able to predict the model’s performance accurately. The cost function is a critical ML parameter to determine the degree of accuracy of the model developed. In all programs/models, the degree of accuracy is examined using the MSE measure. MSE is one of the most commonly employed cost functions. It computes the square of the difference between the predicted value and the actual value (eq 25).

5.1. ANN-PSO Performance

In order to choose the most optimal structure for the ANN-PSO model, different parameters are optimized, such as constants for gBest and pBest, number of particles, number of neurons in the hidden layer, and number of maximum iterations. Figure 8 displays the performance of the model for the datasets of training and testing. The AARE % values of the model for the training and testing phases are 6.57 and 5.33%, respectively.

Figure 8.

Performance of the ANN-PSO model: (a) training and (b) testing.

5.2. CSA-LSSVM Performance

The CSA-LSSVM model is analyzed using both the Gaussian Kernel function (radial basis function) and the polynomial Kernel function. The results obtained in terms of the model performance using both mentioned approaches revealed that the training performance of the Gaussian Kernel function is better than that of the polynomial Kernel function. The best polynomial degree is estimated to be three. The values of MSE for the training phase for the cases of Gaussian Kernel function and polynomial Kernel functions are 0.033 and 0.106, respectively. Therefore, the CSA-LSSVM model performance is evaluated by employing the Gaussian Kernel function. The LSSVM model with the radial Kernel function includes two critical parameters as the tuning parameter (σ²) and the regularization parameter (γ), where their optimal values are determined by the CSA optimization algorithm. These two values significantly influence the prediction accuracy of the model. The calculated optimal values of σ² and γ are 218.52 and 2.89 × 10⁵, respectively. Figure 9 illustrates the performance of the model based on the training and testing datasets. The AARE % values of the model for the training and testing steps are 2.38 and 6.87%, respectively.

Figure 9.

Performance of the CSA-LSSVM model: (a) training and (b) testing.

5.3. ANFIS Performance

The developed ANFIS model algorithm is based on the Takagi–Sugeno Fuzzy inference system. Since the fuzzy part of the ANFIS model employs If-Then rules and linguistic terms, the model is able to learn from the presented data. Table 2 includes the specifications of the developed ANFIS model. The type of MF used for the development of the ANFIS model is Gaussian. MF as a function represents the extent of an independent parameter that belongs to a set. Figure 10 shows MFs of the input parameters (independent parameters) after the training process is carried out. Figure 11 depicts the performance of the developed ANFIS model. The AARE % values of the model for the training and testing phases are obtained to be 1.54 and 6.16%, respectively.

Table 2. Specifications of the ANFIS Model.

parameter	definition/value
number of inputs	4
number of output	1
fuzzy type	Sugeno
FIS generation	Grid partition
optimization method	hybrid
membership function	Gaussian
number of fuzzy rules	9
maximum number of epochs	300
initial step size	0.01
increase rate of step size	1.05
decrease rate of step size	0.7

Figure 10.

Membership functions for the input parameters of the developed ANFIS model.

Figure 11.

Performance of the ANFIS model: (a) training and (b) testing.

5.4. GEP Performance

There are many parameters that influence the accuracy of the GEP model (e.g., number of chromosomes and number of genes). Numerous efforts/runs are made to determine the most suitable model based on the collected data. The model accuracy increases with an increase in the number of chromosomes and the number of genes. There is a slight increase in the model’s accuracy if the head size is increased. The optimal values for the number of chromosomes, number of genes, and head size are 90, 3, and 11, respectively. Table 3 includes the values of different parameters for the most optimal GEP model (optimal evolution). Figure 12 displays the ETs of the developed GEP model based on the specifications, which are summarized in Table 3.

Table 3. Specifications of the GEP Model.

parameter	value
chromosome	90
gene	3
head size	11
root insertion sequence transposition	0.00546
gene transposition	0.00277
inversion rate	0.00546
insertion sequence transposition	0.00546
mutation rate	0.00138

Figure 12.

Expression tree of the developed GEP model (d is the model variables and c is the model constant parameters).

Several runs are carried out in the software environment to find the most suitable correlation which can properly represent the thermal degradation phenomenon. The introduced correlation is given below

27

where

28

29

30

31

The values of the constant parameters involved in the above correlation are provided in Table 4.

Table 4. Values of the Constant Parameters in the GEP Model.

constant	value
g1	2.8459
g2	–1.0751
g3	–2.6345
g4	1.2730
g5	5.9360
g6	5.3664
g7	–9.7546
g8	–6.5825
g9	–0.4391
g10	0.1580

Figure 13 shows the performance of the developed GEP model. The AARE % values of the model for the training and testing stages are determined to be 6.37 and 6.00%, respectively.

Figure 13.

Performance of the GEP model: (a) training and (b) testing.

The results of the developed GEP model are compared with those of the kinetics model developed by Davis.⁵ The values of the R² for the GEP model and the kinetics model are 0.96 and 0.95, respectively. It implies that the developed model has very acceptable accuracy. Highlighting the importance of process variables in the degradation phenomenon, the GEP model prioritizes them, as illustrated in Figure 14.

Figure 14.

Importance of operating variables affecting the adverse phenomenon of degradation predicted by the GEP model.

5.5. Comparison of Developed Models

The statistical criteria of R² (coefficient of determination), MSE, and AARE % are employed to evaluate the performance of the developed models. Figure 15 depicts the performance of the ANN-PSO, CSA-LSSVM, ANFIS, and GEP models in the training and testing steps. Table 5 summarizes the performance of the developed models considering the error analysis based on the statistical criteria. It reveals that the CSA-LSSVM and ANFIS models are more accurate predictive tools.

Figure 15.

Performance of the models according to the training and testing phases: (a) ANN-PSO training; (b) ANN-PSO testing; (c) CSA-LSSVM training; (d) CSA-LSSVM testing; (e) ANFIS training; (f) ANFIS testing; (g) GEP training; and (h) GEP testing.

Table 5. Performance of the Developed Models.

model	R2 (training)	R2 (testing)	MSE (training)	MSE (testing)	AARE % (training)	AARE % (testing)
ANN-PSO	0.975	0.977	0.195	0.211	6.57	5.33
CSA-LSSVM	0.996	0.964	0.033	0.239	2.38	6.87
ANFIS	0.998	0.962	0.016	0.354	1.54	6.16
GEP	0.975	0.974	0.189	0.240	6.37	6.00

5.6. Parametric Sensitivity Analysis

The performance of the ANN-PSO, CSA-LSSVM, and ANFIS models is evaluated based on the trained models. The reliability of the GEP model is also assessed using the correlation generated by GeneXproTool5 5.0. The accuracy of all the models is summarized in Table 6, revealing that the most suitable and accurate model is ANFIS.

Table 6. Performance of the Trained Models.

model	R2	MSE	AARE %
ANN-PSO	0.959	0.318	9.074
CSA-LSSVM	0.989	0.087	3.117
ANFIS	0.992	0.066	2.745
GEP	0.961	0.24	7.18

A sensitivity analysis is performed to determine the relationship between the input parameters and the output/target variable. This analysis is performed using the ANFIS model as the most accurate model. In the context of statistics and probability, correlation matrix theory determines the degree of the linear relationship between two variables in a multi-variable system. Various correlations can be used to calculate the strength of the linear relationship. The Pearson product–moment correlation coefficient, which is computed by dividing the two variables covariance by their standard deviation’s multiplication, is one of the best methods to perform the correlation matrix analysis as follows^98,101,102

32

33

34

where 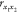is the correlation coefficient; signifies the covariance; 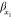and indicate the two variables standard deviation; x₁ and x₂ denote the two variables; and point out the average values of the two variables; and n represents the number of the experimental data. The calculated value for r falls within [−1 1], revealing the strength of the linear relationship between the two variables. If the value of r is close to 1, it implies a positive relationship, while the value of r close to −1 reveals a negative relationship between the two variables. The values close to zero indicate a weak relationship between the proposed variables. Figure 16 depicts the results of the sensitivity analysis of the variables involved in the MEA thermal degradation and the degree of relationship between the input variables and the final concentration of MEA as the output. Based on Figure 16, the solvent initial concentration has a strong linear relationship with the target variable as the remaining concentration of the solvent (r-value of 0.877). Moreover, the variables of temperature, time, and CO₂ loading have a negative relationship with the target variable, meaning that upon an increase in these variables, the final concentration of the solvent in the system decreases. Among these variables, temperature has a stronger negative relationship with the target variable. This finding agrees with the results obtained from the GEP model as depicted in Figure 14.

Figure 16.

Values of correlation coefficients revealing the linear relationship of the input variables to the output variables.

In the operation of a solvent-based PCC, the cost of amine degradation is critical, and it was reported that 10% of the operation cost comes from solvent degradation.¹⁰³ This implies the importance of understanding amine degradation in the performance analysis of solvent-based PCC processes. The solvent’s capacity to absorb CO₂ decreases when it encounters undesirable degradation. The byproducts/impurities of degradation should be removed from the system. They are considered hazardous waste, and their specifications and quantities need to be known for the proper control of the process. The stripper energy requirement can be decreased by increasing the pressure and solution capacity. However, these conditions increase the risk of degradation and corrosion. Considering the fluctuations of the operating parameters in an actual process system, the development of a thermal degradation model, which encompasses the operating conditions outside of normal operating conditions, is required to effectively optimize the system in terms of energy and solvent degradation.¹⁰⁴ Increasing temperature increases the MEA degradation, and the pressure increase in the stripper accelerates the MEA degradation due to increased reboiler temperature. In a constant pressure system, a lower CO₂ concentration results in a higher temperature of the reboiler, which leads to more thermal degradation.⁵ An increase in MEA concentration increases the chance of corrosion and enhances the solution viscosity, leading to enhancement of the mass transfer and pumping characteristics. Based on the model developed by Davis,⁵ an increase in temperature increases the thermal degradation, while an increase in amine concentration and CO₂ loading lowers the thermal degradation. According to this study, increasing temperature and CO₂ loading increases the thermal degradation, while an increase in the MEA concentration decreases the thermal degradation. Therefore, there is a discrepancy between the two models with respect to the CO₂ loading. Note that the results of this study are in agreement with the models developed by Braakhuis et al.³¹ and Léonard et al.²¹ When a change in the CO₂ loading occurs, the CO₂ partial pressure alters. Since the system is isobaric, the temperature alters to balance/compensate for the change. It can be concluded that decreasing pressure is an efficient remedy since this leads to a stripper temperature reduction. However, it adds more costs as the equivalent work of the stripper increases. Therefore, the thermal degradation rate can be reduced by increasing the partial pressure of CO₂. Temperature reduction in the stripper can be implemented by utilizing a greater concentration of amine (e.g., MEA) at higher loading.⁵

6. Conclusions

In this study, thermal degradation of amines in the conventional solvent-based PCC process is examined. The degradation phenomenon is analyzed using hybrid smart models, including ANN-PSO, CSA-LSSVM, and ANFIS. A correlation is introduced using the capability of the GEP based on the concept of maximum fitness and optimal evolution. The statistical analysis shows that the ANFIS model has the highest accuracy, with a coefficient of determination of 0.992. The results reveal that increasing CO₂ loading, time, and temperature increases the thermal degradation, and an increase in MEA initial concentration leads to a reduction in the thermal degradation. These findings are confirmed by the ANFIS model and the GEP correlation. The results indicate that the solvent initial concentration and temperature are the most influential variables affecting solvent degradation. Moreover, the variables of time and CO₂ loading have a relatively equal impact on the degradation of the amine solvent studied in this work. The developed models ignore the complex degradation reactions of the solvent and can be employed to predict the thermal degradation of any solvent in a solvent-based PCC process. Referring to the importance of global warming, this study can provide a suitable platform for the further analysis of the thermal degradation mechanism of the solvents and the development of reliable optimization models, leading to process improvement in terms of cost, energy, and environmental aspects. As a future work, the developed models can be used for the prediction of thermal and oxidative degradation of different solvents and comparison of their potential and capabilities in various CO₂ absorption processes. The most suitable solvent can be then used for conventional PCC processes toward optimal conditions and process sustainability.

The authors declare no competing financial interest.

Notes

A part of this work was presented at the 2022 Canadian Chemical Engineering Conference in Vancouver, BC, October 23–26 (2022). Very small portions of the text were reprinted from the corresponding extended abstract (Azarpour and Zendehboudi, 2022) with considerable modification. Thus, the present work is significantly different from the extended abstract.