Loops and the activity of loop extrusion factors constrain chromatin dynamics

Abstract

The chromosomes—DNA polymers and their binding proteins—are compacted into a spatially organized, yet dynamic, three-dimensional structure. Recent genome-wide chromatin conformation capture experiments reveal a hierarchical organization of the DNA structure that is imposed, at least in part, by looping interactions arising from the activity of loop extrusion factors. The dynamics of chromatin reflects the response of the polymer to a combination of thermal fluctuations and active processes. However, how chromosome structure and enzymes acting on chromatin together define its dynamics remains poorly understood. To gain insight into the structure-dynamics relationship of chromatin, we combine high-precision microscopy in living Schizosaccharomyces pombe cells with systematic genetic perturbations and Rouse model polymer simulations. We first investigated how the activity of two loop extrusion factors, the cohesin and condensin complexes, influences chromatin dynamics. We observed that deactivating cohesin, or to a lesser extent condensin, increased chromatin mobility, suggesting that loop extrusion constrains rather than agitates chromatin motion. Our corresponding simulations reveal that the introduction of loops is sufficient to explain the constraining activity of loop extrusion factors, highlighting that the conformation adopted by the polymer plays a key role in defining its dynamics. Moreover, we find that the number of loops or residence times of loop extrusion factors influence the dynamic behavior of the chromatin polymer. Last, we observe that the activity of the INO80 chromatin remodeler, but not the SWI/SNF or RSC complexes, is critical for ATP-dependent chromatin mobility in fission yeast. Taking the data together, we suggest that thermal and INO80-dependent activities exert forces that drive chromatin fluctuations, which are constrained by the organization of the chromosome into loops.

INTRODUCTION

Chromatin, which is made up of DNA and its associated proteins, is confined within the cell nucleus of eukaryotes, where it takes on a compartmentalized, three-dimensional structure. While we understand the molecular details of nucleosomes, the fundamental unit of chromatin, only recently has a unified model for the intermediate scale of chromatin organization emerged, namely the existence of topologically associating domains (TADs). TADs of 100 kb to Mb scale are now considered to be a characteristic unit of mesoscale chromosomal folding, revealed largely through genome-wide chromosome conformation capture techniques (e.g., Hi-C) (Lieberman-Aiden et al., 2009; Dixon et al., 2012, 2016; Nora et al., 2012; Sexton et al., 2012; Dekker, 2014; Mizuguchi et al., 2014).

The structure of TADs is thought to arise through characteristic chromatin looping interactions. The major molecular machinery responsible for chromatin loops is composed of members of the structural maintenance of chromosome (SMC) complex family of ATPases, most notably in the form of the cohesin and condensin complexes (Banigan and Mirny, 2020). Indeed, high levels of cohesin and condensin reside at boundaries between TADs at steady state (Nora et al., 2012; Mizuguchi et al., 2014). Given the established ability of SMC complexes to topologically engage DNA strands (Haering et al., 2008; Terakawa et al., 2017), it has been widely suggested that SMC complexes are loop extrusion factors (LEFs) that drive the formation of chromatin loops, an activity that can be observed in vitro or in extracts (Ganji et al., 2018; Davidson et al., 2019; Kim et al., 2019; Golfier et al., 2020). Moreover, loss of functional cohesin in fission yeast leads to a complete loss of TADs as assessed by Hi-C through a mechanism distinct from its role in sister chromatid cohesion (Mizuguchi et al., 2014), while complete depletion of cohesin similarly leads to the loss of TADs in mammalian cells (Rao et al., 2017). LEF simulations further demonstrate that the dynamic extrusion of loops by SMC complexes combined with the existence of boundary elements (BEs) encoded in the DNA (e.g., sequence-specific binding of CCCTC-binding factor (CTCF), which is enriched at boundaries and physically interacts with cohesin [Parelho et al., 2008; Wendt et al., 2008]), can give rise to contact maps similar to those revealed experimentally through Hi-C (Fudenberg et al., 2016; Nuebler et al., 2018; Banigan et al., 2020). Consistent with the LEF model, recent experimental studies demonstrate that cohesin and condensin can actively drive loop formation on naked DNA (Haarhuis et al., 2017; Ganji et al., 2018; Davidson et al., 2019; Kim et al., 2019) with additional supportive evidence in vivo (Gabriele et al., 2022; Pradhan et al., 2022). Taken together, these observations suggest that cohesin and condensin are ATP-dependent drivers of dynamic DNA looping.

From a functional perspective, TADs play a critical role in defining the probability of physical contacts along the chromosome; these units correlate with chromatin attributes such as gene expression levels, suggesting that the form and function of TADs are intricately linked (Ibrahim and Mundlos, 2020). It is intuitive that genetic transactions requiring interactions between DNA elements will be influenced by both TAD structure and dynamics. For example, discrete chromatin contacts that underlie critical regulatory processes such as transcriptional enhancement and coregulation are tied to cohesin function, as are insulation and the suppression of genomic interactions with undesirable outcomes (Nora et al., 2012; Shen et al., 2012; Symmons et al., 2014; Lupianez et al., 2015; Flavahan et al., 2016). However, the static, time-averaged view of TADs arising from Hi-C models derived from thousands of cells fails to address the underlying chromatin dynamics on which TADs impinge. Moreover, in situ hybridization approaches that can be applied to individual, fixed cells (Wang et al., 2016; Bintu et al., 2018) also cannot address how chromatin folding influences its dynamics. Indeed, how TADs, and the formation or persistence of looping interactions on which they depend, impact the dynamic properties of chromatin in vivo remains unclear but is a question likely to benefit from a combination of experimental and in silico approaches (Tiana and Giorgetti, 2018).

The chromosomes behave as large polymers that are crowded within the nuclear volume. Given that individual genetic loci are part of these large chromosomes and move through the crowded nucleoplasm, it is not surprising that they display a characteristic subdiffusive behavior across model systems (Marshall et al., 1997; Heun et al., 2001; Weber et al., 2012). A distinguishing feature of the chromatin polymer is that its mobility depends on cellular energy (Marshall et al., 1997; Heun et al., 2001; Weber et al., 2012; Joyner et al., 2016). A persistent mystery is the identity of the energy-dependent process(es) underpinning this observation and whether it reflects changes in the material properties of the nucleoplasm upon energy depletion (Joyner et al., 2016) and/or an activity of an ATP-requiring enzyme(s) to agitate chromatin dynamics. Given that SMC proteins are themselves ATPases capable of translocating DNA fibers relative to each other, they are plausible candidates to be such “agitating” factors.

Here we employ a combination of live-cell imaging of gene loci in fission yeast with polymer dynamics simulations to investigate how the configuration (specifically TADs) and dynamics of chromatin are linked. On short (seconds) timescales, we find that several different gene loci in fission yeast display highly similar subdiffusive dynamics regardless of location on the chromosome. Surprisingly, we find that loss of either cohesin or condensin function increases chromatin locus fluctuations, suggesting that chromatin loops made by SMC complexes predominantly constrain chromatin movement rather than driving chromatin dynamics through the act of loop extrusion. Employing Rouse polymer simulations, we independently show that it is chromatin looping that constrains chromatin mobility into a subdiffusive state characterized by an exponent lower than the expected Rouse polymer value of 0.5, recapitulating our experimental observations. Our experimental data and simulations further argue that both the number and the lifetime of LEFs influence the dynamic behavior of chromatin. Last, we identify the INO80 complex as an important driver of chromatin mobility in fission yeast that likely acts in parallel with loop extrusion. Taking the data together, we demonstrate that energy-dependent chromatin mobility is likely driven, at least in large part, by the action of INO80, while loops, driven by cohesin and to a lesser extent condensin, introduce constraints on chromatin mobility.

RESULTS

Chromatin loci show a characteristic subdiffusive behavior in fission yeast at short timescales

To gain insights into the factors that contribute to dynamic chromatin organization in vivo, we developed a live-cell imaging, tracking, and analysis approach to precisely characterize the spatial and temporal dynamics of chromatin loci at short (millisecond to second) timescales (Figure 1a). We visualized chromosomal loci dynamics in fission yeast by both targeted and random integrations of lac operator (lacO) repeats and expression of fluorescently tagged lac repressor (GFP-LacI). Wide-field fluorescence microscopy movies were obtained at short (58 ms) time steps. The position of each individual locus at each time step was determined by fitting a Gaussian to the diffraction-limited lacO/GFP-LacI focus; the motion of the locus was subsequently tracked using a single particle tracking (SPT) algorithm (Crocker and Grier, 1996). Thousands of individual loci tracks were then subjected to motion analysis by calculating and fitting the mean squared displacement (MSD) versus time to theoretical profiles that take into account localization noise and motion blur (Bailey et al., 2021). Covariance analysis of the particle tracks further revealed that the motion of gene loci in fission yeast can be described by a single diffusive state (Bailey et al., 2021). On the seconds timescale, we observe a characteristic subdiffusive behavior in fission yeast that is nearly identical at six different genomic positions (Figure 1b and Supplemental Figure S1a). On these timescales, this characteristic chromatin motion is well described by a single mean anomalous exponent (α = 0.44 ± 0.04), which provides a good description of all experimental MSDs for the first 29 time points (between 0.058 and 1.7 s) as indicated by the best fit (solid lines) of the anomalous diffusion equation (Eq. 1; see Materials and Methods). Of note, this value is slightly but consistently lower than α = 0.5—the value previously measured for budding yeast chromatin (Weber et al., 2012) and the expected value corresponding to the Rouse model polymer (beads connected by springs) (Doi and Edwards, 1986). Using our approach, we also recapitulate a value close to α = 0.5 for budding yeast harboring a tagged chromatin locus (Supplemental Figure S1b), suggesting that the depressed value that we observe in fission yeast is likely meaningful. Plausible reasons for the difference we observe between fission and budding yeast include smaller chromosome size, differences in histone modifications (absence of histone H3 lysine 9 methylation), or TAD scale (see below). Applying an exponent of α = 0.44, the “diffusion coefficient,’’ D, ranges from 0.0025 to 0.0031 μm²/s^0.44 across the six genetic loci in fission yeast (see Supplemental Table S1). Unless otherwise noted, we used α = 0.44 in all our subsequent analysis. Consistent with prior studies, depletion of ATP by the addition of sodium azide decreases the diffusivity about twofold (from 0.0028 to 0.0015 μm²/s^0.44 for the mmf1 locus [Figure 1c]).

FIGURE 1:

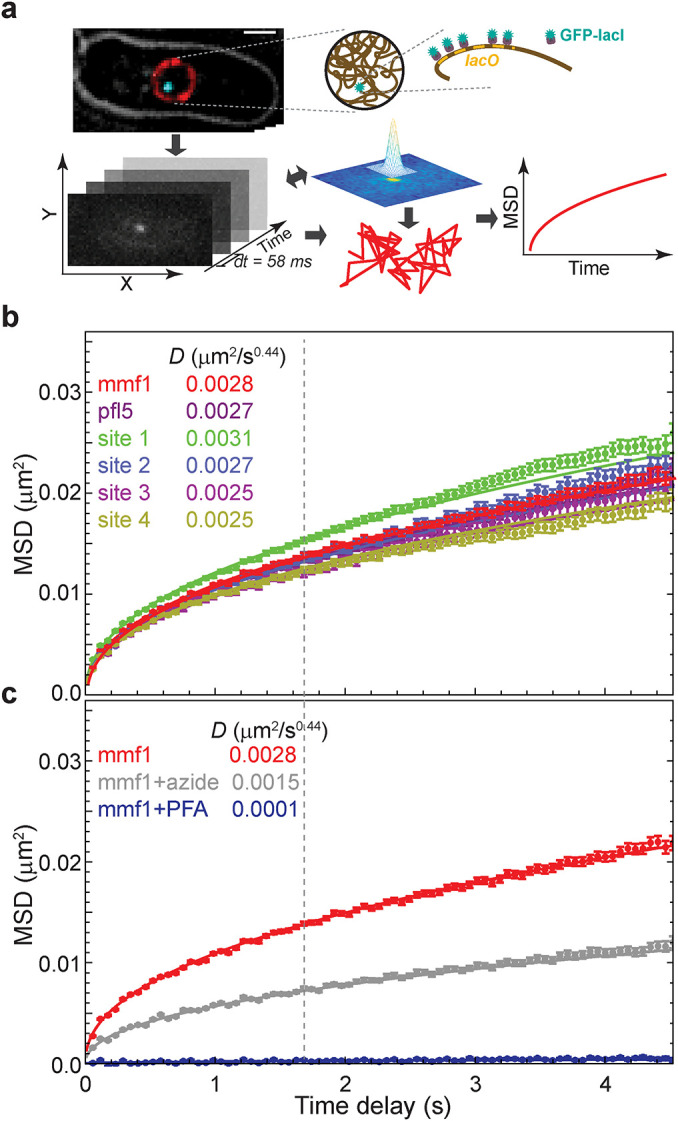
Visualization and tracking of DNA loci over time reveals characteristic, ATP-dependent chromatin dynamics in fission yeast. (a) Cells labeled with a lacO array inserted adjacent to the gene of interest or at random are visualized using GFP-LacI fluorescence. DNA loci are tracked using a custom two-dimensional single particle tracking algorithm (Bailey et al., 2021). (b) Chromatin diffusivity is nearly identical across six different genomic locations as shown by the MSD of each genetic locus as a function of the time. Dashed line marks “window of observation,” along with its calculated diffusion coefficient, D. (c) Cells depleted of ATP by treatment with sodium azide show much slower chromatin dynamics. For comparison, cells fixed with formaldehyde were imaged and analyzed to estimate systematic error in our image acquisition and analysis system. Error bars in panels b and c designate standard errors of the mean. Lines are the best fit of Eq. 1 with the indicated D values.

Microtubule-driven centromere oscillations influence chromatin dynamics on longer timescales

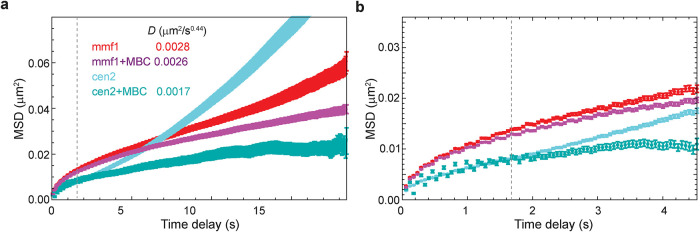
In fission yeast, centromeres are mechanically coupled to the spindle pole body (SPB; the centrosome equivalent) (Funabiki et al., 1993). Thus, forces from microtubule polymerization that drive oscillation of the SPB along the long axis of the cell on the minutes timescale (Tran et al., 2001) could be manifested in chromatin motion, even in regions distal to the centromere. Indeed, we observe clear superdiffusive behavior on the tens-of-seconds timescale (α > 1) for a lacO array integrated directly adjacent to the chromosome II centromere (cen2) (Figure 2a). This superdiffusive motion is driven by microtubules as their depolymerization with carbendazim (methyl benzimidazol-2-yl-carbamate; MBC) leads to a strong depression of motion at cen2 and the adoption of subdiffusive behavior (Figure 2a). Although it is more subtle, we also observe that the motion of a distant mmf1 locus (∼1.8 Mb from the centromere) on the tens-of-seconds timescale is enhanced in cells with intact microtubule dynamics relative to cells treated with MBC (Figure 2a, apparent after time delays of ∼5 s). We exclude that this effect is due to rigid body movement of the nucleus in response to microtubule forces exerted on the SPB on this timescale (Supplemental Figure S2). Interestingly, below the ∼5 s time delay regime, cen2 displays lower diffusivity than the mmf1 locus (D = 0.0017 μm²/s^0.44 in the presence of MBC), suggesting that bridging centromeres to the SPB acts to constrain chromatin motion at short times. Indeed, if we focus on the same time regime explored in Figure 1 (up to a time delay of ∼4 s), microtubule dynamics play a minor role on the diffusivity of cen2, which is far more constrained than mmf1 (Figure 2b). At mmf1, we observe only a nominal contribution of microtubule dynamics to the observed diffusivity at this timescale (D = 0.0026 μm²/s^0.44 in the presence of MBC; Figure 2b). We therefore chose to focus the rest of our study on this seconds-scale time regime, where there is little influence of microtubule dynamics.

FIGURE 2:

Microtubule dynamics actively drive chromatin motion at the centromeres and, to a lesser extent, the chromosome arms in fission yeast. In S. pombe, large-scale chromatin dynamics are influenced by movement of the SPB through its attachment to the centromeres (Funabiki et al., 1993). (a) The centromeres (cen2) demonstrate actively driven motion at the tens-of-seconds timescale as revealed by MSD analysis. Upon addition of the microtubule-depolymerizing agent carbendazim (MBC), this mobility is greatly depressed. The effect of microtubule dynamics is far less prominent for a locus in the chromosome arm (mmf1). (b) On the seconds time scale, the mobility of cen2 is far more constrained than the mmf1 locus and microtubule dynamics play a more muted effect. Error bars indicate standard errors of the mean.

The loop extrusion complexes, cohesin and condensin, primarily constrain chromatin motion in fission yeast

Chromosome conformation is influenced by the activity of cohesin and condensin in fission yeast. Loss of cohesin strongly disrupts TADs as assessed by Hi-C (independent of its role in sister chromatid cohesion) (Mizuguchi et al., 2014), while condensin plays a more subtle but nonetheless discernible role in interphase chromatin organization (Kakui et al., 2020). Condensin and cohesin presumably shape chromosomes through their loop extrusion activity, resulting in a dynamic steady state of DNA loops that appear and disappear in a stochastic manner. To assess how loop extrusion by condensin or cohesin impacts chromatin motion, we examined locus mobility after disruption of condensin function or postreplicative cohesin loading. To this end, we employed critical loss-of-function, temperature-sensitive alleles of the SMC2 subunit of condensin (cut14-208) or cohesin loading factor (mis4-242) and measured the motion of two loci, mmf1 and pfl5, which are distant from their chromosome’s centromere (∼1800 and 2800 kb, respectively). To our surprise, we observed a profound increase in chromatin mobility (∼30 to ∼50% increase in the diffusion coefficient D) upon inactivation of either loop-extruding complexes at mmf1 (Figure 3a), with a greater effect upon disruption of cohesin loading. A similar trend was observed at the pfl5 locus (Figure 3b).

FIGURE 3:

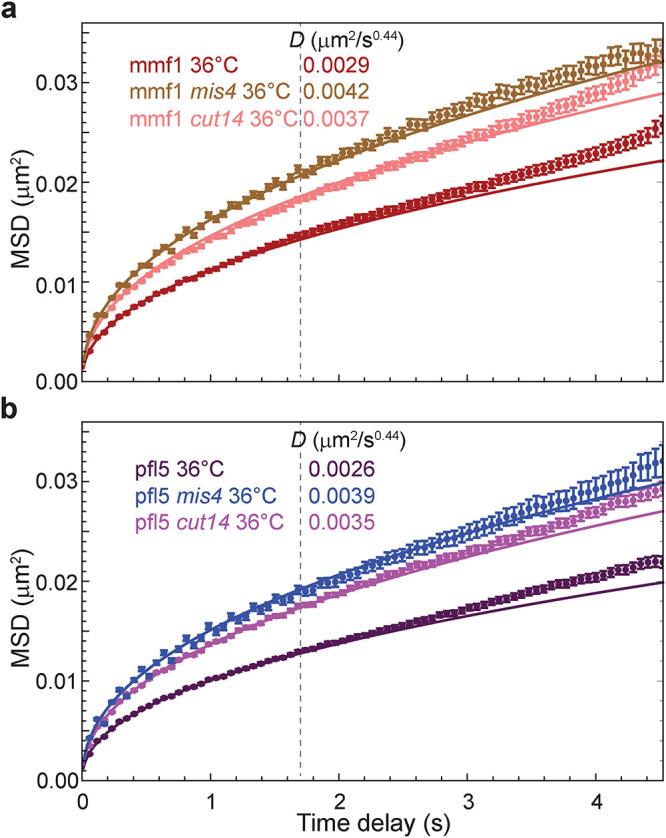
Loss of cohesin or condensin activity increases chromatin mobility. (a) MSD analysis of G2 cells harboring temperature-sensitive alleles of the cohesin-loading protein Mis4 and condensin complex subunit 2 (Cut14). The fluorescently labeled mmf1 locus was imaged at the nonpermissive temperature (36°C) to inhibit G2 cohesin and condensin function, respectively. (b) The same enhancement of chromatin dynamics is observed at a separate genomic locus, pfl5. Error bars indicate standard errors of the mean. Lines are the best fit of Eq. 1 with the indicated D values.

Prior studies in S-phase budding yeast found that cohesin depletion leads to an increase in chromatin diffusivity on the tens-of-seconds timescales (Dion et al., 2012; Cheblal et al., 2020), although this was interpreted as a result of disrupted cohesion between sister chromatids. To further dissect how sister chromatid cohesion versus cohesin-dependent loop extrusion contributes to chromatin dynamics, we took advantage of the fact that most fission yeast cells are in the G2 phase of the cell cycle. During this period, replication and the establishment of sister chromatid cohesion have both taken place, thereby allowing us to critically disrupt dynamic cohesin loading tied to loop extrusion while sister chromatid cohesion is retained. Indeed, although G2 fission yeast cells have two copies of the lacO array, GFP-LacI fluorescence predominantly appears as a single focus (Supplemental Figure S3). Removing Rad21 (a structural component of the cohesin complex) by genetically tagging it with an auxin-inducible degron and adding the auxin analogue 5-IAA in a strain expressing OsTir (Supplemental Figure S3) leads to the visible separation of the two sister chromatin lacO arrays due to loss of cohesion. In contrast, disruption of cohesin loading using the mis4-242 allele at the nonpermissive temperature did not lead to the loss of cohesion (Supplemental Figure S3) despite its strong effect on chromatin mobility (Figure 3). Thus, we conclude that 1) cohesin constrains chromatin mobility independent of its role in sister chromatin cohesion, which could reflect its role in generating loops that underlies its cell cycle–independent role in TAD formation (Mizuguchi et al., 2014); and 2) condensin also contributes to constraining chromatin dynamics, albeit to a lesser extent than cohesin.

Simulations predict that looping interactions constrain chromatin mobility

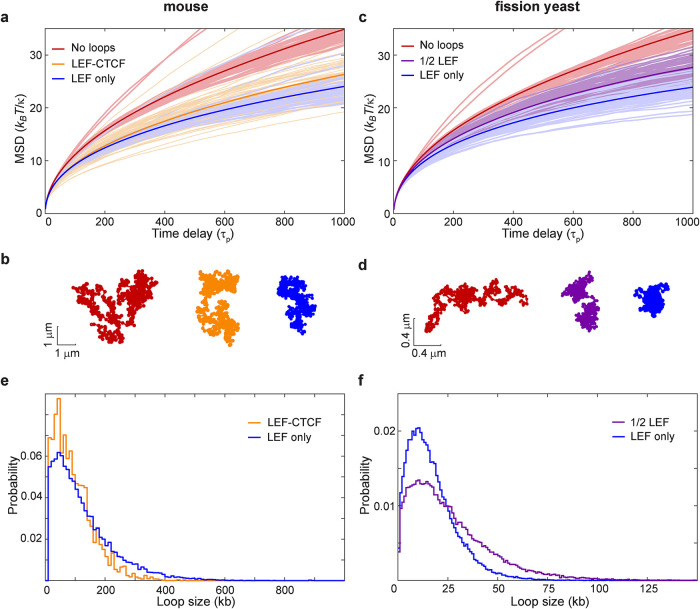
Because chromatin dynamics reflects the response of the chromatin polymer to both active processes and thermal fluctuations, we turned to modeling in order to understand how condensin- and cohesin-mediated loops arising from loop extrusion impact fluctuations of the chromatin polymer. We coupled Rouse model polymer dynamics simulations with LEF model simulations of the loop configuration for a given genomic region. Just as for the classical Rouse model, our version neglects excluded-volume interactions and attachments to the nuclear envelope or other subnuclear structures. We implemented a loop extrusion model that includes 1) random loading of LEFs, 2) followed by bidirectional loop extrusion until a LEF encounters another LEF or a BE such as a site bound by CTCF (Alipour and Marko, 2012; Fudenberg et al., 2016; Nuebler et al., 2018), or 3) until the LEF dissociates, causing the loop to dissipate. As CTCF does not exist in fission yeast but CTCF and its binding sites have been reported for mouse cells, we first simulated dynamics of several 6-Mbp regions of the mouse genome. We described each 10 kb of the genome as a bead connected to its neighbors by springs of stiffness, κ, and experiencing a friction coefficient, ζ. To incorporate loops, we augmented the usual nearest-neighbor Rouse model with additional springs (of the same spring constant) that connect nonadjacent beads, thus representing the base of a loop. The loop configuration (defined by the monomers/beads that are linked) evolves according to the stochastic “LEF-CTCF” model similar to that developed by Mirny and colleagues (Fudenberg et al., 2016; Nuebler et al., 2018) as described above. In the model, CTCF occupancy determines the probability of the LEF passing through the CTCF binding sites. Using reported CTCF occupancy derived from experimental data from chromatin immunoprecipitation followed by sequencing (Bonev et al., 2017) as an input and the parameters outlined in Supplemental Table S2, LEF model simulations resulted in a dynamic steady state of chromatin loops with about 30 loops within a 6-Mbp region. The comparison of MSDs between the Rouse simulations without loops (red curve) and with CTCF-dependent loops (orange curve) reveals that loops constrain chromatin motion (Figure 4a), consistent with our experimental MSD measurements of gene loci in Schizosaccharomyces pombe with and without disrupted SMC complex loading or activity (Figure 3). Increased chromatin motion was tied to chromatin conformations that were less compact in the absence of loops (example shown in Figure 4b, red) compared with more condensed conformations in simulations with LEFs generating loops (Figure 4b, orange).

FIGURE 4:

LEF activity constrains chromatin motion as revealed by Rouse-type polymer simulations. (a) The formation of time-dependent loops driven by loop extrusion according to the LEF-CTCF model with semipermissible boundaries at CTCF binding sites (orange) or LEF-only model lacking explicit boundaries (blue) applied to the mouse genome leads to decreased MSD compared with the polymer without loops (red). MSDs arise from a Rouse model with beads of friction coefficient ζ, connected by springs of spring constant κ; τ_p = ζ /(4κ) is the characteristic time of polymer relaxation. (b) Examples of the instantaneous polymer configurations from simulations for the mouse genome. (c) The same analysis as described in panel a but applied to the fission yeast genome for the LEF-only model (blue) compared with the polymer without loops (red). In magenta is the LEF-only model in which only half of the LEFs are present. (d) Examples of the instantaneous polymer configurations from fission yeast simulations. (e) Loop size distribution for simulations of the mouse chromatin with LEF-CTCF and LEF-only models. (f) Loop size distribution for simulations of the fission yeast chromatin with LEF-only models at “full” or 1/2 numbers of LEFs.

We next developed an analogous simulation approach that could be applied to the fission yeast genome. Yeasts lack CTCF, although they likely have alternative BEs that define experimentally observed TADs (Thon et al., 2002; Mizuguchi et al., 2014). We therefore devised a simulation, which we call the “LEF-only” model, that includes 1) random loading of LEFs and 2) the ability of the LEF to move bidirectionally from its loading site until it encounters another LEF or 3) until it dissociates—a feature of many prior loop extrusion models (Alipour and Marko, 2012; Fudenberg et al., 2016; Nuebler et al., 2018). The LEF-only model is the same as the LEF-CTCF model with one exception—there is no influence of CTCF (or any other explicit factor) on LEF movement. Similar to the CTCF-dependent mouse genome results, we again observe that LEF activity leads to a reduction in the MSD in simulations of a 300-kb region of the fission yeast genome (Figure 4c, compare the blue curve to the red) and more compact polymer conformations (Figure 4d, in blue; compare to without loops, in red). Moreover, subjecting the mouse genome to this alternate LEF-only loop extrusion model also constrains loci motion (Figure 4, a and b, blue curve and polymer conformation). The resulting MSDs in the LEF-only model are suppressed slightly beyond those generated by the LEF-CTCF model (Figure 4a), which is also reflected in more compact polymer conformations (Figure 4b). Greater compaction stems from the lack of CTCF-dependent pausing sites, which allows LEFs to travel a greater genomic distance before encountering another LEF, leading to larger chromatin loops on average (Figure 4e) and therefore a smaller fraction of chromatin existing outside of loops. These results suggest that the distribution of loop sizes can impact chromatin dynamics.

We next investigated how the number of loops impacts the MSD. If we decreased the number of LEFs by half (referred to as the “1/2 LEF” model) in our fission yeast simulation, we observed an MSD profile and polymer compaction that is intermediate between the no-loop conformations and the “full amount” of LEFs (Figure  4c, purple curve). This simulation result can, at least in part, explain the observed effect that inactivating cohesin or condensin has on loci motion (Figure 3), as loss of either increases chromatin mobility despite the continued presence of the other presumed LEF. Indeed, while having fewer SMCs allowed formation of larger loops (reflecting a reduced probability of encountering another SMC during the LEF residence time), the extent of polymer compaction in the 1/2 LEF model was also intermediate, as a greater fraction of the chromatin was outside of loops (Figure 4, d and f). Taken together, these observations again reinforce the trend that loop size and density are important variables of how chromatin conformation impacts its dynamics. Moreover, our observations underscore that while particular LEF models might be different in their details (i.e., with or without CTCF), extruded loops consistently constrain chromatin mobility.

The long residence time of cohesin likely underlies its dominance over condensin in constraining chromatin mobility

Our experimental data suggest that cohesin has a more profound influence on constraining chromatin dynamics than condensin, given that disrupting its loading in G2 cells quantitatively drives up the MSD to a greater extent than loss of condensin function (Figure 3, a and b). While our 1/2 LEF simulation provides an explanation for the sensitivity of chromatin mobility to loss of either cohesin or condensin, it does not explain why they have different impacts on loci dynamics. We hypothesized that the differential effect could stem from distinct lifetimes of cohesin and condensin on chromatin, as supported by prior experimental observations (Gerlich et al., 2006a, b; Hirano, 2016). To begin to explore this hypothesis, we carried out simulations in which we explicitly considered two types of LEFs differing 10-fold in their respective lifetimes while keeping the total number of LEFs constant. As expected, introducing activities of both long- and short-lifetime LEFs (mimicking cohesin and condensin, respectively) resulted in constrained MSDs (Figure 5a and Supplemental Figure S4a, blue vs. red curves), similar to those in previous simulations (Figure 4c). Here, however, inactivation of long-lived LEFs (Figure 5a and Supplemental Figure S4b, dark green) led to a much stronger mobility enhancement compared with the inactivation of short-lived LEFs (Figure 5a and Supplemental Figure S4a, light green). Thus, LEFs with shorter lifetimes have a weaker impact on chromatin dynamics, perhaps because the loops they form during their lifetime are smaller (Supplemental Figure S4c). By contrast, LEFs with longer lifetimes make larger loops (Supplemental Figure S4c) that may explain why they dominate in compacting chromatin and, as a consequence, constraining chromatin mobility.

FIGURE 5:

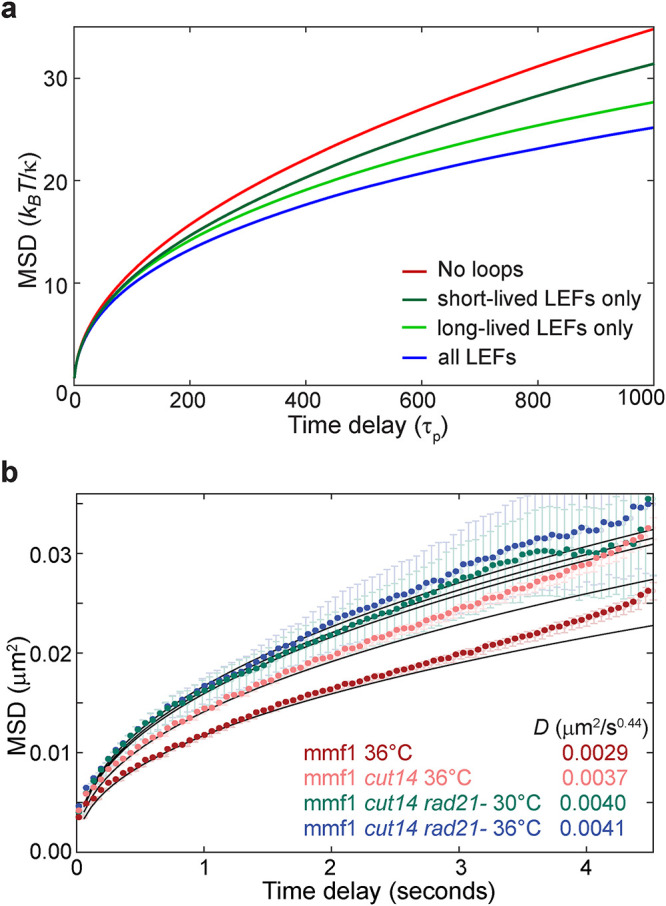
Impact of loop extrusion on chromatin mobility depends on the LEF lifetime. (a) MSD results of the Rouse-type polymer simulations combined with loop extrusion simulations that considered two types of LEF complexes (in equal amounts) with different lifetimes. Blue, simulations with both types of LEFs present; green, only long-lived LEF present; dark green, only short-lived LEF present; red, no LEFs. Lines represent the average over all beads and all simulations. See also Supplemental Figure S3. (b) Experimental MSDs for WT cells at 36°C (red) and cells harboring a temperature-sensitive allele of the condensin complex subunit 2 (Cut14) imaged at the nonpermissive temperature (36°C; pink) and cells harboring the temperature-sensitive allele of Cut14 imaged after depletion of the Rad21 subunit of the cohesin complex at the permissive temperature (30°C; green) and at the nonpermissive temperature (36°C; blue). Lines are the best fit of Eq. 1 with the indicated D values.

To further examine the relative contributions of cohesin and condensin to chromatin mobility experimentally, we engineered a strain that combines critical Rad21 depletion with the temperature-sensitive cut14-208 allele in condensin. While rapid (∼20 min; Supplemental Figure S5) Rad21 degradation at the permissive temperature for cut14-208 led to enhanced mmf1 locus mobility (Figure 5b), similar to inactivation of Mis4 (Figure 3a), additional inactivation of Cut14 by shifting to its nonpermissive temperature had only a nominal effect. These results suggest that cohesin is the dominant factor responsible for damping chromatin dynamics, plausibly due to its longer lifetime. Taking our experimental and simulation findings together suggests that, on this timescale, the loop-extruding activity of cohesin, and to a lesser extent condensin, constrains the MSD of chromatin, which is sensitive to both the number and size of loops.

Loop extrusion decreases the effective exponent describing chromatin diffusivity

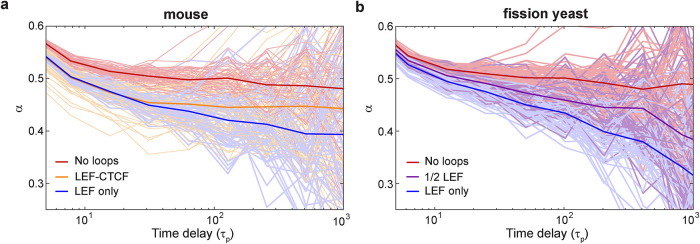
We next inquired whether the loop configuration simulations could provide further insight into our observation that the subdiffusive chromatin motion in fission yeast is described by an exponent, α, of ∼0.44, which deviates from that expected for a Rouse polymer (α = 0.5). To this end, we calculated the effective exponent, α = (log MSD[t_n+1] − log MSD[t_n])/(log t_n+1 − log t_n) from the simulated chromatin configurations and compared how α is influenced by loop extrusion in the simulations. As expected, the effective exponents for the classical Rouse model lacking loops in mouse simulations lie close to 0.5 for the wide range of times longer than the polymer relaxation time, τ_p, τ_p = ζ/(4κ) (Figure 6a, red curve). Remarkably, however, the effective exponent in the presence of loop extrusion employing either the CTCF-LEF model (Figure 6a, orange curve) or the LEF-only model (Figure 6a, blue curve) shows a gently evolving value with a mean that appears to vary continuously from a value near α ≃ 1/2 for t ≃ τ_p to a value near α = 0.4 for t ≃ 10³τ_p. Similarly, loop extrusion depresses the value of the effective exponent in the fission yeast LEF-only or 1/2 LEF simulations (Figure 6b). These results are strikingly similar to our experimental finding that MSDs in S. pombe are well described overall by a value of α ≃ 0.44 (Figure 1 and Supplemental Table S1). Thus, our data support a model in which chromatin looping interactions not only influence its apparent diffusivity, but also are manifested in depressed values for α compared with that of a Rouse polymer.

FIGURE 6:

Loop extrusion decreases the apparent subdiffusive exponent. (a, b) Effective “instant” exponent, α, vs. time for the mouse and fission yeast models presented in Figure 4. Thin lines correspond to individual beads; thick lines represent the average over all beads and simulations.

The INO80 chromatin remodeler drives chromatin mobility in fission yeast

Both our experimental and simulation approaches find that loop extrusion by SMC complexes predominantly suppresses chromatin mobility rather than serving as an activity that promotes its dynamics. Nonetheless, because ATP depletion drastically reduces chromatin fluctuations and motion (Figure 1c), there must be a process(es) tied to cellular metabolism that acts on the chromatin polymer to elicit its fluctuations. ATP-dependent chromatin (nucleosome) remodelers represent attractive alternative candidates for driving energy-dependent chromatin mobility and have been previously implicated in driving enhanced chromatin mobility in response to DNA damage (Neumann et al., 2012; Seeber et al., 2013; Hauer et al., 2017; Cheblal et al., 2020). Whether this activity is also tied to LEF function, and more generally whether and how nucleosomes impact the translocation of LEFs along the DNA, remains incompletely understood. To test whether chromatin remodelers contribute to ATP-dependent chromatin mobility in fission yeast, we examined cells lacking Arp8, an auxiliary component of the essential INO80 remodeling complex, and Arp9, a component of both the SWR1 and RSC remodeling complexes. Strikingly, loss of Arp8 led to a clear suppression of chromatin mobility (D = 0.0024 μm²/s^0.44), representing a 40% decrease in the ATP-dependent diffusivity, that is, above the basal, ATP-depleted motion (Figure 7a). By contrast, loss of Arp9 had little effect (Figure 7a). Importantly, as INO80 is essential for viability, Arp8 deletion is akin to a hypomorphic allele rather than a complete loss of function, leaving open the possibility that INO80 activity contributes to ATP-dependent chromatin diffusivity to an even greater extent than is observed in arp8Δ cells. These results are consistent with a prior study in which INO80 (but not SWR1 or RSC) was both required for a transcription-dependent boost in chromatin mobility and sufficient to impart increased diffusivity when artificially targeted to a chromosomal locus in budding yeast (Neumann et al., 2012), although the unique role for INO80 but not SWR and RSC remains unexplained.

FIGURE 7:

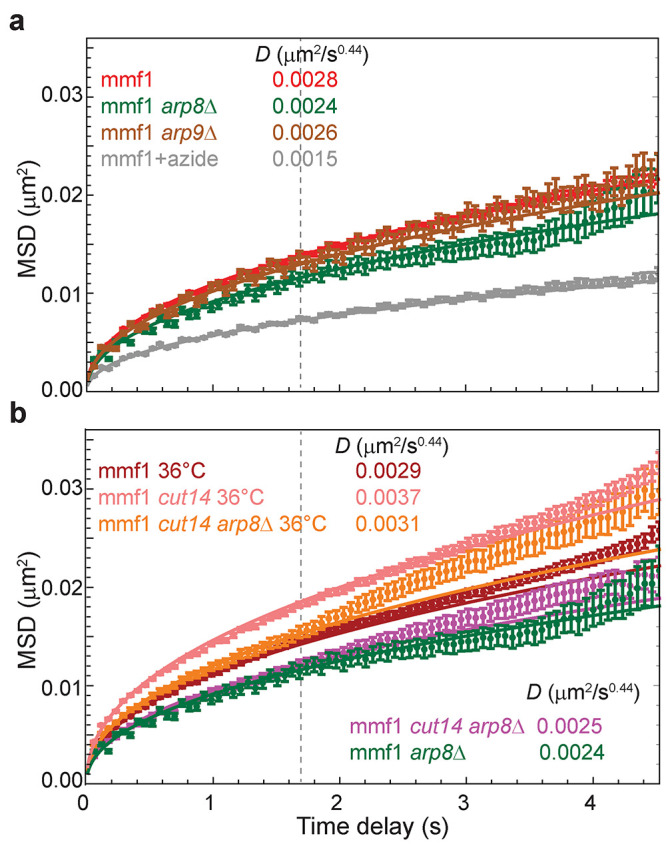
Loss of the nucleosomal remodeling complex protein Arp8 decreases chromatin mobility likely through a mechanism distinct from loop extrusion. (a) Loss of Arp8, a component of the INO80 complex, reduces ATP-dependent chromatin mobility by ∼40%, while loss of Arp9, a component of both the SWR1 and RSC complexes, has a minimal effect. For comparison, cells depleted of ATP (treated with sodium azide) are shown (replotted from Figure 1c). (b) Loss of Arp8 dampens the elevated chromatin dynamics in the cut14-208 background at the nonpermissive temperature to a slightly lesser extent than in WT cells (an ∼30% decrease) but remains much more diffusive than at the permissive temperature. Error bars indicate standard errors of the mean. Lines are the best fit of Eq. 1 with the indicated D values.

To address the interplay between the boosting of chromatin mobility by INO80 and the constraint imposed by LEFs, we examined how loss of Arp8 and the elevated chromatin diffusivity observed in LEF mutants would intersect. At the permissive temperature, cut14-208 arp8Δ cells displayed decreased diffusivity of the mmf1 locus similar to that of arp8Δ cells at the short times used in our analysis, although there is a slight upward trend at longer times in cells also harboring the cut14-208 allele (Figure 7b, D = 0.0025). At the nonpermissive temperature (36°C), loss of Arp8 also dampens the elevated chromatin dynamics observed in the cut14-208 background (Figure 7b, D = 0.0031 μm²/s^0.44). The relative magnitude of the effect (an ∼30% decrease of the ATP-dependent diffusivity; Figure 7b) is only slightly smaller than that observed at the permissive temperature or upon Arp8 deletion in wild-type (WT) cells. Importantly, the level of absolute diffusivity in cut14-208 arp8Δ cells at the nonpermissive temperature remains substantially elevated compared with that in cells lacking only Arp8 (D = 0.0031 vs. 0.0024 μm²/s^0.44). Taken together, these observations suggest that 1) INO80 activity is a major driver of nonthermal chromatin fluctuations in fission yeast and 2) loop extrusion influences the manner in which these fluctuations act on the chromatin polymer.

DISCUSSION

Here we provide new insights into the relationship between chromosome structure and dynamics. Combining live-cell imaging and polymer simulations, we converge on the conclusion that chromatin loops, which arise by SMC-driven loop extrusion, primarily constrain chromatin mobility. This constraint is manifested as a decrease in the MSD of chromatin loci and the effective exponent describing their subdiffusive behavior. We provide evidence that the activity of the INO80 chromatin remodeler is a major source of the as-yet-mysterious, energy-dependent activity that drives chromatin motion. Our findings emphasize that the chromatin conformation and the molecular machines acting on the polymer together determine chromatin dynamics.

Loops as constraints to chromatin mobility

We observe that cohesin and condensin, both harboring ATPase activity, constrain chromatin mobility in vivo; a similar observation was recently reported for the effect of cohesin depletion in mouse ES cells (Mach et al., 2022). These data are consistent with prior observations for cohesin depletion in budding yeast (Cheblal et al., 2020), although the boost in chromatin mobility was ascribed primarily to loss of sister chromatid cohesion rather than loop extrusion. Condensin depletion in G2-arrested fission yeast also led to enhanced chromatin mobility (Kakui et al., 2020), but this was observed concurrent with an increase in DNA damage that, by itself, can lead to increased chromatin mobility (see below).

Our polymer simulations provide a mechanistic explanation for the constraining effect of loop extrusion on chromatin dynamics. Specifically, while loop extrusion can drive changes in the loop configuration, the “polymer” (chromatin) relaxation timescale through which this change is manifested is much shorter (on the subsecond timescale) than our observations of chromatin dynamics (on the seconds timescale). Thus, changes to an explicit loop configuration have less impact on chromatin dynamics than the statistical impact that loops generally exert on the experimentally observed MSD and exponent of α = 0.44, which when related to the simulations in Figure 6b provides a window into the values of τ_p relevant to our measured, second-timescale trajectories. This interpretation is further bolstered by the observation that motion of individual loci is mostly independent of their genomic position (Figure 1b). Taking a different simulation approach for examining the effect of loop extrusion that also accounts for volume exclusion, Mach et al. (2022) likewise found recently that it is the act of loop extrusion rather than the influence of specific boundaries (or barriers) that impacts polymer dynamics, although they did not observe changes to the anomalous exponent, α. Taken together, these observations highlight that chromatin dynamics is dominated by the polymer nature of the chromatin and not by the local genomic conformation on the seconds timescale.

One important ramification of this model is that it provides another, “dynamic,” means by which loop extrusion factors can antagonize inter-TAD interactions and reinforce the relative overrepresentation of local, intra-TAD interactions that extends beyond roles in imposing explicit TAD boundaries. This effect would also be expected to disfavor longer-range, stochastic interactions, consistent with Hi-C studies demonstrating that cohesin antagonizes compartments (Gassler et al., 2017; Rao et al., 2017), suggesting that the loss of loops leads to more unfettered contacts between self-associating chromatin landmarks, for example those driving B compartment cohesion (Falk et al., 2019). We expect that the influence of loops on chromatin dynamics is likely to play a fundamental and conserved role as it is independent of the specific mechanisms determining the position of TADs across eukaryotic models (e.g., organisms outside of bilateria that lack CTCF and/or employ other insulator proteins such as the widely conserved TFIIIC complex [Van Bortle and Corces, 2012]). Indeed, the effect of loops on chromatin dynamics could easily extend beyond cohesin and condensin, for example to so-called tethering elements that mediate non-SMC loops (Batut et al., 2022).

ATP dependence of chromatin mobility and nucleosome remodelers

The source of ATP-dependent chromatin mobility has been a perennial mystery, ever since the first live-cell recordings of chromatin dynamics were made using the lacO-LacI technology more than 20 years ago (Marshall et al., 1997; Heun et al., 2001). Importantly, a study in budding yeast (and extended to fission yeast) demonstrates that caution must be exercised when interpreting experiments that disrupt cellular energy by glucose starvation, which results in altered cell volume, as this can lead to increased crowding that affects not just chromatin mobility but also other large macromolecular complexes (Joyner et al., 2016); for this reason, we have used sodium azide treatment to uncouple effects of ATP depletion from altered crowding in this study.

A renewed interest in actively driven chromatin mobility has arisen through studies of the DNA damage response across multiple model systems (Zimmer and Fabre, 2019). Induction of a DNA double-strand break (DSB) leads to an increase in mobility of not only the broken chromosome region but, surprisingly, the entire genome (Miné-Hattab and Rothstein, 2013; Lawrimore et al., 2020); this effect has been suggested to promote the homology search phase of DSB repair. While many factors contribute to this response, including nuclear and cytoplasmic cytoskeletal proteins (Swartz et al., 2014; Lottersberger et al., 2015; Caridi et al., 2018; Oshidari et al., 2018; Schrank et al., 2018; Zhurinsky et al., 2019; Lawrimore et al., 2020), of note the INO80 nucleosome remodeler appears to play a central role (Neumann et al., 2012; Seeber et al., 2013; Hauer et al., 2017; Cheblal et al., 2020). Indeed, in budding yeast, loss of Arp8 disrupts the observed DSB-dependent boost in chromatin mobility (Neumann et al., 2012; Seeber et al., 2013; Hauer et al., 2017; Cheblal et al., 2020). Although the potential involvement of INO80 in multiple steps of DSB repair complicates the interpretation of the mechanisms at play, it nonetheless underscores the specificity underlying the unique relationship between the INO80 nucleosome remodeler and chromatin dynamics, possibly due to INO80’s role in nucleosome eviction (Cheblal et al., 2020).

Finally, transcription has also been observed to drive a boost to chromatin dynamics across model systems (Chuang et al., 2006; Neumann et al., 2012; Gu et al., 2018). Importantly, in budding yeast, the increase of chromatin mobility upon transcriptional activation again requires INO80 activity (Neumann et al., 2012). Further, in perhaps the most elegant demonstration of sufficiency, simply locally targeting INO80 to a lacO array is sufficient to recapitulate the transcription-driven boost in chromatin mobility even in the absence of transcription; this is not the case for other nucleosome remodeling complexes when similarly targeted (Neumann et al., 2012). Thus, a common theme is that a unique function of INO80 among nucleosome remodeling complexes lies at the heart of enhanced chromatin motion in response to DSBs or transcriptional activation. Our observations suggest that a critical role for INO80 in promoting chromatin mobility extends beyond such specialized contexts and is instead generalizable, driving a component of the ATP-dependent motion characteristic of chromatin.

Cross-talk between loop extrusion, nucleosomes, and chromatin remodelers

The potential role that nucleosome remodelers play in facilitating loop extrusion remains to be fully investigated, as we are just beginning to define mechanistically how nucleosomes impact loading and translocation of cohesin and condensin, particularly in living mammalian cells. Single-molecule experiments show that nucleosomes impede cohesin translocation along DNA (Stigler et al., 2016) and that nucleosome removal promotes efficient loop extrusion in Xenopus egg extracts (Golfier et al., 2020). Moreover, numerous studies suggest that cohesin loading on chromosomes occurs at nucleosome-depleted regions (often associated with transcription start sites) and requires ATP-dependent nucleosome remodeling activities (Garcia-Luis et al., 2019; Munoz et al., 2019; Golfier et al., 2020). In addition, it has been suggested that cohesin translocation requires transcription-coupled nucleosome remodeling (Glynn et al., 2004; Lengronne et al., 2004; Dubey and Gartenberg, 2007; D’Ambrosio et al., 2008; Schmidt et al., 2009; Hu et al., 2011; Ocampo-Hafalla et al., 2016). However, recent studies suggest the possibility that loop extrusion can proceed over nucleosomes, albeit at low nucleosome density (Kim et al., 2019; Golfier et al., 2020) and/or that loop extrusion may not require topological engagement at all, allowing blockades such as nucleosomes to be circumvented (Pradhan et al., 2022). If nucleosomes (or a subset of nucleosomes, if histone modifications have an impact) do serve as barriers to loop extrusion, then ATP-dependent nucleosome remodeling would be expected to play important roles in TAD formation. Our work suggests that the INO80 chromatin remodeler carries out an important role in driving chromatin mobility in a manner that appears to be independent of the impact of looping interactions on chromatin dynamics. Of note, critical depletion of INO80 in budding yeast had a less pronounced effect on contact probability maps than depletion of other nucleosome remodelers (Jo et al., 2021), consistent with a loop extrusion–independent function. However, this does not rule out collaboration of nucleosome remodelers on the act of loop extrusion, which remains an exciting avenue for further study.

MATERIALS AND METHODS

Request a protocol through Bio-protocol.

Strain generation and culturing

All strains used in this study are listed in Supplemental Table S3. S. pombe cells were grown, maintained, and crossed using standard procedures and media (Moreno et al., 1991). Gene replacements were made by exchanging open reading frames with various MX6-based drug resistance genes (Bähler et al., 1998; Hentges et al., 2005). Targeted lacO array insertions were generated using a modified two-step integration procedure that first creates a site-specific DNA DSB to increase the targeting efficiency of the linearized plasmid pSR10_ura4_10.3kb (Leland and King, 2014); integration sites are listed in Supplemental Table S3. Random lacO array insertions were generated by transformation of the GFP-LacI–expressing strain MKSP1120 with linearized plasmid pSR10_ura4_10.3kb followed by selection on plates lacking uracil as in Leland and King (2014). Strains that had successfully inserted the lacO array were identified by fluorescence microscopy. Strains with an auxin-inducible degron (AID) system were constructed as follows. MKSP3626 and MKSP3629 were generated by C-terminally tagging rad21 with the XTEN17-3xsAID-KanMX cassette in DY48569 (Zhang et al., 2022) and in MKSP2760, respectively. DY48569 was provided by the Yeast Genetic Resource Center (NBRP, Japan). The XTEN17-3xsAID-KanMX cassette was obtained by amplifying from pDB4581 plasmid (a gift from Li-Lin Du [National Institute of Biological Sciences, Beijing] Addgene; plasmid #171124) with the megaprimers that were generated using isolated WT S. pombe genomic DNA as a template and primer pairs KL101 (GATTCACTTTTTGACGCTCCTCC)–KL102 (gttaattaacccggggatccgTAGTGATGAAAGTA­GCATTCCACGTTTA) and KL103 (agtttaaacgagctcgaattcatcgGAGGTCGGTTAATATTTTTT­CAAAATCCAATTAGATCTAT)–KL104 (GATCAATCATTGAGAATAAATTAAAAAGCGCGT). Strains MKSP3652 and MKSP3660 are two clones created by crossing MKSP3629 with DY48569. The Saccharomyces cerevisiae strains used in this study were constructed, grown, and imaged as described (Colombi et al., 2018).

Microscopy

Cells were grown in YE5S media (yeast extract plus five supplements: 5 g/l yeast extract (BD Bacto) and 0.25 g/l adenine, 0.25 g/l histidine, 0.25 g/l leucine, 0.25 g/l lysine, and 0.25 g/l uracil (Sunrise Science Products) at 30°C to log phase (OD₆₀₀ 0.5–0.8). To fix cells, cells were incubated with 2% paraformaldehyde for 10 min and washed once with 2× phosphate-buffered saline (PBS). For temperature-sensitive alleles, the cells were grown at 30°C and then shifted for 20 min to the nonpermissive temperature (36°C) before imaging. For pharmacological inhibition studies, cells were incubated at 30°C in YE5S supplemented with sodium azide (0.02% wt/vol) or with 50 μg/ml MBC for 10 min before imaging and then imaged on agarose pads (see below) containing the drug at the same concentration. For auxin-induced degradation, cells were imaged on agarose pads (see below) containing 100 nM 2-[5-(adamantan-1-yl)-1H-indol-3-yl]acetic acid (5-IAA; TCI product number A3390).

For imaging, 1.4 μl of the concentrated cell suspension was transferred to an ∼1 cm × 1 cm × 1 mm pad made of 1.4% agarose (Denville Scientific) in EMM5S (Edinburgh minimal media plus five supplements (0.25 g/l adenine, 0.25 g/l histidine, 0.25 g/l leucine, 0.25 g/l lysine, and 0.25 g/l uracil [Sunrise Science Products]) on a microscope slide. The cell pad was covered with a #1.5, 22 × 22 mm coverslip, and edges were sealed with VALAP (1:1:1 petroleum jelly, lanolin, and paraffin) to limit evaporation during imaging.

Fluorescence and bright-field images were acquired on a DeltaVision wide-field microscope (Applied Precision/GE) equipped with a temperature control chamber, 1.4 NA 100× objective (Olympus), solid-state–based illumination (Lumencor), and an Evolve 512 EMCCD camera (Photometrics). Fluorescence was excited at 488 nm and collected with emission filters between 500 and 550 nm. Typically, 1000 images were continuously acquired with 10 ms exposure time and 58 ms per frame rate.

Western blot

To measure rad21-XTEN17-3sAID degradation, cells were grown exactly as for imaging experiments in YE5S media to OD = 0.6 and split into two samples—with and without the addition of 100 nM 5-IAA for 20 min. Cultures were centrifuged at 2000 × g for 5 min, and cell pellets were washed with 1 mM EDTA. Cells were then pelleted and lysed in 2 M NaOH incubated for 10 min on ice. An equal volume of 50% trichloroacetic acid (TCA) was mixed in before incubation for 10 min on ice and collection of the protein precipitate by centrifugation. The pellet was then washed with –20°C acetone and air-dried for 15 min. The pellet was then dissolved in 5% SDS followed by an equal volume of SDS–PAGE sample buffer containing urea (24 mM Tris-Cl, pH 6.8, 9 M urea, 1 mM EDTA, 1% SDS, 10% glycerol). Samples were then shaken at 37°C for 15 min before being centrifuged at 14,000 × g for 15 min. Approximately equal loads of extracted protein were subjected to SDS–PAGE and transferred to a 0.2 µm nitrocellulose membrane (Bio-Rad; 1620112). Transferred proteins were then stained with Ponceau S solution (Sigma-Aldrich; P3504). Blots were blocked (5% [wt/vol] dry milk/Tris-buffered saline with 0.1% Tween 20) before incubation with primary mouse α-mAID antibody (MBL; M214-3) (diluted 1:1000 in blocking buffer) overnight. The blots were then incubated for 1 h at room temperature with secondary horseradish peroxidase–conjugated goat anti-mouse goat antibodies (Invitrogen; #31430; 1:5000 dilution). The blot was developed using the SuperSignal West Femto Maximum Sensitivity ECL Substrate (Thermo Fisher Scientific; 34094) on a VersaDoc Imaging System (Bio-Rad; 4000 MP).

Loci tracking and trajectory analysis

The localization of each fluorescently labeled chromatin focus was determined by applying a spatial bandpass filter to each raw image frame. Specifically, the centroid of each peak above a determined threshold value was calculated to obtain an approximate position. Then, the final localization was obtained by fitting a radially symmetric Gaussian function around each centroid position. These positions were then linked into time trajectories using the algorithm for single particle tracking introduced in Crocker and Grier (1996). Specifically, we did not allow gaps between frames, we set the maximum displacement between frames to two pixels (0.321 μm), and we set the minimum track length to be 300 frames, or 100 frames for experiments involving arp8Δ, arp9Δ, and cut14-208/arp8Δ genotypes or sodium azide treatment. The MSD versus time delay for each time-lapse image series was calculated as follows. First, the trajectories were split into subtrajectories of 29 steps (with duration ≈ 1.68 s). Then, individual displacements were averaged across all subtrajectories and different time-lapse series for a given experiment. The calculated experimental MSDs were fitted by the theoretical MSD for fractional Brownian motion (fBm) with static and dynamic localization errors taken into account, as described (Bailey et al., 2021):

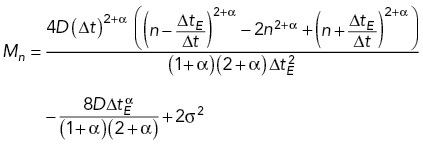1

where D is an effective diffusivity, Δt_E = 10 ms is exposure time, Δt is the time step between frames, and α is an exponent (α< 1 corresponds to subdiffusive motion and α > 1 to superdiffusive motion), n is the number of frames, and σ is the static localization error. Initial MSD fitting, in which D, α, and σ were varied, showed that the values of α grouped around a mean of 0.44 for most measured loci in unperturbed, WT cells (Supplemental Table S1). In all subsequent analyses (see Figures 1, 2b, 3, 5, and 7), α was fixed at α = 0.44, while D and σ were varied, allowing us to directly compare values of D as a measure of locus mobility across different experiments. Supplemental Table S1 contains all the fitting results.

Whole-nucleus motion tracking

To estimate the potential contribution of rigid body motion of the nucleus to our measurements of chromatin dynamics, we analyzed the dynamics of nuclei in a strain expressing a fluorescently tagged form of the nucleoporin, Cut11 (Cut11-mCherry). Single central plane fluorescence images were acquired every 2 s. First, approximate nuclei positions were detected using a custom-written routine in MATLAB. Next, each detected fluorescence image of the nuclear envelope rim was fitted (using a custom-written routine in MATLAB) by a circle convolved with the point spread function with the center position, circled radius, fluorescence amplitude, and background as free parameters. Last, the position of each nuclear center was tracked by the same approach as that described for loci tracking and trajectory analysis.

Quantification of cohesion loss

Because in fission yeast most cells are in G2 phase, that is, after replication and establishment of a sister chromatid cohesion, most cells (in an asynchronous culture) have two copies of the lacO array. However, most of the time GFP-LacI fluorescence predominantly appeared as a single diffraction-limited focus due to close proximity of sister chromatids in cells with unperturbed cohesion. To quantify cohesion loss, we first detected spots using a custom-written MATLAB “findIrregularSpots” function with parameters that allowed detection of close (but not overlapping) spots in the same single-plane, time-lapse movies that were used for MSD analysis. Next, for each movie, all spots were assigned to nuclei based on spatial proximity. We analyzed only nuclei in which at least one spot was observed for at least 100 (not necessarily consecutive) frames. Then, nuclei in which two foci appeared in at least 25% of any (one or two) spot observations were labeled as “two-foci” nuclei, and their fraction was calculated (Supplemental Figure S3). Note that because we used single-plane images, there is always a chance that the lacO array is out of the focal plane optical section.

LEF simulations

We carried out Gillespie-type simulations (Gillespie, 1977) of the chromatin loop configuration using two different models of loop formation and extrusion. First, we simulated a version of the LEF model described in Fudenberg et al. (2016). Subsequent to uniformly distributed random binding, LEF translocation proceeds stochastically and bidirectionally at a certain rate v until either the LEF dissociates or a LEF anchor encounters another LEF or a BE. Only outward translocation (i.e., one increasing the loop) is permitted, with translocation at each loop anchor occurring randomly and independently with equal probability. LEFs cannot pass each other; however, BEs have a nonzero permeability, P, which is implemented as a multiplier to the LEF translocation rate at BEs, that is, the translocation rate through BEs v_BE = P v. CTCF chromatin immunoprecipitation (ChIP)-seq data (Bonev et al., 2017) were used to determine the locations of BEs, as well as their permeability P, which was determined from the CTCF ChIP-seq signal S via a logistic function:

where S₀ and μ are free parameters to choose. We set S₀ = 20 and μ = 3 following the parameters used in Fudenberg et al. (2016). Second, because S. pombe lacks CTCF, we also carried out simulations without any BEs, called the LEF-only model, which is otherwise the same as the previous model. For each set of parameter values, we performed 30 simulations, each comprising 100,000 time steps. Loop dynamics reached a steady state over about 5000 steps as gauged by convergence of the chromatin backbone length, as well as the chromatin’s radius of gyration, to a more-or-less constant value. Genomic regions (6 Mbp [300 kb]) for mice (yeast) were divided into 10 kb (0.5 kb) bins, creating 600 sites that could be occupied by an anchor of a LEF. The LEF model parameters used for both CTCF and random loop models for both mice and yeast are presented in Supplemental Table S2. The parameters used closely follow from the range of values given in Fudenberg et al. (2016). For simulations considering two types of LEFs, an equal number of LEFs with two different dissociation times that bind and move independently of each other (unless they encounter another LEF of the same or different type) were simulated. Our LEF simulation code is online at the Github repository: https://github.com/nilesyan/LEF-Simulation.

Rouse model polymer simulations

Chromatin’s polymer behavior was modeled as a free-end Rouse (bead-spring) chain, in which each 10 kb (0.5 kb) region of the mouse (yeast) genome is represented as a bead that is connected to its nearest neighbors by springs of stiffness κ and experiences fluid friction with coefficient ζ. By treating each Rouse segment as an entropic spring, κ is derived from the chromatin persistence length l_k estimated in Arbona et al. (2017) using the formula 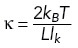, where L is the contour length of the segment. Given the calculated k and measured diffusion coefficient D from our experiments, the friction coefficient ζ can be evaluated by the formula 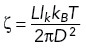, which is derived from the classical Rouse model (Doi and Edwards, 1986). For the simulations shown in Figures 4–6, the characteristic polymer time, defined here as the reciprocal of the largest Rouse model eigenvalue, namely 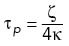, was then calculated and used as a time unit (Supplemental Table S2). To include loops, we augmented the model with additional springs (of the same spring constant) that can connect nonadjacent beads, representing the base of a loop. The sizes and locations of loops evolve according to the loop configurations generated by the LEF model simulation described above. Because the additional springs (loops) lead to far-from-diagonal terms in the Rouse model dynamical matrix, the matrix was diagonalized numerically to find the eigenmodes and corresponding beads-to-eigenmode transformations. Assuming equipartition with an effective temperature, these eigenmodes (and, through transformations, the corresponding bead positions) were then evolved using the exact simulation method as described in Gillespie (1996) until the loop configuration changed. This procedure was then repeated for each new loop configuration. At any time point when the loop configuration changes, we set the beads’ positions immediately after the time point to be the same as the beads’ positions immediately before the time point. Therefore, the beads’ positions evolve continuously, and we can simulate the motion of the chromatin beads in an exact and continuous manner. As a result, we are able to simulate polymer dynamics exactly with arbitrary time steps in our simulations and combine an equally spaced time series (with time step comparable to the polymer time) with the exact times of loop extrusion events, ensuring a recapitulation of the chromatin motion in the presence of loop extrusion. Furthermore, because the polymer relaxation time is much shorter than the characteristic loop extrusion time, the loop dynamics due to active loop extrusion has a negligible effect on the chromatin polymer dynamics. Finally, for the simulations shown in Figures 4–6, we generated an independent Rouse polymer simulation for each of 30 LEF simulations and chose 60 equally separated beads along the chromatin polymer. Each bead’s MSD and effective exponent results were averaged over these 30 independent polymer simulations (shown in light colors), and the dark colored lines are the averaged results of the 60 individual beads (light colored lines).

Abbreviations used:

AID

auxin-inducible degron

BE

boundary element

DSB

double-strand break

5-IAA

2-[5-(Adamantan-1-yl)-1H-indol-3-yl]acetic acid

LEF

loop extrusion factor

MBC

methyl benzimidazole-2-yl-carbamate

MSD

mean square displacement

SMC

structural maintenance of chromosome

SPB

spindle pole body

SPT

single particle tracking

TAD

topologically associating domain.