Microtubule competition and cell growth recenter the nucleus after anaphase in fission yeast

Abstract

Cells actively position their nuclei based on their activity. In fission yeast, microtubule-dependent nuclear centering is critical for symmetrical cell division. After spindle disassembly at the end of anaphase, the nucleus recenters over an ∼90-min period, approximately half of the duration of the cell cycle. Live-cell and simulation experiments support the cooperation of two distinct microtubule competition mechanisms in the slow recentering of the nucleus. First, a push–push mechanism acts from spindle disassembly to septation and involves the opposing actions of the mitotic spindle pole body microtubules that push the nucleus away from the ends of the cell, while a postanaphase array of microtubules baskets the nucleus and limits its migration toward the division plane. Second, a slow-and-grow mechanism slowly centers the nucleus in the newborn cell by a combination of microtubule competition and asymmetric cell growth. Our work underlines how intrinsic properties of microtubules differently impact nuclear positioning according to microtubule network organization and cell size.

INTRODUCTION

Active nuclear positioning through microtubule dynamics is an essential process for many types of cells (Gundersen and Worman, 2013). In fission yeast, the nucleus localizes to the cell center during interphase and instructs the position of the contractile ring to ensure symmetrical division (Tran et al., 2000, 2001; Daga et al., 2006). A microtubule-dependent mechanism centers the nucleus during interphase ahead of cytokinesis. Bundles of interphase microtubules attached to the nuclear envelope at the spindle pole body (SPB) and other sites polymerize until they reach the cell ends (Ding et al., 1997; Hagan and Yanagida, 1997; Tran et al., 2001). Their polymerization against the end of the cell generates pushing forces that are transmitted to the nucleus and push it away from the cell end. Cycles of microtubule polymerization followed by catastrophe pushing at both cell ends result in the oscillation of the nucleus and in its directed recentering when the nucleus is artificially moved off center (Tran et al., 2001; Daga et al., 2006). Simulations of this “core” nuclear positioning mechanism constrained by microtubule dynamics measured in live cells are sufficient to recapitulate the oscillatory and directed motions of the nucleus (Tran et al., 2001; Daga et al., 2006; Foethke et al., 2009).

During anaphase, the daughter nuclei are naturally displaced away from the cell center and pushed to the cell ends by the spindle. How and when the nuclei reposition back to the cell center after spindle disassembly remains unknown. The post-anaphase array (PAA) of microtubules and the mitotic SPB (mSPB) microtubules are potential candidates for repositioning the nucleus after the end of anaphase. The PAA microtubules form a ringlike structure associated with the contractile ring (Hagan and Hyams, 1988; Pichova et al., 1995; Heitz et al., 2001; Pardo and Nurse, 2003). They poly­merize from equatorial microtubule organizing centers (eMTOCs) recruited to the contractile ring in a myosin-II Myp2-dependent manner (Samejima et al., 2010). Different roles have been proposed for these microtubules, including anchoring the contractile ring, reestablishing interphase microtubules before the end of cytokinesis, and keeping the nucleus away from the ingressing septum (Hagan and Yanagida, 1997; Pardo and Nurse, 2003). The mSPB microtubules assemble from the SPB after spindle disassembly (Samejima et al., 2010). Their specific role has not been experimentally determined, but interpretation of fixed and immunostained cells has suggested that the mSPB microtubules coordinate with the PAA microtubules to pull the nucleus back to the cell center after anaphase (Hagan and Yanagida, 1997).

We found that the nucleus is off center from spindle disassembly until septation, a period lasting ∼50 min, and eventually recenters ∼40 min after septation. We identified two microtubule-based mechanisms that reposition the nucleus during this ∼90-min period. First, a push–push mechanism involving two competing networks of microtubules positions the nucleus at a third of the distance between the cell end and the contractile ring before septation. The mSPB microtubules push the nucleus away from the cell end toward the constricting contractile ring, while the PAA microtubules push the nucleus in the opposite direction. After septation, interphase microtubules slowly complete the centering of the nucleus. Simulations constrained by microtubule dynamics show that microtubule competition in the short newborn cell is responsible for the low velocity of nuclear displacement. Importantly, the addition of asymmetric cell growth to the simulation was necessary to explain the profile of nuclear displacement after septation, supporting a slow-and-grow mechanism of nuclear displacement in the newborn cell. Our work establishes that the same intrinsic properties of micro­tubules in cells of different sizes can result in different outcomes on the relative positioning of the nucleus.

RESULTS

Distinct microtubule networks recenter the nucleus after anaphase

At the onset of mitosis, the spindle elongates between the duplicated SPBs and drives the daughter nuclei, hereafter referred to as nuclei, to the opposite ends of the cell (Supplemental Figure 1). To determine when the nucleus recentered, we tracked the position of the nucleus from the time of spindle disassembly in time-lapse micrographs of cells expressing either Cut11p-tdTomato (nuclear marker), GFP-Atb2p (microtubules) and Sad1p-mEGFP (SPB), or Sad1-RFP and mEGFP-Myo2p (contractile ring marker). Coincident with spindle disassembly, the nucleus started to reposition toward the center of the half-cell compartment (Figure 1A). The nucleus moved in a directed manner until it reached a final maximal distance from the cell end and then oscillated about that position. In wild-type cells, the maximal distance of the nucleus from the cell end, measured as the normalized final position of the center of the nucleus from the cell end, was 2.3 ± 0.4 µm (mean ± SD) and from the contractile ring was 3.7 ± 0.5 µm (n = 20 nuclei; Figure 1, A and B). This position corresponds to one-third of the distance between the end of the cell to the contractile ring. After septation, in the newborn cell, the nucleus resumed its motion after ∼10 min and reached a stable position just beyond the cell center ∼40 min after septation (Figure 1, B and C). The total displacement of the nucleus thus happened in two phases, with the first phase spanning the end of anaphase until septation and the second phase occurring over the first 40 min in the newborn cell for a total duration of ∼90 min.

FIGURE 1:

Nucleus is off center from spindle disassembly until ∼40 min after septation. (A) Time series of micrographs in a wild-type cell showing nuclear position from spindle disassembly until septation. (B) Plot of the nuclear position of wild-type cells normalized for the cell length. The closest distance to old cell end is 0. The closest distance to new cell end is 1. The solid line is the mean. The dashed horizontal line is the normalized position of 0.5. Sample size ranged from 12 to 22 cells. (C) Time series of micrographs of a wild-type cell after septation. The red box is the selected region of interest. Inverted gray scale used for single color and merged for two colors. Dotted lines are cell outlines.

These two phases suggested that distinct mechanisms reposition the nucleus after spindle disassembly. We investigated whether microtubules repositioned the nucleus after spindle disassembly by treating cells with 50 µg/ml methyl benzimidazole carbamate (MBC) to depolymerize the microtubule network and then rapidly processing the cell samples for time-lapse imaging (Tran et al., 2000; Tran et al., 2001; Sawin and Snaith, 2004; Castagnetti et al., 2010). At the start of imaging, <7 min after MBC addition, interphase microtubules were already depolymerized. Spindles and the PAA microtubules depolymerized more slowly, with some PAA microtubules visible at the contractile ring throughout the acquisition (Figure 2A). All nuclear motions, both directed and oscillatory, in cells at any stage of the cell cycle ended upon microtubule depolymerization, supporting the conclusion that microtubules reposition the nucleus after spindle disassembly (Figure 2, A and B).

FIGURE 2:

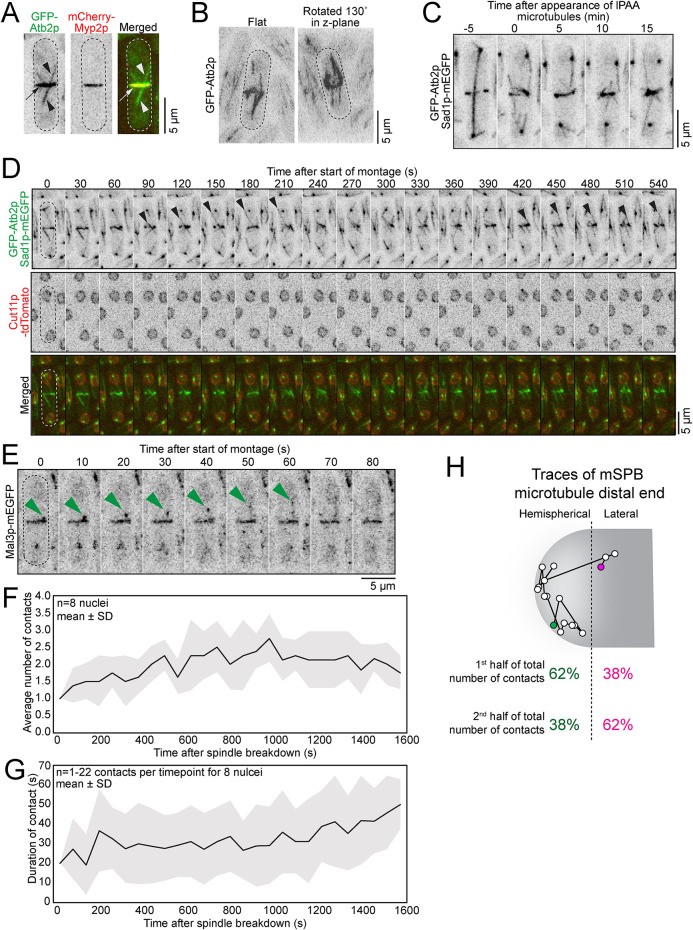
Microtubules position the nucleus after anaphase. (A) Time series of micrographs of wild-type cell treated with either DMSO or MBC. The green arrowhead is the nuclear position at the time of spindle disassembly. The magenta arrowhead is the stable nuclear position after displacement. Some ePAA microtubule signal is detectable during the entire acquisition (black arrow). Time 0 is SPB separation for DMSO-treated cells, and MBC-treated cells were aligned to DMSO-treated cells based on the size of their contractile rings. (B) Kymographs (center) of maximum projections of optical sections of a cell taken at 1-min intervals and diagrams (left, right) for orientation. Dotted lines track the cell ends over time. (C) Diagram showing the three microtubule networks that polymerize from spindle disassembly until septation. (D) Time series of micrographs of a wild-type cell. Colored boxes highlight frame with appearance of each of the three networks of microtubules in this example. Color code same as in C. (E, F) Outcomes plot showing the timing of microtubule network events, E, or nuclear positioning events, F. Number of cells analyzed in parentheses. Inverted grayscale used for single color and merged for two colors. Dotted lines are cell outlines.

Three distinct networks of microtubules polymerize after spindle disassembly: the PAA, the mSPB, and interphase-like microtubules (Figure 2C; Hagan and Hyams, 1988; Hagan and Yanagida, 1997; Samejima et al., 2010). To determine which of these networks contributed to nuclear repositioning, we measured their timing of appearance using time-lapse micrographs (Figure 2, D and E). The PAA microtubules form a complex network with the equatorial PAA (ePAA) microtubules organized in the plane of the contractile ring and the longitudinal PAA (lPAA) microtubules extending from the contractile ring toward both ends of the cell (Figure 2, C and D). The ePAA microtubules appeared at the contractile ring shortly before the spindle disassembled at 25 ± 3 min (mean ± SD, SPB separation = 0 min; Figure 2E). The lPAA microtubules were first detected at 29 ± 5 min. The PAA microtubule network remained until the contractile ring disassembled, ∼65 min after SPB separation. The mSPB microtubules (Samejima et al., 2010) appeared at 30 ± 4 min. This bundle of microtubules appeared to persist beyond septation into the newborn cell and presumably became the interphase microtubule bundle connected to the SPB. Finally, interphase-like microtubules that are not associated with the SPBs appeared at 55 ± 6 min, after the nucleus reached its maximal distance from the cell end. These microtubules also appeared to persist beyond cytokinesis and possibly became interphase microtubules.

We measured the timing of the nuclear movements from spindle disassembly until septation to correlate the appearance of these microtubules with nuclear repositioning (Figure 2F). In wild-type cells, the nucleus reached the cell ends at 27 ± 4 min, roughly coinciding with the onset of constriction of the contractile ring and the moment when the ends of the elongating spindle reached the cell ends at 25 ± 3 min. The spindle then bowed and disassembled at 29 ± 4 min. Over the following 20 ± 11 min, the nucleus moved back toward the contractile ring, reaching its maximal distance from the cell end at 50 ± 12 min, where it oscillated slightly, with no further gain in displacement toward the contractile ring until septation. The contractile ring disassembled ∼15 min later at 66 ± 4 min and septation occurred at 77 ± 8 min. Both the mSPB and PAA microtubules are present from ∼29 to ∼50 min after SPB separation during nuclear repositioning, suggesting that they may cooperate to reposition the nucleus from the end of anaphase until septation. Based on our timing measurements, the interphase-like microtubules were not present during the repositioning of the nucleus, and they were not investigated further.

After septation, bundles of interphase microtubules are present in the cell, suggesting that they may be poised to center the nucleus promptly in the newborn cells (Figure 2D). At that moment, the nucleus is only ∼1 µm away from the cell center, yet this final centering occurs very slowly. The slow centering and the displacement profile during this final phase may indicate that additional factors impact microtubule-based centering core mechanism.

The mSPB and PAA microtubules compete to position the nucleus

The gamma-tubulin complex linker protein Mto1p, a component of MTOCs, is involved in the polymerization of different microtubules throughout the cell cycle (Sawin et al., 2004; Venkatram et al., 2004; Zimmerman and Chang, 2005; Samejima et al., 2008). Deletion of the mto1 gene (∆mto1) causes multiple microtubule defects including the loss of mSPB microtubules and PAA microtubules (Venkatram et al., 2004; Zimmerman and Chang, 2005; Samejima et al., 2010). We leveraged specific mutations in mto1 that disrupt either the PAA or mSPB microtubules to determine their distinct role in repositioning the nucleus. The mto1-427 allele disrupts PAA microtubules, whereas a 30–amino acid deletion at the C-terminus of Mto1p, the mto1(1-1085) allele, disrupts astral and mSPB microtubules specifically (Samejima et al., 2010). In addition, cells lacking the myosin-II Myp2p (∆myp2 cells) also lack PAA microtubules, as Myp2p is required for the recruitment of Mto1p to the contractile ring (Samejima et al., 2010).

We acquired time-lapse micrographs of ∆mto1, mto1-427, ∆myp2, or mto1(1-1085) mutant cells and measured the maximal distance from the cell end before the end of cytokinesis (Figure 3A). We normalized the values according to cell length to account for mild variations in cell length across the different genotypes. A value of 0 represents the position of a nucleus abutting the end of the cell and 1, abutting the contractile ring (Figure 3B). In wild-type cells, the nucleus traveled until it reached a maximal distance from the cell end of 0.33 ± 0.10. In mto1-427 (and ∆myp2) cells that lack PAA microtubules, the nucleus traveled closer to the contractile ring than in wild-type cells, reaching a maximal distance from the cell end of 0.42 ± 0.13 (0.44 ± 0.08 for ∆myp2). When ring constriction was delayed (∆myp2 myo2-E1 cells) in cells that lacked PAA microtubules, the nucleus just crossed the center and reached 0.53 ± 0.14 (Mana-Capelli et al., 2012; Laplante et al., 2015). In contrast, in cells that lacked mSPB microtubules, mto1(1-1085) cells, the nucleus remained close to the end of the cell, with a maximal distance from the cell end of 0.13 ± 0.09. In those cells, a minimal drift of the nucleus away from the cell end occurred upon spindle disassembly and might result from the relief of the pushing forces exerted by the spindle. Interphase-like microtubules were present in mto1(1-1085) cells, supporting the conclusion that these microtubules are insufficient for repositioning the nucleus after anaphase, consistent with their timing of appearance (Figure 2E). In ∆mto1 cells, cells that lack both PAA and mSPB microtubules, the nucleus remained close to the cell end, with a maximal distance from the cell end of 0.15 ± 0.09, comparable to the value measured in mto1(1-1085) cells. Our observations suggest that the mSPB microtubules move the nucleus away from the cell end, while the PAA microtubules limit that movement.

FIGURE 3:

PAA and mSPB microtubules position the nucleus after anaphase until septation. (A) Confocal micrographs of the final position of the nucleus before ring disassembly (left). Kymographs of maximum projections of optical sections of cells containing Cut11p-tdTomato taken at 1-min intervals aligned at the time when the nucleus reached the cell end (right; dotted horizontal lines, cell ends). (B) Swarm plot of the nuclear position normalized for cell length. The closest distance to old cell end is 0.00. The closest distance to new cell end is 1.00. The asterisk marks a significant difference between the indicated comparisons at p < 0.05, Student’s t test. (C) Graph of the displacement of the nucleus. Time 0 is time when nucleus reaches the ends of the cell by the action of the spindle. Tracking of the nucleus ended when the contractile ring was fully disassembled. Number of cells analyzed in parentheses. Inverted gray scale used for single color and merged for two colors. Dotted lines are cell outlines.

To determine how the two networks of microtubules contribute to the motion of the nucleus, we tracked the displacement of the nucleus every minute from the time it reached the end of the cell until the contractile ring disassembled (Figure 3C and Supplemental Figure 2). In wild-type cells, the mean displacement of the nucleus showed an initial rapid phase during the first ∼10 min followed by a slower, more variable phase. During the rapid phase (from 0 min to 10 min), the nucleus moved at a mean velocity (∆x/∆t for entire duration of displacement) of 0.09 ± 0.05 µm/min and then dropped to 0.005 ± 0.018 µm/min during the slower phase of displacement (from 10 min until plateau is reached). The greater coefficient of variation seen in the slower phase of displacement reflects the oscillatory movement of the nuclei after they reached their maximal distance. Some nuclei reach their maximal distance from the cell end sooner than others and are mostly moving “backward” during the slow phase, resulting in negative velocities and a higher variation in velocities during the slow phase (Supplemental Figure 2). The profile of displacement of the nucleus in cells that lacked mSPB microtubules (mto1(1-1085), ∆mto1, and cells treated with MBC) showed a single slow phase of displacement. In those cells, the nucleus displaced slowly from spindle breakdown until the disassembly of the contractile ring (0.05 ± 0.02 µm/min for mto1(1-1085), 0.06 ± 0.03 µm/min for ∆mto1, and 0.04 ± 0.02 µm/min for MBC-treated cells). These results suggest that the initial rapid phase of displacement observed in wild-type cells depends on the actions of the mSPB microtubules (Figure 3C and Supplemental Figure 2). The nuclear displacement traces for cells that lack PAA microtubules (mto1-427, ∆myp2, and ∆myp2 myo2-E1) followed a profile similar to that of wild-type cells, with an initial rapid phase followed by a slow phase (Figure 3C). The velocity of the nuclear movement during the initial phase of displacement in mto1-427, ∆myp2, and ∆myp2 myo2-E1 was comparable to that of wild-type (0.10 ± 0.06 µm/min for mto1-427, 0.09 ± 0.05 µm/min for ∆myp2, and 0.11 ± 0.05 µm/min for ∆myp2 myo2-E1; Supplemental Figure 2). The nuclear velocity of the second phase of displacement was similar to wild-type in mto1-427 (0.01 ± 0.02 µm/min, p = 0.23) and slightly faster in both ∆myp2 (0.02 ± 0.03 µm/min, p < 0.05) and ∆myp2 myo2-E1 cells (0.03 ± 0.02 µm/min, p < 0.001; Supplemental Figure 2). The transition between the initial rapid phase and slow phase was delayed by ∼5–10 min in cells that lacked PAA microtubules. This delayed transition suggests that the PAA microtubules intercept the nucleus ∼10 min after the onset of nuclear motion, thus ending the initial fast phase of motion.

mSPB microtubules push the nucleus away from the cell ends

To understand how mSPB microtubules displace the nucleus toward the division plane, we characterized their organization and dynamics. The entire mSBP microtubule is composed of a proximal and a distal bundle (Figure 4A). We measured the fluorescence intensity of the mSPB bundles labeled with GFP-Atb2p, compared it with that of the interphase microtubule bundles, expected to be composed of four microtubules, and found that mSPB microtubules are bundles of three or four microtubules near the SPB, tapering down to one or two microtubules near their +tips (Tran et al., 2001; Loiodice et al., 2005; Daga et al., 2006). The average length of the proximal bundle gradually increased during nuclear displacement until it reached a maximal length of 2.9 ± 0.7 µm (Figure 4B). The distal bundle was consistently shorter than the proximal, with a maximal length of 1.6 ± 0.7 µm (Student’s t test, p < 0.0001). Both proximal and distal bundles showed dynamic instability characterized by periods of growth followed by rapid depolymerization typical of microtubules. However, the proximal bundle appeared more stable and contacted the ends of the cell for 2.6 ± 1.3 min (n = 20) before shrinking. In contrast, the distal bundle shrank more frequently and did not contact any obvious structure. We concluded from these results that the mSPB microtubules may push rather than pull the nucleus toward the division plane.

FIGURE 4:

Elongation of mSPB microtubules against the cell end rotates and pushes the nucleus. (A) Time series of micrographs of a wild-type cell showing mSPB microtubule dynamics. The green arrowhead marks the proximal mSPB bundle. The magenta arrow marks the distal mSPB bundle. (B) Plot of the length of the proximal mSPB bundle over time in wild-type cells. (C) Representative traces of SPB position taken every 1 min in wild-type and mto1(1-1085) cells from the time the nucleus reached the end of the cell until ePAA disappearance. The green circle represents the starting position. The magenta circle represents the ending position. (D) Stacked bar chart of the percentage of SPBs that rotated to face the contractile ring before septation. Diagram of scoring of SPB rotation (right). Inverted gray scale used for single color and merged for two colors. Dotted lines are cell outlines.

We expected this pushing motion of the mSPB microtubules at the SPB to rotate the nucleus and the rotation to be detectable in the position of the SPBs embedded in the nuclear envelope. At the start of nuclear displacement, shortly after the spindle disassembled, the SPB faced the end of the cell, likely due to the pushing action of the spindle on the SPBs (Figure 4, C and D, and Supplemental Figure 3A; McCully and Robinow, 1971; Tanaka and Kanbe, 1986; Ding et al., 1993). Concurrent with the appearance and elongation of the mSPB microtubules, the SPBs rotated toward the division plane in wild-type cells. In the absence of mSPB microtubules, in mto1(1-1085) and ∆mto1 cells, the SPBs did not rotate and remained facing the cell end (Figure 4, C and D, and Supplemental Figure 3A). Our observations suggest that mSPB microtubules pushed against the cell end and rotated the nucleus, causing the reorientation of the SPBs. Consistent with this conclusion, we often observed the deformation of the nuclear envelope in response to the mSPB microtubules pushing against the SPB. This effect was also observed when interphase microtubules contacted and pushed against the end of the cell, transferring the pushing force to the SPB, thus deforming the nuclear envelope as the nucleus moves away from the cell end (Tran et al., 2001; Daga and Chang, 2005).

The PAA microtubules basket the nucleus and limit its movement toward the contractile ring

The basket shape of the PAA microtubule network suggests that they may physically intercept the incoming nucleus (Figure 5, A and B). The lPAA microtubules are very dynamic, with constant elongation and shortening back to the ePAA microtubules that rearrange the entire network on a time scale of minutes (Figure 5C). We quantified the contacts between the lPAA microtubules and the nucleus in cells expressing GFP-Atb2p or the EB1 homolog Mal3p-mEGFP and Cut11p-tdTomato (Figure 5, D and E). We scored the colocalization of the two markers as contacts between the microtubule and the nucleus. The lPAA microtubules made frequent contacts with the nucleus, either with their +tip or along their side (Figure 5D). The number of contacts between the lPAA microtubules and the nuclear envelope ranged from 1 to 3 per camera frame, and each contact lasted from ∼20 to 50 s (Figure 5, F and G). A visible deformation of the nuclear membrane was often observable where the lPAA microtubules contacted the nuclear envelope (Supplemental Figure 3B). Therefore, the PAA micro­tubules likely make physical contacts with the nucleus, possibly causing the previously measured transition between the fast and slow nuclear displacement phases (Figure 3C). Consistent with this interpretation, the nucleus abruptly moved closer to the division plane when the contractile ring and PAA microtubule network disassembled (Figure 1B).

FIGURE 5:

PAA microtubules position the nucleus through direct, dynamic contact. (A) Confocal micrographs showing ePAA (arrow) and lPAA microtubules (arrowheads) in a wild-type cell. (B) Flat (left) and rotated 130° (right) micrographs of the PAA microtubules. (C) Time series of micrographs showing the dyamics of PAA microtubules in a wild-type cell. (D) Time series of micrographs of strains showing PAA microtubules and nuclei in a wild-type cell. Arrowheads show the contacts between lPAA and nucleus. Timepoints 150, 180, and 210 s are also shown in Supplemental Figure 3B. (E) Time series of micrographs showing +tips of lPAA microtubule (green arrowheads) extending toward nucleus. (F, G) Plots of the number of contacts by the lPAA microtubules with the nuclear membrane, F, and the duration of these contacts, G, over time. (H) (Top) Representative trace of mSPB microtubule position taken every 1 min in a wild-type cell from the time of mSPB microtubule appearance to ring disassembly. The green circle marks the start position. The magenta circle marks the end position. (Bottom) Percentage of location of contacts of the proximal end of the mSPB microtubule during the first and second half of the total number of contacts. n = 20 mSPB microtubules. Inverted gray scale used for single color and merged for two colors. Dotted lines are cell outlines.

In the absence of PAA microtubules, the nucleus moved closer to the contractile ring, suggesting that the proximal mSPB bundles may grow longer in cells lacking PAA microtubules (Figure 3, B and C). However, in mto1-427 cells, the proximal mSPB bundles reached a maximum length of 2.9 ± 0.8 µm (n = 20), while the distal mSPB bundle reached a length of 1.4 ± 0.4 µm, comparable to the lengths measured in wild-type cells (Student’s t test, p = 0.7739 and p = 0.3963, respectively). We mapped the contact points of the +tip of the proximal mSPB microtubules along the inner cell surface from the time of mSPB appearance until ring disassembly. The proximal mSPB bundle contacted the end of the cell transiently in a touch-and-retract manner. For the first half of the total number of measured contacts (∼the first 15 min of repositioning), 62% of contacts were made within the hemispherical end of the cell in wild-type cells (n = 20 mSPB microtubules; Figure 5H). During the second half of all contacts (∼the last 15 min of repositioning), 62% of the contacts were made with the lateral sides of the cell. Therefore, in the absence of PAA microtubules, the proximal mSPB microtubules contact the cell surface progressively closer to the division plane to push the nucleus toward the division plane. Such progressive stepping may explain how short microtubules can push the nucleus to distances that exceed their length. The actions of the PAA microtubules may then restrict the contacts of the mSPB microtubule to the cell ends and prevent their progressive stepping toward the contractile ring.

Simulations support the conclusion that nuclear position within the cell predicts nuclear displacement velocity

Interphase microtubules can reposition an artificially displaced nucleus with a peak displacement velocity ranging from 0.2 to 0.9 µm/min (Tran et al., 2001; Daga and Chang, 2005; Tolic-Norrelykke et al., 2005). We therefore expected the interphase microtubules, present in the newborn cell at the time of septation, to rapidly center the nucleus within 5 min after septation. In contrast, the nucleus slowly reached the cell center over the first ∼40 min after septation (Figure 1, B and C, and Supplemental Figure 4A). The displacement profile of the nucleus in a wild-type cell showed an initial static phase of ∼10 min followed by a slow displacement of ∼0.01 µm/min (mean velocity) until the nucleus reached a final stable position ∼40 min after septation (Figure 1B and Supplemental Figure 4A). The absence of net nuclear movement in the first 10 min after septation suggests that although microtubules are present at that time, their dynamics does not result in any significant nuclear movements.

To understand the molecular mechanisms responsible for this slow displacement, we modified a previous model of nuclear displacement in fission yeast cells (Foethke et al., 2009) to account for asymmetric cell growth (Supplemental Table 2). We first simulated the repositioning of an off-center nucleus located at the cell end in a 12.4 µm–long cell, the same cell length studied by Daga et al. (2006). The simulations effectively repositioned the nucleus to the cell center at a peak displacement velocity, the initial velocity of the displacement, of 0.34 µm/min, in agreement with the range measured by Daga et al. (2006; Supplemental Video 1). We measured a mean velocity of the entire displacement of 0.08 µm/min, nearly 10-fold higher than the nuclear displacement velocity we measured in newborn cells.

Movie S1.

Download video file ^{(2.4MB, mp4)}

Simulated nuclear displacement in 12.4-μm cell. Video output of simulation of nuclear displacement in a 12.4 μm cell with a nucleus positioned at the cell end.

To understand the factors that influence nuclear displacement velocity, we observed the video output from simulations of nuclear displacement in short and long cells that have a nucleus positioned against the end of the cell. Videos showed dynamic microtubules growing nearly parallel to the long axis of the cell from sites anchored at the nuclear envelope (Supplemental Video 1). Cycles of microtubule polymerization followed by sudden catastrophe captured the dynamic instability of microtubules. Microtubules polymerized until they reached the closest cell end, bowed slightly while exerting pushing forces that moved the nucleus away from that cell end, and rapidly underwent catastrophe. We refer to the distance between the nucleus and the proximal end of the cell as the proximal (P) distance and the distance between the nucleus and the distal end of the cell as the distal (D) distance. In a newborn wild-type cell, the proximal end is the old cell end and the distal end refers to the new cell end created by septation. In videos of long cells (12.4 µm) with a nucleus located at the cell end, the proximal microtubules visibly reached the proximal cell end before distal microtubules could reach the distal end of the cell. Therefore, the proximal microtubules had a pushing advantage over the distal microtubules at every round of polymerization and catastrophe due to their closer proximity to the cell end than the distal microtubules. From these observations, we hypothesized that the P/D ratio influenced the velocity of nuclear displacement. We ran simulations with nuclei positioned across a range of physiologically relevant P/D ratios for wild-type cells of different lengths. Nuclear velocity decreased with increasing P/D ratio, supporting the conclusion that the greater the difference between the P and the D distances, the faster the nucleus repositioned to the cell center (Figure 6A). This pushing advantage may be a combination of proximity to the cell end and the capacity of shorter microtubules to sustain greater forces before buckling (Mickey and Howard, 1995; Felgner et al., 1997).

FIGURE 6:

P/D ratio determines nuclear displacement velocity. (A) Correlation plot between the nuclear displacement velocity and the P/D ratios simulated for cells of different lengths. Line is the linear fit. n = 50 simulations per cell length and P/D ratio combination. (B, C) Correlation plots between the matched P/D ratios of cells of different lengths and either ∆t_d-p, B, or ∆c_p-d, C. Line is the linear fit. n = 50 simulations per cell length and P/D ratio combination. (D) Histogram of the probability of microtubules simultaneously touching at both cell ends, touching one cell end or not touching either cell end in cells of different lengths.

This relationship predicts that the proximal microtubules have a pushing advantage over the distal microtubules. We extracted information about the dynamics of microtubules +tips from simulations and measured the additional time required for the distal microtubules to reach the distal cell end over the time required for proximal microtubules to reach the proximal cell end (∆t_d-p) at the start of the simulations. We also measured the additional number of microtubule contacts at the proximal cell end over those at the distal cell end (∆c_p-d) for the first 20 min of the simulation. We used ∆t_d-p and ∆c_p-d as quantitative values for measuring asymmetric pushing advantage. We found that both ∆t_d-p and ∆c_p-d increased with decreasing P/D ratios (Figure 6, B and C). In addition, both ∆t_d-p and ∆c_p-d increased with increasing cell length. Our simulations support that proximal microtubules have a greater pushing advantage when the nucleus is positioned farther off center, that is, at a smaller P/D ratio. Finally, we determined whether the P/D ratio could recapitulate the measured nuclear displacement velocity measured in newborn cells. Simulations of a 7-µm cell with a nucleus located at a relative nuclear position of 0.4 (P/D ratio of 0.83), comparable to a wild-type newborn cell, resulted in a mean nuclear displacement velocity of 0.01 µm/min, the same velocity measured experimentally. Similarly, a P/D ratio of 0.44 in a 7-µm cell, similar to that in mto1-1085 cells, predicted a mean displacement velocity of 0.04 µm/min, comparable to the experimental value of 0.05 µm/min. Our simulations support the conclusion that nuclear displacement velocity increases when the proximal microtubules exert pushing forces that are unopposed by the actions of the distal microtubules while nuclear velocity decreases with increasing simultaneous pushing against both cell ends.

Our simulations predicted a high frequency of simultaneous microtubule contacts at both cell ends in newborn cells. We experimentally measured microtubule contacts with the ends of the cell over time from cell birth (∼7-µm cell) until the disassembly of the interphase microtubules ahead of spindle assembly (∼14-µm cell) while keeping track of cell size (Figure 6D). From those measurements, we calculated the probability of microtubule contacts at both cell ends simultaneously, at one cell end only, and no contact at either end. In cells ranging from 6 to 10 µm in length, the probability of simultaneous contacts was 0.76 while the probability of single contact was 0.2 and the probability of no contact was <0.1. In longer cells ranging from 11 to 15 µm, the probabilities of simultaneous and single contacts were similar at ∼0.4 each. Interestingly, the probability of simultaneous contacts drops when cells reach ∼10 µm in length. Therefore, as predicted from our simulations, we found that the probability of microtubules contacting both ends of the cell simultaneously is highest in short cells and lowest in longer cells.

Our results suggest that the difference between the proximal and the distal distances influences nuclear velocity. Lower P/D ratios result in faster nuclear movements, presumably due to net asymmetric pushing against the proximal cell end, resulting in a greater velocity. In contrast, higher P/D ratios result in frequent simultaneous pushing against both cell ends. These inefficient pushing actions result in slow nuclear displacement velocities. Our experimental data suggest that in short cells, proximal and distal microtubules simultaneously contact their respective cell end with high frequency, likely resulting in a tie in the pushing forces that slows down nuclear displacement.

Cell growth is needed to recapitulate the nuclear displacement profile in the newborn cell in simulations

The nuclear displacement profile generated by our simulations did not fit the profile measured in live cells (Figure 7A). The profile of nuclear displacement in newborn cells showed an initial 10-min static phase immediately after septation, followed by a slow displacement, during which the nucleus moves to its final stable position located just beyond the cell center (normalized position ∼0.54) ∼40 min after septation. In contrast, nuclear displacement profiles from simulations showed no initial plateau and a premature stabilization of the nucleus at the cell center (normalized position ∼0.50) ∼20 min after septation. These results suggested that additional factors influence nuclear displacement in live cells.

FIGURE 7:

Cell growth cooperates with interphase microtubules dynamics to center the nucleus after septation. (A, B) Plots of normalized nuclear position in 7-μm cells with a nucleus positioned at 0.83 P/D ratio in simulations with microtubule dynamics only (A, orange) and simulations with cell growth and microtubule dynamics combined (B, red). Mean of 50 simulations for each A and B. Experimentally measured normalized nuclear position in wild-type cell (same as Supplemental Figure 4A). (C, D) Same plots as in A and B aligned at the start of nuclear displacement in the experimental data 10 min after septation. Horizontal black dashed line marks the center of the cell. Vertical gray dashed lines mark the times of OETO and NETO, respectively. (E) Model of nuclear positioning mechanisms and their expected duration across the cell cycle. In newborn cells, a slow-and-grow mechanism slowly centers the nucleus. Once cells reach 9.5–10 µm in length, the late interphase nuclear positioning mechanism maintains/corrects the center position of the nucleus until anaphase. During anaphase, the spindle pushes the two daughter nuclei to opposite ends of the cells. From spindle disassembly until septation, a push–push mechanism repositions the nucleus from the cell end until a third of the distance from the cell end. Times in parentheses are approximate durations for each mechanism based on a 4-h cell cycle.

Although cell growth occurs at a time scale negligible compared with rapid microtubule dynamics, nuclear displacement in short cells with a nucleus positioned at a high P/D ratio occurs on a time scale similar to cell growth. We thus considered that cell growth may contribute to the nuclear displacement profile in newborn cells. We measured the profile of cell growth in the first 80 min after septation. Mitchison and Nurse (1985) detected an early delay in the growth of the old end (Old End TakeOff, OETO) of some cells after septation. We measured the profile of cell growth by tracking the appearance of For3-3xGFP, a component of the polarisome, or actin patches, marked with GFP-CHD, in newborn wild-type cells (Feierbach et al., 2004; Martin and Chang, 2005; Martin et al., 2005). We first detected For3-3xGFP at the old cell end 12 ± 5 min after septation and at the new end 57 ± 7 min (New End TakeOff, NETO) after septation (Supplemental Figure 4, B and C). We measured the growth rate of a newborn cell from 10 to 40 min after septation to be 0.024 µm/min, similar to the previously measured growth rate (Mitchison and Nurse, 1985). Using the measured asymmetric growth profile and rate, we built a kinematic model with a static nucleus inside an asymmetrically growing cell (Supplemental Figure 4D). The kinematic model reproduced the overall shape of the experimental profile of nuclear displacement including the initial plateau and the final stable position of the nucleus beyond the cell center, suggesting that cell growth may influence the nuclear displacement profile.

The kinematic model assumes an immobile nucleus inside a growing cell, a situation that cannot be experimentally reproduced, as depolymerization of microtubules to immobilize the nucleus also impacts cell polarity and cell growth (Verde et al., 1995; Browning et al., 2000; Brunner and Nurse, 2000; Snaith and Sawin, 2003; Feierbach et al., 2004; Snaith et al., 2005). To test the impact of cell growth on nuclear displacement, we modified our simulation platform to allow the cell to grow according to our measured growth profile. We simulated nuclear displacement in a 7-µm wild-type cell growing asymmetrically from OETO 10 min after septation and then symmetrically starting at NETO 60 min after septation. Growth rate at each cell end was set to the measured rate of 0.024 µm/min. The nucleus was initially positioned at a P/D ratio of 0.83, while all other parameters and variables remained unchanged from our previous simulations (Supplemental Video 2). Nuclear displacement from the simulations with OETO improved the overall fit with the experimental displacement profile and recapitulated the maximal distance of the nucleus to a normalized position of ∼0.54 (Figure 7B). Adding cell growth did not change the mean nuclear displacement velocity of 0.01 µm/min obtained in our previous simulations without cell growth. Although the fit improved, the simulations with OETO still did not capture the initial 10 min plateau in nuclear position (p < 0.001, Tukey’s HSD). The molecular reasons for the initial 10-min plateau remain unknown but suggest that microtubules are incompetent to move the nucleus or that the nucleus may not be movable during that time.

Movie S2.

Download video file ^{(3MB, mp4)}

Simulated nuclear displacement in growing 7-μm cell. Video output of simulation of nuclear displacement in a 7 μm cell with a nucleus positioned at a P/D ratio of 0.83 to mimic a newborn cell. OETO starts at 10 min and NETO at 60 min.

As the simulations reproduced the profile of the active displacement of the nucleus and recapitulated the nuclear displacement velocity measured in live cells, we focused on the section of the profile starting 10 min after septation. We thus aligned the start of our simulations to the 10 min mark of the experimentally measured nuclear displacement in live cells. This realignment resulted in a better agreement between the simulated data with growth and the live cell displacement profile. The simulations with no cell growth still showed poor agreement with the experimentally measured nuclear displacement profile (Figure 7, C and D). These results further support the conclusion that our simulation framework based on microtubule dynamics can explain nuclear displacement after the initial 10-min plateau. Simulations with cell growth showed strong agreement with both the final stable position at 0.54 and the time at which the nucleus reached that position. Together, our simulations suggest that in short newborn cells with a nucleus positioned at a high P/D ratio, nuclear displacement slows down. On such a time scale, cell growth becomes relevant in the overall nuclear displacement.

DISCUSSION

We explored the mechanism that recenters the nucleus after anaphase. Like many other cell types, fission yeast cells use microtubules to reposition their nucleus. Simulations of a nuclear positioning mechanism based on microtubule dynamics reproduced oscillatory motions and repositioning of the nucleus in interphase cells (Daga et al., 2006; Foethke et al., 2009; Tran et al., 2001). This core mechanism relies on the specific dynamics and organization of microtubules in mid- to late interphase cells. The intrinsic properties of microtubules that cause their dynamic instability result in temporary alternating pushing forces from microtubule polymerization against the cell ends. Modifications of this core mechanism were needed to explain how the nucleus recentered after anaphase, since the general organization of the microtubule network after anaphase is different from the organization of interphase microtubules. We found that microtubule competition and cell growth influence the core mechanism of nuclear positioning from anaphase until ∼40 min after septation, covering a large portion of the total duration of a fission yeast cell cycle (Figure 7E).

Our measurements suggest that competition between the mSPB and PAA microtubules drives nuclear displacement in a push–push mechanism from the end of anaphase until septation (Figure 7E). Immediately after spindle disassembly, the mSPB microtubules polymerize until the proximal bundle of mSPB microtubules contacts the proximal end of the cell, where it exerts pushing forces. The force generated by the mSPB microtubules are transferred to the nucleus to rotate the nucleus and push it toward the contractile ring. The PAA microtubule network then intercepts the moving nucleus and stops its progression at a third of the distance from the cell end to the contractile ring.

The basketlike structure of the PAA microtubule network and its attachment to the contractile ring are likely key to providing the counterforce necessary to push against the incoming nucleus. The nature of the connections between the eMTOCs and the contractile ring is not fully understood but relies on direct or indirect interactions between Mto1p and the myosin-II Myp2p (Samejima et al., 2010). To better understand the PAA microtubules, we will need to uncover their molecular organization and the nature of their attachment to the bundle of actin filaments of the contractile ring.

It is tempting to posit that the function of the PAA microtubules is to block the nucleus from entering the contractile ring and prevent fatal DNA damage. Although we cannot rule out that the lack of PAA microtubules could result in a damaged nucleus/DNA under untested conditions, the lack of PAA microtubules did not result in nuclei being cut by the contractile ring in our experiments. In the absence of the PAA microtubules, the nucleus never reached the contractile ring and rarely crossed the center of the half-cell compartment before septation. If the DNA is not in danger of being damaged in the absence of PAA microtubules, what is the purpose of such a complex network of microtubules? The PAA microtubules keep the nucleus at one-third of the distance between the cell end and the contractile ring, because that position may be the optimal target position to avoid nuclear-associated material from becoming unevenly distributed after cytokinesis. For example, the type I interphase nodes containing the kinases Cdr1p and Cdr2p and the Anillin/Mid1p distribute in a broad band around the nucleus before septation (Akamatsu et al., 2014). A nucleus positioned closer to the ring may result in the altered distribution of these nodes and the factors responsible for their distribution. As these nodes contain cell cycle regulation factors, their uneven inheritance between daughter cells may be deleterious.

The final position of the nucleus in the absence of PAA microtubules suggests that other factors prevent the nucleus from reaching the contractile ring and getting damaged by its constriction. Even when contractile ring closure was delayed (∆myp2 myo2-E1), giving the nucleus more time to travel toward the ring, the nucleus stopped just beyond the center of the half-cell compartment. Other dense material in the vicinity of the division plane may prevent the nucleus from reaching the contractile ring. The actin network of the contractile ring is a possible candidate that can exert forces against the nucleus and influence its position (Yukawa et al., 2021). Alternatively, connections between the nuclear envelope and the plasma membrane, such as the cortical endoplasmic reticulum, may slow down the displacement of the nucleus (Zhang et al., 2010). Finally, a local increase in cytoplasmic viscosity in the vicinity of the division plane may impede the motion of the nucleus toward the contractile ring. Any of these putative mechanisms would have the same outcome of impeding the progression of the nucleus toward the contractile ring.

The push–push mechanism leaves the nucleus off center after septation, and at that moment the interphase microtubules finalize the centering of the nucleus. Our simulations suggest that nuclear centering is slowed down by microtubule competition. This competition involves microtubules simultaneously pushing against both cell ends, resulting in a tie in the pushing forces and an ineffective displacement of the nucleus. Our simulations suggest that a tie in the pushing forces arises when proximal and distal microtubules are roughly the same length (i.e., when the nucleus is positioned at a large P/D ratio). This situation occurs naturally in short newborn cells that have a nucleus slightly off center. Our simulations thus predicted a high probability of microtubules simultaneously contacting both cell ends in newborn cells. As predicted, we experimentally measured a high probability of simultaneous microtubule contact at both cell ends in newborn cells. The probability of simultaneous contacts at both cell ends drops once cells reach a length of 9.5–10 µm. The length of microtubules may be a possible explanation for this transition, as short microtubules can sustain a greater amount of stress before buckling than longer microtubules (Felgner et al., 1997; Mickey and Howard, 1995). Therefore, a tie in pushing forces in longer cells is less likely, as longer microtubules buckle more easily under stress. In cells that are ∼10 µm in length, microtubules may reach a length at which the stress exerted by a pushing microtubule exceeds the buckling force of the opposite microtubule, causing it to break and catastrophe. Thus, cell growth may be a built-in natural tiebreaker in the pushing forces that occurs when cells reach ∼10 µm in length.

In simulations, microtubule dynamics was insufficient to explain the profile of nuclear displacement measured in live cells. Cell growth occurs at a timescale similar to that of nuclear positioning in newborn cells, and the change in cell size caused by growth can influence nuclear positioning based on the intrinsic properties of microtubules as discussed earlier. Combining cell growth with microtubule dynamics improved the fit between the simulated and experimentally measured profiles of nuclear displacement and recapitulated the position of the nucleus at the end of the displacement. Our work supports a slow-and-grow mechanism of nuclear positioning in newborn cells (Figure 7E). This model is based on microtubule dynamics in short newborn cells that have a nucleus positioned at a high P/D ratio. A nucleus positioned at a high P/D ratio results in microtubules that frequently contact both ends of the cell simultaneously, presumably resulting in a tie in the pushing forces that reduces the velocity of nuclear displacement. Cell growth in combination with microtubule dynamics in a short cell with a nucleus positioned at a high P/D ratio causes the nucleus to overshoot the center position. This slow-and-grow mechanism reproduced the displacement of the nucleus from 10 to 40 min after septation and may be the leading mechanism of nuclear positioning until the cell is ∼9.5–10 µm in length. When cells reach that length, ∼80 min after septation, nuclear positioning may transition from the slow-and-grow mechanism to the core nuclear positioning mechanism (Figure 7E).

Our simulations could not replicate the initial 10-min plateau in nuclear displacement that we measured in live cells immediately after septation. Instead, simulated data showed that microtubule dynamics recentered the nucleus, even with a high frequency of simultaneous microtubule contacts at both cell ends, combined with cell growth. These results may support the existence of additional factors that influence nuclear displacement immediately after septation. It is possible that microtubule dynamics or that the connections between the microtubules to the nuclear envelope are different during those first 10 min, preventing microtubules from moving the nucleus during that period. Therefore, the parameters we used in our simulations, which were measured experimentally in longer interphase cells, may need adjustments to replicate this nuclear behavior (Foethke et al., 2009). Alternatively, the properties of the nucleus or of its cytoplasmic environment may be different during that time period. Those properties may effectively act as a glue that prevents microtubule dynamics from centering the nucleus during the first 10 min in the newborn cell. An interesting possibility to consider is that the factors that glue the nucleus during the first 10 min after septation may be the same ones that prevent the nucleus from getting into the contractile ring before septation. Connections between the nucleus and the plasma membrane or a high local cytoplasmic viscosity may hinder nuclear motions from ∼20 min before septation until ∼10 min after septation.

Our work suggests that different factors can influence microtubule-based mechanisms of nuclear positioning. The intrinsic properties of microtubules can lead to different outcomes in the position of the nucleus depending on the changes in cell size and shape that occur naturally throughout the cell cycle. The mechanical properties of the nucleus can impact its positioning throughout the cell cycle by tuning its response to force producing changes in the cytoskeleton. These factors may be conserved in microtubule-based nuclear positioning mechanisms across different cell types. Given the abundance of knowledge of microtubule dynamics in fission yeast and the ease of genetics manipulations, fission yeast is a prime model organism to uncover unknown factors that govern nuclear displacements. In combination with computational simulations, this is a powerful toolset to understand mechanisms of nuclear positioning.

METHODS

Request a protocol through Bio-protocol.

Strains, growing conditions, and genetic and cellular methods

Supplemental Table 1 lists the Schizosaccharomyces pombe strains used in this study. Strains were created using PCR-based gene targeting to integrate the constructs into the endogenous locus, except Pnmt41-GFP-CHD, which was integrated into the leu1 locus (Bahler et al., 1998). Either pFA6a-mEGFP-kanMX6 or PFA6a-tdTomato-kanMX6 was used to create templates to generate C-terminal-tagged constructs. The primers had 80 bp of homologous sequence surrounding the integration site (sourced from www.bahlerlab.info/resources/). Except for the Pnmt81-GFP-atb2 and Pnmt41-GFP-CHD constructs, all tagged genes were under the control of their endogenous promoters. Successful integration was confirmed by a combination of fluorescent microscopy, PCR, and DNA sequencing.

Cells were grown to exponential phase for 36–48 h before imaging. Strains containing the Pnmt81-GFP-atb2 and Pnmt41-GFP-CHD constructs were shifted to EMM5S 15-18 h before imaging to allow expression of the construct. To depolymerize the microtubules, 50 µg/ml MBC (methyl-2-benzimidazole-carbamate) was added to the cells immediately before imaging (Sawin and Snaith, 2004; Castagnetti et al., 2010).

Spinning-disk confocal microscopy

Cells were grown to exponential phase at 25°C in YE5S-rich liquid medium in 50-ml baffled flasks in a shaking temperature-controlled incubator in the dark. Cells were concentrated 10- to 20-fold by centrifugation at 2400 × g for 30 s and then resuspended in EMM5S. Five microliters of cells were mounted on a thin gelatin pad consisting of 10 μl of 25% gelatin (Sigma Aldrich; G-2500) in EMM5S, sealed under a #1.5 coverslip with VALAP (1:1:1Vaseline:Lanolin:Parafin), and observed at 22°C.

Fluorescence micrographs of live cells were acquired with a Nikon Eclipse Ti microscope equipped with a 100×/numerical aperture (NA) 1.49 HP Apo TIRF objective (Nikon), a CSU-X1 (Yokogawa) confocal spinning-disk system, 488-/561-nm solid state lasers, and an electron-multiplying cooled charge-coupled device camera (EMCCD IXon 897, Andor Technology). The Nikon Element software was used for acquisition. Cells were imaged at a low laser power (16.1 µW at the objective for the 488-nm laser; 17.8 µW at the objective for the 561-nm laser) and a 19-z image (6.48 µm total range) was acquired either every minute or every 10 s for 2 h, depending on the dataset. To determine whether our imaging setup impacted microtubule dynamics, we analyzed the number of contacts made by interphase microtubules with the cell ends in cells expressing GFP-Atb2p imaged under the same conditions as used for the nuclear positioning analysis (described above). The average number of microtubules contacts in the first 10 min of a 2-h video was 7.8 ± 2.1 (n = 20 cells), while the average number of microtubule contacts in the last 10 min of the same video was 7.5 ± 2.2 (n = 20 cells). This difference was not significant, according to a Student’s t test (p = 0.6570). Therefore, the acquisition setting used in our work appeared to have no measurable impact on microtubule dynamics, based on this test.

ImageJ (Schneider et al., 2012) was used for all image visualization and analyses. Images in the figures are maximum-intensity projections of z-sections spaced at 0.36 μm. Images were systematically contrasted to provide the best visualization, and images within the same figure panel were contrasted using the same settings.

Image analyses

The relative position of the nucleus (Figure 1B and 3B and Supplemental Figure 4A) was calculated by measuring the length of the cell compartment the nucleus inhabited (L_C) and the distance of the center of the nucleus from the cell end (L_E). The distance D₁ from the cell end to the proximal edge of the nucleus was measured using the line tool in Fiji. Similarly, we measured the distance D₂ from the cell end to the distal edge of the nucleus. We calculated the distance of the center of the nucleus using the formula ([D₂ – D₁]/2)+D₁. The radius of each nucleus (R_N) was assumed to be roughly 1 μm (diameter, 2R_N, of 2 μm) based on our measurements in wild-type cells. As the center of the nucleus cannot occupy either the very cell tip or the center of the contractile ring, we calculated the travelable distance as the diameter (2R_N) of the nucleus subtracted from the cell compartment length. Using this travelable distance, these values were then normalized so that a value of 0.00 represented the closest a nucleus could get to the end, while 1.00 represented the closest a nucleus could get to the contractile ring. This was calculated for each value with the following formula:

Cells expressing mEGFP-Myo2p Cut11p-tdTomato were used to calculate the relative position of the nucleus for all time points including and before 10 min after septation, while cells expressing GFP-CHD Cut11p-tdTomato were used to calculate the relative position of the nucleus for all time points occurring later than 10 min after septation.

Timing of microtubule events (Figure 2E) was measured by noting the camera frames when the spindle appeared (t = 0), the spindle reached the cell ends, the spindle broke down, the ePAA appeared, the lPAA appeared, the preinterphase microtubules appeared, and the mSPB microtubules appeared. The spindle was considered fully elongated when the ends of the spindle no longer progressed toward the cell end. The spindle was considered broken down when it was no longer a continuous single entity after the completion of spindle elongation.

The timing of events associated with the nucleus (Figure 2F) was measured by noting the first camera frames when the nucleus reached the cell end, the SPB faced the cell end, SPB rotation was complete, and the displacement of the nucleus after spindle disassembly was complete. Time zero, spindle appearance.

Contractile ring timing (Figure 2F) was measured by noting the camera frame when the spindle pole bodies separated (t = 0) and the contractile ring disassembled. SPB separation was defined as the time when the spindle pole bodies were first distinguishable as two objects. Completion of contractile ring disassembly was defined as the time when the signal from the constricting contractile ring was no longer visible at the end of constriction. All timing data were visualized using an outcomes plot (aka Kaplan–Meier or cumulative distribution function plot) to display the “time-to-event” data as a percentage of the cell population in the relevant section of our methods. A timeline diagram showing the timing of the events used as time zero is included in Supplemental Figure 4E.

To track the position of the nucleus (Figure 3C), the coordinates of the position of the end of the nucleus closest to the contractile ring were measured every minute from the time that the nucleus reached the cell end until the end of ring disassembly. From these measurements, the displacement velocity (Supplemental Figure 2) was calculated by taking the change in position from the start of displacement to the end of displacement and dividing this value by the duration of displacement. All nuclear velocities measured were mean velocities (∆x/∆t for duration of the displacement) except for the proof-of-principle experiment, which compared the peak nuclear displacement velocity reported previously (Tran et al., 2001; Daga and Chang, 2005; Tolic-Norrelykke et al., 2005).

The position of the SPB over time during reorientation (Figure 4C) was tracked using the TrackMate plugin in FIJI (Tinevez et al., 2017). The coordinates of the traces were corrected for the vertical change in position of the nucleus at each time point to account for the displacement away from the cell end that the nucleus undergoes after spindle disassembly.

The extent of SPB rotation (Figure 4D) was calculated by determining whether the SPB rotated from facing the cell end at time of spindle disassembly to occupying the hemisphere of the nucleus facing the contractile ring before completion of septation.

The interactions of the lPAA microtubule +tips with the nucleus (Figure 5, F and G) were measured by merging channels containing the Cut11p-tdTomato and the GFP-Atb2p (or Mal3-mEGFP) markers. After spindle disassembly but before septation, the number of times GFP-Atb2p colocalized with the Cut11p-tdTomato marker was measured every 60 s. The duration of each colocalization event was also measured to determine how stable these interactions were.

To generate traces of the position of the proximal end of the mSPB microtubules over time (Figure 5H), the coordinates of the position of the proximal ends of the mSPB microtubules were determined every minute from the time of appearance to ring disassembly. We then calculated the percentage of contacts with the hemispherical cell end (within 1 µm of the cell end) and the lateral (> 1 µm away from the cell end) portion of the cell edge for the first and second halves of all the contacts.

The elongation and shrinkage velocities of the lPAA microtubules were calculated by dividing the change in position of the lPAA microtubules from the beginning to the end of elongation or shrinkage by the duration of either elongation or shrinkage.

SEM was reported when our conclusions depended on interpreting the average value of a dataset over time and therefore needed a readout of the error associated with that mean. SD was used in all other situations.

The alpha value for all statistical tests was 0.05; that is, we consider p < 0.05 a statistically significant difference.

Computer simulations

Simulations were run using the CytoSim platform (Nédélec and Foethke, 2007), a Brownian dynamics simulator where each component of the cytoskeleton is represented as an individual object with associated physical and interactive properties and subjected to thermal fluctuations. The configuration file from Foethke et al. (2009) was modified to allow for asymmetric cell growth (see config.cym file; Foethke et al., 2009). The 2009 platform, with hemispherical cell ends, does not allow for asymmetric cell growth. To overcome this challenge, we simulated the cell as a long cylinder with two large beads to either side of the cell to demarcate the cell ends. The beads were 100 μm in radius and had a viscosity of 10,000 pN s/µm², so that the force exerted by the microtubules did not push the cell ends. In simulations where growth was considered, the bead representing the old end was moved at a rate of 0.024 μm/min after 10 min of simulation time (OETO), and the new end moved in the opposite direction at a rate of 0.024 μm/min after 60 min (NETO) of simulation time, to reflect our experimental measurements in wild-type cells. At each timepoint in the simulation, we extracted the positions of the old end, the new end, the center of the nucleus, and the +ends of the interphase microtubules. The +tips of the microtubules were considered to contact the cell ends if they came within 0.1 µm of the beads. Significance in the difference of final nuclear position at 30-40 min after start of the simulation between the types of simulations was calculated using Tukey’s HSD. All parameters used in the configuration file are listed in Supplemental Table 2.

All simulations start with de novo microtubule polymerization from sites around the nuclear envelope. This initial growth resulted in the initial 80-s profile of nuclear displacement visible in all simulations. All nuclear displacement traces (Figure 7, A–D) show the position of the center of the nucleus from the proximal cell end over time. The relative position of the nucleus was calculated as previously described for experimental data acquired in live cells (see above). To calculate the peak velocity, we measured the change in position over time during the period of fastest movement at the beginning of displacement using the average of the displacement traces from all simulations within a dataset (Figure 6A). To calculate the average velocity, we measured the change in the position over time during the entire period of nuclear movement using the average of the displacement traces from all simulations within a dataset (Figure 6A). To calculate ∆t_d-p, we measured the time required for either the proximal or distal end of the microtubules to reach the proximal (∆t_p) or distal end (∆t_d) of the cell, respectively; we then subtracted ∆t_p from ∆t_d to determine the additional time needed to reach the distal end (Figure 6, B and C). To calculate ∆c_{p-d, we} measured the total number of microtubules contacts at either the proximal (∆c_p) or distal end (∆c_d) of the cell during the period before the nucleus reached a stable position within the cell (first 20 min of simulation). We then subtracted ∆c_d from ∆c_p to determine the additional contacts present at the proximal end. We were interested in ∆c_p-d only during the period of nuclear displacement, as this is when presence of a net pushing force would be most meaningful.

Abbreviations used:

eMOTC

equatorial microtubule organizing centers

ePAA

equatorial post-anaphase array

lPAA

longitudinal post-anaphase array

MBC

carbendazim

mSPB

mitotic spindle pole body

PAA

post-anaphase array

SPB

spindle pole body

Tukey’s HSD

Tukey’s Honestly Significant Difference