Abstract
Free energy simulations that employ combined quantum mechanical and molecular mechanical (QM/MM) potentials at ab initio QM (AI) levels are computationally highly demanding. Here, we present a machine-learning-facilitated approach for obtaining AI/MM-quality free energy profiles at the cost of efficient semiempirical QM/MM (SE/MM) methods. Specifically, we use Gaussian process regression (GPR) to learn the potential energy corrections needed for an SE/MM level to match an AI/MM target along the minimum free energy path (MFEP). Force modification using gradients of the GPR potential allows us to improve configurational sampling and update the MFEP. To adaptively train our model, we further employ the sparse variational GP (SVGP) and streaming sparse GPR (SSGPR) methods, which efficiently incorporate previous sample information without significantly increasing the training data size. We applied the QM-(SS)GPR/MM method to the solution-phase SN2 Menshutkin reaction, , using AM1/MM and B3LYP/6-31+G(d,p)/MM as the base and target levels, respectively. For 4000 configurations sampled along the MFEP, the iteratively optimized AM1-SSGPR-4/MM model reduces the energy error in AM1/MM from 18.2 to 4.4 kcal/mol. Although not explicitly fitting forces, our method also reduces the key internal force errors from 25.5 to 11.1 kcal/mol/ and from 30.2 to 10.3 kcal/mol/ for the N–C and C–Cl bonds, respectively. Compared to the uncorrected simulations, the AM1-SSGPR-4/MM method lowers the predicted free energy barrier from 28.7 to 11.7 kcal/mol and decreases the reaction free energy from −12.4 to −41.9 kcal/mol, bringing these results into closer agreement with their AI/MM and experimental benchmarks.
I. INTRODUCTION
Accurate free energy profile simulation, which is critical for understanding many chemical and biochemical processes,1 requires proper descriptions of the potential energy surfaces (PESs) of the system. Classical (nonreactive) force fields cannot be directly used to model chemical reactions because they lack proper PES descriptions of bond dissociation/formation processes, for which quantum mechanical methods are needed to characterize the associated changes in electronic structures. In condensed phases, these processes are often simulated by combined quantum mechanical and molecular mechanical (QM/MM) methods,2–7 with which a small-sized, electronically reactive subsystem is modeled using quantum mechanics, whereas the surrounding nonreactive environment is modeled using molecular mechanics. High-quality, ab initio (AI) PES descriptions of the QM region are generally accurate and reliable, but they are usually computationally too time-consuming to obtain. This puts a limitation on the use of AI/MM methods in molecular dynamics (MD)-based free energy simulations, for which significant amounts of phase space sampling are needed to obtain statistically robust free energy profile along the reaction coordinate. By contrast, semiempirical (SE) methods, including molecular orbital (MO) methods based on the neglect of diatomic differential overlap (NDDO) approximation, such as MNDO,8 AM1,9 and PM3,10 and approximate density functional theory (DFT) methods such as the self-consistent-charge density-functional tight-binding (SCC-DFTB) method,11–13 offer efficient PES alternatives to render sufficient sampling affordable, but they usually sacrifice accuracy for speed.
How to combine the accuracy of AI/MM methods and the efficiency of SE/MM methods has therefore posed a significant challenge (and opportunity) in QM/MM free energy simulations. One way to accomplish this is through indirect free energy simulations. Specifically, one carries out free energy perturbation (FEP), in which a correction term is applied to the SE/MM-generated free energy profile using Zwanzig’s exponential average formula based on the single-point energy differences calculated at the respective levels of theory.14 In practice, the accuracy of this treatment, however, strongly depends on the degree of phase-space overlap between the SE/MM and AI/MM Hamiltonians involved. A poor overlap of the two Hamiltonians would hinder the numerical convergence of FEP calculations and limit the accuracy of computed free energies.15,16
An alternative dual-level QM/MM free energy simulation strategy is the reaction path force matching (RP-FM) method.17–19 Through using force as the central bridging quantity, RP-FM and related methods forge direct links between the SE/MM and AI/MM levels by connecting their dynamics, free energies, and phase-space distributions.17–20 RP-FM has previously been used to improve QM/MM free energy results by either fitting Cartesian forces through optimization of SE parameters17 or by fitting reactive internal forces in collective variables (CVs).18 Combined with the weighted thermodynamics perturbation (wTP) method, RP-FM-based SE potential recalibration has proved to be effective in improving the phase-space overlap for dual-level QM/MM FEP calculations.19 A common theme in these FM developments is that they all fit high-level potentials (although implicitly) through some physics-based quantities such as electronic-structure parameters and free energy mean force, whose connections to the potential energy function can be computationally inconvenient to handle. As the complexity of the system increases, a general-purpose mathematics-function-based potential fitting tool may become more desirable.
To this end, several groups have employed delta (Δ) machine learning (ML) potentials, primarily based on neural networks (NN), as a means to directly correct SE/MM potential energy for improved QM/MM simulations.21–25 Despite the overall similarity in the Δ-learning theme following the work of Ramakrishan et al.,26 these works differ in their choice of base levels, NN potentials’ descriptors and topological features, and loss function construction. Building on their earlier work using NN potentials for free energy perturbation,27 Yang and co-workers have developed a method for training artificial neural networks (ANN) to correct DFTB/MM to the DFT/MM level using energy-only-based loss functions during MD simulations.21 Although forces are not directly used in training, the nuclear gradients associated with the NN-predicted energy corrections are incorporated to obtain modified molecular dynamics.21 Since force matching (FM) can greatly improve the phase-space overlap involved and therefore the quality of dynamics,17,19 it is generally desirable to include forces directly in the loss function when training the NN potentials.22–25 For example, Böselt et al.22 used symmetry-function descriptors as input features to train their high-dimensional neural network potentials (HDNNP), based on both energy and forces, for predicting corrections for DFTB/MM in simulating stable and transition-state species in solution. Pan et al. used FM-recalibrated SE method to ensure that the training configurations are sampled in the relevant phase space.23 Based on the DeepPot-SE28 and the DeepMD framework,29,30 their ML model uses an embedding network to encode input features and incorporates both energy and force differences into the loss function to ensure accurate dynamics for MD-based free energy simulations of solution-phase and enzyme reactions.23 Other recent QM/MM developments utilizing DeepPot and local environment descriptors include the range-corrected deep learning scheme of Zeng et al.24 and the DFTB/MM-based ML model of Gomez-Flores et al.25 One notable issue with conventional NN potentials is that they generally do not provide a metric to assess the uncertainties in energy and force predictions. For MD-based QM/MM simulations, in particular, free energy path simulations, this poses a question on how to maintain the robustness of NN models when the trajectories sampled on the NN-predicted PES deviate from the original training configuration space. Although active-learning-based models can be used to adaptively expand the training set,21 the lack of uncertainty analysis capability makes the identification of underrepresented training regions a challenging task without actually encountering a failure of simulation. On the other hand, the novel use of committee-based multiple-NN strategy,31–34 Bayesian NN,35,36 or dropout NN37 can help detect untrustable predictions on the fly during MD simulations, but it can increase the inference cost.
As an alternative ML approach to NN, Gaussian process regression (GPR) can produce well-calibrated prediction uncertainty through predictive variance.38,39 GPR models have been used in computational chemistry for various applications, including generating force fields,40–42 enabling fast and accurate geometry optimization,43–47 improving weighted free energy perturbation results,48 obtaining AI-quality potential energy landscapes,49–51 and making improvements to dynamics.49 GPR-produced PESs have been demonstrated to outperform those constructed using ANNs.52 Additionally, GPR models outperform NN variants in uncertain estimates for predicting adsorption energies.53 However, there are few cases of QM/MM implementation that enable GPR to be used directly for MD-based free energy simulations, which is the focus of the present study.
In this work, we match the SE/MM potential of the system with the target AI/MM potential using a GPR-predicted molecular energy correction term. While several studies utilize Δ-ML potentials as atom-based energy corrections,21,23,25,32 thereby preserving permutational invariance, the objective of this work is to train and deploy a system-specific model for condensed-phase QM/MM simulations along a well-defined free energy path. In this scenario, molecular configurations involving permutations of identical atoms are of lesser concern; therefore, permutational invariance is not strictly enforced here. We have found that the direct prediction of molecular energy corrections is sufficient for the purpose of this work. The training of the GPR models is done based on ensembles of dynamical configurations sampled initially along the SE/MM free energy path and later along the GPR-corrected ones. Specifically, we use the string method in collective variables54,55 (see Ref. 55 for the details of our string implementation) to determine the minimum free energy path (MFEP) through iterative path updates. Incorporation of the GPR-associated nuclear gradients on the geometric input features enables us to perform MD simulations for updating free energy sampling and obtaining the GPR-modified MFEP. Since GPR by nature has a predictive uncertainty, the relationship of the sample input space to the training set can be assessed, which is a significant benefit for dynamics simulations as the configurations sampled along the updated MFEP may differ significantly from the ones used for training the original model. To accommodate the possible shift in MFEP during this learning–relearning process, we employ two sparse GPR models to efficiently incorporate the previous training data when updating our model iteratively for predictions in the new input space.
To demonstrate its effectiveness, we applied the QM-GPR/MM method to free energy simulations of the Menshutkin reaction in aqueous solution. The rest of the paper is organized as follows: In Sec. II, we briefly describe the GPR model and its sparse variants as well as the associated gradient formalism. The computational details of the simulations are provided in Sec. III. We present the results in Sec. IV. The outlook of the method is further discussed in Sec. V. Concluding remarks are given in Sec. VI.
II. METHODS
A. Gaussian process regression
GPR defines a distribution of functions relating a set of input space X, composed of n input vectors x, to a set of n observations y. Any observation y in the set y occurring at the input vector x, composed of m input features [x1, …, xm], in set X can be linked to the input space through an underlying function, f(x), where y = f(x) + ɛ, and ɛ is an observational noise that separates the function value from the observation. The values of ɛ follow a Gaussian distribution centered at zero whose variance is determined by a noise parameter , i.e., (0, ). The prior distribution of the underlying functions, denoted f(X), follows a Gaussian distribution,
| (1) |
where 0 is the mean of the functions and is the covariance kernel matrix of the training dataset based on a given covariance kernel function k that defines the similarity between the two input vectors involved,39
| (2) |
In this study, a radial basis function (RBF) is used as the covariance kernel function k,
| (3) |
where is the vertical variation parameter, l is the length parameter, and d(xi, xj) is the Euclidean distance between the two input vectors xi and xj. To account for noise in the observations, the noise parameter in the form of is added to the covariance kernel matrix of the training data, which modifies the covariance kernel matrix to
| (4) |
where I is the identity matrix.39 Here, , l, and collectively form a set of hyperparameters, θ, that are optimized by maximizing the log marginal likelihood of the data,
| (5) |
where p(y|X, θ) is the probability of y given X and θ. The GP prior distribution can then be used to make a set of predictions, f*, given a set of new input vectors, X*, following the joint distribution,
| (6) |
where K** = K(X*, X*), K* = K(X*,X), and is the transpose of K*, and it is thus K(X, X*). The posterior predictive distribution is then given by
| (7) |
The mean, μ*, and variance, V*, of the posterior predictive distribution of X* are found as follows:
| (8) |
| (9) |
B. Model implementation
Let UAI∕MM and USE/MM denote the potential energies for a given configuration determined at the AI/MM and SE/MM levels, respectively; in practice, they are shifted with respect to the corresponding zero of energy at each level for numerical convenience. Then, the energy gap ΔU between the two levels can be written as
| (10) |
In our GPR model, a collection of ΔU obtained for n configurations forms the training set of observations y,
| (11) |
A similar collection of m-dimensional input feature vectors for each of the n configurations forms the GPR input space in the matrix form . In the present study, we focus on the input features that are specifically based on the interatomic distances within the solute. To convert the interatomic distances to a generic form for GPR input, a preprocessing normalization step is first applied,
| (12) |
where xj,k represents the standardized unitless input feature j for configuration k, and rj,k is the jth distance for configuration k; and sj are the average and standard deviation, respectively, of the jth distances for all n configurations in the training set.
C. GPR gradient
During MD simulations, our GPR model is used to predict ΔU based on the configuration of the solute in the form of x*. The mean of the predictive distribution, μ*, is added to USE/MM. To be consistent with the updated energy during dynamics, the force applied to each atom, expressed as the negative gradient of the potential energy with respect to the atomic coordinates, must be updated accordingly. For each input feature of GPR, the associated force modification on atom c in the Cartesian direction q is given by
| (13) |
where x*,j is the jth input feature of x*, rj is the jth interatomic distance, and qc is the Cartesian variable x, y, or z onto which the force correction to atom c is applied. The first partial derivative term in Eq. (13), , is obtained by differentiating Eq. (8),
| (14) |
where
| (15) |
Where and I is a n × n unit matrix. The second term in Eq. (13) can be obtained by differentiating Eq. (12),
| (16) |
The third partial derivative term in Eq. (13) concerns the dependence of interatomic distances on the atomic Cartesian coordinates involved, which can be obtained in a straightforward manner,
| (17) |
where qc and qd are the atomic Cartesian involved in the interatomic distance rj.
D. Sparse GPR variants for adaptive MFEP optimization
With the GPR gradient available, the QM-GPR/MM model can be used in MD-based free energy path simulations to update the MFEP. When the configurations sampled along the GPR-modified MFEP significantly differ from the ones used to train the original model, the GPR model itself needs to be updated adaptively to incorporate information learned from the new samples. Although this can be done intuitively by merging the old and new samples into an expanded training set and then retraining the GPR model, the scalability of the GPR algorithm with respect to data size makes such a brute-force treatment quickly out of reach.
To achieve a data-efficient relearning process for adaptive MFEP optimization, we employ two sparse variants of the GPR model. First, we reduce the training data size for learning along a single MFEP by introducing a set of inducing points using the sparse variational GP (SVGP) model (Appendix A). Second, for retraining the model using sample information from multiple MFEPs, we use the streaming sparse GPR (SSGPR) model (Appendix B), a variant based on SVGP, to enable adaptive model update in the combined input space without significantly increasing the training data size. For the interested readers, the technical details of these sparse GPR variants as well as the necessary modifications for implementing their nuclear gradients can be found in Appendixes A and B.
III. COMPUTATIONAL DETAILS
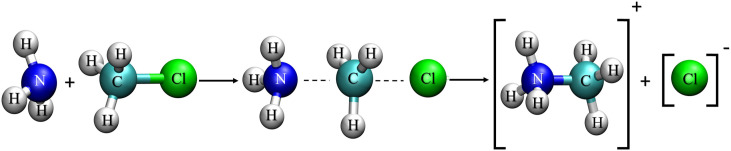
To test the performance of the QM-GPR/MM method, we applied it to free energy simulations of the solution-phase Menshutkin reaction ,56 which involves a nucleophilic attack of ammonia on methyl chloride following an associative SN2 mechanism (Fig. 1). This reaction has served as an important paradigm for developing accurate and efficient potential energy methods and solvation models (see our recent work18 and references therein for a brief review of the QM/MM methods developed for simulating this system).
FIG. 1.
Menshutkin reaction between ammonia and methyl chloride.
At the SE/MM level, we treat the solute molecules by AM19 using the MNDO97 package57 incorporated in Chemistry at HARvard Macromolecular Mechanics (CHARMM),58 whereas the solvent environment is modeled by a 40 × 40 × 40 Å3 box of modified TIP3P59 water molecules under periodic boundary conditions. The nonbonded QM/MM van der Waals (vdW) parameters were initially assigned based on the related atom types in the CHARMM22 force field60 during setup and later replaced by the pair-specific vdW parameters optimized by Gao and Xia61 in the actual simulations. Long-range electrostatics is treated by the particle mesh Ewald (PME)62 and QM/MM-Ewald63 methods for the MM-MM and QM-MM interactions, respectively. The MFEPs and associated free energy profiles were determined by using the string method in CVs.54 For the Menshutkin reaction, we represent the MFEP by two CVs: the forming bond distance, rN−C, and the breaking bond distance, rC−Cl. The initial string path and configurations along it were obtained from a potential energy scan along the one-dimensional reaction coordinate rC−Cl–rN−C at the AM1/MM level. The MFEPs were optimized iteratively by the string method for 10 cycles, in each of which 20 ps MD sampling was used for evaluating the free energy mean forces on the CVs in each of 20 images evenly spaced along the string. For additional details of the MD simulations and string optimization protocols, see our previously published work.18,55
Based on the configurations sampled along the AM1/MM MFEP, AI/MM single-point energy calculations were performed at the B3LYP64–66/6-31+G(d,p)67/MM level using the Gaussian16 program68 interfaced with CHARMM. To generate our testing set, we collected configurations every 100 fs from 20 ps of MD trajectories for each of the 20 images along the MFEP, which gives a training set of 4000 configurations. For GPR training, we draw one in every five of these configurations (i.e., 1 configuration every 500 fs) to build a training set of 800 configurations. For the same set of configurations, AM1/MM single-point energies were retrieved from the MNDO97/CHARMM interface. These single-point energies were then used to determine the energy gaps between the two levels involved, i.e., ΔU = UB3LYP/6−31+G(d,p)/MM − UAM1/MM, as defined in Eq. (10) and used in Eq. (11), for which the training sample size n = 800.
The GPR model was generated and optimized using the Scikit-learn package.69 The SVGP model was generated using the SGPR module in the GPflow 2.0 package.70 The SSGPR models were constructed using the code from the work of Bui et al.,71 updated for compatibility with GPflow 2.042 and TensorFlow 2.0.72,73 Conveniently, Bui and colleagues recently updated their code for compatibility with the updated version of GPflow and TensorFlow, accessible to the reader at Ref. 74. The SVGP and SSGPR models were optimized with respect to their hyperparameters using the ADAM optimizer75 implemented in TensorFlow 2.0.
The optimized GPR, SVGP, and SSGPR models were implemented in CHARMM through its USER module, which enables predictions of energy corrections along MD simulations. The mean of the predictive distribution of ΔU for a given MD configuration was added to the SE/MM energy to acquire the total energy for SE-GPR/MM as well as for its sparse variants. The nuclear gradients were modified by distributing the associated force corrections according to Eq. (13) or its sparse versions based on Eqs. (A5) and (B4).
IV. RESULTS
A. AM1/MM free energy profile
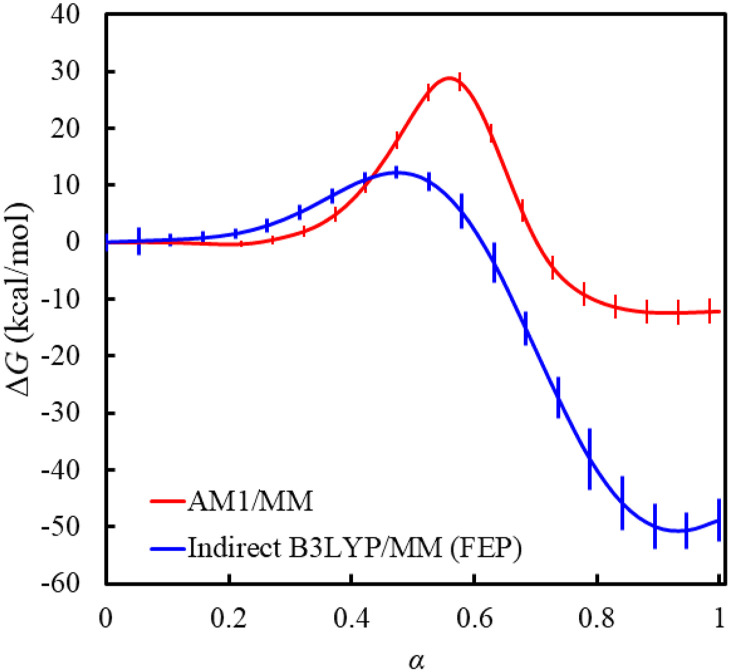
Using the AM1/MM Hamiltonian, we obtained a free energy profile that gives a reaction free energy of −12.4 kcal/mol and a free energy barrier of 28.7 kcal/mol for the Menshutkin reaction (Fig. 2). Compared with the experimentally derived reaction free energy of −34 ± 10 kcal/mol reported by Gao76 or −36 ± 6 kcal/mol reported in the work of Su et al.,77 AM1/MM underestimates the exergonicity of the Menshutkin reaction by 21.6–23.6 kcal/mol. Although no experimental barrier is available for this reaction, the reaction between NH3 + CH3I, which gives a free energy barrier of 23.5 kcal/mol,78 has been previously used as a point of comparison.76,79,80 Compared with this best experimental estimate, AM1/MM overestimates the free energy barrier by 5.2 kcal/mol.
FIG. 2.
AM1/MM and indirect B3LYP/MM free energy profiles for the Menshutkin reaction. The AM1/MM free energy profile was obtained along the string MFEP determined at the same level (with α = 0 for reactant and 1 for product). The indirect free energy profile was obtained by free energy perturbation (FEP) from the AM1/MM to the B3LYP/6-31+G(d,p)/MM level based on the configurations sampled along the AM1/MM MFEP. Even with AI/MM-based free energy corrections, the indirect FEP results still do not adequately reproduce the experimental results. Details on the calculations of the error bars can be found in the supplementary material, Sec. S4.
B. Potential energy gap
Since the AM1/MM free energy profile displays significant discrepancies from experiment, we performed free energy perturbation (FEP) calculations along the AM1/MM free energy path to see if indirect DFT/MM calculations can help improve the results. Unfortunately, FEP on its own, based on the potential energy differences between the AM1/MM and B3LYP/6-31+G(d,p)/MM levels, does not produce a high-quality free energy profile; instead, it generates a free energy barrier of 12.2 kcal/mol and a reaction free energy of −50.7 kcal/mol, both too low compared with experiment (Fig. 2). The modest performance of a simple FEP correction in this case is likely caused by a slow convergence of the results when using inadequate sample size81,82 as well as possible systematic biases linked to poor overlap between the important phase space sampled at the base and target levels.83–85 At the limited sampling performed at AM1/MM, the average standard deviation of the relative energy difference distribution is 3.7 kcal/mol, well exceeding the recommended limits of 1.7 kcal/mol82 for fine results or 2.4 kcal/mol86 for crude results. Furthermore, the failure for our samples to meet the bias metric criterion of Π > 0.5 introduced by Wu and Kofke84,85,87 suggests significant differences in the configurations sampled on the AM1/MM and B3LYP/6-31+G(d,p)/MM PESs; see the supplementary material, Sec. S1. Although indirect FEP calculations can be accelerated when combined with ML approaches,27,88 the issues we identified here collectively highlight the need for a free energy method that directly samples the AI/MM-quality PES.
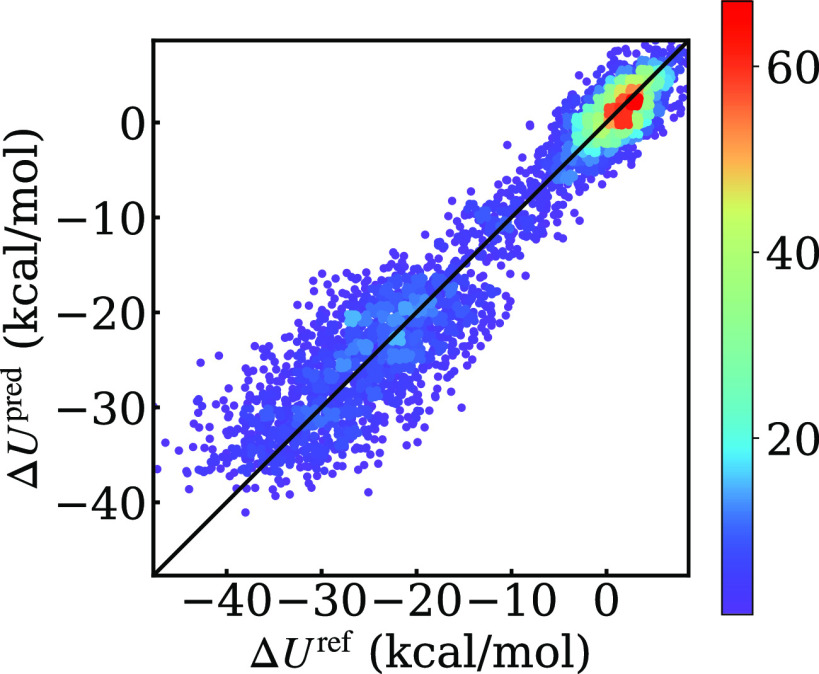
The energy corrections predicted by our GPR model are compared with their reference values in Fig. 3. The root-mean-square errors (RMSEs) of the GPR-predicted energy gaps are 3.1 and 3.7 kcal/mol for the training and testing sets, respectively (Table I). Considering the magnitude of the energy gap as well as its nonuniform distribution along the reaction coordinate, we found this performance acceptable and comparable to that of other machine learning models; see the supplementary material, Sec. S2. As we mentioned earlier in the indirect FEP results, the reference energy gaps along the AM1/MM MFEP display a significant average standard deviation of 3.7 kcal/mol, which suggests that the data are inherently noisy and therefore susceptible to prediction error. The mean of predictive variance, or equivalently the lower bound of the expected mean squared error,38,89,90 is 2.3 and 1.9 (kcal/mol)2 for the training and testing set, respectively. As explained in the supplementary material, Sec. S3, the predictive variance is used to calculate the 95% confidence interval as a measure of the uncertainty of prediction. The average 95% confidence intervals for energy predictions on the testing and training sets are 2.9 and 2.6 kcal/mol, respectively.
FIG. 3.
The GPR-predicted energy corrections (ΔUpred) plotted against the reference energy differences (ΔUref) between the AM1/MM and B3LYP/6-31+G(d,p)/MM levels for configurations sampled along the AM/MM MFEP. The color scale shows the number of configurations found in each region.
TABLE I.
Cross validations of the AM1-(SS)GPR/MM models in energy prediction.a
| Samples | AM1/MM | GPR | SSGPR-0b | SSGPR-1 | SSGPR-2 | SSGPR-3 | SSGPR-4 |
|---|---|---|---|---|---|---|---|
| AM1/MM | 18.2 | 3.7 ± 2.9 (3.1 ± 2.6) | 3.8 ± 3.4 (3.2 ± 3.3) | 3.9 ± 4.2 | 4.1 ± 4.7 | 4.4 ± 5.2 | 4.8 ± 5.8 |
| GPR | 18.2 | 11.6 ± 4.2 | 11.7 ± 3.4 | 12.1 ± 4.2 | 12.5 ± 4.7 | 12.8 ± 5.2 | 13.0 ± 5.8 |
| SSGPR-0 | 21.8 | 7.6 ± 3.7 | 7.1 ± 4.8 | 3.9 ± 3.6 (3.5 ± 3.5) | 3.9 ± 3.9 | 4.0 ± 4.3 | 4.3 ± 4.9 |
| SSGPR-1 | 22.9 | 4.9 ± 3.6 | 4.9 ± 4.3 | 4.9 ± 4.4 | 4.1 ± 3.7 (3.7 ± 3.6) | 4.0 ± 3.9 | 4.1 ± 4.4 |
| SSGPR-2 | 23.9 | 5.2 ± 3.6 | 5.3 ± 4.1 | 4.4 ± 4.0 | 4.5 ± 3.9 | 3.7 ± 3.7 (3.1 ± 3.6) | 3.8 ± 4.1 |
| SSGPR-3 | 23.5 | 5.6 ± 3.5 | 5.8 ± 4.0 | 4.6 ± 4.1 | 4.3 ± 4.1 | 4.6 ± 4.1 | 3.8 ± 4.1 (3.4 ± 4.0) |
| SSGPR-4 | 24.1 | 5.2 ± 2.9 | 5.4 ± 3.9 | 4.3 ± 4.0 | 4.0 ± 3.9 | 4.0 ± 4.0 | 4.4 ± 4.3 |
Root-mean-square errors (RMSEs) in energy prediction (in kcal/mol) are compared against the B3LYP/6-31+G(d,p)/MM benchmark; results for both the testing set and the training set (data in parenthesis) are given when applicable; values following ± correspond to the average 95% confidence interval of energy predictions.
The SVGP model is labeled as SSGPR-0.
Sampling the GPR-corrected potential (AM1-GPR/MM), the free energy path is updated. Because the new path evolves away from the AM1/MM path used for previous training, the GPR model becomes less accurate on the newly sampled configurations, with the RMSE in energy prediction increasing to 11.6 kcal/mol. The average predictive variance along the AM1-GPR/MM MFEP, which offers an assessment of prediction uncertainty in GPR, also increases to 2.3 (kcal/mol)2. Both of these results suggest changes in the sampled phase space and the necessity of retraining the model. Interestingly, the model seems to be more tolerant to such changes in terms of predictive variance than predictive error. Further analysis shows that the newly sampled configurations may not differ too much from those used for training the original model in the input feature space to perturb the prediction distribution (see Sec. S5 in the supplementary material), but the greater baseline errors in AM1/MM for the new samples can quickly worsen the overall RMSE of the GPR-corrected method in energy prediction. Nevertheless, we decided to retrain the model iteratively when updating MFEPs to prevent possible model deterioration.
Due to the matrix inversions involved, GPR does not scale well with training data size. Therefore, a simple retraining strategy by adding new data to the existing dataset could quickly become unmanageable. However, omission of previous samples in the retraining processes could result in model oscillations and divergent free energy results; see the supplementary material, Sec. S6. To address this problem, we first use the sparse variational GP (SVGP) method (Appendix A) to summarize the training set into a set of inducing points using an approximate kernel, which also reduces the memory requirement. The streaming sparse (SSGPR) method (Appendix B) is then used to further allow us to train a “synthesized” model on multiple sets of data from different MFEPs without significantly increasing the kernel’s dimensionality. By substituting the original GPR model with an SVGP model containing 50 inducing points, the RMSEs in energy prediction on the training and testing sets along AM1/MM MFEP increase slightly to 3.2 and 3.8 kcal/mol, respectively (Table I). Using the SVGP model (also referred to as SSGRP-0) as a starting point, the SSGPR-i (i = 1–4) models were trained iteratively until the MFEPs determined in successive iterations converge. Although unnecessary, in practice it can be advantageous to use more inducing points as the sampled input space evolves. For example, we found that increasing the number of inducing points to 200 yields improvements to the RMSE of the entire set of configurations (see, Sec. S7 in the supplementary material). To balance efficiency and accuracy, we added 50 more inducing points every iteration, which results in a use of 250 inducing points in the SSGPR-4 model. This procedure allows us to make predictions and evaluate uncertainties with greater confidence across all the relevant phase space sampled when the MFEP is gradually improved from the AM1/MM toward the DFT/MM level. The RMSE of the SSGPR-4 model in energy predictions for the original AM1/MM testing set is 4.8 kcal/mol. For the configurations sampled along the AM1-SSGPR-3/MM MFEP, based on which the SSGPR-4 model is trained, the RMSE of the model in energy prediction is reduced to 3.4 and 3.8 kcal/mol for the training and testing sets, respectively.
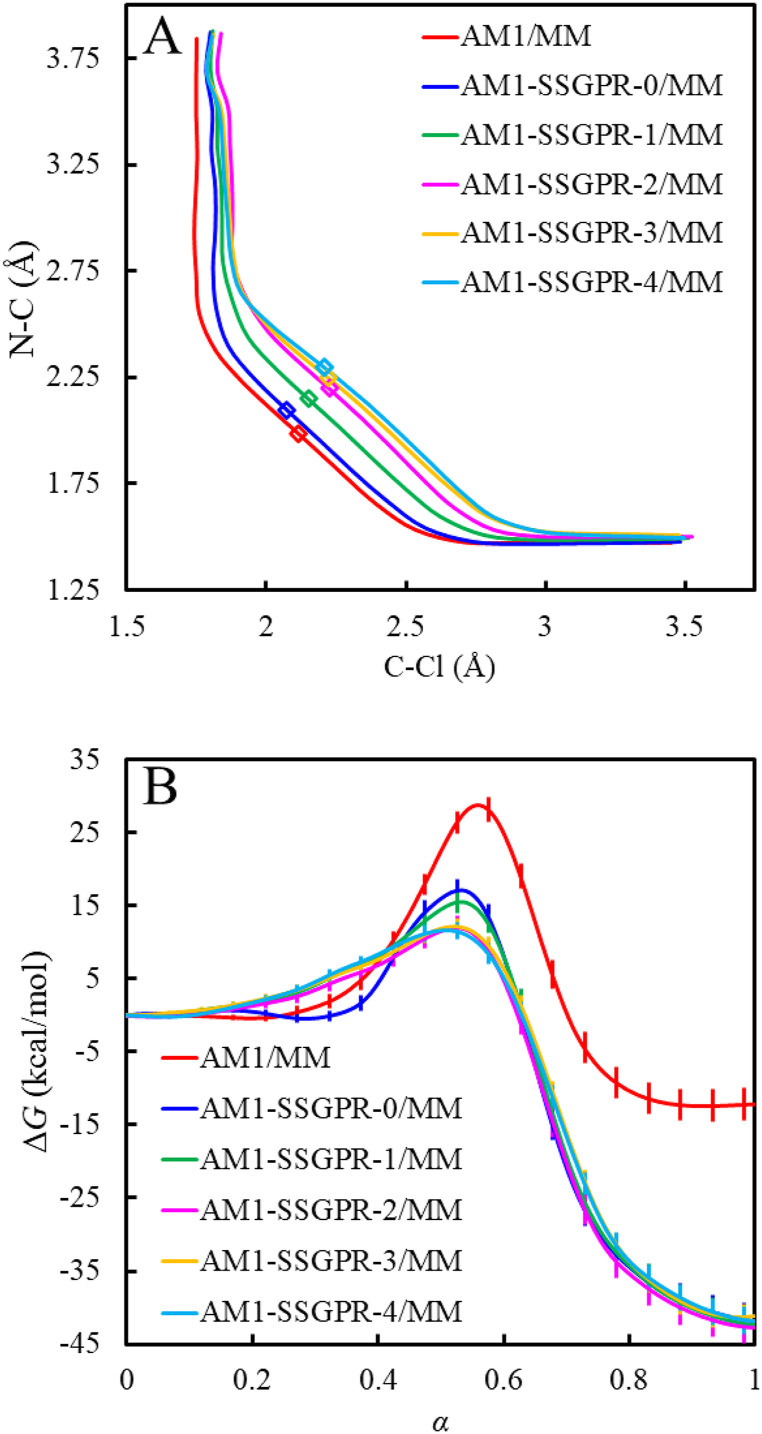
C. AM1-(SS)GPR/MM methods improve free energy profiles and MFEPs
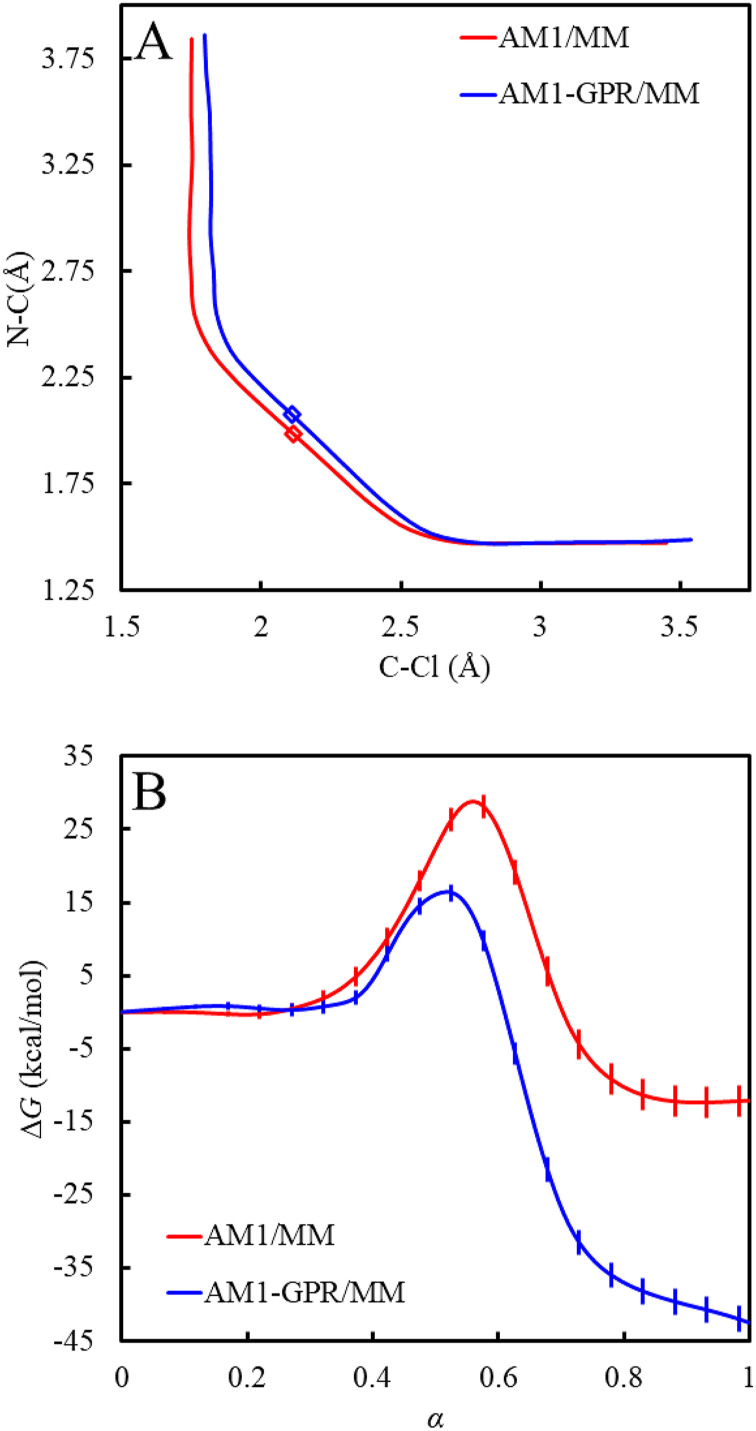
For the Menshutkin reaction, the free energy profile simulated with the AM1-GPR/MM method produces a free energy barrier of 14.3 kcal/mol and a reaction free energy of −44.9 kcal/mol (Fig. 4). The AM1-SVGP/MM method (i.e., AM1-SSGPR-0/MM) yields comparable results with a free energy barrier of 17.1 kcal/mol and a reaction free energy of −41.8 kcal/mol. The free energy profiles obtained by the AM1-SSGPR-i/MM methods converge to a reaction free energy of −41.9 kcal/mol and a free energy barrier of 11.7 kcal/mol (Fig. 5). Compared to a significant overestimate of −12.4 kcal/mol at the AM1/MM level, the reaction free energies predicted by these GPR-corrected methods are greatly improved to close agreements with the experimental values of −34 ± 1076 and −36 ± 6 kcal/mol.77 Although the simulated free energy barriers are still significantly lower than the best experimental estimate of 23.5 kcal/mol,78 the goal of our GPR-corrected methods is to reproduce the target-level AI/MM results. The B3LYP functional used here is known to underestimate the free energy barrier for the Menshutkin reaction, based on previous implicit solvation79 and multilevel QM/MM calculations.18,19 From this perspective, the free energy barrier of 14.3 kcal/mol from our AM1-GPR/MM simulations agrees well with the DFT/MM benchmark value of 15.3 ± 0.1 kcal/mol established in the work of Pan et al.19 from umbrella sampling simulations at the B3LYP/6-31G(d)/MM level and a value of 14.7 kcal/mol obtained in the work of Kim et al.18 through internal-force-matched RP-FM-CV simulations at the B3LYP/6-31+G(d,p):AM1/MM level. On the other hand, the free energy barrier of 11.7 kcal/mol converged from the iteratively optimized AM1-SSGPR-i/MM methods may represent a slight underestimate of the target value. Free energy perturbation was further performed on the AM1-SSGPR-4/MM free energy profile and no statistically significant changes were observed; see the supplementary material, Sec. S8.
FIG. 4.
(a) The AM1/MM and AM1-GPR/MM MFEPs. (b) The AM1/MM and AM1-GPR/MM free energy profiles.
FIG. 5.
(a) The AM1/MM and AM1-SSGPR/MM MFEPs. (b) The AM1/MM and AM1-SSGPR/MM free energy profiles.
The GPR-corrected methods also improve the free energy paths consistently by moving the original AM1/MM MFEP toward the concave side (Figs. 4 and 5). The free energy transition states determined at the AM1-GPR/MM and AM1-SSGPR/MM levels are looser than that obtained at the AM1/MM level. These results are in agreement with our observations in a previous RP-FM-CV study when the AI/MM-level internal forces were directly targeted.18
D. AM1-(SS)GPR/MM methods improve forces
The free energy forces used for string path optimization and the calculations of the free energy profile are estimated based on the fluctuations of the collective variables (CVs) under a set of harmonic restraints.54 For a restrained system whose statistics follows the Boltzmann–Gibbs distribution, such fluctuations are ultimately governed by the system’s potential energy.54 This indicates that correcting the potential energy of the system (e.g., with a GPR model) to the reference level of theory would improve both the string MFEP and the free energy profile accordingly. Using a different strategy, we recently showed that the high-level free energy profile can be restored through force matching (FM) on the CV degrees of freedom along the reaction path (RP-FM-CV),18 which is equivalent to fitting free energy mean force on the reaction coordinate. As both the SE-GPR/MM and RP-FM-CV approaches are able to reproduce the AI/MM-quality free energy profile, the connection between them needs to be established. Although SE-GPR/MM also modifies forces through nuclear gradients of the GPR energy correction term, it is unclear how these force modifications are distributed to various internal degrees of freedom that eventually lead to an improved MFEP. To examine whether forces are also improved along the reaction coordinate, we monitored the internal forces on the CVs before and after applying the GPR corrections, employing the redundant internal coordinate transformation framework we recently developed for RP-FM-CV.18
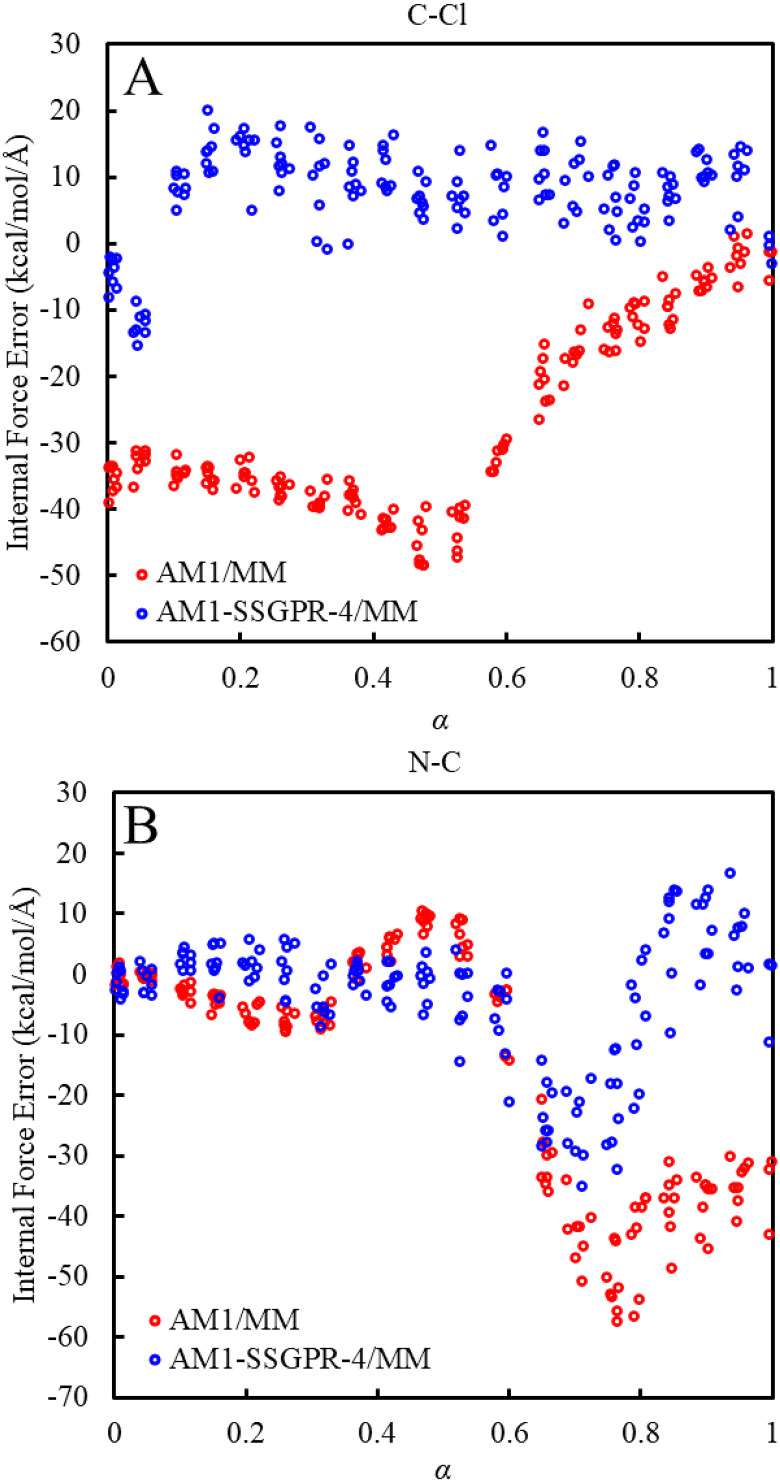
In Fig. 6, we compare the CV internal force errors of using AM1/MM and AM1-SSGPR-4/MM along the converged AM1-SSGPR-4/MM MFEP, with respect to the B3LYP/6-31+G(d,p)/MM benchmark. Unsurprisingly, the AM1-SSGPR-4/MM method based on the converged SSGPR-4 model offers an improved force description of the C–Cl bond nearly across the entire reaction coordinate. The RMSE in C–Cl force decreases from 30.2 to 10.3 kcal/mol/ after the SSGPR-4 corrections are applied to AM1/MM. Similar trends are found for the N–C bond, where the GPR corrections result in a near perfect description of its force in the reactant and transition state regions, and they significantly improve the AM1/MM description of the bond in the product region. The overall description of the N–C bond improves with an RMSE in force reduced from 25.5 to 11.1 kcal/mol/. The RMSE of Cartesian forces among all solute atoms drops from 14.6 to 12.1 kcal/mol/; for the atoms involved in the CVs, the Cartesian force error drops from 19.4 to 14.6 kcal/mol/; see the supplementary material, Sec. S9. These force results offer a possible explanation for the improved free energy profile. The greater force correction found on the C–Cl bond suggests its dominant role in improving the free energy profile. With the C–Cl force description improved, the AM1-SSGPR-4/MM free energy profile shows enhanced agreement with the AI/MM result. We performed a similar comparison for the AM1-GPR/MM method (see Sec. S10 in the supplementary material) but found that along the AM1-GPR/MM MFEP, the quality of both the internal and Cartesian forces deteriorates significantly, which highlights the need for an adaptive model. Regardless of the sampled path and model, the underlying shape of the force differences remains the same. The persistence of these trends in the force differences between the SE/MM and SE-GPR/MM models suggests certain limitations in the energy-based GPR model in terms of distributing the desired force corrections, perhaps due to the selected input features.
FIG. 6.
Internal force differences between the B3LYP/6-31+G(d,p)/MM and AM1-SSGPR-4/MM levels; the force differences on the C–Cl bond (a) and N–C bond (b) were evaluated based on configurations sampled along the AM1-SSGPR-4/MM MFEP.
E. Computational cost of AM1-SSGPR/MM methods
As mentioned in the Introduction, one objective of this work is to obtain AI/MM-quality free energy profiles at the reduced cost comparable to SE/MM simulations. In Table II, we present the wall times for a single-point energy-force calculation, a single MD step, and 20 ps MD sampling (at a timestep of 1 fs), using AM1/MM as the baseline method with and without the SSGRP-predicted corrections. We compare these times with the estimated cost required for completing a single iteration of string MFEP optimization using brute-force DFT/MM simulations. We found that, with only a modest increase in the computational cost relative to AM1/MM, the AM1-SSGPR/MM method can be used to efficiently perform free energy sampling on a timescale comparable to AM1/MM, resulting in a 100-fold speedup of the DFT/MM simulations at the B3LYP/6-31+G(d,p)/MM level. Even when utilizing 24 central processing units (CPUs), the parallel DFT/MM benchmark shown in Table II remains about 50 times slower than a serial AM1-SSGPR/MM calculation.
TABLE II.
Wall time comparison of using the AM1/MM, AM1-SSGPR/MM, and direct DFT/MM methods for simulating the Menshutkin reaction.
| Time per | |||||
|---|---|---|---|---|---|
| Method | CPUs | Energy and force evaluation (s) | Single MD step (s) | 20 ps MD (hr) | Total wall time for MFEPa (hr) |
| AM1/MM | 1 | 0.243 | 0.367 | 2.038 | 408 |
| AM1-SSGPR/MM | 1 | 0.253 | 0.378 | 2.100 | 420 |
| DFT/MMb | 1 | 26.037 | 39.056 | 216.975 | 43 395 |
| DFT/MMb | 24 | 11.888 | 17.832 | 99.069 | 19 814 |
Total wall time for one iteration of string MFEP optimization following the simulation procedures outlined in Sec. III.
At the B3LYP/6-31+G(d,p)/MM level.
V. DISCUSSION
The accuracy of potential energy description plays a critical role in the reliable determination of free energy profile. Motivated by its connection to the free energy perturbation strategy, here we have developed an energy-based GPR method that dynamically predicts the energy corrections needed for an SE/MM Hamiltonian to match a desired AI/MM target. The availability of nuclear gradients associated with the GPR energy correction also allows us to update forces accordingly to achieve improved molecular dynamics and free energy profiles.
An alternative approach would be to treat both energy and force as the GPR observations during model training. It has been suggested that including gradient information in training would improve the performance of ML potentials.91 For ANN-based models, this can be conveniently done by including the force-fitting errors in the loss functions. For GPR models, the gradient of the energy (negative force) needs to be included consistently in an extended set of observations. We have reported our force-extended GPR approach in a separate work,92 where we use GPR with derivative observations (GPRwDO) to simultaneously predict both QM/MM energy and force corrections. Although the GPRwDO approach significantly improves the description of Cartesian forces compared to an energy-only model, it does increase the computational complexity of model training from to and the memory complexity from to , when including d-dimensional derivative observations in each of the n training samples. This poses additional constraints on the training set size and the number of atoms to be considered for explicit force training. For the large number of nonreactive atoms in a QM/MM system, we may still need to rely on differentiating an energy-only model to obtain the related force corrections. Nevertheless, there are other ways to consider to alleviate this problem. For example, Bartok et al.49 incorporated derivative observation into their sparse GP models to improve algorithmic scaling. Alternatively, von Lilienfeld and co-workers developed the kernel-based operator quantum machine learning approach,93,94 which reduces both memory usage and computational complexity. Finally, Meyer and Hausser demonstrated a scheme where internal forces are fitted along with energy for geometry optimization.44
Interestingly, our recent force matching work (RP-FM-CV)18 showed that similar improvements in free energy results can be achieved by directly correcting the internal forces on the CVs without explicit energy correction. Although potential energy dictates the density of state, the dynamics of the system and its evolution are nevertheless determined by the forces on the atoms. Moreover, in the string free energy method we employed,54 potential energy is neither directly used in the MFEP optimization nor used in the determination of free energy profile. Under the RP-FM-CV framework, we attributed the success of our method to an effective fitting of the high-level free energy mean force, the integration of which along the reaction coordinate allows the associated potential of mean force to be faithfully reproduced.18
While direct learning in the force space is appealing, the use of energy-based GPR may offer a few advantages. As previously mentioned, one metric for assessing the degree of phase-space overlap is the distribution of relative energy differences between two levels of theory.82,86 This will permit easy assessment of phase-space overlap without the need for any AI/MM benchmark configurations. The energy-based GPR scheme also reduces the dimensionality of the output space, making prediction and evaluation of its quality less complex. The use of a single molecular energy correction, instead of atomic energies49 or atomic forces, would also reduce the risk of placing disproportionate weights on correcting the fast degrees of freedom, which may cause trajectory instability issues if not handled properly.95 Further investigation is needed to determine if a force-only-based GPR scheme would be sufficient and effective to achieve similar improvements for QM/MM free energy simulations.
In this proof-of-concept work, we use simple geometric features, such as pair-wise distances to describe the input space of the GPR models. Although the GPR-facilitated free energy profile of the Menshutkin reaction simulated in aqueous solution shows good agreement with the AI/MM benchmarks and experimental results, it could be more challenging to achieve similar performance for reactions in a more complex environment, such as an enzymatic reaction treated by QM/MM. The heterogeneity of enzyme active site would likely require additional descriptions of charge changes on the QM atoms, especially when the accuracy in QM/MM interactions plays a large role in the free energy profile. Since charge-dependent GPR gradients may not be straightforward to implement, it may be advantageous to use other features to represent the evolving QM/MM interactions. Descriptors such as atom-centered symmetry functions (ACSF),96 smooth overlap of atomic positions (SOAP),97 or density encoded canonically aligned fingerprint (DECAF)40 may be more applicable to modeling corrections in complex chemical environments. Notably, these atom-centered environment descriptors lend themselves to permutationally invariant models that predict atomic energy corrections. These advanced descriptors and an extension to the SSGPR model to account for permutational invariance will be examined in our future work.
VI. CONCLUDING REMARKS
In summary, we have presented a GPR-assisted dual-level QM/MM method for cost-effective free energy simulations of condensed-phase chemical reactions. Built upon an efficient SE/MM Hamiltonian, this method boosts its PES accuracy to an AI/MM quality by modeling the energy corrections needed through GPR-enabled stochastic inference. Incorporation of the forces associated with the GPR-predicted energy corrections allows for accurate determination and construction of MFEPs and free energy profiles from MD-based QM/MM simulations. Two data-efficient sparse GPR variants, i.e., SVGP and SSGPR, are further employed to facilitate the iterative updates of our model when the sample space evolves along with the MFEP that moves toward its AI/MM target. The great improvements seen in the free energy results for the solution-phase Menshutkin reaction demonstrate the effectiveness of this energy-based QM-(SS)GPR/MM method and suggest its general usefulness for studying reaction mechanisms in complex environments.
SUPPLEMENTARY MATERIAL
See the supplementary material for a description of the Wu and Kofke bias metric for the Menshutkin reaction, illustration of the reference and predicted energy gap along the reaction coordinate and a comparison of GPR prediction performance with existing ANN model in literature, comparison of predictive-variance-based uncertainty estimates, description of FEP calculations and error estimation of the string free energy profile, description of the discrepancy between rising error and stagnant variance in new phase space, demonstration of the model improvements with an increased number of inducing variables, FEP calculations on the AM1-SSGPR/MM converged MFEP, and Cartesian force improvements through energy corrections with the evolving models.
ACKNOWLEDGMENTS
This work was supported by a Research Support Funds Grant (RSFG) from IUPUI, and Grant Nos. R15-GM116057 (J.P.) and R01-GM135392 (Y.S. and J.P.) from the U.S. National Institutes of Health (NIH). The authors thank the Indiana University Pervasive Technology Institute (IU PTI) for providing supercomputing and visualization resources on BigRed3 and Carbonate DL/GPU that have contributed to the research results reported within this paper. This research was supported in part by Lilly Endowment, Inc., through its support for IU PTI.
APPENDIX A: SPARSE VARIATIONAL GAUSSIAN PROCESSES
One deficiency of GPR is its limited ability to scale to large training datasets. Due to the matrix inversions involved, the computational cost of GPR grows as with respect to the sample size n. This can be particularly concerning for free energy path simulations as the training data drawn from the sampled configurations evolve during path update and optimization. To reduce the data requirements, we utilize sparse variational Gaussian processes (SVGP), which summarize the full data X into a series of m inducing points (XM) that maintain the model using an approximate posterior. The inducing variables are trained along with the kernel’s hyperparameters by maximizing the lower bound of the exact marginal likelihood.98 This is accomplished by minimizing the Kullback–Leibler divergence between the exact and approximate posteriors. Using this method, an approximate posterior distribution is used in place of the exact posterior distribution, for which the mean and covariance functions are given by
| (A1) |
| (A2) |
where , and μM and A are the mean vector and covariance matrix of the chosen variational Gaussian distribution of the inducing point function values, respectively, calculated as follows:98
| (A3) |
| (A4) |
where . Under the SVGP model, the gradient in Eq. (14) is updated to
| (A5) |
APPENDIX B: STREAMING SPARSE GPR
As the sampled phase space evolves, the model may no longer accurately predict the potential energy difference between the AI/MM and SE/MM levels. It is therefore necessary to iteratively update the model using data from the new configurations; however, we cannot simply retrain the model on the new data without losing the memory of the previous configurations. We therefore use a streaming sparse GPR (SSGPR) method outlined in the work of Bui et al.71 Here, we stream the new data as a batch and update the model’s hyperparameters and inducing points by leveraging both the old posterior approximation and the new data. Let Xb represent the new inducing points and Xa the old inducing points, and then the predictive mean and covariance for the SSGPR model are given as
| (B1) |
| (B2) |
where , Lb is a lower triangular matrix obtained from the Cholesky decomposition of Kbb such that , , where f is the latent function values at the newly collected training points Xnew, hereon referred to as Xf for the use in subscripts, and
| (B3) |
where ynew is the set of observations encountered at Xf, , μa and Sa are the mean vector and covariance matrix of the old approximate posterior distribution, respectively, is the kernel operation of the old approximate posterior, α is the order of the α-divergence used to generalize the Kullback–Leibler divergence, and diag refers to the diagonal elements of the matrix within the parentheses. Equation (A5) must then be updated to
| (B4) |
Contributor Information
Yihan Shao, Email: mailto:yihan.shao@ou.edu.
Jingzhi Pu, Email: mailto:jpu@iupui.edu.
AUTHOR DECLARATIONS
Conflict of Interest
The authors have no conflicts to disclose.
Author Contributions
Ryan Snyder: Conceptualization (equal); Data curation (equal); Formal analysis (equal); Methodology (equal); Software (equal); Writing – original draft (equal); Writing – review & editing (equal). Bryant Kim: Software (equal); Writing – review & editing (equal). Xiaoliang Pan: Formal analysis (equal); Writing – review & editing (equal). Yihan Shao: Conceptualization (equal); Formal analysis (equal); Funding acquisition (equal); Project administration (equal); Supervision (equal); Writing – review & editing (equal). Jingzhi Pu: Conceptualization (equal); Formal analysis (equal); Methodology (equal); Project administration (equal); Writing – original draft (equal); Writing – review & editing (equal).
DATA AVAILABILITY
The data that support the findings of this study are available from the corresponding author upon reasonable request.
REFERENCES
- 1.McCammon J., Roux B., Voth G., and Yang W., J. Chem. Theory Comput. 10, 2631 (2014). 10.1021/ct500366u [DOI] [PubMed] [Google Scholar]
- 2.Warshel A. and Levitt M., J. Mol. Biol. 103, 227–249 (1976). 10.1016/0022-2836(76)90311-9 [DOI] [PubMed] [Google Scholar]
- 3.Field M. J., Bash P. A., and Karplus M., J. Comput. Chem. 11, 700–733 (1990). 10.1002/jcc.540110605 [DOI] [Google Scholar]
- 4.Singh U. C. and Kollman P. A., J. Comput. Chem. 7, 718–730 (1986). 10.1002/jcc.540070604 [DOI] [Google Scholar]
- 5.Gao J. and Thompson M. A., Combined Quantum Mechanical and Molecular Mechanical Methods (ACS Publications, 1998), Vol. 712. [Google Scholar]
- 6.Lin H. and Truhlar D. G., Theor. Chem. Acc. 117, 185–199 (2007). 10.1007/s00214-006-0143-z [DOI] [Google Scholar]
- 7.Senn H. M. and Thiel W., Angew. Chem., Int. Ed. 48, 1198–1229 (2009). 10.1002/anie.200802019 [DOI] [PubMed] [Google Scholar]
- 8.Dewar M. J. S. and Thiel W., J. Am. Chem. Soc. 99, 4899–4907 (1977). 10.1021/ja00457a004 [DOI] [Google Scholar]
- 9.Dewar M. J. S., Zoebisch E. G., Healy E. F., and Stewart J. J. P., J. Am. Chem. Soc. 107, 3902–3909 (1985). 10.1021/ja00299a024 [DOI] [Google Scholar]
- 10.Stewart J. J. P., J. Comput. Chem. 10, 209–220 (1989). 10.1002/jcc.540100208 [DOI] [Google Scholar]
- 11.Elstner M., Porezag D., Jungnickel G., Elsner J., Haugk M., Frauenheim T., Suhai S., and Seifert G., Phys. Rev. B 58, 7260–7268 (1998). 10.1103/physrevb.58.7260 [DOI] [Google Scholar]
- 12.Elstner M., Frauenheim T., Kaxiras E., Seifert G., and Suhai S., Phys. Status Solidi B 217, 357–376 (2000). [DOI] [Google Scholar]
- 13.Frauenheim T., Seifert G., Elstner M., Niehaus T., Köhler C., Amkreutz M., Sternberg M., Hajnal Z., Carlo A. D., and Suhai S., J. Phys.: Condens. Matter 14, 3015–3047 (2002). 10.1088/0953-8984/14/11/313 [DOI] [Google Scholar]
- 14.Zwanzig R. W., J. Chem. Phys. 22, 1420–1426 (1954). 10.1063/1.1740409 [DOI] [Google Scholar]
- 15.Hudson P. S., Boresch S., Rogers D. M., and Woodcock H. L., J. Chem. Theory Comput. 14, 6327–6335 (2018). 10.1021/acs.jctc.8b00517 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Giese T. J. and York D. M., J. Chem. Theory Comput. 15, 5543–5562 (2019). 10.1021/acs.jctc.9b00401 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhou Y. and Pu J., J. Chem. Theory Comput. 10, 3038–3054 (2014). 10.1021/ct4009624 [DOI] [PubMed] [Google Scholar]
- 18.Kim B., Snyder R., Nagaraju M., Zhou Y., Ojeda-May P., Keeton S., Hege M., Shao Y., and Pu J., J. Chem. Theory Comput. 17, 4961–4980 (2021). 10.1021/acs.jctc.1c00245 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pan X., Li P., Ho J., Pu J., Mei Y., and Shao Y., Phys. Chem. Chem. Phys. 21, 20595–20605 (2019). 10.1039/c9cp02593f [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wu J., Shen L., and Yang W., J. Chem. Phys. 147, 161732 (2017). 10.1063/1.5006882 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shen L. and Yang W., J. Chem. Theory Comput. 14, 1442–1455 (2018). 10.1021/acs.jctc.7b01195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Böselt L., Thürlemann M., and Riniker S., J. Chem. Theory Comput. 17, 2641–2658 (2021). 10.1021/acs.jctc.0c01112 [DOI] [PubMed] [Google Scholar]
- 23.Pan X., Yang J., Van R., Epifanovsky E., Ho J., Huang J., Pu J., Mei Y., Nam K., and Shao Y., J. Chem. Theory Comput. 17, 5745–5758 (2021). 10.1021/acs.jctc.1c00565 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zeng J., Giese T. J., Ekesan S., and York D. M., J. Chem. Theory Comput. 17, 6993–7009 (2021). 10.1021/acs.jctc.1c00201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gómez-Flores C. L., Maag D., Kansari M., Vuong V.-Q., Irle S., Gräter F., Kubař T., and Elstner M., J. Chem. Theory Comput. 18, 1213–1226 (2022). 10.1021/acs.jctc.1c00811 [DOI] [PubMed] [Google Scholar]
- 26.Ramakrishnan R., Dral P. O., Rupp M., and von Lilienfeld O. A., J. Chem. Theory Comput. 11, 2087–2096 (2015). 10.1021/acs.jctc.5b00099 [DOI] [PubMed] [Google Scholar]
- 27.Shen L., Wu J., and Yang W., J. Chem. Theory Comput. 12, 4934–4946 (2016). 10.1021/acs.jctc.6b00663 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zhang L., Han J., Wang H., Saidi W., Car R., and E W., Adv. Neural Inf. Process. Syst. 31, 4436–4446 (2018). [Google Scholar]
- 29.Wang H., Zhang L., Han J., and E W., Comput. Phys. Commun. 228, 178–184 (2018). 10.1016/j.cpc.2018.03.016 [DOI] [Google Scholar]
- 30.Zhang L., Han J., Wang H., Car R., and E W., Phys. Rev. Lett. 120, 143001 (2018). 10.1103/physrevlett.120.143001 [DOI] [PubMed] [Google Scholar]
- 31.Peterson A. A., Christensen R., and Khorshidi A., Phys. Chem. Chem. Phys. 19, 10978–10985 (2017). 10.1039/c7cp00375g [DOI] [PubMed] [Google Scholar]
- 32.Rossi K., Jurásková V., Wischert R., Garel L., Corminbœuf C., and Ceriotti M., J. Chem. Theory Comput. 16, 5139–5149 (2020). 10.1021/acs.jctc.0c00362 [DOI] [PubMed] [Google Scholar]
- 33.Imbalzano G., Zhuang Y., Kapil V., Rossi K., Engel E. A., Grasselli F., and Ceriotti M., J. Chem. Phys. 154, 074102 (2021). 10.1063/5.0036522 [DOI] [PubMed] [Google Scholar]
- 34.Devergne T., Magrino T., Pietrucci F., and Saitta A. M., J. Chem. Theory Comput. 18, 5410–5421 (2022). 10.1021/acs.jctc.2c00400 [DOI] [PubMed] [Google Scholar]
- 35.MacKay D. J. C., Network: Comput. Neural Syst. 6, 469 (1995). 10.1088/0954-898x_6_3_011 [DOI] [Google Scholar]
- 36.Lampinen J. and Vehtari A., Neural Network 14, 257–274 (2001). 10.1016/s0893-6080(00)00098-8 [DOI] [PubMed] [Google Scholar]
- 37.Gal Y. and Ghahramani Z., in Proceedings of The 33rd International Conference on Machine Learning, Proceedings of Machine Learning Research, Vol. 48, edited by Balcan M. F. and Weinberger K. Q. (PMLR, New York, NY, 2016), pp. 1050–1059. [Google Scholar]
- 38.Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, edited by Aarti S. and Jerry Z. (PMLR, 2017), Vol. 54. [Google Scholar]
- 39.Rasmussen C. E. and Williams C. K. I., Gaussian Processes for Machine Learning (MIT Press, Cambridge, 2006). [Google Scholar]
- 40.Tang Y.-H., Zhang D., and Karniadakis G. E., J. Chem. Phys. 148, 034101 (2018). 10.1063/1.5008630 [DOI] [PubMed] [Google Scholar]
- 41.Jinnouchi R., Karsai F., and Kresse G., Phys. Rev. B 100, 014105 (2019). 10.1103/physrevb.100.014105 [DOI] [Google Scholar]
- 42.Vandermause J., Torrisi S. B., Batzner S., Xie Y., Sun L., Kolpak A. M., and Kozinsky B., npj Comput. Mater. 6, 20 (2020). 10.1038/s41524-020-0283-z [DOI] [Google Scholar]
- 43.Schmitz G. and Christiansen O., J. Chem. Phys. 148, 241704 (2018). 10.1063/1.5009347 [DOI] [PubMed] [Google Scholar]
- 44.Meyer R. and Hauser A. W., J. Chem. Phys. 152, 084112 (2020). 10.1063/1.5144603 [DOI] [PubMed] [Google Scholar]
- 45.Raggi G., Galván I. F., Ritterhoff C. L., Vacher M., and Lindh R., J. Chem. Theory Comput. 16, 3989–4001 (2020). 10.1021/acs.jctc.0c00257 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Born D. and Kästner J., J. Chem. Theory Comput. 17, 5955–5967 (2021). 10.1021/acs.jctc.1c00517 [DOI] [PubMed] [Google Scholar]
- 47.Teng C., Wang Y., Huang D., Martin K., Tristan J.-B., and Bao J. L., J. Chem. Theory Comput. 18, 5739–5754 (2022). 10.1021/acs.jctc.2c00546 [DOI] [PubMed] [Google Scholar]
- 48.Hu W., Li P., Wang J.-N., Xue Y., Mo Y., Zheng J., Pan X., Shao Y., and Mei Y., J. Chem. Theory Comput. 16, 6814–6822 (2020). 10.1021/acs.jctc.0c00794 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bartók A. P., Payne M. C., Kondor R., and Csányi G., Phys. Rev. Lett. 104, 136403 (2010). 10.1103/physrevlett.104.136403 [DOI] [PubMed] [Google Scholar]
- 50.Uteva E., Graham R. S., Wilkinson R. D., and Wheatley R. J., J. Chem. Phys. 149, 174114 (2018). 10.1063/1.5051772 [DOI] [PubMed] [Google Scholar]
- 51.Kolb B., Marshall P., Zhao B., Jiang B., and Guo H., J. Phys. Chem. A 121, 2552–2557 (2017). 10.1021/acs.jpca.7b01182 [DOI] [PubMed] [Google Scholar]
- 52.Kamath A., Vargas-Hernández R. A., Krems R. V., Carrington T., and Manzhos S., J. Chem. Phys. 148, 241702 (2018). 10.1063/1.5003074 [DOI] [PubMed] [Google Scholar]
- 53.Tran K., Neiswanger W., Yoon J., Zhang Q., Xing E., and Ulissi Z. W., Mach. Learn.: Sci. Technol. 1, 025006 (2020). 10.1088/2632-2153/ab7e1a [DOI] [Google Scholar]
- 54.Maragliano L., Fischer A., Vanden-Eijnden E., and Ciccotti G., J. Chem. Phys. 125, 024106 (2006). 10.1063/1.2212942 [DOI] [PubMed] [Google Scholar]
- 55.Zhou Y., Ojeda-May P., Nagaraju M., Kim B., and Pu J., Molecules 23, 2652 (2018). 10.3390/molecules23102652 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Menshutkin N., Z. Phys. Chem. 5, 589–600 (1890). [Google Scholar]
- 57.Thiel W., MNDO97 Version 5.0 (University of Zurich, Zurich, Switzerland, 1998). [Google Scholar]
- 58.Brooks B. R., Brooks C. L., Mackerell A. D., Nilsson L., Petrella R. J., Roux B., Won Y., Archontis G., Bartels C., Boresch S., Caflisch A., Caves L., Cui Q., Dinner A. R., Feig M., Fischer S., Gao J., Hodoscek M., Im W., Kuczera K., Lazaridis T., Ma J., Ovchinnikov V., Paci E., Pastor R. W., Post C. B., Pu J. Z., Schaefer M., Tidor B., Venable R. M., Woodcock H. L., Wu X., Yang W., York D. M., and Karplus M., J. Comput. Chem. 30, 1545–1614 (2009). 10.1002/jcc.21287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., J. Chem. Phys. 79, 926–935 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
- 60.MacKerell A. D., Bashford D., Bellott M., Dunbrack R. L., Evanseck J. D., Field M. J., Fischer S., Gao J., Guo H., Ha S., Joseph-McCarthy D., Kuchnir L., Kuczera K., Lau F. T. K., Mattos C., Michnick S., Ngo T., Nguyen D. T., Prodhom B., Reiher W. E., Roux B., Schlenkrich M., Smith J. C., Stote R., Straub J., Watanabe M., Wiórkiewicz-Kuczera J., Yin D., and Karplus M., J. Phys. Chem. B 102, 3586–3616 (1998). 10.1021/jp973084f [DOI] [PubMed] [Google Scholar]
- 61.Gao J. and Xia X., J. Am. Chem. Soc. 115, 9667–9675 (1993). 10.1021/ja00074a036 [DOI] [Google Scholar]
- 62.Darden T., York D., and Pedersen L., J. Chem. Phys. 98, 10089–10092 (1993). 10.1063/1.464397 [DOI] [Google Scholar]
- 63.Nam K., Gao J., and York D. M., J. Chem. Theory Comput. 1, 2–13 (2005). 10.1021/ct049941i [DOI] [PubMed] [Google Scholar]
- 64.Lee C., Yang W., and Parr R. G., Phys. Rev. B 37, 785–789 (1988). 10.1103/physrevb.37.785 [DOI] [PubMed] [Google Scholar]
- 65.Becke A. D., J. Chem. Phys. 98, 5648–5652 (1993). 10.1063/1.464913 [DOI] [Google Scholar]
- 66.Stephens P. J., Devlin F. J., Chabalowski C. F., and Frisch M. J., J. Phys. Chem. 98, 11623–11627 (1994). 10.1021/j100096a001 [DOI] [Google Scholar]
- 67.Francl M. M., Pietro W. J., Hehre W. J., Binkley J. S., Gordon M. S., DeFrees D. J., and Pople J. A., J. Chem. Phys. 77, 3654–3665 (1982). 10.1063/1.444267 [DOI] [Google Scholar]
- 68.Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Petersson G. A., Nakatsuji H., Li X., Caricato M., Marenich A. V., Bloino J., Janesko B. G., Gomperts R., Mennucci B., Hratchian H. P., Ortiz J. V., Izmaylov A. F., Sonnenberg J. L., Williams-Young D., Ding F., Lipparini F., Egidi F., Goings J., Peng B., Petrone A., Henderson T., Ranasinghe D., Zakrzewski V. G., Gao J., Rega N., Zheng G., Liang W., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., Throssell K., J. A. Montgomery, Jr., Peralta J. E., Ogliaro F., Bearpark M. J., Heyd J. J., Brothers E. N., Kudin K. N., Staroverov V. N., Keith T. A., Kobayashi R., Normand J., Raghavachari K., Rendell A. P., Burant J. C., Iyengar S. S., Tomasi J., Cossi M., Millam J. M., Klene M., Adamo C., Cammi R., Ochterski J. W., Martin R. L., Morokuma K., Farkas O., Foresman J. B., and Fox D. J., Gaussian 16 Revision C.01, Gaussian, Inc., Wallingford, CT, 2016. [Google Scholar]
- 69.Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., Dubourg V., Vanderplas J., Passos A., Cournapeau D., Brucher M., Perrot M., and Duchesnay E., J. Mach. Learn. Res. 12, 2825–2830 (2011). [Google Scholar]
- 70.Matthews A. G. De G., Van Der Wilk M., Nickson T., Fujii K., Boukouvalas A., León-Villagrá P., Ghahramani Z., and Hensman J., J. Mach. Learn. Res. 18, 1–6 (2017). [Google Scholar]
- 71.Bui T. D., Nguyen C. V., and Turner R. E., Adv. Neural Inf. Process. Syst. 30, 3299–3307 (2017). [Google Scholar]
- 72.Abadi M., Agarwal A., Barham P., Brevdo E., Chen Z., Citro C., Corrado G. S., Davis A., Dean J., Devin M., Ghemawat S., Goodfellow I., Harp A., Irving G., Isard M., Jia Y., Jozefowicz R., Kaiser L., Kudlur M., Levenberg J., Mané D., Monga R., Moore S., Murray D., Olah C., Schuster M., Shlens J., Steiner B., Sutskever I., Talwar K., Tucker P., Vanhoucke V., Vasudevan V., Viégas F., Vinyals O., Warden P., Wattenberg M., Wicke M., Yu Y., and Zheng X., “TensorFlow: Large-scale machine learning on heterogeneous systems,” arXiv:1603.04467 (2015).
- 73.Abadi M., Barham P., Chen J., Chen Z., Davis A., Dean J., Devin M., Ghemawat S., Irving G., Isard M., Kudlur M., Levenberg J., Monga R., Moore S., Murray D. G., Steiner B., Tucker P., Vasudevan V., Warden P., Wicke M., Yu Y., and Zheng X., “TensorFlow: A system for large-scale machine learning,” in 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16) (USENIX Association, 2016), pp. 265–283. [Google Scholar]
- 74.Bui T. D., Nguyen C. V., and Turner R. E., Streaming sparse gaussian process approximations, https://github.com/thangbui/streaming_sparse_gp.
- 75.Kingma D. P. and Ba J., “Adam: A Method for Stochastic Optimization,” in Proceedings of 3rd International Conference on Learning Representations (2015). [Google Scholar]
- 76.Gao J., J. Am. Chem. Soc. 113, 7796–7797 (1991). 10.1021/ja00020a070 [DOI] [Google Scholar]
- 77.Su P., Wu W., Kelly C. P., Cramer C. J., and Truhlar D. G., J. Phys. Chem. A 112, 12761–12768 (2008). 10.1021/jp711655k [DOI] [PubMed] [Google Scholar]
- 78.Okamoto K., Fukui S., and Shingu H., Bull. Chem. Soc. Jpn. 40, 1920–1925 (1967). 10.1246/bcsj.40.1920 [DOI] [Google Scholar]
- 79.Truong T. N., Truong T.-T. T., and Stefanovich E. V., J. Chem. Phys. 107, 1881–1889 (1997). 10.1063/1.474538 [DOI] [Google Scholar]
- 80.Vilseck J. Z., Sambasivarao S. V., and Acevedo O., J. Comput. Chem. 32, 2836–2842 (2011). 10.1002/jcc.21863 [DOI] [PubMed] [Google Scholar]
- 81.Pohorille A., Jarzynski C., and Chipot C., J. Phys. Chem. B 114, 10235–10253 (2010). 10.1021/jp102971x [DOI] [PubMed] [Google Scholar]
- 82.Ryde U., J. Chem. Theory Comput. 13, 5745–5752 (2017). 10.1021/acs.jctc.7b00826 [DOI] [PubMed] [Google Scholar]
- 83.Heimdal J. and Ryde U., Phys. Chem. Chem. Phys. 14, 12592–12604 (2012). 10.1039/c2cp41005b [DOI] [PubMed] [Google Scholar]
- 84.Wu D. and Kofke D. A., J. Chem. Phys. 123, 054103 (2005). 10.1063/1.1992483 [DOI] [PubMed] [Google Scholar]
- 85.Wu D. and Kofke D. A., J. Chem. Phys. 123, 084109 (2005). 10.1063/1.2011391 [DOI] [PubMed] [Google Scholar]
- 86.Boresch S. and Woodcock H. L., Mol. Phys. 115, 1200–1213 (2017). 10.1080/00268976.2016.1269960 [DOI] [Google Scholar]
- 87.Wu D. and Kofke D. A., J. Chem. Phys. 121, 8742–8747 (2004). 10.1063/1.1806413 [DOI] [PubMed] [Google Scholar]
- 88.Bučko T., Gesvandtnerová M., and Rocca D., J. Chem. Theory Comput. 16, 6049–6060 (2020). 10.1021/acs.jctc.0c00486 [DOI] [PubMed] [Google Scholar]
- 89.Le Gratiet L. and Garnier J., Mach. Learn. 98, 407–433 (2015). 10.1007/s10994-014-5437-0 [DOI] [Google Scholar]
- 90.Zhao Y., Fritsche C., Hendeby G., Yin F., Chen T., and Gunnarsson F., IEEE Trans. Signal Process. 67, 5936–5951 (2019). 10.1109/tsp.2019.2949508 [DOI] [Google Scholar]
- 91.Pinheiro M., Ge F., Ferré N., Dral P. O., and Barbatti M., Chem. Sci. 12, 14396–14413 (2021). 10.1039/d1sc03564a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Snyder R., Kim B., Pan X., Shao Y., and Pu J., Phys. Chem. Chem. Phys. 24, 25134–25143 (2022). 10.1039/d2cp02820d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Christensen A. S. and von Lilienfeld O. A., CHIMIA 73, 1028 (2019). 10.2533/chimia.2019.1028 [DOI] [PubMed] [Google Scholar]
- 94.Christensen A. S., Faber F. A., and von Lilienfeld O. A., J. Chem. Phys. 150, 064105 (2019). 10.1063/1.5053562 [DOI] [PubMed] [Google Scholar]
- 95.Pan X., Van R., Epifanovsky E., Liu J., Pu J., Nam K., and Shao Y., J. Phys. Chem. B 126, 4226–4235 (2022). 10.1021/acs.jpcb.2c02262 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Behler J., J. Chem. Phys. 134, 074106 (2011). 10.1063/1.3553717 [DOI] [PubMed] [Google Scholar]
- 97.Bartók A. P., Kondor R., and Csányi G., Phys. Rev. B 87, 184115 (2013). 10.1103/physrevb.87.184115 [DOI] [Google Scholar]
- 98.Titsias M. K., Variational Learning of Inducing Variables in Sparse Gaussian Processes (AISTATS, 2009), Vol. 5. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See the supplementary material for a description of the Wu and Kofke bias metric for the Menshutkin reaction, illustration of the reference and predicted energy gap along the reaction coordinate and a comparison of GPR prediction performance with existing ANN model in literature, comparison of predictive-variance-based uncertainty estimates, description of FEP calculations and error estimation of the string free energy profile, description of the discrepancy between rising error and stagnant variance in new phase space, demonstration of the model improvements with an increased number of inducing variables, FEP calculations on the AM1-SSGPR/MM converged MFEP, and Cartesian force improvements through energy corrections with the evolving models.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.