Mapping tissue microstructure across the human brain on a clinical scanner with soma and neurite density image metrics

Abstract

Soma and neurite density image (SANDI) is an advanced diffusion magnetic resonance imaging biophysical signal model devised to probe in vivo microstructural information in the gray matter (GM). This model requires acquisitions that include b values that are at least six times higher than those used in clinical practice. Such high b values are required to disentangle the signal contribution of water diffusing in soma from that diffusing in neurites and extracellular space, while keeping the diffusion time as short as possible to minimize potential bias due to water exchange. These requirements have limited the use of SANDI only to preclinical or cutting‐edge human scanners. Here, we investigate the potential impact of neglecting water exchange in the SANDI model and present a 10‐min acquisition protocol that enables to characterize both GM and white matter (WM) on 3 T scanners. We implemented analytical simulations to (i) evaluate the stability of the fitting of SANDI parameters when diminishing the number of shells; (ii) estimate the bias due to potential exchange between neurites and extracellular space in such reduced acquisition scheme, comparing it with the bias due to experimental noise. Then, we demonstrated the feasibility and assessed the repeatability and reproducibility of our approach by computing microstructural metrics of SANDI with AMICO toolbox and other state‐of‐the‐art models on five healthy subjects. Finally, we applied our protocol to five multiple sclerosis patients. Results suggest that SANDI is a practical method to characterize WM and GM tissues in vivo on performant clinical scanners.

We present a novel robust and clinically feasible 10‐min diffusion MRI protocol with b values up to 6000 s/mm² for 3 T which can reliably assess gray and white matter microstructure according to the soma and neurite density image (SANDI) model. Using analytical simulations we investigated the potential impact of neglecting water exchange. Then we demonstrated the feasibility and assessed the repeatability and reproducibility of our approach in vivo.

1. INTRODUCTION

Diffusion MRI (dMRI) is a powerful technique to probe brain tissue microstructure in vivo (Basser et al., 1994; Le Bihan et al., 1991; Moseley et al., 1990). Since its introduction, and with the establishment of multi‐shell protocols, several microstructural models and signal representations have been proposed (see, e.g., Alexander et al., 2019; Jelescu & Budde, 2017; Novikov, Kiselev, et al., 2018) and applied to study how different neurological diseases affect the integrity of brain tissues. The first signal representation proposed was the diffusion tensor imaging (DTI; Le Bihan et al., 2001), which assumes that the diffusion displacement of water molecules follows a Gaussian distribution and can be thus described by the tensor of covariances. From DTI, it is possible to derive scalar indices such as the axial diffusivity (AD), radial diffusivity (RD), and mean diffusivity (MD), which quantify the magnitude of principal, radial, and average diffusion within a voxel, and the fractional anisotropy (FA), which measures the directionality of diffusion. Because of its straightforward interpretation and the ease of data acquisition (which necessitates a standard pulsed gradient spin echo [PGSE] sequence [Stejskal & Tanner, 1965] with a unique shell with b value ~1000 s/mm² and ~32 directions that can be run on the vast majority of clinical MRI scanners in less than 5 min), DTI has proven to be a valuable tool for investigating diverse pathological features in brain and body tissues (Van Hecke et al., 2016). However, despite its good sensitivity in detecting diseased tissue and following it over time, DTI has low pathological specificity, which does not allow to discriminate between the different pathological processes underlying the diverse pathogenesis. Indeed, while in regions of approximately parallel fibers, like the corpus callosum, the DTI model and the derived scalar indices provide contrasts that reflect tissue properties, such as myelination or fiber density, in general, the effects of orientation dispersion dominate such contrast and more sophisticated models are necessary to describe the underlying microstructure (Alexander et al., 2019).

To overcome this issue, many multi‐compartment models based on geometrical assumptions have been proposed (Alexander et al., 2019; Chiang et al., 2014; Coelho et al., 2022; Jelescu et al., 2020; Jespersen et al., 2010; Novikov, Kiselev, et al., 2018; Novikov, Veraart, et al., 2018; Shemesh et al., 2015; Suh et al., 2003; Wang et al., 2014). Among these, two very popular models that can be fitted using a clinically feasible two‐shell acquisition and that are often employed in clinical applications are the neurite orientation dispersion and density imaging (NODDI) (Zhang et al., 2012) and the multi‐compartment spherical mean technique (SMT) (Callaghan et al., 1979; Kaden et al., 2016). NODDI distinguishes three microstructural environments: intra‐neurite, extra‐neurite, and cerebrospinal fluid compartments. All these compartments have fixed diffusivities (with a relationship between the external AD and RD), and geometrical assumptions that affect diffusion in a unique way, resulting in three separate dMRI signals. Similarly, the multi‐compartment SMT estimates microscopic features specific to the intra‐neurite and extra‐neurite compartments in the white matter (WM). The use of the spherical mean in the fitting allows the minimization of the confounding effects derived from axonal fiber crossings and orientation dispersion (OD). Moreover, comparing it to NODDI, although it can only indirectly capture the presence of free water, it does not fix any values for the intra‐neurite and extra‐neurite axial diffusivities allowing to estimate them from the measured signal. More precisely the axial intra‐neurite and extra‐neurite diffusivities are assumed to have the same value and the corresponding perpendicular extra‐neurite diffusivity is linked to the estimated axial one via the tortuosity assumption (Kaden et al., 2016). This means that perpendicular extra‐neurite diffusivity is linked to not just the axial diffusivity, but also intra‐neurite signal fraction binding the intra‐neurite and extra‐neurite spaces together. However, these assumptions are not always satisfied in realistic conditions (Henriques et al., 2019). Although in some clinical studies these two models have been proved to be sensitive to tissue alterations caused by diverse pathologies, they are rarely used in clinical practice. This is due to several reasons among which we highlight: (i) the lack of a harmonized dMRI acquisition scheme available on most clinical scanners, which should guarantee repeatability and reproducibility of the estimated metrics of interest across vendors/systems, with good accuracy and precision; (ii) most of the advanced models are based on geometrical assumptions that are specific to WM tissue, and thus cannot be reliably applied to study gray matter (GM) microstructure; (iii) the clinical translation of usage of multi‐shell sequences to fit multi‐compartment models is far from established and especially the GM microstructure is mostly studied on “super scanners” (e.g., Connectom or 7 T) (Foo et al., 2020; Jones et al., 2018; McNab et al., 2013; Setsompop et al., 2013) or on preclinical scanners (Jelescu et al., 2020); (iv) validation against histopathology as well as in large patient cohorts of the proposed models is lacking; (v) parameter estimation is potentially biased if the amount of data available for short scanning times is not sufficient to fit model parameters accurately while avoiding degeneracy. However, being able to investigate GM tissue injury in clinically feasible settings would be important for diagnostic and prognostic purposes and for determining the biological processes underlying clinical deficits (Todea et al., 2020).

Recently, the soma and neurite density imaging (SANDI) (Palombo et al., 2020) model has been proposed to adapt the multi‐compartment models' formalism to the geometrical properties of GM thus recovering meaningful microstructural information from GM. In the original paper, the authors showed that, by using signals obtained from a multi‐shell sequence with b values up to 10,000 s/mm², SANDI provides maps of soma and neurite signal fractions, that remarkably mirror contrasts of histological images of brain cyto‐ and myelo‐architecture. Subsequently, it was demonstrated (Genc et al., 2021) that measures of soma and neurite signal fractions and apparent soma radii obtained with SANDI were highly reproducible and repeatable across multiple GM regions of the healthy human brain also using images acquired on a Connectom scanner (Koller et al., 2021) with lower maximum b value = 6000 s/mm²; it was also shown (Ianuş et al., 2022) that parameter estimates are stable in in vivo healthy mouse brain when the dMRI protocol is reduced from eight shells to five shells, and the SANDI soma signal fraction strongly correlates with cell density from the Allen Brain Atlas of adult mouse brain. Finally, in a recent work (Schiavi et al., 2022), an implementation of SANDI inside the AMICO toolbox (Daducci et al., 2015) was proposed, which makes the computation feasible on standard workstations.

However, to disentangle the MR signal contribution of water diffusing in soma from that diffusing in neurites and extracellular space, SANDI requires b values that are at least six times higher than those used in clinical practice. Moreover, such high b values should be reached while keeping the diffusion time and the gradient pulse duration as short as possible to minimize bias due to potential water exchange between neurites and extracellular space (Jelescu et al., 2022; Olesen et al., 2022). These requirements have thus far limited the translation of SANDI to clinical scanners, where high b values can be reached only at the expense of longer diffusion times and gradient pulse duration.

Inspired by these works, and with the intent of bringing a more informative GM model to clinical applications, here we propose a clinically feasible 10‐min multi‐shell acquisition protocol suitable for performant 3 T scanners which, coupled with the AMICO fitting procedure, allows the characterization of both GM and WM microstructure. The potential bias due to water exchange at longer diffusion times (~30 ms) in the SANDI estimates is evaluated using analytical simulations. To assess the stability of the fit for the chosen protocol parameters we performed numerical simulations using different number of shells and different signal‐to‐noise‐ratios (SNRs). Simulations describe the impact of exchange and SNR on the estimations of SANDI parameters with the selected protocol. Finally, we assess the repeatability and reproducibility of our approach in vivo on healthy subjects (HS) and show the feasibility and clinical application in five patients affected by multiple sclerosis (MS). We focused on MS since the lesions caused by the disease are known to have very heterogeneous and complex pathophysiology, difficult to characterize using only a single modality (Rahmanzadeh et al., 2021) and we demonstrate how with a single 10‐min acquisition scan we can obtain complementary information from DTI, NODDI, SMT, and SANDI, enabling the quantification of complementary informative microstructural features.

2. METHODS

2.1. Proposed sequence

We implemented a protocol based on a prototype PGSE sequence (Feinberg et al., 2010; Moeller et al., 2010; Xu et al., 2013) for multi‐shell dMRI acquisition on a 3 T Siemens MAGNETOM Prisma (Siemens Healthcare) equipped with a 64CH receiver head/neck coil and the following parameters: repetition time 2600 ms, echo time 80 ms, pulse duration δ = 24.66 ms, time interval between the pulses Δ = 39.07 ms, maximum gradient strength 67 mT/m, spatial resolution 2 × 2 × 2 mm³, 72 slices, axial orientation, FOV = 200 × 200, GRAPPA = 2, multiband = 4, partial Fourier = 6/8, with b values = 0/500/1000/2000/3000/4000/6000 s/mm² with 15/6/32/40/40/40/40 measurements per shell in anterior–posterior phase encoding (acquisition time 10′01″) as well as one b value = 0 s/mm² with reversed phase encoding (acquisition time 47″). The set of directions was generated using the electrostatic repulsion model (Caruyer et al., 2013), with an inhouse implementation. The complete acquisition scheme of gradient directions and associated b values is reported in Table S1.

2.2. Analytical simulations

We performed numerical simulations with two aims: (i) to demonstrate that the six shells used in the proposed protocol are sufficient to reliably estimate the SANDI parameters, (ii) to show the impact of exchange time and SNR on estimated parameters with the predefined setting. Given the physical and technical constraints of a 3 T scanner with maximum gradient strength of 80 mT/m, the smallest achievable pulse duration and distance were δ = 24.66 ms and Δ = 39.07 ms, respectively. These values allow to obtain a maximum b value of 6000 s/mm² on our clinical scanner and thus were fixed for all the simulations.

To achieve the first aim, we tested five different PGSE protocols with maximum b value of 6000 s/mm², fixed δ and Δ, and different number of shells: from 6 (corresponding to the proposed approach) to 14. The b values chosen for each protocol were:

• 6 shells: 0/500/1000/2000/3000/4000/6000 s/mm²;

• 8 shells: 0/500/1000/1500/2000/3000/4000/5000/6000 s/mm²;

• 10 shells: 0/500/700/1000/1500/2000/3000/4000/5000/5500/6000 s/mm²;

• 12 shells: 0/500/700/1000/1500/2000/3000/3500/4000/4500/5000/5500/6000 s/mm²;

• 14 shells: 0/300/500/700/1000/1500/2000/2500/3000/3500/4000/4500/5000/5500/6000 s/mm².

For each choice of number of shells, we generated: 10,000 random combinations of SANDI model parameters, by sampling neurite and soma signal fractions (fneurite and fsoma) using a Dirichlet distribution to ensure uniform coverage of the simplex fneurite + fsoma + fextra = 1 (where fextra is the extra‐axonal signal fraction); two uniform distributions in [0.25, 3] μm²/ms for the intra‐neurite and extra‐axonal diffusivities (Din ad De); a uniform distribution in [1, 15] μm for the soma radii (Rsoma). For each combination, we computed the PGSE normalized direction‐averaged signals without noise (corresponding to SNR = ∞), and with added Rician or Gaussian noise separately to obtain also signals with SNR = 50 and SNR = 100. We note that the SNRs simulated here are referred to the images obtained after the spherical mean, thus they are approximately $\sqrt{\#\text{directions}}$ times higher than those measured on images acquired in a single direction. We then fit the SANDI model to the generated signals with different SNR using the nonlinear least square (NLLS) method implemented in the “lsqcurvefit” function in MATLAB with initial condition either the ground truth (GT) values to simulate the ideal case of known initial conditions or GT values with 25% of Gaussian noise added to simulate cases of good initial guess with some uncertainty. The results corresponding to the latter choice of initial conditions are reported in Figure S1. To evaluate the quality of the fit, we computed the root‐mean‐squared error (RMSE), the adjusted coefficient of determination, R ², and the bias as intercept of the linear fitting of the simulated GT SANDI parameters versus the estimated ones for each protocol at each SNR. Moreover, similarly to what has been done in Epstein et al. (2022), for the 6 and 14 shells protocols and three representative values of SNRs (50, 100 and, $\infty$), we also computed the mean bias (defined as mean error, i.e., mean difference between simulated and estimated parameters), the standard deviation, and the RMSE of parameter estimates with respect to GT values. For each model parameter, we computed these three metrics using a sliding window of 200 consecutive simulated points and we plotted the values as a function of the synthetic test dataset.

To evaluate the impact of water exchange, we fixed the PGSE protocol being the one with six shells, we sampled the space of SANDI parameters in the same way as in the previous experiments, but generating three different types of normalized direction‐averaged signals for the same GT parameters as follows:

1. according to the SANDI models with additive Rician or Gaussian noise separately, to obtain SNRs of 30, 50, 100, 500, $\infty$;

2. according to the neurite exchange imaging model (Jelescu et al., 2022) with the addition of a third non‐exchanging compartment modeling diffusion restricted in sphere, like the SANDIX model in Olesen et al. (2022) using exchange time values between neurite and extracellular compartments of 5, 10, 15, 20, 30, 50, 100, 300, 500, and $\infty$ ms;

3. As in Point 2, but with the addition of Rician or Gaussian noise separately with SNRs of 30, 50, 100, 500, and $\infty$.

We then fit the SANDI model using GT values as initial condition and we computed the RMSE, the adjusted R² and the intercept of the linear fitting of the simulated GT SANDI parameters versus the estimated ones for each type of signals. Finally, for three representative values of exchange times (tex = 5, 50, and 300 ms) and two of SNRs (100 and $\infty$), we also computed the mean bias (defined as mean error, i.e., mean difference between simulated and estimated parameters), the standard deviation, and the RMSE of parameter estimates with respect to GT values. In all simulations, for each model parameter, we computed these three metrics using a sliding window of 200 consecutive simulated points and we plotted the values as a function of the synthetic test dataset.

2.3. In vivo data acquisition

Five HS (25–32 years old, two females) were scanned twice using the proposed acquisition scheme with six b shells, with head and bed repositioning to reset scanner settings and test the repeatability of both dMRI acquisition protocol and microstructural models. In addition, for each subject, we also acquired a three‐dimensional (3D) sagittal T1‐MPRAGE image (repetition time 2300 ms, inversion time 929 ms, echo time 2.96 ms, flip angle 8°, spatial resolution 1 × 1 × 1 mm³, acquisition time 5′12″), suitable for tissue segmentation.

Five MS patients (25–42 years old, all females with relapsing–remitting course; Thompson et al., 2018) underwent a scanning protocol including the proposed multi‐shell dMRI sequence (total acquisition time 10′01″ plus 47″ to acquire the reverse phased b = 0 s/mm² images), the 3D sagittal T1‐MPRAGE sequence (5′12″) as well as a 3D sagittal T2‐FLAIR (repetition time 5000 ms, inversion time 1800 ms, echo time 393 ms, spatial resolution 0.4 × 0.4 × 1 mm³, acquisition time 6′37″) and a 3D sagittal double inversion recovery (DIR) based on a prototype 3D turbo spin echo sequence (Costagli et al., 2022) (repetition time 5500 ms, inversion recovery times 2500 and 450 ms, T2 preparation time 125 ms, echo time 270 ms, spatial resolution 1.2 × 1.2 × 1.2 mm³, acquisition time 4′41″) suitable for MS lesion segmentation. Institutional Review Board approval was obtained to perform this study.

2.4. Image processing

We processed the MPRAGE images with FreeSurfer 6.0 (http://surfer.nmr.mgh.harvard.edu) (Fischl et al., 2002, 2004) and we used the standard Desikan‐Killiany (Desikan et al., 2006) atlas for the automatic segmentation that provides cortical and subcortical parcellation of 84 (42 per hemisphere) region of interest (ROI) as well as a 35 WM ROI per hemisphere which subtend the corresponding cortical ones. In addition, for the five MS subjects, lesions were manually segmented by a neurologist with more than 5 years of experience in neuroimaging on MPRAGE, FLAIR, and DIR images using a segmentation technique based on user‐supervised local thresholding (Jim 7.0, Xinapse System; http://www.xinapse.com) as described in Petracca et al. (2018) to create WM and GM lesion masks. The corresponding MPRAGE images underwent lesion filling using a T1‐hypointense lesion mask and FMRIB Software Library (FSL).

Given that our acquisition protocol uses parallel imaging, to compute the SNR from the b = 0 s/mm² images, we used the following definition, in accordance with Dietrich et al. (2007):

$$\mathrm{SNR}=\frac{1}{\sqrt{2}}\frac{{\text{mean}}_{\mathrm{ROI}}\left(S_1\left(b=0\right)+S_2\left(b=0\right)\right)}{{\mathrm{std}}_{\mathrm{ROI}}\left(S_1\left(b=0\right)-S_2\left(b=0\right)\right)},$$

where $S_1\left(b=0\right)$ and $S_2\left(b=0\right)$ are the first two consecutive b = 0 s/mm² images acquired. The SNR was calculated in three ROIs: the WM and GM masks, as well as their sum.

We then preprocessed each dMRI dataset using a combination of the FSL (Smith et al., 2004) and MRtrix3 (Tournier et al., 2019) software as well as the DESIGNER (Ades‐Aron et al., 2018) pipeline following these steps: denoise (Cordero‐Grande et al., 2019; Tournier et al., 2019), degibbs (Kellner et al., 2016), Rician bias correction (Koay & Basser, 2006), correction of movement artifacts and removal of susceptibility induced distortions (Andersson et al., 2016, 2003; Smith et al., 2004), N4‐bias correction (Tustison et al., 2010). As term of comparison with the existing literature, we also computed the apparent SNR obtained after the adopted preprocessing procedure as defined in Mosso et al. (2022), that is the SNR as defined in the equation above, but replacing $S_1\left(b=0\right)$ and $S_2\left(b=0\right)$ with the signals of the same b = 0 s/mm² volumes after all the preprocessing steps.

Using the preprocessed images we fit the following models recovering the relative microstructural maps: SANDI (Palombo et al., 2020); NODDI (Zhang et al., 2012); multi‐compartment SMT (Kaden et al., 2016); and DTI (Le Bihan et al., 2001).

To fit the SANDI and NODDI model we used the AMICO software (https://github.com/daducci/AMICO; Daducci et al., 2015). More in details, for SANDI we fixed the intra‐soma diffusivity to 3 μm²/ms, set the dictionary as 6 radii evenly spaced in the interval [1, 15] μm for the soma compartment, four intra‐neurite diffusivities equally distributed in [0.25, 3] μm²/ms, five isotropic diffusivities in [0.25, 3] μm²/ms, and the ${\mathcal{L}}_2$ regularization term equal to 7.5 × 10⁻⁴. This value for the regularization term was computed following the method described in Schiavi et al. (2022) adapted to the proposed protocol. With these choices, we obtained maps of neurite, extra‐neurite, and soma signal fractions (fneurite, fextra, and fsoma), apparent soma radius (Rsoma), intra‐ and extra‐neurite diffusivities (Din and De). Hereafter, we will refer to SANDI‐AMICO to refer to in vivo maps computed according to the SANDI model through the AMICO toolbox.

To fit the NODDI model, we used only the measurements with b ≤ 3000 s/mm² with the default AMICO settings and obtained the maps of intra‐neurite and isotropic volume fraction (ICVF and ISOVF) and OD index. The former describes the intra‐axonal environment, the second the free water in the extracellular environment, whereas the latter describes the fiber dispersion parametrised through the Watson distribution (Zhang et al., 2012).

To fit the multi‐compartment SMT model, we used the online open‐source software (https://github.com/ekaden/smt) on measurements with b ≤ 3000 s/mm² with the default settings. We derived maps of intra‐neurite diffusivity (diff), intra‐neurite signal fraction (intra), and extra‐neurite mean and transversal diffusivities (extramd and extratrans).

To compute microstructural maps from the DTI model, we used the measurements with b ≤ 1000 s/mm² for the fitting of the diffusion tensor in FSL (O'Donnell & Westin, 2011) using the default settings. We retrieved the microstructural maps of FA, MD, AD, and RD. The first describes the degree of the diffusion process anisotropy, the second is the mean of the three eigenvalues of the diffusion tensor, whereas the third describes the diffusion perpendicular to the main diffusion direction (Le Bihan et al., 2001).

Finally, using FSL FLIRT with boundary‐based optimization, we rigidly co‐registered (Greve & Fischl, 2009; Jenkinson et al., 2002) the 84 GM ROIs and grouped those and the corresponding WM ones to form the classical major brain macroregions: temporal, cingulate, occipital, frontal and parietal lobes, as well as insula, subcortical, and cerebellum regions. For each model, we extracted the mean value of every microstructural map in each ROI. We used subject‐specific ROIs instead of whole‐brain voxel‐wise statistics to remove potential bias due to different brain positions and deformations. For the statistical tests, we grouped the ROIs into the corresponding lobes. In patients, by using the previously obtained transformation matrix, the WM and GM lesion masks were rigidly co‐registered to the dMRI space to extract mean values of microstructural metrics also inside these ROIs and compare them with those extracted from normal‐appearing white matter (NAWM) and normal‐appearing gray matter (NAGM) tissues obtained by subtracting the lesion masks from the WM and GM masks estimated by applying FreeSurfer on the lesion‐impainted T1 images.

2.5. Statistics

Following what was done in Palombo et al. (2023) and Veraart et al. (2021), to evaluate the reliability of each diffusion metric per subject and lobes, we used the test–retest variability (TRV), the intraclass correlation coefficient (ICC) as well as Pearson's r and derived coefficient of determination R ². As done in Veraart et al. (2021), the Pearson r, the coefficient of determination R ², and the ICC enabled the assessment the repeatability of the computed microstructural metrics, while TRV values were used to assess reproducibility.

The TRV of estimates of parameter $\theta$ was computed across N ROIs in each lobe as:

$$\mathrm{TRV}=\frac{\sqrt{\pi }}{2N}\sum _{i=1}^N\frac{\left|{\mathrm{\Delta }}_{\theta }\left(x_i\right)\right|}{{\mu }_{\theta }\left(x_i\right)},$$

with ${\mathrm{\Delta }}_{\theta }\left(x_i\right)$ and ${\mu }_{\theta }\left(x_i\right)$ being the difference and the average of the test and retest estimates of parameter $\theta$ in the ith ROI $x_i$, respectively.

The ICC was calculated for two‐way mixed effects, single measurement, with absolute agreement using the pingouin package of Python 3 (https://pingouin-stats.org). As in Veraart et al. (2021), the ICC estimates were interpreted based on the following guidelines: values less than 0.5 indicate poor reliability, values between 0.5 and 0.75 indicate moderate reliability, values between 0.75 and 0.9 indicate good reliability, and values greater than 0.90 indicate excellent reliability. ICC values were interpreted considering the 95% confidence interval (CI).

Finally, Pearson correlation r and R ² were computed using the stats module in the scipy package of Python 3 (https://scipy.org).

To evaluate the clinical utility of the SANDI metrics computed from our optimized protocol with the AMICO toolbox, we compared the distributions of all the diffusion metrics in HS WM, MS NAWM, MS FLAIR hyperintense lesions, HS GM, MS NAGM, and MS GM lesions using Mann–Whitney U nonparametric test when comparing HS with MS patients and paired Wilcoxon test when comparing normally appearing tissues and lesions within MS subjects.

3. RESULTS

We present the results obtained with the newly proposed dMRI protocol in four sections. First, we present analytical simulations to show the stability of parameter estimations using six shells and assess the effect of noise and increasing exchange time. Second, we show an example of the images obtained with the acquisition and present the SNR and apparent SNR estimated on the five HS. Third, we show the reproducibility and repeatability of the SANDI microstructural maps derived on five HS who were scanned twice. Finally, we present a clinically meaningful application demonstrating the utility of such metrics when studying MS lesions in five patients with relapsing–remitting course (Thompson et al., 2018).

3.1. Simulations

Figure 1 reports the results of the numerical simulations conducted to investigate the stability of the fit at decreasing number of shells and Rician noise with different SNR. Analogous results for Gaussian noise are reported in Figure S1. For each SANDI microstructural metric, we show the RMSE, adjusted R ² and intercept estimated using a different number of shells and three choices of SNR: $\infty$ (i.e., no noise), 100 (which approximates our in vivo experiments), and 50. As expected, all the reported measures show that at SNR = $\infty$ the performances do not get worse when lowering the number of shells. By decreasing the SNR instead, we see very small biases in all the reported measures which for SNR = 100 are at most ~15% (for De) in the worst‐case scenario. However, the protocol with 6 shells allows an acquisition time of 10 min, while the acquisition of 14 shells require the ~24 min, which prevents application in clinical settings. Analogous results hold also when we initialized NLLS using GT data with 25% Gaussian noise (results shown in Figure S2 for Rician noise and Figure S3 for Gaussian noise).

FIGURE 1.

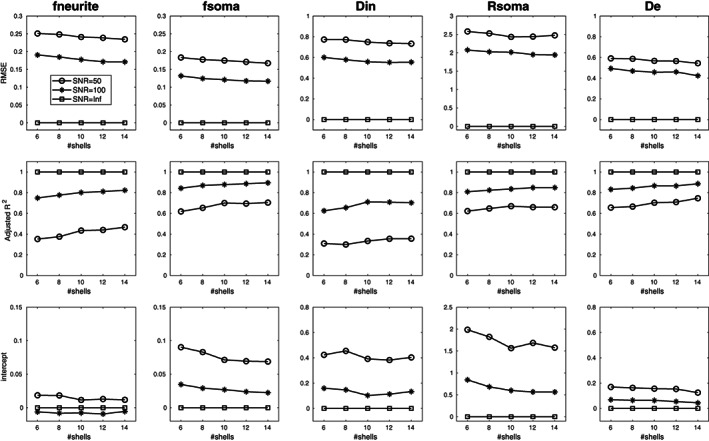
Root mean square error (RMSE), adjusted R ², and intercept estimated for each parameter of SANDI model computed using the same parameters and maximum b value, but a different number of shells: from 6 corresponding to our protocol to 14. The three curves represent simulations preformed for different signal‐to‐noise ratio (SNR) of the spherical average: circle markers for SNR = 50, asterisk markers for SNR = 100 and squares in absence of noise (i.e., SNR equal infinite). Diffusivities are reported in μm²/ms and Rsoma in μm.

Figure 2 reports the mean bias, standard deviation, and RMSE of parameter estimates with respect to GT values computed for the 6 and 14 shells protocols and three representative values of SNRs (50, 100, and Inf) using a sliding window of 200 consecutive simulated points. Again, we observe only small differences between the two protocols, while the effect of SNR is predominant. In particular, fneurite is more sensitive to the SNR than fsoma and the accuracy is lower for larger values of fneurite (higher bias). Rsoma is better estimated in the central values of our parameter space (from 5 to 10 μm), while Din and De have the same trend of fneurite, but they show good accuracy (bias close to 0) for reasonable values estimated in vivo (i.e., between 1 and 2.5 μm²/ms).

FIGURE 2.

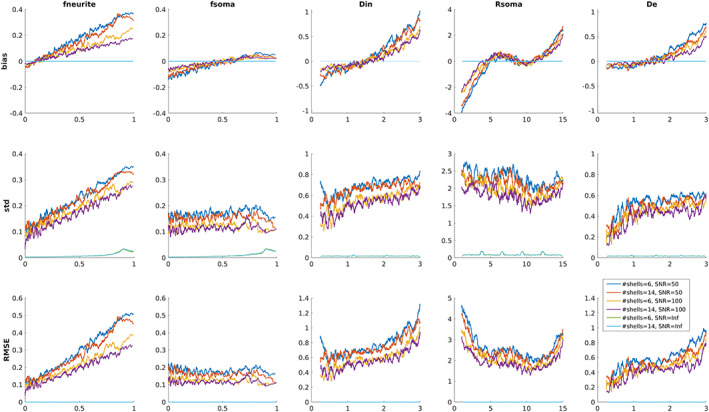
Parameter estimation performance as a function of the ground truth parameter for the 6 and 14 shells protocols and three representative values of SNRs (50, 100, and Inf). For each plot a single point represents the metric computed using a sliding window of 200 consecutive simulated points. Diffusivities are reported in μm²/ms and Rsoma in μm.

Figure 3 reports the results of the simulations conducted to investigate the biases caused by exchange with different characteristic exchange times (tex) between neurite and extracellular compartments and decreasing SNR adding Rician noise. Analogous results for Gaussian noise are reported in Figure S4. For each SANDI microstructural metric, we show the RMSE, adjusted R ² and intercept obtained using the proposed acquisition protocol and by varying only the exchange time with no noise (black curve), only the SNR with no exchange (dashed lines with different colors corresponding to different SNR levels) and the exchange time at different SNR levels (continuous lines with different colors corresponding to different SNR). Our results suggest that the impact of exchange on the accuracy and precision of SANDI model parameters estimates becomes dominant over that of noise only at high SNR and short tex. In particular, for tex ~20–50 ms, like those estimated in vivo in cortex (Jelescu et al., 2022), and SNR = 100, as in our experimental conditions, our simulations predict: (a) an increase of RMSE with respect to its reference value due to only noise of ~7.9%–2.9% for fneurite, ~7.5%–3.5% for fsoma, ~12.8%–5.9% for Din, ~7.5%–3.3% for Rsoma and ~9.0%–4.0% for De; (b) a decrease of R ² with respect to its reference value due to only noise of ~12.9%–2.1% for fneurite, ~5.5%–2.4% for fsoma, ~7.8%–6.5% for Din, ~1.6%–0.6% for Rsoma, ~8.3%–2.5% for De; (c) a less clear trend of the intercept: a decrease of intercept value with respect to its reference value due to only noise of ~62.9%–66.2% for fneurite, but an increase of intercept value with respect to its reference value due to only noise of ~36.9%–22.7% for fsoma, ~104.2%–109.5% for Din, ~89.9%–86.2% for Rsoma, and of ~108.4%–117.6% for De.

FIGURE 3.

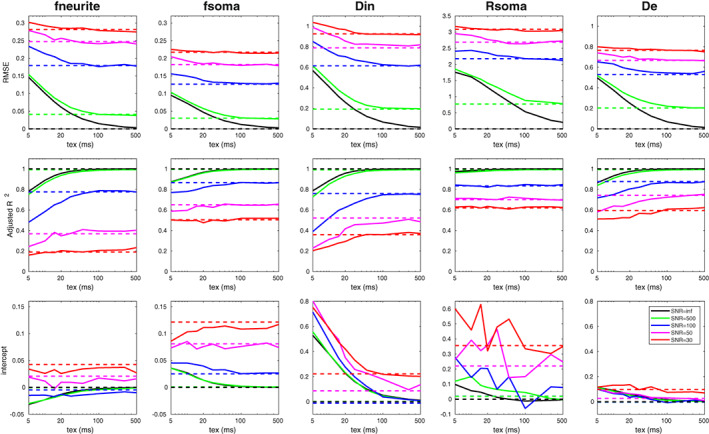
Root mean square error (RMSE), adjusted R ² and intercept estimated for each parameter of SANDI model computed using the proposed acquisition protocol and by varying the exchange time without noise (continuous black line) and with additive Rician noise (continuous colored lines: green for SNR = 500, blue SNR = 100, magenta SNR = 50, and red SNR = 30). Dashed lines refer to simulations without exchange for different SNR levels. Diffusivities are reported in μm²/ms and Rsoma in μm.

Figure 4 reports the mean bias, standard deviation, and RMSE of parameter estimates with respect to GT values computed for three representative values of tex (5, 30, and 300 ms) and two SNRs (100 and Inf) using a sliding window of 200 consecutive simulated points. Again, for SNR = 100 the impact of exchange is small: curves representing different tex are more similar to each other, with respect to curves referring to SNR = Inf. In the absence of noise fneurite is more sensitive to tex at the center of the simulated parameter space, but when we lower the SNR to the realistic values we observe a similar behavior to that in Figure 2 where the accuracy and precision decrease for increasing values of fneurite (higher bias). On the contrary, the accuracy and precision of fsoma are higher for larger values of this parameter (bias close to zero and small standard deviation and RMSE). In the absence of noise Rsoma is more sensitive to tex for lower values, but for values bigger than 5 μm for realistic SNR levels the estimates are more accurate. Similarly, for Din and De at SNR = 100 the effect of tex is much smaller than that of noise and in the range of values expected in vivo (i.e., between 1 and 2.5 μm²/ms) the estimates are rather accurate.

FIGURE 4.

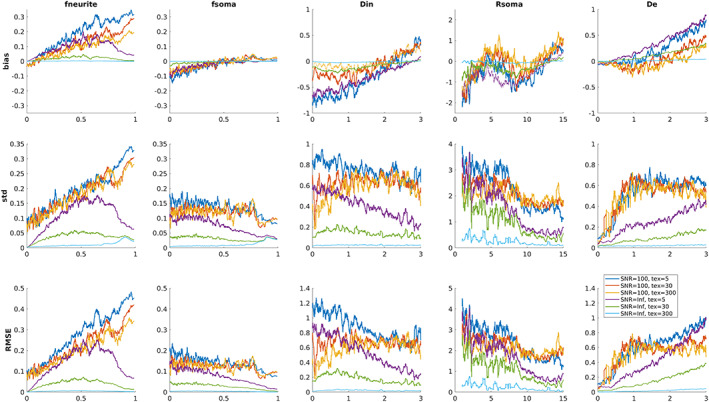
Parameter estimation performance as a function of the ground truth for three representative values of tex (5, 30, and 300 ms) and two SNRs (100 and Inf). For each plot, a single point represents the metric computed using a sliding window of 200 consecutive simulated points. Diffusivities are reported in μm²/ms and Rsoma in μm.

3.2. Quality assessment of images

Figure 5 shows sample images of the proposed acquisition scheme on one HS for qualitative evaluation. The top row shows representative images for the same gradient direction at all b values; in the middle row we show the spherical average at each b value, while in the bottom row we show the estimated maps of intra‐neurite (fneurite), extra‐neurite (fextra), and intra‐soma (fsoma) signal fractions, apparent soma radii (Rsoma), and intra‐ and extra‐neurite diffusivities (Din, De), obtained with SANDI‐AMICO. In Table 1, we report for each HS the estimated SNR and apparent SNR values in three ROIs (WM, GM, and WM + GM) computed on the raw and preprocessed b = 0 s/mm² images, respectively. In WM we obtained SNR = 15.85 ± 1.18 and apparent SNR = 57.37 ± 6.22, in GM SNR = 17.33 ± 1.56, and apparent SNR = 53.04 ± 11.17, and in the WM + GM mask SNR = 16.72 ± 1.39 and apparent SNR = 57.76 ± 10.95. Thus, our in vivo estimations correspond to the results obtained for SNR ~ 100 in simulations which suppose an SNR computed after averaging over all the gradient directions (spherical mean). Since each shell of our protocol has from 6 to 40 directions, using the spherical mean definition, multiplying the numbers in Table 1 by √(#directions) our in vivo SNRs ranges between 65 and 113.

FIGURE 5.

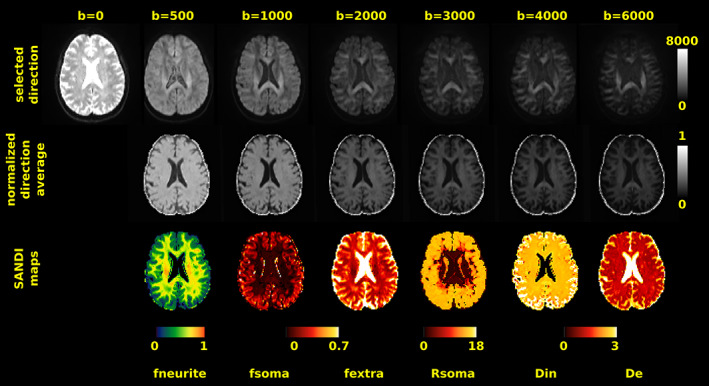
Quality assessment. Visual inspection of raw dMRI data (first row) acquired in one healthy subject with our sequence and corresponding normalized spherical average (second row) and SANDI microstructural maps (third row). Intensity of raw dMRI in the first row is in arbitrary unit. Scaling was kept constant across b values to visually assess the signal drop for increasing b values. In the bottom row, diffusivities are reported in μm²/ms, Rsoma in μm and b values in s/mm².

TABLE 1.

Estimated SNR (on raw b = 0 s/mm² images) and apparent SNR (on preprocessed b = 0 s/mm² images) for white matter (WM), gray matter (GM), and the sum of the two (WM + GM).

Subject	SNR			Apparent SNR
	WM	GM	WM + GM	WM	GM	WM + GM
S001	17.48	19.03	18.40	66.02	69.30	67.93
S002	16.12	18.39	17.47	56.59	56.34	56.16
S003	14.88	15.47	15.23	49.24	46.51	49.68
S004	14.54	15.91	15.32	54.91	50.98	63.36
S005	16.25	17.86	17.16	60.09	52.08	61.67

Note: Each row represents the value obtained for one HS.

3.3. Reproducibility analyses

To assess the reproducibility of the microstructural metrics we compared those derived using the SANDI model—computed from the entire dMRI dataset—with those obtained from the widely used models in clinical research: NODDI, SMT, as well as DTI which is the gold standard in clinical practice—computed from the appropriate low shells of the dMRI dataset. Figure 6 reports the scatter plots, Pearson r and coefficient of determination R ² of scan–rescan mean metric values in the predefined 84 GM ROIs derived from the FreeSurfer Desikan‐Killiany atlas (Desikan et al., 2006). Points are color‐coded by subjects and markers indicate different brain regions (frontal, parietal, occipital, temporal, cingulate, insula, subcortical, or cerebellum). For the GM ROIs the R ² of metrics derived using the SANDI model are in the range [0.501, 0.926], the ones from NODDI model in [0.641, 0.961], from the SMT model in [0.842,0.961], and from the DTI signal representation in [0.794, 0.914]. Figure S5 shows the same analysis performed on five GM and five WM ROIs defined using the classical subdivision in “macro brain regions.” In that case we obtained R ² in the range [0.736, 0.974] for SANDI, [0.952, 0.991] for NODDI, [0.886, 0.976] for SMT, and [0.958, 0.998] for DTI.

FIGURE 6.

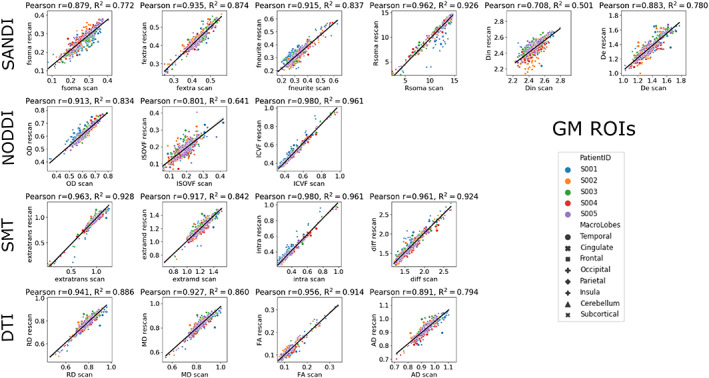
Repeatability of microstructural metrics. Scatter plots of scan–rescan microstructural metrics extracted from the 84 GM ROIs of the Desikan‐Killiany atlas. Points are color‐coded by subjects and markers indicate the macro region they were extracted from. Diffusivities are reported in μm²/ms and Rsoma in μm. Above each plot, Pearson r and coefficient of determination R ² are reported.

In Figure 7 we show the Bland–Altman plots as well as TRV, ICC and 95% CI of scan–rescan microstructural values in the same ROIs. For the GM ROIs the TRV and ICC values are in the range [8.2%, 32.1%] and [0.702, 0.956] for SANDI, [11.2%, 48.1%] and [0.8, 0.974] for NODDI, [10.9%, 18.8%] and [0.917, 0.975] for SMT, and [8.3%, 23.6%] and [0.878, 0.954] for DTI. In Figure S6, we show the same indices for the combined WM and GM ROIs. For those the TRV and ICC values are in the range [0.9%, 4.4%] and [0.859, 0.987] for SANDI, [1.4%, 3.7%] and [0.973, 0.994] for NODDI, [0.9%, 2.2%] and [0.942, 0.984] for SMT, and [0.8%, 1.6%] and [0.975, 0.999] for DTI. These plots and indices (Figures 6, 7, S5, and S6) show that the repeatability and reproducibility of the SANDI model are comparable with those of DTI, NODDI, and SMT (ICC always >0.7 and R ² > 0.7). Moreover, besides the information obtained with DTI, NODDI and SMT, SANDI provides additional indices of fsoma and Rsoma that can be used to obtain a more specific description of the underlying tissues microstructure.

FIGURE 7.

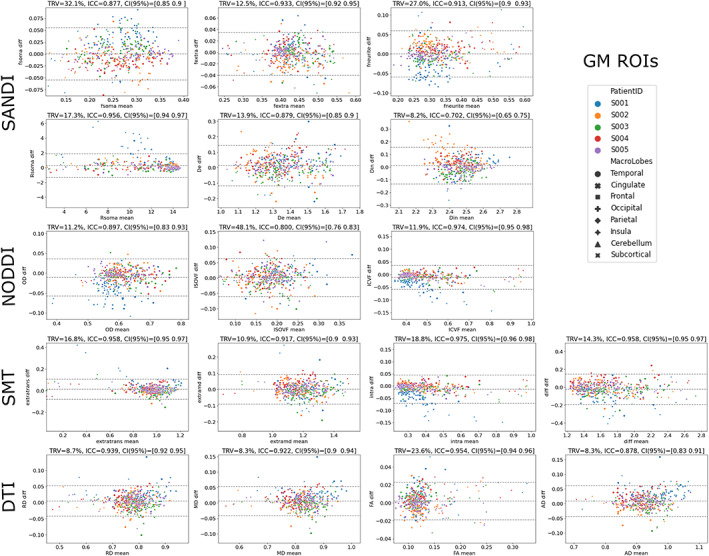
Repeatability and reproducibility of microstructural metrics. Bland–Altman plots of scan–rescan microstructural metrics extracted from the 84 GM ROIs of the Desikan‐Killiany atlas. Points are color‐coded by subjects and markers indicate the macroregion they were extracted from. Diffusivities are reported in μm²/ms and Rsoma in μm. Above each plot, the estimated TRV, ICC, and 95% confidence interval (CI) are reported.

3.4. Clinical application

Given the repeatability and reproducibility showed for SANDI‐AMICO microstructural metrics derived from the proposed sequence on a clinical scanner, we assessed if additional information on fsoma and Rsoma obtained from SANDI can provide important additional insights in diseased brains. To present a practical example, we acquired the proposed sequence in five MS patients, and we qualitatively and quantitatively evaluated the resulting maps in NAWM and NAGM as well as in lesions identified by an experienced neurologist as hyperintense ROIs on FLAIR images or hypointense ROIs on MPRAGE images. Figure 8 reports selected sagittal slices of the microstructural metrics estimated on a 30‐year‐old female MS patient. The arrows indicate a lesion within a cortical area. For DTI, NODDI, and SMT, we show that AD, MD, RD, ISOVF, extramd, and extratrans values were higher, while ICVF and intra‐axonal signal fraction values were lower in the lesion compared to the surrounding GM. Of note, FA and OD did not show visible abnormalities. In the same cortical region, SANDI showed a decrease in fsoma, Rsoma, and fneurite.

FIGURE 8.

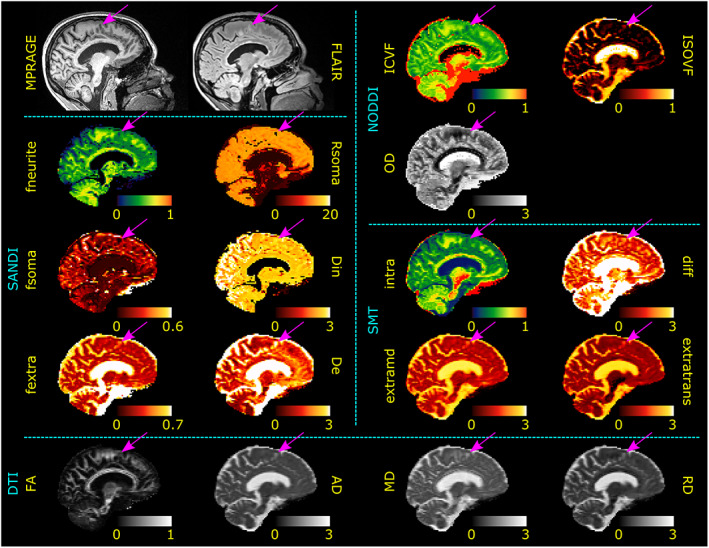
Gray matter lesion. Sagittal views of MPRAGE and FLAIR images as well as SANDI, NODDI, and DTI metrics of an MS subject. Diffusivities are in μm²/ms and Rsoma in μm. Purple arrows indicate the location of a cortical lesion to be compared with the surrounding normal‐appearing GM tissue. Although alterations in DTI, NODDI, and SMT metrics are visible (increased AD, MD, RD, ISOVF, extramd, and extratrans as well as a decrease in ICVF and intra), SANDI provides a deeper understanding of the pathological process underlying the lesioned tissue showing a decrease in fneurite, fsoma, Rsoma, and increase in fextra and De.

Figure 9 shows selected sagittal maps of the microstructural metrics estimated from a 33‐year‐old female MS patient. The arrows indicate two different WM lesions. Here, the DTI metrics show the same alteration in both lesions (increase in AD, MD, RD); NODDI maps show an increase in ISOVF only in the dorsal one (purple arrow) while SMT maps show an increase in extramd only in the dorsal lesion and a decrease in diff only in the other one. Similarly, SANDI maps show a decrease in fneurite and an increase of fextra in both lesions but fsoma, Rsoma and De appear altered only in the rostral lesion indicated by the blue arrow.

FIGURE 9.

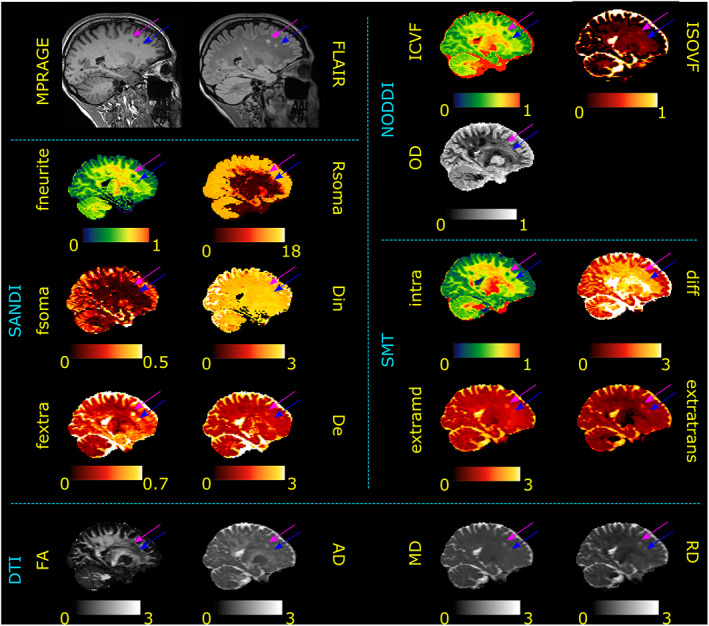
Lesions discrimination in white matter. Sagittal view of MPRAGE, FLAIR images, and SANDI, NODDI, and DTI metrics of an MS subject. Diffusivities are in μm²/ms and Rsoma in μm. Purple and blue arrows indicate the location of two WM lesions to be compared with the normal‐appearing WM tissue. DTI shows an increase in AD, MD, RD in both lesions; NODDI shows a decrease in ICVF in both lesions and an increase in ISOVF only in the lesion indicated by the purple arrow; SMT shows a decrease in intra and an increase in extratrans in both lesions, a decrease in diff in the rostral (blue arrow) lesion and an increase in extramd only in the lesion indicated by the purple arrow; SANDI shows a decrease in fneurite and an increase in fextra in both lesions and an increase in Rsoma and De only in the lesion indicated by the purple arrow.

To quantitatively evaluate the SANDI‐derived metrics, we compared their mean values in WM and GM between HS and MS patients and among NAWM, NAGM, FLAIR visible lesions, and GM lesions in MS patients. Figure 10 reports the boxplots of these comparisons for all the microstructural metrics, while Table 2 the respective summary statistics. Regarding WM (fourth column in the table), we observed that the MS patients have clearly altered parameters of fneurite and fextra (p = .009) in NAWM compared to WM from HS. Moreover, the MS FLAIR visible lesions resulted very different from both WM of HS (p = .009) and the same subjects NAWM (p = .043). Conversely, in GM, only fextra and De resulted altered in MS NAGM compared to GM of HS. Finally, regarding GM lesions, we observed a clear distinction from GM of HS of all the tissue densities (p < .02), while only fsoma and fextra resulted altered with respect to NAGM of the same subjects (p = .043) with fneurite showing a trend (p = .080). For the same ROIs, NODDI, SMT, and DTI also detected several differences between HS and MS patients in NAWM (p ranging between .009 and .047) and NAWM and lesions (p = .009). However, some differences were less marked compared to those shown by SANDI. Moreover, for these models the interpretation of GM findings was far from straightforward (e.g., the decrease of ICVF for NODDI and increase of FA for DTI in GM lesions compared to NAGM which should be directly correlated instead).

FIGURE 10.

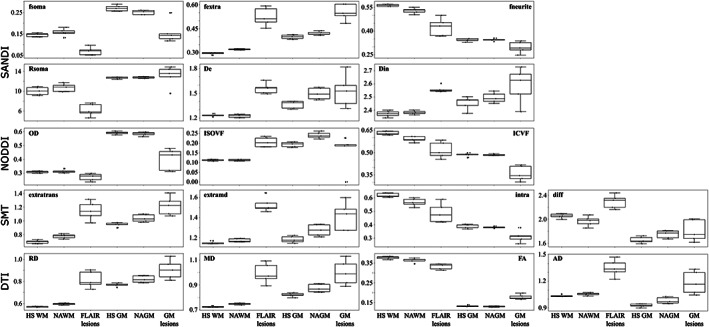
Clinical application. Box plots comparing SANDI, NODDI, SMT, and DTI metrics between five healthy subjects (HS) white matter (WM) and gray matter (HS GM) with normal‐appearing white and gray matter (NAWM and NAGM), white matter FLAIR hyperintense lesions, and GM lesions of five patients affected by multiple sclerosis (MS). Values of single subjects are displayed as dots for both groups. Diffusivities are in μm²/ms and Rsoma in μm. We observe that the lack of description of the cell body compartment prevents NODDI, SMT, and DTI to clearly identifying the different mechanisms underlying NAWM and WM FLAIR hyperintense lesions microstructural alterations, while SANDI metrics describe a different trend of damage according to the specific region. It is worth noting, in gray matter, the not easily interpretable increased FA in lesions compared to NAGM found with DTI which is in contradiction with the decrease in ICVF found by NODDI.

TABLE 2.

Summary statistics relative to the boxplots reported in Figure 10.

	HS		MS NA		MS lesions		HS vs. MS NA		HS vs. MS lesion		MS NA vs. MS lesion
	Mean	std	Mean	std	Mean	std	Z	p	Z	p	Z	p
White matter
SANDI
fneurite	0.5636	0.0070	0.5293	0.0175	0.4248	0.0562	−2.611	.009	−2.611	.009	−2.023	.043
fsoma	0.1450	0.0084	0.1565	0.0176	0.0690	0.0186	−1.358	.175	−2.611	.009	−2.023	.043
fextra	0.2953	0.0062	0.3204	0.0035	0.5245	0.0582	−2.611	.009	−2.611	.009	−2.023	.043
Rsoma (μm)	10.015	0.811	10.699	0.818	6.192	1.243	−1.149	.251	−2.611	.009	−2.023	.043
De (μm2/ms)	1.2331	0.0138	1.2261	0.0202	1.5563	0.0652	−0.522	.602	−2.611	.009	−2.023	.043
Din (μm2/ms)	2.3711	0.0231	2.3809	0.0138	2.5577	0.0257	−0.94	.347	−2.611	.009	−2.023	.043
NODDI
ICVF	0.6298	0.0124	0.5897	0.0182	0.5162	0.0546	−2.611	.009	−2.611	.009	−2.023	.043
ISOVF	0.1121	0.0038	0.1127	0.0039	0.2051	0.0249	−0.104	.917	−2.611	.009	−2.023	.043
OD	0.3075	0.0067	0.3128	0.0126	0.2707	0.0264	−0.731	.465	−2.611	.009	−2.023	.043
SMT
diff (μm2/ms)	2.0530	0.0376	1.9636	0.0827	2.2906	0.1122	−1.776	.076	−2.611	.009	−2.023	.043
extramd (μm2/ms)	1.1478	0.0125	1.1720	0.0166	1.5274	0.0729	−1.984	.047	−2.611	.009	−2.023	.043
extratrans (μm2/ms)	0.6954	0.0245	0.7762	0.0319	1.1458	0.1339	−2.611	.009	−2.611	.009	−2.023	.043
intra	0.6188	0.0153	0.5661	0.0291	0.4866	0.0725	−2.611	.009	−2.611	.009	−2.023	.043
DTI
FA	0.3765	0.0071	0.3636	0.0111	0.3322	0.0146	−1.776	.076	−2.611	.009	−2.023	.043
MD (μm2/ms)	0.7248	0.0048	0.7476	0.0069	0.9930	0.0812	−2.611	.009	−2.611	.009	−2.023	.043
AD (μm2/ms)	1.0350	0.0115	1.0546	0.0152	1.3478	0.0952	−1.984	.047	−2.611	.009	−2.023	.043
RD (μm2/ms)	0.5690	0.0038	0.5944	0.0080	0.8154	0.0750	−2.619	.009	−2.619	.009	−2.023	.043
Gray matter
SANDI
fneurite	0.3437	0.0100	0.3436	0.0076	0.2966	0.0364	−0.104	.917	−2.402	.016	−1.753	.080
fsoma	0.2690	0.0139	0.2502	0.0100	0.1569	0.0525	−1.776	.076	−2.611	.009	−2.023	.043
fextra	0.3987	0.0136	0.4206	0.0121	0.5531	0.0514	−2.193	.028	−2.611	.009	−2.023	.043
Rsoma (μm)	12.677	0.186	12.764	0.165	13.048	2.109	−0.94	.347	−1.567	.117	−0.674	.500
De (μm2/ms)	1.3623	0.0464	1.4940	0.0700	1.5248	0.1977	−2.611	.009	−1.149	.251	−0.405	.686
Din (μm2/ms)	2.4528	0.0500	2.4941	0.0386	2.5870	0.1351	−1.149	.251	−1.776	.076	−1.483	.138
NODDI
ICVF	0.4854	0.0116	0.4848	0.0049	0.3599	0.0503	−0.731	.465	−2.611	.009	−2.023	.043
ISOVF	0.1931	0.0127	0.2402	0.0164	0.1591	0.0904	−2.611	.009	−0.313	.754	−2.023	.043
OD	0.5913	0.0104	0.5845	0.0137	0.3990	0.0783	−0.522	.602	−2.611	.009	−2.023	.043
SMT
diff (μm2/ms)	1.6524	0.0540	1.7472	0.0651	1.8040	0.1809	−1.776	.076	−1.358	.175	−0.674	.500
extramd (μm2/ms)	1.1812	0.0335	1.2736	0.0574	1.4122	0.1415	−2.193	.028	−2.611	.009	−1.753	.080
extratrans (μm2/ms)	0.9458	0.0290	1.0376	0.0543	1.2166	0.1365	−2.611	.009	−2.611	.009	−2.023	.043
intra	0.3891	0.0151	0.3805	0.0059	0.3115	0.0438	−0.731	.465	−2.402	.016	−1.753	.080
DTI
FA	0.1316	0.0035	0.1293	0.0027	0.1773	0.0130	−0.731	.465	−2.611	.009	−2.023	.043
MD (μm2/ms)	0.8206	0.0157	0.8738	0.0329	0.9986	0.1011	−2.611	.009	−2.611	.009	−2.023	.043
AD (μm2/ms)	0.9270	0.0189	0.9830	0.0357	1.1830	0.1300	−2.611	.009	−2.611	.009	−2.023	.043
RD (μm2/ms)	0.7678	0.0147	0.8194	0.0317	0.9064	0.0876	−2.514	.012	−2.611	.009	−1.761	.078

Note: For both white and gray matter, we compared mean values of SANDI, NODDI, SMT, and DTI microstructural maps between (i) healthy subjects (HS) and normal‐appearing tissue of multiple sclerosis patients (MS NA) and (ii) HS and MS lesioned tissue with a Mann–Whitney U‐test; (iii) MS NA and MS lesioned tissue with a paired Wilcoxon test. The first three columns report the mean and standard deviations (std) of each metric in the selected region of interest. For each comparison we report both Z scores and exact significance p values and we highlight in bold those resulting statistically significant after accounting for multiple comparisons to control the type I error in each separate diffusion model.

4. DISCUSSION

To the best of our knowledge, this is the first time that reproducibility and repeatability of a PGSE acquisition protocol suitable for in vivo SANDI parameter estimation in human brain on a clinical 3 T scanner is assessed. Specifically, inspired by the work of Genc et al. (2021), where the authors proved the reproducibility of SANDI parameters estimations in GM regions on subjects acquired on Connectom scanner with maximum b value = 6000 s/mm², we customized an advanced multi‐shell dMRI protocol (Feinberg et al., 2010; Moeller et al., 2010; Xu et al., 2013) to simultaneously minimize the diffusion time and maximize the gradient strengths to reach the high b values needed to disentangle and quantify the dMRI signal coming from the brain cell bodies (Palombo et al., 2020). In particular, given the lesser presence of myelinated neurites in the GM compared to WM, in GM, exchange between tissue compartments (e.g., intra‐neurite and extracellular space) may play an important role, resulting in a bias in the estimation of any microstructural features, from any model or representation that does not explicitly account for it, such as DTI (Le Bihan et al., 2001), NODDI (Zhang et al., 2012), SMT (Callaghan et al., 1979; Kaden et al., 2016), and SANDI (Palombo et al., 2020), just to mention a few (Jelescu et al., 2022; Olesen et al., 2022). For this reason, a dMRI acquisition aiming to characterize the microstructure of both WM and GM with these methods should be designed with the constraint of keeping the diffusion time constant and the shortest possible.

Because of physical and technical constraints of a 3 T scanner with maximum gradient strength of 80 mT/m, the smallest duration pulse and distance between the pulses we could achieve to obtain a maximum b value of 6000 s/mm² were δ = 24.66 ms and Δ = 39.07 ms, which corresponds to a diffusion time of ~30 ms. Using these values, another requirement of SANDI model is the acquisition of at least three b values ≥3000 s/mm². To define the final setting, we performed simulations starting from 14 shells and lowering them until 6 (minimum number needed to estimate the five parameters of SANDI model). Our analyses on synthetic data reported in Figures 1 and S1–S3, show that for a realistic SNR (i.e., ~80–120), the error in the estimations caused by lowering the number of shells at the minimum possible value is small (maximum RMSE at SNR = 100 after spherical mean comparable to our in vivo setting is 15% obtained in the estimation of De), but this enables shortening the acquisition time (i.e., we reduce it from ~24 min needed to acquire 14 shells to 10 min for 6 shells). Regarding the selection of number of directions for each shell we optimized it according to previous work highlighting the minimum number of directions needed for preforming reliable constrained spherical deconvolution (Tournier et al., 2007) and the recent work investigating the number of sampling directions needed for robust measures of the spherical mean diffusion weighted signal (Schilling et al., 2022). Similar to the analyses conducted in Epstein et al. (2022), in Figure 2 our simulations also evaluated the accuracy and precision in the parameter estimation by computing the mean bias, the standard deviation and the RMSE with respect to the GT values for the 6 and 14 shells protocols and three representative values of SNRs (50, 100, and Inf). The results shown in Figure 2 confirmed that the reduction from 14 to 6 shells has no major impact on the parameter estimation, and allowed us to better delineate the accuracy in the estimation for each single parameter when varying the SNR. In particular, for realistic noise levels, both accuracy and precision decrease for larger values of fneurite (bigger than 0.5), while fsoma is accurate in the entire parameter space with slightly less precision for small values. Rsoma resulted well estimated in the middle of the parameter space (between 5 and 10 μm), while Din and De had the same behavior of fneurite, but with a better accuracy for reasonable values expected in vivo (i.e., approximately mean bias 0 for diffusivities between 1 and 2.5 μm²/ms).

After defining the protocol parameters, we also performed simulations to investigate the potential bias caused by noise and/or exchange. Based on these simulations, indeed the exchange can decrease the accuracy and precision of SANDI parameters estimates, but this decrease depends on the characteristic exchange time and the SNR. For both simulated types of noise (Rician noise in Figure 3 and Gaussian noise in Figure S4), at very high SNR (> ~ 500) the impact of exchange is more severe than at lower SNR (<~100). In particular, for tex <20 ms, the impact of exchange is not negligible, while for tex ~20–50 ms (as estimated in vivo in rat brain cortex by Jelescu et al., 2022), the impact of exchange is lower than the impact of noise for SNR <~100. In particular, for SNR = 100 (which is comparable to our in vivo setting) and tex ~20–50 ms, we observe a 3%–13% increase of RMSE (with maximum reached for Din at tex = 20) and 2%–13% decrease of R ² (with maximum reached for fneurite at tex = 20), ascribable to exchange in that time range. Moreover, as already highlighted in Dhital et al. (2019) and Howard et al. (2022), the simulations also show that independently from the tex and SNR, the estimation of Din cannot be very accurate and precise in clinical setting where ultra‐high b values or the combination of linear and planar tensor encoding acquisitions cannot be used. Finally, Figure 4 reported the accuracy and precision in the parameter estimation for three representative values of tex (5, 30, and 300 ms) and two SNRs (100 and ∞). These plots confirmed that SNR has more impact than different tex, and allowed us to better delineate the accuracy in the estimation for each single parameter when varying the SNR for three representative values of tex (a very small one, 5 ms; a typical in vivo one, 30 ms; and a very high one, 300 ms). In the absence of noise (SNR = ∞), exchange biases each SANDI parameter in a specific way, e.g., fneurite is most biased (underestimated) for GT values around 0.5. However, with noise levels as those in our measurements (SNR = 100), the bias due to exchange is overcome by the bias due to noise. In other words, the bias due to noise covers the exchange‐specific misestimation. For example, noise level corresponding to SNR = 100 leads to an increasing underestimation of fneurite with increasing GT values. On the contrary, the accuracy and precision of fsoma are higher for larger values of this parameter, although even for small values we observe a good accuracy (small standard deviation and low RMSE). In absence of noise, Rsoma is more sensitive to tex for lower values, but at realistic SNR levels we have a good accuracy and precision for values bigger than 5 μm. Similarly, for Din and De the effect of tex is less predominant than the one of noise at realistic SNR levels, and we obtain good estimations for values expected in vivo (i.e., between 1 and 2.5 μm²/ms).

The SNR in WM and GM masks of the five HS scanned with the proposed protocols resulted in values in line with state‐of‐the‐art literature and stable across the subjects. Moreover, based on the values reported in Table 1, the unprocessed data have an SNR after spherical mean between 65 and 113 (considering the number of directions used for each shell) which suggests that the stability of the fitting of SANDI‐AMICO parameters and the bias caused by exchange are comparable with those in our simulations at SNR = 100. The qualitative evaluation of estimated SANDI‐AMICO metrics in Figure 5 shows a good contrast between WM and GM in fneurite, fsoma, fextra, and Rsoma. Only few voxels at the boundary of GM and CSF showed unexpectedly high fsoma, which is likely an artifact due to a partial volume with CSF in those voxels that were not part of the GM mask. This limitation does not compromise the advantages of using the proposed sequence and relative tissue characterization through SANDI‐AMICO.

As proof of the feasibility of our protocol on 3 T scanners and to demonstrate the possible clinical utility of the proposed sequence, we demonstrated the high repeatability (via Pearson r, coefficient of determination R ², and ICC) and reproducibility (via TRV) of all the model parameters on five HS. The plots and relative indices in Figures 6, 7, S5, and S6 show that the repeatability and reproducibility of SANDI metrics are comparable with those of DTI, NODDI, and SMT (ICC > 0.7 and R ² > 0.7). This further supports indirectly that unaccounted exchange effects do not significantly impact the repeatability and reproducibility of SANDI‐AMICO estimates. Moreover, although they were obtained with a different parcellation of GM, these results are in line with those obtained on the MICRA dataset (Genc et al., 2021) where—with a similar acquisition protocol as the one proposed here (same resolution and maximum b value but shorter pulse duration and diffusion time thanks to the high gradient strength achievable on Connectom scanner)—the authors looked at the reproducibility of fneurite, fextra, fsoma, and Rsoma in GM and found that the mean ICC for these four metrics in all the ROIs tested was 0.95 and the lowest was 0.66. As expected, in our analyses the worse performances are always achieved for Din which is affected by technical factors that are not related to the translation of a multi‐shell sequence suitable for SANDI on a clinical scanner. Indeed, to gain accuracy and precision on the estimation of Din we would need either ultra‐high b values (Howard et al., 2022), or combine linear and planar tensor encoding acquisitions (Dhital et al., 2019), which is not straightforward on clinical scanners yet.

In addition to the information obtained with DTI, NODDI and SMT, SANDI provides new indices such as fsoma and Rsoma that enable more specific characterization of GM and that likely reflect the cell body population (neurons, astrocytes, microglia) (Ianuş et al., 2022; Palombo et al., 2020) in the WM, which can potentially help better characterize the complex tissue substrates. In particular, this was evident in Figures 8 and 9 which show how SANDI metrics depict the changes in microstructure in both GM and WM tissues in MS lesions. In the GM lesion shown in Figure 8, SANDI depicts a decrease in fsoma, Rsoma, and fneurite. As previously described in Wegner et al. (2006), a decrease in neuronal density and size highlighted by the decrease in fneurite and Rsoma might be related to a depletion of dendritic processes and an increase in the free water content (reflected by the increase in fextra). If confirmed on a larger cohort of subjects, this feature may represent the histopathological hallmarks of demyelinating cortex in MS (Trapp et al., 2018). In the two WM lesions in Figure 9, which appear hyperintense in FLAIR and hypointense in MPRAGE images, SANDI depicts an increase of fextra in both lesions, but fsoma results altered only in one. In particular, NODDI and SMT showed altered ISOVF and extramd respectively only in one lesion suggesting that the higher component of free water is what best describes the underlying pathological process in this region. However, when using SANDI, while both lesions present a higher extra‐axonal signal fraction than the surrounding NAWM (increased fextra), what distinguishes the two is instead the presence of a cell body compartment (increased fsoma). This might be biologically explained by infiltration of blood‐derived monocytes or activated microglia and, to a lesser extent, of T cells, in the perivascular space as well as throughout the lesion area (Kuhlmann et al., 2017). Considering recent evidence, which has highlighted the role of compartmentalized inflammation (both in NAWM and FLAIR hyperintense lesions) as a key mechanism in driving disability progression (Gillen et al., 2018), being capable of detecting resident inflammatory components inside WM lesions (increase of fsoma) might provide specific targets for new therapeutic approaches which could potentially delay and/or reverse clinical deficits. Future deeper investigations to validate this hypothesis should be conducted by complementing the acquisition protocol with other MRI contrasts like iron‐sensitive maps from quantitative susceptibility mapping (Deistung et al., 2017). However, a recent study (Margoni et al., 2023) applying the SANDI model to a cohort of MS subjects showed exciting promising results despite a coarser resolution (2.5 mm isotropic vs. our proposed 2 mm isotropic), a larger exchange bias (diffusion time of ~39 vs. ~31 ms) and fewer sampling directions (resulting in a less robust estimation of spherical mean diffusion weighted signal; Schilling et al., 2022) than those adopted in our protocol.

To provide a more quantitative evaluation of SANDI‐AMICO metrics in both GM and WM, we compared mean values of HS WM and GM with NAWM, NAGM, WM FLAIR visible hyperintense lesions, and GM lesions from MS patients (Figure 10 and Table 2). Even with the few subjects acquired (five HS and five relapsing–remitting MS patients), we observed a good separation in median values between HS WM/GM and MS patients NAWM/NAGM as well as NAWM and FLAIR hyperintense WM lesions and NAGM and GM lesions within patients. Regarding the WM, SANDI metrics show that the NAWM of MS patients has evident lower fneurite and higher fextra compared to HS WM but also a trend of higher fsoma and Rsoma suggesting the possible presence of microglial activation and astrogliosis due to widespread inflammation (increased fsoma and Rsoma), together with expected axonal damage (decreased fneurite). In patients, FLAIR hyperintense WM lesions compared to NAWM showed lower fneurite, fsoma, and Rsoma, as well as higher De and Din confirming previous histopathological (Lassmann et al., 2001) and MRI (Rahmanzadeh et al., 2021; Schiavi et al., 2021) studies suggesting that nonactive WM lesions are mostly characterized by demyelination, axonal loss, and hypocellularity. For the same ROIs, also NODDI, SMT, and DTI detect differences between HS WM and MS NAWM as well as NAWM and lesions in patients. However, once again the lack of description of the cell body compartment prevents a precise identification of the different mechanisms underlying NAWM and lesions alterations. Indeed, all metrics are altered in the same direction except for the diff parameter in SMT which results significantly higher in FLAIR lesions (p = .009) and lower in NAWM (p = .076) compared to HS WM and thus has no straightforward biological interpretation. In GM, in contrast with the conflicting increased FA in GM lesions compared to NAGM found with DTI (p = .009), SANDI shows lower fsoma and higher fextra and De in MS NAGM than HS GM (p < .028), while lower fsoma and higher fextra when comparing NAGM and GM lesions within patients (p = .043) with a trend of lower fneurite (p = .080). If confirmed in a larger patients' sample, this would suggest that there is a gradient of destruction between NAGM and GM lesions with a severe loss in cell body density and a more moderate neuroaxonal damage. Specifically, the results found in our MS patients could be explained by the fact that neuroaxonal alteration in GM appears in a later stage of the pathology (Jürgens et al., 2016; Möck et al., 2021).

5. LIMITATIONS AND FURTHER CONSIDERATIONS

Although we showed high repeatability and reproducibility of SANDI metrics in HS, we acknowledge that in the implementation of the dMRI sequence on our clinical scanners we could not obtain the diffusion time shorter than 20 ms suggested in (Jelescu et al., 2022; Olesen et al., 2022; Palombo et al., 2020), where a non‐exchanging multi‐compartment model can be used with minimal bias due to unaccounted exchange mechanisms. Thus, since we used longer gradient pulses (24 ms) and diffusion times (39 ms), our SANDI estimates may be biased by unaccounted inter‐compartmental exchange (Jelescu et al., 2022; Olesen et al., 2022). However, this bias affects all the microstructural models that do not account for exchange (i.e., also NODDI, SMT, and DTI) and is present for both HS and MS patients analyzed. Moreover, the simulations provided here for SANDI parameters highlight that the bias caused by exchange between neurite and extracellular compartments depends on the characteristic exchange time and the SNR. In particular, in the realistic scenario of SNR = 100 after spherical average (which is comparable to our in vivo setting) and tex ~20–50 ms, the impact of exchange is lower than that of noise and our simulations suggest that exchange on those time scales decreases of less than 13% the accuracy and precision of SANDI parameters. Therefore, by interpreting with care the resulting maps we can use this tool to better characterize the pathology.

We also highlight that, to minimize the acquisition time, we acquired all the diffusion directions with monopolar echo planar images and only the b = 0 images were acquired twice with the reverse phase encoding. Thanks to the application of the eddy toolbox we were able to apparently remove the frontal distortions, but not to recover the lost signal in those area. Thus, we advise to revise the protocol if the focus of certain application is on those areas known to be greatly affected by EPI phase encoding‐dependent distortions.

Another limitation is the small number of subjects enrolled in this study. Indeed, while five HS can be considered sufficient to assess the reproducibility of the metrics in such experiment as previously reported (Veraart et al., 2021), five MS subjects are certainly not sufficient to characterize this complex and heterogeneous pathology. However, the goal of our work was not to present an extensive analysis of tissue alterations in MS, but rather to demonstrate the potential of better capturing differences between tissue alterations that might appear identical with other sequences (like MPRAGE and FLAIR) or are difficult to be resolved and interpreted using other models like NODDI, SMT, and DTI. Indeed, our results suggest that SANDI metrics computed via AMICO toolbox can provide a more informative characterization of both GM and WM, compared to the other currently available methods.

Finally, this study was based solely on simulations and in vivo data, thus the interpretations made in the case of pathological data must be taken with care in absence of an accurate validation with histology.

6. CONCLUSIONS

For the first time, we implemented a clinically feasible dMRI protocol for 3 T scanners that can reliably assess GM and WM microstructure in a clinical setting according to the SANDI model fitted through the AMICO toolbox. The results presented here emphasize the importance of adopting more advanced signal models than the standard WM‐based model to investigate GM and demonstrate the clinical feasibility of a dMRI technique that can be implemented on performant 3 T scanners available at hospital sites. Indeed, as suggested by our preliminary results on MS patients, making such a tool available on clinical scanners provides the opportunity to study simultaneously GM and WM alterations and to better characterize brain development and neurological diseases.

AUTHOR CONTRIBUTIONS

Simona Schiavi and Matilde Inglese conceptualized the present work. Simona Schiavi, Marco Palombo, Mauro Costagli, and Domenico Zacà developed and optimized the dMRI acquisition protocol as well as acquired all the data. Simona Schiavi and Marco Palombo developed the pipeline of analyses and statistical assessment and visualized the results. Francesco Tazza, Caterina Lapucci, and Matilde Inglese enrolled and performed clinical evaluations of multiple sclerosis patients. Simona Schiavi wrote the first draft of the manuscript with help from Marco Palombo, Caterina Lapucci, Mauro Costagli, and Matilde Inglese. Simona Schiavi, Marco Palombo, Caterina Lapucci, Francesco Tazza, Domenico Zacà, Lucio Castellan, Mauro Costagli, and Matilde Inglese discussed the results and revised the manuscript.

CONFLICT OF INTEREST STATEMENT

Domenico Zacà is an employee of Siemens Healthcare, Italy. Other authors declare no conflict of interest.

Supporting information

DATA S1. Supporting Information.

Schiavi, S. , Palombo, M. , Zacà, D. , Tazza, F. , Lapucci, C. , Castellan, L. , Costagli, M. , & Inglese, M. (2023). Mapping tissue microstructure across the human brain on a clinical scanner with soma and neurite density image metrics. Human Brain Mapping, 44(13), 4792–4811. 10.1002/hbm.26416

DATA AVAILABILITY STATEMENT

Images acquired at the University of Genoa and IRCCS San Martino Hospital with the newly proposed protocol may be provided to interested researchers upon request to the corresponding author, after clearance from the IRB. All the codes used in this work are freely available and the corresponding links are listed in the Methods section of the manuscript. The parameters to replicate the newly proposed sequence are listed in the subsection “Proposed sequence and MRI acquisition” and the pulse sequence used can be requested from the University of Minnesota under the c2p agreement with Siemens Healthcare.