Mitigating biomass composition uncertainties in flux balance analysis using ensemble representations

Abstract

The biomass equation is a critical component in genome-scale metabolic models (GEMs): it is used as the de facto objective function in flux balance analysis (FBA). This equation accounts for the quantities of all known biomass precursors that are required for cell growth based on the macromolecular and monomer compositions measured at certain conditions. However, it is often reported that the macromolecular composition of cells could change across different environmental conditions and thus the use of the same single biomass equation in FBA, under multiple conditions, is questionable. Herein, we first investigated the qualitative and quantitative variations of macromolecular compositions of three representative host organisms, Escherichia coli, Saccharomyces cerevisiae and Cricetulus griseus, across different environmental/genetic variations. While macromolecular building blocks such as RNA, protein, and lipid composition vary notably, changes in fundamental biomass monomer units such as nucleotides and amino acids are not appreciable. We also observed that flux predictions through FBA is quite sensitive to macromolecular compositions but not the monomer compositions. Based on these observations, we propose ensemble representations of biomass equation in FBA to account for the natural variation of cellular constituents. Such ensemble representations of biomass better predicted the flux through anabolic reactions as it allows for the flexibility in the biosynthetic demands of the cells. The current study clearly highlights that certain component of the biomass equation indeed vary across different conditions, and the ensemble representation of biomass equation in FBA by accounting for such natural variations could avoid inaccuracies that may arise from in silico simulations.

Graphical Abstract

Highlights

• •Evaluated natural variations in macromolecular compositions in three model species.
• •Conducted sensitivity analysis to explore impact of biomass compositions on FBA.
• •Identified proteins and lipids to be most sensitive in phenotype predictions.
• •Proposed new approach FBAwEB to mitigate the uncertainty in biomass equations.

1. Introduction

Flux balance analysis (FBA) is a popular approach for analyzing cellular metabolic behaviors in silico [1]. Unlike dynamic modelling, which requires detailed kinetic parameters, FBA simply uses the information on metabolic reaction stoichiometry and mass balances around the metabolites, under pseudo-steady state assumption [2], [3]. Such simplicity of FBA and the availability of massive amounts of genome sequences from public databases have enabled the development of thousands of genome-scale metabolic models (GEMs) for a multitude of species across all three domains of life [4]. These GEMs have been successfully applied in various studies including microbial evolution, metabolic engineering, drug targeting, context-specific analysis of high throughput omics data and the investigation of metabolic interactions among cells and/or organisms [4], [5].

FBA is an optimization-based approach where a particular cellular objective is maximized or minimized while simultaneously constraining the mass balance, thermodynamic and enzyme capacity of a metabolic network to determine the plausible steady-state fluxes [6]. Maximization of biomass production has been the most commonly used objective function in FBA with a principal hypothesis that living cells typically strive to grow as fast as possible, particularly under the exponential growth phase [7], [8]. Almost all reconstructed GEMs include an artificial reaction, referred to as the ‘biomass equation’, that accounts for the stoichiometric proportions of various compounds that make up macromolecules of the cellular biomass, e.g., protein, DNA, RNA, carbohydrate, and lipid, for the use as objective function during FBA. In most cases, the macromolecular and monomer compositions used to derive this biomass equation are empirically determined under a certain experimental condition and assumed to remain similar across a wide range of growth environments. However, it is well-documented that cellular volume and the compositions of macromolecular components may vary depending on growth conditions and/or genetic makeup of cells [9], [10], [11]. For example, the RNA/protein ratio of Escherichia coli exhibits robust correlation with their growth phase and culture conditions such as nutrient utilization/depletion and waste-product accumulation [12]. Recent studies also demonstrated variation in protein and lipid composition in immortalized mammalian cell lines derived from the same original tissue [11], and dynamic nature of macromolecular composition in photoautotroph, Chlorella vulgaris, in phototropic and autotrophic conditions [13]. Therefore, the perseverative use of a biomass equation formulated from a single compositional dataset is questionable as the FBA phenotype predictions are sensitive to any variations in individual biomass components [14], [15], [16], [17], [18], [19], [20].

Efforts were recently undertaken to address the uncertainty associated with the biomass equation formulation in FBA. Lachance et al. [21] proposed “BOFdat”, in which genetic algorithm was used to obtain a particular biomass equation from a series of biomass equations which were stochastically generated by including/removing certain metabolites to best-fit the known gene essentiality data [21]. While this approach utilizes data from multiple environmental conditions to draft the biomass equation with relevant metabolites that make up the cell, it still cannot address the quantitative variations within each macromolecular/monomer component(s). In order to address the quantitative variations of biomass compositions, another study proposed two approaches [22]: 1) an optimal set of trade-off weights were assigned to multiple biomass equations so that it can fit the maximal growth rate; and 2) the coefficients of metabolites in the biomass equation are estimated by interpolation of known sets of macromolecular/monomer compositional data measured under different environmental conditions, assuming linearity between compositions and the environmental changes. The key limitation of this approach is the theoretical treatment of biomass variations, i.e., linear variation across environments, as macromolecules vary only within a certain range and not necessarily exhibit a linear relationship. The development of genome-scale metabolism and expression models (ME-models) systematically eliminated the use of a biomass equation by expanding the scope through the inclusion of pathways that constitute the cellular transcription and translation, and thus able to predict compositions of proteome and transcriptome with the constant structural composition [23], [24], [25]. However, it is often difficult to collect all the required kinetic parameters such as transcription/translation rates and catalytic turnover constants specific to each mRNA or enzyme to establish a good quality ME-model.

To address the uncertainties in the biomass equation and make it applicable across multiple environmental conditions, we first need to find answers to the following open questions: Do all macromolecular and monomer compositions in biomass vary across environmental conditions? If so, how significant are those variations? Do phylogenetically close organisms have similar monomer compositions? How reliable is the estimation of biomass composition from omics datasets? How much does such a natural variation of biomass composition impact model predictions? In this study, we first examined the variations in biomass compositions in three representative host organisms, namely E. coli, Saccharomyces cerevisiae and Chinese hamster (Cricetulus griseus) ovary (CHO) cells to answer all the above-mentioned questions. We also investigated the quantitative variation between monomer compositions obtained from omics datasets and the experimentally measured ones. Based on the analysis results, we newly propose the use of an ensemble of biomass equations within the FBA framework, to better capture the natural variation in biomass compositions.

2. Methods

2.1. Compilation of macromolecule and monomer compositions and the estimation of their natural variations

Macromolecular and monomer composition data for three representative species, E. coli, S. cerevisiae, and CHO cells, was collected through a targeted literature search. Data was collected from various studies which reported macromolecular and monomer composition across various conditions including changes in environmental conditions including temperature, dilution rates, oxygen concentrations, media compositions, and growth phases. Similar data was also collected from multiple mutants, strains, and cell lines of the same species. In addition, we also obtained the monomer composition for the species that are phylogenetically close to either of E. coli, S. cerevisiae, or CHO cells. The full list of biomass composition data and its source are available in Supplementary File S1.

Natural variability of all macromolecules and monomers were calculated using the coefficient of variation (CV). It was calculated by dividing the standard deviation of collected and/or processed composition data (mass % or mole %) by the mean value of the corresponding biomass component. The CVs of monomers necessitated an additional step, where the average of multiple monomer CVs was taken to represent a final CV. The variability of monomers in DNA was simply determined based on multiple guanine-cytosine (GC)-content data crawled with a query of each species name of the three organisms from NCBI genome database. Note that the estimation of ribonucleotides composition from omics data was not taken into consideration when we evaluated the CVs.

2.2. Estimation of monomer composition from omics-data

We collected multi-omics data of E. coli, S. cerevisiae, and CHO cells to estimate ribonucleotide and amino acid composition. Genome data were obtained from NCBI RefSeq database [26], transcriptomic datasets were collected from the Sequence Read Archive [27] and NCBI Gene Expression Omnibus (GEO) [28], and proteomic data was downloaded from PaxDB [29]. Note that amino acid composition is not estimated from proteome for CHO cells due to lack of whole proteomic data for CHO cells in PaxDB. The source information of each omics data used in this study is listed in Supplementary File S2.

For the transcriptome and proteome data, list of genes that were expressed were used to extract corresponding coding sequences to estimate the ribonucleotide and amino acid compositions. These gene lists were then classified into two categories: all expressed and top 10% highly expressed genes. In case of genome data, all known genes encoded were considered. The gene sets from each category were first labelled according to their respective source: Genome, Transcriptome-all, Transcriptome-high, Proteome-all, and Proteome-high for estimating amino acid composition, and Genome, Transcriptome-all and Transcriptome-high for ribonucleotide composition. While the coding sequences of genes were considered as it is for genome and transcriptome data, a corresponding amino acid sequence was first obtained using the ExPasy translate tool. Then the frequency of monomer i ($p_M^i)$ is obtained from the coding sequences as follows:

$${\mathrm{p}}_{\mathrm{M}}^{\mathrm{i}}=\{\begin{array}{cc}\frac{{\mathrm{\theta }}^{\mathrm{i}}}{{\mathrm{\theta }}_{All}}\forall i\in G,\hfill & ifGenome,Transcriptome-all,Proteome-all\hfill \\ \frac{{\theta }^i}{{\theta }_{Top10\%}}\forall i\in G,\hfill & ifTranscriptome-high,Proteome-high\hfill \end{array}$$

$$G=\{\begin{array}{cc}\{1,2,3,4\}\hfill & ifM=Ribonucleotide\hfill \\ \left\{\begin{array}{l}1,2,\dots 20\hfill \end{array}\right\},\hfill & ifM=\mathit{A}\mathit{min}\mathit{o}\mathit{a}\mathit{c}\mathit{i}\mathit{d}\hfill \end{array}$$

$$G=\left\{\begin{array}{c}\{1,2,3,4\},\\ \{1,2,...20\},\end{array}\right)\mathit{if}M=\mathit{Ribonucleotide}$$

$$\mathit{if}M=\mathit{Amino}\mathit{acid}$$

where ${\theta }^i$ stands for the occurrence of monomer i, and ${\theta }_{\mathit{All}}$ is the total number of monomers. Total number of monomers in genome was based on coding sequences of all genes while in transcriptome and proteome data it was based on expressed genes only. ${\theta }_{\mathit{Top}10\%}$ denotes the total number of monomer units encoded by top 10% expressed genes in transcriptome or proteome data while ${\theta }_{\mathit{All}}$ considers all genes expressed (count >10).

2.3. Sensitivity analysis of growth rates and intracellular metabolic fluxes upon biomass composition variations

We used parsimonious flux balance analysis (pFBA) [30] for analyzing the sensitivity of growth rate and intracellular fluxes upon varying biomass compositions. In this method, the GEM is first converted into irreversible one by converting all reversible reactions into two reactions in which one represent forward and the reverse direction, respectively. Then, the maximum possible growth rate is simulated by solving the following linear programming problem:

$$\max {Z=v}_{\mathit{biomass}}$$ (P1)

$$s.t{S}_{\mathit{irrev}}\bullet v_{\mathit{irrev}}=0$$

$$0\le v_{\mathit{irrev},j}\le v_{\max ,j}$$

where $S_{\mathit{irrev}}$ is a stoichiometric matrix where all reactions are represented as irreversible, $v_{\mathit{irrev},j}$ is the irreversible flux through reaction j, $v_{\max ,j}$ is the maximum allowable flux through reaction j, and $v_{\mathit{biomass}}$ denotes the flux through biomass equation. Subsequently, the following linear problem is solved where the sum of all irreversible fluxes is minimized while simultaneously constraining the previously obtained flux through biomass Eq. (P1) as the lower bound

$$\min \sum _j{v}_{\mathit{irrev},j}$$ (P2)

$$s.t.v_{\mathit{biomass}}\ge Z$$

$$S_{\mathit{irrev}}\bullet v_{\mathit{irrev}}=0$$

$$0\le v_{\mathit{irrev},j}\le v_{\max }$$

To investigate how flux predictions are affected by variations in biomass composition, we modified the coefficient of a specific component in a reference biomass equation. The reference equation was established based on the average composition of biomass. We altered the coefficient of the target component by 25% of the average mass fraction (g/g dry cell weight, DCW) and normalized the equation so that the total sum of all components equaled 1gDCW. We maintained the original relative amounts of the other macromolecules in the equation. Furthermore, we maintained the original monomer compositions when varying the mass fractions of the macromolecules, and vice versa. The biomass equation (B) can be represented as follows:

$$\mathit{B}\left(p,d,r,c,l,o\right)=$$

$$\mathit{P}\left(p,q_{\mathit{amino}\mathit{acid}}\right)+\mathit{D}(d,q_{\mathit{DNA}})+\mathit{R}(r,q_{\mathit{RNA}})+\mathit{C}(c,q_{\mathit{carb}})+\mathit{L}(l,q_{\mathit{fa}})+\mathit{O}(o,q_{\mathit{others}})$$

where p, d, r, c, l, o denotes the macromolecular weight fraction of protein, DNA, RNA, carbohydrate, lipid, and others such as ions/cofactors, respectively. The macromolecular synthesis equations, symbolized by P, D, R, C, L, O, are functions of q vectors representing the composition of monomers or ions.

By varying the biomass components iteratively, we first evaluated the change in in silico growth rate predictions using problem (P1). Next, we sought to estimate the sensitivity of metabolic flux distributions of all reactions to change in each biomass component. Flux vectors were obtained under two conditions: the reference condition, which was based on the average biomass composition, and an altered biomass composition condition where we modified the biomass equations. To obtain the sensitivity (s), we first obtained flux vectors (v) by solving problem (P2). We then calculated sensitivity (s) using equation as follows:

$$v_{\mathit{ref}}=v,\mathit{when}\mathit{B}\left(p_{\mathit{mean}},d_{\mathit{mean}},r_{\mathit{mean}},c_{\mathit{mean}},l_{\mathit{mean}}\right)$$

$$s={\sum }_i^N\frac{1}{2}\left(\frac{\left|v_{i,\mathit{ref}}-v_{i,\min }\right|}{v_{i,\mathit{ref}}}+\frac{\left|v_{i,\mathit{ref}}-v_{i,\max }\right|}{v_{i,\mathit{ref}}}\right)$$

where $p_{\mathit{mean}},d_{\mathit{mean}},r_{\mathit{mean}},c_{\mathit{mean}},l_{\mathit{mean}}$ are the average fractions of protein, DNA, RNA, carbohydrate, and lipid, respectively. N is the number of reactions in a GEM. To calculate the sensitivity of protein, for instance, we increased or decreased its mass fraction by 25% of the average fraction value and normalized the fraction of the other components (d’, r’, c’, l’), as shown below:

$$v_{\min }=v,\mathit{when}\mathit{B}\left({(1-0.25)\times p}_{\mathit{mean}},d\prime ,r\prime ,c\prime ,l\prime \right)$$

$$v_{\max }=v,\mathit{when}\mathit{B}\left((1+0.25){\times p}_{\mathit{mean}},d\prime ,r\prime ,c\prime ,l\prime \right)$$

Finally, we divided the absolute sensitivity by the sum of absolute sensitivities for all macromolecules and monomers to obtain the relative sensitivity.

All simulations were performed using the COBRA Toolbox v2.0 [31] implemented within MATLAB with Gurobi 7 as the optimization solver. The following GEMs were used for each organism: E. coli - iML1515 [32], S. cerevisiae - Yeast8.0.0 [33] and CHO cells - iCHO2291 [34].

2.4. Ensemble representations of biomass

In order to represent biomass equation as ensembles and implement pFBA using each of the biomass equation, the first step is to establish a single set of ‘reference’ macromolecular/monomer compositions, which can be determined by calculating the mean of multiple measurements. The subsequent step involves randomly generating a set of 'n' number, e.g., 5000, of biomass equations by altering the composition of the individual biomass components which either vary across environmental conditions or highly sensitive to flux predictions. Our analysis revealed that either all macromolecules vary significantly or are sensitive to flux predictions and thus need to be varied. On the other hand, we noted that compositions of all monomers, except fatty acids, neither vary across conditions nor found to be sensitive to flux predictions and need not be varied in biomass equations. The variation in each biomass composition should be carried out within a specified range indicated by the coefficient of variation (CV). Once the ‘n’ number of biomass equations is generated, pFBA is implemented ‘n’ times, with each iteration using a different biomass equation, and the resulting flux distribution is analyzed as range of fluxes for each reaction.

3. Results

3.1. Assessing the validity of common assumptions made while drafting the biomass equation

To understand the natural variations within biomass components, we first compiled relevant macromolecular and monomer composition data for three highly divergent and representative organisms, E. coli (a prokaryote), S. cerevisiae (a unicellular eukaryote), and CHO cells (immortalized cells derived from a multicellular eukaryote) from literature. In total, we obtained 352 (105, 127 and 120 for E. coli, S. cerevisiae and CHO cells, respectively) different cellular composition data from various studies which were measured across various environmental and/or genetic conditions: conditions which reported the cells grown in different substrates, different levels of oxygenation and data from mutants (see Methods, Supplementary File S1). We then calculated the coefficient of variation (CV) of each macromolecule within unit biomass, i.e., 1 g of DCW, and each monomer within a particular unit macromolecule for each species. This analysis revealed that macromolecules show larger variation than monomers across the three species (CV = 6–87% compared to that of 2–50%). Within macromolecules, lipids, which are biomolecular compounds involved in long term energy storage and cellular membrane reconstitution, have substantially higher variability than other macromolecules in all three species. We also observed that all macromolecules showed increasing CVs in sequence of CHO cells, S. cerevisiae, and E. coli (Fig. 1a). Since prokaryotic cells are more adept in adapting to various niches through their faster exchange of various molecules with adjacent environments, their metabolism as well as cell growth can be stimulated much faster than eukaryotes, and thus could result in a faster turnover of cellular components, e.g., macromolecular composition [35]. Among monomers, while amino acids and nucleotides showed relatively less variability, fatty acids showed very large variations across different growth conditions (Fig. 1b). The high variability of fatty acids distributions could be attributed to the dynamic requirements of cellular membranes to adapt against perturbed environments, e.g., temperature, pH, salt, or dietary conditions [36], [37], [38]. In summary, the comparisons of biomass compositions from multiple conditions clearly showed that while monomers except fatty acids are relatively stable, distribution of macromolecules within unit biomass vary considerably.

Fig. 1.

Inherent variations in macromolecules and monomers compositions across various species and comparison of monomer composition from experiments and omics data. The coefficient of variations (CVs) of five macromolecules classes (a) and 4 monomer groups (b) is provided for three species: E. coli, S. cerevisiae, and CHO cells. N denotes the number of each biomass composition data. The bar graphs in (c) represent relative frequency distributions (y-axis) of the Euclidean expression distance (x-axis, root mean squared deviation, rmsd) between monomer (amino acid and ribonucleotide) compositions obtained from experiments and estimated values from various combinations of omics data.

It has been previously suggested that amino acid and nucleotide composition can be estimated from genome or transcriptome datasets [39], [40]. Alternatively, previous studies have borrowed such data from phylogenetically close species: multiple yeast GEMs have used the nucleotide and/or monomer composition from S. cerevisiae [41], [42], [43], [44]. We therefore evaluated which of these methods provide a better approximation for monomer composition. To do so, we first collected relevant multi-omics datasets: genome, transcriptome, and proteome for all three species (Supplementary File S2). We then estimated the ribonucleotide composition from whole transcriptome datasets and evaluated its “closeness” with the experimentally measured monomer composition across various conditions using the Euclidean distance metric – a measures of divergence between two datasets (see Methods). We also compared the experimentally measured and “-omics” estimated values with the data obtained from phylogenetically close species. The distance between experimentally measured ribonucleotide distributions (including the natural variation) and transcriptome data estimated ones was much lesser (indicated by a high relative frequency at low distances) compared to the distance calculated from phylogenetically close species (Fig. 1c). Next, we calculated the amino acid composition using genome, transcriptome, and proteome datasets and compared it with experimentally measured values. It is important to note that we utilized two combinations of transcriptome and proteome datasets: "all" and "highly expressed", respectively. Based on previous suggestions, we separately considered the highly expressed datasets (top 10%) of mRNA transcripts and proteins. This approach was adopted because highly expressed mRNA transcripts and proteins are known to contribute significantly to the overall proteome outputs. While the amino acid composition estimated from whole “-omics” datasets were distant from the experimentally measured ones (including natural variation), the distances from highly expressed transcripts/proteins were significantly less than that of experimental measurements from close organisms, and thus highlighting the estimation of amino acid composition from highly expressed transcripts/proteins is a good choice (Fig. 1c). Overall, our analysis indicates that “-omics” data, i.e., genome or transcriptome for ribonucleotide and highly expressed proteins or transcripts for amino acids, can be reliably used for deriving monomer composition within each macromolecule rather than borrowing it from close organisms.

3.2. Sensitivity of macromolecular/monomer composition in phenotype predictions

It has been earlier shown that FBA phenotype predictions are sensitive to any variations in individual biomass components. For the first time, Pramanik and Keasling showed that both growth rates and intracellular fluxes predicted from the metabolic model are sensitive to monomer compositions in E. coli [19]. Feist et al. later examined how growth rate predictions change in E. coli when the macromolecular composition is varied and observed no major influence [14]. Another study which performed similar sensitivity analysis in S. cerevisiae and reported biomass composition is indeed sensitive to flux predictions [15]. Such mixed observations in literature could be mainly due to lack of standardization in the sensitivity analyses performed; some studies focused only on the variations in intracellular fluxes while others focused on growth rate predictions, some studies analyzed the effect of changes in monomers while some other studies focused on macromolecular variations, etc. Therefore, we next examined the sensitivity of predicted in silico growth rates and intracellular metabolic fluxes upon varying both macromolecular and monomer compositions in all three species across diverse environments. Particularly, the sensitivity analysis was carried out under aerobic and anaerobic conditions in E. coli, in three different carbon sources (glucose, xylose and ethanol) in S. cerevisiae and three different cell lines in CHO cells by using the relevant GEMs (see Methods).

Initially, we examined the sensitivity of macromolecular and monomer composition on growth rate predictions. Our analysis indicated that protein compositions were the most sensitive among different macromolecules, while DNA was found to be the least sensitive, except E. coli (Supplementary Fig. S2). Such a trend is expected since proteins and lipids have the largest fraction (by mass) in dry cell weight while the composition of DNA is almost negligible. Interestingly, although protein fraction of E. coli was three times greater than RNA, the growth rate prediction in E. coli was more sensitive to RNA than protein. Our analysis also unraveled condition specific sensitivities of macromolecular composition. The sensitivity of protein predicted under aerobic condition was higher than that of anaerobic conditions in E. coli. Similarly, the sensitivities of protein and carbohydrate were lower in reduced substrate ethanol than that of glucose and xylose. Among monomers, only amino acid composition was observed to be relatively sensitive in growth rate predictions.

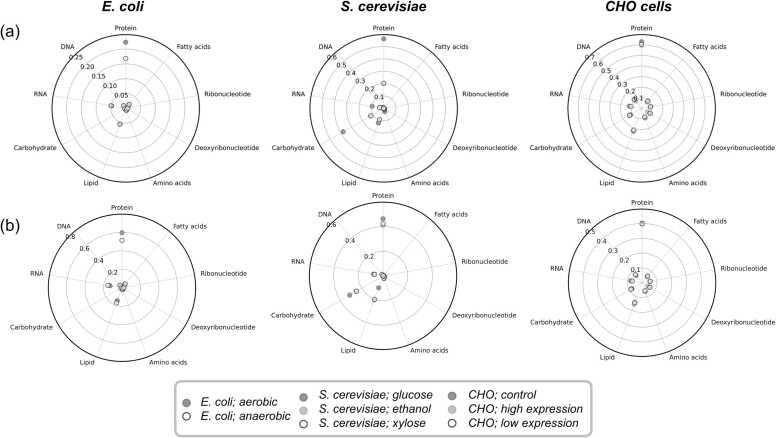
Subsequently, we explored the effect of macromolecular and monomer compositions on flux distribution of all the intracellular reactions (Supplementary Fig. S3). The flux sensitivity was quantified by comparing the predicted fluxes in the reference state, i.e., original biomass equation, and those in a perturbed state, i.e., modified biomass equation (see Methods). Similar to the variations in growth rates, macromolecular compositions were sensitive to reaction flux predictions than the monomers (Fig. 2). Among macromolecules, intracellular fluxes were highly sensitive to protein composition in all three species as more than 40% of overall sensitivity is accounted by them. This is expected since protein is the most abundant component in unit biomass, and the number of reactions required to synthesize the 20 proteinogenic amino acids constitutes a large metabolic network. Similarly, we noted lipids to be second most sensitive component, as they are usually second most abundant constituent in cells next to proteins in all three species despite their low abundance in unit biomass. Within monomers, amino acids had the largest sensitivity coefficients (but still negligible compared to macromolecules) while fatty acids had almost dispensable sensitivities. This is mainly because amino acids biosynthesis pathways are made up of diverse reactions across the metabolic network while all fatty acids of different chain lengths are synthesized using the same set of reactions within the same pathway. Finally, we noted CHO cells to be relatively more sensitive to all monomers than E. coli or S. cerevisiae.

Fig. 2.

Sensitivity of metabolic fluxes predicted by GEMs upon varying individual biomass components. The flux distributions of reference condition, i.e., default biomass equation, and the perturbed condition, i.e., biomass equation obtained by varying each biomass component by 25%, were compared to obtain absolute (a) and relative (b) sensitivities of biomass components under various conditions. A relative sensitivity was calculated by normalizing an absolute sensitivity by the sum of the absolute sensitivities of all macromolecules and monomers for every model condition.

3.3. Ensemble representation of biomass equation to account for natural variation in macromolecular and monomer components

By analyzing the natural variations and the sensitivity to flux predictions, we note that both these parameters could contribute to any potential errors in FBA. For example, a biomass component with high natural variability but low sensitivity, e.g., lipids, can result in more significant changes in flux prediction. On the other hand, components with small CV and high sensitivity, e.g., protein, should also be considered as critical since even a small measurement error may lead to large differences in flux predictions (Fig. 3). We thus propose to label certain biomass components as “critical”, if it falls in any of the following three categories: 1) high CV & high sensitivity, 2) high CV & low sensitivity, and 3) low CV & high sensitivity. Based on this definition, we observed all the macromolecules were critical in E. coli. In S. cerevisiae and CHO cells, we observed all macromolecules except DNA and RNA to be critical. On the other hand, fatty acid was the only critical component observed in the monomer category.

Fig. 3.

Natural variation and the flux sensitivity of various biomass component. The distribution of biomass components based on their coefficient of variation (CV) on the x-axis and sensitivity on the y-axis. Biomass components exhibiting high CV or high sensitivity are identified as critical components within our method.

To address both the natural variation in macromolecular components and potential experimental errors in the measurement of sensitive biomass constituents, we propose ensemble representation of biomass within the FBA framework (Supplementary Fig. S4). In this approach, the critical biomass components that either significantly vary or are highly sensitive to FBA results are sampled several times within a range, i.e., range of natural variation, and “n” number of biomass reactions with various combinations were generated and normalized to make up 1 g of cell in total (see Methods). Subsequently, FBA is implemented “n” times with each of the newly generated “n” biomass equation as the objective function. The distribution of fluxes obtained from “n” number of simulations are then analyzed to extract the plausible flux ranges for each reaction, similar to that in flux sampling approaches. Note that FBA with ensemble biomass is not a method with new types of constraints as in parsimonious FBA (pFBA) [30] or enzyme capacity constrained FBA (ecFBA) [34], [45], rather it is an extension of FBA and can be incorporated into any constraint-based flux analysis method such as pFBA or ecFBA.

To demonstrate the utility of ensemble biomass representations in FBA, we implemented pFBA with ensemble biomass (pFBAwEB) and compared its performance to pFBA with a singular biomass equation which was derived from the average values of all macromolecular and monomer compositions collected. We used relevant experimentally measured growth phenotypic data of E. coli under various environmental conditions and genetic manipulations [46], [47], [48], [49], and employed 5000 different biomass permutations to obtain 5000 flux solutions for each pFBAwEB simulation (see Supplementary Note and Supplementary Fig. S1 for details). In general, when evaluating the accuracy of growth rate predictions, pFBAwEB had smaller error values compared to pFBA. This improvement is attributed to the fact that pFBAwEB predicts a range of growth rates rather than a single value (two-sample Kolmogorov-Smirnov statistic 0.7 compared to that of 1, Fig. 4a).

Fig. 4.

Comparison of flux distributions with and without ensemble biomass. (a) Growth rate predictions by pFBA (grey bar) and pFBAwEB (white bar), compared to experimental measurements (black bar), across different environmental conditions and mutants. All predictions used the same reference biomass composition. (b) Detailed comparison of experimentally estimated fluxes (¹³C MFA, solid magenta line with confidence interval range) with predicted fluxes by different methods: pFBAwEB (blue density plot), pFBA with the reference biomass composition (dashed black line), pFBA with BOFdat (dashed purple line) by Lachance et al. (2019), and pFBA with Biomass Trade-off Weighting (BTW) (dashed orange line) and Higher-dimensional-plane InterPolation (HIP) (dashed green line) by Schulz et al. [22]. The figure illustrates the central carbon metabolism, including the Pentose Phosphate Pathway (PPP, blue box), the TCA cycle (green box), and various amino acid metabolism pathways (yellow box), in E. coli under aerobic (left graph) and anaerobic (right graph) conditions.

To further evaluate the performance of pFBAwEB in estimating internal metabolic flux distributions, we compared it with other methods that address biomass composition uncertainty (BOFdat [21], BTW and HIP [22]) using the E. coli iML1515 model [32], under aerobic and anaerobic conditions. We used the same macromolecular composition as in pFBAwEB to derive a biomass equation for BOFdat. In the case of BTW, we generated different biomass equations for varying glucose and oxygen levels. For HIP, we obtained biomass equations for both aerobic and anaerobic conditions using four datasets of macromolecular composition, along with the corresponding glucose and oxygen uptake rates. The complete list of retrieved biomass equations for each method can be found in Supplementary File S3. We compared the resulting flux predictions from each method with experimentally measured flux data obtained through ¹³C isotope labeling [50]. The flux predictions across glycolysis and fermentative pathways were more or less similar in all methods, while pFBAwEB, BOFdat and BTW performed better in simulating fluxes through anabolic pathways such as the Krebs cycle and amino acid biosynthetic reactions (Fig. 4b). The comparison of ¹³C-flux analysis with pFBAwEB and other methods highlights two main strengths of biomass ensemble representations. First, pFBAwEB presents biologically relevant flux ranges by accounting for the uncertainty in the anabolic demands while other methods provide just a single solution which may have variable accuracy across the entire metabolic network. Second, despite using an ensemble biomass representation, the predicted flux spans presented distinguishable patterns when comparing two different conditions, e.g., E. coli growing in aerobic vs. anaerobic conditions.

4. Discussion

Understanding the degree of natural variation in macromolecules and monomers is fundamental for mitigating the uncertainties in biomass equations and their influence in intracellular flux predictions using FBA. The current study investigated the natural variations in biomass of three representative organisms and gives a comprehensive overview on how cellular composition varies across organisms under different conditions. While most macromolecules varied significantly, the composition of monomers, except fatty acids, remained relatively stable across conditions. CV values of carbohydrate, DNA, and RNA were much greater than that of their corresponding monomers while protein and lipid showed less variability in most cases. Considering that the mean value and the CV are in an inverse relation, relatively small CV values of protein compared to other macromolecules are reasonable because protein accounts for the largest amount of cell weight (approx. 50% mass fraction). Unlike macromolecules, composition of monomers did not vary appreciably across different conditions, except fatty acids. Although perturbations in fatty acid composition brought almost negligible differences in growth rate predictions, its influence on internal fluxes was evident in CHO cells. These observations together clearly indicate the necessity of accurate measurements of various biomass components, particularly the macromolecular composition. To this end, Beck et al. (2018) reviewed multiple analytical techniques and suggested guidelines for accurate quantitative measurement of five major macromolecules [9].

In this study, we also examined how reliable it is to estimate biomass components from omics datasets and noted that it is better to use such estimates than borrowing this data from phylogenetically close organisms. Interestingly, even though omics data sets provide good estimate for monomer compositions, still, there exists difference between experimental and estimated values (Fig. 1c), particularly genome data estimates had poor concordance. This may stem from two main reasons. Firstly, not all the encoded genes get transcribed; only around 5% of the genome is transcribed into RNA at any given time [51]. Second, nucleotide, ribonucleotide and amino acid compositions are known to vary locally in individual members of a population. Nucleotide composition varies locally in different areas of a given genome [52], and consequently could result in mRNA transcripts with varying ribonucleotide composition. Similarly, amino acid composition differs across protein functional categories, probably related to consideration of translation rate [53]. Fortunately, even though monomer composition estimated from omics-data varies marginally from experimental values, it does not impact intracellular flux distribution significantly as the sensitivity of compositions of ribonucleotide and amino acids is negligible.

Not surprisingly, all biomass uncertainty methods rely on variation in macromolecular and monomer composition as fundamental input data. However, the key distinction among all the methods lies in their data requirements and prediction capabilities. BOFdat requires a single macromolecular composition as input and optionally incorporates gene essentiality data specific to the desired environmental condition in the final step to determine the suitable biomass equation. BTW, on the other hand, necessitates multiple biomass compositions obtained from measurements conducted under diverse environmental conditions. When we applied the BTW method using four distinct biomass equations derived from different macromolecular compositions with specific glucose and oxygen uptake rates, we observed that flux only flowed through one of the equations, deviating from the intended distribution across multiple biomass equations. HIP method relies on biomass composition data along with corresponding uptake rates of different substrates. For example, to simulate E. coli growth under aerobic and anaerobic conditions, multiple biomass composition datasets with corresponding glucose and oxygen uptake rates are required. Uniquely, pFBAwEB does not require any additional phenotypic data to simulate across the environmental conditions. Moreover, pFBAwEB provides flux spans representing the range of possible flux values for each reaction rather than single value, which allows us to better handle the inherent variability and uncertainty in cellular systems.

5. Conclusion

Overall, we conclude that among various components of biomass, all macromolecules except DNA, and fatty acids among monomers, vary considerably under different environments. Thus, these need to be accounted for its natural variation carefully while drafting the biomass equation. We also found that the omics data-estimated composition of monomers, is within the observed natural variation and could be reliably used. Based on such observations, we propose to use ensemble representations of biomass instead of a solitary equation in FBA, to account for both the natural variations and the intracellular flux sensitivities to cellular composition. While such ensemble biomass representations can be easily obtained for an organism with multiple cellular compositional measurements available, we suggest using the range of CVs reported in this study for each biomass component to derive an ensemble biomass equation when appropriate data is not available.

CRediT authorship contribution statement

Y.-M. Choi: Formal analysis, Implementation, Software, Visualization, Writing – original draft. D.-H. Choi: Software, Writing – original draft. Y. Q. Lee: Data curation. L. Koduru: Methodology, Writing – review & editing. N. E. Lewis: Conceptualization, Writing – review & editing. M. Lakshmanan: Conceptualization, Writing – review & editing, Supervision. D.-Y. Lee: Conceptualization, Writing – review & editing, Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

Supplementary material

.

Supplementary material

.

Supplementary material

.

Supplementary material

.