General analytical solution expressions for analyzing Langmuir-type kinetics of sonochemical degradation of nonvolatile organic contaminants in water

Highlights

• •Ultrasonic oxidation of nonvolatile contaminants in water was examined under different conditions.
• •Two solution expressions of the Langmuir-type model were used to predict degradation kinetics.
• •Degradation increased as initial concentration and frequency decreased and as intensity increased.
• •The two solution expressions provided an excellent description of the ultrasonic oxidation data.

Abstract

Detailed kinetic studies of the ultrasonic decomposition of contaminants in water are scarce. Most of the work has used a pseudo-first order kinetics law, which is unrealistic. The model based on a Langmuir-type mechanism has been shown to fit the sonolytic decomposition data well, especially by using the non-linear technique. To avoid unrealistic assumptions, general analytical solutions to a time-dependent non-linear Langmuir-type equation may be the appropriate method. In this work, the sonolytic oxidation of organic contaminants, i.e., naphthol blue black and furosemide, in water was analyzed using two general analytical solution expressions of the Langmuir-type kinetics model, which describe the pollutant concentration in water. The validity of the two general analytical solution expressions was tested under a diversity of operating conditions, such as initial substrate concentration and varying ultrasonication frequency and intensity. As the initial substrate concentration increased, the sonolytic oxidation kinetics decreased, while the initial ultrasonic decomposition rate increased and then plateaued. Consequently, a heterogeneous kinetics equation based on a Langmuir-type mechanism can be used to simulate the sono-decomposition process. The decomposition yield increased with increasing sonication intensity and decreasing frequency. The two analytical solution expressions seem to be in excellent agreement with the experimental results of the sonochemical decomposition of the nonvolatile organic contaminants tested for the different operating conditions examined. These expressions provide a valuable tool for the analysis and simulation of advanced sonochemical oxidation processes under various experimental conditions.

1. Introduction

As the harm that emerging contaminants pose to water resources has become more widely recognized, attention to these pollutants has increased exponentially. These contaminants cannot be removed by classical water treatment techniques [1]. Advanced oxidation processes are highly effective techniques used to degrade contaminants found in water and wastewater. Due to the harsh conditions created by sonochemically active cavitation bubbles [2], ultrasonic degradation processes are believed to be an effective alternative for the removal of contaminants from waters [3], [4], [5], [6], [7], [8], [9], [10], [11].

The central event in ultrasonic decomposition of contaminants in aqueous solution is the cavitation bubble. Acoustic cavitation occurs when a solution is exposed to ultrasound. Bubbles can expand and burst abruptly [12], [13], [14]. The resulting bubbles can be either stable cavities with lifetimes of many cycles oscillating around an equilibrium size, or transient cavities with lifetimes of no more than a few acoustic cycles [15], [16]. During strong collapse, the pressure and temperature in the interior of the bubble rise to several hundred bar and several thousand degrees Kelvin [17]. Consequently, the presence of non-condensable gases and water vapor in the hot regions leads to the generation of a diversity of radicals, such as H^•, ^•OH and HO₂^•, and reactive entities, H₂O₂ for example, which can lead to other secondary chemical reactions [18], [19], [20], [21]. In other words, high-energy chemical reactions can occur inside the bubble, at the bubble–liquid interface, and in the liquid bulk when acoustic cavitation concentrates diffused ultrasonication energy into petite hot spots that quickly transform into microreactors.

Each microreactor can release huge amounts of energy quickly and efficiently. There are two different mechanisms by which organic contaminants in diluted aqueous media undergo sonolysis [16]: (i) during the expansion cycle, volatile substances vaporize and then undergo pyrolysis/combustion reactions within the collapsing acoustic cavitation bubble and (ii) it happens as a result of a reaction between ^•OH radicals and the substrate adsorbed at the bubble boundary, in the bulk, and to a certain extent in the interior of the acoustic cavitation bubbles.

In ultrasonic degradation of nonvolatile contaminants in aqueous phase, it has been suggested to use kinetics equations based on Langmuir-type model. Two equations linking the reaction rate with the concentration regime have been used to characterize the kinetics pattern of ultrasonic decomposition of nonvolatile hydrophilic pollutants to clarify the local reaction zone. According to Serpone et al. [22], the rate of sonication-induced elimination of chlorophenols is both concentration independent and concentration dependent. The key mechanistic relevance is that at low chlorophenol concentrations, the reaction happens in most of the solution, but at higher concentrations, the reaction takes place mainly at the gas bubble–liquid interface. An equation alike to that of Serpone et al. has been proposed by Kidak and Ince [23] for the sonolytic degradation of phenol. Okitsu et al. [24], [25], [26] showed that the sonolytic oxidation of alkylbenzene sulfonates, benzoic acid, butyric acid and azo dyes can be studied using a Langmuir-type kinetics equation based on heterogeneous reaction systems. For the sonochemical destruction of rhodamine blue and rhodamine B, Priya and Giridhar [27] established an equation analogous to that of Okitsu et al. [24], [25], [26].

In our previous work [28], the sonochemical decomposition of nonvolatile organic contaminants, i.e., phenol, 4-isopropylphenol, and rhodamine B, was predicted using kinetics equations based on a Langmuir-type process. The nonlinear curve fitting analysis approach was ascertain to be the most suitable technique to identify the equation parameters, according to the study of degradation data by the model of Okitsu et al. [24], [25], [26]. Using the model of Serpone et al. [22], an excellent description of the experimental data of the sonochemical decomposition of rhodamine B was achieved. For phenol and 4-isopropylphenol, the model of Serpone et al. [22] provides a poorer fit to the sonolytic oxidation data.

Due to its non-linearity, the kinetics equation of the Langmuir-type shows that the sonolytic degradation of contaminants in water is not agreeable to a rigorous analytical solution. The concentration of contaminants during ultrasonic degradation is described by the nonlinear Langmuir-type model of Okitsu et al. [24], [25], [26], but a general analytical expression has not yet been reported. Therefore, the purpose of the current paper is to apply two general analytical solution expressions, developed by Loghambal et al. [29] using the perturbation-iteration algorithms, for the pollutant concentration decay by sonochemical decomposition of naphthol blue black and furosemide in aqueous media. The validity of the general analytical solution expressions for the nonlinear Langmuir-type model of Okitsu et al. [24], [25], [26] was verified for various experimental conditions, i.e., initial substrate concentration and ultrasonication frequency and intensity.

2. Experimental

2.1. Chemicals

Ultrapure water was used for all aqueous solutions. Analytical grade chemicals were used in this study. Naphthol blue black, furosemide and ammonium hepta-molybdate were supplied by Sigma-Aldrich. Potassium iodide and acetonitrile were provided by Riedel-de Haën.

2.2. Ultrasonication reactor

The ultrasonication tests were conducted in a high-frequency reactor (Meinhardt Ultrasonics E/805/T/M) containing 300 mL of aqueous solution, equipped with a jacketed glass cylinder of 5.9 cm internal diameter and a 7.5 cm in diameter transducer (5.3 cm active area diameter) mounted at the bottom. The transducer is capable of generating ultrasonic irradiation at three different ultrasonication frequencies (585, 860, and 1140 kHz). Both frequency and intensity can be adjusted. In all experiments, a chiller (Lauda RE 630 SN) was used to maintain the solution temperature at 25 ± 1 °C during sonolysis. The calorimetric technique was used to calculate the actual ultrasonication power [30].

2.3. Procedures

A solution volume of 300 mL was used throughout the various sonochemical studies involving the decomposition of naphthol blue black and furosemide and the generation of hydrogen peroxide in pure Milli-Q water. Cooling solution was circulated through an envelope surrounding the reactor to maintain the temperature of the ultrasonicated solution at 25 ± 1 °C.

A UV–visible Lightwave II (Biochrom WPA) spectrophotometer set at 620 nm was used to measure the concentration of naphthol blue black in water samples taken at regular intervals from the reacting medium.

Furosemide concentration was quantitatively analyzed by YL Instruments HPLC (YL9100) using a Supelcosil column (LC-18, 4.6 mm internal diameter, 250 mm length, and 4 μm particle diameter) and a YL9120 UV–vis detector adjusted at 230 nm. A flow rate of 0.6 mL/min in isocratic mode was used for the mobile phase (70/30 (v/v) water/acetonitrile and 0.1% formic acid).

Iodometry was used to measure the accumulation of sono-formed hydrogen peroxide [31]. A quartz cuvette containing 1000 µL of KI (0.1 M) and 20 µL of ammonium heptamolybdate (0.01 M) was filled with a 200 µL sample aliquot collected from the sonoreactor. After 5 min, a UV–visible Lightwave II (Biochrom WPA) spectrophotometer was employed to determine the absorbance at 350 nm.

3. Mathematical models

The Langmuir-type model describes the kinetics of ultrasonic degradation of contaminants and is represented by the following equation [28]:

$$\mathrm{r}=-\frac{\mathrm{d}\mathrm{C}}{\mathrm{d}\mathrm{t}}=\frac{\mathrm{k}\mathrm{K}\text{C}}{1+\mathrm{K}\text{C}}$$ (1)

where r is the rate of contaminant sonochemical degradation as a function of time in mg/L·min, C is the contaminant concentration at any time t (min) in mg/L, K is the equilibrium constant in L/mg and k is the pseudo-rate constant in mg/L·min.

Equation (1) can be reduced to zero-order reaction kinetics when KC ≫ 1:

$$\mathrm{r}=-\frac{\mathrm{d}\mathrm{C}}{\mathrm{d}\mathrm{t}}=\mathrm{k}$$ (2)

If KC ≪ 1, equation (1) can be reduced to pseudo-first-order reaction kinetics:

$$\mathrm{r}=-\frac{\mathrm{d}\mathrm{C}}{\mathrm{d}\mathrm{t}}=\mathrm{k}\mathrm{K}\mathrm{C}={\mathrm{K}}_{\mathrm{a}\mathrm{p}\mathrm{p}}\mathrm{C}$$ (3)

where K_app is the pseudo-first-order constant in 1/min.

Equation (3) and its integrated form (ln(C/C₀) = K_app t) are the most commonly used to describe the ultrasonic decomposition kinetics of contaminants in aqueous solutions because the pollutant concentration seems to decrease exponentially as a function of time. However, contrary to what would be expected from a first-order kinetics equation, there was no linear relationship between the initial sono-degradation rate and the initial contaminant concentration [3], [6], [7], [9], [28], [32], [33], [34], [35]. It is evident that the sonolytic oxidation process does not obey to a first-order kinetics and cannot be adequately considered by a single rate constant stated in 1/time [3], [6], [7], [9], [28], [32], [33], [34], [35].

The use of a Langmuir-type kinetics equation in the sonolytic degradation of contaminants in water was first proposed by Okitsu et al. [24], [25], [26]. Based on the local reaction region at the interfacial zone of the acoustic cavitation bubbles, they have proposed a Langmuir-type mechanism of adsorption and desorption. During acoustic bubble oscillation, contaminant molecules are adsorbed from the bulk liquid at the bubble/solution interface and desorbed in the forward direction, leading to the degradation of contaminants that were previously present in the local reaction zone. If θ is the fractional coverage of the contaminant molecules in the interfacial zone of the acoustic cavitation bubbles, the following assumptions are included in this kinetics model:

• •The adsorption rate of the pollutant (r_a) from the bulk liquid to the interfacial zone of the acoustic cavitation bubbles is in proportion to (1 − θ) and the contaminant concentration in the bulk liquid.
• •The desorption rate of the contaminant (r_d) from the bubble − solution interface to the solution bulk is correlated with θ.

Consequently, the adsorption and desorption rates are given by:

$${\mathrm{r}}_{\mathrm{a}}={\mathrm{k}}_{\mathrm{a}}\mathrm{C}(1-\theta )$$ (4)

$${\mathrm{r}}_{\mathrm{d}}={\mathrm{k}}_{\mathrm{d}}\theta$$ (5)

where C is the initial contaminant concentration, k_a is the adsorption rate constant and k_d is the desorption rate constant.

The following equation can be written after pseudo-steady state:

$${\mathrm{k}}_{\mathrm{a}}\mathrm{C}(1-\theta )={\mathrm{k}}_{\mathrm{d}}\theta$$ (6)

Substituting k_a/k_d for K, θ is then given by

$$\theta =\frac{\text{K C}}{1+\mathrm{K}\text{C}}$$ (7)

In an ultrasonic field, cavitation bubbles oscillate, which causes the size of the bubbles to fluctuate. During an ultrasonic rarefaction cycle, the size increases, and during a compression cycle, it decreases. The approach to equilibrium can be affected by such fluctuations in bubble size. Determining the lifetime of the cavitation bubbles is another challenge. As a result, it is necessary to assume a pseudo-steady state in the current situation.

The sonochemical decomposition rate of contaminant molecules in the interfacial zone of acoustic cavitation bubbles is expressed as

$$\mathrm{r}=-\frac{\mathrm{d}\mathrm{C}}{\mathrm{d}\mathrm{t}}=\mathrm{k}\theta =\frac{\mathrm{k}\mathrm{K}\text{C}}{1+\mathrm{K}\text{C}}$$ (8)

A variety of techniques have been developed to find solutions that are admissible without the need for a small parameter [29], [36]. The principles of a class of recently proposed alternative perturbation-iteration algorithms have been described for first-order differential equations. The fact that the developed method does not necessitate any initial transformation of the equations into another form is one of its main features. In fact, the method was initially established for algebraic equations before being modified for use with ordinary differential equations. Two approximate solution expressions to the Langmuir-type kinetics model can be obtained [29]:

$$\mathrm{C}={\mathrm{C}}_0{\mathrm{e}}^{-\mathrm{k}\mathrm{K}\mathrm{t}}\left(1+{\mathrm{C}}_0\mathrm{K}(1-{\mathrm{e}}^{-\mathrm{k}\mathrm{K}\mathrm{t}})\right)$$ (9)

$$\mathrm{C}={\mathrm{C}}_0{\mathrm{e}}^{-\mathrm{k}\mathrm{K}\mathrm{t}}\left(1-\frac{{\mathrm{C}}_0\mathrm{K}\left(2\left({\mathrm{e}}^{-\mathrm{k}\mathrm{K}\mathrm{t}}-1\right)+{\mathrm{C}}_0\mathrm{K}\left({\mathrm{e}}^{-2\mathrm{k}\mathrm{K}\mathrm{t}}-1\right)\right)}{2\left(1+{\mathrm{C}}_0\mathrm{K}{\mathrm{e}}^{-\mathrm{k}\mathrm{K}\mathrm{t}}\left(2+{\mathrm{C}}_0\mathrm{K}{\mathrm{e}}^{-\mathrm{k}\mathrm{K}\mathrm{t}}\right)\right)}\right)$$ (10)

where C (mg/L) is the concentration of contaminant at any time t, C₀ (mg/L) is the initial concentration of contaminant, K (L/mg) is the equilibrium constant and k (mg/L·min) is the pseudo-rate constant.

Using Kaleidagraph® software and the non-linear curve fitting analytical approach, the sonochemical degradation results for the investigated nonvolatile contaminants were analyzed to fit the two general analytical equation solutions. The model parameters are then derived and the decomposition kinetics curves are then reconstructed using the calculated values. The resulting curves are a superposition of the theoretically predicted data and the experimental results.

The analytical expression that best describes the ultrasonic decomposition kinetics of nonvolatile organic contaminants in the aqueous phase is selected based on its goodness of fit. Correlation coefficient and nonlinear chi-square test are the functions that were used to evaluate model fit.

4. Results and discussion

Since naphthol blue black (vapor pressure: 4.85 × 10⁻²⁹ mm Hg at 25 °C, Henry’s law constant: 1.25 × 10⁻³¹ atm·m³/mol at 25 °C, log K_ow = 0.82, solubility: 10–50 mg/mL) and furosemide (vapor pressure: 3.11 × 10⁻¹¹ mm Hg at 25 °C, Henry’s law constant: 3.95 × 10⁻¹⁶ Pa·m³/mol [37], log K_ow = 2.03, solubility: > 49.6 µg/mL at pH 7.4 (73.1 µg/mL at 30 °C)) are nonvolatile materials, they cannot enter the acoustic cavitation bubble and instead must be decomposed by reacting with ^•OH radicals on the outside of the collapsing bubble [9], [10].

The present study intends to apply two general analytical solution expressions of the Langmuir-type kinetics equation, developed by perturbation-iteration algorithms, which describe the pollutant concentration in aqueous solution that can accurately represent the experimental findings of the ultrasonic decomposition kinetics of nonvolatile organic contaminants in water.

4.1. Impact of initial substrate concentration

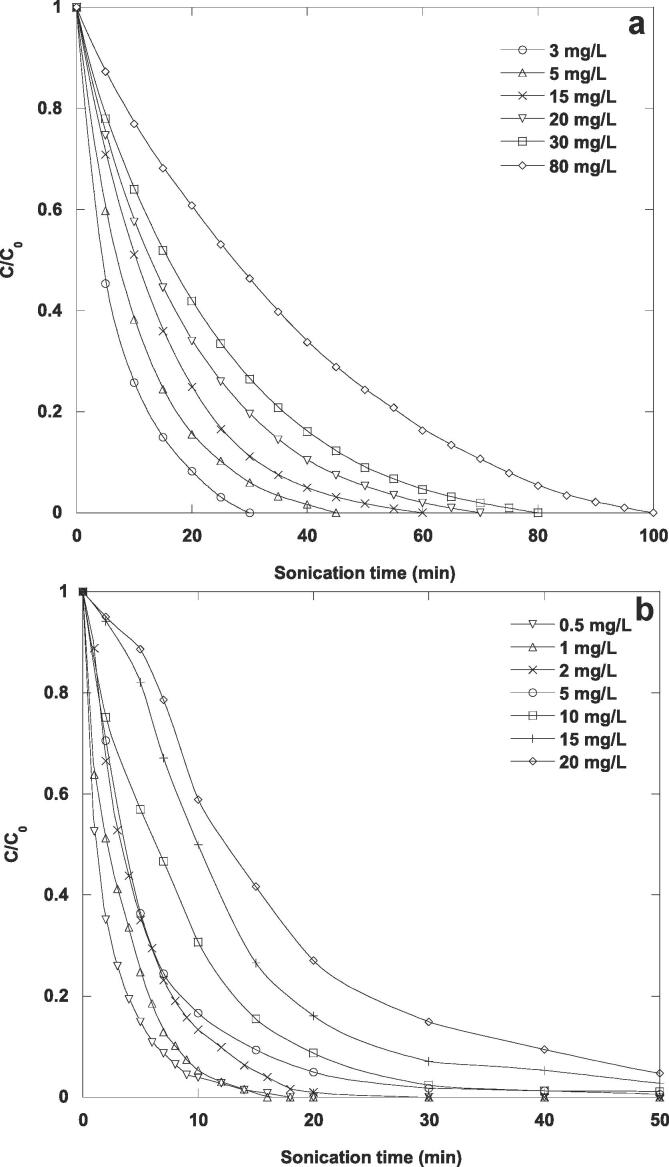
Ultrasonication at 585 kHz was applied to contaminants aqueous solutions at diverse initial substrate concentrations in the interval of 3–80 mg/L for naphthol blue black (sonication intensity of 3.58 W/cm²) and in the interval of 0.5–20 mg/L (sonication intensity of 4.30 W/cm²) for furosemide. The sonolytic decomposition kinetics for both contaminants in water were plotted in Fig. 1(a) and 1(b). As the initial substrate concentration increased, the results exhibited that the ultrasonic oxidation kinetics decreased. Nevertheless, the initial ultrasonic decomposition rate increased as a function of initial substrate concentration and then reached a plateau (figure not shown). These observations suggest that the ultrasonic oxidation data for both contaminants do not follow a first-order kinetics law. The same behavior has been observed for the decomposition of different nonvolatile organic contaminants by sonolysis in the aqueous phase [34], [38], [39], [40], [41], [42], [43]. At high substrate concentration, contaminant molecules accumulate at the interface of the acoustic cavitation bubbles where they react with ^•OH radicals, which are present in high concentration in this region, conducting to an improvement in the decomposition rate. At higher substrate concentrations, the substrate molecules attain a saturation limit at the bubble surface, resulting in a nearly constant degradation rate. At low substrate concentration, due to the low accumulation of substrate molecules in the interfacial zone of the acoustic cavitation bubbles, a small amount of hydroxyl radicals is scavenged by the pollutant, which results in a lower degradation rate. This indicates that the degradation process occurring in the interfacial zone of acoustic cavitation bubbles can be represented by a heterogeneous kinetics equation based on a Langmuir-type mechanism. Additionally, ultrasonication of the contaminated solutions resulted in the simultaneous production of hydrogen peroxide, which was formed to a lesser extent than in uncontaminated water (figure not shown). The reaction between hydroxyl radicals leading to hydrogen peroxide formation dominates at low contaminant concentrations [9], [10]. As the substrate solution concentration increases, the possibility of interaction between the contaminant molecules and the hydroxyl radicals increases. This results in an intensification in degradation rate.

Fig. 1.

Sonochemical degradation kinetics of NBB (a) and FSM (b) in water at different initial substrate concentrations (conditions: volume: 300 mL, initial concentrations: 3–80 mg/L (NBB) and 0.5–20 mg/L (FSM), frequency: 585 kHz, acoustic intensity: 3.85 W/cm² (NBB) and 4.3 W/cm² (FSM), temperature: 25 °C, pH: natural (∼6 (NBB) and 5.2 (FSM))).

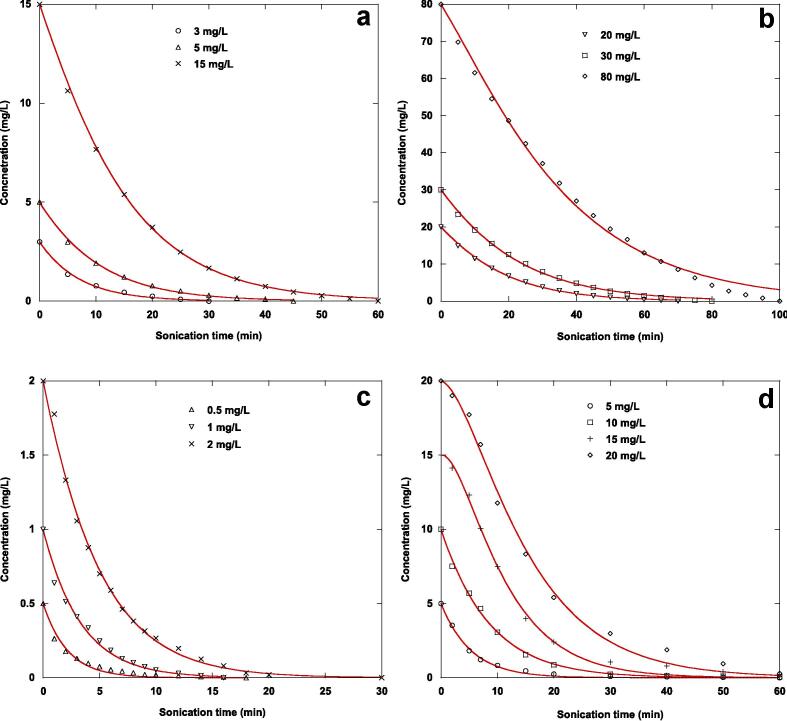
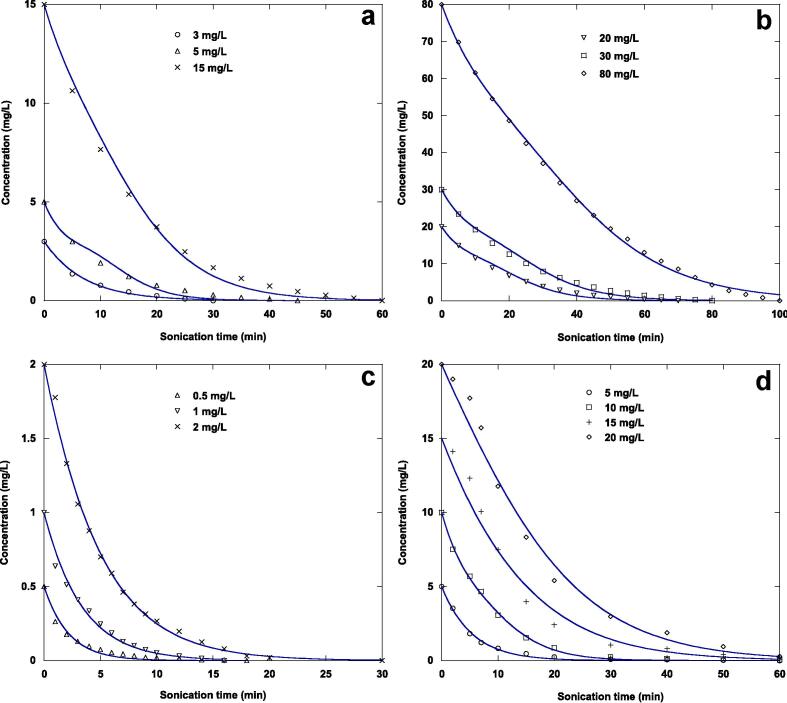
To evaluate the applicability of the Langmuir-type mechanism to the ultrasonic degradation process of the nonvolatile organic contaminants tested, the analytical solution expressions (Eqs. (9), (10)) obtained for the heterogeneous model were applied to the degradation kinetics data using a non-linear technique, and the results are shown in Fig. 2(a-d) and 3(a-d) and Table 1. The best fit of the analytical solution expression of the Langmuir-type model is assessed by evaluating the correlation coefficients and chi-square test values. Additionally, the predicted substrate concentrations must be in reasonably good agreement with the experimental values, with maximum correlation coefficients and minimum chi-square values.

Fig. 2.

Comparison of experimental and predicted sonochemical degradation kinetics of NBB (a and b) and FSM (c and d) in water at different initial substrate concentrations by the first analytical solution (Eq. (9)) of the Langmuir-type model under the same conditions of Fig. 1.

Fig. 3.

Comparison of experimental and predicted sonochemical degradation kinetics of NBB (a and b) and FSM (c and d) in water at different initial substrate concentrations by the second analytical solution (Eq. (10)) of the Langmuir-type model under the same conditions of Fig. 1.

Table 1.

Parameters of the Langmuir-type model obtained using two analytical solution expressions by nonlinear regression technique for different initial concentrations of substrate (conditions: volume: 300 mL, initial concentrations: 3–80 mg/L (NBB) and 0.5–20 mg/L (FSM), frequency: 585 kHz, acoustic intensity: 3.85 W/cm² (NBB) and 4.3 W/cm² (FSM), temperature: 25 °C, pH: natural (∼6 (NBB) and 5.2 (FSM))).

	Naphthol blue black
	Initial concentration (mg/L)
	3	5	15	20	30	80
First analytical solution expression (Equation(9))
k (mg/L·min)	162.39	0.43073	3.7979	5.3573	8.4799	5.9581
K (L/mg)	0.8666 × 10−3	0.11815	21.604 × 10−3	11.616 × 10−3	5.9128 × 10−3	6.1151 × 10−3
χ2	0.030703	0.080682	0.22753	0.87051	2.5848	63.369
R	0.99771	0.99875	0.99957	0.99915	0.99900	0.99735
Second analytical solution expression (Equation(10))
k (mg/L·min)	327.2	0.23042	1.089	0.67434	0.84859	1.8838
K (L/mg)	0.42998 × 10−3	0.28218	0.11238	0.16426	0.107	28.484 × 10−3
χ2	0.030703	0.026339	1.4407	4.4098	8.0804	15.284
R	0.99771	0.99959	0.99727	0.99569	0.99688	0.99936
	Furosemide
	Initial concentration (mg/L)
0.5	1	2	5	10	15	20
	First analytical solution expression (Equation(9))
k (mg/L·min)	36.906	31.713	3.3089	150.24	3.9591	1.7846	1.9331
K (L/mg)	12.571 × 10−3	9.5099 × 10−3	66.452 × 10−3	1.2584 × 10−3	37.642 × 10−3	70.078 × 10−3	47.32 × 10−3
χ2	0.0063756	0.01459	0.022793	0.10316	0.19023	0.93609	3.0115
R	0.98723	0.99327	0.99813	0.9981	0.99923	0.99862	0.99744
	Second analytical solution expression (Equation(10))
k (mg/L·min)	72.862	67.408	4.5732	151.98	4.0099	2.5861	2.419
K (L/mg)	6.3641 × 10−3	4.4691 × 10−3	47.723 × 10−3	1.2447 × 10−3	40.806 × 10−3	35.206 × 10−3	34.236 × 10−3
χ2	0.0063759	0.014595	0.022821	0.10316	0.18285	6.7934	7.8539
R	0.98723	0.99327	0.99813	0.9981	0.99926	0.98996	0.99331

Fig. 2(a-d) present the experimental and predicted degradation kinetics of the two contaminants by ultrasonication examined at different initial substrate concentrations by the first analytical solution expression of the Langmuir-type model, while Fig. 3(a-d) show those determined by using the second analytical solution equation. These figures show that both analytical solution expressions (Eqs. (9), (10)) of the Langmuir-type model accurately describe the experimental data of the ultrasonic oxidation of naphthol blue black and furosemide at diverse initial substrate concentrations in water. This finding is based on the chi-square values and the correlation coefficients of the nonlinear regression analysis (Table 1). According to the correlation coefficient values, the analytical solution expressions fit the experimental results well. The correlation coefficients vary from 0.98723 to 0.99957 for the first analytical solution expression (Eq. (9)) and from 0.98723 to 0.99936 for the second analytical solution equation (Eq. (10)). The differences in the correlation coefficient values obtained for the two analytical solution expressions and for the two tested contaminants are very marginal (sometimes null) and cannot be used to draw any conclusions. On the other hand, the difference between the actual data and the data that would be predicted by the analytical solution expressions if there were no difference is summed to obtain the chi-square value, which is a single number. The chi-square value is equals zero when the experimental data and the predicted data (assuming no differences) are identical. The value of the chi-square will increase as the difference increases. The results in Table 1 show that the chi-square test values for the two analytical solution expressions increase with increasing initial substrate concentration of the two pollutants studied. For the two analytical solution expressions, the lower chi-square test values are obtained for furosemide, indicating that the experimental results of the sonolytic decomposition of furosemide are best described than those of naphthol blue black. This is probably due to the low solubility and high vapor pressure, octanol–water partition coefficient (log K_ow) and Henry’s law constant of furosemide compared to those of naphthol blue black, which leads to more accumulation of furosemide in the interfacial zone of the acoustic cavitation bubbles.

For naphthol blue black, at an initial concentration of the substrate of 3 mg/L, the two analytical solution expressions of the Langmuir-type equation give the same value of chi-square, whereas the chi-square values for the first analytical solution expression (Eq. (9)) are lower than those determined for the second analytical solution equation (Eq. (10)), except at an initial contaminant concentration of 80 mg/L, where this tendency is reversed. It appears that at low initial substrate concentrations (5–30 mg/L), the best fit was obtained by the first analytical solution expression, while at high initial contaminant concentrations the second analytical expression was better.

For furosemide, at an initial contaminant concentration in the interval of 0.5–5 mg/L, a practically identical chi-square value was obtained using the two analytical solution expressions. At an initial contaminant concentration of 10 mg/L, the experimental data were well predicted by the second analytical solution expression. The first analytical solution equation fits well the experimental results of sonolytic oxidation of furosemide at initial concentrations of 15 and 20 mg/L. Overall, it appears that the first solution equation of the Langmuir-type model (Eq. (9)) is better than the second one (Eq. (10)) for describing the ultrasonic decomposition of furosemide in water.

An excellent description of the experimental data of the ultrasonic decomposition of naphthol blue black and furosemide in water at different initial contaminant concentrations was accomplished using the two analytical solution expressions of the Langmuir-type equation. The results of this work indicate that the tested contaminants undergo oxidation mainly at the bubble − solution interface.

4.2. Impact of ultrasonication frequency

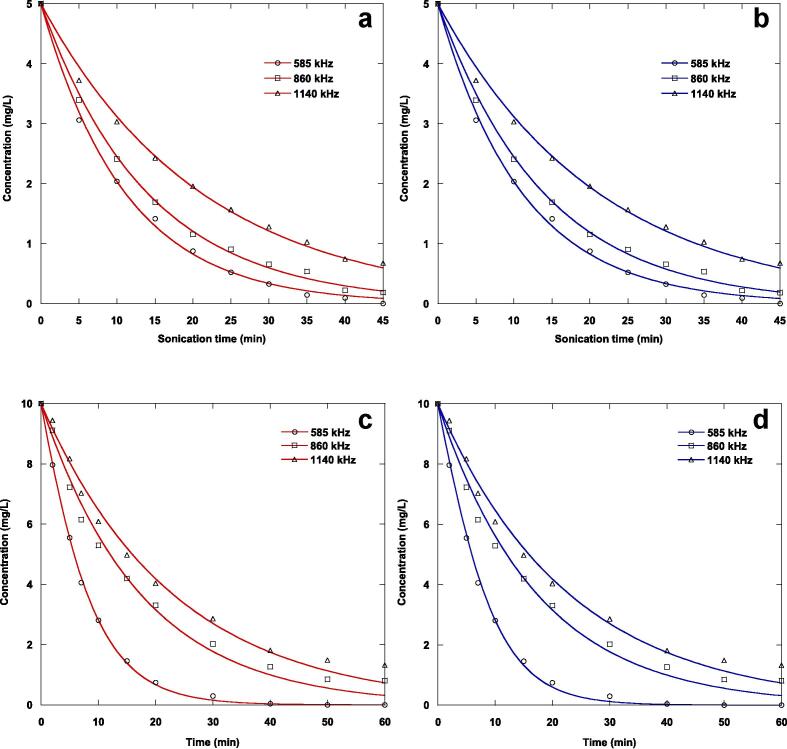
Ultrasonication experiments were accomplished at three frequencies of 580, 860 and 1140 kHz, with the ultrasonic intensity kept constant at 3.58 W/cm² for naphthol blue black (5 mg/L) and 4.3 W/cm² for furosemide (10 mg/L). Fig. 4 shows the impact of ultrasonication frequency on the oxidation of the nonvolatile organic contaminants tested. The decomposition yield decreases with increasing ultrasonication frequency in the investigated range for both contaminants examined. The number of active acoustic cavitation bubbles and the single bubble yield are both significant parameters that affect this result. These parameters are sensitive to ultrasonication frequency variations. In other words, the number of active acoustic cavitation bubbles increased notably with increasing ultrasonication frequency. In another way, a lower frequency gives the bubble more time to expand, resulting in a stronger collapse. This leads to higher temperatures during the collapse and accelerating free radical generation. Furthermore, the generation of acoustic cavitation bubbles at higher frequencies and the subsequent production of free radicals are accelerated. Therefore, a reduced rate of hydroxyl radical formation would be expected as both the temperature of the collapsing bubble and the time it takes to collapse decrease with increasing ultrasonic frequency. Thus, the single bubble yield, which was found to be less efficient at higher frequencies, was primarily responsible for the net effect of ultrasonication frequency on the ultrasonic oxidation of the contaminants in water.

Fig. 4.

Comparison of experimental and predicted sonochemical degradation kinetics of NBB (a and b) and FSM (c and d) in water at different ultrasonic frequencies by the first analytical solution expression (Eq. (9), red curves) and second analytical solution expression (Eq. (10), blue curves) of the Langmuir-type model (conditions: volume: 300 mL, initial concentrations: 5 mg/L (NBB) and 10 mg/L (FSM), acoustic intensity: 3.85 W/cm² (NBB) and 4.3 W/cm² (FSM), temperature: 25 °C, pH: natural (∼6 (NBB) and 5.2 (FSM))).

The comparison of the experimental and predicted sonolytic oxidation kinetics of the two contaminants studied at different ultrasonication frequencies by the first analytical solution expression (red curves) and the second analytical solution equation (blue curves) of the Langmuir-type model was shown in Fig. 4(a-d). The parameter values of the Langmuir-type equation determined by using the two analytical solution expressions were tabulated in Table 2 for the sonolytic destruction of the two experienced contaminants. The lower chi-square values were obtained for naphthol blue black compared to those of furosemide at a given frequency using the two analytical solution expressions. The chi-square test value is a single number that sums up all the differences between the experimental data and the data we would expect if there were no differences. The chi-square value is zero when the data are identical to what would be expected (if no differences exist). The chi-square value increases as the discrepancy increases. The correlation coefficients obtained using the two analytical solution expressions were good, and those for naphthol blue black are higher than those calculated for furosemide, except at a frequency of 585 kHz. For a given ultrasonication frequency, the correlation coefficients obtained by the two analytical solution expressions are almost identical for both contaminants. Using the two analytical solution expressions for a selected frequency and contaminant, the chi-square values obtained are practically equal, except those calculated at 585 kHz. For the two analytical solution expressions and for both contaminants, the equilibrium constant decreased with increasing ultrasonication frequency, while the pseudo-rate constant increased with increasing ultrasonication frequency.

Table 2.

Parameters of the Langmuir-type model obtained using two analytical solution expressions by nonlinear regression technique for different ultrasonic frequencies (conditions: volume: 300 mL, initial concentrations: 5 mg/L (NBB) and 10 mg/L (FSM), acoustic intensity: 3.85 W/cm² (NBB) and 4.3 W/cm² (FSM), temperature: 25 °C, pH: natural (∼6 (NBB) and 5.2 (FSM))).

	Naphthol blue black
	Ultrasonic frequency (kHz)
	585	860	1140
	First analytical solution expression (Equation(9))
k (mg/L·min)	0.43073	13.668	77.269
K (L/mg)	0.11815	5.3295 × 10−3	0.61332 × 10−3
χ2	0.080682	0.048099	0.078134
R	0.99875	0.99891	0.99783
	Second analytical solution expression (Equation(10))
k (mg/L·min)	0.23042	27.367	169.5
K (L/mg)	0.28218	2.655 × 10−3	0.27947 × 10−3
χ2	0.026339	0.04809	0.078139
R	0.99959	0.99891	0.99783
	Furosemide
	Ultrasonic frequency (kHz)
585	860	1140
	First analytical solution expression (Equation(9))
k (mg/L·min)	3.9591	257.18	159.31
K (L/mg)	37.642 × 10−3	0.22439 × 10−3	0.27377 × 10−3
χ2	0.19023	0.98309	0.92624
R	0.99923	0.99541	0.99542
	Second analytical solution expression (Equation(10))
k (mg/L·min)	4.0099	534.39	324.17
K (L/mg)	40.806 × 10−3	0.10796 × 10−3	0.13451 × 10−3
χ2	0.18285	0.98305	0.92623
R	0.99926	0.99541	0.99542

All the above statements demonstrate that both analytical solution expressions of the Langmuir-type equation predict well the experimental data of the ultrasonic oxidation of the tested contaminants in water at the three investigated frequencies.

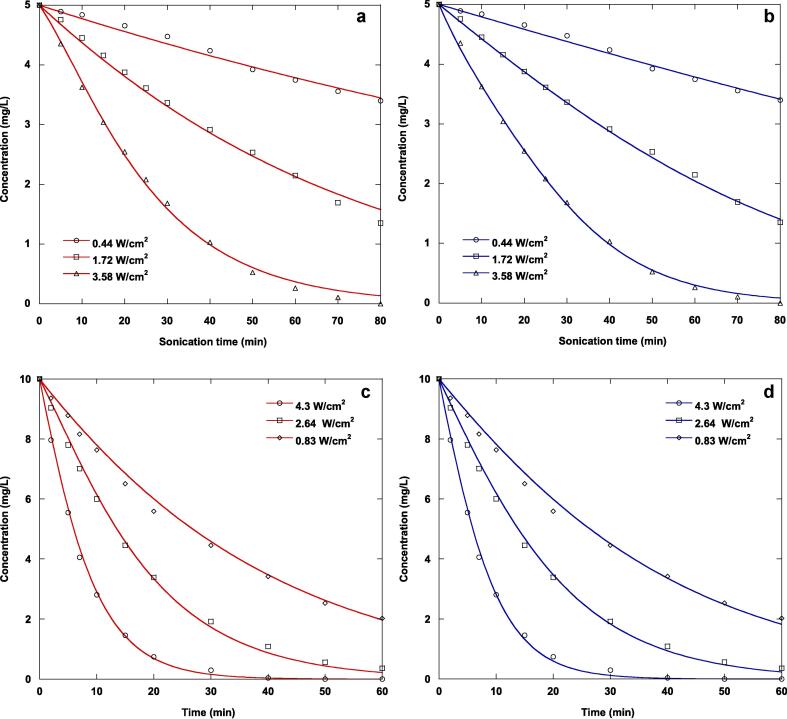
4.3. Impact of ultrasonication intensity

For an ultrasonication frequency of 585 kHz, the impact of ultrasonic intensity in the range of 0.44–3.58 W/cm² for naphthol blue black (5 mg/L) and in the interval of 0.83–4.3 W/cm² for furosemide (10 mg/L) on the ultrasonic decomposition of the examined nonvolatile organic contaminants in water was investigated. Fig. 5 depicts the results of the sonolytic experiments. These results obviously demonstrate that the decomposition of the substrates improves notably with the ultrasonic intensity. This is due to an increase in the ultrasonic amplitude, resulting in a greater sonochemical impact in the collapsing acoustic cavitation bubble. This can be used to explain why ultrasonic intensity has a positive impact on contaminant decomposition. Additionally, more acoustic cavitation bubbles are created, increasing the amount of hydroxyl radical formation as the ultrasonic intensity increases. Similar patterns have been described in the literature for the decomposition of organic contaminants in water by sonolysis [40], [42], [44].

Fig. 5.

Comparison of experimental and predicted sonochemical degradation kinetics of NBB (a and b) and FSM (c and d) in water at different ultrasonic intensities by the first analytical solution expression (Eq. (9), red curves) and second analytical solution expression (Eq. (10), blue curves) of the Langmuir-type model (conditions: volume: 300 mL, initial concentrations: 5 mg/L (NBB) and 10 mg/L (FSM), frequency: 585 kHz, temperature: 25 °C, pH: natural (∼6 (NBB) and 5.2 (FSM))).

In Fig. 5(a-d), the first analytical solution equation (red lines) and the second analytical solution expression (blue lines) of the Langmuir-type model were used to compare the predicted and experimental ultrasonic decomposition kinetics of the two studied contaminants in water at different ultrasonication intensities. For the sonolytic decomposition of the two examined pollutants, the parameters of the Langmuir-type model predicted using the two analytical solution expressions were summarized in Table 3. For a given ultrasonication intensity, the chi-square value calculated for naphthol blue black was lower than that obtained for furosemide for both analytical solution expressions of the Langmuir-type model. Additionally, for both contaminants tested, the chi-square test value obtained using the first analytical solution equation increased with increasing ultrasonication intensity, but decreased with increasing ultrasonic intensity using the second solution expression. The correlation coefficient values for both analytical solution expressions are good, and those obtained for furosemide are slightly higher than those determined for naphthol blue black. The correlation coefficient values increased slightly with increasing the ultrasonic intensity. When the second solution expression was used, the equilibrium constant for both contaminants increased with increasing ultrasonication intensity, but only that of naphthol blue black increased with acoustic intensity when the second solution equation was used. The pseudo-rate constant for both contaminants increased with increasing ultrasonication intensity for the second solution expression, but only that of naphthol blue black increased with intensity for the first solution equation.

Table 3.

Parameters of the Langmuir-type model obtained using two analytical solution expressions by nonlinear regression technique for different ultrasonic intensities (conditions: volume: 300 mL, initial concentrations: 5 mg/L (NBB) and 10 mg/L (FSM), frequency: 585 kHz, temperature: 25 °C, pH: natural (∼6 (NBB) and 5.2 (FSM))).

	Naphthol blue black
	Ultrasonic intensity (W/cm2)
	0.44	1.72	3.58
	First analytical solution expression (Equation(9))
k (mg/L·min)	0.89155	0.47103	0.43073
K (L/mg)	5.3251 × 10−3	33.637 × 10−3	0.11815
χ2	0.04548	0.10691	0.080682
R	0.99263	0.99664	0.99875
	Second analytical solution expression (Equation(10))
k (mg/L·min)	0.077202	0.16387	0.23042
K (L/mg)	96.79 × 10−3	0.13948	0.28218
χ2	0.027112	0.027033	0.026339
R	0.99561	0.99915	0.99959
	Furosemide
	Ultrasonic intensity (W/cm2)
0.83	2.64	4.3
	First analytical solution expression (Equation(9))
k (mg/L·min)	1.4804	1.4695	3.9591
K (L/mg)	20.632 × 10−3	47.72 × 10−3	37.642 × 10−3
χ2	0.34418	0.30937	0.19023
R	0.99782	0.99873	0.99923
	Second analytical solution expression (Equation(10))
k (mg/L·min)	1.5402	1.6751	4.0099
K (L/mg)	20.96 × 10−3	42.091 × 10−3	40.806 × 10−3
χ2	0.49949	0.27414	0.18285
R	0.99684	0.99888	0.99926

All of the aforementioned discussions illustrate that the two analytical solution expressions of the Langmuir-type equation accurately predict the experimental data of the ultrasonic decomposition of the tested pollutants in the aqueous phase at the three ultrasonication intensities examined.

5. Conclusion

For the ultrasonic decomposition of naphthol blue black and furosemide in aqueous solution, two general analytical solution expressions of the Langmuir-type heterogeneous model, developed using perturbation-iteration techniques, were used in this study to predict the sono-oxidation kinetics of these contaminants. The validity of the two general analytical solution expressions was examined under diverse operating conditions, such as initial substrate concentration and ultrasonic frequency and intensity. The results obtained showed that the sonolytic oxidation kinetics of both contaminants decreased as the initial substrate concentration increased. However, as a function of the initial contaminant concentration, the initial ultrasonic decomposition rate increased and then plateaued. Naphthol blue black and furosemide, as nonvolatile substances, cannot diffuse in the bubble interior and must instead be oxidized by reaction with ^•OH radicals in the interfacial zone of acoustic cavitation bubbles. Therefore, a heterogeneous kinetics equation based on a Langmuir-type mechanism can be used to simulate the sono-decomposition process. Using the two analytical solution expressions of the Langmuir-type model, an excellent description of the experimental data of the sono-oxidation of contaminants in water at various initial concentrations was obtained. This confirms that the oxidation of the examined contaminants occurs primarily at the bubble-solution interface. The decomposition yield increases with decreasing ultrasonic frequency in the investigated range and with increasing the intensity of the ultrasound waves. The findings show that the experimental data of sonolytic oxidation of the tested pollutants in the aqueous phase at the three sonolytic intensities and frequencies investigated are well predicted by the two analytical solution expressions of the Langmuir-type equation.

In conclusion, the two general analytical solution expressions of the nonlinear Langmuir-type model are very advantageous for predicting the degradation kinetics of nonvolatile contaminants in aqueous phase by sonolysis process.

CRediT authorship contribution statement

Oualid Hamdaoui: Investigation, Conceptualization, Methodology, Formal analysis, Project administration, Supervision, Visualization, Writing – original draft, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

Data will be made available on request.