Optical single-pixel volumetric imaging by three-dimensional light-field illumination

Significance

Three-dimensional single-pixel imaging (3D SPI) offers a powerful method for 3D imaging and ranging. However, the resolution of depth sensing is fundamentally limited by the time-of-flight or stereovision implementations of current optical 3D-SPI techniques. We propose and experimentally demonstrate an optical single-pixel volumetric imaging approach by 3D light-field illumination, which achieves a near-diffraction-limit 3D optical resolution. In particular, our method is capable of label-free 3D visualization of optical absorption contrasts of single living cells. Our work opens a door to high-performance 3D SPI with applications in biomedical research and optical sensing.

Abstract

Three-dimensional single-pixel imaging (3D SPI) has become an attractive imaging modality for both biomedical research and optical sensing. 3D-SPI techniques generally depend on time-of-flight or stereovision principle to extract depth information from backscattered light. However, existing implementations for these two optical schemes are limited to surface mapping of 3D objects at depth resolutions, at best, at the millimeter level. Here, we report 3D light-field illumination single-pixel microscopy (3D-LFI-SPM) that enables volumetric imaging of microscopic objects with a near-diffraction-limit 3D optical resolution. Aimed at 3D space reconstruction, 3D-LFI-SPM optically samples the 3D Fourier spectrum by combining 3D structured light-field illumination with single-element intensity detection. We build a 3D-LFI-SPM prototype that provides an imaging volume of ∼390 × 390 × 3,800 μm³ and achieves 2.7-μm lateral resolution and better than 37-μm axial resolution. Its capability of 3D visualization of label-free optical absorption contrast is demonstrated by imaging single algal cells in vivo. Our approach opens broad perspectives for 3D SPI with potential applications in various fields, such as biomedical functional imaging.

Single-pixel imaging (SPI) has emerged as an attractive three-dimensional (3D) imaging modality due to its capability of 3D imaging and ranging with a single-pixel detector (1–3). The single-pixel detectors could offer improved performance beyond the conventional array sensors in spectral range, detection efficiency, and timing response (1). Over the last decade, there have been many demonstrations of single-pixel cameras capable of imaging at wavelengths outside the visible spectrum, such as the infrared (4–6), terahertz (7–9), and X-ray range (10, 11). Moreover, the single-pixel cameras have shown superior performance in imaging at weak intensity, single-photon level (12–14), and precise timing resolution (15–17). Benefiting from these advantages, 3D SPI is uniquely positioned for biomedical imaging and remote sensing, especially in harsh environments. For instance, SPI has been adopted in deep tissue imaging (18–21), fluorescence lifetime imaging (22), ultrathin 3D fiber endoscopy (21), and optical diffraction tomography (23) for in vivo applications where light scattering and absorption are commonly involved. Additionally, the 3D precise ranging and sensing ability of SPI has been exploited for various LiDAR systems (14, 15, 24–27) and non-line-of-sight 3D imaging (28–30) with promising applications in 3D situation awareness for autonomous vehicles as well as real-time visualization of hazardous gas leaks (31).

Depth mapping lies at the heart of 3D imaging technology. The majority of current 3D-SPI techniques rely on the stereovision (32–35) or time-of-flight (TOF) (36, 37) principle to extract depth information from backscattered light while the transverse spatial resolution is obtained by the single-pixel image reconstruction. To apply the stereovision principle in SPI, it is necessary to detect two or more images of a scene from different viewpoints using multiple single-pixel detectors (32, 34), which, however, need to be aligned well in an appropriate geometry. In contrast, a TOF measurement directly determines the distance to a scene by illuminating it with pulsed laser light and measuring the time delay of the back-scattered pulses (21, 36, 37). TOF can be used in an SPI configuration to realize precise 3D ranging and sensing using a photodiode, where the depth precision is determined by the temporal resolution of the detector and the width of the laser pulses. The state-of-the-art 3D-SPI system achieves depth mapping to an accuracy of ~3 mm via TOF measurements (15). However, such a depth resolution is far from the requirement of imaging microscopic objects, for instance, biological cells. Besides, optical TOF imaging is so far limited to 3D surface mapping, precluding volumetric imaging. By exploiting the TOF of photoacoustic wave, the depth resolution of 3D SPI can be improved for microscopic imaging but restricted to acoustic diffraction limit (18). Alternatively, by single-pixel diffraction tomography (38, 39), holographic imaging together with a sample rotation enables volumetric reconstruction of a 3D object. However, the imaging operation relies on the stability of mechanical rotation as well as the ability to position the sample precisely at the microscope focus, which inevitably limits the applicability in microscopic imaging.

In this work, we present a single-pixel volumetric imaging technique that aims at direct 3D image reconstruction of microscopic objects, without using any above-mentioned schemes for depth resolving. By exploiting wavefront engineering of a digital micromirror device (DMD), we develop 3D light-field illumination to optically sample the 3D Fourier spectrum via single-element detection in a motionless manner. The proposed approach is termed 3D light-field illumination single-pixel microscopy (3D-LFI-SPM). As a proof of concept, we build a 3D-LFI-SPM prototype that achieves an imaging volume of ∼390 × 390 × 3,800 μm³ and a resolution of up to 2.7 μm laterally and better than 37 μm axially. The high-resolution volumetric imaging performance is demonstrated by imaging spatially distributed algal cells in vivo and in situ. Particularly, the significant merits of our method lie in imaging with a near-diffraction-limit 3D optical resolution, and 3D visualization of label-free optical absorption contrasts of living cells. By harnessing the superiority of single-pixel detectors in spectral range, we expect that 3D-LFI-SPM can be extended to visualize various absorption contrasts of objects at their corresponding wavelengths for biomedical functional imaging.

Results

Principle of 3D-LFI-SPM.

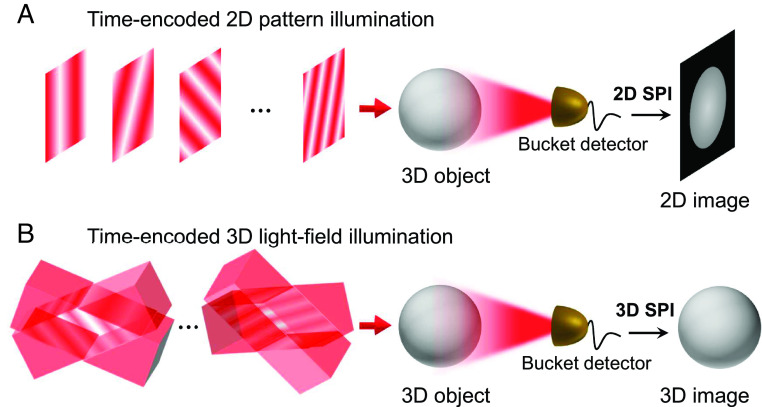
SPI utilizes structured illumination light to sequentially encode the spatial information of objects into the temporal signals collected by a bucket detector and recovers the images with appropriate algorithms computationally. To capture a two-dimensional (2D) image, time-encoded 2D structured patterns, for example, the Fourier patterns (12) (also known as “sinusoidal fringes”) with various spatial frequencies $\left(k_x,k_y\right)$ , are projected to obtain the transverse spatial information of the object, as illustrated in Fig. 1A. To capture a 3D image, however, the structured illumination light should provide three degrees of freedom that encode both the transverse and depth information. For this purpose, we develop 3D light-field illumination exhibiting sinusoidal fringes at any depth and propagating in various directions ( $k_z$ ), which essentially incorporates 3D spatial frequency $\left(k_x,k_y,k_z\right)$ of light (Fig. 1B). This capability allows us to optically sample the 3D Fourier spectrum and reconstruct 3D images of the object via Fourier transform (SI Appendix, Fig. S1).

Fig. 1.

Concept of 3D SPI by 3D-LFI-SPM. (A) 2D SPI shifts the transverse spatial information of an object onto 2D time-varying structured patterns. (B) By 3D light-field illumination, 3D-LFI-SPM is able to encode the 3D spatial information, achieving reconstruction of the 3D image of the object.

Corresponding to each 3D Fourier basis, the structured illumination light presents a normalized 3D intensity profile of

$$I\left(x,y,z;\phi \right)=\frac{1}{2}\left[1+\cos \left(\overrightarrow{k}·\overrightarrow{r}+\phi \right)\right],$$ [1]

where $\overrightarrow{k}=\left(k_x,k_y,k_z\right)$ is a vector in the frequency domain (Fig. 2A), $\overrightarrow{r}=\left(x,y,z\right)$ indicates the position vector, and $\phi$ is a shifting phase. To generate such an intensity distribution, we use a superposition of two plane waves ${\overrightarrow{E}}_1$ and ${\overrightarrow{E}}_2$ with complex amplitudes of $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right. \exp \left[i\left(\overrightarrow{k_1}·\overrightarrow{r}\text{+}\raisebox{1ex}{$\text{φ}$}\!\left/ \!\raisebox{-1ex}{$\text{2}$}\right.\right)\right]$ and $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right. \exp \left[i(\overrightarrow{k_2}·\overrightarrow{r}- \raisebox{1ex}{$\phi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.)\right]$ , where i is the imaginary unit. The two plane waves interfere in the 3D space and generate an optical field (Fig. 2B), which reads

$$E\left(x, y, z; \phi \right)=\exp \left(i\frac{\overrightarrow{k_{\mathit{1}}}+\overrightarrow{k_{\mathit{2}}}}{2}\mathit{·}\overrightarrow{\mathit{r}}\right) \cos \left(\frac{\overrightarrow{k}·\overrightarrow{r}}{2}+\frac{1}{2}\phi \right),$$ [2]

Fig. 2.

Sampling domain and flow chart of 3D-LFI-SPM. (A) Illustration of the $\overrightarrow{k}$ -space that can be sampled for generation of the 3D light fields. (B) The 3D light field created by the interference of two plane waves with varying wave-vectors. (C) Acquisition of the 3D Fourier spectrum by scanning the 3D structured light fields in the 3D OTF domain. (D) 3D image reconstruction of the object by 3D inverse Fourier transform.

where $\overrightarrow{k}={\overrightarrow{k}}_1-{\overrightarrow{k}}_2$ . The wave-vectors ${\overrightarrow{k}}_1$ and ${\overrightarrow{k}}_2$ satisfy ${\left|{\overrightarrow{k}}_1\right|}^2={\left|{\overrightarrow{k}}_2\right|}^2={k_0}^2$ , where $k_0=\frac{2\pi }{\lambda }$ and $\lambda$ are the wavenumber and wavelength of light. In a practical imaging system, ${\overrightarrow{k}}_1$ and ${\overrightarrow{k}}_2$ are limited by the numerical aperture (NA) of the system (Fig. 2A). As a result, the spatial frequencies $\left(k_x,k_y,k_z\right)$ that can be sampled are limited and the corresponding optical transfer function (OTF) domain is shown in Fig. 2C, where ${k_x}^2+{k_y}^2\le {\left(2k_0\mathrm{N}\mathrm{A}\right)}^2$ , and ${k_z}^2\le {{k_0}^2\left(1-\sqrt{1-{\mathrm{N}\mathrm{A}}^2}\right)}^2$ (see details in SI Appendix, Note S1).

Although the optical field is a 3D field, it can be formed by free-space propagation of $E_{\mathrm{m}\mathrm{o}\mathrm{d}}\left(x,y;\phi \right)=E\left(x,y,z=0;\phi \right)$ , the field that is modulated on the focal plane of an objective. When the structured light field illuminates a 3D object (Fig. 2B), the resultant intensity of the signal light collected by a single-pixel detector is proportional to

$$\begin{array}{c}{I}_S\left(k_x,k_y,k_z;\phi \right)={\iiint }_{\mathrm{\Omega }}\left[1-\mu \left(x,y,z\right)\right]\times I\left(x,y,z;\phi \right)\mathrm{d}x\mathrm{d}y\mathrm{d}z\hfill \\ =\frac{1}{2}{\iiint }_{\mathrm{\Omega }}\left[1-\mu \left(x,y,z\right)\right]\hfill \\ \times \left[1+cos\left(\overrightarrow{k}·\overrightarrow{r}+\phi \right)\right]\mathrm{d}x\mathrm{d}y\mathrm{d}z,\hfill \end{array}$$ [3]

where $\mathrm{\Omega }$ represents the illumination volume and $\mu \left(x,y,z\right)$ is the normalized optical absorption distribution of the object. Our microscope works in the transmission mode, so the detected signal is the total intensity of the unabsorbed light. Then the Fourier coefficient corresponding to the spatial frequency $(k_x,k_y,k_z)$ is extracted by using the phase-shifting method (Materials and Methods). Therefore, by scanning all the frequencies in the frequency domain for the structured light-field illumination, the 3D Fourier spectrum of the object can be optically sampled with single-pixel intensity detections. Finally, the reconstruction of 3D optical absorption distribution in the illumination volume is achieved by applying 3D inverse Fourier transform to the obtained Fourier spectrum (Fig. 2D). Distinguished from the conventional single-pixel diffraction tomography, 3D-LFI-SPM enables the acquisition of 3D microscopic images without the need for rotating the sample (SI Appendix, Fig. S2).

Experimental Setup and Characterization.

To perform 3D structured light-field illumination, we exploited the ability of complex field modulation of a DMD to generate the 3D interference fields of two plane waves with varying wave-vectors (see Materials and Methods section). In particular, the high switching rate (up to 17.8 kHz in our case) of the DMD enables rapid switching among various structured illumination fields in a digital manner. Based on such a DMD-modulation scheme, we built a 3D-LFI-SPM prototype in a transmission mode to perform motionless volumetric SPI, which is schematically illustrated in Fig. 3A (for a detailed description, see Materials and Methods section). Note that, 3D-LFI-SPM can also be implemented in a reflection mode for surface mapping of 3D objects.

Fig. 3.

Experimental setup and characterization of the depth resolving ability. (A) Schematic illustration of the 3D-LFI-SPM system. L1-L7: lens; TIRP: total internal reflection prism; DMD: digital micromirror device; BS: beam splitter; PD1, PD2: photodiode; ASL: aspheric lens; DAQ, data acquisition card. (B) Demonstration of depth resolving by tracking a single particle translated along the axial axis. Two 3D Fourier coefficients were sampled by the 3D light-field illumination. (C) Experimental result of the axial tracking. Red circles and the blue line are the measured data and preset line.

The ability to resolve depths by 3D light-field illumination was first verified by tracking a moving particle along the axial axis, as illustrated in Fig. 3B. Specifically, a particle adhered to a coverslip was translated with a 20-μm step size in depth, and at each position, two Fourier coefficients $G\left(k_{x0},k_{y0},k_{z0}\right)$ and $G\left(k_{x0},k_{y0},0\right)$ were acquired. According to the shift theorem of Fourier transform, the depth position can be extracted from the phase shift of the two complex-valued coefficients (40, 41) (see details in SI Appendix, Note S2). As presented in Fig. 3C, the depth positions of the particle are precisely tracked in good agreement with the theoretical prediction. Distinguished from conventional single-particle tracking techniques by holographic imaging (42), our method achieves axial tracking of single particle by acquiring only two Fourier coefficients instead of capturing the whole images, providing a way for high-speed tracking.

Because the illumination light beams have a size and impact angle limited by the DMD and the relay system, the field of view (FOV) and axial range of the 3D-LFI-SPM system are actually limited. The imaging volume was directly measured by imaging a United States Air Force (USAF) resolution target placed at different depths. As shown in Fig. 4A and SI Appendix, Fig. S3, all the features in Group 6 (highest resolution of 114.0 line pairs per mm) can be resolved with our system over an imaging volume of ∼390 μm × 390 μm (lateral) × 3,800 μm (axial, determined by the overlap of the two collimated beams in Fig. 3B). In addition, the lateral and axial resolutions of the system were further characterized within the imaging volume. To measure the lateral resolution, a sharp edge of the square on the USAF target was imaged. Fig. 4G shows the image of the edge at the focal plane, from which the edge spread function was measured. Its corresponding line spread function (LSF) was fitted to compute the lateral resolution, which, defined by the full-width at half-maximum of the LSF, was 2.7 μm (Fig. 4F). This value almost approaches the theoretical lateral resolution limit of 2.2 μm, given by $0.35\lambda /\mathrm{N}\mathrm{A}$ (SI Appendix, Note S3).

Fig. 4.

Characterization of imaging volume and resolution by 3D imaging. (A) Images of a USAF resolution target placed at different depths acquired by 3D-LFI-SPM. The result shows our system achieves an imaging volume of ∼390 × 390 × 3,800 μm³. (B) Depth-encoded image of multilayer carbon fibers. The depth interval between every two layers is ~37 μm. (C–E) Three en-face image slices taken from the 3D reconstruction at the depths of 0 μm, 18 μm, and 37 μm. (F) Normalized (Norm.) edge spread function measured at the focal plane using a sharp edge on the USAF target. The corresponding line spread functions were fitted to compute the lateral resolutions defined by the full-width at half-maximum (Inset). (G) Image of the sharp edge of a square. (Scale bars, 50 µm.)

To quantify the axial resolution, we first calculated the diffraction-limit resolution by $\lambda /2{\mathrm{N}\mathrm{A}}^2$ , that is, 31.7 μm for $\mathrm{N}\mathrm{A}=0.1$ . Then our system performed 3D imaging to test the expected axial resolution. We used a specially designed 3D object made of multilayer carbon fibers (about 7-µm diameter) for the testing. Adjacent layers were separated by a 30-µm-thick coverslip, and thus the average distance between them was ~37 µm. 3D-LFI-SPM achieved imaging the spatial distribution of carbon fibers at different depths. Fig. 4B depicts the reconstructed image of the multilayer object, with imaging depths encoded in color. For further examination, three en-face image slices taken at adjacent layers are presented in Fig. 4 C–E and SI Appendix, Fig. S4. Although there exists some edge enhancement due to sparse Fourier sampling near the direct current component, the images clearly show that the carbon fibers placed at different depths can be resolved, suggesting that our system achieves an axial resolution of better than 37 μm. Our experimental data agree with the expected resolution prediction. Overall, these results establish that 3D-LFI-SPM is capable of volumetric imaging with a near-diffraction-limit optical resolution in three dimensions.

Label-Free 3D Imaging of Living Haematococcus pluvialis Cells.

Benefiting from the low phototoxicity due to wide-field structured illumination, 3D-LFI-SPM allows noninvasive 3D imaging of living biological specimens. To demonstrate the superior performance, we applied 3D-LFI-SPM for 3D imaging of living algal cells and in-situ cell counting inside a target volume. In experiment, H. pluvialis cells in a suspension were the target objects to be imaged, and the living algal cells were immobilized with 2% melted agarose while kept alive in the meantime (see Materials and Methods section). Fig. 5A and the video in Movie S1 show the volume-rendered images of the spatially distributed cells. For this volumetric reconstruction with ∼2.7 × 10⁵ voxels, we measured 59,061 Fourier samples of the 3D OTF domain (Fig. 2C). As seen, the single cells inside the target volume are clearly depth-resolved, which can be examined by the z-slices taken from the 3D reconstruction, as presented in Fig. 5 B–D. In contrast, the out-of-plane cells are hardly recognized from the image (Fig. 5E) captured by a conventional microscope under wide-field illumination. Because of the depth-resolved imaging ability, we are able to localize and count the living cells in situ within the volume. As plotted in Fig. 5F, the 3D positions (centers of gravity) of all the algal cells imaged and the total number can be obtained. This capability might be potentially applied for monitoring cell morphology and growth in situ.

Fig. 5.

Label-free volumetric imaging of living H. pluvialis cells. (A) Volume-rendered image of spatially distributed living algal cells reconstructed by 3D-LFI-SPM. (B–D) Three en-face image slices taken at imaging depths of –180 μm, 78 μm, and 239 μm. The single cells inside the imaging volume are depth-resolved. (E) Image of the cell sample captured by a conventional inverted microscope. The out-of-plane cells are hardly recognized from the image. (F) 3D positions of the single algal cells inside the target volume for in-situ cell counting. (G and H) 3D visualization of optical absorption contrast of a single algal cell from lateral and side views.

Apart from the depth resolving ability, our approach achieves 3D visualization of optical absorption contrasts of single algal cells without labeling, as demonstrated in Fig. 5 G and H. This is particularly distinguished from conventional optical 3D-SPI techniques that generally measure the surface reflectivity of objects. Our observations confirm that noninvasive, label-free, and in-vivo 3D imaging of spatially distributed single cells with a near-diffraction-limit resolution has been achieved by 3D-LFI-SPM. Foreseeably, our approach can readily be extended to visualize various labeled or unlabeled absorption contrasts of biological samples at their corresponding wavelengths for biomedical functional imaging.

Discussion

Larger imaging volume and higher resolution are both desired for 3D-LFI-SPM. However, there is an inherent tradeoff between these performances, which is determined by the NA of the imaging system. With the proposed system, the effective NA is given by $\lambda /4p$ , where $p$ is the size of the super pixel on the DMD (SI Appendix, Note S3). The product of the FOV and the NA is restricted by the pixel count of the DMD (SI Appendix, Eq. S10 in Note S3). So is the case with the product of the depth range and the NA squared (SI Appendix, Eq. S12). We can improve the imaging volume and the resolution simultaneously by increasing the pixel count on the DMD that has a smaller pixel pitch. Besides, the finite NA of the imaging system leads to a well-known missing cone problem because the Fourier spectrum contains no information in a conical region along the optical axis (Fig. 2C and SI Appendix, Fig. S5). Sample rotation can offer an effective way to mitigate its impact (43). Due to the fast time response of the photodiode, the refreshing rate (17.8 kHz) of our DMD is fully exploited to project structured light fields for high-speed illumination. However, large voxels in the 3D images correspond to a large amount of Fourier samples, limiting the frame rate of our imaging system. For instance, capturing a 3D image as Fig. 5A requires the projection of 236,244 patterns in total on the DMD, taking 13.27 s. The acquisition time can be shortened by equipping a higher-speed DMD. Alternatively, the compressed sensing strategy (44) can be adopted to decrease the number of samples. The update of the setup and reconstruction algorithm may further improve 3D-LFI-SPM for potential video-rate volumetric imaging.

By combing raster scanning with single-pixel detection, 3D imaging can be performed to obtain volumetric images of objects. In contrast, our 3D-LFI-SPM exploits structured light illumination method, which sometimes allows us to obtain the whole images even when the number of measurements is fewer than that of a raster scanning. For example, the compressed sensing strategy can be used for this purpose, and SI Appendix, Fig. S6 presents the imaging results of the two methods as a demonstration. In addition, SPI also allows coherent holographic image reconstruction, by which 3D imaging is possible with sparse objects such as particle tracking. However, as Emil Wolf pointed out in 1969 (45), tomography is necessary for high-resolution 3D imaging. Actually, our 3D-LFI-SPM can be taken as a kind of tomography based on the rotation illumination.

In conclusion, we have proposed and implemented 3D-LFI-SPM by combining 3D structured light-field illumination with single-element intensity detection to sample the 3D Fourier spectrum. Remarkably, 3D-LFI-SPM is capable of imaging 3D optical absorption contrasts of objects with a near-diffraction-limit optical resolution. To implement motionless 3D structured light-field illumination, we built a 3D-LFI-SPM system based on a DMD that digitally generated the 3D light fields. Our system achieves an imaging volume of ∼390 × 390 × 3,800 μm³, a lateral resolution of 2.7 μm, and an axial resolution of better than 37 μm. The superior performance of high-resolution volumetric imaging was demonstrated by visualization of spatially distributed living algal cells and in-situ cell counting inside a 3D volume. Our approach can readily be extended to nonvisible wavebands, thus opening broad perspectives for various 3D-SPI modalities with potential applications in biomedical research and optical sensing.

Materials and Methods

3D Fourier Coefficient Extraction by Phase Shifting.

The 3D Fourier coefficient is extracted by a structured light field corresponding to each 3D Fourier basis indicated by Eq. 1. When the structured light field illuminates a 3D object with an absorption distribution of $\mu \left(\overrightarrow{r}\right)$ , the intensity of the signal light indicated by Eq. 3 can be expressed in regard to the Fourier coefficient as

$$\begin{array}{c}{I}_S\left(\overrightarrow{k};\phi \right)=\frac{1}{2}\left[G\left(0\right)+\frac{1}{2}G\left(\overrightarrow{k}\right)\exp \left(-i\phi \right)+\frac{1}{2}G\left(-\overrightarrow{k}\right)\exp \left(i\phi \right)\right].\hfill \end{array}$$ [4]

The Fourier coefficient $G\left(\overrightarrow{k}\right)$ is $\begin{array}{c}\mathcal{F}\left[1-\mu \left(\overrightarrow{r}\right)\right]={\iiint }_{\mathrm{\Omega }}\left(1-\mu \left(\overrightarrow{r}\right)\right) \hfill \end{array}$$\begin{array}{c} \exp \left(-\overrightarrow{k}·\overrightarrow{r}\right)\mathrm{d}\overrightarrow{r}\hfill \end{array}$ , where $\mathcal{F}$ denotes the Fourier transform operator. It can be extracted by using the phase-shifting method, where the shifting phase $\phi$ can be set as $0$ , $\pi /2$ , $\pi$ , and $3\pi /2$ . Accordingly, the intensities of the four-step measurements read

$$\begin{array}{c}\left\{\begin{array}{c}{I}_S\left(\overrightarrow{k};0\right)=\frac{1}{2}\left[G\left(0\right)+\frac{1}{2}G\left(\overrightarrow{k}\right)+\frac{1}{2}G\left(-\overrightarrow{k}\right)\right],\hfill \\ I_S\left(\overrightarrow{k};\frac{\pi }{2}\right)=\frac{1}{2}\left[G\left(0\right)-\frac{1}{2}iG\left(\overrightarrow{k}\right)+\frac{1}{2}iG\left(-\overrightarrow{k}\right)\right],\\ I_S\left(\overrightarrow{k};\pi \right)=\frac{1}{2}\left[G\left(0\right)-\frac{1}{2}G\left(\overrightarrow{k}\right)-\frac{1}{2}G\left(-\overrightarrow{k}\right)\right],\\ I_S\left(\overrightarrow{k};\frac{3\pi }{2}\right)=\frac{1}{2}\left[G\left(0\right)+\frac{1}{2}iG\left(\overrightarrow{k}\right)-\frac{1}{2}iG\left(-\overrightarrow{k}\right)\right].\end{array}\right.\hfill \end{array}$$ [5]

Thus, the Fourier coefficient can be calculated by

$$G\left(\overrightarrow{k}\right)=\left[I_S\left(\overrightarrow{k};0\right)-I_S\left(\overrightarrow{k};\pi \right)\right]+i\left[I_S\left(\overrightarrow{k};\frac{\pi }{2}\right)-I_S\left(\overrightarrow{k};\frac{3\pi }{2}\right)\right],$$ [6]

where i is the imaginary unit.

3D Structured Light Fields Generated by a DMD.

The light fields used for 3D Fourier samples were created by the interference of two plane waves with varying wave-vectors. In practice, the desired 3D light-field distribution can be formed by the free-space propagation of the optical field $E_{\mathrm{m}\mathrm{o}\mathrm{d}}\left(x,y;\phi \right)$ on the focal plane ( $z=0$ ), which was produced by a DMD. To generate the complex optical field with a binary DMD, a binary hologram encoding the complex field was calculated with the super-pixel method (46, 47). In this method, the square regions of nearby pixels (4×4 pixels within 1,080×1,080 pixels in our case) were grouped into various super pixels to define a complex field in the imaging plane, using the first-order diffraction beam. Once the binary hologram was loaded onto the DMD, the desired light field was produced in the target plane and its propagating field presents the 3D intensity profile given by Eq. 1. SI Appendix, Fig. S7 presents the 3D intensity distribution of a generated structured field as well as its cross-sections on given planes, which agrees with the theoretical distribution. In regard to a different 3D Fourier basis, the corresponding interference field of two plane waves with different wave-vectors was generated. In this manner, we were able to scan the structured illumination beams by switching the holograms projected on the DMD. By exploiting the high switching rate of the DMD, digital scanning of 3D structured light fields with a speed of up to 17.86 kHz was achieved.

Details of the Experimental Setup.

Our DMD-based 3D-LFI-SPM system is sketched in Fig. 3A. A He-Ne laser (HNL210LB, Thorlabs, Inc.) with a wavelength of 633 nm is used as the light source. A 20-time beam expander enlarges the laser beam to fully illuminate the surface of a DMD (1,920×1,080 pixels; ALP 4395, ViALUX GmbH, Corp.) with an incident angle of 24° via a total internal reflection prism. With a 4-f configuration (3× demagnification) and a pinhole filter, the DMD is able to generate complex 3D structured light fields. The modulated light fields are relayed to illuminate the 3D objects by a converging lens (f = 180 mm) and an objective lens (10×; UPLSAPO10X2, Olympus, Corp.). The transmitted signal light is then collected by an aspheric lens (f = 40 mm; ACL5040U-A, Thorlabs, Inc.) and its total intensity is detected by a photodiode (PD2, PDB420A, Thorlabs, Inc.). Meanwhile, because of the fluctuant laser power and the varying modulation efficiency for different illumination beams, another photodiode (PD1, PDB420A, Thorlabs, Inc.) monitors the light intensities to compensate for the intensity fluctuations. The output voltage signals from the two photodiodes are acquired and digitalized by a 14-bit data acquisition (DAQ) card (NI PXIe-5122, National Instruments, Corp.), which is controlled by a computer. The computer also instructs the DMD to project and switch the illumination beams. Synchronous acquisition of the DAQ corresponding to time-varying illumination light is triggered by the trigger-out source from the DMD. Finally, the reconstruction algorithm is executed using MATALB on the computer and 3D visualization of the objects is performed with 3D Viewer plugin of ImageJ (48).

Cell Sample Preparation for Imaging Experiments.

H. pluvialis cell samples (FACHB-827) were purchased from the Freshwater Algae Culture Collection at the Institute of Hydrobiology, CAS. The algal cells were cultured in water at room temperature. 3D-LFI-SPM requires immobilizing the living cells inside the imaging volume. For this purpose, we used a mixture of 2% melted agarose (A5030, Sigma-Aldrich) and a cell suspension with a volume ratio of 1:2. Immediately, ~200-microliter solution was injected into a cuvette using a pipette. After gelling on standing below 17 °C for several minutes, the cell sample could be used for the imaging experiments. This preparation minimized the movement of the living cells during the experiments.

Supplementary Material

Appendix 01 (PDF)

Movie S1.

The volume-rendered movie of the spatially distributed cells.

Data, Materials, and Software Availability

All study data are included in the article and/or supporting information.