Integrated NMR/Molecular Dynamics Determination of the Ensemble Conformation of a Thermodynamically Stable CUUG RNA Tetraloop

Abstract

Both experimental and theoretical structure determinations of RNAs have remained challenging due to the intrinsic dynamics of RNAs. We report here an integrated nuclear magnetic resonance/molecular dynamics (NMR/MD) structure determination approach to describe the dynamic structure of the CUUG tetraloop. We show that the tetraloop undergoes substantial dynamics, leading to averaging of the experimental data. These dynamics are particularly linked to the temperature-dependent presence of a hydrogen bond within the tetraloop. Interpreting the NMR data by a single structure represents the low-temperature structure well but fails to capture all conformational states occurring at a higher temperature. We integrate MD simulations, starting from structures of CUUG tetraloops within the Protein Data Bank, with an extensive set of NMR data, and provide a structural ensemble that describes the dynamic nature of the tetraloop and the experimental NMR data well. We thus show that one of the most stable and frequently found RNA tetraloops displays substantial dynamics, warranting such an integrated structural approach.

Introduction

Conformational dynamics of RNA molecules is intimately linked to their function. In RNA, double-stranded regions are intersected by nonbase-paired single-stranded regions containing loops and bulges. These nonbase-paired regions undergo conformational transitions with rates that can span orders of magnitude. Even though NMR spectroscopy is powerful in detecting these transitions, deriving an underlying microscopic model to describe the structural dynamics has remained challenging.¹⁻³ The integration of NMR spectroscopy contains time information on both the averaged structure and their underlying interconversion kinetics, and molecular dynamics (MD) simulations appear to be the best approach to provide such a microscopic model of the ensemble properties of RNAs.^4,5 To interlink NMR and MD, the measurement of extensive sets of experimental data allows the calibration of potential energy functions, cross-validation of the simulation results, or through simulations a posteriori.⁶⁻¹⁰

Tetraloops are frequently occurring nonbase-paired elements in the RNA secondary structure, and their stabilities differ substantially, as shown by mfold¹¹ predictions of all 4⁴ = 256 tetraloop sequences (Figure 1), embedded in a fixed stem sequence containing 5 nucleobase pairs. It is important to note here that the stabilities are influenced by the already known and analyzed tetraloops by the mfold algorithm.¹² Here, we report NMR and MD investigations of the CUUG tetraloop that is among the most stably predicted tetraloops. The 14mer RNA is sufficiently small to allow for detailed structural characterization by NMR spectroscopy and extensive MD simulations. Further, the structure of the CUUG tetraloop has been solved by Pardi et al. in 1995,¹³ thus showing its general suitability for NMR spectroscopic studies. In fact, the structure presented here is in good agreement with the earlier elucidated NMR-based structure.

Figure 1.

Predicted stabilities for all 256 tetraloops in a 14 nts hairpin RNA with the indicated target sequence. Eight tetraloops are predicted to be stabilized by more than −8 kcal mol^–1. The box plot covers all tetraloop sequences that are not shown in individual data points. ΔGs were predicted using the program mfold11. The stabilities of all 256 tetraloops with sequences 5′-ggcacXXXXgugcc-3′ were predicted (shown in black). In addition, the stabilities of all tetraloops with an inverted closing base pair (5′-ggcagXXXXcugcc-3′) were predicted (shown in red).

Previously, we have investigated the structure and dynamics of the UUCG tetraloop.¹⁴ The NMR structure was based on the incorporation of an extensive set of NMR restraints including NOEs, homo- and heteronuclear J-coupling constants, cross-correlated relaxation rates (CCRs), and residual dipolar couplings (RDCs).¹⁵⁻²¹ In the work described here, we provide an equally extensive set of NMR restraints for a second tetraloop sequence and, in combination with MD simulations, determine a structural ensemble of the CUUG tetraloop to capture its dynamics. The stem sequence comprising five nucleobase pairs from a previously determined 5′-cUUCGg-3′ RNA 14mer tetraloop was mostly retained for cross-validation, where only the closing base pair had to be changed from the 5′-cCUUGg-3′ sequence to the 5′-gCUUGc-3′ sequence to avoid duplex formation apparent in the former RNA construct.

The integrative NMR/MD approach provides a detailed dynamic model of this RNA tetraloop that could not be obtained by either technique alone. The outlined procedure is likely to provide a standard for the description of dynamic RNA conformations.^22,23 In fact, there is growing evidence that the RNA function is linked to the ensemble properties even in vivo, and representing RNA conformation by a single structure fails to capture this structure–function relation for this important class of biomacromolecules.²⁴⁻²⁶

Materials and Methods

NMR Sample Preparation

In brief, all 5′-PO₄^3–-GGCAGCUUGCCGCC-2′-3-cyclic phosphate samples were produced using T7-polymerase in vitro transcription. In the in vitro transcription, the 5′ end of the RNA is triphosphorylated. Over time, hydrolysis of the 5′-monophosphate can be observed. In HCP experiments, however, we observe cross-peaks from the 5′-terminal residue to the 5′-phosphate, showing that the 5′-terminus is not completely dephosphorylated over time. The plasmids were ordered from Eurofins containing the gCUUGc tetraloop 14mer sequence incorporated between the EcorR1 and SmaI sites. The plasmid also contained an HDV ribozyme sequence to generate homogeneous 3′-ends. Plasmids were amplified using the DH5α Escherichia coli strain and purified by Gigaprep (Qiagen). Linearization of the plasmid was achieved by using the SmaI enzyme. For preparative transcriptions, the T7-polymerase mutant P226L was used.²⁷ All RNAs were produced as follows: preparative transcriptions were run for 18 h at 37 °C and purified using anion-exchange columns. Fractions containing RNA were precipitated with pure ethanol. Target 14mer RNA and byproduct HDV were separated by preparative HPLC using a Kromasil RP18 column. After a LiClO₄ precipitation (2% w/v in acetone), a buffer exchange to NMR buffer was performed using centrifugal concentrators with a cutoff membrane of 3 kDa. The final buffer concentrations were optimized to 10 mM potassium phosphate and 1 mM EDTA and pH 6.4. For folding, the sample was heated to 95 °C for 5 min and allowed to cool down at room temperature. Final sample concentrations range from 0.64 mM to 1.3 mM in a volume of 280 μL. All samples contained 50 μM DSS and, if not specified otherwise, 5% D₂O. An additional sample for RDC measurements contained 200 μM of RNA and 20 mg mL^–1 of Pf1 phages (ASLA Biotech AB, RNase, and protease free) in 10 mM KP_i buffer.

Several NMR samples of the CUUG tetraloop to determine a close-to-complete NMR data set were prepared. Two samples contained unlabeled RNA in either 95% H₂O/5% D₂O ([RNA] = 860 μM) and one in 100% D₂O ([RNA] = 980 μM). In addition, two samples with ¹³C/¹⁵N labeling were prepared. The sample in H₂O contained 600 μM of RNA, and the sample in D₂O contained 1.26 mM of RNA. Further, a sample for RDC measurements was prepared containing 200 μM of RNA and 20 mg mL^–1 of Pf1 phages (ordered from Asla Biotech) in a total volume of 550 μL. A reference sample containing 200 μM of RNA without Pf1 phages was produced as well.

All preparations of the 5′-gCUUGc-3′ tetraloop 14mer contained duplex regardless of the range of sample concentrations between 100 μM and 1.2 mM. The amount of duplex could be significantly reduced by heating the sample to 95 °C and allowing it to cool at room temperature.

Still, a weak band corresponding to the duplex was detected on a native gel by UV shadowing. At NMR concentration, the duplex population was determined to be less than 5% based on the quantification of cross-peak intensities in the well-resolved H1′ and C1′ regions of ¹H-¹³C-HSQC spectra. Duplex and hairpin conformations were found to be in slow exchange. While no changes in the duplex concentration were observable during measurements (>10 days at 308 K), increases of the duplex population to roughly 30% over the course of ∼2 months were observed. These increases were reversible by reapplying the folding protocol. Even repeating this refolding more than 10 times had no effect on the overall stability and integrity of the CUUG 14mer samples.

NMR Experiments

We recorded NMR experiments on Bruker 600, 700, 800, 900, and 950 MHz spectrometers equipped with either AVIIIHD or AV NEO consoles. The spectrometers were equipped with cryogenic triple resonance probes and a z-axis pulsed-field gradient accessory. The Bruker 700 AVIIHD spectrometer was equipped with a quadruple-resonance QCI-P probe. The Bruker 800 MHz AVIII spectrometer was equipped with a carbon-optimized TXO cryogenic probe. We processed and analyzed all NMR data using the software Topspin 3.6.3 and Topspin 4.1.3 (Bruker). NMR resonance assignments were performed in NMRFAM-Sparky.²⁸ Chemical shift referencing was based on internal DSS and its proton chemical shifts as described by Wishart.²⁹

NMR Structure Calculations

NMR structure calculations were performed with CNS 1.1³⁰ through the ARIA 1.2 adapted setup and protocols using the nucleic acid force field (dna-rna-allatom-hj), which includes optimized potentials for liquid simulation (OPLS) charges and nonbonded parameters.^14,31 Standard annealing protocols were used, and NOE distance calibration was carried out with the correction of spin diffusion. Weak base-planarity restraints were included, as was the possibility for the H5′/H5″ ambiguous assignment and swapping. For 13 out of 14 nucleobases, a stereospecific assignment was possible. Furthermore, dihedral angle restraints were added based on ³J-couplings and CCRs as well as RDCs. 100 starting structures were generated based on a linear template, and for each successive iteration (1–7), in which again 100 structures were calculated, the NOE distance restraints were recalibrated based on the 20 lowest-energy structures of the preceding iteration. The violation tolerance was progressively reduced to 0.1 Å in iteration 8 in which 200 structures were calculated. For the calculations, a four-stage simulated annealing (SA) protocol with torsion angle dynamics (TAD) was used. A high-temperature stage of 10,000 steps at 10,000 K was followed by three cooling steps consisting of 8000 steps to 2000 K, 20,000 steps to 1000 K, and 15,000 steps to 50 K. The force constant for the NOE restraints during the SA protocol was set to 0, 10, 10, and 50 kcal mol^–1 Å^–1. Water refinement was performed for the final bundle of 20 lowest-energy structures.³²

Alignment Tensor Free Structure Calculations

Structure refinement using restraint sets A–F was repeated using the program SCULPTOR-CNS (structure calculation using long-range, tensorial, and orientational restraints).³³ This program allows for the full freedom of the 5 independent parameters defining the alignment tensor (Aa, Ar, α, β, and γ) simultaneously to the structure refinement.

Ten structures determined with all experimental restraints except RDCs using ARIA (as described above) were individually subjected to the following refinement protocol:^34,35 the alignment tensor was initially fitted to the starting structure in its initial conformation using the C–H and N–H RDCs. Both the structure and tensor are released to freely evolve, and RDCs and all other restraints (described above) are applied. Conformational space was sampled at a nominal temperature of 1000K using Cartesian dynamics with a time step of 0.3 fs, and NOEs, dihedral angle, and hydrogen-bonding restraints were applied using 20 kcal mol^–1 Å^–2, 100 kcal mol^–1 deg^–2, and 20 kcal mol^–1 Å^–2, respectively. RDC force constants were linearly ramped from 0.0 to 0.5 kcal mol^–1 Hz^–2 over 8 ps at this temperature, followed by a 2 ps sampling. The system was slow-cooled to 100 K under these restraints over 12 ps prior to minimization. 100 structures (10 per starting structure) were calculated for each restraint combination, and the 10 conformers with the lowest target function from each starting structure were included in each final bundle.

System Preparation and MD Simulations

To generate a diverse set of initial tetraloop structures, we searched the Protein Data Bank (PDB) for all RNA three-dimensional (3D) structures containing the 5′-ngCUUGcn-3′ sequence and forming a Watson–Crick base pair between the first and the last nucleotides. We performed a complete-linkage hierarchical clustering of the 161 tetraloop structures obtained from the PDB, using the eRMSD to measure distances; the number of clusters was set to 20.³⁶ Next, an ideal A-form helix of residues G1–G5 and C10–C14 was generated using an in-house python script (https://github.com/sbottaro/build_aform). To build the 20 chimeric 14mer structures, we aligned all heavy atoms in residues 5 and 10 and heavy backbone atoms in residues 4 and 11 of the stem and loop sequence.

We modeled the RNA using the Amber ff99SB force field together with the parmbsc0 and χ_OL3 corrections.^37,38 First, we minimized the RNA in vacuo for up to 50,000 steps of steepest descent, placed in a dodecahedral box with a 1.4 nm padding between the RNA and the box and solvated with about 4300 OPC water molecules.³⁹ Before the addition of ions, the system was again minimized for up to 25,000 steps. The negative charge of −13 was neutralized with K⁺ ions, and further K⁺/CL^– ions were added to reach a concentration of 10 mM and again minimized as before. Next, we equilibrated the system in the NVT ensemble for 200 ps using the velocity rescaling thermostat with a reference temperature of 308 K and a thermostat time scale of 1 ps.⁴⁰ A force constant of 1000 kJ mol^–1 nm^–2 was used for harmonic position restraints on all heavy atoms of the RNA molecule during minimization and NVT equilibration. The system was then equilibrated for 10 × 200 ps in the NPT ensemble, gradually releasing the force constants of positional restraints from 1000 to 0 kJ mol^–1 nm^–2. We used the Parrinello–Rahman barostat for pressure coupling with a reference pressure of 1 bar, a time scale of 2 ps, and an isotropic compressibility of 4.5 × 10^–5 bar^–1. Finally, we performed production runs in the NPT ensemble for 200 ns per simulation. Equations of motions were integrated using the leapfrog algorithm, and a cutoff of 1.4 nm was used for van der Waals and Coulomb interactions. The particle-mesh Ewald summation was employed for long-range electrostatics with a fourth-order cubic interpolation and a 0.16 nm Fourier grid spacing.⁴¹ For each starting structure, 5 independent simulations were run totaling to 20 μs of simulation time after pooling all 100 simulations. We used one frame saved every 1 ns for analyses.

MD Simulation Analysis and Reweighting

We calculated eRMSDs, base-pairing interactions, ³J-couplings, and dihedral angles using the Barnaba python library with default settings.⁴² NOE distances were calculated using the compute_distances module in the MDTraj python library, and r^–6 averaging was employed to calculate simulation averages.⁴³ CCRs were calculated using an in-house python script (https://github.com/sbottaro/CCRR), and RDCs were calculated with the PALES software.⁴⁴ For this, we used the Rod LC model (pf1) for alignment tensor prediction with a crystal concentration of 0.05 mg mL^–1 and included all atoms. To compare calculated RDCs to experimental measurements, we rescaled all calculated values using a linear regression model considering all 14 residues.

We fitted the simulations against experimental RDCs and ³J-couplings using the Bayesian/maximum entropy reweighting method implemented in the BME python library.⁴⁵ The hyperparameter θ was set to 20 after choosing a suitable range using 5-fold cross-validation and cross-validation against NOEs and CCRs (see Figures S9 and S10 in the Supporting Information). To generate the MD subensemble, we sampled 100 out of 20,100 structures with replacement using the weights from BME reweighting with the random.choice module from the Numpy python library. Finally, we clustered the structures in the new ensemble based on eRMSDs using the quality threshold algorithm with an eRMSD cutoff of 0.7 Å and a minimum cluster size of 5.⁴⁶ Analysis and visualization were done with python and ChimeraX, respectively.⁴⁷ Data and scripts for analysis scripts are available on GitHub [https://github.com/KULL-Centre/_2023_oxenfarth_CUUG].

Results and Discussion

Heteronuclear two-dimensional (2D) experiments revealed substantial temperature-dependent changes, indicating the presence of different conformations. The gCUUGc 14mer undergoes significant dynamics in the temperature range of 278–308 K. These dynamics arise for nucleotides within the loop (C6, G9) and the closing GC-nucleobase pair (C10). In the following sections, we show that a single structure containing a C6–G9 nucleobase pair within the loop is not sufficient to adequately describe the conformation of the CUUG 14mer.

To rule out that the temperature-dependent changes of nucleotides C6, G9, and C10 are due to changes in the extent of dimerization or monomer dimer conversion kinetics, we analyzed the temperature-dependent intensities of the signals of the imino protons of U7 and U8 from the minor dimer conformation in ¹H-1D temperature rows (1D temperature row shown in Figure S2 in the Supporting Information). No temperature-dependent changes in the intensity of U7 and U8 were observable, indicating no changes in the slow exchange regime of the dimer and hairpin monomer, ruling out that temperature-dependent effects C6, G9, and C10 can be attributed to the presence of the minor duplex conformation. We observe similar temperature independence of C1′–H1′ resonances of the duplex. They remain in slow exchange at all temperatures in ¹H,¹³C-HSQCs (Figure 5b). These observations are supported by previous investigations that report the time scale for refolding of hairpins into duplexes involving the opening of several base pairs, which are of the order of seconds to days.^48,49

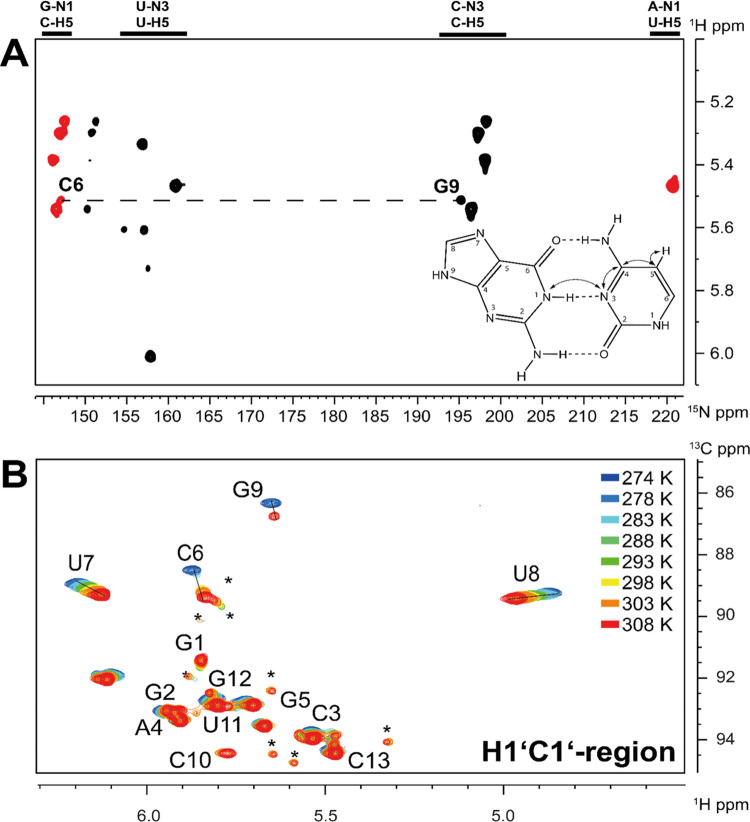
Figure 5.

Experiments to detect the loop GC base pair at 308 K and temperature series of the C1′–H1′ region. (A) Spectra of the H(CC)NN-COSY experiment. The spectrum was measured at 308 K on a ¹³C, ¹⁵N CUUG 14mer sample in D₂O. (B) the ¹H¹³C-HSQC spectra were measured on the ¹³C, ¹⁵N CUUG 14mer sample in D₂O from 278 to 308 K. All experiments were measured at 800 MHz. The asterisks indicate peaks originating from the low amount of duplex in the sample.

Derivation of NMR Restraints

To analyze the impact of the loop-closing base pair on the structure of the stem of the tetraloop, we compared ribose ¹³C chemical shifts of the two tetraloops 5′-P0₄^3–-GGCAgCUUGcCGCC-3′ and 5′-P0₄^3–-GGCAcUUCGgCGCC-3′ (Figure S1: comparison chemical shifts of UUCG and CUUG stems in the Supporting Information). All moieties of the ribose show a strong correlation ranging from R = 0.98 for chemical shifts of C4′ sites to R = 0.81 of C2′ sites, indicating that the structures of the A-form helical stems of both RNA constructs are nearly identical.

Distance restraints were obtained from ¹H,¹H-NOESY experiments at T = 308 K (Figure 3B and annotated version in Figure S8 in the Supporting Information) using cross-peak intensities from spectra with three different mixing times (50, 100, and 150 ms) measured in D₂O. Spectra in D₂O are preferred because of the better spectral quality (resolution and resolving sugars near the water). Moreover, the signals in the imino and amino regions are more prone to diffusion and exchange, especially at higher temperature. On average, 13 distance restraints were obtained per residue (9 intraresidue and 4 sequential). This resulted on average in 13 distance restraints per residue, excluding NOEs between the diastereotopic H5′/H5″ protons as well as the close-proximity pairs H5–H6 and H1′–H2′. Assessment of spin diffusion and distance calibration was performed with ARIA for each cross-peak. Additionally, a set of NOESY experiments were performed at 283 K using the same mixing times. In comparison to the NOESYs at 308 K, about two fewer NOE contacts were detected per nucleotide.

Figure 3.

Representative set of NMR spectra documenting the quality of the experimental data to extract structural information from torsion angle-dependent J-coupling constants, cross-correlated relaxation rates, NOEs, and residual dipolar couplings. If not stated otherwise, experimental data were measured at 308 K. (A) HNN-COSY was used to determine donor and acceptor nitrogen atoms involved in base pairs. (B) Aromatic and sugar region of ¹H–¹H-NOESY spectra. A larger version of the NOESY with annotated cross-peaks is shown in Figure S6. (C) Forward-directed HCC-TOCSY-CCH-E.COSY yields ³J(H,H) coupling constants for the ribose moieties of the nucleotides to determine torsion angles. Right of panel C, close-ups of examples of cross-peaks for stem and loop nucleotides are shown. (D) Cross- and reference spectra of the quantitative Γ-HCCH experiment yield cross-correlated relaxation rates to determine project angles of C–H dipolar vectors. From experimental data shown in panels C and D, the sugar pucker (pseudorotation phase and amplitude) was derived. (E) IPAP spectra from unaligned (isotropic) and phage-aligned (anisotropic) RNA samples yield 1D(C,H) residual dipolar couplings to determine C–H dipolar vector orientations.

When RNA structures are calculated solely by using NOE-derived distance restraints, the ensemble often does not converge to high resolution. In these cases, dihedral angle restraints (Figure 2 and Table 1) and residual dipolar couplings provide useful complementary sets of local conformational and global orientational restraints. Both sets of NMR restraints were determined for the CUUG 14mer (Figure 3C,D) using previously developed methodologies.^19−21,51

Figure 2.

Overview of the dihedral angles in RNA.

Table 1. Data Used for the Determination of Dihedral Angles Using NMR.

angle	NMR-parameter
α	Γ(C5′,H5′,P)DD,CSA Γ(C5′,H5″,P)50
β	3J(H5′,P)-, 3J(H5″,P)-51 and 3J(C4′,P)52
γ	3J(H4′,H5′)-, 3J(H4′,H5″)-19 and 2J(C4′,H5′)-, 3J(C4′,H5″)53
δ, P	3J(H1′,H2′)-, 3J(H2′,H3′)-, 3J(H3′H4′)-, Γ(C1′H1′,C2′H2′)DD,DD Γ(C3′H3′,C4′H4′)15,53,54
ε	3J(H3′,Pi+1)-,51 and 3J(C4′,Pi+1)-, 3J(C2′,Pi+1)52
ζ	ΓC3′,H3′,Pi+1DD,CSA50
χ	Γ(C8H8,C1′H1′)DD,DD (purines), Γ(C6H6,C1′H1′) (pyrimidines)20

The conversion of J-coupling constants into dihedral restraints (Figure 3) relies on Karplus parameterizations.⁵⁵⁻⁵⁷ The accuracy of torsion angle determination is, however, not as good as for proteins since Karplus parameters for oligonucleotides were often parameterized from a small set of model compounds of low molecular weight, especially for heteronuclear coupling constants. In addition, for larger-sized RNAs, systematic errors, in particular, for the determination of ³J(H,H) coupling constants, can be observed as theoretically outlined by Harbison.^57,58

Cross-correlated relaxation rates (CCRs) similarly report on the local conformation. CCRs are linearly dependent on τ_c and do not require additional parameterization.⁵⁹ For determination of the ribose sugar moieties, ratios of cross-correlated relaxation rates Γ_{(H1′C1′,H2′C2′)}^DD,DD/Γ_{(H3′C3′,H4′C4′)} can be used, which compensate the effect of differential local dynamics in different nucleotides, for example, between those in stem regions vs those in loop regions of the RNA, assuming that the local dynamics in the furanosyl ring moieties of the dipolar H–C vector are coupled.

Torsion Angles

We first discuss NMR data reporting on the pseudorotation phase P and the torsion angle γ. The conformation of the ribofuranosyl ring in RNA is described by the pseudorotation phase (P) and amplitude ν_max. ¹³C chemical shifts are sensitive to the local ribofuranosyl ring conformation and can be converted into the so-called canonical coordinates.^60,61 Canonical coordinates are empirical parameterization comparable to TALOS predictions of the protein backbone conformation.⁶² As a second parameter reporting on P and ν_max, we determined ³J(H,H) coupling constants. From a total of 70 ³J(H,H) coupling constants, 56 ³J(H,H) could be measured and analyzed (Table S1). Further, the conformational analysis was corroborated by the measurement of CCR. From a total of 28 CCRs, 23 CCRs could be measured and analyzed.

The derivation of the P can serve as an example to compare the three methods described above. An initial assessment of the P based on ¹³C chemical shifts via canonical coordinates indicates that the entire loop is in the noncanonical C2′-endo conformation, while the entire stem is in the canonical α-helical conformation with the ring adopting a C3′-endo conformation (Table S3). We confirmed these observations with the analysis of ³J(H,H)-coupling constants and CCRs (shown in Figure 4A–C and Tables S1–S3). Overall, the canonical coordinates are in better agreement with values acquired by ³J-couplings than those obtained from CCRs.

Figure 4.

Compilation of NMR restraints derived from the NMR parameters of the CUUG tetraloop. Panel (A) shows the canonical coordinates of the CUUG tetraloop determined from the ¹³C shifts of the ribose ring at 308 K. The x axis shows the pseudorotation phase P, while the y axis shows the γ angle. The entire loop nucleotide samples C2′-endo conformations, while stem nucleotides adapt C3′-endo conformations. Panel (B) shows the determination P based on the CCR. Red shows P determined from Γ_{(H1′C1′,H2′C2′)}^DD,DD, while the blue graph corresponds to Γ_{(H3′C3′,H4′C4′)}. The yellow graph shows the ratio of blue and red. For C6, a ratio could not be calculated since the Γ_{(H3′C3′,H4′C4′)}^DD,DD rate was outside of the possible parameter values, presumably due to too low signal-to-noise. (C) Derivation of the pseudorotation phase P based on the ³J(H1′,H2′) and ³J(H3′,H4′) couplings derived from the HCC-TOCSY-CCH-E.COSY experiment. ³J(H1′,H2′) couplings are shown in red, ³J(H3′,H4′) couplings are shown in blue, and ³J(H2′,H3′) couplings are shown in green. Panel (D) shows the Karplus-based determination of the ε angle of C3. The blue-colored graphs show the simulated ²J and ³J-couplings, while the red graph shows the lowest possible rmsJ for the angle C3. Panel (E) shows the determination of the angle χ based on CCR. The gray graph shows calculated values for χ for an S² of 0.9. The red and blue graphs were generated using S² values of 0.8 and 0.7, respectively. For all nucleotides except G9, the choice of the S² value does not change the result of the determination of the angle χ. Panel (F) shows aromatic ¹D(C,H) RDCs measured at 283 K (blue) and 308 K (red).

Next to an empirical estimate provided by the canonical coordinates, qualitative information regarding the backbone angle γ can be derived from heteronuclear geminal ²J(C4′,H5′)- and ²J(C4′,H5″)-coupling constants^53,63 together with homonuclear ³J(H4′,H5′)- and ³J(H4′,H5″)-coupling constants. The two hydrogens H5′ and H5″ covalently bound to C5′ are diastereotopic. In general, they thus give rise to two different chemical shift positions, e.g., in ¹H,¹³C-HSQC experiments. As stereotopic annotation, we use the H5′ and H5″ nomenclatures. At the same time, the nomenclatures proR and proS and H5′1 and H5′2 are used. IUPAC has defined the following nomenclature:⁶⁴ the H5′ (H5′1) is the proS hydrogen atom (proton) and the H5″ (H5′2) is the proR hydrogen (proton). H5′ and H5″ are thus not assigned due to their downfield and highfield chemical shifts, respectively, but they represent stereochemical denominators.

Rotamer states (periplanar and clinal^–) are distinguishable by the magnitudes and signs of the ²J(C4′,H5′)- and ²J(C4′,H5″)-coupling constants. For the synclinal (sc+) conformation, a negative sign of the coupling constant for the H5′ and a positive sign for the H5″ are expected.

In addition, both the ³J(H4′,H5′)- and ³J(H4′,H5″)-coupling constants are small for the synclinal configuration. For the synclinal (sc-) configuration, negative couplings ²J(C4′,H5′)- and ²J(C4′,H5″)-coupling constants, a large ³J(H4′,H5″) coupling, and a small ³J(H4′,H5″) coupling are observed.

For some nucleotides, the determination of the ³J-coupling constants proved to be difficult due to weak signals of the correlations involving H5′/H5″ protons in the forward-directed HCC-TOCSY-CCH-E.COSY experiment. In most cases, however, the ²J(C4′,H5′)- and ²J(C4′,H5″)-coupling constants were sufficient to assign the torsion angle γ. In all cases except G9 and C10, the rotamer state was synclinal (sc+). For G9, the analysis of the ²J(C4′,H5′/H5″) and ³J-coupling constants resulted in the trans (antiperiplanar) conformation, where H5″ is the downfield-shifted proton and H5′ is the upfield-shifted proton.

Determination of the conformation and diastereotopic assignments of C10 proved difficult. The determination of the ³J(H4′,H5′)- and ³J(H4′,H5″)-coupling constants was not feasible since the H4′ and the H5′ protons share the same chemical shift. Without these couplings, it is not possible to distinguish between the synclinal (sc+) and antiperiplanar conformations. Canonical coordinates indicate that the antiperiplanar conformation is more likely because the angle is determined at 155°, which fits well with a canonical angle of 160° of the antiperiplanar conformation.

The conformation of angle χ determining the orientation of the nucleobase relative to the ribose ring is described (an example for purines is shown in Figure 4E). χ typically adopts an anti-conformation in RNA stems but can also adopt syn-conformations in loops. Determination of χ is possible from cross-correlated relaxation rates (Γ_{(C1′H1′,C6H6)}^DD,DD and Γ_{(C1′H1′,C8H8)}) in combination with information on local dynamics (S² values) for each nucleotide (Table S8).²⁰ We performed a preliminary calculation with homology-modeled S² values. We fixed stem S² values to the experimentally determined stem S² of the UUCG 14mer, as the values for the stem are expected to be very similar.⁶⁵ For the loop residues, we estimated the lowest value of S² = 0.7. Interestingly, χ angles of purines were less dependent on S² for the range of CCRs determined. The CCR is small for χ in anti-conformation and large for χ in syn-conformation (see Figure 4E). Reduction of S² further reduced the size of the rate. One exception was G9. Here, no fit was possible for any S² below 0.9. For S² = 0.9, χ = 171°, and for S² = 1, χ = 178°. This finding could indicate a second, less populated conformation of G9 where the nucleobase populates either the syn-conformation or the high anti-conformation. In fact, our MD simulations also point to a second, less populated state (∼10%) with high anti-conformation. To further check this, we analyzed the integrals of several H1′–H8 cross-peaks in D₂O NOESYs. For a nucleotide in the syn-conformation, a strong cross-peak between H1′–H8 would be expected (data shown in Figure S6 in the Supporting Information). As a reference, we analyzed the integral of a H1′–H2′ cross-peak. Our analysis showed that the integral of G9 is in the same order as G1, G2, and G5, suggesting that it is mostly present in the anti-conformation.

In comparison to nucleotides with purine nucleobases, the derived conformations for nucleotides with pyrimidine nucleobases were more dependent on the S² parameter. We note that using different S² values had almost no impact on the χ angle of most nucleotides for which we obtained CCRs except for C10. Here, the χ angle varied by about 15–20° between the different S² values and the determined CCR. Nonetheless, even the smallest theoretically determined angle would still be 180°, thus strongly indicating the anti-conformation.

To determine backbone angles β and ε, we measured ³J-couplings using quantitative HCP, J-modulated HSQCs, and P-FIDS experiments (Tables S4–S6).^51,52 In the quantitative HCP experiment, correlations were observed between ³¹P nuclei to several sugar atoms including H3′, H4′, H5′/H5″, and C4′/C2′ (Figure S7: spectrum of the quantitative HCP in the Supporting Information). Due to the unfavorable resolution of the C5′H5′ region, not all coupling constants could be determined. Additionally, only upper bounds for ³J(C2′_i,P_i+1) couplings could be derived as these couplings are small and could thus not be detected in the cross-experiment due to insufficient signal to noise. For the reference experiment, all peaks were observable, and intensities for every peak except G1 could be determined. Therefore, we assumed ³J(C2′_i,P_i+1)-couplings for all stem residues to be 0.8 Hz. For the stem nucleotides, we determined ε ∼ 205° in most cases, which is also the canonical value for A-form RNA. The derivation of ε for residue U3 is shown in Figure 4D. We determined 19 out of the 28 backbone angles β and ε.

Interestingly, even residues C6, U7, and G9 were placed in the canonical A-form angle of ε = 205° with their angles determined at ε = −203, 215, and 205°, respectively. Determination of ε for U8 and C10 was less clear. Here, minima were located at 0° with additional minima at 120/250 and 125/265° for U8 and C10, respectively. The minima at 0° would indicate the eclipsed rotamer configuration for these nucleotides. These values might, however, indicate that several populations for the angle ε are possible and support the dynamic averaging of the structure.

Once the angles β and ε are determined, it is possible to also determine the backbone angles α and ζ by measuring dipole-CSA (chemical shift anisotropy) CCR between CH-dipoles and the P chemical shift anisotropy.²¹ In 2D and 3D reference experiments, we observed peaks for all nucleotides, allowing us to derive Γ_{(C3′H3′,P)}^DD,CSA, Γ_{(C4′H4′,P)}, and Γ_{(C4′H4′,Pi+1)}^DD,CSA (Table S7). By contrast, the detection of correlations depending on Γ_{(C5′H5′,P)} proved to be more difficult to observe. Nevertheless, we could determine 12 out of 14 rates. For some of the rates, we can determine upper bounds for the maximal size of the cross-correlated relaxation rate. In the reference experiment, no peaks were observable for the nucleotides A4 and G12. In the cross-experiment, less peaks were observable. Despite these difficulties, we evaluated the angles α and ζ following the procedure outlined in Nozinovic et al.²¹ For each angle, four different solutions were possible for each β and ε combined with the respective cross-correlated relaxation rate (Table S6). In a boot-strapping procedure, the most likely solutions were first determined by analyzing initial structure calculations containing all determined NOEs, nucleobase pairing patterns, and all previously determined backbone angles. The best-fitting solution for α and ζ was then chosen (Table S7). In cases where multiple solutions were possible, the nearest value was chosen. Afterward, the initial choice was confirmed by running a follow-up structure calculation. Since some loop residues did not match the previously chosen angle, we checked whether a different solution would be a better fit, which allowed us to improve ζ of C6 and α of U7, U8, and G9. In total, we determined 18 of the 26 possible angles.

Residual dipolar couplings were measured at two different temperatures (T = 283 and 308 K) (Tables S9–S12). We measured RDCs for all imino NH sites, the aromatic C5H5, C6H6, C8H8, and C2H2 as well as for the sugar C1′H1′ sites (data for aromatic RDC shown in Figure 4F) summing up to a total of 39 RDCs. The NH RDCs of the iminos were strongly temperature-dependent, presumably due to accelerated solvent exchange rates at higher temperatures and associated self-decoupling. Surprisingly, the values of all CH-based RDCs did not change with an increase in temperature. We note that signals are lacking, especially in the dynamic loop region as well as for the C14 residue. While a change in intensity for all loop nucleotides and C10 is observable in ¹³C-HSQCs, it was still surprising that no signal was detectable in the aligned samples for these residues.

Structural Characteristics and NMR Structure Calculations

One interesting feature of this RNA tetraloop is the base pair between loop residues C6 and G9. This base pair was observed and incorporated in the structure determination by Jucker et al. in 1995.¹³ It is observable, though weak, in an HNN-COSY experiment at 278 K but cannot be detected with the same experiment at higher temperatures. This temperature dependence for base pair formation should be taken into account for structure calculations of the CUUG 14mer when performed with data measured at higher temperatures (298 K in 1995 and 308 K in this work). Merging of NMR data recorded at different temperatures is usual for RNA structure calculations. For this CUUG 14mer, however, this is likely not valid. To investigate whether the C6–G9 base pair observed at 278 K is still (partially) formed at 308 K, we conducted a H(CC)NN-COSY experiment.⁶⁶ Since this experiment starts on the nonexchangeable H5 proton of cytidines, it is independent of chemical solvent exchange of the hydrogen-bonded imino proton that is the starting nucleus in the HNN-COSY experiment.

Using the H(CC)NN-COSY experiment, we confirmed the presence of the nucleobase pair between C6 and G9 even at 308 K (Figure 5A). We note that the intensities of the diagonal peak of C6 and the cross-peak of C6–G9 are less strong compared to cross-peaks for the nucleobase pairs of the stem. This observation suggests that the base-paired state is possibly not completely populated at higher temperatures. We determined ^2HJ(N,N) coupling according to Dingley et al.⁶⁷ and found that the determined ^2HJ(N,N) coupling constants do not differ for the two 278 and 308 K data sets for the C6–G9 base pair. We interpret these seemingly controversial experimental observations to indicate that the chemical exchange of the imino proton with solvent water is temperature-sensitive. At higher temperatures, the intensity of imino signals becomes lower and, in fact, not detectable even if the population of the base-paired state remains high. The strength of the base pair once formed is, however, not changed.

Temperature series of ¹³C HSQCs of the ribose region show that C1′H1′ signals of the loop nucleotides are temperature-sensitive. While the signals for U7 and U8 are visible at all temperatures, signals for residues C6 and G9 are visible at the low and the high temperatures but not in between. This behavior of signals for C6 and G9 indicates that the conformational transition features intermediate exchange kinetics at temperatures between 283 and 298 K (shown in Figure 5B). In addition, C1′H1′ of C10 is not observable at temperatures below 288 K.

Given the substantial temperature dependence, we initially aimed to determine two structures, a low-temperature structure (T = 283 K) and a high-temperature structure (T = 308 K). 283 K was chosen since this was the lowest temperature at which most peaks were detectable. The amount of cross-peaks in the NOESY experiment was, however, significantly smaller, and experiments to extract J-coupling constants and cross-correlated relaxation could not be obtained at sufficient signal to noise. Therefore, the determination of a high-resolution, low-temperature structure is practically infeasible.

Because of that, we carried out NMR structure calculations using high-temperature data. The structure calculation was performed in several steps to validate the impact of the restraints: six different structures were determined (Figure S3: compilation of all determined structures in the Supporting Information). First, two structures using all angles were determined with and without the C6–G9 base pair (Figure S3: bundles A and B, respectively, in the Supporting Information). Second, two structures using all angles except for α and ζ and using all RDC data were determined. Again, one structure was calculated using the C6–G9 base pair and one without it (Figure S3: bundles C and D in the Supporting Information). Lastly, two structures using all acquired data (all distance and angular data and all RDCs) were determined, again with the distinction that one contained the C6–G9 base pair and one did not (Figure S3: bundles E and F in the Supporting Information).

Defining features of bundles A, C, and E are that nucleotides U7 and U8 are both pointing toward the groove (detailed view shown in Figure S5 in the Supporting Information). U7 is nearly perpendicular to the C6–G9 base pair, and U8 is stacked on top of G9. The nucleobase of loop-closing nucleotide C10 is slightly twisted compared to the other nucleobases in the stem. The turn of the loop itself is rather smooth, and all of the determined backbone angles fit well to the determined structures. Comparison to the structure published by Jucker and Pardi in 1995 is striking: both structures share the same stacking of U8 and G9 as well as the perpendicular position of U7 to the base pair of C6 and G9. We note, however, that the stem of our structure is much better defined compared to the structure published in 1995, likely due to the substantially larger number of restraints collected in this study. Differences between these three bundles are mainly in the amount of small violations and the overall RMSD of the bundles. Bundle A has the highest RSMD with 1.24 Å. Both bundles C and E converge to a higher-resolution ensemble with an RMSD of 0.64 and 0.67 Å, respectively. This convergence is indicated by the pairwise RMSD of 1 Å.

Comparison of the bundles B, D, and F, which all do not contain the C6–G9 base pair, shows that U7 and U8 are similarly oriented to the bundles A–E (detailed depiction shown in Figure S5 in the Supporting Information). No striking differences can be observed for those two loop residues. The loop residue C6 shows similarly to U7 and U8 no significant structural heterogeneity in all 20 structures of each of the three bundles. G9 is pointing in several different directions. In addition, it seems that in bundle D containing only all RDCs but not the angles α and ζ, C6 and G9 are at rather close distance. Such a close distance is also observed in bundles A, C, and E. This cannot be observed for bundles B and F where the loop opens up between C6 and G9. These observations are also reflected in the overall RMSD of the three different bundles. Bundle B has the highest RMSD with 1.27 Å, followed by bundle F with 0.96 Å and bundle D with 0.80 Å. Small NOE violations (<0.4 Å) are found for all structures, but bundle D contained the least and F the most. The same is true for dihedral violations. Violations are only observable for stem nucleotides and in few cases also involving C10.

In addition, we performed structure calculations including RDCs using floating tensors to verify structures (shown in Figure S4 in the Supporting Information). The two structure calculations applying different protocols were performed independently in two different laboratories. Structures calculated with floating tensors are in good agreement with the structures determined by ARIA and further verifying them. Especially, the floating alignment tensor structures equivalent to bundles C and F are most similar, while the structure corresponding to bundle D differs the most. Here, several different structures are observed rather than a single state. Pairwise RMSDs were determined for all structures with floating tensor as well as pairwise RMSD between the ARIA and floating tensor structures (Table S13).

The small but evident increase in violations with increasing amounts of restraints in addition to the temperature-dependent data apparent in HSQC experiments points to the necessity to determine a more dynamic RNA structural ensemble as opposed to fitting the NMR data to a single structural state as implicit in all three NMR bundles. This is in line with observations other groups made showing that an ensemble fit often depicts the RNA better than a single structure.²⁴⁻²⁶

Lastly, the differences between the two different base pair possibilities for this tetraloop are beyond the scope of this manuscript, especially at concentrations required for more complex NMR experiments. Further experiments on the other construct are required in this case.

Computational Studies and Integrative Structural Ensemble Determination

The results shown above suggest that the structural interpretation of the NMR data of RNA is particularly complex and that the presence of multiple conformational states must be considered to explain the experimental results. We thus performed molecular dynamics (MD) simulations of the CUUG tetraloop and validated these results with experimental NMR data. The result of such an integrative approach is a structural ensemble of multiple conformations that more closely agrees with the measured experimental data.

To provide an independent starting point for the structure determination, we performed MD simulations of the CUUG tetraloop using 20 structurally different initial conformations modeled based on tetraloop structures in the PDB. For each of these starting structures, we ran five replicates of 200 ns of MD simulations (see the Materials and Methods section for details). The resulting pool of 20,100 structures (henceforth termed MD) is thus obtained from 100 separate simulations for a total of 20 μs of sampling.

For each individual structure in the MD ensemble, we calculated the expected RDCs, ³J-couplings, CCRs, and NOE distances of residues G5–C10 for comparison with the experimentally measured values. Figure 6 (panels A–D) reports the root-mean-square error (RMSE) between the ensemble averages and experimental measurements for the distinct types of data: RDCs (panel A), ³J scalar couplings (panel B), NOEs (panel C), and CCRs (panel D). The RMSE values of the MD ensemble are compared to the values calculated for bundles E and F as well as the previously determined NMR structure (PDB bundle 1RNG). Note that while we treat the MD as an ensemble (hence, comparing each experimental measurement to the average back-calculated value), NMR bundles E, F, and 1RNG are considered as a collection of individual structures. Hence, each point in Figure 6A–D reports the RMSE for each individual structure in these bundles.

Figure 6.

Comparison of simulation ensembles and structure bundles to experimental data. (A–D) Root-mean-squared-errors (RMSEs) between back-calculated and experimental (A) RDCs, (B) ³J-couplings, (C) CCRs, and (D) NOEs for the different ensembles and structure bundles. (E) Upper panel: experimental and back-calculated distributions of Γ_{(H1′C1′,H2′C2′)}^DD,DD and Γ_{(H3′C3′,H4′C4′)} CCRs of residue G5. Lower panel: distributions of the corresponding δ torsion angle. (F) Upper panel: RMSE in Hz between back-calculated and experimental measurements probing the δ torsion angle of residues G5 and C6 (i.e., CCRs: Γ_{(H1′C1′,H2′C2′)}^DD,DD, Γ_{(H3′C3′,H4′C4′)}; 3J-couplings: H1′H2′, H2′H3′, H3′H4′). Lower panel: C2′-endo population of residues G5 and C6. Asterisks mark values that are 0. Ensemble averages are shown as bars, while all NMR structures are shown individually (filled marker) with their respective average (nonfilled marker). Colors and markers are as follows: experimental (black square including errors), MD (dim-gray bars/solid line), MD+Exp (dark-gray bars/dashed line), bundle MD+Exp (lightgray bars/circles), bundle E (blue diamonds), bundle F (green hexagons), and 1RNG (red left-pointing triangles).

In the case of the RDCs, 30% of structures in bundle E agree better with the experimental data compared to MD (min. RMSE bundle E = 5.88 Hz, RMSE MD = 6.79 Hz). Bundle F and 1RNG show worse agreement (Figure 6A).

In contrast to the RDCs, the MD simulations performed the best for all other measurements (Figure 6C,D). This is a remarkable result considering that no explicit NMR data were used to produce the MD ensemble except for the use of the PDB-derived initial configurations and suggests that ensemble averaging is key for this tetraloop.

Looking at the NMR bundles, bundle E agreed best with the experimental data on average and thus was better than bundle F. The only difference between these two bundles is whether the C6–G9 base pair was restrained (bundle E) or not (bundle F) during the structure calculations. Although none of the two bundles has a proper Watson–Crick base pair according to the definitions by Barnaba, bundle F shows more structural flexibility with respect to the base of G9.⁴² This finding might indicate that the presence of the C6–G9 base pair observed experimentally, in at least some structures, is critical to achieving good agreement and is in fact present at high temperatures, although not always populated (see the discussion above).

To further improve the agreement between simulations and experiments, we refined the MD ensemble using RDC and ³J-coupling constant data. In such refinement procedures, the weight of each structure in an ensemble is modified so that the resulting ensemble averages match experimental measurements better compared to the original ensemble.^10,68 As described in previous studies, we used the Bayesian maximum entropy (BME) scheme to refine the MD ensemble using RDCs and ³J-couplings. CCRs and NOEs were instead used for cross-validation (Figure S10 in the Supporting Information).⁴⁵ We determined θ between 10 and 30 as an adequate range for the reweighting using k-fold cross-validation (Figure S9 in the Supporting Information) and finally chose θ = 23 because lower values quickly reduce ϕ_eff, which is a measure of the effective number of frames and thus gives information about how much of the original simulation data is retained (see the Materials and Methods section). We used RDCs and ³J-couplings to reweight the simulation data and cross-validated against CCRs and NOEs (Figure S10 in the Supporting Information).

As per construction, the reweighted ensemble (here called MD+Exp) improved the agreement with experimental RDCs (RMSE = 2.11 Hz) and ³J-couplings (RMSE = 2.25 Hz), while the RMSE for both NOEs and CCRs changed only marginally (Figure 6).

While the optimized weights can be used to calculate any observable or quantities of choice, it is sometimes more intuitive and convenient to analyze a small set of structures with identical weights rather than many structures (20,100 in this case) and their associated weights. For this reason, we subsampled a new ensemble of 100 structures obtained from the BME-refined MD ensemble (MD+Exp). As expected, the subsampled ensemble (which we term bundle MD+Exp) agreed nearly as well with the experimental data as the full simulation set (Figure 6).

From the above-described results, the question arises as to why the simulated ensemble seemingly agrees better with the experimental data than the NMR bundles E and F, considering that experimentally derived restraints were used to calculate the latter. The dihedral angle distributions strongly indicate that this arises from the fact that in some cases only a bi- or multimodal distribution of states can explain experimental measurements. One example is the δ torsion angle, which reports on the puckering of the sugar moiety, in C6. Experimentally, the δ torsion angle can be probed by measuring, for instance, the Γ_{(C1′H1′,C2′H2′)}^DD,DD and Γ_{(C3′H3′,C4′H4′)} or ³J(H1′,H2′) and ³J(H2′,H3′) and ³J(H3′,H4′) coupling constants. We compared the CCRs, back-calculated from the NMR bundles, to the values from the experimental measurements and verified that they did not match them very well. The MD simulations appeared to match the experimental data much better. Looking at the underlying distribution, it became evident that multiple states were observed for both C6:H1′–C1′–C2′–H2′ and C6:H3′–C3′–C4′–H4′ (Figure 6E). This was highlighted by the distribution of the δ torsion angle for C6 where the simulations showed two states around 86° and 149°, indicating both C2′-endo and C3′-endo populations, while all NMR bundles and 1RNG only showed C2′-endo population. This is further supported by the fact that the simulations had a lower RMSE for all CCRs and ³J-couplings of that residue compared with the NMR bundles. For G5, both the simulations and all NMR bundles agree very well with the experiments, whereby only a C2′-endo population is observed for that residue (Figure 6F). Similar observations were made for other torsion angles and measurements (Figures S11–S17 in the Supporting Information). This shows a limitation of classical NMR structure calculations where usually a restraint has to be fulfilled by each structure in the bundle, which might lead to artifacts in the case of experimental data averaging due to the existence of multiple conformational states. MD-based ensemble generation can help to overcome this limitation if all relevant conformations are sampled in the simulation.

Both the experiments by Jucker and Pardi in 1995 and our NMR findings indicated the presence of the C6-G9 base pair. However, the presence of this base pair appears to be temperature-dependent. MD simulations indicated that the C6-G9 Watson–Crick base pair is only partially stable at 308 K, which is also in line with the experimental evidence (Figure 7A). The population of the base-paired state in the MD ensemble is 57%, and reweighting against experimental data increases that to ∼65%. Due to the inclusion of this base pair restraint by Jucker and Pardi, all structures in 1RNG have the C6-G9 base pair. It was also included in the restraints of bundle E; however, our calculations actually resulted in 0% C6-G9 base pairing. While C6 and G9 are close to each other in all structures of bundle E, the relative orientation of the two nucleobases does not fulfill the requirements for a proper Watson–Crick base pair as defined in Barnaba. The MD+Exp simulations also indicated the presence of the U8–G9 stacking (Figure 7B,C), with a population of 29%. More in detail, we observe both the outward stacking and upward stacking (as in 1RNG), while none of the NMR bundles shows any stacking of U8–G9.

Figure 7.

Structural analysis of the simulated ensembles and structure bundles. (A) Percentage of structures with the C6–G9 Watson–Crick base pair formed within MD ensembles and the different NMR structure bundles including the consensus structure 1RNG,¹³ as labeled. (B) U8–G9 outward stacking population and (C) U8–G9 upward stacking population. Asterisks mark values that are 0. (D–F) Structural representations of the three clusters after clustering the subsampled MD ensemble (bundle MD+Exp) with quality threshold clustering using the eRMSD metric. Loop residues C6 (blue), U7 (purple), U8 (pink), and G9 (salmon) are highlighted in color, and stem residues are gray. If shown, the 1RNG bundle is colored yellow. (G) eRMSD distribution within the cluster. (H) Average eRMSD of the MD starting structures to 1RNG (ref 1RNG), and error bars indicate the standard deviation over the five individual structures from 1RNG.

To get a better understanding of the structural features of the MD-based subensemble, we clustered the corresponding structures based on eRMSDs of G5–C10 using the quality threshold algorithm.^46,69 The clustering returned three clusters, containing 28, 20, and 6% of the structures (Figures 7D–F and S18A). The remaining 46 structures did not fit in clusters with at least five structures. We note that about 89% of the structures can be sorted into different clusters when using an eRMSD cutoff of 1.1 Å corresponding to grouping “similar” structures (Figure 7G). One of the clusters (no. 2) containing 20% of the structures is fully composed of 1RNG-like structures (centroid eRMSD = 0.7 ± 0.08). The major structural features of this fold are the stacking of U8/U9, Watson–Crick-like base pairing of C6–G9, and that U7 is folded into the minor groove, interacting with the C6–G9 base pair and the loop-closing base pairs G5–C10 (Figure 7E). The main difference between this fold and the other two clusters 1 and 3 is the location of U7. In clusters 1 and 3, U7 does not interact with the aforementioned base pairs but instead takes on a variety of bulged-out states (Figure 7D,F). Clusters 1 (28%) and 3 (6%) are quite similar to each other and mainly differ in the dihedral angle distributions of U8. While the structures in cluster 1 exclusively populate the anti-conformation of the χ angle, structures in cluster 3 populate either the syn or the high anti-conformation. For the same residue, cluster 3 also shows more variation of the α and β angles compared to cluster 1. We note that the strong presence of 1RNG-like structures is not necessarily expected because only one of the 20 starting structures was 1RNG-like (Figure 7H). However, this is also in line with the experimental data and is highlighted by the fact that 1RNG-like structures receive, on average, greater weights from the reweighting process.

We found that about 20% of the MD structures and 14% in the MD subensemble miss the G5–C10 base pairing (Figure S19A in the Supporting Information). We tested the importance of structures missing this base pair by calculating RMSEs to the experiments only considering structures with or without the base pair. It turns out that both data sets (with and without G5–C10 base pair) showed worse agreement with the experiments than the full ensemble, demonstrating that both sets of structures are necessary for the improved recapitulation of the experimental data (Figure S19B, RMSE deviations of different parameters to determined structures). This could indicate that the opening of the G5–C10 base pair might be necessary to allow some structural rearrangements in the loop, which, however, could happen on time scales to which the experimental measurements are not sensitive enough in order to detect this state by NMR. This is further supported by the fact that we find the remaining small violation in our NMR structure calculations in the region of G5–C6 and G9–C10.

Finally, we asked whether the loop structure of CUUG and UUCG showed any similarities since both systems are unusually stable. Figure 8 shows a comparison of the loop region of our three main clusters from the subsampled MD ensemble with the NMR structure of the UUCG tetraloop (PDB: 2KOC).¹⁴ We found that both systems have a similar overall structure: L1 forms a base pair with L4, L3 stacks on the L1–L4 base pair, and L2 is either extruded (clusters 1 and 3) or folded into the minor groove (clusters 3 and 2KOC). However, in contrast to CUUG, the L1–L4 base pair in UUCG is established by a trans sugar Watson–Crick (SWt) base pair. This is related to the conformation of the χ angle of the G9 residue, which is syn in UUCG and high anti in all three clusters of CUUG. We found only a small population of the SWt base pair in our CUUG simulations (<1%). However, we note that it is difficult to assess whether the stability of the two systems is related to a similar overall structure without comparing the systems to other less stable tetraloops, which is beyond the scope of this work.

Figure 8.

Comparison of the UUCG tetraloop and the CUUG MD subensemble. Dynamic secondary structure annotation following the Leontis–Westhof nomenclature and renders of the extended loop region (residues 5–10) of (A) 2KOC, (B) cluster 1, (C) cluster 2, and (D) cluster 3 from the subsampled MD ensemble. The color bar represents the population of each secondary structure element. In the renders, only the centroid structures are shown and residues are colored by base type (yellow, C; red, G; and turquoise, U). For each bundle or cluster, the most common hydrogen bonds are shown as blue dashed lines (>50% population).

Conclusions

In this work, we show that the structure of the CUUG RNA tetraloop, which is one of the thermodynamically most stable tetraloops, is not well described by a structural bundle derived from conventional NMR structure calculations. By conducting independent MD simulations starting from high-resolution models deposited in the protein data bank and subsequent reweighting with experimental NMR data, we are able to provide a structural ensemble featuring substantial dynamics. We argue that the structure determination of RNA benefits greatly from such an integrated NMR/MD approach as many common RNA secondary structure motifs such as loops and bulges cannot be represented by a single conformational state. Thermodynamic stability is thus not solely ascribed to the sampling of a single structure, and for the system investigated here, these dynamics are sampled within the physiologically relevant temperature range.

Data Availability Statement

mFold: http://unafold.rna.albany.edu/?q=mfold. Sedphat: http://www.analyticalultracentrifugation.com/sedphat/download.htm. NITPIC: http://biophysics.swmed.edu/MBR/software.html. Sparky: https://www.cgl.ucsf.edu/home/sparky/. Topspin: https://www.bruker.com/service/support-upgrades/software-downloads/nmr/free-topspin-processing/nmr-topspin-license-for-academia.html. Structural coordinates of the MD ensemble are available at 8CLR. NMR experimental data including chemical shifts, J-couplings, cross-correlated relaxation rates, and residual dipolar couplings are available at 34796.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.3c03578.

• Detailed experimental data; experimental restraints; structure calculations; and detailed MD simulation results (PDF)

Author Contributions

^⊥ A.O. and F.K. contributed equally.

This work was supported by DFG collaborative research center 902: Molecular principles of RNA-based regulation and the EU horizon program iNEXT-discovery. R.S. was supported by the Fonds der Chemischen Industrie. Work at BMRZ was supported by the state of Hesse. This research was also supported by the Lundbeck Foundation BRAINSTRUC initiative in structural biology (R155-2015-2666 to K.L.-L.). The authors also acknowledge access to computational resources from the ROBUST Resource for Biomolecular Simulations (supported by the Novo Nordisk Foundation; NNF18OC0032608) and Biocomputing Core Facility at the Department of Biology, University of Copenhagen. Funding for open access charge: institutional funds.

The authors declare no competing financial interest.