Abstract
DNA strand displacement networks are a critical part of dynamic DNA nanotechnology and are proven primitives for implementing chemical reaction networks. Precise kinetic control of these networks is important for their use in a range of applications. Among the better understood and widely leveraged kinetic properties of these networks are toehold sequence, length, composition, and location. While steric hindrance has been recognized as an important factor in such systems, a clear understanding of its impact and role is lacking. Here, a systematic investigation of steric hindrance within a DNA toehold-mediated strand displacement network was performed through tracking kinetic reactions of reporter complexes with incremental concatenation of steric moieties near the toehold. Two subsets of steric moieties were tested with systematic variation of structures and reaction conditions to isolate sterics from electrostatics. Thermodynamic and coarse-grained computational modeling was performed to gain further insight into the impacts of steric hindrance. Steric factors yielded up to 3 orders of magnitude decrease in the reaction rate constant. This pronounced effect demonstrates that steric moieties can be a powerful tool for kinetic control in strand displacement networks while also being more broadly informative of DNA structural assembly in both DNA-based therapeutic and diagnostic applications that possess elements of steric hindrance through DNA functionalization with an assortment of chemistries.
Introduction
DNA has become a central material in a variety of applications including diagnostics (both medical and non-medical),1−8 therapeutics,3,9,10 molecular computation,11−13 and nanodevices.14,15 The wide-scale adoption of DNA for uses in nanotechnology can be largely attributed to its predictable Watson–Crick binding16,17 and comprehensive understanding of its hybridization thermodynamics18−23 and kinetics.24−29 Such fundamental understanding, as well as thorough characterization of DNA, has enabled engineering of sophisticated structures30−33 and the execution of complex dynamic systems including chemical reaction networks, which possess immense computational power facilitated by the specificity of dynamic DNA interactions.34−37 These interactions permit Turing-universality through deterministic mass-action kinetics and indicate that chemistry can be used to compute anything.34 Dynamic DNA nanotechnology, specifically, relies on toehold-mediated strand displacement,38 which uses a short single-stranded sequence, immediately adjacent to its larger hybridized portion, to expedite exchange of its complementary strand. Toehold-mediated strand displacement is responsible for nanomachines,38−41 including molecular motors,42,43 controllers,44,45 logic circuits capable of computation,46 signal restoration,46,47 and amplification.48−51 Much work has been done to understand the intricacies of toeholds on strand displacement including toehold length,25,27,52,53 toehold sequence and composition,24 and toehold location.41,54−56 Despite our knowledge about the behavior of these networks, key unexplored structural features, such as steric hindrance, remain.
Over the past twenty years, there have been many studies attributing a significant influence of steric hindrance on DNA networks.17,27,57−61 However, the effect of steric hindrance on the operation of these networks has not been studied in detail. Steric hindrance is a term adopted from organic chemistry62 and refers to the partial blocking of a molecule’s reaction sites caused by the physical presence of its parts. Steric hindrance can be seen as the three-dimensional contribution of structures to influence their reactivity. A more thorough understanding of steric hindrance could provide an additional parameter for the design and analysis of DNA strand displacement networks, helping efforts to mitigate undesired reactions of metastable species such as in leaky amplifiers.63−71 Beyond strand displacement networks, the knowledge of steric moieties’ roles in reaction kinetics can more broadly inform the creation of DNA nanotechnology within structural applications,72 synthetic biology,73 surface bound chemistries,74 and biosensing applications.75−78
Here, we report a simple system to investigate the effects of steric moieties on DNA strand displacement reactions. We use a basic DNA reporter as the test object, as shown in Figure 1A. The simplicity of the reporter construct makes the interactions straightforward to monitor and analyze. In addition to this simple reporter, we modify the reporter to possess an internal toehold rather than an external toehold, as detailed in Figure 1B. This modification involves concatenating a duplex to the opposite side of the toehold from the dye and quencher duplex. While “external” and “internal” descriptors have been used by Turberfield et al. to describe the location of a toehold in reference to a DNA loop structure,55,79 others have used it to describe the whereabouts of a toehold in reference to strand anatomy.80,81 We use this latter meaning: internal toeholds describe toeholds made from medial nucleotides of the strand, while external toeholds are constructed from terminal nucleotides of the strand. The investigation of the internal toehold, in addition to the external toehold, (1) helps assess the effect of steric hindrance on the inner strand regions rather than just the terminal regions, (2) helps confirm that the results are not anomalous and valid only with the use of simple external toehold reporters, (3) serves as a steppingstone to validate steric moieties as a versatile approach to tuning reaction kinetics, that are adaptable to a variety of complexes, and (4) facilitates an extra location to tether steric moieties.
Figure 1.
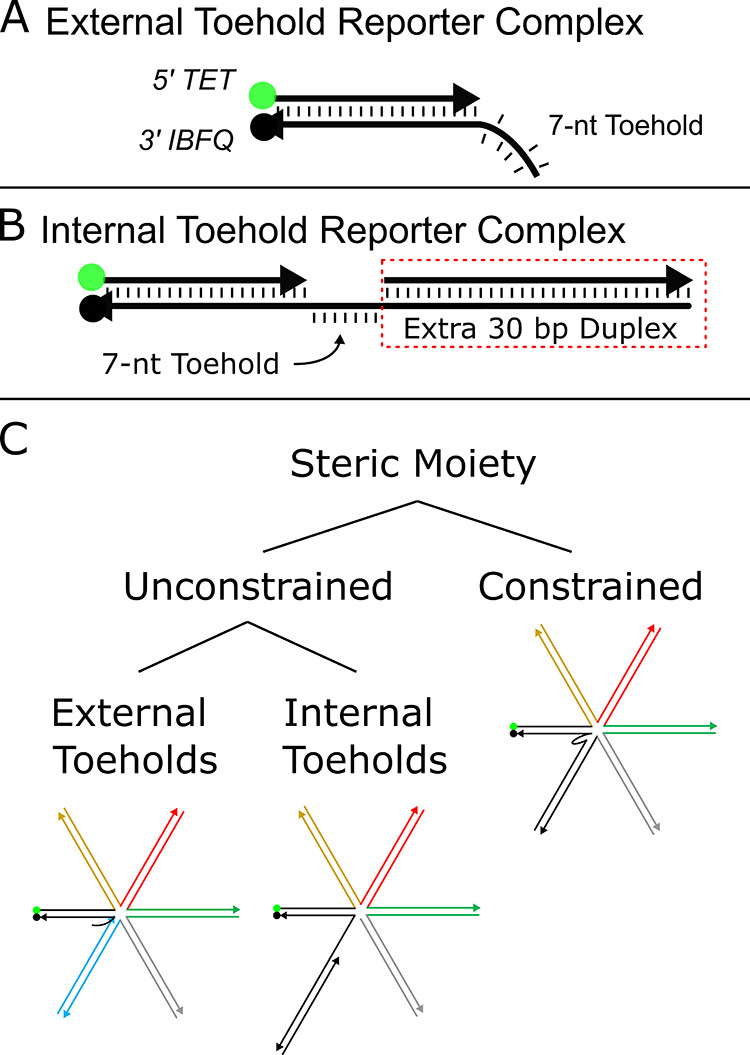
Reporter and multi-arm complex representations. (A) Base external toehold reporter complex consists of a 5′ TET fluorophore paired with a 3′ Iowa Black fluorophore quencher, twenty base pair duplex, and seven-nucleotide toehold. (B) Base internal toehold reporter complex possesses identical fluorophores and sequences of the duplex and toehold as the external toehold reporter complex and has an additional duplex concatenated to the opposite end of the toehold. This extra duplex is not involved in branch migration but is used specifically to internalize the toehold. (C) Quintessential representations of multi-arm complex structures are shown within a highly simplified steric moiety taxonomy. Steric moieties investigated here are divided into two categories: unconstrained and constrained. Unconstrained steric moieties are further divided into two sub-categories: external toehold junction complexes and internal toehold junction complexes.
To systematically vary the steric hindrance, we chose multi-arm junctions. Multi-arm junctions consist of a series of DNA duplexes connected at their terminals. These DNA duplexes serve as physical obstacles to hinder the invasion of potential reactant molecules from their connection point, known as the junction, which is located next to the toehold. Multi-arm junctions are easy to position and scale while keeping the system simple. These junctions form at the immediate terminus of complementary domains, which makes their position controllable and helps them straddle desired locations, such as the toehold, closely. Scaling the number of arms in the junction is also straight forward. Scaling requires only a concatenated domain to the end of the last arm in the multi-arm chain and an introduction of a complementary sequence to the concatenated strand (illustrated in Figure S1 of the Supporting Information). Multi-arm junctions are also simpler than elaborate origami structures to construct and position, making them a good starting point for steric studies. Multi-arm junctions do not require any additional chemistries that complicate the interactions between other molecules or the available nucleotides in the toehold.
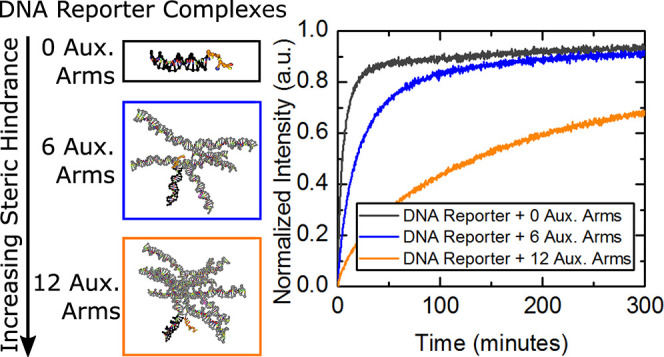
The reporters are paired with multi-arm junctions to form two different sets of complexes including unconstrained and constrained multi-arm junction complexes. Unconstrained complexes (U.C.s) are divided into two sub-categories, “external toehold complexes” and “internal toehold complexes” (Figure 1C). External toehold complexes consist of a twenty-nucleotide reporter duplex with a seven-nucleotide toehold at the end of the quencher strand as shown in Figure 1A. To increase the steric hindrance of this simple external toehold reporter, a thirty-nucleotide strand is concatenated to the dye strand opposite the toehold on the quencher strand. This concatenated strand enables hybridization of a complementary strand, creating an auxiliary arm that serves as a steric moiety to obstruct invasion and nucleation of an invader strand to the toehold. By further concatenating another thirty-nucleotide sequence to each complementary strand, the complex can increase its number of arms, and thus the level of steric hindrance, incrementally. An illustration of this process can be found in the Supporting Information (Figure S1). A maximum of twelve auxiliary arms were added to the initial external toehold reporter complex. Strand sequences and complex illustrations of this complete set are found in Table S1 and Figure S2, respectively, of the Supporting Information. Internal toehold complexes are identical in their sequences to external toehold complexes except that internal toehold complexes possess a duplexed domain on the opposite side of the toehold from the reporter, connected via concatenation to the toehold of the quencher strand (Figure 1B). Strand sequences and complex illustrations of all these complexes can be found in the Supporting Information in Table S1 and Figure S3, respectively.
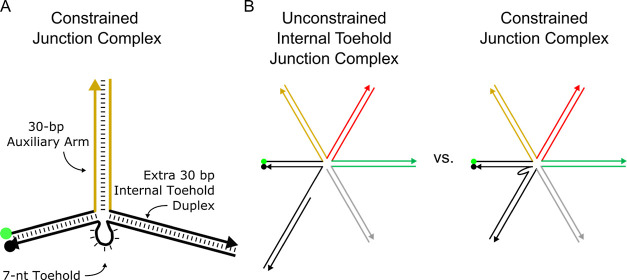
Constrained complexes (CCs) are modified internal toehold complexes where the last strand of the internal toehold complex is concatenated to a domain complementary to the quencher strand on the opposite side of the toehold from the reporter. Figure 2A illustrates a detailed C.C. with one auxiliary arm while Figure 2B illustrates the subtle difference between an internal toehold complex and constrained junction complex with four auxiliary arms. The connection of the extra duplex (black) and the last auxiliary arm (gray) closes the geometry of the complex and constrains the auxiliary arms to surround the toehold. Only six C.C.s were tested. C.C. sequences can be found in Tables S1 and S4 of the Supporting Information, while illustrations of these structures can be found in Figure S4 of the Supporting Information.
Figure 2.
Constrained complex schematics. (A) C.C.s are a modified internal toehold complex where the duplex opposite the toehold from the reporter duplex, is concatenated to the complementary strand of the last auxiliary arm in the complex. (B) A side by side schematic helps depict the transformation of a four-auxiliary-arm internal toehold complex (left) to a constrained complex (right) through the connection of the last auxiliary arm with the extra duplex.
To determine the effects of the incremental addition of auxiliary arms to reporter complexes on toehold-mediated strand displacement, an invader strand is introduced to each complex. The invader interacts with each complex via toehold-mediated strand displacement and produces an invader/quencher duplex as well as a fluorescent signaling complex as shown in Figure 3. Specific reactions are outlined for the unconstrained external toehold reaction (Figure 3A), the unconstrained internal toehold reaction (Figure 3B), and the C.C. reaction (Figure 3C). Equal concentrations of both complexes and invaders were used throughout all complex variation experiments (with specifics found in the Methods and Materials section of the Supporting Information). Reaction kinetics were monitored by recording fluorescence intensity versus time and are provided in Figures S11–S13 of the Supporting Information. Bimolecular reaction kinetics were assumed, and the fluorescence data were fit with the equation presented in the Supporting Information (eq S1).
Figure 3.
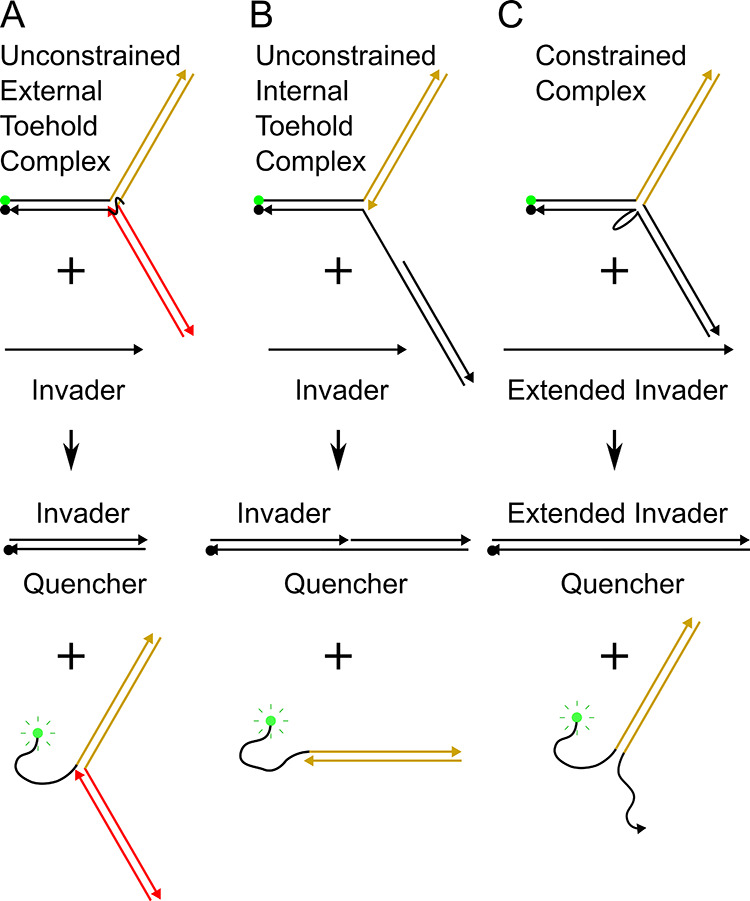
Reaction pathways are represented for each category of complexes. (A) External toehold complex with two auxiliary arms reacts with an invader to yield an invader-quencher duplex and a free TET fluorophore. (B) Internal toehold complex with one auxiliary arm reacts with the invader strand and yields an invader-quencher duplex and free TET fluorophore. (C) Constrained junction complex with one auxiliary arm reacts with an extended invader strand that yields an invader-quencher duplex and free TET fluorophore.
Results and Discussion
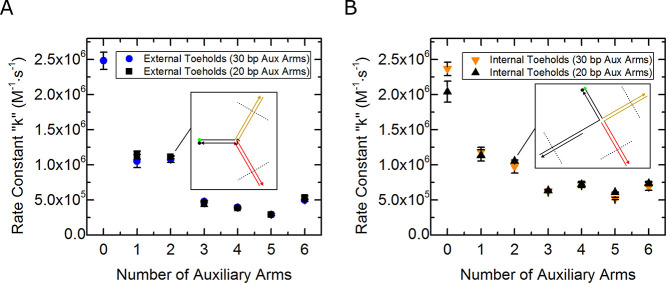
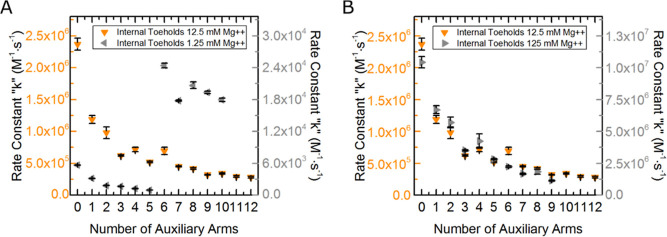
Figure 4 shows a plot of reaction rate constant versus the number of auxiliary arms for each type of complex tested. Unconstrained external toehold complex data show that the reporter complex without any auxiliary arms has the highest reaction rate constant at approximately k = 2.5 × 106 (M–1 s–1). Addition of each auxiliary arm continuously reduced the reaction rate constant with two exceptions, two and six auxiliary arms, where the rate constants were shown to increase from those with one less arm (rate constant data shown in Tables S8–S10, Supporting Information). Internal toehold complex data show a similar trend as the external toehold complexes, with a decrease in reaction rate constant as the number of auxiliary arms are increased. A pattern is observed in Figure 4 of large decreases in the rate constant followed by smaller decreases, or even increases, in the rate constant with each additional auxiliary arm. To see this pattern more clearly, Figure 5 details the difference in the rate constant of each complex compared to the rate constant of the complex with one less auxiliary arm. There is a considerable swing in differential rate constant values. For example, increasing the complex size from zero to one auxiliary arm results in a large decrease in the reaction rate constant. Further increasing the complex size from one arm to two arms shows a shallower decrease than there is from zero to one arm. Adding a third auxiliary arm results in another large decrease and adding a fourth arm a smaller decrease (increase for internal toehold complex). This “swinging” of the differential rate constant is sustained, and the smaller decreases, on occasion, turn into increases in the reaction rate constant.
Figure 4.
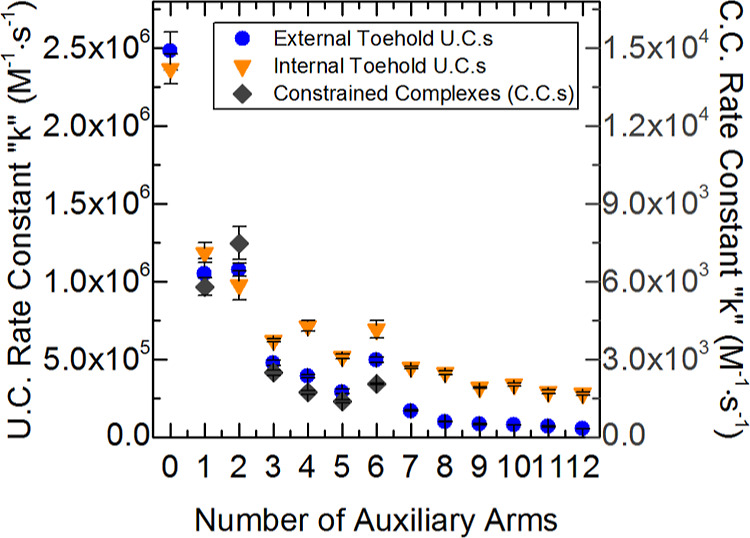
Average invasion reaction rate constants for external and internal toehold U.C.s (left scale), as well as C.C.s (right scale). Complexes are presented with the number of auxiliary arms, which does not include the reporter arm and in the case of internal toehold and C.C.s; the duplex on the opposite side of the toehold is also omitted. Average external toehold complex rate constants are shown as blue circles. Average internal toehold complex rate constants are shown as orange down-pointing triangles. Reaction rate constants of C.C.s are shown as gray diamonds and measured using the scale on the right of the plot. Averages are taken from technical triplicates of each complex.
Figure 5.
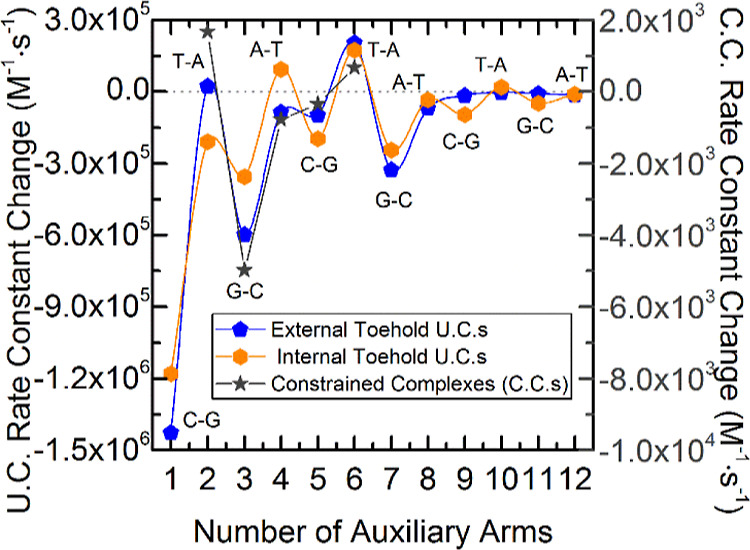
Difference of the rate constants with an increasing number of auxiliary arms for both U.C. (left scale) and C.C. (right scale). Plot labels indicate the base pair of each arm closest to the junction to show the similarity in the trends. The rate constant change values are relative to the complexes with one less arm. For example, the rate constant change shown at one auxiliary arm is compared to complexes with no auxiliary arms. Blue pentagons show the decreases of rate constants of unconstrained external toehold complexes, while orange hexagons show the decrease of unconstrained internal toehold complexes, and dark gray stars depict the rate constant decreases of C.C.s. There is a noticeable swing of big decreases and small decreases which in some cases (two and six auxiliary arms) turn into mild increases of the rate constant with increasing numbers of arms. This pattern is remarkably consistent among all three sets of complexes.
Reaction rate constants for a set of constrained multi-arm junctions are shown as gray diamonds in Figure 4. The rate constants are seen trending downward with the same pattern as the external toehold complexes. The reaction rate constants of C.C.s are shown to decrease dramatically from the U.C.s. The considerable drop in reaction rate constant values of C.C.s compared to their unconstrained analogues is attributed to the more comprehensive protection that the auxiliary arms impart by being in more immediate proximity of the toehold.
Between all sets of complexes, the unconstrained internal toeholds possess the greatest reaction rate constants throughout a majority of the tests (auxiliary arms 3–12). Looking at the reaction pathways in Figure 3A,B, we can see that the product of the internal toehold invader can coaxially base stack with the additional duplex. This additional base stacking can assist the invader in hybridizing to the toehold, thus speeding up the kinetics as shown in the work of Yuan et al.82 The exceptions occur with complexes with 0–2 auxiliary arms. These data for both external and internal complexes show no significant difference in reaction rate constants. This lack of difference is attributed to the steric hindrance produced by the extra duplex that the internal toehold complex possesses. With the addition of the third auxiliary arm, it is suspected that the steric hindrance provided by the extra duplex of the internal toehold is negated by the growing presence of the auxiliary arms. At this point the faster kinetics due to the additional base stacking component of hybridization is observed with the internal toehold complexes and significantly elevates their reaction rate constants over their external toehold complex analogues.
External toehold complexes, with two and six auxiliary arms, were the exceptions to the downward trending reaction rate constants. These exceptions may be attributed to the auxiliary-arm sequences at the junction. Complex junction sequences come from the design borrowed from Wang and Seeman83 where the ultimate base pairs of each arm at the junction site are recycled every four arms so that each fourth arm possesses the same base pairs at the junction, as is shown in Figure 5 plot labels. Auxiliary arms two and six possess a T–A ultimate base pair at the junction terminal. This sensitivity to the identity of the terminal base pairs suggests that the overall trend of decreasing reaction rate constants could be related to the increase of partially available nucleotides put in closer proximity of the toehold.65 Internal toehold complex data show the same type of behavior with arms terminating in either T–A or A–T pairs elevating reaction rate constants in the cases of 4, 6, 8, 10, and 12 total arms. As the number of arms increases, the significance of terminal pair looks to dissipate. A deeper investigation of this pattern and an alternative explanation for its existence is given in the subsequent sections.
oxDNA Modeling of Experimental Complexes
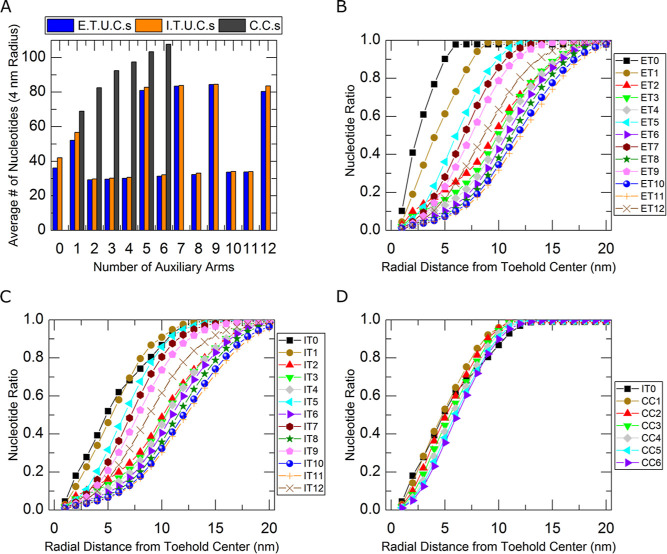
To help understand the experimental data, complexes were modeled using oxDNA.84−89 Simulation details are listed in the oxDNA Simulation Details section of the Supporting Information including in Figures S5–S7 and Tables S4–S6. The oxDNA model is not equipped with a divalent cation option to mimic our experiments directly but still yields qualitative information to compare the varying complexes through using identical input parameters. Specifically, we looked for increases in nucleotides surrounding the complexes’ toeholds. A simple program, presented at the end of the oxDNA Simulation Details section, was implemented to count the number of nucleotides within increasing radial distances from the middle (4th) nucleotide of the toehold out to 20 nm for each complex. The data in Tables S4 and S5 of the Supporting Information show that outside of 1 nm, the average number of nucleotides trends upward as auxiliary arms are added for all three types of complexes (external/internal U.C.s and C.C.s). A significant pattern in the U.C. simulation data can be seen by choosing a radial distance (such as 4 nm) and comparing the average number of nucleotides across complexes. A bar chart is provided in Figure 6A illustrating this suggested 4 nm example. Large jumps in nucleotide counts are seen in complexes with one, five, seven, nine, and twelve arms for both U.C.s. This pattern dissipates at higher radial distances, where the increased number of nucleotides achieved by adding more arms is more apparent. Figure 6B,C shows the pattern in normalized plots for all radial distances in external and internal U.C.s. Nucleotide ratios in Figure 6B–D are calculated by dividing the data in Tables S4–S6 by the total number of nucleotides in each structure. For example, the complex ET5 (shown as light blue left-pointing triangles in B) has an average of 125.1 nucleotides within a 5 nm radius of the central toehold (tabulated in Table S4) over the course of the simulation. There are 347 total nucleotides in the ET5 complex (5 auxiliary arms x 60 nucleotides each + reporter duplex with 40 nucleotides + 7 nucleotide toehold = 347 nucleotides), and 125.1 nucleotides of 347 is approximately 0.36. Normalizing the data in this way helps give an idea of the dispersion of nucleotides in each complex. The pattern found in the oxDNA simulation data shows a striking resemblance to the experimental rate constant reductions found in Figure 5. Figure S8 of the Supporting Information shows a plot of the experimental rate constant reduction data from Figure 5 and the normalized nucleotide data from Figure 6B,C. Pearson correlation coefficients of −0.85 and −0.89 were found suggesting good agreement between oxDNA simulations and experimental results.
Figure 6.
Nucleotide counts and ratios surrounding complex toeholds show oxDNA simulations register similar effects as experimental results. (A) Nucleotide counts within a four-nanometer radius from the central toehold nucleotide are displayed in a bar chart for external and internal unconstrained complexes (E.T.U.C.s and I.T.U.C.s) in blue and orange, respectively, and C.C.s in dark gray. (B–D) Ratios of nucleotides within a given radial distance of the central toehold to the total nucleotides in each complex are shown for E.T.U.C.s, I.T.U.C.s, and C.C.s, respectively. Plots in B–D were color coded so curves match the color of the last added arms of the complex schematics in Figures S2–S4.
C.C.s were also modeled using oxDNA and are featured in Figure S7 of the Supporting Information. In contrast to the U.C. data tabulated in Table S4 and S5, the C.C. simulations did not show any intermittent spikes in nucleotides when comparing across complexes as detailed in Figure 6A and tabulated in Table S6. The experimental data from Figure 5, however, show similar behavior to that of the unconstrained toeholds suggesting that the simulations of C.C.s should possess similar large nucleotide increases. It is not known why these constrained data are not as well aligned with experimental data.
To investigate the increased protection facilitated by constraining the complexes, oxDNA models of unconstrained internal toehold and constrained toehold complexes as shown in Figures S9 and S10 of the Supporting Information, respectively, were compared. Data extracted from oxDNA simulations showed that the nucleotide density (a suspected form of steric protection) increased for all C.C.s over their unconstrained internal toehold analogues and increased as much as 287% at just 6 nm away from the toehold (Supporting Information, Table S7). Even with the large nucleotide spikes of the internal toehold complexes discussed previously and illustrated in Figure 6A, C.C. counterparts still possessed higher nucleotide densities across the board. In addition to higher densities, it is possible that C.C.s attain a more even arrangement of nucleotides due to the extra attachment point helping disperse the obstructing nucleotides and shielding the toehold from a broader range of angles. The experimental data, supported by the modeling, indicate that increasing steric hindrance through constraining a complex can decrease the kinetic reaction rate constant by over 3 orders of magnitude. While the data point to the steric hindrance as the main contributor behind the large drop, further experiments are needed to rule out the role of toehold sequestration from the effect of toehold conformation or topological trapping90 that the constraint may cause. Although oxDNA simulations look to closely depict the experimental data, simulations may need to be run on a longer time scale or with appropriate salt to bring the simulation and experimental results into greater alignment.
Experimental results showed that increasing the number of arms across all complexes decreased the reaction rate constants. Modeling data help reinforce the idea that rate constant decreases stem from steric hindrance. While the effect is clear and modeling data indicate that the effect originates from increased steric hindrance imparted by additional auxiliary arms, other possible alternatives such as the concomitant components of additional mass, increased electrostatic concentration at the junction, near the toehold, and additional nucleotides may contribute to the effect. Further experiments were run to give a better understanding of each of these variables.
Effects of Increasing Mass on Decreasing the Average Reaction Rate Constants
To test the relationship of additional mass and the reduction of the reaction rate constant, arm lengths of the original U.C.s were reduced from 30 to 20 bp as the inset example complexes show in Figure 7A,B. Truncating the arms of these structures reduces their mass by approximately one-third but keeps the junction the same so the mass is the only considerable change. Figure 7A,B compares the original 30 bp auxiliary-arm complex data with the truncated 20 bp auxiliary-arm complex data of external and internal toehold complexes, respectively. Data from each set of complexes match each other closely and are numerically listed in Tables S11 and S12 of the Supporting Information. There is one exception with the zero-arm internal toehold featured in Figure 7B; the complex with a 20 bp duplex is shown to have a slower rate constant than with a 30 bp duplex, which is opposite of the expected result and thus does not support mass as a considerable factor in the decrease of reaction rate constants with the addition of more auxiliary arms.
Figure 7.
Illustration and data of complexes with decreased mass. (A) Data from the original unconstrained external toehold complex with 30 base pair arms are shown in blue circles and compared to the truncated 20 base pair arms of each of their analogue complexes, shown as black squares. The inset depicts an external toehold complex with two auxiliary arms and dotted lines that demark the truncation of auxiliary arms from 30 to 20 bp. (B) Data of the original unconstrained internal toehold complexes with 30 base pair arms are shown as orange downward-pointing triangles and compared to the truncated 20 base pair arms of each of their analogue complexes, black upward-pointing triangles. The inset depicts an internal toehold complex with two auxiliary arms with dotted lines that demark truncation of auxiliary arms from 30 to 20 bp.
Long-Range Electrostatic Effects with Increasing Steric Moieties
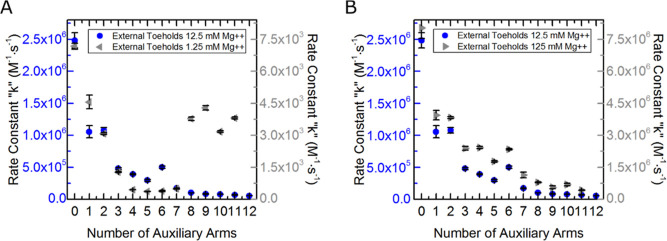
To examine long-range electrostatic effects of the complexes, buffer salt concentrations were increased and decreased by an order of magnitude from the default 12.5 mM concentration. Figure 8A shows data of external toehold complex reaction rate constants at 1.25 mM magnesium listed in Table S13 of the Supporting Information. Reaction rate constants collected at this lower salt concentration were two to three orders of magnitude slower than those run in our default 12.5 mM magnesium buffer. These data show decreases in reaction rate constants with increasing numbers of arms up until six arms. With the addition of the seventh arm, the reaction rate constants begin to subtly increase and drastically spike with the addition of the eighth arm before leveling off with the addition of the ninth, tenth, and eleventh arms.
Figure 8.
Unconstrained external toehold complex data of three different salt concentrations. Data sets in A and B are kept separate to help communicate the similarities between data in the default salt concentration between data in the low and high concentrations. (A) Original external toehold data under default salt concentration of 12.5 mM magnesium chloride (shown in blue circles and rate constant scale on the left of the plot in blue) and external toehold data at an order of magnitude lower salt concentration of 1.25 mM magnesium chloride (shown in left pointing gray triangles with the rate constant scale in gray on the right of the plot). (B) Original external toehold data under default salt concentrations is again shown in blue as it is in (A), and external toehold data at an order of magnitude elevated concentration of 125 mM magnesium chloride is depicted in gray right pointing triangles with a gray scale on the right.
Strand invasion experiments for external toehold complexes were also run in buffer with 125 mM magnesium concentration, and the reaction rate constant data are shown in Figure 8B and tabulated in Table S15 of the Supporting Information. These data (depicted as gray right pointing triangles) show a trend of decreasing reaction rate constants with an increase in the number of arms added to the complexes. This trend is nearly identical to that seen with the complexes at the default 12.5 mM magnesium salt concentrations, which are shown as blue circles in Figure 8B. While the data depict a similar trend at high salt concentrations, the reaction rate constants themselves are four-fold higher in the higher salt concentration (125 mM Mg2+) than the default salt concentration (12.5 mM Mg2+).
The results from experiments run at varied salt concentrations reveal a few things. First, decreased reaction rate constants for lower salt concentrations, and increased reaction rate constants for higher salt concentrations, are expected, and the data unsurprisingly confirm this behavior. Salt helps buffer the electrostatic repulsion of each of the negatively charged DNA backbones allowing for more efficient hybridization to occur.91 Second, they show that the decrease in reaction rate constants with increasing number of auxiliary arms is not just a product of niche ideal conditions but is demonstratable over a span of conditions. Third, lower salt concentrations helped steady the rate of decrease in the reaction rate constants with the addition of arms one through six. This suggests that the oscillations in rate constants, previously illustrated in Figure 5, stem from a phenomenon that can be masked with decreased salt. The lower salt concentrations also revealed, by the spike in reaction rate at the addition of the eighth auxiliary arm that the trend of decreased reaction rate is likely due to structural contributions.
Reactions of internal toehold complexes that were run at low salt concentrations (1.25 mM Mg2+) are shown as gray left-pointing triangles in Figure 9A and listed in Table S14 of the Supporting Information. Reaction rate constants showed a similar trend to those of the external toehold complexes at low salt concentrations. Initially, there was a steady decrease in reaction rate constants from zero to five arms. With the addition of the sixth arm, there was an increase of over an order of magnitude from the previous arm and to nearly five times the rate constant of the internal toehold complex control without any additional auxiliary arms (zero auxiliary arms). The addition of the seventh, eighth, ninth, and tenth arms yield decreases in the reaction rate constants from the eighth but still were nearly three times the control complex of zero auxiliary arms.
Figure 9.
Unconstrained internal toehold complex data of three different salt concentrations. Data sets in A and B are kept separate to help communicate the similarities between data in the common salt concentration between data in the low and high concentrations. (A) Original internal toehold data under common salt concentration of 12.5 mM magnesium chloride (shown in orange downward pointing triangles and rate constant scale on the left of the plot in orange) and internal toehold data at an order of magnitude lower salt concentration of 1.25 mM magnesium chloride (shown in left pointing gray triangles with the rate constant scale in gray on the right of the plot). (B) Original internal toehold data under common salt concentrations is again shown in orange as it is in (A), and internal toehold data at an order of magnitude elevated concentration of 125 mM magnesium chloride is depicted in gray right pointing triangles with a gray scale on the right.
The drastic increase of the reaction rate constants with the addition of the sixth arm of the internal toehold complex, and the eighth arm of the external toehold complex, might suggest that these are critical points where the complexes break apart due to weaker charge screening effect at low salt concentrations and have at least a portion of the complex dissociated, causing a reduction in the steric hindrance and thus an increase in reaction rate constant. However, the reaction rate constant should then become similar to the previous complexes with fewer arms. Instead, the reaction rate constant far exceeds any of these previous complexes for internal toehold complexes. If the complexes were to break apart, the rates would then no further be affected by the addition of more arms because additional arms would be added to the dissociated portion of the complex, not to the portion possessing the dye and quencher. Thus, it is more likely that an increase in the number of arms reaches a critical point in which the complex junction adjusts to allow more space for electrostatic repulsion among arm duplexes and dissociates one or more base pairs of the dye quencher arm, increasing the size of the toehold while simultaneously creating more space between the toehold and the protection of the arms, producing a more conducive path for the invader to reach the toehold. This would explain the large increase in the reaction rate with the addition of the sixth arm, above the control, due to the larger toehold, and explain the subsequent decrease in reaction rates with increases in further auxiliary arms that would be impactful because they have not been completely severed from the complex.
Reaction rate constants were collected for internal toehold complexes at high salt concentrations (125 mM Mg2+) shown as gray right-pointing triangles in Figure 9B and tabulated in Table S16 in the Supporting Information. These data depict a very similar trend to the data collected for these complexes at the default 12.5 mM magnesium salt concentration shown as orange triangles, possessing a similar rate of decrease in the reaction rate constant with increasing arms and mimicking the swing of rate constants.
Nucleotide Availability Near the Toehold
The presence of more nucleotides near the toehold, resulting from increasing the number of arms, could increase toehold interactions and thus could decrease the availability of nucleotides in the toehold to react with invader strands and decrease the overall reaction rate constant. The initial data suggest that the nucleotides made partially available through fraying of auxiliary arms at the terminal may have at least minor effects on the reaction rate constants as shown in Figure 5. The trend for both external and internal toeholds shows that having an A–T pair terminating an auxiliary arm at the junction increased reaction rate constant for an A–T versus a G–C pair. This is seen in the swing of the reaction rate constant values between arms that end at the junction in A–T versus G–C base pairs (Figure 5). The differences seen in the reaction rate constants seem to coincide with the identity of the base pairs.
The oscillating rate constant changes in Figure 5 suggests that the identity of the terminating base pairs may impact the reaction rate. To assess whether this effect may result from corresponding changes in availability of toehold nucleotides, we analyzed minimum free-energy (MFE) structures using NUPACK22,92−95 (see Figures S22–S24 in the Supporting Information). Overall, the MFE structures did not reveal any significant impacts on toehold availability; however, there may be limitations in NUPACK’s ability to accurately model the nucleotide interactions in these multi-arm structures.
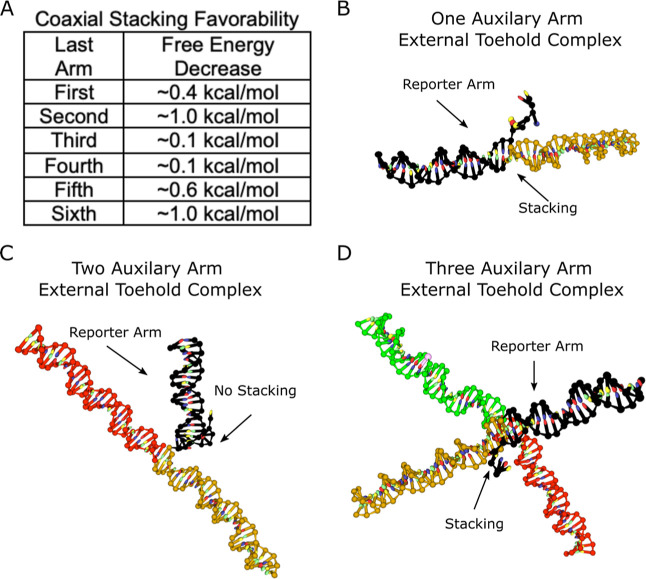
A more fitting explanation for the noticeable reaction rate constant difference between arms terminating at the junction with different base pairs is coaxial base stacking. Coaxial base stacking, or coaxial stacking, occurs when duplexes align with one another to allow base stacking between duplexes and a possible reduction in free energy. Two studies have shown that the favorability of coaxial stacking is sequence dependent.96,97 The multi-arm junction design employed in our research cycles through four unique terminal sequences. According to these two studies, the most conducive of our used sequences for coaxial stacking is introduced with the addition of the second, sixth, and tenth arms, with ∼2–10 times the favorability of the other sequence combinations (Figure 10A). The jump in reaction rate constants, especially with the addition of the second and sixth auxiliary arms, as shown in Figure 4, suggests that the last arm added to the complex can dictate the structure of these molecules through base stacking with the previous arm. This base stacking behavior propagates in a way to maximize stacking interactions between all duplexes. Because the last arm preferentially stacks with the next available arm and the next two available arms coaxially stack with one another, the reporter duplex is last in line to stack and thus has a more or less frequent stacking partner based on the number of arms in the complex. Complexes with an odd number of auxiliary arms result in the reporter duplex base stacking with the first auxiliary arm and those with an even number of auxiliary arms result in the reporter duplex not stacking because the first auxiliary arm is instead preferentially stacking with the second auxiliary arm. For example, in a one arm complex, it is likely that the reporter duplex coaxially stacks with the first auxiliary arm, causing large disruptions to toehold access and branch migration. This point is illustrated by an oxDNA84−89 simulation of an external toehold complex featured in Figure 10B but is also present in internal and C.C.s, as shown in Supporting Information, Figures S6 and S7. When the second arm is introduced, the first arm then preferably stacks with the second arm instead of the reporter arm as shown in Figure 10C, and thus has a more accessible toehold and elevated reaction rate constant. Once the third auxiliary arm is introduced, the favorability of the sequence of the second arm is interrupted by the concatenation of the third arm (Figure 10D) and thus, the second arm no longer has the favorability it had as the last arm to continue stacking with the first arm. This change allows the first arm to more frequently base stack with the reporter arm causing another large reduction in the reaction rate constant. The reaction rate constant does not return to the former rate constant despite the same coaxial stacking behavior because there are now more auxiliary arms increasing the steric hindrance from that of the last complex. Furthermore, the oxDNA simulation data discussed previously suggest that the base stacking mechanism orients the structures in a way that increases the nucleotide density, and thus protection, around the toehold. Low salt concentration data in previous Figures 8A and 9A showed much steadier decreases in reaction rate constants (before the spike) compared to the common salt concentrations, suggesting that the complex configuration caused by stacking interactions subsided with a decrease in charge screening while the steric effects remained.
Figure 10.
Coaxial stacking in multi-arm junction complexes. (A) Table of values interpreted from Vaskiliskov et al.96 shows that the second and sixth arms have a higher free-energy decrease than other arms, thereby more strongly influencing the complex structure. (B) Unconstrained external toehold complex modeled in OxDNA84−89 shows an instance of coaxial stacking of the reporter arm with the first auxiliary arm. (C) External toehold complex with two auxiliary arms modeled in OxDNA shows coaxial stacking between the last added arm (second) and the second to last added arm (first), while the reporter does not coaxially stack. (D) External toehold complex with three auxiliary arms modeled in OxDNA returns to a conformation in which the reporter arm coaxially stacks with the first auxiliary arm while the second auxiliary arm coaxially stacks with the third auxiliary arm.
Sterically Programmable Kinetics
The previous sections have presented and discussed data to elucidate the extent of impact that steric hindrance has on DNA strand displacement and attempted to determine a primary mechanism for this impact. In this section, steric hindrance is explored for increasing kinetic control over strand displacement networks. Unlike other methods for controlling displacement kinetics, steric moieties do not necessitate nucleotide manipulation like mismatches, do not require competitive reactions such as thresholding, and do not need to possess network specific sequences to be integrated as if a network component. Due to their separate mechanism of implementation, steric moieties can be used in concert with other kinetic control methods. In some instances, steric moieties may even be preferable over other kinetic control mechanisms. For example, changing toehold length achieves large discrete changes in the rate constant,24 while steric moieties can achieve arbitrarily small changes on a continuous spectrum, as will be demonstrated in this section. Additionally, changing the toehold length affects all strand displacement reactions where a toehold length may be beneficial for one reaction in a cascade but not another. In contrast, steric moieties can be added, eliminated, or their sizes can be changed without affecting the rates of strand displacement reactions in the whole network. While steric moieties possess high compatibility with other kinetic control mechanisms, they also offer preferable advantages such as dynamic control and fine kinetic control.
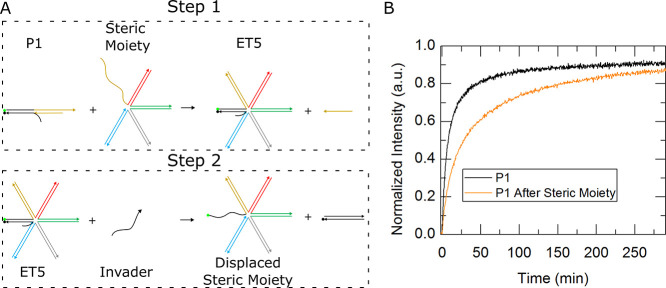
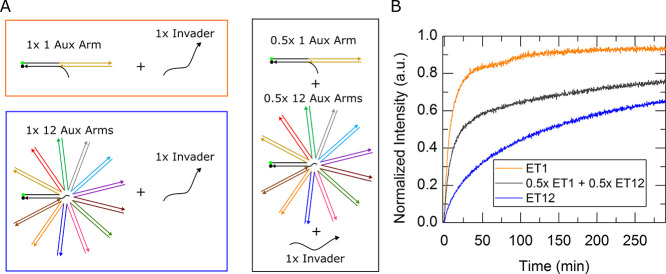
Dynamic control is one advantage that steric moieties possess compared to other methods of kinetic control and is reached through their programmability. Steric moieties can be stripped away or added over the course of a reaction. This allows for kinetic control beyond a dynamic effective rate constant. To demonstrate this capability of steric moieties, an unconstrained external toehold complex possessing one auxiliary arm was made programmable by using a shorter cap strand to create a 10 nt toehold on the auxiliary arm. Steric hindrance of this complex, which we call “P1” (programmable complex with one auxiliary arm), was increased through a toehold-mediated exchange of P1’s 20 nt cap strand with a four and a half arm steric moiety shown in step 1 of Figure 11A via the residual 10 nt single strand from the auxiliary arm of P1. After 24 h, the resulting five arm external toehold complex, or “ET5”, illustrated in step 2 of Figure 11B was then introduced to an invasion strand to complete toehold-mediated strand displacement. Figure 11B shows a plot with kinetic traces of both P1 and ET5. The kinetic rate constants of both P1 and ET5 complexes match the rate constants of one and five arm external toehold complexes presented in Figure 4, indicating complete reaction of steric moiety with the one arm complex.
Figure 11.
Programming an increase in steric presence. (A) Schematic shows a one-auxiliary-arm external toehold complex interacting with a steric moiety to become a five-auxiliary-arm complex in step 1, and in step 2 the five-auxiliary-arm complex underwent a subsequent reaction with an invasion strand to dissociate the quencher strand and creating a signal. (B) Plot depicts the kinetics traces of an invasion reaction of the programmable external toehold complex with one auxiliary arm (P1) in black and an invasion reaction involving one-auxiliary-arm complex after the introduction of the steric moiety (ET5) in orange.
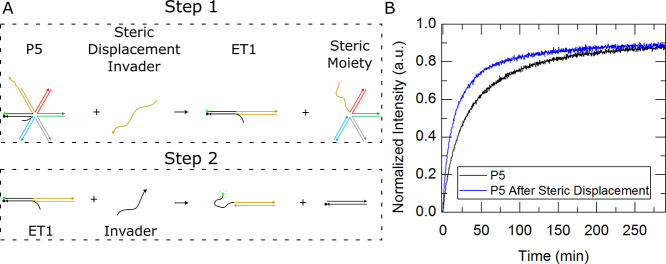
In addition to increasing the steric presence, decreasing the steric presence can be accomplished by changing a five-auxiliary arm to a one-auxiliary arm external toehold complex. Figure 12A shows a schematic of a five-auxiliary-arm complex, called “P5”, interacting with a disassembler strand to produce a one-auxiliary-arm external toehold complex (ET1) in step 1. An invasion strand was then introduced to the resulting ET1 complex in step 2 of Figure 12A. Figure 12B shows the kinetic traces of P5 (black) and ET1 (blue). A lower-than-expected reaction rate constant was found after stripping the steric moiety. Gel analysis in Figure S25 confirmed that steric moieties were being stripped successfully. Upon further investigation, it was found that while the toehold was not shown to be affected by the freshly unhybridized region of the steric moiety, the invader strand did show considerable interaction. A NUPACK MFE structure depicting this interaction is given in Supporting Information, Figure S26. The strands used in these experiments were borrowed from our previous experiments and thus were not designed to avoid the interference realized here but can easily be optimized to achieve better performance. Additionally, for proof of principle, we waited 24 h and used 1.3× of the displacing species to ensure full conversion of reactants. It is suspected that much shorter wait times are sufficient to fully convert the programmable steric moieties and can be shortened with even higher concentrations of the displacing species.
Figure 12.
Programming an increase in steric presence. (A) Schematic shows a five-auxiliary-arm external toehold complex (P5) interacting with a steric displacer strand to yield a one-auxiliary-arm complex (ET1) and a steric moiety. ET1 had a subsequent interaction with an invasion strand to dissociate the quencher strand and create a signal. (B) Plot depicts the kinetics traces of an invasion reaction of the P5 black and the sterically stripped ET1 complex in blue.
Another advantage that steric moieties offer is the capability of finer kinetic control. The data from Figure 4 show that by holding the component concentrations constant, discrete reaction rate constants can be attained. While this discrete level of control may be sufficient for some applications, finer control of the ensemble kinetic rate is possible by using different combinations of steric moiety sizes. A simple demonstration of this is shown in Figure 11, where half of the complexes employ a small (one auxiliary arm) steric moiety, and the other half of the complexes employ a large (twelve auxiliary arm) steric moiety. A schematic representation of this reaction is shown inside the dark gray box in Figure 13A. Schematics of reactions with only the one-auxiliary-arm complex and only the twelve-auxiliary-arm complex are depicted in the orange and blue boxes, respectively. Figure 13B shows a plot with color-coded kinetics traces for each reaction depicted in Figure 13A. The dark gray trace of the mixed steric complexes helps illustrate the fine control of kinetics that steric moieties allow. The mixture results in a kinetic rate proportional to the steric ratio. As a result, a continuous rather than discrete spectrum of kinetic control is attainable.
Figure 13.
Schematically represented reactions and kinetics traces for individual and combinatorial steric complexes. (A) Orange box contains the reactants for a one auxiliary arm only steric complex invasion reaction. The blue box contains the reactants for a twelve auxiliary arm only steric complex invasion reaction. The dark gray box contains the reactants of a half 1 auxiliary arm and half twelve auxiliary arm invasion reaction. (B) Kinetics traces are color coded with the boxes in A showing the one auxiliary arm only reaction as the fastest orange trace, twelve auxiliary arm only reaction as the slowest blue trace and the combination reaction of half the one arm and half the twelve arm complexes shown as the middle dark gray trace.
In addition to these broader implications of kinetic control imparted by steric moieties, the multi-arm junction steric moieties employed in this study showed potential as an assay. The auxiliary arms that were incrementally added to grow the steric presence in these structures introduced distinct sequence patterns at the junction. As it was discussed in the last section, these distinct sequences showed substantial rate constant changes attributed to different coaxial base stacking favorability. This sensitivity indicates that these structures are a feasible approach for measuring sequence-dependent coaxial base stacking stabilities.
Conclusions
We have investigated the effects of steric moieties on toehold-mediated strand displacement reactions. Specifically, two categories—unconstrained and constrained—of multi-arm junction complexes were studied. Unconstrained external toehold complexes were found to be capable of decreasing the reaction rate constant by nearly 2 orders of magnitude, while C.C.s were found to be capable of decreasing the reaction rate constant by over 3 orders of magnitude from the control reporter complex. For both categories of U.C.s and C.C.s, a clear trend of decreasing reaction rate constants shows that the more obstructions are added, the smaller the reaction rate constant becomes. Furthermore, the coinciding coaxial stacking favorability and reaction rate constant jumps indicate that the conformation of the structures help shape their reactivity. It is not clear if this steric contribution is decreasing the reaction rate constant through inhibiting the nucleation of the invader on the toehold or if the moieties surrounding the branch migration domain make branch migration more challenging. Both possibilities are supported by the data. Additional experimental and computational studies are required to establish which of these mechanisms underlies the steric hindrance behavior observed. The discovery of exact mechanisms would help to predictively model reaction kinetics based on reactant structures, allowing for the leverage of steric moieties to slow undesired leaky reactions and increase usability of DNA in a wide array of nanotechnological applications. Additionally, we have demonstrated the use of steric hindrance as a new way to dynamically control individual and ensemble reaction kinetics in DNA strand displacement networks.
Acknowledgments
We thank members of the Nanoscale Materials and Device Group for valuable assistance. This work was supported partially by the National Science Foundation Award no. 1706065.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.3c04344.
Materials and methods, strand sequences, complex construction schematic, complex schematics, MFE structures, kinetics curves, tabulated rate constants, kinetics fitting equation, oxDNA simulation details, oxDNA simulation images, and oxDNA simulation data (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Agasti S. S.; Rana S.; Park M.-H.; Kim C. K.; You C.-C.; Rotello V. M. Nanoparticles for Detection and Diagnosis. Adv. Drug Deliv. Rev. 2010, 62, 316–328. 10.1016/j.addr.2009.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung C.; Ellington A. D. Diagnostic Applications of Nucleic Acid Circuits. Acc. Chem. Res. 2014, 47, 1825–1835. 10.1021/ar500059c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campolongo M. J.; Tan S. J.; Xu J.; Luo D. DNA nanomedicine: Engineering DNA as a polymer for therapeutic and diagnostic applications. Adv. Drug Delivery Rev. 2010, 62, 606–616. 10.1016/j.addr.2010.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doran J. L.; Collinson S. K.; Burian J.; Sarlós G.; Todd E. C.; Munro C. K.; Kay C. M.; Banser P. A.; Peterkin P. I.; Kay W. W. DNA-based diagnostic tests for Salmonella species targeting agfA, the structural gene for thin, aggregative fimbriae. J. Clin. Microbiol. 1993, 31, 2263–2273. 10.1128/jcm.31.9.2263-2273.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gasser R. B.; Bott N. J.; Chilton N. B.; Hunt P.; Beveridge I. Toward practical, DNA-based diagnostic methods for parasitic nematodes of livestock — Bionomic and biotechnological implications. Biotechnol. Adv. 2008, 26, 325–334. 10.1016/j.biotechadv.2008.03.003. [DOI] [PubMed] [Google Scholar]
- Lau H. Y.; Botella J. R. Advanced DNA-based point-of-care diagnostic methods for plant diseases detection. Front. Plant Sci. 2017, 8, 1–14. 10.3389/fpls.2017.02016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahenthiralingam E.; Bischof J.; Byrne S. K.; Radomski C.; Davies J. E.; Av-Gay Y.; Vandamme P. DNA-Based Diagnostic Approaches for Identification of Burkholderia cepacia Complex, Burkholderia vietnamiensis, Burkholderia multivorans,Burkholderia stabilis, and Burkholderia cepacia Genomovars I and III. J. Clin. Microbiol. 2000, 38, 3165–3173. 10.1128/JCM.38.9.3165-3173.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathur D.; Medintz I. L. The Growing Development of DNA Nanostructures for Potential Healthcare-Related Applications. Adv. Healthcare Mater. 2019, 8, 1801546. 10.1002/adhm.201801546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- You M.; Peng L.; Shao N.; Zhang L.; Qiu L.; Cui C.; Tan W. DNA “nano-claw”: logic-based autonomous cancer targeting and therapy. J. Am. Chem. Soc. 2014, 136, 1256–1259. 10.1021/ja4114903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang P.; Wang C.; Zhao J.; Xiao A.; Shen Q.; Li L.; Li J.; Zhang J.; Min Q.; Chen J.; et al. Near infrared-guided smart nanocarriers for microRNA-controlled release of doxorubicin/siRNA with intracellular ATP as fuel. ACS Nano 2016, 10, 3637–3647. 10.1021/acsnano.5b08145. [DOI] [PubMed] [Google Scholar]
- Adleman L. M. Molecular computation of solutions to combinatorial problems. Science 1994, 266, 1021–1024. 10.1126/science.7973651. [DOI] [PubMed] [Google Scholar]
- Arter W. E.; Yusim Y.; Peter Q.; Taylor C. G.; Klenerman D.; Keyser U. F.; Knowles T. P. J. Digital Sensing and Molecular Computation by an Enzyme-Free DNA Circuit. ACS Nano 2020, 14, 5763–5771. 10.1021/acsnano.0c00628. [DOI] [PubMed] [Google Scholar]
- Sakamoto K.; Gouzu H.; Komiya K.; Kiga D.; Yokoyama S.; Yokomori T.; Hagiya M. Molecular computation by DNA hairpin formation. Science 2000, 288, 1223–1226. 10.1126/science.288.5469.1223. [DOI] [PubMed] [Google Scholar]
- Sherman W. B.; Seeman N. C. A precisely controlled DNA biped walking device. Nano Lett. 2004, 4, 1801. 10.1021/nl048887a. [DOI] [Google Scholar]
- Simmel F. C.; Dittmer W. U. DNA nanodevices. Small 2005, 1, 284–299. 10.1002/smll.200400111. [DOI] [PubMed] [Google Scholar]
- Watson J. D.; Crick F. H. Molecular structure of nucleic acids: a structure for deoxyribose nucleic acid. Nature 1953, 171, 737–738. 10.1038/171737a0. [DOI] [PubMed] [Google Scholar]
- Kool E. T. Hydrogen Bonding, Base Stacking, and Steric Effects in DNA Replication. Annu. Rev. Biophys. Biomol. Struct. 2001, 30, 1–22. 10.1146/annurev.biophys.30.1.1. [DOI] [PubMed] [Google Scholar]
- Lu M.; Guo Q.; Marky L. A.; Seeman N. C.; Kallenbach N. R. Thermodynamics of DNA branching. J. Mol. Biol. 1992, 223, 781–789. 10.1016/0022-2836(92)90989-w. [DOI] [PubMed] [Google Scholar]
- SantaLucia J.; Allawi H. T.; Seneviratne P. A. Improved nearest-neighbor parameters for predicting DNA duplex stability. Biochemistry 1996, 35, 3555–3562. 10.1021/bi951907q. [DOI] [PubMed] [Google Scholar]
- SantaLucia J. Jr A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl. Acad. Sci. U.S.A. 1998, 95, 1460–1465. 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SantaLucia J.; Hicks D. The thermodynamics of DNA structural motifs. Annu. Rev. Biophys. Biomol. Struct. 2004, 33, 415–440. 10.1146/annurev.biophys.32.110601.141800. [DOI] [PubMed] [Google Scholar]
- Dirks R.; Bois J.; Schaeffer J.; Winfree E.; Pierce N. Thermodynamic Analysis of Interacting Nucleic Acid Strands. SIAM Rev. 2007, 49, 65–88. 10.1137/060651100. [DOI] [Google Scholar]
- Bommarito S.; Peyret N.; Jr J. S. Thermodynamic parameters for DNA sequences with dangling ends. Nucleic Acids Res. 2000, 28, 1929–1934. 10.1093/nar/28.9.1929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang D. Y.; Winfree E. Control of DNA strand displacement kinetics using toehold exchange. J. Am. Chem. Soc. 2009, 131, 17303–17314. 10.1021/ja906987s. [DOI] [PubMed] [Google Scholar]
- Yurke B.; Mills A. P. Using DNA to power nanostructures. Genet. Program. Evolvable Mach. 2003, 4, 111–122. 10.1023/a:1023928811651. [DOI] [Google Scholar]
- Panyutin I. G.; Hsieh P. The kinetics of spontaneous DNA branch migration. Proc. Natl. Acad. Sci. U.S.A. 1994, 91, 2021–2025. 10.1073/pnas.91.6.2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srinivas N.; Ouldridge T. E.; Šulc P.; Schaeffer J. M.; Yurke B.; Louis A. A.; Doye J. P. K.; Winfree E. On the biophysics and kinetics of toehold-mediated DNA strand displacement. Nucleic Acids Res. 2013, 41, 10641–10658. 10.1093/nar/gkt801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sikora J. R.; Rauzan B.; Stegemann R.; Deckert A. Modeling stopped-flow data for nucleic acid duplex formation reactions: The importance of off-path intermediates. J. Phys. Chem. B 2013, 117, 8966–8976. 10.1021/jp404550a. [DOI] [PubMed] [Google Scholar]
- Graugnard E.; Cox A.; Lee J.; Jorcyk C.; Yurke B.; Hughes W. L. Kinetics of DNA and RNA hybridization in serum and serum-SDS. IEEE Trans. Nanotechnol. 2010, 9, 603–609. 10.1109/TNANO.2010.2053380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothemund P. W. Folding DNA to create nanoscale shapes and patterns. Nature 2006, 440, 297–302. 10.1038/nature04586. [DOI] [PubMed] [Google Scholar]
- Zheng J.; Birktoft J. J.; Chen Y.; Wang T.; Sha R.; Constantinou P. E.; Ginell S. L.; Mao C.; Seeman N. C. From molecular to macroscopic via the rational design of a self-assembled 3D DNA crystal. Nature 2009, 461, 74–77. 10.1038/nature08274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ke Y.; Ong L. L.; Shih W. M.; Yin P. Three-dimensional structures self-assembled from DNA bricks. science 2012, 338, 1177–1183. 10.1126/science.1227268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei B.; Dai M.; Yin P. Complex shapes self-assembled from single-stranded DNA tiles. Nature 2012, 485, 623–626. 10.1038/nature11075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clamons S.; Qian L.; Winfree E. Programming and simulating chemical reaction networks on a surface. J. R. Soc. Interface 2020, 17, 20190790. 10.1098/rsif.2019.0790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soloveichik D.; Seelig G.; Winfree E. DNA as a universal substrate for chemical kinetics. Proc. Natl. Acad. Sci. U.S.A. 2010, 107, 5393–5398. 10.1073/pnas.0909380107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srinivas N.; Parkin J.; Seelig G.; Winfree E.; Soloveichik D. Enzyme-free nucleic acid dynamical systems. Science 2017, 358, eaal2052 10.1126/science.aal2052. [DOI] [PubMed] [Google Scholar]
- Lai W.; Ren L.; Tang Q.; Qu X.; Li J.; Wang L.; Li L.; Fan C.; Pei H. Programming Chemical Reaction Networks Using Intramolecular Conformational Motions of DNA. ACS Nano 2018, 12, 7093–7099. 10.1021/acsnano.8b02864. [DOI] [PubMed] [Google Scholar]
- Yurke B.; Turberfield A. J.; Mills A. P.; Simmel F. C.; Neumann J. L. A DNA-fuelled molecular machine made of DNA. Nature 2000, 406, 605–608. 10.1038/35020524. [DOI] [PubMed] [Google Scholar]
- Shin J.-S.; Pierce N. A. A synthetic DNA walker for molecular transport. J. Am. Chem. Soc. 2004, 126, 10834–10835. 10.1021/ja047543j. [DOI] [PubMed] [Google Scholar]
- Bath J.; Turberfield A. J.. DNA nanomachines. In Nanoscience And Technology: A Collection of Reviews from Nature Journals; World Scientific, 2010; pp 124–133. [Google Scholar]
- Turberfield A. J.; Mitchell J. C.; Yurke B.; Mills A. P.; Blakey M. I.; Simmel F. C. DNA Fuel for Free-Running Nanomachines. Phys. Rev. Lett. 2003, 90, 118102. 10.1103/PhysRevLett.90.118102. [DOI] [PubMed] [Google Scholar]
- Mao C.; Sun W.; Shen Z.; Seeman N. C. A nanomechanical device based on the B–Z transition of DNA. Nature 1999, 397, 144–146. 10.1038/16437. [DOI] [PubMed] [Google Scholar]
- Shu W.; Liu D.; Watari M.; Riener C. K.; Strunz T.; Welland M. E.; Balasubramanian S.; McKendry R. A. DNA molecular motor driven micromechanical cantilever arrays. J. Am. Chem. Soc. 2005, 127, 17054–17060. 10.1021/ja0554514. [DOI] [PubMed] [Google Scholar]
- Chen Y. J.; Dalchau N.; Srinivas N.; Phillips A.; Cardelli L.; Soloveichik D.; Seelig G. Programmable chemical controllers made from DNA. Nat. Nanotechnol. 2013, 8, 755–762. 10.1038/nnano.2013.189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fern J.; Schulman R. Modular DNA strand-displacement controllers for directing material expansion. Nat. Commun. 2018, 9, 3766–3768. 10.1038/s41467-018-06218-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seelig G.; Soloveichik D.; Zhang D. Y.; Winfree E. Enzyme-free nucleic acid logic circuits. science 2006, 314, 1585–1588. 10.1126/science.1132493. [DOI] [PubMed] [Google Scholar]
- Qian L.; Winfree E. Scaling up digital circuit computation with DNA strand displacement cascades. science 2011, 332, 1196–1201. 10.1126/science.1200520. [DOI] [PubMed] [Google Scholar]
- Dirks R. M.; Pierce N. A. Triggered amplification by hybridization chain reaction. Proc. Natl. Acad. Sci. U.S.A. 2004, 101, 15275–15278. 10.1073/pnas.0407024101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seelig G.; Yurke B.; Winfree E. Catalyzed relaxation of a metastable DNA fuel. J. Am. Chem. Soc. 2006, 128, 12211–12220. 10.1021/ja0635635. [DOI] [PubMed] [Google Scholar]
- Zhang D. Y.; Turberfield A. J.; Yurke B.; Winfree E. Engineering entropy-driven reactions and networks catalyzed by DNA. Science 2007, 318, 1121–1125. 10.1126/science.1148532. [DOI] [PubMed] [Google Scholar]
- Yin P.; Choi H. M. T.; Calvert C. R.; Pierce N. A. Programming biomolecular self-assembly pathways. Nature 2008, 451, 318–322. 10.1038/nature06451. [DOI] [PubMed] [Google Scholar]
- Chen X. Expanding the rule set of DNA circuitry with associative toehold activation. J. Am. Chem. Soc. 2012, 134, 263–271. 10.1021/ja206690a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X.; Tang Y.; Traynor S. M.; Li F. Regulation of DNA Strand Displacement Using an Allosteric DNA Toehold. J. Am. Chem. Soc. 2016, 138, 14076–14082. 10.1021/jacs.6b08794. [DOI] [PubMed] [Google Scholar]
- Genot A. J.; Zhang D. Y.; Bath J.; Turberfield A. J. Remote toehold: a mechanism for flexible control of DNA hybridization kinetics. J. Am. Chem. Soc. 2011, 133, 2177–2182. 10.1021/ja1073239. [DOI] [PubMed] [Google Scholar]
- Green S. J.; Lubrich D.; Turberfield A. J. DNA hairpins: Fuel for autonomous DNA devices. Biophys. J. 2006, 91, 2966–2975. 10.1529/biophysj.106.084681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader A.; Cockroft S. L. Conformational enhancement of fidelity in toehold-sequestered DNA nanodevices. Chem. Commun. 2020, 56, 5135–5138. 10.1039/d0cc00882f. [DOI] [PubMed] [Google Scholar]
- Hong F.; Šulc P.. Strand displacement: a fundamental mechanism in RNA biology?. 2019, arXiv preprint arXiv:1903.12199. [Google Scholar]
- Zhang D. Y.; Winfree E. Dynamic allosteric control of noncovalent DNA catalysis reactions. J. Am. Chem. Soc. 2008, 130, 13921–13926. 10.1021/ja803318t. [DOI] [PubMed] [Google Scholar]
- Liang X.; Mochizuki T.; Fujii T.; Kashida H.; Asanuma H.. Design of a Functional Nanomaterial with Recognition Ability for Constructing Light-Driven Nanodevices; Springer, 2010; pp 112–122. [Google Scholar]
- Liu J.; Lu Y. Stimuli-responsive disassembly of nanoparticle aggregates for light-up colorimetric sensing. J. Am. Chem. Soc. 2005, 127, 12677–12683. 10.1021/ja053567u. [DOI] [PubMed] [Google Scholar]
- Zhang D. Y.; Winfree E. Robustness and modularity properties of a non-covalent DNA catalytic reaction. Nucleic Acids Res. 2010, 38, 4182–4197. 10.1093/nar/gkq088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes E. D. Steric hindrance. Q. Rev. Chem. Soc. 1948, 2, 107–131. 10.1039/QR9480200107. [DOI] [Google Scholar]
- Wang B.; Thachuk C.; Ellington A. D.; Winfree E.; Soloveichik D. Effective design principles for leakless strand displacement systems. Proc. Natl. Acad. Sci. U.S.A. 2018, 115, E12182–E12191. 10.1073/pnas.1806859115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lysne D.; Jones K.; Stosius A.; Hachigian T.; Lee J.; Graugnard E. Availability-Driven Design of Hairpin Fuels and Small Interfering Strands for Leakage Reduction in Autocatalytic Networks. J. Phys. Chem. B 2020, 124, 3326–3335. 10.1021/acs.jpcb.0c01229. [DOI] [PubMed] [Google Scholar]
- Olson X.; Kotani S.; Padilla J. E.; Hallstrom N.; Goltry S.; Lee J.; Yurke B.; Hughes W. L.; Graugnard E. Availability: A Metric for Nucleic Acid Strand Displacement Systems. ACS Synth. Biol. 2017, 6, 84–93. 10.1021/acssynbio.5b00231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kotani S.; Hughes W. L. Multi-Arm Junctions for Dynamic DNA Nanotechnology. J. Am. Chem. Soc. 2017, 139, 6363–6368. 10.1021/jacs.7b00530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song T.; Gopalkrishnan N.; Eshra A.; Garg S.; Mokhtar R.; Bui H.; Chandran H.; Reif J. Improving the Performance of DNA Strand Displacement Circuits by Shadow Cancellation. ACS Nano 2018, 12, 11689–11697. 10.1021/acsnano.8b07394. [DOI] [PubMed] [Google Scholar]
- Olson X.; Kotani S.; Yurke B.; Graugnard E.; Hughes W. L. Kinetics of DNA Strand Displacement Systems with Locked Nucleic Acids. J. Phys. Chem. B 2017, 121, 2594–2602. 10.1021/acs.jpcb.7b01198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang Y. S.; Bhadra S.; Li B.; Ellington A. D. Mismatches Improve the Performance of Strand-Displacement Nucleic Acid Circuits. Angew. Chem., Int. Ed. 2014, 53, 1845–1848. 10.1002/anie.201307418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhadra S.; Ellington A. D. Design and application of cotranscriptional non-enzymatic RNA circuits and signal transducers. Nucleic Acids Res. 2014, 42, e58 10.1093/nar/gku074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zarubiieva I.; Spaccasassi C.; Kulkarni V.; Phillips A. Automated Leak Analysis of Nucleic Acid Circuits. ACS Synth. Biol. 2022, 11, 1931–1948. 10.1021/acssynbio.2c00084. [DOI] [PubMed] [Google Scholar]
- Pinheiro A. V.; Nangreave J.; Jiang S.; Yan H.; Liu Y. Steric crowding and the kinetics of DNA hybridization within a DNA nanostructure system. ACS Nano 2012, 6, 5521–5530. 10.1021/nn301448y. [DOI] [PubMed] [Google Scholar]
- Ang J.; Harris E.; Hussey B. J.; Kil R.; McMillen D. R. Tuning response curves for synthetic biology. ACS Synth. Biol. 2013, 2, 547–567. 10.1021/sb4000564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanna M.; Munshi M.; Kedzierski N. A.; Chung P. N.; Huang T.; Mok A. K.; Lukeman P. S. Photocleavage control of nucleated DNA nanosystems – the influence of surface strand sterics. Nanoscale 2014, 6, 2094–2096. 10.1039/C3NR05875A. [DOI] [PubMed] [Google Scholar]
- Ranallo S.; Rossetti M.; Plaxco K. W.; Vallée-Bélisle A.; Ricci F. A modular, DNA-based beacon for single-step fluorescence detection of antibodies and other proteins. Angew. Chem., Int. Ed. 2015, 54, 13214–13218. 10.1002/anie.201505179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei W.; Zhang L.; Ni Q.; Pu Y.; Yin L.; Liu S. Fabricating a reversible and regenerable electrochemical biosensor for quantitative detection of antibody by using “triplex-stem” DNA molecular switch. Anal. Chim. Acta 2014, 845, 38–44. 10.1016/j.aca.2014.07.015. [DOI] [PubMed] [Google Scholar]
- Mahshid S. S.; Camiré S. b.; Ricci F.; Vallée-Bélisle A. A highly selective electrochemical DNA-based sensor that employs steric hindrance effects to detect proteins directly in whole blood. J. Am. Chem. Soc. 2015, 137, 15596–15599. 10.1021/jacs.5b04942. [DOI] [PubMed] [Google Scholar]
- Peng Y.; Li X.; Yuan R.; Xiang Y. Steric hindrance inhibition of strand displacement for homogeneous and signal-on fluorescence detection of human serum antibodies. Chem. Commun. 2016, 52, 12586–12589. 10.1039/c6cc06893f. [DOI] [PubMed] [Google Scholar]
- Turberfield A. J.; Mitchell J. C.; Yurke B.; Mills A. P.; Blakey M. I.; Simmel F. C. DNA Fuel for Free-Running Nanomachines. Phys. Rev. Lett. 2003, 90, 118102–118104. 10.1103/PhysRevLett.90.118102. [DOI] [PubMed] [Google Scholar]
- Taylor D. N.; Davidson S. R.; Qian L. A cooperative DNA catalyst. J. Am. Chem. Soc. 2021, 143, 15567–15571. 10.1021/jacs.1c07122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engelen W.; Meijer L. H.; Somers B.; De Greef T. F.; Merkx M. Antibody-controlled actuation of DNA-based molecular circuits. Nat. Commun. 2017, 8, 14473–14478. 10.1038/ncomms14473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan B.-f.; Zhuang X.-y.; Hao Y.-h.; Tan Z. Kinetics of base stacking-aided DNA hybridization. Chem. Commun. 2008, 6600–6602. 10.1039/b812929k. [DOI] [PubMed] [Google Scholar]
- Wang X.; Seeman N. C. Assembly and Characterization of 8-Arm and 12-Arm DNA Branched Junctions. J. Am. Chem. Soc. 2007, 129, 8169–8176. 10.1021/ja0693441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henrich O.; Gutierrez Fosado Y. A.; Curk T.; Ouldridge T. E. Coarse-grained simulation of DNA using LAMMPS: An implementation of the oxDNA model and its applications. Eur. Phys. J. E: Soft Matter Biol. Phys. 2018, 41, 57. 10.1140/epje/i2018-11669-8. [DOI] [PubMed] [Google Scholar]
- Poppleton E.; Bohlin J.; Matthies M.; Sharma S.; Zhang F.; Šulc P. Design, optimization and analysis of large DNA and RNA nanostructures through interactive visualization, editing and molecular simulation. Nucleic Acids Res. 2020, 48, e72 10.1093/nar/gkaa417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poppleton E.; Romero R.; Mallya A.; Rovigatti L.; Šulc P. OxD. N. A. OxDNA.org: a public webserver for coarse-grained simulations of DNA and RNA nanostructures. Nucleic Acids Res. 2021, 49, W491–W498. 10.1093/nar/gkab324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snodin B. E. K.; Randisi F.; Mosayebi M.; Šulc P.; Schreck J. S.; Romano F.; Ouldridge T. E.; Tsukanov R.; Nir E.; Louis A. A.; et al. Introducing improved structural properties and salt dependence into a coarse-grained model of DNA. J. Chem. Phys. 2015, 142, 234901. 10.1063/1.4921957. [DOI] [PubMed] [Google Scholar]
- Šulc P.; Romano F.; Ouldridge T. E.; Rovigatti L.; Doye J. P. K.; Louis A. A. Sequence-dependent thermodynamics of a coarse-grained DNA model. J. Chem. Phys. 2012, 137, 135101. 10.1063/1.4754132. [DOI] [PubMed] [Google Scholar]
- Ouldridge T. E.; Louis A. A.; Doye J. P. K. Structural, mechanical, and thermodynamic properties of a coarse-grained DNA model. J. Chem. Phys. 2011, 134, 085101. 10.1063/1.3552946. [DOI] [PubMed] [Google Scholar]
- Bois J. S.; Venkataraman S.; Choi H. M. T.; Spakowitz A. J.; Wang Z.-G.; Pierce N. A. Topological constraints in nucleic acid hybridization kinetics. Nucleic Acids Res. 2005, 33, 4090–4095. 10.1093/nar/gki721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wetmur J. G. Hybridization and renaturation kinetics of nucleic acids. Annu. Rev. Biophys. Bioeng. 1976, 5, 337–361. 10.1146/annurev.bb.05.060176.002005. [DOI] [PubMed] [Google Scholar]
- Zadeh J. N.; Steenberg C. D.; Bois J. S.; Wolfe B. R.; Pierce M. B.; Khan A. R.; Dirks R. M.; Pierce N. A. NUPACK: Analysis and design of nucleic acid systems. J. Comput. Chem. 2011, 32, 170–173. 10.1002/jcc.21596. [DOI] [PubMed] [Google Scholar]
- Dirks R. M.; Pierce N. A. A partition function algorithm for nucleic acid secondary structure including pseudoknots. J. Comput. Chem. 2003, 24, 1664–1677. 10.1002/jcc.10296. [DOI] [PubMed] [Google Scholar]
- Dirks R. M.; Pierce N. A. An algorithm for computing nucleic acid base-pairing probabilities including pseudoknots. J. Comput. Chem. 2004, 25, 1295–1304. 10.1002/jcc.20057. [DOI] [PubMed] [Google Scholar]
- Fornace M. E.; Porubsky N. J.; Pierce N. A. A unified dynamic programming framework for the analysis of interacting nucleic acid strands: Enhanced models, scalability, and speed. ACS Synth. Biol. 2020, 9, 2665–2678. 10.1021/acssynbio.9b00523. [DOI] [PubMed] [Google Scholar]
- Vasiliskov V. A.; Prokopenko D. V.; Mirzabekov A. D. Parallel multiplex thermodynamic analysis of coaxial base stacking in DNA duplexes by oligodeoxyribonucleotide microchips. Nucleic Acids Res. 2001, 29, 2303–2313. 10.1093/nar/29.11.2303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peyret N.Prediction of Nucleic Acid Hybridization: Parameters and Algorithms; Wayne State University, 2000. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.