Abstract
The thalamus is composed of functionally and structurally distinct nuclei. Previous studies have indicated that certain cortical areas may project across multiple thalamic nuclei, potentially allowing them to modulate distributed information flow. However, there is a lack of quantitative investigations into anatomical connectivity patterns within the thalamus. Consequently, it remains unknown if cortical areas exhibit differences in the spread of their thalamic connectivity patterns. To address this knowledge gap, we used diffusion magnetic resonance imaging (dMRI) to compute brain-wide probabilistic tractography using data from 828 healthy adults collected by the Human Connectome Project. To measure the spatial extent of anatomical connectivity patterns within the thalamus, we developed an innovative framework that quantifies the spatial properties of each cortical area’s within-thalamus connectivity patterns. We then leveraged resting-state functional MRI, cortical myelin, and human neural gene expression data to test if the spread of within-thalamus connectivity patterns varied along the cortical hierarchy. These results revealed two broad cortico-thalamic tractography motifs: 1) a sensorimotor cortical motif characterized by focal thalamic connections targeting posterolateral thalamus, which potentially supports fast, feed-forward information flow; and 2) an associative cortical motif characterized by diffuse thalamic connections targeting anteromedial thalamus, which potentially supports slower, feed-back information flow. These results were consistent among human subjects and were also observed in macaques, indicating cross-species generalizability. In summary, these findings demonstrate that sensorimotor and association cortical areas exhibit differences in the spatial extent of their within-thalamus connectivity patterns, which may support functionally-distinct cortico-thalamic information transmission.
Keywords: thalamus, spatial topography, thalamo-cortical, diffusion MRI, anatomical connectivity, tractography
Introduction
Mapping the anatomical connections of the brain is a fundamental goal in neuroscience, as these pathways tether different brain areas together and impose constraints on their functional interactions. The thalamus is a central subcortical brain structure that is extensively connected to the entire cortex through long-range white matter fiber bundles (1). These bundles form parallel cortico-thalamic circuits, which enable the thalamus to relay, sustain, and coordinate information across the entire cortex (2–4). Notably, the thalamus lacks reciprocal excitatory connections (5). Thus, sensorimotor and associative neural computations involving the thalamus heavily rely on its long-range inputs from and outputs to the cortex (6). Mapping these long-range connections can provide critical insight into the role of the thalamus in shaping cortical information flow and the neural basis of higher-order cognitive functions, which are critically reliant on the long-range interactions between the thalamus and cortex in vertebrates (2, 7–12).
Research on the anatomy of cortico-thalamic connectivity date back to the early 19th century, yet we still lack a comprehensive understanding of the organizing principles of these connections, particularly in humans (see 13 and 14 for review). The traditional view of the thalamus has largely been informed by its histologically-defined nuclear structure (6). This view has also been supported by evidence showing that certain cortical areas project to individual thalamic nuclei. However, some cortical areas exhibit widespread connections across the thalamus, projecting to multiple thalamic nuclei (15–21). One proposed role for such cross-nuclei targeting is to allow for spatial overlap of connections from different cortical areas, thereby facilitating information integration within the thalamus (22–24). However, knowledge of how within-thalamus connectivity patterns vary across cortical areas, especially in humans, remains incomplete.
Primate studies investigating cortico-thalamic circuitry have primarily relied on anatomical tracer data in monkeys (e.g., 18–20, 25–27). However, such invasive studies cannot be replicated in humans. Fortunately, advancements in magnetic resonance imaging (MRI) have enabled the examination of white matter pathways in vivo using diffusion MRI (dMRI), which measures the diffusion properties of water molecules in brain tissue (28–30). These properties are then used by tractography algorithms to reconstruct white matter pathways, known as streamlines (31–34).
State-of-the-art tractography techniques can now map streamlines at high spatial resolutions to reveal connectivity patterns within the thalamus (15, 16, 35–37). Tractography studies have unveiled a diverse array of cortico-thalamic circuits. These circuits are characterized by distinct origins, targets, strengths, and microstructural profiles, which are optimized for specialized roles in information transmission (15, 37–40). Emerging evidence suggests that certain cortical areas may exhibit more widespread connectivity patterns within the thalamus (37), which may grant them privileged access for integrating or modulating whole-brain functional interactions (41). However, it is uncertain whether the extent of within-thalamus connectivity patterns systematically varies across cortical areas in humans and what implications such variation may have for information processing within cortico-thalamic systems.
Furthermore, there are few studies that have directly compared cortico-thalamic anatomical circuitry between humans and non-human primates using tractography methods (e.g., 40, 42). Such studies form a bridge to the existing macaque tract tracing literature. They also provide validation for human dMRI findings, as macaque dMRI can be collected at much higher resolutions, without confounds such as motion artifacts (43).
The aim of this study was to investigate the spatial extent of cortical connectivity within the thalamus in both humans and non-human primates and explore how it may vary between sensorimotor and association cortical areas. To this end, we leveraged probabilistic tractography derived from 3T diffusion data for 828 healthy human adults from the Human Connectome Project (HCP) and 7T diffusion data from six post-mortem macaque monkeys. We first developed an innovative approach to quantify the spatial properties of tractography-derived anatomical connectivity patterns. We then examined inter-cortical differences in the extent of within-thalamus connectivity patterns. We found that the spatial extent of the cortico-thalamic connections varies within the thalamus across the cortical hierarchy, such that sensorimotor cortical areas exhibited more focal thalamic connectivity patterns, while association cortical areas have more diffuse, or widespread, connectivity patterns. Our findings provide convergent evidence using resting-state functional MRI, cortical myelin, and human neural gene expression data to demonstrate distinct patterns of thalamic connectivity between sensory and associative cortical areas in humans. Additionally, we show that these differences are generalized in macaques. Overall, our findings highlight that sensorimotor and association cortical areas exhibit distinct anatomical connectivity patterns within the thalamus, which may underlie functionally distinct cortico-thalamic computations.
Results
Cortical areas differ in the extent of their thalamic connectivity patterns.
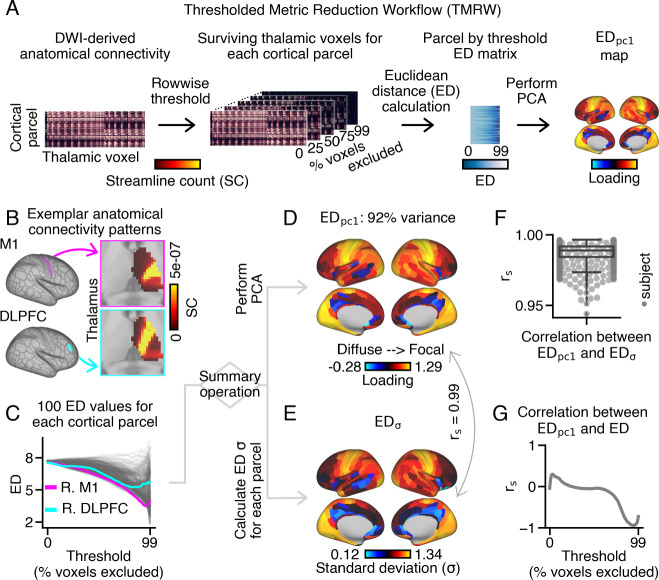
We first examined whether there are systematic differences in the spatial extent of anatomical connectivity patterns within the thalamus across cortical areas. To achieve this, we developed a thresholding framework to investigate the spatial properties of brain connectivity patterns (Fig. 1A). Briefly, the framework involved iteratively excluding a percentage of thalamic voxels based on their streamline count, which represents the likelihood that a voxel is connected to the given cortical area. For each cortical parcel, we then calculated the average pairwise Euclidean distance (ED) between these ‘surviving’ thalamic voxels. To obtain a single measure for each cortical area, each cortical area’s ED values across all thresholds were used as input into principal components analysis (PCA), yielding a loading value for the first principal component ( loadings; see SI Appendix for additional methodological details). loadings serve as an index of the spatial extent of thalamic connectivity patterns for each cortical area.
Fig. 1.
Workflow for quantifying the extent of each cortical area’s thalamic anatomical connectivity pattern using Euclidean distance (ED). (A) Schematic overview of the thresholding and ED calculation framework applied to group-level and individual-level human probabilistic tractography data (). ED was used to measure the extent of each cortical parcel’s anatomical connectivity pattern within ipsilateral thalamus (see Fig. S8 for bilateral calculation). (B) Thalamic connectivity patterns for right motor area 1 (M1) and dorsolateral prefrontal cortex (DLPFC). M1 and DLPFC illustrate focal and diffuse thalamic connectivity patterns, respectively. (C) ED matrix depicting pairwise distances calculated between surviving thalamic voxels for 100 thresholds. Cortical parcels with more diffuse thalamic connectivity patterns exhibited higher ED values across thresholds (e.g., DLPFC). (D) Cortical loading map obtained through principal component analysis (PCA) of the ED matrix. The first PC accounted for 92% of the variance. (E) Cortical map representing the standard deviation of ED across 100 thresholds for each cortical parcel. values were highly correlated with loadings , with p-values estimated using spatial-autocorrelation (sa) preserving surrogate brain maps (44). : Spearman rho. (F) Correlations between and were highly consistent across subjects. (G) loadings and ED values negatively correlated at more conservative thresholds, indicating that higher loadings correspond to more focal thalamic connectivity patterns.
We applied the thresholding framework to dMRI-derived probabilistic tractography data from healthy adults from the Human Connectome Project (; see SI Appendix Fig. S1 for preprocessing steps). Here, we parcellated dense (grey-ordinate to grey-ordinate) streamline count connectivity data along one dimension to generate a cortico-thalamic ‘connectome’. This connectome represents the likelihood of the presence of connections between 360 cortical parcels and all thalamic voxels. Only ipsilateral thalamic voxels were considered, unless otherwise specified in supplementary analyses. Each cortical parcel exhibited a distinct thalamic connectivity pattern, as exemplified by motor area 1 (M1; top magenta panel) and dorsolateral prefrontal cortex (DLPFC; bottom cyan panel) (Fig. 1B). Thalamic voxels displayed varying probabilities of connectivity to each cortical area, where warmer colors indicated voxels with a higher likelihood of having a connection to the seeded cortical area relative to cooler colors.
For each cortical parcel, we iteratively calculated the average pairwise ED between between thalamic voxels, after progressively excluding a percentage (0 to 99%) of thalamic voxels with the lowest streamline counts (Fig. S2 shows the surviving thalamic voxels for a subset of thresholds). This process generated a matrix of ED values for each cortical parcel and threshold combination (360×100) (Fig. 1C).
We then conducted PCA using the ED matrix as input. The first principal component accounted for almost all of the variation of ED across cortical parcels (92%) (Fig. 1D). Cortical parcels with lower loadings included bilateral anterior cingulate areas (such as areas 25 and 24), bilateral precuneus, and right temporal cortex. In contrast, cortical parcels with higher loadings included bilateral visual areas, right somatosensory cortex, and left entorhinal cortex (refer to Fig. S3 for visualizations of their respective thalamic connectivity patterns).
We then compared loadings with alternative measures of the exent of cortical connections within the thalamus. Based on the qualitative observation that some cortical parcels had ED values that remained higher across conservative thresholds, the standard deviation of ED across thresholds was calculated for each cortical parcel, denoted as (Fig. 1E). Remarkably, the and measures exhibited an almost perfect correlation , with statistical significance determined using spatial-autocorrelation (SA) preserving surrogate maps (see SI Appendix for further details) (44). The high correlation between and was consistently observed across subjects (, ) (Fig. 1F).
Moreover, we explored other alternative measures to capture the extent of cortical connections within the thalamus (see Fig. S4). However, based on the superior agreement with ED calculated at more conservative thresholds, we selected loadings for further analysis. These alternative measures largely replicated the main findings of this study (Fig. S4).
We next examined whether the measure can distinguish between focal and diffuse thalamic connectivity patterns. For this purpose, we compared loadings with the ED values calculated at individual thresholds (Fig. 1G). We observed a strong negative correlation between and ED at more conservative thresholds (e.g., 78–99%; Fig. S5). Additionally, we investigated the relationship between loadings and the mean and standard deviation of ED across different threshold ranges. Similar to the correlation observed with individual thresholds, these measures also displayed a high correlation with loadings at more conservative thresholds (Fig. S6). In essence, cortical parcels exhibiting focal thalamic connectivity patterns were characterized by higher loadings compared to those with diffuse thalamic connectivity patterns.
We proceeded to examine the properties of bilateral (Fig. S8) and contralateral (Fig. S9) thalamic connectivity patterns. Bilateral loadings exhibited a strong correlation with ipsilateral loadings . Conversely, contralateral loadings demonstrated a weaker, yet still significant, correlation with ipsilateral loadings . Furthermore, bilateral loadings successfully differentiated cortical parcels with unilateral and bilateral thalamic connectivity patterns (Fig. S8), indicating that the measure can distinguish between focal and diffuse thalamic connectivity patterns within and across hemispheres.
Finally, we conducted extensive control analyses to ensure the robustness of these findings. Firstly, we found that loadings were not associated with inter-subject variation in motion (Fig. S14) or volumes of gray or white matter in the cortex, subcortex, or thalamus (Fig. S15). Additionally, inter-cortical variation in did not correspond with average streamline count (Mean SC) or streamline length (Fig. S10), anatomical overlap with thalamic fractional anisotropy and mean diffusivity values (Fig. S11), or cortical geometry, distortion, or bias (Fig. S12). loadings also remained largely unchanged after accounting for volume differences between the left and right thalamus (Fig. S13) and inter-cortical variation of cortical curvature (Fig. S16).
Lastly, we also calculated isotropy, or evenness of spread, to capture thalamic connectivity pattern shape (Fig. S7), which also did not correspond highly with loadings.
Sensory cortical parcels have more focal thalamic connectivity patterns relative to association cortical parcels.
Animal studies have provided evidence that corticothalamic anatomical connectivity is hierarchically-organized, with a progression from sensory to association cortical areas (46–49). Building upon this, we hypothesized that the extent of within-thalamus connectivity patterns would also vary along the cortical hierarchy in humans. To test this hypothesis, we compared loadings between sensory and association cortical parcels using both network and gradient approaches (Fig. 2). Overall, these results show that sensory cortical parcels have more focal thalamic connectivity patterns relative to association cortical parcels.
Fig. 2.
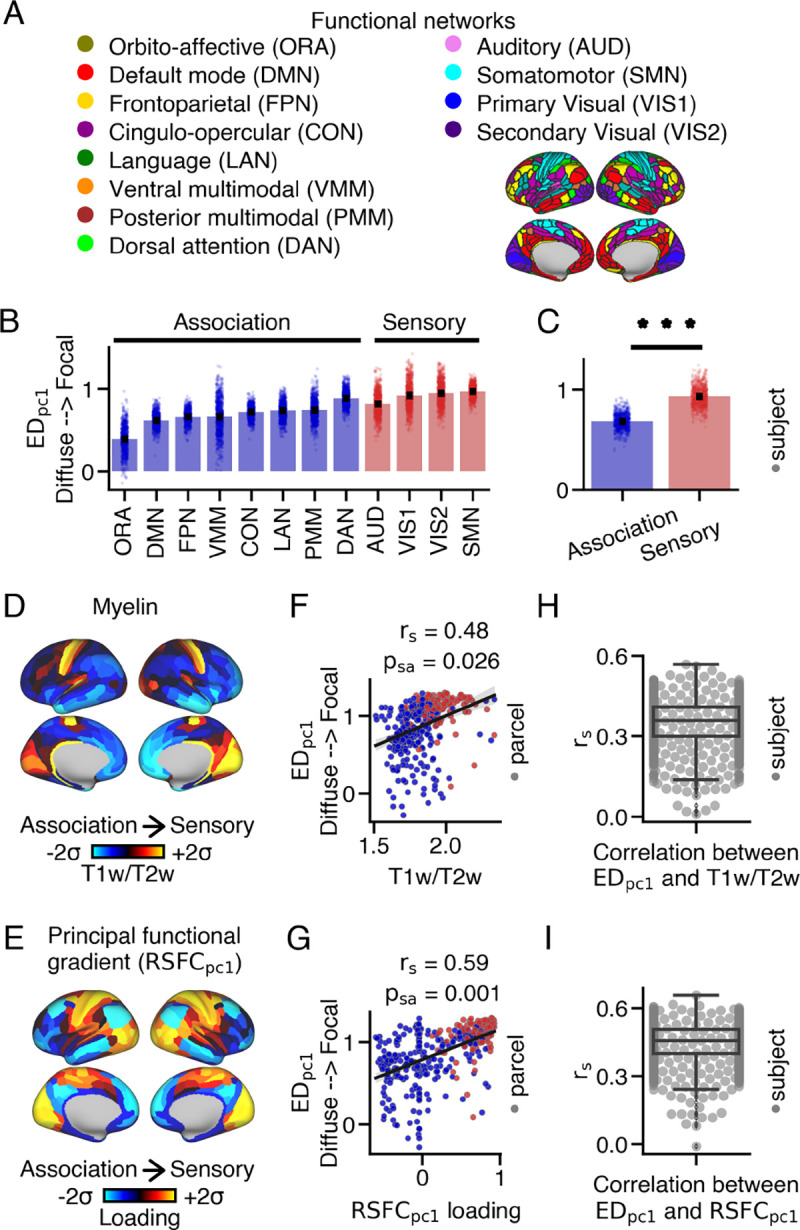
Differences in thalamic connectivity patterns between sensory and association cortical parcels. (A) Resting-state functional connectivity networks identified by Ji et al. (45). The 360 cortical parcels were assigned to twelve functional networks, including eight association and four sensory networks. (B) loadings for each network, representing the average loading within the network for each subject. Barplots show the mean and standard error. (C) Sensory networks exhibited significantly higher loadings compared to association networks (two-sided Wilcoxon signed-rank test; *** p < 0.001). (D) Cortical myelin map calculated by averaging T1w/T2w values across subjects. (E) Cortical principal functional gradient loading () map derived from PCA on cortico-cortical resting-state functional connectivity data. Sensory cortical parcels displayed higher T1w/T2w values and loadings compared to association cortical parcels. (F,G) Correlations between loadings and T1w/T2w values, as well as loadings, across the cortex. (H,I) On average, a moderate relationship was observed between loadings and T1w/T2w values, as well as loadings, across subjects.
First, we assigned each cortical parcel to specific networks based on the work of Ji et al. (45), which categorized the 360 cortical parcels into twelve functional resting-state networks, encompassing sensorimotor (referred to as ‘sensory’) and higher-order associative (referred to as ‘association’) networks (Fig. 2A). loadings exhibited variations within and across these networks (Fig. 2B). Notably, sensory cortical networks demonstrated higher loadings () compared to association cortical parcels () (Wilcoxon signed-rank test: ) (Fig. 2C).
Recently, novel methods have emerged to characterize brain organization along gradients, which exhibit smooth spatial transitions in brain features (50). Many of these gradients demonstrate hierarchical variations from sensory to association cortical areas, including the T1w/T2w ratio, a proxy measure of cortical myelin (51), and the principal resting-state functional gradient , which is derived from cortico-cortical resting-state blood-oxygen-level-dependent (BOLD) functional connectivity (52). T1w/T2w values and loadings are higher in sensory unimodal cortical parcels compared to associative transmodal cortical parcels (Fig. 2D,E). Additionally, they significantly correlate with one another Fig. S17A).
loadings demonstrated a strong positive correlation with both T1w/T2w values (Fig. 2F) and loadings across cortex (Fig. 2G). On average, the correlations between each subject’s loadings and T1w/T2w values (mean: 0.35, median: 0.36, ) and loading (mean: 0.45, median: 0.45, , ) were moderate (Fig. 2H,(I). However, there were instances where a weak relationship was observed between these cortical maps. This discrepancy may be attributed to the presence of biologically implausible connections originating from certain cortical parcels (Fig. S18), which was associated with a weaker correlation between loadings and T1w/T2w values, as well as loadings, across subjects (Fig. S19).
The finding that loadings significantly correlated with T1w/T2w values, as well as loadings, was replicated using bilateral thalamic connectivity patterns (Fig. S8), but not contralateral patterns (Fig. S9). This finding was replicated using an alternate tractography seeding strategy (Fig. S20), dense connectivity data (Fig. S21), and structurally and functionally defined thalamic masks (Fig. S22). Lastly, at more conservative thresholds, ED calculated at individual thresholds (Fig. S5) and the mean and standard deviation of ED calculated for a range of thresholds (Fig. S6) demonstrated variations between sensory and association cortical parcels.
To determine specificity, we tested the correspondence between loadings and the anteroposterior cortical gradient or the secondary principal functional gradient, which reflects functional specialization along a sensory-association-motor cortical axis (52). Neither cortical gradient significantly correlated with loadings (Fig. S23).
Cortical parcels with focal thalamic connectivity patterns preferentially couple to sensorimotor thalamus.
Thalamic nuclei are known to play a role in various sensorimotor and associative cognitive processes (9, 54). We hypothesized that cortical parcels with diffuse thalamic connectivity patterns would anatomically couple with associative thalamic nuclei, while those with focal connectivity patterns would anatomically couple with sensorimotor thalamic nuclei. To test this hypothesis, we compared loadings to quantitative indices that capture anatomical coupling across the thalamic subregions. These findings demonstrate that cortical parcels with more focal thalamic connectivity patterns primarily couple with thalamic subregions associated with sensorimotor processes, predominantly located in the lateral and posterior thalamus, referred to as ‘first-order’ nuclei. Interestingly, cortical parcels with diffuse thalamic connectivity patterns only preferentially coupled with a few nuclei, such as the mediodorsal nucleus (Fig. S24). In contrast, ‘higher-order’ medial and anterior nuclei exhibited more balanced coupling to cortical parcels with both focal and diffuse thalamic connectivity patterns.
First, we investigated the relationship between loadings and anatomical coupling to discrete thalamic nuclei. For this analysis, we used the Morel histological thalamic atlas to segment the thalamus into 28 thalamic nuclei (Fig. 3A). Previous studies have proposed different classifications of these nuclei based on their spatial proximity (e.g., anterior, medial, posterior, and lateral groups), primary input sources (e.g., higher-order vs first-order; (55)), or molecular architecture (e.g., primary, secondary, and tertiary; (56)). (Fig. S25). See Table 1 for all nuclei labels and subgroup assignments. We tested if anatomical overlap across thalamic nuclei, or their associated classes, corresponded with loadings across the cortex.
Fig. 3.
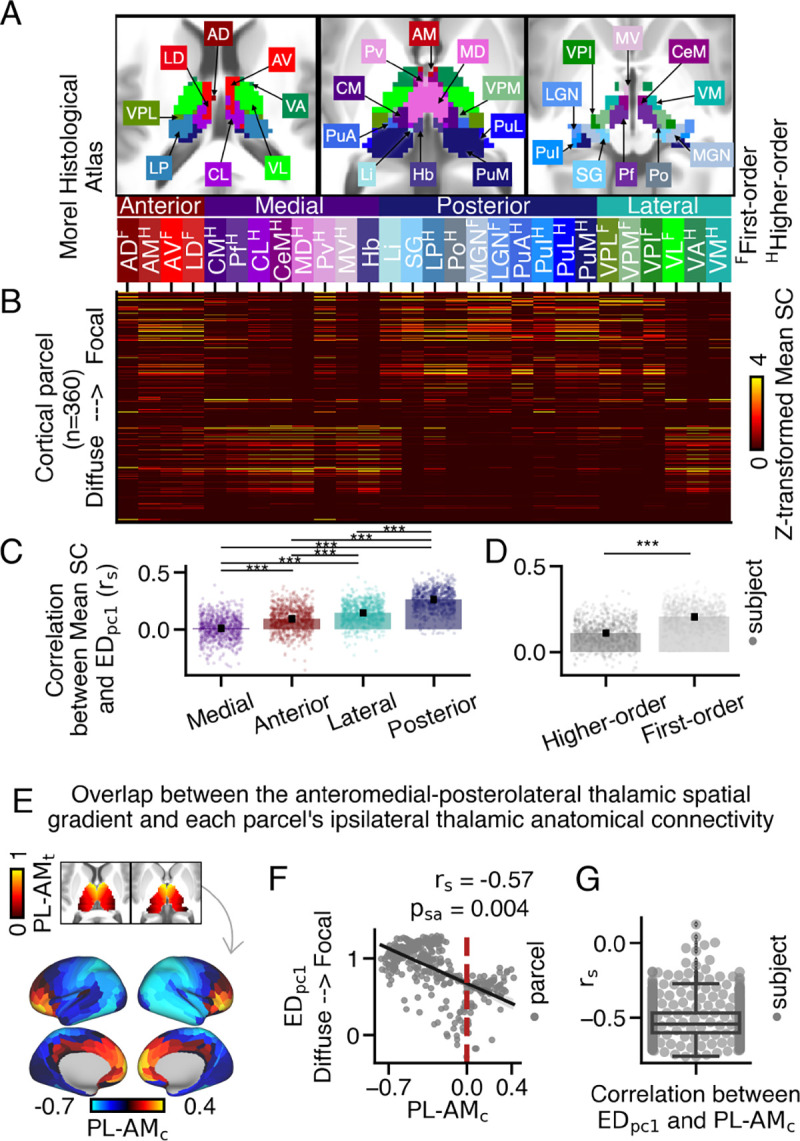
Mapping the extent of cortico-thalamic connectivity patterns onto anatomical coupling with the anteromedial-posterolateral thalamic gradient. (A) Axial view displaying 28 histologically-defined thalamic nuclei from the Morel thalamic atlas (53). (B) An anatomical connectivity matrix between each cortical parcel and each thalamic nucleus. The y-axis is sorted such that cortical parcels with more focal thalamic connectivity patterns (higher loadings) are positioned near the top. (C-D) The correlation between loadings and Mean SC values was calculated for each thalamic nucleus in each subject. Higher values indicate thalamic nuclei that preferentially couple with cortical parcels exhibiting focal thalamic connectivity patterns. (C) Cortical parcels with focal thalamic connectivity patterns preferentially coupled with posterior nuclei, followed by lateral, anterior, and medial nuclei (Friedman test; *** p = 0.001 for Nemenyi post-hoc tests). Each dot represents the averaged value of a subject across thalamic nuclei. (D) Cortical parcels with focal thalamic connectivity patterns preferentially coupled with first-order thalamic nuclei (two-sided Wilcoxon signed-rank test). (E) The overlap between each cortical parcel’s anatomical connectivity along the anteromedial-posterolateral thalamic spatial gradient was calculated for each cortical parcel. Across cortex, higher values denote cortical parcels that preferentially couple with anteromedial thalamus . (F) Cortical parcels with higher loadings preferentially coupled with the posterolateral thalamus, resulting in lower rho values. (G) On average, a moderate relationship was observed between loadings and values across subjects.
First, we constructed an anatomical connectivity matrix to assess the strength of connectivity between each thalamic nucleus and every cortical parcel (Fig. 3B). Each element in the matrix represents the mean streamline count (Mean SC) between a cortical parcel and a thalamic nucleus, normalized within each nucleus. The cortical parcels with the highest group-averaged loadings are positioned at the top.
Anterior and medial thalamic nuclei are commonly associated with higher-order cognitive functions, while lateral and posterior nuclei are primarily associated with sensorimotor cognition (8, 41, 57, 58). Qualitatively, we observed that medial and anterior nuclei coupled to cortical parcels exhibiting both focal and diffuse thalamic connectivity patterns. Posterior nuclei preferentially coupled to those with focal thalamic connectivity patterns. Lateral nuclei displayed a split pattern, with ventroposterior thalamic nuclei preferentially coupling to cortical parcels with focal patterns, while ventrolateral, ventroanterior, and ventromedial nuclei preferred those with diffuse patterns.
To quantify these relationships, we correlated loadings with Mean SC values across cortex separately for each thalamic nucleus. We then compared these values between the four classes of thalamic nuclei. A Friedman test revealed a significant difference in the correlations between loadings and Mean SC across the posterior (median: 0.27), lateral (median: 0.15), anterior (median: 0.1), and medial (median: 0.01) thalamic nuclei (Fig. 3C). Post-hoc Nemenyi tests indicated significant differences between all group comparisons . We also examined the correlation between Mean SC and for each of the 28 thalamic nuclei, which showed modest correlations that did not survive correction for multiple comparisons (Fig. S24).
Previous studies have classified thalamic nuclei based on their driving inputs. First-order nuclei, which receive primary sensory inputs, transmit sensory information to the cortex. On the other hand, higher-order thalamic nuclei receive sensory inputs and inputs from layer 5 of cortex, facilitating trans-thalamic information processing (55, 59). We hypothesized that cortical parcels with focal thalamic connectivity patterns would preferentially couple with first-order thalamic nuclei, while those with diffuse thalamic connectivity patterns would preferentially couple with higher-order thalamic nuclei. We observed a stronger correlation between loadings and Mean SC for first-order (median: 0.20) compared to higher-order (median: 0.11) thalamic nuclei (Wilcoxon signed-rank test; W: 2067, ). These findings indicate that cortical parcels with diffuse thalamic connectivity patterns preferentially couple with both first-order and higher-order thalamic nuclei, while those with focal thalamic connectivity patterns preferentially couple with first-order nuclei. We also examined the correspondence between loadings and Mean SC within thalamic classes defined based on gene expression data (56), which largely replicated these results (Fig. S25). It is worth noting that other classifications of thalamo-cortical nuclei exist (e.g., 60), which we did not consider in this study.
Previous research has demonstrated that cortico-thalamic connectivity may continuously vary along the anteroposterior and mediolateral thalamic axes axes (16, 21, 61). Based on these data, we hypothesized that the extent of connections within the thalamus would also continuously vary along these axes. To investigate this hypothesis, we examined corticothalamic anatomical connectivity along Cartesian spatial gradients within the thalamus.
First, we calculated the position of each thalamic voxel along the anteromedial-posterolateral spatial gradient. Next, we computed the Spearman correlation between a thalamic voxel’s position along the anteromedial-posterolateral gradient and its streamline count for each cortical parcel, representing its coupling strength (schematized in Fig. S26) (Fig. 3E). We then correlated values with loadings (Fig. 3F). These findings revealed that cortical parcels with focal thalamic connectivity patterns exhibited a significant preference for coupling with the posterolateral thalamus ( compared to cortical parcels with diffuse thalamic connectivity patterns, which was largely consistent across subjects (mean: −0.53, median: −0.54, ) (Fig. S28I).
Additionally, we conducted specificity analyses using the dorsoventral gradient and combinations of the anteroposterior, mediolateral, and dorsoventral gradients (Fig. S28). Across subjects, the average correlation between loadings and overlap across the anteromedial-posterolateral thalamic spatial gradient was the highest compared to other thalamic spatial gradients (Fig. 3G).
The extent of cortical connections within the thalamus is associated with distinct cortical information processing roles.
Given that the extent of thalamic connectivity patterns varied along the cortical hierarchy, we hypothesized that the extent of cortical connections within the thalamus would correspond to different information processing roles in the cortex. These findings support this hypothesis, revealing that cortical parcels with focal thalamic connectivity patterns are associated with faster, relay-like feed- forward information flow, whereas parcels with diffuse thalamic connectivity patterns are associated with slower, modulatory feed-back information flow.
We compared the extent of thalamic connectivity patterns in each cortical parcel to their anatomically coupling across two thalamic subpopulations: ‘core’ and ‘matrix’. Thalamic neurons of the ‘core’ type project focally to middle cortical layers, while ‘matrix’ type neurons project diffusely to superficial cortical layers (5, 64). The ‘core’ fibers are associated with relay-type, feed-forward information flow, suited for sensory processing, while the ‘matrix’ fibers support slower, modulatory information flow, ideal for associative processing (5, 64). Recent BOLD-derived functional connectivity work in humans demonstrated that sensory cortical areas functionally couple to ‘core’ thalamus while associative cortical areas functionally couple to ‘matrix’ thalamus (62). Building upon these findings, we hypothesized that cortical parcels with more focal thalamic connectivity patterns would anatomically couple with ‘core’ thalamus, while parcels with more diffuse thalamic connectivity patterns would anatomically couple with ‘matrix’ thalamus.
To examine this, we used the relative mRNA expression levels of calcium-binding proteins Parvalbumin (PVALB; ‘core’ thalamus) and Calbindin (CALB1; ‘matrix’ thalamus) to index each thalamic voxel’s position along the corematrix thalamic gradient (62) (Fig. 4A). Remarkably, the gradient demonstrated a strong correlation with the anteromedial-posterolateral thalamic gradient (Fig. 4B). While other calcium-binding proteins, like Calretinin, are expressed by thalamic neurons as well (65), we did not consider them in this study.
Fig. 4.
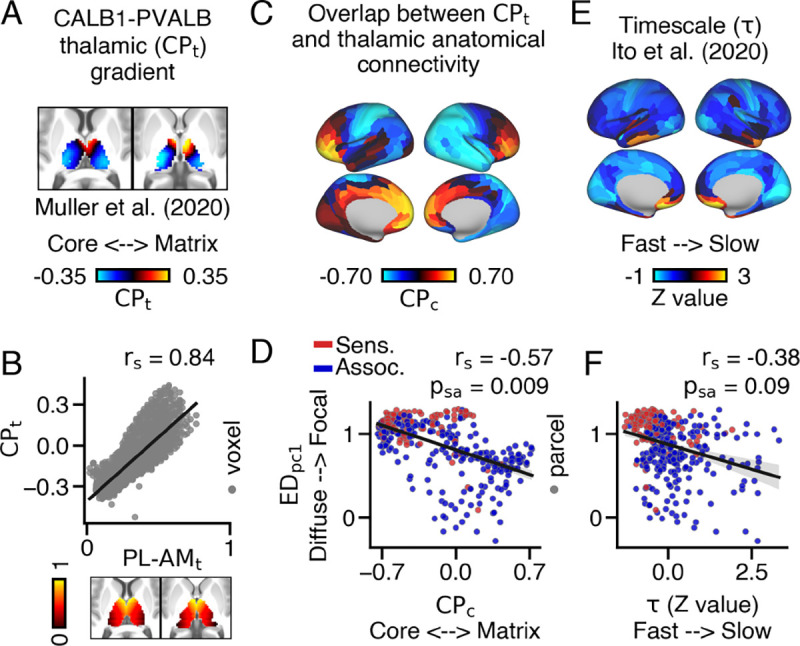
Relationship between the extent of cortical connections within the thalamus and overlap with thalamic subpopulations and intrinsic timescale across cortex. (A) Thalamic gradient reflecting the relative mRNA expression of Parvalbumin (PVALB) and Calbindin (CALB1)-expressing thalamic subpopulations () (62). Warmer colors indicate higher CALB1 expression relative to PVALB. (B) and values strongly correlated with one another. (C) Cortical map showing the overlap between anatomical connectivity and values (). Warmer colors denote preferential coupling with CALB1-expressing thalamic populations. (D) loadings and values significantly correlated with one another. (E) Cortical map of z-transformed intrinsic timescale , calculated from group-averaged resting-state data (63). (F) loadings and z-transformed values exhibited a trending correspondence when accounting for spatial-autocorrelation.
We then examined the correlation between thalamic streamline counts for each cortical parcel and their corresponding values, resulting in a cortical map of values (Fig. 4C). We found that cortical parcels with higher loadings also displayed higher values (Fig. 4D). In essence, cortical parcels with focal thalamic connectivity patterns exhibited preferential coupling with ‘core’ thalamus, while parcels with diffuse thalamic patterns exhibited preferential coupling with ‘matrix’ thalamus . Moreover, consistent with previous research on cortico-thalamic functional connectivity, association cortical parcels exhibited higher anatomical values compared to sensory cortical parcels (62) (Fig. S29).
Cortical parcels are known to exhibit differences in the timescales of their intrinsic BOLD fluctuations, with feed-forward processing parcels operating at relatively faster timescales compared to those involved in feedback processing (63, 66). In line with this, we hypothesized that cortical parcels with more diffuse thalamic connectivity patterns would also exhibit longer intrinsic timescales. To investigate this, we compared the extent of thalamic connectivity patterns in each cortical parcel to their intrinsic timescale derived from resting-state functional connectivity (Fig. 4E) (63). This analysis revealed a modest correlation between loadings and values, indicating that cortical parcels with focal thalamic connectivity patterns operated at faster timescales during rest. However, this relationship only showed a trending significance when accounting for spatial auto-correlation (Fig. 4F).
Generalized hierarchical variation of the extent of cortical connections within the thalamus in macaques.
Following previous work comparing cortico-thalamic connectivity patterns between humans and macaques (40), we investigated within-thalamus connectivity patterns in macaque monkeys. We hypothesized that the extent of cortical connections within the macaque thalamus would show similarities to the human data, albeit to a lesser extent. To test this, we analyzed tractography data from six post-mortem macaque brains, obtained from 7T diffusion MRI scans. Our results revealed a similar organization of thalamo-cortical connectivity in macaques compared to humans.
We parcellated macaque tractography data to derive connectivity between 128 cortical parcels from the Markov atlas across all ipsilateral thalamic voxels (67). Macaque M1 (area F1; magenta panel) projected to the lateral portion of the thalamus, while DLPFC (area 9/46d; cyan panel) projected to medial and anterior thalamic regions (Fig. 5A). Comparing ED values across thresholds, we observed greater similarity between M1 and DLPFC in macaque compared to humans. We then followed the framework developed in humans to calculate macaque loadings, which accounted for 82% of the variance (Fig. 5B–C).
Fig. 5.
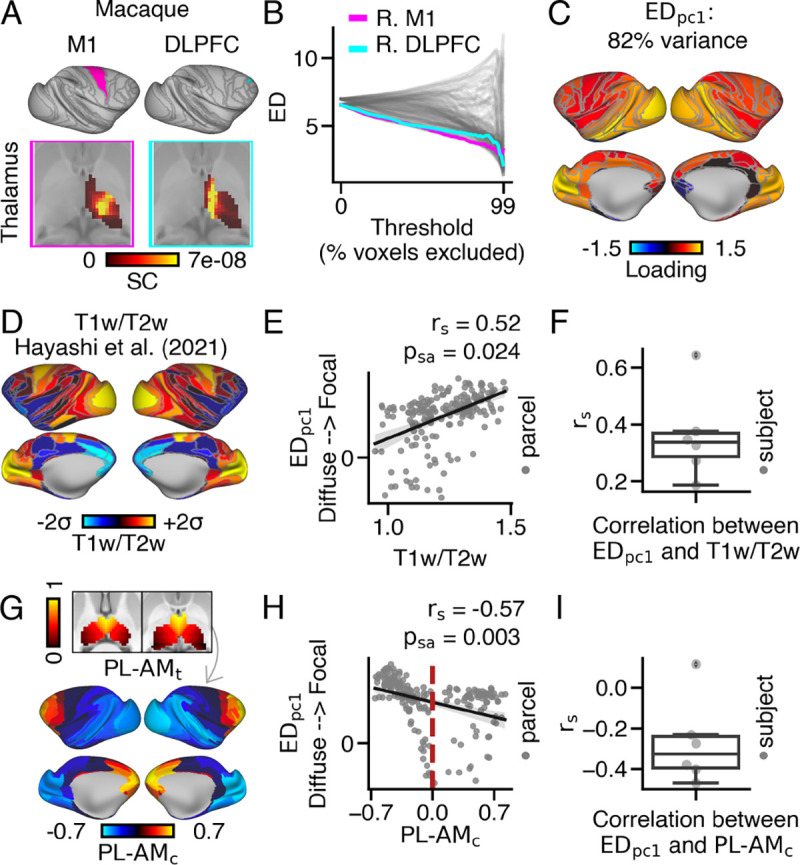
Generalized pattern of cortical variation in the extent of cortical connections within the thalamus observed in macaques. (A) Parcellation of macaque cortex based on the Markov Atlas (67). Exemplar thalamic connectivity patterns for M1 (area F1) and DLPFC (area 9/46d) are displayed in the magenta and cyan panels, respectively. (B) ED matrix. (C) Cortical map showing loadings. (D) Cortical myelin map, calculated by averaging T1w/T2w values across 30 macaque monkeys (68). (E) Across cortex, loadings positively correlated with T1w/T2w values at the group level and (F) at the subject level. (G) Cortical map depicting anatomical coupling with the anteromedial-posterolateral thalamic spatial gradient . Higher values indicate cortical parcels that preferentially couple with anteromedial thalamus . (H) Cortical parcels with higher loadings preferentially coupled with posterolateral thalamus. The red dashed line represents parcels with balanced coupling along the gradient. (I) On average, loadings and value negatively corresponded.
To examine the variation of loadings between sensory and association cortical parcels in macaques, we correlated macaque loadings and group-averaged T1w/T2w values obtained from (68) (Fig. 5D). We observed a strong positive correlation between loadings and T1w/T2w values at the group level (Fig. 5E), which was consistent on average across subjects (mean: 0.36, median: 0.34, ). Surprisingly, the median value was not significantly different from the human data (Fig. 5F; Fig. S30D).
We also conducted further analysis to investigate whether cortical parcels with focal thalamic connectivity patterns in macaques preferentially coupled with the posterolateral thalamus, similar to the findings in humans. Consistent with the human data, macaque loadings showed a strong negative correlation with values at both the group level and the subject-level (mean: −0.27, median: −0.33, , ) Fig. 5G–I). This association was more pronounced compared to other thalamic spatial gradients (Fig. S31). Lastly, the correlation between loadings and values showed a trending difference between humans and macaques, while no significant differences were observed for any other thalamic gradients (Fig. S30E).
The relationship between macaque and was slightly weaker and more nonlinear compared to the human data, likely due to cortical parcels with exceptionally high ED values, resulting in an underestimation of the extent of cortical connections within the thalamus by the measure. Conversely, the measure accurately captured the extent of thalamic connectivity patterns for these cortical parcels (Fig. S30A–C).
Discussion
This study contributes to the rich body of literature investigating the organization of cortico-thalamic systems in humans and non-human primates. By employing dMRI-derived tractography across species, we tested if different cortical areas show differences in the spatial extent of their connections within the primate thalamus. This is critical to establish the anatomical architecture of how information flows within distinct cortico-thalamic systems. Here, we show that thalamic connectivity patterns systematically varied across cortical areas in humans and macaques. Our results implicate distinct tractography motifs corresponding to sensorimotor and association cortico-thalamic circuits. These motifs were consistent across people and generalized in macaques. Collectively, this study offers convergent evidence that different cortical areas exhibit systematic hierarchical variation in how they spatially project onto the thalamus, which may support distinct computations across cortico-thalamic loops.
Spatial properties of thalamic connectivity patterns vary along the cortical hierarchy.
Here we replicate findings from prior tracer and tractography studies, providing confirmation that each cortical area exhibits a distinct pattern of anatomical connectivity within the thalamus (15, 16, 18–20, 25–27, 37, 40). Moreover, this study’s findings are consistent with previous animal studies that demonstrate a correspondence between thalamic organization and the sensory-association cortical hierarchy (5, 46–49, 55). Here we build on this body of work to systematically characterize variation in the extent of cortical connections within the thalamus across the entire cortex. The core innovation here is that we demonstrate that sensory cortical areas exhibit more focal thalamic connectivity patterns relative to association cortical areas. Our findings suggest that the spatial distribution of within-thalamus connectivity patterns is a key distinguishing feature of cortico-thalamic circuits, potentially associated with their roles in sensorimotor and higher-order associative information processing. In line with this notion, other quantitative measures derived from dMRI, including connectivity strength and microstructure, do not exhibit significant variation along the cortical hierarchy.
We offer convergent evidence for this phenomenon by demonstrating that cortical areas that exhibit focal projections target posterolateral thalamus, whereas cortical areas that exhibit diffuse projections generally target anteromedial thalamus (55). This finding is consistent with previous studies showing the organization of thalamic functional connectivity, microstructure, and gene expression along the anteroposterior and mediolateral thalamic axis (16, 21, 56, 69–71). Prior work has shown that axon guidance cues along the anteromedial-posterolateral thalamic gradient shape the topography of thalamo-cortical connections (72). Powell et al. provide insight into the molecular mechanisms that may shape cortex-to-thalamus connectivity patterns. Here, it will be vital to characterize the mechanisms that give rise to hierarchical differences in the spatial extent of within-thalamus connectivity patterns, which may be critical for distinct information flow across cortico-thalamic systems and compromised in neurodevelopmental disorders (73–75).
Building on human quantitative dMRI, we show convergent effects in macaques, which mitigate limitations related to lower resolution, shorter collection time, and motion bias in humans (43). Using macaque dMRI data, previous studies have identified both similarities and differences in cortico-thalamic anatomical connectivity patterns relative to humans (76). Despite notable inter-species differences in many cortical areas, here we present data that support a generalized cortex-wide hierarchical organization of the extent of cortical connections within the thalamus across both humans and macaques. The integration of macaque tractography and tracer data in cortico-thalamic systems remains limited (77, 78), but future studies incorporating tracer data could provide more specific insights into cortico-thalamic system organization by considering directionality. For example, it has been previously suggested that feed-forward non-reciprocal cortex-to-thalamus signals may allow information from segregated cortical pathways to converge within the thalamus (23, 24). Consequently, cortical areas with more spatial extent in their thalamic connectivity may receive a greater number of thalamic feedback projections, perhaps enabling such areas to perform broader computational modulation across distributed circuits. These hypotheses will need to be tested in future animal studies.
In addition to area-level projection patterns onto the thalamus discussed above, dMRI-derived tractography data can address gaps in the non-human primate tracer literature. For instance, it can reveal patterns regarding contralateral cortico-thalamic connections. These connections have received less attention in macaque tracer studies (19, 79, 80), yet hold potential for investigating the influence of cortico-thalamo-cortical circuits on inter-hemispheric communication.
Implications of large-scale cortico-thalamic projection patterns for understanding levels of anatomical architecture.
Cortex-to-thalamus and thalamus-to-cortex neuronal fibers exhibit distinct patterns in their axonal projections (5, 19, 64). We hypothesized these distinct patterns of neuronal connectivity may also be reflected in the patterns of large-scale white matter tract terminations within the thalamus. Specifically, ‘core’ neurons display focal projections to middle cortical layers, while ‘matrix’ neurons exhibit diffuse projections to superficial cortical layers that often span architectonic boundaries (5). Moreover, prefrontal neurons have been observed to exhibit either dense, focal projections to the ipsilateral thalamus or sparse, diffuse projections to bilateral thalamus (19, 81). Therefore, the extent of axonal projections distinguishes both cortical and thalamic fibers within cortico-thalamic systems.
In this study, we show that the extent of cortical terminations within the thalamus distinguishes cortico-thalamic white matter tracts. Furthermore, we linked human neural gene expression and tractography to show that cortical areas with focal and diffuse thalamic connectivity patterns preferentially couple with PVALB-expressing ‘core’ and CALB1-expressing ‘matrix’ thalamus, respectively. This finding highlights a mirrored anatomical principle of variation between individual neuronal fibers and large-scale tracts within cortico-thalamic systems. This finding suggests that corticothalamic white matter tracts may be composed of individual neuronal fibers with similar termination patterns.
This finding aligns with theoretical proposals that hypothesize similar principles governing connectivity at multiple levels of analysis (82, 83). Moreover, it implies that core principles of variation in thalamic fibers provide insights into the properties of large-scale white matter tracts. For instance, thalamic neurons exhibit variations in the extent of their axonal projections across cortical layers (5, 64). Future studies employing dMRI tractography can investigate if this effect extends to the extent of streamline terminations from thalamic nuclei to individual cortical areas.
Additionally, previous studies have shown that cortical projections onto the contralateral thalamus primarily involve non-reciprocal connections (9, 19). We found that cortical areas with stronger contralateral thalamic connectivity display more focal thalamic connectivity patterns across the contralateral thalamus. This suggests that cortical areas may relay information to the opposite hemisphere via feed-forward connections onto the contralateral thalamus.
Interrogating cortico-thalamic anatomical connectivity to better understand the role of the thalamus in shaping brain-wide information flow.
While early studies suggested that the thalamus primarily relays information through parallel and segregated circuits from the sensory periphery, accumulating empirical and computational evidence supports the notion that the thalamus is a crucial integration hub capable of coordinating and sustaining signals across the cortex (11, 12, 49, 84–86). The structural properties of cortico-thalamic circuits invariably constrain the types of computations these circuits can support (6), and prior work has established a relationship between the extent of axonal terminations in cortico-thalamic systems and both feed-forward and feed-back information flow (5, 19). While the present findings do not directly support directional interpretations, our data raise the possibility that diffuse thalamic connectivity patterns may be associated with slower, feedback brain dynamics that may support integrative information transmission, whereas focal thalamic connectivity patterns may be associated with faster, feed-forward brain dynamics that may support the relay of sensory information.
Complementary functional neuroimaging studies have revealed areas of integration and segregation within the human thalamus (58, 87, 88). The anatomical basis for thalamic integration is not fully understood, but it has been proposed that overlapping terminations may contribute to this process (22, 23, 37). It is hypothesized that overlapping thalamic connections emerging from segregated cortical circuits may enable the integration of information across different cortical areas (41). In this study, we demonstrate that certain cortical areas, such as the anterior cingulate and precuneus, exhibit diffuse thalamic connectivity, allowing them to impact thalamo-cortical information in a distributed manner. Specifically, the anterior cingulate demonstrates widespread connections across the thalamus, aligning with observations by Phillips et al. that area 24 exhibits diffuse anatomical terminations across the mediodorsal nucleus of the thalamus (37). This property has been hypothesized to support the integration of signals within the prefrontal cortex (41).
Circuits connecting the cortex, thalamus, and the basal ganglia have also been implicated in integrative functions (23, 89). The patterns of anatomical connections between the basal ganglia and thalamus may also exhibit variation in their spatial properties. Future studies can better elucidate the variation in the spatial properties of anatomical connections between the thalamus and basal ganglia and how such variation may correspond to integrated vs. segregated cortico-basal ganglia-thalamo-cortical functional interactions
Our findings indicate that cortical areas with diffuse thalamic connectivity patterns couple to both anteromedial and posterolateral thalamic subregions. Surprisingly, these results did not support the hypothesis that ‘higher-order’ thalamic nuclei preferentially couple with cortical areas displaying diffuse thalamic connectivity. Instead, these nuclei display more balanced coupling to cortical areas with both focal and diffuse thalamic connectivity patterns. Previous studies have shown that ‘higher-order’ thalamic nuclei receive input from cortical and subcortical regions (90, 91). This could be one mechanism for how the integration of higher-order and first-order signals in the thalamus may support complex cognitive functions (92).
Our findings indicate that cortical areas with diffuse thalamic connectivity patterns are coupled to both anteromedial and posterolateral thalamic subregions. Surprisingly, these results did not support the hypothesis that ‘higher-order’ thalamic nuclei preferentially couple with cortical areas displaying diffuse thalamic connectivity. Instead, these nuclei showed more balanced coupling to cortical areas with both focal and diffuse thalamic connectivity patterns. Previous studies have demonstrated that ‘higher-order’ thalamic nuclei receive input from cortical and subcortical regions (90, 91). This mechanism may explain how the integration of higher-order and first-order signals in the thalamus supports complex cognitive functions (92).
Although we did not directly compare cortico-thalamic structure and function in this study, we offer an anatomical framework to complement the findings of a previous investigation on cortico-thalamic functional coupling (62). Muller et al. (62) examined cortico-thalamic BOLD-derived functional connectivity and demonstrated that sensory cortical areas exhibited stronger functional coupling with ‘core’ thalamus, whereas association cortical areas exhibited stronger functional coupling with ‘matrix’ thalamus, and this dichotomy was found to align with patterns of whole-brain dynamics. However, the specific ways in which thalamocortical anatomical connectivity constraints may shape functional connectivity remain unknown. A possible future direction would be to investigate how thalamo-cortical anatomical connections contribute to both intra- and inter-hemispheric functional interactions.
Lastly, these data imply that cortical areas with diffuse thalamic connectivity patterns may selectively overlap with thalamic subregions implicated in functional integration and multimodal cognitive processes (58, 88). This observation warrants future investigations in combination with functional modalities.
Study limitations.
While powerful, probabilistic tractography has notable limitations, such as the possibility of producing false positives and lacking directionality information (93, 94). In this study, we did not find any specific confounding factors systematically influencing the patterns of thalamic connectivity derived from tractography. However, we did observe that cortical curvature and sulcal depth were positively correlated with an increased mean streamline count, potentially reflecting gyral bias.
Furthermore, we observed significant individual variation in thalamic connectivity patterns. Notably, we identified biologically unlikely tractography patterns in some subjects. The nature of these differences, whether they represent true individual variation or false positive connections, remains unclear, but it is likely a combination of both. While these variations did not appear to produce a spurious difference in the extent of cortical connections within the thalamus between sensory and association cortical areas, these data are consistent with previous reports suggesting that interpretations of tractography data have inherent limitations (e.g., (93, 94)).
Importantly, tractography-based anatomical connectivity has shown strong agreement with invasive tract tracing studies conducted in monkeys, providing validation for its use (43, 95–101). However, it is worth noting that the majority of these investigations have primarily focused on cortico-cortical connections and connectivity at the areal level. In comparison, studies directly assessing the correspondence of tractography-derived connectivity with tracer-derived connectivity in thalamo-cortical systems are limited (94, 102). Consequently, future research should prioritize examining the correspondence between tracer-based and tractography-derived anatomical terminations within subcortical gray matter structures while also investigating factors that may contribute to the presence of biologically implausible connections across different individuals. This is vital for a comprehensive understanding of inter-individual variation in anatomical connectivity and its implications for cognition and behavior in both health and disease.
Conclusions
The thalamus plays a key role in various neural functions involving multiple sensory modalities (8, 41, 103). Dysfunction of the thalamus has been linked to severe neuropsychiatric disorders such as psychosis (104–109), and the symptoms of these disorders have been associated with abnormal anatomical cortico-thalamic connectivity (73–75). However, our understanding of the contribution of the thalamus to healthy whole-brain information transmission and its dysfunction in diseases has been hindered by limited knowledge of the underlying circuitry, especially in humans (6, 110).
Since the first in vivo examinations of cortico-thalamic anatomy in humans (35, 36), neuroimaging studies have made significant progress in mapping thalamo-cortical circuitry and investigating its role in shaping whole-brain functional interactions (54, 111). This study provides quantitative evidence that the spatial properties of within-thalamus anatomical connectivity patterns exhibit variation across cortical areas, following established hierarchical principles of cortical organization, which may reflect variations associated with different types of information processing. Here we demonstrate that an in-depth investigation of corticothalamic anatomical circuitry can offer insights into how the thalamus supports segregated and integrated information flow throughout the brain, which may underlie the computations enabling higher-order cognition in humans.
Experimental Procedures
Human Dataset and diffusion processing pipeline.
We obtained minimally pre-processed 1.25 mm isotropic 3T dMRI data for 828 healthy adults from the Washington University – Minnesota (WU-Min) Human Connectome Project (HCP). The imaging protocol details can be found at the following link: https://protocols.humanconnectome.org/HCP/3T/imaging-protocols.html (112, 113).
To generate dMRI-derived probabilistic tractography data, we utilized the Quantitative Neuroimaging Environment & Toolbox (QuNex) (114). Specifically, FSL’s Bedpostx was employed to estimate diffusion parameters, including up to three fiber orientations per voxel, using a model-based deconvolution approach with zeppelins (33, 115, 116). The parameters used were as follows: burn-in period of 3000, 1250 jumps (sampled every 25), automatic relevance determination, and Rician noise. We then obtained whole-brain probabilistic tractography using FSL’s probtrackx (31, 36, 117). We performed dense gray-ordinate-by-gray-ordinate streamline connectivity, seeding from each white ordinate 3000 times (shown in all figures unless otherwise specified), and from each gray-ordinate 10,000 times (Fig. S20) with distance correction. Streamline length data was also extracted.
We then performed several processing steps on the FSL-generated dense data (Fig. S1). To account for inter-subject streamline count differences, dense streamline count data were waytotal normalized. We further applied log normalization to account for distance effects. Each subject’s data were then parcellated along one dimension, averaging the streamline count between all grey-ordinated with a cortical parcel. The partition used was defined by Ji et al. (45), and the analysis was restricted to the 360 symmetrical bilateral cortical parcels defined by Glasser et al. (118). These data were masked with the thalamic gray matter mask used during tractography, which consisted of 2539 voxels (Fig. S22). Group-level cortical-parcel by dense thalamic-voxel streamline count connectivity matrices were generated by averaging data across participants. In some visualizations, standardized streamline counts were shown, which were z-scored for each cortical parcel. Finally, before group averaging, an alternative processing step was performed which consisted of regressing cortical curvature from streamline counts for each subject. The residuals from this regression were then group-averaged (Fig. S1, step 5) and used for supplementary analyses.
We replicated our findings using multiple functional and structural thalamic masks derived from different atlases: the Yeo 2011 parcellation (119) (https://github.com/ryraut/thalamic-parcellation), Melbourne Atlas (120), and the Morel thalamic atlas (53) (Fig. S22). Furthermore, we replicated the main results using dense ED values (Fig. S21) and an alternative seed strategy, which consisted of seeding each white-ordinate 10,000 times (Fig. S20).
To assess microstructural properties, we extracted fractional anisotropy (Fa) and mean diffusivity (Md) using FSL’s DTIFIT. We then examined the overlap between each voxel’s Fa and Md values and its streamline count to each cortical parcel (Fig. S11). We compared the cortical variation of this overlap with loadings and measures of cortical geometry and hierarchy.
Human BOLD acquisition and processing.
For each subject, we obtained four runs of minimally preprocessed blood-oxygen-level-dependent (BOLD) resting-state data from the HCP (Atlas_MSMAll_hp2000_clean). The first 100 frames of each BOLD time series were dropped, and the data were demeaned. The four resting-state scans were concatenated in the order of 2-1-4-3. These data were parcellated using the partition defined by Ji et al. (45), and we included only the 360 cortical parcels defined by Glasser et al. (118). Functional connectivity was computed by calculating pairwise Pearson correlations between the time series of each cortical parcel, resulting in a parcellated functional connectivity matrix. This matrix was then used as input into a principal component analysis (PCA) to derive the first and second principal functional gradients. See ‘Deriving cortical gradients’ for more details.
Macaque Dataset and diffusion processing pipeline.
We obtained diffusion-weighted 7T MRI data with 0.6 mm isotropic resolution from a previously collected dataset of six postmortem macaques (4–16 years old), as described in previous work (121, 122). These data are publicly available through the PRIMatE Data Exchange (PRIME-DE) repository (http://fcon_1000.projects.nitrc.org/indi/PRIME/oxford2.html) (123). Nonlinear surface transformation to macaque F99 standard space was performed, as described elsewhere (124, 125). Subcortical structures were registered to F99 standard space using FNIRT and templates from the HCP Non-Human Primate Minimal Preprocessing Pipelines (68, 113).
Connectivity matrices for the macaques were derived using FSL’s Bedpostx and Probtrackx pipeline. We seeded each white-ordinate 3,000 times to obtain a gray-ordinate-by-gray-ordinate connectivity matrix. The parameters used were the same as those used for tractography in the human data, with the exception that no distance correction was applied and the step length was reduced from 0.5 to 0.2. The macaque data were waytotal and log normalized, and then parcellated using the Markov 2014 atlas (67, 126). This workflow resulted in a parcel-by-dense (128×71401) connectivity matrix for each macaque. These data were masked with the thalamic mask used for tractography seeding, which consisted of 1539 voxels (649 right; 890 left), and data were then averaged to create a group matrix.
Framework to quantify the spread of cortico-thalamic connectivity patterns via Euclidean distance (ED).
Commonly used quantitative measures derived from tractography studies lack consideration of the spatial properties of anatomical terminations, such as the number of streamlines or streamline length (34). Developing a spatially-informed quantitative tractography measure presents methodological challenges, particularly in probabilistic tractography where lower streamline counts are less likely to represent a white matter connection compared to higher streamline counts. Thresholding is a common approach to address this limitation by excluding connections with lower streamline counts, but determining an appropriate threshold remains uncertain (32, 34). In this study, we addressed this challenge by calculating the measure while sampling the entire spectrum of possible thresholds.
Our thresholding framework utilizes a dense, weighted connectivity matrix as input. We iteratively exclude voxels with lower streamline counts for each cortical parcel based on proportional thresholding, ensuring an equal proportion of connections (i.e., the same number of included voxels) for each parcel (127). At each threshold, ED is computed on the thresholded connectivity values, resulting in a matrix of ED values for each brain area across thresholds. This matrix is then subjected to principal component analysis (PCA) to derive a single loading for each brain area. While alternative thresholding approaches have been proposed, this framework optimizes the examination of spatial patterns by proportionally thresholding the data, enabling equitable sampling of each cortical area’s spatial pattern of connections. This approach controls for inter-areal differences in anatomical connection strength that could bias ED estimates. Subsequently, PCA is used to condense multiple ED measurements across thresholds into a single value, maximizing variation across brain areas. This framework was used to calculate two spatially-informed measures: ED (how spread out is the pattern?) and isotropy (is the spread even in all direction?).
First, we used tractography-derived cortical parcel to thalamic voxel connectivity data from 828 healthy adults from the Human Connectome Project (HCP) (Fig. 1A). We then iteratively thresholded these data by excluding 0% to 99% of thalamic voxels with the lowest streamline counts for each cortical parcel (Fig. 1B). For each threshol, only surviving thalamic voxels were used in the ED calculation. This resulted in an ED value for each threshold for each cortical parcel (Fig. 1C). The pairwise ED calculation was performed using the following equation:
| (1) |
Where:
represents the average pairwise ED,
is the number of surviving thalamic voxels,
and are indices of thalamic voxels,
is the ED between thalamic voxels and .
The Euclidean distance between two thalamic voxels, , can be computed using the formula:
| (2) |
where and represent the coordinates of the thalamic voxels and in 2mm space. This calculation is performed for each cortical parcel across its surviving thalamic voxels (i.e., voxels with streamline counts above the cutoff) for each threshold, generating a cortical parcel-by-threshold matrix with ED values. The procedure is performed separately for the left and right thalamus. In the case of bilateral connectivity, the ED values for each threshold are summed across the left and right thalamus.
Additionally, we can calculate the relative ED (rED) to compare brain areas of different sizes:
| (3) |
Where:
denotes the relative ED,
represents the ED value for each cortical parcel at threshold ,
represents the ED value for each cortical parcel at threshold 1 (when no threshold is applied and no voxels are excluded).
This relative measure allows for a direct comparison of ED between target brain areas of different sizes or shapes (e.g., left and right thalamus), across subjects, and across species. In this study, due to the similarity between the left and right thalamus, and loadings were nearly identical (Fig. S13).
Measure calculations.
loading calculation:
Principal component analysis (PCA) using Singular Value Decomposition was performed on the threshold by cortical parcel (100×360) ED matrix. The resulting first principal component (PC1) represents the dominant spatial pattern of Euclidean distance (ED) variation across cortical parcels. is a vector containing the loadings of PC1 for each of the 360 cortical parcels. The loadings were calculated as:
| (4) |
Where:
is the first PC’s eigenvector for cortical parcel c,
is the first PC’s eigenvalue.
This procedure was also performed for group-averaged dense cortico-thalamic connectivity data to examine the spread of thalamic connectivity for 59,000 cortical vertices (Fig. S21).
calculation:
represents the population standard deviation of ED across thresholds for each cortical parcel. It was computed using the following equation:
| (5) |
Where:
is the standard deviation of ED values across thresholds for cortical parcel ,
is the total number of thresholds (in this case 100),
is the ED of surviving thalamic voxels for parcel at threshold ,
is the mean ED for cortical parcel across the thresholds.
In addition to the standard deviation of ED across all thresholds, we also calculated the standard deviation (STD) of ED across specific ranges of thresholds (as shown in Fig. S6). We then compared these values to , T1w/T2w, and measures.
Streamline count (SC) mean calculation and analysis:
The mean streamline count (Mean SC) within the thalamus was computed for each cortical parcel using the formula:
| (6) |
Where:
represents the square root normalized mean of streamline counts for cortical parcel ,
is the index of the thalamic voxel,
is the number of thalamic voxels,
is the streamline count between cortical parcel and thalamic voxel .
We then correlated Mean SC with , T1w/T2w, , and average streamline length values. These analyses were performed separately for the left and right thalamic voxels for each cortical parcel.
Streamline length calculation and analysis:
The average streamline length (1) for each cortical parcel was computed using the formula:
| (7) |
Where:
represents the average streamline length for cortical parcel across all thalamic voxels,
is the index of the thalamic voxel,
is the number of thalamic voxels,
is the average length of streamlines between cortical parcel and thalamic voxel .
Streamline lengths were obtained from FSL’s probtrackx using the –ompl flag. Separate calculations were performed for the left and right thalamic voxels for each cortical parcel.
Isotropy () calculation:
To quantify the isotropy of thalamic connectivity patterns for each cortical parcel, we modified the thresholding framework. The following equation was used:
| (8) |
Here, values are derived from the covariance matrix calculated on the x, y, and z coordinates of surviving thalamic voxels for each threshold and cortical parcel . Separate calculations were performed for the left and right thalamic voxels for each cortical parcel. This matrix was then subjected to PCA, and the loadings from the first principal component (PC1) were calculated as described in the ED loading calculation section.
score calculation:
PCA was performed on the cortical parcel by threshold (360×100) ED matrix. The PC1 scores for each cortical parcel were computed using the equation:
| (9) |
Here, represents the PC1 score for cortical parcel , which was obtained from the PCA on the cortical parcel by threshold ED matrix , and is the eigenvector corresponding to the first principal component for cortical parcel .
Mean ED calculation:
The average Euclidean distance (ED) across thresholds was computed for each cortical parcel by taking the arithmetic mean of the ED values. The calculation was performed using the following equation:
| (10) |
Where:
represents the mean ED for cortical parcel across thresholds,
refers to the total number of thresholds (in this study, we used 100),
denotes the index of the threshold,
represents the ED of surviving thalamic voxels for parcel at threshold .
In addition to the mean ED across all thresholds, we also calculated the mean ED across ranges of thresholds (as shown in Fig. S6) and compared these values to , T1w/T2w, and values.
Weighted Mean ED calculation:
We applied a weighting scheme to calculate the weighted mean ED. The weights were assigned based on the conservativeness of each threshold, with more conservative thresholds receiving higher weights. The calculation was performed using the following equations:
| (11) |
| (12) |
| (13) |
Where:
represents the weighted mean ED for cortical parcel across thresholds,
refers to the total number of thresholds (in this study, we used 100),
denotes the index of the threshold,
represents the weight for the threshold.
The weight assigned to each threshold is determined by the exponential function, with more conservative thresholds having higher weights. Specifically, a threshold of , where no voxels are excluded, has a weight of zero, while a threshold of , where 99% of voxels are excluded, has a weight of 1.
Streamline count (SC) skewness calculation:
The robust skewness of streamline counts (SCs) within the thalamus was computed for each cortical parcel using the mean-median difference standardized by the absolute deviation. The calculation was performed using the following equation:
| (14) |
Where:
represents the robust skewness of SCs for cortical parcel ,
refers to the mean of square-root normalized streamline counts for cortical parcel ,
median denotes the median of streamline counts between cortical parcel and thalamic voxel ,
represents the index of the thalamic voxel,
is the number of thalamic voxels.
This calculation was performed separately for the left and right thalamic voxels for each cortical parcel.
Weighted Nuclei Mean SC calculation:
The mean streamline count between each cortical parcel and each thalamic nucleus was weighted by the volume of the nucleus. These weighted values were then summed across thalamic nuclei. The calculation was performed using the following equation:
| (15) |
Where:
represents the standardized mean streamline count across all thalamic nuclei, weighted by the volume of each nucleus ,
represents the index of the thalamic nucleus,
represents the total number of thalamic nuclei from the Morel thalamic atlas ,
, represents mean streamline count between cortical parcel and thalamic nucleus , standardized within cortical parcels.
Control analyses.
Cortical maps for various surface features, including cortical thickness, curvature, sulcal depth, bias field, edge distortion, spherical distortion, and areal distortion, were obtained from the HCP and group-averaged across subjects. The surface area of each cortical parcel from the Glasser et al., 2013 atlas was computed as the number of vertices within each parcel. These cortical maps were then examined for associations with loadings (Fig. S12).
Additionally, fractional anisotropy (Fa) and mean diffusivity (Md) values were extracted for each subject using FSL’s DTIFIT. The correlation between the streamline counts of each cortical parcel within the thalamus and their corresponding thalamic Fa and Md values was computed. These correlations were then compared to loadings of each cortical parcel (Fig. S11).
Network analysis.
The network assignments for the 360 bilateral cortical parcels were based on the work by Ji et al. (45). The parcels were categorized into 12 functionally-defined networks, including sensory networks (somatomotor, SMN; visual 1, VIS1; visual 2, VIS2; auditory, AUD) and association networks (cingulo-opercular, CON; default-mode, DMN; dorsal attention, DAN; frontoparietal network, FPN; language, LAN; posterior multimodal, PMM; ventral multimodal, VMM; orbito-affective, ORA) (Fig. 2A). loadings were averaged within these 12 networks and within the sensory and association networks for each subject (Fig. 2B–C). The averaged loadings for the sensory and association networks were compared across subjects using a Wilcoxon signed-rank test (Fig. 2C).
Cortical gradients.
To capture systematic variation across the cortex, we derived multiple cortical gradients and examined their similarity to loadings.
T1w/T2w maps, reflecting cortical myelin content (128), were obtained from the HCP dataset and group-averaged across 828 subjects. Similarly, group-averaged dense T1w/T2w maps from 30 macaques were acquired (https://balsa.wustl.edu/study/Klr0B) (68). These maps were also parcellated using respective atlases.
Functional cortical gradients were derived from group-averaged and individual-level () resting-state functional cortical connectivity matrices. After thresholding to include the top 20% of connections, PCA was performed, and the loadings from the first () and second () principal components were calculated, following previous work (52, 129).
T1w/T2w values and loadings serve as quantitative measures of cortical hierarchy, with sensory cortical parcels showing higher T1w/T2w content and loadings compared to association cortical parcels. Similarity between individual-level T1w/T2w maps and maps and the group maps highly correlated across subjects (see SI Appendix, Fig. S17).
loadings represent the sensory-association-motor cortical hierarchy, indicating functional specialization. (52).
To assess the anteroposterior cortical gradient, we calculated the Cartesian distance between each cortical parcel and the ipsilateral V1, separately for human and macaque data.
Non-parametric method for assessing correspondence of cortical brain maps.
We assessed the correspondence between cortical brain maps using Spearman correlations and determined the significance of each correlation using a non-parametric approach. To preserve spatial autocorrelation, we generated 1000 surrogate maps for each target brain map (e.g., T1w/T2w values, loadings) using brainSMASH with default parameters (44). Specifically, 500 surrogate maps were generated for the left cortex and 500 for the right cortex. These surrogates were then mirrored contralaterally to create bilateral surrogate maps. We correlated these bilateral surrogate maps with the empirical cortical map (e.g., loadings) to generate a null distribution. Non-parametric p-values were calculated by dividing the number of surrogate maps with a higher correlation coefficient than the empirical value by the total number of surrogates generated (i.e., 1000).
For dense maps, surrogates were generated separately for the left and right cortex using resampling. We used default parameters with the exception of the knn parameter, which was set to the number of vertices in the brain map based on optimization (130).
Non-parametric method for assessing differences between sensory and association cortical parcels.
To determine if a value significantly differed between sensory and association cortical parcels, we employed a non-parametric approach. We estimated a p-value by calculating the median value of sensory and association regions from 1000 surrogate maps generated from the target cortical map. The p-value was computed by dividing the number of surrogate maps with a higher absolute difference between sensory and association regions compared to the empirical value by the total number of surrogates generated (Fig. S19E).
Individual variability.
We also investigated the variability of loadings across individuals and its relationship with cortical connectivity patterns. To quantify the inter-subject variability of , we calculated the coefficient of variation for each cortical parcel across all subjects (Fig. S18A). To test the hypothesis that the variability of loadings would be higher in association compared to sensory cortical parcels, we examined the standard deviation of loadings across subjects for each cortical parcel (Fig. S18A).
We found that variability did not significantly correspond with T1w/T2w values but it did correlate with loadings (Fig. S19B–C). Moreover, we observed higher variability of loadings in association cortical parcels compared to sensory cortical parcels (Fig. S19D–E). Interestingly, the variability of was strongly associated with Mean SC , indicating that cortical parcels with greater individual variability in also exhibited weaker anatomical connectivity within the thalamus (Fig. S18B). Additionally, the variability of loadings across subjects significantly correlated with group-averaged loadings, even after controlling for group-averaged Mean SC (Fig. S18C).
We previously observed low hierarchical variation in subject-level loadings, as indicated by weak correlations with T1w/T2w values and loadings in some subjects (Fig. 2H,I). To investigate this further, we examined individual subjects’ thalamic connectivity patterns to understand why some subjects exhibited a weak relationship between and T1w/T2w and values. Notably, visual area 1 (V1) displayed higher variability across subjects compared to other sensorimotor areas, such as M1 (Fig. S19A), despite having a high average Mean SC value (Fig. S10F). Moreover, the primary axis of variation in individual subjects, derived from the first principal component (PC) of loadings across 828 subjects, exhibited strong loadings on bilateral visual cortices, as well as right posterior parietal and temporal cortices (Fig. S19F–H).
Considering existing literature on tract tracing, we expected V1 streamlines to terminate in visual thalamic areas such as the lateral geniculate nucleus and pulvinar in the posterior thalamus (131). While some subjects exhibited V1 terminations in the visual thalamus, as exemplified by subject 1, others displayed terminations spreading along the anterior and dorsal axis of the thalamus, as seen in subject 2 (Fig. S18D). To assess the generalizability of this observation, we calculated the ratio of streamline terminations in the visual thalamus relative to terminations outside of the visual thalamus for the right V1. A higher ratio indicated a larger proportion of V1 streamlines terminating in the visual thalamus, including the pulvinar and lateral geniculate nucleus (Fig. S18E). As we anticipated V1 terminations primarily in the pulvinar and lateral geniculate nucleus, subjects with higher ratios exhibited more biologically plausible V1 termination patterns. All subjects demonstrated right V1 terminations preferentially coupled to the pulvinar and lateral geniculate nucleus (ratios > 1). However, many subjects had ratios close to 1, indicating a substantial portion of streamline terminations outside of the visual thalamus. A strong negative correlation was observed between each subject’s right V1 loading and their right V1 SC ratio, confirming that subjects with more diffuse thalamic connectivity patterns from the right V1 had a greater number of terminations outside the visual thalamus (Fig. S18E).
Finally, we investigated the hypothesis that V1 terminations outside of the expected thalamic nuclei could undermine the correspondence between and the T1w/T2w and cortical maps. To assess this hypothesis specifically for right V1, we compared each subject’s ratio of streamline counts between visual and nonvisual thalamic regions to their respective Spearman rho values between their loadings and cortical myelin (; purple) and the principal functional gradient (; green) (Fig. S18F). We observed a weak to moderate positive correlation between these variables, indicating that subjects with weaker correspondence between and the T1w/T2w and cortical maps also had more right V1 terminations outside of the visual thalamus.
Thalamic nuclei segmentation.
Thalamic nuclei were defined using the Morel histological atlas (53), resampled to 2mm Montreal Neurological Institute (MNI) space and converted to cifti format (Fig. 3A). Each thalamic voxel was assigned to one of the 28 thalamic nuclei based on the highest scaled mask value. The sPF nucleus from the Morel atlas was combined with the PF nucleus as their voxels overlapped. Thalamic nuclei were further categorized into posterior, medial, lateral, and anterior subdivisions (132), and some were designated as higher-order or first-order (59) or primary, secondary, and tertiary (56) based on prior work. The complete list of 28 thalamic nuclei, along with their abbreviations, is provided in Table 1. The volume of each nucleus was determined by counting the number of 2mm thalamic voxels assigned to it Table 1. The volume for each nucleus was calculated by counting the number of 2mm thalamic voxels assigned to each nucleus Table. 1.
For each cortical parcel, we computed the mean streamline count across thalamic voxels within each thalamic nucleus. This was performed for each subject, resulting in a cortical parcel by thalamic nucleus (360×28) Mean SC connectivity matrix. The matrix was then averaged across all subjects and z-scored to visualize the cortical connectivity patterns within each thalamic nucleus (Fig. 3B). The Mean SC matrix is organized along the y-axis such that cortical parcels located at the bottom exhibit lower average loadings, indicating more diffuse thalamic connectivity patterns.
Subsequently, each subject’s loadings were correlated with the Mean SC values of each cortical parcel for each thalamic nucleus, resulting in 28 rho values per subject (Fig. 3C). A positive rho value indicates that cortical parcels with more focal thalamic connectivity patterns have stronger connectivity (higher Mean SC) to a specific nucleus, while a negative rho value indicates that cortical parcels with more diffuse thalamic connectivity patterns exhibit stronger connectivity to a given thalamic nucleus.
To assess the significance of differences between subject-level rho values, we conducted a Friedman test to compare the averaged rho values between and Mean SC across posterior, lateral, anterior, and medial thalamic nuclei. Post-hoc analyses were performed using the Wilcoxon–Nemenyi–McDonald–Thompson test, which corrected for family-wise error (Fig. 3C). A similar procedure was conducted to examine the differences in average subject-level rho values between and Mean SC for primary, secondary, and tertiary nuclei (56) (Fig. S25). Furthermore, a two-sided Wilcoxon signed-rank test was employed to determine the significance of differences between subject-level rho values for first-order and higher-order thalamic nuclei (Fig. 3D). Additionally, we explored correlations between cortical Mean SCs for each thalamic nucleus and the minor and major subdivisions of thalamic nuclei (Fig. 1Suppl); however, none of these comparisons survived correction for multiple comparisons using the Holm-Bonferroni correction.
Cartesian thalamic gradient calculation and analysis.
To capture thalamic anatomical coupling along continuous gradients, we examined the overlap between each cortical parcel’s streamline count and Cartesian spatial gradients. We correlated each voxel’s streamline count and position along each thalamic spatial gradient for each cortical area. Specifically, the anteroposterior and dorsoventral gradients were defined by the Y and Z coordinates and , respectively. The mediolateral gradient was determined by the distance from the cortical midline.
First, we calculated the distance to the cortical midline using the formula:
| (16) |
Where:
represents the distance to the cortical midline for thalamic voxel ,
is the coordinate of each thalamic voxel,
median is the median coordinate across all thalamic voxels.
, represents mean streamline count between cortical parcel and thalamic nucleus , standardized within cortical parcels.
Subsequently, we computed the distance to the thalamic midline with the equation:
| (17) |
Where:
indicates the position of each thalamic voxel along the mediolateral thalamic axis (i.e., the distance between the thalamic voxel and the medial part of the thalamus),
represents the distance to the midline for each thalamic voxel,
is the distance between the midline and the most medial portion of the thalamus corresponding to the thalamic voxel’s Y-axis position,
refers to the coordinate of a given thalamic voxel,
represents the indices of thalamic voxels that share the same coordinate as the thalamic voxel at position .
By subtracting the distance to the midline thalamus from each thalamic voxel’s distance to the cortical midline, we obtained the mediolateral thalamic gradient. See SI Appendix to view thalamic gradients (Fig. S28).
We also examined combined thalamic gradients that integrated the anteroposterior, mediolateral, and dorsoventral gradients. Firstly, we min-max transformed the and values to scale them between 0 and 1. Then, each thalamic voxel’s position along six thalamic spatial gradients following the equations:
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
Where:
denotes index of thalamic voxel,
: anterodorsal-posteroventral gradient,
: mediodorsal-lateroventral gradient,
: anteromedial-posterolateral gradient,
: anterolateral-posteromedial gradient,
: anteroventral-posterodorsal gradient,
: medioventral-laterodorsal gradient.
These values were also min-max scaled between 0 and 1 (see Fig. S28 to view the thalamic gradients). Using the same overlap procedure described earlier, we generated six cortical maps representing the overlap with each of the six combined thalamic gradients and compared these maps to the empirical cortical map (Fig. S28). We performed this procedure for both human and macaque data (see Fig. S31 for the macaque results).
Furthermore, we computed the mediolateral thalamic gradient based on the distance from the midline and re-evaluated the correlation between loadings and the , and thalamic gradients. These findings largely mirrored the main text results, with the anteromedial-posterolateral thalamus showing the strongest relationship with loadings (Fig. S27). However, since the thalamus is slightly oblique to the cortical midline, the distance to the midline had a stronger correspondence with the anteroposterior thalamic axis compared to the distance to midline thalamus (Fig. S27A). Therefore, we utilized the distance to midline thalamus to quantify the mediolateral thalamic spatial gradient in the main text.
The median correlation coefficient (rho) between ipsilateral loadings and T1w/T2w values, as well as the overlap across thalamic spatial gradients, was compared between humans and macaques using an independent two-sample t-test (Fig. S30D). Additionally, a 2-way analysis of variance (ANOVA) was conducted to compare the rho values between loadings and overlap across thalamic spatial gradients between the two species. The residuals of the ANOVA model were assessed for normal distribution using a QQ plot. Both species exhibited equal variances (Bartlett’s test; , but the gradients, despite having the same sample size, showed unequal variances (Bartlett’s test; ). To avoid introducing an artificial interaction between gradients and species, the sign of the rho values between loadings and overlap across the mediolateral gradient was flipped prior to conducting the statistical tests. Post-hoc Tukey’s Honestly Significant Difference (HSD) tests were subsequently performed (Fig. S30E).
PVALB and CALB1 thalamic gradient calculation and analysis.
The thalamic gradient of the relative mRNA levels of Calbindin (CALB1) and Parvalbumin (PVALB) () was obtained from the Allen Brain Atlas and downloaded from https://github.com/macshine/corematrix. This gradient was derived using mRNA expression probes and reflects the expression levels of PVALB and CALB1 in the thalamus. Cooler values on the gradient indicate higher relative expression of PVALB, associated with the ‘core’ thalamus, while warmer values indicate higher relative expression of CALB1, associated with the ‘matrix’ thalamus (Fig. 4A). We also correlated the gradient with the anteromedial thalamic gradient (Fig. 4B).
To determine the spatial overlap between thalamic anatomical connectivity patterns of each cortical parcel and ‘core’ and ‘matrix’ thalamic subpopulations, we performed a correlation analysis between the gradient and the thalamic streamline counts for each cortical parcel (see Fig. S26 for overlap procedure). This analysis was limited to voxels that were common between the map and the thalamic mask used for tractography. Only voxels with PVALB-CALB1 and streamline count data were included (1,684 bilateral thalamic voxels). The resulting cortical map () displayed a single correlation coefficient () value for each cortical parcel, where cooler values indicated a greater overlap with PVALB-expressing thalamic neurons, and warmer values indicated a greater overlap with CALB1-expressing thalamic neurons (Fig. 4C). Subsequently, we correlated the cortical map with the cortical map (Fig. 4D).
Intrinsic timescale.
To estimate the intrinsic timescale, we conducted an autocorrelation analysis using BOLD functional connectivity data from the Human Connectome Project (HCP) (133). The data were obtained from Ito et al. (2020) (https://github.com/ColeLab/hierarchy2020) (63). For each cortical parcel, an exponential decay function was fitted to the HCP data using the equation:
| (24) |
Where:
represents the exponential decay function for each cortical parcel ,
is a scaling factor,
is an offset,
denotes the rate of decay (i.e., intrinsic timescale),
represents the time lag (we used a lag of 100 time-points.
The model was fit individually for each cortical parcel using the ‘Trust Region Reflective’ algorithm (scipy.optimize.curvefit), and the data were standardized. Subsequently, the parcellated dense values were correlated with values
Visualization.
All cortical brainmaps were generated using Connectome Workbench. Subcortical axial visualization were generated using Nilearn Plotting in python. Neuroimaging files will be made available on the Brain Analysis Library of Spatial maps and Atlases (BALSA) website.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Jie Lisa Ji, Grega Repovš, Jure Demsar, and Takuya Ito for assistance with data processing and analysis and Amy F.T. Arnsten, Jane R. Taylor, John H. Krystal, Maxwell Shinn, Rachel Cooper, Jacob A. Miller, and Warren W. Pettine for helpful discussions. This work was supported by the Gruber Foundation (AMH) and the National Institute of Mental Health (Grant Nos. U01 MH121766-03, R01 MH112189) (AA). Diffusion data collection and sharing for this project was provided by the Human Connectome Project (HCP) and the PRIMatE Data Exchange (PRIME-DE).
Data and Code Availability.
Neuroimaging files used in this study will be made available on the Brain Analysis Library of Spatial maps and Atlases (BALSA) website. The 1mm Morel thalamic atlas was obtained elsewhere with permission (53). As such, we cannot provide the thalamic segmentation files directly, but we can provide the code to create the segmentation for Morel nuclei in 2mm space. All code related to this study will be made publicly available on BitBucket. All analyses were implemented using Python (version 3.10) and the following packages were used: numpy v1.21.2 (134), pandas v1.4.4 (135), scipy v1.10.1 (136), nibabel v3.2.1 (https://zenodo.org/record/7795644), seaborn v0.12.2 (137), sklearn v0.10.0 (138), matplotlib v3.4.3 (139), wbplot (https://github.com/jbburt/wbplot), pingouin v0.5.3 (https://pingouin-stats.org/build/html/index.html), statsmodels v0.13.1 (140), and nilearn (141). Figures were constructed in python with CanD v0.0.2 (https://github.com/mwshinn/CanD).
Bibliography
- 1.Sherman S Murray and Guillery R W. Distinct functions for direct and transthalamic corticocortical connections. J Neurophysiol, 106(3):1068–1077, Sep 2011. ISSN 1522-1598 (Electronic); 0022-3077 (Linking). doi: 10.1152/jn.00429.2011. [DOI] [PubMed] [Google Scholar]
- 2.Bolkan Scott S, Stujenske Joseph M, Parnaudeau Sebastien, Spellman Timothy J, Rauffenbart Caroline, Abbas Atheir I, Harris Alexander Z, Gordon Joshua A and Kellendonk Christoph. Thalamic projections sustain prefrontal activity during working memory maintenance. Nat Neurosci, 20(7):987–996, Jul 2017. ISSN 1546–1726 (Electronic); 1097–6256 (Print); 1097–6256 (Linking). doi: 10.1038/nn.4568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Rikhye Rajeev V, Wimmer Ralf D and Halassa Michael M. Toward an integrative theory of thalamic function. Annu Rev Neurosci, 41:163–183, Jul 2018. ISSN 1545–4126 (Electronic); 0147–006X (Linking). doi: 10.1146/annurev-neuro-080317-062144. [DOI] [PubMed] [Google Scholar]
- 4.. Nakajima Miho and Halassa Michael M. Thalamic control of functional cortical connectivity. Curr Opin Neurobiol, 44:127–131, Jun 2017. ISSN 1873–6882 (Electronic); 0959–4388 (Print); 0959–4388 (Linking). doi: 10.1016/j.conb.2017.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jones E G. The thalamic matrix and thalamocortical synchrony. Trends Neurosci, 24 (10):595–601, Oct 2001. ISSN 0166–2236 (Print); 0166–2236 (Linking). doi: 10.1016/s0166-2236(00)01922-6. [DOI] [PubMed] [Google Scholar]
- 6.Halassa Michael M and Sherman. S Murray Thalamocortical circuit motifs: A general framework. Neuron, 103(5):762–770, Sep 2019. ISSN 1097–4199 (Electronic); 0896–6273 (Print); 0896–6273 (Linking). doi: 10.1016/j.neuron.2019.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Roy Dheeraj S, Zhang Ying, Halassa Michael M and Feng Guoping. Thalamic subnetworks as units of function. Nat Neurosci, 25(2):140–153, Feb 2022. ISSN 1546–1726 (Electronic); 1097–6256 (Print); 1097–6256 (Linking). doi: 10.1038/s41593-021-00996-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Saalmann Yuri B and Kastner. Sabine The cognitive thalamus. Front Syst Neurosci, 9: 39, 2015. ISSN 1662–5137 (Print); 1662–5137 (Electronic); 1662–5137 (Linking). doi: 10.3389/fnsys.2015.00039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wolff Mathieu and Vann Seralynne D.. The cognitive thalamus as a gateway to mental representations. Journal of Neuroscience, 39(1):3–14, 2019. ISSN 0270–6474. doi: 10. 1523/JNEUROSCI.0479–18.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yang Weiguo, Tipparaju Sri Laasya, Chen Guang and Li Nuo. Thalamus-driven functional populations in frontal cortex support decision-making. Nat Neurosci, 25(10):1339–1352, Oct 2022. ISSN 1546–1726 (Electronic); 1097–6256 (Print); 1097–6256 (Linking). doi: 10.1038/s41593-022-01171-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Schmitt L. Ian, Wimmer Ralf D., Nakajima Miho, Happ Michael, Mofakham Sima and Halassa. Michael M. Thalamic amplification of cortical connectivity sustains attentional control. Nature, 545(7653):219–223, 2017. doi: 10.1038/nature22073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Guo Zengcai V, Inagaki Hidehiko K, Daie Kayvon, Druckmann Shaul, Gerfen Charles R and Svoboda. Karel Maintenance of persistent activity in a frontal thalamocortical loop. Nature, 545(7653):181–186, May 2017. ISSN 1476–4687 (Electronic); 0028–0836 (Print); 0028–0836 (Linking). doi: 10.1038/nature22324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Miguel Ángel García-Cabezas Isabel Pérez-Santos and Cavada Carmen. Mapping the primate thalamus: historical perspective and modern approaches for defining nuclei. Brain Struct Funct, 228(5):1125–1151, Jun 2023. ISSN 1863–2661 (Electronic); 1863–2653 (Print); 1863–2653 (Linking). doi: 10.1007/s00429-022-02598-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cassel Jean-Christophe and Anne Pereira de Vasconcelos. Routes of the thalamus through the history of neuroanatomy. Neuroscience Biobehavioral Reviews, 125:442–465, 2021. ISSN 0149–7634. doi: 10.1016/j.neubiorev.2021.03.001. [DOI] [PubMed] [Google Scholar]
- 15.Zhang Dongyang, Snyder Abraham Z, Shimony Joshua S, Fox Michael D and Raichle. Marcus E Noninvasive functional and structural connectivity mapping of the human thalamocortical system. Cereb Cortex, 20(5):1187–1194, May 2010. ISSN 1460–2199 (Electronic); 1047–3211 (Print); 1047–3211 (Linking). doi: 10.1093/cercor/bhp182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lambert Christian, Simon Henry, Colman Jordan and Barrick Thomas R.. Defining thalamic nuclei and topographic connectivity gradients in vivo. NeuroImage, 158:466–479, 2017. ISSN 1053–8119. doi: 10.1016/j.neuroimage.2016.08.028. [DOI] [PubMed] [Google Scholar]
- 17.Xiao D., Zikopoulos B. and Barbas H.. Laminar and modular organization of prefrontal projections to multiple thalamic nuclei. Neuroscience, 161(4):1067–1081, 2009. ISSN 0306–4522. doi: 10.1016/j.neuroscience.2009.04.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Barbas H, Henion T H and Dermon. C R Diverse thalamic projections to the prefrontal cortex in the rhesus monkey. J Comp Neurol, 313(1):65–94, Nov 1991. ISSN 0021–9967 (Print); 0021–9967 (Linking). doi: 10.1002/cne.903130106. [DOI] [PubMed] [Google Scholar]
- 19.Preuss T M and Goldman-Rakic P S. Crossed corticothalamic and thalamocortical connections of macaque prefrontal cortex. J Comp Neurol, 257(2):269–281, Mar 1987. ISSN 0021–9967 (Print); 0021–9967 (Linking). doi: 10.1002/cne.902570211. [DOI] [PubMed] [Google Scholar]
- 20.Romanski L M, Giguere M, Bates J F and Goldman-Rakic P S. Topographic organization of medial pulvinar connections with the prefrontal cortex in the rhesus monkey. J Comp Neurol, 379(3):313–332, Mar 1997. ISSN 0021–9967 (Print); 0021–9967 (Linking). [PubMed] [Google Scholar]
- 21.Oldham Stuart and Ball Gareth. A phylogenetically-conserved axis of thalamocortical connectivity in the human brain. bioRxiv, page 2022.11.15.516574, January 2022. doi: 10.1101/2022.11.15.516574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Draganski Bogdan, Kherif Ferath, Klöppel Stefan, Cook Philip A, Alexander Daniel C, Parker Geoff J M, Deichmann Ralf, Ashburner John and Frackowiak Richard S J. Evidence for segregated and integrative connectivity patterns in the human basal ganglia. J Neurosci, 28(28):7143–7152, Jul 2008. ISSN 1529–2401 (Electronic); 0270–6474 (Print); 0270–6474 (Linking). doi: 10.1523/JNEUROSCI.1486-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Haber Suzanne N and Calzavara Roberta. The cortico-basal ganglia integrative network: the role of the thalamus. Brain Res Bull, 78(2–3):69–74, Feb 2009. ISSN 1873–2747 (Electronic); 0361–9230 (Print); 0361–9230 (Linking). doi: 10.1016/j.brainresbull.2008.09.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.McFarland Nikolaus R and Haber Suzanne N. Thalamic relay nuclei of the basal ganglia form both reciprocal and nonreciprocal cortical connections, linking multiple frontal cortical areas. J Neurosci, 22(18):8117–8132, Sep 2002. ISSN 1529–2401 (Electronic); 0270–6474 (Print); 0270–6474 (Linking). doi: 10.1523/JNEUROSCI.22-18-08117.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Goldman-Rakic P S and Porrino L J. The primate mediodorsal (md) nucleus and its projection to the frontal lobe. J Comp Neurol, 242(4):535–560, Dec 1985. ISSN 0021–9967 (Print); 0021–9967 (Linking). doi: 10.1002/cne.902420406. [DOI] [PubMed] [Google Scholar]
- 26.Siwek D F and Pandya D N. Prefrontal projections to the mediodorsal nucleus of the thalamus in the rhesus monkey. J Comp Neurol, 312(4):509–524, Oct 1991. ISSN 0021–9967 (Print); 0021–9967 (Linking). doi: 10.1002/cne.903120403. [DOI] [PubMed] [Google Scholar]
- 27.Selemon L D and Goldman-Rakic P S. Common cortical and subcortical targets of the dorsolateral prefrontal and posterior parietal cortices in the rhesus monkey: evidence for a distributed neural network subserving spatially guided behavior. J Neurosci, 8(11):4049–4068, Nov 1988. ISSN 0270–6474 (Print); 1529–2401 (Electronic); 0270–6474 (Linking). doi: 10.1523/JNEUROSCI.08-11-04049.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Jbabdi Saad, Sotiropoulos Stamatios N, Haber Suzanne N, Essen David C Van and Behrens Timothy E. Measuring macroscopic brain connections in vivo. Nat Neurosci, 18(11):1546–1555, Nov 2015. ISSN 1546–1726 (Electronic); 1097–6256 (Linking). doi: 10.1038/nn.4134. [DOI] [PubMed] [Google Scholar]
- 29.Basser P J, Mattiello J and LeBihan D. Mr diffusion tensor spectroscopy and imaging. Biophys J, 66(1):259–267, Jan 1994. ISSN 0006–3495 (Print); 1542–0086 (Electronic); 0006–3495 (Linking). doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Le Bihan Denis. Diffusion mri: what water tells us about the brain. EMBO Mol Med, 6(5):569–573, May 2014. ISSN 1757–4684 (Electronic); 1757–4676 (Print); 1757–4676 (Linking). doi: 10.1002/emmm.201404055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Behrens T.E.J., Berg H. Johansen, Jbabdi S., Rushworth M.F.S. and Woolrich M.W.. Probabilistic diffusion tractography with multiple fibre orientations: What can we gain? NeuroImage, 34(1):144 – 155, 2007. ISSN 1053–8119. doi: 10.1016/j.neuroimage.2006.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sotiropoulos Stamatios N and Zalesky Andrew. Building connectomes using diffusion mri: why, how and but. NMR Biomed, 32(4):e3752, Apr 2019. ISSN 1099–1492 (Electronic); 0952–3480 (Print); 0952–3480 (Linking). doi: 10.1002/nbm.3752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Jbabdi Saad and Johansen-Berg Heidi. Tractography: where do we go from here? Brain Connect, 1(3):169–183, 2011. ISSN 2158–0022 (Electronic); 2158–0014 (Print); 2158–0014 (Linking). doi: 10.1089/brain.2011.0033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhang Fan, Daducci Alessandro, He Yong, Schiavi Simona, Seguin Caio, Smith Robert E, Chun-Hung Yeh, Zhao Tengda and O’Donnell Lauren J. Quantitative mapping of the brain’s structural connectivity using diffusion mri tractography: A review. Neuroimage, 249: 118870, Apr 2022. ISSN 1095–9572 (Electronic); 1053–8119 (Print); 1053–8119 (Linking). doi: 10.1016/j.neuroimage.2021.118870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Johansen-Berg Heidi, Behrens Timothy E J, Sillery Emma, Ciccarelli Olga, Thompson Alan J, Smith Stephen M and Matthews Paul M. Functional-anatomical validation and individual variation of diffusion tractography-based segmentation of the human thalamus. Cereb Cortex, 15(1):31–39, Jan 2005. ISSN 1047–3211 (Print); 1047–3211 (Linking). doi: 10.1093/cercor/bhh105. [DOI] [PubMed] [Google Scholar]
- 36.Behrens T E J, Johansen-Berg H, Woolrich M W, Smith S M, Wheeler-Kingshott C A M, Boulby P A, Barker G J, Sillery E L, Sheehan K, Ciccarelli O, Thompson A J, Brady J M and Matthews P M. Non-invasive mapping of connections between human thalamus and cortex using diffusion imaging. Nat Neurosci, 6(7):750–757, Jul 2003. ISSN 1097–6256 (Print); 1097–6256 (Linking). doi: 10.1038/nn1075. [DOI] [PubMed] [Google Scholar]
- 37.Phillips Jessica M, Fish Lesenia R, Kambi Niranjan A, Redinbaugh Michelle J, Mohanta Sounak, Kecskemeti Steven R and Saalmann Yuri B. Topographic organization of connections between prefrontal cortex and mediodorsal thalamus: Evidence for a general principle of indirect thalamic pathways between directly connected cortical areas. Neuroimage, 189:832–846, Apr 2019. ISSN 1095–9572 (Electronic); 1053–8119 (Print); 1053–8119 (Linking). doi: 10.1016/j.neuroimage.2019.01.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Jakab András, Blanc Rémi and Berényi Ervin L. Mapping changes of in vivo connectivity patterns in the human mediodorsal thalamus: correlations with higher cognitive and executive functions. Brain Imaging Behav, 6(3):472–483, Sep 2012. ISSN 1931–7565 (Electronic); 1931–7557 (Linking). doi: 10.1007/s11682-012-9172-5. [DOI] [PubMed] [Google Scholar]
- 39.Giraldo-Chica Monica, Rogers Baxter P, Damon Stephen M, Landman Bennett A and Woodward Neil D. Prefrontal-thalamic anatomical connectivity and executive cognitive function in schizophrenia. Biol Psychiatry, 83(6):509–517, Mar 2018. ISSN 1873–2402 (Electronic); 0006–3223 (Print); 0006–3223 (Linking). doi: 10.1016/j.biopsych.2017.09.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Klein Johannes C, Rushworth Matthew F S, Behrens Timothy E J, Mackay Clare E, de Crespigny Alex J, D’Arceuil Helen and Johansen-Berg. Heidi Topography of connections between human prefrontal cortex and mediodorsal thalamus studied with diffusion tractography. Neuroimage, 51(2):555–564, Jun 2010. ISSN 1095–9572 (Electronic); 1053–8119 (Print); 1053–8119 (Linking). doi: 10.1016/j.neuroimage.2010.02.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Phillips Jessica M, Kambi Niranjan A, Redinbaugh Michelle J, Mohanta Sounak and Saalmann Yuri B. Disentangling the influences of multiple thalamic nuclei on prefrontal cortex and cognitive control. Neurosci Biobehav Rev, 128:487–510, Sep 2021. ISSN 1873–7528 (Electronic); 0149–7634 (Print); 0149–7634 (Linking). doi: 10.1016/j.neubiorev.2021.06.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Croxson Paula L., Johansen-Berg Heidi, Behrens Timothy E. J., Robson Matthew D., Pinsk Mark A., Gross Charles G., Richter Wolfgang, Richter Marlene C., Kastner Sabine and Rushworth Matthew F. S.. Quantitative investigation of connections of the prefrontal cortex in the human and macaque using probabilistic diffusion tractography. Journal of Neuroscience, 25(39):8854–8866, 2005. ISSN 0270–6474. doi: 10.1523/JNEUROSCI.1311-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Yendiki Anastasia, Aggarwal Manisha, Axer Markus, Howard Amy F D, van Cappellen van Walsum Anne-Marie and Haber Suzanne N. Post mortem mapping of connectional anatomy for the validation of diffusion mri. Neuroimage, 256:119146, Aug 2022. ISSN 1095–9572 (Electronic); 1053–8119 (Print); 1053–8119 (Linking). doi: 10.1016/j.neuroimage.2022.119146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Burt Joshua B., Helmer Markus, Shinn Maxwell, Anticevic Alan and Murray John D.. Generative modeling of brain maps with spatial autocorrelation. NeuroImage, 220:117038, 2020. ISSN 1053–8119. doi: 10.1016/j.neuroimage.2020.117038. [DOI] [PubMed] [Google Scholar]
- 45.Jie Lisa Ji, Spronk Marjolein, Kulkarni Kaustubh, Grega Repovš, Anticevic Alan and Cole Michael W. Mapping the human brain’s cortical-subcortical functional network organization. NeuroImage, 185:35–57, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Harris Julie A, Mihalas Stefan, Hirokawa Karla E, Whitesell Jennifer D, Choi Hannah, Bernard Amy, Bohn Phillip, Caldejon Shiella, Casal Linzy, Cho Andrew, Feiner Aaron, Feng David, Gaudreault Nathalie, Gerfen Charles R, Graddis Nile, Groblewski Peter A, Henry Alex M, Ho Anh, Howard Robert, Knox Joseph E, Kuan Leonard, Kuang Xiuli, Lecoq Jerome, Lesnar Phil, Yaoyao Li, Luviano Jennifer, McConoughey Stephen, Mortrud Marty T, Naeemi Maitham, Lydia Ng, Seung Wook Oh, Ouellette Benjamin, Shen Elise, Sorensen Staci A, Wakeman Wayne, Wang Quanxin, Wang Yun, Williford Ali, Phillips John W, Jones Allan R, Koch Christof and Zeng Hongkui. Hierarchical organization of cortical and thalamic connectivity. Nature, 575(7781):195–202, Nov 2019. ISSN 1476–4687 (Electronic); 0028–0836 (Print); 0028–0836 (Linking). doi: 10.1038/s41586-019-1716-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ma Guofen, Liu Yanmei, Wang Lizhao, Xiao Zhongyi, Song Kun, Wang Yanjie, Peng Wanling, Liu Xiaotong, Wang Ziyue, Jin Sen, Tao Zi, T Li Chengyu, Xu Tianle, Xu Fuqiang, Xu Min and Zhang Siyu. Hierarchy in sensory processing reflected by innervation balance on cortical interneurons. Sci Adv, 7(20), May 2021. ISSN 2375–2548 (Electronic); 2375–2548 (Linking). doi: 10.1126/sciadv.abf5676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Farishta Reza Abbas, Boire Denis and Casanova Christian. Hierarchical Organization of Corticothalamic Projections to the Pulvinar. Cerebral Cortex Communications, 1(1), 07 2020. ISSN 2632–7376. doi: 10.1093/texcom/tgaa030. tgaa030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Mukherjee Arghya, Bajwa Navdeep, Lam Norman H, Porrero César, Clasca Francisco and Halassa Michael M. Variation of connectivity across exemplar sensory and associative thalamocortical loops in the mouse. eLife, 9:e62554, oct 2020. ISSN 2050–084X. doi: 10.7554/eLife.62554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Bernhardt Boris C, Smallwood Jonathan, Keilholz Shella and Daniel S Margulies. Gradients in brain organization. Neuroimage, 251:118987, Feb 2022. ISSN 1095–9572 (Electronic); 1053–8119 (Linking). doi: 10.1016/j.neuroimage.2022.118987. [DOI] [PubMed] [Google Scholar]
- 51.Burt Joshua B, Demirtas Murat¸, Eckner William J, Navejar Natasha M, Jie Lisa Ji, Martin William J, Bernacchia Alberto, Anticevic Alan and Murray John D. Hierarchy of transcriptomic specialization across human cortex captured by structural neuroimaging topography. Nat Neurosci, 21(9):1251–1259, Sep 2018. ISSN 1546–1726 (Electronic); 1097–6256 (Print); 1097–6256 (Linking). doi: 10.1038/s41593-018-0195-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Margulies Daniel S., Ghosh Satrajit S., Goulas Alexandros, Falkiewicz Marcel, Huntenburg Julia M., Langs Georg, Bezgin Gleb, Eickhoff Simon B., Castellanos F. Xavier, Petrides Michael, Jefferies Elizabeth and Smallwood Jonathan. Situating the default-mode network along a principal gradient of macroscale cortical organization. Proceedings of the National Academy of Sciences, 113(44):12574–12579, 2016. ISSN 0027–8424. doi: 10.1073/pnas.1608282113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Krauth Axel, Blanc Remi, Poveda Alejandra, Jeanmonod Daniel, Morel Anne and Székely Gábor A mean three-dimensional atlas of the human thalamus: generation from multiple histological data. Neuroimage, 49(3):2053–2062, Feb 2010. ISSN 1095–9572 (Electronic); 1053–8119 (Linking). doi: 10.1016/j.neuroimage.2009.10.042. [DOI] [PubMed] [Google Scholar]
- 54.Sherman S Murray. Functioning of circuits connecting thalamus and cortex. Compr Physiol, 7(2):713–739, Mar 2017. ISSN 2040–4603 (Electronic); 2040–4603 (Linking). doi: 10.1002/cphy.c160032. [DOI] [PubMed] [Google Scholar]
- 55.Sherman S Murray and Guillery R W. The role of the thalamus in the flow of information to the cortex. Philos Trans R Soc Lond B Biol Sci, 357(1428):1695–1708, Dec 2002. ISSN 0962–8436 (Print); 1471–2970 (Electronic); 0962–8436 (Linking). doi: 10.1098/rstb.2002. 1161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Phillips James W, Schulmann Anton, Hara Erina, Winnubst Johan, Liu Chenghao, Valakh Vera, Wang Lihua, Shields Brenda C, Korff Wyatt, Chandrashekar Jayaram, Andrew L Lemire Brett Mensh, Dudman Joshua T, Nelson Sacha B and Hantman Adam W A repeated molecular architecture across thalamic pathways. Nat Neurosci, 22(11):1925–1935, Nov 2019. ISSN 1546–1726 (Electronic); 1097–6256 (Print); 1097–6256 (Linking). doi: 10.1038/s41593-019-0483-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Saalmann Yuri B. Intralaminar and medial thalamic influence on cortical synchrony, information transmission and cognition. Front Syst Neurosci, 8:83, 2014. ISSN 1662–5137 (Print); 1662–5137 (Electronic); 1662–5137 (Linking). doi: 10.3389/fnsys.2014.00083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Kawabata Kazuya, Bagarinao Epifanio, Watanabe Hirohisa, Maesawa Satoshi, Mori Daisuke, Hara Kazuhiro, Ohdake Reiko, Masuda Michihito, Ogura Aya, Kato Toshiyasu, Koyama Shuji, Katsuno Masahisa, Wakabayashi Toshihiko, Kuzuya Masafumi, Hoshiyama Minoru, Isoda Haruo, Naganawa Shinji, Ozaki Norio and Sobue Gen. Bridging large-scale cortical networks: Integrative and function-specific hubs in the thalamus. iScience, 24(10):103106, Oct 2021. ISSN 2589–0042 (Electronic); 2589–0042 (Linking). doi: 10.1016/j.isci.2021.103106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Sherman S Murray. The thalamus is more than just a relay. Curr Opin Neurobiol, 17(4):417–422, Aug 2007. ISSN 0959–4388 (Print); 1873–6882 (Electronic); 0959–4388 (Linking). doi: 10.1016/j.conb.2007.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Clascá Francisco, Rubio-Garrido Pablo and Jabaudon Denis. Unveiling the diversity of thalamocortical neuron subtypes. Eur J Neurosci, 35(10):1524–1532, May 2012. ISSN 1460–9568 (Electronic); 0953–816X (Linking). doi: 10.1111/j.1460-9568.2012.08033.x. [DOI] [PubMed] [Google Scholar]
- 61.Yang Siqi, Meng Yao, Li Jiao, Li Bing, Fan Yun-Shuang, Chen Huafu and Liao Wei. The thalamic functional gradient and its relationship to structural basis and cognitive relevance. NeuroImage, 218:116960, 2020. ISSN 1053–8119. doi: 10.1016/j.neuroimage.2020.116960. [DOI] [PubMed] [Google Scholar]
- 62.Müller Eli J., Munn Brandon, Hearne Luke J., Smith Jared B., Fulcher Ben, Arnatkevičiūtė Aurina, Lurie Daniel J., Cocchi Luca and Shine James M.. Core and matrix thalamic subpopulations relate to spatio-temporal cortical connectivity gradients. NeuroImage, 222: 117224, 2020. ISSN 1053–8119. doi: 10.1016/j.neuroimage.2020.117224. [DOI] [PubMed] [Google Scholar]
- 63.Ito Takuya, Hearne Luke J and Cole Michael W. A cortical hierarchy of localized and distributed processes revealed via dissociation of task activations, connectivity changes, and intrinsic timescales. Neuroimage, 221:117141, Nov 2020. ISSN 1095–9572 (Electronic); 1053–8119 (Print); 1053–8119 (Linking). doi: 10.1016/j.neuroimage.2020.117141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Jones Edward G. Synchrony in the interconnected circuitry of the thalamus and cerebral cortex. Ann N Y Acad Sci, 1157:10–23, Mar 2009. ISSN 1749–6632 (Electronic); 0077–8923 (Linking). doi: 10.1111/j.1749-6632.2009.04534.x. [DOI] [PubMed] [Google Scholar]
- 65.Münkle M.C, Waldvogel H.J and Faull R.L.M. The distribution of calbindin, calretinin and parvalbumin immunoreactivity in the human thalamus. Journal of Chemical Neuroanatomy, 19(3):155–173, 2000. ISSN 0891–0618. doi: 10.1016/S0891-0618(00)00060-0. [DOI] [PubMed] [Google Scholar]
- 66.Murray John D, Anticevic Alan, Gancsos Mark, Ichinose Megan, Philip R Corlett, Krystal John H and Wang Xiao-Jing. Linking microcircuit dysfunction to cognitive impairment: effects of disinhibition associated with schizophrenia in a cortical working memory model. Cereb Cortex, 24(4):859–872, Apr 2014. ISSN 1460–2199 (Electronic); 1047–3211 (Print); 1047–3211 (Linking). doi: 10.1093/cercor/bhs370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Markov N T, Ercsey-Ravasz M M, Gomes A R Ribeiro, Lamy C, Magrou L, Vezoli J, Misery P, Falchier A, Quilodran R, Gariel M A, Sallet J, Gamanut R, Huissoud C, Clavagnier S, Giroud P, Sappey-Marinier D, Barone P, Dehay C, Toroczkai Z, Knoblauch K, Essen D C Van and Kennedy H. A weighted and directed interareal connectivity matrix for macaque cerebral cortex. Cereb Cortex, 24(1):17–36, Jan 2014. ISSN 1460–2199 (Electronic); 1047–3211 (Print); 1047–3211 (Linking). doi: 10.1093/cercor/bhs270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Hayashi Takuya, Hou Yujie, Glasser Matthew F, Autio Joonas A, Knoblauch Kenneth, Inoue-Murayama Miho, Coalson Tim, Yacoub Essa, Smith Stephen, Kennedy Henry and Van Essen David C. The nonhuman primate neuroimaging and neuroanatomy project. NeuroImage, 229:117726, 2021. ISSN 1053–8119. doi: 10.1016/j.neuroimage.2021.117726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Yang Siqi, Meng Yao, Li Jiao, Li Bing, Fan Yun-Shuang, Chen Huafu and Liao Wei. The thalamic functional gradient and its relationship to structural basis and cognitive relevance. Neuroimage, 218:116960, Sep 2020. ISSN 1095–9572 (Electronic); 1053–8119 (Linking). doi: 10.1016/j.neuroimage.2020.116960. [DOI] [PubMed] [Google Scholar]
- 70.Brysch W, Brysch I, Creutzfeldt O D, Schlingensiepen R and Schlingensiepen K H. The topology of the thalamo-cortical projections in the marmoset monkey (callithrix jacchus). Exp Brain Res, 81(1):1–17, 1990. ISSN 0014–4819 (Print); 0014–4819 (Linking). doi: 10.1007/BF00230095. [DOI] [PubMed] [Google Scholar]
- 71.Höhl-Abrahão J Cand Creutzfeldt O D. Topographical mapping of the thalamocortical projections in rodents and comparison with that in primates. Exp Brain Res, 87(2):283–294, 1991. ISSN 0014–4819 (Print); 0014–4819 (Linking). doi: 10.1007/BF00231845. [DOI] [PubMed] [Google Scholar]
- 72.Powell Ashton W, Sassa Takayuki, Wu Yongqin, Tessier-Lavigne Marc and Polleux Franck. Topography of thalamic projections requires attractive and repulsive functions of netrin-1 in the ventral telencephalon. PLoS Biol, 6(5):e116, May 2008. ISSN 1545–7885 (Electronic); 1544–9173 (Print); 1544–9173 (Linking). doi: 10.1371/journal.pbio.0060116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Giraldo-Chica Monica and Woodward Neil D. Review of thalamocortical resting-state fmri studies in schizophrenia. Schizophr Res, 180:58–63, Feb 2017. ISSN 1573–2509 (Electronic); 0920–9964 (Print); 0920–9964 (Linking). doi: 10.1016/j.schres.2016.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Sheffield Julia M, Huang Anna S, Rogers Baxter P, Giraldo-Chica Monica, Landman Bennett A, Blackford Jennifer Urbano, Heckers Stephan and Woodward Neil D. Thalamocortical anatomical connectivity in schizophrenia and psychotic bipolar disorder. Schizophr Bull, 46(5):1062–1071, Mar 2020. ISSN 1745–1701 (Electronic); 0586–7614 (Print); 0586–7614 (Linking). doi: 10.1093/schbul/sbaa022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Avery Suzanne N, Huang Anna S, Sheffield Julia M, Rogers Baxter P, Vandekar Simon, Anticevic Alan and Woodward Neil D. Development of thalamocortical structural connectivity in typically developing and psychosis spectrum youths. Biol Psychiatry Cogn Neurosci Neuroimaging, 7(8):782–792, Aug 2022. ISSN 2451–9030 (Electronic); 2451–9022 (Print); 2451–9022 (Linking). doi: 10.1016/j.bpsc.2021.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Blostein Nadia, Devenyi Gabriel A., Patel Sejal, Patel Raihaan, Tullo Stephanie, Plit-man Eric, Costantino Manuela, Markello Ross, Parent Olivier, Bedford Saashi A., Sherwood Chet C., Hopkins William D, Seidlitz Jakob, Raznahan Armin and Chakravarty M. Mallar. Variation in subcortical anatomy: relating interspecies differences, heritability, and brain-behavior relationships. bioRxiv, page 2022.04.11.487874, 01 2022. doi: 10.1101/2022.04.11.487874. [DOI] [Google Scholar]
- 77.Yan Mingchao, Yu Wenwen, Lv Qian, Lv Qiming, Bo Tingting, Chen Xiaoyu, Liu Yilin, Zhan Yafeng, Yan Shengyao, Shen Xiangyu, Yang Baofeng, Hu Qiming, Yu Jiangli, Qiu Zilong, Feng Yuanjing, Zhang Xiao-Yong, Wang He, Xu Fuqiang and Wang Zheng. Mapping brain-wide excitatory projectome of primate prefrontal cortex at submicron resolution and comparison with diffusion tractography. eLife, 11:e72534, may 2022. ISSN 2050–084X. doi: 10.7554/eLife.72534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Bezgin Gleb, Solodkin Ana, Bakker Rembrandt, Ritter Petra and McIntosh Anthony R.. Mapping complementary features of cross-species structural connectivity to construct realistic “virtual brains”. Human Brain Mapping, 38(4):2080–2093, 2017. doi: 10.1002/hbm.23506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Dermon C Rand Barbas H. Contralateral thalamic projections predominantly reach transitional cortices in the rhesus monkey. J Comp Neurol, 344(4):508–531, Jun 1994. ISSN 0021–9967 (Print); 0021–9967 (Linking). doi: 10.1002/cne.903440403. [DOI] [PubMed] [Google Scholar]
- 80.Adeyelu Tolulope, Gandhi Tanya and Lee Charles C. Crossed connections from insular cortex to the contralateral thalamus. Front Neural Circuits, 15:710925, 2021. ISSN 1662–5110 (Electronic); 1662–5110 (Linking). doi: 10.3389/fncir.2021.710925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Scheibel Madge E. and Scheibel Arnold B.. Structural organization of nonspecific thalamic nuclei and their projection toward cortex. Brain Research, 6(1):60–94, 1967. ISSN 0006–8993. doi: 10.1016/0006-8993(67)90183-7. Forebrain Inhibitory Mechanisms. [DOI] [PubMed] [Google Scholar]
- 82.Scholtens Lianne H, Pijnenburg Rory, de Lange Siemon C, Huitinga Inge and van den Heuvel Martijn P. Common microscale and macroscale principles of connectivity in the human brain. J Neurosci, 42(20):4147–4163, May 2022. ISSN 1529–2401 (Electronic); 0270–6474 (Print); 0270–6474 (Linking). doi: 10.1523/JNEUROSCI.1572-21.2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.van den Heuvel Martijn P and Sporns Olaf. Rich-club organization of the human connectome. J Neurosci, 31(44):15775–15786, Nov 2011. ISSN 1529–2401 (Electronic); 0270–6474 (Print); 0270–6474 (Linking). doi: 10.1523/JNEUROSCI.3539-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Groh Alexander, Bokor Hajnalka, Mease Rebecca A, Plattner Viktor M, Hangya Balázs, Stroh Albrecht, Deschenes Martin and Acsády László. Convergence of cortical and sensory driver inputs on single thalamocortical cells. Cereb Cortex, 24(12):3167–3179, Dec 2014. ISSN 1460–2199 (Electronic); 1047–3211 (Print); 1047–3211 (Linking). doi: 10.1093/cercor/bht173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Gu Qinglong L., Lam Norman H., Halassa Michael M. and Murray John D.. Circuit mechanisms of top-down attentional control in a thalamic reticular model. bioRxiv, page 2020.09.16.300749, 01 2020. doi: 10.1101/2020.09.16.300749. [DOI] [Google Scholar]
- 86.Jaramillo Jorge, Mejias Jorge F. and Wang Xiao-Jing. Engagement of pulvino-cortical feedforward and feedback pathways in cognitive computations. Neuron, 101(2):321 – 336.e9, 2019. ISSN 0896–6273. doi: 10.1016/j.neuron.2018.11.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Greene Deanna J, Marek Scott, Gordon Evan M, Siegel Joshua S, Gratton Caterina, Laumann Timothy O, Gilmore Adrian W, Berg Jeffrey J, Nguyen Annie L, Dierker Donna, Van Andrew N, Ortega Mario, Newbold Dillan J, Hampton acqueline M, Nielsen shley N, McDermott Kathleen B, Roland Jarod L, Norris Scott A, Nelson Steven M, Snyder Abraham Z, Schlaggar Bradley L, Petersen Steven E and Dosenbach Nico U F. Integrative and network-specific connectivity of the basal ganglia and thalamus defined in individuals. Neuron, 105(4):742–758, Feb 2020. ISSN 1097–4199 (Electronic); 0896–6273 (Print); 0896–6273 (Linking). doi: 10.1016/j.neuron.2019.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Hwang Kai, Bertolero Maxwell A, Liu William B and D’Esposito Mark. The human thalamus is an integrative hub for functional brain networks. J Neurosci, 37(23):5594–5607, Jun 2017. ISSN 1529–2401 (Electronic); 0270–6474 (Print); 0270–6474 (Linking). doi: 10.1523/JNEUROSCI.0067-17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Haber Suzanne and Mcfarland Nikolaus R.. The place of the thalamus in frontal cortical-basal ganglia circuits. The Neuroscientist, 7(4):315–324, 2001. doi: 10.1177/107385840100700408. [DOI] [PubMed] [Google Scholar]
- 90.Beltramo Riccardo and Scanziani Massimo. A collicular visual cortex: Neocortical space for an ancient midbrain visual structure. Science, 363(6422):64–69, Jan 2019. ISSN 1095–9203 (Electronic); 0036–8075 (Linking). doi: 10.1126/science.aau7052. [DOI] [PubMed] [Google Scholar]
- 91.Wurtz Robert H., Sommer Marc A. and Cavanaugh James. Drivers from the deep: the contribution of collicular input to thalamocortical processing. In Cortical Function: a View from the Thalamus, volume 149 of Progress in Brain Research, pages 207–225. Elsevier, 2005. doi: 10.1016/S0079-6123(05)49015-9. [DOI] [PubMed] [Google Scholar]
- 92.Wolff M., Morceau S., Folkard R., Martin-Cortecero J. and Groh A.. A thalamic bridge from sensory perception to cognition. Neuroscience Biobehavioral Reviews, 120:222–235, 2021. ISSN 0149–7634. doi: 10.1016/j.neubiorev.2020.11.013. [DOI] [PubMed] [Google Scholar]
- 93.Maier-Hein Klaus H., Neher Peter F., Houde Jean-Christophe, Côté Marc-Alexandre, Garyfallidis Eleftherios, Zhong Jidan, Chamberland Maxime, Fang-Cheng Yeh, Ying-Chia Lin, Qing Ji, Reddick Wilburn E., Glass John O., Chen David Qixiang, Feng Yuanjing, Gao Chengfeng, Wu Ye, Jieyan Ma, Renjie He, Qiang Li, Westin Carl-Fredrik, Deslauriers-Gauthier Samuel, González J. Omar Ocegueda, Paquette Michael, St-Jean Samuel, Girard Gabriel, Rheault François, Sidhu Jasmeen, Tax Chantal M. W., Guo Fenghua, Mesri Hamed Y., Dávid Szabolcs, Froeling Martijn, Heemskerk Anneriet M., Leemans Alexander, Boré Arnaud, Pinsard Basile, Bedetti Christophe, Desrosiers Matthieu, Brambati Simona, Doyon Julien, Sarica Alessia, Vasta Roberta, Cerasa Antonio, Quattrone Aldo, Yeatman Jason, Khan Ali R., Hodges Wes, Alexander Simon, Romascano David, Barakovic Muhamed, Auría Anna, Esteban Oscar, Lemkaddem Alia, Jean-Philippe Thiran, Cetingul H. Ertan, Odry Benjamin L., Mailhe Boris, Nadar Mariappan S., Pizza-galli Fabrizio, Prasad Gautam, Villalon-Reina Julio E., Galvis Justin, Thompson Paul M., Requejo Francisco De Santiago, Laguna Pedro Luque, Lacerda Luis Miguel, Barrett Rachel, Dell’Acqua Flavio, Catani Marco, Petit Laurent, Caruyer Emmanuel, Daducci Alessandro, Dyrby Tim B., Holland-Letz Tim, Hilgetag Claus C., Stieltjes Bram and Descoteaux Maxime. The challenge of mapping the human connectome based on diffusion tractography. Nature Communications, 8(1):1349, 2017. doi: 10.1038/s41467-017-01285-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Schilling Kurt G, Petit Laurent, Rheault Francois, Remedios Samuel, Pierpaoli Carlo, Anderson Adam W, Landman Bennett A and Descoteaux Maxime. Brain connections derived from diffusion mri tractography can be highly anatomically accurate-if we know where white matter pathways start, where they end, and where they do not go. Brain Struct Funct, 225(8):2387–2402, Nov 2020. ISSN 1863–2661 (Electronic); 1863–2653 (Print); 1863–2653 (Linking). doi: 10.1007/s00429-020-02129-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Delettre Céline, Messé Arnaud, Dell Leigh-Anne, Foubet Ophélie, Heuer Katja, Larrat Benoit, Meriaux Sebastien, Mangin Jean-Francois, Reillo Isabel, de Juan Romero Camino, Borrell Victor, Toro Roberto and Hilgetag Claus C. Comparison between diffusion mri tractography and histological tract-tracing of cortico-cortical structural connectivity in the ferret brain. Netw Neurosci, 3(4):1038–1050, 2019. ISSN 2472–1751 (Electronic); 2472–1751 (Linking). doi: 10.1162/netn{\_}a{\_}00098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Donahue Chad J, Sotiropoulos Stamatios N, Jbabdi Saad, Hernandez-Fernandez Moises, Behrens Timothy E, Dyrby Tim B, Coalson Timothy, Kennedy Henry, Knoblauch Kenneth, Essen avid C Van and Glasser Matthew F. Using diffusion tractography to predict cortical connection strength and distance: A quantitative comparison with tracers in the monkey. J Neurosci, 36(25):6758–6770, Jun 2016. ISSN 1529–2401 (Electronic); 0270–6474 (Print); 0270–60474 (Linking). doi: 10.1523/JNEUROSCI.0493-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.van den Heuvel Martijn P, de Reus Marcel A, Barrett Lisa Feldman, Scholtens Lianne H, Coopmans Fraukje M T, Schmidt Ruben, Preuss Todd M, Rilling James K and Longchuan Li. Comparison of diffusion tractography and tract-tracing measures of connectivity strength in rhesus macaque connectome. Hum Brain Mapp, 36(8):3064–3075, Aug 2015. ISSN 1097–0193 (Electronic); 1065–9471 (Print); 1065–9471 (Linking). doi: 10.1002/hbm.22828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Grisot Giorgia, Haber Suzanne N. and Yendiki Anastasia. Diffusion mri and anatomic tracing in the same brain reveal common failure modes of tractography. NeuroImage, 239: 118300, 2021. ISSN 1053–8119. doi: 10.1016/j.neuroimage.2021.118300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Schilling Kurt G., Gao Yurui, Stepniewska Iwona, Janve Vaibhav, Landman Bennett A. and Anderson Adam W.. Anatomical accuracy of standard-practice tractography algorithms in the motor system - a histological validation in the squirrel monkey brain. Magnetic Resonance Imaging, 55:7–25, 2019. ISSN 0730–725X. doi: 10.1016/j.mri.2018.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Dauguet Julien, Peled Sharon, Berezovskii Vladimir, Delzescaux Thierry, Warfield Simon K., Born Richard and Westin Carl-Fredrik. Comparison of fiber tracts derived from in-vivo dti tractography with 3d histological neural tract tracer reconstruction on a macaque brain. NeuroImage, 37(2):530–538, 2007. ISSN 1053–8119. doi: 10.1016/j.neuroimage.2007.04.067.. [DOI] [PubMed] [Google Scholar]
- 101.Gao Yurui, Choe Ann S, Stepniewska Iwona, Li Xia, Avison Malcolm J and Anderson Adam W. Validation of dti tractography-based measures of primary motor area connectivity in the squirrel monkey brain. PLoS One, 8(10):e75065, 2013. ISSN 1932–6203 (Electronic); 1932–6203 (Linking). doi: 10.1371/journal.pone.0075065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Thomas Cibu, Frank Q Ye, Irfanoglu M Okan, Modi Pooja, Saleem Kadharbatcha S, Leopold David A and Pierpaoli Carlo. Anatomical accuracy of brain connections derived from diffusion mri tractography is inherently limited. Proc Natl Acad Sci U S A, 111(46):16574–16579, Nov 2014. ISSN 1091–6490 (Electronic); 0027–8424 (Print); 0027–8424 (Linking). doi: 10.1073/pnas.1405672111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Hwang Kai, Shine James M, Bruss Joel, Tranel Daniel and Boes Aaron. Neuropsychological evidence of multi-domain network hubs in the human thalamus. eLife, 10:e69480, oct 2021. ISSN 2050–084X. doi: 10.7554/eLife.69480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Anticevic Alan, Yang Genevieve, Savic Aleksandar, Murray John D, Cole Michael W, Repovs Grega, Pearlson Godfrey D and Glahn David C. Mediodorsal and visual thalamic connectivity differ in schizophrenia and bipolar disorder with and without psychosis history. Schizophr Bull, 40(6):1227–1243, Nov 2014. ISSN 1745–1701 (Electronic); 0586–7614 (Print); 0586–7614 (Linking). doi: 10.1093/schbul/sbu100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Anticevic Alan, Haut Kristen, Murray John D, Repovs Grega, Yang Genevieve J, Diehl Caroline, McEwen Sarah C, Bearden Carrie E, Addington Jean, Goodyear Bradley, Cadenhead Kristin S, Mirzakhanian Heline, Cornblatt Barbara A, Olvet Doreen, Mathalon Daniel H, McGlashan Thomas H, Perkins Diana O, Belger Aysenil, Seidman Larry J, Tsuang Ming T, van Erp Theo G M, Walker Elaine F, Hamann Stephan, Woods Scott W, Qiu Maolin and Cannon Tyrone D. Association of thalamic dysconnectivity and conversion to psychosis in youth and young adults at elevated clinical risk. JAMA Psychiatry, 72(9):882–891, Sep 2015. ISSN 2168–6238 (Electronic); 2168–622X (Print); 2168–622X (Linking). doi: 10.1001/jamapsychiatry.2015.0566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Murray John D and Anticevic Alan. Toward understanding thalamocortical dysfunction in schizophrenia through computational models of neural circuit dynamics. Schizophr Res, 180:70–77, Feb 2017. ISSN 1573–2509 (Electronic); 0920–9964 (Print); 0920–9964 (Linking). doi: 10.1016/j.schres.2016.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Woodward Neil D, Karbasforoushan Haleh and Heckers Stephan. Thalamocortical dysconnectivity in schizophrenia. Am J Psychiatry, 169(10):1092–1099, Oct 2012. ISSN 1535–7228 (Electronic); 0002–953X (Print); 0002–953X (Linking). doi: 10.1176/appi.ajp.2012.12010056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Woodward Neil D and Heckers Stephan. Mapping thalamocortical functional connectivity in chronic and early stages of psychotic disorders. Biol Psychiatry, 79(12):1016–1025, Jun 2016. ISSN 1873–2402 (Electronic); 0006–3223 (Print); 0006–3223 (Linking). doi: 10.1016/j.biopsych.2015.06.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Hwang Wu Jeong, Kwak Yoo Bin, Cho Kang Ik K, Tae Young Lee, Harin Oh, Minji Ha, Minah Kim and Kwon Jun Soo. Thalamic connectivity system across psychiatric disorders: Current status and clinical implications. Biol Psychiatry Glob Open Sci, 2(4):332–340, Oct 2022. ISSN 2667–1743 (Electronic); 2667–1743 (Linking). doi: 10.1016/j.bpsgos.2021.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Bell Peter T. and Shine James M.. Subcortical contributions to large-scale network communication. Neuroscience Biobehavioral Reviews, 71:313–322, 2016. ISSN 0149–7634. doi: 10.1016/j.neubiorev.2016.08.036. [DOI] [PubMed] [Google Scholar]
- 111.Shine James M.. The thalamus integrates the macrosystems of the brain to facilitate complex, adaptive brain network dynamics. Progress in Neurobiology, 199:101951, 2021. ISSN 0301–0082. doi: 10.1016/j.pneurobio.2020.101951. [DOI] [PubMed] [Google Scholar]
- 112.Van Essen David C, Smith Stephen M, Barch Deanna M, Behrens Timothy E J, Yacoub Essa and Ugurbil Kamil. The wu-minn human connectome project: an overview. Neuroimage, 80:62–79, Oct 2013. ISSN 1095–9572 (Electronic); 1053–8119 (Print); 1053–8119 (Linking). doi: 10.1016/j.neuroimage.2013.05.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Glasser Matthew F, Sotiropoulos Stamatios N, Wilson J Anthony, Coalson imothy S, Fischl Bruce, Andersson Jesper L, Junqian Xu, Jbabdi Saad, Webster Matthew, Polimeni Jonathan R, Van Essen David C and Jenkinson Mark. The minimal preprocessing pipelines for the human connectome project. Neuroimage, 80:105–124, Oct 2013. ISSN 1095–9572 (Electronic); 1053–8119 (Print); 1053–8119 (Linking). doi: 10.1016/j.neuroimage.2013.04.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Ji Jie Lisa, Demšar Jure, Fonteneau Clara, Tamayo Zailyn, Pan Lining, Kraljič Aleksij, Matkovič Andraž, Purg Nina, Helmer Markus, Warrington Shaun, Winkler Anderson, Zerbi Valerio, Coalson Timothy S, Glasser Matthew F, Harms Michael P, Sotiropoulos Stamatios N, John D, Anticevic Alan and Repovš Grega. Qunex-an integrative platform for reproducible neuroimaging analytics. Front Neuroinform, 17:1104508, 2023. ISSN 1662–5196 (Print); 1662–5196 (Electronic); 1662–5196 (Linking). doi: 10.3389/fninf.2023.1104508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Sotiropoulos Stamatios N, Hernández-Fernández Moisés, Vu An T, Andersson Jesper L, Moeller Steen, Yacoub Essa, Lenglet Christophe, Ugurbil Kamil, Behrens Timothy E J and Jbabdi Saad. Fusion in diffusion mri for improved fibre orientation estimation: An application to the 3t and 7t data of the human connectome project. Neuroimage, 134: 396–409, Jul 2016. ISSN 1095–9572 (Electronic); 1053–8119 (Print); 1053–8119 (Linking). doi: 10.1016/j.neuroimage.2016.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Sotiropoulos Stamatios N, Jbabdi Saad, Xu Junqian, Andersson Jesper L, Moeller Steen, Auerbach Edward J, Glasser Matthew F, Hernandez Moises, Sapiro Guillermo, Jenkinson Mark, Feinberg David A, Yacoub Essa, Lenglet Christophe, Van Essen David C, Ugurbil Kamil and Behrens Timothy E J. Advances in diffusion mri acquisition and processing in the human connectome project. Neuroimage, 80:125–143, Oct 2013. ISSN 1095–9572 (Electronic); 1053–8119 (Print); 1053–8119 (Linking). doi: 10.1016/j.neuroimage.2013.05.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Hernandez-Fernandez Moises, Reguly Istvan, Jbabdi Saad, Giles Mike, Smith Stephen and Sotiropoulos Stamatios N. Using gpus to accelerate computational diffusion mri: From microstructure estimation to tractography and connectomes. Neuroimage, 188:598–615, Mar 2019. ISSN 1095–9572 (Electronic); 1053–8119 (Print); 1053–8119 (Linking). doi: 10.1016/j.neuroimage.2018.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Glasser Matthew F., Coalson Timothy S., Robinson Emma C., Hacker Carl D., Harwell John, Yacoub Essa, Ugurbil Kamil, Andersson Jesper, Beckmann Christian F., Jenkinson Mark, Smith Stephen M. and Van Essen David C.. A multi-modal parcellation of human cerebral cortex. Nature, 536(7615):171–178, 2016. doi: 10.1038/nature18933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Yeo B T Thomas, Krienen Fenna M, Sepulcre Jorge, Sabuncu Mert R, Lashkari Danial, Hollinshead Marisa, Roffman Joshua L, Smoller Jordan W, Zöllei Lilla, Polimeni Jonathan R, Fischl Bruce, Liu Hesheng and Buckner Randy L. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J Neurophysiol, 106(3):1125–1165, Sep 2011. ISSN 1522–1598 (Electronic); 0022–3077 (Print); 0022–3077 (Linking). doi: 10.1152/jn.00338.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Tian Ye, Margulies Daniel S, Breakspear Michael and Zalesky Andrew. Topographic organization of the human subcortex unveiled with functional connectivity gradients. Nat Neurosci, 23(11):1421–1432, Nov 2020. ISSN 1546–1726 (Electronic); 1097–6256 (Linking). doi: 10.1038/s41593-020-00711-6. [DOI] [PubMed] [Google Scholar]
- 121.Warrington Shaun, Bryant Katherine L, Khrapitchev Alexandr A, Sallet Jerome, Charquero-Ballester Marina, Douaud Gwenaëlle, Jbabdi Saad, Mars Rogier B and Sotiropoulos Stamatios N. Xtract - standardised protocols for automated tractography in the human and macaque brain. Neuroimage, 217:116923, Aug 2020. ISSN 1095–9572 (Electronic); 1053–8119 (Print); 1053–8119 (Linking). doi: 10.1016/j.neuroimage.2020.116923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Folloni Davide, Sallet Jerome, Khrapitchev Alexandre A, Sibson Nicola, Verhagen Lennart, Mars Rogier B, Heilbronner Sarah, Gold Joshua I and de Schotten Michel Thiebaut. Dichotomous organization of amygdala/temporal-prefrontal bundles in both humans and monkeys. eLife, 8:e47175, 2019. doi: 10.7554/eLife.47175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Milham Michael P., Ai Lei, Koo Bonhwang, Xu Ting, Amiez Céline, Balezeau Fabien, Baxter Mark G., Blezer Erwin L.A., Brochier Thomas, Chen Aihua, Croxson Paula L., Damatac Christienne G., Dehaene Stanislas, Everling Stefan, Fair Damian A., Fleysher Lazar, Freiwald Winrich, Froudist-Walsh Sean, Griffiths Timothy D., Guedj Carole, Hadj-Bouziane Fadila, Hamed Suliann Ben, Harel Noam, Hiba Bassem, Jarraya Bechir, Jung Benjamin, Kastner Sabine, Klink P. Christiaan, Kwok Sze Chai, Laland Kevin N., Leopold David A., Lindenfors Patrik, Mars Rogier B., Menon Ravi S., Messinger Adam, Meunier Martine, Mok Kelvin, Morrison John H., Nacef Jennifer, Nagy Jamie, Rios Michael Ortiz, Petkov Christopher I., Pinsk Mark, Poirier Colline, Procyk Emmanuel, Rajimehr Reza, Reader Simon M., Roelfsema Pieter R., Rudko David A., Rushworth Matthew F.S., Russ Brian E., Sallet Jerome, Schmid Michael Christoph, Schwiedrzik Caspar M., Seidlitz Jakob, Sein Julien, Shmuel Amir, Sullivan Elinor L., Ungerleider Leslie, Thiele Alexander, Todorov Orlin S., Tsao Doris, Wang Zheng, Wilson Charles R.E., Yacoub Essa, Ye Frank Q., Zarco Wilbert, di Zhou Yong, Margulies Daniel S. and Schroeder Charles E.. An open resource for non-human primate imaging. Neuron, 100(1):61–74.e2, 2018. ISSN 0896–6273. doi: 10.1016/j.neuron.2018.08.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Warrington Shaun, Thompson Elinor, Bastiani Matteo, Dubois Jessica, Baxter Luke, Slater Rebeccah, Jbabdi Saad, Mars Rogier B. and Sotiropoulos Stamatios N.. Concurrent mapping of brain ontogeny and phylogeny within a common space: Standardized tractography and applications. Science Advances, 8(42):eabq2022, 2023/June/06 . doi: 10.1126/sciadv.abq2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Mars Rogier B, Sotiropoulos Stamatios N, Passingham Richard E, Sallet Jerome, Verhagen Lennart, Khrapitchev Alexandre A, Sibson Nicola, Jbabdi Saad and Stephan Klaas Enno. Whole brain comparative anatomy using connectivity blueprints. eLife, 7:e35237, 2018. doi: 10.7554/eLife.35237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Van Essen David C, Donahue Chad J, Coalson Timothy S, Kennedy Henry, Hayashi Takuya and Glasser Matthew F. Cerebral cortical folding, parcellation, and connectivity in humans, nonhuman primates, and mice. Proc Natl Acad Sci U S A, 116(52):26173–26180, Dec 2019. ISSN 1091–6490 (Electronic); 0027–8424 (Print); 0027–8424 (Linking). doi: 10.1073/pnas.1902299116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.van den Heuvel Martijn P., de Lange Siemon C., Zalesky Andrew, Seguin Caio, Yeo B.T. Thomas and Schmidt Ruben. Proportional thresholding in resting-state fmri functional connectivity networks and consequences for patient-control connectome studies: Issues and recommendations. NeuroImage, 152:437–449, 2017. ISSN 1053–8119. doi: 10.1016/j.neuroimage.2017.02.005. [DOI] [PubMed] [Google Scholar]
- 128.Glasser Matthew F and Van Essen David C. Mapping human cortical areas in vivo based on myelin content as revealed by t1- and t2-weighted mri. J Neurosci, 31(32):11597–11616, Aug 2011. ISSN 1529–2401 (Electronic); 0270–6474 (Print); 0270–6474 (Linking). doi: 10.1523/JNEUROSCI.2180-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Ito Takuya and Murray John D. Multitask representations in the human cortex transform along a sensory-to-motor hierarchy. Nat Neurosci, 26(2):306–315, Feb 2023. ISSN 1546–1726 (Electronic); 1097–6256 (Linking). doi: 10.1038/s41593-022-01224-0. [DOI] [PubMed] [Google Scholar]
- 130.Markello Ross D. and Misic Bratislav. Comparing spatial null models for brain maps. NeuroImage, 236:118052, 2021. ISSN 1053–8119. doi: 10.1016/j.neuroimage.2021.118052. [DOI] [PubMed] [Google Scholar]
- 131.Bourassa J, Pinault D and Deschênes M. Corticothalamic projections from the cortical barrel field to the somatosensory thalamus in rats: a single-fibre study using biocytin as an anterograde tracer. Eur J Neurosci, 7(1):19–30, Jan 1995. ISSN 0953–816X (Print); 0953–816X (Linking). doi: 10.1111/j.1460-9568.1995.tb01016.x. [DOI] [PubMed] [Google Scholar]
- 132.Kumar Vinod Jangir, Beckmann Christian F., Scheffler Klaus and Grodd Wolfgang. Relay and higher-order thalamic nuclei show an intertwined functional association with cortical-networks. Communications Biology, 5(1):1187, 2022. doi: 10.1038/s42003-022-04126-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Murray John D, Bernacchia Alberto, Freedman David J, Romo Ranulfo, Wallis Jonathan D, Cai Xinying, Padoa-Schioppa Camillo, Pasternak Tatiana, Seo Hyojung, Lee Daeyeol and Xiao-Jing Wang. A hierarchy of intrinsic timescales across primate cortex. Nat Neurosci, 17(12):1661–1663, Dec 2014. ISSN 1546–1726 (Electronic); 1097–6256 (Print); 1097–6256 (Linking). doi: 10.1038/nn.3862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Harris Charles R., Millman K. Jarrod, van der Walt Stéfan J., Gommers Ralf, Virtanen Pauli, Cournapeau David, Wieser Eric, Taylor Julian, Berg Sebastian, Smith Nathaniel J., Kern Robert, Picus Matti, Hoyer Stephan, van Kerkwijk Marten H., Brett Matthew, Haldane Allan, Río Jaime Fernández del, Wiebe Mark, Peterson Pearu, Gérard-Marchant Pierre, Sheppard Kevin, Reddy Tyler, Weckesser Warren, Abbasi Hameer, Gohlke Christoph and Oliphant Travis E.. Array programming with NumPy. Nature, 585(7825):357–362, September 2020. doi: 10.1038/s41586-020-2649-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.McKinney Wes. Data Structures for Statistical Computing in Python. In Stéfan van der Walt and Millman Jarrod, editors, Proceedings of the 9th Python in Science Conference, pages 56 – 61, 2010. doi: 10.25080/Majora-92bf1922-00a. [DOI] [Google Scholar]
- 136.Virtanen Pauli, Gommers Ralf, Oliphant Travis E., Haberland Matt, Reddy Tyler, Cournapeau David, Burovski Evgeni, Peterson Pearu, Weckesser Warren, Bright Jonathan, van der Walt Stéfan J., Brett Matthew, Wilson Joshua, Millman K. Jarrod, Mayorov Nikolay, Nelson Andrew R. J., Jones Eric, Kern Robert, Larson Eric, Carey C J, ˙Polat Ilhan, Feng Yu, Moore Eric W., VanderPlas Jake, Laxalde Denis, Perktold Josef, Cimrman Robert, Henriksen Ian, Quintero E. A., Harris Charles R., Archibald Anne M., Ribeiro Antônio H., Pedregosa Fabian, van Mulbregt Paul and SciPy 1.0 Contributors. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nature Methods, 17:261–272, 2020. doi: 10.1038/s41592-019-0686-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Waskom Michael L.. seaborn: statistical data visualization. Journal of Open Source Software, 6(60):3021, 2021. doi: 10.21105/joss.03021. [DOI] [Google Scholar]
- 138.Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., Dubourg V., Vanderplas J., Passos A., Cournapeau D., Brucher M., Perrot M. and Duchesnay E.. Scikit-learn: Machine learning in Python. Journal of Machine Learning Research, 12:2825–2830, 2011. [Google Scholar]
- 139.Hunter J. D.. Matplotlib: A 2d graphics environment. Computing in Science & Engineering, 9(3):90–95, 2007. doi: 10.1109/MCSE.2007.55. [DOI] [Google Scholar]
- 140.Seabold Skipper and Perktold Josef. statsmodels: Econometric and statistical modeling with python. In 9th Python in Science Conference, 2010. [Google Scholar]
- 141.Abraham Alexandre, Pedregosa Fabian, Eickenberg Michael, Gervais Philippe, Mueller Andreas, Kossaifi Jean, Gramfort Alexandre, Thirion Bertrand and Varoquaux Gael. Machine learning for neuroimaging with scikit-learn. Frontiers in Neuroinformatics, 8, 2014. ISSN 1662–5196. doi: 10.3389/fninf.2014.00014. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Neuroimaging files used in this study will be made available on the Brain Analysis Library of Spatial maps and Atlases (BALSA) website. The 1mm Morel thalamic atlas was obtained elsewhere with permission (53). As such, we cannot provide the thalamic segmentation files directly, but we can provide the code to create the segmentation for Morel nuclei in 2mm space. All code related to this study will be made publicly available on BitBucket. All analyses were implemented using Python (version 3.10) and the following packages were used: numpy v1.21.2 (134), pandas v1.4.4 (135), scipy v1.10.1 (136), nibabel v3.2.1 (https://zenodo.org/record/7795644), seaborn v0.12.2 (137), sklearn v0.10.0 (138), matplotlib v3.4.3 (139), wbplot (https://github.com/jbburt/wbplot), pingouin v0.5.3 (https://pingouin-stats.org/build/html/index.html), statsmodels v0.13.1 (140), and nilearn (141). Figures were constructed in python with CanD v0.0.2 (https://github.com/mwshinn/CanD).