Efficient DLPNO-CCSD(T)-Based Estimation of Formation Enthalpies for C, H, O, and N-Containing Closed-Shell Compounds Validated Against Critically-Evaluated Experimental Data

Abstract

An accurate and cost-efficient methodology for the estimation of the enthalpies of formation for closed-shell compounds composed of C, H, O, and N atoms is presented and validated against critically-evaluated experimental data. The computational efficiency is achieved through the use of the Resolution-of-Identity (RI) and Domain-Based Local Pair-Natural Orbital Coupled Cluster (DLPNO-CCSD(T)) approximations, which results in drastic reduction in both the computational cost and the number of necessary steps for a composite quantum chemical method. The expanded uncertainty for the proposed methodology evaluated using a data set of 45 thoroughly vetted experimental values for molecules containing up to 12 heavy atoms is about 3 kJ·mol⁻¹, competitive with those of typical calorimetric measurements. For the compounds within the stated scope, the methodology is shown to be superior to a representative, more general, and widely-used composite quantum chemical method, G4.

Graphical Abstract

Introduction

The importance of reliable and readily-accessible values for the gas-phase enthalpies of formation (Δ_fH^○) of organic compounds is well recognized. Reliable experimental data are available only for a limited number of cases, resulting in a long history of estimation method development. The oldest and most widely used approach is the application of empirical group-contribution schemes.^1–3 Group-contribution methods are very accessible as they require almost no computational effort. However, they are limited both in scope (group value availability) and in accuracy (additivity approximation within the chosen group decomposition scheme). The alternative is the use of quantum chemical methods which are free of these limitations. Unlike the group-contribution approaches, quantum chemical methods do not yield Δ_fH^○ directly; it is derived from either the enthalpy of atomization or the enthalpy of suitable, preferably isodesmic, reaction (subject to availability of reliable experimental enthalpies of formation for all participants except for the one under consideration). The former approach can be formally viewed as a direct method, given tabulated experimental and precomputed data for all atoms involved. However, strong multireference nature of atomic configurations necessitates advanced quantum chemical calculations to obtain atomization enthalpies of acceptable accuracy. Practical application of quantum chemistry for prediction of Δ_fH^○ requires at least two steps: one needs (1) to obtain the optimized model geometry and its electronic energy (E) and (2) to compute vibrational frequencies needed for evaluation of zero-point vibrational energy (ZPVE) and the enthalpy change from 0 K to the reference temperature of 298.15 K (${\Delta }_0^{T}H$). These two calculations are very computationally-expensive and one has to use relatively low levels of theory and small basis sets even for moderately-sized compounds. Consequently, the energies obtained after optimization are rarely of acceptable accuracy and additional steps, in the form of single-point energy calculations at higher levels of theory and with larger basis sets, need to be taken. As using both at the same time is often also computationally-prohibitive, several multiple-step procedures were proposed, including Gaussian (Gn, n=1,2,3,4),^4–7 Complete Basis Set (CBS),^8–11 HEAT,^12,13 ATOMIC,^14,15 and Weizmann (Wn, n=1,2,3,4)^16–18 protocols; more sophisticated schemes are under active development.^19,20 Most of these approaches involve multiple single-point energy calculations with balanced combinations of theory levels and basis set sizes, thus reducing the overall computational requirements. The final energy is derived from the results of these multiple steps. It should also be noted that routine use of high-accuracy HEAT or the Wn theories is extremely computationally-expensive on modern mainstream hardware, even for moderately-sized molecules. Consequently, the “budget” Gn and CBS procedures presently dominate the practical estimation of the enthalpies of formation.^21–25 Most methods from these families approximate coupled-cluster with single, double, and perturbative triple excitations (CCSD(T)) level of theory with large (or extrapolated to infinite) basis set. Recent benchmarking for Δ_fH^○ derived from atomization enthalpies reported the best performance at the level of 2.5–3 kJ·mol⁻¹ standard deviation (s) for C/H/O systems²² and nitrogen-containing organics,²³ although reliable experimental data for nitrogen compounds are limited,^24,25 making large-scale assessment problematic.

This brings another issue related to the performance assessment: the method performance is normally evaluated by comparing predictions with reliable experimental data. The majority of Δ_fH^○ for organic compounds are determined from their energies of combustion measured in bomb calorimeters. This requires a few grams of a sample of very high purity, preferably above 99.9 %. The high purity is important since the relative standard uncertainty in the energies of combustion is typically about 0.02 %. Accurate chemical analysis of the combustion products is also necessary to achieve this data quality. This analysis is especially important for large molecules and cases involving heteroatoms. Furthermore, since bomb experiments are usually conducted with compounds in the condensed state, the enthalpy of vaporization or sublimation is required to derive the gas-phase Δ_fH^○. While the standard uncertainty in gas-phase enthalpies of formation is about 1 kJ·mol⁻¹ for state-of-the-art studies, uncertainties of a few kJ·mol⁻¹ are typical for the majority of the competent measurements. This imposes a limitation on determination of the performance metrics as one cannot achieve accuracy better than that of the data themselves.

The focus of this work is the development of a method for efficient estimation of Δ_fH^○ suitable for practical applications with moderate computational resources. Of note is the fact that most of composite (multiple-step) methods rely on numerical solution of exact model equations. However, a number of methods based on efficient approximate solution exist, and some of them have evolved to a level of practical maturity. Specifically, the “Resolution-of-Identity” (RI) (also referred to as “Density-Fitted”, DF) methods can substantially accelerate Self-Consistent Field (SCF), Density Functional Theory (DFT), and the Møller-Plesset second-order perturbation theory (MP2) calculations.^26–28 With the use of the RI approximations, the first step of a composite method, geometry optimization, can be conducted very efficiently and with significantly larger basis sets as compared to those that can be afforded in a course of the canonical solution. Furthermore, if a sufficiently accurate and efficient CCSD(T) approximation is available, one can bypass multiple steps and use this approximation with a large basis set as a final step of the method. The recently reported DLPNO-CCSD(T) approach^29–32 offers a very efficient and accurate approximation of the canonical CCSD(T) with nearly linear scaling of the computational time with the system size. Provided that the approximations are sufficiently accurate for the application considered here, a drastic reduction in computational time and memory requirements can be achieved or, alternatively, the calculations for very large molecules become possible. This represents the basic idea of the proposed method. The specific implementation details are given below.

Methods

Computational methods

In this study, we focus on efficient estimation of the enthalpies of formation for closed-shell compounds with compositions restricted to C, H, O, and N elements. We consider two methods, B3LYP-D3(BJ)³³ and RI-MP2, for geometry optimization and frequency calculations, and DLPNO-CCSD(T) for single-point electronic energy calculations. The balanced Karlsruhe “def2” triple- and quadruple-zeta basis sets³⁴ were used in these calculations. Additional computations with the popular G4 method, representative of the current budget composite methods, were also done for comparison. The direct estimation of the enthalpy of formation is performed with the following equation:

$${\Delta }_{\text{f}}{H}^{\circ }=E+\text{ZPVE+}{\Delta }_0^{T}H-\sum _{i=1}^N{n}_i{h}_i.$$ (1)

The summation in the last term of Eq. (1) is performed over all chemical elements present in the compound (N equals to 4 in this study); n_i is the ith element count, and h_i is the element-specific constant. Eq. (1) is mathematically equivalent to the derivation of Δ_fH^○ using the enthalpy of atomization, and h_i can be formally defined via computed atomic electronic energies, reference enthalpies of formation, and reference enthalpy changes for individual atomic species. The present implementation of DLPNO-CCSD(T) does not support open-shell systems, a restriction that does not apply to gas-phase atomic species in their ground states considered in this study. To circumvent this problem, we treat h_i as empirical constants and determine them from the regression analysis against the experimental data. This approach resembles earlier semi-empirical “atom-equivalent” proposals^35–37 to convert SCF and DFT energies to Δ_fH^○, but with the full rigor of explicitly accounting for ZPVE and ${\Delta }_0^{T}H$ terms. Our tests have shown that exclusion of these terms results in a nearly 4-fold increase in the standard deviation between the experiment and the model. It should also be noted that absolute DLPNO-CCSD(T) energies used in Eq. (1) are very sensitive to the DLPNO threshold parameters;³¹ consequentely, the h_i regression constants depend on them as well. “TightPNO” settings³¹ were used in all cases and need to be applied if h_i constants reported here are used to predict Δ_fH^○. The use of default, “NormalPNO” settings³¹ leads to larger data scatter, manifested in about 0.1–0.2 kJ·mol⁻¹ increase in the standard deviation and wider ranges of deviations between the experimental and predicted values. Because h_i constants are determined empirically using the experimental data, they are also expected to compensate, at least to some extent, for the deficiencies in the computed ZPVE and the lack of the post-CCSD(T)³⁸ contributions.

The computational schemes tested using the present approach are listed in Table 1. They include four schemes based on RI-MP2 geometries (“small”, “small+”, “medium”, and “large”); the naming follows an increase in the basis sets used in the scheme. Additionally, the combination based on B3LYP-D3(BJ) geometry, “medium-DFT”, with the basis sets corresponding to the “medium” scheme was tested. Energies in all schemes, except for the “small+”, were obtained from a single-point DLPNO-CCSD(T) calculation. The “small+” scheme is a test of a more complex composite protocol that includes additional MP2 energy correction, similar to the Gaussian theory methodology.⁵ In comparison with the “small”, “small+” includes an additional single-point RI-MP2/def2-QZVP calculation, and the DLPNO-CCSD(T)/def2-TZVP energy is corrected by the energy increment between the corresponding RI-MP2/def2QZVP and RI-MP2/def2-TZVP values.

Table 1:

Computational schemes tested^a

scheme	E	ZPVE & ${\Delta }_0^{T}H$
small	DLPNO-CCSD(T)/def2-TZVP//RI-MP2/def2-TZVP	B3LYP-D3(BJ)/def2-TZVP
medium	DLPNO-CCSD(T)/def2-QZVP//RI-MP2/def2-TZVP	B3LYP-D3(BJ)/def2-TZVP
large	DLPNO-CCSD(T)/def2-QZVP//RI-MP2/def2-QZVP	B3LYP-D3(BJ)/def2-TZVP
medium-DFT	DLPNO-CCSD(T)/def2-QZVP//B3LYP-D3(BJ)/def2-TZVP	B3LYP-D3(BJ)/def2-TZVP
small+	E (small) + A E (RI-MP2)b	B3LYP-D3(BJ)/def2-TZVP
G4c	G4	G4
G4-E	G4	B3LYP-D3(BJ)/def2-TZVP

a unless specified, Δ_fH^○ were computed via Eq. (1);

b ΔE(RI-MP2)= E(RI-MP2/def2-QZVP//RI-MP2/def2-TZVP)−E(RI-MP2/def2-TZVP//RI-MP2/def2-TZVP);

c Δ_fH^○ were computed via conventional atomization procedure using atomic data from Ref. 39

Finally, two schemes based on the popular G4 procedure were evaluated for comparison. The scheme labeled “G4” represents canonical G4 calculation of Δ_fH^○ via the enthalpy of atomization. The scheme “G4-E” is the case when only E was taken from the G4 results, while Δ_fH^○ was computed using Eq. (1) with ZPVE, ${\Delta }_0^{T}H$, and the h_i constants determined in the same manner as for the schemes based on DLPNO-CCSD(T).

From the initial tests, it was recognized that the vibrational frequency analysis needed for evaluation of ZPVE and ${\Delta }_0^{T}H$ terms posed a significant “bottleneck” in practical RI-MP2 calculations. To keep the computational costs down, the vibrational frequencies used in all proposed schemes (except for the canonical G4) were computed with B3LYP-D3(BJ)/def2-TZVP using the geometries optimized at the same level. For the schemes based on geometries other than those produced with B3LYP-D3(BJ)/def2-TZVP, this introduces an additional optimization step. However, the overall computational effort still remains lower as compared to the alternative of using RI-MP2 for frequency calculations. Prior to their use, the computed frequencies were scaled with the factors of 0.96 for hydrogen stretches and 0.985 for all other modes. The ${\Delta }_0^{T}H$ terms were evaluated using conventional rigid rotor - harmonic oscillator approximation,⁴⁰ and anharmonicities due to internal rotations were ignored. The compounds for which anharmonicities can significantly affect ${\Delta }_0^{T}H$ were deliberately avoided during the data set selection.

The assignments for scaling factors used here are consistent with reported recommendations^41–43 and the results do not show strong sensitivity to variations in their values. Their fidelity was also tested by including them in the optimization procedure along with h_i constants. This did not lead to significant performance improvements (standard deviation reduction was within 0.1 kJ·mol⁻¹) or variations in the scaling factor for the lower frequencies, but resulted in unrealistically low values of the scaling factor for hydrogen stretches, about 0.8.

All computations (except for G4) were performed with ORCA⁴⁴ v.3.0.3 package. The G4 calculations were performed with Gaussian 09.⁴⁵

Critically-evaluated data set

The data set of reliable, critically-evaluated experimental enthalpies of formation at 298.15 K for 45 compounds compiled from evaluated data reviews^39,46,47 and from the original experimental works is given in Table 2. Only cases with at least two independent experimental verifications were considered. If the values in the reviews were consistent and no new data were available, the recommended values from the reviews were used. Otherwise, the experimental data and their uncertainties were evaluated to identify outliers. The uncertainties included contributions due to repeatability, calibration, auxiliary compounds, and chemical analysis, if this information was available. The most reliable combustion energies were weight-averaged and the condensed-state enthalpies of formation were derived using the enthalpies of formation for carbon dioxide and water recommended by CODATA.⁴⁸ The uncertainties in the enthalpies of formation also included the uncertainties in Δ_fH^○ for reference compounds present in the combustion equations. Similar analysis for the enthalpies of vaporization and sublimation included both calorimetric results and temperature-dependent vapor pressures. An effort was made to achieve a balanced representation of different functional groups and to avoid cases exhibiting significant conformational ambiguity or, as mentioned earlier, vibrations with strong anharmonicity affecting evaluation of ${\Delta }_0^{T}H$ terms. The expanded uncertainties (0.95 confidence level) were below 2 kJ·mol⁻¹ in all cases. We note that much larger data sets with the same restrictions on elemental composition and electronic structure as applied here were reported in the literature (e.g., Ref. 37). However, the imposed strict requirements of the confirmed experimental accuracy are critical for robust determination of parameters in Eq. (1) and meaningful assessment of the method performance, and they firmly constrain any significant extension of the present set of compounds. It should be emphasized that development of the present data set (inclusive of the associated critical evaluation procedures) is significant and absolutely critical part of the present effort.

Table 2:

List of compounds, experimental Δ_fH^○, and deviations between the experiment and the calculations^a

		experimentalb			$({\Delta }_{\text{f}}{H}^{\circ },\text{exp}-{\Delta }_{\text{f}}{H}^{\circ },\text{calc})$ c
name	formula	${\Delta }_{\text{f}}{H}^{\circ }$	U	Ref.	S	M	L	M-DFT	S+	G4	G4-E
methane	CH4	−74.53	0.06	39	0.6	−1.7	−1.7	−1.6	−1.7	0.1	1.7
ethane	C2H6	−83.78	0.15	39	1.6	−0.3	−0.3	−0.2	−0.3	−0.6	1.1
propane	C3H8	−104.6	0.2	39	1.8	0.2	0.2	0.3	0.2	−1.2	0.8
butane	C4H10	−125.8	0.3	39	1.8	0.4	0.4	0.5	0.3	−1.5	0.8
isobutane	C4H10	−135.1	0.5	49–51	0.2	−1.5	−1.5	−1.4	−1.6	−2.5	−0.2
neopentane	C5H12	−168.0	0.8	46	1.0	−1.6	−1.6	−1.4	−1.6	−0.7	1.7
cyclohexane	C6H12	−123.3	0.8	46	1.1	0.2	0.2	0.3	0.1	−3.7	−1.9
ethylene	C2H4	52.53	0.14	39	2.3	0.3	0.3	0.1	0.7	0.2	1.1
propene	C3H6	20.3	0.3	39	1.8	0.3	0.3	0.2	0.6	−0.4	0.9
(E)-2-butene	C4H8	−11.2	0.5	39	0.8	−0.6	−0.6	−0.7	−0.5	−1.6	0.1
(z)-2-butene	C4H8	−7.3	0.5	39	−1.1	−1.8	−1.9	−1.9	−1.7	−3.2	−1.7
cyclohexene	C6H10	−5.0	1.0	52–54	0.8	0.4	0.4	0.4	0.5	−3.5	−2.5
norbornene	C7H10	81.9	1.7	55–57	3.7	2.7	2.6	3.0	2.8	1.0	1.7
1,3-butadiene	C4H6	110.0	1.0	46	−0.1	−1.7	−1.7	−1.9	−1.1	−1.8	−0.8
ethyne	C2H2	228.32	0.14	39	3.1	0.7	0.8	0.5	1.0	−0.5	−0.2
propyne	C3H4	185.1	0.5	58–60	2.5	0.0	0.2	−0.2	0.2	−0.7	−0.5
1-butyne	C4H6	165.4	0.9	39	1.4	−0.8	−0.7	−0.9	−0.7	−2.2	−1.7
benzene	C6H6	82.9	0.9	47	0.1	0.9	1.0	0.9	1.1	−1.8	−2.0
styrene	C8H8	148.0	1.4	46	−2.0	−1.4	−1.4	−1.7	−1.3	−1.1	−1.4
naphthalene	C10H8	150.6	1.5	47	−0.6	1.0	1.0	1.2	0.6	3.6	2.0
biphenyl	C12H10	180.2	1.8	61–68	−0.8	0.8	0.9	0.8	0.6	3.2	1.6
water	H2O	−241.83	0.04	48	−13.5	−0.4	−0.3	−0.5	−0.6	−1.8	−1.2
carbon dioxide	CO2	−393.51	0.13	48	9.6	1.5	1.5	1.9	2.0	3.6	1.6
methanol	CH 4 O	−200.7	0.2	39	−3.8	1.0	1.0	0.9	0.9	0.2	0.9
ethanol	C2H6O	−234.6	0.2	39	−3.8	0.9	1.0	0.9	0.8	−0.7	0.2
2-propanol	C3H8O	−272.8	0.4	39	−3.5	0.8	0.8	0.8	0.6	−0.9	0.3
2-methylpropan-2-ol	C4H10O	−312.5	0.8	46	−3.5	−0.2	−0.2	−0.1	−0.4	−0.2	1.2
phenol	C6H6O	−95.7	1.1	69–74	−7.8	−2.8	−2.7	−2.8	−2.8	−4.9	−5.6
1-naphthol	C10H8O	−27.5	1.7	75–77	−7.2	−1.7	−1.7	−1.4	−2.2	2.0	0.1
dimethyl ether	C2H6O	−184.0	0.4	39	2.6	0.7	0.7	0.5	0.9	0.7	1.6
anisole	C7H8O	−69.9	1.0	78–82	0.3	−0.3	−0.4	−0.6	−0.2	0.0	−0.7
methanal	CH 2 O	−109.16	0.11	39	6.5	2.1	2.1	1.9	2.8	2.7	2.3
ethanal	C2H4O	−165.5	0.3	39	4.6	0.8	0.8	0.8	1.2	0.6	0.6
propanone	C3H6O	−216.1	0.4	39	3.5	0.2	0.2	0.3	0.4	−0.3	0.0
formic acid	CH2O2	−378.5	0.2	39	1.9	1.3	1.3	1.2	1.2	0.2	−0.6
acetic acid	C2H4O2	−432.8	0.6	39	−1.2	−1.4	−1.4	−1.4	−1.8	−2.8	−3.4
benzoic acid	C7H6O2	−294.1	1.0	83, d	0.8	1.5	1.6	1.5	0.9	1.2	−0.9
ammonia	H3N	−45.56	0.03	39	−7.2	−0.2	−0.1	−0.2	−0.5	−2.8	−0.6
acetonitrile	C2H3N	74.0	0.3	46	11.0	2.2	2.4	2.4	2.8	1.2	2.0
urea	CH4N2O	−237.8	0.5	84–92	−5.5	−2.0	−2.0	−2.1	−2.8	−5.6	−3.6
piperidine	C5H11N	−47.3	0.8	93–97	2.2	2.6	2.6	2.8	2.7	−0.8	1.5
pyridine	C5H5N	140.4	0.7	46	5.5	2.0	2.0	2.0	2.6	0.6	0.8
aniline	C6H7N	87.1	1.2	98–102	−3.7	0.6	0.7	0.4	0.6	−1.5	−0.5
nitrobenzene	C6H5NO2	66.0	1.1	102–104,e	5.6	−1.7	−1.8	−1.5	−0.4	8.5	6.6
benzamide	C7H7NO	−99.8	1.0	98,99,105–109	−2.6	−1.7	−1.7	−1.7	−2.2	−2.1	−2.5
standard deviation					4.6	1.4	1.4	1.4	1.5	2.5	2.0

a energy units are kJ·mol⁻¹;

b U represents expanded uncertainty (0.95 level of confidence);

c S, M, L, M-DFT, and S+ refer to “small”, “medum”, “large”, “medium-DFT”, and “small+” schemes, respectively (see Table 1);

d enthalpy of sublimation was evaluated using the NIST ThermoData Engine 10.1 software¹¹⁰ with full list of literature sources available;¹¹¹

e the enthalpy of combustion reported in Ref. 103 was corrected to −(3086.7 ± 0.7) kJ·mol⁻¹ because the term for adjustment to the standard pressure (estimated to be 6 J·g⁻¹) had an incorrect sign; the resulting liquid-phase standard enthalpy of formation is 11.1 ± 1.0 kJ·mol⁻¹

Performance metric and uncertainty of predictions

For the main model performance metric, the standard deviation was used:

$$s=[{(\sum _{j=1}^M{({\Delta }_{\text{f}}{H}_j^{\circ },\text{exp}-{\Delta }_{\text{f}}{H}_j^{\circ },\text{calc})}^2)/(M-n_p)]}^{1/2},$$ (2)

where ${\Delta }_{\text{f}}{H}_j^{\circ }$, exp and ${\Delta }_{\text{f}}{H}_j^{\circ }$, calc are experimental and computed enthalpies of formation for the jth compound, respectively, M the total number of compounds in the data set, and n_p the number of optimized parameters (equals N for all schemes except for the canonical G4 method, for which it is zero).

For the model with optimized parameters, the standard uncertainty of the predicted value can be estimated as¹¹²

$$u({\Delta }_{\text{f}}{H}^{\circ })={[s^2+{\mathbf{\text{nVn}}}^{\mathbf{\text{T}}}]}^{1/2},$$ (3)

where n is the row-vector of the chemical element counts in the compound for which the prediction was made, and V is the covariance matrix:

$${\text{V=s}}^{\text{2}}{({\mathrm{N}}^{\text{T}}\text{N})}^{-1}.$$ (4)

In the above equation, N is the M × N design matrix of the linear least squares problem defined by Eq. (1) and composed of row-vectors of element counts for the compounds in the data set. Combining Eqs (3) and (4), one can obtain

$$u({\Delta }_{\text{f}}{H}^{\circ })=s{[1+{\text{n(N}}^{\text{T}}{\text{N)}}^{\text{-1}}{\mathrm{n}}^{\text{T}}]}^{1/2}.$$ (5)

As seen, the expression in the brackets of Eq. (5) has no dependency on the computational scheme used in the method; it depends only on compositions of the compounds in the data set and the compound for which the estimate is being made. It is, therefore, possible to precompute (N^TN)⁻¹ matrix for the data set adopted here and use it for a priori assessment of the relative contributions of the two terms in Eq. (5) to the standard uncertainty. The (N^TN)⁻¹ matrix computed for the present data set is given in Table 3. Clearly, some off-diagonal terms (e.g., carbon-hydrogen) are rather significant, indicative of the obvious fact that element counts in closed-shell organic compounds are correlated following the chemical bonding patterns. All off-diagonal terms are negative, suggesting the rate of uncertainty increase with compound size that is slower than what would be expected for uncorrelated element counts. For all compounds in the present data set (with sizes ranging from water to biphenyl), the term in Eq. (5) associated with (N^TN)−¹ can be neglected and u(Δ_fH^○) N is nearly equal to the corresponding standard deviation s.

Table 3:

Matrix (N^TN)⁻¹ from Eq. (5) computed for the data set listed in Table 2

	C	H	O	N
C	0.005073	−0.003146	−0.001 679	−0.000443
H	−0.003146	0.002 544	−0.000692	−0.001579
O	−0.001679	−0.000 692	0.037142	−0.008760
N	−0.000443	−0.001579	−0.008 760	0.103257

Finally, the commonly reported expanded uncertainty (coverage factor of 2, corresponding to 0.95 confidence for normal distribution) is twice of the standard uncertainty,

$$U({\Delta }_{\text{f}}{H}^{\circ })=2\times u({\Delta }_{\text{f}}{H}^{\circ }).$$ (6)

Results and Discussion

The results for all schemes are presented in Table 2 (deviations between the experiment and predictions for individual compounds and standard deviations for each scheme), Table 4 (regression constants h_i), and Fig. 1 (box-and-whisker diagram of deviation distributions). As seen, the “small” scheme based on def2-TZVP basis set yields rather high standard deviation of 4.6 kJ·mol⁻¹ and 3 outliers. Elevating the basis set for the singlepoint DLPNO-CCSD(T) energy calculations to def2-QZVP results in dramatic improvement over the “small” scheme. All three schemes using DLPNO-CCSD(T)/def2-QZVP energies, “medium”, ”large”, and ”medium-DFT”, exhibit very similar performance. They differ only in terms of the method used to generate the optimized model geometry; no noticeable effect on performance is observed for the choices tested (Table 2 and Fig. 1). The obtained regression constants h_i are also very close for these three cases (Table 4). The standard deviations for “medium”, ”large”, and ”medium-DFT” schemes do not exceed 1.5 kJ·mol⁻¹ (corresponding to about 3 kJ·mol⁻¹ expanded uncertainty), and they feature no apparent outliers. Δ_fH^○ for all compounds in the set are predicted within 3 kJ·mol⁻¹ for all three schemes. Among the three, “medium-DFT” is the most economical computationally and can be suggested as the first choice to consider. However, the other two schemes, “medium” and ”large”, do not pose significantly higher computational expenses and may be considered in situations that can benefit from the use of RI-MP2 geometries over those obtained with B3LYP-D3(BJ).

Table 4:

Regression constants −h_i in Eq. (1) for the tested computational schemes

	$-h_i/\text{kJ}\cdot {\text{mol}}^{\text{-1}}$
scheme	C	H	O	N
small	99 880.13	1516.17	197071.22	143562.88
medium	99 904.57	1525.81	197129.56	143 605.50
large	99 904.58	1525.78	197129.66	143605.53
medium-DFT	99 904.56	1525.80	197129.63	143605.41
small+	99 907.55	1527.03	197131.91	143608.06
G4-E	100044.38	1528.35	197275.39	143749.04

Figure 1:

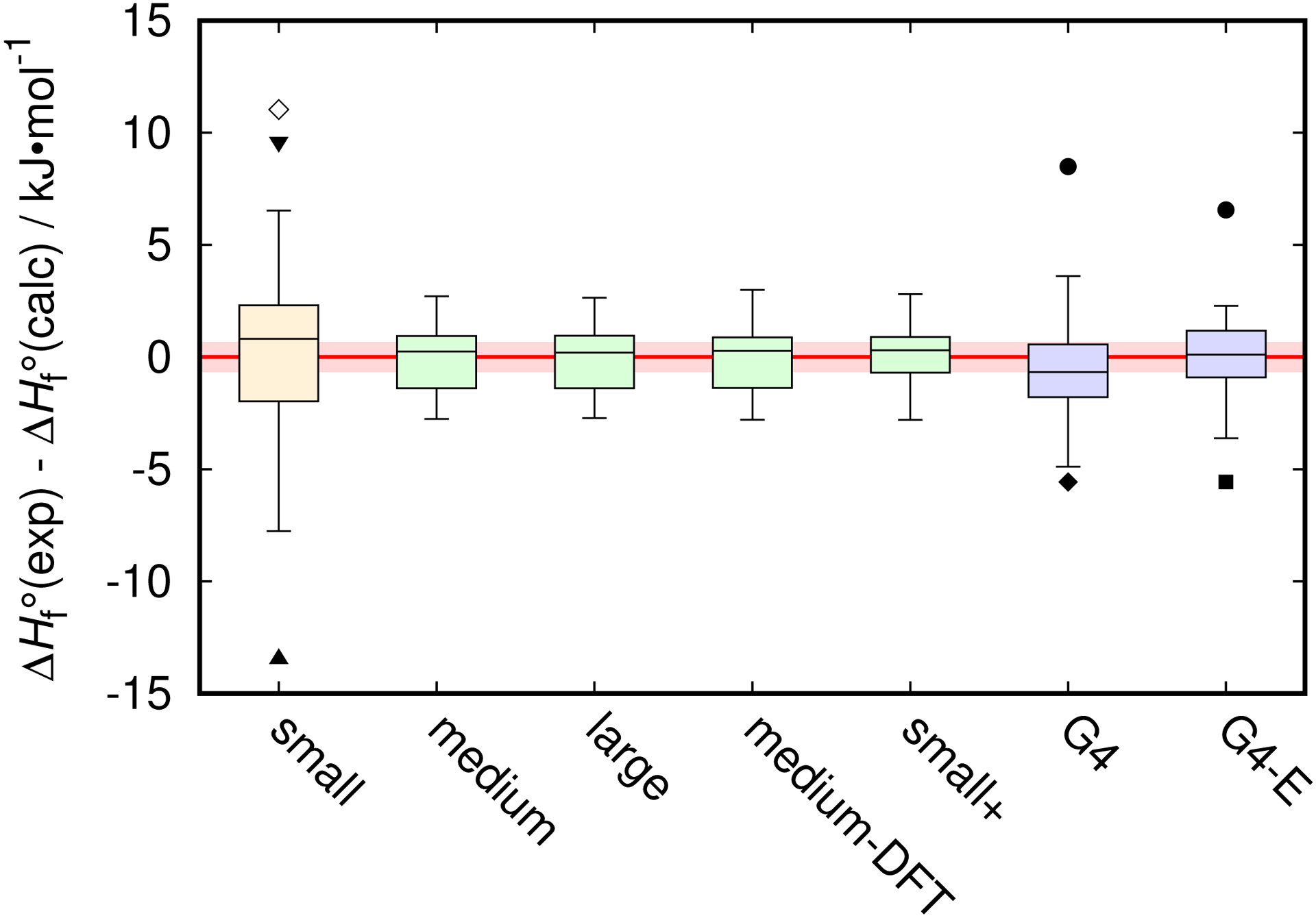
Box-and-whisker diagram of the deviations between the experimental and computed Δ_fH^○. Whiskers indicate data extrema within 1.5 of the interquartile range from the corresponding box edges.¹¹³ The outliers: ● - nitrobenzene, ◆ - urea, ■ - phenol, ▴ - water, ▾ - carbon dioxide, ◇ - acetonitrile. The shaded area represents a 50 % confidence interval (consistent with the box sizes) for the state-of-the-art calorimetric measurements corresponding to 0.95 confidence level of 2 kJ·mol⁻¹.

The “small+” scheme presents an interesting dilemma. Formally, it can be viewed as an intermediate case between the “small” and the “‘medium” schemes: instead of performing full DLPNO-CCSD(T)/def2-QZVP calculation as in the case of the “medium” scheme, the DLPNO-CCSD(T)/def2-TZVP energy of “small” scheme is corrected with the RI-MP2 energy increment due to basis set increase from def2-TZVP to def2-QZVP. The resulting standard deviation for the “small+” scheme is nearly the same as those for the three DLPNO-CCSD(T)/def2-QZVP-based methods discussed above (only about 0.1 kJ·mol⁻¹ increase). However, the distribution of deviations between the experimental and predicted values for this scheme appears noticeably different (Fig. 1). The deviations span over approximately the same range as for the DLPNO-CCSD(T)/def2-QZVP-based schemes, but the interquartile range (box size in Fig. 1) is smaller. This implies a narrower middle portion of the distribution with higher “tails”. More detailed analysis of the data in Table 2 indicates that the changes in the distribution are not uniform across the data set: while improvement is generally observed for the hydrocarbons (which represent the largest fraction of the data set), it is accompanied by some degradation of predictions for oxygenates and especially nitrogen-containing compounds, mainly responsible for the elevated “tails” of the distribution. This is not unexpected as oxygen and nitrogen contributions are more affected by the basis set size and the theory level. Therefore, although “small+” represents an attractive budget alternative, the DLPNO-CCSD(T)/def2-QZVP-based schemes are expected to be more reliable for the general use.

As seen in Fig. 1, the canonical G4 atomization scheme shows significant bias (systematically overpredicts Δ_fH^○) for the present data set, consistent with prior observations.²² Two outliers, urea and nitrobenzene, are present. “Parametrization” of G4 via Eq. (1), “G4-E” scheme, allows more objective comparison of G4 procedure with the present results by introducing the same set of adjustable parameters (it should be noted, however, that G4 energies already incorporate an empirical term, “the higher-level correction”⁷). “G4-E” does have significantly reduced bias as compared to the canonical G4. However, the outliers still persist (nitrobenzene and phenol), resulting in only moderate reduction in the standard deviation, from 2.5 to 2.0 kJ·mol⁻¹ (Table 2). With the outliers excluded, the remaining compounds are predicted within 4.9 and 3.7 kJ·mol⁻¹ for “G4” and “G4-E“ schemes, respectively. Comprehensive and scrupulous analysis of the original experimental data for the outliers exhibited by the G4-based methods (urea, phenol, and nitrobenzene) carried out in this study did not yield reasons to suspect significant experimental errors. Similar problem with the G4 method for nitrobenzene was reported previously, and the discrepancy was circumvented with an empirical correction.¹⁰⁴ Recent extensive G4 investigation¹¹⁴ suggested revision to the experimental Δ_fH^○ of phenol based on their theoretical findings. The reported G4 results¹¹⁴ are consistent with the present G4-based predictions. On the other hand, the deviation of the present DLPNO-CCSD(T)/def2-QZVP-based results from our critically-evaluated experimental value is within 2.8 kJ·mol⁻¹. Although it is one of the highest deviations for this data set, it remains within two standard deviations, giving no sufficient grounds for revision.

Finally, the computational performance of the presented procedures needs to be mentioned. The efficiency of the most expensive step, DLPNO-CCSD(T), was documented in detail by its developers.³² In the present study with the “TightPNO” settings,³¹ DLPNOCCSD(T)/def2-QZVP calculations took about 30 min for butane (4 heavy atoms) and 9.5 hours for biphenyl (12 heavy atoms) on 10 Intel Xeon E5–4617 CPU cores at 2.9 GHz with 100 Gb of RAM and 7200 rpm mechanical disk RAID storage. This performance opens possibility for large-scale applications of the presented methodology over a wide range of molecular sizes.

Conclusions

The proposed computational schemes provide simple and economical approach to estimate the enthalpies of formation of closed-shell organic compounds requiring only 3–5 steps performed using very cost-efficient approximations. The results obtained with the critically-evaluated experimental data set containing molecules with up to 12 heavy atoms suggest the expanded uncertainties of predicted values to be about 3 kJ·mol⁻¹, well below 4 kJ·mol⁻¹ of the target “chemical accuracy”¹⁹ and competitive with the typical experimental uncertainties. For the compounds within the stated scope, the proposed schemes were also found to be superior to the more general, budget composite method (G4) widely used at present. Due to their efficiency, the schemes can be used for large-scale validation of the existing data collections and emerging new data.¹¹⁵ Furthermore, as more accurate and efficient methods become available,¹¹⁶ the approach presented here can be easily upgraded via straightforward reparametrization of Eq. (1).