Genotype by environment interaction and heteroscedasticity influence the expression of parasite resistance in Katahdin sheep

Abstract

Increasingly, sheep producers are choosing breeds that express resistance to gastrointestinal parasites due to reduced efficacy of anthelminthic drugs. One such breed is Katahdin. Katahdins are raised in various climates and management systems in the United States, which can be combined into eco-management clusters to describe production environments more holistically. The objectives of this study were to determine if genotype by environment interaction (G × E) and heteroscedasticity existed across these eco-management clusters for traits indicative of parasite resistance. Body weights (BW), FAMACHA scores (FAM), and fecal egg counts (FEC) were collected at around 90 d in 3,527 Katahdin lambs delineated into nine eco-management clusters. A tri-variate animal model including birth-rearing type, sex, and dam age (as a quadratic covariate) as fixed effects, and eco-management cluster, direct additive, uncorrelated maternal environmental (for BW), and residual as random effects, was fitted with ASReml. Heritability estimates for BW, FEC, and FAM were 0.36 ± 0.07, 0.31 ± 0.07, and 0.26 ± 0.05, respectively. The genetic (additive) correlation between BW with FEC was −0.26 ± 0.08 and with FAM was −0.16 ± 0.08, and thereby favorable. Heritabilities were also estimated univariately within eco-management clusters and ranged from 0.30 ± 0.05 to 0.37 ± 0.05 for BW, 0.18 ± 0.12 to 0.50 ± 0.13 for FEC, and 0.07 ± 0.06 to 0.40 ± 0.19 for FAM. Significant genetic and phenotypic heteroscedasticity among eco-management clusters was detected in FEC and FAM. A sire by eco-management cluster interaction term was added to the initial model fitted to evaluate G × E. This interaction defined substantial variation (P < 0.01) in all traits and explained 12% (FEC) to 20% (BW) of the phenotypic variation. Accounting for G × E and heteroscedasticity in the design and implementation of breeding programs may introduce operational challenges. Still, doing so would improve the efficacy of selection programs to improve parasite resistance.

Climatic and management practices were combined into eco-management clusters to describe environmental conditions distinctive to subsets of Katahdin flocks. Across these clusters, heritabilities differed with evidence of genotype by environment interaction for traits indicative of parasite resistance with potential consequences on the design and implementation of breeding programs.

Introduction

In small ruminant, pasture-based systems, gastrointestinal nematode (GIN) parasitism is recognized to substantially affect animal performance and wellbeing, with economic consequences (Bowman, 2021). Since their introduction, anthelmintics have been used to treat GIN infections. However, increasing resistance of GIN to these treatments has been documented (Li et al., 2017). In the United States, the primary GIN of concern is the Haemonchus contortus, a blood-sucking nematode (Courtney et al., 1985). The parasite burden of H. contortus is commonly quantified using fecal egg counts (FEC). FAMACHA score (FAM) is a subjective measure of the impact of parasitism due to anemia based on the color of the ocular mucous membrane (Kaplan et al., 2004). By measuring both FEC and FAM, parasite resistance—the ability of the host to exert some degree of control over the pathogen life cycle—and resilience—the productivity of an animal in the face of infection—can be assessed (Bishop and Woolliams, 2014).

Variation in GIN resistance exists within and among sheep breeds (Vanimisetti et al., 2004; Brown and Fogarty, 2016) with genetic selection for resistance possible using indicator traits such as FEC and FAM. Selection based on these traits may, however, influence others of economic importance. Therefore, not only the heritability of these indicator traits but their correlations with other production traits need to be considered in the design of selection programs.

Katahdin are a relatively prolific maternal composite hair breed comparable to other medium-sized maternal breeds in adult body weight (BW) and lamb growth (Ngere et al., 2018). Katahdin sheep are distributed across the United States and thereby in production systems differing in climatic conditions and management practices. Arisman et al. (2023) combined these factors into eco-management clusters to holistically define the environmental conditions distinctive to subsets of flocks.

Eco-management clusters capture differences in production environments. Therefore, they likely reflect distinct environmental challenges (Arisman et al., 2023). Heteroscedasticity in additive and phenotypic variation in GIN resistance may therefore exist across eco-management clusters (Nakaoka et al., 2007), necessitating adjustment to genetic evaluation programs. Furthermore, interactions between animal genotypes and eco-management clusters may exist. The first objective of this study was to test for heterogeneity in variances across eco-management clusters in BW, FEC, and FAM in Katahdin sheep. The second objective was to test for genotype by environment interaction (G × E) for this same suite of traits in this breed. The relevance of these considerations in the implementation of genetic evaluation was discussed.

Materials and Methods

Animal handling and sample collection was conducted by the animal’s owner in participating commercial flocks and, therefore, did not require institutional animal care and use approval. Survey data were collected and stored in accordance with the University of Nebraska—Lincoln Institutional Review Board approval and standards.

Data collection

Over 3 yr (2017 to 2019), data were collected on 3,527 lambs from 142 sires and 1,855 dams spanning 17 Katahdin flocks from across the United States. These flocks were members of the National Sheep Improvement Program (NSIP; Notter, 1998), and volunteered to participate. The full pedigree consisted of 88,880 animals. The performance data included BW (kg), FEC (eggs/g), and FAM (1 = red or healthy; 5 = pale or anemic; Bath et al., 1996), collected in lambs at around 90 d of age (91.5 [SD 8.5] d). Drenching protocols were also available. The FEC were collected via stool samples directly from the rectum and quantified using the modified McMaster technique (Whitlock, 1948).

BW were adjusted to 90 d equivalents (Arisman et al., 2023). The FEC were not normally distributed and were therefore transformed as log(FEC + 25) (Ngere et al., 2018). The FAM were positively skewed with several transformations considered (log, square root, reciprocal). As described by Arisman et al. (2023), none significantly improved the distributional properties of the trait. For simplicity, and to facilitate interpretations, a Gaussian distribution for FAM therefore was assumed. Only FEC and FAM from animals for which no anthelmintic was given 30 d prior to measurement were used. The data were further edited for outliers with observations for BW, FEC, and FAM that were ± 4 SD from the mean removed.

Eco-management clusters

Eco-management clusters were defined to quantify environmental differences in climate and management practices among 40 Katahdin sheep producers across the United States engaged in NSIP (Arisman et al., 2023). These included the 17 flocks that also provided BW, FEC, and FAM data. The clusters were formed by combining climate data from the U.S. National Weather Service summarized over a 30-yr time frame (1991 to 2020) with management survey data collected in 2021 from the producers. A Factor Analysis on Mixed Data followed by Hierarchical Clustering on Principal Components were utilized to group flocks with similar management practices and climate data into eco-management clusters utilizing the Factoextra package in R (Mundt and Kassambara, 2020).

Performance records from the 17 flocks providing data were aligned with their eco-management cluster. This coincided with 9 of the 18 clusters identified. From an earlier study (Arisman et al., 2023), the combined eco-management clusters explained more variation in BW, FAM, and FEC than clusters based on climate or on management alone. The main environmental factors delineating the eco-management clusters were temperature, precipitation, grain supplementation while the lambs were on pasture, and the age of which lambs were introduced to pasture. Arisman et al. (2023) showed that these factors corresponded with risks of GIN parasitism. That said, the eco-management clusters were not delineated based on parasitism and, therefore, did not inherently represent differences in parasitism. Consequently, the nine eco-management clusters were used to capture the environmental challenge to parasite infection.

Model selection and parameter estimation

For each eco-management cluster, the number of observations for BW, FEC, and FAM are given in Table 1. Their means and distributions are provided in Table 2.

Table 1.

Number of observations for BW, FEC, and FAMACHA score by eco-management cluster and for the full dataset¹

Trait	Eco-management cluster									Full
	1	2	3	4	5	6	7	8	9
No. of lambs	763	498	625	460	315	183	334	31	318	3,527
BW	761	414	513	460	265	183	183	31	311	3,121
FEC	531	377	591	460	291	122	314	31	259	2,976
	614	498	625	460	131	183	202	31	313	3,057

¹Measures collected at around 90 d of age.

Table 2.

Mean, SD, and co-efficient of variation (CV) for BW (kg), log transformed FEC [log(eggs/gram + 25)], and FAMACHA (FAM, score) by eco-management cluster and for the full dataset¹

Trait	Statistic	Eco-management cluster									Full
		1	2	3	4	5	6	7	8	9
BW	Mean	18.96	26.32	22.03	23.23	24.51	26.63	18.23	24.83	29.78	22.39
	SD	4.48	4.43	5.79	4.64	5.68	6.41	3.06	4.88	7.44	6.54
	CV	0.24	0.17	0.26	0.20	0.23	0.24	0.17	0.20	0.25	0.29
Log FEC	Mean	2.70	2.64	2.62	2.71	2.46	2.73	2.88	3.22	2.34	2.66
	SD	0.69	0.75	0.64	0.48	0.59	0.55	0.56	0.64	0.48	0.77
	CV	0.26	0.28	0.24	0.18	0.24	0.20	0.19	0.20	0.21	0.29
FAM	Mean	1.48	1.79	1.67	1.70	2.15	2.57	1.86	2.17	2.30	1.85
	SD	0.70	0.78	0.71	0.74	1.04	1.06	0.74	1.03	0.72	0.83
	CV	0.47	0.44	0.43	0.44	0.48	0.41	0.40	0.47	0.31	0.45

¹Measures collected at around 90 d of age.

Systematic effect.

The systematic (fixed) effects included in the statistical models fitted were determined using stepwise regression in R (Venables and Ripley, 2002). The models tested included birth and rearing type (BR), which was defined as a concatenated variable with six levels: single-single, twin-single, twin-twin, triplet plus-single, triplet plus-twin, triplet plus-triplet plus, where the first adjective was the birth type, and the second adjective was the rearing type; a triplet plus indicated a triplet or higher birth or rearing type. There were limited instances of cross fostering. Birth year, the lamb’s sex (male, including castrates, or female), the linear and quadratic effect of its dam’s age (d), and the sex by BR interaction were also considered. For all three traits, only BR, the linear and quadratic effects of dam age, and sex defined significant variation (P < 0.05). These terms were included in the final models fitted.

Random effects.

Univariate analyses were conducted using ASReml V4.2 (Gilmour et al., 2021) to determine the most parsimonious animal model to fit. Beyond the systematic effects, the random effect terms initially considered were eco-management cluster, direct additive, uncorrelated maternal environment, and residual error. Eco-management cluster was fitted as a random to subsequently consider including a sire by eco-management cluster interaction effect if deemed appropriate. The assumption was that the distribution of phenotypes for a trait were homogenous across the eco-management clusters (Ducrocq et al., 2022).

A random contemporary group effect capturing the effects of flock, birth year, and management group combination was initially included in the models fitted. However, some eco-management clusters were defined by single flocks with data in a single lambing season, so fitting both eco-management cluster and contemporary group caused singularities in the design matrix. The contemporary group effect, therefore, was necessarily excluded.

Based on exploration of the data structure (Lewis and Beatson, 1999), there was little information available through maternal ancestry because of a limited number of dams and granddams with records; the maternal additive effect was therefore excluded. The significance of adding the uncorrelated maternal environmental effect to a model already including the eco-management cluster, direct additive and residual effects was tested using a log-likelihood ratio test (chi-square test with 1 degree of freedom; Woolf, 1957). The Akaike information criterion (AIC; Akaike, 1998) and Bayesian information criterion (BIC; Schwarz, 1978) were also considered in defining a “best fit” model for each trait.

Using the selected univariate model for each trait, a tri-variate animal model was also fitted that included eco-management cluster and direct additive covariances between traits. For BW, the model fitted included the uncorrelated maternal environmental effect.

The total phenotypic variance was estimated as the sum of the estimated variance from all components, including eco-management cluster. Direct (h²) heritabilities were calculated as the ratio of the direct additive and total phenotypic variances. The maternal environmental effect for BW was summarized as the ratio of its variance and the total phenotypic variance.

Heteroscedasticity

Separately for BW, FEC, and FAM, each eco-management cluster was defined as a distinct trait. Nine univariate models—one for each cluster—were then fitted within each trait that included the systematic, direct additive, and residual effects. For BW, an uncorrelated maternal environment effect was also included.

The log-likelihood value from the evaluation of each eco-management cluster was obtained. Since these clusters formed independent samples, log-likelihoods could be summed and compared against that from the full data. In the absence of heteroscedasticity, the sum of the log-likelihoods from the independent samples and the log-likelihood from the complete data would be expected to be equal (Márquez et al., 2015). A log-likelihood ratio test with 8 degrees of freedom was used to test whether the sum of the log-likelihoods from the independent clusters differed from the log-likelihood obtained with the full data.

Genotype by environment interaction

To investigate the presence of G × E, where the environment was defined by the eco-management cluster, univariate animal models were fitted adding a random sire by cluster (S × C) interaction term (Dickerson, 1962). Systematic and random effects were otherwise the same as those used in the analyses of the full data. To test for significance of the additional interaction term, a log-likelihood ratio test was performed. The ratio of S × C to total variance was calculated to quantify the extent of a G × E in the population.

To establish if the S × C interaction was caused by heterogeneous variances, the traits were standardized to the largest eco-management cluster. The models where each eco-management cluster was fitted as a separate trait were rerun. The standardization used was (Márquez et al., 2012):

$${\displaystyle \begin{array}{l}{\displaystyle t_i={{\displaystyle \widehat{\mu }}}_{C{L}_j}+z_i\times {{\displaystyle \widehat{\sigma }}}_{LCL}}\end{array}}$$ (1)

where t_i was the ith transformed observation for a trait for an animal i, ${\widehat{\mu }}_{C{L}_j}$ was the mean of the cluster to which the animal belonged, z_i was the standard normal deviate, and ${\widehat{\sigma }}_{LCL}$ was the SD of the cluster with the largest number of records (cluster 3). As noted by Márquez et al. (2012), this transformation ensured that the variances of t_i across eco-management clusters were homogenous. Differences in the estimates of the heritability would indicate persistence of heterogeneity.

Connectedness

To determine if biases in the estimates of S × C were a risk, familial relationships or connectedness among the eco-management clusters were calculated. These were based on prediction error co-variances among estimated breeding values for direct additive effects (Lewis et al., 2005; Kuehn et al. 2007, 2008). The greater the value of connectedness statistic, the less bias in predictions of breeding values. At a connectedness statistic threshold of 0.1, bias is nearly at its minimum indicating sufficient familial relationship between groups (Kuehn et al., 2007). Using BW as the representative trait, and its heritability of 0.36 derived from this study, connectedness correlations were determined among pairs of eco-management clusters. The animal model fitted included BR, dam age (as age categories 1, …, 5+), and sex as systematic effects, and direct additive and residual as random effects.

Results

Model selection and parameter estimation

The results of model selection are summarized in Table 3 for analyses of the full data. For FEC and FAM, only eco-­management cluster, direct additive effects, and residual effects were included in the final model selected. For BW, however, including the uncorrelated maternal environment effect explained significant additional variation in performance levels.

Table 3.

Random effects fitted in univariate models, and deviations of the log-likelihood ratio test (ΔLogL), AIC, and BIC from the model of best fit, for BW, log transformed FEC, and FAMACHA score¹

Trait	Random effects2	ΔLogL3	AIC4	BIC3
BW	${\sigma }_e^2$ , ${\sigma }_{em}^2$, ${\sigma }_a^2$	−28.08	54.15	47.92
	${\sigma }_e^2$ , ${\sigma }_{em}^2$, ${\sigma }_a^2$, ${\sigma }_c^2$	0	0	0
Log transformed FEC	${\sigma }_e^2$ , ${\sigma }_{em}^2$, ${\sigma }_a^2$	0	0	0
	${\sigma }_e^2$ , ${\sigma }_{em}^2$, ${\sigma }_a^2$, ${\sigma }_c^2$	−0.23	1.54	7.73
FAMACHA score	${\sigma }_e^2$ , ${\sigma }_{em}^2$, ${\sigma }_a^2$	0	0	0
	${\sigma }_e^2$ , ${\sigma }_{em}^2$, ${\sigma }_a^2$, ${\sigma }_c^2$	−0.31	1.62	4.50

¹Measures collected at around 90 d of age.

² ${\sigma }_e^2$ , residual variance; ${\sigma }_{em}^2$, eco-management cluster variance, ${\sigma }_a^2$, direct additive variance; ${\sigma }_c^2$, uncorrelated maternal (permanent) environmental variance.

³Minus two times the log-likelihood expressed as a deviation from the model chosen as the “best-fit” model (in bold). Effects were included sequentially. Positive values refer to an increase in the log-likelihood, indicating a “better” fit (with 1 df, threshold for significance of an effect was ${\mathrm{\chi }}_{\mathrm{\alpha }=0.01,1}^2=6.64$).

⁴Expressed as a deviation from the model chosen as the “best-fit” model (in bold). Positive values refer to a loss in information or “poorer” fit.

Heritabilities, and direct additive and phenotypic correlations, from the tri-variate analyses are shown in Table 4. The heritability estimates were 0.36 ± 0.07 for BW, 0.31 ± 0.07 for FEC, and 0.26 ± 0.05 for FAM. For BW, the uncorrelated maternal environmental variance ratio explained 8.3% of the total phenotypic variation. The phenotypic and genetic correlations between FEC and FAM were positive and moderate (0.39 ± 0.09) and low (0.15 ± 0.08), respectively. Body weight had favorable relationships with FEC and FAM, as indicated by their low to moderate negative correlations (−0.14 ± 0.11 to −0.26 ± 0.08).

Table 4.

Estimates of additive (${\sigma }_a^2$), eco-management cluster (${\sigma }_{em}^2$), and total phenotypic variances (${\sigma }_p^2$), and heritabilities and correlations, for BW (kg), log transformed FEC [log (eggs/g + 25)], and FAMACHA (FAM) score¹

Trait	${\sigma }_{\mathbf{a}}^{\mathbf{2}}$	${\sigma }_{\mathbf{e}\mathbf{m}}^{\mathbf{2}}$	${\sigma }_{\mathbf{p}}^{\mathbf{2}}$	BW	(Co)variance ratios2
					Log transformed FEC	FAM score
BW3	15.64 (1.19)	13.67 (8.12)	43.78 (8.15)	0.36 (0.07)	−0.14 (0.11)	−0.18 (0.08)
Log transformed FEC	0.20 (0.05)	0.09 (0.06)	0.64 (0.08)	−0.26 (0.08)	0.31 (0.07)	0.39 (0.09)
FAM score	0.21 (0.04)	0.13 (0.03)	0.77 (0.06)	−0.16 (0.08)	0.15 (0.08)	0.26 (0.05)

¹Measures collected at around 90 d of age.

²Heritabilities are provided on the diagonal in bold, additive genetic correlations are provided below the diagonal, and phenotypic correlation are provided above the diagonal. Standard errors of estimates are shown in parentheses.

³Uncorrelated maternal (permanent) environment variance was estimated as 3.62 ± 0.47 kg².

Heteroscedasticity

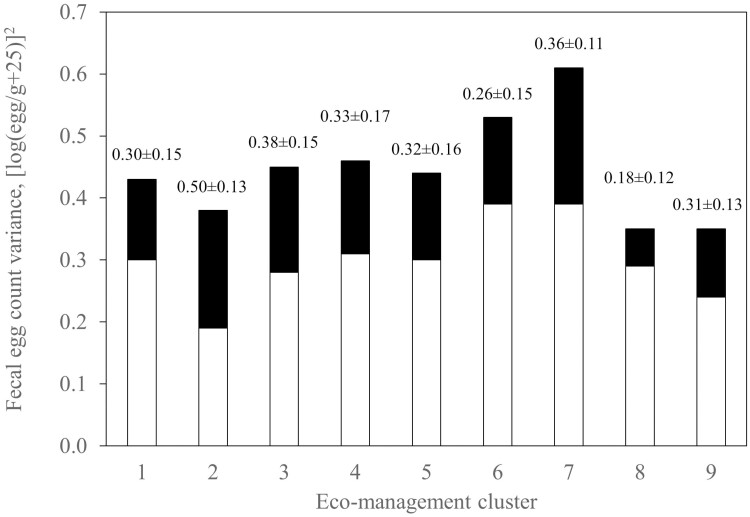
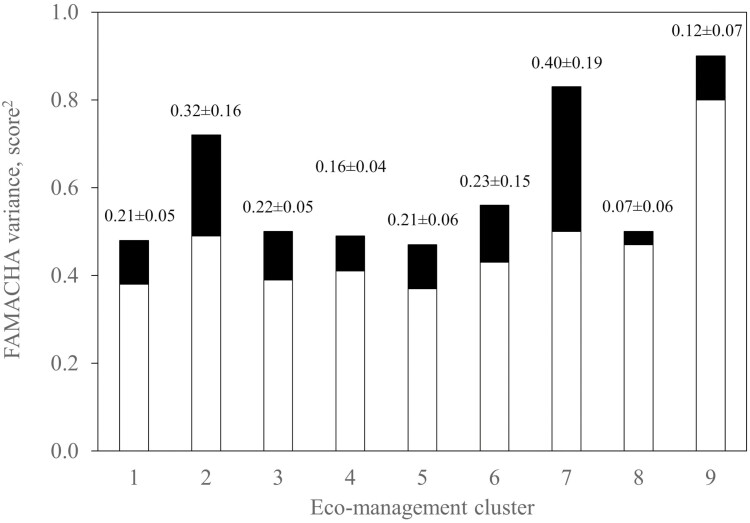
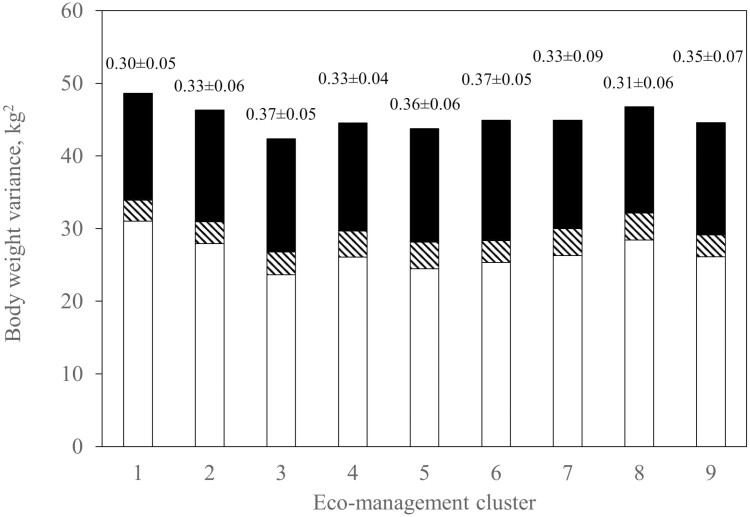
When the data were separated into eco-management clusters there was evidence of heterogeneity in variance for FEC and FAM based on the log-likelihood ratio test (P < 0.01; Table 5). From the heritabilities estimated from the univariate analysis for each cluster within a trait, the ratios of additive to phenotypic variances differed among eco-management clusters for FEC (Figure 1) and FAM (Figure 2). However, such was not the case for BW (Figure 3). Even once standardized for differences in phenotypic variances, the heritability estimates for FEC and FAM varied among clusters (data not shown). Therefore, heteroscedasticity in both direct additive and phenotypic variance was evident in these two traits, but not in BW.

Table 5.

Log-likelihood values for test of heteroscedasticity in BW, log transformed FEC, and FAMACHA score

Comparison	BW	Log transformed FEC	FAMACHA score
Sum independent samples log-likelihood values1	−5945.12	−464.33	−680.73
Full data log-likelihood value2	−5978.19	−266.03	−577.31
Log-likelihood ratio test3	−66.14	396.61	206.84

¹Sum of log-likelihood values for data separated as different traits for each eco-management cluster.

²Log-likelihood value for data combined across eco-management clusters.

³Minus two times the log-likelihood expressed as a deviation between the sum of the log-likelihoods from the independent samples and the log-likelihood from the full data. Positive values refer to an increase in the log-likelihood, indicating a “better” fit (with 8 degrees of freedom, threshold for significance was ${\mathrm{\chi }}_{\mathrm{\alpha }=0.01,8}^2=20.09$).

Figure 1.

Additive (black) and residual (white) variance in log transformed FEC [(log(egg/g + 25))²] by eco-management cluster. The ratio of additive to phenotypic variance (heritability ± s.e.) is given above each bar of the histogram.

Figure 2.

Additive (black) and residual (white) variance in FAMACHA (score²) by eco-management cluster. The ratio of additive to phenotypic variance (heritability ± s.e.) is given above each bar of the histogram.

Figure 3.

Additive (black), uncorrelated maternal (permanent) environment (diagonal stripes), and residual (white) variance in BW (kg²) by eco-management cluster. The ratio of additive to phenotypic variance (heritability ± s.e.) is given above each bar of the histogram.

Genotype by environment interaction

For the three traits, including the S × C term improved model fit as indicated by a log-likelihood ratio test, and the AIC and BIC (Table 6). The heritability was lower for BW when the model included (0.26 ± 0.06) vs. excluded (0.36 ± 0.07) this interaction term, although with only small changes in the other two traits. Correspondingly, the ratio of the S × C to the total variance was lower for FEC and FAM than for BW (Table 7).

Table 6.

Comparison of univariate models including vs. excluding a sire by eco-management cluster interaction for BW, log transformed FEC, and FAMACHA score

Trait	ΔLogL1	AIC2	BIC2
BW	135.56	−269.13	−262.88
Log transformed FEC	28.93	−55.85	−49.71
FAMACHA score	53.09	−104.18	−97.98

¹Minus two times the log-likelihood expressed as a deviation between the sum of the log-likelihoods from the model including vs. excluding a sire by eco-management interaction. Positive values refer to an increase in the log-likelihood, indicating a “better” fit (with 1 degrees of freedom, threshold for significance was ${\mathrm{\chi }}_{\mathrm{\alpha }=0.01,1}^2=6.64$).

²AIC and BIC expressed as deviations between the model including vs. excluding a sire by eco-management interaction. Positive values refer to a loss in information or “poorer” fit.

Table 7.

Estimates of variances and heritabilities for the genotype by environment interactions models for BW (kg), log-transformed FEC [log(eggs/g + 25)], and FAMACHA (FAM, score) as observed and standardized for heterogeneity in phenotypic variation among eco-management clusters¹

	Observed scale			Standardized scale2
	BW	Log FEC	FAM	BW	Log FEC	FAM
Additive variance	11.05 (1.50)	0.17 (0.02)	0.16 (0.03)	10.01 (0.88)	0.16 (0.03)	0.11 (0.03)
S × C variance3	8.28 (1.55)	0.07 (0.01)	0.12 (0.03)	7.80 (0.77)	0.06 (0.02)	0.08 (0.03)
Heritability4	0.26 (0.06)	0.33 (0.05)	0.23 (0.05)	0.25 (0.03)	0.32 (0.06)	0.18 (0.05)
G × E4,5	0.20 (0.05)	0.13 (0.03)	0.17 (0.03)	0.19 (0.05)	0.12 (0.03)	0.12 (0.03)

¹Standard errors of estimates are shown in parentheses. Measures collected at around 90 d of age.

²Total phenotypic variances were standardized to the SD of the largest eco-management cluster as per model (1).

³Sire by eco-management cluster interaction.

⁴Heritability and G × E are without units.

⁵G × E defined as the proportion of sire by eco-management cluster variance as a proportion of total phenotypic variance.

When the phenotypic variances across eco-management clusters were standardized for heteroscedasticity, the same trend held true. The direct additive and S × C variance, and their corresponding ratios with phenotypic variances, in general, only decreased slightly following the standardization (Table 7). The reductions were somewhat larger with FAM.

Connectedness

Among pairs of eco-management clusters, the connectedness correlations ranged from 0.04 to 0.57. Kuehn et al. (2008) showed that correlations of 0.10 and higher were indicative of strong connectedness, with minimum bias in the estimation of breeding values in a genetic evaluation. Only one eco-management cluster (cluster 9) was poorly connected with the others, with connectedness correlations of less than 0.10. Predictions of breeding values and comparisons of parameter estimates, therefore, suffered from little bias due to these strong levels of connectedness. For the one cluster with the low connectedness value, the risk of bias in the estimates was greater.

Connectedness is typically established through sharing of sires across flocks. In the current data, the most represented sire had progeny in three eco-management clusters. Most sires, however, only had progeny in one eco-management cluster. The high level of connectedness among most eco-management clusters was through ancillary relatives of sires.

Discussion

Parameter estimation

With moderate heritabilities, and favorable genetic correlations, there is opportunity to increase BW and improve parasite resistance concurrently through selection. Such could also be deduced from previous studies. Safari et al. (2005), Fogarty (1995), Van Wyk and Bath (2002), Riley and Van Wyk (2000), and Ngere et al. (2018) reported similar ­estimates for heritabilities and genetic correlations for these traits.

In the current study, eco-management cluster was fitted as a random effect, with its variance included in the total phenotypic variance. In other studies, this proxy for a contemporary group effect would instead be considered fixed. When excluding the eco-management variance from the total phenotypic variance, the heritabilities were higher as expected (BW: 0.52 ± 0.08; FEC: 0.36 ± 0.07; FAM: 0.31 ± 0.05), although still broadly consistent with literature values. Excluding the eco-management (co)variances had little effect on estimates of phenotypic correlations.

The range in heritability estimates across eco-management clusters for FEC (0.18 to 0.50) also aligns with those reported elsewhere for Katahdin lambs within NSIP flocks (Notter, 2013; Notter et al., 2017; Ngere et al., 2018). Like this study, the findings of Notter (2013) were based on a limited sample of flocks and years. Even with our constraints in data size, the variation in heritability estimates across eco-management clusters indicates that selection responses among flocks may differ depending on their environmental conditions.

Maternal effects were not observed for FEC. Such was also the case for Ngere et al. (2018), Pollott and Greeff (2004), and Huisman and Brown (2009). Even so, due to the size and structure of the current data, the suite of possible genetic and environmental maternal factors that may affect performance levels could not be fully explored. Ngere et al. (2018), for instance, hypothesized that maternal influences on a litter, including dominance, might impact FEC in lambs. Such effects may be unique to a litter due to the grazing patterns of an ewe, and thereby her offspring, on infected pasture (Ngere et al., 2018). Further investigations of maternal effects on parasite resistance would clearly be worthwhile.

Correlations between FEC or FAM with BW were small to moderate and negative between the traits in agreement with Ngere et al. (2018). Such negative correlations are favorable. They suggest that individuals with a greater potential for growth also have lower FEC and FAM, and therefore greater parasite resistance. The slight negative phenotypic correlations between FEC and FAM with BW also indicate that lighter lambs are at greater risk to a parasite challenge.

The direct additive and phenotypic correlations between FEC and FAM were low (0.15 ± 0.08) and moderate (0.39 ± 0.09), respectively. These positive correlations suggest that animals that are more resistant to a parasite challenge (lower FEC), may also be more resilient to such infection (lower FAM). In addition, these positive correlations support the presence of H. contortus in the GIN infection as higher FEC coincided with evidence of greater anemia (Ngere et al., 2018).

Heteroscedasticity

Heteroscedasticity across eco-management clusters was observed in FEC and FAM, but not in BW. From the fit of univariate models in which each eco-management cluster was considered a separate trait, significant heterogeneity in phenotypic variance was detected in FEC and FAM. When comparing heritability estimates, the proportion of phenotypic variance defined by additive effects also varied among eco-management clusters. Such remained the case even once standardizing to a common phenotypic variance for all clusters. Taken together, there was clear heteroscedasticity in both the direct additive and phenotypic variance for FEC and FAM.

For BW, additive and phenotypic variances were homogenous across eco-management clusters. This is consistent with Canavesi et al. (1995) and Márquez et al. (2015), who also did not detect heteroscedasticity in BW across production environments.

Ignoring heterogeneous variances in a genetic evaluation risks reranking of sires across environments (Santana Jr et al., 2013). Some of the risks can be mitigated through the implementation of a heterogeneous variance model as done in other livestock species (Gianola, 1986; Nakaoka et al., 2007). Another approach to mitigate such bias would be to strengthen connectedness among the eco-management clusters, or among production environments generally. In sheep, where artificial insemination is less common, this can be achieved through designed breeding programs in which rams are shared among flocks (Lewis and Simm, 2000). The progeny of these shared sires create genetic relationships among flocks and thereby environments (Kuehn et al., 2008; Márquez et al., 2015).

Genotype by environment interaction

Variation defined by sire by eco-management interaction was used as a predictor of G × E (Dickerson, 1962). The ratio of the S × C to phenotypic variance was slightly lower in FAM and FEC as compared to BW. This indicates that G × E may have more influence on BW than indicator traits specific to parasitism. Still, in the three traits considered, G × E defined a substantial proportion of phenotypic variability (12% to 20%).

When adding S × C to the statistical model, the heritability of BW and, to a smaller extent, FAM was reduced. That was due to a portion of additive variance being partitioned to G × E, as also observed by Márquez et al. (2015) and Ngere et al. (2018). Although the reduction was small, the heritabilities for BW and FAM decreased further when observations within eco-management clusters were standardized to the same phenotypic variance as the largest cluster (cluster 3). Notably, the phenotypic variance of that cluster was intermediary to others.

FEC exhibited substantial G × E in accordance with Carrick and van der Werf (2007). Although that study involved a different breed of sheep (Merino), they reflected flocks managed across the diversity of climates found in Australia. Bishop (2012) suggested that variation in parasite challenge and nutritional resources across environments may lead to reranking of animal performance, consistent with a G × E. In the current study, the FEC varied considerably across eco-management clusters. Furthermore, although H. contortus was presumed to be the primary GIN species associated with parasitism, such was not verified. Carrick and van der Werf (2007) reported that G × E may reflect the population structure of the GIN infection. Therefore, worm species admixture in a parasite challenge would be anticipated to affect the expression of G × E in FAM.

Connectedness

Misztal (1990) proposed that a small sire by herd interaction could be explained by sires having progeny in few herds. In the current study, sires were not well-represented across eco-management clusters. The most well-represented sire had progeny in only three of the nine clusters. However, genetic connectedness was strong among eight of the clusters, reflecting genetic relationships established through ancillary relatives of sires. Despite limited direct sharing of sires, sufficient connectedness was still present to allow reliable estimation of parameter values including interactions between sires and eco-management clusters.

Implications

In selection programs animals are often reared in different environments. Therefore, ignoring G × E in genetic evaluation may lead to reductions in selection response (Garrick and Van Vleck, 1987; Mulder and Bijma, 2006). Even though disregarding G × E may increase selection intensity, response may be slower because of a decrease in selection accuracy (Slagboom et al., 2021). By accounting for G × E, genetically superior individuals could be more reliably identified benefiting the outcomes of a breeding program.

When G × E is present, breeding programs may need to be modified to account for the differences in genetic expression across environments. A common across-flock breeding goal remains appropriate. However, the mating design may benefit from strategic use of sires across eco-management clusters. With enough progeny per sire within each of the collaborating flocks, stronger connectedness would be established among clusters. The estimate of a sire by eco-management cluster interaction would thereby be improved.

Although important, incorporating G × E into a routine genetic evaluation has complications. Perhaps most challenging would be defining pertinent eco-management clusters. For this study, these clusters were derived from a multivariate analysis of climatic and management data using principal component loadings to group flocks into environmental categories (Arisman et al., 2023). Since management practices change, such an exercise would need to be repeated periodically.

Perhaps an alternative approach for accommodating G × E would be through utilizing random regression. Ducrocq et al. (2022) included individual climate variables (e.g., temperature, solar radiation, perception) as a reaction norm variable in a random regression model. They compared solutions to identify the most important climate variables contributing to G × E. A potential modification would be to substitute and test individual principal component loadings as the climate variable.

Conclusions

Resistance to GIN infection is moderately heritable with favorable genetic correlations with BW. However, there was heterogeneity in both direct additive and phenotypic variances across environments (eco-management clusters) in FEC and FAM. A significant G × E was also detected in all three traits and defined substantial phenotypic variation. Accounting for such heteroscedasticity and G × E in the design and implementation of breeding programs, despite operational challenges, may improve the efficacy of selection programs to improve parasite resistance.

Glossary

Abbreviations

AIC

Akaike information criterion

BIC

Bayesian information criterion

BW

body weight

S × C

sire by eco-management cluster interaction

FAM

FAMACHA score

FEC

fecal egg counts

GIN

gastrointestinal nematode

G × E

genotype by environment interaction

NSIP

National Sheep Improvement Program

Conflict of Interest Statement

The authors declare no real or perceived conflict of interest.