Effect of nanoparticle loading and magnetic field application on the thermodynamic, optical, and rheological behavior of thermoresponsive polymer solutions

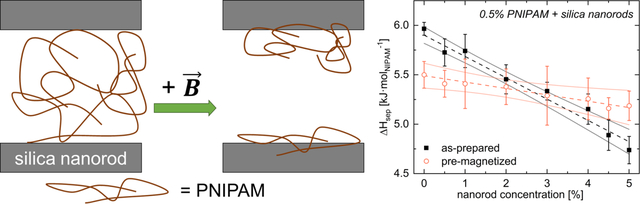
Abstract

Although processing via external stimuli is a promising technique to tune the structure and properties of polymeric materials, the impact of magnetic fields on phase transitions in thermoresponsive polymer solutions is not well-understood. As nanoparticle (NP) addition is also known to impact these thermodynamic and optical properties, synergistic effects from combining magnetic fields with NP incorporation provide a novel route for tuning material properties. Here, the thermodynamic, optical, and rheological properties of aqueous poly(N-isopropyl acrylamide) (PNIPAM) solutions are examined in the presence of hydrophilic silica NPs and magnetic fields, individually and jointly, via Fourier-transform infrared spectroscopy (FTIR), magneto-turbidimetry, differential scanning calorimetry (DSC), and magneto-rheology. While NPs and magnetic fields both reduce the phase separation energy barrier and lower optical transition temperatures by altering hydrogen bonding (H-bonding), infrared spectra demonstrate that the mechanism by which these changes occur is distinct. Magnetic fields primarily alter solvent polarization while NPs provide PNIPAM-NP H-bonding sites. Combining NP addition with field application uniquely alters the solution environment and results in field-dependent rheological behavior that is unseen in polymer-only solutions. These investigations provide fundamental understanding on the interplay of magnetic fields and NP addition on PNIPAM thermoresponsivity which can be harnessed for increasingly complex stimuli-responsive materials.

Graphical Abstract

1. INTRODUCTION

Stimuli-responsive polymers and soft materials have shown incredible potential for applications that require dynamic, tunable, and functionalized materials. These systems have been designed to respond to a wide range of external stimuli such as shear,^1–3 temperature,^4–9 pH,^6,10 small molecules,^6,8,9,11 electric fields,^12,13 and magnetic fields.^14–18 Application of external fields can alter the microstructure and orientation of these responsive materials, facilitating control of macroscopic properties such as optical clarity,^19–21 thermal and electrical conductivity,^22–24 small molecule transport,^6,25,26 and mechanical strength.^23,24,26 In contrast to external stimuli such as shear and electric fields, magnetic fields are a particularly promising external field for processing soft materials as they provide a homogeneous, contactless stimulus without compromising the mechanical and chemical stability of the system.^27,28

The magnetically-induced response of diamagnetic materials, such as the polymers and anisotropic particles discussed in this work, are usually driven by the alignment of anisotropic constituents.^29–31 The magnetic force driving this alignment is proportional to the magnetic susceptibility anisotropy, Δχ, which originates from the electromagnetic anisotropy of chemical bonds.^29,31 This effect on the molecular level yields magnetically-induced alignment behaviors in various constituents with overall shape anisotropy such as polymer chains, semi-crystalline polymers, block copolymer phases, and various polymer additives.^18,29–31 This effect can enhance ordering, increase grain size, and induce/align block copolymer phases and has been leveraged for widespread applications in adhesives, biotechnology, and storage media.^29,32

While the majority of prior work examining magnetic field effects in polymeric systems has focused on neat polymers, the behavior of polymer solutions in magnetic fields can be complicated by the presence of solvent, which often experiences magnetically-induced effects independent of the presence of polymer. Vshivkov and co-workers showed that applying magnetic fields can increase the phase separation temperature in diamagnetic polyelectrolyte solutions, though the presence of this effect depends on solvent type.^33,34 The magnitude of changes in separation temperature were dependent upon the ability of the polyelectrolytes to align in solvents, with more polar solvents leading to lower changes in separation temperature.³⁴ Vshivkov et al. also examined flexible polymer melts and solutions in magnetic fields, noting an increase in crystallization temperature of polyethylene, also attributed to chain orientation along magnetic field lines.³³

Magnetic fields also drive changes in water, altering hydrogen bonding (H-bonding) and the structure of water, which subsequently changes macroscopic properties such as specific heat and boiling point.^35–43 Application of magnetic fields have been shown to alter the polarization of electrons in water molecules, impacting molecular vibrations and the strength of their hydrogen bonds.^35,37,40 Sronsri et al. demonstrated that changes in the Raman and infrared spectra of water due to magnetization depend on magnetization time and magnetic field strength.⁴⁴ Variations in the polarization of water impact the solubility of certain small molecules,^42,44 transport of ions,^37,40,42 and thermal conductivity.^37,40,42

Aqueous poly(N-isopropyl acrylamide) (PNIPAM) is an ideal system for examining responsive behavior under a range of external stimuli, as this well-studied thermoresponsive polymer displays a lower critical solution temperature transition around 32 °C in aqueous solution.^45–47 Above the transition temperature, PNIPAM chains dehydrate and liberate water molecules, forming inter- and intra-chain PNIPAM hydrogen bonds.^46,47 At low concentrations (c~0.01% wt.) – typically used to deposit thermoresponsive coatings or to develop drug delivery vectors^10,48,49 – dehydrated PNIPAM chains aggregate into stable mesoglobules that remain suspended in water.⁴⁷ The formation of these mesoglobules leads to an optical transition where the transition temperature can be characterized via turbidimetry.⁴⁵ At higher concentrations (c≳1% wt.), these mesoglobules can coarsen into physical hydrogels, often used for tissue engineering,⁵⁰ water desalination,⁵¹ and flow controllers.⁵² The properties of these physical hydrogels, such as their swelling and de-swelling kinetics,⁵³ can be controlled via nanoparticle (NP) addition.^54–56 Grafting thermoresponsive polymers to NPs also aids in self-cleaning and can prevent fouling in polymer nanocomposites, highlighting the utility of these mixed polymer/NP systems.⁵⁷ Given that the properties of water can be controlled via magnetic fields and that PNIPAM-water interactions and phase separation behavior can be altered via NP addition, the thermodynamic and optical transitions in aqueous PNIPAM can likely be controlled in unique ways via a combination of temperature, field application, and NP inclusion.

Hydrophilic silica NPs disrupt hydrogen bonding interactions between PNIPAM amide groups and water by providing surface hydroxyl and siloxane groups for H-bonding,^54–56 enabling a fine tuning of the optical and thermodynamic properties associated with phase separation.^54,58 Through these H-bonding interactions with PNIPAM amide groups, hydrophilic silica NPs partially dehydrate PNIPAM, decreasing the entropic penalty for PNIPAM dehydration and collapse^59,60 and the required enthalpy for phase separation, ΔH_sep.^54,55,58 Liberation of hydrogen bonds between water and the amide group and restructuring of water molecules in hydration shell surrounding PNIPAM both contribute to the energy required for phase separation.^55,61,62 Beyond altering PNIPAM-water hydrogen bonding, NP addition can increase physical network connectivity following phase separation, increasing mechanical properties such as viscosity and dynamic moduli.^56,63–65

Recently, we showed that the reduction in phase separation enthalpy (ΔH_sep) with silica NP addition for aqueous PNIPAM is largely dominated by changes in NP surface area and surface charge – rather than NP aspect ratio – in the limit where the NP size is much larger than the polymer size.⁵⁶ In this regime, NP curvature is inconsequential and changes in ΔH_sep and Fourier transform infrared spectroscopy (FTIR) signatures with NP aspect ratio can be explained by normalizing to the total NP surface area, and by accounting for differences in NP ζ-potential (zeta-potential) caused by changes in surface silanol density.⁵⁶ At high NP aspect ratio (A8, A14), NP-containing solutions had the highest colloidal stability (highest magnitude ζ₋potential) and NP surface properties such as surface silanol density and mesoporosity were virtually independent of NP aspect ratio.⁵⁶ Interestingly, despite small changes in thermodynamics, significant differences in the rheological behavior of PNIPAM-NP solutions were observed with NP aspect ratio. Here, longer NPs led to higher dynamic moduli as the temperature increased above the onset of transition.⁵⁶

As the application of magnetic fields^35,37,40 and introduction of silica nanoparticles⁵⁶ are known to alter hydrogen bonding in poly(N-isopropyl acrylamide) and water, respectively, here we examine the application of magnetic fields and NP addition on the thermodynamic, optical, and rheological properties of aqueous PNIPAM. Here, anisotropic NPs with an aspect ratio (A = L/D) of 8 are used, as they require significantly lower concentrations than isotropic NPs to induce anisotropy in microstructure and macroscopic properties.^60,66–69 Additionally, A8 NP-containing PNIPAM solutions provide good modulus enhancement upon temperature elevation, and are also colloidally stable and less prone to settling in dilute polymer solutions than higher A NPs.⁵⁶ Supplementary experiments utilizing longer NPs (A14) with similar surface properties⁵⁶ and spherical NPs (A1) are used to further strengthen the findings (SI.25). Using a combination of Fourier-transform infrared spectroscopy (FTIR), magnetoturbidimetry, differential scanning calorimetry (DSC), and magneto-rheology, the solution behavior of PNIPAM is examined in the presence of magnetic fields, NPs, and both magnetic fields and NPs to determine how polymer-solvent interactions are altered to impact the thermoresponsivity. Changes in the phase separation enthalpy and optical transition temperatures detected by DSC and magneto-turbidimetry are linked to altered polymer-solvent interactions measured via FTIR; these properties are then used to rationalize unique steady shear flow behavior observed in magneto-rheology. These investigations provide fundamental understanding on how the interplay between external field application and NP addition can be used to control application relevant solution properties like optical transmission and steady shear flow behavior, providing a new route for developing soft materials with well-controlled stimuli-responsiveness.

2. EXPERIMENTAL

2.1. Materials

Hexanes (mixture of isomers, >98.5%), 1,4-dioxane (>99.0%), and sodium citrate dihydrate (>99%) were used as received from Sigma-Aldrich. Diethyl ether (99%, stabilized), 1-pentanol (99%) and tetraethyl orthosilicate (98%) were used as received from Acros Organics. Tetrahydrofuran (Fisher scientific, >95%, stabilized), was used as received. Poly(vinyl pyrrolidone) (Alfa Aesar, 40 kDa, powder), ethanol (Pharmco-Aaper, 200 proof), and ammonia (Supelco, 25% (v/v)) were used as received. 2,2’-Azobis(2-methylpropionitrile) (AIBN, Sigma-Aldrich, 98%) was recrystallized three times in methanol and dried under vacuum. N-isopropyl acrylamide (NIPAM, Fisher scientific, 98.0%, stabilized) was purified via sublimation. Distilled water was used as received. The chain transfer agent (CTA) for RAFT polymerization, 2-(ethylsulfanylthio-carbonylsulfanyl)-2-methylpropionic acid (EMP), was synthesized per the method presented in SI.1.

2.2. Synthesis of poly(N-isopropyl acrylamide homopolymers)

N-isopropyl acrylamide (NIPAM, 12.5 g, 1105 equiv.), EMP (22.5 mg, 1 equiv.), and AIBN (1.65 mg, 0.1 equiv.) were mixed in 54 mL 1,4-dioxane and degassed three times via freeze-pump-thaw cycles. Polymerization occurred at 70 °C for 18 hours in a mineral oil bath and terminated through quenching in liquid nitrogen and exposure to air. Product was purified through three subsequent precipitations using THF and 3:2 diethyl ether: hexanes a total of three times and vacuum dried overnight at 40 °C. Polymer characterization data (Nuclear-magnetic resonance (NMR), Size-exclusion chromatography) are provided in SI.2 and show the product has number-averaged molecular weight (M_n) = 87 kDa and Ð = 1.43; in this work, the polymer is designated by the code P87 for poly(N-isopropyl acrylamide) (PNIPAM) of 87 kDa.

2.3. Nanoparticle synthesis and purification

Silica nanorods were synthesized following established procedures from Murphy^70,71 and Kuijk.¹² In short, 30 g of poly(vinyl pyrrolidone), 300 mL of 1-pentanol, 30 mL ethanol, 8.4 mL deionized water, 2 mL of 0.18 M aqueous sodium citrate, and 6 mL of 25% (v/v) ammonia were added, with 60 seconds of vortexing between each component. To initiate synthesis 4.5 mL of tetraethyl orthosilicate (TEOS) was added in two equal additions, six hours apart. After each addition, reactors were gently swirled for ten seconds to mix. About 18 hours after initiation, nanoparticles were purified and fractionated using the centrifugation protocol described in SI.3. Then, nanoparticles were dried under vacuum at 50 °C, ground with a mortar and pestle, and calcined in a crucible in air at 500 °C for 5 hours to remove residual polymer and organics.

2.4. Silica nanoparticle characterization

Silica NP size and shape were characterized using a JEOL 6010 scanning electron microscope operated at 5 kV; a characteristic image is shown in Fig. 2. NPs were suspended in ethanol and drop cast onto a stainless-steel plate to image. ImageJ software was used to analyze approximately 150 particles to provide statistical distributions of length, diameter, and aspect ratio (A = L/D), shown in Fig. 2. The aspect ratio of resulting nanorods was 8, designated A8 NPs (see explanation in SI.4 for a description on nanorod growth shape). BET surface area and DLS ζ-potential (zeta-potential) analyses are provided in SI.5 and SI.6, respectively; results show nanoparticles have high surface roughness and good colloidal stability in water.

FIGURE 2.

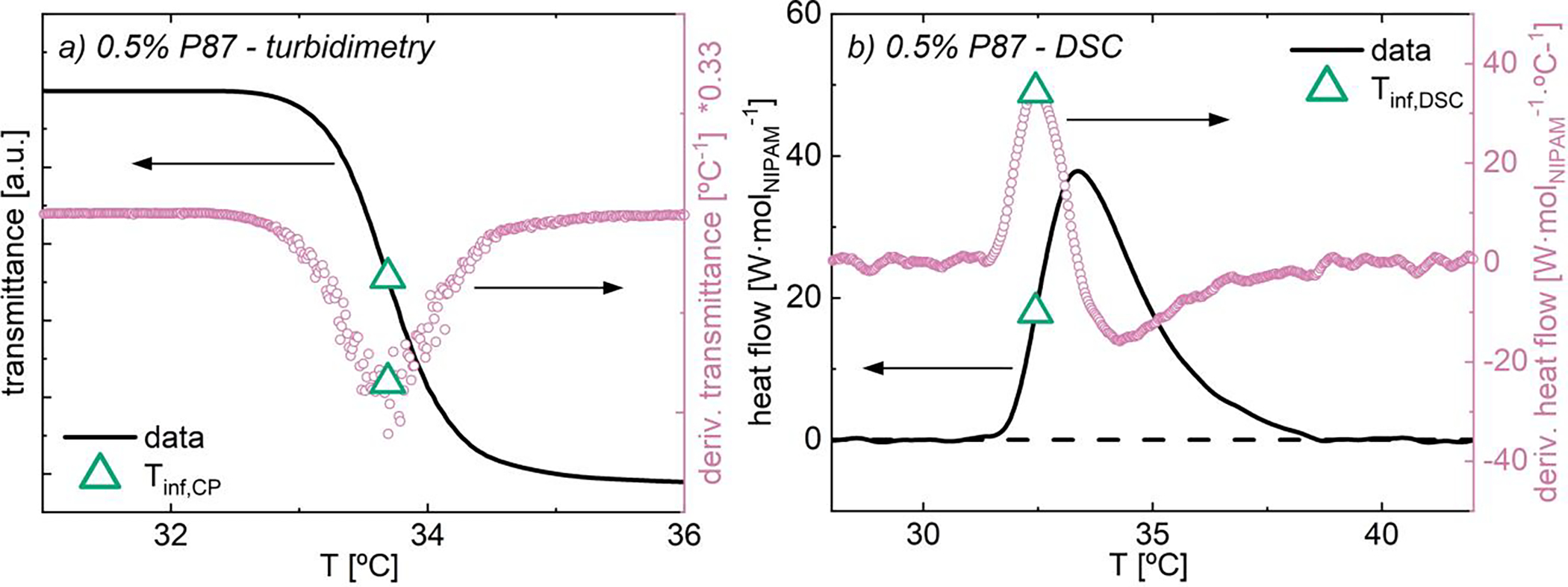
(a) Transmittance and (b) heat flow as functions of temperature for 0.5% P87 in water. Data collected at (a) 0.2 °C/min and (b) 1 °C/min. Overlain are derivatives of (a) transmittance and (b) heat flow, as well as inflection separation temperatures (T_inf; hollow green triangle) for each method.

2.5. Polymer-nanoparticle sample preparation

Polymer-nanoparticle aqueous suspensions were created with 0.5% PNIPAM and between 0 and 5% A8 silica nanoparticles. For differential scanning calorimetry experiments, silica concentrations of 0, 0.1, 0.19, 0.3, 0.4, 0.5, 1, 2, 3, 4, 4.5 and 5% were used. For turbidimetric experiments, only silica contents up to 0.4% silica were used due to absorbance of light from particles. For simplicity, codes of x% P87/ y% A8 NPs were used, where x signifies the P87 concentration and y signifies the silica concentration.

Solutions in the absence of NPs are called ‘bare’. All percentages were based on mass fractions of the total target solution mass.

For each solution, the appropriate amount of dry silica nanorods were added to a 2 dram vial. The appropriate amount of dry polymer and then water were subsequently added. Vials were capped and shaken with vortex mixing for approximately 1 minute and sonicated under ice for approximately 6 hours to thoroughly break up aggregates. The solutions were then shaken under refrigeration for at least 4 days. To counteract any potential settling which occurs over the course of half a day, solution vials were vortex mixed on medium for approximately 30 seconds to re-suspend particles and sonicated for 5 seconds to remove air bubbles immediately before use.

2.6. Turbidimetry measurements

Turbidimetric transition temperatures were quantified using a visible light cell modified in-house to allow for in situ magnetic field application (see SI.12 for setup). Light transmittance as a function of temperature was measured using semi-micro 2 mL 10 mm pathlength acrylic cuvettes, a red laser (5 mW, class 3R, 650 nm), and a standard CdS photoresistor. A cartridge heater and PTD thermocouple control the temperature of the cell (resolution = 0.03 °C), and a Peltier module and CPU fan provide active cooling. All components are controlled by an Arduino Uno. Transmittance was recorded from 25 °C to 40 °C at a rate of 0.2 °C/min. For in situ magneto-turbidimetry, various combinations of neodymium permanent magnets were used to apply 80, 140, 200 and 340 mT during investigation; higher magnetic field strengths were not practical due to the use of permanent magnets. Further, pre-magnetized solutions were run by holding the solution in a magnetic field (~180 mT) for 3 days prior to magneto-turbidimetry with 200 mT in situ application (see SI.11). To account for potential evaporation during pre-magnetization, equivalent as-prepared solutions were also allowed to sit for three days. Due to the use of permanent magnets to apply magnetic fields in situ, fields above 340 mT were not practical in this examination.

An example turbidimetric transition trace of transmittance versus temperature is provided for as-prepared 0.5% P87 in Fig. 1a. The derivative of transmittance with respect to temperature is overlaid in pink circles. The turbidimetric transition temperature, T_inf,CP, is defined as the minimum in the derivative of transmittance, corresponding to the inflection point of transmittance. In Fig. 1a, T_inf,CP is shown as a hollow green triangle. Data analysis information and full results are provided in SI.14.

FIGURE 1.

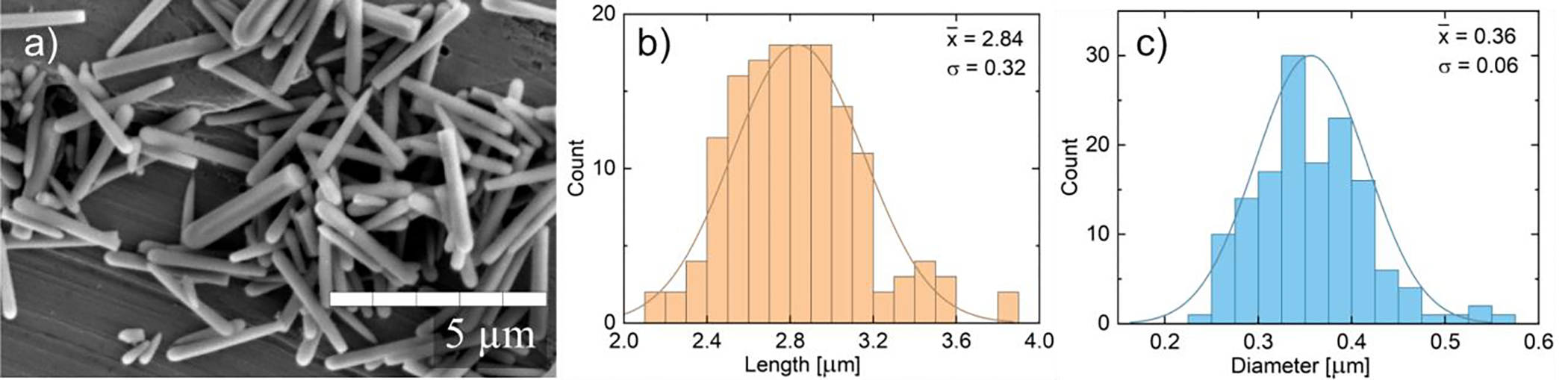
(a) SEM images of silica nanorods with aspect ratio A8 at 10,000x magnification. Nanorods were drop-cast from ethanol onto stainless steel multi-well plate. Scratches in background correspond to imperfections on plate surface. See the SI for more images and to compare similar magnifications. Distributions of length (b) and diameter (c) are also provided, showing average and standard deviation of each dimension.

2.7. Fourier-transform infrared (FTIR) spectroscopy

FTIR spectra were collected using a Thermo Nicolet 6700 spectrometer using attenuated total reflection (ATR) mode to probe the effects of silica nanoparticles and magnetic field application on intermolecular modes. Solutions for pre-magnetization were placed on neodymium permanent magnets for at least 3 days (see SI.15). Using a Gauss meter, the average magnetic field acting on the solution during pre-magnetization was ~150 mT; higher magnetic field strengths were not practical due to the use of permanent magnets. To account for potential evaporation during pre-magnetization, equivalent as-prepared solutions were also allowed to sit for three days. Approximately 2 uL of solution used for each examination. 64 scans were collected for each solution from 650 cm⁻¹ to 4000 cm⁻¹ with a reported resolution of 0.964 cm⁻¹. Data was baseline corrected through the Thermo Fisher software. Thorough assignments for FTIR peaks and vibrational modes are provided in SI.15.1. Sronsri et al. found that magnetic increases on the FTIR intensity of water persisted for up to 48 hours; as spectra were collected in under 2 minutes temporal relaxation during collection was assumed to be minimal.⁴⁴

2.8. Differential scanning calorimetry (DSC)

Phase separation enthalpy was quantified as functions of NP content and pre-magnetization using a TA Instruments DSC Q2000 and hermetically-sealed aluminum Tzero pans (~ 20 μL solution). Pans were loaded at 20 °C and equilibrated at 20 °C for 1 minute. The temperature increased from 20 °C to 50 °C at a rate of 1 °C/min; see Fig. 1b for an example of heat flow vs. temperature for 0.5% P87. Data was baseline-corrected utilizing a tangential sigmoid model through TA Instruments Universal Analysis software which draws baselines tangent to data from 25–30 °C and 42–48 °C. The integral of phase separation peaks results in an enthalpy of separation, ΔH_sep, which was normalized to the mass of solution and moles of NIPAM, [kJ/mol_NIPAM]. Pre-magnetized solutions were loaded into Tzero pans and held between neodymium permanent magnets (~ 230 mT) for 3 days prior to quantification (see SI.8); higher magnetic field strengths were not practical due to the use of permanent magnets. Pans were removed from magnet immediately prior to trial. To account for potential evaporation during pre-magnetization, equivalent as-prepared solutions were also allowed to sit for three days.

An example of heat flow versus temperature for as-prepared 0.5% P87 is provided in Fig. 1b. The derivative of heat flow with respect to temperature is shown in hollow pink circles. The thermodynamic phase separation temperature, T_inf,DSC, is defined as the maximum in the derivative of heat flow, corresponding to the inflection point of heat flow. In Fig. 1b, T_inf,DSC is shown as a hollow green triangle. Data analysis information and full results are provided in SI.9.

2.9. Magneto-rheological flow curves

Viscosity as a function of shear rate was collected on an Anton Paar MCR 702 stress-controlled rheometer with an MRD180/1T magneto-rheological device and 20 mm parallel plate operating at a 0.5 mm gap. Extensive calibration studies were used to ensure the temperature acting on the solution was within 20 ± 0.1 °C for all times, shear rates and magnetic field strengths. Prior to examination, solutions were sheared at 10 s⁻¹ for 5 min and then allowed to recover at 0.1%, 0.1 rad/s for 5 min. Solutions were then pre-treated under oscillatory shear (0.1%, 0.1 rad/s) at the respective magnetic field strength for 20 min. For each shear rates, viscosity was collected over 4-second points for 50 points; the average and standard deviation of viscosity were then extracted from the final 25 points for each respective shear rate. Data was fit utilizing Mathworks MATLAB curve fitting software which also provides 95% confidence intervals for fitting parameters.

2.10. Magneto-rheological temperature ramps and amplitude sweeps

Dynamic moduli as a function of temperature were collected on the MRD180/1T accessory (Sec. 2.9). First, solutions were sheared at 10 s⁻¹ for 5 min and then oscillated at 0.1%, 0.1 rad/s for 5 min. Solutions were then pre-treated under oscillatory shear (1%, 1 rad/s) at their respective magnetic field strengths for 20 min. Using the same oscillatory shear and field parameters, the dynamic moduli were recorded during temperature ramps from 20 °C to 40 °C, at a temperature ramp rate of 0.2 °C/min. Once at 40 °C, solutions were allowed to recover at 0.1%, 0.1 rad/s for 10 min. Finally, dynamic moduli were collected across strain amplitudes from 0.1% to 1000% under their respective magnetic field strengths.

3. RESULTS AND DISCUSSION

3.1. Magnetic field impacts on poly(N-isopropyl acrylamide) (PNIPAM) thermodynamic and optical transitions

Turbidimetry on bare 0.5% 87 kDa poly(N-isopropyl acrylamide) (P87) solutions demonstrates that magnetic field application shifts the pseudo-sigmoidal optical transmittance curves to lower temperatures with minimal change in curve shape (Fig. 3a). The inflection point in these curves, T_inf,CP, decreases linearly with increasing field strength, by −1.2 °C/T up to 0.34 T (Fig. 3b). Here, T_inf,CP is the temperature where long-range polymer aggregation increases most rapidly and is a function of system specific parameters such as polymer-solvent interactions and additives (or fillers) containing hydrophilic interacting sites.^10,49 Further, this inflection point is characteristic of S-shaped transitions and is relatively insensitive to changes in magnitude of the transmittance change or transition width,⁴⁵ enabling accurate comparison between solutions with varying polymer, solvent, and additive content.

FIGURE 3.

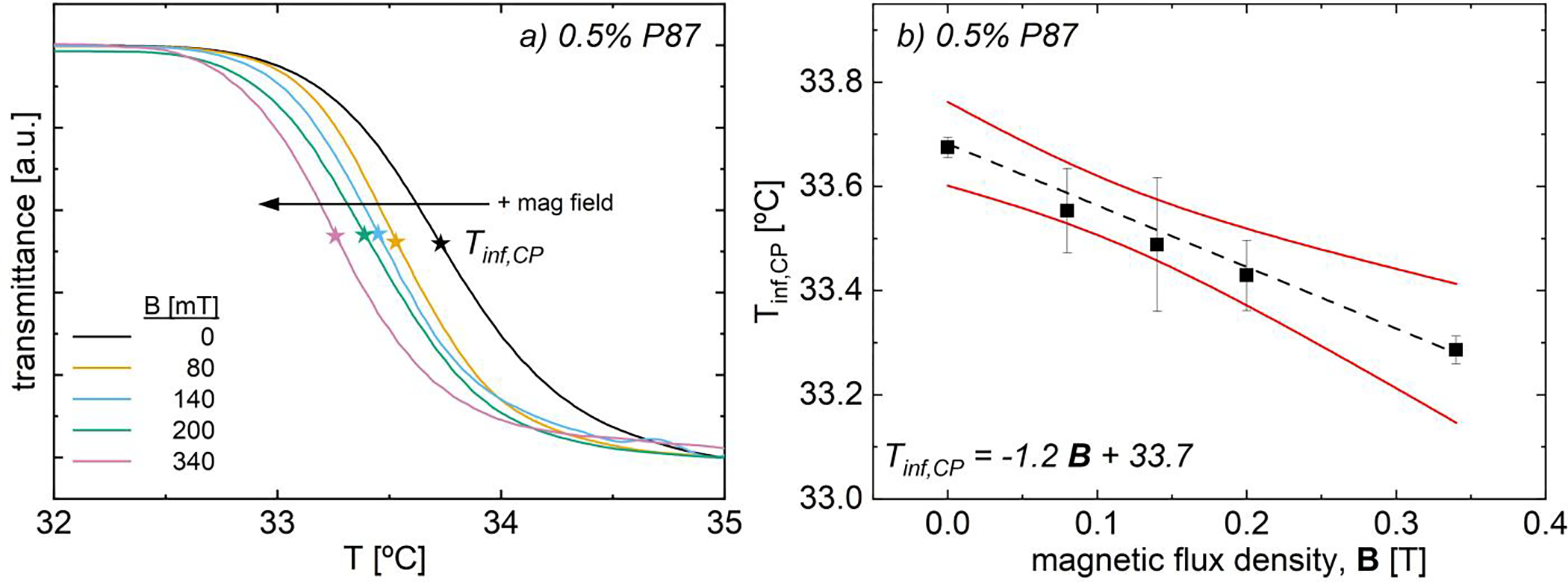
(a) Transmittance as a function of temperature and magnetic field strength for bare 0.5% P87. (b) Turbidimetric inflection temperature, T_inf,,_CP vs. field strength. T_inf,CP decreases linearly with 𝐵 (−1.2 °C/T, black dashed line); 95% confidence band is in solid red lines.

The decreasing T_inf,CP with increasing field strength suggests that magnetic fields decrease the affinity for polymer-solvent interactions, making transition more favorable at lower temperatures; in contrast, Vshivkov and co-workers noted increases in phase transition temperatures in polyelectrolyte and polymer solutions.^33,34 With little change in the curve shape or width, magnetic fields do not appear to dramatically vary the PNIPAM aggregation pathway, but only the temperature at which the optical transition occurs (Fig. 3a). Magnetic fields change the polarization of water molecules,⁴⁴ which has dramatic impacts on the thermodynamic properties of pure water^{35–38,40,44} and the interactions with other species in aqueous environments.^{36,39,41–43} As polymer-solvent interactions are thermodynamically unfavorable above the transition temperature, a decrease in T_inf,CP with increasing field strength may suggest that magnetic fields decrease the favorability of PNIPAM-water H-bonds, such that transition and aggregation occur at lower temperatures (Table 1).

TABLE 1.

Turbidimetric and thermodynamic transition inflection temperatures, T_inf,CP and T_inf,DSC′, phase separation enthalpy, ΔH_sep; and DSC heat flow full width at half-maximum, FWHM_DSC for 0.5% P87 solutions a function of magnetic field flux density. Note that turbidimetry was run with magnetic field in situ whereas DSC solutions were pre-magnetized.

Magnetic Field [mT]	Tinf,CP [°C]	Tinf,DSC [°C]	Δ Hsep kJ/molNIPAM	FWHMDSC [°C]
0	33.7 ± 0.0	32.45 ± 0.01	5.97 ± 0.06	2.40 ± 0.02
80	33.6 ± 0.0
140	33.5 ± 0.1
200	33.4 ± 0.1	32.46 ± 0.01	5.50 ± 0.13	2.36 ± 0.02
340	33.3 ± 0.0

To further explore field-induced changes in thermodynamics, bare 0.5% P87 solutions were ‘pre-magnetized’ prior to differential scanning calorimetry (DSC), resulting in a net decrease in phase separation enthalpy, ΔH_sep, of ~8% (Table 1). For corresponding non-magnetized, ‘as-prepared’ solutions, ΔH_sep = 5.97 ± 0.06 kJ/mol_NIPAM (Table 1), in agreement with the widely accepted range of 4.6 to 7.1 kJ/mol_NIPAM depending on PNIPAM molecular weight and end groups.^55,72,73 For both as-prepared or pre-magnetized solutions, DSC traces exhibit a single broad peak beginning around 31 °C that slowly taper above 40 °C (see SI.9.3 for raw data). Interestingly, the DSC inflection point temperature, T_inf,DSC,, and full-width half-maximum (FWHM) of the heat flow trace are not impacted by pre-magnetization (Table 1). The only noticeable change in the DSC trace due to pre-magnetization is a decrease in the maximum heat flow, which leads to a lower ΔH_sep; this negligible change in peak shape suggests that magnetic fields do not dramatically impact the PNIPAM dehydration pathway, in agreement with magneto-turbidimetry (Fig. 3a).

The reduction in ΔH_sep and the temperature onset of the optical transition suggest a decreasing favorability for PNIPAM-water hydrogen bonding (H-bonding) with field application, which may be due to weaker and/or fewer hydrogen bonds. Prior Raman spectroscopy by Sronsi and co-workers suggests that pre-magnetization of pure water results in a net increase dipole moment and higher hydrophilicity of water molecules;⁴⁴ their results are consistent with Fourier-transform infrared (FTIR) spectra on 0.5% P87 solutions at ambient conditions, which exhibit similar increases in the peak intensity in regions corresponding to water-water H-bonding (3000–3600 cm⁻¹, Fig. S62). Though the magnitude of these intensity increases with pre-magnetization is small (~1% increase), these differences are similar to those previously observed (~5%⁴⁴) and are statistically significant and reproducible across solutions and acquisitions; see SI.15.3 for confidence intervals, raw data, and additional analysis.

Similar to the findings on 0.5% P87 solutions, Sronsri and coworkers saw no change in peak positions in magnetized water, concluding that peak intensity changes corresponded to alignment of water dipoles and consequently disruption of water molecule structure.⁴⁴ These findings suggest that pre-magnetizing 0.5% P87 solutions thus increases the difference between the polarity of PNIPAM and water by increasing the polarization of water and total water-water H-bonding (Fig. S62b). In this event, the reduction in ΔH_sep and T_inf,CP with magnetization may in part be explained by a lower likelihood of water molecules to hydrophobically hydrate regions of the NIPAM sidechain like the isopropyl group.^34,62,74 This hypothesis is supported by thermal cycling experiments in 0.5% P87 (SI.26), where the decrease in T_inf,CP persists over multiple cycles with in situ 0.2 T magnetization (Fig. S80). Though increasing temperature can disrupt hydrogen bonding interactions and the structure of water, here in situ field application preserves some field-induced changes. However, when pre-magnetized solutions are thermally cycled at 0 T, magnetization effects are mitigated with thermal cycling, and T_inf,CP, of as-prepared and pre-magnetized PNIPAM solutions start to converge with increasing cycle number (Fig. S81). This convergence suggests that increasing temperature at 0 T slowly erases the impact of field application, likely due to disruption of hydrogen bonds in solution.

Similar increases in water-water H-bonding modes are seen in pre-magnetized PNIPAM solutions of higher concentration (SI.16) and higher molecular weight (SI.17). Notably, no statistically significant differences in H-bonding are observed in the FTIR spectra between water and the PNIPAM amide group (SI.15.3), lending credence to the hypothesized changes in water structure and hydrophobic hydration^34,62,74 with field application rather than changes in the amide group hydration. Thus while the FTIR spectra cannot be used to determine field-induced changes in H-bonding interactions with increasing temperature that may also explain reductions in ΔH_sep and T_inf,CP, these measurements suggest that pre-magnetization alters the H-bonding in PNIPAM solutions at ambient conditions, in both dilute liquid-like solutions and more concentrated solid-like gels.

3.2. Silica nanoparticle reduction of transition temperature and phase separation enthalpy

Adding Α8 silica NPs to bare 0.5% P87 solutions has a similar impact to magnetizing bare P87 solutions, with approximately linear reductions in T_inf,CP (Fig. 4a) and ΔH_sep (Fig. 4b) with increasing NP content. This linear reduction in ΔH_sep with increasing NP content is also observed in A1, A2.5, and A14 NPs with similar diameters to the A8 NPs.⁵⁶ These findings are in agreement with prior reports,^55,56 which attribute the decrease in ΔH_sep to hydrogen bonds between the PNIPAM amide group and NPs replacing a small number of polymer-solvent H-bonds. Turbidimetry reveals that T^inf,CP decreases by roughly −1.5 °C/% NP up to 0.4% NP (Fig. 3a); higher NP contents caused substantial light scattering at ambient conditions, precluding additional measurements. In contrast with prior work in 2% P87,⁵⁶ adding 0.025% NPs narrows the turbidimetric transition from that of the bare solutions (SI.14.3), as determined by the FWHM of the derivative of transmittance vs. temperature (see SI.14.5 for values and raw data). These differences likely arise from the difference in polymer content and thus lower percentage of non-interacting PNIPAM chains in this work (see SI.10). This turbidimetric transition gradually increases in width with increasing NP content until the FWHM of the bare solution is recovered at 0.4% NP (see SI.14.3). PNIPAM bound to NPs preferentially concentrates around a few initiation sites where chains require less rearrangement to aggregate and phase separate.⁵⁵ Additionally, bound PNIPAM attenuates the inter-particle repulsion between silica NPs while unbound PNIPAM induces weak attractive depletion forces between NPs.⁵⁶ Both of these factors likely lead to formation of polymer-NP clusters (which strongly scatter light) at lower temperatures than in bare PNIPAM solutions; note that the short-range steric stabilization provided by the bound polymer layer does not preclude formation of weakly associated clusters.⁵⁶ Thus at low NP content, the larger number of chains associated with each NP⁵⁵ and larger number of unbound chains likely narrow the optical transition vs. higher NP content solutions due to the different balance of inter-particle forces; this transition may broaden with increasing NP content due to the smaller number of unbound chains in solution and the smaller number of chains associated with each NP, weakening both the depletion attractions and attenuation of the NP surface charge on a per particle basis. However, the larger number of NPs reduces the average interparticle distance thereby increasing the likelihood of forming polymer-NP clusters, which likely explains the decreasing T_inf,CP with increasing NP content.

FIGURE 4.

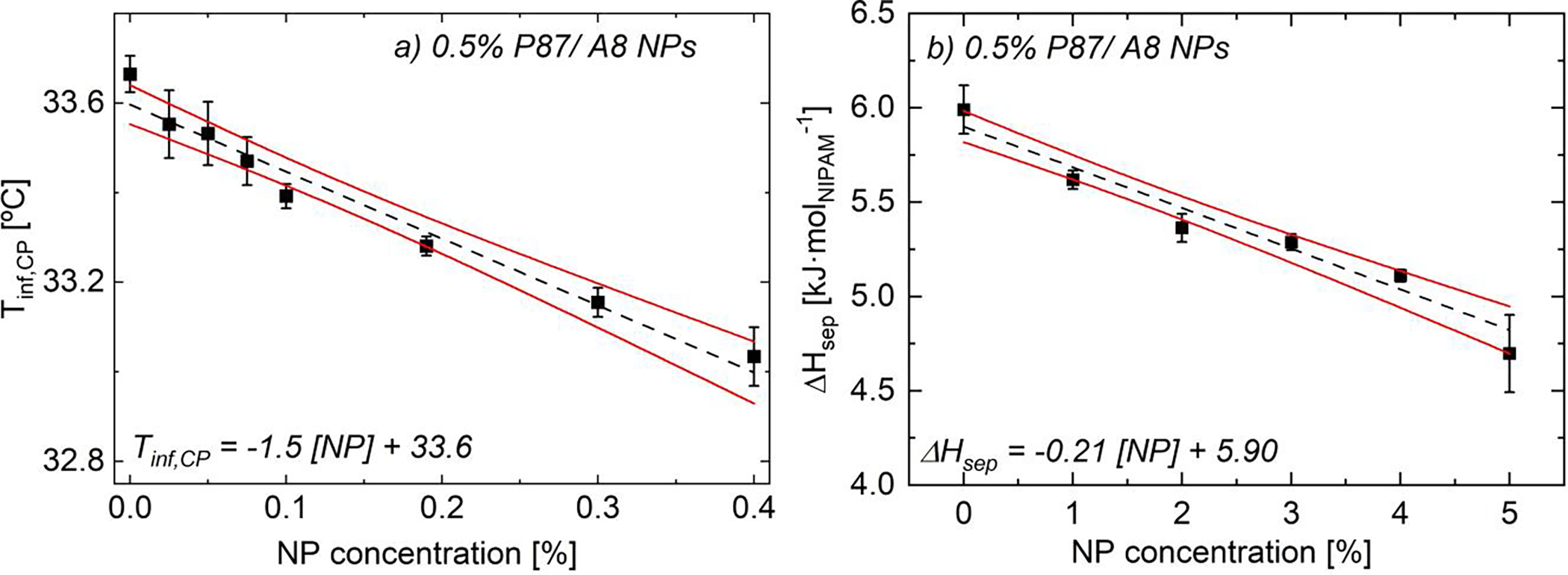
(a) Turbidimetric inflection temperatures, T_inf,CP,, and (b) DSC separation enthalpies, ΔH_sep, of as-prepared 0.5% P87/ A8 NPs (0 T). As NP content increases, T_inf,CP and ΔH_sep linearly decrease (black --) due to PNIPAM-NP H-bonding. Error bars are standard error of the mean (n ≥ 3). Solid red lines are 95% confidence bands on the linear regression. See Table S1 and Table S4 for additional data.

DSC measurements over a wider range of NP contents reveal a greater than 20% decrease in ΔH_sep from bare 0.5% P87 to 0.5% P87/ 5% A8 NPs (−0.21 kJ/mol_NIPAM/ % NP, Fig. 3b). Using zero enthalpy forecasts as done by Larrson,⁷⁵ Shönhoff,⁷⁶ and Petit⁵⁵, the total surface coverage per area is ~0.38 ± 0.08 mg P87 per m²_NP and the estimated percentage of PNIPAM interacting with NPs is ~18 ± 4% for the 5% NP solution. This reduction in ΔH_sep with increasing NP content is rationalized in part by ambient FTIR measurements (Fig. 5); for detailed analysis of spectral changes, see ref. 56. In short, as NP content increases, changes in spectroscopic signatures arise in three distinct regions: silica intra-particle modes (1000–1250 cm⁻¹), PNIPAM amide-water H-bonding modes (1500–1750 cm⁻¹) and water-water H-bonding modes (3000–3700 cm⁻¹). Silica intra-particle modes measure the siloxane network (Si-O-Si) and surface silanol (Si-O-H) groups present in the solution; these modes increase in intensity with increasing NP content due to the higher concentration of siloxane and silanol groups in the solutions. A reduction in intensity of the modes associated with amide-water H-bonding interactions (1500–1750 cm⁻¹) indicates that NPs disrupt these H-bonds, in agreement with prior work (Fig. S60).^55,56,61,77 These changes are consistent with the hypothesis that a number of PNIPAM-water H-bonds are replaced by PNIPAM-NP H-bonds, decreasing ΔH_sep.

FIGURE 5.

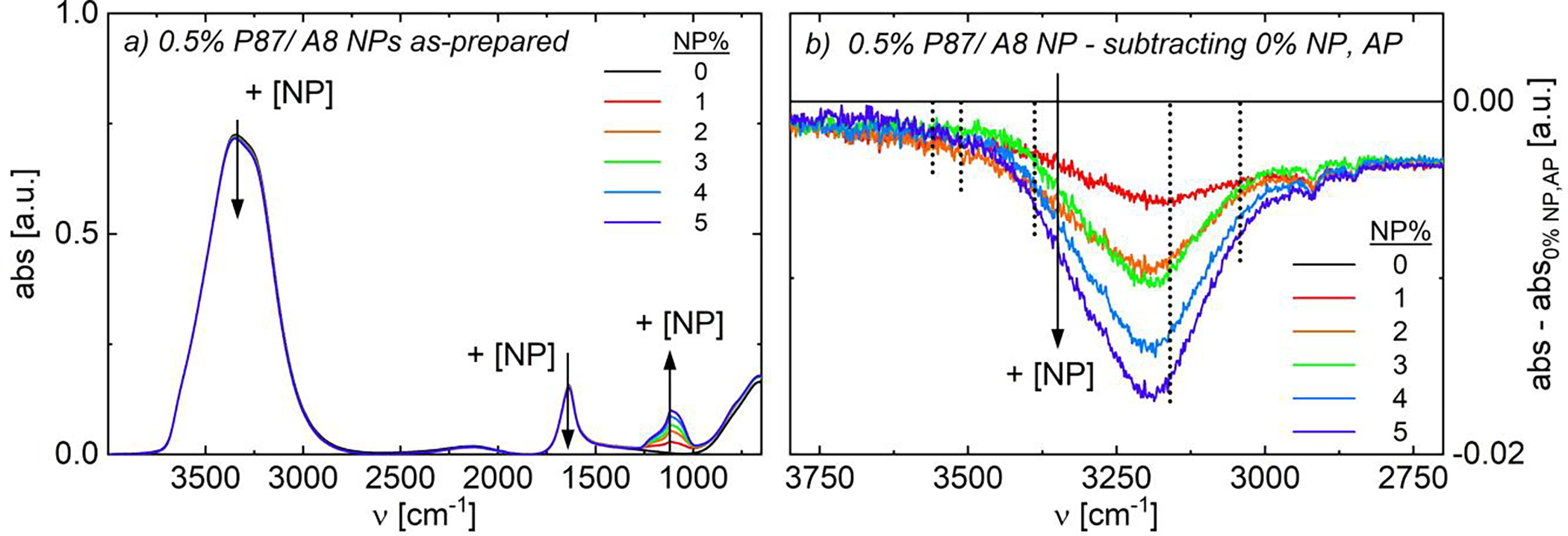
Fourier-transform infrared spectra of as-prepared (non-magnetized) 0.5% P87/ A8 NPs. (a) Full spectra and (b) zoomed spectra from 2700–3800 cm⁻¹ subtracted from 0% NP data. As NP content increases, water-water (ν ~ 3000–3700 cm⁻¹) and amide-water (ν ~ 1500–1700 cm⁻¹) H-bonding modes decrease. Water-water H-bonding modes are shown in vertical dotted lines in (b).

In contrast to the increase in intensity with pre-magnetization, the decreasing intensity in water-water H-bonding modes (3000–3700 cm⁻¹) with increasing NP content suggests disruption in bulk water H-bonding interactions and of the hydration shells surrounding PNIPAM.^44,61,62 The water-water H-bonding modes between 3000–3700 cm⁻¹ are a convolution of five peaks, indicating the number of hydrogen bonds donated and accepted by each molecule^44,78,79; see SI.15.3 for explanations of water H-bonding modes. Briefly, increasing NP content most substantially decreases the intensity of the mode at 3160 cm⁻¹, corresponding to double-donor, double-acceptor (DDAA; Fig. 5b) water-water H-bonding.^44,78,79 DDAA H-bonding corresponds to water molecules with the maximum number of allowable hydrogen bonds and is the structure commonly attributed to H-bonding in ice.^44,78,79 Thus in contrast to pre-magnetization which increase the intensity of these modes (Fig. S62b), the presence of NPs likely breaks down the extensively-coordinated ‘ice-like’ water clusters both in bulk solution and surrounding the polymer, though given the low polymer content, this effect is primarily due to changes in the bulk water structure.⁵⁶ Notably, little change in peak intensity occurs with NP addition for free O-H (3650 cm⁻¹) and double-donor single acceptor (DDA, 3512 cm⁻¹) modes; the intensity of the single-donor double acceptor mode (DAA, 3042 cm⁻¹) minorly decreases with NP content, either due to breakup of the bulk H-bonding network or overlap with the decreasing DDAA mode.

3.3. Combined impact of NPs and magnetic fields

To examine the interplay between NP addition and magnetization on the temperature-dependent solution behavior, magnetoturbidimetry, DSC and FTIR were conducted on solutions of 0.5% P87 and 0–5% A8 NPs, with supplementary experiments using A14 NPs with similar surface properties⁵⁶ (SI.25). As NP addition decreased–while pre-magnetization increased–the FTIR peak intensities corresponding to solvent hydrogen bonding modes, FTIR spectra before and after magnetization were first compared to determine potential competing effects of NP addition and pre-magnetization; here, changes in spectra for pre-magnetized solutions are examined vs. the analogous as-prepared solution to isolate the role of pre-magnetization (Fig. 6a) and vs. a non-magnetized solution without NPs to examine the combined effect of pre-magnetization and NP inclusion (Fig. 6b). Similar to findings on pre-magnetized P87-only solutions, pre-magnetization causes a net intensity increase in water-water H-bonding modes in both A8 and A14 NP-containing solutions (Fig. 6a and Fig. S76c, respectively; also see SI.27 for raw FTIR traces of solutions with A14 NPs). Notably, substantially larger increases in peak intensities vs. as-prepared solutions are observed for the double-donor, double acceptor (DDAA, 3160 cm⁻¹) and single-donor, single acceptor (DA, 3388 cm⁻¹) H-bonding modes in solutions with A8 NPs vs. P87-only solutions (color lines vs. black line, Fig. 6a). However when compared to as-prepared solutions of equivalent NP content, pre-magnetization effects on these hydrogen bonding modes are independent of NP content, illustrated by the nearly overlaying spectra (Fig. 6a). One possible explanation is that pre-magnetization worsens the solvent quality for the polymer, causing the polymer to adopt a less extended conformation in solution and enabling more extensive H-bonding networks to form in the bulk.

FIGURE 6.

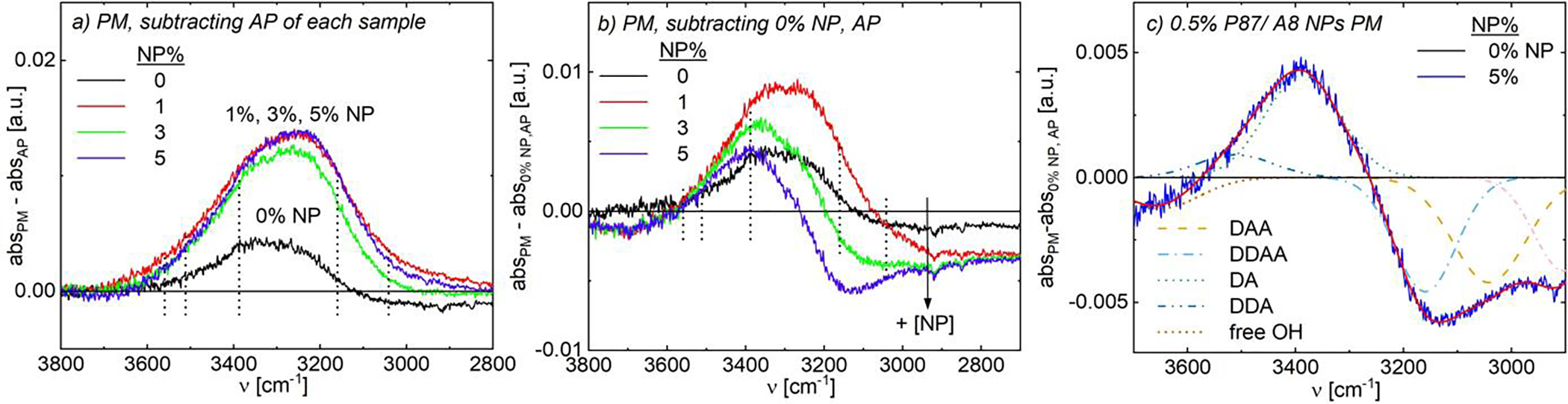
FTIR spectra of aqueous 0.5% P87/ A8 NPs. Data with: (a) corresponding as-prepared solution subtracted to isolate spectral changes due to pre-magnetization; (b,c) as-prepared, 0% NP data subtracted to examine spectral changes due to both pre-magnetization and NP inclusion. (c) Deconvolution of pre-magnetized, 5% NP solution using Gaussians for each of the five water-water H-bonding modes (see SI.15.2): DDA (yellow – –); DDAA (light blue -⋅-); DA (green --), DDA (dark blue -⋅⋅-), and free OH (orange ⋅⋅⋅), plus a correction for changes in PNIPAM backbone intensities (pink -⋅-). Summed fit is in solid red.

When the combined impact of pre-magnetization and NP inclusion is instead examined, intensities of FTIR H-bonding modes change non-monotonically, in a similar fashion for both A8- and A14-containing solutions (Fig. 6b and Fig. S76d, respectively). As changes in the free O-H, DAA, and DDA modes are consistent with those observed in non-magnetized P87 solutions, this analysis focuses on DDAA and DA modes. While the presence of NPs breaks up the extensively-coordinated water H-bonding network thereby decreasing the intensity of DDAA and DA H-bonding modes, magnetic fields increase the intensity of these modes due to changes in electron distribution and water polarization promoting increased solvent H-bonding.⁴⁴ For solutions containing 1% NPs, pre-magnetization outweighs disruption of the bulk H-bonding network by NPs, leading to a net increase in DDAA and DA peaks vs. as-prepared and pre-magnetized solutions without NPs (Fig. 6b). Conversely for the pre-magnetized 3% NP solution, the DA peak intensity decreases relative to the 1% solution but remains higher than that of both as-prepared and pre-magnetized bare P87 solutions; the intensity of the DDAA mode decreases relative to bare solutions. These trends continue with increasing NP content, where the DA peak intensity further decreases but still exceeds that of the as-prepared P87-only solution; consistent with NPs disrupting the well-coordinated bulk H-bonding network, the DDAA peak also further decreases vs. the bare solutions and vs. lower NP content solutions. The increase in DA H-bonding due to magnetic fields persists even at relatively high (5%) NP content, confirmed via peak deconvolution (Fig. 6c). This finding is consistent with a competition mechanism developed from experiments and theory suggesting that magnetic fields yield smaller and more numerous water clusters⁸⁰ which favor these less-coordinated H-bonding modes. Complementary experiments on A14 NPs suggest similar changes in hydrogen bonding structure upon magnetization (see SI.25, Fig. S77).

Similar to solutions that were only pre-magnetized or only contained NPs, magneto-turbidimetry (0.2T in situ) reveals that T_inf,CP decreases with increasing NP content in pre-magnetized 0.5% P87 solutions for all examined aspect ratios (Figs. 7a, S76, S78). Interestingly, the decrease in T_inf,CP, with Α8 NP content is significantly weaker in pre-magnetized (−1.0 °C/% NP) than as-prepared solutions (−1.5 °C/% NP). While pre-magnetized solutions have lower T_inf,CP at low NP content, T_inf,CP is statistically identical at 0.4% NP (Fig. 7a). While higher NP contents could not be measured, changes in both ΔH_sep (Fig. 7b) and FTIR peak intensities (Fig. 6b) at higher NP content suggest such that changes in T_inf,CP may also persist at higher NP content. The lower slope and y-intercept of T_inf,CP with increasing NP content in pre-magnetized vs. as-prepared solutions can be rationalized by the similar impact of NP addition and magnetization on lowering T_inf,CP. In the absence of NPs or at low NP content, magnetic fields likely weaken the hydrophobic hydration shell surrounding PNIPAM, decreasing T_inf,CP. However with increasing NP content, a larger number of PNIPAM chains interact with NPs, which also strongly reduces T_inf,CP,. In this event, the number of PNIPAM-water interactions that can be disrupted by field application is reduced, leading to a weaker scaling of T_inf,CP with NP content for magnetized solutions. A nearly identical trend in T_inf,CP is observed between solutions with A8 and A14 NPs (SI.25) which is attributed to similarities in surface properties⁵⁶; when normalized normalized based on total surface silanol groups, results from Α1, Α8, and Α14 NPs quantitatively converge across NP aspect ratios (Fig. S79b).

FIGURE 7.

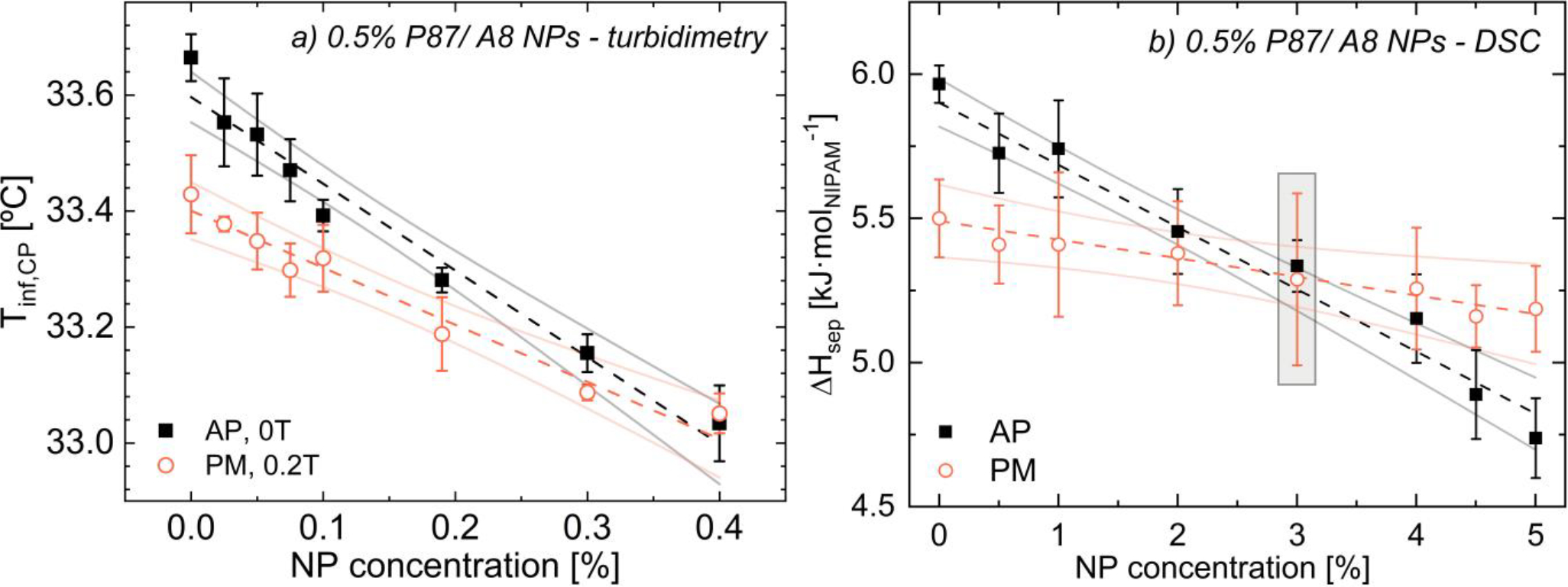
(a) T_inf,CP, and (b) ΔH_sep for 0.5% P87/ A8 NPs vs. NP content for as-prepared (black ◼) and pre-magnetized (orange ◦) solutions, with associated linear fits (--) and 95% confidence bands (–). See Fig. 7 for spectra from shaded points. For clarity, some data points are excluded; however, all points are used to calculate confidence bands; see Table S1 for all data.

Similar to the reduction in turbidimetric inflection temperatures with increasing NP content, ΔH_sep decreases at a weaker rate in pre-magnetized (−0.06 kJ/mol_NIPAM/% NP) vs. as-prepared (−0.21 kJ/mol_NIPAM/% NP) A8 NP-containing solutions (Fig. 6b). Similar reductions in ΔH_sep with increasing NP content are observed for A14 NPs (Fig. S75b). Below 3% A8 NPs, pre-magnetized solutions of 0.5% P87 require less energy to undergo phase separation than as-prepared solutions (Fig. 6b), whereas above this intersection point, ΔH_sep is higher for pre-magnetized solutions. The differences in the NP content in which T_inf,CP and ΔH_sep converge for pre-magnetized and as-prepared solutions likely reflect the different transitions being probed: optical (aggregation) vs. thermodynamic (dehydration). As previously discussed, NPs strongly impact optical transmission, and formation of polymer-NP clusters may artificially reduce T_inf,CP, relative to the thermodynamic transition, lowering the NP content at which this convergence occurs.

While solutions of 0.5% P87 and 3% A8 NPs had statistically identical ΔH_sep (Fig. 6b), FTIR spectra illustrate stark differences in ambient H-bonding interactions (Fig. 7). In the as-prepared solution, NP addition primarily reduces the FTIR peak intensity corresponding to DDAA H-bonding, suggesting a breakup of the bulk water network and the hydrophobic hydration shell surrounding PNIPAM vs. the 0% NP, as-prepared solution. For this solution, the PNIPAM amide-water H-bonding peak also decreases (Fig. 5a), largely accounting for the reduction in ΔH_sep.^56,61,77 However for the pre-magnetized solution, the peak intensity for the DA mode increases due to magnetization while the intensity for the DDAA mode decreases due to the presence of NPs, but less substantially than in the as-prepared solution. Additionally, the amide-water H-bonding peak intensity also decreases due to the presence of NPs, but not as substantially as in the as-prepared solutions (see SI.15.5); as such, fewer amide-water H-bonds may be disrupted for an equivalent NP content in pre-magnetized solutions, helping rationalize the weaker slope in Fig. 6b with pre-magnetization. As magnetic fields alter the structure of bulk water^35–43,80 and likely the clusters of water interacting with PNIPAM, the lower ΔH_sep in pre-magnetized solutions at low NP content is likely due to complex changes in the solution H-bonding environment, where hydrophobic hydration shells consisting of more singly coordinated (DA) H-bonds may break more easily with increasing temperature.

3.4. Field effects at higher PNIPAM content solutions

In pre-magnetized P87-only solutions, the magnitude of the magnetic field effect on reducing ΔH_sep decreases with increasing PNIPAM content (Fig. 8). For non-magnetized PNIPAM solutions, ΔH_sep per mol NIPAM is statistically independent of PNIPAM concentration dependence below ~6% polymer (Fig. 8a). Above ~6% PNIPAM, ΔH_sep decreases with increasing polymer content, as polymer-polymer interactions replace a number of polymer-solvent interactions thereby reducing the overall chain hydration.⁸¹ Interestingly, ΔH_sep for pre-magnetized solutions increases with polymer content up to ~6% PNIPAM (Fig. 8a), suggesting that although polymer-polymer interactions are insufficient to reduce ΔH_sep in this concentration regime, these interactions are substantial enough to reduce the impact of field application. When polymer-polymer interactions become significant (>6% PNIPAM), the field effect is diminished and ΔH_sep is indistinguishable between as-prepared and pre-magnetized solutions (Fig. 8a). Notably, ΔH_sep for as-prepared solutions is non-monotonic with increasing PNIPAM content; however, the relative difference in ΔH_sep between as-prepared and pre-magnetized solutions monotonically decreases with PNIPAM content until plateauing above ~6% polymer (Fig. 8b). While Vshivkov and co-workers saw an increase rather than decrease in phase transition temperatures in magnetized polymer solutions, these results are consistent with their observations that the field effect is diminished as solvent quality worsens.³³

FIGURE 8.

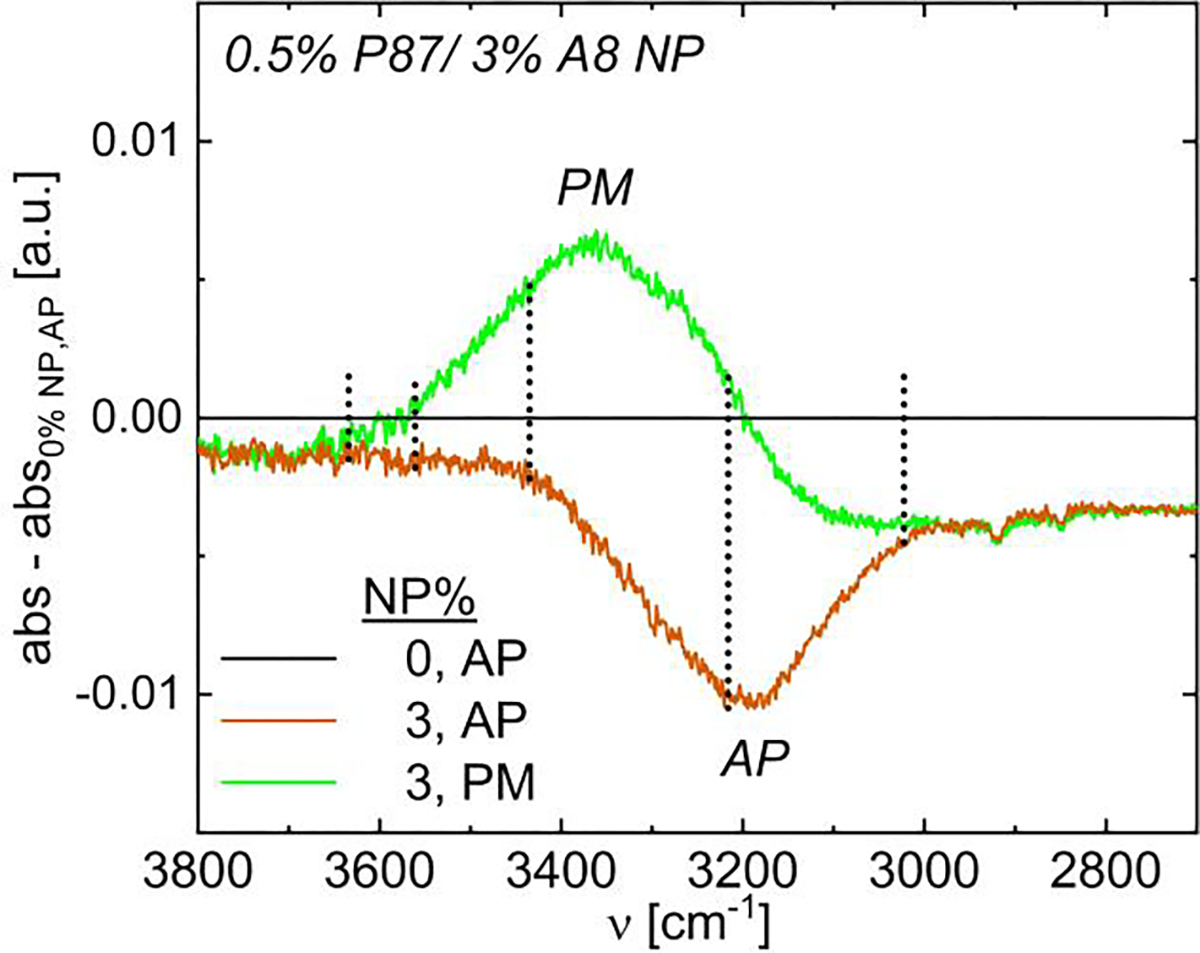
FTIR spectra of water H-bonding modes in 0.5% P87 and 3% A8 NPs as-prepared (AP, 0 T, orange) and pre-magnetized (PM, 0.15 T, green). Data have 0.5% P87 as-prepared subtracted; negative indicates a decrease in intensity from as-prepared to pre-magnetized.

Magneto-turbidimetry on 2, 6, and 10% P87 solutions shows that the field effect on the optical transition is diminished with increasing PNIPAM content, as the reduction in T_inf,CP with increasing field strength is less substantial at high polymer content (SI.13). As is characteristic of lower-critical solution temperature (LCST) polymer solutions,^72,83 the FWHM narrows and T_inf,CP is reduced for as-prepared solutions with increasing PNIPAM content, ascribed to more favorable de-mixing due to spatial proximity of the polymer chains. In pre-magnetized solutions, the decrease in T_inf,CP with increasing field strength is statistically identical for 0.5% and 2% P87 solutions (Figs. 2, S26). However with increasing polymer content (≥6% PNIPAM), the reduction in T_inf,CP with increasing B weakens, nearly disappearing at 10% PNIPAM (Figs. S27,S28). As with prior evidence, these DSC and magneto-turbidimetry results suggest that magnetic fields reduce solvation and polymer-solvent hydrogen bonding, as field effects are most pronounced when polymer chains are well-solvated and disappear when chains are less hydrated.

Interestingly, while changes in phase separation enthalpy and clouding due to magnetization are negligible at higher (~ 10%) P87 concentrations (Fig. 8b), oscillatory rheological temperature ramps and high-temperature (40 °C) amplitude sweeps suggest that magnetic fields strengthen the resulting physical hydrogel of 10% P87 at elevated temperatures (Fig. 9). As 10% P87 rheological transition (solutions are well above the critical overlap concentration,⁵⁶ T ≤ 30 °C). These interacting chains aggregate into PNIPAM mesoglobules which coarsen to form a significant inter-chain interactions occur below the onset of the strong hydrogel with increasing temperature,⁴⁷ with a storage modulus, G′, of over 10 kPa at 35 °C (Fig. 9a).

FIGURE 9.

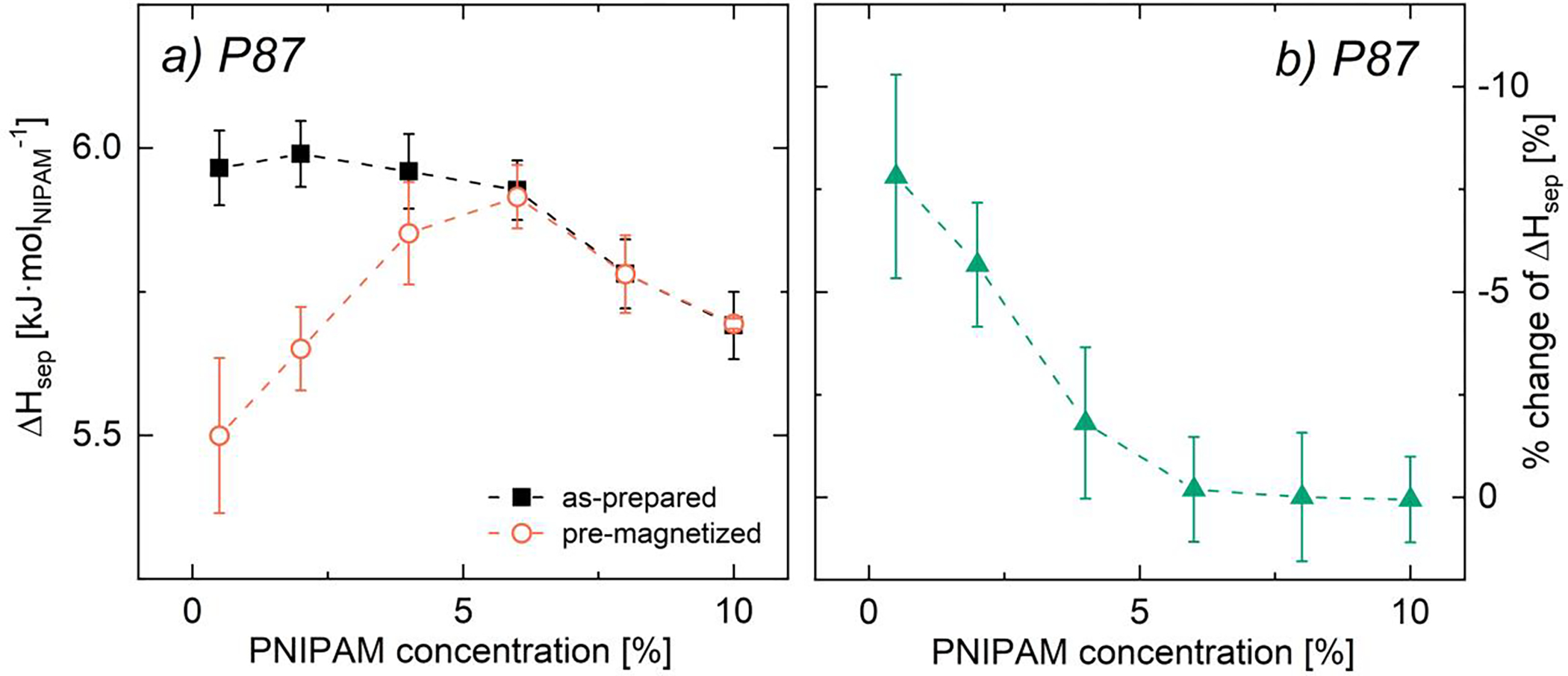
(a) Phase separation enthalpy and (b) % change in ΔH_sep due to pre-magnetization as functions of PNIPAM concentration for bare PNIPAM solutions as-prepared (black filled squares) and pre-magnetized for 3 days at 0.1 T (orange open circles). Error bars designate (a) standard error of the mean (n ≥ 3) and (b) error propagation from standard error of the mean (see SI.7).⁸² Lines are for visual aid only.

Applying a 0.4 T magnetic field to 10% P87 during this rheological temperature ramp results in substantially higher dynamic moduli in the hydrogel coarsening regime (T > 32 °C, Fig. 9a); these higher moduli persist in amplitude sweeps of 10% P87 at 40 °C following the temperature ramps up to ~10% strain (Fig. 9b). At low strain amplitudes, the dynamic moduli of magnetized 10% P87 (blue triangles) are nearly an order of magnitude higher than its non-magnetized counterpart. Near ~10% strain, a yielding transition is observed for both magnetized and non-magnetized solutions. Non-magnetized solutions exhibit a gradual yielding transition, whereas this transition appears more abrupt for the magnetized solutions – which could reflect an increase in hydrogel brittleness or sample slip. Above this transition, the dynamic moduli for both solutions are nearly indistinguishable; however, given the high polymer content and high strain amplitudes, these similarities could be due to slip or fracture. Finally, while magnetic fields appear to have little influence on the dynamic moduli or transition onset at lower temperatures, low torque signal prevents further analysis; this lower temperature behavior will thus be further investigated with higher torque steady shear measurements (see Sec. 3.5).

Although the exact mechanism leading to modulus increase in the magnetized solutions is unclear, the FTIR above, paired with results from others,^44,80,84,85 suggest that the size and coordination of water clusters – and the strength of inter-cluster hydrogen bonds – are altered by field application. If this direct hydration shell, or hydrophobic hydration shell, surrounding PNIPAM is altered, the size of the PNIPAM mesoglobules that form may change, which directly impacts the dynamic moduli. Although the reduction in T_inf,CP with magnetization is less pronounced at higher polymer content (SI.13), a change in mesoglobule size would alter the light scattering from those globules, potentially explaining the shift in T_inf,CP with magnetization. Magnetic fields may also orient mesoglobules differently, or cause secondary structures to form, as was postulated in prior work on magnetized polymer solutions. Finally, during hydrogel formation, polymer chain dehydration occurs from the outside of the mesoglobule inwards.⁸⁶ As such, a shell of tightly-aggregated PNIPAM chains can form on the outside of the PNIPAM mesoglobules at these high PNIPAM concentrations, which can prevent removal of water clusters from the mesoglobules.^47,86 Any change in the water cluster size or coordination due to field application will likely impact this complex process of mesoglobule formation and water removal, thus altering the ultimate hydrogel properties. Thus while the effects of magnetic fields on thermoresponsive polymer solutions appear to decrease with increasing polymer content (Fig. 8), unexpected differences in rheological properties may still emerge (Fig. 9), which should be taken into account when considering specific applications.

3.5. Shear magnetorheology of P87/NP solutions

Given the surprising changes in oscillatory rheology upon magnetization despite minimal changes in DSC and cloud point for higher polymer concentrations, the impact of magnetic fields during shear processing was examined further for solutions of polymers and NPs at concentrations relevant for hydrogel applications.^63,87,88 Here, steady shear magnetorheology was conducted on 10% P87 solutions both with and without 1% A8 NPs below the phase transition temperature; flow curves were fit with the Carreau model to extract the relaxation time, τ. All solutions with and without NPs exhibit similar steady shear behavior, with a Newtonian plateau below ~20 s⁻¹ and pronounced shear thinning with increasing shear rate (Figs. 10, S71); all zero-shear viscosities, η₀, fall between 30 and 40 mPa⋅s and all τ between 25 and 35 ms. Note that measurements became unstable prior to observing an infinite rate viscosity; as such, Carreau models excluded fitting to infinite-shear data though is shown in SI.20. Rotational Péclet number (Pe, SI.24) and Mason number (Mn, SI.23) calculations suggest that NP alignment occurs at shear rates as low as 0.1 s⁻¹ and that expected flow alignment greatly exceeds magnetic alignment for all conditions; thus the observed shear thinning is likely dominated by changes in flow-induced polymer chain alignment rather than field-induced alignment.^33,34

FIGURE 10.

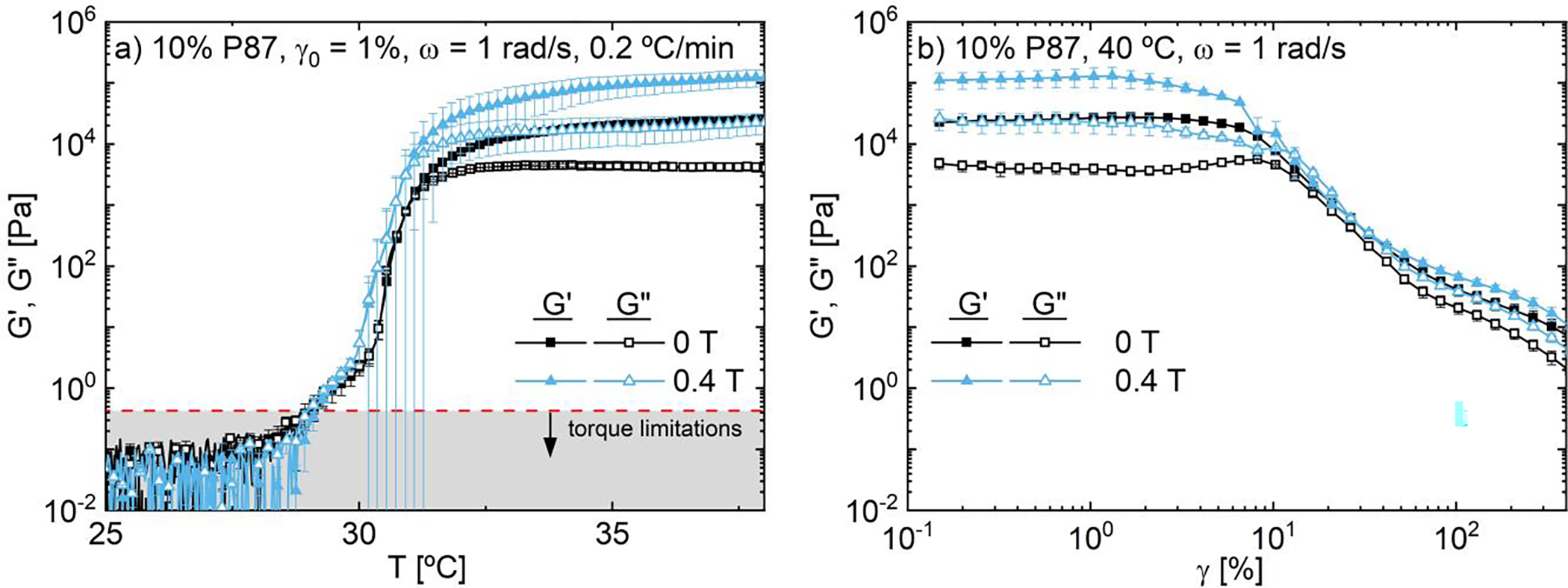
Dynamic moduli of 10% P87 as functions of (a) temperature at γ₀ = 1%, ω = 1 rad/s and (b) amplitude at 40 °C and ω = 1 rad/s. As temperature increases, 10% P87 solutions aggregate into a physical hydrogel which strengthens with magnetic field strength.

In the absence of NPs, η₀ increases with magnetic field strength while τ is independent of field strength between 0 T and 0.4 T (Table 2, SI.18). These findings are in contrast to DSC results that showed pre-magnetization effects were minimized at higher polymer contents, suggesting that the temperature change during DSC may minimize or erase the impact of pre-magnetization. Pre-magnetization effects are also time-dependent, with larger viscosity increases observed at longer pre-magnetization times; these viscosity increases also persist following high shear and upon field removal (SI.21). Conversely in NP-containing solutions, increasing the field strength from 0 T to 0.4 T increases η₀ by ~10% but decreases τ by ~20% (Fig. 11, Table 2). As field application does not impact the relaxation time of magnetized P87-only solutions, the decreasing τ in magnetized NP-containing solutions is attributed to presence of silica NPs. The relaxation time of polymer solutions often increases with increasing polymer content like in the Doi-Edwards reptation model.⁸⁹ Thus the decreasing τ with increasing magnetic field strength suggests that magnetic fields decrease the effective concentration of PNIPAM when in the presence of NPs. As magnetic fields likely alter the PNIPAM hydration environment, magnetic fields may increase the number of PNIPAM chains bound to NPs or cause formation of secondary structures,³⁴ decreasing bulk PNIPAM content. While pre-magnetizing P87 solutions led to fewer polymer-NP interactions than as-prepared samples, here the higher field strength and the in situ field may instead increase these polymer-NP interactions. As 20 °C is below the transition temperature, interactions between these non-bound PNIPAM chains, including entanglements and H-bonding interactions, are largely responsible for determining the relaxation behavior and resistance to flow.

TABLE 2.

Relaxation time, τ, and zero-shear viscosity, η₀, of 10% P87/ A8 NP solutions from Carreau model fits (see SI.18).

concentration	τ [ms]			η0 [mPa·s]
[%]	0 T	0.2 T	0.4 T	0 T	0.2 T	0.4 T
0	33.6 ± 4.8	29.4 ± 6.0	33.3 ± 7.4	32.4 ± 0.1	33.6 ± 0.1	34.9 ± 0.3
1	33.7 ± 2.8	28.2 ± 1.4	26.3 ± 3.6	35.0 ± 0.0	37.1 ± 0.0	38.8 ± 0.1

FIGURE 11.

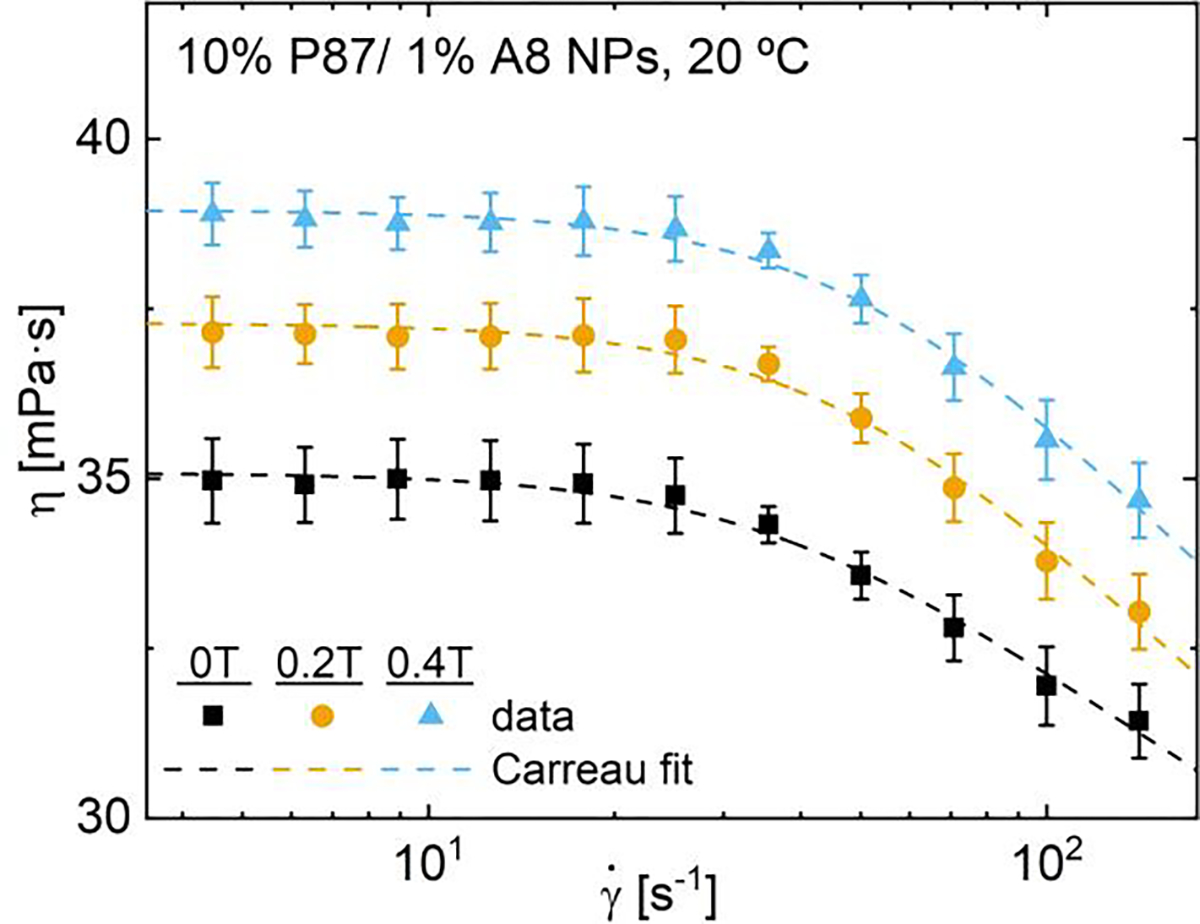
Steady shear viscosity and Carreau model fits of 10% P87/1% A8 NPs at 20 °C and 0, 0.2 or 0.4 T (see SI.18).

The zero-shear viscosity increases in the presence of magnetic fields whether or not NPs are present, suggesting that varying the magnetic field strength is one route for controlling flow properties like viscosity for a range of aqueous solutions. The increase in η₀ with increasing field strength is attributed in part to the increase in water-water H-bonding, and potentially a closer proximity to the thermal phase transition, which is known to increase the viscosity.⁵⁶ In magnetized water, the increased water polarization leads to more hydrogen bonding, increasing the resistance to flow and the viscosity.^36,85,90 Notably, Cai et al. showed that the viscosity of pure water increases by >10% after magnetization at 1 T for 14 minutes.⁸⁵ Typically magnetic field effects increase with longer magnetization times,^{35–37,40,44} consistent with the more pronounced increases in viscosity observed after longer pre-magnetization periods (SI.21).

Shear flow may also amplify magnetic effects on rheological properties (see SI.21). Sronsri et al. found that increasing flow rate increased FTIR peak intensities of water-water hydrogen bonds, increased electrical conductivity, and decreased heat capacity in pure water.⁴⁴ As the shear rate increases, the Lorentz force acting on the polar water molecules increases (see SI.22), amplifying changes in water properties due to magnetic fields. Finally, some have postulated that fields induce formation of secondary structures like polymer bundles.³⁴ Thus shear flow, magnetic field strength, and NP addition–and the interplay between each–all impact and can be used to tune the rheological properties of aqueous PNIPAM for a range of applications.

4. CONCLUSION

Individually and in tandem, anisotropic silica nanoparticles and magnetic field application alter the molecular interactions and macroscopic flow properties of aqueous poly(N-isopropyl acrylamide) (PNIPAM); these effects persist across a range of particle aspect ratios. In dilute (0.5%) PNIPAM solutions, both NP addition and field application independently reduce the energy barrier to phase separation, ΔH_sep, and lower the temperature at which the optical clouding transition occurs, T_inf,CP. However, Fourier transform infrared (FTIR) spectra suggest that the mechanism by which these changes occur is distinct. Consistent with literature on magnetized water, magnetic fields increase the polarization and hydrogen bonding of water molecules, specifically increasing the number of single-donor single-acceptor (DA) and double-donor double acceptor (DDAA) H-bonds in solution, which also alters the hydration environment around the polymer. Conversely, hydrophilic silica NPs provide alternative H-bonding sites for PNIPAM amide groups, partially dehydrating polymer chains and thereby lowering ΔH_sep. Here, the number of DA and DDAA H-bonds in solution also decrease, as the presence of NPs disrupts the bulk water H-bonding network.

Despite that both magnetic fields and silica NPs lead to qualitatively similar reductions in T_inf,CP and ΔH_sep, combining NPs and magnetic fields leads to competing effects regarding H-bonding in solution. At low NP content, field application dominates and DA and DDAA H-bonding increase in solution. Around 3% NPs, the disruption of ‘solid-like’ DDAA H-bonding clusters due to NP addition outweighs the increase in DDAA H-bonds due to magnetic fields; however, the increase in DA H-bonding due to field application persists. The formation of a higher number of less-coordinated water clusters in magnetized solutions likely contributes to the reduced T_inf,CP and ΔH_sep; however, pre-magnetized NP-containing solutions exhibit fewer PNIPAM-NP interactions than as-prepared solutions, causing a weaker decrease in these parameters due to NP inclusion. Finally, magnetizing 10% PNIPAM solutions in the presence or absence of NPs increases the steady shear viscosity across a range of shear rates. Interestingly, the combination of magnetic fields and NP inclusion (1%) alters the shear thinning and relaxation behavior distinctly from field application alone. Although the impact of magnetization on the phase separation enthalpy and cloud point transition are minimized in higher polymer content solutions, magnetization still leads to higher dynamic moduli at elevated temperatures for hydrogel-forming 10% P87 solutions, suggesting that field application may be useful in altering the properties of both dilute and semi-dilute polymers for wide-ranging applications. These studies reveal that both magnetic fields and hydrophilic silica NPs can profoundly impact the thermodynamic, optical, and rheological properties of aqueous PNIPAM solutions, unlocking novel routes for controlling these properties in aqueous, thermoresponsive polymers.

Abbreviations:

NP

silica nanoparticles

P87

PNIPAM with number-average molecular weight = 87 kDa

PNIPAM

poly(N-isopropyl acrylamide)

AIBN

2,2’Azobis(2-methylpropionitrile)

EMP

2-(ethylsulfanylthio-carbonylsulfanyl)-2-methylpropionic acid

Biographies

Christopher A. P. Neal, Department of Chemical Engineering and Materials Science, University of Minnesota, Twin Cities. 421 Washington Ave SE, Minneapolis, Minnesota 55455, United States of America

Grace V. Kresge, Department of Chemical Engineering and Materials Science, University of Minnesota, Twin Cities. 421 Washington Ave SE, Minneapolis, Minnesota 55455, United States of America

Michelle C. Quan, Department of Chemical Engineering and Materials Science, University of Minnesota, Twin Cities. 421 Washington Ave SE, Minneapolis, Minnesota 55455, United States of America

Valeria León, Mechanical Engineering Department, University of Texas Rio Grande Valley. ENGR 3.222, Edinburg, Texas 78541, United States of America

Nondumiso O. Chibambo, Department of Chemical Engineering and Materials Science, University of Minnesota, Twin Cities. 421 Washington Ave SE, Minneapolis, Minnesota 55455, United States of America

Michelle A. Calabrese, Department of Chemical Engineering and Materials Science, University of Minnesota, Twin Cities. 421 Washington Ave SE, Minneapolis, Minnesota 55455, United States of America