Abstract
Clay has been reported as an active absorbent for the removal of toxic heavy metals from aqueous medium. In this study, pristine and acid modified kaolinite clays (PKC and AMKC) were prepared, characterized using various analyses, and tested for Cd2+ ion adsorption from textile industry wastewater. After acid modification, the specific surface area of clay increased from 84.2 to 389.4 m2/g. Adsorption isotherm, kinetics and thermodynamics behaviour process were examined. The pH at (pHpzc) of 8.5 indicate that AMKC surface is positively charged for pH below the pHpzc attracting anions. Response surface methodology was used to investigate the effect of adsorption process factors on Cd2+ ion removal uptake. At the optimum process conditions of 45.3 °C temperature, 0.63 g/L adsorbent dosage, and 120.9 min contact time, the percentages of Cd2+ adsorbed by PKC and AMKC were 77.82% and 99.19%, respectively. Various models were employed to analyzed the kinetic and equilibrium data. The Pseudo-first order, Pseudo-second order and Intra-particle diffusion were used to evaluate the kinetic data, while the Langmuir, Freundlich and Temkin isotherm models were applied to analyzed the equilibrium data. The sorption kinetics was found to be best described by Pseudo-second order considering the high correlation coefficient (R2), smaller Chi-square (ᵪ2) and sum of square error (SSE). The Freundlich model was the most accurate in describing the equilibrium data followed by Langmuir and Temkin respectively. The thermodynamic reveal that the reaction is spontaneous and endothermic in nature, and increase in randomness between the adsorbent and adsorbate. The obtained activation energy (Ea) value suggest that the adsorption mechanism of Cd(II) is a physisorption dominated.
Keywords: Kaolinite clay, Cadmium ions, Adsorption, Optimization, Response surface methodology
1. Introduction
Water pollution is identified as one of the social issues posing health risks to humans and their environment [1,2]. Water pollution caused by toxic heavy metal discharge from process industries and mining sites is a major concern [3]. Despite being an essential micronutrient, excessive heavy metal intake can have a variety of toxic effects [4]. Cadmium is one of the toxic heavy metals and longstanding environmental contaminants [5]. Numerous process industries such as electroplating, textile, metal plating and battery manufacturing generate huge quantities of wastewater contaminated by cadmium ions (Cd2+) [6,7]. Over the years, the researchers' main focus has been on water, which contains heavy metals because of their negative effects on the environment and humans [8]. However, when these heavy metals are present in humans and biological systems in concentrations that exceed the threshold limits, they are known to cause health problems. For example, persistent exposure to Cd2+ ions can lead to skin irritation, nasal cancer, liver and heart damage [7,9]. As a result, the removal of Cd2+ from aqueous medium is an urgent focus of research [10]. Several methods for Cd2+ ions removal from water/wastewater have been investigated over the last several decades, including chemical precipitation [11], membrane separation [12], ion exchange [13], and adsorption [7, 14, 15]. Amongst these techniques, adsorption has emerged to be the most promising treatment technology because of its high removal efficiency, low cost and ease of operation [[16], [17], [18], [19]].
Among the various adsorbents utilized for wastewater treatment, the abundant clays have derived one large adsorbent family endowed with natural physicochemical properties, high specific surface area, extraordinary cation exchange capacity (CEC) and cation exchange selectivity, surface hydrophilicity and surface electronegativity, attracting widespread attention on environmental remediation [20,21]. According to earlier research, the adsorption capacity of local clay samples for heavy metals removal was improved through acid modification [22]. The purpose of this study is to analyze the properties of locally sourced clay that has been treated with hydrochloric acid, in order to enhance its economic value and useability. The uses of locally sourced natural material, offers several benefits such as reducing environmental challenges and supporting local economy. Acids are commonly used for surface modification and impurity removal from clay minerals. Acid activation has been shown to increase the adsorption capacity of clay material by opening pore spaces and edges clay minerals, thereby increasing their adsorption capacity [23,24]. Clay activation also removes cations such as magnesium, potassium, calcium and metal oxides that may be present in the clay, increasing the number of empty sites for heavy metal adsorption [25]. Hydrochloric, phosphoric, nitric, sulfuric, lactic and acetic acids are the most commonly used acids for clay modification [[26], [27], [28]]. Therefore, clay modified with acid can serve as a promising adsorbent in industrial wastewater treatments [24,28]. When compared to other commercial adsorbents, clay has a wide range of benefits and utility, including excellent specific surface area, high mechanical and chemical stability, availability, affordability, ion exchangeability, surface and structural property variety and good adsorption capacity [27].
In the past, researchers have typically applied one variable at time (OFAT) to study the impact of operating factors on adsorption of heavy metals onto adsorbent materials. However, this approach requires a large number of experiments and fails to reveal the iterative behaviour of process factors [29]. Additionally, it can be time consuming and expensive when dealing with high number of variables [30]. By utilizing statistical experimental design such as response surface methodology (RSM), it becomes possible to eliminate the limitations of a classical methods by optimizing all parameters collectively.
The objectives of study is to examine the potential of pristine and acid-modified kaolinite clay (PKC and AMKC) as effective adsorbents for the removal of Cd2+ ions from textile industry wastewater. These adsorbents prepared were characterized using various techniques. Moreover, the optimum adsorption process factors needed for the maximum removal Cd2+ ions uptake have been evaluated using design of experiment.
In conclusion, to the best of our knowledge, there is limited or no available literature on the use of pristine and acid-modified kaolinite clay for decontamination of Cd2+ from wastewater. If there is any available material, no central composite design (CCD) method of RSM was conducted for the design of experiment. Nevertheless, the limitation of this research further revealed that simulated wastewater was used for the adsorption experiments of all the reviewed papers. Hence, the current study establishes the performance evaluation of the developed pristine and acid-modified kaolinite clay adsorbents on textile industry wastewater.
2. Materials and methods
2.1. Materials
Pristine kaolinite clay (PKC) was sourced from Umunze, Nigeria, while effluent used was collected from a textile industry, Kaduna, Nigeria. All reagents used in this study which include hydrochloric acid (HCl, 36%), sodium hydroxide (NaOH, 95%), acetic acid (CH3COOH, 97%) were supplied by Panlac Scientific Limited, Minna Nigeria. The chemical composition of PKC, as determined by chemical analysis, were 67.8% SiO2, 12.9% Al2O3, 6.7% Fe2O3, 1.5% TiO2, 1.5% MgO, 1.7% other metal oxides and 7.9% Loss on ignition (LOI).
2.2. Preparation of acid-modified kaolinite clay adsorbent
10 g of PKC was gently ground and washed with distilled water to get rid of dirt. The washed PKC was thereafter dried in an oven at 105 °C overnight and then sieved using sieve mesh size of 125 μm to obtain fine particle. In order to activate the PKC powder, 5 g of the fine PKC was suspended in 2.0 M HCl aqueous solution in an Erlenmeyer beaker, stirred on hot plate at 80 °C for 2 h. Following the clay activation process, the slurry was severally washed with distilled water until the solution pH attained neutral, filtered, oven-dried at 108 °C for 3 h and finally stored in a covered container. Henceforth, the acid-modified kaolinite clay will be referred to as AMKC.
2.3. Characterization of acid-modified kaolinite clay adsorbents
The surface structure, surface functional groups, crystallographic structure and textural characteristics of as-synthesized clay-based adsorbents were evaluated using scanning electron microscope (SEM, Zeiss Sigma, Germany), Fourier-transform infrared (FTIR) spectrometer (FTIR, Agilent Cary 600), powder X-ray diffractometer (GBC eMMA XRD) and surface area analyzer (Tristar™ II 3020, Micromeritics, USA).
2.4. Equilibrium batch adsorption studies
Adsorption capacities of the PKC and AMKC adsorbents were assessed through batch an equilibrium adsorption study, which was carried out in a set of each 250 mL Erlenmeyer flasks containing 50 mL of effluent without adjusting the wastewater pH. The flasks were agitated in a water bath shaker at different operating conditions, contact time (10–120 min), adsorbent dosage (0.1–0.5 g) and temperature (25–45 °C) until equilibrium was reached. Following the completion of the process, the concentrations of Cd(II) ions before and after adsorption were measured using atomic absorption spectrophotometer (AAS, PinAACLE 900Z, USA.). The percentage removal (R) of Cd(II) ions by both adsorbents was determined by Eq. (1)
| (1) |
Where M (g) is the mass of sorbent, V (L) is termed the volume of the solution, (mg/L) is the final concentration of the Cd(II) ions; Co (mg/L) is the initial concentration of the Cd(II) ions and is the Cd(II) ions concentration at equilibrium (mg/L).
The amount of adsorption of Cd(II) ions can be calculated using Eq. (2)
| (2) |
2.5. Optimization of Cd(II) ions adsorption by acid-modified clay
The central composite design (CCD) of response surface methodology (RSM) was used to study the effects of adsorption process conditions (time, adsorbent dosage and temperature) on equilibrium uptake of Cd(II) ions by PKC and AMKC adsorbents. For considering three process factors, a total of 20 experimental runs, comprising of 6 axial points, 8 factional runs and 6 center runs, were employed. Experimental data were analyzed using Design Expert software (statistical) version 7.0 (STAT-EASE Inc., Minneapolis, USA). The experimental ranges and the levels of the process input variables for Cd(II) ions removal are given in Table 1. However, the adsorption removal efficiency (Y) which is the dependent variable was evaluated using batch techniques. To analyze the data, a second order quadratic polynomial expression relate the three independent factors to the response (Y). The equation for this model is given in Eq. (3).
| Y = bo + ∑ biXi + ∑biiXi2 + ∑ bijXiXj | (3) |
Table 1.
Experimental ranges and levels of the independent factors.
| Independent variable | Code | Unit | Levels |
||
|---|---|---|---|---|---|
| −1 | 0 | +1 | |||
| Temperature | A | oC | 25 | 35 | 45 |
| Adsorbent dosage | B | g/L | 0.1 | 0.3 | 0.5 |
| Contact time | C | Min | 10 | 65 | 120 |
The experimental data is analyzed using the analysis of variance (ANOVA). The choice of ANOVA is due to its ability to analyze multiple independent variables and their effects on the dependent variables and also to identified the optimal levels of each independent variables. In this analysis, Y is considered as the dependent variable representing the removal efficiency, while Xi and Xj are the independent process variables. Here i and j takes the value of 1, 2 and 3, but i is not equal to 1. The model incorporates constant regression coefficients bo, bi, bii, and bij. To determine the quality of fit for the polynomial model, both the adjusted R square (R2) and determination coefficient (R2) are utilized as evaluation metrics. In order to evaluate the statistical significance and adequacy of the model, the probability value (Prob > F), Fisher variation ratio (F value) and adequate precision value are taken into consideration.
2.6. Point of zero charge (pHpzc)
[7] described the essence of zero-point charge as a means of evaluating the net surface charge. The pHpzc was examined using a method of salt solution. 0.1 g of sorbent samples was added with 0.1 M of KNO3 which were thoroughly mixed in six conical flask at operating condition of 25 °C. The mixture pH was adjusted to (pHi) value of 2, 4, 6, 8, 10 and 12 respectively by adding several drops of H2SO4. The agitation of the mixture was carried out in an isothermal water bath shaker at 180 rpm for 24 h, following the evaluation of pHf of each solution. The plot of (pHf – pHi) versus pHi was plotted and pHpzc was obtained at the intercept on X axis.
2.7. Isotherm study
This study employs isotherm models to investigate the interaction between sorbate and sorbent in adsorption process. To examine the adsorption of Cd(II) onto AMKC. Langmuir, Freundlich and Temkin model were applied. According to Langmuir isotherm model, adsorbate molecules form a monolayer on the surface of a solid, and it is assumed that once a site on the adsorbent is saturated with metals ion, no further adsorption occurs at that site. The model further proposed that all adsorption site have equivalent energy. The equation for this model was developed by Irving Langmuir (1916).
The Langmuir non-linearized form is given as Eq. (4)
| (4) |
Where Qmax (mg/g) is the maximum number of adsorption capacity of metal ion adsorbed, qe (mg/g) is the metal ion adsorption capacity at equilibrium, Ce is the concentration of the adsorbate in solution at equilibrium (mg/L) and KL which is the Langmuir equilibrium constant (L/mg) which reflect the energy of adsorption, quantitatively indicating the degree of affinity between the adsorbent and adsorbate. Although the Langmuir adsorption isotherm model is unable to explain the mechanism behind the adsorption process, it is useful in providing information on both the adsorption capacity and equilibrium state [31]. The model is visually identifiable by plateau that represent the point of equilibrium saturation, where no further adsorption can occur once a molecule occupies the site [32].
The Freundlich model isotherm assumes that adsorption takes places on a surface with heterogeneous characteristic and it can be applied to both chemisorption (monolayer adsorption) and van Der Waals adsorption (multilayer adsorption) [33]. The nonlinear form of the Freundlich equation, originally proposed by Ref. [34] is represented by Eq. (5)
| (5) |
Where 1/n is the coefficient of heterogeneity, Ce is the concentration of the adsorbate, while KF is the Freundlich constant associated with adsorption capacity. The higher value of KF suggest a greater adsorption capacity. The values of n give favourability information on the adsorption process [35,36].
The Temkin isotherm postulates that the reduction in the heat of adsorption is proportional to the adsorption heat, and that the adsorption process is characterized by uniform distribution of binding energies.
Temkin model non-linearized equation can be expressed as Eq. (6)
| (6) |
where qe (mg/g) is the adsorption capacity, Ce (mg/L) is the concentration of metals ion at equilibrium, KT is the equilibrium constant (L/g), is related to heat of adsorption, the gas constant R (8.314 J mol−1. K−1) and T is the absolute temperature (K) [37].
2.8. Kinetic study
Kinetics is a crucial aspects of adsorption process because it provides valuable insight into the reaction pathways and rate controlling mechanism of the reaction [38]. To investigate the adsorption rates of Cd(II) ion onto AMKC, this study utilizes the Pseudo-first order, Pseudo-second order and intra-particle diffusion model. The removal mechanism of Pseudo-first order kinetics model introduced by Refs. [39,40], involves diffusion through a boundary that precedes the adsorption process. The non-linear version of the model is represented by Eq. (7)
| (7) |
qt denotes the quantity of metal ion at time t, the volume of adsorption at equilibrium is qe, while k1 (min−1) is the rate constant of the first order kinetic models and time t (min). The Pseudo-first order assumes that each active site on the adsorbent surface bind to only one adsorbate molecules.
[41] introduced the Pseudo-second order kinetics, which assumes that adsorption follows a second order kinetics mechanism. According to this model, the sorption process is controlled by chemisorption where electron are shared or exchanged between the solute and the adsorbent. The model also assumes that a single adsorbate molecule binds to two active sites on the surface of the sorbent. The equation for this model can be expressed as Eq. (8)
| (8) |
The Pseudo-second order rate constant denoted as K2 (g/mgmin), amount of Cd(II) adsorbed at equilibrium (qe) and at time t (qt) and time t (min) respectively.
From analytical view point, experimental kinetics data is interpreted using the intra-particle diffusion model, which is based on the theory presented by Weber and Morris (1963). The equation is expressed using Eq. (9)
| (9) |
The quantity of Cd(II) ion adsorbed per unit mass of adsorbent is represented by qt, while C (measured in mg/g) is a constant that provides information about the boundary layer. The term “t” is the contact time and "Kid" (mg g−1 min−1/2) refers to intraparticle diffusion rate constant. When C equals zero, the intraparticle diffusion is the only factor that limits the rate of adsorption. However, if C is not equal to zero, it indicates that there is some degree of boundary layer control the reaction and therefore, intraparticle diffusion is not the only factor limiting the rate of adsorption.
2.9. Non-linear regression method
The parameter of adsorption isotherm model can be estimated through the non-linear regression analysis, which involves the original form of the isotherm equation. This method shares the same objectives with linear regression method, which is to obtain the model parameters estimate by minimizing the squared difference between the experimental data and the model output. However, the non-linear regression method differs from linear regression because it requires an iterative process [42].
The process of estimating adsorption isotherm model parameters involves inputting the experimental data’s, including the equilibrium concentration (Ce), the amount of metals ion adsorbed at equilibrium (qe) as well at time t, (qt) into Excel spreadsheet and creating a graph. Initial estimates of the unknown parameters in the model equations are then made to calculate theoretical qe or qt values. The squared sum of the difference (SS) between the experimental data and theoretical model output is computed. Subsequent iteration are performed by slightly adjusting the initial estimated parameters values and recalculating the (SS) multiples until the parameters value yield the lowest possible (SS) value. Unlike the non-linear regression method which is an iterative process, linear regression typically only needs one calculation to produce lowest (SS) values. The solver add in function in Microsoft Excel is a convenient tool which was used for performing non-linear regression analysis. Generally, the non-linear regression method considered more appropriate and accurate in determining model parameter than the linear method [43].
2.10. Error analysis
To validate the fitness of these isotherm models in describing the adsorption process further, error analysis methods such as chi-square (χ2) and sum of square error (ERRSQ/SSE) were used and compared to the correlation coefficient (R2). Because it only represents the fitness between linear forms of isotherm equations and experimental data, the coefficient correlation (R2) alone may not be sufficient to validate the basis for the best adsorption model selection. Non-linear regression is commonly used to distribute experimental data and predicted isotherms based on convergence criteria, minimization and maximization error. The difference between the experimental data and data obtained from the model can be quantify by chi square test (χ2). It is calculated as the sum of squares of this difference divided by the corresponding data calculated from models as described in Eq. (10). If the qe, exp values are similar to qe model values, the χ2 value approaches zero. Conversely, a higher χ2 indicates a significant discrepancy between the experimental and the calculated model values, which suggest a high level of bias [44]. The smaller χ2 and ERRSQ/SSE values for the isotherm models studied, the better the fit to the adsorption process. The χ2 and SSE values were calculated using the following Eqs. (10), (11) below; [45].
| (10) |
| (11) |
The quantity of Cd(II) adsorbed at equilibrium is denoted as qe, exp (mg/g) and the amount of Cd(II) uptake from the model after using solver Add-in is qe,cal (mg/g).
2.11. Thermodynamic study
The behaviour of the adsorption process was evaluated using the thermodynamic parameters which include Gibbs free energy changes ΔGo (kJ/mol), ΔHo (kJ/mol) for enthalpy change and change in entropy ΔSo (J mol −1 K-1). The adsorption thermodynamic studies were evaluated using the following Eqs. (12), (13), (14) respectively [27].
| (12) |
| (13) |
| (14) |
| (15) |
Where Cad is the concentration of the metal ion, Keq is the constant at equilibrium, T(K) is the temperature, and the gas constant is R (8.314 Jmol −1K−1). The Arrhenius equation, as shown in equation (15), was utilized to calculate the activation energy (Ea). Ea is the activation energy (KJ/mol), Arrhenius constant is denoted as A. An adsorption activation energy (Ea) value of 5–40 kJ/mol or below suggests physisorption, whereas a value between 40 and 800 kJ/mol indicates chemisorption.
2.12. Desorption study
The reusability and recoverability of AMKC was tested using batch desorption studies. 10 ml of 0.1 N H2SO4 solution was added with the adsorbent saturated with metal ions after the process of adsorption. The solution mixture was agitated at 160 rpm for 120min, thereafter the desorbed metal ion concentration of each sample was analyzed [46].
The desorption percentage (DS) of metal ions was expressed as Eq. (16)
| (16) |
M1 = Amount of metal ion desorbed (mg)
M2 = Amount of metal ion adsorbed (mg)
3. Results and discussion
3.1. Adsorbent characterizations
The surface features of the two adsorbents (PKC and AMKC) are presented in Table 2. As seen from the results, it was obvious that the specific surface area of the unmodified clay material was lesser than that of the modified clay, indicating that acid modification of the clay resulted in a surface characteristics improvement. These observations were in agreement with study reported by Ref. [47] who found that the modification of clay material by mineral acid facilitated an ion exchange between H+ and those components of the clay. Furthermore, the process led to leaching of Al3+ from tetrahedral and octahedral sites of the clay while the silicate groups remained largely intact, thus improving the performance of the AMKC sample. As also seen in Table 2, the pore volume of the clay largely improved upon modification, suggesting that active sorption sites were available on the external surface of the AMKC sample, and it could enhance the adsorption of Cd2+ ions onto its surface.
Table 2.
Surface characteristics of the PKC and AMKC.
| Sample | Specific surface area | Pore volume (cm3/g) | Pore diameter (Å) |
|---|---|---|---|
| PKC | 84.2 | 0.05 | 2.12 |
| AMKC | 389.4 | 0.22 | 2.13 |
The microstructures of pristine and acid modified clay are displayed in Fig. 1. As seen from Fig. 1a, PKC exhibited a leaf-like structure. However, these leaf-like layers vanished upon modification of the raw clay by HCl, forming thin films which reduce the sharp edge features of the parent clay. It is worthy of note that the AMKC sample showed a wide pore distribution, size asymmetric cavity and smaller particles. The presence of the pores on the AMKC adsorbent suggested a good possibility for metal ions to be adsorbed [19,48].
Fig. 1.
SEM images of (a) PKC and (b) AMKC.
Fig. 2 revealed the FTIR spectra of pristine and modified clay samples within the wavenumber range of 4000–500 cm−1. The peaks at around 3638-3449 cm−1 were as a result of moisture presence on the samples which could be attributed to hydroxyl (O–H) group. The presence of peaks at around 1650 cm−1 and 1000-900 cm−1 in both PKC and AMKC samples could be assigned to the deformation of Si–O-M+ and O–Si–O stretching, respectively [49]. A series of absorption bands in both samples at 867-876 cm−1, 768 cm−1 and 698 cm−1 could be respectively attributed to CH out-of-plane deformation, Al–Mg–OH and Si–O–Al vibration of the clay sheet [20]. It is noteworthy that a peak at 876 cm−1 in AMKC suggested the presence of acid group in the modified clay [50]. Overall, the presence of the functional groups on the surfaces of the two samples contributed to their better performances.
Fig. 2.
FTIR spectra of PKC and AMKC samples.
The XRD patterns of pristine and acid-modified kaolinite clay are shown in Fig. 3. The XRD intensity of the clay was changed by modification with acid. Fig. 3 illustrates the characteristic peaks of SiO2 in form of kaolinite and tridymite for the AMKC adsorbent. The acid-modified clay was sufficiently active in the adsorptive removal of cadmium ions because of the intensity of kaolinite (21.3°, 39.1°, 43.7°, 50.3° and 56.1°), quartz (27.4°), tridymite (63.1°) and CaSiO2 (74.6°). It is clear that the presence of silica and alumina in the as-synthesized clay-based adsorbent would play a critical role in the adsorptive removal of Cd ions from wastewater. According to Refs. [19,27], SiO2 is an inorganic adsorbent with the presence of silanol (SiOH) group on its surface, which acts as sorption sites during the adsorption process.
Fig. 3.
XRD pattern of PKC and AMKC samples.
3.2. Response surface methodology for Cd ions removal by PKC and AMKC
The 3-factor CCD matrix as generated by the software and the removal efficiencies obtained in adsorption of Cd2+ ions by PKC and AMKC at different adsorption process conditions are listed in Table 3. The polynomial (second-order) equations (Eqs. (17), (18))) were used to illustrate the adsorption process parameters and Cd2+ removal uptake by AMKC and PKC.
| YAMKC = 93.74–2.60A - 0.22B + 2.37AB + 3.68AC + 0.50BC - 6.49A2 + 3.04B2 + 2.34C2 | (17) |
| YPKC = 71.24 + 5.81A - 8.58B + 3.53 + 10.95C + 7.57AB - 2.96AC +5.7BC - 2.13A2 - 3.53B2 - 6.71C2 | (18) |
Table 3.
3-factor central composite design matrix and the value of response function.
| Run | Temperature, A (oC) | Dosage, B (g) | Time, C (min) | YAMKC | YPKC |
|---|---|---|---|---|---|
| 1 | 35.00 | 0.30 | 65.00 | 93.89 | 70.14 |
| 2 | 35.00 | 0.30 | 10.00 | 93.67 | 55.32 |
| 3 | 25.00 | 0.50 | 10.00 | 93.25 | 17.14 |
| 4 | 25.00 | 0.30 | 65.00 | 90.08 | 64.22 |
| 5 | 45.00 | 0.10 | 10.00 | 82.22 | 62.82 |
| 6 | 35.00 | 0.10 | 65.00 | 97.07 | 77.29 |
| 7 | 35.00 | 0.30 | 65.00 | 93.68 | 69.89 |
| 8 | 35.00 | 0.30 | 65.00 | 93.84 | 69.22 |
| 9 | 35.00 | 0.30 | 65.00 | 93.67 | 70.78 |
| 10 | 25.00 | 0.10 | 10.00 | 99.39 | 61.25 |
| 11 | 35.00 | 0.30 | 120.00 | 98.44 | 75.97 |
| 12 | 45.00 | 0.50 | 10.00 | 85.58 | 49.63 |
| 13 | 35.00 | 0.30 | 65.00 | 93.82 | 70.99 |
| 14 | 35.00 | 0.50 | 65.00 | 96.44 | 60.37 |
| 15 | 35.00 | 0.30 | 65.00 | 93.67 | 73.73 |
| 16 | 25.00 | 0.50 | 120.00 | 92.01 | 56.61 |
| 17 | 25.00 | 0.10 | 120.00 | 96.10 | 77.22 |
| 18 | 45.00 | 0.30 | 65.00 | 84.37 | 76.23 |
| 19 | 45.00 | 0.50 | 120.00 | 99.00 | 77.44 |
| 20 | 45.00 | 0.10 | 120.00 | 93.67 | 68.39 |
As seen from Eqs. (17), (18), the positive terms indicate synergistic effect on the response whereas negative terms suggest an antagonistic effect on the process output. Coefficient of determination ( and ) standard deviation (SD), p-value, F-value and analysis of variance (ANOVA) were used in judging the model fitness. As shown in Table 4, Table 5, the coefficients of determination values = 0.9987 and = 0.9953 for AMKC and = 0.9940 and = 0.9826 for PKC) were high, thus suggesting that the predicted values matched the experimental values reasonably well and ensuring a satisfactory adjustment of the second-order regression model with the experimental data. Furthermore, the low values of SD for both adsorbents (SD = 0.17 for AMKC and SD = 1.48 for PKC) reaffirmed the model fitness as the smaller SD suggests more accurate prediction of response by the model [8].
Table 4.
Response Surface (ANOVA) for Cd2+ adsorption using AMKC.
| Source | Sum of Squares | Df | Mean square | F/value | P –value prob > F | Comment |
|---|---|---|---|---|---|---|
| Model | 403.14 | 9 | 44.79 | 1563.6 | <0.0001 | S.D = 0.17 |
| A – temp | 67.55 | 1 | 67.55 | 2357.89 | <0.0001 | Mean = 93.19 |
| B – dosage | 0.47 | 1 | 0.47 | 16.44 | 0.0023 | |
| C - time | 63.05 | 1 | 63.05 | 2200.91 | <0.0001 | C.V = 0.18 |
| AB | 44.75 | 1 | 44.75 | 1561.93 | <0.0001 | R2 = 0.9987 |
| AC | 108.05 | 1 | 108.05 | 3777.1 | <0.0001 | R2(adj)=0.9953 |
| BC | 2.02 | 1 | 2.02 | 70.51 | <0.0001 | AP = 144.365 |
| A2 | 115.67 | 1 | 115.67 | 40.37 | <0.0001 | |
| B2 | 25.49 | 1 | 25.49 | 889.79 | <0.0001 | |
| C2 | 15.12 | 1 | 15.12 | 527.67 | <0.0001 | |
| Residual | 0.29 | 10 | 0.029 | |||
| Lack of fit | 0.24 | 5 | 0.047 | 4.79 | 0.0553 | |
| Pure Error | 0.049 | 5 | 9.897E-003 | |||
| Cor Total | 403.43 | 19 |
Table 5.
Response Surface (ANOVA) for Cd2+ ions adsorption using PKC.
| Source | Sum of squares | Df | Mean square | F/value | P –value Prob > F | Comment |
|---|---|---|---|---|---|---|
| Model | 3635.64 | 9 | 403.96 | 185.61 | <0.0001 | S.D = 1.48 |
| A -temp | 337.21 | 1 | 337.21 | 154.94 | <0.0001 | Mean = 65.23 |
| B- Dosage | 735.82 | 1 | 735.82 | 338.10 | <0.0001 | R2 = 0.9940 |
| C- Time | 1198.37 | 1 | 1198.37 | 550.63 | <0.0001 | R2(adj)=0.9826 |
| AB | 458.74 | 1 | 458.74 | 210.78 | <0.0001 | AP = 57.602 |
| AC | 60.83 | 1 | 60.83 | 27.95 | 0.0004 | C.V = 2.26 |
| BC | 261.52 | 1 | 261.52 | 120.78 | <0.0001 | |
| A2 | 12.50 | 1 | 12.50 | 5.74 | 0.0375 | |
| B2 | 34.21 | 1 | 34.21 | 15.72 | 0.0027 | |
| C2 | 123.88 | 1 | 123.88 | 56.92 | <0.0001 | |
| Residual | 21.76 | 10 | 2.18 | |||
| Lack of fit | 9.38 | 5 | 1.88 | 0.76 | 0.6158 | |
| Pure Error | 12.38 | 5 | 2.48 | |||
| Cor. Total | 3657.90 | 19 |
Moreover, the ANOVA results for the Cd2+ adsorption by AMKC and PKC adsorbents are presented in Table 4, Table 5, respectively. The adequacies of the regression models were further judged by P-value, lack of fit, F-value and signal to noise ratio. The P-value less than 0.05 suggests that the model term is significant, whereas the lack of fit value greater than 0.0500 signifies an insignificant model. Non-significant lack of fit is good as it confirms the adequacy of the model fit. Also, an adequate precision (a parameter that measures ratio of signal to noise) value greater than 4 is desirable as it indicates an adequate signal [51]. As shown in Table 4, Table 5, the models for the Cd2+ ions removal efficiencies for AMKC and PKC satisfied those above-mentioned criteria, thus confirming the model’s fitness [19]. In addition to this, it was noticed that all the three independent variables studied were significant to the adsorption of Cd2+ ions by the acid-modified kaolinite clay.
3.3. Effect of parameters as response surface plots
3.3.1. Response surface plots for Cd2+ uptake removal by AMKC
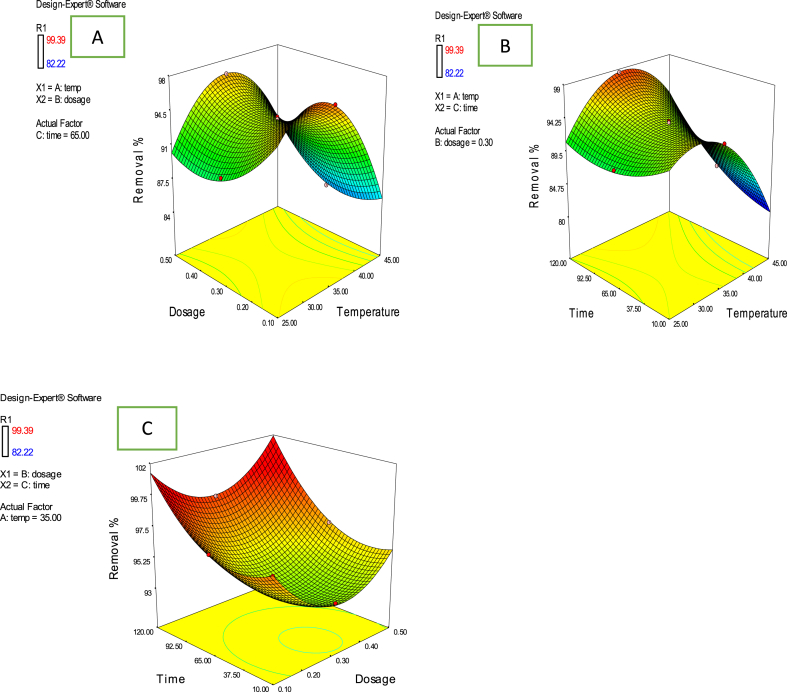
The interaction influence of independent process factors studied (temperature, adsorption dosage and contact time) on Cd2+ ions removal uptake by AMKC is illustrated in Fig. 4. Fig. 4a displays the combined effect between adsorbent dosage and temperature on Cd2+ ions removal uptake for a contact time of 65 min. As displayed in Fig. 4a, the removal efficiency decreased with increasing adsorbent dosage and temperature. This observation indicated that the small amount of AMKC adsorbent was needed to adsorb larger amount of Cd2+ ions and also implied that the process was endothermic [52]. Fig. 4b shows that the removal efficiency of Cd2+ ions increased with increasing contact time. The figure also showed that little amount of heat was needed to achieve maximum removal uptake of Cd2+ ions. Fig. 4c depicts the interaction effect between contact time and adsorbent dosage on Cd2+ ions removal efficiency (%) for a temperature of 35 °C. From the figure, it was observed that as the contact time increased, the removal efficiency also increased until it attains 120 min. This observation indicated that the time required to attain adsorption equilibrium was established at maximum value of contact time [7]. The same trend is also observed in the case of removal efficiency versus adsorbent dosage.
Fig. 4.
Combined effect of process factors (a) dosage and temperature (b) time and temperature (c) time and dosage on percentage removal of Cd(II) on AMKC.
3.3.2. Response surface plots for Cd2+ ions uptake removal by PKC
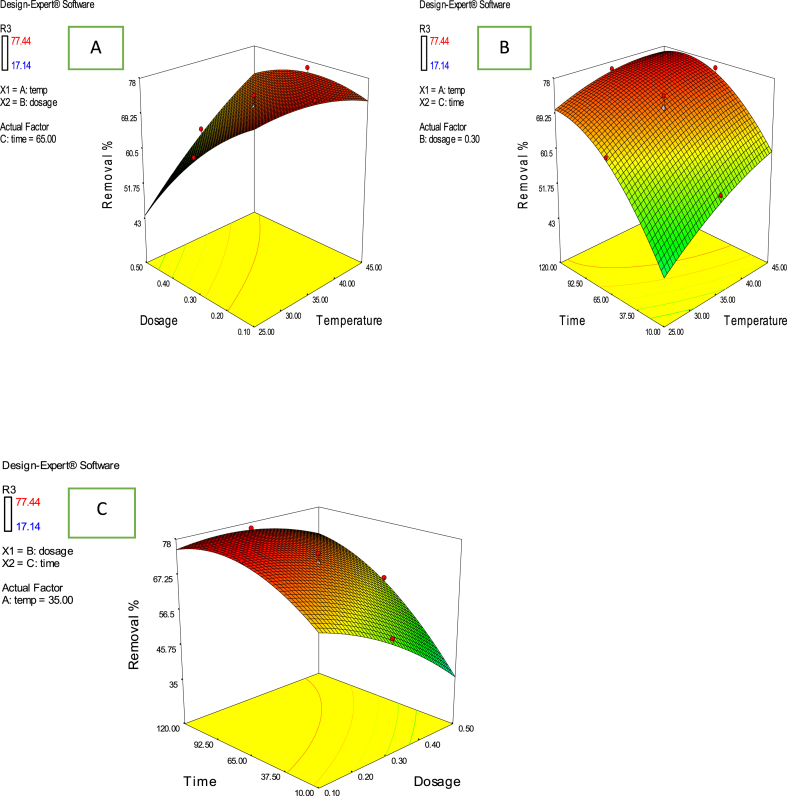
Fig. 5a shows the response surface plots of Cd2+ ions removal efficiency as a function of adsorbent dosage and adsorption temperature. It was revealed that the removal efficiency of Cd2+ ions rapidly decreased with increasing adsorbent dosage, while it increased with an increase with in the temperature. This observation may be due to more active sites of adsorbent remained unsaturated during the Cd2+ ions adsorption. Fig. 5b shows an increase in removal efficiency with an increase in contact time and temperature. At the beginning of adsorption, the high rate of adsorption of Cd2+ ions on the PKC adsorbent was due to the availability of an abundance of adsorption sites. However, the increase in removal efficiency with the increase in temperature indicated that Cd2+ ions adsorption by PKC was endothermic in nature [52]. Fig. 5c shows that the Cd2+ ions uptake decreased with an increase in adsorbent dosage. It could be deduced from the figure that to achieve maximum adsorption, cadmium ions-containing solution needs to be treated with 0.10 g/L PKC, and this indicated that the adsorbent dosage is the most influential factor among the variables studied.
Fig. 5.
Combined effect of process factors (a) dosage and temperature (b) time and temperature (c) time and dosage on percentage removal of Cd2+ ions on PKC.
The experimental data was also analyzed to assess the correlation between the predicted and experimental adsorption efficiency of AMKC and PKC in removal of Cd(II) ion. Fig. 6a depicts the correlation between Normal % probability and studentized residual plot which indicates a satisfactory distribution of data points near the straight line, while that of Fig. 6b indicate a strong correlation between the experimental and predicted values of Cd(II) ion removal efficiency as calculated by Eqs. (17), (18)). Fig. 7a and b Shows a similar trend. This suggest a positive relationship between the experimental and predicted response values and that the assumption underlying the analysis were appropriated as noted in similar study by Ref. [53]. Furthermore, the results suggest that the quadratic models selected was sufficient in predicting the response variables for the experimental data.
Fig. 6.
a. Plot of a Normal % probability versus residual error b. Actual values versus predicted values for AMKC.
Fig. 7.
a. Plot of a Normal % probability versus residual error b. Actual values versus predicted values for PKC.
3.4. Process optimization
The numerical optimization feature of the DOE software version 7.0.0 was used to determine the best operating conditions for the removal of Cd2+ ions by AMKC and PKC adsorbents. Table 6 shows the optimum process variable values for maximum removal uptakes. The predicted removal efficiencies for AMKC and PKC at these optimum values were 97.61% and 76.32%, respectively. A comparison between the experimental and predicted results revealed that the error between them is less than 0.3% indicating that the generated model is reliable. However, by repeating the experiment under the established optimal conditions, the observed percentage adsorbed of Cd2+ ions by AMKC and PKC were 99.19% and 77.82%, respectively. The obtained results show that the strategy used in optimizing the conditions of Cd2+ ion uptake by both PKC and AMKC, as well as achieving the maximum percentage removal by RSM for batch adsorption of Cd2+ ions, is feasible. To further validate the model, a dosage of 0.2 g, temperature of 30 °C and time of 80 min which were within the working range but not tested before were also evaluated. The predicted removal efficiency was 96.81% and 75.42% for AMKC and PKC. This was substantiated experimentally in the laboratory, where 95.97% and 74.53% efficiency were obtained. This established the reliability and accuracy of the model in predicting other random independent runs.
Table 6.
Optimal condition and model validation of Cd2+ ions adsorption by AMKC and PKC adsorbents.
| A (oC) | B (g/L) | C (min) | Cd2+ removal uptake (%) by AMKC | Cd2+ removal uptake (%) by PKC | ||
|---|---|---|---|---|---|---|
| Predicted | Experimental | Predicted | Experimental | |||
| 45.3 | 0.63 | 120.9 | 97.61 | 99.19 | 76.32 | 77.82 |
| 30 | 0.2 | 80 | 96.81 | 95.97 | 75.42 | 74.53 |
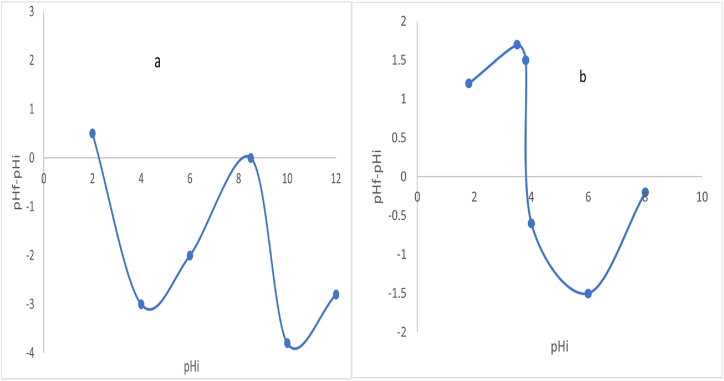
3.5. Point of zero charge determination
The value of pHpzc obtained on the surface of prepared adsorbent (PKC and AMKC) was gotten to be 8.5 (basic) and 3.8 (acidic) which can be seen in Fig. 8 (a, b). Due to acid activation, the pH decreased from 8.5 to 3.8. The results indicate the AMKC would be good enough to eliminate metal ions at pH > 3.8 [54]. A basic idea, samples develop positive charge when the pH of substance is lesser than the pHpzc. In contrast, samples develop negative charge when the pH is greater than pHpzc. Making it the chosen materials for cation adsorption [55,56].
Fig. 8.
Determination of pH at point zero charge (pHpzc) on surface (a) PKC and (b) AMKC.
3.6. Effect of pH
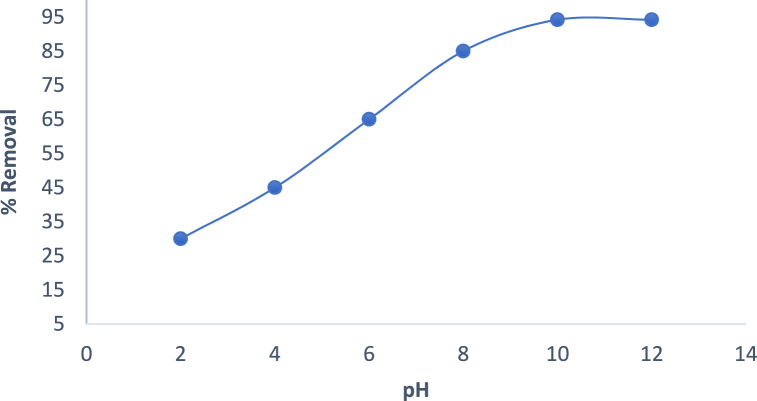
The effect of solution pH was carried out to evaluate the maximum percentage of Cd(II) ions onto the adsorbent AMKC in an aqueous solution. The result of effect of pH as illustrated in Fig. 9 showed that as the pH of Cd(II) ion increases from 2 to 10, the percentage removal also increase from 32.5% to 92.4% and beyond the point of (pH > 8) the percentage remain constant. At low value of pH the uptake percentage is low which may be due to protonation on the surface of the adsorbent in an acidic medium thereby leading to electrostatic repulsion between the adsorbent surface and Cd(II) ions [57].
Fig. 9.
Effect of pH on Cd(II) ions adsorption by AMKC. (Adsorbent dosage of 0.63 g/L, temperature of 45.3 °C and time of 120 min).
3.7. Adsorption isotherms study
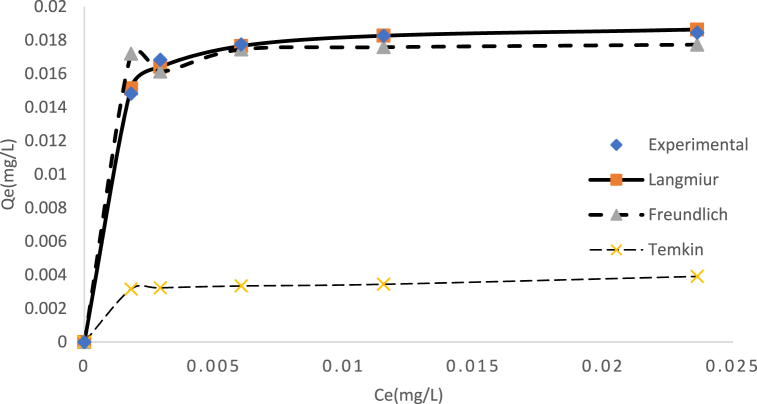
The parameters of adsorption isotherm model and the results of error analysis are displayed in Table 8 alongside Fig. 10. A comparison of R2, ᵪ2 and SSE values for the model used was evaluated. Based on the experimental data, it was observed that the adsorption isotherm model fit the data in the following order; Freundlich > Langmiur > Temkin. The Freundlich isotherm model provided the best description of the experimental data, with the highest R2 value of 0.997 with the lowest ᵪ2 and SSE values of 2.02E-7 and 8.6E-6 respectively. This further suggests that the studied adsorption process could be described as either non-ideal or reversible sorption, not limited to the formation of a monolayer on a heterogeneous surface [45,58,59]. Also, the (1/n) was determined to be 0.146 (corresponding to an n value of 6.84) as shown in Table 8. This value indicate that the adsorption of Cd(II) ion onto AMKC is favourable, as an exponent value between 0 and 1 suggests favourable adsorption process [60]. The adsorption process follows monolayer and homogeneous mechanism with high-capacity uptake and also as a result of ionic properties (See Table 7). Lastly the strong attraction of Cd(II) to the adsorbent surface is due to its high electronegativity value [22 ,61].
Table 8.
Isotherm parameter constant and coefficients correlation for adsorption onto Cd(II).
| Isotherm | Value |
|---|---|
| Langmuir | |
| Qmax (mg/g) | 388.80 |
| KL (L/g) | 0.024 |
| R2 | 0.988 |
| ᵪ2 | 4.9E-5 |
| SSE | 2.2E-5 |
| Freundlich | |
| KF(mg/g) (L/g) | 0.0386 |
| 1/n | 0.146 |
| R2 | 0.997 |
| ᵪ2 | 2.02E-7 |
| SSE | 8.6E-6 |
| Temkin | |
| KT (L/g) | 123.68 |
| B (J/mol) | 263.64 |
| R2 | 0.737 |
| ᵪ2 | 0.0540 |
| SSE | 2.11E-4 |
Fig. 10.
Predicted curve fits for equilibrium isotherm for Cd(II) adsorption on AMKC.
Table 7.
Cd(II) ions ionic property.
| Property | Cd(II) |
|---|---|
| Atomic weight | 112.41 |
| Ionic radii (Ao) | 0.95 |
| Molecular weight | 769.52 |
| Hydrated radii (Ao) | 4.260 |
| Electronegativity | 1.69 |
| Coordination number | 6 and 4 |
Source [61].
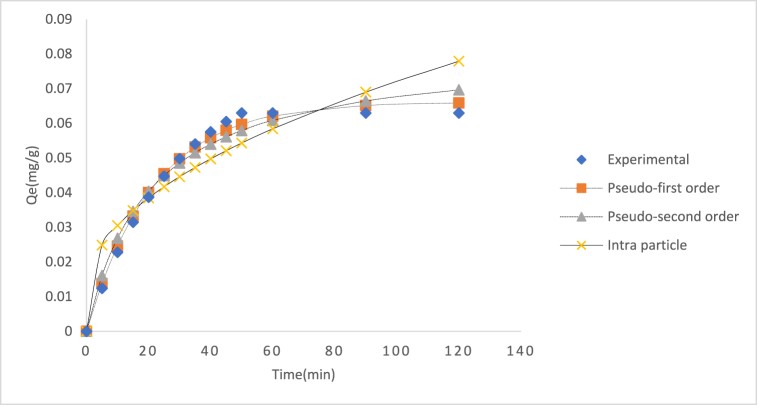
3.8. Adsorption kinetics study
The kinetic model for adsorption of Cd(II) ion adsorption was carried out using three models namely Pseudo-first order, Pseudo-second order and intra particle diffusion model respectively, and the resulting kinetics parameters and error function data are displayed in Table 9 and their plots in Fig. 11. Regarding the Cd(II)ion, the R2 value for Pseudo second order kinetic equation was observed to be superior to that of Pseudo-first order and intra particle diffusion. Additionally, the calculated qe value for the Pseudo-second order (0.0658 mg/g) was found to be closer to the experimental qe value (0.0661 mg/g) as compared to the pseudo-first order model (0.0620 mg/g). Although both Pseudo first order and Pseudo-second order exhibited good correlation with experimental data. The fitness of Pseudo-second order model was further attested to the smaller value of SSE (9.0E-8) and ᵪ2 (1.3E-6). It is worth nothing that both physisorption and chemisorption could be occurring simultaneously on the surface of the adsorbent as a layer of molecules may be physically adsorbed on top of an underlying chemisorbed layer [62,63]. The decrease in the rate constant (K2) attest to the fact that at lower concentration the Cd(II) ion attain equilibrium faster [64].
Table 9.
Kinetic models for adsorption of Cd(II) ion onto AMKC.
| Kinetic model | Equation | Parameter | Adsorbate (Cd(II) |
|---|---|---|---|
| Pseudo-first order | qe,cal (mg/g) | 0.0621 | |
| qe,exp (mg/g) | 0.0661 | ||
| K1 (min−1) | 0.0464 | ||
| SSE | 1.68E-5 | ||
| R2 | 0.9850 | ||
| ᵪ2 | 2.7E-4 | ||
| Pseudo-second order | qe,cal (mg/g) | 0.0658 | |
| qe exp | 0.0661 | ||
| K2 (g/mg min) | 0.00603 | ||
| SSE | 9.0E-8 | ||
| R2 | 0.9991 | ||
| ᵪ2 | 1.3E-6 | ||
| Intraparticle diffusion | Kid (mg/gmin1/2) | 0.00608 | |
| C | 0.0112 | ||
| SSE | 1.64E-2 | ||
| ᵪ2 | 4.2E-5 | ||
| R2 | 0.92618 |
Fig. 11.
Predicted curve fits for kinetics of Cd(II) adsorption onto AMKC.
3.9. Adsorption thermodynamics study
The adsorption thermodynamics study for the adsorption of Cd(II) onto AMKC and results obtained were depicted in Table 10. The entropy (ΔSo) and enthalpy (ΔHo) values were determined by analyzing the slope and intercept of the linear graph generated by plotting log against . The negative ΔGo values obtained for the metal ion onto the sorbent showed that the adsorption process is feasible and spontaneous. The positive value of ΔHo indicate that the adsorption process was endothermic. The positive ΔSo value implies increase in the degree of freedom at the adsorbate-adsorbent interface during the adsorption process [21]. Also the activation energy Ea was calculated using equation (15), based on the obtained Ea value of 7.439 kJ/mol, it can be inferred that the adsorption of Cd(II) was primarily due to physical adsorption (physisorption).
Table 10.
Thermodynamic parameters for adsorption of Cd(II) ion onto AMKC.
| Adsorbate | Temp (0K) | ΔHo(kJmol−1) | ΔSo(KJmol−1K−1) | ΔGo (kJmol−1) |
|---|---|---|---|---|
| Cd(II) | 298 | 26.5324 | 0.093009 | −1.18413 |
| 303 | −1.64917 | |||
| 308 | −2.11422 | |||
| 313 | −2.57926 | |||
| 318 | −3.04432 |
3.10. Desorption study
In terms of broad utilization, the recyclable and stability of AMKC is important. The desorption efficiency results depicted in Table 11 revealed the number of metal ions removed. The modified adsorbent decreased slightly after the first and second cycles, respectively. The reduction is attributed to the repetition of the desorption process which also decreased the adsorption capacity [7,65].
Table 11.
Desorption efficiency of Cd(II) ion after 3 cycles.
| Desorption efficiency (%) | ||||
|---|---|---|---|---|
| Adsorbent | Adsorbate | Cycle 1 | Cycle 2 | Cycle 3 |
| AMKC | Cd(II) | 98.73 | 86.41 | 65.39 |
Table 12 presents a comparison of the adsorption capacities of various clay materials for Cd(II) ion. The Langmuir adsorption capacity of AMKC is also compared to previous studies reported in the literature. The results demonstrate that AMKC exhibit a high adsorption capacity, indicating its effectiveness and appropriateness for the removal of heavy metals from wastewater.
Table 12.
Comparison of Cd(II) ion maximum adsorption capacity using different clays and other materials.
| Metal ion | Adsorbent | Maximum adsorption capacity Qmax (mg/g) | Reference |
|---|---|---|---|
| Cd(II) | Ball clay | 27.27 | [16] |
| Commercial (AC) | 31.9 | [66] | |
| Pure smectite | 3.87 | [67] | |
| Waste eggshell | 23.4 | [37] | |
| Recycled ligno-cellulose | 51.28 | [68] | |
| Cork biomass | 14.77 | [69] | |
| Luffa cylidrica | 7.29 | [70] | |
| Bone meal apatite | 116.16 | [13] | |
| AMKC | 388.80 | Present Study |
4. Conclusions
The adsorptive removal of Cd2+ ions from textile industry wastewater was investigated using pristine and acid-modified clay. When the clay was activated with HCl acid, its physicochemical and structural properties improved significantly, allowing AMKC to adsorb more Cd2+ ions than PKC. The percentages of Cd2+ ions adsorbed by the AMKC and PKC was 99.19% and 77.82%, respectively, under optimum conditions (temperature = 45.3 °C, adsorbent dosage = 0.63 g/L, contact time = 120.9 min). Freundlich isotherm was found to be the most suitable model for describing the adsorption isotherm, with the highest R2 value of 0.997 and the lowest ᵪ2 and SSE values of 2.02E-7 and 8.6E-6 respectively. The result obtained from kinetic model showed that the adsorption process follows Pseudo-second order. Investigation on thermodynamics behaviour showed that the process was spontaneous and endothermic in nature. The adsorption mechanism of Cd(II) ion was shown to be primarily dominated by physisorption. Maximum desorption efficiency was recorded at 98.73% which create an avenue for reuse of adsorbent. From the various analysis conducted this suggests that modifying kaolinite clay with mineral acid may be a better option than unmodified clay for Cd2+ ion adsorption from contaminated water.
Author contribution statement
Lukman Shehu MUSTAPHA: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Adeyinka Sikiru YUSUFF: Analyzed and interpreted the data; Wrote the paper.
Paul Egwuonwu DIM: Contributed reagents, materials, analysis tools or data.
Data availability statement
Data included in article/supp. Material/referenced in article.
Funding Statement
This research did not receive any specific grant from funding agencies in the private, public, or not-for-profit sectors.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The following names and the department are appreciated for their immense effort which facilitate the prompt results of the analysis carried out during the course of work. They are: Dr Remy Bucher (ithemba Labs XRD), Prof. S. J. Moir (Scientific Services, XRF), Cape Town, South Africa and Dr Franc¸ois Cummings (Physics Department, SEM/EDS), University of Western Cape (UWC), South Africa.
References
- 1.Igunnu E.T. Isothermal, kinetic, and thermodynamic parameters for adsorption of cadmium. J. Low Carbon Technol. 2014;9(3):157–177. [Google Scholar]
- 2.Alqadami A.A., Ghfar A.A., Naushad M., Abdalla M.A., Aloothmanions T. Efficient removal of toxic metal from wastewater using a recyclable nanocomposite: a study of adsorption parameters and interaction mechanism. J. Clean. Prod. 2017:426–436. [Google Scholar]
- 3.Tanihara A., Kiikuchi K., Konno H. Insight into the mechanism of heavy metal removal from water by monodisperse ZIF-8 fine particles. Inorg. Chem. Commun. 2021;54(131):3358–3371. 108782. [Google Scholar]
- 4.Briffa J., Singagra E., Blundell R. Heavy metal pollution in the environment and their toxicological effects on humans. Heliyon. 2020;6 doi: 10.1016/j.heliyon.2020.e04691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Rifaqat A.K.R., Kashifuddin M. Adsorption studies of Cd(II) on ball clay Comparison with other natural clays. Arab. J. Chem. 2016;9:S1233–S1244. [Google Scholar]
- 6.Lim S.F., Lee A.Y.W. Kinetic study on removal of heavy metal ions from aqueous solution by using soil. Environ. Sci. Pollut. Res. Int. 2015;22(13):10144–10148. doi: 10.1007/s11356-015-4203-6. [DOI] [PubMed] [Google Scholar]
- 7.Yusuff A.S. Adsorption of hexavalent chromium from aqueous solution by Leucaenaleucocephala seed pod activated carbon: equilibrium, kinetic and thermodynamic studies. Arabian J. Basic Appl. Sci. 2019;26:89–102. [Google Scholar]
- 8.Yusuff A.S., Owolabi J.O., Igbomezie C.O. Optimization of process parameters for adsorption of heavy metals from aqueous solutions by alumina-onion skin composite. Chem. Eng. Commun. 2021;208(1):14–28. [Google Scholar]
- 9.Sharma Y.C. Thermodynamics of removal of cadmium by adsorption on indigenous clay. Chem. Eng. J. 2010;145:64–68. [Google Scholar]
- 10.Gupta V.K., Rastogi A., Naya K.A. Adsorption studies on the removal of hexavalent chromium from aqueous solution using a low- cost fertilizer industry waste material. J. Colloid Interface Sci. 2012;342(1):135–141. doi: 10.1016/j.jcis.2009.09.065. [DOI] [PubMed] [Google Scholar]
- 11.Liu W.J., Zeng F.X., Zhang X.S. Preparation of high adsorption capacity bio-chars from waste biomass. J. Bioresource. Technol. 2012;102(17):8247–8252. doi: 10.1016/j.biortech.2011.06.014. [DOI] [PubMed] [Google Scholar]
- 12.Zhang T., Wang W., Zhao Y., Bai H., Kang T., Song Komarneni S. Removal of heavy metals and dyes by clay-based adsorbents: from natural clays to 1D and 2D nano-composites. Chem. Eng. J. 2021;420(2):127–574. [Google Scholar]
- 13.Ofudje E.A., Adeogun I.A., Idowu M.A., Kareem S.O. Simultaneous removals of cadmium(II) ions and reactive yellow 4 dye from aqueous solution by bone meal-derived apatite: kinetics, equilibrium and thermodynamic evaluations. J. Anal. Sci. and Technol. 2020;11:7–15. [Google Scholar]
- 14.Batool F., Jamshed I., Iqbal S., Noreen S., Bukahari S.N.A. Study of isothermal, kinetics thermodynamics of parameter of cadmium. J. Bioinorganic Chemist. Applicat. 2018;18 doi: 10.1155/2018/3463724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Duraisamy R.T., Henni A.H.A. InTech; London: 2013. State of the Art Treatment of Produced Water,” Water Treatment; pp. 199–222. [Google Scholar]
- 16.Rao R.A.K., Ikram S., Uddin M.K. Removal of Cr(VI) from aqeous solution on seed of artimsia arbisithium (novel plant materials) Appl. J. Desalined Wastewater Manag. Water Treatm. 2015;54:3358–3371. [Google Scholar]
- 17.Khan S., Dan Z., Mengling Y., Yang Y., Hao J. Isotherms, kinetics and thermodynamic studies of adsorption of Ni and Cu by modification of Al2O3 nanoparticles with natural organic matter. Fullerenes, Nanotub. Carbon Nanostruct. 2018;26:158–167. [Google Scholar]
- 18.Burakov A.E., Galunin E.V., Agarwal A.E., Tkachev A.G. Adsorption of heavy metals on conventional and nanostructure materials for wastewater treatment purposes: a review. J. Ecotoxicol. Environm. Saf. 2018;148:702–712. doi: 10.1016/j.ecoenv.2017.11.034. [DOI] [PubMed] [Google Scholar]
- 19.Yusuff A.S., Popoola L.T., Igbafe A.I. Response surface modeling and optimization of hexavalent chromium adsorption onto eucalyptus tree bark-derived pristine and chemically-modified biochar. Chem. Eng. Res. Des. 2022;182:592–603. [Google Scholar]
- 20.Olutoye M.A., Hameed B.H. A highly active clay-based catalyst for the synthesis of fatty acid methyl ester from waste cooking palm oil. Appl. Catal. Gen. 2013;450:57–62. [Google Scholar]
- 21.Dim P.E., Mustapha L.S., Tertanum M., Okafor J.O. Adsorption of chromium (VI) and iron (III) ions onto acid-modified kaolinite: isotherm, kinetics, and thermodynamics studies. Arab. J. Chem. 2021:1–14. King Saud University. [Google Scholar]
- 22.Dim P.E., Mustapha L.S., Tertanum M. Isotherm, Kinetics and Thermodynamics studies of adsorption of Cadmium (II) and Nickel (III) ions from textile effluent with acid modified clay. J. Chemical Technol. Metallurgy. 2021;56(5):1016–1029. [Google Scholar]
- 23.O’Connell D.W C., Burkinshaw T.F., Dwyer O. Heavy metal adsorbents prepared from the modification of cellulose: biosorption of copper ions from aqueous solutions by Spirulina platensis biomass. Bio Resources. Technol. 2008;99:6709–6724. doi: 10.1016/j.biortech.2008.01.036. [DOI] [PubMed] [Google Scholar]
- 24.Espana V.A., Sarkar A., Biswas B., Naidu R. Environmental applications of thermally modified and acid activated clay minerals: current status of the art. Environ. Technol. Innov. 2019;13:383–397. [Google Scholar]
- 25.Otunola B.O., Ololade O.O. A review on the application of clay minerals as heavy metal adsorbents for remediation purposes, Environmental Technology & Innovation. Overv. Linear Nonlinear Appr. Error Anal. 2020;18(18):10–62. 100692. [Google Scholar]
- 26.Obayomi K.S., Manasse A. Development of microporous activated Aloji clay for adsorption of lead (II) ions for aqueous solution. Heliyon. 2019;5 doi: 10.1016/j.heliyon.2019.e02799. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 27.obayomi K.S., Manasse A., Kovo A.S. Isotherm, Kinetic and thermodynamics studies for the adsorption of Pb(ll) onto modified Aloji clay. Desalinat. Water Treat. 2020;181:376–384. [Google Scholar]
- 28.Yavuz O.A. Removal of nickel, cobalt, and manganese from aqueous solution by kaolinite. Water Res. 2003;37:948–952. doi: 10.1016/s0043-1354(02)00409-8. [DOI] [PubMed] [Google Scholar]
- 29.Karmaker S.C., Elijamal O., Sah B.B. Response surface methodology for strontium removal process optimization from contaminated water using zeolite nano composite. Environ. Sci. Pollut. Res. 2021:1–17. doi: 10.1007/s11356-021-14503-3. [DOI] [PubMed] [Google Scholar]
- 30.Cheng J., Gao J., Zhang J., Yan W., Zhou J. Optimization of hexavalent chromium biosorption by shewanella putre using the box- behken design. Water Air Solut. 2021;232(3) [Google Scholar]
- 31.Puri S., Sumana G. Highly effective adsorption of crystal violet dye from contaminated water using graphene oxide intercalated montmorillonite nanocomposite. Appl. Clay Sci. 2018;166:102–112. [Google Scholar]
- 32.Allen S.J., Mckay G., Porter I.F. Adsorption isotherm models for basic dye adsorption by peat in single and binary component systems. J. Colloid Interface Sci. 2004;280(2):322–333. doi: 10.1016/j.jcis.2004.08.078. [DOI] [PubMed] [Google Scholar]
- 33.Yang C. Statistical mechanical study on the Freundlich isotherm equation. J. Colloid Interface Sci. 1998;208:379–387. doi: 10.1006/jcis.1998.5843. [DOI] [PubMed] [Google Scholar]
- 34.Freundlich H.M.F. Over the adsorption in solution. Z. Phys. Chem. 1906;57:385–470. [Google Scholar]
- 35.Daifullahi A.A.M., Girgis B.S., Gad H.N.M. A study of the factors affecting the removal of humic acid by activated carbon prepared from biomass material. Colloids Surf A Physicochem. Eng. Aspects. 2004;235:1–10. [Google Scholar]
- 36.Pillay K., Cukrowska E.M., Coville N.J. Multi-walled carbon nanotubes as adsorbents adsorbents for the removal of parts per billion levels of hexavalent chromium from aqueous solution. J. Hazard Mater. 2009;166:1067–1075. doi: 10.1016/j.jhazmat.2008.12.011. [DOI] [PubMed] [Google Scholar]
- 37.Balaz M., Buinakova Z., Balaz P., Zorkovoska A., Brinancin J. Adsorption of cadmium(II) on waste biomaterial. J. Colloid Interface Sci. 2015;454:121–133. doi: 10.1016/j.jcis.2015.03.046. [DOI] [PubMed] [Google Scholar]
- 38.Balarak D., Jaffari J., Hassani G., Mahdavi Y., Gupta V.K. The use of low-cost adsorbent (Canola Residues) for the adsorption of methylene blue from aqueous solution: isotherm, kinetic and thermodynamic studies. Colloids Interf. Sci. Communi. 2015;7:16–19. [Google Scholar]
- 39.Lagergren S. About the theory of so-called adsorption of soluble substances. Kungliga Svenska Vetenskapsakademiens Handlingar. 1898;24 [Google Scholar]
- 40.Li Q., Yue Q., Su Y., Gao B., Sun H. Equilibrium, thermodynamics and process design to minimize adsorbent amount for the adsorption of acid dyes onto cationic polymer-loaded bentonite. Chem. Eng. J. 2010:158–489. [Google Scholar]
- 41.Blanchard G., Maunaye M., Martin G. Removal of heavy metals from waters by means of natural zeolites. J. Water Resour. 1984;18(12):1501–1507. [Google Scholar]
- 42.Brown A.M. A step-by-step guide to non-linear regression analysis of experimental data using a microsoft excel spreadsheet. Comput. Methods Progr. Biomed. 2001;65:191–200. doi: 10.1016/s0169-2607(00)00124-3. [DOI] [PubMed] [Google Scholar]
- 43.Crini G., Badot P. Presses Universitaires de Franche-Comté; Besançon: 2010. Sorption Processes and Pollution: Conventional and Non-conventional Sorbents for Pollutant Removal from Wastewaters. [Google Scholar]
- 44.Enebi E.T., Victor O.A., Jude C.O. Nonlinear regression analysis of the sorption of crystal violet and methylene blue from aqueous solution onto an agro-waste derived activated carbon. Appl. Water Sci. 2020;10(132):2–11. [Google Scholar]
- 45.Foo K.Y., Hameed Insights into the modeling of adsorption isotherm systems. Chem. Eng. J. 2010;156:2–10. [Google Scholar]
- 46.Khan S.D. Isotherms, kinetics and thermodynamic studies of adsorption of Ni and Cu by modification of Al2O3 nanoparticles with natural organic matter. Fullerenes, Nanotub. Carbon Nanostruct. 2018;26:158–167. [Google Scholar]
- 47.Kooli F., Liu R., Al-Faze A., Suhaimi I.I. Effect of acid of Saudi local clay minerals on removal properties of basic blue 41 from an aqueous solution. Appl. Clay Sci. 2015:23–30. [Google Scholar]
- 48.Hameed B.H., Krishni R.R., Sata S.A. A novel agricultural waste adsorbent for the removal of cationic dye from aqueous solution. Vol. 162. 2009. A novel agricultural waste adsorbent for the removal of cationic dye from aqueous solution; pp. 305–311. [DOI] [PubMed] [Google Scholar]
- 49.Olutoye M.A., Wong S.W., Chin L.H., Amani S.W., Hameed B.H. Synthesis of fatty acid methyl esters via the transesterification of waste cooking oil by methanol with a barium-modified montmorillonite K10 catalyst. Renew. Energy. 2016;86:392–398. [Google Scholar]
- 50.Seyf-Laye A.M., Ibrahim T., Gbandi D.B., Moctar B.L.’, Honghan C. Investigation of different electrodes in electrocoagulation of domestic wastewater treatment. International. J. Eng. Sci. Res. Technol. 2018;7(5):50–54. [Google Scholar]
- 51.Ahmadkhaniha D., Heyarzadeh M., Hanzaki A.Z. Taguchi optimization of process parameters in friction stir processing of pure Mg. J. Magnesium Alloy. 2015;3:168–172. [Google Scholar]
- 52.Gorzin F., Abadi M.M.B.R. Adsorption of Cr(VI) from aqueous solution by adsorbent prepared from paper mill sludge: kinetics and thermodynamic studies. Adsorpt. Sci. Technol. 2017;24:1–12. [Google Scholar]
- 53.Ani J.U., Okoro U.C., Ameka L.E., Onkuwuli O.D. Application of responds surface methodology for optimization of dissolved solid adsorption by activated coal. Appl. Water Sci. 2019:1–11. [Google Scholar]
- 54.Hattab A., Bagane M., Chlendi M. Characterisation of Tataouine's raw and activated clay. J. Chem. Eng. Process Technol. 2013;4:155–165. [Google Scholar]
- 55.Ayari F., Manai G., Khelifi S., Trabelslayadi M. Treatment of anionic dye solution using Ti, HDTMA and Al/Fe pillard bentonite Essay to regenerate the adsorbent. J. Saudi Chem. Soc. 2019;23:294–306. [Google Scholar]
- 56.Sedef D., Gulgin Y., Ertugrul Y., Emine K. Zeta potential study of natural–and acid–activated sepiolites in electrolyte solutions. Can. J. Chem. Eng. 2011;90:785–792. [Google Scholar]
- 57.Padmavathy K., Madhub G., Haseena P. A study on effects of pH, adsorbent dosage, time, initial concentration and adsorption isotherm study for the removal of hexavalent chromium (Cr (VI)) from wastewater by magnetite nanoparticles. Environ. Technol. 2016;24:585–594. [Google Scholar]
- 58.Berizi Z., Hashemi S.Y., M Hadi, Azari A. The study of Non-linear kinetics and adsorption isotherm models for Acid Red 18 from aqueous solutions by magnetite nanoparticles and magnetite nanoparticles modified by sodium alginate. Water Sci. Technol. 2016;74(5):1235–1242. doi: 10.2166/wst.2016.320. [DOI] [PubMed] [Google Scholar]
- 59.Rahim A.A., Garba Z.N. Efficient adsorption of 4-Chloroguiacol fromaqueous solution using optimal activated carbon: equilibrium isotherms and kinetics. J. Assoc. Arab Univ. Basic Appl. Sci. 2015;15:1–10. [Google Scholar]
- 60.Karthikeyan T., Rajgopal S., Miranda L.R. Chromium (VI) adsorption from aqueous solution by Hevea brasilinesis sawdust activated carbon. J. Hazard Mater. 2005;124:192–199. doi: 10.1016/j.jhazmat.2005.05.003. [DOI] [PubMed] [Google Scholar]
- 61.Jain M., Kadirvelu V.K., Garg M., Sillanpa M. Adsorption of heavy metals from multi-metal aqueous solution by sunflower plant biomass-based carbons, Ower Plant Biomass-based carbons. Int. J. Environ. Sci. Technol. 2016;13:493–500. [Google Scholar]
- 62.Denizili A., Say R., Y Removal of heavy metals ion from aquatic solution by membrane chromatography. Sep. Purif. Technol. 2000;21:181–190. [Google Scholar]
- 63.Herma M., Arivoli S. Adsorption kinetics and thermodynamic of malchite green dye unto acid activated low cost carbon. J. Appl. Sci. 2008:43–51. [Google Scholar]
- 64.Aravindhan R., Fathima N.N., Rao J./.R., Nau B.U. Equilibrium and thermodynamic studies on the removal of Basic Black dye using calcium alginate beads. J. Coll. Surface Physico Chem. Eng. Aspect. 2007;299:232–238. [Google Scholar]
- 65.Balaž M., Ficeriova J., Brain J. Influence of milling on the adsorption ability of eggshell waste. J. Chemisph. 2016;146:458–471. doi: 10.1016/j.chemosphere.2015.12.002. [DOI] [PubMed] [Google Scholar]
- 66.Tran H.T., Nuguyen L.H., Vigneswaran S. Characteristics and mechanisms of cadmium adsorption onto biogenic aragonite shells-derived biosorbent: batch and column studies. J. Environ. Manag. 2018;241:535–548. doi: 10.1016/j.jenvman.2018.09.079. [DOI] [PubMed] [Google Scholar]
- 67.Bedouin K., Bekri- Abass I., Srasra E. Removal of cadmium (II) from aqueous solution using pure smectite and Lewatite S 100, the effect of time and metal concentration. J. Desalinat. 2008;223:269–273. [Google Scholar]
- 68.Birol K. Cadmium removal mechanisms from aqeous solution by using recycled lignocellulose. Alex. Eng. J. 2022:443–456. [Google Scholar]
- 69.Fouad K., Noureddine A., Mohammed C.N. Adsorptive removal of cadmium from aqueous Neuacer and M., Diedid. “Adsorptive removal of cadmium from aqeous solution by cork biomas. Equilibrum, dynamic and thermodynamic studies. Arab. J. Chem. 2016:1077–1083. [Google Scholar]
- 70.Ad C., Benalla M., Laidani Y., Saffedine F., Neuacer I., Diedid M. Adsorptive removal of cadmium from aqeous solution by luffa cylindrica, equilibrium, dynamic thermody. 2015;7(12):388–397. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data included in article/supp. Material/referenced in article.