New regression models to predict fat mass in intermediate-level male padel players

Abstract

Purpose

Padel is a racquet team sport that has generated great interest in recent years, but the anthropometric and body composition characteristics of padel players have not widely been investigated. So, this study has a threefold aim: i) to draw two specific linear regression models to estimate fat mass from Dual X-ray Absorptiometry (DXA) to anthropometry or bioelectrical impedance analysis (BIA); ii) to provide a BIA-vector (BIVA) profile of intermediate level padel players; iii) to understand if anthropometric, body composition and handgrip strength differ among padel's roles.

Methods

Participants were 15 padel players (26.66 ± 11.84 years, 71.6 ± 12.51 kg, 173.13 ± 7.63 cm) who competed in the same championship. DXA, anthropometry, BIA and vector analysis were assessed. The stepwise procedure for the best general linear model was performed. The one-way ANOVA was used to compare right and left-side players. The Bland-Altman method, concordance correlation and Pearson's correlation coefficients, and statistical power achieved were computed.

Results

The regression models achieved high goodness of fits in fat mass estimation (anthropometric adj. R² = 0.984, BIA adj. R² = 0.949) with four and two regressors, respectively. Padel players showed BIVA features close to teams' (D = 0.22) and power's (D = 0.37) sports. Also, no significant differences between left and right players were found in body composition and handgrip strength.

Conclusion

This study provided novel and useful information on players' body profiles for coaches and trainers. Also, our resulting equations provide easy-to-assess field methods in the accurate estimation of players’ body composition characteristics.

1. Introduction

Padel is a racquet team sport played on a 20 × 10 m rectangular court divided in the middle by a tennis net and surrounded by a glass wall and metallic mesh area that is 3–4 m tall [1,2]. Although padel uses the same scoring system and similar rules as tennis, it requires specific physiological, mechanical, technique-tactical and physical demands [3]. Padel matches include high-intensity activities with intermittent efforts, with an average point-rest duration ratio of about 1:2 (7.24 and 14.12 s, respectively), and a total distance covered of 1117 m at an average speed of 7 km/h [4]. However, performance characteristics can vary depending on the competition level [5].

Speed, power, strength, and endurance are performance parameters related to athletes' physical characteristics and body composition [6]. Body size and composition play a key role in the performance of professional athletes in multiple disciplines [6] including racket sports [7]. Although elite padel and tennis players exhibited similar profiles [8], different body characteristics could affect the specific sport's performance. For example, anthropometric features such as height and weight can affect the technical-tactical patterns of padel players [2]. Also, body composition component as Body Fat-Mass (FM) and Fat Free-Mass (FFM) varied among different padel competitive levels [3,9]. To date, the anthropometric characteristics, body composition and somatotype of male [10] and female [10,11] elite padel players have been described, but further information on low and mid-level players is needed.

Thus, body composition analysis and monitoring are of interest to team sports clubs participating in padel competitions. In addition, padel adherence has worldwide increased in the last decade and it could be an effective strategy to enhance physical activity practice and improve cardiovascular fitness, muscle strength and body composition in sedentary people [12]. However, the gold-standard methods used to quantify FM and FFM require specific laboratory techniques such as hydrostatic weighing or expensive instruments such as dual-X-ray absorptiometry (DXA) [13,14]. To provide easier and cheaper methods, both bioelectrical impedance analysis (BIA) and anthropometry have been well-debated. Also, bioimpedance vector analysis (BIVA) could provide interesting details to identify the specific sport's profile in terms of body fluids and hydration status [15]. Despite several authors having proposed equations for generally healthy adults and athletes, it is unclear which methods could better predict FM and FFM. Also, few studies have drawn sports-specific regression models to estimate body composition [16]. To date, only one research evaluated players' body composition with DXA in padel [5], and all the regression equations used in FM estimation were derived from the unspecific population [3,8].

To the best of our knowledge, no study has calculated any specific regression model for estimating body composition parameters in padel. In addition, no research study has reported BIVA graphs and profiles of male padel players. Furthermore, there is no report on body composition differences between right and left players’ positions. So, the first aim of the following study is to draw two different equations that may accurately estimate FM and FFM using portable and field instruments such as the skinfold calliper and the bio-impedance analyser. The second purpose is to provide the specific BIVA characteristics of male padel players, which allows us to compare them with other sports athletes and generate a reference ellipsis for future investigation. The final aim is to compare anthropometric and body composition features between right and left players.

2. Materials & methods

2.1. Study design

This study used a cross-sectional experimental design. One racket sports association with an intermediate level padel team of 16 players, who competed for the Italian third category, was selected for the experiment. Due to the lack of a female competitive team, only male players were included in the study. All the players were examined on one day in September 2022, from 10 a.m. to 2 p.m., at the Medical University Centre of Bari. Before enrolling the participants in the study, they were informed about the experimental procedures and risks, and they could voluntarily decide to participate in the study. For minor participants, their parents were informed and allowed them to participate. After the enrollment, one participant was excluded due to a leg injury, and 15 players completed all evaluations. The players trained for three days (2 h per training), of which 2 h per week of strength and conditioning and 4 h per week of technical-tactical training. In addition, all players played two matches per week. The researchers did not collect information on their dietary intake.

This study was conducted in accordance with the Declaration of Helsinki and approved by the Ethics Committee of the Alma Master Bologna University (code 0122481, May 23, 2022). All participants or their parents gave their written consent before enrolling on the study.

2.2. Dual-energy X-ray absorptiometry (DXA)

One specialized physician assessed the DXA measurements. Each participant was asked to lie in a supine position on a bed for the evaluation. The Hologic Horizon Wi (S/N 300294 M) densitometer with InnerCore™ Visceral Fat Assessment was used to measure total and segmental (upper limbs, lower limbs, thorax, and head) body composition parameters such as body fat mass (FM, g), percentage of body fat (%F) and total lean mass (FFM, g). This feature uses a source that generates X-rays at two energies, and it has a switching-pulse system that alternates the voltage of the X-rays generator, producing two beams of high and low energies. The subject's differential attenuation of the two energies is used to determine the body composition within 5 min. Then, an interface with a computer system produces colour images displaying the distribution of fat, lean mass, bone, and fat mass index. The information is translated into an easy-to-interpret report for improved patient management and counselling. The Horizon DXA system incorporates the National Health and Nutrition Examination Survey (NHANES) whole-body composition reference data [17]. The accuracy and precision of the instrument were previously tested [17].

2.3. Anthropometry

Two trained researchers cooperated and assessed the anthropometric evaluations according to standardized procedures [18]. Height and sitting height were measured to the nearest 0.1 cm using a stadiometer (GPM, Zurich, Switzerland), and leg length was derived by the subtraction of sitting height from height. Body weight was measured to the nearest 0.1 kg (light indoor clothing, without shoes) using a calibrated analogue scale. Body mass index (BMI) was computed as the ratio between the body weight (kg) and the stature squared (m²).

Circumferences (relaxed and contracted upper arm, thigh, and calf) were measured to the nearest 0.1 cm with a non-stretchable tape and widths (humerus and femur) to the nearest 0.1 cm with a sliding calliper, both on the left side of the body. The upper arm circumference was taken at the mid-point between the shoulder acromion and the olecranon process point, with the participant's elbow relaxed along the body side (relaxed evaluation) or to be flexed 90° with palm facing upward (contracted evaluation); the thigh circumference was taken at the mid-point between the inguinal fold and the superior kneecap point, with the participant in a standing position (thigh muscles relaxed); the calf circumference was taken at the bulkiest calf point, with the participant in a standing position (calf muscles relaxed); the humerus and femoral widths were taken, respectively, between the own lateral and medial epicondyles, with participant's elbow and knee flexed 90°. Skinfold thicknesses (biceps, triceps, subscapular, supraspinal, supra-iliac, thigh, and calf) were measured to the nearest 1 mm using a Lange skinfold calliper at the left side of the body (Beta Technology Inc., Houston, TX, USA) at the following sites [19]: triceps and biceps, vertically at the midpoint between the acromion process and the olecranon process, respectively, a posterior and anterior upper arm face; subscapular, at an angle of 45″ to the lateral side of the body, about 20 mm below the tip of the scapula; supra-iliac, about 20 mm above the iliac crest (in the axillary line); thigh, vertically at the mid-point between the inguinal fold and the superior kneecap point; and calf, vertically at the bulkiest calf point both medially and laterally.

2.4. Bioelectric Impedance and vector analysis

Two trained researchers performed the bioimpedance analysis using the BIA 101 BIVA® PRO (Akern®, Florence, Italy). The current frequency was settled at 50 kHz. A total body patient cable with four insulated alligator clips was used for connection to proximal (black) and distal (red) electrodes (Biatrodes™, Florence, Italy). The analyser was tested at the beginning of the evaluation day to check its validity. To conduct the evaluation, each participant was asked to lie down on a bed in the supine position, with a lower limb angle of 45° compared to the median line of the body and the upper limb angle of 30° from the trunk. Before recording the measurement, each participant waited 2 min to allow for uniform distribution of bodily fluids. After cleaning the skin with alcohol, the electrodes (Ag/AgCl) were placed homolaterally on the right hand and foot, keeping them at least 5 cm apart [15]. The day before the evaluation, each participant was asked to abstain from foods and liquids for at least 4 h before the test. The raw parameters (R, resistance; Xc, reactance; PhA, phase angle) were measured and gathered.

BIVA was carried out using the classic methods, e.g., normalizing R (Ω) and Xc (Ω) for height in meters [15]. Due to the lack of padel players' ellipses, the Elite male tennis players’ bioelectrical specific values were used as a reference to build the 50%, 75%, and 95% tolerance ellipses on the R/H–Xc/H graph. BIVA plots the parameters recorded in BIA (R, Xc, PhA) as a vector within a specific tolerance ellipse (specific profile for each sport and competitive level), and it allows to evaluate of soft tissues through patterns based on percentiles of their electrical characteristics. A BIVA vector that falls out of the 75% tolerance ellipses exhibits an abnormal tissue impedance, while vectors that fall in the 50% represent a normal tissue impedance.

2.5. Statistical analysis

The descriptive statistics were calculated and reported as mean ± standard deviation (SD) for continuous variables. The variables' distribution was previously checked graphically and then verified with the Shapiro-Wilk and the Kolmogorov-Smirnov tests. When a variable showed a non-well-shaped distribution, a check for curve skewness and kurtosis was assessed. A location and scale (logarithm) transformation was applied when the curve functions appeared right-skewed. The one-way ANOVA was performed to compare differences between left and right players. The stepwise backward procedure was performed to draw the best regression model, with a significant level for removal from the model equal to 0.10 and a significant level for additions to the model equal to 0.10. To meet the general linear regression model assumptions, the heteroskedasticity was checked by the White and Breusch-Pagan/Cook-Weisberg tests. The variance inflation factor (VIF) checked the multicollinearity, where a value lower than 5 was considered acceptable (moderate correlation [20]). The leverage plot and Cook's distance were computed to look for the outlier presence. When the presence of some outlier affected the model, it was removed, and a new model was performed. To report the goodness of fit, the adjusted R² was calculated and the plot with the residuals of any regressors was computed. A p-value (P) < 0.05 was considered significant. In addition, the F value (with (k-1, n-k) degrees of freedom, where k is the groups' number, and n is the sample size), the Root MSE, the regression coefficient (β), the standard error (SE), the student's t-test (t) value, the 95% confidence interval and the partial η² for each slope were reported. Then, the Bland-Altman plot and the pairwise correlation coefficient (r) were computed to assess agreement between the new method and the gold standard [21]. In addition, the concordance correlation coefficient (CCC) was computed and reported. Finally, a post hoc test was assessed to compute the achieved power given the type I error value, sample size, effect size (R² of the tested model) and the number of coefficients tested. A 1-β value ≥ 0.90 was considered optimal.

As regards BIVA outcomes, the Mahalanobis’ distance (D) was computed to quantify the degrees of BIA similarity between padel and other sports.

3. Results

3.1. Participants characteristics

Table 1 shows the anthropometric and body composition for the whole sample and the comparisons between right and left players. As reported, no significant differences emerged between the two groups. Although two of the right players were left-arm dominant, both FM and FFM resulted similarly in the left and right halves. However, a greater variability appeared in the arm fat percentages of the left group (%FM arm left range = 29.6; %FM arm right range = 24.4). Regarding BIA, despite no significant differences appearing, right players showed a greater resistance average value than those who played at left (Δ = 18.89 Ω).

Table 1.

Anthropometric, Body Compositions and Hand-Grip strength characteristics.

Variable	Total sample (n = 15)	Right Players (n = 7)	Left Players (n = 8)	Roles differences
	Mean (±SD)	Mean (±SD)	Mean (±SD)	F(1, 13)	P
Age [year]	26.66 (11.84)	29.31 (13.26)	24.30 (10.83)	0.65	0.435
Weight [kg]	71.6 (12.51)	70.93 (11.43)	72.19 (14.15)	0.04	0.854
Height [cm]	173.13 (7.63)	174.19 (7.71)	172.21 (7.97)	0.24	0.635
leg length [cm]	53.9 (4.3)	121.19 (5.04)	117.53 (4.63)	2.15	0.166
Trunk Height [cm]	119.23 (5.02)	53.00 (3.11)	54.69 (5.22)	0.56	0.469
BMI [kg/m2]	23.73 (2.66)	23.23 (1.89)	24.17 (3.25)	0.45	0.514
R [Ω]	426.21 (49.46)	436.29 (50.8)	417.4 (49.89)	0.53	0.481
Xc [Ω]	55.75 (6.36)	56.14 (6.75)	55.41 (6.45)	0.05	0.834
PhA	7.43 (0.49)	7.30 (0.42)	7.54 (0.54)	0.88	0.364
Arm stretch. [cm]	28.18 (3.36)	27.57 (3.30)	28.71 (3.54)	0.41	0.532
Arm contract. [cm]	31.03 (3.45)	30.93 (3.76)	31.11 (3.41)	0.01	0.922
Calf circum. [cm]	35.69 (2.24)	34.96 (2.38)	36.33 (2.05)	1.44	0.252
Thigh circum. [cm]	50.75 (4.65)	51.21 (4.41)	50.35 (5.12)	0.12	0.734
Waist circum. [cm]	76.31 (7.7)	75.10 (7.06)	77.38 (8.56)	0.31	0.587
Pelvis circum. [cm]	93.31 (6.37)	92.14 (5.92)	94.34 (6.96)	0.43	0.526
Humeral diam. [cm]	6.41 (0.38)	6.44 (0.44)	6.39 (0.35)	0.07	0.788
Femural diam. [cm]	9.53 (0.52)	9.61 (0.55)	9.46 (0.52)	0.3	0.592
Biceps SK [mm]	4.73 (1.68)	4.64 (1.49)	4.81 (1.93)	0.03#	0.953
Triceps SK [mm]	10.93 (3.09)	11.36 (3.57)	10.56 (2.8)	0.23	0.637
Subscap SK [mm]	10.83 (3.55)	9.86 (2.48)	11.69 (4.27)	0.33#	0.563
Supra-iliac SK [mm]	10.53 (3.68)	9.71 (1.60)	8.88 (3.64)	0.40#	0.524
Supraspinal SK [mm]	8.4 (2.59)	9.43 (2.88)	9.88 (4.70)	0.05	0.831
Calf med. SK [mm]	9.73 (4.1)	10.14 (3.89)	9.38 (4.50)	0.12	0.731
Calf lat. SK [mm]	10.07 (3.28)	10.43 (3.21)	9.75 (3.54)	0.15	0.705
Thigh SK [mm]	13.9 (3.34)	14.64 (3.4)	13.25 (3.37)	0.63	0.441
FM arm left [kg]	1.04 (0.83)	0.86 (0.24)	1.20 (1.13)	0.59	0.458
FM arm right [kg]	1.02 (0.69)	0.87 (0.26)	1.16 (0.92)	0.65	0.434
FM thorax [kg]	7.04 (2.3)	7.09 (1.69)	7.00 (2.85)	0.01	0.941
FM leg left [kg]	3.14 (0.78)	3.27 (0.89)	3.02 (0.71)	0.37	0.553
FM leg right [kg]	3.23 (0.78)	3.31 (0.82)	3.15 (0.79)	0.13	0.72
FM total [kg]	16.69 (4.8)	16.62 (3.49)	16.75 (5.97)	0	0.959
%FM arm left	23.17 (6.9)	21.91 (1.85)	24.26 (9.46)	0.01#	0.91
%FM arm right	21.93 (6.05)	20.96 (2.51)	22.77 (8.13)	0.01#	0.91
%FM thorax	22.05 (3.54)	22.30 (2.69)	21.83 (4.32)	0.06	0.81
%FM leg left	24.81 (3.77)	26.14 (4.25)	23.65 (3.10)	1.72	0.21
%FM leg right	24.83 (3.53)	25.66 (3.61)	24.10 (3.53)	0.71	0.41
%FM total	23.49 (3.25)	23.77 (2.51)	23.25 (3.95)	0.09	0.77
FFM arm left [kg]	2.98 (0.81)	2.92 (0.81)	3.03 (0.86)	0.06	0.809
FFM arm right [kg]	3.21 (0.79)	3.08 (0.80)	3.32 (0.82)	0.34	0.567
FFM thorax [kg]	23.58 (3.57)	23.69 (3.11)	23.49 (4.14)	0.01	0.92
FFM leg left [kg]	13.88 (19.33)	8.61 (1.37)	8.49 (26.34)	0.97	0.342
FFM leg right [kg]	9.17 (1.39)	8.99 (1.54)	9.32 (1.33)	0.21	0.657
FFM total [kg]	50.75 (7.65)	50.24 (7.52)	51.20 (8.25)	0.05	0.82

Note: n, number of observations; SD, standard deviation; min, minimal value; max, maximal value; F, Snedecor-Fisher test value; P, p-value; R, resistance; Xc, reactance; PhA, phase angle; stretch., stretched; contract., contracted; circum., circumference; diam., diameter; SK, skinfold; med., medial; lat., lateral; FM, fat mass; FFM, fat-free mass; #, the parametric comparison was assessed on a logarithm transformed variable.

3.2. Linear regression models for fat mass estimation

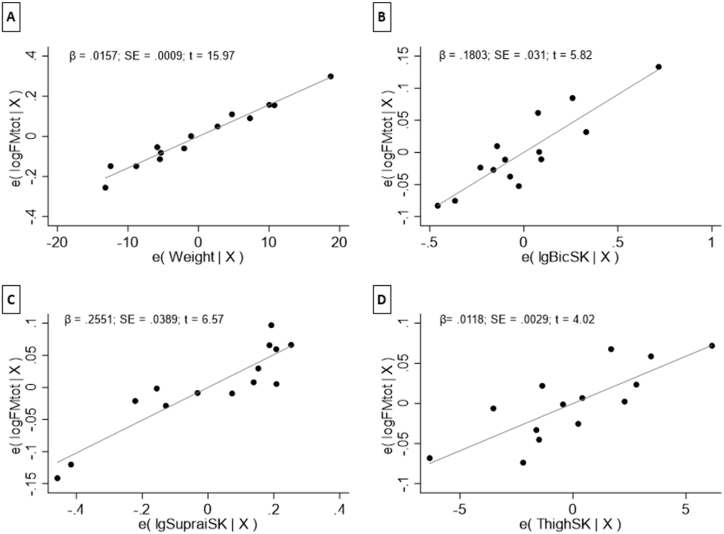
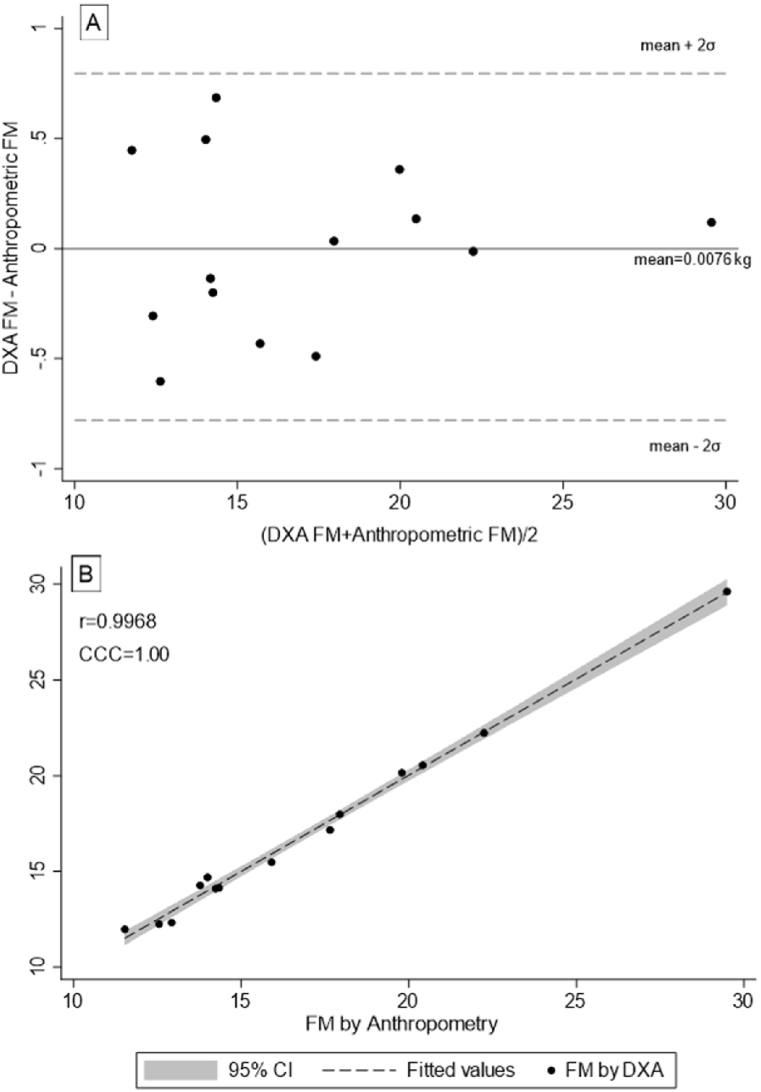
Table 2 shows the best regression model assessed by the stepwise method (n = 14). The mean VIF was 1.49, the χ²₍₁₎ obtained by the Breusch–Pagan/Cook–Weisberg was 3.13 (P = 0.08), and the F _{(2, 11)} of the White test equalled 2.15 (P = 0.159). Before this, the first model was affected by an outlier (Cook's distance), which was deleted from the latest model. Fig. 1 shows scatter plots with the error estimation of each model regressor. Fig. 2 shows the Bland-Altman plot (A) and the scatter plot (B) with the new calculation method and the gold standard (DXA).

Table 2.

Regression model for FM estimation with Anthropometry.

Source	SS	df	MS	F(4, 9)	P	R2	Adj R2	Root MSE
Model	0.880474	4	0.220118	196.23	<0.001	0.9887	0.9836	0.03349
Residual	0.010096	9	0.001122
Total	0.890569	13	0.068505
log Fat-Mass	β	SE	t	P	95% CI		η2 [95% CI]
Weight	0.016	0.001	15.97	<0.001	0.014	0.018	0.966 [0.867; 0.980]
log biceps SK	0.180	0.031	5.82	<0.001	0.110	0.250	0.790 [0.358; 0.882]
log suprail SK	0.255	0.039	6.57	<0.001	0.167	0.343	0.827 [0.441; 0.902]
Thigh SK	0.012	0.003	4.02	0.003	0.005	0.018	0.642 [0.130; 0.800]
Intercept	0.658	0.085	7.76	<0.001	0.466	0.850

Note: SS, the sum of squares; df, degrees of freedom; MS, mean of squares; F, Snedecor-Fisher statistical test; P, p-value; R², the goodness of fit; Adj R², adjusted R²; MSE, mean of squares error; β, regression coefficient; SE, standard error; t, student's statistical test; CI, confidence interval; η², eta-squared effect size; suprail., supra-iliac; SK, skinfold thickness.

Fig. 1.

Scatter plots with the error of DXA FM and each anthropometric regressor: (A) body weight, (B) logarithm biceps skinfold thickness, (C) logarithm of supra-iliac skinfold thickness, (D) thigh skinfold thickness.

Fig. 2.

Bland-Altman plot (A) and scatter plot (B) between DXA FM and new FM estimation by anthropometry. Note: σ, standard deviation; r, Pearson correlation coefficient; CCC, concordance correlation coefficient.

The first model generates equation (1)

$$\log \text{FM}=\left(0.016\bullet \text{BW}\right)+(0.180\bullet \log \text{Bic}\text{SK})+(0.255\bullet \log \text{Sup}\text{SK})+\left(0.012\bullet \text{th}\text{SK}\right)+0.658$$ (1)

where BW is body weight, log Bic SK is the logarithm of the biceps skinfold thickness, log Sup SK is the logarithm of the supra-iliac skinfold thickness and th SK is the skinfold thickness of the thigh; all the skinfold measures are expressed in millimetres. The exponential function is required to obtain the real FM value ($e^{logFM}$). The mean for the new method was 16.917 (±4.851), while the DXA mean was 16.925 (±4.894; r = 0.997). The achieved power (1-β) ∼ 1.00 (Δ = 87.5).

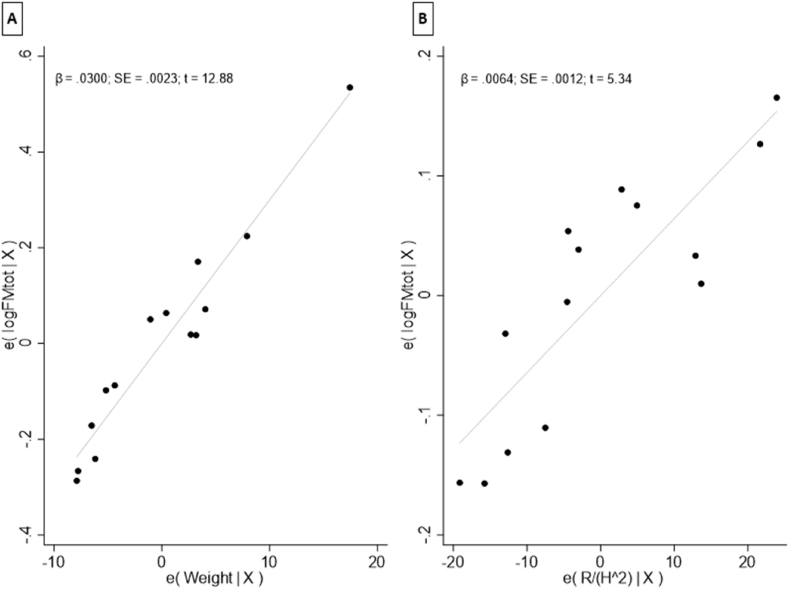
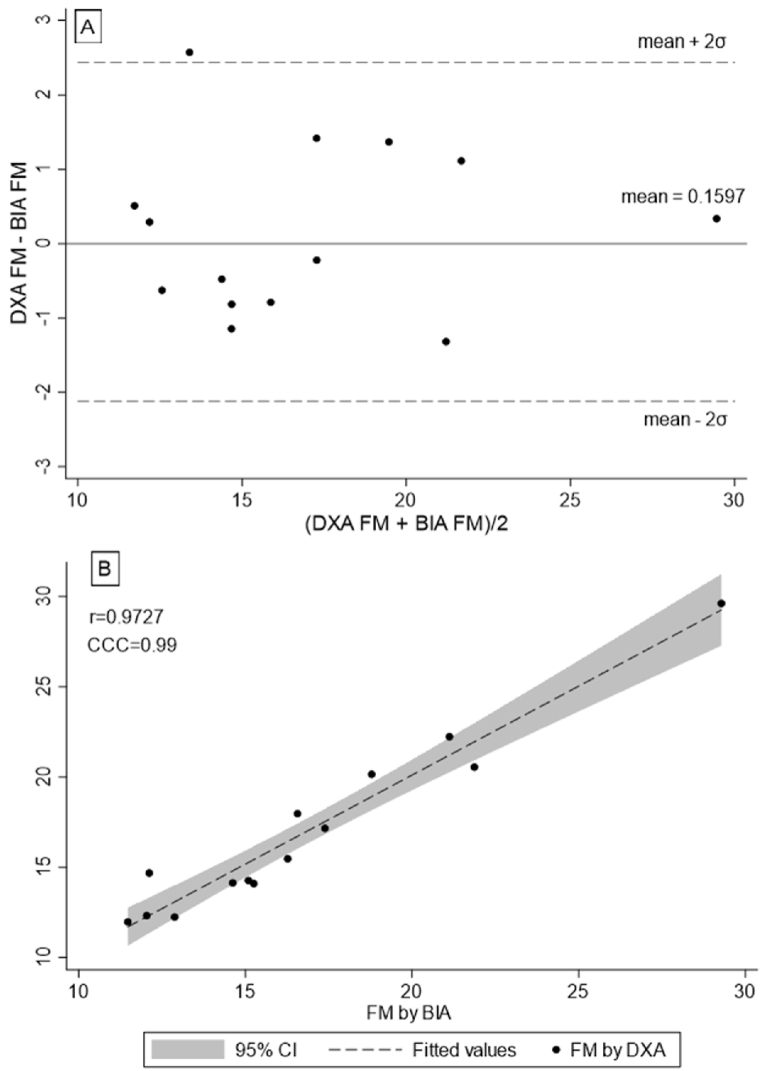
Table 3 shows the best regression model assessed by the stepwise method (n = 14). The mean VIF was 2.97; the χ²₍₁₎ obtained by the Breusch–Pagan/Cook–Weisberg was 0.01 (P = 0.954), and the F _{(2, 11)} of the White test equalled 2.47 (P = 0.126). Before this, the first model was affected by an outlier (Cook's distance), which was deleted from the latest model. Fig. 3 shows the scatter plot with the error estimation of each model regressor. Fig. 4 shows the Bland-Altman plot (A) and the scatter plot (B) with the new calculation method and the gold standard (DXA).

Table 3.

Regression model for FM estimation with BIA.

Source	SS	df	MS	F(2, 11)	P	R2	Adj R2	Root MSE
Model	0.878596	2	0.439298	122.3	<0.001	0.957	0.9491	0.05993
Residual	0.039511	11	0.003592
Total	0.918107	13	0.070624
log Fat-Mass	β	SE	t	P	95% CI		η2 [95% CI]
Weight	0.030007	0.002329	12.88	<0.001	0.02488	0.035133	0.938 [0.799; 0.963]
R/h2	0.006438	0.001205	5.34	<0.001	0.003785	0.00909	0.722 [0.296; 0.839]
intercept	−0.3035	0.324187	−0.94	0.369	−1.01703	0.410028

Note: SS, the sum of squares; df, degrees of freedom; MS, mean of squares; F, Snedecor-Fisher statistical test; P, p-value; R², the goodness of fit; Adj R², adjusted R2; MSE, mean of squares error; β, regression coefficient; SE, standard error; t, student's statistical test; CI, confidence interval; η², eta-squared effect size.

Fig. 3.

Scatter plots with the error of DXA FM and Weight (A) and Resistance/Height [2] (B) regressors.

Fig. 4.

Bland-Altman plot (A) and scatter plot (B) between DXA FM and new FM estimation by BIA, Height, and Weight. Note: σ, standard deviation; r, Pearson correlation coefficient; CCC, concordance correlation coefficient.

The model with the BIA parameter generates equation (2)

$$\log \text{FM}=\left(0.0300007\bullet \text{BW}\right)+(0.006438\bullet \frac{\mathrm{R}}{{\mathrm{H}}^2})-0.3035$$ (2)

Where log FM is the logarithm of the fat mass, BW is the body weight, R is the bio-electrical resistance and H is the height (expressed in meters). The exponential function is required to obtain the real FM value ($e^{logFM}$). The mean for the new method was 16.766 kg (±4.83; r = 0.973). The achieved power (1-β) ∼ 1.00 (Δ = 22.26).

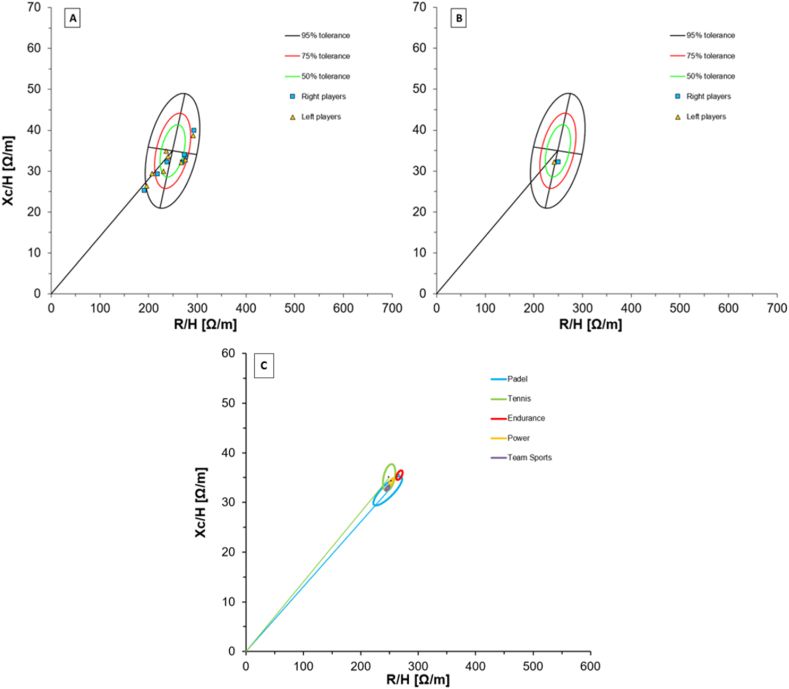
3.3. BIVA

Fig. 5 shows the BIVA qualitative analysis of all players (A), and the two roles mean respectively (B), where the reference ellipse referred to elite tennis players. Despite the wide variability between each participant, the means of the two groups exhibited similar vectorial characteristics and lay in the 50% tolerance of the ellipse of tennis players. In addition, Fig. 5 (C) shows the BIVA confidence ellipses of padel, tennis, endurance, power, and elite team sport. There, padel players exhibited more similar characteristics to team sports (T² = 0.70; D = 0.22, p = 0.71) than elite tennis players (T² = 3.71; D = 0.62, p = 0.18), while significant differences appeared compared to endurance sports (T² = 8.52; D = 0.79, p = 0.01).

Fig. 5.

BIVA tolerance patterns of all (A) or right and left Padel players means (B) in elite tennis players reference ellipse; (C) BIVA confident ellipses of Padel and Tennis, Endurance, Power, and Team Sports elite players.

4. Discussion

This study first aimed to draw two specific linear regression models to estimate FM with simpler field methods such as anthropometry or BIA in padel players. To the best of our knowledge, the literature is lacking specific models and no previous studies have tried to fill this gap. Regarding anthropometry, previous authors [[8], [9], [10]] who investigated body composition in padel players used classic methods such as Siri's equation [22] to convert the body density (BD) estimated by Withers and colleagues' model [23]. Although BD conversion has been widely applied since 1961 and the Withers et al. yielded their regression equation on 185 subjects, the correlation coefficient of their predicted model was less than 80% and the sample was composed of lacrosse and football players. Differently, Sánchez-Muñoz and colleagues [3] used five different equations derived from 1967 to 1974 to estimate the body density of elite padel athletes [14,[23], [24], [25], [26]]. These pioneering studies used underwater weighting as the gold standard to calculate BD, which requires higher expertise in maximum exhalation to ensure the correct measure of participants' residual volumes. Three works assessed the analysis of healthy college and university USA students and did not report any information about their training status or sports classification; the correlation coefficients between the observed and predicted BD values were r = 0.867 (16.8–36.8 years, 133 men [26]) r = 0.861 (18–26 years, 50 white men [25]) and r = 0.86 (53 men [14]), respectively. Durnin and Womersley [24] analyzed 209 healthy men classified by their age (from 16 up to 72 years) and assessed many models to estimate BD by one through four skinfolds (r varied from 0.7 up to 0.9). Despite these articles reporting both the standard error and the correlation coefficient of each measurement, they lacked several statistical applications such as checking collinearity, heteroscedasticity, and the presence of any outliers, testing the reliability and the power achieved and reporting the goodness of fit of each model. Our model met all the assumptions the generalized linear model requested and reported a higher correlation coefficient value in predicting players' FM. Differently, Stewart and Hannan [13] used rigorous statistical criteria to draw different regression models for predicting FM and FFM through anthropometry in 106 athletes of several disciplines. Although twelve of them were racket sports players and DXA was used, the models considered the whole sample with no discipline differentiation. In addition, 24 of them did not compete in their sports and 19 were international athletes. Contrarily, our model was computed on only padel players who trained and competed at the same level. The new equation calculates precise players' body composition through field measurements such as body weight, biceps, supra-iliac, and thigh skinfolds.

Regarding Bio Impedance Analysis, a recent review showed that many BIA-based predictive equations for FM estimation in general and athletic populations are available, but sport-specific models are needed [16]. To the best of our knowledge, no authors have computed any regression model in racket sports such as padel. Related to other sports, Matias and colleagues developed an accurate regression equation from DXA to BIA in elite futsal players, for predicting FFM [27]. In 44 collegiate footballers, three authors compared BIA evaluation for predicting total FM with DXA measurements, and found that multifrequency BIA underestimated FM and overestimated FFM [28]; however, no regression model was reported. In addition, Matias et al. reported a high goodness of fit (R² = 0.94) using the BIA resistance as a predictor to estimate FFM derived from the 4-C model, but the study included 105 male and 37 female general athletes [29]. Although our model was derived from only 14 players who were male, the achieved statistical power was very high, and the explained variance equalled 95%. However, more efforts are needed for padel and other sports.

The second aim of our research was to provide a BIVA profile of padel players. Many studies observed the vector trajectory to measure hydration status in several disciples [[30], [31], [32], [33]], but no references are available in padel. Martins and colleagues included seven players of badminton, tennis or tennis table in a sample of 167 university athletes (18–35 years), but they only compared team and individual sports [31]. Just one study reported the BIVA comparisons between 23 sports, including tennis, which was classified as a velocity-power discipline [34]. According to their classification, we compared padel players with tennis, endurance, power, and team sports vectors. Reversely to what was expected from sports features, padel players exhibited vector direction and angle closer to power and team sports than tennis, while endurance athletes appeared significatively different with a longer vector (less hydrated athletes). Despite padel and tennis sharing several rules and game situations, padel has confirmed to possess team sports body composition parameters. However, padel became widely played in the last five years and many of our participants played different team sports before its occurrence.

The final purpose of this study was to understand whether anthropometric and body composition differs among padel roles. Despite technical-tactical, physiological and mechanical demands being expected to be similar, the probability to possess a dominant left hand on the right court side is higher. Contrary to our expectation, the sample showed no differences in BC among left and right players. Many studies exhibited how body characteristics could variate among roles of different team sports [[35], [36], [37], [38]]. Due to its misleading classification close to tennis, previous authors who investigated Padel players' body composition did not discriminate between right and left positions [3,8]. Left and right padel players involved in our research appeared homogeneous in all anthropometric measurements and BIVA positions. However, the sample size achieved in this study was small and a larger analysis could detect specific roles’ features. In addition, more efforts are needed to explore the physiological demands of roles as done among gender [39] and competitive levels [5].

This study presents some limitations: a) the sample size was small to detect any difference between left and right players; b) the participants were male, and their ages varied from 16 up to 47 years. The equations are specific for these sex and age targets; c) although all participants played padel at least for five years, many of them practised team or individual sports such as soccer or tennis before becoming Padel players, and d) no diet information was recorded, e) these equations may not be generalized.

5. Conclusions

Padel has aroused great interest in the last five years, showing increased participation in amatorial and professional competitions. This study provides for the first time two specific regression equations that allow us to precisely estimate the body composition in padel players through anthropometry instruments and BIA. Also, it adds novel to the growing literature related to padel training evaluation assessments and body characteristics, and it draws a specific BIVA profile. These methods may have practical implications for enhancing the accuracy of longitudinal player monitoring such as in a game season or a multi-season plan, and to provide a cheap and easy method to evaluate padel players. Evaluating body composition characteristics and comparing body dimensions and requests among sports ranks could increase the fundamental knowledge needed for players’ best performances and sport advancement.

Authors’ contributions

MM, ST, and GG participated in the design of the study, contributed to data collection and data reduction/analysis, and drafted the manuscript; SDG and GDG participated in the design of the study and contributed to data collection; BM contributed to interpretation of results; KMH, SC, LM and FF reviewed and edited the manuscript. All authors contributed to the manuscript writing. All authors have read and approved the final version of the manuscript and agree with the order of presentation of the authors.

Data availability statement

Data will be made available on request.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.