Causal inference during closed-loop navigation: parsing of self- and object-motion

Abstract

A key computation in building adaptive internal models of the external world is to ascribe sensory signals to their likely cause(s), a process of causal inference (CI). CI is well studied within the framework of two-alternative forced-choice tasks, but less well understood within the cadre of naturalistic action–perception loops. Here, we examine the process of disambiguating retinal motion caused by self- and/or object-motion during closed-loop navigation. First, we derive a normative account specifying how observers ought to intercept hidden and moving targets given their belief about (i) whether retinal motion was caused by the target moving, and (ii) if so, with what velocity. Next, in line with the modelling results, we show that humans report targets as stationary and steer towards their initial rather than final position more often when they are themselves moving, suggesting a putative misattribution of object-motion to the self. Further, we predict that observers should misattribute retinal motion more often: (i) during passive rather than active self-motion (given the lack of an efference copy informing self-motion estimates in the former), and (ii) when targets are presented eccentrically rather than centrally (given that lateral self-motion flow vectors are larger at eccentric locations during forward self-motion). Results support both of these predictions. Lastly, analysis of eye movements show that, while initial saccades toward targets were largely accurate regardless of the self-motion condition, subsequent gaze pursuit was modulated by target velocity during object-only motion, but not during concurrent object- and self-motion. These results demonstrate CI within action–perception loops, and suggest a protracted temporal unfolding of the computations characterizing CI.

This article is part of the theme issue ‘Decision and control processes in multisensory perception’.

1. Introduction

We do not directly access environmental objects and events. Instead, our biological sensors (i.e. retina, cochlea, etc.) detect noisy, incomplete and often ambiguous sensory signals. In turn, our brains ought to leverage these signals to build adaptive internal models of the external world [1]. A key step in building these models is to ascribe sensory signals to their likely (and hidden) cause(s), a process of causal inference (CI; [2–4]).

CI has been well studied in human psychophysics, and a growing body of literature is starting to elucidate the neural mechanisms underpinning this computation, both in human [5–10] and in animal models [11–13]. Namely, whether localizing audio-visual stimuli [2,5,11], estimating heading [6,12], perceiving motion relations in visual scenes [9,10] or inferring the location of one's own body based on visual, tactile and proprioceptive cues [7,8,13], humans and non-human primates behave as if they hold and combine (sometimes optimally) multiple interpretations of the same sensory stimuli. From a neural standpoint, CI appears to be subserved by a cascade of concurrent interpretations; sensory areas may respond to their modality of preference, intermediate ‘associative’ nodes may always combine cues (sometimes called ‘forced-fusion’), and finally higher-order fronto-parietal areas may flexibly change their responses based on the causal structure inferred to generate sensory observations [4,14,15] (see [16,17] for similar findings across time, from segregation to integration to causal inference). If and how this inferred causal structure subsequently and dynamically biases lower-level sensory representations is unknown (but see [18]).

More broadly, the study of CI has heavily relied on static tasks defined by binary behavioural outcomes and artificially segregating periods of action from periods of perception (see [19] for similar arguments). These tasks not only are a far cry from the complex, closed-loop and continuous-time challenges that exist in human behaviour, but may also limit and colour our understanding of CI. For instance, while feed-forward-only mechanistic models of CI may account for decisions during two-alternative forced-choice tasks [20], our brains (i) are decidedly recurrent, and (ii) largely dictate the timing, content and relative resolution of sensory input via motor output (i.e. active sensing). The focus on open-loop tasks when studying CI also limits our ability to bridge between CI and other foundational theories of brain function [21]—particularly those derived from reinforcement learning, which are best expressed within closed loops.

Here, we take a first step toward understanding CI under closed-loop active sensing by studying how humans attribute optic flow during navigation to self- and object-motion. Namely, human observers are tasked with navigating in virtual reality and stopping at the location of a briefly flashed target, much akin to ‘catching a blinking firefly’ (see [22–26]). The virtual scene is composed solely of flickering ground plane elements, and thus, when observers move by deflecting a joystick (velocity control), the ground plane elements create optic flow vectors. Observers continuously integrate this velocity signal into an evolving estimate of position [27]. Importantly, in the current instantiation of the task, the target itself may move (i.e. object-motion; constant lateral motion within a range from 0 to 40 cm s⁻¹, either leftward or rightward). Thus, in the case of concurrent self- and object-motion, observers must parse the total retinal motion into components caused by self-motion and/or those caused by object-motion, a process of CI.

First, we derive a normative account specifying how observers ought to intercept hidden and moving targets given their belief about (i) whether retinal motion was (at least partially) caused by the target moving, and (ii) if so, at what velocity. Then, we demonstrate that humans' explicit reports and steering behaviour concord with the model's predictions. Further, we support the claim that humans misattribute flow vectors caused by object-motion to their self-motion by showing that these misattributions are larger (i) when self-motion is passive (i.e. lacking an efference copy) and (ii) when objects are presented eccentrically (such that object- and self-motion vectors are congruent in direction). Lastly, via eye-movement analyses, we show a gradual unfolding of behaviour during CI. Early saccades are largely accurate and directed toward the last visible location of the target. Thus, during this time period eye movements behave as if participants perceive targets as moving. Subsequent gaze pursuit of the invisible target is accurate when there is no concurrent self-motion, but is consistent with the target being perceived as stationary during concurrent self- and object-motion. Together, the results demonstrate CI in attributing retinal motion to self- and object-motion during closed-loop goal-directed navigation. This opens a new avenue of study wherein we may attempt to understand not only the perceptual networks underpinning CI, but also the joint sensorimotor ones.

2. Results

(a) . A normative model of intercept behaviour during visual path integration

We identify behavioural signatures of CI during path integration toward a (potentially) moving target by formulating a normative model (figure 1). We take the example of a briefly visible target moving at a constant, potentially zero, speed (i.e. no acceleration) and with a constant direction along a lateral plane (i.e. side-to-side, figure 1a). The task of the model is to form a belief about the target's location and velocity given a brief observation period (i.e. period over which the target is visible), and then use this belief to navigate and intercept the target (think of a predator intercepting its prey, figure 2a). The observation period may occur while the observer is stationary (and thus all retinal motion is caused by object-motion), or during concurrent observer and object-motion (and thus retinal motion has to be ascribed to self and/or object). We model concurrent self- and object-motion (versus object-motion only) by increasing the noise associated with target observations (these being corrupted by a concurrent flow field). For simplicity, within this work we only consider linear trajectories wherein the model selects a direction and duration over which to travel (figure 1a, middle panel). We expect this trajectory to reasonably approximate the steering endpoints of the continuously controlled steering trajectories of our human participants.

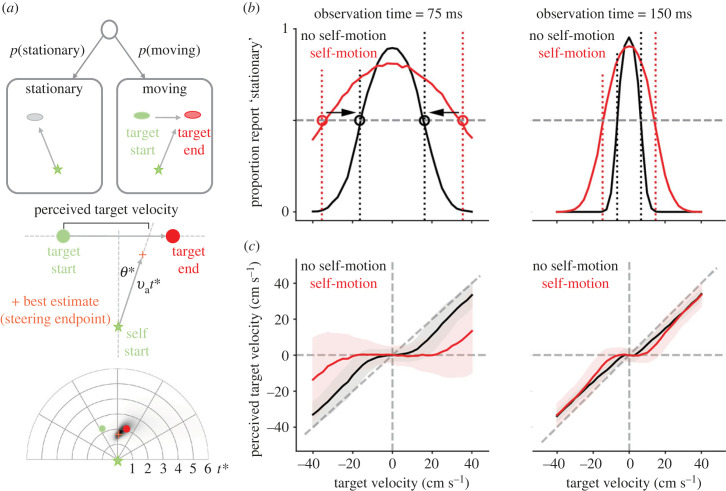
Figure 1.

Predicted behavioural signatures of causal inference when navigating to intercept a briefly observed moving target. (a) Task and trajectories of a normative model. We derived the normative strategy for intercepting a briefly presented target that provided the model with an uncertain estimate of the target velocity and whether the target was moving at all. Top: the model first estimates whether the target is stationary or moving. Middle: we assumed that the model aimed to intercept the target by travelling along a straight line at a certain angle (θ*) and for a certain distance (velocity × duration, v_at*). To compensate for the model overshooting or undershooting the target (given uncertainty in path integration, see bottom panel), we assessed the model's perceived velocity by computing when the model's trajectory intercepted the target's path. The middle panel shows a schematized example, while the bottom panel shows an example simulation including the best estimate endpoint (orange) and full posterior (shades of black). (b) Stationary reports. The model perceived the target as stationary if its noisy velocity estimate fell below a velocity threshold (dotted vertical lines). Noise in the velocity estimates resulted in a bell-shaped fraction of stationary reports when plotted over the target's true velocities. For a Bayesian decision strategy, and in contrast to simpler heuristics, the velocity thresholds increased for larger observation noise induced by self-motion (red versus black) and for shorter observation times (left versus right). The bell-shaped curves widened accordingly, and the point at which they intersected the 0.5 proportion (grey dashed line) changed. We highlight this threshold change here for the self-motion versus no self-motion case by the circles and associated black arrows. (c) Perceived target velocities. Causal inference causes the perceived velocities to be biased toward zero for small target velocities, and to approach true target velocities (down-weighted by the slow-velocity prior) for larger target velocities. This bias increases for larger observation noise (red versus black) and shorter observation periods (left versus right). (b,c) Mean (lines) and s.d. (shaded area, (c) only) across 1000 simulated trajectories for each target velocity, ranging from −40 to 40 cm s⁻¹ in steps of 2.5 cm s⁻¹.

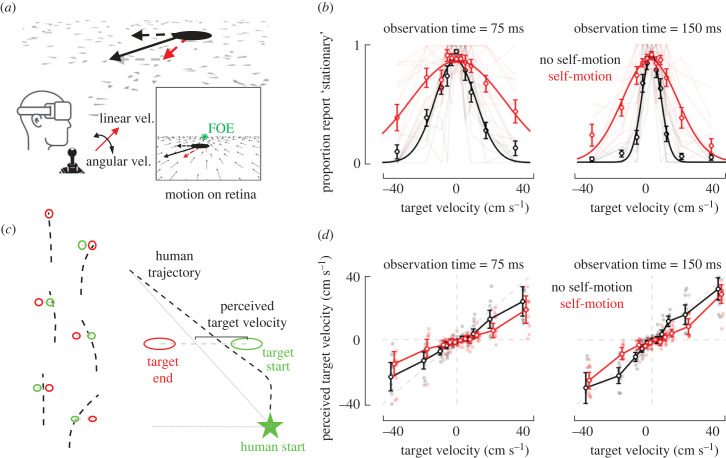
Figure 2.

Intercepting a briefly visible moving target by path integration demonstrates features of causal inference. (a) Experimental protocol and setup. Participants are placed in a virtual scene composed of intermittently flashing textural elements providing an optic flow signal when participants are moving. Subjects are in closed-loop, at all times being in control of their linear and angular velocity. When the target has an independent motion in the environment (dashed black arrow) and subjects move toward it (red arrows), the retinal motion of the target (solid black arrow) is composed of both object- and self-motion components. Inset additionally shows flow vectors. FOE (in green) indicates the focus of expansion. (b) Stationary reports. The proportion of trials in which participants reported the target as stationary (y-axis) is plotted as a function of target velocity (x-axis), whether the subject was moving (self-motion, red) or not (no self-motion, black) during target presentation, and target observation time (left versus right panels). Circles denote means across subjects, and error bars represent ±1 s.e.m. Pale lines in the background show data for individual subjects. (c) Example steering trajectories and quantification. Left: six example trials (arbitrarily staggered). Bird's-eye view of the target's starting (green circle) and ending (red circle) locations, as well as individual trajectories (dashed black). The distance between the start of the dashed black line (origin) and the target's starting location is always 300 cm. Right: To estimate the perceived target velocity, we computed for each trial the distance between the target's initial location and the location where the target's trajectory intersects a straight line connecting the human's starting and ending locations. This recapitulates the definition from figure 1 and defines the lateral displacement of an individual trajectory above and beyond the starting location of the target, while also considering the depth overshooting. (d) Perceived target velocity. The perceived target velocity (as quantified in (c), y-axis)) is plotted as a function of actual target velocity (x-axis), whether the subject was moving (self-motion, red) or not (no self-motion, black) during target presentation, and target observation time (left versus right panels). Circles denote means, and error bars represent ±1 s.e.m. Pale dots in the background show data for individual subjects.

On each trial, before making any observation, the model assumes the target to be stationary with a certain probability, and to move otherwise (i.e. a prior for stationarity). If moving, the model assumes that slower targets are more likely than faster ones (i.e. a slow-velocity prior, [28,29]). When the target is rendered visible, the model gathers noisy observations of the target's location (e.g. noisy percepts in each video frame, potentially corrupted by a concurrent flow field) that it uses to infer whether the target is stationary or moving, and if moving, with what velocity. Once the model has formed these target motion estimates, it uses a simple steering policy in which it moves a certain distance (determined by a velocity and optimal stopping time) along a straight-line trajectory to best intercept the target (figure 1a, see Methods and the electronic supplementary material for details).

Simulating the model across multiple trials led to two predictions. The first prediction is that whether the target is perceived as stationary or moving should depend on the target's actual velocity, the observation time, and observation noise (i.e. ‘no self-motion’ versus ‘self-motion’, respectively in black and red; figure 1b). Noisy observations during concurrent self-motion imply that a moving target might be mistaken for a stationary one, in particular if this is a priori deemed likely. Our model defaults to such a stationary target percept as long as the target velocity estimate remains below a specific velocity threshold (figure 1b, dotted vertical lines). Noise in the target velocity estimates thus leads to a bell-shaped relationship between the probability of a stationary target percept and the target's actual velocity. This relationship is modulated by observation time and observation noise magnitude: both larger observation noise magnitudes and shorter observation times require stronger evidence to perceive a target as moving (figure 1b, black versus red and left versus right). Our model implements this by increasing the threshold on the target velocity estimate. This change in threshold provides a test for whether observer (i.e. human) behaviour is sensitive to changes in the observation quality, in line with rational Bayesian behaviour. If the moving/stationary decision is instead implemented by a simpler threshold on the target velocity estimate that is insensitive to such changes, then the target velocity that leads to a probability of stationary percepts of 0.5 would not shift with a change in observation noise or time (in contrast to the arrows shown in figure 1b). Observing such a shift (figure 2) rules out this simpler heuristic model with fixed threshold.

The second prediction relates the target's true velocities to those perceived by the model. In each simulated trial, the model uses the target motion estimate to steer along a straight trajectory that maximizes the likelihood of intercepting the target, while accounting for standard path integration properties (e.g. increasing location uncertainty with distance travelled, see Methods and [22]). To estimate our model's perceived target velocity, we intersected a straight line connecting steering start- and endpoints with the line that the target moved along (which was the same across trials; figure 1a, middle panel). This procedure compensates for the steering endpoint occasionally overshooting or undershooting the target's location, given noisy path integration and speed priors (see [22] and below). Plotting these perceived velocities against true target velocities revealed characteristic S-shaped curves (figure 1c). For large target velocities, the perceived velocities linearly increase with target velocities, but consistently underestimate them owing to the slow speed prior. Smaller target velocities reveal signatures of CI: as small target velocities occasionally make the target appear stationary, the perceived velocities are further biased toward zero. Both larger observation noise magnitudes and shorter observation times expand the range of true target velocities for which the perceived velocities are biased toward zero (figure 1c, black versus red and left versus right), in line with the stationarity reports (figure 1b).

In summary, therefore, according to the normative model, if concurrent self- and object-motion leads to increased observation noise (vis-à-vis a condition with no concurrent self-motion), then we ought to expect (i) a larger velocity range over which targets are reported as stationary, and (ii) a characteristic S-shaped curve where observers more readily navigate toward the starting rather than ending location of targets, particularly when object velocity is not very high (and thus unambiguous).

(b) . Human observers perform causal inference when navigating during concurrent object-motion

We test predictions of the model by having human observers (n = 11) navigate by path integration to the location of targets that could be either stationary (i.e. no object velocity) or moving with different velocities relative to the virtual environment (figure 2a, dashed black arrow denotes object velocity). As in the model, targets moved at a constant speed (range from 0 to 40 cm s⁻¹) and with a constant lateral direction (i.e. leftward or rightward, if moving). Further, at the end of each trial participants explicitly reported whether they perceived the target as moving or not relative to the scene. Most importantly, in different blocks of trials the observers themselves could either be stationary (i.e. labelled ‘no self-motion’ and requiring participants to maintain a linear velocity under 1 cm s⁻¹ for 1 s for targets to appear) or moving during the time period when the target was visible (i.e. labelled ‘self-motion’ and requiring participants to maintain a linear velocity over 20 cm s⁻¹ for 1 s for targets to appear, see Methods for further detail). The optic flow caused by self-motion introduces additional observation noise and requires the parsing of total flow vectors into self- and object-components.

Explicit stationarity reports were well accounted for by Gaussian distributions (mean r² = 0.74). As expected, participants most readily reported targets as stationary in the world when the object velocity was close to 0 (mean of Gaussian fits pooled across ‘self-motion’ and ‘no self-motion’ conditions; 75 ms observation time: μ = −4.65 × 10⁻⁴; 150 ms observation time: μ = 9.2 × 10⁻³), regardless of the target observation time (p = 0.47). Most importantly, as predicted by the model, during concurrent self- and object-motion (red, figure 2b) participants reported targets as stationary at increasing object velocities, both for lower (75 ms; Gaussian standard deviation, mean ± s.e.m., no self-motion: 10.89 ± 2.37 cm s⁻¹; self-motion: 29.39 ± 7.06 cm s⁻¹; paired t-test, p = 0.021) and higher (150 ms; no self-motion: 4.59 ± 0.51 cm s⁻¹; self-motion: 15.15 ± 3.01 cm s⁻¹; p = 0.0025) observation times (figures 1b and 2b). This suggests that participants putatively misattributed flow vectors caused by object-motion to self-motion.

We similarly analysed the endpoints of participants' steering behaviour. This behaviour was heterogeneous, with participants frequently stopping at the target's end location (figure 2c, top left and right; examples of stationary and moving targets), but also at times navigating to the starting and not ending target location (figure 2c, middle left) or navigating to some intermediary location (figure 2c, bottom left). Likewise, participants often overshot targets in depth (figure 2c, middle and bottom right (also see [22,24]), radial response divided by radial target distance, no self-motion = 1.44 ± 0.08; self-motion = 1.32 ± 0.09; no self-motion versus self-motion, t = 1.55, p = 0.15). To quantify this performance, for each trial we computed a perceived target velocity analogously to the modelling approach (figures 1a and 2c). Results demonstrated that, on average, subjects underestimated the target's velocity (linear fit to no self-motion condition, grand average slope = 0.82 ± 0.08; slope = 1 indicates no bias), and this effect was exacerbated during low observation times (figure 2d, slopes of linear fits, 75 versus 150 ms observation times paired t-test, p = 0.05). Interestingly, when targets were presented during concurrent self-motion (figure 2d, red), intermediate target velocities were perceived (or at least steered toward) as if moving more slowly than when the same object velocity was presented in the absence of self-motion (figure 2d, red versus black, paired ANOVA interaction term, 75 ms observation time, p = 8.12 × 10⁻⁵; 150 ms observation time, p = 1.53 × 10⁻⁹; Bonferroni-corrected p < 0.05 for 75 ms observation time at −20, −6 and +10 cm s⁻¹, and for 150 ms observation time at −20, −10 and +10 cm s⁻¹). This is precisely the behaviour predicted by the model (compare figure 1c and figure 2d), wherein CI causes the perceived target velocities to be biased toward zero for small and intermediate velocities, and to approach true target velocities for larger target velocities. Only relatively slow target velocities are biased toward zero as these may not be unambiguously ascribed to object-motion.

(c) . Steering behaviour suggests a misattribution of flow vectors during concurrent self- and object-motion

To further test the possibility that during concurrent object-motion and path integration participants may misattribute flow vectors related to the object and self, we can make two further qualitative predictions. First, we predict that the location of the target at its onset will affect how object- and self-motion derived flow vectors are misattributed. That is, early in trials, participants move forward, toward the target. During this forward self-motion, lateral flow vectors on the retina—i.e. those matching the direction of target movement—are essentially null straight-ahead and have much greater speed in the periphery (figure 2a, inset). Thus, we predict that flow vectors should be more readily misattributed under our current protocol for eccentric, rather than central, targets. Second, within the current closed-loop experiment, self-motion is not estimated solely based on optic flow signals, but also by an efference copy of hand movements (and thus joystick position, which drives virtual velocity). In turn, we can predict that if self-motion during object-motion were passive (i.e. no efference copy), the estimate of self-motion would be more uncertain, and thus putatively more amenable to misattribution between object- and self-motion cues. We test these qualitative predictions while focusing our analysis on (1) the 150 ms target observation time given that participants are more accurate in this condition, and (2) steering behaviour (versus explicit reports) given that these are an implicit measure of CI and less prone to response biases [30].

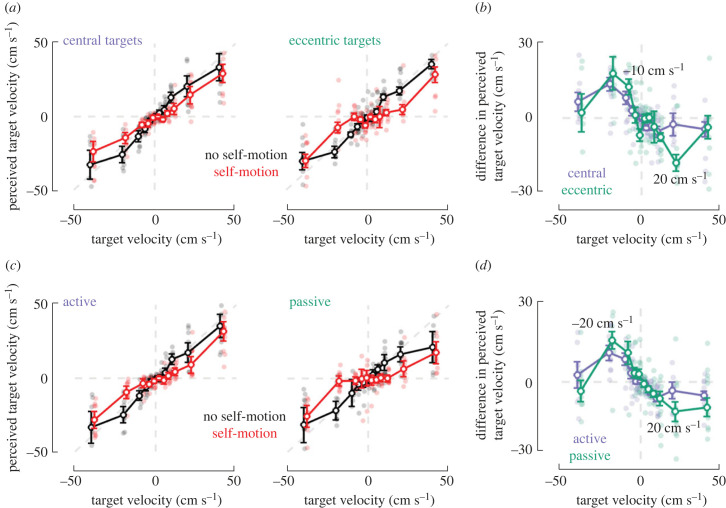
We test the first prediction by dividing the dataset into trials for which the target was presented centrally (i.e. within −5° and +5°; 48.5% of total dataset) or eccentrically (i.e. within −10° and −5°, or within +5° and +10°). As shown in figure 3a, during both central and eccentric presentations, targets were seemingly perceived as if moving less rapidly during self-motion rather than during no self-motion. Thus, even when dividing our dataset in two (and thus reducing statistical power) concurrent self- and object-motion resulted in targets being perceived as slower. To quantitatively ascertain whether flow vectors were more readily misattributed during eccentric rather than central presentations, for each condition (central versus eccentric) and target velocity we computed the difference in perceived target velocity (self-motion minus no self-motion). This difference is illustrated in figure 3b, and statistical contrasts indicated that the impact of self-motion was greater for eccentric rather than central presentation for targets moving at −10 and 20 cm s⁻¹ (red versus black, paired ANOVA object velocity × self-motion condition interaction term, p = 0.03, post hoc comparisons at each velocity, p < 0.05 Bonferroni-corrected at −10 and 20 cm s⁻¹). The fact that eccentricity of the target most readily impacted velocity perception of intermediate speeds (approx. 10 and 20 cm s⁻¹) concords with the modelling results (figure 1c, ‘S-curves’) suggesting that the impact of concurrent self-motion during object-motion is most prominent when retinal motion may not be unambiguously attributed to a given cause (e.g. to the target during high object velocity). The effect sizes at these intermediate speeds (i.e. 10 and 20 cm s⁻¹) were large compared with a hypothesis suggesting no effect (i.e. y = 0 in figure 3b, central targets: Cohen's d = 1.03; eccentric targets: Cohen's d = 1.19), and of small to moderate magnitude when contrasting central and eccentric targets (Cohen's d = 0.35). For further corroboration that eccentric targets were more likely to be perceived as stationary (relative to central targets), we fitted the difference in perceived velocity (self-motion versus no self-motion, data from figure 3b) to sinusoidal functions (amplitude, phase and frequency as free parameters). These fits were of good and equal quality across target locations (central R² = 0.65 ± 0.07; eccentric R² = 0.64 ± 0.09; p = 0.89). Importantly, the amplitude of these sinusoids were larger for eccentric (0.205 ± 0.03) than for central target locations (0.094 ± 0.014, p = 0.01), indicating a larger perceptual bias in the former condition. Phase (p = 0.50) and frequency (p = 0.12) were not different across target locations.

Figure 3.

Misattribution of optic flow vectors during concurrent self- and object-motion is exacerbated for eccentric targets and during passive rather than active self-motion. (a) Effect of target location. Perceived target velocity (y-axis, as estimated based on steering endpoint) as a function of true target velocity (x-axis), whether participants were moving (red; self-motion) or not (black; no self-motion) while the target was visible, and whether targets at onset were central (left) or eccentric (right). Circles represent means, error bars denote ±1 s.e.m., and pale dots in the background show data for individual subjects. (b) Impact of self-motion on perceived object velocity as a function of target location. Difference in perceived target velocity as a function of self-motion condition (self-motion − no self-motion; or red − black from (a), and whether targets were central (purple) or eccentric (green) at onset. Circles indicate means, error bars denote ±s.e.m., and pale dots in the background show data from individual subjects. (c) Active versus passive self-motion. Similar to (a), but panels are separated as a function of whether self-motion during target presentation was active (i.e. closed-loop; left, data are reproduced from figure 2d, right) or passive (i.e. open-loop; right). (d) Impact of active versus passive self-motion on perceived object velocity. Similar to (b), but separated according to whether self-motion during target presentation was active (purple) or passive (green).

To test the second prediction, we conducted an additional experiment (same participants but on a different day, see Methods) wherein participants' linear velocity during target presentation (and only during this time period) was under experimental control and was varied from trial to trial (either 0 cm s⁻¹ or a Gaussian profile ramping over 1 s to a maximum linear velocity of 200 cm s⁻¹). Angular velocity during this period was always held at 0° s⁻¹). In turn, we contrast the impact of self-motion on perceived target velocity either during closed-loop, active navigation (figure 3c, left, same data as in figure 2d, 150 ms observation time) or during passive self-motion (figure 3c, right). Firstly, we note that the passive data replicate the observation that intermediate target velocities were perceived as slower than when the same object velocity was presented in the absence of self-motion (figure 2c, passive, red versus black, paired ANOVA interaction term, p = 3.68 × 10⁻¹⁰; Bonferroni-corrected p < 0.05 at −20, −10, +10 and +20 cm s⁻¹, all Cohen's d > 0.7). Further, as above, for both active and passive conditions we compute the difference in perceived target velocity between self-motion and no self-motion conditions. Results show that when targets moved at a velocity of −20 and +20 cm s⁻¹ (figure 3d; ANOVA object velocity × active versus passive interaction term, p = 0.04; post hoc comparisons, p < 0.05, Bonferroni-corrected at −20 and 20 cm s⁻¹), the misattribution of flow vectors during self-motion was greater during passive rather than active self-motion. The difference between active and passive conditions (at −20 and +20 cm s⁻¹) was relatively small in effect size (Cohen's d = 0.24), an observation that is perhaps not surprising given that within the context of this experiment the major contributors to self-motion estimates are likely the optic flow and (the lack of) vestibular signals, not the presence or absence of efference copies. As further corroboration, fitting sinusoidal functions to the difference in perceived target velocity as a function of self-motion (data from figure 3d) again suggested larger perceptual biases (i.e. in amplitude parameter) during passive (0.14 ± 0.01) than active (0.09 ± 0.01) self-motion (p = 0.002; difference in R², p = 0.25; phase, p = 0.18; frequency, p = 0.14). Together, these results support our qualitative predictions, suggesting that optic flow vectors were misattributed during concurrent self- and object-motion.

(d) . Eye movements suggest a temporal cascade from segregation to integration to causal inference

Lastly, we attempt to leverage the continuous-time nature of the task to gain insight into the time-course of the computations supporting CI during closed-loop navigation. Namely, the above analyses were restricted to trajectory endpoints, the outcome of the computation. However, we may also use the eye movements occurring during and near the time of target presentation, which is the critical period during which the task-relevant inference ought to occur.

Eye movements were composed of a rapid, ballistic saccade (figure 4a, thin lines show example trials and thicker lines show mean values, arrows indicate the mean latency to saccade offset for eccentric targets) followed by a more protracted smooth pursuit (figure 4a, slow drift after arrow). In prior work, we have demonstrated that humans (and non-human primates) intuitively saccade to the visible target, and then track it via smooth pursuit, even when hidden ([23,26]). Unlike in these prior studies, however, here the target itself moved, and the presentation times were half as long (300 ms before versus maximum of 150 ms here). Thus, the saccade itself happens after target offset (figure 4a). In turn, saccades and gaze pursuit may aim toward the target onset position, its final visible offset location, an intermediate location, and/or track an evolving location.

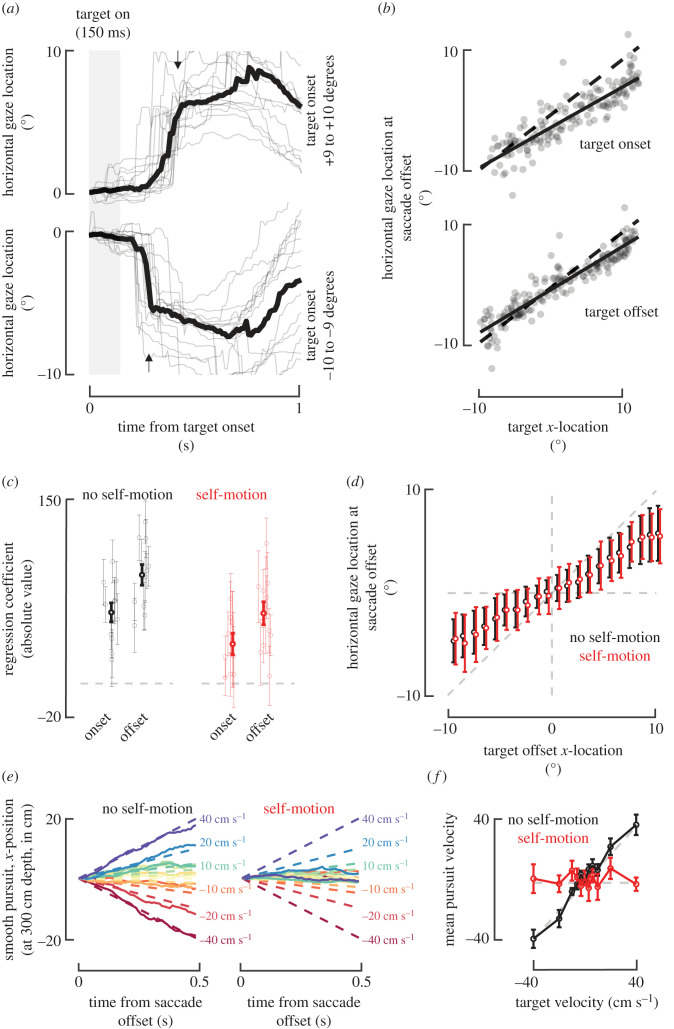
Figure 4.

Saccade and smooth pursuits during and following the target presentation. (a) Example lateral gaze position. Top panel shows gaze (eye + head) direction along the lateral plane for targets far to the right (positive values: +9 to +10°). Bottom panel shows gaze direction along the lateral plane for targets far to the left. Thin grey lines are examples (no self-motion condition), while the thick black line is the average. Arrows represent the mean latency of saccade. These representative data show a ballistic saccade (marked by the arrows) followed by smooth pursuit. (b) Saccade landing locations along the lateral plane for a representative subject. Top: lateral gaze location (in degrees) at saccade offset as a function of the target's initial (onset) location (also in degrees). Bottom: as above, for target offset location (i.e. last visible location). Dashed line shows the identity, while solid line shows the best linear fit. Individual dots represent trials. (c) Coefficients (absolute value) for a regression accounting for saccade offset location as a function of target onset and offset location. Grey circles with thin error bars denote individual subjects and their s.e., while black circles with thick opaque and error bars show the mean and s.e.m. Coefficients were larger for the offset than onset target location, for both the no self-motion and self-motion conditions. (d) Lateral gaze location at saccade offset as a function of target offset. Target offset locations were categorized in 21 bins (every degree, from −10 to +10°) and gaze offset location was averaged for each subject within these bins. Circles show means across subjects, and error bars represent ±1 s.e.m. Dashed grey line is the unity-slope diagonal, demonstrating that subjects slightly undershot targets, but were largely accurate. (e) Baseline-corrected lateral gaze position after saccade offset during no self-motion (left) and self-motion (right) conditions. The time-course of gaze (500 ms after saccade offset) shows modulation as a function of the target velocity (gradient: from warm to cold colours, −40 to +40 cm s⁻¹) in the no self-motion condition, but no modulation during the self-motion condition. Solid lines are averages across all subjects. Dashed lines show the evolving location of targets. (f) Smooth pursuit velocity as a function of target velocity and self-motion condition. During self-motion (red), gaze velocity (y-axis) was not modulated as a function of target velocity (x-axis). By contrast, gaze velocity did accurately track target velocity in the no self-motion condition (black). Circles show means across subjects, and error bars represent ±1 s.e.m. Dashed grey lines show y = 0 and y = x.

To examine saccades, we expressed gaze location along azimuth by adding eye-in-head orientation and head orientation. Similarly, we expressed the onset and offset locations of the target in polar coordinates. As shown in figure 4b for a representative subject, saccades were well accounted by both the onset (representative subject r² = 0.83, mean ± s.e.m.: 0.81 ± 0.01) and offset (representative subject r² = 0.88, 0.87 ± 0.01) target location, yet better by the latter than the former (paired t-test, t₁₀ = 14.74, p = 4.12 × 10⁻⁸; self-motion and no self-motion conditions considered jointly). In general, participants were reasonably accurate, but tended to undershoot the lateral location of targets with their gaze (onset, slope: 0.77 ± 0.03; offset: 0.79 ± 0.03; onset versus offset, paired t-test, t₁₀ = 7.44, p = 2.18 × 10⁻⁵). To ascertain whether humans saccade to the initial target location or incorporate knowledge of object-motion and saccade to its offset location, we fitted a regression model ($y\sim 1+{\beta }_1\mathrm{onset}+{\beta }_2\mathrm{offset}$) with β₁ and β₂ respectively weighting the target onset and offset locations and y being the measured lateral gaze. As shown in figure 4c, subjects placed more weight on the target offset than onset locations (onset versus offset, no self-motion and self-motion, paired t-test, both t > 2.21 and p < 0.04). Similarly, while the offset regressor was significant for 11 (no self-motion) and 8 (self-motion) of the 11 subjects, the onset regressor was significant for 9 (no self-motion) and 4 (self-motion). These results replicate the early observation that humans [31] (and monkeys [32]) can make accurate eye movements to moving targets, and that observers are able to programme the saccade not to where the target is when its position enters the oculomotor system, but rather to an estimate of where the moving target will be at the end of the saccade [33]. Finally, given (i) our interest in comparing between a concurrent object- and self-motion condition requiring CI, and an object-motion only condition not requiring CI, and (ii) the above evidence that saccade behaviour was mostly dictated by the target's offset location, we binned the latter and examined whether gaze to target offset location was modulated by self-motion. Results showed no impact of self-motion on the landing saccade position (figure 4d, unpaired ANOVA, interaction term, p = 0.95). Thus, subjects' initial inference of target position, as reflected by saccades, does not appear to be affected by misattribution of retinal velocity to object-motion versus self-motion.

We similarly examined the smooth pursuit that occurred after saccade offset. That is, for each trial we epoched and baseline-corrected the 500 ms of eye movements following saccade offset. We split trials as a function of target velocity and self-motion condition. Strikingly, as shown in figure 4e (means across all subjects), while smooth pursuit was modulated by target velocity in the no self-motion condition, it was not during concurrent self- and object-motion. We quantify this effect by computing the mean velocity of eye displacement across the 500 ms following saccade offset. This analysis reveals no dependence of eye velocity on target velocity in the self-motion condition (one-way ANOVA, F_10,110 = 0.41, p = 0.93), and the presence of a strong modulation when object-motion was presented alone (one-way ANOVA, F_10,110 = 21.7, p = 6.66 × 10⁻²², figure 4f). In fact, the gaze velocity along azimuth matched the target velocity in the absence of self-motion (one-way ANOVA on the difference between target and gaze velocity, F_10,110 = 0.75, p = 0.67).

Together, the pattern of eye movements shows largely accurate saccading to the target offset regardless of the self-motion condition, followed by smooth pursuit of the target, which is absent in the case of concurrent self- and object-motion, in contrast to the object-motion only condition and our prior work (where the target never moved; [23,26]). That is, during the no self-motion condition gaze velocity matches that of targets, while it is null after concurrent self- and object-motion. Crucially, during smooth pursuit, the target is invisible in both cases, such that this difference is not simply a visually driven effect.

3. Discussion

A wide array of studies have argued that human perception is scaffolded on the process of CI: we first hypothesize a generative structure (i.e. how ‘data’ are generated by the world), and then use this hypothesis in perceiving [2,5–10,14–16,30,34–40]. As such, some [3] have argued that CI is a unifying theory of brain function. Here, our main contribution is the derivation of CI predictions for a more naturalistic and continuous-time task, and the demonstration of these signatures during closed-loop active sensing and navigation. Further, we demonstrate how using continuous-time tasks may allow us to index the temporal unfolding of computations that mediate CI.

We take the example of concurrent self- and object-motion where observers have to infer whether flow vectors on their retina are generated entirely by self-motion, by object-motion, or by some combination of the two. Empirically, we show that, in line with the derived predictions, humans are more likely to report moving targets as stationary at high velocities during concurrent self-motion. Similarly, during concurrent self- and object-motion, observers navigate to locations closer to the initial target location, as if the target were not moving. This effect is most pronounced when targets move at intermediate velocities: those that cannot be easily ascribed to a single interpretation, either self- or object-motion. We further support the claim that observers misattribute flow vectors caused by object-motion to self-motion by testing and corroborating two additional qualitative predictions. First, we note that lateral flow vectors at the focus of expansion are essentially null when moving forward and toward the focus of expansion (see inset in figure 2a). Thus, in the current setup there should be less misattribution of flow vectors when targets are presented centrally (i.e. near the focus of expansion), and this prediction was confirmed (figure 3b). Second, we highlight that our estimates of self-motion are not solely derived from optic flow, but also from efference copies of motor commands, among other signals. Thus, we ran a second experiment in which the self-motion experienced during object-motion was not under the subjects' control. We argue that passive self-motion, by virtue of lacking efference copies of motor commands that are present during active self-motion, should result in a less certain estimate of self-motion and thus in a greater likelihood of misattributions. This prediction was also confirmed (figure 3d). Together, these findings suggest that observers perform CI when navigating in the presence of objects that may or may not move.

The third and final experimental finding allowed us to gain some insight into the time-course of the processes constituting CI. That is, we show that saccades to hidden targets already incorporate knowledge of the object velocity [31–33], with target offset position accounting for a larger fraction of variance than target onset position. The fact that these saccades to target were largely accurate may suggest that, at the time of saccade onset (approx. 200–300 ms from target onset), object-motion was appropriately parsed from self-motion. A prior study [11] has shown CI during saccades, but in this study saccades were used as a reporting mechanism, as opposed to allowing observers to use saccades in a natural and continuous-time environment. Next, we show that smooth gaze pursuit of the target following the initial saccade was strikingly different between the self-motion and no self-motion conditions. While in the no self-motion condition gaze velocity showed a gradient consistent with the target velocity, there was no modulation of gaze velocity by target velocity in the self-motion condition. This difference cannot be attributed to differences in optic flow, as at the time of smooth pursuit (approx. 400–900 ms after target onset) participants were moving and experiencing optic flow in both conditions. These results suggest that at the time of smooth pursuit, flow vectors caused by object- and self-motion were not properly parsed. Speculatively, these findings (i.e. parsing at the time of saccades but not at the time of smooth pursuit) are evocative of a cascade of events observed in neural data [4,14–16] wherein primary sensory cortices segregate cues, later ‘associative’ areas always integrate cues, and finally ‘higher-order’ regions perform flexible CI. Interestingly, the established neural cascade occurs earlier than the herein described behavioural one (cf. fig. 4f in [17]; neurally, segregation occurs between 0 and 100 ms post-stimulus onset, forced integration occurs between 100 and 350 ms, and CI thereafter).

From a mechanistic standpoint, our view of the literature is that most others have suggested that a decision regarding causal structure (e.g. optic flow ascribed to self and object with varying degrees) subsequently biases perception and perceptual biases (e.g. [12]). This hypothesis naturally arises from the CI formalism, wherein mathematically one first deduces causal structures, and then uses this inference in estimating features of hidden sources in the environment [2]. This conjecture has received nascent empirical support, with neural activity in the parietal cortex dynamically updating sensory representations to maintain consistency with the causal structure inferred in premotor cortex [18]. However, others have suggested that a purely feed-forward architecture (with no feedback for instance from pre-motor to parietal cortex) leveraging appropriately tuned neurons (i.e. ‘congruent’ versus ‘opposite’ cells, see [41,42]) may be sufficient to engender CI [20]. In our view, our results suggest a protracted cascade of processing not unlike that described neurally [14–17], wherein potentially early estimates demonstrate segregation (i.e. saccades results), intermediate time points show forced fusion (i.e. gaze pursuit results), and finally latter time points flexibly demonstrate CI (i.e. steering behaviour). Further, our results demonstrate CI within closed action–perception loops. Nonetheless, whether this protracted cascade and closed observer–environment loop relies exclusively on feed-forward mechanisms or not remains a question for further inquiry and likely will require large-scale neurophysiology.

We must mention a number of limitations in the current work. While our aim is to study CI within dynamic action–perception loops, much of our analysis relied on specific events frozen in time, and particularly at the end of trials (e.g. trajectory endpoints and explicit reports). This was somewhat mitigated by the eye-movement analyses and is a reflection of (i) challenges associated with jointly modelling CI, path integration and control dynamics, as well as (ii) the fact that within the current paradigm inference over object-motion occurs only once, during the observation period. In future work we hope to leverage the full trajectories generated by participants in attempting to intercept moving, hidden targets. This, however, will require accounting for idiosyncrasies emanating from path integration (e.g. putatively a slow-speed prior [22,24] and cost functions that evolve with time and distance travelled [22,24,25]), as well as derivation of optimal control policies (see [43–45] for recent attempts to model continuous behaviour as rational, and then invert this model to deduce the dynamics of internal models). Similarly, at risk of losing generalizability, the modelling approach could be expanded to explicitly take flow vectors as input (i.e. ‘image-computable modelling’). More generally, however, these next steps in our modelling approach are designed to account for evolving beliefs, and thus require just that, behaviour reflecting a protracted unfolding of an evolving belief. Examination of steering trajectories (figure 2c) did not suggest frequent and abrupt re-routings, as one would expect to occur during changing interpretations of the target motion (e.g. from moving to stationary). Instead, it appears that within the current paradigm observers made a causal inference once, early in the trial and while the target was visible. The complexity in properly modelling and accounting for all aspects of the behaviour (i.e. CI, path integration, control dynamics) also resulted in a lack of alternative models tested. This will also be rectified by attempts to model the task within the framework of inverse rational control [43–45], wherein we can use reinforcement learning to hypothesize a whole set of models (i.e. ‘forward models’) and then determine which accounts best for human performance. Lastly, we must acknowledge the relatively small sample size (n = 11), which may have resulted in limited statistical power and thus relatively small effect sizes (particularly in figure 3b,d).

Altogether, we derive normative predictions for how observers ought to intercept moving and hidden targets by inferring (i) whether objects are independently moving in the world, and (ii) if so, with what velocity. We then support the conjecture that humans perform CI in attributing flow vectors on their retina to different elements (i.e. self and object) during navigation. Lastly, we show that when allowed to evolve naturally in time, behaviour may demonstrate a protracted unfolding of the computations characterizing CI. In the past we have shown that macaques will intuitively track the ongoing location of moving and hidden targets [25]. Hence, the current results demonstrating signatures of CI in attempting to ‘catch’ moving targets open the avenue for future studies of naturalistic and closed-loop CI at the single-cell level.

4. Methods

(a) . Participants

Eleven participants (age range = 21–35 years old; 5 females) took part in the study. This number of participants was not determined via statistical power calculation, but is larger than prior reports employing a similar task (7 subjects [22] and 9 subjects [27]), and two to three times as large as other ‘continuous psychophysics' experiments [46,47]. All participants had normal or corrected-to-normal vision, normal hearing, and no history of neurological or musculoskeletal disorders. The experimental protocol was approved by the University Committee on Activities Involving Human Subjects at New York University.

(b) . Experimental materials and procedure

Participants were tasked with virtually navigating to and stopping at the location of a briefly presented target (i.e. the ‘firefly’) via an analogue joystick with two degrees of freedom (linear and angular velocity; CTI Electronics, Ronkonkoma, USA). The explicit instruction given was to stop ‘on top’ of the target and that if the target were to move, it would move throughout the entire trial. Visual stimuli were rendered via custom code in Unity (Unity Technologies, San Francisco, USA) and displayed on a virtual reality (VR) head-mounted display with a built-in eye tracker (90 Hz; HTC VIVE Pro, New Taipei, Taiwan). The subjective vantage point was set to a height of 100 cm above the ground, and participants had a field of view of 110° of visual angle.

The virtual scene comprised ground plane textural elements (isosceles triangles, base × height = 8.5 × 18.5 cm) that were randomly positioned and reoriented at the end of their lifetime (lifetime = 250 ms; floor density = 1.0 elements per 1 m²). For each trial, subjects were (programmatically) positioned at the centre of the virtual world, and a target (a black circle of radius 30 cm, luminance and colour matched to ground plane triangles) was displayed at a radial distance of 300 cm, and within a lateral range spanning from −10° to +10° (uniform distribution; 0° being defined as straight-ahead). In 10% of trials, the target was visible throughout the duration of the trial. In the rest, targets were presented for either 75 or 150 ms (equal probability). In 25% of trials, the target did not move (i.e. object velocity = 0 cm s⁻¹). In the remaining 75% of trials, the target moved laterally at 3, 6, 10, 20 or 40 cm s⁻¹, either leftward or rightward (equal probability). From a subjective standpoint, the experiment was well balanced with regard to the probability of observing a moving target. Namely, in the case of no concurrent self- and object-motion (see below), 53.35% of trials were reported as stationary (61.98 and 44.73% respectively for 75 and 150 ms observation times). Further, in pilot experiments (different set of participants, n = 7), we manipulated the fraction of trials in which targets moved, and this variable did not significantly impact stationarity reports (see electronic supplementary material; range tested from 55 to 75% of trials in which the target moved). Target presentation time, velocity and direction were randomly interleaved across trials and within blocks. Participants navigated toward the target with a maximum linear velocity (v_max) of 200 cm s⁻¹, and a maximum angular velocity (w_max) of 90° s⁻¹. In every trial, after participants stopped to indicate their perceived location of the (hidden) target, they were asked to explicitly report whether the target had moved or not, by deflecting the joystick leftward (target did not move) or rightward (target moved). Participants were informed that their responses were logged via an auditory tone. No feedback on performance was given. Inter-trial intervals were not defined to participants (i.e. ground plane elements were always visible and continuous with the previous frame, there was no transient artefact indicating a new trial even when virtually participants were instantaneously re-positioned to the origin of the virtual environment at the beginning of each trial) and of random duration (uniform) between 300 and 600 ms.

Every participant took part in two experiments, on separate days (each session lasting approx. 1 h). Prior to each experiment the subjects were allowed a dozen practice trials in which they understood that, in the case of a non-zero velocity target, even when invisible, the target kept moving (see [25] for evidence that macaques also intuitively understand this). In the first experiment, participants performed two blocks of 200 trials, in which they were always under full closed-loop conditions (i.e. motor output dictated sensory input). In one block, targets were presented given that participants were not moving (linear velocity <1 cm s⁻¹; no self-motion condition). In the other block, targets were presented given that participants were moving (linear velocity >20 cm s⁻¹; self-motion condition). Block order was randomized across subjects and participants were informed prior to each block whether they had to ‘maintain a linear velocity’ (‘self-motion’ condition) or remain static (‘no self-motion’ condition) for targets to appear. In practice, all subjects adapted an all-or-none approach wherein they would either deflect the joystick maximally (200 cm s⁻¹) or not at all (0 cm s⁻¹) prior to target presentation. Deflecting the joystick maximally during inter-trial intervals minimized experimental time. Angular velocity was kept near zero (mean absolute angular velocity during inter-trial interval less than 1° s⁻¹ on 98.2% of trials) given that targets could appear either leftward or rightward from straight ahead. In the second experiment, participants performed four blocks of 200 trials. Different from the first experiment, here linear velocity was set (open-loop, under experimental and not subject control) during the target presentation. Linear velocity was either null (0 cm s⁻¹; no self-motion condition) or had a Gaussian profile with peak amplitude equal to 200 cm s⁻¹ (self-motion condition). Angular velocity was kept fixed at 0° s⁻¹ and thus passive motion during inter-trial interval was always straight ahead. When participants were passively displaced, the linear perturbation lasted 1 s, and the target was presented during the peak of the perturbation (200 cm s⁻¹) such that it would be at a distance of 300 cm. After the perturbation, participants gained full access to the control dynamics (as in Experiment 1). Self-motion and no self-motion conditions were interleaved within a single block in Experiment 2. In total each participant completed 1200 trials.

(c) . Modelling

We here provide a basic outline of the normative model. A more detailed description is provided in the electronic supplementary material. At the beginning of each trial, we assume the target to be visible for some observation time T = Nδt, where δt is the duration of individual, discrete time steps in which our model is formulated. These time steps can be thought of as the time between individual video frames. While our results are independent of the specific choice of δt, discretization simplifies the model description and derivation of its properties. In the nth time step the target's true location is z_n = z_N − (N − n)vδt, where z_N is the target's true location at the end of the observation period, and where v is the target's velocity. The target's initial location z₁ is assumed to be drawn from a uniform distribution over a wide range of values of z₁. Its velocity is v = 0 (stationary target, γ = 0) with probability 1 − p_γ and otherwise (moving target, γ = 1) drawn from a normal distribution $N(v|0,{\sigma }_0^2)$ with mean zero and variance ${\sigma }_0^2$. This latter distribution effectively implements a slow-velocity prior, which has been widely used as an effective means of conceptually recapitulating known biases in human perception [28,29,48] and neural tuning [48,49] (also see [50] for a recent mechanistic explanation of the putative origin of this prior). The observer has noisy observations, x_n|z_n ∼ N(z_n,σ²/δt), whose variance is scaled by 1/δt to keep the results invariant to the choice of δt (i.e. choosing a smaller δt provides more, but individually less-informative observations per unit time). Based on all observations, x_{1 : N} ≡ x₁, … ,x_N, the model estimates the probability of the target being stationary, p(γ = 0|x_{1 : N}), and the target's velocity p(v|x_{1 : N}, γ = 1) if it is moving. The first probability is used for its stationary reports (figure 1b). Both are used to decide on the model's steering trajectory (figure 1c).

A lengthy derivation that is provided in the electronic supplementary material yields the required posteriors. The resulting expressions are rather lengthy and thus not detailed here. We assume that the model reports that the target is stationary if p(γ = 0|x_{1 : N}) > p(γ = 1|x_{1 : N}), that is, if $p(\gamma =0|x_{1\hspace{0.17em}:\hspace{0.17em}N})>1/2$, which is the case if

$${\displaystyle \frac{1}{2}\log {\displaystyle \frac{12{\sigma }^2}{12{\sigma }^2+T^3{\sigma }_0^2}+{\displaystyle \frac{T^6{\sigma }_0^2{\hat{v}}^2}{24{\sigma }^2(12{\sigma }^2+T^3{\sigma }_0^2)}<\log {\displaystyle \frac{1-p_{\gamma }}{\hspace{0.17em}{p}_{\gamma }},}}}}$$

where $⟨\hat{v}=v|x_{1\hspace{0.17em}:\hspace{0.17em}N},\hspace{0.17em}\gamma =1⟩$ is the mean estimate of the target's velocity under the assumption that it is moving. This decision rule imposes a threshold on this velocity estimate that depends on observation noise magnitude σ² and observation time T, and leads to the stationary reports shown in figure 1b.

The model chooses the optimal steering angle and distance to maximize the probability of intercepting the target. To do so, we assume it uses the self-motion estimation model from Lakshminarasimhan et al. [22] in which the uncertainty (here measured as the variance of a Gaussian posterior over location) grows as k²d^2λ, where d is the distance travelled, and k and λ are model parameters. For a given angle θ and travel time t (at fixed velocity v_a) this provides a Gaussian posterior p(z_a|t,θ) over 2-dimensional self-location z_a. Furthermore, assuming a known initial target distance and a lateral target motion, the model provides a similar posterior p(z_o|x_{1 : N},t) over 2-dimensional target location at time t, given by a weighted mixture of two Gaussians. The model then chooses t* and θ* that maximize p(z_a = z_o|x_{1 : N},t,θ), that is, the likelihood of ending up at the target's location when moving for some time t* at angle θ* (see electronic supplementary material for respective expressions). Unfortunately, this maximization cannot be performed analytically, and thus we find the maximum by discretizing t and θ.

The model parameters were hand-tuned to provide a qualitative match to the human data. However, it is worth noting that the qualitative model behaviour described in the main text is generic (i.e. fine-tuning is not necessary). Owing to the simple nature of the model, and the simplified steering (i.e. control) model that only moved along a straight line, we did not attempt to achieve a quantitative match. The target was assumed to be at a fixed, known distance of 4 m during the target observation period, and the observer moved at a constant v_a = 2 m s⁻¹ thereafter. A priori, the target was assumed to be moving with p_γ = 0.3 and the standard deviation of its slow-velocity prior was σ₀ = 0.5 m s⁻¹. Observation times were set to either T = 0.075 s or T = 0.150 s, matching those of the experiment. Observation noise was set to σ = 0.0004 m (no self-motion) or σ = 0.001 m (self-motion). The path integration uncertainty parameters were set to k = 0.5 and λ = 0.5 (Wiener diffusion).

Ethics

The experimental protocol was approved by the University Committee on Activities Involving Human Subjects at New York University (protocol 18-505).

Data accessibility

Data and code are available at: https://osf.io/72e6w/. Additional figures and results are included in the electronic supplementary material [51].

Authors' contributions

J.-P.N.: conceptualization, data curation, formal analysis, investigation, methodology, software, visualization, writing—original draft, writing—review and editing; J.B.: conceptualization, formal analysis, investigation, methodology, software, writing—review and editing; H.D.: software; J.V.: conceptualization, investigation, methodology, software, writing—review and editing; G.C.D.: conceptualization, funding acquisition, project administration, supervision, writing—review and editing; D.E.A.: conceptualization, funding acquisition, project administration, supervision, writing—review and editing; J.D.: conceptualization, formal analysis, funding acquisition, project administration, software, supervision, writing—original draft, writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed herein.

Conflict of interest declaration

We declare we have no competing interests.

Funding

This work was supported by NIH U19NS118246 (to G.C.D., D.E.A. and J.D.) and K99NS128075 (to J.-P.N.).