Abstract
When the buried pipeline is subjected to the external explosion load, stress and deformation will occur. When the stress and deformation value exceed a specific range, it will affect the normal use of the buried pipeline. In this paper, a multiphase coupled model of pipeline, soil and fluid within the pipeline is established. The penalty function coupling method is used to describe the load between soil and pipeline and the fluid within the pipeline. By specifying the boundary conditions of the coupled system, the multiphase coupled global solution variational principle function of the soil-pipe-fluid is derived. According to the established multiphase coupled calculation method, the numerical simulation analysis of the response of pipeline to external explosion is carried out. The maximum error of the experimental and numerical simulation results is about 5%, which verifies the accuracy of the multiphase coupled calculation method. The soil-pipeline-fluid multiphase coupled numerical calculation model is established to analyze the response of the buried pipeline under the external explosion load. The results show that during the explosion shock wave propagating in the soil, the peak value of the explosion pressure in different positions in the soil of the gas pipeline is greater than that of the oil pipeline. As for the structural response, the maximum radial displacement value of the oil pipeline is reduced by 3.83 mm compared with the gas pipeline, the maximum stress value is reduced by 3.75%. The maximum radial displacement value of the pipeline with a fluid velocity of 1.5 m/s is 2.65 mm larger than that of the pipeline with a fluid velocity of 1 m/s, and the maximum stress value is increased by 5.72%. The deformation resistance and explosion resistance of the oil pipeline are both stronger than that of the gas pipeline. The higher the fluid velocity, the weaker the pipeline's resistance to deformation and explosion will be.
Keywords: Buried pipeline, External explosion load, Multiphase coupling, Penalty function coupling, Structural response, Explosion resistance
1. Introduction
With the development of cities and the national economy, more and more gas and oil are transported by buried pipelines, which are highly likely to be destroyed by human-made and war explosions [1,2]. Such as third-party blasting construction, military strikes, parallel pipeline leakage and combustion explosion, can cause damage to the buried pipeline. After the destruction of oil and gas pipelines, it will further lead to pipeline leakage and explosion, resulting in inevitable casualties and economic losses, and even bring significant impact on the country's political and military activities. Therefore, it is especially important to study the structural response of pipelines under the action of external explosion loads [3].
At present, the experimental and numerical simulation methods are mainly used to study the response of buried pipelines under the action of an external explosion. In the experimental research, Dejian Du et al. [[4], [5]] used the acquisition and analysis system to measure the impact pressure generated by the explosion vibration, and found that the back of the buried pipeline section under the stress wave was easily damaged by the axial tensile stress, and it was a transient stress process. Bonalumi P and Michael R. Acton et al. [[6], [7]] measured the acceleration and pressure generated by the explosion shock wave in the soil through a full-scale pipeline explosion construction field test. When the explosion shock wave propagates in the soil, it will be affected by the pipeline, which makes the propagation process of the explosion wave more complicated. The numerical calculation method can obtain the accurate explosion load and the pipeline response under more complicated conditions, so the numerical simulation calculation method has been widely used in the calculation of the external explosion of buried pipelines [8]. Nan Jiang et al. [[9], [10]] carried out field blasting tests on a full-size buried high-density polyethylene pipe (HDPE) to verify the distribution characteristics of blasting vibration velocity and dynamic strain. Taolong Xu et al. [11] established the interaction mode between explosive load, soil and gas pipeline, and found out the main factors affecting the safety of parallel paved pipelines. Boohyoung Bang et al. [12] conducted a numerical simulation comparison analysis of inner-air pipelines under different explosion distances and different pipeline shell thickness conditions. Lan Zhang et al. [13] analyzed the response of the ground explosion load to the buried pipeline, and obtained the influence of internal pressure, TNT size, shell thickness and buried depth on the pipeline stress. Ping Liu et al. [14] conducted a numerical analysis of the response of buried gas pipelines under the impact of soil explosion and compared the pipeline response under different distances to the explosion center. Nan Jiang et al. [15,16] established the prediction models of pipeline and ground blasting vibration velocity under blasting action and peak effective stress of pipeline respectively, and the dynamic response of pipelines induced by blasting vibration, the possible damage characteristics of pipelines and the dynamic response data related to pipe-soil interaction are analyzed. The results show that the vertical vibration is the main deformation of buried pipelines and soil layers, and the axial tensile deformation is the main deformation of pipelines. Chong Fang et al. [17] conducted numerical simulation of the dynamic response of the pressurized pipe and the empty pipe under the impact of air explosion. The results showed that the deformation resistance of the pressurized pipe was stronger, and the stability was higher. Gianfranco Totani et al. [18] used numerical simulation to simplify the contact between soil and pipeline into a sliding finite element model and analyzed the effect of soil slope on pipeline collapse. Aursand E et al. [19] used the finite element software to establish a fluid-solid coupled interaction model and simulated the crack length, crack propagation velocity and pressure of CO2 pipelines. Limin Peng et al. [20] used finite element software to simulate the large-scale water pipeline tunnel, analyzed the deformation and stress response of the pipeline during each construction process, and evaluated the safety of tunnel construction and pipeline. G Valsamos et al. [21] simulated the explosion load by the numerical simulation method and calculated and assessed the fatal and non-lethal risks of the explosion.
It can be seen from the comparative analysis of the above literature that the existing research mainly focuses on the external explosion response of the pipeline under different influencing factors. However, the existing studies are little concerned with the load transfer mode between the soil, pipeline, and fluid within the pipeline during the explosion process or with the calculation method of multiphase coupling between the pipeline and soil. Therefore, by establishing a multiphase coupled model of the solid domain of the pipeline and the fluid domain within the pipeline, the penalty function coupling method is used to analyze the solid domain of the pipeline and the fluid domain within the pipeline, and the soil-pipeline-fluid multiphase coupled global solution for the variational principle functional is derived by specifying the boundary conditions of the coupled system. Finally, according to the multiphase coupled calculation method, a numerical simulation analysis is performed on the explosion load and buried pipeline's response to external explosion load under different fluid media and different flow conditions. Thus, the laws of explosion pressure propagation in the soils and the pipeline response are obtained.
2. Soil-pipeline-fluid multiphase coupled load transfer calculation method
2.1. Multiphase coupled dynamics model
As shown in Fig. 1, under the action of the external explosion load, the soil transmits the explosion pressure to the pipeline, and the pipeline transmits the displacement generated by the explosion pressure to the fluid within the pipeline through the coupled interface, and the fluid within the pipeline transmits the fluid pressure to the pipeline through the coupled interface.
Fig. 1.
Soil-pipeline-fluid multiphase coupled interface physical quantity transfer.
The process of the liquid-filled buried pipeline under external explosion load is simplified into a multiphase coupled dynamics model, as shown in Fig. 2. The soil, pipeline and the fluid within the pipeline are taken as the research objects, as shown in Fig. 2(a). The model is divided into three domains, the solid domain of the pipeline , the soil solid domain , and the fluid domain within the pipeline . It is assumed that the pipeline is an ideal elastic body, and the pipeline is of equal section, the cross-section is always circular, the ends of the pipeline are hinged boundaries, and the boundary of the soil is a fixed constraint.
Fig. 2.
Multiphase coupled dynamics model: (a) Pipeline-soil coupled system, (b) Pipeline-soil interface penalty function coupling and (c) Pipeline solid domain.
The contact between the pipeline and the soil is a penalty function coupling. As shown in Fig. 2(b), after the explosion shock wave acts, the pipeline is deformed by the action of the soil. The deformation of the pipeline along the length and in the circumferential direction does not change with the deformation of soil. As shown in Fig. 2(c), the inlet of the pipeline is the boundary of the velocity, the velocity is , and the outlet is the pressure boundary, which is indicated by . The interface between the fluid within the pipeline and the pipeline is the coupled fluid-solid boundary, which is represented by . The interface of pipeline-soil interaction is the penalty function contact surface, which is represented by .
The boundary conditions for the fluid domain within the pipeline are shown in equation (1):
| (1) |
Where , , and are the outer normal unit vector, velocity vector, and pressure vector of the fluid domain interface, respectively; is the pipeline inlet velocity; p is the pipeline outlet pressure.
2.2. Multiphase coupled calculation of pipeline and fluid domain within the pipeline
In the model establishment and numerical analysis, the fluid within the pipeline and the pipeline are considered together, and the governing equations of the fluid and the solid are simultaneously solved in the same solver. In this paper, the Lagrangian multiplier method is applied to introduce the constraints of the coupled fluid-solid interface, and the fluid within the pipeline is coupled to the pipeline into a system. The force acting on the coupled fluid-solid interface is taken as the unknown quantity to be solved. The functional describing the mechanism of interaction between the fluid within the pipeline and pipeline is constructed. The coupled fluid-solid system equation of the pipeline and the fluid within the pipeline is established.
The fluid domain and the solid domain in the coupled fluid-pipeline system respectively satisfy the corresponding basic equations and boundary conditions. The generalized variational principle functional for the coupled system of fluid domain within the pipeline and solid domain of the pipeline is shown in equation (2):
| (2) |
Where is the generalized variational principle functional for the fluid domain within the pipeline and the solid domain of the pipeline [22]; and are the functional correction terms for introducing the fluid-solid coupled constraint condition and the coupled force work in the Lagrangian multiplier method.
For , there is:
| (3) |
Among them:
; ;Where the superscripts and represent fluid and solid, respectively; and are the surface force tensors on the coupled boundary between fluid and solid; x is the vector in the Cartesian coordinates; represents the coordinate in the x, y, z direction, successively; represents the coordinate in the y, z, x direction successively; is the velocity vector of fluid or solid; sequentially indicates the v, w, u direction displacement; sequentially indicates the v, w, u direction velocity; sequentially indicates the w, u, v direction velocity; and are the volumetric force vector of the fluid and the solid respectively; and are the densities of the fluid and solid, respectively; is the solid stress tensor, is the strain rate tensor.
On the coupled fluid-solid interface :
| (4) |
| (5) |
Where , , , , and are Lagrangian multipliers.
The displacement, velocity, and pressure at any point in the fluid domain within the pipeline and the solid domain of the pipeline are expressed as:
| (6) |
| (7) |
Where is the number of element nodes, for an eight-node hexahedral element, n = 8; for a six-node tetrahedral element, n = 6. is the shape function of fluid velocity, displacement and pressure; and are the displacement of the fluid element node and the tensor of the velocity along the i direction, respectively; and are the displacement of the solid element node and the tensor of the velocity along the i direction, respectively; is the velocity and displacement shape function of the pipeline element.
It can be concluded that the generalized variational principle functional for the coupled fluid-solid discrete model is given by:
| (8) |
Where and are the numbers of discrete elements in the fluid domain within the pipeline and the solid domain of the pipeline, respectively. is the number of nodes on the coupled fluid-solid interface.
By taking the variational variation of the velocity and pressure p in equations (3), (4), (5), (6), (7), (8), the finite element equation of the coupled dynamics analysis of the fluid domain within the pipeline and the solid domain of the pipeline can be obtained. The constraints of the coupled fluid-solid interface can be obtained by taking the variational variation of the Lagrangian multiplier and . The control equations and constraints are written in a matrix form, and the dynamic finite element governing equations for the coupling of the pipelines and the fluids in the pipelines are shown in equation (9):
| (9) |
Among them:
; ; ; ;
; ; ; ;
; ;
; .Where is the fluid-solid coupling matrix sub-block; is the mass matrix for the solid domain of the pipeline; is the stiffness matrix for the solid domain of the pipeline; and are the strain matrix and elastic matrix for the solid domain of the pipeline, respectively; is the damping matrix for the solid domain of the pipeline, for which the Rayleigh damping is usually adopted; , are the structural damping coefficients and related to the structural frequency and damping ratio; is the mass matrix of the fluid domain within the pipeline; is the convection matrix of the fluid domain within the pipeline; is the pressure matrix for the fluid domain within the pipeline; is the wear matrix for the fluid domain within the pipeline; is the continuous matrix; is a fluid force vector; is the fluid volume force vector; is the external load term at the fluid domain boundary when the pressure term and the convection term are integrated by parts; is the fluid and solid force vector on the coupled fluid-solid interface; H is the boundary velocity vector; is the known load column vector of the coupled fluid-solid boundary; , and are the acceleration, velocity and displacement vector of the fluid domain within the pipeline respectively; , and are the acceleration, velocity and displacement vector of the solid domain of the pipeline; is the fluid force vector on the coupled fluid-solid interface; , and are a column vector indicating the interpolation function or its derivative, a row vector number; and are the velocity of the fluid boundary and pressure interpolation functions, respectively.
3. Numerical calculation method and experimental verification based on multiphase coupling
3.1. Experimental setup and numerical model establishment
In order to verify the numerical calculation method based on multiphase coupling, the numerical simulation analysis of the pipeline explosion experiment in Ref. [23] is carried out, where the pipeline material in is Q235, the pipeline length is 100 cm, the outer diameter is 10 cm, and the shell thickness is 0.275 cm. The experimental device is shown in Fig. 3(a). The explosive used in the experiment is a 3cm × 3cm × 7 cm TNT explosive. The explosive is fixed at a certain distance above the pipeline, and the ends of the pipeline are simply supported.
Fig. 3.
The experimental setup and numerical calculation model: (a) Experimental device and (b) Numerical simulation finite element model.
In the experiment, the explosive explodes in the air, and the blast wave is transmitted to the pipeline through the air. In the numerical calculation, the air, the pipeline and the air within the pipeline are divided into three phases, and the finite element model is established as shown in Fig. 3(b). The model includes three different material types: TNT explosives, air, and pipeline. The explosion pressure of TNT explosives PCJ = 21.0 GPa, density = 1.61 g/cm3, and explosion velocity a = 6930 m/s. The equation of state for TNT explosives is Jones-Wilkens-Lee [24]. The air mass density and initial internal energy E0 were 1.29 g/cm3 and 0.25 J/cm3, respectively. The pipeline material model is described by the Johnson-Cook constitutive equation [25]. The numerical simulation analysis of the pipeline response is carried out when the distance between the explosion center and pipeline surface is 2 cm, 4 cm, 6 cm and 8 cm, respectively.
3.2. Comparison of numerical simulation and experimental results
According to the calculation, the deformation of the burst surface of the pipeline under different explosion distance conditions is compared, as shown in Fig. 4(a–d). It can be seen from Fig. 4(a–d) that at the position where the pipeline directly facing TNT, the elliptical pit is formed due to the explosion shock wave, and as the distance between the explosion center and pipeline surface increases, the elliptical pit area gradually becomes smaller, and the depth gradually becomes shallower.
Fig. 4.
Pipeline deformation under different distance between the explosion center and pipeline surface (experimental and numerical simulation): (a) Distance between the explosion center and pipeline surface of 2 cm, (b) Distance between the explosion center and pipeline surface of 4 cm, (c) Distance between the explosion center and pipeline surface of 6 cm and (d) Distance between the explosion center and pipeline surface of 8 cm.
In order to further analyze the radial deformation of the pipeline section under different distances between the explosion center and pipeline surface, the angle between the pits on the burst surface of the pipeline is shown in Fig. 5. The variation of the angle of the pit under different distances between the explosion center and pipeline surface is shown in Table 1. The radial deformation curve of the pipeline section under different distances between the explosion center and pipeline surface is shown in Fig. 6, and the specific values are shown in Table 2.
Fig. 5.
Deformation angle of pipeline pit.
Table 1.
Pit angle under distance distances between the explosion center and pipeline surface.
| Explosion center distance (cm) | Pit angle (°) |
Relative difference (%) | |
|---|---|---|---|
| Experiment | Numerical Simulation | ||
| 2 | 70 | 73 | +4.3 |
| 4 | 88 | 91 | +3.4 |
| 6 | 92 | 96 | +4.3 |
| 8 | 108 | 106 | −1.9 |
Fig. 6.
Radial deformation of the burst surface of the pipeline under distance between the explosion center and pipeline surface.
Table 2.
Radial deformation of pipelines under distance distances between the explosion center and pipeline surface.
| Explosion center distance (cm) | Radial deformation of the pipeline (cm) |
Relative difference (%) | |
|---|---|---|---|
| Experiment | Numerical Simulation | ||
| 2 | 7.51 | 7.88 | +4.9 |
| 4 | 5.70 | 5.56 | −2.5 |
| 6 | 4.22 | 4.35 | +3.1 |
| 8 | 2.43 | 2.30 | −5.3 |
It can be seen from the data in Table 1, Table 2 and Fig. 6 that the radial deformation curves of pipelines obtained via experiment and numerical simulation are in good agreement. With the increase of the distance between the explosion center and pipeline surface, the angle of the pits on the burst surface of the pipeline gradually increases, while the deformation gradually decreases. Comparing the experimental and numerical simulation results, the maximum relative difference of the angle of the pipeline pit is 4.3%, and the maximum relative difference of the radial deformation is 5.3%, which indicates that the multiphase coupled numerical calculation method and model established in this paper can accurately calculate the external explosion load of the buried pipeline and pipeline response.
4. Calculation of external explosion load of buried pipeline based on multiphase coupling
4.1. Establishment of the numerical model for multiphase coupling of buried pipelines
The buried pipeline geometry model is shown in Fig. 7. The TNT package size is 20cm × 20cm × 20 cm; the outer diameter of the pipeline is 81.3 cm, the shell thickness is 0.95 cm, the length is 1000 cm, the pipeline bury depth is 100 cm, and the distance between the outer surface of the pipeline and the center of the TNT package is 200 cm. The observation points 1 and 2 are established at a distance of 50 cm from the burst surface of the pipeline and in the soil close to the pipeline, respectively. The observation points 1 and 2 are parallel to the centerline of the explosive. According to the symmetry of the geometric structure, a three-dimensional finite element model of the buried pipeline is established as shown in Fig. 8. The model fluid domain is the fluid within the pipeline, which is divided by tetrahedral solid elements. The solid domain is divided into two parts: the pipeline and the soil. The pipeline is discretized by shell elements, and the soil part is meshed by hexahedral solid elements. During the calculation, the model mesh is continuously modified by different sizes. When the stress of the pipeline gradually converges to a stable value, the mesh is considered to be suitable. After calculation and analysis, the size of the fluid mesh in the pipeline and the pipeline is 0.9cm × 0.9 cm. The size of the whole soil mesh is 10cm × 10 cm. The size of the explosive mesh is 5cm × 5 cm.
Fig. 7.
Geologic model of buried pipeline under external explosion.
Fig. 8.
Finite element model of buried pipeline under external explosion.
In the calculation model, the central axis of the pipeline coincides with the Z-axis, and the side of the positive X direction of the soil is an infinite soil boundary condition, and the displacement constraint in the Z direction is restricted. The pipeline and the soil are described by a penalty function coupling method to limit the Z-direction displacement and rotation constraint of the pipeline. The coupled interface of the fluid domain within the pipeline is set as a moving mesh, the inlet boundary condition is set to a velocity of 1 m/s (By coupling the ICFD solver with the structural solver, set the boundary conditions of the pipeline), and the outlet boundary condition is set to a pressure of 8 MPa. In the calculation, the fluid within the pipeline is oil and natural gas respectively (By modifying the keywords such as fluid material density, dynamic viscosity, and surface tension), and the pipeline material model is described by the Johnson-Cook constitutive equation. The pipeline material adopts ×70 and follows the Von Mises yield criterion.
4.2. Material description in the calculation model
4.2.1. Explosive material model
The external explosive of the buried pipeline adopts the TNT high-energy explosive material model, and the JWL equation of state is used to describe the explosive explosion process. The equation of state is shown in equation (10):
| (10) |
Where P is the TNT explosion pressure; A1, B1, R1, R2, and are the TNT material constants; E0 is the TNT initial specific energy; , is the explosion product density; is the explosive density.
4.2.2. ipeline material model
The pipeline material is described by a high strain rate constitutive equation (11):
| (11) |
Where A, B, C, n and m are input constants; is the effective plastic strain; , EPSO is quasi-static threshold rate; is the effective total strain rate; is the homologous temperature .
4.2.3. Soil material model
The soil material adopts the × MAT_SOIL_AND_FOAM material model, and the stress yield function of the material is shown in equation (12):
| (12) |
Where represents the Cauchy deviatoric stress tensor of the soil material; is the Kronecker symbol of the soil material; a0 is the influence of the soil friction angle; a1 is the influence of soil cohesion; a2 is the influence of the soil explosive dynamic load effect.
4.3. Numerical analysis of the explosion field
4.3.1. Propagation of explosion shock waves
The changes of explosion pressure when the explosion shock wave propagates in the soil under the two working conditions of oil pipeline and gas pipeline are calculated. Fig. 9 shows the pressure propagation cloud map of the explosion shock wave in the soil at different times when the medium in the pipeline is oil.
Fig. 9.
Explosion pressure cloud map at different times (10 [5]MPa): (a) 0 μs, (b) 5200 μs, (c) 9100μs and (d) 20000 μs?
It can be seen from Fig. 9 that the explosion shock wave rapidly decreases during the propagation of the soil shock wave, and the pressure wave area gradually expands during the propagation process, showing a spherical wave surface. It can be seen from Fig. 9(a) that the pressure generated by the explosive at the moment of ignition is as high as several gigapascals, and the maximum pressure position is at the center of the explosive. As can be seen from Fig. 9(b), when the pressure wave is transmitted to the observation point 1, the explosion pressure of the area with the maximum value has dropped to 4.41 MPa. From Fig. 9(c), it can be seen that when the pressure wave reaches the observation point 2, the explosion pressure of the area with the maximum value has dropped to 2.39 MPa. At 20000 μs, the explosion pressure wave has completely covered the buried pipeline.
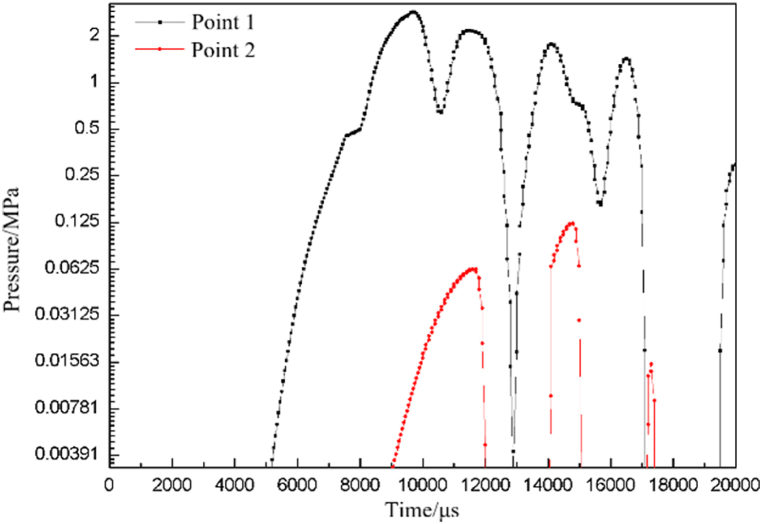
In order to compare the pressure changes of observation point 1 and observation point 2 with time at different times, Fig. 10 shows the pressure-time history curves of observation point 1 and observation point 2, respectively.
Fig. 10.
Explosion pressure curve of each observation point.
From the pressure-time history curve of observation point 1, it can be seen that the pressure of the explosion shock wave propagates to the observation point 1 at 5200 μs, and then the pressure rapidly increases and reaches a peak pressure of 2.86 MPa at 9700 μs, and reaches a secondary peak pressure of 2.16 MPa at 11500 μs? The shock wave pressure repeatedly oscillates and reduces. From the pressure-time history curve of observation point 2, it can be seen that the explosion shock wave pressure propagates to the observation point 2 at 9100 μs, which is just the time when the observation point 1 reaches the peak pressure moment. This indicates that due to the reflection from the pipeline, the explosion shock wave pressure undergoes reflection enhancement. Then, at 11600 μs, the observation point 2 reaches a peak pressure of 0.062 MPa, which is close to the secondary peak pressure of observation point 1 at 11500 μs, and the shock wave pressure repeatedly oscillates after reaching the secondary peak pressure of 0.13 MPa at 14600 μs?
4.3.2. Analysis of the impact of explosion shock waves under different media conditions in the pipeline
Table 3 shows the time and pressure values at which the peak pressure and the secondary peak pressure occur at observation points 1 and 2 when the medium in the pipeline is oil and gas, respectively.
Table 3.
Calculation results of explosion pressure at observation points 1 and 2 (different media).
| Observation points | Working condition | First pressure peak |
Second pressure peak |
||
|---|---|---|---|---|---|
| Time (μs) | Value (MPa) | Time (μs) | Value (MPa) | ||
| 1 | Gas pipeline | 9500 | 3.26 | 11,200 | 2.21 |
| Oil pipeline | 9700 | 2.86 | 11,500 | 2.16 | |
| 2 | Gas pipeline | 16,100 | 0.12 | 17,800 | 0.16 |
| Oil pipeline | 11,600 | 0.06 | 14,800 | 0.12 | |
It can be seen from the data in Table 3 that due to the buffering effect of the oil in the pipeline, the pits generated on the surface of the oil pipeline are shallow and the area is large, and the pits generated on the surface of the gas pipeline are deep and the area is relatively small, so the oil pipeline quickly reflects the shock wave, and the reflected explosion pressure is small. Therefore, the time at which observation point 2 of the oil pipeline reaches the pressure peak is 8.64% earlier than the gas pipeline, and the pressure peak is reduced by 8.33%. For observation point 1, because the reflection pressure of the oil pipeline is smaller, the propagation speed is slower after the reflection. Therefore, the time when the oil pipeline observation point 1 reaches the pressure peak is 2.73% longer than the gas pipeline, and the pressure peak decreases by 3.32%.
5. Structural dynamic response of the buried pipeline under the external explosion load
5.1. Structural response under different fluid media within the pipeline
5.1.1. Radial deformation response of the pipeline under different fluid media within the pipeline
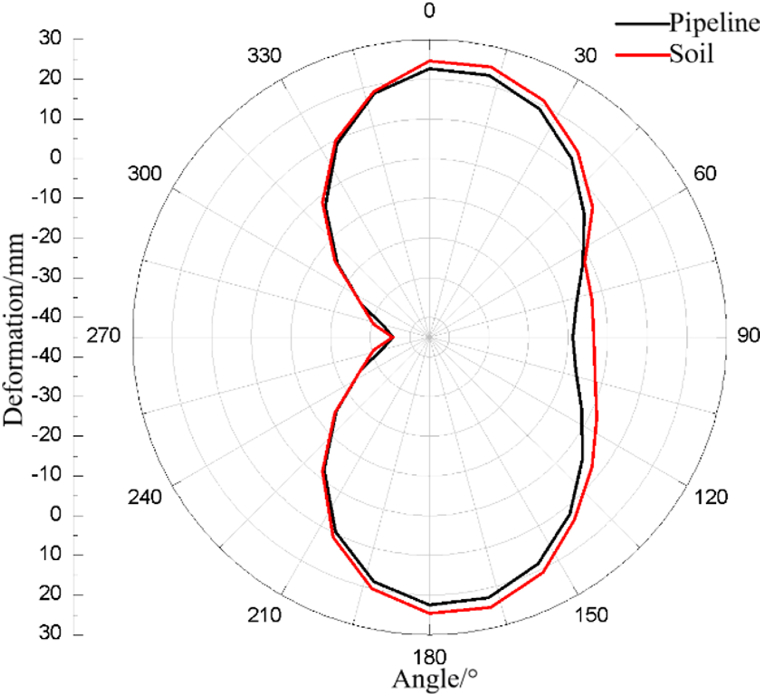
Numerical simulation analysis of the pipeline subjected to external explosion under the condition of oil and gas in the pipeline is carried out. In order to better explain the deformation relationship between the pipeline and the surrounding soil after the external explosion, the gas pipeline is taken as an example. The deformation of the pipeline at the explosion center and the surrounding soil at the time of 20000μs is selected as shown in Fig. 11 (the clockwise direction is recorded as 0°∼270° of the pipeline).
Fig. 11.
Radial deformation of the pipeline and surrounding soil (20000 μs)
It can be seen from Fig. 11 that between 30° and 180°, the difference between the deformation of the pipeline and that of the surrounding soil is large. Between 180° and 360° and 0°∼60°, the difference between the deformation of the pipeline and that of the surrounding soil is small. The radial deformation of the central section of the pipeline is negative between 231.5° and 309° of the burst surface and 64°∼116° of the backburst surface, indicating that the pipeline is deformed inward between the two sections. In other angles, the pipeline experiences outward convex deformation. The concave interval of the soil around the pipeline is between 235° and 306.1° of the burst surface and 62°∼113° of the backburst surface. The concave range of the pipeline is larger than that of the surrounding soil, and the deformation value is also large.
At 20000 μs, the radial deformation curves at the central section of the pipeline with different media in the pipeline are compared in Fig. 12. The radial displacement peaks of the four directions of 0°, 90°, 180° and 270° in the center section of the pipeline are shown in Table 4. The radial deformation of the pipeline in the axial direction is shown in Fig. 13.
Fig. 12.
Radial deformation curve at the center section of the pipeline (different media).
Table 4.
Radial displacement peaks in different directions of pipeline center section (different media).
| Element position (°) | Radial displacement peak of the gas pipeline (mm) | Radial displacement peak of the oil pipeline (mm) | Displacement peak relative difference (mm) |
|---|---|---|---|
| 0 | 25.50 | 22.87 | −2.63 |
| 90 | −9.21 | −9.12 | −0.9 |
| 180 | 25.50 | 22.85 | −2.65 |
| 270 | −41.29 | −37.46 | −3.83 |
Fig. 13.
Element radial deformation curve in the axial direction the pipeline burst surface (different media).
It can be seen from Fig. 12 and Table 4 that the radial deformation of each section of the pipeline is symmetrical along the horizontal line of the pipeline and the maximum radial deformation occurs at 270° on the burst surface. The radial deformation on the burst surface is all greater than that on the backburst surface. Due to the incompressibility of petroleum, the buffering effect on the pipeline subjected to external force is large, and the radial deformation everywhere in the central section of the pipeline is smaller than that of the gas pipeline. The concave range on the burst surface of the gas pipeline has a concave area of 77.5° and that of the oil pipeline is 104°. Compared with the oil pipeline, the concave section of the gas pipeline is small, and the concave deformation is larger. The burst surface of the gas pipeline presents a trend of large deformation with small intervals, while the burst surface of the oil pipeline presents a trend of small deformation with large intervals. The concave sections on the backburst surfaces of the gas pipeline and the oil pipeline are all in the range of 52°, i.e., the concave range is the same. The concave deformation of the gas pipeline is slightly larger than that of the oil pipeline. For pipelines conveying different fluid media, the maximum difference in radial deformation at various angles is 3.83 mm.
As can be seen from Fig. 13, the radial deformation on the axis of the pipeline is symmetrically distributed along the central section. The middle of the pipeline is inwardly concaved. The closer to the center of the pipeline, the greater the degree of inward concave and the greater the radial deformation will be. The concave section of the gas pipeline is 0.89 m–9.11 m (between point A and point F), and the concave section of the oil pipeline is 0.71 m–9.29 m (between point B and point E). The concave interval of the gas pipeline is smaller than the concave interval of the oil pipeline. Between point C and point D (between 1.8 m and 8.2 m), the radial deformation of the gas pipeline is greater than the radial deformation of the oil pipeline. At 5 m to the center of the longitudinal direction of the pipeline, the radial deformation values of the gas pipeline and oil pipeline both reach the peak values. The radial deformation law of the pipeline section is the same as the axial deformation law. In the longitudinal direction of the pipeline, the radial deformation of the gas pipeline shows a tread of large deformation with small intervals and the oil pipeline presents a trend of small deformation with large intervals.
5.1.2. Stress response of pipelines under different fluid media conditions
In order to study the stress response of the pipeline, the oil pipeline is taken as an example to analyze the change process of the stress distribution on the pipeline surface at different times. Fig. 14(a–c) shows the surface stress distribution map of the oil pipeline at different times.
Fig. 14.
Stress response cloud map of the oil pipeline at different times (MPa): (a) 6400 μs, (b) 9700μs and (c) 20000 μs?
It can be seen from Fig. 14(a–c) that the stress on the burst surface of the pipeline directly facing the explosion center is the largest. With the propagation of the explosion shock wave, the surface stress of the pipeline increases gradually. At 6400 μs, the surface stress of the pipeline increases to 115.49 MPa, and at 9700 μs, the surface stress of the pipeline reaches 461.55 MPa. At 20000 μs, the pipeline surface stress reached a peak of 473.54 MPa.
In order to compare and analyze the pipeline stress response with different fluid media in the pipeline, the stress values at the center section of the gas pipeline and the oil pipeline at 20000μs are selected, respectively. The comparison curve is shown in Fig. 15. The stress peaks of elements in the four directions (0°, 90°, 180° and 270°) of the pipeline section are shown in Table 5, and the element stress comparison in the axial direction of the pipeline burst surface is shown in Fig. 16.
Fig. 15.
Pipeline center section stress curve (different media).
Table 5.
Stress peaks in different directions of pipeline center section (different media).
| Element position (°) | Gas pipeline stress peak (MPa) | Oil pipeline stress peak (MPa) | Stress peak relative difference (%) |
|---|---|---|---|
| 0 | 486.59 | 475.15 | −2.35 |
| 90 | 387.95 | 384.77 | −0.82 |
| 180 | 487.61 | 475.43 | −2.50 |
| 270 | 495.42 | 476.86 | −3.75 |
Fig. 16.
Element stress curve in the axial direction of the pipeline burst surface (different media).
It can be seen from Fig. 15 and Table 5 that the stress on the burst surface of the pipeline is greater than the stress on the backburst surface, where the stress at the 270° position of the burst surface is the largest, and the stress values of the individual elements of the oil pipeline are smaller than those of the corresponding elements of the gas pipeline. It can be seen from Fig. 16 that the stress on the axis of the pipeline is symmetrically distributed along the central section, and the closer to the center, the greater the stress value. Due to the buffering effect of oil in the pipeline, the overall stress value of the oil pipeline is smaller than that of the gas pipeline. The stress variation of the gas pipeline is relatively small in the range of 4.1 m–5.8 m and that of the oil pipeline is also small in the range of 3.9 m–6.1 m.
5.2. Structural response of the pipelines under different fluid flow conditions
In order to compare and analyze the change of pipeline response under different flow conditions, the pipeline response is calculated under the two conditions with a medium velocity of 1 m/s and 1.5 m/s.
5.2.1. Radial deformation response of the pipelines under different flow conditions
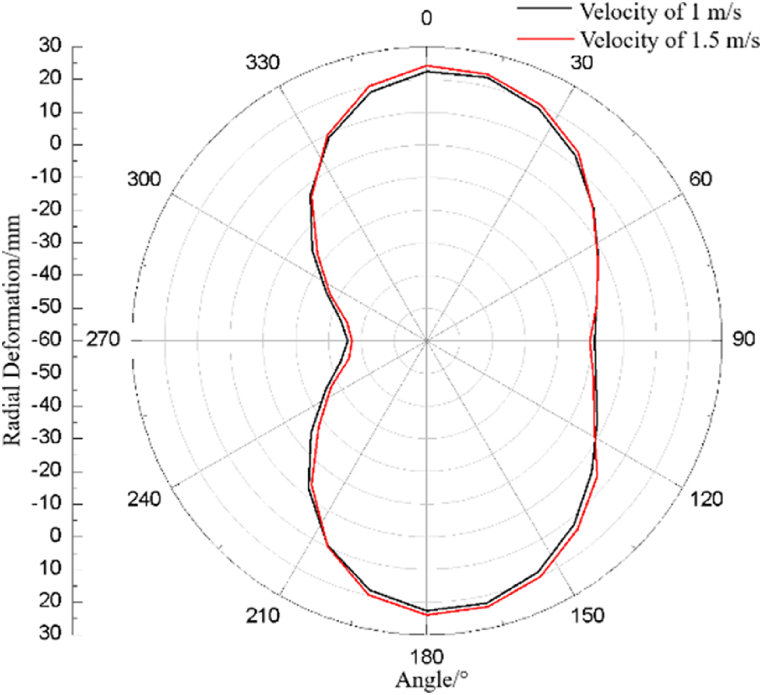
At 20000 μs, the radial deformation curves at the center section of the pipeline at different velocities are compared in Fig. 17. The radial displacement peaks of the four directions of 0°, 90°, 180° and 270° in the center section of the pipeline are shown in Table 6. The radial deformation of the pipeline in the axial direction is shown in Fig. 18.
Fig. 17.
Radial deformation curve at the center Section of the pipeline (different velocities).
Table 6.
Radial displacement peaks in different directions of pipeline center section (different velocities).
| Element position (°) | Radial displacement peak at a velocity of 1 m/s (mm) | Radial displacement peak at a velocity of 1.5 m/s (mm) | Displacement peak relative difference (mm) |
|---|---|---|---|
| 0 | 22.87 | 24.26 | 1.39 |
| 90 | −7.21 | −8.28 | 1.07 |
| 180 | 22.85 | 23.99 | 1.14 |
| 270 | −37.46 | −40.11 | 2.65 |
Fig. 18.
Radial deformation curve of elements in the axial direction of the burst surface of the pipeline (different velocities).
It can be clearly seen from the data in Fig. 17 and Table 6 that the radial deformation of the center section under the condition of the fluid velocity of 1 m/s is smaller than the velocity of 1.5 m/s, indicating that the larger the medium velocity, the weaker the resistance to deformation of the pipeline. When the velocity of the fluid within the pipeline is 1.5 m/s, the concave surface of the pipeline burst surface has a concave range of 102.9°. Under the condition of 1 m/s, the concave surface of the pipeline burst surface has a concave range of 104°. Under the condition with a fluid velocity of 1.5 m/s, the burst surface of the pipeline shows a trend of large deformation with small interval. When the velocity is 1 m/s, the burst surface of the pipeline exhibits a trend of small deformation with large interval. Under different flow conditions of the fluid within the pipeline, the maximum difference of radial deformation of the pipeline at each angle is 2.65 mm, and the minimum difference is 1.07 mm.
It can be seen from Fig. 18 that the concave interval of the pipeline is 1.04–8.96 m (between point A and point F) under the condition with a fluid velocity of 1.5 m/s. When the fluid velocity in the pipeline is 1 m/s, the concave interval is 0.71 m–9.29 m (between point B and point E). When the fluid velocity in the pipeline is 1.5 m/s, the concave interval of the pipeline is smaller than that when the fluid velocity of the pipeline is 1 m/s. Between point C and point D (between 1.8 m and 8.1 m), the radial deformation of the pipeline at a fluid velocity of 1.5 m/s is higher than the radial deformation of the pipeline at a velocity of 1 m/s. The radial deformation law of the pipeline section is the same. In the longitudinal direction of the pipeline, the pipeline radial deformation presents a trend of small interval with larger deformation when the fluid velocity is 1.5 m/s, but the trend becomes large interval with small deformation when the fluid velocity is 1 m/s.
5.2.2. Stress response of the pipelines under different flow conditions
In order to compare and analyze the stress response of the pipeline at different velocities, the stress response at the center of the pipeline at 20000μs when the medium velocity in the pipeline 1 m/s and 1.5 m/s is selected. The comparison curve is shown in Fig. 19. The stress peak changes of center section elements in four directions 0°, 90°, 180° and 270° are shown in Table 7, and the element stress comparison of the axial direction of the pipeline burst surface is shown in Fig. 20.
Fig. 19.
Pipeline center section stress curve (different velocity).
Table 7.
Stress peaks in different directions in the center of the pipeline (different velocities).
| Element position (°) | Pipeline stress peak at a velocity of 1 m/s (MPa) | Pipeline stress peak at a velocity of 1.5 m/s (MPa) | Stress peak absolute difference (%) |
|---|---|---|---|
| 0 | 475.15 | 502.33 | 5.72 |
| 90 | 384.77 | 385.89 | 0.29 |
| 180 | 475.43 | 501.24 | 5.43 |
| 270 | 476.86 | 482.21 | 1.12 |
Fig. 20.
Element stress curve in the axial direction of the pipeline burst surface (different velocity).
It can be seen from Fig. 19 and Table 7 that the stress on the burst surface of the pipeline is greater than the stress on the backburst surface of the pipeline, where the stress at the 270° position is the largest, and the stress value of each element under the condition that the fluid velocity in the pipeline is 1 m/s is less than the stress value corresponding to the 1.5 m/s working condition. It can be seen from Fig. 20 and Table 7 that the axial overall stress value of the pipeline with a fluid velocity of 1.5 m/s is greater than that of the pipeline with a fluid velocity of 1 m/s. Due to the increase of the medium velocity in the pipeline, the explosion resistance of the pipeline becomes weaker. The pipeline stress variation is small for the pipeline in the range of 4.0 m–6.0 m when the fluid velocity is 1 m/s and the pipeline in the range of 3.9 m–6.1 m when the fluid velocity is 1.5 m/s.
6. Conclusion
-
(i)
The global solution variational principle functional and load transfer calculation methods of soil-pipeline-fluid multiphase coupled are proposed, and the experimental pipeline is analyzed by numerical simulation method, which verifies the accuracy of the multiphase coupled numerical calculation method and model established in this paper.
-
(ii)
During the propagation process of the blast wave, the explosion pressure decreases rapidly, and the area of the pressure wave expands gradually, showing a spherical wave surface. The peak surface pressure of oil pipeline is 8.33% lower than that of gas pipeline due to the buffering effect of the medium in the pipeline.
-
(iii)
For different fluid transport media, the radial deformation and stress of gas pipelines under explosive impact load are greater than those of oil pipelines. Due to the non compressibility of petroleum, oil pipelines have stronger anti deformation and anti explosion capabilities. With the increase of fluid velocity, the radial deformation and stress of pipeline increase. The higher the fluid velocity of the medium inside the pipe, the weaker the resistance to deformation and explosion ability of the pipeline will be.
Author contribution statement
Ye Lu: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Yuqi Ding: Conceived and designed the experiments; Analyzed and interpreted the data; Wrote the paper.
Jiahe Zhang, Ming Yang: Performed the experiments; Contributed reagents, materials, analysis tools or data.
Data availability statement
Data included in article/supp. Material/referenced in article.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors are grateful for the support from the Natural Science Foundation of Heilongjiang Province (Grant No. LH2022A003).
References
- 1.Zhang R.M., Zeng X.G., Wang H. Numerical simulation of dynamic response of buried pipelines under blast loading. CHN. Petro. Mach. 2017;2(2):26–30. [Google Scholar]
- 2.Zhang J., Liang Z., Han C.J., Feng D., Zhang H., Yang X. Analysis on response of overhead oil and gas pipeline impacted by rock-fall. J. Safe. Sci. Technol. 2015;11(7):11–17. [Google Scholar]
- 3.Liu F.J., Ling Z.W., Kong S., Qian Y.Q., Zheng M.L., et al. Real-time calculation of gas pipeline leakage diffusion and prediction of explosion hazard. Vessel. Technol. 2010;27(10):21–29. Press. [Google Scholar]
- 4.Du D.J., Ma S.G., Yang J.D. Experimental study on the impact of buried pipeline explosion. Eng. Blast. 2006;12(2):19–23. [Google Scholar]
- 5.Liang X.Q., Xie M.L., Xie Q., Zhang W.H., Wei S.Q. Safety test and monitoring of blasting vibration of underground pipelines. Eng. Blast. 2009;15(4):66–68. [Google Scholar]
- 6.Bonalumi P., Colombo M., Comina C., Prisco M., Foti S., Galli A. Characterization of blast effects on surrounding soil: internal detonations in underground pipes. Appl. Mech. Mater. 2011;82:302–307. [Google Scholar]
- 7.Acton M.R., Allason D., Creitz L.W., Lowesmith B.J. Large scale experiments to study hydrogen pipeline fires. Proc. Biennial Int. Pipeline Conf. 2010:593–602. [Google Scholar]
- 8.Du D.J., Liang X.Y., Deng Z.D., Ma X.W. Analytical solution calculation of buried pipeline explosion impact. Blasting. 2011;28(3):21–25. [Google Scholar]
- 9.Jiang N., Zhang Y., Wu T., Yao Y., Luo X. Determination of blasting vibration safety criterion for HDPE pipeline using vibration and strain data in a coastal metro line. Sensors. 2021;21(21):7252. doi: 10.3390/s21217252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jiang N., Zhu B., Zhou C., Luo X., Li H., Wu T., Lu G. Safety criterion of gas pipeline buried in corrosive saturated soft soil subjected to blasting vibration in a coastal metro line. Thin-Walled Struct. 2022;180 [Google Scholar]
- 11.Xu T.L., Yao A.L., Zeng X.G., Li Y.L. Study on the security conditions of parallel laying gas transmission pipelines under blast loading. Int. Conf. Pipelines Trenchless Technol. 2011 [Google Scholar]
- 12.Bang B., Park H., Kim J. Simplified method for estimating the effect of a hydrogen explosion on a nearby pipeline. J. Loss Prevent. Proc. 2016;2(6):112–116. [Google Scholar]
- 13.Zhang L., Liang Z., Zhang J. Mechanical response of a buried pipeline to explosion loading. J. Fail. Anal. Prev. 2016;16:576–582. [Google Scholar]
- 14.Liu P., Cao X.K., Cai X.S., Yang R.Q. Numerical analysis of the impact response of buried gas pipelines under the impact of soil explosion. West Exp. Eng. 2018;2:26–31. [Google Scholar]
- 15.Jiang N., Zhu B., Zhou C., Li H., Wu B., Yao Y., Wu T. Blasting vibration effect on the buried pipeline: a brief overview. Eng. Fail. Aanal. 2021;129 [Google Scholar]
- 16.Zhu B., Jiang N., Zhou C., Luo X., Li H., Chang X., Xia Y. Dynamic interaction of the pipe-soil subject to underground blasting excavation vibration in an urban soil-rock stratum. Tunn. Undergr. Space Technol. 2022;129 [Google Scholar]
- 17.Fang C., Deng Z.D., Wang G.Y. Numerical simulation analysis of water filling and inner air pipeline under explosive impact load. Proc. 2016 Annu. Conf. China Civil Eng. Soc. 2016:396–405. [Google Scholar]
- 18.Totani G., Totani F., Celli D. Post-event site investigation, monitoring, stability analysis, and modeling of a gas pipeline explosion. J. Fail. Anal. Prev. 2016;17(1):1–7. [Google Scholar]
- 19.Aursand E., Dumoulin S., Hammer M. Fracture propagation control in CO2 pipelines: validation of a coupled fluid–structure model. Eng. Struct. 2016;123:192–212. [Google Scholar]
- 20.Peng L.M., An Y.L., Zhao D., Wu Z.B. Safety evaluation of liuyanghe tunnel beneath a water pipe with a big cross section. Saf. Sci. 2008;7:247–251. [Google Scholar]
- 21.Valsamos G., Casadei F., Solomos G., Larcher M. Risk assessment of blast events in a transport infrastructure by fluid-structure interaction analysis. Saf. Sci. 2019;118:887–897. [Google Scholar]
- 22.Liu Y.H. Xi'an Jiaotong University; China: 2001. Fluid-solid Dynamic Coupling Theory and Application of Hydraulic Engineering, PhD Thesis. [Google Scholar]
- 23.Song K.J., Long Y., Ji C., Gao F.Y. Plastic deformation of metal tubes subjected to lateral blast loads. Math. Probl. Eng. 2014 doi: 10.1155/2014/250379. [DOI] [Google Scholar]
- 24.Livermore Software Technology Corporation (LSTC) Version 960; Livermore, Calif: 2003. LS-DYNA Keyword User's Manual. [Google Scholar]
- 25.Johnson G.R., Cook W.H. Proc. 7th Int. Symposium on Ballistics. The Hague. The Netherlands; 1983. A constitutive model and data for metals subjected to large strain, high strain rates and high temperature; pp. 541–548. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data included in article/supp. Material/referenced in article.