Abstract
Due to enhanced heat transfer rate, the nanofluid and hybrid nanofluids have significant industrial uses. The principal objective of this exploration is to investigate how thermal radiation influences the velocity and temperature profile. A water-based rotational nanofluid flow with constant angular speed is considered for this comparative study. A similarity conversion is applied to change the appearing equations into ODEs. Three different nanoparticles i.e., copper, aluminum, and titanium oxide are used to prepare different nanofluids for comparison. The numerical and graphical outputs are gained by employing the bvp-4c procedure in MATLAB. The results for different constraints are represented through graphs and tables. Higher heat transmission rate and minimized skin friction are noted for triple nanoparticle nanofluid. Skin coefficients in the x-direction and y-direction have reduced by 50% in trihybrid nanofluid by keeping mixed convection levels between the range . The heat transmission coefficient with raising the levels of thermal radiation between and Prandlt number has shown a 60% increase.
Subject terms: Applied mathematics, Fluid dynamics
Introduction
Incompressible fluid movement above a extending surface has numerous applications in the industrial field like aerodynamics, extrusion of plastic sheets, continuous metallic plate extrusion, artificial fibers, and stretching of plastic films. In each of these cases, the amount of heat transfer at the stretchy surface influences the effectiveness of the final form of the product. To learn the fundamentals of these processes, it is essential to examine dynamics and thermal transmission within a fluid above a continuously extending sheet/surface. Sakiadis1 examined boundary layer (BL) behavior over continuous solid surfaces elaborating on the two-dimensional axisymmetric movement. Erickson et al.2 discussed the injection/suction influence on heat and mass transmission above a moving flat plate. Crane3 explored the flow past the stretchable surface and Chen and Stroble4 scrutinized the buoyancy influence on a flat plate. Turkyilmazoglu5 explored the stretching wall in magneto-hydrodynamic rotating flow frames. Takhar and Nath6 explored three-dimensional movement over the stretched surface. Several investigators have examined stretching surfaces for heat and mass transfer under different under-applying forces7–12.
The dispersion of NPs in a host fluid is known as nanofluid (NF). Similarly, the addition of one or more nanoparticles in NF is termed as a hybrid nanofluid (HNF). Susrutha et al.13 elaborated that the NPs bond to and through the other molecules which govern different properties like heat transfer rate and electrical conductivity. Phule et al.14 studied the shape and size of -NPs and - using the electron microscope at high voltage. Behra and Ram15–19 investigated the mechanism of solubilizing, and stabilization in the form of nanofluid in an alcoholic medium, and variations in optical properties in fullerene with the existence of poly (vinyl pyrrolidone) molecules in water. Singh and Ram20 magnetic NF’s synthetization and their applications.
Stretchable surfaces in fluid environments are known to produce significant features of industrial and technological value. With the aid of a cutting-edge spectral relaxation technique, Ghasemi et al.21 investigated NF flow over the stretched surface with radiation and magnetic field influence. They observed that high magnetic field intensities have a significant impact on temperature profile. Arshad and Hassan22 explored HNF between rotating systems. Nasir and Hassan et al.23–25 discussed the flow of water and ethylene glycol magnetized NP over a flexible surface. Additionally, elaborated on the flow of different NFs with an energy source and entropy analysis on the transportation of MHD advanced NF embedded in the porous surface.
Due to the intrinsic rotation of the fluid particles and their tendency to ascend with fluid motion, fluid rotation occurs in nature. Researchers investigated rotational fluid paired with different properties because of engineering and industrial applications. Mehmood and Ali26 have investigated the impact of MHD in a revolving system of overstretched and porous media. Hussain et al.27 examined the rotating nanofluid flow over the stretchable surface by considering the magnetic effect. Shah and Ullah28 considered forced convection for ferrofluid treatment with the insertion of the electric field. Dadheech et al.29,30 explored the copper oxide and silver with ethylene glycol as host fluid with porous medium effect and modified NF flow above non-linear stretching surface with MHD effect. Shah et al.31 computationally studied engine oil base HNF with variable heat transfer.
The thermal radiation impact on the free convection flow is important in many engineering applications, such as in advanced types of power plants for nuclear rockets, reentry vehicles, high-speed flights, and procedures involving high temperatures. Sheikholeslami et al.32 explored radiation impact on MHD NF utilizing two-phase simulation with heat transfer. Safdar et al.33 examined Maxwell NF using the Buongiorno model with thermal radiation. Micro-organism profiles diminish under higher bioconvection levels they remarked. Asghar et al.34 presented the mixed convection HNF with slip conditions and heat generation/absorption. Jawad et al.35–37 studied the bioconvection and thermal radiation effect of Williamson and Casson NF with micro-organism migration over a stretching surface. They discovered that migration of micro-organisms declines with increment in bio convection and Peclet number. Similarly, numerous researchers38–41 have explored different NF's flow over stretchable surfaces considering diverse assumptions. Tang et al.42 presented a computational study on magnetized gold-blood NF flow and heat transmission. Farooq et al.43 employed the Cattaneo-Christov model with the bio-convectional flow of Williamson fluid under the thermal radiation effect over the slandering cylinder.
In the above-conducted literature review, it is demonstrated that the comparison between the three different types of NFs has not been yet investigated. Hussain8 discussed the effects of radiation and magnetization on water-based NFs, and Hassan10 elaborated on linear and nonlinear radiation effects on distinct-based HNFs. Adnan and Jawad et al.36 examined the Arrhenius energy and heat transport activates effect on gyrotactic microorganisms with Nield boundary conditions. Arshad and Hassan22 discussed the HNFs using different nanoparticles. The objective of the present research is to comparatively discuss the three distinct types of water-based nanofluids above dual stretching surface inserted in a porous medium, namely, NF ; HNF and trihybrid nanofluid (THNF) for heat transfer rate. The novelty of this study is that we have incorporated the Rosseland thermal radiation approximation to investigate the mixed convection in rotating nanofluids flow. Turkyilmazoglu5 used the spectral Chebyshev collocation method, Shafiq18 employed the optimal homotopy method, Hayat44 studied heat transfer with the homotopy analysis method and in this study we use the BVP-4c technique to examine the comparative flow of different NFs with radiation effect over dual stretching. Related researches45–49 can be studied. The governing equations are transformed into the ordinary differential equation by employing a similarity transformation and tackled a MATLAB by applying the boundary value problem method (BVP-4c). The outcomes of the present study are described through graphs and tables for different parameters. The main research questions of the present research are designed as follows:
How different parameters change the temperature and velocity profiles?
How primary and secondary velocity is effected by mixed convection and porous medium parameter.
Increase in Prandtl number and radiation parameter how effects both profiles?
Which type of NF, HNF, or THNF shows the maximum heat transfer rate?
Governing equations
The basic flow governing equalities for viscid incompressible liquid over the permeable surface in the existence of Rosseland radiation are:
Continuity equation
| 1 |
Momentum equation
| 2 |
Energy equation
| 3 |
Formulation of problem
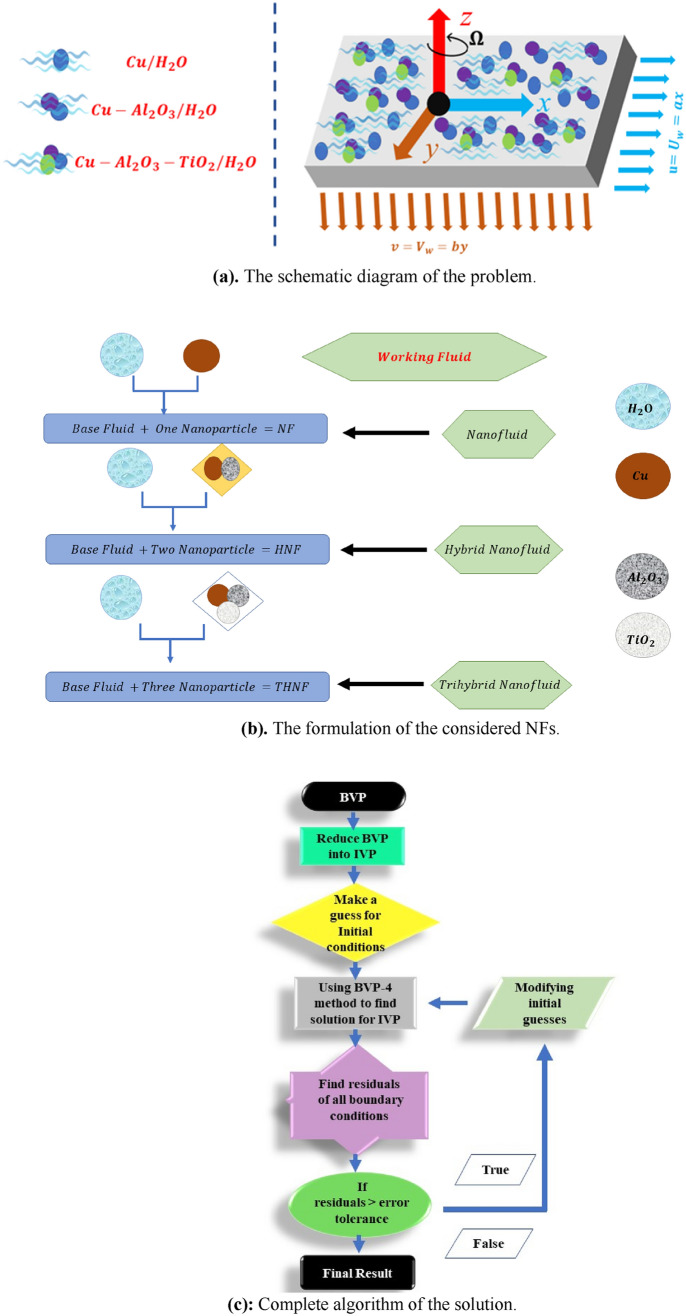
Let us consider an in-compressible, flow over the stretchable surface with the stretching velocities embedded in a permeable medium. The flow is contained on the surface and the surface is stretchable with surface velocities and in and -directions correspondingly. It is assumed that the flow of chemically reactive trihybrid nanofluids is restricted above the plane, in other words, . Based on the situation, the flow assumptions are as follows:
The flow is rotational with a constant angular speed and along the z-axis, as shown in Fig. 1a.
We have considered three different types of fluids, namely, NF, HNF, and THNF.
Water is used as a working fluid and 49,50 as NPs which is presented in Fig. 1b.
The surface is inserted in a porous medium and the chemical reaction and thermal radiation effect are considered while modelling.
Figure 1.
(a) The schematic diagram of the problem. (b) The formulation of the considered NFs. (c) Complete algorithm of the solution.
The thermophysical possessions of NPs and water are defined in Table 1. The flow equations of continuity, momentum, and energy for these assumptions can be presented as:
Table 1.
Thermophysical46 properties of base fluid and nanoparticles.
| Physical properties | Density (kg m−3) | Specific heat (J kg−1 K) | Thermal conductivity (W m−1 K) | Thermal expansion (K−1) |
|---|---|---|---|---|
| Water | 997 | 4179 | 0.614 | 21 × 10−5 |
| Copper (s1) | 8933 | 385 | 400 | 1.67 × 10−5 |
| Aluminum oxide (s2) | 3970 | 765 | 40 | 0.85 × 10−5 |
| Titanium oxide (s3) | 4250 | 686 | 8.96 | 0.90 × 10−5 |
Continuity equation51:
| 4 |
Momentum equation along the x-axis51:
| 5 |
Momentum equation along -axis51:
| 6 |
Energy equation51:
| 7 |
Here , and are velocity components in the , and directions respectively. is temperature, is the porosity, radiation, and gravitational acceleration respectively. is the density, viscosity, and thermal diffusivity of a hybrid nanofluid. By applying the Rosseland approximation, the radiative heat flux is defined by:
| 8 |
Here is the Stefan-Boltzmann coefficient and is the mean absorption constant. This model considers optically thick radiation. Assuming that there is not much of a temperature differential within the flow, the expression of the term by using Taylor series expansion is expanded as follows:
| 9 |
Now by neglecting higher order terms beyond the first degree in , we get.
| 10 |
By using Eqs. (9) and (10), the relation takes the form:
| 11 |
Therefore, the energy equation takes the form:
| 12 |
The corresponding boundary conditions48 are:
| 13 |
Transformation methodology
We define the following transformation46:
| 14 |
Here differential is concerned . Using this similarity transformation Eq. (14), the Eq. (4) is satisfied. Equations (5), (6), and Eq. (12) take the following transformed form for HNF:
| 15 |
| 16 |
| 17 |
The non-dimensional quantities and are defined as and the thermophysical formulation relations are defined in Table 2 for NF, in Table 3 for HNF, and in Table 4 for THNF.
| 18 |
Table 2.
Thermophysical46 formulation for nanofluid (NF).
| Properties | Nanofluid |
|---|---|
| Density | |
| Dynamic viscosity | |
| Heat capacity | |
| Thermal expansion | |
| Thermal conductivity |
Table 3.
Thermophysical46 formulation for hybrid nanofluid.
| Properties | Hybrid nanofluid |
|---|---|
| Density | |
| Dynamic viscosity | |
| Heat capacity | |
| Thermal expansion | |
| Thermal conductivity |
Here |
Table 4.
Thermophysical52 formulation for trihybrid nanofluid.
| Properties | Tri-Hybrid nanofluid |
|---|---|
| Density | |
| Dynamic viscosity | |
| Heat capacity | |
| Thermal expansion | |
| Thermal conductivity |
Here and |
The modified boundary conditions are as follows:
| 19 |
Here is the dimensionless stretching ratio parameter.
Quantities of engineering interest
The most significant physical quantities of importance from an engineering perspective are the skin friction coefficients , , and Nusselt number , which are defined as follows:
| 20 |
Here and denote the shear stress along the stretched wall along the x-axis and y-axis and are defined as
| 21 |
The dimensionless form of Eq. (18) is:
| 22 |
By using the temperature field to define the thermal transmission rate as a Nusselt number:
| 23 |
Or
| 24 |
Numerical scheme and validation
The numerical outcomes for the present study are obtained through the bvp-4c at MATLAB. The complete algorithm in graphical form is presented in Fig. 1c. The Eqs. (15)–(17) which are highly non-linear are changed to first-order ODEs by using a new set of variables. Subsequently, the initial guesses are chosen which satisfy the boundary conditions. A convergence criterion of is set for the acquired solution.
| 25 |
A new set of variables are defined as follows in MATLAB to obtain the numerical solution.
| 26 |
| 27 |
| 28 |
| 29 |
| 30 |
| 31 |
| 32 |
| 33 |
The transformed boundary conditions changed into the subsequent form:
| 34 |
The skin friction and Nusselt number changed into the following form:
| 35 |
| 36 |
The attained results present the influence on different profiles. The results are assessed with the literature in Table 5.
Table 5.
The assessment of the present numerical outcomes with literature.
Results and discussion
The formulation of the problem presented in the preceding section is for HNF. The outputs of the present problem for NF, HNF, and THNF are obtained separately for each nanofluid i.e., copper–water NF, copper/aluminum oxide–water HNF, and copper/aluminum oxide/titanium oxide–water THNF. The effects of different parameters by employing the boundary value problem technique at MATLAB are described in this section.
Velocity profile
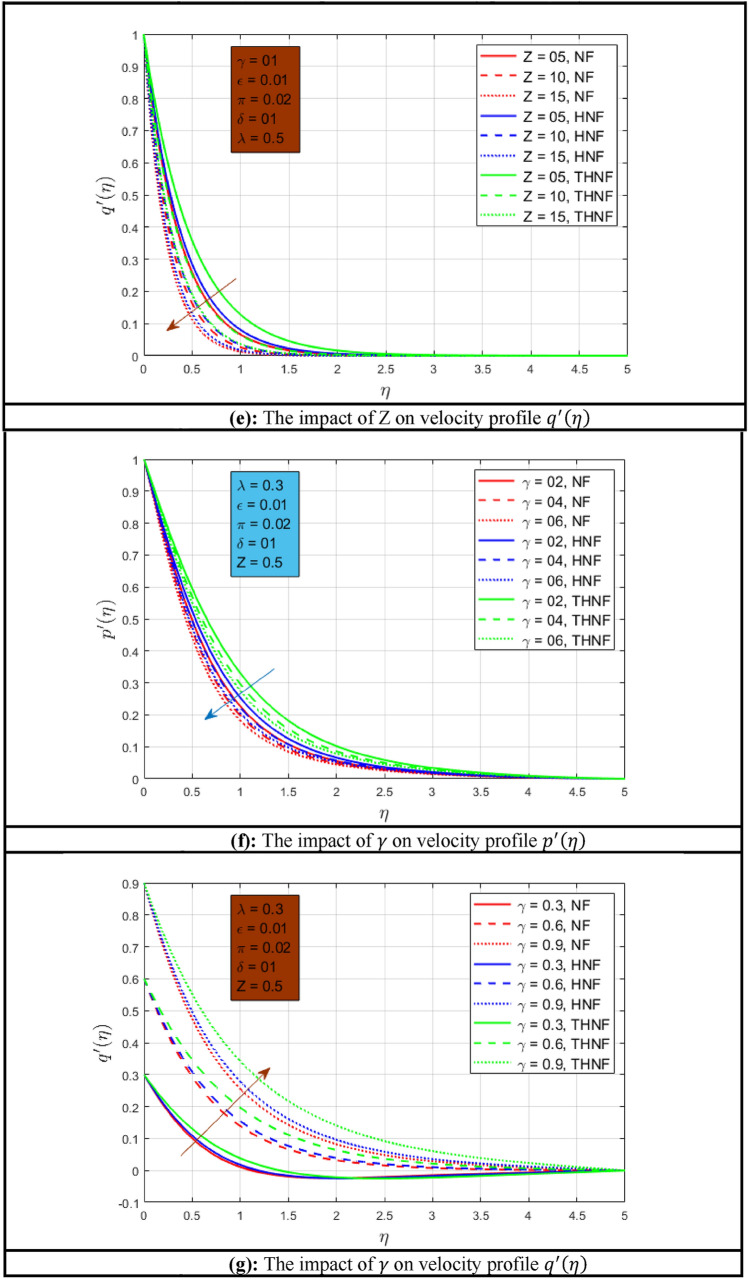
The impact of rotation parameters on velocity profiles and is presented in Fig. 2a,b for NF, HNF, and THNF where water is the host fluid. Figure 2a illustrates the effect of rotational motion on the primary velocity profile . It is examined that when the rotational motion is increased the velocity profile decline for NF, HNF, and THNF. Observations indicate form that has an inverse relationship with . In addition, the momentum boundary layer has considerably extended under rotation influence in the case of THNF as associated with NF and HNF. The reason behind this phenomenon is that when three nanoparticles are dispersed in base liquid the volumetric concentration increases as compared to NF and HNF. When the influence of rotation on velocity profiles is compared with46, it is observed that a wider momentum boundary layer is noted. Figure 2b depicts the influence of rotation on secondary velocity . The velocity in the secondary direction has declined for all the fluid types under consideration. The significant decline in velocities profiles is the direct relation of with the rotational angular velocity of flow. The change of mixed convection constraint on velocity profile is shown in Fig. 2c for all types of fluids considered in this comparative study. The velocity profile has a direct relation with mixed convection constraint as shown in this Fig. When mixed convection occurs, the buoyancy on free convection becomes significant. That’s why if the mixed convection constraint increases the buoyancy will increase and as a result, the velocity profiles will increase. The lower momentum boundary layer is noted for NF and higher for THNF. When the influence of the mixed convection parameter is compared with46, it is observed that a thinner momentum boundary layer is noted. Figure 2d,e show the effect of porosity constraint on velocity profile and respectively. Here also a similar trend is noted for NF, HNF, and THNF for a rise in porous medium parameters. The velocity profiles and decay as the permeability of the medium increases. This is due to the permeability of the stretchable surface. When the influence of the porosity parameter is compared with46, it is observed that a similar momentum boundary layer is noted. The effect of stretching ratio constraint on profiles and is presented in Fig. 2f,g. It can be observed that when the stretching rate in the y-direction raises the velocity profile declines and when the stretching rate increases along the x-axis, the velocity profile improves and the wide momentum boundary layer is observed for THNF.
Figure 2.
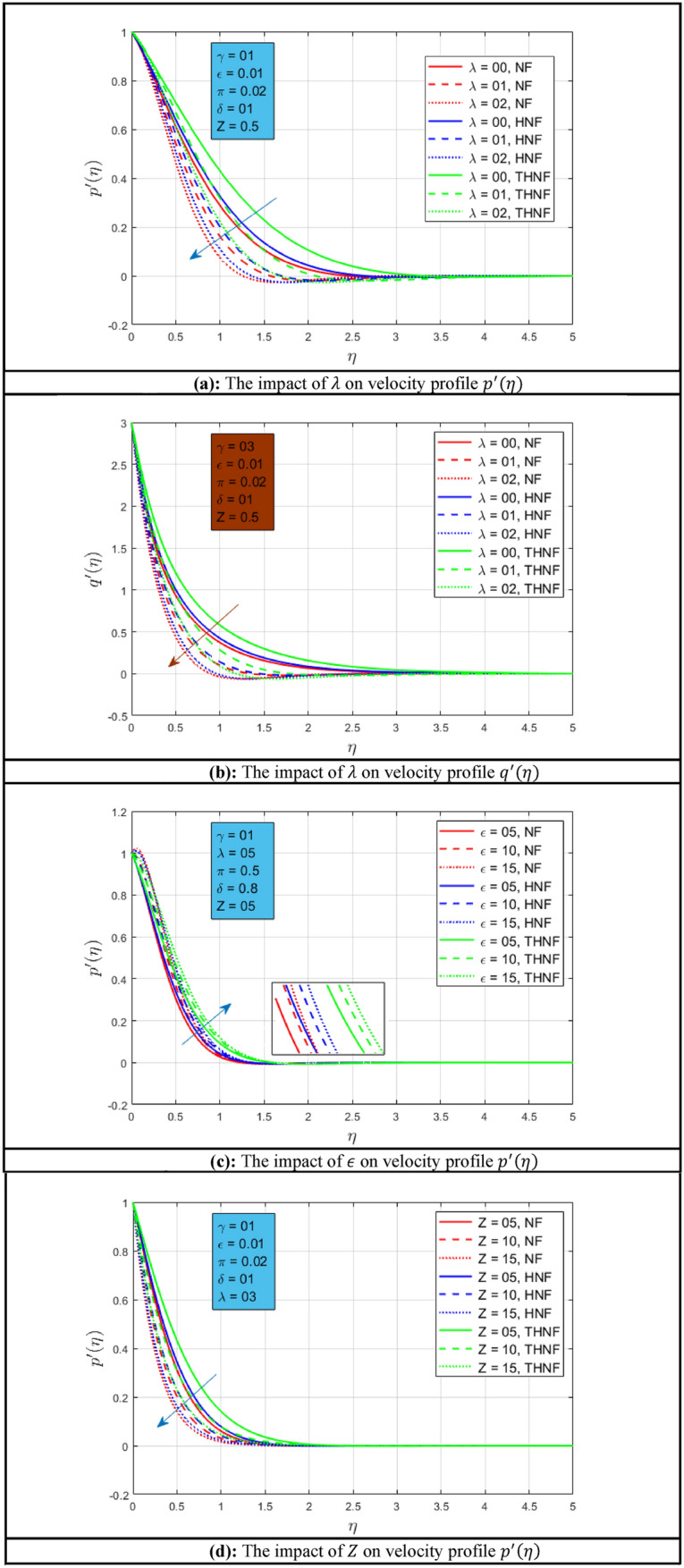
(a) The impact of on velocity profile . (b) The impact of on velocity profile . (c) The impact of on velocity profile . (d) The impact of on velocity profile . (e) The impact of Z on velocity profile . (f) The impact of on velocity profile . (g) The impact of on velocity profile .
Temperature profile
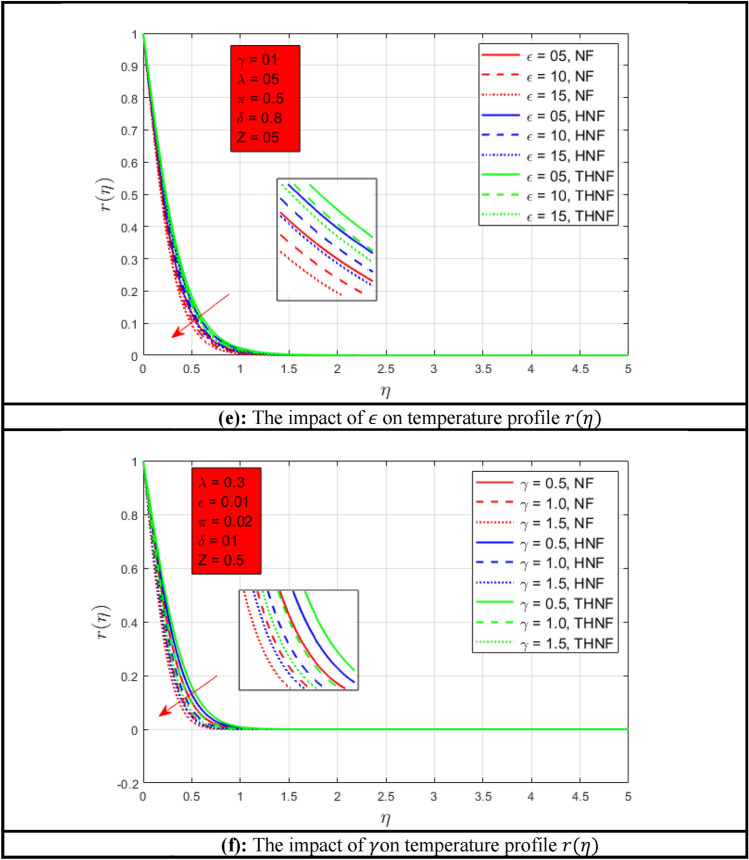
The following Figures show the influence of different parameters on temperature profile . Figure 3a shows the influence of rotation parameter on temperature profile . As the rotation of the NFs enhances the heat transfer rate of NF, HNF, and THNF increases. A higher rate of heat transmission is observed for THNF due to the combination of three nanoparticles. Comparatively, a thinner energy profile is noted when compared with46. The effect of Prandtl number on temperature profile is presented in Fig. 3b. The Prandtl number and temperature profile have inverse relations as depicted in Figure. Temperature profile decays as the Prandtl number increases for NF, HNF, and THNF nanofluid. However, a consistent thermal boundary layer is examined for THNF. The Prandtl number has a greater influence on energy profile as compared to46. Permeability effects on temperature profile are shown in Fig. 3c. When porosity of the stretchable surface improves, the heat transfer of all types of NFs increases because the fluid flow rate improves. Porosity has a huge difference between the present study and46. The change of radiation parameter is presented in Fig. 3d. It can be observed that when the radiation effect is zero, the thermal boundary layers a closer to each other for all types of nanofluids. Suddenly, when the radiation parameter increases the temperature boundary layers get closer due to resistance which does not allow the fluid to flow easily. As an outcome, the temperature profile reduces when the radiation parameter increases. Comparatively46 have a wider energy profile as associated with the present study. The impact of mixed convection constraint and stretching rate parameter is described in Fig. 3e,f respectively. As the mixed convection constraint increases the temperature profile decreases accordingly. The highest rate of heat transfer is observed for THNF. The effect of stretching surface parameter for temperature profile is represented in Fig. 3f. The higher stretching rate along the y-axis, x-axis, and the same stretching rate for NF, HNF, and THNF are presented. The consistent and higher temperature profile is observed for THNF as compared to other both NFs.
Figure 3.
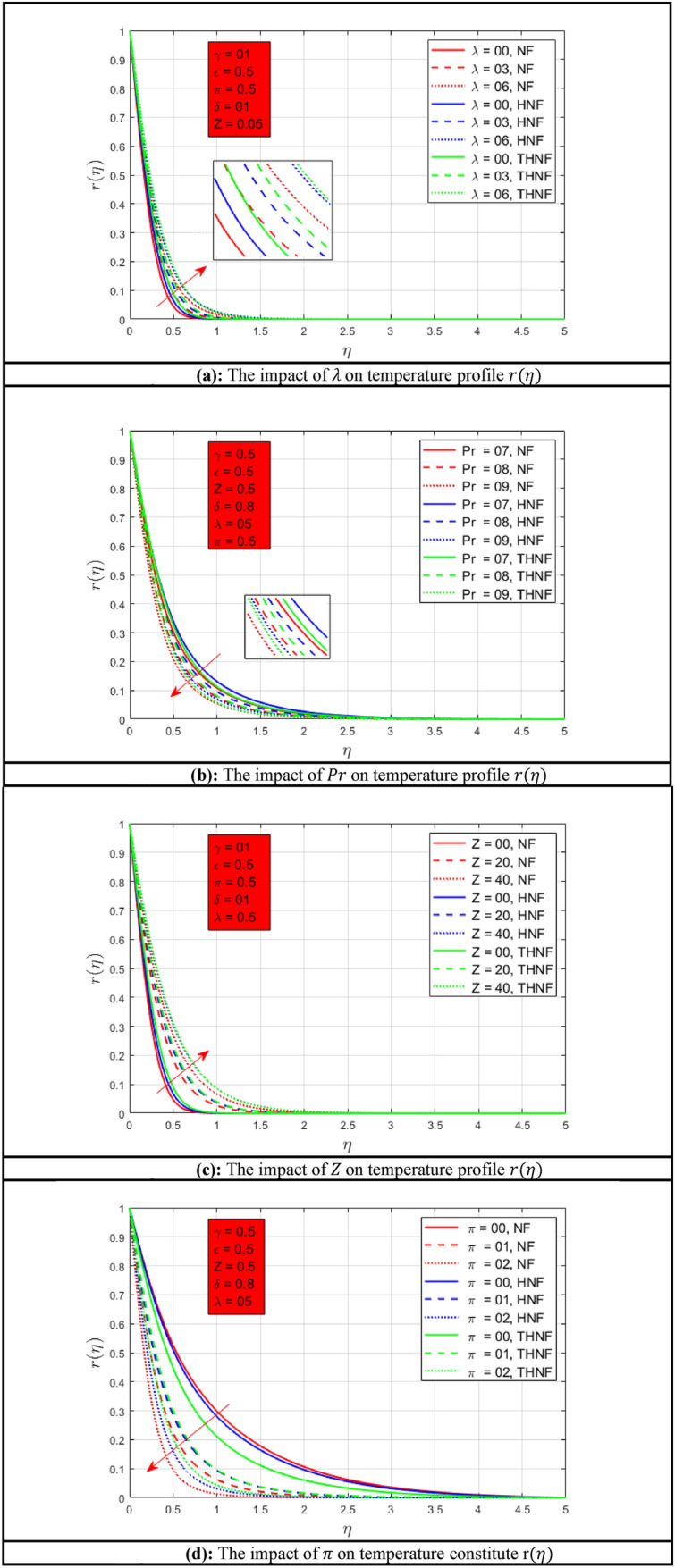
(a) The impact of on temperature profile . (b) The impact of on temperature profile . (c) The impact of on temperature profile . (d) The impact of on temperature constitute r. (e) The impact of on temperature profile . (f) The impact of on temperature profile .
Skin frictions and Nusselt number
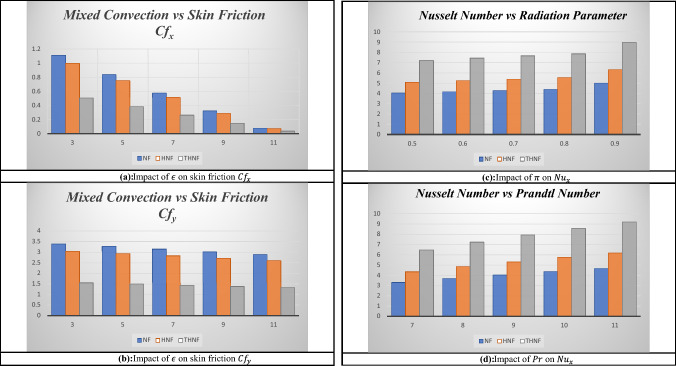
In this section, the solutions for skin frictions , , and Nusselt number are presented. The influence of mixed convection on skin friction along the x-axis and y-axis is presented in Fig. 4a,b. These figures show that the skin friction gradually decreases as the mixed convection parameter increases for NF, HNF, and THNF. Higher skin friction along the is observed as compared to the . Minimum resistance is noted for THNF. The influence of radiation constraint and Prandtl number is presented in Fig. 4c,d. A rise in radiation parameters increases the Nusselt number for all types of NFs. A higher change is observed for THNF in Fig. 4c. Figure 4d shows the influence of the Prandtl number on the Nusselt number for NF, HNF, and THNF. The highest Nusselt number for THNF is noted when the Prandtl number increases as compared to NF and HNF. Table 6 shows the numerical results of skin friction along the x-axis and the y-axis and Table 7 shows the numerical outcomes of the Nusselt number for NF, HNF, and THNF by changing the values of different constraints. In the absence of rotation, a maximum heat transfer rate and reduced skin friction are noted. Porosity has a direct relation with heat transfer and skin friction constants. Minimum skin friction and maximum Nusselt number are observed when the surface stretching rate along the y-axis is high as compared to the x-axis. As the mixed convection constraint increases the skin friction along both axis and the heat transfer rate increases. The thermal radiation and Prandtl number have the same relation with skin friction and the Nusselt number constant. They both increase by raising the values of thermal radiation and Prandtl number.
Figure 4.
(a) Impact of on skin friction . (b) Impact of on skin friction . (c) Impact of on . (d) Impact of on .
Table 6.
Numerical results of different parameters for skin frictions along x-axis and y-axis respectively.
| Z | for NF | for NF | for HNF | HNF | for THNF | for THNF | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.5 | 0.8 | 0.3 | 0.5 | 6.2 | − 1.6519 | − 0.70939 | − 1.3778 | − 0.596258 | − 0.575551 | − 0.253026 |
| 1.0 | − 1.07303 | − 1.97035 | − 0.898143 | − 1.64223 | − 0.378037 | − 0.684988 | |||||
| 2.0 | − 0.94837 | − 2.92488 | − 0.795099 | − 2.43386 | − 0.335846 | − 1.0117 | |||||
| 0.7 | 0.5 | 0.8 | 0.3 | 0.5 | 6.2 | − 1.1588 | − 1.61871 | − 0.969137 | − 1.35058 | − 0.407187 | − 0.564586 |
| 0.8 | − 1.31191 | − 1.69061 | − 1.09617 | − 1.41021 | − 0.459695 | − 0.589201 | |||||
| 1.0 | − 1.40886 | − 1.7388 | − 1.17662 | − 1.45018 | − 0.492948 | − 0.605703 | |||||
| 0.7 | 0.5 | 0.9 | 0.3 | 0.5 | 6.2 | − 1.10348 | − 1.75272 | − 0.922987 | − 1.46165 | − 0.387843 | − 0.610427 |
| 1.0 | − 1.04933 | − 1.89452 | − 0.877833 | − 1.57915 | − 0.368984 | − 0.658858 | |||||
| 1.1 | − 0.99663 | − 2.04558 | − 0.833897 | − 1.70435 | − 0.350649 | − 0.710478 | |||||
| 0.7 | 0.5 | 0.8 | 0.0 | 0.5 | 6.2 | − 1.23184 | − 1.68788 | − 1.02257 | − 1.40115 | − 0.423177 | − 0.579995 |
| 0.3 | − 1.15882 | − 1.61873 | − 0.96915 | − 1.35063 | − 0.407145 | − 0.564684 | |||||
| 0.6 | − 1.0864 | − 1.55002 | − 0.91613 | − 1.30039 | − 0.391188 | − 0.549428 | |||||
| 0.7 | 0.5 | 0.8 | 0.3 | 0.8 | 6.2 | − 1.16542 | − 1.62446 | − 0.972939 | − 1.3539 | − 0.407938 | − 0.565385 |
| 1.0 | − 1.16892 | − 1.62756 | − 0.975049 | − 1.35575 | − 0.408404 | − 0.565802 | |||||
| 1.2 | − 1.17191 | − 1.63023 | − 0.976906 | − 1.35739 | − 0.408829 | − 0.56618 | |||||
| 0.7 | 0.5 | 0.8 | 0.3 | 0.5 | 6.2 | − 1.15882 | − 1.61873 | − 0.96915 | − 1.35063 | − 0.407145 | − 0.564684 |
| 7.2 | − 1.16333 | − 1.62263 | − 0.972452 | − 1.35348 | − 0.408138 | − 0.565564 | |||||
| 8.2 | − 1.16746 | − 1.62626 | − 0.97547 | − 1.35612 | − 0.40904 | − 0.56638 |
Table 7.
Numerical outcomes of different parameters for Nusselt number .
| Z | for NF | for HNF | for THNF | |||||
|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.5 | 0.8 | 0.3 | 0.5 | 6.2 | 5.65765 | 6.83338 | 9.3672 |
| 1.0 | 5.49454 | 6.63341 | 9.13085 | |||||
| 2.0 | 5.27139 | 6.35964 | 8.81215 | |||||
| 0.7 | 0.5 | 0.8 | 0.3 | 0.5 | 6.2 | 5.56119 | 6.71513 | 9.22685 |
| 0.8 | 5.52006 | 6.66491 | 9.16575 | |||||
| 1.0 | 5.49329 | 6.6322 | 9.12599 | |||||
| 0.7 | 0.5 | 0.9 | 0.3 | 0.5 | 6.2 | 5.74435 | 6.9371 | 9.5261 |
| 1.0 | 5.91972 | 7.14956 | 9.81305 | |||||
| 1.1 | 6.08786 | 7.35321 | 10.0886 | |||||
| 0.7 | 0.5 | 0.8 | 0.0 | 0.5 | 6.2 | 5.54197 | 6.69438 | 9.20895 |
| 0.3 | 5.56118 | 6.7151 | 9.22679 | |||||
| 0.6 | 5.58889 | 6.73545 | 9.24443 | |||||
| 0.7 | 0.5 | 0.8 | 0.3 | 0.8 | 6.2 | 9.37348 | 10.1468 | 12.3225 |
| 1.0 | 9.96987 | 10.6638 | 12.7641 | |||||
| 1.2 | 10.5351 | 11.1587 | 13.1919 | |||||
| 0.7 | 0.5 | 0.8 | 0.3 | 0.5 | 6.2 | 5.56118 | 6.7151 | 9.22679 |
| 7.2 | 5.98464 | 7.2274 | 9.92313 | |||||
| 8.2 | 6.4251 | 7.7602 | 10.64739 |
Conclusions
In this investigation, the authors studied three-dimensional, rotating, incompressible, NF, HNF, and THNF above permeable stretchable surfaces for the heat transmission rate. The major implications are as follows:
The velocity profile declines with a rising in stretching ratio, rotation, and porosity parameters.
The velocity profile increases with a rise in the stretching ratio parameter while it decays with a rise in porosity and rotation.
The temperature profile declines by an increase in stretching ratio, radiation, Prandtl number, and mixed convection parameter while it rises by increasing the rotation and porous medium parameter.
The skin friction decays when mixed convection constraint increases and higher skin friction along the y-axis is noted when compared to the x-axis skin friction.
The Nusselt number increases by rising the radiation constraint and the Prandtl number increases. Nusselt numbers have increased by 50% in the case of tri-hybrid nanoparticles when compared with hybrid and mono particles.
Reduced skin friction and higher heat transfer rate are noted for triple nanoparticle nanofluid.
Future recommendations In the future, this study can be extended to discuss heat and mass transfer by selecting the mixed combination of solid NPs and oxide NPs by using different base fluids like ethylene glycol, engine oil, etc.
Acknowledgements
Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R443), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors express their gratitude to the Deanship of Scientific Research at King Khalid University for funding this work through the Large Research Group Project under grant number RGP.2-285-44. This study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2023/R/1444).
List of symbols
Angular speed
Specific heat
Volume fraction of nanoparticles
Similarity variable
Temperature
Skin frictions
Stretching rate along x and y axis
Prandtl number
Temperature profile
Heat flux
- bvp-4c
Boundary value problem
- R
Reynolds number
Gravitational acceleration
Stretching ratio parameter
Thermal conductivity
Nusselt number coefficient
Nanofluid
- , w
Velocity components in direction
- Z
Porosity parameter
Dimensionless velocity
Hybrid nanofluid
Trihybrid nanofluid
Kinematic viscosity
Dynamic viscosity
- ODE
Ordinary differential equation
- 3D
Three dimensional
Greek symbols
Temperature diffusivity
Rotational velocity
Density
Thermal radiation parameter
Shear stress
Mixed convection parameter
Author contributions
M.M.A.: Funding, Data curation, M.A., and F.M.A.: Conceptualization, Writing—Original draft preparation, Writing—Reviewing and Editing, L.A.A.-E.: Funding, visualization, Investigation, A.H. and A.M.S.: Formal Analysis, Methodology, S.M.E.: Software, Validation. Supervision, Q.H. and A.M.G.: Project Administration, Data Curation. All the authors reviewed the final version of the manuscript and agreed to submit it.
Data availability
All data generated or analyzed during this study are included in this published article.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Sakiadis BC. Boundary-layer behavior on continuous solid surfaces: I. Boundarylayer equations for two- dimensional and axisymmetric flow. AIChE J. 1961;7(1):26–28. [Google Scholar]
- 2.Erickson LE, Fan LT, Fox VG. Heat and mass transfer on moving continuous flat plate with suction or injection. Ind. Eng. Chem. Fundam. 1966;5(1):19–25. [Google Scholar]
- 3.Crane LJ. Flow past a stretching plate. Z. Angew. Math. Phys. 1970;21:645–647. [Google Scholar]
- 4.Chen TS, Strobel FA. Buoyancy effects in boundary layer adjacent to a continuous, moving horizontal flat plate. ASME J. Heat Transf. 1980;102:170–172. [Google Scholar]
- 5.Turkyilmazoglu M. Wall stretching in magnetohydrodynamics rotating flows in inertial and rotating frames. J. Thermophys. Heat Transf. 2011;25(4):606–613. [Google Scholar]
- 6.Takhar HS, Nath G. Unsteady three-dimensional flow due to a stretching flat surface. Mech. Res. Commun. 1996;23(3):325–333. [Google Scholar]
- 7.Arshad M, Hassan A, Haider Q, Alharbi FM, Alsubaie N, Alhushaybari A, et al. Rotating hybrid nanofluid flow with chemical reaction and thermal radiation between parallel plates. Nanomaterials. 2022;12(23):4177. doi: 10.3390/nano12234177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hussain A, Elkotb MA, Arshad M, Rehman A, Sooppy Nisar K, Hassan A, Saleel CA. Computational investigation of the combined impact of nonlinear radiation and magnetic field on three-dimensional rotational nanofluid flow across a stretchy surface. Processes. 2021;9(8):1453. [Google Scholar]
- 9.Arshad M, Karamti H, Awrejcewicz J, Grzelczyk D, Galal AM. Thermal transmission comparison of nanofluids over stretching surface under the influence of magnetic field. Micromachines. 2022;13(8):1296. doi: 10.3390/mi13081296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hassan A, Hussain A, Arshad M, Awrejcewicz J, Pawlowski W, Alharbi FM, Karamti H. Heat and mass transport analysis of MHD rotating hybrid nanofluids conveying silver and molybdenum di-sulfide nano-particles under effect of linear and non-linear radiation. Energies. 2022;15(17):6269. [Google Scholar]
- 11.Arshad M, Hussain A, Elfasakhany A, Gouadria S, Awrejcewicz J, Pawłowski W, et al. Magneto-hydrodynamic flow above exponentially stretchable surface with chemical reaction. Symmetry. 2022;14(8):1688. [Google Scholar]
- 12.Hady FM, Ibrahim FS, Abdel-Gaied SM, Eid MR. Radiation effect on viscous flow of a nanofluid and heat transfer over a nonlinearly stretching sheet. Nanoscale Res. Lett. 2012;7:1–13. doi: 10.1186/1556-276X-7-229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Susrutha B, Ram S, Tyagi AK. Effects of gold nanoparticles on rheology of nanofluids containing poly (vinylidene fluoride) molecules. J. Nanofluids. 2012;1(2):120–127. [Google Scholar]
- 14.Phule AD, Ram S, Tyagi AK. Anchoring silver with poly (vinylidene fluoride) molecules in model flocculates and its effects on rheology in stable nanofluids. J. Nanofluids. 2013;2(4):249–260. [Google Scholar]
- 15.Behera M, Ram S. Mechanism of solubilizing fullerene C60 in presence of poly (vinyl pyrrolidone) molecules in water. Fuller. Nanotub. Carbon Nanostruct. 2015;23(10):906–916. [Google Scholar]
- 16.Behera M, Ram S. Poly (vinyl pyrrolidone) mediated solubilization and stabilization of fullerene C60 in the form of nanofluid in an alcoholic medium. Fuller. Nanotub. Carbon Nanostruct. 2015;23(12):1064–1072. [Google Scholar]
- 17.Behera M, Ram S. Variation of optical properties, rheology, and microstructure in fullerene/poly (vinyl pyrrolidone) nanofluids with fullerene content in n-butanol. Fuller. Nanotub. Carbon Nanostruct. 2016;24(2):154–161. [Google Scholar]
- 18.Behera M, Ram S. Strongly optical absorptive nanofluids and rheology in bonded fullerene C60 via poly (vinyl pyrrolidone) molecules in water. Fuller. Nanotub. Carbon Nanostruct. 2017;25(3):143–150. [Google Scholar]
- 19.Behera M, Ram S. Intense quenching of fluorescence intensity of poly (vinyl pyrrolidone) molecules in presence of gold nanoparticles. Appl. Nanosci. 2013;3:543–548. [Google Scholar]
- 20.Singh, G. P. & Ram, S. Magnetic nanofluids: Synthesis and applications. In Nanofluids, Research, Development and Applications (Nova Publisher, 2013).
- 21.Ghasemi SE, Mohsenian S, Gouran S, Zolfagharian A. A novel spectral relaxation approach for nanofluid flow past a stretching surface in presence of magnetic field and nonlinear radiation. Results Phys. 2022;32:105141. [Google Scholar]
- 22.Arshad M, Hassan A. A numerical study on the hybrid nanofluid flow between a permeable rotating system. Eur. Phys. J. Plus. 2022;137(10):1126. [Google Scholar]
- 23.Nasir S, Berrouk AS, Aamir A, Gul T. Significance of chemical reactions and entropy on Darcy–Forchheimer flow of H2O and C2H6O2 convening magnetized nanoparticles. Int. J. Thermofluids. 2023;17:100265. [Google Scholar]
- 24.Hassan A, Hussain A, Fernandez-Gamiz U, Arshad M, Karamti H, Awrejcewicz J, et al. Computational investigation of magneto-hydrodynamic flow of Newtonian fluid behavior over obstacles placed in rectangular cavity. Alex. Eng. J. 2023;65:163–188. [Google Scholar]
- 25.Nasir S, Berrouk AS, Tassaddiq A, Aamir A, Akkurt N, Gul T. Impact of entropy analysis and radiation on transportation of MHD advance nanofluid in porous surface using Darcy–Forchheimer model. Chem. Phys. Lett. 2023;811:140221. [Google Scholar]
- 26.Mehmood A, Ali A. Analytic solution of three-dimensional viscous flow and heat transfer over a stretching flat surface by homotopy analysis method. J. Heat Transf. 2008;130(12):121701. [Google Scholar]
- 27.Hussain A, Arshad M, Rehman A, Hassan A, Elagan SK, Ahmad H, Ishan A. Three-dimensional water-based magneto-hydrodynamic rotating nanofluid flow over a linear extending sheet and heat transport analysis: A numerical approach. Energies. 2021;14(16):5133. [Google Scholar]
- 28.Shah Z, Ullah A. Ferrofluid treatment with insertion of electric field inside a porous cavity considering forced convection. Waves Random Complex Media. 2023;1:19. doi: 10.1080/17455030.2023.2169386. [DOI] [Google Scholar]
- 29.Dadheech PK, Agrawal P, Purohit SD, Kumar D. Study of flow and heat transfer of CuO−Ag/C2H6O2 hybrid nanofluid over a stretching surface with porous media and MHD effect. Sci. Technol. Asia. 2021;26:174–181. [Google Scholar]
- 30.Dadheech PK, Agrawal P, Sharma A, Nisar KS, Purohit SD. Transportation of Al2O3–SiO2–TiO2 modified nanofluid over an exponentially stretching surface with inclined magnetohydrodynamic. Therm. Sci. 2021;25(Spec. issue 2):279–285. [Google Scholar]
- 31.Shah Z, Rooman M, Shutaywi M. Computational analysis of radiative engine oil-based Prandtl–Eyring hybrid nanofluid flow with variable heat transfer using the Cattaneo–Christov heat flux model. RSC Adv. 2023;13(6):3552–3560. doi: 10.1039/d2ra08197k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sheikholeslami M, Ganji DD, Javed MY, Ellahi R. Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model. J. Magn. Magn. Mater. 2015;374:36–43. [Google Scholar]
- 33.Safdar R, Jawad M, Hussain S, Imran M, Akgül A, Jamshed W. Thermal radiative mixed convection flow of MHD Maxwell nanofluid: Implementation of Buongiorno's model. Chin. J. Phys. 2022;77:1465–1478. [Google Scholar]
- 34.Asghar A, Chandio AF, Shah Z, Vrinceanu N, Deebani W, Shutaywi M, Lund LA. Magnetized mixed convection hybrid nanofluid with effect of heat generation/absorption and velocity slip condition. Heliyon. 2023;9(2):e13189. doi: 10.1016/j.heliyon.2023.e13189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Jawad M, Mebarek-Oudina F, Vaidya H, Prashar P. Influence of bioconvection and thermal radiation on MHD Williamson nano Casson fluid flow with the swimming of gyrotactic microorganisms due to porous stretching sheet. J. Nanofluids. 2022;11(4):500–509. [Google Scholar]
- 36.Jawad M, Hameed MK, Majeed A, Nisar KS. Arrhenius energy and heat transport activates effect on gyrotactic microorganism flowing in Maxwell bio-nanofluid with Nield boundary conditions. Case Stud. Therm. Eng. 2023;41:102574. [Google Scholar]
- 37.Jawad M, Shehzad K, Safdar R. Novel computational study on MHD flow of nanofluid flow with gyrotactic microorganism due to porous stretching sheet. Punjab Univ. J. Math. 2021;52(12):43–60. [Google Scholar]
- 38.Safdar R, Gulzar I, Jawad M, Jamshed W, Shahzad F, Eid MR. Buoyancy force and Arrhenius energy impacts on Buongiorno electromagnetic nanofluid flow containing gyrotactic microorganism. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2022;236(17):9459–9471. [Google Scholar]
- 39.Majeed A, Zeeshan A, Jawad M. Double stratification impact on radiative MHD flow of nanofluid toward a stretchable cylinder under thermophoresis and Brownian motion with multiple slip. Int. J. Mod. Phys. B. 2023 doi: 10.1142/S0217979223502326. [DOI] [Google Scholar]
- 40.Jawad M, Hameed MK, Nisar KS, Majeed AH. Darcy–Forchheimer flow of Maxwell nanofluid flow over a porous stretching sheet with Arrhenius activation energy and Nield boundary conditions. Case Stud. Therm. Eng. 2023;44:102830. [Google Scholar]
- 41.Majeed A, Zeeshan A, Jawad M, Alhodaly MS. Influence of melting heat transfer and chemical reaction on the flow of non-Newtonian nanofluid with Brownian motion: Advancement in mechanical engineering. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022 doi: 10.1177/09544089221145527. [DOI] [Google Scholar]
- 42.Tang TQ, Rooman M, Shah Z, Jan MA, Vrinceanu N, Racheriu M. Computational study and characteristics of magnetized gold-blood Oldroyd-B nanofluid flow and heat transfer in stenosis narrow arteries. J. Magn. Magn. Mater. 2023;569:170448. [Google Scholar]
- 43.Farooq U, Waqas H, Makki R, Ali MR, Alhushaybari A, Muhammad T, Imran M. Computation of Cattaneo–Christov heat and mass flux model in Williamson nanofluid flow with bioconvection and thermal radiation through a vertical slender cylinder. Case Stud. Therm. Eng. 2023;42:102736. [Google Scholar]
- 44.Hayat T, Qasim M, Mesloub S. MHD flow and heat transfer over permeable stretching sheet with slip conditions. Int. J. Numer. Meth. Fluids. 2011;66(8):963–975. [Google Scholar]
- 45.Arshad M, Alharbi FM, Alhushaybari A, Eldin SM, Ahmad Z, Galal AM. Exploration of heat and mass transfer subjected to first order chemical reaction and thermal radiation: Comparative dynamics of nano, hybrid and tri-hybrid particles over dual stretching surface. Int. Commun. Heat Mass Transf. 2023;146:106916. [Google Scholar]
- 46.Li S, Khan MI, Alzahrani F, Eldin SM. Heat and mass transport analysis in radiative time dependent flow in the presence of Ohmic heating and chemical reaction, viscous dissipation: An entropy modeling. Case Stud. Therm. Eng. 2023;42:102722. [Google Scholar]
- 47.Bafakeeh OT, Raghunath K, Ali F, Khalid M, Tag-ElDin ESM, Oreijah M, et al. Hall current and Soret effects on unsteady MHD rotating flow of second-grade fluid through porous media under the influences of thermal radiation and chemical reactions. Catalysts. 2022;12(10):1233. [Google Scholar]
- 48.Abbasi A, Farooq W, Tag-ElDin ESM, Khan SU, Khan MI, Guedri K, et al. Heat transport exploration for hybrid nanoparticle (Cu, Fe3O4): Based blood flow via tapered complex wavy curved channel with slip features. Micromachines. 2022;13(9):1415. doi: 10.3390/mi13091415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Shah SAGA, Hassan A, Karamti H, Alhushaybari A, Eldin SM, Galal AM. Effect of thermal radiation on convective heat transfer in MHD boundary layer Carreau fluid with chemical reaction. Sci. Rep. 2023;13(1):4117. doi: 10.1038/s41598-023-31151-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wong KV, De Leon O. Applications of nanofluids: Current and future. Adv. Mech. Eng. 2010;2:519659. [Google Scholar]
- 51.Das S, Jana RN. Natural convective magneto-nanofluid flow and radiative heat transfer past a moving vertical plate. Alex. Eng. J. 2015;54(1):55–64. [Google Scholar]
- 52.Guedri K, Khan A, Gul T, Mukhtar S, Alghamdi W, Yassen MF, Tag Eldin E. Thermally dissipative flow and entropy analysis for electromagnetic trihybrid nanofluid flow past a stretching surface. ACS Omega. 2022;7(37):33432–33442. doi: 10.1021/acsomega.2c04047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Wang CY. Stretching a surface in a rotating fluid. Z. Angew. Math. Phys. 1988;39(2):177–185. [Google Scholar]
- 54.Arshad M, Alharbi FM, Hassan A, Haider Q, Alhushaybari A, Eldin SM, et al. Effect of inclined magnetic field on radiative heat and mass transfer in chemically reactive hybrid nanofluid flow due to dual stretching. Sci. Rep. 2023;13(1):7828. doi: 10.1038/s41598-023-34871-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Nazar R, Amin N, Pop I. Unsteady boundary layer flow due to a stretching surface in a rotating fluid. Mech. Res. Commun. 2004;31(1):121–128. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data generated or analyzed during this study are included in this published article.