MOCSS: Multi-omics data clustering and cancer subtyping via shared and specific representation learning

Summary

Cancer is an extremely complex disease and each type of cancer usually has several different subtypes. Multi-omics data can provide more comprehensive biological information for identifying and discovering cancer subtypes. However, existing unsupervised cancer subtyping methods cannot effectively learn comprehensive shared and specific information of multi-omics data. Therefore, a novel method is proposed based on shared and specific representation learning. For each omics data, two autoencoders are applied to extract shared and specific information, respectively. To reduce redundancy and mutual interference, orthogonality constraint is introduced to separate shared and specific information. In addition, contrastive learning is applied to align the shared information and strengthen their consistency. Finally, the obtained shared and specific information for all samples are used for clustering tasks to achieve cancer subtyping. Experimental results demonstrate that the proposed method can effectively capture shared and specific information of multi-omics data and outperform other state-of-the-art methods on cancer subtyping.

Graphical abstract

Highlights

• •Obtain shared information and specific information from multi-omics data
• •Apply contrastive learning to align representations of shared information
• •The proposed method has a stronger capability for molecular subtyping of cancer

Biocomputational method; Cancer systems biology; Cancer; Omics

Introduction

Cancer is an extremely complex genomic disease. Each type of cancer will show changes in molecular biology or genes at different stages of development which result in differences in invasion ability and drug sensitivity. Due to the significant heterogeneity of cancer, it is necessary to formulate specific clinical treatment options and prognosis for different patients. Therefore, it is of great significance to accurately identify cancer subtypes, which can provide patients with precise treatment¹ and develop new treatment strategies.²

At present, the identification of cancer subtypes has shifted from traditional morphological subtyping to molecular subtyping which is more precise. Most previous cancer subtyping methods only used single-omics data, and studied a certain level of biomolecular changes. However, different levels of molecules are related to each other in reprogramming cellular function.^3,4,5 As a result, any research limited to a certain molecular level is not enough to understand the complex pathogenesis of cancer and is difficult to meet the need for accurate molecular subtyping of cancer. With the rapid development of high-throughput biotechnology, it has become more and more feasible to obtain stable, reliable, and large-scale multi-omics data from cancer patients. International collaborative projects, such as The Cancer Genome Atlas (TCGA)⁶ and the International Cancer Genome Consortium (ICGC)⁷ have collected a large amount of multi-omics data from different cancer patients. Multi-omics data can provide a more macro perspective for understanding, recognizing, and identifying cancer subtypes. This is because biological data at different levels collectively influence and modulate multiple biological processes, providing more comprehensive and reliable information for cancer formation and development. Comprehensive and integrated molecular subtyping can identify molecular relationships among multiple cancers, which provides a new direction for exploring the clinical feasibility of cancer therapy.⁸

How to realize cancer molecular subtyping by integrating multi-omics data has become an appealing research problem in recent years. Although the acquisition of multi-omics data has been relatively easy, obtaining the ground-truth label of cancer subtypes is still difficult and costly. Therefore, multi-omics clustering methods are often used in the study of cancer molecular subtyping. Currently, many multi-omics data clustering methods have been developed, which can be roughly divided into five categories: multi-kernel learning, matrix factorization, dimensionality reduction, network-based methods and deep learning.^{9,10,11,12,13}

Methods based on multi-kernel learning aim to learn a convex combination of kernel functions for each omics data, exploiting comprehensive multi-omics information for better clustering performance.^14,15 However, these methods often have a large overhead in optimization and memory when facing a large-size dataset. Matrix factorization methods perform joint matrix factorization of different omics data, with the goal of finding a shared low-rank matrix in the latent space. Especially methods based on non-negative matrix factorization, such as MultiNMF,¹⁶ iNMF,¹⁷ and jNMF,¹⁸ have attracted extensive attention due to their flexible interpretability. However, since the objective function of non-negative matrix factorization is not convex, it may lead to local optimal solutions. Methods based on dimensionality reduction include CCA¹⁹ and MCCA.²⁰ CCA linearly projects two omics data to a lower dimension and maximizes their correlation, while MCCA extends CCA with more than two omics. Such CCA-based methods can only calculate linear correlations while multi-omics data may be non-linearly correlated. Network-based methods construct a similarity network for each multi-omics data and then integrate them into a single one for clustering. This category of methods is most widely used in cancer subtyping. Representative methods that use this approach include SNF,²¹ ANF,²² NEMO,²³ CIMLR,²⁴ MCSM,²⁵ DeFusion²⁶ and MDICC.²⁷ But network-based methods have the problem of inaccurate similarity measurement when constructing the interaction network, which easily leads to poor clustering performance. Deep learning methods utilize multiple neural networks to train multi-omics data for obtaining latent representations, which are somehow integrated and fed into downstream clustering tasks.^{28,29,30,31,32,33,34} It should be noted that the above-mentioned methods may belong to more than one category at the same time.

Although some deep learning methods have been applied for cancer subtyping, they have not paid attention to the shared and specific information in multi-omics data at the same time, ignoring the complementarity and consistency. Multi-omics data, such as multi-view data and multi-modal data in other fields, are multi-source data. They are descriptions of the same sample from different perspectives or levels. Multiple different omics data could form a complete biological signal flow, and provide complementary and common information. The information contained in multi-omics data can be divided into the following two categories: consistent information (inter-omics shared information) and unique information (intra-omics specific information). In order to fully mine and utilize the shared and specific information in multi-omics data, we propose a novel method for multi-omics data clustering and cancer subtyping via shared and specific representation learning (MOCSS). For each omics data, the method applies two autoencoders (AEs) to extract shared and specific information, respectively. To reduce redundancy and mutual interference, orthogonality constraint is introduced to separate shared and specific information. In addition, contrastive learning is applied to align the shared information extracted from different omics data in subspace and strengthen their consistency. Through the above process, a unified form of representation is learned for each sample, which contains inter-omics shared information and intra-omics specific information. Finally, the representation matrix of all samples is fed into the downstream clustering task, and the K-means clustering algorithm is applied to obtain the cluster label assigned to each sample, which represents its cancer subtype.

The key contributions of this study include the following three points:

The model proposed in this study can effectively obtain inter-omics shared information and intra-omics specific information from multi-omics data, and reduce the redundancy and mutual interference among them; The representations of shared information in multi-omics data are aligned in subspaces by using contrastive learning to enforce consistency; Experimental results show that the proposed model has better clustering performance and effectively achieves cancer subtyping, which is superior to other state-of-the-art methods.

Results

Datasets

To evaluate the performance of our proposed method, we choose five publicly available cancer multi-omics datasets for experimental analysis, including BRCA, GBM, LUAD, SARC, and STAD. These datasets all include the following three types of omics data: mRNA expression, miRNA expression, and DNA methylation. The above datasets are obtained from MOGONET³⁵ or downloaded from TCGA, and the data are preprocessed using the method mentioned in.³⁶ It should be noted that in SARC, because the number of samples of the two subtypes (MPNST: 5, SS: 10) is far less than that of other subtypes, we only uses the remaining four subtypes for experimental analysis. The details of five datasets are summarized in Table 1. In order to eliminate the influence of different value ranges of multi-omics data, it is necessary to normalize the original data first. We use Min-Max Normalization to map the original data to the range of [0, 1], which is defined as follows:

$$X^{\ast }=\frac{X-\mathit{min}}{\mathit{max}-\mathit{min}}$$

where $X$ represents the original single omics data. $\mathit{max}$ and $\mathit{min}$ are the maximum and minimum values in the original omics data, and $X^{\ast }$ denotes the normalized data.

Table 1.

Details of the datasets used in the experiments

Dataset	mRNA expression	miRNA expression	DNA methylation	Samples	Subtypes
BRCA	1000	1000	503	875	5
GBM	6000	534	5000	272	4
LUAD	6000	554	6000	144	3
SARC	6000	820	5000	191	4
STAD	6000	519	6000	198	4

Evaluation metrics and empirical setting

To evaluate the clustering performance of our method, we use three evaluation metrics: Normalized Mutual Information ($NMI)$, Adjusted Rand Index ($ARI)$ and Accuracy ($ACC)$. A larger value of them indicates a better clustering result.

NMI is a typical metric to evaluate the consistency between the obtained cluster labels and ground-truth labels of the sample. NMI is defined as:

$$NMI\left(Y,\hat{Y}\right)=\frac{2\times I\left(Y;\hat{Y}\right)}{H\left(Y\right)+H\left(\hat{Y}\right)}$$

where $Y$ and $\hat{Y}$ are the ground-truth labels and cluster labels, respectively. $I(·)$ is the mutual information, and $H(·)$ represents the entropy. The value range of NMI is [0, 1].

ARI is a widely used metric to measure the concordance between two clustering results. ARI is defined as:

$$ARI=\frac{2\times \left(TP·TN-FN·FP\right)}{\left(TP+FN\right)\left(FN+TN\right)+\left(TP+FP\right)\left(FP+TN\right)}$$

where $TP$ represents the number of true positive samples, and $TN$ represents the number of true negative samples in the prediction. $FN$ represents the number of false negative samples, and $FP$ represents the number of false positive samples in the prediction. The value range of ARI is [0, 1].

ACC is used to compare the match between the obtained cluster labels and the ground-truth labels, which is defined as:

$$ACC=\frac{{\sum }_{i=1}^N\delta \left(y_i,map\left({\hat{y}}_i\right)\right)}{N}$$

where $y_i$ and ${\hat{y}}_i$ denote the ground-truth labels and cluster labels, respectively. $N$ is the number of samples, and $map(·)$ denotes the permutation mapping function, which can generally be done by the Hungarian Algorithm. $\delta (·)$ represents an indicator function, which is defined as follows:

$$\delta \left(x,y\right)=\{\begin{array}{c}1ifx=y\\ 0otherwise\end{array}$$

The hyperparameters in MOCSS include the layers of AE network $l$, the training batch size $M$, the representation dimension $d_z$, and the temperature parameter $\tau$. The hyperparameter settings are shown in Table 2.

Table 2.

Hyperparameters of the MOCSS model

Hyperparameters	Setting
Layers of autoencoder network($l$)	$\left\{\mathrm{5,7,9,11,13}\right\}$
Training batch size($M$)	$\left\{\mathrm{32,64,128,256}\right\}$
Dimension($d_z$)	$\left\{\mathrm{32,64,128,256}\right\}$
Temperature parameter($\tau$)	$\left[\mathrm{0,1}\right]$

Comparison with state-of-the-art clustering methods

To evaluate the clustering performance of our model, we compared MOCSS with the following six state-of-the-art clustering methods for multi-omics data integration in comparative experiments.

SNF constructs a sample-sample similarity network for each omics data and updates them iteratively through a message-passing process to make these networks become more and more similar. NEMO constructs a similarity network between samples for each omics data, and then modifies the similarity to relative similarity (RS), thus improving comparability between omics. It integrates different omics data by averaging relative similarity in different similarity networks. DeFusion introduces a denoised network regularization to uncover a consistent latent representation among multi-omics data by capturing noise and data-specific patterns in the error term. MDICC constructs an affinity network for each omics data and uses a sparse subspace learning framework to reduce noise interference and fuse multi-omics data. Subtype-GAN proposes a deep adversarial learning approach based on the multiple-input multiple-output neural network to model the complex omics data accurately. Subtype-DCC proposes an end-to-end multi-omics clustering approach using decoupled contrastive learning to identify cancer subtypes. The above methods perform clustering algorithms on the obtained fusion network or latent representation matrix to realize cancer subtyping.

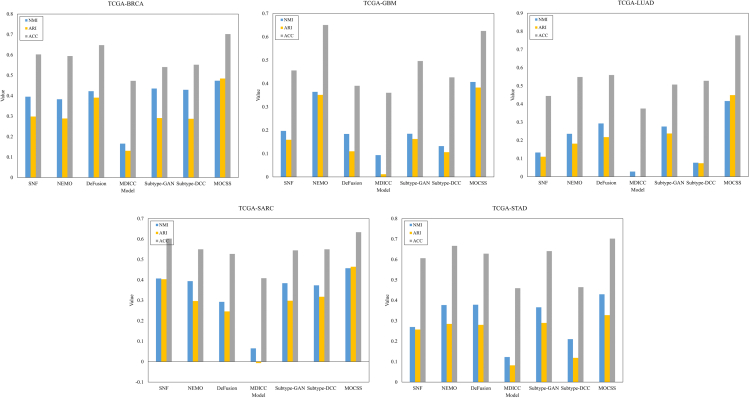
It is worth mentioning that all of the above methods except Subtype-DCC are two-stage multi-omics clustering methods. The hyperparameter settings for these models are chosen from the values recommended in the relevant papers. In this part, we set the representation dimension $d_z=128$, the layers of network $l=9$, and the temperature parameter $\tau =0.4$. The experimental results are shown in Figure 1. It can be seen that our model achieves the best performance in most metrics of all datasets. This illustrates that MOCSS has shown an excellent ability to identify cancer subtypes in multiple datasets. The above four comparison methods all involve calculating the similarity between different samples, which has higher requirements on the similarity measure function. Since multi-omics data are often high-dimensional and noisy, the similarity networks obtained in the above four methods may be difficult to accurately describe the real relationship between samples, which greatly affects their performance. Since our proposed model takes advantage of the powerful feature learning ability of neural networks, it can not only obtain high-quality representations, but also learn complementary and consistent information from multi-omics data. Therefore, MOCSS can exploit and utilize the information of multi-omics data more effectively than the network-based methods.

Figure 1.

Clustering performance of different models on five datasets

Parameters study

To illustrate the impact of hyperparameters on model performance, we conducted parameter-tuning experiments. Since the sample size of the BRCA dataset is the largest, we conduct experiments on this dataset.

Figure 2A shows the effect of different values of $M$ on the model performance. In this part, the values of $M$ are taken in the range of $\left\{32,62,128,256\right\}$ and the rest of the hyperparameters are set to $d_z=128$, $l=$ 9, $\tau =0.4$. According to the results, the model’s performance increases and then decreases as the training batch becomes larger, and all metrics achieves optimal values when $M=128$. The reason may be that when the training batch is appropriately increased, more negative samples are provided for the anchor samples in contrastive learning, which is helpful for the learning of representations. However, when continuing to increase the training batch, too many negative samples may cause some hard samples that are originally of the same category as the anchor samples to be farther away in the latent space. This will result in that these hard samples may be assigned wrong cluster labels.

Figure 2.

The impact of hyperparameters on the performance of MOCSS

(A) The impact of the training batch size $M$ on the clustering performance of MOCSS for the BRCA dataset.

(B) The impact of the dimension $d_z$ on the clustering performance of MOCSS for the BRCA dataset.

(C) The impact of the number of layers $l$ on the clustering performance of MOCSS for the BRCA dataset.

(D) The impact of the temperature τ on the clustering performance of MOCSS for the BRCA dataset.

Figure 2B demonstrates the impact of representations of different dimensions on clustering performance. We set the representation dimension $d_z=\left\{32,62,128,256\right\}$, $M=128$, $l=$ 9, $\tau =0.4$ . When the dimension of representation increases in a certain range, the more adequate information it can express. When $d_z=128$, the model reach the highest value among the three metrics, and the dimension size at this time is enough to represent the comprehensive information of the sample. When the dimension continues to increase, it may lead to noise and redundancy, resulting in a decrease in the clustering performance.

Figure 2C shows the impact of AEs with different numbers of layers on the clustering performance. In this part, we set the layers $l=\left\{5,7,9,11,13\right\}$, $M=128$, $d_z=128$, $\tau =$ 0.4. When the number of layers $l=9$, the model performance reaches the optimal value among the three metrics. As the number of network layers increases, the learning ability of the model and the quality of the representation gradually improve. However, when $l$ continues to increase, the parameters that the model needs to train are also increasing. Limited by the number of samples, model training may be difficult to converge, resulting in a significant drop in clustering performance.

Figure 2D shows the effect of different τ. We set $\tau =\left\{0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0\right\}$, $M=128,d_z=128$, $l=$ 9. When the temperature parameter $\tau$ = 0.4, the model performs best. The temperature parameter is able to adjust the attention to hard samples. As the value of $\tau$ increases, the model can better retain the learned latent semantic structure, which facilitates the performance of downstream clustering task. However, when $\tau$ continues to increase, the model ignores the learning of hard samples, and some hard samples that are not in the same class as the anchor samples cannot be distinguished, which leads to them being assigned the wrong cluster labels. Therefore, when $\tau =0.4$, our model achieves a better balance in terms of attention to hard samples.

Ablation study

To verify the validity of each component in MOCSS, we conduct ablation study to illustrate the effect of AEs, orthogonality loss, and nonlinear projection function in contrastive learning on model performance. The results are illustrated in Table 3.

Table 3.

Ablation study results

$AE$	$Orthogonality$ $Constraint$	$Projection$$function$	$NMI$	$ARI$	$ACC$
×	✓	✓	0.4094	0.3519	0.6229
✓	×	✓	0.4722	0.4770	0.6857
✓	✓	×	0.4634	0.4679	0.6823
✓	✓	✓	0.4737	0.4845	0.7017

AEs are employed in MOCSS to obtain a robust initial representation for each sample. In the ablation experiments, we use deep neural networks with the same number of layers as the encoder to complete the representation extraction instead of the AEs. The performance of using AEs for feature extraction is obviously better than that using DNN network. This is due to the ability of the AE to reconstruct the original data and learn a high-quality representation by minimizing the loss between the reconstructed data and the original data.

We introduce orthogonality constraint in the model to separate the shared and specific information. We compared the impact of using orthogonality constraint or not on the model’s clustering performance. It’s clear that the model shows better performance when using orthogonality loss. This is because when the orthogonality constraint is not used, the two types of information may be redundant and pollute each other, which affects the performance of the model to a certain extent.

Furthermore, we apply a two-layer nonlinear projection function in instance-level contrastive learning. We investigate the importance of non-linear projection function. It can be found that nonlinear projection function can improve the clustering performance. This is due to the loss of information caused by contrastive learning, which removes information that may be useful for downstream clustering task. By using the nonlinear projection function $f(·)$, more useful information can be formed and maintained in the representation $z_{c,i}^v$.

Visualization

As shown in Figure 3, Umap³⁷ is used to visualize the trained representations of the above five datasets in a 2-dimensional space. It can be observed that the labeled points from the same category are relatively concentrated in the five datasets, and the clusters of different categories can be better distinguished. This validates the representation capability and clustering performance of our model. For the GBM dataset, there is one class (marked in red) that cannot be clearly distinguished from the other three classes. According to investigation, it is found that the subtype labels of GBM may have some errors. Recent studies suggest that GBM should be classified into three subtypes instead of the four subtypes labeled by TCGA.³⁸

Figure 3.

Umap visualization of five cancer datasets

Survival analysis

To validate the effect of prognostic prediction of the model on different cancer subtypes, five cancer datasets from TCGA⁶ are used for survival analysis experiments, including BRCA-sur, BLCA-sur, LUAD-sur, LUSC-sur, and SKCM-sur. The reason for choosing these five datasets is that they have a large number of samples and the experimental results could be more accurate. Since the original feature dimensions of three omics in the five cancer datasets differ greatly, we also use the method in³⁶ for data preprocessing. The details of these datasets are shown in Table 4.

Table 4.

Details of the datasets used in the survival analysis

Dataset	mRNA expression	miRNA expression	DNA methylation	Samples
${BRCA}_{-sur}$	6000	513	6000	506
${BLCA}_{-sur}$	6000	549	6000	333
${LUAD}_{-sur}$	6000	554	6000	310
${LUSC}_{-sur}$	6000	878	5000	343
${SKCM}_{-sur}$	6000	901	5000	438

We applied MOCSS and the other four state-of-the-art methods on these five datasets and calculated Cox proportional risk regression P-values. Specifically, we selected three different cluster numbers (3/4/5) for each dataset, and calculated the P-value of each method under different clusters. Statistical significance was determined using $-{\mathit{log}}_{10}P$-$value$ from the log rank test. The results are shown in Table 5. It can be seen that MOCSS has a relatively high $-{\mathit{log}}_{10}P$-$value$ in most of the results, which means that MOCSS shows a stronger ability to detect cancer subtypes than the other four methods. Although NEMO on the SKCM-sur dataset (cluster = 4) had the most significant $-{\mathit{log}}_{10}P$-$value$ (6.64) among the six comparing methods, $-{\mathit{log}}_{10}P$-$value$ obtained by MOCSS also reached a higher level (5.66). It is worth mentioning that the number of cancer subtypes in both BRCA-sur and LUAD-sur datasets is generally considered to be definitive (BRCA-sur: 5; LUAD-sur: 3).³⁸ MOCSS achieved the highest $-{\mathit{log}}_{10}P$-$value$ under these two subtype settings, which further confirms that MOCSS has a strong ability to detect cancer subtypes and can be used as an effective tool for cancer molecular subtyping. In addition, using LUAD as an example, we plot the survival curves of all methods. The results are shown in Figure 4. Obviously, the differentiation between different cancer subtypes identified by MOCSS is the highest, showing the best ability to identify cancer subtypes. When the number of cancer subtypes is set to 3, there is a clear survival difference between subtype 0 (marked in blue) and the other two subtypes (marked in red and black). This means that patients with this subtype face a higher risk and may need to be focused on in clinical treatment.

Table 5.

Survival analysis on the five datasets using MOCSS and other methods

Dataset	SNF	NEMO	DeFusion	MDICC	Subtype-GAN	SubtypeDCC	MOCSS
${BRCA}_{-sur}$ (3)	1.08	1.04	1.79	0.08	1.72	0.33	0.25
(4)	1.03	1.23	1.19	0.03	1.23	0.72	1.31
(5)	0.26	0.57	1.33	0.02	0.84	1.36	1.83
${BLCA}_{-sur}$ (3)	2.54	2.04	3.38	1.18	1.81	0.11	2.38
(4)	2.08	1.74	2.85	0.98	1.58	1.57	3.47
(5)	2.01	1.44	1.00	1.74	1.61	2.87	3.45
${LUAD}_{-sur}$ (3)	0.28	0.83	0.48	0.37	0.05	0.86	2.76
(4)	1.16	1.76	0.07	0.28	0.21	0.45	2.56
(5)	0.06	0.74	0.38	0.20	0.31	0.19	1.90
${LUSC}_{-sur}$ (3)	1.23	1.46	0.65	0.45	1.09	0.66	1.07
(4)	1.24	1.23	1.08	0.43	1.44	0.44	1.75
(5)	1.61	0.74	0.98	0.07	1.21	1.23	1.89
${SKCM}_{-sur}$ (3)	1.55	1.33	2.17	0.61	2.12	0.32	2.18
(4)	1.06	6.64	2.35	0.48	3.64	0.77	5.66
(5)	2.56	4.07	3.25	0.72	3.98	0.22	4.30

Statistical significance was determined using −log10P-values from the log-rank test. Three different dataset clusters were formed; the cluster number is in parentheses. The best results are in boldface. Suboptimal results are underlined.

Figure 4.

Survival curves obtained using MOCSS and four state-of-the-art methods on the LUAD-sur dataset

Case study

Since LUAD is one of the most common types of lung cancer, we use LUAD-sur dataset as an example in the following analysis. In fact, each of omics data exhibits a distinct molecular pattern across the three different molecular subtypes of LUAD. As shown in Figure 5A, we present a heatmap of features among these subtypes. Specifically, we selected and demonstrated features whose Normalized Mutual Information (NMI) values are ranked in the top 50 of all NMI values across all feature types. Notably, each subtype showed distinct mRNA expression, miRNA expression, and DNA methylation profiles, with a particularly evident signature difference observed between subtype 1 and subtype 3. The results indicate that these three subtypes may involve distinct molecular mechanisms. Furthermore, these features have the potential to serve as reliable biomarkers for distinguishing different LUAD subtypes.

Figure 5.

Patterns across the three different molecular subtypes of LUAD

(A) Heatmap of features significantly differential among LUAD subtypes that are identified by using MOCSS.

(B–E) Survival analysis of the association between the expression levels of important features and overall survival time in LUAD. Patients were classified in three different categories according to mRNA expression of important features.

(F) Distribution of stage at diagnosis across three subtype groups.

(G) Distribution of the number of packs smoked each year across three subtype groups.

To bolster the credibility of these putative molecular biomarkers, we studied the biological contextualization in some cases. Among the top 5 important features of mRNA expression, four genes (SLC14A2, TTK, KIAA1524 and CENPA) are shown as potential biomarkers in LUAD according to previous researches.^{39,40,41,42,43,44} As shown in Figures 5B–5E, the four genes also significantly affect the prognosis of patients with LUAD. Furthermore, the contribution of deregulated miRNAs to the pathogenesis of LUAD has been studied in recent years, and some miRNAs have been shown to carry potential diagnostic and prognostic values. Among the top 5 important features of miRNA expression in this study, four miRNAs (hsa-miR-4746-5p, hsa-miR-375-3p, hsa-miR-4709-3p and hsa-miR-196b-5p) were found associated with LUAD aggressiveness and prognosis in LUAD according to previous researches.^45,46 Collectively, these features may serve as diagnostic and prognostic markers for LUAD.

Moreover, we also found associations between the subtypes and clinical variables. The pathologic stage combines the results of both the clinical staging (physical exam, imaging test) with surgical results. It estimates the extent of the cancer, where stage IV is the most serious condition. Tumors in subtype 3 tend to be diagnosed at more advanced stages (IV) (Figure 5F). For the number of packs smoked each year, the patients with subtype 3 obviously have more smoking (Figure 5G). These results hint a correlation between smoking and the severity of LUAD. It has been established that smoking plays a significant role in the initiation and progression of LUAD.^47,48,49,50

Discussion

In this study, we propose a deep learning-based multi-omics clustering method for molecular subtyping of cancer. The proposed MOCSS can effectively mine and utilize consistent information and unique information in multi-omics data. We extract inter-omics shared information and intra-omics specific information from each omics. Contrastive learning is applied to align the shared information between different omics and reinforce their consistency. In addition, the orthogonality constraint can effectively separate the two types of information and reduce their redundancy and mutual interference. MOCSS finally learns complete representations for each sample, which contain more comprehensive information and can better distinguish different classes of samples.

We conducted a series of experiments on 10 cancer datasets. Experimental results demonstrate that MOCSS exhibits better clustering performance than the currently available state-of-the-art multi-omics clustering methods. We show the representations learned by MOCSS in a low-dimensional space using visualization technique. It is obviously that the representations learned on five datasets have a better distribution of clusters and the samples of each category are differentiable. At the same time, the results of survival analysis also support our conclusions. MOCSS can distinguish biologically meaningful clusters. In addition, we perform the case study to give the significant biomarkers of each subtype and found associations between the subtypes and clinical variables.

Overall, our proposed MOCSS is able to adapt to a wide range of omics data and serve as an effective tool for molecular subtyping of cancer.

Conclusion

Currently, deep learning (DL) has achieved impressive success in the field of bioinformatics due to its excellent feature representation ability and high learning capability. DL-based clustering methods for multi-omics data have emerged as a powerful tool for cancer subtyping. In this study, we propose a novel method for multi-omics data clustering and cancer subtyping via shared and specific representation learning (MOCSS). It applies multiple AEs to extract inter-omics shared information and intra-omics specific information, then uses instance-level contrastive learning to reinforce the consistency of shared information across omics. In addition, to avoid redundancy and mutual contamination between the two types of information, we introduce an orthogonality constraint to separate shared and specific information. MOCSS learns the effective clustering information of the samples and improves the accuracy of unsupervised cancer subtyping. The superiority of the model was demonstrated by conducting several comparative experiments on five different cancer datasets. Meanwhile, we conducted the ablation study to demonstrate the effectiveness of introducing various constraints and components. We also further validated the ability of the model to distinguish between different cancer subtypes through visualization.

Although MOCSS has relatively good performance in cancer subtyping, our work still faces some challenges. First, due to the lack of ground-truth labels for cancer subtypes in unsupervised learning, we do not select appropriate negative samples or positive samples when applying contrastive learning, which may limit the clustering performance. It would be beneficial to introduce high-quality pseudo-labels to further improve the model performance. It is also important to mention that our model is a two-stage clustering model. The downstream clustering information can be used to guide the learning of the representation for end-to-end training, which may be beneficial to improve clustering performance.

In conclusion, MOSCC based on DL effectively exploits the consistency and complementarity in multi-omics data and can be used as an unsupervised model for the identification of cancer subtypes. Performing cancer subtyping on existing multi-omics data will facilitate precise diagnosis and prognostic stratification of patients with cancer.

Limitations of the study

The sample size of different cancers from TCGA is different, as an example, the sample size of LUAD is smaller than those of other cancer datasets, which may lead to statistical bias. In BRCA, based on gene expression profiling criteria, there may be ambiguity in the classification of Luminal A and Luminal B so that Luminal A and Luminal B subtypes are difficult to distinguish. In addition, the significant prognostic markers identified by MOCSS need to be further investigated to further verify the impact on LUAD.

STAR★Methods

Key resources table

REAGENT and RESOURCE	SOURCE	IDENTIFIER
Deposited data
TCGA cancer program	The Cancer Genome Atlas Program (TCGA) - NCI	https://github.com/ChenyuxinXMU/MOCSS/dataset
Software and algorithms
Python 3.7.11	Python	https://www.python.org
Numpy 1.21.2	Numpy	https://numpy.org
Pytorch 1.10.1	Pytorch	https://pytorch.org
Scikit-learn 1.0.2	scikit-learn: machine learning in Python	https://scikit-learn.org
MOCSS	MOCSS	https://github.com/ChenyuxinXMU/MOCSS

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Zhongnan Zhang (zhongnan_zhang@xmu.edu.cn).

Materials availability

This study did not generate new unique materials.

Method details

Problem definition

A cancer multi-omics dataset is denoted as $X=\left\{X^1,X^2,\dots ,X^V\right\}$, where $V$ represents the number of omics. $X^v=\left\{x_1^v,x_2^v,\dots ,x_N^v\right\}\in R^{N\times d_v}$ represents the $v$-th omics data with $N$ samples, each with $d_v$-dimensional features. $Y=\left\{y_1,y_2,\dots ,y_N\right\}$ is denoted as the ground-truth label set of $N$ samples, where $y_i$ represents the ground-truth label of the $i$-th $\left(1\le i\le N\right)$ sample $x_i$, that is, the cancer subtype. There are $K$ cancer subtypes in all $N$ samples, so $y_i\in \left\{\mathrm{1,2},\dots ,K\right\}$. Based on the given multi-omics data set $X$, a clustering algorithm is applied to obtain the corresponding cluster label set $\hat{Y}=\left\{{\hat{y}}_1,{\hat{y}}_2,\dots ,{\hat{y}}_N\right\}$, where ${\hat{y}}_i$ represents the cluster label assigned to the $i$-th $\left(1\le i\le N\right)$ sample, that is, the cancer subtype predicted by the proposed model. Our goal is to predict the labels of all $N$ samples as accurately as possible, so that the predicted labels in $\hat{Y}$ are more consistent with the corresponding ground-truth labels in $Y$.

Method overview

The cancer subtyping method proposed in this study is a two-stage method. The first stage is based on shared and specific representation learning, which aims to learn a unified form of representation for each sample. First, we employ two AEs for each omics data to extract shared and specific information, respectively, and then apply instance-level contrastive learning to enforce the consistency of shared information among different omics data. At the same time, the orthogonality constraint is applied to separate these two types of information, and finally the representation of each sample is output. The second stage is to perform the K-means clustering algorithm on the learned representation matrix of all samples and assign cluster labels for each sample to realize cancer subtyping. The overview of MOCSS is shown in Figure S1.

Shared and specific representation learning

Multi-omics data and multi-view data belong to multi-source data, and they are essentially descriptions of the same sample from different perspectives. We learn from the shared and specific representation learning in multi-view learning to achieve the multi-omics data fusion learning. Figure S2 shows the basic idea of shared and specific representation learning based on two views.

The purpose of multi-view learning is to enable the model to achieve better performance in downstream tasks by effectively exploiting the comprehensive information contained in multiple views. Previously, most methods can be roughly divided into two categories: joint representation learning and aligned representation learning. The former method applies single-view learning method on each view for dimensionality reduction, and then concatenates the representations learned from all views. This kind of methods only learns complementary information from each view. In addition, simply concatenating all representations is not interpretable and prone to the dimensional disaster. Aligned representation learning assumes that there is a low-dimensional subspace shared by multiple views. This kind of methods only considers the consistency of multi-view data, which may lose some specific information that are beneficial for reconstructing each view. For multi-view data in the real world, it is not enough just to consider consistency or complementarity. Therefore, neither of the above two kind of methods can learn comprehensive information for samples.

To solve the above problem, shared and specific representation learning is proposed as a novel multi-view learning architecture: Such method aims to effectively exploit and utilize complementary and consistent information from different views. Complementary information is also named specific information, which represents the unique information of each view itself. Consistent information is also named shared information, which are some common properties among different views. In addition, the shared information learned from different views should be consistent with each other. This kind of methods first utilizes multiple networks to extract shared and specific information from each view, and then aligns all shared information of different views. Finally, the specific information of each views and the consistency information they shared are fused into a complete representation of all samples.

Representation initialization

In order to extract shared and specific information from multi-omics data, two AEs are employed to extract corresponding features for each omics data. Each omics has its individual encoder so that to fit the specific size of input data. Specifically, for the $v$-th omics dataset $X^v$, the encoders $E_c^v$ and $E_s^v$ learn the representations $z_{c,i}^v$ and $z_{s,i}^v$ of sample $x_i^v\left(1\le i\le N\right)$, respectively. $z_{c,i}^v$ and $z_{s,i}^v$ represent the shared information and the specific information of $x_i^v$ respectively, denoted as:

$$z_{c,i}^v=E_c^v\left(x_i^v\right)$$ (Equation 1)

$$z_{s,i}^v=E_s^v\left(x_i^v\right)$$ (Equation 2)

For the representations $z_{c,i}^v$ and $z_{s,i}^v$, decoders $D_c^v$ and $D_s^v$ reconstruct the data sample respectively and obtain ${\tilde{x}}_{c,i}^v$ and ${\tilde{x}}_{s,i}^v$. Each omics has a corresponding decoder to reconstruct the data. The structure of the decoder is the opposite of the encoder. The reconstruction process of ${\tilde{x}}_{c,i}^v$ and ${\tilde{x}}_{s,i}^v$ are denoted as:

$${\tilde{x}}_{c,i}^v=D_c^v\left(z_{c,i}^v\right)$$ (Equation 3)

$${\tilde{x}}_{c,i}^v=D_c^v\left(z_{c,i}^v\right)$$ (Equation 4)

According to the above equations, the corresponding reconstruction loss $L_{rec}$ of multi-omics data in each training batch can be denoted as:

$$L_{rec}=\sum _{v=1}^V\sum _{i=1}^M{\Vert x_i^v-{\tilde{x}}_{c,i}^v\Vert }_2^2+\sum _{v=1}^V\sum _{i=1}^M{\Vert x_i^v-{\tilde{x}}_{s,i}^v\Vert }_2^2$$ (Equation 5)

where $M$ represents the number of samples in each training batch.

Instance-level contrastive learning

The shared information of different omics obtained in the previous step often lacks consistency. Therefore, we need to align the extracted representations ${\left\{z_{c,i}^v\right\}}_{v=1}^V$ from $V$ omics data. In previous studies, most methods utilize adversarial training for alignment, which discriminate the distribution of each shared information by training a generative adversarial network (GAN). When the discriminator is unable to distinguish differences between shared information from different omics, it is considered that these shared information are sufficiently similar.⁵¹ However, GAN is often difficult to train and thus prone to model crashes, which cannot be improved well even with longer training time. In addition, since adversarial alignment only considers the representation distributions, a given cluster from one omics might be aligned with a different cluster from another omics.

To overcome the shortcomings of adversarial training, new alignment methods are needed to reinforce the consistency of shared information and contrastive learning has made impressive achievements in unsupervised representation learning.^52,53 The basic idea of contrastive learning is that in the feature learning process, the distance between positive pairs is brought closer, while the distance between negative pairs is drawn farther apart. Contrastive learning learns the representation by comparing a given anchor sample with its corresponding positive and negative samples in subspace. In Figure S3, we take two omics data as an example to illustrate the basic idea of unsupervised instance-level contrastive learning. In instance-level contrastive learning, the consistency between different augmented instances of the same sample is maximized for representation learning to address the problem of adversarial learning in representation alignment.^53,54 This provides a new idea for the alignment of shared information in multi-omics. Therefore, we perform instance-level contrastive learning instead of adversarial learning to achieve the alignment of shared information.

If contrastive learning is directly applied to $z_{c,i}^v$, it may lead to information loss,⁵³ which could make against downstream tasks. Therefore, instead of using $z_{c,i}^v$ directly, we apply a two-layer nonlinear projection function $f(·)$ to map $z_{c,i}^v$ to $h_{c,i}^v$ so that to preserve more useful information in $z_{c,i}^v$, that is:

$$h_{c,i}^v=f\left(z_{c,i}^v\right)$$ (Equation 6)

Since the ground-truth labels are unknown in unsupervised learning, for a given sample, we cannot accurately distinguish its positive samples and negative samples. It is necessary to define the positive and negative samples in instance-level contrastive learning first. We define ${\left\{x_i^v\right\}}_{v=1}^V$ as different instances of the $i$-th $\left(1\le i\le N\right)$ sample. Assuming that there are $M$ samples in each training batch, any two omics data $X^v$ and $X^u\left(u\ne v\right)$ include $2\ast M$ instances. For a given instance $x_i^v$ in $X^v$, the corresponding instance $x_i^u$ in $X^u$ is considered as a positive sample, while the remaining $\left(2\ast M-2\right)$ instances are considered as negative samples. The cosine similarity $Sim\left(\right)$ measures the similarity of two instances:

$$Sim\left(h_{c,i}^v,h_{c,j}^u\right)=\frac{{h_{c,i}^v}^T·h_{c,j}^u}{\Vert h_{c,i}^v\Vert ·\Vert h_{c,j}^u\Vert }$$ (Equation 7)

where $i,j\in \left\{\mathrm{1,2},\dots ,M\right\}$, $v,u\in \left\{\mathrm{1,2},\dots ,V\right\}$.

To complete the instance-level contrastive learning, we introduce the $NT$-$Xent$ loss for these $2\ast M$ instances. For an instance $x_i^v$, its contrastive loss $l_i^{v,u}$ in omics $v$ and $u$ is denoted as:

$$l_i^{v,u}=-\log \frac{\mathit{exp}\left(Sim\left(h_{c,i}^v,h_{c,i}^u\right)/\tau \right)}{{\sum }_{j=1,j\ne i}^M\mathit{exp}\left(Sim\left(h_{c,i}^v,h_{c,j}^v\right)/\tau \right)+{\sum }_{j=1}^M\mathit{exp}\left(Sim\left(h_{c,i}^v,h_{c,j}^u\right)/\tau \right)}$$ (Equation 8)

where $i,j\in \left\{\mathrm{1,2},\dots ,M\right\}$, $v,u\in \left\{\mathrm{1,2},\dots ,V\right\}$, M denotes the number of samples in the training batch, and $\tau$ is the temperature parameter to control the softness.

In clustering tasks, hard samples are defined as samples with high similarity to a given anchor sample. Contrastive loss is a hardness-aware loss function, and the temperature τ play a role in controlling attention on hard samples. Lower temperature focuses more on separating hard samples which are similar to anchor samples, and thus tend to result in generating more uniform representations. However, there are many hard samples, such as different instances belonging to the same category, which are actually potential positive samples. If paying excessive attention to distinguish hard samples, it may break the semantic structure of the embedding distribution. An appropriate temperature should be a compromise to balance uniformity and tolerance.⁵⁵

For omics $v$ and $u$, the contrastive loss $L_{con}^{v,u}$ for all instances is:

$$L_{con}^{v,u}=\frac{1}{2\mathrm{M}}\sum _{i=1}^M\left(l_i^{v,u}+l_i^{u,v}\right)$$ (Equation 9)

If more than two omics are available, the above formula is applied between the two omics and summed. Therefore, we can obtain the contrastive loss function $L_{con}$ of multi-omics:

$$L_{con}=\sum _{v=1}^{V-1}\sum _{u=v+1}^V{L}_{con}^{v,u}$$ (Equation 10)

By minimizing the contrastive loss $L_{con}$, the shared information between different omics will have high cosine similarity to achieve representation alignment. At the same time, contrastive learning will make the distribution of clusters among different omics data as consistent as possible, which enables the omics data with better original cluster distribution to guide the learning of other omics.

Separation of shared and specific information

The shared and specific information extracted by the AEs are not automatically separated, and they may be redundant and pollute each other, which affects the purity of the information. Therefore, orthogonality constraint is applied to separate these two types of information. Suppose $C^v$ and $S^v$ represents the shared and specific information matrix composed of the shared representation ${\left\{z_{c,i}^v\right\}}_{i=1}^N$ and specific representation ${\left\{z_{s,i}^v\right\}}_{i=1}^N$ , which are extracted from the $v$-th omics. Applying the orthogonality constraint on $C^v$ and $S^v$ to obtain the corresponding orthogonality loss $L_{ort}$, denoted as:

$$L_{ort}=\sum _{v=1}^V{\Vert {{C^v}^{T}S}^v\Vert }_F^2$$

$$C^v={\left[z_{c,1}^v,z_{c,2}^v,\dots ,z_{c,n}^v\right]}^T$$ (Equation 11)

$$S^v={\left[z_{s,1}^v,z_{s,2}^v,\dots ,z_{s,n}^v\right]}^T$$

where ${\Vert ·\Vert }_F^2$ is the squared Frobenius norm.

Accordingly, the total loss function $L$ of MOCSS is formulated as:

$$L=L_{rec}+L_{con}+L_{ort}$$ (Equation 12)

Algorithm 1 Summarizes the process of shared and specific representation learning.

Algorithm 1: Shared and Specific Representation Learning

Input: Multi-omics dataset $X=\left\{X^1,X^2,\dots ,X^V\right\}$, number of clusters $K$, batch size $M$, temperature parameter $\tau$ 1:Normalization 2:Initialize the parameters of autoencoders and projection head $f(·)$ 3:While not reaching the maximum epoch $T$ do 4: randomly select M samples from $X^v$ 5: generate shared and specific representation from eachomic using $Eq.\left(1\right)$-$\left(4\right)$ 6: compute reconstruction loss $L_{rec}$ by $Eq.\left(5\right)$ 7: compute contrastive loss $L_{con}$ by $Eq.\left(6\right)$-$\left(10\right)$ 8: compute orthogonality loss $L_{ort}$ by $Eq.\left(11\right)$ 9: compute overall loss $L$ and updata entire network by $Eq.\left(12\right)$ 10: generate the shared information matrix $C^v$ and specific information matrix $S^v$ for all samples 11:End while Output: Shared information matrix $C^v$ and specific information matrix $S^v$

Sample clustering

When the model is trained, for a given sample $x_i$, the shared information $Z_{c,i}={\left\{z_{c,i}^v\right\}}_{v=1}^V$ and specific information ${Z_{s,i}=\left\{z_{s,i}^v\right\}}_{v=1}^V$ are obtained from $V$ omics data. Since the shared information of different omics is highly similar after contrastive learning, we only use the average $z_{c,i}$ in final representation:

$$z_{c,i}=\frac{1}{V}\sum _{v=1}^V{z}_{c,i}^v$$ (Equation 13)

Finally, we concatenate $z_{c,i}$ and specific information ${\left\{z_{s,i}^v\right\}}_{v=1}^V$ from all omics to represent the sample $x_i$, denoted as:

$$z_i=z_{c,i}\parallel z_{s,i}^1\parallel z_{s,i}^2\parallel \dots \parallel z_{s,i}^V$$ (Equation 14)

Therefore, the representation matrix $Z$ of all samples is:

$$Z={\left[z_1,z_2,\dots ,z_n\right]}^T$$ (Equation 15)

The K-means clustering algorithm is applied on $Z$ to separate all samples into $K$ clusters, and each cluster represents a cancer subtype so that to realize the unsupervised cancer subtyping.

Quantification and statistical analysis

All statistical analyses were performed in Python version 3.7.11. The details of data filtering, network structure and hyperparameters setting have been indicated in the respective method details. The datasets are used for repetitive experiments and the selected features and the methodology is repeatable, the details have been included in the previous sections.

Published: July 13, 2023

Data and code availability

• •The datasets used in this study have been deposited in github at https://github.com/ChenyuxinXMU/MOCSS/dataset.
• •All original code have been deposited in github at https://github.com/ChenyuxinXMU/MOCSS.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.