Abstract
Purpose:
To develop a single-shot multi-slice T1 mapping method by combing simultaneous multi-slice (SMS) excitations, single-shot inversion-recovery (IR) radial fast low-angle shot (FLASH) and a nonlinear model-based reconstruction method.
Methods:
SMS excitations are combined with a single-shot IR radial FLASH sequence for data acquisition. A previously developed single-slice calibrationless model-based reconstruction is extended to SMS, formulating the estimation of parameter maps and coil sensitivities from all slices as a single nonlinear inverse problem. Joint-sparsity constraints are further applied to the parameter maps to improve T1 precision. Validations of the proposed method are performed for a phantom and for the human brain and liver in six healthy adult subjects.
Results:
Phantom results confirm good T1 accuracy and precision of the simultaneously acquired multi-slice T1 maps in comparison to single-slice references. In-vivo human brain studies demonstrate the better performance of SMS acquisitions compared to the conventional spoke-interleaved multi-slice acquisition using model-based reconstruction. Apart from good accuracy and precision, the results of six healthy subjects in both brain and abdominal studies confirm good repeatability between scan and re-scans. The proposed method can simultaneously acquire T1 maps for five slices of a human brain (0.75 × 0.75 × 5 mm3) or three slices of the abdomen (1.25 × 1.25 × 6 mm3) within four seconds.
Conclusion:
The IR SMS radial FLASH acquisition together with a non-linear model-based reconstruction enable rapid high-resolution multi-slice T1 mapping with good accuracy, precision, and repeatability.
Keywords: simultaneous multi-slice, model-based reconstruction, T1 mapping, radial FLASH
Introduction
Quantitative mapping of MR relaxation times such as T1 finds increasing applications in a variety of clinical use cases [1, 2]. Mapping of T1 relaxation time commonly relies on the inversion-recovery (IR) Look-Locker sequence where RF excitations are continuously applied after inversion followed by computation of a T1 map in a postprocessing step [3–5]. While efficient, the conventional IR Look-Locker method may still require segmented data acquisitions with multiple inversions [4, 5]. As a sufficient delay is necessary between inversions, these techniques still suffer from long measurement time. Most recently, advances in sequence development such as non-Cartesian sampling together with state-of-the-art reconstruction techniques have enabled faster parameter mapping [6–13], including accelerated T1 mapping within a single inversion recovery [14–16]. These methods usually consist of two steps: First, reconstruction of contrast-weighted images from undersampled datasets and, second, subsequent voxel-by-voxel fitting of the T1 map. In contrast, nonlinear model-based reconstruction methods [6, 17–26] estimate parameter maps directly from k-space, completely bypassing the intermediate step of image reconstruction and voxel-by-voxel fitting. Moreover, a priori information such as sparsity constraints can be applied to the parameter maps to improve precision [6, 20, 22, 25].
So far, most of the above efforts have focused on the acceleration of single-slice parameter mapping. However, in clinical applications, multi-slice parameter mapping is highly desirable. For example, it has been recommended to perform myocardial T1 mapping in at least three short-axis sections to capture potential heterogeneity across the left ventricular wall [27, 28]. Methods exploiting the conventional multi-slice acquisition strategy have been reported [29–32]. On the other hand, the simultaneous multi-slice (SMS) technique [33] is a promising way to accelerate multi-slice quantitative MRI. SMS allows for the distribution of undersampling along the additional slice dimension and exploits sensitivity encoding in all three spatial dimensions. Applications of SMS in quantitative MRI include but are not limited to simultaneous three-slice MR fingerprinting [34], simultaneous three-slice cardiac T1 mapping [28] based on the SAPPHIRE technique and simultaneous multi-slice T2 mapping using the Cartesian multi-echo spin-echo sequence with a model-based iterative reconstruction [35].
To further enable fast T1 mapping of multiple slices, in this work, we aim to combine simultaneous multi-slice excitations and single-shot IR radial FLASH with a nonlinear model-based reconstruction to enable multi-slice T1 mapping within a single inversion recovery. In particular, we first combine SMS excitation with the single-shot IR radial FLASH sequence using a golden-angle readout. Next, we extend a previously developed single-slice calibrationless model-based reconstruction to SMS, formulating the estimation of parameter maps and coil sensitivities from all slices as a single nonlinear inverse problem. In this way, no additional coil-calibration steps are needed. Further, joint-sparsity constraints are applied on the parameter maps to improve T1 precision. Performance of the proposed method is validated first on an experimental phantom and then on human brain and liver studies of six healthy adult subjects.
Methods
Sequence Design
The sequence starts with a non-selective adiabatic inversion pulse, followed by a radial FLASH readout using continuous SMS excitations and a tiny golden angle between successive spokes (≈ 23.63°) [36]. In the partition dimension, radial spokes can be designed to follow an aligned or non-aligned distribution as shown in Figure 1. The aligned scenario allows decoupling of SMS data using an inverse Fourier transform along the partition dimension, followed by independent reconstruction of each slice. In such a way, there is still the SNR benefit of a SMS acquisition over the spoke-interleaved multi-slice scheme. However, the main advantage of SMS - acceleration in the direction perpendicular to the slices - only comes into play when distinct k-space samples are acquired in each partition [37, 38]. Figure 1 (bottom) depicts the latter case, where a larger k-space coverage could be achieved within a given readout time. In this work, we applied the tiny golden angle (≈ 23.63°) sampling in the partition dimension as well. Accordingly, throughout this manuscript, we adopt the terms ”SMS aligned” and ”SMS golden-angle” to refer to the two SMS acquisition strategies, respectively. To reconstruct images/parameter maps in the latter SMS golden-angle acquisition scheme, conventional slice-by-slice reconstruction can not be used. A more general SMS model-based reconstruction method is therefore developed, which is explained in the following.
Figure 1.
Single-shot IR radial multi-slice data acquisition schemes. (Top) Conventional spoke-interleaved multi-slice acquisition scheme. (Middle and bottom) Radial SMS with spokes distributed following aligned and golden-angle distribution in the partition dimension, respectively. Note that the longitudinal axis represents slice direction for the conventional spoke-interleaved multi-slice scheme and the partition dimension for the SMS acquisitions. For a certain slice, the SMS golden-angle acquisition scheme could cover more k-space within a given readout time after inversion.
SMS Model-based Reconstruction
Following a similar notation introduced in [38], we define as the partition index and the slice index, respectively, where is the total number of partitions/slices. In SMS acquisitions, the signal from the partition can be written as
| (1) |
where is an SMS encoding matrix. In this study, it is chosen as the Fourier matrix, i.e., . The signal for the slice of the coil is given by
| (2) |
where is the corresponding coil sensitivity map, is the position in image space, and is the chosen k-space trajectory. is the relaxation model for the slice at the inversion time :
| (3) |
where is defined as the center of each acquisition window. , and are the steady-state signal, equilibrium signal and effective relaxation rate, respectively. After estimation of , values of the slice can be calculated by [3,4,30]:, with the delay between inversion and the start of data acquisition, which is around 15 ms for the sequence used in this study. To estimate parameter maps and coil sensitivity maps from all slices, equations (1) and (2) are understood as a nonlinear inverse problem with a nonlinear operator , mapping all the unknowns from all slices to the measured undersampled SMS data :
| (4) |
| (5) |
Here is the sampling operator for the given k-space trajectory and is the two dimensional Fourier transform. represents a set of coil sensitivity maps for the slice. is the relaxation model described in Equation (3). The unknowns are with , which are then estimated by solving the following regularized nonlinear inverse problem:
| (6) |
with the joint -Wavelet regularization in the parameter dimension [25] and the Sobolev norm [39] enforcing the smoothness of coil sensitivity maps. and and , and are the regularization parameters for the parameter and coil-sensitivity maps, respectively. is a convex set ensuring to be nonnegative. The above nonlinear inverse problem is then solved by the iteratively regularized Gauss-Newton method (IRGNM) where in each Gauss-Newton step the nonlinear problem is linearized and solved by the fast iterative shrinkage-thresholding algorithm (FISTA) [40]. More details on the IRGNM-FISTA algorithm can be found in [25].
Data Acquisition
All MRI experiments were conducted on a Magnetom Skyra 3T (Siemens Healthineers, Erlangen, Germany) with approval of the local ethics committee. The proposed method was first validated on a commercial reference phantom (Diagnostic Sonar LTD, Scotland, UK) consisting of six compartments with defined T1 values surrounded by water. Phantom and brain studies were conducted with a 20-channel head/neck coil, whereas abdominal scans were performed with a combined thorax and spine coil with 26 channels. Six subjects (4 females, 2 males, 26 ± 5 years old) without known illness were recruited. For each subject, both brain and liver measurements were performed. In all experiments, simultaneously acquired slices using IR radial FLASH are separated by a fixed distance d. All single-slice and multi-slice acquisitions employed the same nominal flip angle . Acquisition parameters for phantom and brain measurements were: FOV: 192×192 mm2, matrix size: 256×256, TR/TE = 4.10/2.58 ms, bandwidth 630 Hz/pixel, slice thickness mm, slice distances mm and mm for phantom and in-vivo studies, respectively. A gold standard T1 mapping was performed on the center slice of the phantom using an IR spin-echo method [41] with 9 IR scans (TI = 30, 530, 1030, 1530, 2030, 2530, 3030, 3530, 4030 ms), TR/TE = 4050/12 ms, FOV: 192 × 192 mm2, matrix size: 192×192, and a total acquisition time of 2.4 hours. Parameters for the abdominal measurements were: FOV: 320 × 320 mm2, matrix size: 256 × 256, TR/TE = 2.70/1.69 ms, bandwidth 850 Hz/pixel, mm, mm. All single-shot measurements were acquired within a 4-second duration, which was chosen to compromise between good T1 accuracy, SNR while still keep the acquisition time short [15]. The SMS golden-angle acquisitions were executed twice to evaluate the repeatability of the proposed method. Abdominal experiments were performed during a brief breathhold.
Numerical Implementation
All SMS image reconstruction was done offline based on the software package BART [42] using a 40-core 2.3 GHz Intel Xeon E5–2650 server with a RAM size of 512 GB. For abdominal studies, coil elements far away from the regions of interest (i.e., coils near the arm regions) were manually excluded to image reconstruction to remove residual streaking artefacts [43]. After gradient-delay correction [44] and channel compression to 8 principle components, the multi-coil radial raw data were gridded onto a Cartesian grid, where all successive iterations were then performed using FFT-based convolutions with the point-spread function [45, 46]. Parameter maps were initialized with and all coil sensitivities were initialized with zeros for all slices. The regularization parameters and were initialized with 1.0 and subsequently reduced by a factor of three in each Gauss-Newton step. A minimum value of was used to control the noise of the estimated parameter maps even with a larger number of Gauss-Newton steps. The optimal value was chosen manually to optimize SNR without compromising the quantitative accuracy or delineation of structural details. 10 Gauss-Newton steps were employed to ensure convergence. With these settings, it took around 10 hours to reconstruct a five-slice SMS brain dataset and 6 hours to reconstruct a three-slice SMS abdominal dataset on the CPU system. For single-slice references, reconstructions were able to run on a GPU (Tesla V100 SXM2, NVIDIA, Santa Clara, CA), which then took only 8 to 12 min per dataset.
Model-based reconstruction techniques generally offer a flexible choice of temporal binning, i.e., even a single radial spoke per k-space frame could be employed for accurate parameter estimation [23]. However, a certain amount of temporal binning effectively reduces the computational demand as long as the T1 accuracy is not compromised [4, 23]. Here, the number of binned spokes was chosen such that the temporal bin size does not exceed 85 ms, which is sufficiently low to keep the quantification error below 1% as shown previously [23]. More specifically, 15, 6 and 4 spokes per k-space frame were selected for single-slice, simultaneous three-slice and five-slice model-based brain reconstructions, respectively. For abdominal studies, 25 and 10 spokes per k-space frame were used for single-slice and simultaneous three-slice reconstructions.
T1 Analysis
All quantitative T1 results are reported as mean ± standard deviation (SD). Regions-of-interest (ROIs) were carefully selected to minimize partial volume errors using the arrayShow [47] tool in MATLAB (Math-Works, Natick, MA). For further analysis, relative difference maps and normalized relative errors were calculated, respectively, with the reference T1 map estimated from a single-slice acquisition [25] and the T1 map reconstructed from the corresponding multi-slice acquisition. Moreover, the repeatability error between scans was calculated using , with the T1 difference between different measurements and the number of subjects. In addition, synthetic images are computed for all inversion times and this image series is then converted into a movie showing the recovery of the longitudinal magnetization after the inversion.
Results
The proposed method was first validated in a phantom study using the SMS golden-angle acquisition and the developed SMS model-based reconstruction. Figure 2 (a) shows T1 maps of three slices reconstructed with the proposed method together with an IR spin-echo reference and the T1 maps estimated from single-slice IR radial acquisition [25] of the center slice. Visual inspection reveals that the proposed method can completely disentangle the superposed slices and all multi-slice T1 maps are in good agreement with the references. These findings are confirmed by the T1 values of the ROIs in the center slice in Figure 2 (b), where preservation of good precision (low standard deviation) of the SMS T1 mapping method is also observed. Quantitative results for T1 maps from the other two slices are shown in the Supporting Information Table S1, which confirms good T1 accuracy and precision of these two slices as well.
Figure 2.
a. T1 maps for three simultaneously acquired slices for a phantom using a three-slice SMS golden-angle IR FLASH acquisition and model-based reconstruction in comparison to a single-slice IR spin-echo reference method (center slice) and a single-slice IR FLASH acquisition using model-based reconstruction. b. Quantitative T1 values (mean and standard deviation) within ROIs of the six phantom tubes for the center-slice T1 maps of all three methods.
Figure 3 demonstrates the effect of the minimum regularization parameter used in the SMS model-based reconstruction with a multi-slice factor of five. Low values of result in increased noise in the T1 maps, while high values lead to blurring. A similar effect can be seen in the synthesized image series presented in the Supporting Information Video S1. A value of was chosen to balance noise reduction and preservation of image details. This value was used for all multi-slice brain reconstructions. Similarly, was used for all multi-slice abdominal reconstructions.
Figure 3.
Five-slice SMS brain T1 maps (center slice) obtained using model-based reconstruction for different choices of the minimum regularization parameters . A value is used for all multi-slice brain studies.
Figure 4 (a) compares the center-slice T1 maps of a human brain for different multi-slice acquisitions and using model-based reconstruction for a multi-slice factor of three. Both SMS methods produce T1 maps with less noise than the conventional spoke-interleaved multi-slice method. Further, the SMS T1 values are closer to the single-slice reference, as seen in the relative difference maps as well as the normalized errors. In line with the three-slice results, Figure 4 (b) shows for a multi-slice factor of five that both SMS T1 maps have better SNR and are closer to the reference than the conventional multi-slice method. For both acceleration factors, the SMS golden-angle method further helps to reduce artifacts in the border areas and has less quantitative errors than the SMS aligned method. The T1 values for white- and gray-matter ROIs in Figure 5 confirm the above findings: Apart from similar mean T1 values among all multi-slice methods, both SMS approaches produce T1 values with higher precision than the spoke-interleaved multi-slice method. In addition, all SMS brain T1 values are in close agreement with the single-slice reference as well as literature values [48, 49]. Note the 5-slice SMS aligned T1 map looks slightly less noisier than the 3-slice SMS aligned one but has a higher normalized error. This may be due to the fact that streaking artifacts start to appear in the border areas of the 5-slice SMS aligned T1 map.
Figure 4.

a. (Top) Center-slice of three-slice brain T1 maps from different multi-slice acquisitions using model-based reconstructions with (middle) magnified T1 regions and (bottom) their relative difference maps (× 5) to the single-slice reference T1 map. b. Similar comparisons at a multi-slice factor of five. Normalized errors are presented at the bottom left on all relative-difference T1 maps.
Figure 5.
Quantitative T1 values (mean and standard deviation) within ROIs that were manually drawn into the frontal white matter (WM), occipital WM, frontal gray matter (GM) and occipital GM of all T1 maps in Figure 4.
Figure 6 (a) presents the center-slice abdominal T1 maps for different three-slice acquisitions using model-based reconstructions. Similar to the brain results, both SMS T1 maps have better SNR than the spoke-interleaved multi-slice result. The SMS golden-angle method further helps to reduce streaking artifacts on the T1 maps. The ROI-analyzed quantitative liver T1 values in Figure 6(b) confirm good accuracy of all multi-slice methods in comparison to the single-slice T1 map with a best quantitative precision achieved by the SMS golden-angle method.
Figure 6.
a. (Top) Center-slice of three-slice abdominal T1 maps from different multi-slice acquisitions using model-based reconstructions with (bottom) magnified T1 regions. b. Quantitative T1 values (mean and standard deviation) within ROIs that were manually drawn into the liver region as indicated in a.
Figure 7 (a) depicts all T1 maps estimated from a five-slice SMS golden-angle acquisition as well as the corresponding single-slice T1 maps. All five-slice T1 maps are visually in good agreement with the corresponding single-slice maps. This is also observed for the other five subjects as shown in the Supporting Information Figure S1, indicating that the combination of the SMS golden-angle acquisition with SMS model-based reconstructions can be used to simultaneously acquire T1 maps for five slices of a human brain in good quality within four seconds. A similar comparison is presented for simultaneous three-slice abdominal T1 mapping in Figure 7(b) and Supporting Information Figure S2. In this case, the simultaneous three-slice datasets were acquired within a single four-second breathhold. Again, good agreement is reached between the simultaneous three-slice abdominal T1 maps and the single-slice maps. These results suggest an acceleration factor of three can be used for abdominal T1 mapping with the proposed method. Images for all inversion times were synthesized for the five-slice brain and three-slice liver studies and are presented in the Supporting Information Videos S2 and S3, respectively.
Figure 7.
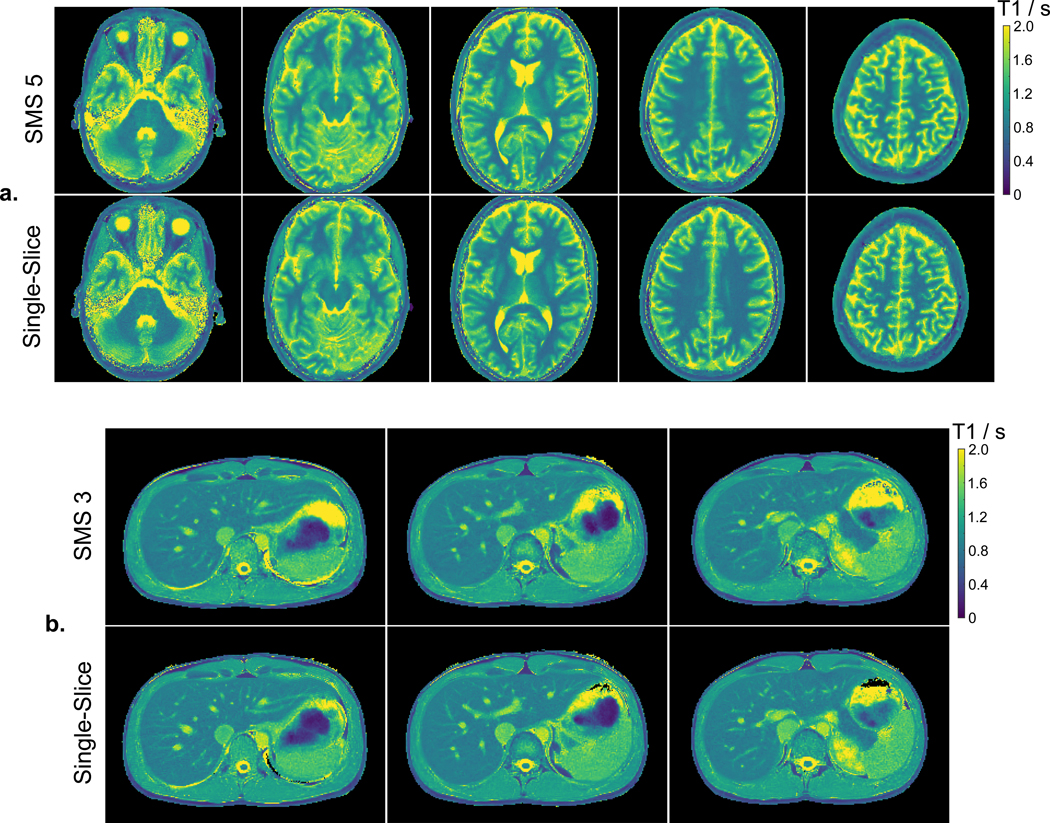
a. (Top) T1 maps of five simultaneously acquired slices of a human brain obtained using the SMS golden-angle acquisition and the proposed model-based reconstruction technique. (Bottom) The corresponding single-slice T1 maps. b. Similar comparisons for simultaneous three-slice abdominal T1 mapping. The abdominal acquisition was performed within a single breathhold of four seconds.
Figure 8 and Figure 9 show T1 values of all six subjects for the two repetitive scans in both SMS brain and liver studies. The small T1 difference between the repetitive scans demonstrates good intra-subject repeatability of the proposed method. The repeatability errors are: Frontal white matter: 13 ms (1.8% of the mean), occipital white matter: 4 ms (0.5% of the mean), frontal gray matter: 15 ms (1.1% of the mean), occipital gray matter: 18 ms (1.3% of the mean) and liver: 4 ms (0.5% of the mean). Figure 9 additionally confirms good quantitative agreement between single-slice and SMS liver T1 values for all subjects.
Figure 8.
Quantitative brain T1 values (s) in the four ROIs of the center slice when using the five-slice SMS T1 methods for all six subjects and two repetitive scans. FWM - frontal white matter, OWM - occipital white matter, FGM - frontal gray matter and OGM - occipital gray matter.
Figure 9.
Quantitative liver T1 values (s) of the center slice when using the three-slice SMS T1 methods for all six subjects and two repetitive scans. Note that dashed black lines represent the corresponding liver T1 values from single-slice acquisitions.
Figure 10 illustrates the use of the proposed SMS T1 mapping technique for the acquisition of a whole-brain T1 map consisting of 25 contiguous slices with a resolution of 0.75 × 0.75 × 5 mm3. These datasets were acquired using five consecutive five-slice SMS acquisitions with each having slice distance of 25 mm. As a sufficient delay is necessary between the non-selective inversions, the total acquisition took around one minute: Four seconds for each five-slice SMS acquisition with a waiting period of 10 seconds in between to ensure full recovery of the magnetization.
Figure 10.

Full brain T1 map consisting of 25 contiguous slices at a resolution of 0.75 × 0.75 × 5 mm3. These 25 T1 maps were acquired using five consecutive five-slice SMS acquisitions with a slice distance of 25 mm each.
Discussion
This work describes a fast multi-slice T1 mapping technique which combines simultaneous multi-slice excitations and single-shot IR radial FLASH with an extended nonlinear model-based reconstruction. The present method avoids any coil-calibration steps for SMS reconstruction and uses sparsity constraints to improve precision. Validation studies on a phantom and in six healthy subjects show that the combination of SMS golden-angle acquisition and the developed SMS model-based reconstruction technique can obtain high-resolution simultaneous five-slice brain T1 maps and simultaneous three-slice abdominal T1 maps with good accuracy, precision and repeatability within a single inversion recovery of four seconds.
In comparison, to reconstruct a fully-sampled image at each time point while still keeping bin size small, the conventional IR Look-Locker technique needs to employ multiple inversions and acquire complementary k-space data in each inversion to fulfill the Nyquist criterion. With a bin size of 20 radial spokes (singleslice) and a 256 × 256 matrix, at least 20 ≈ (256×π/2)/20 inversions are needed. Thus, the undersampling factor is 20 for model-based reconstruction in the single-shot single-slice method. With the extension to SMS described in the present work, the acceleration factor is further enhanced by an additional factor of 3–5. The present method achieves 0.8 to 1.33 seconds per T1 map within a single inversion recovery and 2.8 to 4.67 seconds per map when taking into account a 10 second delay in a multi-slice protocol with several inversions. This compares well to other recent radial T1 mapping approaches with IR Look-Locker based acquisitions recently described in the literature [26, 32].
In contrast to many other quantitative SMS MRI techniques [28, 34, 35], the proposed method integrates coil-sensitivity estimation into the model-based reconstruction framework, avoiding additional calibration scans, which further reduces miscalibration errors in case of motion, especially when imaging moving organs such as abdomen or heart. Moreover, the proposed method dispenses with intermediate image reconstruction, enabling the reconstruction of high-quality T1 maps directly from k-space which does not require binning. This property is especially beneficial for T1 mapping of multiple slices at higher acceleration factors where other methods need to trade off image quality against accuracy when choosing the bin size [30, 50]. The spoke-interleaved results in this study are noisier than the ones presented in [31]. The main reason might be that measurements in the previous work [31] were done on a different scanner using a 64-channel head coil while this study employed a 20-channel head coil. Different parameter choices for sequence and reconstruction may also be a contributing factor. In this study, we used identical parameters as used in the proposed SMS model-based method to make a direct comparison possible.
In the present work, we use a radial FLASH readout while other studies employ EPI or 3D spiral to achieve high-resolution brain mapping [51, 52]. While radial FLASH is less efficient in covering k-space, with short echo times it is much less sensitive to off-resonance effects than spiral or EPI trajectories and is not affected by geometric distortions. Due to the intrinsic oversampling of the k-space center, radial FLASH is also more robust to motion, which will be beneficial in abdominal and cardiac applications. An alternative to multi-slice T1 mapping is 3D imaging using a radial stack-of-stars sequence or other 3D sequences [52]. 3D sequences should provide even better SNR than 2D SMS imaging and allow for isotropic T1 mapping [26, 52]. The proposed model-based reconstruction method is also applicable to 3D T1 mapping. However, 3D sequences need to employ multi-shot acquisitions, in which case data over the duration of a complete scan (usually in the order of minutes) have to be combined for parameter estimation. This makes 3D imaging much more sensitive to motion than their 2D SMS counterparts [34].
For radial sampling, the use of a golden angle in the partition dimension has been shown to have better performance than the use of aligned spokes for undersampled stack-of-stars 3D volume MRI [37] and 2D radial SMS parallel imaging using NLINV [38]. In this work, we have adopted the same strategy for SMS model-based parameter mapping. Our results confirm a slightly better performance of this golden-angle strategy over the aligned case. Combination of such a sampling strategy and model-based reconstructions may be further exploited for single-shot SMS myocardial T1 mapping, where part of the IR data (e.g., systolic data) would be discarded prior to model-based T1 estimations [53]. The proposed method is also applicable to whole-liver imaging where we need to perform the single-shot acquisition multiple times, i.e., with multiple breathholds to achieve the desired volume coverage. As the delay time can be as short as 3 seconds for liver studies [54], covering the entire liver with 30 slices using ten 4-second breathhold SMS-3 acquisitions interrupted by nine 3-second time gaps when the subject is allowed to breath freely required a minimum acquisition time of 67 seconds. With a longer delays of 10 seconds between breathholds for more patient convenience this scan could still be performed in two minutes.
The non-selective inversion pulse used in this study is not optimal for whole-brain T1 mapping as it necessitates a delay time between successive SMS acquisitions. The 10-second delay time we employed is very high as usually 3–4 seconds should be enough for brain applications [26]. Furthermore, it has been reported [30, 32] that there is little difference in T1 accuracy between non-selective and slab-selective inversion pulses for brain T1 mapping. With adapted excitation pulses and acquisition strategies, we expect to eliminate most of the delay time when combining a slab-selective inversion with the proposed simultaneous multi-slice T1 mapping technique for full brain applications in future studies.
The other limitation of the proposed method is the long computation time, especially for model-based reconstruction of the SMS golden-angle datasets: All the data from multiple slices have to be held in memory simultaneously during iterations, which still prevents the use of GPUs. In principle, the alternative methods such as subspace methods have to deal with the same amount of data, but recent implementations use smart computational strategies to reduce the amount of memory and can then achieve very fast reconstruction [12, 42, 55]. The key difference between subspace and the nonlinear methods is that the latter does not need any approximations for the signal models, i.e., a minimal number of physical parameters could describe the desired MR signal precisely. In contrast, subspace methods have to approximate the MR signal using a few principal coefficients, which then leads to compromised accuracy or precision. While computation times reported in this work for the proposed model-based reconstruction on CPUs are still very high, newer generations of GPUs with larger memory will enable much faster reconstructions. Preliminary results obtained by using a smaller matrix size are very encouraging: When reducing the in-plane resolution from 0.75 × 0.75 mm2 (matrix size: 512 × 512) to 1.0 × 1.0 mm2 (matrix size: 384 × 384), the SMS 5-slice model-based reconstructions could already run on a GPU, which then took only around 14 min per dataset. Similarly, the 1.0 × 1.0 mm2 SMS 3-slice reconstruction took around 8 min per dataset.
Conclusion
The proposed combination of simultaneous multi-slice excitations, single-shot IR radial FLASH, and calibrationless model-based reconstruction allows for efficient high-resolution multi-slice T1 mapping with good accuracy, precision and repeatability.
Supplementary Material
Supporting Information Table S1. T1 relaxation times (ms, mean ± SD) for the experimental phantom in Figure 2.
Supporting Information Figure S1. T1 maps for five simultaneously acquired slices of the human brain and the corresponding single-slice T1 maps for five subjects.
Supporting Information Figure S2. T1 maps for three simultaneously acquired abdominal slices and the corresponding single-slice T1 maps for five subjects.
Supporting Information Video S1. Synthesized image series representing recovery of the longitudinal magnetization after inversion for the five-slice SMS brain study (center-slice) using model-based reconstruction with different minimum regularization parameters, i.e., αmin = 0.0005, 0.001, 0.0015, 0.002, from left to right, respectively.
Supporting Information Video S2. Synthesized image series representing recovery of the longitudinal magnetization after inversion of five simultaneously slices of a human brain when using a bin size of 82 ms. The acquisition time for all five slices is four seconds.
Supporting Information Video S3. Synthesized image series representing recovery of the longitudinal magnetization after inversion for three simultaneously acquired slices of a human liver using a bin size of 81 ms. The acquisition time for all three slices is four seconds.
Acknowledgments
This work was supported by the DZHK (German Centre for Cardiovascular Research), by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy - EXC 2067/1-390729940, and funded in part by NIH under grant U24EB029240.
Footnotes
Conflict of Interest
The authors declare no competing interests.
Data Availability Statement
In the spirit of reproducible research, code to reproduce the experiments is available on https://github.com/mrirecon/sms-T1-mapping The raw k-space data used in this study can be downloaded from DOI:10.5281/zenodo.3969809.
References
- [1].Cheng HL, Stikov N, Ghugre NR, Wright GA. Practical medical applications of quantitative MR relaxometry. J Magn Reson Imaging. 2012; 36:805–824. [DOI] [PubMed] [Google Scholar]
- [2].Kellman P, Hansen MS. T1-mapping in the heart: accuracy and precision. J Cardiovasc Magn Reson. 2014; 16:2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Look DC, Locker DR. Time saving in measurement of NMR and EPR relaxation times. Rev Sci Instrum. 1970; 41:250–251. [Google Scholar]
- [4].Deichmann R, Haase A. Quantification of T1 values by SNAPSHOT-FLASH NMR imaging. J Magn Reson. 1992; 96:608–612. [Google Scholar]
- [5].Messroghli DR, Radjenovic A, Kozerke S, Higgins DM, Sivananthan MU, Ridgway JP. Modified Look-Locker Inversion recovery (MOLLI) for high-resolution T1 mapping of the heart. Magn Reson Med. 2004; 52:141–146. [DOI] [PubMed] [Google Scholar]
- [6].Block KT, Uecker M, Frahm J. Model-Based Iterative Reconstruction for Radial Fast Spin-Echo MRI. IEEE Trans Med Imaging. 2009; 28:1759–1769. [DOI] [PubMed] [Google Scholar]
- [7].Doneva M B örnert P, Eggers H, Stehning C, Sénégas J, Mertins A. Compressed sensing reconstruction for magnetic resonance parameter mapping. Magn Reson Med. 2010; 64:1114–1120. [DOI] [PubMed] [Google Scholar]
- [8].Petzschner FH, Ponce IP, Blaimer M, Jakob PM, Breuer FA. Fast MR parameter mapping using k-t principal component analysis. Magn Reson Med. 2011; 66:706–716. [DOI] [PubMed] [Google Scholar]
- [9].Huang C, Graff CG, Clarkson EW, Bilgin A, Altbach MI. T2 mapping from highly undersampled data by reconstruction of principal component coefficient maps using compressed sensing. Magn Reson Med. 2012; 67:1355–1366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Velikina JV, Alexander AL, Samsonov A. Accelerating MR parameter mapping using sparsity-promoting regularization in parametric dimension. Magn Reson Med. 2013; 70:1263–1273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn Reson Med. 2015; 73:655–661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Tamir JI, Uecker M, Chen W, Lai P, Alley MT, Vasanawala SS, Lustig M. T2 shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging. Magn Reson Med. 2017; 77:180–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Feng L, Benkert T, Block KT, Sodickson DK, Otazo R, Chandarana H. Compressed sensing for body MRI. J Magn Reson Imaging. 2017; 45:966–987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Gensler D M örchel P, Fidler F, Ritter O, Quick HH, Ladd ME, Bauer WR, Ertl G, Jakob PM, Nordbeck P. Myocardial T1 quantification by using an ECG-triggered radial single-shot inversion-recovery MR imaging sequence. Radiology. 2014; 274:879–887. [DOI] [PubMed] [Google Scholar]
- [15].Wang X, Joseph AA, Kalentev O, Merboldt KD, Voit D, Roeloffs VB, van Zalk M, Frahm J. Highresolution myocardial T1 mapping using single-shot inversion recovery fast low-angle shot MRI with radial undersampling and iterative reconstruction. Br J Radiol. 2016; 89:20160255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Marty B, Coppa B, Carlier P. Fast, precise, and accurate myocardial T1 mapping using a radial MOLLI sequence with FLASH readout. Magn Reson Med. 2018; 79:1387–1398. [DOI] [PubMed] [Google Scholar]
- [17].Fessler JA. Model-based image reconstruction for MRI. IEEE Signal Process Mag. 2010; 27:81–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Sumpf TJ, Uecker M, Boretius S, Frahm J. Model-based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin-echo MRI. J Magn Reson Imaging. 2011; 34:420–428. [DOI] [PubMed] [Google Scholar]
- [19].Tran-Gia J, Stäb D, Wech T, Hahn D, Köstler H. Model-based acceleration of parameter mapping (MAP) for saturation prepared radially acquired data. Magn Reson Med. 2013; 70:1524–1534. [DOI] [PubMed] [Google Scholar]
- [20].Zhao B, Lam F, Liang ZP. Model-based MR parameter mapping with sparsity constraints: parameter estimation and performance bounds. IEEE Trans Med Imaging. 2014; 33:1832–1844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Peng X, Liu X, Zheng H, Liang D. Exploiting parameter sparsity in model-based reconstruction to accelerate proton density and T2 mapping. Med Eng Phys. 2014; 36:1428–1435. [DOI] [PubMed] [Google Scholar]
- [22].Knoll F, Raya JG, Halloran RO, Baete S, Sigmund E, Bammer R, Block T, Otazo R, Sodickson DK. A model-based reconstruction for undersampled radial spin-echo DTI with variational penalties on the diffusion tensor. NMR Biomed. 2015; 28:353–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Roeloffs V, Wang X, Sumpf TJ, Untenberger M, Voit D, Frahm J. Model-based reconstruction for T1 mapping using single-shot inversion-recovery radial FLASH. Int J Imag Syst Tech. 2016; 26:254–263. [Google Scholar]
- [24].Zhao B, Setsompop K, Ye H, Cauley SF, Wald LL. Maximum likelihood reconstruction for magnetic resonance fingerprinting. IEEE Trans Med Imaging. 2016; 35:1812–1823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Wang X, Roeloffs V, Klosowski J, Tan Z, Voit D, Uecker M, Frahm J. Model-based T1 mapping with sparsity constraints using single-shot inversion-recovery radial FLASH. Magn Reson Med. 2018; 79:730–740. [DOI] [PubMed] [Google Scholar]
- [26].Maier O, Schoormans J, Schloegl M, Strijkers GJ, Lesch A, Benkert T, Block T, Coolen BF, Bredies K, Stollberger R. Rapid T1 quantification from high resolution 3D data with model-based reconstruction. Magn Reson Med. 2019; 81:2072–2089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Moon JC, Messroghli DR, Kellman P, Piechnik SK, Robson MD, Ugander M, Gatehouse PD, Arai AE, Friedrich MG, Neubauer S et al. Myocardial T1 mapping and extracellular volume quantification: Society for Cardiovascular Magnetic Resonance (SCMR) and CMR Working Group of the European Society of Cardiology consensus statement. J Cardiovasc Magn Reson. 2013; 15:92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Weingärtner S, Moeller S, Schmitter S, Auerbach E, Kellman P, Shenoy C, Akçakaya M. Simultaneous multislice imaging for native myocardial T1 mapping: Improved spatial coverage in a single breath-hold. Magn Reson Med. 2017; 78:462–471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Shah NJ, Zaitsev M, Steinhoff S, Zilles K. A new method for fast multislice T1 mapping. Neuroimage. 2001; 14:1175–1185. [DOI] [PubMed] [Google Scholar]
- [30].Deichmann R. Fast high-resolution T1 mapping of the human brain. Magn Reson Med. 2005; 54:20–27. [DOI] [PubMed] [Google Scholar]
- [31].Wang X, Voit D, Roeloffs V, Uecker M, Frahm J. Fast interleaved multislice T1 mapping: Model-based reconstruction of single-shot inversion-recovery radial FLASH. Comput Math Methods Med. 2018; 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Li Z, Bilgin A, Johnson K, Galons JP, Vedantham S, Martin DR, Altbach MI. Rapid high-resolution T1 mapping using a highly accelerated radial steady-state free-precession technique. J Magn Reson Imaging. 2019; 49:239–252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Barth M, Breuer F, Koopmans PJ, Norris DG, Poser BA. Simultaneous multislice (SMS) imaging techniques. Magn Reson Med. 2016; 75:63–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Ye H, Cauley SF, Gagoski B, Bilgic B, Ma D, Jiang Y, Du YP, Griswold MA, Wald LL, Setsom- pop K. Simultaneous multislice magnetic resonance fingerprinting (SMS-MRF) with direct-spiral sliceGRAPPA(ds-SG) reconstruction. Magn Reson Med. 2017; 77:1966–1974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Hilbert T, Schulz J, Marques JP, Thiran JP, Krueger G, Norris DG, Kober T. Fast model-based T2 mapping using SAR-reduced simultaneous multislice excitation. Magn Reson Med. 2019; 82:2090–2103. [DOI] [PubMed] [Google Scholar]
- [36].Wundrak S, Paul J, Ulrici J, Hell E, Geibel MA, Bernhardt P, Rottbauer W, Rasche V. Golden ratio sparse MRI using tiny golden angles. Magn Reson Med. 2016; 75:2372–2378. [DOI] [PubMed] [Google Scholar]
- [37].Zhou Z, Han F, Yan L, Wang DJ, Hu P. Golden-ratio rotated stack-of-stars acquisition for improved volumetric MRI. Magn Reson Med. 2017; 78:2290–2298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Rosenzweig S, Holme HCM, Wilke RN, Voit D, Frahm J, Uecker M. Simultaneous multi-slice MRI using cartesian and radial FLASH and regularized nonlinear inversion: SMS-NLINV. Magn Reson Med. 2018; 79:2057–2066. [DOI] [PubMed] [Google Scholar]
- [39].Uecker M, Hohage T, Block KT, Frahm J. Image reconstruction by regularized nonlinear inversion joint estimation of coil sensitivities and image content. Magn Reson Med. 2008; 60:674–682. [DOI] [PubMed] [Google Scholar]
- [40].Beck A, Teboulle M. Fast Gradient-Based Algorithms for Constrained Total Variation Image Denoising and Deblurring Problems. IEEE Trans Image Process. 2009; 18:2419–2434. [DOI] [PubMed] [Google Scholar]
- [41].Barral JK, Gudmundson E, Stikov N, Etezadi-Amoli M, Stoica P, Nishimura DG. A robust methodology for in vivo T1 mapping. Magn Reson Med. 2010; 64:1057–1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Uecker M, Ong F, Tamir JI, Bahri D, Virtue P, Cheng JY, Zhang T, Lustig M. Berkeley advanced reconstruction toolbox. In: Proc. Intl. Soc. Mag. Reson. Med. 23, Toronto, 2015. p. 2486.
- [43].Block KT, Chandarana H, Milla S, Bruno M, Mulholland T, Fatterpekar G, Hagiwara M, Grimm R, Geppert C, Kiefer B. Towards routine clinical use of radial stack-of-stars 3D gradient-echo sequences for reducing motion sensitivity. J. Korean Soc. Magn. Reson. Med. 2014; 18:87–106. [Google Scholar]
- [44].Block KT, Uecker M. Simple method for adaptive gradient-delay compensation in radial MRI. In: Proc. Intl. Soc. Mag. Reson. Med. 19, Montreal, 2011. p. 2816.
- [45].Wajer FTAW, Pruessmann KP. Major speedup of reconstruction for sensitivity encoding with arbitrary trajectories. In: Proc. Intl. Soc. Mag. Reson. Med. 9, Glasgow, 2001. p. 0767.
- [46].Uecker M, Zhang S, Frahm J. Nonlinear inverse reconstruction for real-time MRI of the human heart using undersampled radial FLASH. Magn Reson Med. 2010; 63:1456–1462. [DOI] [PubMed] [Google Scholar]
- [47].Sumpf T, Unterberger M. arrayshow: a guide to an open source matlab tool for complex mri data analysis. In: Proc. Intl. Soc. Mag. Reson. Med. 21, Salt Lake City, 2013. p. 2719.
- [48].Wansapura JP, Holland SK, Dunn RS, BallJr WS. NMR relaxation times in the human brain at 3.0 tesla. J Magn Reson Imaging. 1999; 9:531–538. [DOI] [PubMed] [Google Scholar]
- [49].Preibisch C, Deichmann R. Influence of RF spoiling on the stability and accuracy of T1 mapping based on spoiled FLASH with varying flip angles. Magn Reson Med. 2009; 61:125–135. [DOI] [PubMed] [Google Scholar]
- [50].Wang X, Roeloffs V, Merboldt KD, Voit D, Schätz S, Frahm J. Single-shot multi-slice T1 mapping at high spatial resolution–inversion-recovery FLASH with radial undersampling and iterative reconstruction. Open Med Imaging J. 2015; 9. [Google Scholar]
- [51].Cohen O, Polimeni JR. Optimized inversion-time schedules for quantitative T1 measurements based on high-resolution multi-inversion EPI. Magn Reson Med. 2018; 79:2101–2112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Cao X, Ye H, Liao C, Li Q, He H, Zhong J. Fast 3D brain MR fingerprinting based on multi-axis spiral projection trajectory. Magn Reson Med. 2019; 82:289–301. [DOI] [PubMed] [Google Scholar]
- [53].Wang X, Kohler F, UnterbergBuchwald C, Lotz J, Frahm J, Uecker M. Model-based myocardial T1 mapping with sparsity constraints using single-shot inversion-recovery radial FLASH cardiovascular magnetic resonance. J Cardiovasc Magn Reson. 2019; 21:60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Chen Y, Lee GR, Aandal G, Badve C, Wright KL, Griswold MA, Seiberlich N, Gulani V. Rapid volumetric T1 mapping of the abdomen using three-dimensional through-time spiral GRAPPA. Magnetic resonance in medicine 2016; 75:1457–1465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Mani M, Jacob M, Magnotta V, Zhong J. Fast iterative algorithm for the reconstruction of multishot non-cartesian diffusion data. Magn Reson Med. 2015; 74:1086–1094. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information Table S1. T1 relaxation times (ms, mean ± SD) for the experimental phantom in Figure 2.
Supporting Information Figure S1. T1 maps for five simultaneously acquired slices of the human brain and the corresponding single-slice T1 maps for five subjects.
Supporting Information Figure S2. T1 maps for three simultaneously acquired abdominal slices and the corresponding single-slice T1 maps for five subjects.
Supporting Information Video S1. Synthesized image series representing recovery of the longitudinal magnetization after inversion for the five-slice SMS brain study (center-slice) using model-based reconstruction with different minimum regularization parameters, i.e., αmin = 0.0005, 0.001, 0.0015, 0.002, from left to right, respectively.
Supporting Information Video S2. Synthesized image series representing recovery of the longitudinal magnetization after inversion of five simultaneously slices of a human brain when using a bin size of 82 ms. The acquisition time for all five slices is four seconds.
Supporting Information Video S3. Synthesized image series representing recovery of the longitudinal magnetization after inversion for three simultaneously acquired slices of a human liver using a bin size of 81 ms. The acquisition time for all three slices is four seconds.
Data Availability Statement
In the spirit of reproducible research, code to reproduce the experiments is available on https://github.com/mrirecon/sms-T1-mapping The raw k-space data used in this study can be downloaded from DOI:10.5281/zenodo.3969809.









