Design of an Electrostatic Frequency Map for the NH Stretch of the Protein Backbone and Application to Chiral Sum Frequency Generation Spectroscopy

Abstract

We develop an electrostatic map for the vibrational NH stretch (amide A) of the protein backbone with a focus on vibrational chiral sum frequency generation spectroscopy (chiral SFG). Chiral SFG has been used to characterize protein secondary structure at interfaces using the NH stretch and to investigate chiral water superstructures around proteins using the OH stretch. Interpretation of spectra has been complicated because the NH stretch and OH stretch overlap spectrally. Although an electrostatic map for water OH developed by Skinner and coworkers was used previously to calculate the chiral SFG response of water structures around proteins, a map for protein NH that is directly responsive to biological complexity has yet to be developed. Here, we develop such a map, linking the local electric field to vibrational frequencies and transition dipoles. We apply the map to two protein systems and achieve much better agreement with experiment than was possible in our previous studies. We show that couplings between NH and OH vibrations are crucial to the lineshape, which informs the interpretation of chiral SFG spectra, and that the chiral NH stretch response is sensitive to small differences in structure. This work increases the utility of the NH stretch in biomolecular spectroscopy.

Graphical Abstract

Introduction

Of the four key vibrational normal modes of the protein amide group, the NH stretch mode (amide A) is perhaps the least studied. This is most likely because the NH group and the OH group of water vibrate in the same frequency range (3000–4000 cm⁻¹), and in most vibrational spectra of biological systems, the water signal overwhelms the signal from the NH stretch. However, because the NH group participates in hydrogen bonding interactions with both other parts of the protein during the formation of secondary structures as well as the water around the protein, the NH stretch contains valuable information about the local environment. Unfortunately, this information is hidden in conventional vibrational spectroscopy, and it cannot be brought out with the use of D₂O to shift the water response because the hydrogen atom of the NH group exchanges with water and shifts in the same way.

The NH stretch can be isolated in higher-order spectroscopies. Vibrational chiral-selective sum frequency generation spectroscopy (chiral SFG) with homodyne detection can detect the NH stretch and help characterize protein secondary structures.^{1, 2} Ultrafast methods such as two-dimensional infrared spectroscopy (2D-IR) can pick up the NH stretch through its interaction with other modes as a cross-peak.^{3, 4} Methods to model 2D-IR and chiral SFG of large systems are closely related,^{5, 6} so being able to model one method computationally corresponds to being able to model the other method as well. The key task is to find a way to relate local environments seen in molecular dynamics (MD) simulations to a fluctuating exciton Hamiltonian, which contains vibrational frequencies and couplings,^{5, 7–15} and thereby extract structural and dynamic information about molecular systems from spectra.

Simpson and coworkers have established symmetry-based chiral SFG theory to describe vibrational chiral SFG in the absence of electronic resonance as surface-selective in uniaxial (C_∞) systems.^{16, 17} Over the past decade, chiral SFG has developed into a powerful technique for probing the secondary structure of chiral biomacromolecules at interfaces and the solvent around them.^{1, 18–25} There are aspects of chiral SFG that are not yet understood. For example, we do not have a straightforward mapping from chiral phase (signal sign) to dipole orientation, unlike in conventional (achiral) SFG. However, the chiral SFG response of the NH stretch can provide vibrational signatures for identifying the secondary structure of proteins,² and the phase of the response correlates with the absolute chirality of protein.²⁰ Hence, being able to simulate the chiral SFG response of the protein NH stretch can help interpret chiral SFG spectra of proteins and extract information about protein structure.

In addition, Petersen’s group used chiral SFG to demonstrate the existence of a chiral spine of hydration in the minor groove of DNA.²⁶ Later, we showed that chiral SFG can also detect hydration structures around proteins.^20–22 In particular, we demonstrated that this technique is specifically sensitive to the first hydration shell of water around a protein.²⁵ However, the chiral OH signals produced by water overlap with the chiral NH signals produced by the protein.^{8, 27} Although signal at 3600–3800 cm⁻¹ can be unmistakably assigned to the OH stretch, signal at lower frequencies may be due to the NH or OH stretch. Previously, we showed that isotope labeling with H₂¹⁸O allows identification of OH stretch peaks by red-shifting water peaks by roughly 12 cm⁻¹.^{20, 22, 25} However, NH and OH interact with each other. Thus, the spectral perturbation induced by the ¹⁸O substitution may also be due to a delocalized mode involving OH and NH. Furthermore, the NH stretch peaks provide useful structural information as well as information about hydrogen-bonding interactions within the protein and between the protein and water. Hence, the ability to model the NH stretch spectra will reveal information about not only protein structures but also local interactions of water with the protein.

Vibrational spectra can be modeled computationally using MD simulations with an electrostatic mapping approach or with a direct dipole-polarizability time-correlation function approach.^{6, 8–12, 14, 15, 28–38} Recently we used the Skinner group’s OH stretch electrostatic map^{6, 8–10, 39–41} to predict chiral SFG signals produced by water around proteins. This map links the electric field along the OH bond at the OH hydrogen to the vibrational frequency, transition dipole, and transition polarizability. Although the map was developed for pure water,^{6, 9, 10, 42, 43} it can be extended to aqueous systems that include biomolecules and their atomic partial charges, as shown in our previous work.^{19, 20, 25} Of particular interest is LK₇β, which forms a stable antiparallel β-sheet at the air-water interface. This system is an ideal model system for SFG, which is inherently surface selective.^44–48 Although qualitative agreement was achieved between our computational and experimental spectra of water hydrating LK₇β at interfaces,^{19, 20, 25} the lack of NH peaks in the computational spectra made comparison between experiment and theory challenging. Any insights hidden in the NH response remained elusive.

The Mukamel group has developed maps for the vibrational modes of the peptide bond group, including the NH stretch using N-methyl acetamide (NMA).^{49, 50} Although NMA contains all the relevant vibrational modes, it is very different from an actual protein environment. The frequencies extracted from this map range from ~3400 to 3500 cm⁻¹. This range does not match the full range of frequencies exhibited by the NH stretch in biological systems.^{24, 27} An alternative approach is needed to model lower frequencies and understand complex biological environments.

Here, we report the development of an electrostatic map for the NH stretch of the protein backbone. Previous work has demonstrated that the NH signal produced by proteins is primarily due to the backbone.^{1, 24} Our map applies to all NH groups in the backbone except C-terminal amide (NH₂) capping groups that most likely contribute little to the total NH response. This map, together with previously developed maps for the OH stretch, enables computational modeling of the full chiral SFG spectra, including both OH and NH modes and the coupling between them. These full spectra contain information about the local hydrogen-bonding environment and the protein-solvent interactions. In the future, our map may allow simulation of 2D-IR and related spectra that directly probe energy exchange between a protein and the surrounding solvent. Our map is validated using a combination of previously published and new experimental data. We focus on two closely related protein systems – LK₇β (Ac-LKLKLKL-NH₂) and LE₇β (Ac-LELELEL-NH₂). Each is a seven-residue peptide consisting of alternating nonpolar and polar residues. The nonpolar residue is leucine and the polar residue is positively charged lysine in LK₇β or negatively charged glutamate in LE₇β. These protein systems form antiparallel β-sheets at the air-water interface. We find that the map reproduces the experimental chiral SFG spectra of these systems quite well. Moreover, analysis of the spectra provides insights into subtle differences in hydrogen bonding between the two apparently similar protein systems. This analysis demonstrates that the NH group is a useful probe for the local environment in biological systems when heterodyne chiral SFG attenuates the overwhelming OH stretch background.

Computational methods

Designing the NH stretch electrostatic map.

Our NH stretch electrostatic map was based on Skinner’s method of mapping electric fields around water molecules to spectroscopic quantities (i.e., vibrational frequency, transition dipole, transition polarizability, vibrational couplings). In brief, Skinner’s method⁶ consists of running an MD simulation of bulk water using a water model such as TIP4P,⁵¹ extracting small water clusters from the trajectory, performing density functional theory (DFT) calculations to determine local vibrational frequencies and other quantities, and correlating these properties to the local electric field (as calculated from local point charges – this is distinct from the long range electric field that is typically calculated using the Ewald method). Importantly, rather than optimizing the geometry of the water cluster and using the Hessian to compute the harmonic frequencies, Skinner’s group stretched the O–H bond and solved the vibrational Schrödinger equation for the resulting one-dimensional potential energy curve.⁶ This procedure results in more accurate vibrational frequencies because it accounts for anharmonic effects and does not involve relaxing (i.e., changing) the configuration for which the electric field is measured.

The first step of our development of an NH stretch electrostatic map was to generate configurations of a relatively small protein that was amenable to DFT calculations but also captured the essence of protein secondary structure. As both α-helices and β-sheets, the two most common secondary structures in proteins, involve hydrogen bonds (H-bonds) between NH groups and carbonyl groups, we focused on reproducing this interaction. We selected a tetraalanine peptide that is able to fold on itself to produce an intramolecular NH/carbonyl H-bond between the first (C=O) and fourth (NH) alanine residue (Figure 1). Because the NH stretch is highly local,⁵² the “folded” structure could effectively simulate NH interactions that would occur in both α-helices and β-sheets. Capping groups (acetyl on the N-terminal, –NH₂ on the C-terminal) were used to avoid charged terminus effects. To overcome the significant thermodynamic barriers to this kind of folding, we conducted a metadynamics enhanced sampling simulation with the distance between the NH nitrogen and carbonyl oxygen as the collective variable and collected configurations sampling the H-bonded state.⁵³ The simulation was performed in explicit TIP4P-Ew water⁵⁴ with ~1000 water molecules. See the SI for details about the metadynamics simulation.

Figure 1.

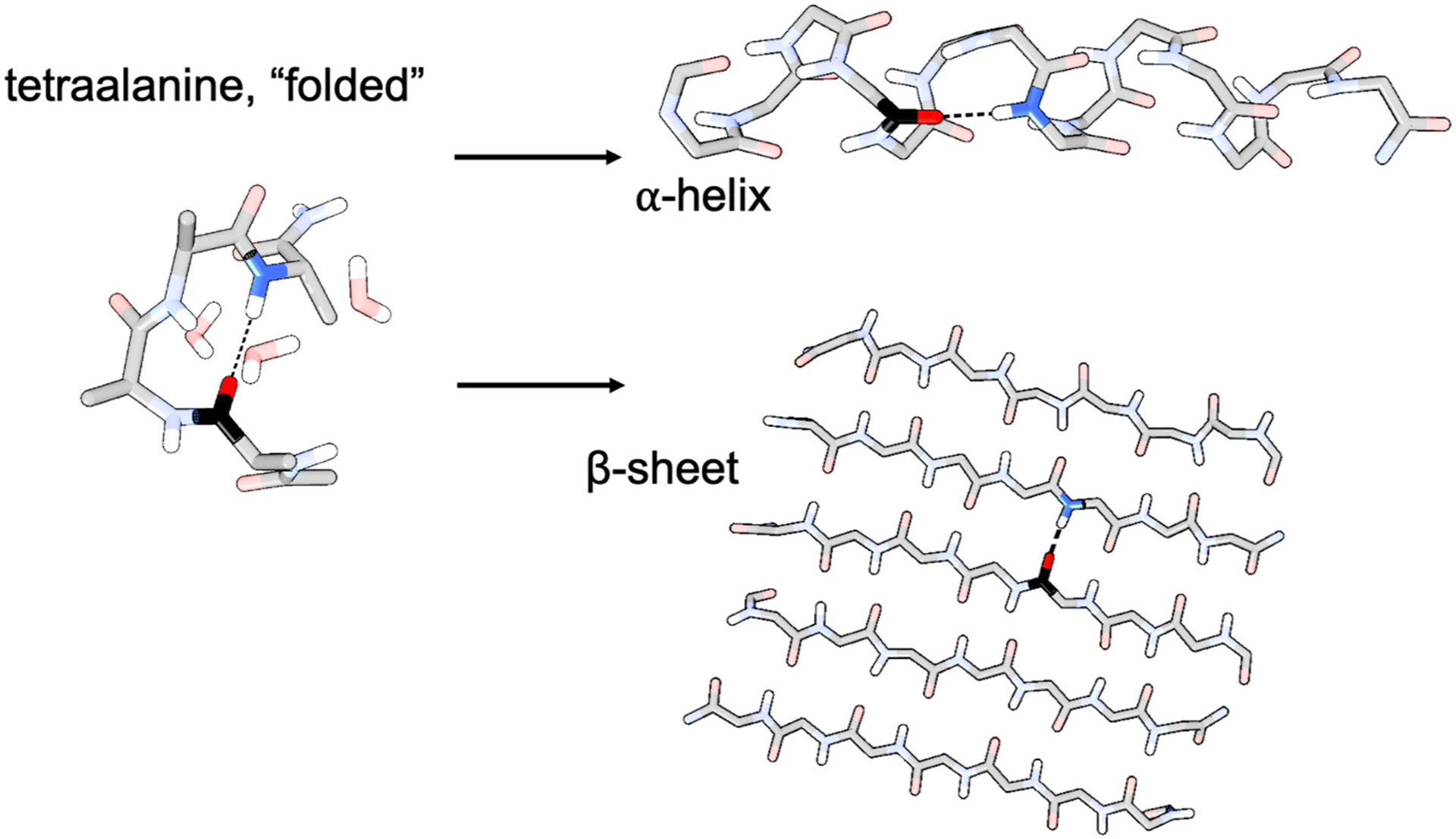
The mapping procedure relied on a small molecule (tetraalanine) mimic of the protein secondary structure environment, which is a H-bond between a backbone NH group and a backbone carbonyl group.

We also extracted configurations by sampling the non-H-bonded state and created a separate electrostatic map for that case. In total, we extracted 400 “H-bonded” and 400 “free” configurations. Note that in the free configurations, the NH group may still donate a H-bond to a water molecule. (Note that NH as an acceptor from water is vanishingly rare in this type of system.) We defined a H-bond using a heavy atom donor−acceptor distance cutoff of 3.2 Å and an angle greater than 135°. Because most free configurations of interest would involve NH groups on the outer edge of β-sheets or in unstructured loops, to ensure that the free configurations were not close to the H-bonded ones, we only considered free configurations where the donor−acceptor distance between the carbonyl oxygen and the amide nitrogen was greater than 4.5 Å, corresponding mostly to extended conformations of tetraalanine. Intermediate configurations (3.2–4.5 Å) were not considered for the maps.

After gathering these configurations, we extracted the entire peptide and the three closest water molecules to the fourth residue’s NH hydrogen. We then stretched the NH bond about the NH center of mass, keeping all other atoms frozen. The center of mass remained stationary during the stretch, so each atom moved in inverse proportion to its mass. The NH distance ranged from 0.58 Å to 1.70 Å over 15 evenly spaced configurations. We then performed single-point energy calculations on each configuration at the B3LYP/6–311G++(d,p)^55–59 level of theory using Gaussian 16⁶⁰ with default convergence criteria.⁶ We also included implicit water using the conductor-like polarizable continuum model (C-PCM) to account for polarization effects due to long range interactions with the bulk solvent.^61–64 The inclusion of implicit water was necessary to bring the frequencies down to the experimental range (~3200–3500 cm⁻¹). We then solved the one-dimensional Schrödinger equation for the resulting potential energy curve using the Fourier grid Hamiltonian method⁶⁵ using 1,500 quadratically interpolated grid points for high accuracy. We used the reduced mass of NH as the effective mass because both atoms were moving about their center of mass. We used a scaling factor of 1.0006 for the frequency based on comparing an analogous calculation with NMA in vacuum to the experimental value cited by Mukamel and coworkers.^{49, 66} To estimate the NH dipole derivative, we also performed a constrained geometry optimization for each configuration, allowing only the hydrogen of the NH group to relax, followed by a dipole derivative calculation for the NH stretch mode.⁸

We then calculated the electric field at various points around the NH group. We found that computing the electric field at points slightly past the hydrogen atom along the NH bond led to better correlations. To maximize the accuracy of the map in complex environments, we sampled the electric field at 51 (3 × 17) points, with one group of 17 points centered at 1.0 Å past the N toward the H along the NH bond, a second group centered at 1.5 Å, and a third group centered at 2.0 Å (See Figure S1 for details). For each central point, the group of 17 points included 16 points located 0.1 and 0.2 Å in all four directions from the central point along y and z. Moreover, the electric field was sampled in three directions for a total of 153 electric field components. The directions were defined by the NH bond (unit vector x), the vector perpendicular to the NH bond vector and pointing toward the adjacent residue’s carbonyl carbon (unit vector y) and the cross product of these vectors, z = x × y. We used these directions to set up our 51 points at each center.

For both the design and application of this model, the electric fields were calculated from the solvent charges (i.e., water molecules and ions) and the charges of the bound carbonyl carbon and oxygen for the H-bonded configurations and from only the solvent charges for the free configurations. TIP4P-Ew⁵⁴ charges were used for the water, standard parameters associated with the TIP4P-Ew model were used for the ions when present,^{67, 68} and the AMBER ff14SB force field⁶⁹ was used for the carbonyl group charges. Solvent charges within 10 Å of the NH sampling points were included. The distance cutoff was applied to individual atoms. We found that including whole water molecules (if any atom was within 10 Å of the sampling point) produced essentially the same distribution of frequencies and transition dipoles as an individual atom cutoff (Figure S5).

During the model design stage, the calculated electric fields, as well as the frequencies and transition dipole derivatives, were used to train a random-forest regression model. The input is the 153 electric field components described above, and the output is the frequency and transition dipole derivative for the specified NH group. We chose this nonlinear model both because it offered better inference about the data than linear regression (measured by r²) and because it tends to give more reasonable predictions for rare cases where the input data falls outside the bounds of the training data. Such a model is robust to unexpected and complex environments. Random forest models tend to respond to an extreme input with an output close to the edge of that produced by the training data, which is a reasonable response for spectroscopy, where peaks do not generally shift past a certain point regardless of the extremes of the environment. In contrast, linear regression can produce wildly inaccurate predictions for even a small deviation from the training data bounds. However, the 153-point model was designed to capture as much local complexity as possible to avoid such edge cases. All r² values from the model were above 0.90 (see the SI for details).

In addition, a linear regression model was designed to determine the transition, off-diagonal, position matrix element defined as

$$x_{01}=\langle {\psi }_0\left|\widehat{x}\right|{\psi }_{\text{1}}\rangle$$ (1)

where ψ₀ is the ground state vibrational wave function and ψ₁ is the first excited vibrational state wave function. In the model, the input is the frequency of the specified NH mode, and the output is the transition position matrix element. The transition dipole could then be approximated to first order by multiplying the transition dipole derivative by the transition position matrix element. The combination of the random forest model and the linear regression model constitutes the NH mapping model developed herein. The SI provides more details about this model, including binaries that enable its direct use with Python.

To apply this model, an MD trajectory of the system is propagated using the same force fields as those used to train the model. For each configuration sampled, the electric fields induced by the solvent and ion charges, as well as the H-bonded carbonyl group charges for the H-bonded cases, are calculated for each NH group. The random forest regression map is used to determine the frequency and transition dipole derivatives from these electric fields, and the linear regression model is used to obtain the transition position matrix element from the frequency. These quantities can be used to compute IR, Raman, or SFG spectra. Note that the same map can also be used to compute higher-dimensional spectra from correlation functions, including 2D-IR. The development of the NH map is summarized in Figure 2.

Figure 2.

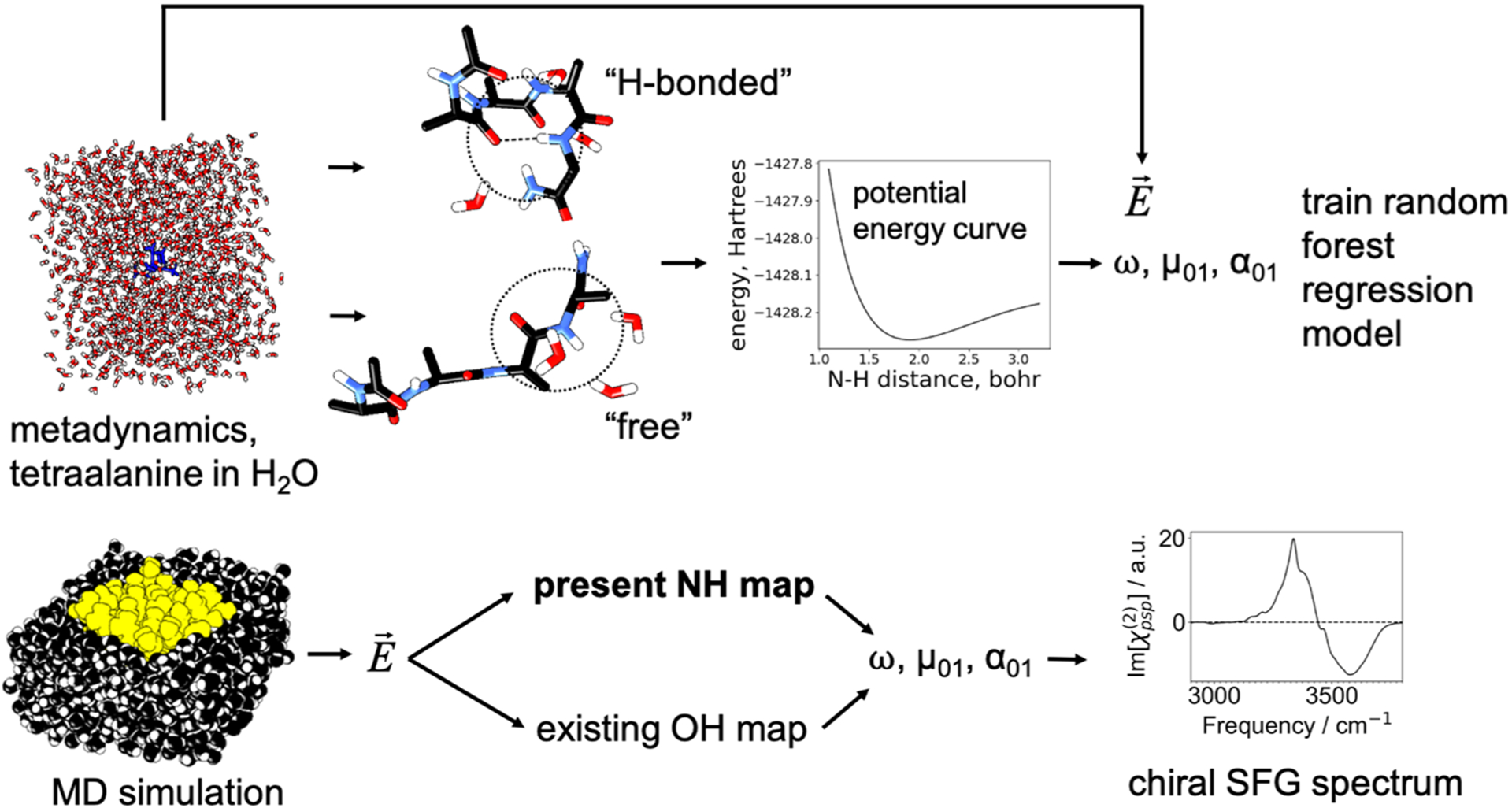
Top: H-bonded and free structures (400 each) were collected from a metadynamics simulation of tetraalanine in water, and each type of structure was used to produce a map for the corresponding type of environment. For a small cluster extracted from the system, the NH bond was stretched to map out a potential energy curve, and an anharmonic vibrational frequency was calculated. The transition dipole derivatives were estimated for a partially minimized structure of this cluster, and the transition dipole was approximated as the product of the dipole derivative and the transition position matrix element given in equation 1. The electric field was calculated near the NH group (Figure S1) from the MD simulation. The vibrational frequency and transition dipole were mapped to the electric field by a random forest regression model combined with a linear regression model. The transition polarizability was inferred partially from the transition position matrix element (equation 2). Bottom: The map was then used to estimate these quantities from an MD simulation of the protein (yellow) in aqueous solution (black), and a chiral SFG spectrum was generated.

Estimating the relative intensities of the NH and OH vibrational response.

When spectra due to both NH and OH responses are calculated, the relative magnitudes of quantities, such as the transition dipole and transition polarizability, are important. The polarizability was approximated as a bond polarizability, so that the transition polarizability is given by^{8, 70}

$${\alpha }_{01,\mathit{\text{ij}}}=(({{\alpha }^{\prime }}_{\parallel }-{{\alpha }^{\prime }}_{\perp })u_i{u}_j+{{\alpha }^{\prime }}_{\perp }(\widehat{i}·\widehat{j}))$$ (2)

where α₀₁ is the transition polarizability tensor, x₀₁ is given by equation 1, ${{\alpha }^{\prime }}_{\parallel }$ is the component of the bond polarizability parallel to the bond axis, ${{\alpha }^{\prime }}_{\perp }$ is the component of the bond polarizability perpendicular to the bond axis, u is the bond unit vector, and i and j are indices or unit vectors representing the x, y, and z directions. The second term is zero for chiral SFG, where the relevant polarizability component is either zy or zx,¹² so only the magnitude of the first term needs to be evaluated. For OH groups, Skinner and coworkers used an ${{\alpha }^{\prime }}_{\parallel }/{{\alpha }^{\prime }}_{\perp }$ ratio of 5.6.⁸ The precise value of this ratio only controls the magnitude of the chiral spectrum and does not change the lineshape, so for NH we chose to use the same ratio. The ratio of the magnitudes of the polarizability derivative $({{\alpha }^{\prime }}_{\text{iso,NH}}/{{\alpha }^{\prime }}_{\text{iso,OH}})$ was estimated by calculating the transition polarizability derivative matrix associated with the OH stretch for water and the NH stretch for NMA in vacuum to obtain the isotropic transition polarizability derivative magnitude using⁴³

$${{\alpha }^{\prime }}_{\mathit{\text{iso}}}=\frac{1}{3}({{\alpha }^{\prime }}_{\mathit{\text{xx}}}+{{\alpha }^{\prime }}_{\mathit{\text{yy}}}+{{\alpha }^{\prime }}_{\mathit{\text{zz}}})$$ (3)

where ${{\alpha }^{\prime }}_{xx}$, ${{\alpha }^{\prime }}_{yy}$, and ${{\alpha }^{\prime }}_{zz}$ are the diagonal components of the resulting tensor. This ratio (1.23/0.82) was then applied to the transition polarizability of NH as a prefactor in equation 2 to estimate the ratio of its magnitude to that of OH. Note that this ratio is quite close to unity, so the relative prominence of NH peaks in the combined NH and OH spectrum does not reflect a substantially larger transition dipole or polarizability, but rather the greater chiral ordering of the NH groups relative to the water and the contribution of only the first hydration shell to the water signal.²⁵ If we had simply assumed the transition polarizability derivatives were the same, the predicted spectra would have been very similar.

Intermediate configurations.

The design of the map considered only groups that were very far from a recipient carbonyl group to be free NH. In real systems, however, occasionally there is a nearby carbonyl but the H-bond between it and an NH group does not quite conform to our definition of a H-bond (i.e., the heavy atom donor−acceptor distance is greater than 3.2 Å). In this case, we assigned the NH group in question to the H-bonded map as long as the heavy atom donor−acceptor distance was less than 3.4 Å.

Calculating chiral SFG spectra using MD trajectories with electrostatic maps.

Chiral SFG spectra were calculated from MD trajectories as previously reported by our group,^{19, 20, 25} using a method originally developed by Skinner and coworkers.⁴¹ In brief, the spectra were calculated using an inhomogeneous limit approximation, which neglects dynamical effects but is much more computationally efficient than the time-dependent approach.^{8, 35} In particular, the absorptive (imaginary) component of the second-order response tensor component ${\chi }_{\text{IJK}}^{(2)}$ is approximated as⁴¹

$$\text{Im}[{\chi }_{\mathit{\text{IJK}}}^{(2)}(\omega )]\approx \text{Im}\left[\langle \sum _a^{N_{\mathit{\text{OH}}/\mathit{\text{NH}}}}\frac{\left(\sum _b^{N_{OH/NH}}{U}_{\mathit{\text{ba}}}{\alpha }_{01,}{}_b^{IJ}\right)\left(\sum _b^{N_{\mathit{\text{OH}}/\mathit{\text{NH}}}}{U}_{ba}{\mu }_{01,}{}_b^K\right)}{{\lambda }_a-\omega -\frac{i}{2\tau }}\rangle \right]$$ (4)

where ω is the response frequency, U is the eigenvector matrix of the exciton Hamiltonian, λ is the eigenvalue vector of the exciton Hamiltonian, α₀₁ is the transition polarizability tensor, μ₀₁ is the transition dipole vector, τ is the vibrational lifetime, and the indices a and b run over each OH and each NH group. The average is over all configurations sampled in the MD trajectory. The exciton Hamiltonian matrix in the local-mode basis contains vibrational frequencies on the diagonal and vibrational couplings on the off-diagonal. The technical details for the calculation of the couplings have been described in previous work.^{6, 8, 71} The transition dipole, transition polarizability, frequencies, and couplings are obtained from the electrostatic maps described above and in previous work.^{6, 8, 10, 19, 20, 25, 41, 43} To calculate chiral SFG spectra, the component ${\chi }_{\text{ZYX}}^{(2)}$ must be obtained from a uniaxial system (i.e., a system with C_∞ symmetry). To simulate the effect of a uniaxial system from an MD trajectory, the quantity ${\chi }_{\text{ZYX}}^{(2)}$ was obtained as ${\chi }_{\text{ZYX}}^{(2)}-{\chi }_{\text{ZYX}}^{(2)}$, as described in prior work.¹²

Experimental methods

The (L-) LK₇β (Ac-Leu-Lys-Leu-Lys-Leu-Lys-Leu-NH₂) (98.39% purity) and (L-) LE₇β (Ac-Leu-Glu-Leu-Glu-Leu-Glu-Leu-NH₂) (98.51% purity) peptides were obtained as lyophilized powders (GL Biochem Ltd., Shanghai). For heterodyne experiments on quartz substrate, stock solutions of (L-) LK₇β at 1.0 mM and (L-) LE₇β at 0.5 mM were made by dissolving the powders in H₂O (Millipore Synergy UV-R system, 18.2 MΩ), or in H₂¹⁸O (97%, SIGMA-ALDRICH Co., St. Louis, MO). The quartz substrate used in these experiments was a right-handed z-cut α-quartz crystal (Conex Systems Technology inc., San Jose, CA), which was rinsed with copious H₂O, dried with nitrogen, and plasma-cleaned (Harrick Plasma; PDC-32G) on “low” for 15 min. Samples were prepared by applying 5 – 10 μL of peptide solution directly onto the clean quartz substrate, which was subsequently dried in a sealed container, with desiccant. The quartz substrate was used as the phase reference to obtain internal heterodyne spectra using a broad-bandwidth SFG spectrometer⁷² following the procedure described previously.^{20, 25, 47} For the experiments at the air-water interface, 1 mM stock solutions of (L-) LK₇β and (L-) LE₇β were prepared. (L-) LE₇β was dissolved in phosphate buffer (10 mM pH = 7.4) and (L-) LK₇β was dissolved in H₂O. Then, 100 μL of the stock solutions were added to 3.9 mL of 10 mM phosphate buffer (pH = 7.4) in a Teflon dish using a Hamilton syringe to give a final peptide concentration of 25 μM. The intensity of the main NH peak was monitored to determine when the system reached equilibrium, roughly two hours after addition of peptide. Homodyne spectra were then obtained (see the SI). All stock solutions of the peptides were prepared in batches and separated into aliquots, which were then flash frozen in liquid nitrogen and stored at –80 °C. Aliquots were thawed on the day of the experiment and discarded after use.

Results and discussion

Model protein systems.

After developing our NH map, we applied to it two related protein systems, LK₇β and LE₇β. LK₇β is a seven-residue peptide consisting of alternating lysine residues (polar, hydrophilic) and leucine residues (nonpolar, hydrophobic).⁷³ LK₇β forms antiparallel β-sheets at the air-water interface, where the leucine residues point into the air and the lysine residues point into the water (Figure 3). LK₇β is positively charged due to the lysines and has been used as a model system for SFG studies.^44.74 LE₇β is a closely related peptide that has negatively charged glutamate residues instead of lysines. LE₇β is negatively charged but also forms β-sheets at the air-water interface. Folding at the interface makes LK₇β and LE₇β ideal model systems for chiral SFG, which is interface-selective. Computationally, we model LK₇β and LE₇β as pentamers consisting of antiparallel β-sheets surrounded by ~1350 water molecules at the vacuum-water interface. We also added 15 Cl⁻ ions to the LK₇β system and 15 Na⁺ ions to the LE₇β system to neutralize the charged residues. We have previously published both experimental spectra and calculations of the OH stretch response for LK₇β,^{20, 25} whereas LE₇β is a new system. We chose LE₇β as a second test system because although it is similar to LK₇β, it has a different polar sidechain with an opposite charge. Our aim was to determine if we could detect any differences in the antiparallel β-sheet structure between the two systems experimentally and computationally. By so doing, we could generate experimental benchmarks to test our computational methods. We have achieved qualitative agreement with experiment for LK₇β in the past.^{19, 20, 25} For example, the phase of our calculated spectra of water OH flips when the (D-) enantiomer is used instead of the native (L-) enantiomer, and the OH peaks appear approximately at the correct frequencies. However, the quantitative agreement was limited due to our inability to model the NH response of the protein backbone, which dominates the total chiral SFG response. Here, we test our new NH map with the LK₇β and LE₇β systems and compare to our experimental results.

Figure 3.

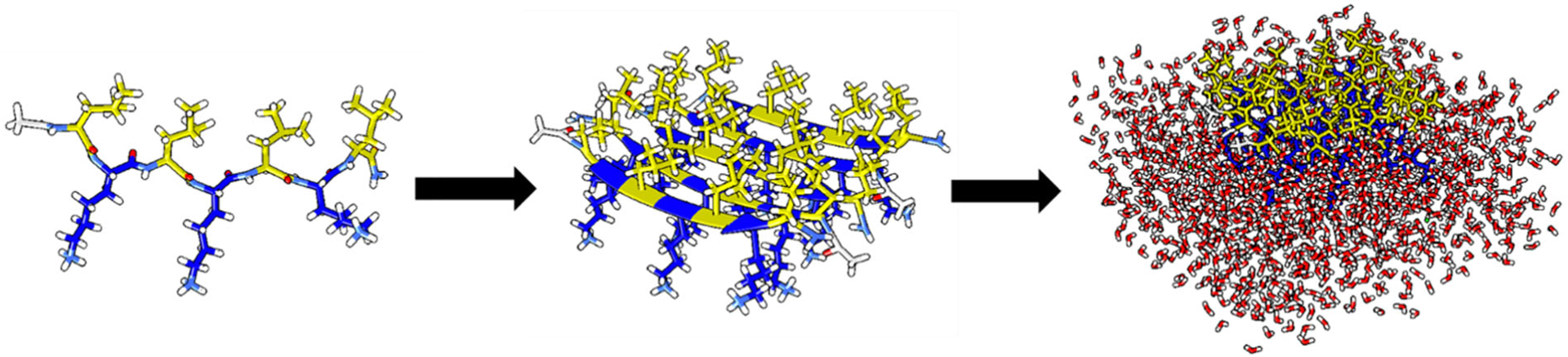
LK₇β is a peptide (Ac-LKLKLKL-NH₂) that assembles into antiparallel β-sheets at the air-water interface. Leucine residues are in yellow, lysine residues are in blue, and water molecules in the computational model are red. The polar lysine residues face into the aqueous phase, while the hydrophobic leucine residues face into the vacuum. LK₇β is modeled as a five-strand β-sheet with ~1350 water molecules around it. LE₇β forms the same structure (Figure S7), but with negatively charged glutamate residues facing the solvent instead of positively charged lysines.

Infrared (linear) response.

Although the NH response dominates chiral SFG, it is but a small component of the total vibrational response of these systems. Figure 4 shows the calculated IR spectrum of the LK₇β system, for water alone (black) and for the whole system (NH and OH), including vibrational couplings between and among NH and OH groups (red). The two spectra are almost identical. Therefore, the NH stretch contributes very little to the IR signal. This is the central problem with using the NH group as a probe of local hydrogen bonding structure – it is obscured by the water response. Chiral SFG solves this problem because the water signal is heavily suppressed due to the small number of water molecules in the first hydration shell. In addition, water molecules are not intrinsically chiral, and their chirality is a higher-order and therefore more subtle effect.²⁵ In contrast, the NH groups on the protein backbone are directly bonded to a chiral center, the α-carbon. Heterodyne detection further resolves NH and OH peaks from each other.

Figure 4.

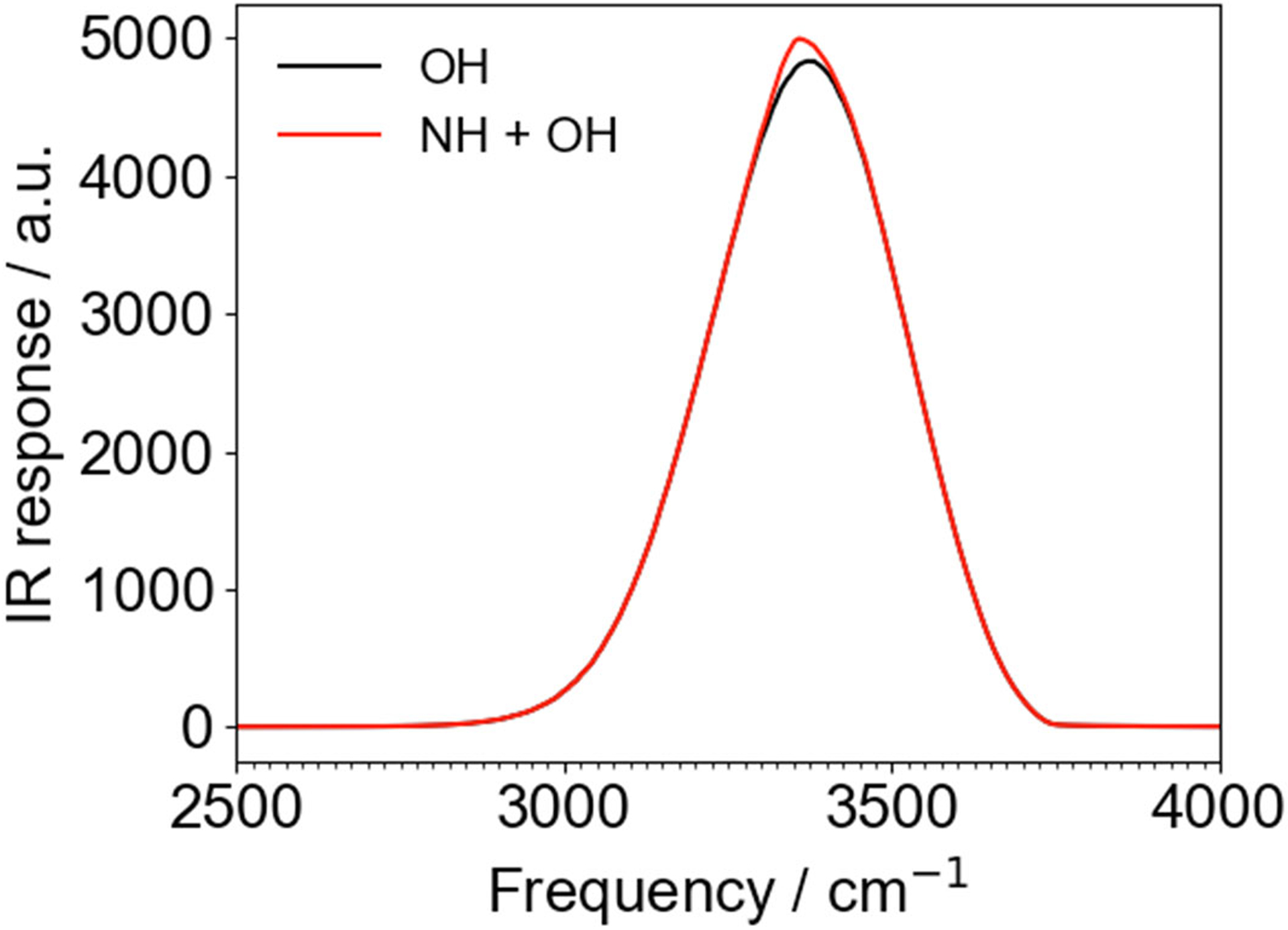
Computational IR spectra of the LK₇β system for water alone (OH, black) and for NH + OH (red), including all vibrational couplings between and within each type of stretch. The NH stretch contributes very little to the total IR spectrum. Spectra were obtained from 1 ns of sampling (100,000 configurations) using Skinner’s time averaging approximation⁷¹ to achieve a realistic peak width. All vibrational couplings were included. a.u. = arbitrary units.

Comparing computational and experimental results.

After calculating the IR response with a combination of Skinner’s OH map and our new NH map, we moved on to chiral SFG. Figure 5 shows the results of our calculations for the heterodyne response of LK₇β and LE₇β. The calculated spectrum for LK₇β (Figure 5a, i) consists of a positive, main peak at ~3336 cm⁻¹, a negative peak at ~3575 cm⁻¹, a small but distinct negative feature at ~3457 cm⁻¹, and a positive shoulder at ~3387 cm⁻¹. The calculated LE₇β spectrum (Figure 5a, ii) consists of a small low-frequency negative peak at ~3243 cm⁻¹, a shoulder at ~3303 cm⁻¹, a main peak at ~3346 cm⁻¹, a distinct but small negative feature at ~3467 cm⁻¹, and a high-frequency negative feature at ~3610 cm⁻¹. Comparison to heterodyne SFG experiments (Figure 5a, iii-iv) illustrates that we have achieved quite good agreement between experiment and theory for both systems, with both the main peaks and the subtler features. Almost every peak in the calculated spectra has a corresponding peak of the same phase and description in the experimental spectra. For example, the “main” positive peak in the LK₇β spectra at 3336 cm⁻¹ (Figure 5a, i) corresponds to a similar peak in the experiment at 3277 cm⁻¹ (Figure 5a, iii). Similarly, the calculated spectra capture the subtler features, for example the small negative feature at 3457 cm⁻¹ in the LK₇β calculated spectra (Figure 5a, i) corresponds to a very similar feature at 3463 cm⁻¹ in the experiment (Figure 5a, iii). The peak at ~3336 cm⁻¹ in the LK₇β spectrum is assigned to NH because it does not shift in the presence of H₂¹⁸O.²⁵ The shoulder to the blue of the main peak in the LK₇β spectrum and the small negative, kink-like, feature in both the LK₇β and LE₇β spectra are due to complex interactions between a broad OH peak and the main NH peak, as revealed in Figure 5b, i-iv. The high-frequency negative peak is due mostly to the OH stretch in both systems. The shoulder and the smaller, kink-like feature reveal how crucial it is to calculate the NH response as well as the OH response even if one is not interested in the protein response – some OH-related peaks appear only due to an NH/OH interaction. It is important to note that while the sign of a chiral SFG peak may depend in some way on orientation, there is currently no clear way to infer orientation from the sign of a peak, as is possible with some forms of conventional (achiral) SFG (for example, the ssp polarization setting).

Figure 5.

(a) Comparison of calculated chiral SFG spectra with heterodyne experimental results for LK₇β and LE₇β. Note the blue-shift of the main peak in LE₇β vs. LK₇β in both the experiment and the theory. All possible vibrational couplings are included. (b) NH-only and OH-only spectra, including only vibrational couplings within these groups. All peaks are labeled. Calculated spectra are averaged over 10,000,000 configurations spanning 100 ns. Data for LK₇β in panel 5a, iii was obtained from Konstantinovsky, Perets et al.²⁵ a.u. = arbitrary units.

The only major features missing in the calculated spectra are the low-frequency experimental signals at around 3125 cm⁻¹ in the LK₇β spectrum (Figure 5a, iii) and 3100 and 3175 cm⁻¹ in the LE₇β spectrum (Figure 5a, iv). This overall feature is common to both systems in the experiment and is perturbed when H₂¹⁸O is used as solvent, indicating a contribution from water.²⁵ This feature may be due to a Fermi resonance or other interaction not considered in the computational model. However, it is unlikely to originate from the Fermi resonance between the OH stretch and the water bend, because the resonance usually leads to features with higher frequency (around 3200 cm⁻¹).⁷⁵ Indeed, we tried including this Fermi resonance phenomenologically as a vibrational coupling with the OH stretch following Skinner’s recent work.⁷⁵ However, we could not computationally reproduce these low-frequency peaks (Figure S6). Our group continues to investigate the complex origins of these features.

The main peak in the theoretical and experimental heterodyne spectra (Figure 5), which is mostly due to the NH stretch, as revealed by comparison to the NH-only and OH-only peaks in Figure 5b, shifts by 10−15 cm⁻¹ between LK₇β and LE₇β in both the experimental and calculated spectra. In the experiment, it shifts from 3277 cm⁻¹ for LK₇β to 3290 cm⁻¹ for LE₇β. In the computed spectra, the shift is from 3336 cm⁻¹ to 3346 cm⁻¹. This suggests that at least some NH groups in LE₇β may experience weaker or fewer hydrogen bonds than the NH groups of LK₇β. This is somewhat unexpected because both systems form stable antiparallel β-sheet structures as revealed by Fourier-transform infrared (FTIR) characterization (Figure S7) and MD simulation. However, we analyzed the average number of backbone H-bonds in the two simulated systems, and found that an LK₇β pentamer typically contains ~20 “strong” H-bonds (r < 3.4 Å, angle > 135°) out of a possible ~24, whereas an LE₇β pentamer contains only ~17 on average. There are roughly 24 possible H-bonds between the strands because there are roughly six possible H-bonds between each pair of strands and there are four inter-strand spaces in a pentamer. The average “strong” H-bond length in LE₇β is also slightly longer (only by 0.005 Å, although this is statistically significant, p < 0.001 from a two-sided t-test). It seems that the lysine residues are a greater force for stabilizing the antiparallel β-sheet structure than are glutamate residues. Alternatively, the shift may be due to a more complicated interaction between the organizing forces of the nonpolar and polar residues. In any case, this finding illustrates how the NH stretch can be used as a sensitive probe of hydrogen bonding environments in proteins when its response is unmasked from the OH water stretches, even when the proteins are very closely related. These results demonstrate that it is possible to extract local structural information from the chiral SFG response of the protein NH stretch.

The chiral SFG spectra suggest that LE₇β has a weaker antiparallel β-sheet structure than LK₇β, but the differences do not stop there. Figure 5b shows that in the calculated OH-only spectra, the peaks due to the OH stretch are significantly red-shifted in the LE₇β spectrum (Figure 5b, iv) compared to the LK₇β spectrum (Figure 5b, iii) (from 3328 cm⁻¹ to 3290 cm⁻¹ for the positive peak, and from 3590 cm⁻¹ to 3560 cm⁻¹ for the negative peak). This suggests, perhaps paradoxically, that although LE₇β has a weaker β-sheet structure, its interactions with and chirality transfer to water may be somewhat stronger than the analogous LK₇β interactions. LE₇β possibly gives up some of its inter-strand interactions in favor of interactions with water molecules. In any case, it is clear how, together, the OH and NH stretch responses reveal a detailed picture of the structural similarities and differences of the two related biological systems.

Theory matches experiments at the air-water interface.

The heterodyne experiments were done with a quartz surface as a phase reference. This is somewhat of a different environment compared to the computational model, where the antiparallel β-sheet pentamers of LK₇β and LE₇β are at the vacuum-water interface. We wanted to see if a true air-water interface experiment would agree with our theoretical predictions as to the difference between LK₇β and LE₇β. We obtained the homodyne chiral SFG spectra at the air-water interface with both LK₇β and LE₇β in the spectral region of 3000–3800 cm⁻¹ and compared to the homodyne chiral SFG spectra predicted by the OH and NH maps (Figure 6). We find that the computational results match the experimental blue shift of the main peak for LE₇β relative to LK₇β (from 3340 to 3350 in the calculated spectra and from 3280 to 3305 in the experimental spectra) and correctly predict the lower-frequency peak to be by far the dominant feature. In the experiment the high-frequency response is very small, especially for LK₇β, although it is not zero (see inset, Figure 6). In the calculated spectrum, the high-frequency features are larger relative to the main peak, although they are still much smaller than the main peak. Overall, the calculated and experimental results exhibit good qualitative agreement.

Figure 6.

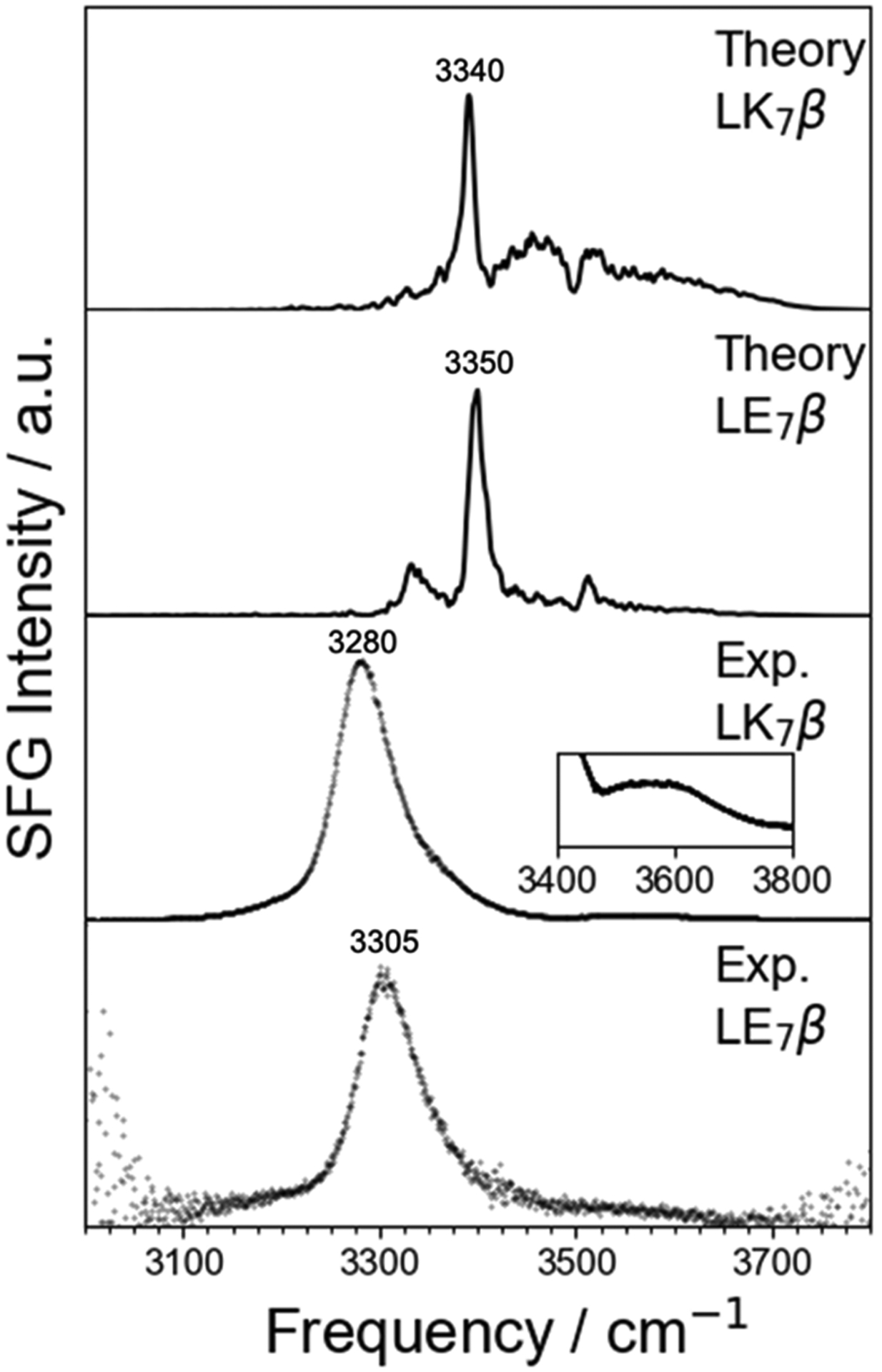
Comparison of calculated homodyne spectra and experimental homodyne results for LK₇β and LE₇β. Note the blue shift in both theory and experiment between LK₇β and LE₇β. The inset in the second plot from the bottom shows a detailed view of the high-frequency peak in the spectrum of LK₇β that is in relatively low in intensity but undergoes some fluctuation (see Figure S12). Key peaks are labeled. The computational spectra are not smoothed because the key peaks are very sharp. Calculated spectra are averaged over 10,000,000 configurations spanning 100 ns. a.u. = arbitrary units.

Although our map was designed to be robust and sensitive to complex biological environments, there are features that may affect its accuracy. The map was designed to work primarily with solvent-adjacent secondary structures. As a result, deeply buried structures, for which water is far away, may not perform as well as structures closer to the solvent. On the other hand, the electric field in the H-bonded configurations was dominated by the H-bonded carbonyl group, so buried NH groups interacting with carbonyl bonds could be expected to perform well using this map. Our observation of a disagreement between experiment and theory for the lower-frequency peaks in the homodyne spectra (Figure 6) as well as in the heterodyne spectra (Figure 5) suggests that the differences are due to a deficiency of the map rather than a difference in experimental and computational setups. The map was derived using a small, computationally tractable peptide surrounded by water molecules and implicit water solvent. It is possible that this environment was too aqueous and did not faithfully reproduce the environment experienced by secondary structures with more hydrophobic surroundings. Future applications of the NH map to larger proteins with true hydrophobic cores will test this assertion further. It may be necessary to develop an extended NH map using less polar implicit solvents to mimic hydrophobic cores. Another possibility is that the tetraalanine peptide used to develop the map does not adequately sample strongly hydrogen-bonded configurations as much as an actual protein backbone samples such configurations. Future refinements of the map may weight strongly bound configurations more in the training of the model to capture low frequencies more faithfully. In any case, the agreement with experiment found in the present work represents a significant step forward in the modeling of chiral SFG. This map may also be extendable to model other kinds of vibrational spectroscopy, including higher-order techniques such as 2D-IR.

It should be noted that although the lower frequencies are less accurate than higher frequencies using the current NH map, the map correctly predicts the qualitative effect of a strong H-bonding environment. Figure 7 shows the average NH stretch frequency predicted by the current map for each NH group in LK₇β. NH groups directly facing the solvent are shown as blue bars, and those facing inward are shown as yellow bars. It is clear, with a few exceptions, that the NH groups facing inward have a lower frequency than the NH groups facing the solvent. This is a result of a more stable H-bonding environment “inside” the structure compared to the exterior surface of the protein. The lowest average frequencies are found in the very center of the structure, as expected. Note that there are actually two different maps being used here (see Computational Methods), one for NH groups experiencing H-bonds with the protein and one for those not experiencing such H-bonds. Future studies using this map might reproduce Figure 7 for globular proteins and other structures with highly buried NH groups.

Figure 7.

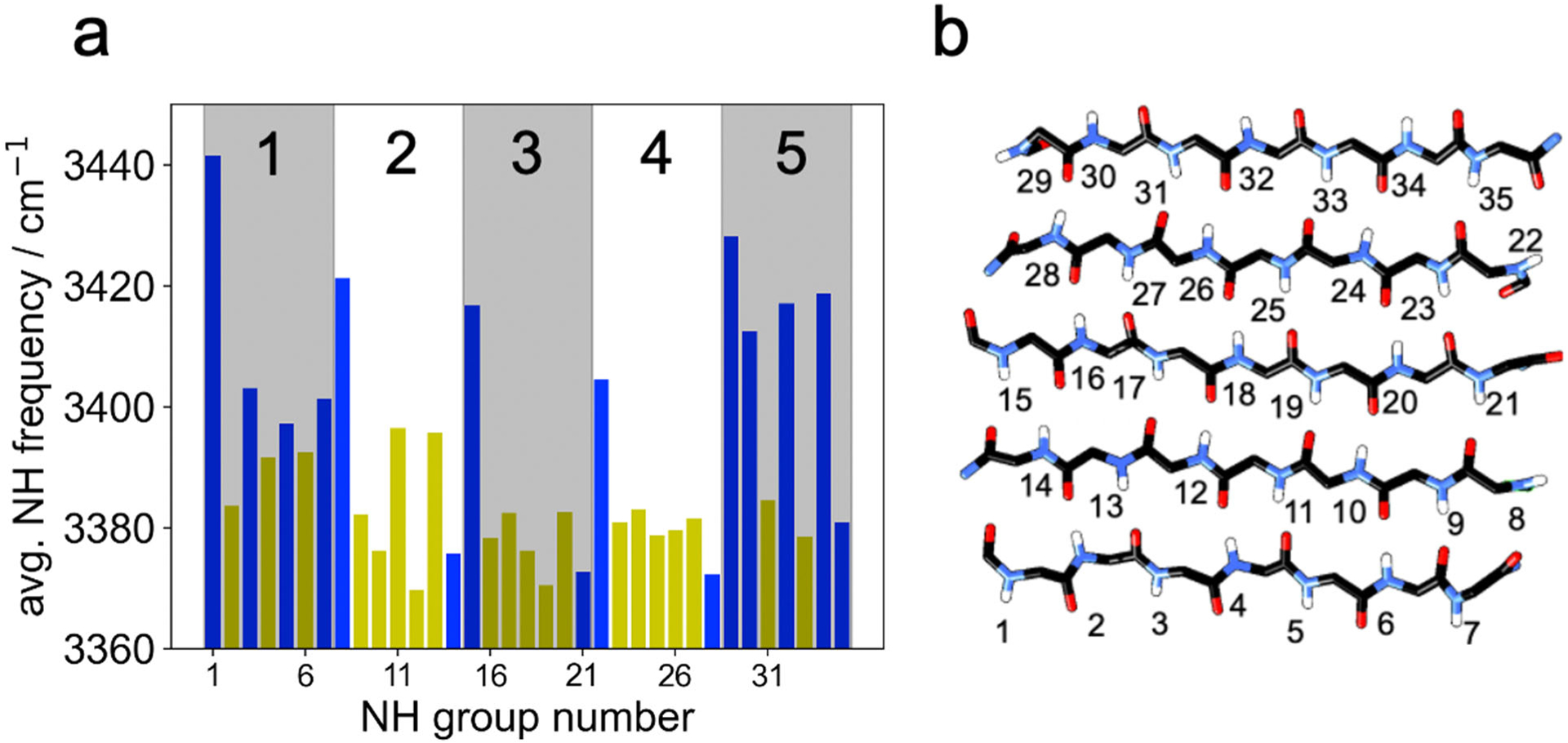
(a) Average NH frequencies in LK₇β by NH group number computed using our map. The shading highlights the different β-strands, which are numbered at the top. The blue bars correspond to NH groups pointing into the solvent, and the yellow bars correspond to NH groups on the inside of the β-sheet. The average frequencies were based on analysis of 100,000 configurations spanning 100 ns. For the most part, the NH groups pointing toward the core of the LK₇β pentamer (yellow) experience stronger H-bonding interactions than those facing the solvent (blue), corresponding to lower vibrational frequencies. (b) An illustration of the numbering scheme.

The role of vibrational couplings.

One of the central advantages of being able to model the NH stretch response is the newfound ability to model interactions between the NH and OH stretches, here modeled as transition dipole vibrational couplings.⁴² The data in Figure 8 shows the unexpected importance of these interactions for both systems we studied. The NH-only spectra for both systems look very little like the NH-derived components of the full spectra and exhibit poor agreement with experimental spectra. In particular, the NH-only spectra have a large negative peak at ~3352 cm⁻¹ (Figure 5b,i-ii and Figure 8) that is not present in the full spectra. Similarly, the OH-only spectra have a large negative peak at ~3590 cm⁻¹ (LK₇β) and ~3560 cm⁻¹ (LE₇β) (Figure 5b,iii-iv and Figure 8) that is severely attenuated and reshaped in the full spectra, even though there is no corresponding positive NH peak that could attenuate these peaks by simple addition. In fact, adding the NH-only and OH-only responses produces “total” spectra that are much farther from the experimental spectra than the modeled spectra that include vibrational couplings (Figure 8, uncoupled spectra). This suggests that vibrational couplings between NH and OH groups are a key component of the chiral SFG response, which is perhaps not surprising given that vibrational couplings play a formative role in the chiral SFG response of water by itself for fundamental, symmetry-related, reasons.¹⁹ Although these findings do not negate the assignment of chiral SFG peaks as “NH” or “OH” (the couplings are much smaller in magnitude than the vibrational frequencies), they do suggest that an OH peak may contain the influence of an NH oscillation, and vice versa. This may not be surprising, as we previously found that the majority of the chiral SFG signals of water arises from the first hydration shell of the protein.²⁵ In general, the true picture of these condensed-phase systems is one of highly delocalized vibrational excitons including many different molecular species. These findings show that vibrational chiral SFG is more than a way to enumerate molecular environments experienced by OH and NH groups. It is a way to study and document the complex interactions between these species. Thus, interactions that would produce a slight frequency shift (if that) in linear (e.g., IR) spectroscopy radically reshape chiral SFG spectra and are more visible as a result.

Figure 8.

The effect of vibrational coupling between NH and OH groups on the calculated chiral SFG spectra and comparison with experimental spectra. (a) Spectra for LK₇β and (b) spectra for LE₇β. Experimental data for LK₇β in (a) was obtained from Konstantinovsky, Perets et al.²⁵ a.u. = arbitrary units.

Treatment of hydrogen bonds of intermediate length.

When we gathered tetraalanine configurations for the H-bonded and free NH maps, we used a H-bond cutoff of 3.2 Å between the heavy atom donor and acceptor. This cutoff was chosen to ensure that the H-bonded configurations accurately represented the typical situation of an NH group inside a β-sheet or α-helix. Free configurations were gathered exclusively from unfolded tetraalanine molecules for the same reason. In real systems, however, H-bonds within a secondary structure are occasionally slightly longer but in all other ways resemble the H-bonded tetraalanine configurations more than the free configurations. These situations were treated using the H-bonded map rather than the free map, and the H-bond distance cutoff used for the calculation of the SFG spectra was 3.4 Å to capture these edge cases. We found that assigning the edge cases to the H-bonded versus free map did not significantly change the chiral SFG spectrum, except by making the OH-related shoulder at 3380 cm⁻¹ more pronounced in the 3.4 Å case (Figure S2). This similarity also shows that the H-bonded and free maps generally agree quite well on the edge cases, where an inter-residue H-bond is nearly broken. This analysis suggests that the two maps cover the entire range of likely environments around an NH group with some degree of overlap.

The NH group as a useful vibrational probe.

Although a great deal of effort has been directed toward developing electrostatic maps for water and the amide modes,^{6, 8, 11, 12, 14, 15, 71} few groups have pursued the NH stretch.⁴⁹ The main reason for the smaller number of models developed for the NH stretch is that this mode is difficult to observe experimentally due to the overwhelming OH stretch of water. This problem is largely solved by chiral SFG, where the NH signal is prominent due to the chiral nature of proteins and the enhanced peak resolution afforded by heterodyne detection. In contrast, the water signal is relatively small because only the water molecules in the first hydration shell contribute significantly to the chiral SFG signal from OH groups.²⁵ Thus, chiral SFG is an ideal technique to study the environments experienced by NH groups in complex biological systems with the caveat that “NH” peaks may contain solvent contributions as well if they are not buried in a hydrophobic pocket. The presence of NH-like groups on amino acid sidechains is unlikely to cause problems for chiral SFG. The fact that we were able to reproduce almost all spectral features computationally for LK₇β while completely ignoring the lysine NH₃⁺ groups suggests that the high degree of chiral ordering of the backbone eclipses any signal from the flexible sidechains. We have also shown previously that the water molecules near the NH₃⁺ groups produce minimal chiral SFG signal, possibly due to the ability of positive charge to disrupt water structure.²⁵

Conclusion

The NH stretch map developed in this paper enables the simulation of full chiral SFG spectra of aqueous proteins in the 3000–4000 cm⁻¹ range. The NH maps developed herein have distinct advantages over previously developed maps for modeling vibrational responses. First, they were designed to model the protein environment around the NH group using a tetraalanine peptide. Second, the design of these maps included the effect of solvent both explicitly (through the inclusion of nearby water molecules in the tetraalanine configurations) and implicitly (through C-PCM implicit solvation in the DFT calculations of the NH frequencies), thereby driving the NH frequency down to the experimental range. Third, the map is based on a complete survey of the local environment through the electric field at 51 points around the NH, including points beyond the NH bond. Finally, the dependence of the transition dipole moment on the local environment is included by mapping the transition dipole to the local electric field. However, one limitation of the current map is that it was created with the AMBER ff14SB force field⁶⁹ and TIP4P-Ew⁵⁴ water and therefore must be used with these force fields to ensure accuracy.

Most importantly, this work has revealed the NH stretch to be a potent reservoir of information about the local environment of the amide group, on par with the more-studied amide I mode. Chiral SFG is ideally suited to probing this mode, as the problems of OH interference almost disappear with this technique. One aspect of the OH stretch response that does not disappear, however, is the coupling of this response to the NH response. We show that coupling between the OH and NH stretch modes is vital to the creation of the chiral SFG lineshape. This finding has implications for the ability of researchers to label peaks as “OH” or “NH” via fitting or even with H₂¹⁸O labeling. This work paves the way for the NH stretch to become a more useful, informative probe in the biological spectroscopy community. Although it can be probed easily by chiral SFG, the NH stretch can also serve as a probe for other vibrational spectroscopy methods such as 2D-IR, which can be modeled with the same type of NH electrostatic maps. Thus, the NH maps developed in this work have implications for a wide range of vibrational spectroscopies applied to diverse chemical and biological systems.