Dual-energy CT Based Mass Density and Relative Stopping Power Estimation for Proton Therapy Using Physics-informed Deep Learning

Abstract

Proton therapy requires accurate dose calculation for treatment planning to ensure the conformal doses are precisely delivered to the targets. The conversion of CT numbers to material properties is a significant source of uncertainty for dose calculation. The aim of this study is to develop a physics-informed deep learning (PIDL) framework to derive accurate mass density and relative stopping power (RSP) maps from dual-energy computed tomography (DECT) images. The PIDL framework allows deep learning (DL) models to be trained with a physics loss function, which includes a physics model to constrain DL models. Five DL models were implemented including a fully connected neural network (FCNN), dual-FCNN (DFCNN), and three variants of residual networks (ResNet): ResNet-v1 (RN-v1), ResNet-v2 (RN-v2), and dual-ResNet-v2 (DRN-v2). An artificial neural network (ANN) and the five DL models trained with and without physics loss were explored to evaluate the PIDL framework. Two empirical DECT models were implemented to compare with the PIDL method. DL training data were from CIRS electron density phantom 062M (Computerized Imaging Reference Systems, Inc., Norfolk, VA). The performance of DL models was tested by CIRS adult male, adult female, and 5-year-old child anthropomorphic phantoms. For density map inference, the physics-informed RN-v2 was 3.3%, 2.9% and 1.9% more accurate than ANN for the adult male, adult female, and child phantoms. The physics-informed DRN-v2 was 0.7%, 0.6%, and 0.8% more accurate than DRN-v2 without physics training for the three phantoms, respectfully. The results indicated that physics-informed training could reduce uncertainty when ANN/DL models without physics training were insufficient to capture data structures or derived significant errors. DL models could also achieve better image noise control compared to the empirical DECT parametric mapping methods. The proposed PIDL framework can potentially improve proton range uncertainty by offering accurate material properties conversion from DECT.

1. Introduction

Proton therapy can deliver conformal doses to tumor targets and spare normal tissues with minimum irradiation to reduce patients’ short- or long-term side effects. Conventional proton treatment planning systems (TPS) utilize either analytical dose calculation (ADC) (Schuemann et al., 2015; Yepes et al., 2018; Liang et al., 2019) or Monte Carlo dose calculation (MCDC) algorithms (Paganetti et al., 2008; Saini et al., 2017; Chang et al., 2020) to design treatment plans. These dose calculation algorithms require information on the relative stopping power (RSP) or mass density (MD) of patients. This information is typically acquired from single-energy computed tomography (SECT) applying CT-number-to-RSP or CT-number-to-mass-density conversion curves, calibrated using the stoichiometric method (Schneider et al., 1996; Schneider et al., 2000). However, this method relies on linear fitting. The model performance can be compromised by the data quality (Dinh, 2013) such as data quantity and uncertainty of calibration materials. Besides, the linear model form limits the model performance even if extensive data are used (Ratner, 2011). Furthermore, materials with different compositions may have the same CT number from SECT, and the conventional calibration curves cannot settle this ambiguity problem. Hence, a margin of 3.5% is typically reserved for proton range uncertainty (Paganetti, 2012).

Dual-energy computed tomography (DECT) has been deployed to characterize human tissues for diagnosis (McCollough et al., 2015), and DECT's virtual monochromatic images (VMI) can improve beam-hardening artifacts and increase image quality (Yu et al., 2012). DECT can be also used to estimate effective atomic number (${\mathit{Z}}_{\mathit{eff}}$) and relative electron density to that of water (${\mathit{\rho }}_{\mathit{e}}$), and these parametric maps can be used to determine proton RSP (Bär et al., 2017) for ADC (Wohlfahrt et al., 2017). In general, DECT can be utilized to infer more exact proton RSP than SECT (Yang et al., 2012). However, the DECT-based stoichiometric method (Bourque et al., 2014) used a fixed form of the fitting model, and it is not trivial to simultaneously include additional DECT’s images such as VMI with multiple energies, ${\mathit{Z}}_{\mathit{eff}}$, and ${\mathit{\rho }}_{\mathit{e}}$ in an existed calibration model. To develop a new model to adapt additional DECT images, it generally requires extensive efforts to gain the insights and mechanistic understanding. As an alternative to mechanistic and semi-analytical models, it is viable to disclose the underlying correlations between DECT parametric maps and material mass density and RSP by modern machine learning (ML) methods.

Model inference of many traditional ML algorithms tend to follow Occam’s razor: the simplest model is preferable due to its interpretability and generalizability (Blumer et al., 1987; Domingos, 1999). However, the approach is limited by data complexity (Champion et al., 2019). On the contrary, deep learning (DL) (LeCun et al., 2015) can deploy hierarchical model layers to uncover complex structures from data. Hornik et al. (Hornik et al., 1989) proved that neural networks with multilayer perceptrons are universal approximators that can capture the properties of any measurable information. Su et al. (Su et al., 2018) used electron density phantoms to demonstrate that ML models achieved DECT parametric mapping for RSP with the uncertainty of ~9% and ~3% for lung and bone.

Physics-informed machine learning (Chang and Dinh, 2019; Karniadakis et al., 2021) has exhibited the advantage of integrating noisy data, insufficient data, and physics models during DL training. In the present work, we couple a physics model in the training of DL models and formulate a physics-informed DL framework to learn the human tissue surrogates from electron density phantoms and predict mass density and RSP maps for anthropomorphic phantoms with different body sizes and material compositions. The framework can adapt various DL models with different degrees of freedom. To evaluate the framework's performance for clinical applications, we investigate conditions by which DL models can benefit from the physics-informed training to work compatibly, stably, and effectively for DECT parametric mapping.

2. Materials and methods

2.1. Data acquisition and phantoms

The images of a CIRS electron density 062M phantom (Computerized Imaging Reference Systems, Inc., Norfolk, VA, USA) scanned with DECT was used to train DL models to establish correlations between DECT images and material properties. Table 1 gives the physical properties of CIRS 062M, which includes 17 inserts from 9 types of tissue surrogate. Each tissue surrogate has redundant inserts except for the bone 1250 mg/cc. A Siemens SOMATOM Definition Edge scanner was used to scan phantoms, and the CT acquisition and reconstruction parameters for all scans includes the tube voltage of 120 kVp, single collimation width of 0.6 mm, reconstruction method and kernel of sinogram-affirmed iterative reconstruction (SAFIRE) and Qr40 with iterative beam hardening correction using Siemens Syngo.CT VB20A. The phantom was scanned using TwinBeam dual-energy (TBDE) protocols with a CT dose index (CTDI_vol, _32cm) of 11.57 mGy and effective milliampere-seconds (${\text{mAs}}_{\text{eff}}$) of 541.

Table 1.

Ground truth mass densities and RSPs (based on Eq. (1)), as well as mean excitation energies and elemental compositions for the CIRS 062M and CIRS Atom M701, M702, and M705 phantoms.

	Tissue surrogate	$\mathit{\rho }\left(\text{g/c}{\text{m}}^{\text{3}}\right)$	RSP	$\text{I}\left(\text{eV}\right)$	H	C	N	O	Mg	P	S	Cl	Ca	Ba
CIRS062M	Lung (Inhale)	0.203	0.202	67.8	8.59	65.92	3.52	19.27				1.69	1.01
	Lung (Exhale)	0.494	0.492	67.3	8.87	66.00	2.38	20.41				0.61	1.73
	Adipose	0.965	0.977	64.2	9.97	71.36	1.79	16.37				0.19	0.32
	BreastTissue	0.996	1.003	65.2	9.60	70.33	1.92	17.02				0.19	0.94
	Muscle	1.059	1.059	66.6	9.07	69.78	2.07	16.80				0.12	2.16
	Liver	1.072	1.070	66.8	8.97	69.45	2.12	17.14				0.13	2.19
	Bone 200 mg/cc	1.157	1.116	76.2	7.00	56.30	2.00	22.70		3.30		0.20	8.50
	Bone 800 mg/cc	1.520	1.404	90.4	4.45	39.11	0.87	33.72				0.05	21.77	0.03
	Bone 1250 mg/cc	1.830	1.647	101. 5	3.60	28.82	1.09	31.99		10.79	0.08	0.04	23.27	0.32
CIRS Atom	Lung	0.205	0.204	67.8	8.59	65.89	3.52	19.29				1.69	1.01
	Breast	0.991	0.982	70.4	9.60	70.26	1.93	17.00				0.20	9.40
	Soft Tissue	1.055	1.041	70.4	8.47	57.44	1.65	24.59	7.62			0.19
	Spinal Cord	1.065	1.035	73.4	7.36	54.27	2.17	26.59	9.37			0.22
	Brain	1.069	1.049	72.2	8.16	53.60	1.53	26.49	9.98			0.19
	(M701/M702)	1.586	1.410	88.3	4.83	37.03	0.97	35.66	6.19			0.05	15.24
	Bone (M705)	1.518	1.422	85.5	5.23	41.63	1.11	33.31	3.54			0.05	15.09

The RSP of each tissue surrogate is calculated by Eq. (1) (Bichsel, 1969) where ${\mathit{\rho }}_{\mathit{e}}$, $m_{\text{e}}$, $c$, $\beta$, and $I_m$ are the relative electron density, electron mass, speed of light, proton velocity relative to the speed of light, and mean ionization potential of phantom media. The $\beta$ and ${\text{I}}_{\mathit{water}}$ in Eq. (1) are obtained using proton energy of 210 MeV and mean ionization potential of 78 eV (Seltzer S M, 2014).

$$RSP\hspace{0.17em}=\hspace{0.17em}{\rho }_e\left\{\frac{\text{ln}\left[\frac{2m_e{c}^2{\beta }^2}{l_m\left(1-{\beta }^2\right)}\right]-{\beta }^2}{\text{ln}\left[\frac{2m_e{c}^2{\beta }^2}{l_{water}\left(1-{\beta }^2\right)}\right]-{\beta }^2}\right\}$$ (1)

Two DECT scans were acquired with different insert arrangements, and each scan contained $512 \text{x} 512 \text{x}\hspace{0.17em}79$ voxels. Figure 1 depicts the setup of DECT scans. During the scans, the electron density phantom was placed between solid water phantoms with a thickness of 10 cm to avoid CT artifacts.

Figure 1.

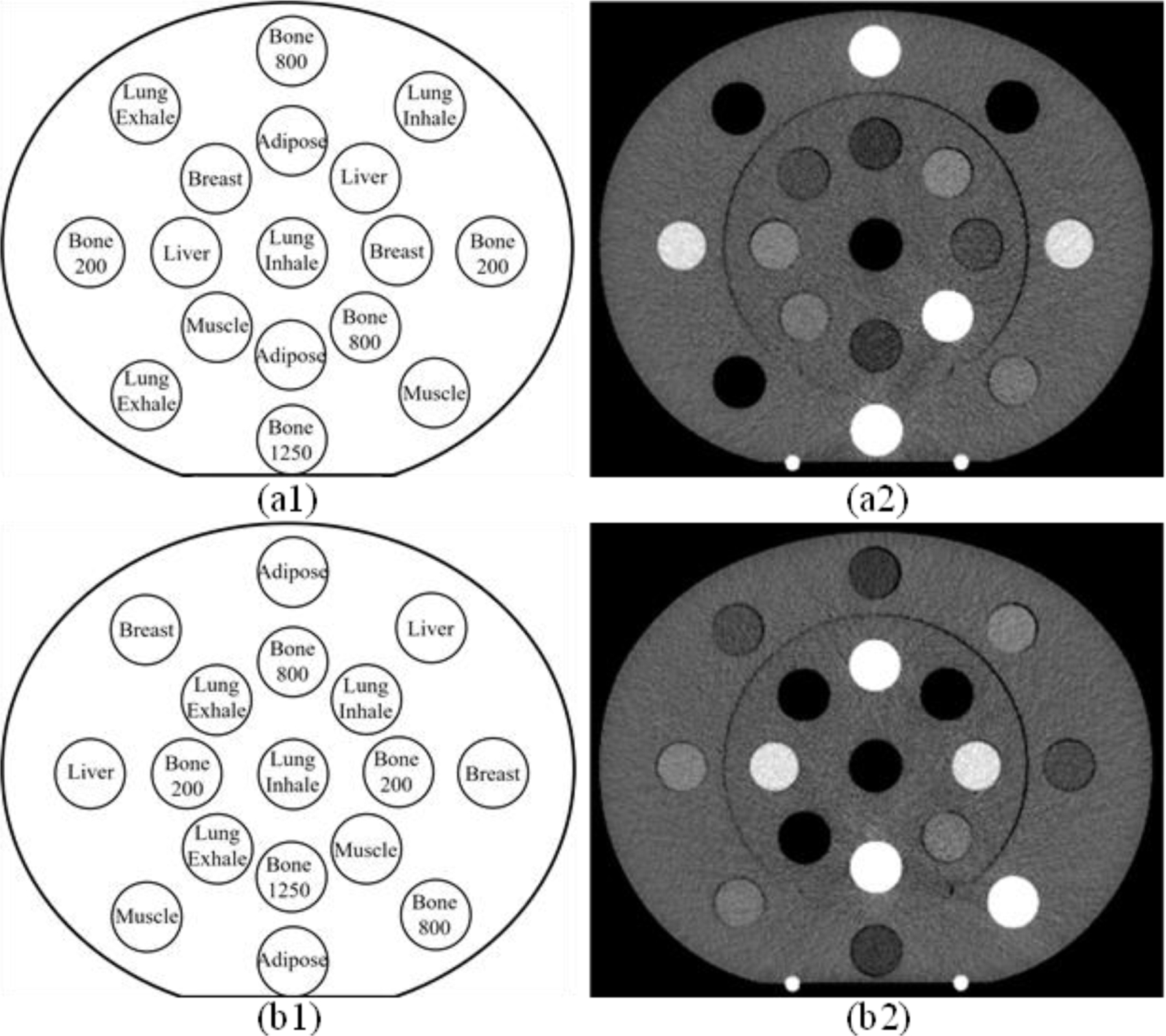
Transversal representation of CIRS 062M electron density phantom configuration for (a1) the first DECT scan and (a2) corresponding VMI of 80 keV and (b1) the second DECT scan and (b2) corresponding VMI of 80 keV.

The CIRS ATOM M701 (adult male), M702 (adult female), and M705 (5-year-old child) anthropomorphic phantoms (Computerized Imaging Reference Systems, Inc., Norfolk, VA) were used to validate DL results. Separate CT scans were made for the head-and-neck (HN), thorax, and pelvis regions of the phantoms, applying body-site specific TBDE CT protocols for each region. For a head-and-neck (HN) TBDE protocol, scans of M701, M702, and M705 contain $\text{512 x 512 x 683}$, $\text{512 x 512 x 605}$, and $\text{512 x 512 x 1286}$ voxels. For M701 and M702, thorax TBDE scans include $\text{512 x 512 x 641}$ and $\text{512 x 512 x 625}$ voxels while pelvis scans involve $\text{512 x 512 x 415}$ and $\text{512 x 512 x 517}$ voxels, respectively. Table 2 shows the CTDI_vol, _32cm and effective milliampere-seconds for different TBDE protocols at each site. For the 5-year-old child phantom, only a TBDE HN protocol was used. The material properties of the anthropomorphic phantoms are provided in Table 1. The tissue-mimicking materials are almost the same for each phantom except for bone. All DECT images were reconstructed using the same reconstruction setting with a diameter of 500 mm and slice thickness of 0.5 mm. Siemens Syngo.Via was used to generate DECT parametric maps such as relative electron density (${\mathit{\rho }}_{\mathit{e}}$), effective atomic number (${\text{Z}}_{\mathit{eff}}$), and VMI of 80, 135, and 190 keV. Table 3 and Table 4 give the reference and Syngo.Via values of ${\mathit{\rho }}_{\mathit{e}}$ and ${\text{Z}}_{\mathit{eff}}$ for the electron density and anthropomorphic phantoms.

Table 2.

CTDI_{vol, 32cm} and effective milliampere-seconds for DECT scans of the CIRS anthropomorphic phantoms using different TBDE protocols at each body site.

		CTDIvol, 32cm (mGy) / effective milliampere-seconds (mAseff)
		HN	Thorax	Pelvis
M701	15.63 / 729		6.99 / 327	9.63 / 450
M702	15.70 / 732		3.97 / 186	6.09 / 284
M705	11.51 / 537		-	-

Table 3.

Values of relative electron densities (${\rho }_e$) and effective atomic numbers ($Z_{eff}$) from reference and Syngo.Via for the CIRS 062M electron density phantom.

	Reference		Syngo.Via
	${\rho }_e$	$Z_{eff}$	${\rho }_e$	$Z_{eff}$
Lung (Inhale)	0.190	7.332	0.227 ± 0.021	-
Lung (Exhale)	0.488	7.382	0.504 ± 0.021	-
Adipose	0.949	6.370	0.965 ± 0.019	6.420 ± 0.972
BreastTissue	0.976	6.766	0.992 ± 0.020	6.656 ± 0.815
Muscle	1.042	7.383	1.035 ± 0.020	7.514 ± 0.626
Liver	1.052	7.409	1.054 ± 0.021	7.459 ± 0.655
Bone 200 mg/cc	1.116	10.055	1.107 ± 0.025	9.804 ± 0.442
Bone 800 mg/cc	1.454	12.566	1.391 ± 0.029	12.802 ± 0.277
Bone 1250 mg/cc	1.694	13.456	1.621 ± 0.036	13.652 ± 0.285

Table 4.

Values of relative electron densities (${\rho }_e$) and effective atomic numbers ($Z_{eff}$) from reference and Syngo.Via for the CIRS adult male (M701), adult female (M702), and 5-year-old child (M705) phantoms.

	Reference			Syngo.Via
	${\rho }_e$		$Z_{eff}$	${\rho }_e$			$Z_{eff}$
				M701	M702	M705	M701	M702	M705
Lung	0.200		7.332	0.207 ± 0.019	0.208 ± 0.018	0.216 ± 0.015	-	-	-
Breast	0.976		6.769	-	0.965 ± 0.022	-	-	7.282 ± 0.687	-
Soft Tissue	1.028		7.187	1.031 ± 0.029	1.031 ± 0.025	1.025 ± 0.014	7.110 ± 1.044	7.165 ± 0.859	7.342 ± 0.360
Spinal Cord	1.027		7.426	1.062 ± 0.031	1.060 ± 0.023	1.046 ± 0.013	6.691 ± 1.590	6.921 ± 1.139	7.537 ± 0.428
Brain	1.039		7.438	1.053 ± 0.011	1.047 ± 0.010	1.046 ± 0.008	7.408 ± 0.315	7.420 ± 0.303	7.433 ± 0.219
Bone (M701/M702)	1.495		11.634	1.437 ± 0.050	1.443 ± 0.042	-	11.741 ± 0.742	11.651 ± 0.654	-
Bone (M705)	1.436		11.481	-	-	1.387 ± 0.028	-	-	11.475 ± 0.284

2.1.1. RSP measurement for CIRS M701 adult male phantom using protons

We used a 208 MeV proton spot and Zebra (IBA Dosimetry, Germany) to measure the RSP of lung, soft tissue, brain, and bone surrogates for the CIRS M701 adult male phantom since the material compositions of these tissue surrogate are identical for the CIRS anthropomorphic phantoms. The proton spot was delivered by Varian ProBeam System (Varian Medical Systems, Palo Alto) with a cyclotron current of 20 nA and the spot sigma of 3.79 mm at the ISO center. Figure 2 depicts the experiment setup. The beam ISO center was set at the phantom surface. The thickness of each phantom slab is 25 mm. The 80% distal range (R80) differences from the measurement with and without phantom slabs were used to compute the water equivalent thickness (WET). The Zebra measurement includes range uncertainty of $\pm \text{0}.5 mm$. The measured RSP can be obtained using WET divided by the thickness of phantom slabs. Then we derived the reference mass density using Eq. (1) by adjusting material mass densities to match the measured RSP. The measured RSP values for lung, soft tissue, brain, and bone surrogates are 0.201, 1.040, 1.050, and 1.410, and the reference mass densities are 0.202, 1.054, 1.070, and 1.517 g/cm³, respectively.

Figure 2.

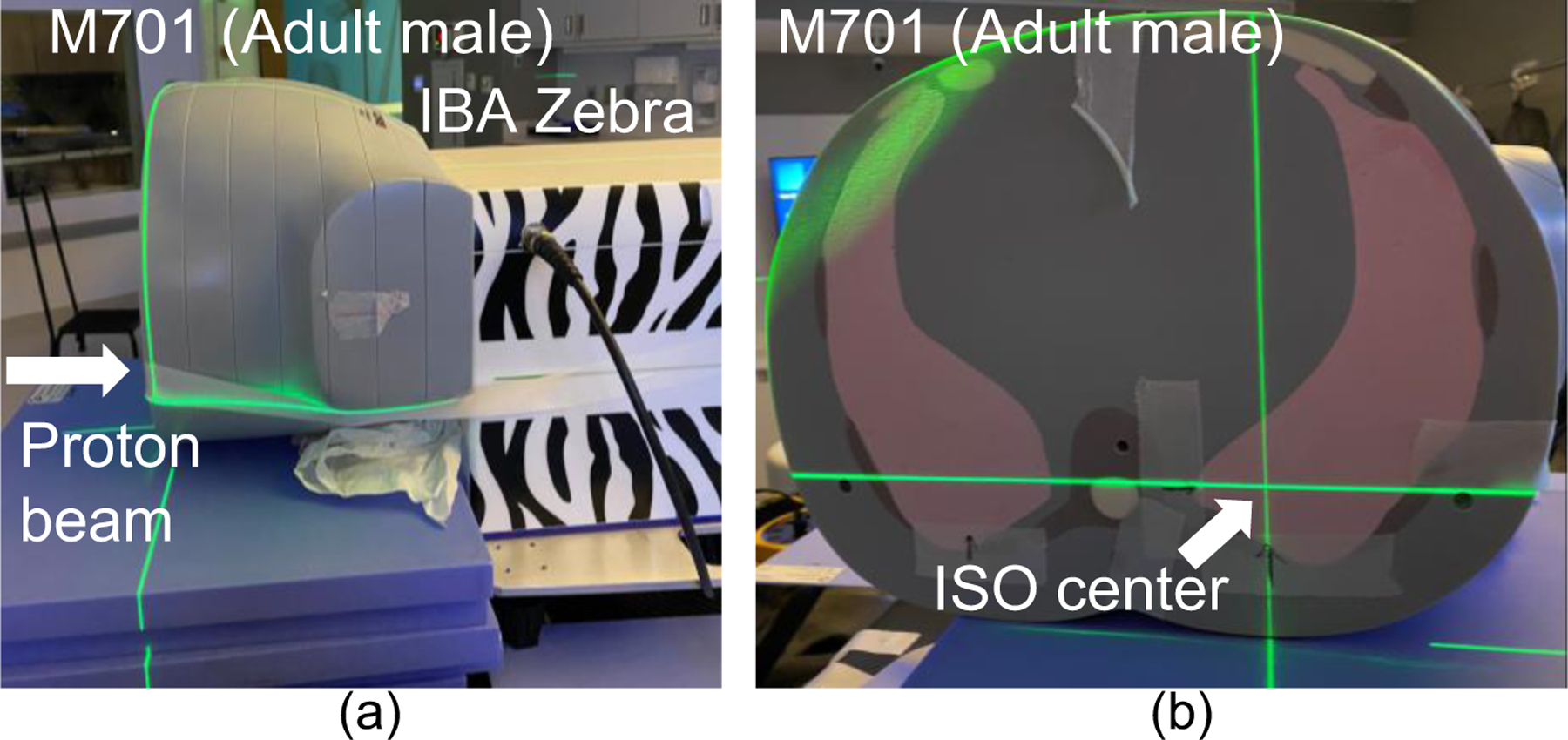
(a) Proton RSP measurement setup for CIRS M701 adult male phantom using Zebra with a 208 MeV proton beam. (b) ISO center of the proton beam for lung RSP measurement.

2.2. Physics-informed deep learning for DECT parametric mapping

Figure 3 portrays the physics-informed deep learning (PIDL) framework to achieve DECT parametric mapping and generate mass density and RSP maps. PyTorch (Paszke, 2019) was used for DL model implementation, and the model inputs include DECT parametric maps of ${\text{Z}}_{\mathit{eff}}$, ${\mathit{\rho }}_{\mathit{e}}$, VMI of 80, 135, and 190 keV, and DECT images from high/low energy spectra. At the training phase, central 79 CT slices from the two scans (given in Figure 1) of the electron density phantom were used, and we manually contoured circular regions of interest for each insert with a diameter of 24 pixels. Then each insert region from each DECT image was arranged to a 1-dimensional (1D) array such that the training input layer contains the size of 1242828 x 7 (total voxels x input images), and the output layer returns values of mass density and RSP simultaneously. Section 2.2.2. provides details about how the physics model tightly interacts with DL models utilizing physics quantities based on material compositions from a CIRS electron density phantom. This approach allows the model response to be constrained by physics knowledge. The performance of the PIDL framework is assessed by three CIRS anthropomorphic phantoms that include different body sizes and bone material compositions.

Figure 3.

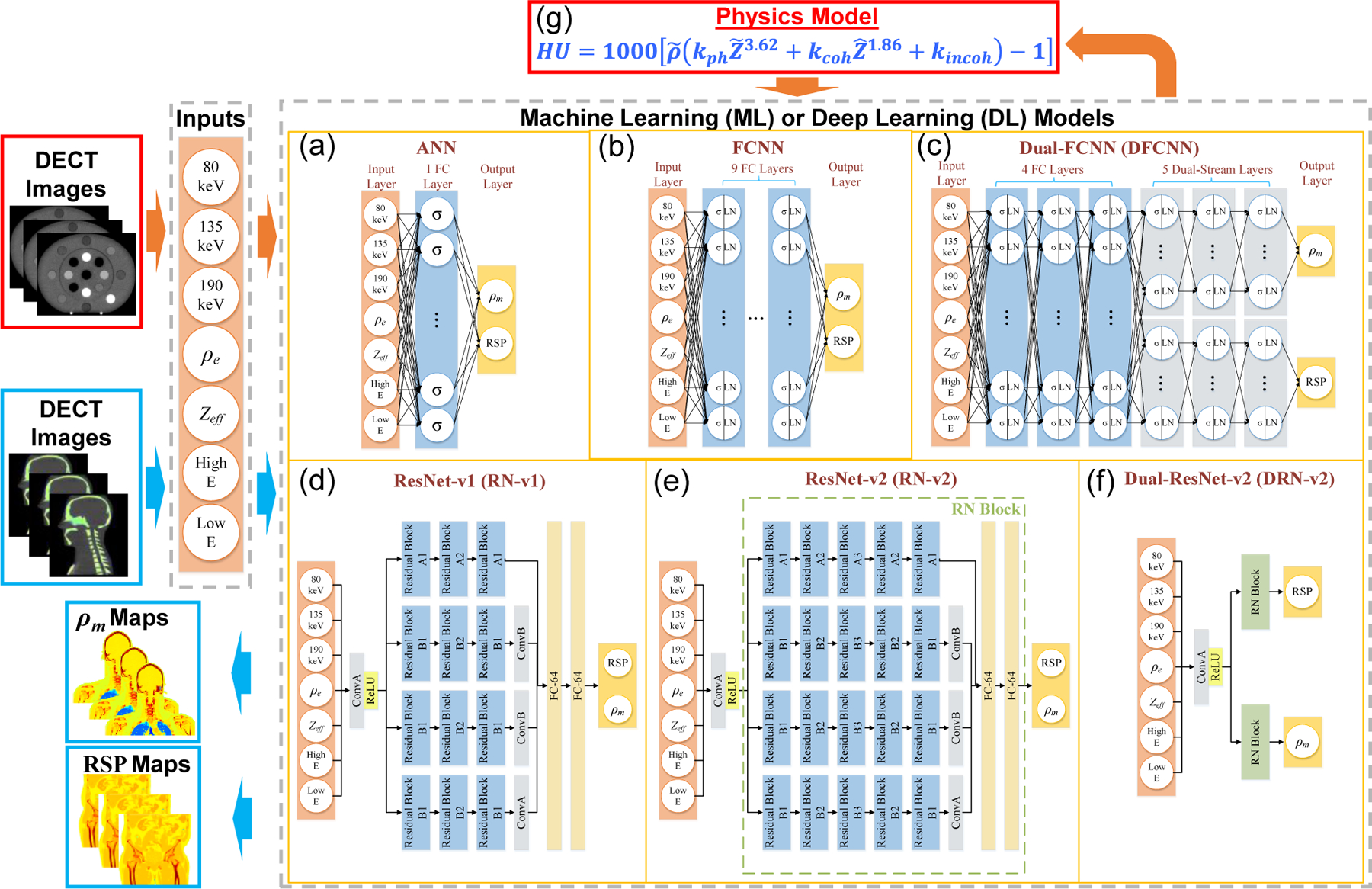
Physics-informed deep learning framework for DECT parametric mapping where the orange and blue arrows denote training and application workflows. The orange arrows represent the training workflow that starts from using DECT images of the electron density phantom as inputs for ML/DL models. The physics model in (g) is only for physics-informed training instead of conventional training. The blue arrows denote the application workflow that starts from using DECT images of CIRS anthropomorphic phantoms as testing data for ML/DL models. The application workflow outputs RSP and mass density (${\mathit{\rho }}_{\mathit{m}}$) maps. The $\text{σ}$ and LN denote activation functions of ReLU (Nair and Hinton, 2010) and layer normalization (Jimmy Lei Ba, 2016). ConvA and ConB are two different convolutional layers defined in Table A1 (Appendix A). The RN block is described in Table A1.

2.2.1. Deep learning models

The PIDL framework is not limited to DL models, and we implemented one traditional ML and five DL models in the framework to further explore relations of the predictive capability and model complexity. Figure 3(a)–(f) shows the six ML/DL models and the model complexity is increased from Figure3(a) to Figure 3(f) due to the increase of trainable parameters and model layers. The ML model in this work was artificial neural networks (ANN) and we implemented ANN with 30 hidden units according to the previous work conducted by Su et al. (Su et al., 2018). Figure 3(a) depicts the ANN structure applied in this study. The σ in Figure 3(a)–(c) denotes activation functions of ReLU (Nair and Hinton, 2010). Meanwhile, we implemented five DL models (Fukushima, 1980; He et al., 2016) to demonstrate the predictive capability of the proposed PIDL framework. Figure 3(b)–(f) show that the five DL models are a fully connected neural network (FCNN) (Bebis and Georgiopoulos, 1994), dual-FCNN (DFCNN) (Schmidhuber, 2015), and three variants of residual networks (ResNet) (Wang et al., 2018) including ResNet-v1 (RN-v1), ResNet-v2 (RN-v2), and dual-ResNet-v2 (DRN-v2). For the DL models with fully connected (FC) layers in Figure 3(b)–(c), there are 200 hidden units in each layer with layer normalization (LN) (Jimmy Lei Ba, 2016) to prevent gradient vanishing issues during training (Hochreiter et al., 2001). FCNN includes nine fully connected (FC) layers, while DFCNN has four FC and five dual-stream layers (Simonyan and Zisserman, 2014). The model complexity of DFCNN is increases compared to FCNN whereby DFCNN potentially can discover more structures from data (Naitzat et al., 2020). The detail structures of RN-v1 and RN-v2 are given in Appendix A. Figure 3(e) shows the structure of a ResNet (RN) block (marked with a green dashed line in Figure 3(e)). The utilization of RN blocks allows us to increase the model complexity compared to neural networks without residual implementation while preventing accuracy degradation issues (He et al., 2016). Figure 3(f) depicts the DRN-v2 architecture built based on two RN blocks. In Section 2.2.2, we described details about how to implement the physics model (given in Figure 3(g)) into a loss function for DL training.

2.2.2. Supervised loss function and physics loss

We use supervised DL models to establish correlations between DECT images and material mass densities and RSP. This inverse learning minimizes the loss function given by Eq. (2), which includes mean square error (MSE) loss and physics loss. The $\delta$ is equal to 1 for physics-informed training and the value is 0 for conventional training. The physics-informed deep learning (PIDL) and DL use identical ANN/DL model structures given in Figure 3(a)–(f) but with different loss functions during the model training. Therefore, ANN/DL models trained by physics-informed and conventional approaches will learn differently from data and result in distinct values of model parameters. For the conventional approach, DL models (given in Figure 3) are trained with only MSE loss, and we use abbreviations of ANN, FCNN, DFCNN, RN-v1, RN-v2, and DRN-v2 for the models trained with only MSE loss. For the physics-informed training, each model (given in Figure 3) is trained with both MSE and physics loss, and we use abbreviations of PANN, PFCNN, PDFCNN, PRN-v1, PRN-v2, and PDRN-v2 for the models trained with MSE and physics losses.

$$L_{total}\hspace{0.17em}=\hspace{0.17em}{L}_{MSE}\hspace{0.17em}+\hspace{0.17em}\delta \hspace{0.17em}\times \hspace{0.17em}\hspace{0.17em}{L}_{physics}\hspace{0.17em}$$ (2)

Eq. (3) defines the MSE loss which is based on mass density and RSP with reference values for the electron density phantom (upper part of Table 1). The ${\mathit{\rho }}_{\mathit{model}}$, ${\rho }_{\mathit{ref}}$, $\mathit{RS}{P}_{\mathit{ref}}$, $\mathit{RS}{P}_{\mathit{model}}$, $\mathit{N}$, and $\mathit{i}$ denote the mass density predicted by ANN/DL models, ground truth mass density, RSP predicted by ANN/DL models, ground truth RSP, total number of CT voxels, and i^th voxel.

$$L_{MSE}\hspace{0.17em}=\hspace{0.17em}\frac{1}{N}\hspace{0.17em}{\sum _{i=1}^N‖{\rho }_{\mathit{i,model}}\hspace{0.17em}-\hspace{0.17em}{\rho }_{\mathit{i,ref}}‖}_2^2\hspace{0.17em}+\hspace{0.17em}\frac{1}{N}\hspace{0.17em}{\sum _{i=1}^N‖RS{P}_{\mathit{i,model}}\hspace{0.17em}-\hspace{0.17em}RS{P}_{\mathit{i,ref}}‖}_2^2$$ (3)

Eq. (4) defines the physics loss where $N$, $i$, and $y_{\mathit{i,meas}}$ denote total number of CT voxels, i^th voxel, and measured quantities of interest that is CT numbers in this work. The $y_{\mathit{i,physics insight}}$ represents physics insights that is empirical HU model in this work given by Eq. (5) (Rutherford et al., 1976; Jackson and Hawkes, 1981), assuming $\mathit{Hounsfield unit (HU) = 1000(}\mu \text{/}{\mu }_{\text{w}}\mathit{-}\mathit{1)}$ where $\mathit{\mu }$ is the linear attenuation coefficient.

$$L_{physics}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}\frac{1}{N}\hspace{0.17em}{\sum _{i=1}^N‖y_{\mathit{i,physics insight}}\hspace{0.17em}-\hspace{0.17em}{y}_{\mathit{i,meas}}‖}_2^2$$ (4)

Eq. (5) is the physics model given in Figure 3(g), and the model is used to compute the physics loss given by Eq. (4). The ${\text{k}}_{\mathit{ph}}$, ${\text{k}}_{\mathit{coh}}$, and ${\text{k}}_{\mathit{incoh}}$ are energy-dependent coefficients corresponding to the photoelectric effect, coherent scattering, and incoherent scatting. These coefficients can be obtained by a least-square fit with VMI of 80keV from the scan of the CIRS 062M electron density phantom. The estimated values for ${\text{k}}_{\mathit{ph}}$, ${\text{k}}_{\mathit{coh}}$, and ${\text{k}}_{\mathit{incoh}}$ in Eq. (5) are $\text{1}{\text{.392 x 10}}^{-\text{5}}$, $\text{1}{\text{.629 x 10}}^{-3}$, and $\text{9}{\text{.166 x 10}}^{-\text{1}}$.

$$y_{physics\hspace{0.17em}insight}\hspace{0.17em}=\hspace{0.17em}H{U}_{80keV}\hspace{0.17em}=\hspace{0.17em}1000\hspace{0.17em}\left[\tilde{\rho }\hspace{0.17em}(k_{ph}\hspace{0.17em}{\tilde{z}}^{3.62}\hspace{0.17em}+\hspace{0.17em}{k}_{coh}\hspace{0.17em}{\widehat{z}}^{1.86}\hspace{0.17em}\hspace{0.17em}+k_{incoh})\hspace{0.17em}-1\hspace{0.17em}\right]$$ (5)

By defining $\tilde{z}$ and $\widehat{z}$ equal to z_3.62 and z_1.86, the values can be derived by Eq. (6) (Mayneord, 1937; Spiers, 1946) where $\text{i}$, $\omega$, $\text{Z}$, and $\text{A}$ denote i^th element, weight fraction, atomic number, and atomic mass.

$$z_n\hspace{0.17em}=\hspace{0.17em}{\left(\sum _i\frac{{\omega }_i\frac{Z_i}{A_i}}{{\sum }_i{\omega }_i\frac{Z_i}{A_i}}{Z}_i^n\right)}^{\frac{1}{n}}$$ (6)

Eq. (7) defines the relative electron density ($\tilde{\rho }$) where ${\mathit{\rho }}_{\text{e,w}}$ is the electron density for water and it is a constant value of $\text{3}{\text{.343 x 10}}^{\text{23}}$ e⁻/cm³. The ${\rho }_{m,DL}$ is the predicted mass density from the output of DL models.

$$\tilde{\rho }\hspace{0.17em}\equiv \hspace{0.17em}\frac{{\rho }_{m,DL}{{\displaystyle \sum }}_i{\omega }_i\frac{Z_i}{A_i}}{{\rho }_{\text{e,}}{}_w}$$ (7)

For the physics-informed training, the value of ${\rho }_{m,DL}$ is queried during each training iteration, allowing the physics model given by Eq. (5) and in Figure 3(g) to be used to compute the physics loss defined by Eq. (4) to train a physics-informed DL model. The CT numbers in the physics loss (given by Eq. (4)) are acquired from the VMI with an energy of 80 keV from the scan of the CIRS 062M electron density phantom.

The 80-keV VMI is used because VMI with an energy around 80 keV can lead to the optimal image-noise ratio and beam-hardening ratio (Yu et al., 2012; Wohlfahrt et al., 2017; Wang et al., 2019) to reduce CT number variations between patients with different body sizes.

2.3. Empirical model for DECT parametric mapping

We implemented two empirical DECT models using MATLAB R2021a, and we compared the performance of DL models to the empirical models. Eq. (8) (Beaulieu et al., 2012) and Eq. (9) (Hünemohr et al., 2013; Kassaee et al., 2021) give empirical models to which can be used to estimate the material mass density and RSP maps from DECT where ${\mathit{\rho }}_{\mathit{e}}$ and ${\text{Z}}_{\mathit{eff}}$ are obtained from Siemens Syngo.Via. The linear mass density model involves considerable uncertainty for the inflated lung, and a constant value of 0.26 g/cm³ is assigned for it (Eq. (8)). The RSP model includes multiple correlations for different tissues, for example, soft tissues (${\text{Z}}_{\mathit{eff}}\text{ < 8}.5$) and bony tissues (${\text{Z}}_{\mathit{eff}}\text{ < 10}$). Syngo.Via has a limitation that the ${\text{Z}}_{\mathit{eff}}$ is assigned to 0 for low-density tissues ($\text{HU < }-\text{500}$), and, therefore, Eq. (9) includes a region of ${\text{Z}}_{\mathit{eff}}$ values < 0.5 for lung tissues.

$$\rho \left(\raisebox{1ex}{$g$}\!\left/ \!\raisebox{-1ex}{$c{m}^3$}\right.\right)\hspace{0.17em}=\hspace{0.17em}\left\{\begin{array}{l}-0.1746\hspace{0.17em}+\hspace{0.17em}1.176{\rho }_{e\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\rho }_{e\hspace{0.17em}}\ge 0.37\\ 0.26\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\rho }_{e\hspace{0.17em}}<0.37\end{array}\right.$$ (8)

$$RSP\hspace{0.17em}=\hspace{0.17em}\left\{\begin{array}{l}{\rho }_{e\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}0\hspace{0.17em}\le \hspace{0.17em}{Z}_{eff}\hspace{0.17em}<\hspace{0.17em}0.5\\ \left(1.1114\hspace{0.17em}-\hspace{0.17em}0.0148Z_{eff}\right){\rho }_e\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0.5\hspace{0.17em}\le \hspace{0.17em}{Z}_{eff}\hspace{0.17em}<\hspace{0.17em}8.5\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\\ 0.9905{\rho }_{e\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}8.5\hspace{0.17em}\le \hspace{0.17em}{Z}_{eff}\hspace{0.17em}<\hspace{0.17em}10\hspace{0.17em}\hspace{0.17em}\\ \left(1.1117\hspace{0.17em}-\hspace{0.17em}0.0116Z_{eff}\right){\rho }_{e,}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{Z}_{eff}\hspace{0.17em}\ge \hspace{0.17em}10\hspace{0.17em}\hspace{0.17em}\end{array}\right.$$ (9)

2.4. Evaluation

To prepare the reference images of CIRS anthropomorphic phantoms, we first generated contours for each tissue surrogate from phantom images. We used RayStation 10B model-based segmentation (RayPhysics, 2021) to obtain contours for the brain, spinal cord, and lung. The threshold CT number was 250 HU for bone. The breast contour was manually contoured from phantom images. The soft tissue was first contoured by using RayStation 10 function to create external regions of interest (ROI). Then we subtracted the external ROI by each tissue contour to acquire the soft tissue contour. To avoid the partial volume and edge effects (Wohlfahrt et al., 2018; Polf et al., 2019), all contours were uniformly contracted by 3 mm, and the tissue materials within the contours were uniform for CIRS anthropomorphic phantoms. Then the mass density and RSP from Table 1 were allocated to each contour as the reference.

Eq. (10)–(11) give the evaluation metrics using absolute percentage error (APE) and mean APE (MAPE) where $\text{i}$, $\text{x}$, and $\text{N}$ represent the i^th voxel, voxel quantity, and total voxels. For anthropomorphic phantoms, the APE is used to generate error maps for whole phantoms to visualize the error distribution, and the MAPE provides error estimation for each tissue contour. Both APE and MAPE were computed for each contour within CIRS anthropomorphic phantoms.

$$AP{E}_i\hspace{0.17em}=\hspace{0.17em}\left|\frac{x_i\hspace{0.17em}-\hspace{0.17em}{x}_{i,REF}}{x_{i,REF}}\right|\hspace{0.17em}\times \hspace{0.17em}100\%$$ (10)

$$MAPE\hspace{0.17em}=\hspace{0.17em}\frac{1}{N}\sum _{i=1}^{N}AP{E}_i$$ (11)

3. Results

We used MAPE to assess the performance of the PIDL framework regarding mass density and RSP map generation and compared the results to the conventional DL models (without the extra physics insight loss term, Eq. (4)) and the empirical models. In Section 3.1–3.3, the reference RSP and mass density for the CIRS anthropomorphic phantoms were from the vendor (lower part of Table 1). In Section 3.4, the reference RSP and mass density for the CIRS M701 adult male phantom were from the proton measurement as described in Section 2.1.1.

3.1. Site-specific analysis using an HN TBDE protocol for CIRS M701, M702, and M705 phantoms

Figure 4 depicts the quantitative evaluation results of the empirical and DL-based DECT parametric mapping for mass densities utilizing CIRS M701, M702, and M705 phantoms. For lung tissue surrogate, the empirical model results in significant uncertainty for low HU materials. Accordingly, the density of the inflated lung is set to be a constant value of 0.26 g/cm³ (Beaulieu et al., 2012), and the error is about 26.8%. In contrast, the DL models can achieve an error of ~1% for lung. Meanwhiles, DL models achieved lower errors than the empirical model for soft tissue, spinal cord, and brain. For M701 bone, the errors are 3.9% and 4.2% for the empirical model and RN-v2. However, the empirical model shows a significant standard deviation (SD) of 5.3%, while the SD of RN-v2 is 0.9%. Compared to the empirical model, DL models usually have a smaller SD. In case where the conventional DL models results in a high MAPE, the physics-informed DL models generally improve the accuracy of density map generations. For instance, the soft tissue errors are 2.2% and 2.4% for conventional ANN and DRN-v2, but the errors are reduced to 1.0% and 1.3% when training the DL models with physics constraints. The bone density generated by RN-v2 shows good agreement to the reference, with a small MAPE (0.2%), while the empirical model results in a MAPE of 4.1% for M705 bone density prediction. For the bone surrogate in M705, the conventional DRN-v2 yields a MAPE of 4.8% but the physics-informed training can reduce the error to 1.5%. In this case, DRN-v2 comprises complicated model architectures and can lead to large MAPE. However, these errors generally can be improved with constraints from the physics model, as shown in Figure 4(c5). Appendix B gives MAPE values of mass density and RSP comparisons for each model.

Figure 4.

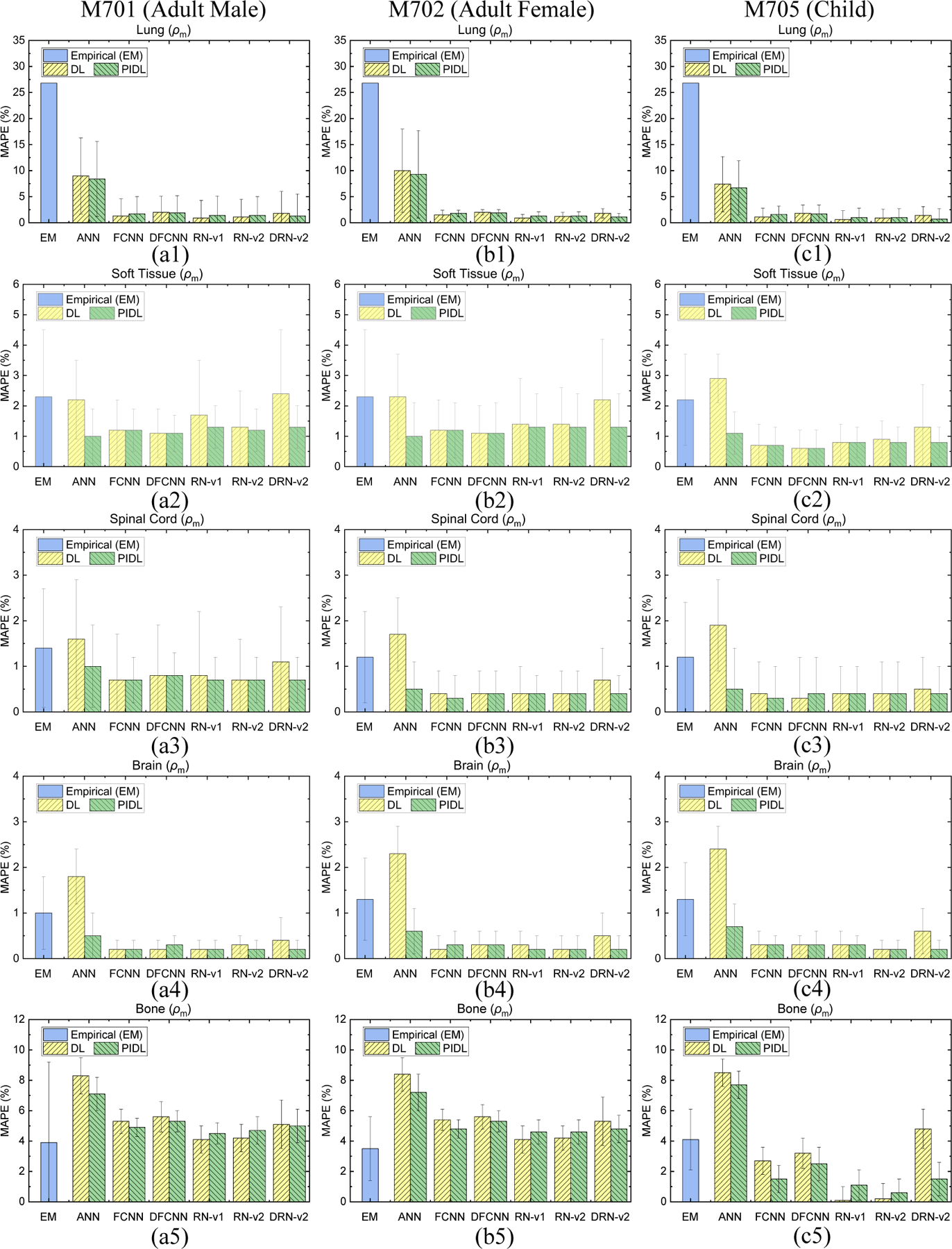
MAPE comparisons of mass densities between the reference and DECT parametric mapping models for an HN site from (a1)-(a5) CIRS M701 adult male, (b1)-(b5) CIRS M702 adult female, and (c1)-(c5) CIRS M705 child phantoms with five tissue surrogates using an HN TBDE scan.

Figure 5 shows the MAPE of RSP by the empirical and DL models. The empirical model can generate RSP maps using Eq. 8, and the MAPE is 8.1% for lung while the error is 1.1% by RN-v1. Compared to the empirical model, the DL models consistently yield smaller MAPE and SD for soft tissues for M701 and M702. The empirical model can achieve smaller MAPE of brain and bone tissues compared to DL models,but the SD for the empirical model is about four times greater than for the DL models as demonstrated by M701 and M702. For M705 bone, RN-v2 leads to an error of $\text{1}.4\% \pm 0.8\%$ but the empirical model results in an error of $\text{4}.6\% \pm 2.0\%$. ANN gives optimal MAPE of RSP for soft tissue, spinal cord, and brain at the HN site.

Figure 5.

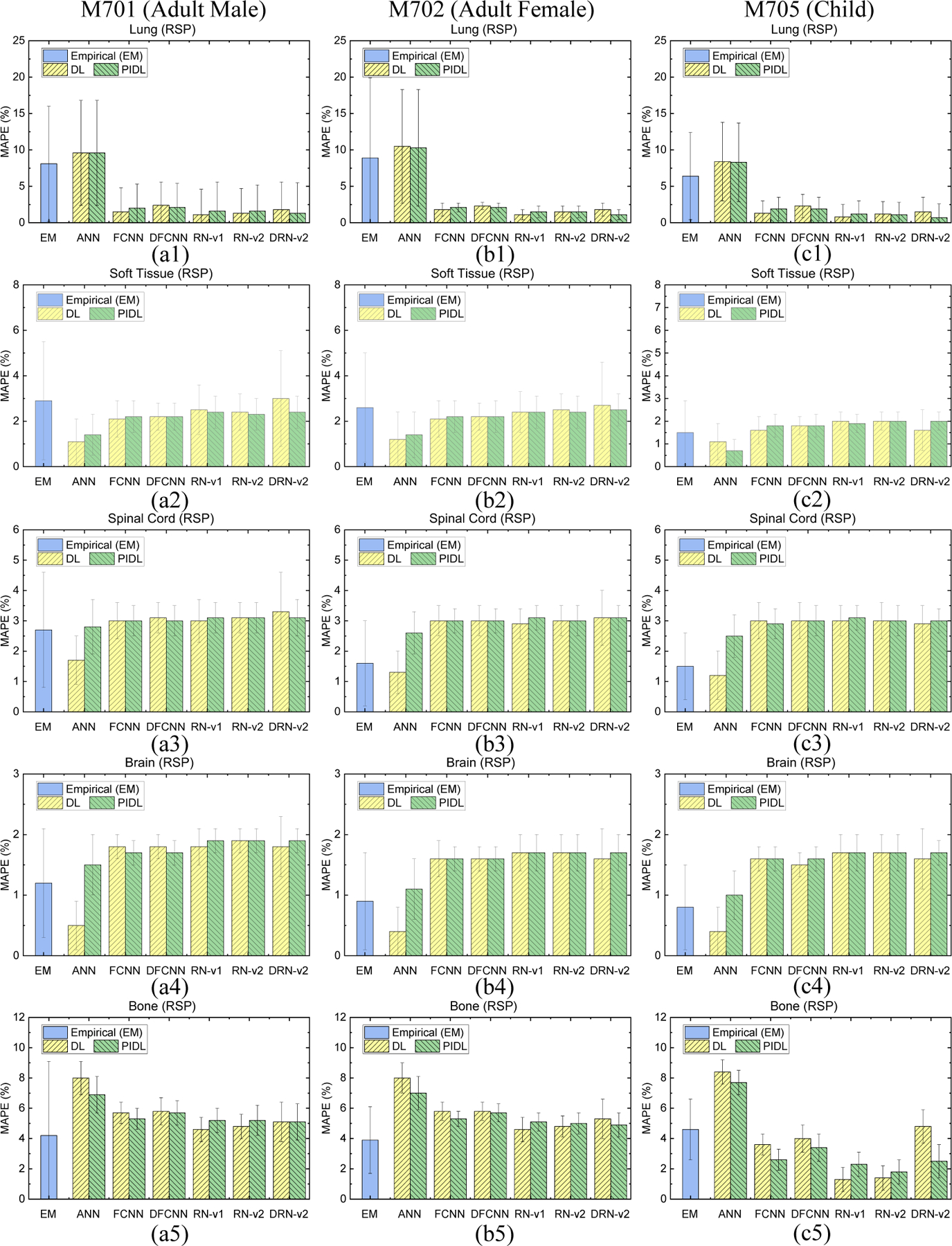
MAPE comparisons of RSP between the reference and DECT parametric mapping models for an HN site from (a1)-(a5) CIRS M701 adult male, (b1)-(b5) CIRS M702 adult female, and (c1)-(c5) CIRS M705 child phantoms with five tissue surrogates using an HN TBDE scan.

3.2. Site-specific analysis using a thorax TBDE protocol for CIRS M701 and M702 phantoms

Figure 6 shows MAPE values of mass densities and RSP for each tissue using the empirical models and ML/DL models with and without physics training including ANN, FCNN, DFCNN, RN-v1, RN-v2, and DRN-v2. The DL models show lower errors than the empirical models for most tissues. Meanwhiles, the physics-informed training can further reduce the errors for DL models without physics training. For instance, Figure 6(b1) and (b3) show that the errors of soft tissue and bone are 2.9% and 6.1% by DRN-v2 while the errors are 0.6% and 4.8% by physics-informed DRN-v2 (PDRN), respectfully. Appendix B gives MAPE values of mass density and RSP comparisons for each model.

Figure 6.

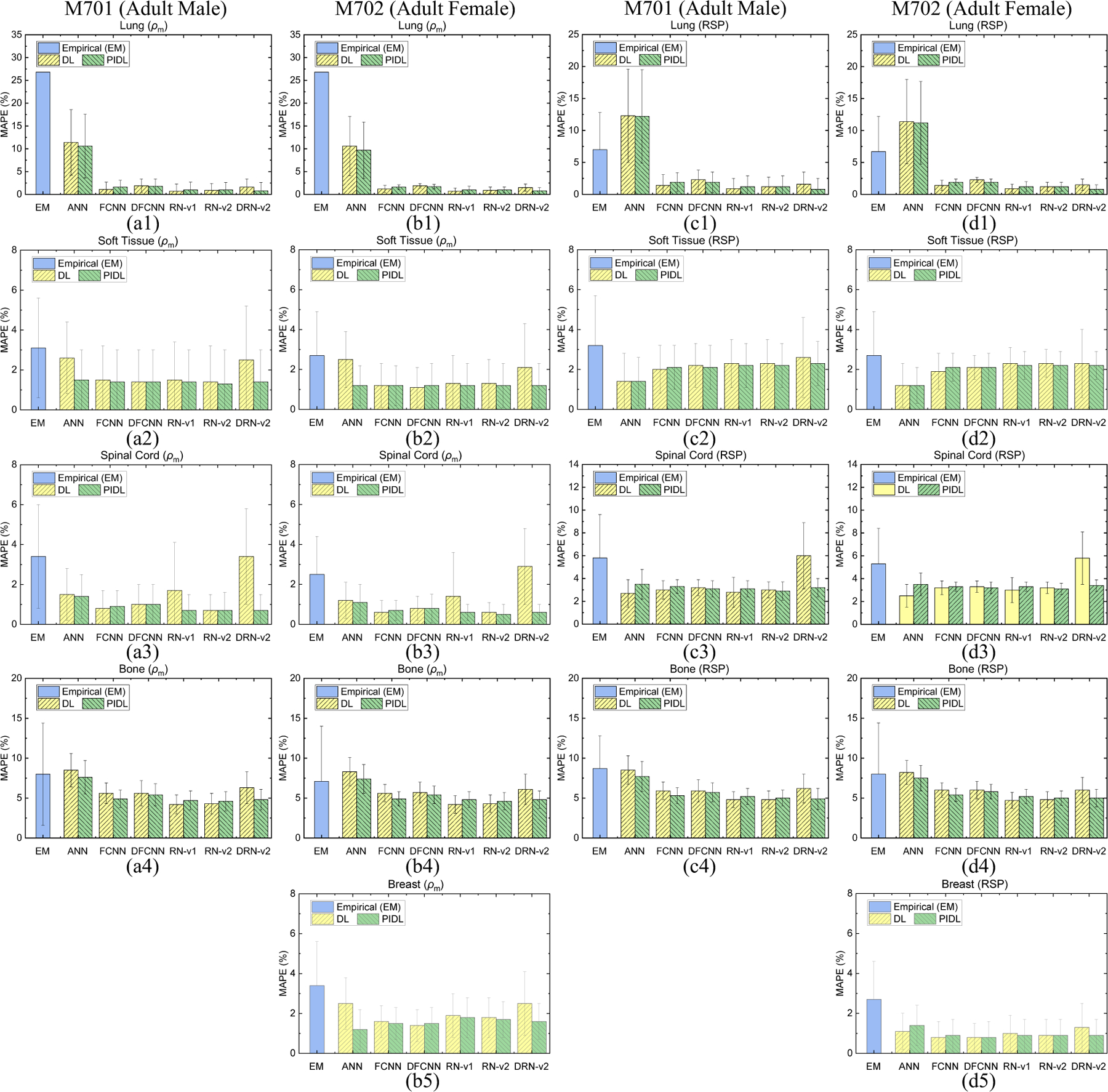
MAPE comparisons of mass densities between the reference and DECT parametric mapping models for a thoracic site from (a1)-(a4) CIRS M701 adult male and (b1)-(b5) CIRS M702 adult female phantoms. MAPE comparisons of RSP between the reference and DECT parametric mapping models for a thoracic site from (c1)-(c4) CIRS M701 adult male phantom with four tissue surrogates and (d1)-(d5) CIRS M702 adult female phantom with five tissue surrogates using a thorax TBDE scan.

3.3. Site-specific analysis using a pelvic TBDE protocol for CIRS M701 and M702 phantoms

Figure 7 shows the MAPE values of mass densities and RSP for M701 and M702 from the empirical model and ML/DL models with and without physics training. For M701 soft tissue and spinal cord given in Figure 7(a1) and (a2), DRN-v2 results in errors of 1.7% and 2.5%, and the physics-informed training can further lower these errors to 0.9% and 1.0%. Figure 7(c1)–(c2) and (d1)–(d2) depict that DL models can achieve smaller RSP MAPE than the empirical model for M701 soft tissue and spinal cord. Appendix B gives MAPE values of mass density and RSP comparisons for each model.

Figure 7.

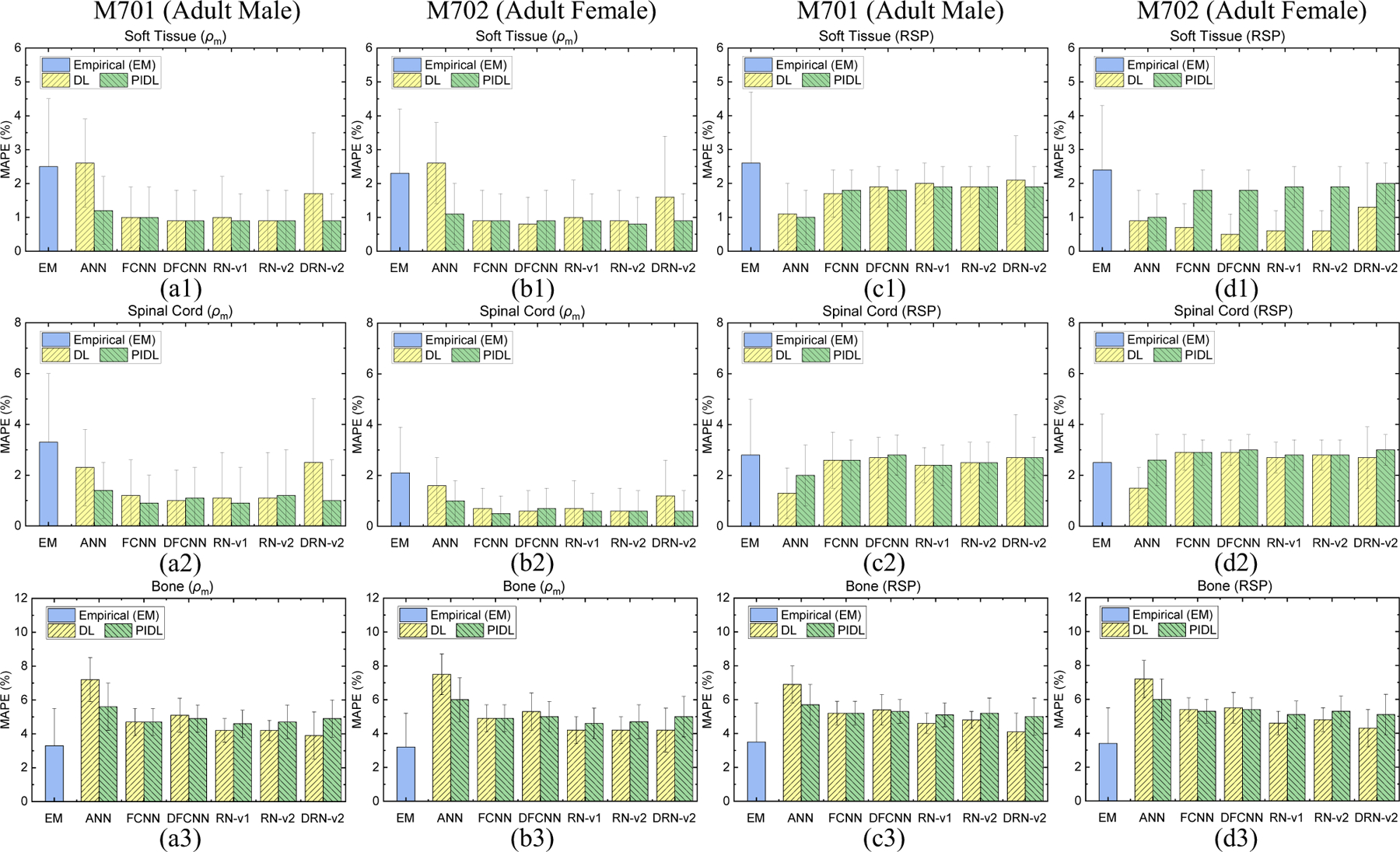
MAPE comparisons of mass densities between the reference and DECT parametric mapping models for a pelvic site from (a1)-(a3) CIRS M701 adult male and (b1)-(b3) CIRS M702 adult female phantoms. MAPE comparisons of RSP between the reference and DECT parametric mapping models for a pelvic site from (c1)-(c3) CIRS M701 adult male and (d1)-(d3) CIRS M702 adult female phantoms with three tissue surrogates using a pelvic TBDE scan.

3.4. Analysis of CIRS M701 phantom using measured tissue-surrogate data

We compared the empirical and DL results to the measured data (given in Section 2.1.1) for CIRS M701 adult male phantom. The results in this section were averaged from the three treatment sites using the CIRS adult male phantom (M701) images scanned by HN, thorax, and pelvic TBDE protocols. Figure 8(a1)–(a4) depicts the MAPE values of the phantom mass densities for each tissue. DL models achieved lower errors than the empirical model. The physics-informed training can generally improve the model errors compared to the models without physics training. For instance, Figure 8(a2) and (a4) show that the errors from physics-informed ANN (PANN) are 1.3% and 2.5% for soft tissue and bone while the errors from ANN without physics training are 2.5% and 3.8%, respectfully. The physics-informed RN-v2 (PRN-v2) achieved the optimal errors of 0.8%, 1.1%, 0.2%, and 0.5% for lung, soft tissue, brain, and bone. Figure 8(b1)–(b4) show the MAPE values of RSP for each tissue from various models.

Figure 8.

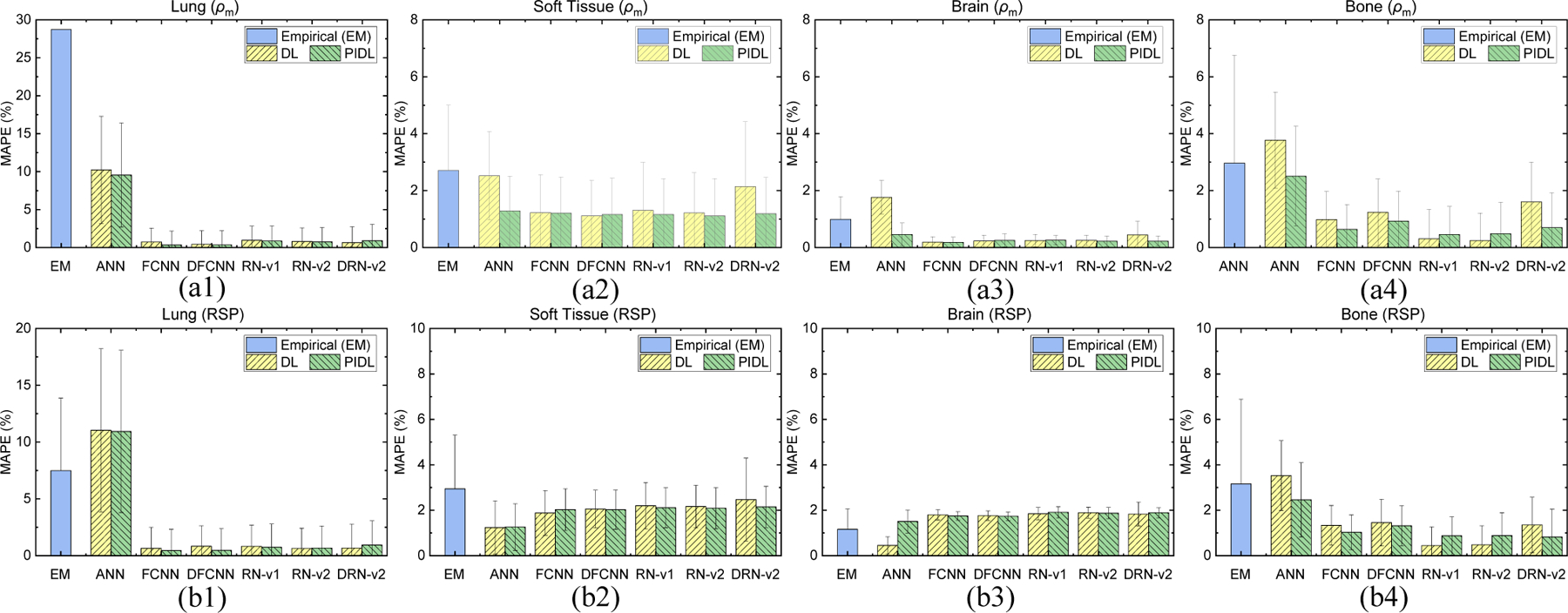
MAPE of (a1-a4) mass density and (b1-b4) RSP between the reference and DECT parametric mapping models for five tissue surrogates from the CIRS adult male anthropomorphic phantom (M701).

Figure 9 illustrates APE maps to evaluate error distributions of mass density for CIRS M701 adult male phantom. The VMI shows the anatomy of the phantom at three sites, including HN, thorax, and pelvis. The empirical and ANN model results in considerable uncertainty at the peripheral of the body and bone. When training an ANN with physics constraints, physics-informed ANN (PANN) error maps show improvement compared to the map by ANN. There is no significant difference between RN-v2 and PRN-v2. Both models can better control the errors across all tissues and the regions of the body peripheral compared to the results by the empirical model. Figure 10 shows the APE maps of RSP. The empirical and ANN models still involve significant uncertainty for the bone and regions of the body peripheral. However, the ANN model reveals optimal results for the soft tissue and brain. RN-v2 and PRN-v2 can still achieve the optimal APE for bone and lung compared to ANN and the empirical models.

Figure 9.

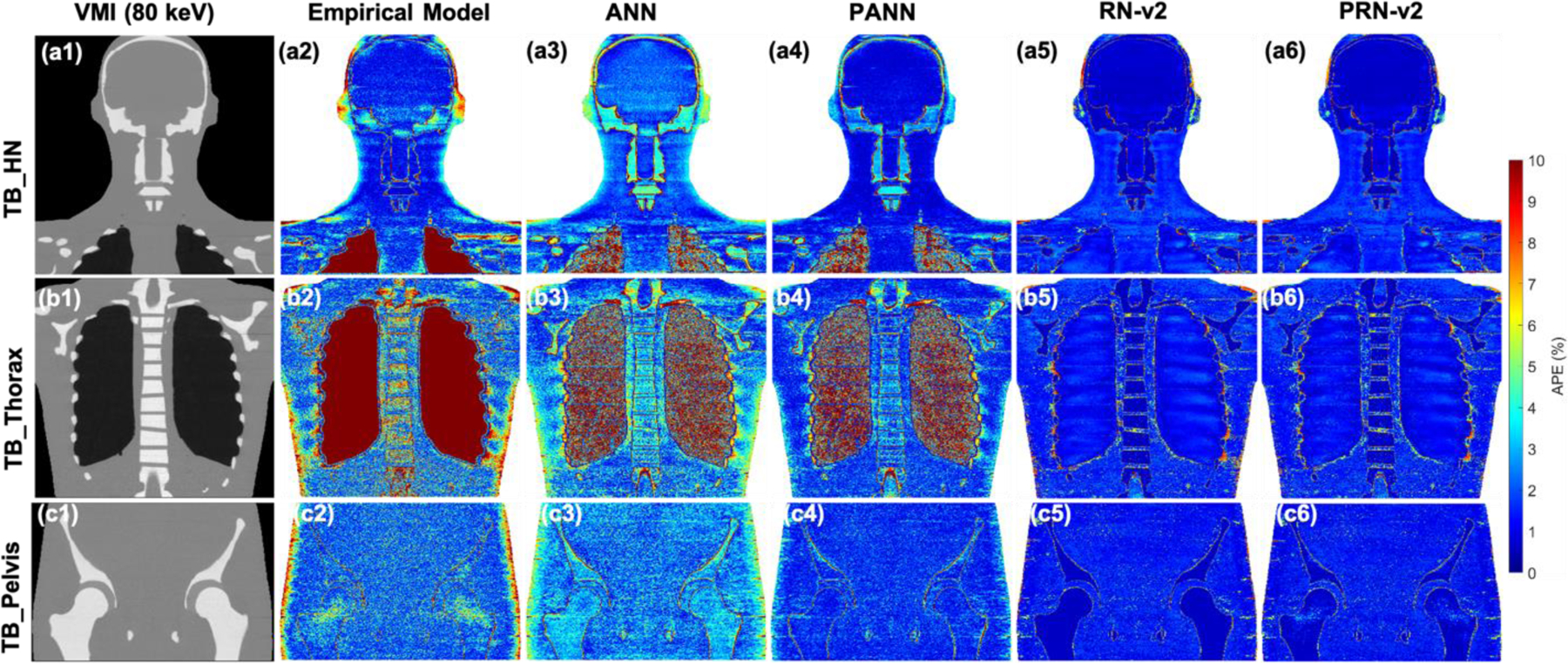
(a1), (b1), and (c1) VMI of 80 keV by different TB protocols. APE maps of mass densities between the reference and DECT parametric models at (a2-a6) HN, (b2-b6) thoracic, and (c2-c6) pelvic sites using CIRS M701 adult male phantom.

Figure 10.

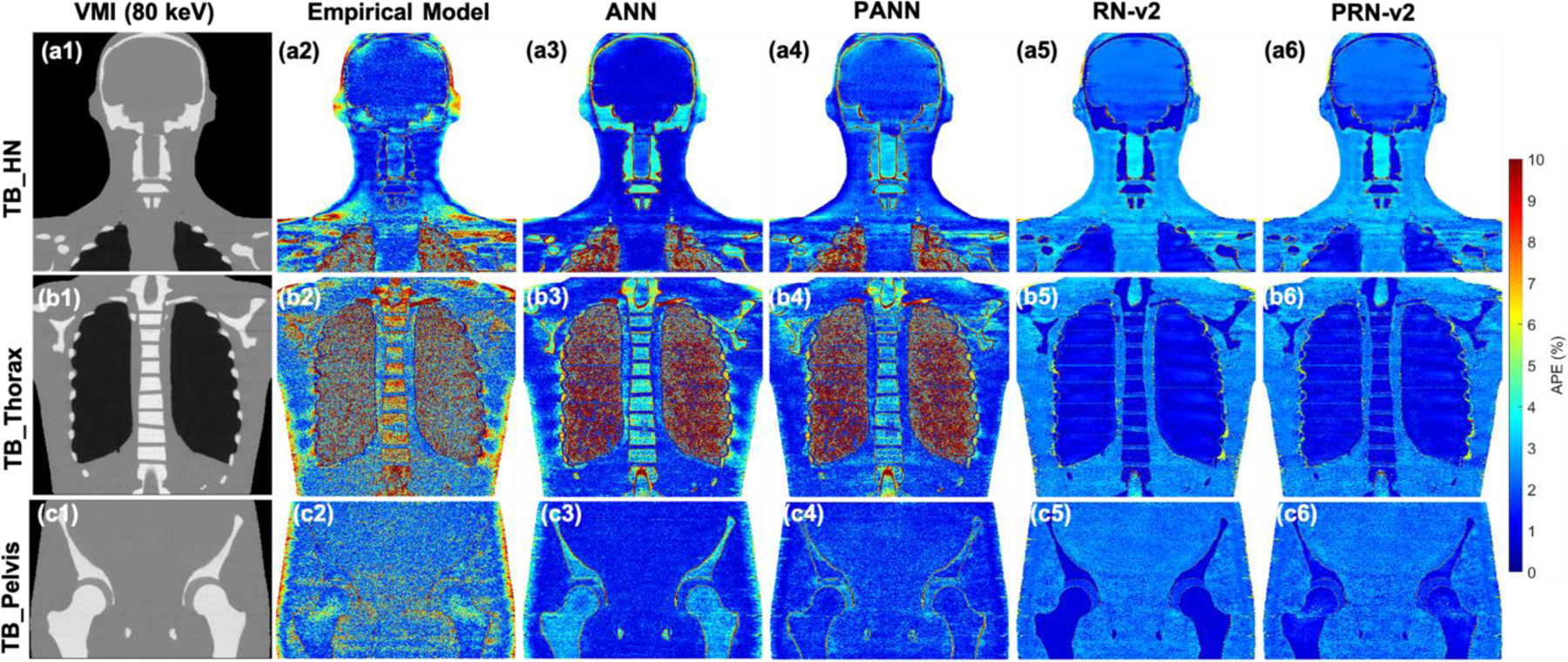
(a1), (b1), and (c1) VMI of 80 keV by different TB protocols. APE maps of RSP between the reference and DECT parametric models at (a2-a6) HN, (b2-b6) thoracic, and (c2-c6) pelvic sites using CIRS M701 adult male phantom.

4. Discussions

Su et al. (Su et al., 2018) employed machine learning methods to establish the correlations between DECT images and parametric maps such as RSP. In this work, we proposed a physics-informed deep learning (PIDL) framework, for the first time, to tightly incorporate a physics model to constrain DL training for DECT parametric mapping. The framework can predict the parametric maps of mass density and RSP to support proton MCDC and ADC for treatment planning. With physics constraints, machine learning models with simplistic structures such as ANN can also reduce mass density errors by 1.2%, 1.3%, and 1.3% for soft tissue, brain, and bone compared to ANN without physics training, as shown in Figure 8(a2)–(a4). Figure 8 also implies that the model errors do not tightly depend on different DL models tested in this work; instead, physics-informed training can improve the model accuracy when conventional DL models lead to large uncertainty. Meanwhiles, Figure 4, Figure 6, and Figure 8–9 show that the empirical DECT model given by Eq. (8) results in large uncertainty for lung surrogates from CIRS anthropomorphic phantoms. Since the model use a constant value for inflated lung, we can match the constant value to the reference mass density of lung surrogates to have zero uncertainty. However, this approach cannot be applied to patient study, and this result shows the limitation of Eq. (8).

The physics-based empirical models (Yang et al., 2010; Landry et al., 2013; Garcia et al., 2015; Zhu and Penfold, 2016) had demonstrated the capabilities of DECT parametric mapping. Nonetheless, the accuracy of those methods was impacted by CT noise and artifacts. Figure 9(c2) illustrates that the empirical model is affected by CT noise, and the phantom anatomy cannot be identified. In contrast, the DL models can suppress the noise, as shown in Figure 9(c2) and (c6) where the standard deviations of APE for whole bodies are 2.3% (empirical model) and 1.4% (PRN-v2), respectfully. Meanwhile, those methods generally involve different degrees of uncertainty due to model forms of regression methods such as linear fitting. The relations between CT numbers and quantities of interest may not always be described as a one-to-one function (Su et al., 2018). To prevent this ambiguity, DL with hierarchical structures has the potential to figure out the hidden correlations behind DECT data and achieve the accuracy and robustness of DL-based parametric mapping methods.

Hünemohr et al. (Hünemohr et al., 2014) concluded that the accuracy of mass density prediction dominates the uncertainty of RSP. Proton MCDC is accurate for particle transport in heterogeneous tissues (Schuemann et al., 2015; Huang et al., 2018; Lin et al., 2021) and can improve treatment planning quality. Accordingly, in the current work, we focus on using a physics model to constrain DL training based on the mass density, and Figure 8(a1)–(a4) depicts that PRN-v2 can achieve MAPE within 1.1%. Besides, when comparing DECT mass density mapping results to bone measurement data, both empirical and PRN-v2 reduce the errors by $\text{~1}.7\%$ and $\text{~4}.2\%$. PRN-v2 performs adequately for both CIRS adult and child anthropomorphic phantoms. The model involves complicated convolutional layers to uncover structures of high-dimensional data and residual blocks to prevent accuracy degradation. We will incorporate PRN-v2 for future dosimetric study to further explore the impacts for treatment planning.

Figure 11 depicts density map prediction for two patients employing HN and pelvis TBDE scans with contrast. All density maps can qualitatively reflect the patients’ anatomy. Figure 11(a1)–(a4) display that the internal jugular vein (IJV) can impact the CT numbers that cause the variation of density curves by RN-v2 and PRN-v2 as shown in Figure 11(a5) and (b5) (pointed by red and blue arrows). Figure 11(a5) demonstrates that the density line profiles by DL models agree with the trend of the HU line profile by VMI. The empirical model is not affected by the variation of CT numbers induced by the contrast injection. It is because iodine is a high $\text{Z}$ material, and it enhances the photo electric effect that impacts CT number. However, the contrast injected in IJV was OMNIPAQUE™ with the specific gravity of 1.406, and 100 ml of the iodine contrast was injected into the patient. The injection of contrast may cause local density variation. Meanwhile, DL models were not trained with iodine that increases the uncertainty from DL models. The patients with contrast become the limitation of the current PIDL framework due to lack of training data. Including more training datasets with iodine contrast may address this issue. Figure 11(b6) exhibits a line profile across soft tissue and bone, and both empirical and DL models agree with the trend of the VMI HU profile. Nevertheless, DL line profiles are smooth that implies the ability to suppress CT noise.

Figure 11.

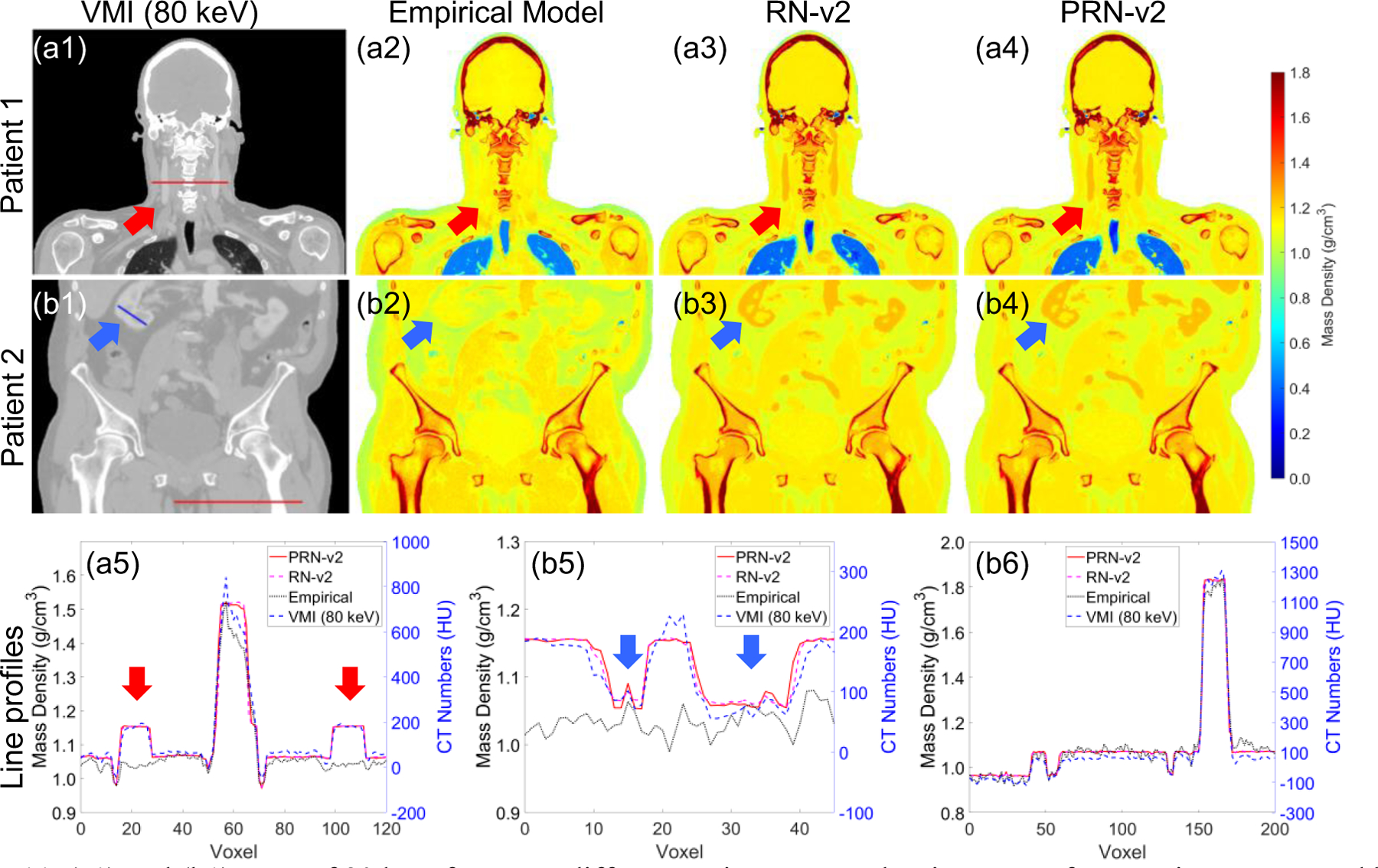
(a1) and (b1) VMI of 80 keV from two different patients. Mass density maps of two patients generated by different DECT parametric mapping models at (a2-a4) HN and (b2-b4) pelvic sites. (a5) the line profile of the red line from (a1). (b5-b6) the line profiles of the blue and red lines from (b1). The red and blue arrows indicate the vascular system contains DECT contrast.

Although Figure 8 indicates that the uncertainty for RSP prediction is more significant than that of mass density prediction by DL models, Figure 8(b1)–(b4) still shows improvement achieved by DL models for lung, soft tissue, spinal cord, and bone compared to the empirical model. Meanwhile, the reference RSP values are calculated by Eq. (1), and the uncertainty of reference RSP comes from elemental compositions and $\text{I}$ values. For instance, Table 1 demonstrates that the density discrepancy between CIRS 062M muscle and CIRS M701 soft tissue is less than 0.5%, but the RSP and $\text{I}$ value differences are $\text{~1}.7\%$ and $\text{~5}.4\%$ due to different material compositions. Additional human tissue surrogates are required to broaden the coverage of training data and to accurate DL models. MC simulation (Hünemohr et al., 2013) can also be an alternative to derive RSP. Correlating DECT data to the parametric maps requires models to capture features from high dimensional data in the domain of extrapolation (Balestriero et al., 2021).

The DL framework serves as a high-order approximation for a well-defined physics problem that can be solved if the exact relative electron density and effective atomic number are known for patients. Hence, the accuracy of image-based relative electron density and effective atomic number dominate the uncertainty of physics-based models for material mass density and RSP inferences. Unlike mechanistic models (empirical models), the robustness of DL can be compromised if the training datasets are not sufficiently covered the physics problem that we attack. In this work, we aim to demonstrate the feasibility of using physics-informed training to enhance model accuracy for conventional ML and DL models. The evaluation of dosimetric impacts using the proposed PIDL framework with meat phantoms such as pig’s loin, belly, rib, and femur, is a crucial step for accessing the feasibility of clinical implementation.

Future work will incorporate additional physics models to regularize DL training to enhance accuracy and robustness (Chang and Dinh, 2019). The current model inputs include VMI of 135 keV and 190 keV because of their potential to mitigate artifacts from surgical implants of various sizes (Wellenberg et al., 2018a; Wellenberg et al., 2018b). Future investigation will likewise integrate the proposed framework to regulate DL-based metal artifact reduction methods (Gjesteby et al., 2019; Liao et al., 2020; Yu et al., 2021a; Yu et al., 2021b) to improve proton range uncertainty (Paganetti, 2012; Chang et al., 2020).

5. Conclusions

A physics-informed deep learning (PIDL) framework was developed to assimilate rich information from DECT and to generate mass density and RSP maps that can be used to inform proton analytical dose calculation and Monte Carlo dose calculation. Physics-informed deep learning models can enhance the accuracy of DECT parametric mapping for voxel-specific material mass densities, mainly when conventional DL models incorporate significant uncertainty. Machine learning models with basic structures can benefit the most from physics-informed training. DL models with complicated structures are not necessary to achieve the optimal DECT parametric mapping; alternatively, physics regularization can effectively improve the performance of DL models. The proposed framework also demonstrated the capability of suppressing CT noise, and the method has the potential to reduce proton range uncertainty to increase the quality of proton therapy.

Appendix A. Structure of ResNet-v1 (RN-v1) and ResNet-v2 (RN-v2)

Table A1 gives the structure of RN-v1 and RN-v2 as given in Figure 3(d)–(e). Each residual block includes two convolutional layers and one residual connection.

Table A1.

Architecture of the 1D convolution components for ResNet (RN). ConvA and ConvB denotes convolutional layer A and B with different parameters.

Network	Layer	Number of channels	Kernel size	Stride	Pad
	ConvA	64	7	2	3
	ConvB	64	3	1	0
Residual Block A1	Convolutional	64	3	2	1
	Convolutional	64	3	1	1
	Residual	64	1	2	0
Residual Block A2	Convolutional	128	3	2	1
	Convolutional	128	3	1	1
	Residual	128	1	2	0
Residual Block A3	Convolutional	256	3	2	1
	Convolutional	256	3	1	1
	Residual	256	1	2	0
Residual Block B1	Convolutional	64	2	2	1
	Convolutional	64	2	1	1
	Residual	64	1	2	0
Residual Block B2	Convolutional	128	2	2	1
	Convolutional	128	2	1	1
	Residual	128	1	2	0
Residual Block B3	Convolutional	256	2	2	1
	Convolutional	256	2	1	1
	Residual	256	1	2	0

Appendix B. MAPE comparisons of mass densities and RSP for CIRS anthropomorphic phantoms

Table B1–B2 give the MAPE comparisons of mass densities and RSP using an HN TBDE protocol for CIRS adult male, adult female, and child phantoms. Table B3–B4 show the MAPR comparisons of mass densities and RSP using a thorax TBDE protocol for CIRS adult male and female phantoms. Table B5–B6 indicate the MAPE comparisons of mass densities and RSP using a pelvic TBDE protocol for CIRS adult male and female phantoms.

Table B1.

MAPE comparisons of mass densities between the reference and DECT parametric mapping models for an HN site with five tissue surrogates using a TBDE HN scan.

M701		Lung	Soft Tissue	Spinal Cord	Brain	Bone
Empirical Model		26.8 ± 0.0	2.3 ± 2.2	1.4 ± 1.3	1.0 ± 0.8	3.9 ± 5.3
Conventional	ANN	9.0 ± 7.3	2.2 ± 1.3	1.6 ± 1.3	1.8 ± 0.6	8.3 ± 1.2
	FCNN	1.3 ± 3.3	1.2 ± 1.0	0.7 ± 1.0	0.2 ± 0.2	5.3 ± 0.8
	DFCNN	2.0 ± 3.1	1.1 ± 0.8	0.8 ± 1.1	0.2 ± 0.2	5.6 ± 1.0
	RN-v1	0.9 ± 3.4	1.7 ± 1.8	0.8 ± 1.4	0.2 ± 0.2	4.1 ± 0.9
	RN-v2	1.1 ± 3.4	1.3 ± 1.2	0.7 ± 0.9	0.3 ± 0.2	4.2 ± 0.9
	DRN-v2	1.8 ± 4.2	2.4 ± 2.1	1.1 ± 1.2	0.4 ± 0.5	5.1 ± 1.6
Physics-informed	ANN	8.4 ± 7.2	1.0 ± 0.9	1.0 ± 0.9	0.5 ± 0.5	7.1 ± 1.1
	FCNN	1.7 ± 3.3	1.2 ± 0.7	0.7 ± 0.5	0.2 ± 0.2	4.9 ± 0.6
	DFCNN	1.9 ± 3.3	1.1 ± 0.6	0.8 ± 0.5	0.3 ± 0.2	5.3 ± 0.7
	RN-v1	1.4 ± 3.7	1.3 ± 0.7	0.7 ± 0.5	0.2 ± 0.2	4.5 ± 0.7
	RN-v2	1.4 ± 3.6	1.2 ± 0.7	0.7 ± 0.5	0.2 ± 0.2	4.7 ± 0.9
	DRN-v2	1.3 ± 4.2	1.3 ± 0.7	0.7 ± 0.5	0.2 ± 0.2	5.0 ± 1.1
M702		Lung	Soft Tissue	Spinal Cord	Brain	Bone
Empirical Model		26.8 ± 0.0	2.3 ± 2.2	1.2 ± 1.0	1.3 ± 0.9	3.5 ± 2.1
Conventional	ANN	10.0 ± 8.0	2.3 ± 1.4	1.7 ± 0.8	2.3 ± 0.6	8.4 ± 1.1
	FCNN	1.5 ± 0.9	1.2 ± 1.0	0.4 ± 0.5	0.2 ± 0.3	5.4 ± 0.7
	DFCNN	2.0 ± 0.5	1.1 ± 0.9	0.4 ± 0.5	0.3 ± 0.3	5.6 ± 0.8
	RN-v1	0.9 ± 0.7	1.4 ± 1.5	0.4 ± 0.6	0.3 ± 0.3	4.1 ± 0.9
	RN-v2	1.2 ± 0.8	1.4 ± 1.2	0.4 ± 0.5	0.2 ± 0.3	4.2 ± 0.8
	DRN-v2	1.8 ± 0.9	2.2 ± 2.0	0.7 ± 0.7	0.5 ± 0.5	5.3 ± 1.6
Physics-informed	ANN	9.3 ± 8.4	1.0 ± 1.1	0.5 ± 0.6	0.6 ± 0.5	7.2 ± 1.2
	FCNN	1.8 ± 0.6	1.2 ± 0.9	0.3 ± 0.5	0.3 ± 0.3	4.8 ± 0.6
	DFCNN	1.9 ± 0.6	1.1 ± 1.0	0.4 ± 0.5	0.3 ± 0.3	5.3 ± 0.7
	RN-v1	1.3 ± 0.8	1.3 ± 1.1	0.4 ± 0.4	0.2 ± 0.3	4.6 ± 0.8
	RN-v2	1.3 ± 0.8	1.3 ± 1.1	0.4 ± 0.5	0.2 ± 0.3	4.6 ± 0.8
	DRN-v2	1.1 ± 0.7	1.3 ± 1.1	0.4 ± 0.4	0.2 ± 0.3	4.8 ± 0.9
M705		Lung	Soft Tissue	Spinal Cord	Brain	Bone
Empirical Model		26.8 ± 0.0	2.2 ± 1.5	1.2 ± 1.2	1.3 ± 0.8	4.1 ± 2.0
Conventional	ANN	7.4 ± 5.3	2.9 ± 0.8	1.9 ± 1.0	2.4 ± 0.5	8.5 ± 0.9
	FCNN	1.1 ± 1.7	0.7 ± 0.7	0.4 ± 0.7	0.3 ± 0.3	2.7 ± 0.9
	DFCNN	1.8 ± 1.6	0.6 ± 0.6	0.3 ± 0.9	0.3 ± 0.2	3.2 ± 1.0
	RN-v1	0.6 ± 1.7	0.8 ± 0.6	0.4 ± 0.6	0.3 ± 0.3	0.1 ± 0.9
	RN-v2	0.9 ± 1.7	0.9 ± 0.6	0.4 ± 0.7	0.2 ± 0.2	0.2 ± 1.0
	DRN-v2	1.4 ± 1.7	1.3 ± 1.4	0.5 ± 0.7	0.6 ± 0.5	4.8 ± 1.3
Physics-informed	ANN	6.7 ± 5.2	1.1 ± 0.7	0.5 ± 0.9	0.7 ± 0.5	7.7 ± 0.9
	FCNN	1.6 ± 1.6	0.7 ± 0.6	0.3 ± 0.7	0.3 ± 0.2	1.5 ± 0.9
	DFCNN	1.7 ± 1.7	0.6 ± 0.6	0.4 ± 0.8	0.3 ± 0.3	2.5 ± 1.1
	RN-v1	1.0 ± 1.8	0.8 ± 0.5	0.4 ± 0.6	0.3 ± 0.2	1.1 ± 1.0
	RN-v2	1.0 ± 1.7	0.8 ± 0.5	0.4 ± 0.7	0.2 ± 0.2	0.6 ± 0.9
	DRN-v2	0.7 ± 2.0	0.8 ± 0.5	0.4 ± 0.6	0.2 ± 0.2	1.5 ± 1.1

Table B2.

MAPE comparisons of RSP between the reference and DECT parametric mapping models for an HN site with five tissue surrogates using a TBDE HN scan.

M701		Lung	Soft Tissue	Spinal Cord	Brain	Bone
Empirical Model		8.1 ± 7.9	2.9 ± 2.6	2.7 ± 1.9	1.2 ± 0.9	4.2 ± 4.9
Conventional	ANN	9.6 ± 7.2	1.1 ± 1.0	1.7 ± 0.8	0.5 ± 0.4	8.0 ± 1.1
	FCNN	1.5 ± 3.3	2.1 ± 0.8	3.0 ± 0.6	1.8 ± 0.2	5.7 ± 0.7
	DFCNN	2.4 ± 3.2	2.2 ± 0.6	3.1 ± 0.5	1.8 ± 0.2	5.8 ± 0.9
	RN-v1	1.1 ± 3.5	2.5 ± 1.1	3.0 ± 0.7	1.8 ± 0.3	4.6 ± 0.8
	RN-v2	1.3 ± 3.4	2.4 ± 0.8	3.1 ± 0.5	1.9 ± 0.2	4.8 ± 0.8
	DRN-v2	1.8 ± 3.8	3.0 ± 2.1	3.3 ± 1.3	1.8 ± 0.5	5.1 ± 1.3
Physics-informed	ANN	9.6 ± 7.2	1.4 ± 0.9	2.8 ± 0.9	1.5 ± 0.5	6.9 ± 1.2
	FCNN	2.0 ± 3.3	2.2 ± 0.7	3.0 ± 0.5	1.7 ± 0.2	5.3 ± 0.7
	DFCNN	2.1 ± 3.3	2.2 ± 0.6	3.0 ± 0.5	1.7 ± 0.2	5.7 ± 0.8
	RN-v1	1.6 ± 4.0	2.4 ± 0.7	3.1 ± 0.5	1.9 ± 0.2	5.2 ± 0.8
	RN-v2	1.6 ± 3.6	2.3 ± 0.7	3.1 ± 0.5	1.9 ± 0.2	5.2 ± 1.0
	DRN-v2	1.3 ± 4.2	2.4 ± 0.7	3.1 ± 0.6	1.9 ± 0.2	5.1 ± 1.2
M702		Lung	Soft Tissue	Spinal Cord	Brain	Bone
Empirical Model		8.9 ± 11.0	2.6 ± 2.4	1.6 ± 1.4	0.9 ± 0.8	3.9 ± 2.2
Conventional	ANN	10.5 ± 7.8	1.2 ± 1.2	1.3 ± 0.7	0.4 ± 0.4	8.0 ± 1.0
	FCNN	1.8 ± 0.9	2.1 ± 0.8	3.0 ± 0.5	1.6 ± 0.3	5.8 ± 0.6
	DFCNN	2.3 ± 0.5	2.2 ± 0.6	3.0 ± 0.5	1.6 ± 0.2	5.8 ± 0.6
	RN-v1	1.1 ± 0.7	2.4 ± 0.9	2.9 ± 0.5	1.7 ± 0.3	4.6 ± 0.8
	RN-v2	1.5 ± 0.8	2.5 ± 0.7	3.0 ± 0.5	1.7 ± 0.3	4.8 ± 0.7
	DRN-v2	1.8 ± 0.9	2.7 ± 1.9	3.1 ± 0.9	1.6 ± 0.5	5.3 ± 1.3
Physics-informed	ANN	10.3 ± 8.0	1.4 ± 1.0	2.6 ± 0.7	1.1 ± 0.5	7.0 ± 1.1
	FCNN	2.1 ± 0.6	2.2 ± 0.7	3.0 ± 0.4	1.6 ± 0.2	5.3 ± 0.5
	DFCNN	2.1 ± 0.6	2.2 ± 0.7	3.0 ± 0.4	1.6 ± 0.2	5.7 ± 0.6
	RN-v1	1.5 ± 0.8	2.4 ± 0.7	3.1 ± 0.4	1.7 ± 0.3	5.1 ± 0.6
	RN-v2	1.5 ± 0.8	2.4 ± 0.7	3.0 ± 0.5	1.7 ± 0.3	5.0 ± 0.7
	DRN-v2	1.1 ± 0.7	2.5 ± 0.7	3.1 ± 0.4	1.7 ± 0.3	4.9 ± 0.8
M705		Lung	Soft Tissue	Spinal Cord	Brain	Bone
Empirical Model		6.4 ± 6.0	1.5 ± 1.4	1.5 ± 1.1	0.8 ± 0.7	4.6 ± 2.0
Conventional	ANN	8.4 ± 5.4	1.1 ± 0.8	1.2 ± 0.8	0.4 ± 0.4	8.4 ± 0.8
	FCNN	1.3 ± 1.7	1.6 ± 0.6	3.0 ± 0.6	1.6 ± 0.2	3.6 ± 0.7
	DFCNN	2.3 ± 1.6	1.8 ± 0.4	3.0 ± 0.6	1.5 ± 0.2	4.0 ± 0.9
	RN-v1	0.8 ± 1.7	2.0 ± 0.4	3.0 ± 0.5	1.7 ± 0.3	1.3 ± 0.8
	RN-v2	1.2 ± 1.7	2.0 ± 0.4	3.0 ± 0.6	1.7 ± 0.3	1.4 ± 0.8
	DRN-v2	1.5 ± 2.0	1.6 ± 0.9	2.9 ± 0.6	1.6 ± 0.5	4.8 ± 1.1
Physics-informed	ANN	8.3 ± 5.4	0.7 ± 0.5	2.5 ± 0.7	1.0 ± 0.4	7.7 ± 0.8
	FCNN	1.9 ± 1.6	1.8 ± 0.5	2.9 ± 0.5	1.6 ± 0.2	2.6 ± 0.7
	DFCNN	1.9 ± 1.6	1.8 ± 0.5	3.0 ± 0.5	1.6 ± 0.2	3.4 ± 0.9
	RN-v1	1.2 ± 1.8	1.9 ± 0.4	3.1 ± 0.4	1.7 ± 0.3	2.3 ± 0.8
	RN-v2	1.1 ± 1.7	2.0 ± 0.4	3.0 ± 0.5	1.7 ± 0.3	1.8 ± 0.8
	DRN-v2	0.7 ± 1.9	2.0 ± 0.4	3.0 ± 0.4	1.7 ± 0.2	2.5 ± 1.1

Table B3.

MAPE comparisons of mass densities between the reference and DECT parametric mapping models for a thoracic site with five tissue surrogates using a TBDE thorax scan.

M701		Lung	Breast	Soft Tissue	Spinal Cord	Bone
Empirical Model		26.8 ± 0.0	-	3.1 ± 2.5	3.4 ± 2.6	7.8 ± 3.9
Conventional	ANN	11.4 ± 7.2	-	2.6 ± 1.8	1.5 ± 1.3	8.5 ± 2.1
	FCNN	1.1 ± 1.6	-	1.5 ± 1.7	0.8 ± 0.9	5.6 ± 1.3
	DFCNN	1.9 ± 1.5	-	1.4 ± 1.6	1.0 ± 1.0	5.6 ± 1.6
	RN-v1	0.7 ± 1.6	-	1.5 ± 1.9	1.7 ± 2.4	4.2 ± 1.2
	RN-v2	0.9 ± 1.5	-	1.4 ± 1.8	0.7 ± 0.8	4.3 ± 1.3
	DRN-v2	1.6 ± 1.8	-	2.5 ± 2.7	3.4 ± 2.4	6.3 ± 2.0
Physics-informed	ANN	10.6 ± 7.0	-	1.5 ± 1.5	1.4 ± 1.1	7.6 ± 2.1
	FCNN	1.6 ± 1.5	-	1.4 ± 1.6	0.9 ± 0.8	4.9 ± 1.1
	DFCNN	1.8 ± 1.6	-	1.4 ± 1.6	1.0 ± 1.0	5.4 ± 1.4
	RN-v1	1.0 ± 1.7	-	1.4 ± 1.6	0.7 ± 0.8	4.7 ± 1.2
	RN-v2	1.0 ± 1.6	-	1.3 ± 1.7	0.7 ± 0.9	4.6 ± 1.2
	DRN-v2	0.8 ± 1.8	-	1.4 ± 1.6	0.7 ± 0.8	4.8 ± 1.3
M702		Lung	Breast	Soft Tissue	Spinal Cord	Bone
Empirical Model		26.8 ± 0.0	3.4 ± 2.2	2.7 ± 2.2	2.5 ± 1.9	7.1 ± 6.9
Conventional	ANN	10.6 ± 6.5	2.5 ± 1.3	2.5 ± 1.4	1.2 ± 0.9	8.3 ± 1.8
	FCNN	1.2 ± 0.8	1.6 ± 0.8	1.2 ± 1.1	0.6 ± 0.6	5.6 ± 1.1
	DFCNN	1.9 ± 0.5	1.4 ± 0.8	1.1 ± 1.0	0.8 ± 0.6	5.7 ± 1.3
	RN-v1	0.7 ± 0.7	1.9 ± 1.1	1.3 ± 1.4	1.4 ± 2.2	4.2 ± 1.1
	RN-v2	0.9 ± 0.7	1.8 ± 1.0	1.3 ± 1.2	0.6 ± 0.5	4.3 ± 1.1
	DRN-v2	1.5 ± 0.8	2.5 ± 1.6	2.1 ± 2.2	2.9 ± 1.9	6.1 ± 1.9
Physics-informed	ANN	9.7 ± 6.2	1.2 ± 1.0	1.2 ± 1.0	1.1 ± 0.9	7.4 ± 1.8
	FCNN	1.6 ± 0.5	1.5 ± 0.8	1.2 ± 1.0	0.7 ± 0.5	4.9 ± 0.9
	DFCNN	1.7 ± 0.5	1.5 ± 0.8	1.2 ± 1.1	0.8 ± 0.7	5.4 ± 1.1
	RN-v1	1.0 ± 0.8	1.8 ± 1.0	1.2 ± 1.1	0.6 ± 0.4	4.8 ± 1.0
	RN-v2	1.0 ± 0.6	1.7 ± 0.9	1.2 ± 1.1	0.5 ± 0.5	4.6 ± 1.1
	DRN-v2	0.8 ± 0.7	1.6 ± 0.9	1.2 ± 1.1	0.6 ± 0.4	4.8 ± 1.1

Table B4.

MAPE comparisons of RSP between the reference and DECT parametric mapping models for a thoracic site with five tissue surrogates using a TBDE thorax scan.

M701		Lung	Breast	Soft Tissue	Spinal Cord	Bone
Empirical Model		7.0 ± 5.8	-	3.2 ± 2.5	5.8 ± 3.8	8.7 ± 4.1
Conventional	ANN	12.3 ± 7.3	-	1.4 ± 1.4	2.7 ± 1.2	8.5 ± 1.8
	FCNN	1.4 ± 1.7	-	2.0 ± 1.2	3.0 ± 0.8	5.9 ± 1.1
	DFCNN	2.3 ± 1.5	-	2.2 ± 1.1	3.2 ± 0.7	5.9 ± 1.4
	RN-v1	0.9 ± 1.6	-	2.3 ± 1.2	2.8 ± 1.3	4.8 ± 1.0
	RN-v2	1.2 ± 1.5	-	2.3 ± 1.2	3.0 ± 0.7	4.8 ± 1.1
	DRN-v2	1.6 ± 1.9	-	2.6 ± 2.0	6.0 ± 2.9	6.2 ± 1.8
Physics-informed	ANN	12.2 ± 7.3	-	1.4 ± 1.2	3.5 ± 1.3	7.7 ± 1.9
	FCNN	1.9 ± 1.5	-	2.1 ± 1.1	3.3 ± 0.6	5.3 ± 1.0
	DFCNN	1.9 ± 1.6	-	2.1 ± 1.1	3.1 ± 0.7	5.7 ± 1.2
	RN-v1	1.2 ± 1.7	-	2.2 ± 1.1	3.1 ± 0.7	5.2 ± 1.0
	RN-v2	1.2 ± 1.7	-	2.2 ± 1.1	2.9 ± 0.8	5.0 ± 1.0
	DRN-v2	0.8 ± 1.7	-	2.3 ± 1.1	3.2 ± 0.8	4.9 ± 1.3
M702		Lung	Breast	Soft Tissue	Spinal Cord	Bone
Empirical Model		6.7 ± 5.5	2.7 ± 1.9	2.7 ± 2.2	5.3 ± 3.1	8.0 ± 6.4
Conventional	ANN	11.4 ± 6.6	1.1 ± 0.9	1.2 ± 1.1	2.5 ± 1.0	8.2 ± 1.5
	FCNN	1.4 ± 0.8	0.8 ± 0.8	1.9 ± 0.9	3.2 ± 0.6	6.0 ± 0.9
	DFCNN	2.3 ± 0.4	0.8 ± 0.7	2.1 ± 0.6	3.3 ± 0.5	6.0 ± 1.1
	RN-v1	0.9 ± 0.7	1.0 ± 0.9	2.3 ± 0.8	3.0 ± 1.1	4.7 ± 1.0
	RN-v2	1.2 ± 0.7	0.9 ± 0.8	2.3 ± 0.7	3.2 ± 0.5	4.8 ± 1.0
	DRN-v2	1.5 ± 0.9	1.3 ± 1.2	2.3 ± 1.7	5.8 ± 2.3	6.0 ± 1.6
Physics-informed	ANN	11.2 ± 6.5	1.4 ± 1.0	1.2 ± 0.9	3.5 ± 1.0	7.5 ± 1.6
	FCNN	1.9 ± 0.5	0.9 ± 0.8	2.1 ± 0.7	3.3 ± 0.4	5.4 ± 0.8
	DFCNN	1.9 ± 0.5	0.8 ± 0.8	2.1 ± 0.7	3.2 ± 0.5	5.8 ± 0.9
	RN-v1	1.2 ± 0.8	0.9 ± 0.8	2.2 ± 0.7	3.3 ± 0.4	5.2 ± 0.9
	RN-v2	1.2 ± 0.7	0.9 ± 0.8	2.2 ± 0.7	3.1 ± 0.5	5.0 ± 0.9
	DRN-v2	0.8 ± 0.7	0.9 ± 0.8	2.2 ± 0.7	3.4 ± 0.5	5.0 ± 1.1

Table B5.

MAPE comparisons of mass densities between the reference and DECT parametric mapping models for a pelvic site with three tissue surrogates using a TBDE pelvis scan.

M701		Soft Tissue	Spinal Cord	Bone
Empirical Model		2.5 ± 2.0	3.3 ± 2.7	3.3 ± 2.2
Conventional	ANN	2.6 ± 1.3	2.3 ± 1.5	7.2 ± 1.3
	FCNN	1.0 ± 0.9	1.2 ± 1.4	4.7 ± 0.8
	DFCNN	0.9 ± 0.9	1.0 ± 1.2	5.1 ± 1.0
	RN-v1	1.0 ± 1.2	1.1 ± 1.8	4.2 ± 0.7
	RN-v2	0.9 ± 0.9	1.1 ± 1.8	4.2 ± 0.6
	DRN-v2	1.7 ± 1.8	2.5 ± 2.5	3.9 ± 1.4
Physics-informed	ANN	1.2 ± 1.0	1.4 ± 1.1	5.6 ± 1.4
	FCNN	1.0 ± 0.9	0.9 ± 1.1	4.7 ± 0.8
	DFCNN	0.9 ± 0.9	1.1 ± 1.2	4.9 ± 0.8
	RN-v1	0.9 ± 0.8	0.9 ± 1.4	4.6 ± 0.8
	RN-v2	0.9 ± 0.9	1.2 ± 1.8	4.7 ± 1.0
	DRN-v2	0.9 ± 0.8	1.0 ± 1.6	4.9 ± 1.1
M702		Soft Tissue	Spinal Cord	Bone
Empirical Model		2.3 ± 1.9	2.1 ± 1.8	3.2 ± 2.0
Conventional	ANN	2.6 ± 1.2	1.6 ± 1.1	7.5 ± 1.2
	FCNN	0.9 ± 0.9	0.7 ± 0.8	4.9 ± 0.8
	DFCNN	0.8 ± 0.8	0.6 ± 0.8	5.3 ± 1.1
	RN-v1	1.0 ± 1.1	0.7 ± 1.1	4.2 ± 0.8
	RN-v2	0.9 ± 0.9	0.6 ± 0.9	4.2 ± 0.8
	DRN-v2	1.6 ± 1.8	1.2 ± 1.4	4.2 ± 1.3
Physics-informed	ANN	1.1 ± 0.9	1.0 ± 0.8	6.0 ± 1.3
	FCNN	0.9 ± 0.8	0.5 ± 0.7	4.9 ± 0.8
	DFCNN	0.9 ± 0.9	0.7 ± 0.8	5.0 ± 0.9
	RN-v1	0.9 ± 0.8	0.6 ± 0.7	4.6 ± 0.9
	RN-v2	0.8 ± 0.8	0.6 ± 0.8	4.7 ± 1.0
	DRN-v2	0.9 ± 0.8	0.6 ± 0.8	5.0 ± 1.2

Table B6.

MAPE comparisons of RSP between the reference and DECT parametric mapping models for a pelvic site with three tissue surrogates using a TBDE pelvis scan.

M701		Soft Tissue	Spinal Cord	Bone
Empirical Model		2.6 ± 2.1	2.8 ± 2.2	3.5 ± 2.3
Conventional	ANN	1.1 ± 0.9	1.3 ± 1.0	6.9 ± 1.1
	FCNN	1.7 ± 0.7	2.6 ± 1.1	5.2 ± 0.7
	DFCNN	1.9 ± 0.6	2.7 ± 0.8	5.4 ± 0.9
	RN-v1	2.0 ± 0.6	2.4 ± 0.7	4.6 ± 0.6
	RN-v2	1.9 ± 0.6	2.5 ± 0.8	4.8 ± 0.5
	DRN-v2	2.1 ± 1.3	2.7 ± 1.7	4.1 ± 1.1
Physics-informed	ANN	1.0 ± 0.8	2.0 ± 1.2	5.7 ± 1.2
	FCNN	1.8 ± 0.6	2.6 ± 0.8	5.2 ± 0.7
	DFCNN	1.8 ± 0.6	2.8 ± 0.8	5.3 ± 0.7
	RN-v1	1.9 ± 0.6	2.4 ± 0.8	5.1 ± 0.7
	RN-v2	1.9 ± 0.6	2.5 ± 0.8	5.2 ± 0.9
	DRN-v2	1.9 ± 0.6	2.7 ± 0.8	5.0 ± 1.1
M702		Soft Tissue	Spinal Cord	Bone
Empirical Model		2.4 ± 1.9	2.5 ± 1.9	3.4 ± 2.1
Conventional	ANN	1.0 ± 0.9	1.5 ± 0.8	7.2 ± 1.1
	FCNN	1.7 ± 0.7	2.9 ± 0.7	5.4 ± 0.7
	DFCNN	1.9 ± 0.5	2.9 ± 0.5	5.5 ± 0.9
	RN-v1	2.0 ± 0.6	2.7 ± 0.6	4.6 ± 0.7
	RN-v2	2.0 ± 0.6	2.8 ± 0.6	4.8 ± 0.7
	DRN-v2	2.1 ± 1.3	2.7 ± 1.2	4.3 ± 1.1
Physics-informed	ANN	1.0 ± 0.7	2.6 ± 1.0	6.0 ± 1.2
	FCNN	1.8 ± 0.6	2.9 ± 0.5	5.3 ± 0.7
	DFCNN	1.8 ± 0.6	3.0 ± 0.6	5.4 ± 0.7
	RN-v1	1.9 ± 0.6	2.8 ± 0.6	5.1 ± 0.8
	RN-v2	1.9 ± 0.6	2.8 ± 0.6	5.3 ± 0.9
	DRN-v2	2.0 ± 0.6	3.0 ± 0.6	5.1 ± 1.2