Tensor-based insights into systems immunity and infectious disease

Abstract

Profiling immune responses across several dimensions, including time, patients, molecular features, and tissue sites, can deepen our understanding of immunity as an integrated system. These studies require new analysis approaches to realize their full potential. We highlight the recent application of tensor methods and discuss several future opportunities.

Infection and immunity are integrated systems

Host-pathogen interactions involve complex, co-adaptive responses that have posed considerable challenges to computational modeling and prediction. Outcomes of infectious diseases derive from multifactorial intersections among host immune responses, pathogen immune subversion, and vaccine or anti-infective efficacy; each is subject to dynamic adaptation and selection pressures [1,2]. Integrating data across different scales, units, and systems—spanning molecular immunity to global epidemiology—is necessary to advance optimally informative models of infection risk, co-evolution of host and pathogen, anti-infective efficacy, and public health. In addition to enabling new insights into systems immunology, accurate models of infection and immunity have the potential to identify unforeseen risk factors and therapeutic targets [2].

The opportunities and challenges in the computational modeling of infectious diseases are illustrated by the successes and setbacks during the COVID-19 pandemic. Specifically, despite the unprecedented number of resources applied to understanding the immunological determinants of COVID-19 disease severity, approximately 85% of critical outcomes in patients remain unexplained [3]. Important advances have been made in understanding what distinguishes protective immune responses by systematically profiling the variation among patients. One such example involves type I and III interferon (IFN) responses, where a subset of patients have been identified with auto-antibodies against these cytokines, impairing protective immunity and leading to severe disease [3]. Indeed, dysfunctional immune responses likely lead to severe outcomes when such front-line innate mechanisms are unable to control viral pathogenesis. At the same time, the pandemic has revealed an acute need to coordinate the study of viral evolution, virulence strategies, immune responses associated with protective versus non-protective immunity, and transmissibility across many families of potential pandemic viruses, along with identifying the shared patterns in these features between viruses [4]. Accurate and predictive computational modeling that spans molecular and cellular immunology, disease epidemiology, and anti-infective development is essential to addressing these challenges.

Outcomes of infection or immunity result from complex molecular and cellular interactions: First, host genetic and epigenetic factors define programs of innate and adaptive immunity. Second, pathogen virulence and immune evasion occur based on mutation and recombination events. Third, the impacts of preventive (vaccine) and therapeutic (anti-microbial; immune modifying) anti-infective regimens coordinately modify both host and pathogen responses [6]. Host biological variables—including age, sex, comorbidity, and environment—affect the immune response and influence each of these interactions. Host and pathogen interactions may also vary depending on the tissue site or are defined by a confluence of interactions across tissues. Thus, taken together, no single series of measurements, even ‘omic in scale, presents a complete picture of one’s immunologic state across a temporal span reflecting holistic immunity. These distinct dimensions of immunologic state are myriad and present significant challenges to computational modeling.

The multidimensional challenge of systems immunology studies

Given the scale of measurements necessary to profile infection and immunity on a systems level, researchers typically turn to tools such as principal components analysis (PCA), t-distributed stochastic neighbor embedding (t-SNE), and uniform manifold approximation and projection (UMAP) to capture patterns in data. These tools reduce a series of measurements (such as the expression of many genes within a cell) into a smaller set of patterns that capture overall trends. However, to work with these methods, researchers must “flatten” multidimensional datasets by concatenating dimensions to fit data into a matrix representation; for instance, a measurement collected over time would be expanded such that each measurement-time point pair becomes a separate variable. While flattening data enables one to use standard methods, it also destroys the critical structure in such studies that can help in data exploration and modeling. Immunological signatures can manifest across specific study dimensions, such as in certain parts of a dynamic response [1,7], or specific subsets of subjects; recognizing these biological phenomena requires joint analysis of measurements, time points, and patient cohorts. Flattening data limits the datasets to two dimensions and confounds the axes over which flattening occurs, impeding the definition of immunological signatures and their significance. Therefore, avoiding this flattening step is advantageous for insights into these studies.

Tensor approaches to data analysis in systems immunology

Rather than flattening data, structuring it into a tensor can greatly improve the modeling and interpretation of systematic measurements (Figure 1). Higher-dimensional generalizations of scalars, vectors, and matrices, tensors are organized arrays of data with typically three or more dimensions [8]. Each study dimension (e.g., biological modalities, time, patients) can be represented as one axis, or mode, in the tensor. Each element in the tensor, therefore, corresponds to a unique combination of modes; for instance, within a gene expression tensor comprised of time, gene, and patient modes, each element corresponds to the expression of a gene for a chosen patient at a single time point. This representation consequently preserves the natural organization of the study (Figure 1).

Figure 1. Tensors, tensor factorization techniques, and canonical polyadic decomposition (CPD) results.

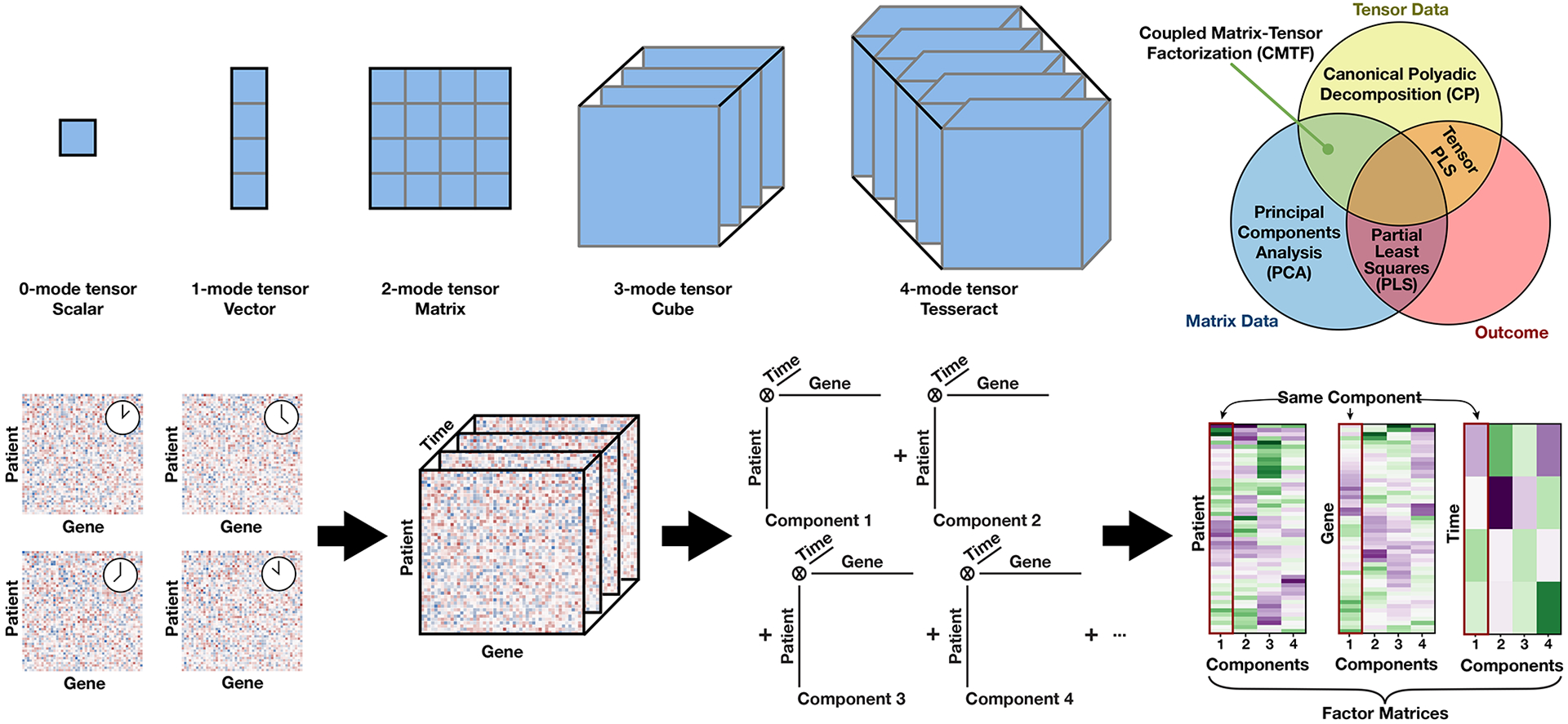
Tensors are organized collections of data with any number of dimensions; these dimensions are called “modes”. Tensors with 0, 1, or 2 modes are commonly referred to as scalars, vectors, and matrices. Each tensor mode represents a distinct axis of variation within a dataset. For instance, longitudinal gene expression measurements from a cohort of patients could be organized into a 3-mode tensor with ‘gene’, ‘patient’, and ‘time’ modes; each position would correspond to the expression of a gene for a specific patient and time point.

Tensor factorization methods, such as canonical polyadic decomposition (CPD), serve a similar purpose as methods like principal components analysis (PCA). Similar to PCA, CPD reduces data to a series of patterns (components) [8]. CPD generalizes to tensor-structured datasets while still identifying patterns summarized as components. The effect of each component is also still added together to re-create the original dataset.

To interpret the biological significance of each component, CPD produces its description of these patterns within a ‘factor matrix’ that relates each mode to the components. In parallel, tracing a component across factor matrices describes the representation of that pattern across the modes. Finally, evaluating differences in components within a factor matrix describes how each pattern identified by CPD is distinct.

Beyond CPD, other tensor factorization methods can be useful for specific types of datasets: For instance, coupled decompositions jointly factorize several tensors that share modes, such as two datasets derived from the same patients. Tensor partial least squares identifies only the shared variation between two tensors, which can be helpful when one wishes to identify the patterns related to a specific outcome, such as resolution of an infection [13].

The additional structure allows tensor factorization methods to better capture and interpret biological patterns. Tensor factorization leverages the tensor structure to isolate a pattern’s association with each tensor mode and reduce data more concisely and accurately than a flattening approach. There are many tensor factorization methods—including canonical polyadic decomposition (CPD), tensor partial least squares regression (tPLS), and Tucker decomposition; we will focus on CPD due to its ease of interpretation [8].

CPD reduces tensor-structured data into a series of components that capture patterns across the data [8]. Each component can be thought of as a unique biological mechanism spread across the tensor modes; in our example tensor with modes of time, gene, and patient, each component would correlate to a functional group of genes with similar dynamics and representation across patients. To interpret the biological significance of each component, CPD produces factor matrices—one for each tensor mode—that relate the tensor factorization components to the dimensions of the original data.

Interpreting the biological patterns highlighted by these components can provide novel insights. Evaluating variations in component associations across factors can reveal variance in immune responses to disease and identify whether distinct processes coordinate in their contribution to a disease [9], [10]. In considering multiple cohorts, individual or collective signature components can reveal common and distinct patterns that exist across subsets of patients, studies, and conditions [9]–[11]. When paired with prediction models, these components can be used to identify biological patterns related to an outcome of interest [9], [10], [12].

There are instances where physiological measurements do not have one common structure, such as multi-omics datasets where some measurements might be antigen-specific while others lack this dimension. Coupled tensor factorizations allow one to find the predominant patterns either restricted to one dataset or shared across both, increasing the range of applications for tensor factorization, especially for multi-omics studies. Identifying patterns across datasets provides dual benefits: First, it can better define molecular mechanisms, particularly for those that manifest across datasets. For instance, cytokine programs with gene expression effects can be identified as the same pathway. Second, it is possible to better predict outcomes by integrating mechanisms that appear in only one measurement type. For example, we observed that tensor factorization recognized and integrated transcriptomic- and proteomic-specific patterns that improved our ability to predict methicillin-resistant Staphylococcus aureus (MRSA) infection persistence [9]. Taken together, tensor factorization can help identify immunological signatures and their patterns of presentation to improve the identification and interpretation of specific immunologic mechanisms.

Prospects in systems immunology enabled by a tensor-centric approach

New scientific questions can be addressed by adopting consilience in experimental and computational approaches that explicitly consider the many dimensions of infection and immunity (Figure 2). Given the extent to which immune responses dynamically evolve over an infection, longitudinal studies and tensor analysis will help to delineate phases of infection and immune responses to dissect how they vary in temporal, spatial, and qualitative features. Coupling different types of measurements—according to their shared timing or presentation in patients—distinguished by their tissue site, molecular profiling technology, or other dimensions—can deepen our ability to analyze immunity as an integrated system. In infectious diseases, coupling measurements of host and infection features will help to define host-pathogen crosstalk.

Figure 2. Examples of research questions enabled by tensor-based analysis.

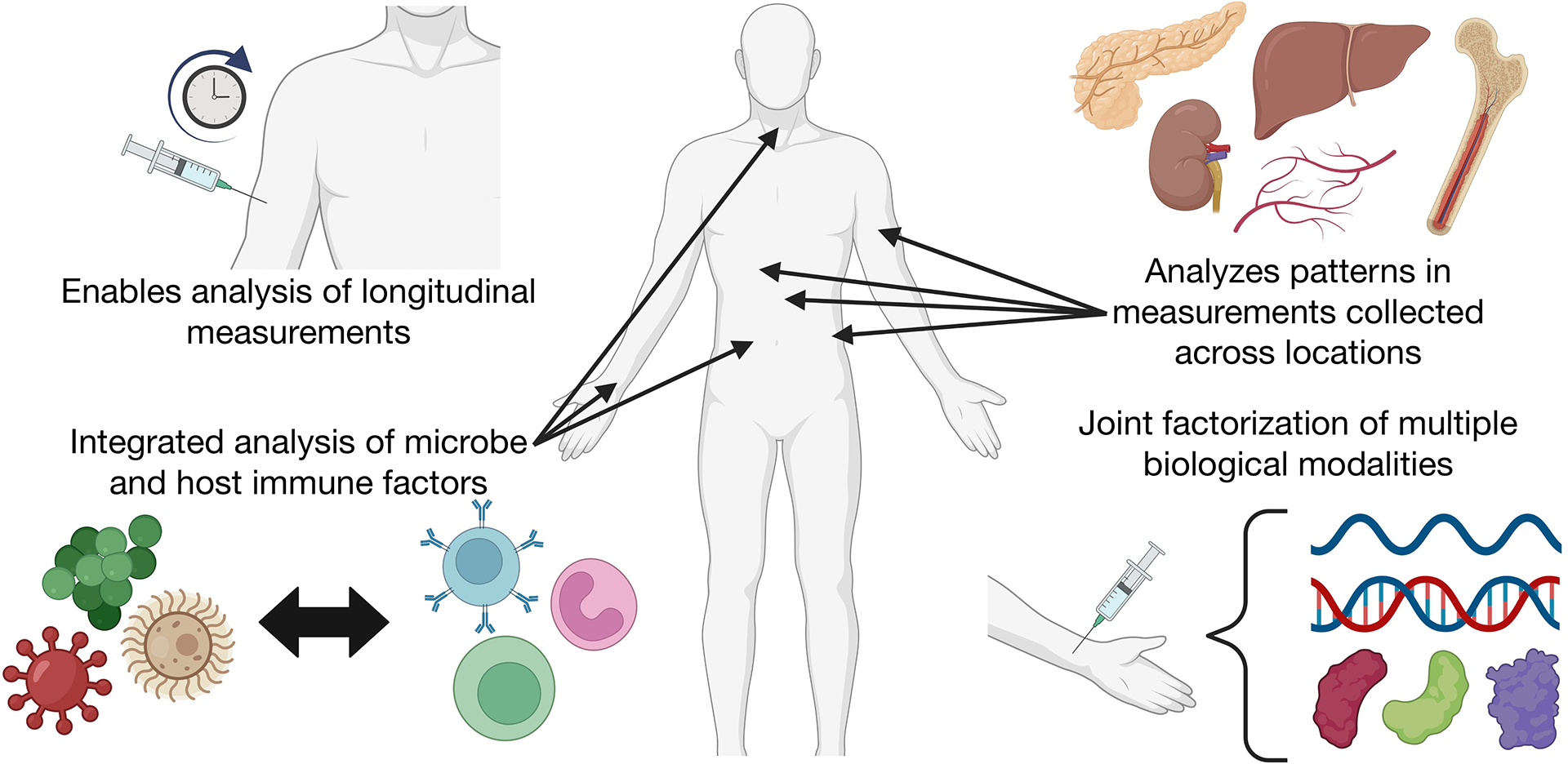
By leveraging the structural information encoded in tensor-formatted data, tensor factorization enables data analyses that better capture patterns between the biological dimensions represented along the tensor modes. This allows users to better understand the relationships between biological dimensions and enables novel research questions in immunology. For example, with tensor analyses, users may be able to better understand the relationships between biological mechanisms, temporal dynamics, host/microbe factors, and tissue sites. This figure was created using BioRender (https://biorender.com/).

In total, leveraging the structure of high-dimensional, systematic studies improves one’s ability to discriminate immune response signals and their association with pathology. By systematically tracking the dimensions over which immune responses vary, it should additionally become possible to ascertain more subtle differences beyond just those most obvious signals in pathologic cases, such as the signals that are absent in a pathologic response and most abundant when infections successfully resolve. Both ‘gas’ and ‘brakes’ are important: the presence of infection must weigh against potential damage from immunity, and positive immune signals must be balanced with regulatory control. Furthermore, it should be possible to take an even broader view and compare molecular signatures across infection types. Indeed, such a perspective has been useful in the oncology space; focusing on the molecular variation of tumors has led to the idea of both defining and treating tumors, not by their site of origin, but by predictive molecular features [13]. A wide array of molecular technologies has finally made it possible to more comprehensively profile immunity; we posit that defining signatures both within and across infections will lead to a similar pan-infection perspective.

Glossary

Canonical polyadic decomposition (CPD)

a tensor factorization technique that reduces tensor-structured data to a series of components that capture the patterns’ associations across the tensor modes

Components

distinct patterns within a dataset that are separated by factorization

Factor matrices

the output of CPD that relates each tensor mode to the CPD components

Immunological signatures

coordinated biological patterns represented by a change in a series of measurements

Matrix

an organized, two-dimensional array of data; equivalent to a two-mode tensor

Omics

collective characterization of a certain class of molecules, such as genomic, transcriptomic, or proteomic measurements

Principal components analysis (PCA)

a dimensionality reduction technique that reduces matrix-structured data into a series of principal components capturing distinct patterns

Scalar

a single value; equivalent to a zero-mode tensor

t-distributed stochastic neighbor embedding (t-SNE)

a nonlinear dimensionality reduction technique that projects high-dimensional data to a lower-dimensional space while grouping similar points in a dataset

Tensor

an organized array of data, usually with three or more dimensions

Tensor factorization

factorization techniques that reduce and capture patterns in tensor-structured data

Mode

one axis over which measurements can be organized in a tensor

Tensor partial least squares

a tensor factorization technique that reduces tensor-structured data to a series of components that capture the shared patterns between two tensors

Tucker decomposition

a tensor factorization technique that decomposes tensor-structured data into the product of mode-specific matrices and a smaller core tensor

Uniform manifold approximation and projection (UMAP)

similar to t-SNE; a nonlinear dimensionality reduction technique that projects high-dimensional data to a lower-dimensional space while grouping similar points in a dataset

Vectors

a one-dimensional array of values