Abstract
Generation of single photons carrying spin and orbital angular momenta (SAM and OAM) opens enticing perspectives for exploiting multiple degrees of freedom for high-dimensional quantum systems. However, on-chip generation of single photons encoded with single-mode SAM-OAM states has been a major challenge. Here, by using carefully designed anisotropic nanodimers fabricated atop a substrate, supporting surface plasmon polariton (SPP) propagation, and accurately positioned around a quantum emitter (QE), we enable nonradiative QE-SPP coupling and the SPP outcoupling into free-space propagating radiation featuring the designed SAM and OAM. We demonstrate on-chip room-temperature generation of well-collimated (divergence < 7.5°) circularly polarized (chirality > 0.97) single-mode vortex beams with different topological charges (𝓁 = 0, 1, and 2) and high single-photon purity, g(2)(0) < 0.15. The developed approach can straightforwardly be extended to produce multiple, differently polarized, single-mode single-photon radiation channels and enable thereby realization of high-dimensional quantum sources for advanced quantum photonic technologies.
Single-photon sources of circularly polarized single-mode vortex beams are demonstrated based on the QE-coupled metasurfaces.
INTRODUCTION
Structuring single-photon emission and engineering photon states triggers breakthroughs in fundamental physics (1, 2) and underpins a broad range of modern quantum technologies (3–6). One of the forefront research fields is chiral quantum optics making use of unique degrees of freedom associated with photon spin orbital momentum (SAM) (7–9) and orbital angular momenta (OAM) (10–12). The superpositions of right- and left-circular SAM states (∣R⟩ and ∣L⟩) and OAM states (±𝓁) encoded in single photons can advantageously be exploited for advanced applications in high-dimensional quantum information processing (5, 13–16). Chiral (i.e., SAM encoded) photon emission has been realized at low temperatures by applying a strong magnetic field (17, 18) and then splitting the excitation transitions in specially engineered nanostructures, e.g., a photonic crystal waveguide (18). The low-temperature generation of single photons with different SAM-OAM superposition states has also been demonstrated using quantum emitters (QEs) coupled to microring resonators (19, 20). Although the requirement of low-temperature operation restricts eventual practical applications, the reported configurations suggest possibilities for on-chip generation of single photons encoded with SAM-OAM states by coupling QEs with individual nanostructures, an approach that is different from using spontaneous parametric down conversion in bulk nonlinear crystals (21, 22) or external mode transformation (23–25), all suffering from low photon generation efficiency, low scalability, and complicated transformation process.
Metasurfaces, representing extended surface nanostructures, exhibit unique capabilities for arbitrarily shaping electromagnetic fields, becoming a staple in classical optics (26–31). Very recently, metasurfaces have been introduced to empower single-photon sources (32–36), opening thereby design pathways unattainable for configurations that involve QEs coupled to individual nanostructures. The “meta-atom” approach, in which a QE is efficiently and nonradiatively coupled to surface plasmon polariton (SPP) modes that are in turn outcoupled to free-space propagating radiation by QE-encircling dielectric nanoridges (37), is especially attractive due to its efficiency (38), versatility (33, 35), and the possibility for room-temperature generation of circularly polarized single photons (37, 39). A careful analysis of the underlying physics involved in the photon generation by such a meta-atom revealed a daunting fundamental challenge: Conventional configurations of QE-encircling nanoridges, such as constant-width (33, 38) and width-varying (37) concentric nanoridges or Archimedean spiral gratings (39), can efficiently generate only radially polarized photons (35). Generation of purely circularly right or left polarized (RCP or LCP) photons is impossible with spiral or concentric nanoridges because the SPP outcoupling by these ridges does not change the (radially oriented) SPP polarization. As a result, any spiral or concentric grating would always generate, simultaneously and with equal efficiency, RCP and LCP beams carrying the same total angular momentum (determined by the number of spirals used), i.e., with their OAM (topological charges) being different by two (35, 39). Similar fundamental limitations are also found in other configurations, rendering single-photon generation of single-mode SAM-OAM vortex beams extremely challenging if not impossible (40).
In this work, we propose the general approach that enables independent manipulation of the single-photon SAM (∣Ψ⟩SAM) and OAM (∣Ψ⟩OAM) states by using dimers of orthogonal nanorods (DONRs), generating high-purity ∣Ψ⟩SAM, arranged in metasurface arrays controlling ∣Ψ⟩OAM. Using nanodiamonds (NDs) containing nitrogen-vacancy (NV) centers positioned precisely within dielectric DONR-based metasurfaces atop silver (Ag) films, we demonstrate a set of room-temperature on-chip single-photon sources of well-collimated circularly polarized single-mode vortex beams. The DONRs are carefully designed to efficiently convert SPP modes (by outcoupling) to free-space propagating RCP photons with near-perfect purity (98% for S3 > 0.9) and with the negligibly small (<0.3%) spatial overlap between RCP and residual LCP photons. Furthermore, by arranging the DONRs along different (spiral and concentric) trajectories, high-purity SAM states are superimposed with OAM states corresponding to different phase-front helicities (topological charges): 𝓁 = 0, 1, and 2. The generated single-photon RCP single-mode vortex beams exhibit a low divergence (< 7.5°) and robust characteristics with respect to small QE misalignments (±50 nm).
RESULTS
Design of on-chip SAM-OAM photon sources
The general design concept is based on devising individual nanostructures that would outcouple (radially polarized) SPP waves into circularly polarized free-space propagating radiation and aligning these nanostructures along trajectories chosen according to the desired OAM. One could opt for resonant plasmonic (metal) nanorods, whose perpendicular dipole moments scatter with the π/2 phase difference (41, 42), but the inevitable photon absorption by metal nanorods would jeopardize the single-photon generation efficiency. We suggest using instead pairs of orthogonal dielectric nanorods, i.e., DONRs, whose separation along the SPP propagation ensures the proper phase difference between their main dipole moments. Following this concept, we place ND-NVs on a Ag substrate covered by a silica (SiO2) spacer and arrange the designed DONRs made of hydrogen silsesquioxane (HSQ) along the OAM-corresponding trajectories (Fig. 1A). Note that the ND-NVs are considered being excited with a tightly focused radially polarized laser beam (not shown in Fig. 1A), an excitation that favors vertical electric dipoles exciting cylindrically diverging SPP waves propagating along the multilayer substrate surface (37–39, 43).
Fig. 1. Design of QE-coupled metasurfaces for SAM-OAM photon emission.
(A) Schematic of QE-coupled metasurfaces generating single-mode SAM-OAM photon emission with different topological charges: lR = 0, 1, and 2. The ND-NVs are surrounded by DONRs aligned along the OAM-corresponding trajectories. Insets: Angular view scanning electron microscopy (SEM) image of the central part of the fabricated metasurface along with the ND-NV schematic. Scale bar, 500 nm. (B) Illustration of SAM generation by DONR outcoupling of the QE-excited SPP wave. An individual DONR consists of two orthogonal nanorods with the width (w) = 100 nm, length (l) = 400 nm, and height (h) = 150 nm. (C) Intensity ratio of RCP and LCP components (left axis) and Stokes parameter S3 (right axis) as a function of the nanorod separation d calculated at the radiation wavelength of 670 nm by considering the outcoupling of a plane SPP wave incident on a rectangular (7 μm by 6 μm) periodic array composed of DONRs. (D) Three-dimensional (3D) representation of the superimposed far-field intensity and polarization distribution of the outcoupled beam produced by the rectangular DONR array with the optimized in (C) nanorod separation. The color indicates the value of Stokes parameter S3. a.u., arbitrary units.
In general, the polarization of the photon emission outcoupled from QE-excited SPPs by a DONR can be represented as the SAM superposition state in the circularly polarized basis (∣R⟩ and ∣L⟩) (44)
| (1) |
with C1 being unequal to C2 due to scattering anisotropy, unlike the case of outcoupling with nanoridges (39). Arranging metasurface DONRs (oriented identically with respect to radially diverging SPP wave) along spiral trajectories separated by the SPP wavelength in the radial direction results in the corresponding OAM superposition states as follows (39)
| (2) |
Here, m is the number of spiral arms with m < 0 for counterclockwise spirals. In our approach, we first design an individual DONR to obtain a high purity SAM state ∣Ψ⟩SAM (e.g., with C1 → 1 and C2 → 0) and then arrange the DONR elements along the spiral trajectories to ensure the generation of a desirable OAM state superimposed with a given SAM state. For example, by outcoupling QE-excited SPPs with azimuthally arranged DONRs, each producing the RCP photons, along diverging (counterclockwise) spiral, concentric, and converging (clockwise) spiral trajectories, RCP vortex beams with correspondingly different OAMs—lR = 0, 1, and 2—are generated (Fig. 1A).
The individual DONR represents a pair of orthogonal dielectric nanorods equally inclined (i.e., having ±45°) with respect to the SPP propagation direction (Fig. 1B). In a qualitative treatment (note S1), the QE-excited SPP wave propagating along the x axis is outcoupled by the DONR having the nanorod separation d = λspp/4 into the RCP (LCP) radiation produced by dipole moments generated along the long (short) sides of the nanorods (fig. S1), with the former being the main contribution. The suppression of the unwanted LCP contribution can be very close to total for nanorods with large aspect [length-to-width (l/w)] ratios. Thereby, the generation of high-purity RCP photon emission with C1 → 1 and C2 → 0 is feasible, resulting in turn in the generation of the pure superposition state, having a desired OAM (Eq. 2). Likewise, a high-purity LCP superposition state, i.e., with C1 → 0 and C2 → 1, can be generated with the DONR mirrored with respect to the x axis (fig. S1).
Nanofabrication of DONRs and the corresponding limitations on the nanorod dimensions, especially on the height-to-width ratio, h/w, result in relatively large nanorod dimensions as compared to the radiation wavelength. Consequently, the nanorods can no longer be treated within the electrostatic approximation and disregarding the interparticle near-field coupling, as implicitly assumed in the qualitative treatment (note S1). Carefully conducted numerical simulations (Materials and Methods) confirmed that the suppression of the unwanted LCP contribution, IRCP/ILCP, can indeed be close to total, reaching 85, with the Stokes parameter S3 attaining 0.98 for a slightly larger than expected (from the qualitative treatment) nanorod separation d = 3λspp/8 (Fig. 1C). The simulated performance of the plane SPP outcoupling by a rectangular DONR array with the optimized nanorod separation demonstrates an efficient SPP outcoupling into a well-collimated pure RCP photon beam (Fig. 1D). This excellent performance of an outcoupling DONR array, efficiently performing the SPP-to-circular polarization transformation, has further been verified in the experiment with SPPs being excited by a periodic nanoridge grating illuminated with free-space laser light at 670 nm (note S2 and fig. S2).
With the designed DONR at hand, it is straightforward to devise DONR location trajectories that would efficiently convert radially polarized and cylindrically diverging (QE-excited) SPP waves into circularly polarized photon emission, generating a desirable OAM state superimposed with the SAM state determined by the DONR orientation, i.e., generating a single-mode SAM-OAM encoded vortex beam (Eq. 2 and note S1). The azimuthal arrangements with different spiral trajectories for the generation of three different SAM-OAM states of single photons are schematically shown in Fig. 1A and described in Table 1. The correspondingly designed configurations are displayed in Fig. 2A with the color representing the SPP propagation phase variation (note S1).
Table 1. Three arrangements (M1, M2, and M3) for different SAM-OAM single-photon states generated by QE-coupled quantum metasurfaces.
| Metasurfaces arrangement | ∣Ψ⟩OAM | ∣Ψ⟩SAM |
|---|---|---|
| M1: Diverging spiral trajectory | ∣𝓁 = 0⟩ | ∣R⟩ |
| M2: Concentric trajectory | ∣𝓁 = 1⟩ | ∣R⟩ |
| M3: Converging spiral trajectory | ∣𝓁 = 2⟩ | ∣R⟩ |
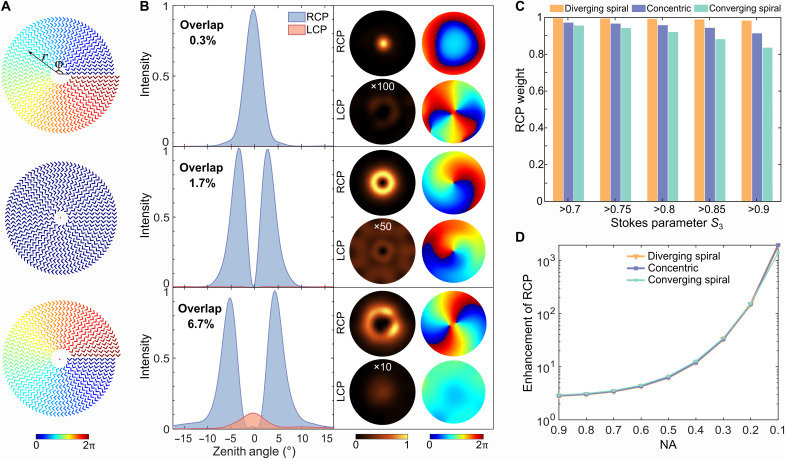
Fig. 2. Generation of single-mode dominated circularly polarized vortex beams.
(A) DONR azimuthal arrangements for generating high-purity circularly polarized vortices with (from top to bottom) diverging spiral, concentric, and converging spiral trajectories, which are colored according to the SPP propagation phase. (B) Simulated intensity and phase distributions of the RCP and LCP contributions for the corresponding configurations. First column: The RCP and LCP intensity profiles with their spatial overlap quantified as 0.3, 1.7, and 6.7%, respectively. Second and third columns: The intensity [numerical aperture (NA) = 0.2] and corresponding phase distributions. The LCP intensity distributions have been enhanced by 100, 50, and 10 times, respectively, to improve their visibility. (C) RCP weight indicating the relative RCP contribution in the total emission for the considered configurations and different chirality thresholds. (D) Enhancement of the RCP emission with respect to the emission without metasurfaces as a function of the collecting objective NA.
SAM-OAM generation
We first confirm that the RCP states dominate the photon emission for all three configurations (Fig. 2B) as expected from the qualitative considerations above. The spatial overlaps of the RCP and LCP intensity distributions are found to be negligibly small—0.3, 1.7, and 6.7%, respectively—much smaller than those obtained previously with the QE-coupled metasurfaces consisting of continuous nanorods (37, 39). At the same time, the conservation of the total angular momentum noted previously (35, 39) is manifested also with these DONR metasurfaces. For example, the diverging (counterclockwise) spiral results in the dominant RCP radiation concentrated in the far field within a collimated bright spot with the uniform phase distribution, signifying the topological charge 𝓁 = 0, while the LCP radiation (weaker by two orders of magnitude) is distributed in a doughnut shape with the phase distribution featuring a singularity with the topological charge 𝓁 = −2 (Fig. 2B). Contrary to that, the converging (clockwise) spiral results in the strong RCP radiation shaped as a doughnut, carrying the topological charge 𝓁 = +2, while the weak LCP radiation is concentrated within a phase homogenous spot with the topological charge 𝓁 = 0 (Fig. 2B).
The RCP relative contribution (weight) can be defined as the ratio of the emission into the RCP radiation, i.e., that with a sufficiently large Stokes parameter S3 > ξ (ξ is the chiral threshold), to the total emitted power, and it can be estimated from the far-field intensity distribution as follows: . For the considered configurations, the RCP weight is rather high (>80%) even when requiring S3 > 0.9, with the largest value of 98.2% found for the RCP generation with the diverging spiral trajectory while being somewhat lower for the concentric and converging spiral trajectories (Fig. 2C). The enhancement of RCP emission as compared with the QE emission without metasurfaces, when calculated as a function of the numerical aperture (NA) of the collecting radiation objective, emphasizes strong collimation of the RCP emission, exceeding three orders of magnitude for NA = 0.1(Fig. 2D).
We have verified the underlying physics of conversion from cylindrically diverging SPP waves into different SAM-OAM states with different DONR trajectories by using an ideal DONR consisting of two orthogonal electric dipoles with the π/2 phase difference to compose the same spiral arrangements. All dipoles are considered to have the same strength with the phases being set in accordance with the SPP propagation phase. The simulation results demonstrated indeed the generation of perfect RCP (LCP contribution of <1%) vortex beams with the corresponding topological charges: 𝓁 = 0, 1, and 2 (fig. S3). Similar results have been obtained with the mirrored DONR configuration producing perfect LCP vortices. We should note that the analytical derivation of SAM and OAM components generated by arrays of angular-distributed dipoles is, in principle, possible (45) but goes beyond the scope of our work limited to the simple model described above. This simple model, which does not require heavy calculations, might also be found useful when analyzing the performance of other QE-coupled metasurfaces. Similar to the orthogonal electric dipoles, the designed DONR with sufficient number of rings can efficiently outcouple SPPs into well-collimated far-field photon emission (figs. S4 to S7). The simulated decay rate enhancement (Purcell factor) with respect to that in free space is ~3.3 with the quantum efficiency (QE), ηQE, (the ratio between the radiative and total decay rates) being ~0.32, which is a moderate value due to the use of low-index (n = 1.41) HSQ polymer to fabricate metasurface nanostructures. Outcoupling metasurfaces made of high-index dielectrics would increase the outcoupling efficiency and thereby decrease the influence of SPP absorption, increasing consequently the quantum efficiency (38). Thus, in our case, the quantum efficiency can be increased to ~0.73 simply by using TiO2 (n = 2.56) metasurface nanostructures (fig. S8). Last, because of very good collimation of the outcoupled radiation by the designed metasurfaces, the collection efficiency, ηCE, is evaluated to be ~0.9 for the collecting emission objective with the NA = 0.9 (fig. S8).
Demonstration of high-purity SAM states
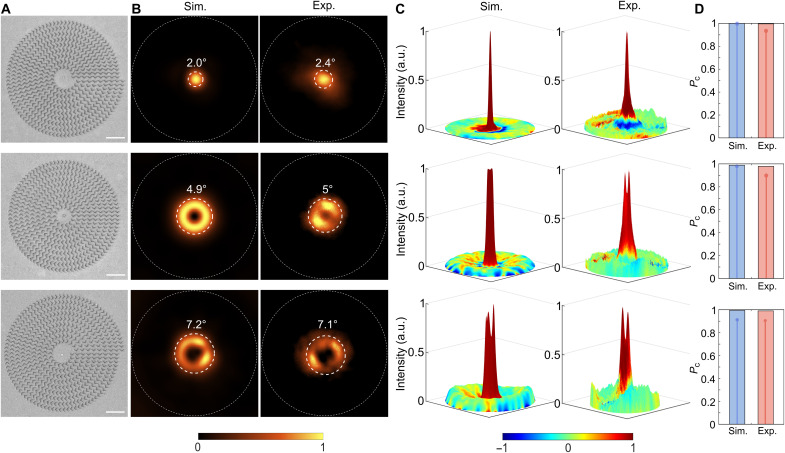
Following the design described above, various SAM-OAM photon sources were fabricated using NDs containing multiple NVs or single NV centers, respectively (fig. S9). The scanning electron microscopy images of the fabricated metasurfaces with DONRs lined up along different spiral trajectories evidence accurate positioning of NDs with multiple NVs (Fig. 3A) as well as high quality and homogeneity of the fabricated nanostructures (figs. S10 and fig. S11). The performance of photon sources was characterized by evaluating the Stokes parameters (S0, S1, S2, and S3), in which S0 represents the total emission intensity; S1 represents the intensity difference between two orthogonal linear polarizations; S2 represents the intensity difference between other orthogonal linear polarizations, which are rotated by 45° with respect to the former one; and S3 represents the intensity difference between the right- or left-hand circular polarizations (all normalized to the total intensity obtained in each measurement) (37, 46, 47). The Stokes parameters were directly measured with the photon emission passing through a quarter–wave plate and linear polarizer (fig. S12 and note S3). We evaluate the chirality (i.e., the degree of circular polarization) of the observed photon emission using the chiral parameter S3 weighted with the other parameters: . Far-field photon emission patterns feature well-collimated beams, with a very good correspondence between the simulated and experimentally observed intensity distribution (Fig. 3B and fig. S13). Note that the experimentally obtained divergence angles, 2.4°, 5°, and 7.1°, are very close to those expected from the simulations. The simulated and measured photon emission intensity and polarization distributions superimposed in three-dimensional (3D) representations exhibit a very good correspondence (Fig. 3C), ascertaining the generation of single-mode SAM-OAM beams. To quantitatively characterize the performance with respect to the chirality of generated photon beams, we define the degree of circular polarization averaged over the intensity distribution: . The photon beam chirality can thus be evaluated as the average chirality calculated from the high-intensity data area (i.e., within the divergence angle indicated by the dashed line in Fig. 3B). This procedure results in the average beam chirality values of 0.934, 0.902, and 0.893 for the three realized (diverging spiral, concentric, and converging spiral) configurations, respectively. Moreover, the maximum chirality values are measured to be 0.996, 0.978, and 0.991 for these configurations, confirming further the generation of high-purity RCP beams (Fig. 3D).
Fig. 3. Demonstration of high-purity SAM states.
(A) SEM images of the fabricated quantum metasurfaces for generating circularly polarized vortex photon beams. Scale bars, 2 μm for all SEM images. (B) Simulated (Sim.) and experimentally (Exp.) measured intensity distributions of the photon emission from the corresponding quantum metasurfaces (NA = 0.3). The white dashed circles encircle the areas corresponding to the full width at half maximum intensities. (C) 3D representation of the superimposed intensity and polarization distributions. The height indicates the intensity, and the color indicates the degree of the circular polarization, with the red (blue) color representing the RCP (LCP). (D) Intensity-weighted and maximum Pc in the high-intensity areas.
The OAM states of generated SAM-OAM photon beams were characterized by using a spatial light modulator (SLM), whose reflection was encoded with different orders of spiral phases, to demodulate phase profiles of OAM beams (39, 44). When changing the topological charge of the SLM phase distribution, the azimuthal intensity pattern of a photon beam reflected by the SLM should change in accordance with the topological charge of the generated vortex beam. A bright spot is expected to be formed when the topological charge of the SLM phase is opposite to that of the vortex beam (fig. S14). Our experimental characterization (Materials and Methods) demonstrated that the azimuthal intensity patterns observed for different SLM spiral phase distributions exhibit indeed well-pronounced and concentrated bright spots for the corresponding topological charges of the SLM phase distribution (fig. S15), indicating thereby high quality of the fabricated SAM-OAM photon sources. We have also observed that the metasurfaces composed of the mirrored DONRs result in the generation of high-quality LCP photon Gaussian and vortex beams (fig. S16).
Single-photon single-mode SAM-OAM beams
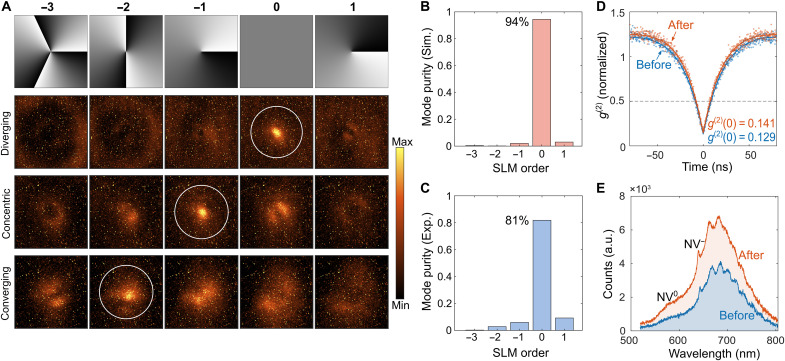
Following the design, fabrication, and characterization procedures described above (but using NDs containing only single NV centers; fig. S17), we realized and characterized single-photon sources of well-collimated single-mode SAM-OAM beams. The main differences in the results of optical characterization are related to considerably weaker photon signals from the single-photon sources, resulting in the optical images being more influenced by the background noise. Thus, the azimuthal intensity distributions observed for different SLM spiral phase distributions when characterizing three different single-photon sources exhibited essentially the same patterns (Fig. 4A), ascertaining also in this case, with the diverging, concentric, and converging spiral DONR trajectories, the generation of the RCP vortex beams carrying the corresponding topological charges 𝓁 = 0, +1, and +2. The generated SAM-OAM photon modes were of high purity, especially the Gaussian RCP mode exhibited the impressive mode purity of 81%, with 94% being expected from simulations (Fig. 4, B and C). The second-order correlation functions of photon emission measured before and after NV-ND coupling to the corresponding metasurface feature the zero-delay level g(2)(0) = 0.129 and 0.141, respectively (Fig. 4D), indicating excellent and stable single-photon properties. In addition, the NV-ND lifetimes (fig. S18) and fluorescence spectra of photon emission (Fig. 4C) did not change notably when measured before and after NV-ND coupling to the metasurface. The single-photon emission spectrum obtained after the NV-ND coupling features two zero-phonon lines, appearing at 575 and 637 nm and indicating, respectively, the charge state of NV dominated by negative (NV−) and neutral (NV0) charge state (47), and the emission peak at ~670 nm, which is the target wavelength of the designed metasurfaces. We note that the proposed design approach is general and can be used for other QEs with different wavelengths and emission decay rates. Regarding the single-photon purity and photon indistinguishability, it has been demonstrated that these two characteristics can be maintained at a very high level (at cryogenic temperatures) even after QE coupling to nanostructures (48–50).
Fig. 4. Characterization of single-photon single-mode SAM-OAM beams.
(A) Intensity distributions of the single-photon emission obtained with different DONR spiral trajectories measured after the reflection from the SLM encoded with different orders of spiral phases. First row present the phase distribution for the SLM holograms with the topological charges of −3, −2, −1, 0, and 1. Second, third, and fourth rows present the intensity distributions obtained with the diverging, concentric, and converging spiral arrangements, respectively. (B and C) Mode purity of the single-photon source simulated (B) and measured (C) with the diverging spiral trajectory. (D) Second-order correlation function g(2) of single-photon emission measured before and after the ND-NV coupling with the metasurface using 100 μW of 532-nm continuous laser. (E) Fluorescence spectrum of the single-photon emission measured before and after the ND-NV coupling.
DISCUSSION
In this work, we proposed the general approach for designing single-photon circularly polarized single-mode vortex beams, with the SAM and OAM states being separately controlled by the DONR configuration and array arrangement. The developed approach provides thereby a straightforward flexible way to precisely engineer the SAM-OAM states of single photons emitted by the DONR-based quantum metasurface. A set of room-temperature single-photon sources has been designed, fabricated, and characterized, demonstrating the generation of high-purity circularly polarized vortex beams by the fabricated QE-coupled quantum metasurfaces. Our successful experimental realizations of high-quality SAM-OAM encoded single-photon sources confirm the robustness of the developed approach with respect to small QE displacements with respect to the DONR arrangement as indicated by the numerical simulations (figs. S6 and S7). This approach can straightforwardly be extended to produce linearly polarized photon beams by interleaving two metasurfaces (51), i.e., DONR arrangements for providing the RCP and LCP photons. Interleaving two metasurfaces for generating different SAM-OAM states opens a way for producing entangled SAM-OAM states, similarly to what has recently been demonstrated (39), but with a very substantial difference: The total angular momentum of entangled states does not have to be the same—it can be arbitrarily different in accordance with the design of the individual metasurfaces (fig. S19). Moreover, high-order OAM modes can also be realized with the proposed DONR-based quantum metasurfaces by increasing the number of spiral arms (fig. S20). Furthermore, by gradually changing the chirality of composing DONRs, the SAM and OAM of the photon emission can be flexibly manipulated with different ratios (fig. S21). Last, by combining the interleaving procedure (51) and recently established holographic formalism (35), the general approach developed in this work can further be extended to produce multiple, differently polarized radiation channels and enable thereby realization of high-dimensional quantum sources for advanced quantum photonic technologies. The on-chip room-temperature versatile handling of photon states opens thereby exciting perspectives for designing advanced single-photon sources and would contribute to further developments within chiral quantum optics, concerned with advanced functionalities such as spin/angular controlled photon switching and high-dimensional quantum information processing.
MATERIALS AND METHODS
Numerical simulations
Numerical simulations of QE-coupled metasurfaces were performed with 3D finite-difference time-domain (FDTD) method. A z-direction electric dipole was placed 30 nm atop the SiO2 spacer (with the thickness of 20 nm) and silver film (with thickness of 150 nm) and in the center of dielectric nanostructures (with height of 150 nm and refractive index of 1.41). The wavelength of the dipole was set as 670 nm, fitting the emission peak wavelength of ND-NVs. The period of the metasurfaces was set to be equal to the SPP wavelength (λspp = 580 nm with the effective SPP mode index nspp = 1.16). The start radius r0 is 1.7λspp. The number of windings was N = 9, enabling efficiently outcoupling SPPs into well-collimated far-field photon emission (figs. S4 and S5). A 2D monitor 30 nm atop the configuration was used to collect far-filed electric field by near- to far-field transformation method.
Device fabrication
Fabrication of QE-coupled metasurfaces followed a well-established sequence of technological steps (fig. S9) (37, 46). A 150-nm-thick silver film was first deposited on the silicon substrate by the thermal evaporation, followed by a 20-nm-thick SiO2 layer being deposited by the magnetron sputtering method. Then, a group of gold markers were fabricated on the substrate by the electron beam lithography (EBL), gold deposition, and the lift-off. Subsequently, ND-NVs were spin-coated with proper concentration. After that, the dark-field microscope image or the fluorescence scan image was taken to determine the position of, respectively, multiple or single ND-NVs with the help of alignment markers. It should be noted that the accurate positioning of DONR arrangements with respect to singles NV centers was more problematic as compared to the positioning of NDs with multiple NVs because it had to be relied on fluorescence images (fig. S17) that were noisier than the dark-field images (fig. S9). After determining the position of ND-NVs with the precise alignment procedure, a negative photoresist (HSQ) was subsequently spin-coated at 4000 rpm, for 45 s, and heated at the hotplate on 160°C for 2 min to form a ~150-nm layer, which was examined by the atomic force microscopy (NT-MDT NTEGRA). The EBL direct writing of metasurface patterns was then carried out on the resist around NV-NDs (JEOL-6490 system; accelerating voltage of 30 kV). Last, QE-coupled metasurfaces were obtained by development with the tetramethylammonium hydroxide solution (for 4 min) and isopropanol (60 s).
Optical characterization
Characterization of QE-coupled metasurfaces was conducted using essentially the same experimental setup as in the previous experiments (fig. S12) (37, 39).
Excitation of single photons
A linearly polarized 532-nm continuous wave or pulsed laser beam, after passing through a radially polarized converter (AR Coptix RPC), was used to driven NV-NDs to form a dominant dipole moment perpendicular to the substrate surface. The excitation and collection of emission were by the same objective with NA = 0.9 (×100; The Olympus MPLFLN).
SAM and OAM states measurement
In SAM states, the Stokes parameters (S0, S1, S2, and S3) were measured to characterize the SAM states. S1 and S2 were measured by orienting the linear polarizer and taking Fourier plane images. S3 was measured by the combination of a quarter-wave plate and a linear polarizer. In OAM states, an SLM working at 670 nm was used to generate the computed holograms with different topological charges. As the SLM only responds to the linear polarized light, the RCP component generated from the QE-coupled metasurface was converted to the linearly polarized photons by a 45°-oriented quarter–wave plate combined with a vertically placed linear polarizer. The reflected light from the incident light was filtered out by a set of dichroic mirrors (Semrock FF535-SDi01/FF552-Di02) and with long-pass filter of 550 nm (Thorlabs FELH0550) and band-pass filter of 676 nm (with 29-nm bandwidth; Edmund Optics).
Single-photon characterization
The photon emission was guided to spectrometer or single-photon detectors for the measurement of correlation, spectrum, and fluorescence image via the flip mirror. Fluorescence imaging (for ND-NV positioning process) was performed by a synchronous movement of piezo stage with mounted sample and projecting the collected fluorescence emission to the avalanche photo diodes (APDs). The decay rate measurements were carried out with a pulsed laser (PicoQuant LDH-PFA-530L) at 1 MHz together with APD1 (τ-SPAD, PicoQuant). Fluorescence spectra were measured using the spectrometer (Andor Ultra 888 USB3-BV) operating within 540 to 820 nm. Second-order correlation was recorded by registering the temporal delay between APD1 and APD2 in a start-stop configuration using an electronic timing box (PicoHarp 300, PicoQuant).
Acknowledgments
We appreciate F. Ding for helpful discussions and Y. Deng for assistance with the experiment.
Funding: This work was supported by the National Natural Science Foundation of China grant 52120105009 (to C.Z.), National Natural Science Foundation of China grant 62105150 (to Y.K.), European Union’s Horizon Europe Research and Innovation Programme under the Marie Skłodowska-Curie Action grant 101064471 (to Y.K.), Natural Science Foundation of Jiangsu Province grant BK20210289 (to Y.K.), Shanghai Key Fundamental Research grant 20JC1414800 (to C.Z.), State Key Laboratory of Advanced Optical Communication Systems Networks of China grant 2022GZKF023 (to Y.K.), and Villum Kann Rasmussen Foundation (award in Technical and Natural Sciences 2019) (to S.I.B.).
Author contributions: S.I.B. conceived the idea. X.J.L. and Y.H.K. performed theoretical modeling. X.J.L. with assistance from Y.H.K. and D.K. fabricated samples. X.J.L. and Y.H.K. with assistance from S.K. and D.K. performed experimental measurement. X.J.L., Y.H.K., S. K., and S.I.B. analyzed the data. S.I.B., Y.H.K., and C.Y.Z supervised the project. X.J.L., Y.H.K. and S.I.B wrote the manuscript with contributions from all authors.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Supplementary Materials
This PDF file includes:
Supplementary Text
Figs. S1 to S21
References
REFERENCES AND NOTES
- 1.A. Mair, A. Vaziri, G. Weihs, A. Zeilinger, Entanglement of the orbital angular momentum states of photons. Nature 412, 313–316 (2001). [DOI] [PubMed] [Google Scholar]
- 2.G. Molina-Terriza, J. P. Torres, L. Torner, Twisted photons. Nat. Phys. 3, 305–310 (2007). [Google Scholar]
- 3.C. H. Bennett, D. P. DiVincenzo, Quantum information and computation. Nature 404, 247–255 (2000). [DOI] [PubMed] [Google Scholar]
- 4.N. Gisin, R. Thew, Quantum communication. Nat. Photon. 1, 165–171 (2007). [Google Scholar]
- 5.X.-L. Wang, X.-D. Cai, Z.-E. Su, M.-C. Chen, D. Wu, L. Li, N.-L. Liu, C.-Y. Lu, J.-W. Pan, Quantum teleportation of multiple degrees of freedom of a single photon. Nature 518, 516–519 (2015). [DOI] [PubMed] [Google Scholar]
- 6.A. Sit, F. Bouchard, R. Fickler, J. Gagnon-Bischoff, H. Larocque, K. Heshami, D. Elser, C. Peuntinger, K. Günthner, B. Heim, C. Marquardt, G. Leuchs, R. W. Boyd, E. Karimi, High-dimensional intracity quantum cryptography with structured photons. Optica 4, 1006–1010 (2017). [Google Scholar]
- 7.A. Fleischer, O. Kfir, T. Diskin, P. Sidorenko, O. Cohen, Spin angular momentum and tunable polarization in high-harmonic generation. Nat. Photonics 8, 543–549 (2014). [Google Scholar]
- 8.P. Lodahl, S. Mahmoodian, S. Stobbe, A. Rauschenbeutel, P. Schneeweiss, J. Volz, H. Pichler, P. Zoller, Chiral quantum optics. Nature 541, 473–480 (2017). [DOI] [PubMed] [Google Scholar]
- 9.A. Javadi, D. Ding, M. H. Appel, S. Mahmoodian, M. C. Löbl, I. Söllner, R. Schott, C. Papon, T. Pregnolato, S. Stobbe, L. Midolo, T. Schröder, A. D. Wieck, A. Ludwig, R. J. Warburton, P. Lodahl, Spin–photon interface and spin-controlled photon switching in a nanobeam waveguide. Nat. Nanotechnol. 13, 398–403 (2018). [DOI] [PubMed] [Google Scholar]
- 10.J. Wang, J.-Y. Yang, I. M. Fazal, N. Ahmed, Y. Yan, H. Huang, Y. Ren, Y. Yue, S. Dolinar, M. Tur, A. E. Willner, Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photon. 6, 488–496 (2012). [Google Scholar]
- 11.N. Bozinovic, Y. Yue, Y. Ren, M. Tur, P. Kristensen, H. Huang, A. E. Willner, S. Ramachandran, Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 340, 1545–1548 (2013). [DOI] [PubMed] [Google Scholar]
- 12.Z.-Y. Zhou, Y. Li, D.-S. Ding, W. Zhang, S. Shi, B.-S. Shi, G.-C. Guo, Orbital angular momentum photonic quantum interface. Light Sci. Appl 5, e16019 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.H. H. Arnaut, G. A. Barbosa, Orbital and intrinsic angular momentum of single photons and entangled pairs of photons generated by parametric down-conversion. Phys. Rev. Lett. 85, 286–289 (2000). [DOI] [PubMed] [Google Scholar]
- 14.X. Chen, X. Lu, S. Dubey, Q. Yao, S. Liu, X. Wang, Q. Xiong, L. Zhang, A. Srivastava, Entanglement of single-photons and chiral phonons in atomically thin WSe2. Nat. Phys. 15, 221–227 (2019). [Google Scholar]
- 15.S. Liu, Y. Lou, J. Jing, Orbital angular momentum multiplexed deterministic all-optical quantum teleportation. Nat. Commun. 11, 3875 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.G. Li, A. S. Sheremet, R. Ge, T. C. H. Liew, A. V. Kavokin, Design for a nanoscale single-photon spin splitter for modes with orbital angular momentum. Phys. Rev. Lett. 121, 053901 (2018). [DOI] [PubMed] [Google Scholar]
- 17.D. Braukmann, E. R. Glaser, T. A. Kennedy, M. Bayer, J. Debus, Circularly polarized zero-phonon transitions of vacancies in diamond at high magnetic fields. Phys. Rev. B 97, 195448 (2018). [Google Scholar]
- 18.I. Söllner, S. Mahmoodian, S. L. Hansen, L. Midolo, A. Javadi, G. Kiršanskė, T. Pregnolato, H. El-Ella, E. H. Lee, J. D. Song, S. Stobbe, P. Lodahl, Deterministic photon–emitter coupling in chiral photonic circuits. Nat. Nanotechnol. 10, 775–778 (2015). [DOI] [PubMed] [Google Scholar]
- 19.B. Chen, Y. Wei, T. Zhao, S. Liu, R. Su, B. Yao, Y. Yu, J. Liu, X. Wang, Bright solid-state sources for single photons with orbital angular momentum. Nat. Nanotechnol. 16, 302–307 (2021). [DOI] [PubMed] [Google Scholar]
- 20.Y. Ma, H. Zhao, N. Liu, Z. Gao, S. S. Mohajerani, L. Xiao, J. Hone, L. Feng, S. Strauf, On-chip spin-orbit locking of quantum emitters in 2D materials for chiral emission. Optica 9, 953–958 (2022). [Google Scholar]
- 21.P. G. Kwiat, K. Mattle, H. Weinfurter, A. Zeilinger, A. V. Sergienko, Y. Shih, New high-intensity source of polarization-entangled photon pairs. Phys. Rev. Lett. 75, 4337–4341 (1995). [DOI] [PubMed] [Google Scholar]
- 22.T. Santia-Cruz, S. D. Gennaro, O. Mitrofanov, S. Addamane, J. Reno, I. Brener, M. V. Chekhova, Resonant metasurfaces for generating complex quantum states. Science 377, 991–995 (2022). [DOI] [PubMed] [Google Scholar]
- 23.T. Stav, A. Faerman, E. Maguid, D. Oren, V. Kleiner, E. Hasman, M. Segev, Quantum entanglement of the spin and orbital angular momentum of photons using metamaterials. Science 361, 1101–1104 (2018). [DOI] [PubMed] [Google Scholar]
- 24.K. Wang, J. G. Titchener, S. S. Kruk, L. Xu, H.-P. Chung, M. Parry, I. I. Kravchenko, Y.-H. Chen, A. S. Solntsev, Y. S. Kivshar, D. N. Neshev, A. A. Sukhorukov, Quantum metasurface for multiphoton interference and state reconstruction. Science 361, 1104–1108 (2018). [DOI] [PubMed] [Google Scholar]
- 25.W. J. M. Kort-Kamp, A. K. Azad, D. A. R. Dalvit, Space-time quantum metasurfaces. Phys. Rev. Lett. 127, 043603 (2021). [DOI] [PubMed] [Google Scholar]
- 26.N. Yu, F. Capasso, Flat optics with designer metasurfaces. Nat. Mater. 13, 139–150 (2014). [DOI] [PubMed] [Google Scholar]
- 27.N. Meinzer, W. L. Barnes, I. R. Hooper, Plasmonic meta-atoms and metasurfaces. Nat. Photon. 8, 889–898 (2014). [Google Scholar]
- 28.A. V. Kildishev, A. Boltasseva, V. M. Shalaev, Planar photonics with metasurfaces. Science 339, 1232009 (2013). [DOI] [PubMed] [Google Scholar]
- 29.C.-W. Qiu, T. Zhang, G. Hu, Y. Kivshar, Quo Vadis, metasurfaces? Nano Lett. 21, 5461–5474 (2021). [DOI] [PubMed] [Google Scholar]
- 30.Y. Ming, Y. Intaravanne, H. Ahmed, M. Kenney, Y. Lu, X. Chen, Creating composite vortex beams with a single geometric metasurface. Adv.Mater. 34, 2109714 (2022). [DOI] [PubMed] [Google Scholar]
- 31.A. H. Dorrah, F. Capasso, Tunable structured light with flat optics. Science 376, eabi6860 (2022). [DOI] [PubMed] [Google Scholar]
- 32.A. S. Solntsev, G. S. Agarwal, Y. S. Kivshar, Metasurfaces for quantum photonics. Nat. Photonics 15, 327–336 (2021). [Google Scholar]
- 33.Y. Kan, F. Ding, C. Zhao, S. I. Bozhevolnyi, Directional off-normal photon streaming from hybrid plasmon-emitter coupled metasurfaces. ACS Photonics 7, 1111–1116 (2020). [Google Scholar]
- 34.R. Bekenstein, I. Pikovski, H. Pichler, E. Shahmoon, S. F. Yelin, M. D. Lukin, Quantum metasurfaces with atom arrays. Nat. Phys. 16, 676–681 (2020). [Google Scholar]
- 35.Y. Kan, S. I. Bozhevolnyi, Molding photon emission with hybrid plasmon-emitter coupled metasurfaces. Adv. Optical Mater. 10, 2102697 (2022). [Google Scholar]
- 36.L. Li, Z. Liu, X. Ren, S. Wang, V. C. Su, M. K. Chen, C. H. Chu, H. Y. Kuo, B. Liu, W. Zang, G. Guo, L. Zhang, Z. Wang, S. Zhu, D. P. Tsai, Metalens-array–based high-dimensional and multiphoton quantum source. Science 368, 1487–1490 (2020). [DOI] [PubMed] [Google Scholar]
- 37.Y. Kan, S. K. H. Andersen, F. Ding, S. Kumar, C. Zhao, S. I. Bozhevolnyi, Metasurface-enabled generation of circularly polarized single photons. Adv. Mater. 32, 1907832 (2020). [DOI] [PubMed] [Google Scholar]
- 38.D. Komisar, S. Kumar, Y. Kan, C. Wu, S. I. Bozhevolnyi, Generation of radially polarized single photons with plasmonic bullseye antennas. ACS Photonics 8, 2190–2196 (2021). [Google Scholar]
- 39.C. Wu, S. Kumar, Y. Kan, D. Komisar, Z. Wang, S. I. Bozhevolnyi, F. Ding, Room-temperature on-chip orbital angular momentum single-photon sources. Sci. Adv. 8, eabk3075 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.J. Ni, C. Huang, L.-M. Zhou, M. Gu, Q. Song, Y. Kivshar, C.-W. Qiu, Multidimensional phase singularities in nanophotonics. Science 374, eabj0039 (2021). [DOI] [PubMed] [Google Scholar]
- 41.A. Pors, M. G. Nielsen, G. D. Valle, M. Willatzen, O. Albrektsen, S. I. Bozhevolnyi, Plasmonic metamaterial wave retarders in reflection by orthogonally oriented detuned electrical dipoles. Opt. Lett. 36, 1626–1628 (2011). [DOI] [PubMed] [Google Scholar]
- 42.A. Pors, S. I. Bozhevolnyi, Efficient and broadband quarter-wave plates by gap-plasmon resonators. Opt. Express 21, 2942–2952 (2013). [DOI] [PubMed] [Google Scholar]
- 43.S. Kumar, C. Wu, D. Komisar, Y. Kan, L. F. Kulikova, V. A. Davydov, V. N. Agafonov, S. I. Bozhevolnyi, Fluorescence enhancement of a single germanium vacancy center in a nanodiamond by a plasmonic Bragg cavity. J. Chem. Phys. 154, 044303 (2021). [DOI] [PubMed] [Google Scholar]
- 44.A. Forbes, M. De Oliveira, M. R. Dennis, Structured light. Nat. Photonics 15, 253–262 (2021). [Google Scholar]
- 45.J. Zhu, Y. Chen, Y. Zhang, X. Cai, S. Yu, Spin and orbital angular momentum and their conversion in cylindrical vector vortices. Opt. Lett. 39, 4435–4438 (2014). [DOI] [PubMed] [Google Scholar]
- 46.H. G. Berry, G. Gabrielse, A. E. Livingston, Measurement of the Stokes parameters of light. Appl. Optics 16, 3200–3205 (1977). [DOI] [PubMed] [Google Scholar]
- 47.S. K. H. Andersen, S. Bogdanov, O. Makarova, Y. Xuan, M. Y. Shalaginov, A. Boltasseva, S. I. Bozhevolnyi, V. M. Shalaev, Hybrid plasmonic bullseye antennas for efficient photon collection. ACS Photonics 5, 692–698 (2018). [Google Scholar]
- 48.H. Wang, Y. M. He, T. H. Chung, H. Hu, Y. Yu, S. Chen, X. Ding, M. C. Chen, J. Qin, X. Yang, R. Z. Liu, Z. C. Duan, J. P. Li, S. Gerhardt, K. Winkler, J. Jurkat, L. J. Wang, N. Gregersen, Y. H. Huo, Q. Dai, S. Yu, S. Höfling, C. Y. Lu, J. W. Pan, Towards optimal single-photon sources from polarized microcavities. Nat. Photonics 13, 770–775 (2019). [Google Scholar]
- 49.J. Liu, R. Su, Y. Wei, B. Yao, S. F. C. da Silva, Y. Yu, J. Iles-Smith, K. Srinivasan, A. Rastelli, J. Li, X. Wang, A solid-state source of strongly entangled photon pairs with high brightness and indistinguishability. Nat. Nanotechnol. 14, 586–593 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.H. Wang, H. Hu, T. H. Chung, J. Qin, X. Yang, J. P. Li, R. Z. Liu, H. S. Zhong, Y. M. He, X. Ding, Y. H. Deng, Q. Dai, Y. H. Huo, S. Höfling, C. Y. Lu, J. W. Pan, On-demand semiconductor source of entangled photons which simultaneously has high fidelity, efficiency, and indistinguishability. Phys. Rev. Lett. 122, 113602 (2019). [DOI] [PubMed] [Google Scholar]
- 51.A. Pors, M. G. Nielsen, S. I. Bozhevolnyi, Plasmonic metagratings for simultaneous determination of Stokes parameters. Optica 2, 716–723 (2015). [Google Scholar]
- 52.A. Yariv, P. Yeh, Optical Waves in Crystals (Wiley, 1984), vol. 5. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Text
Figs. S1 to S21
References