Abstract
In photosystem II (PSII), one-electron oxidation of the most stable oxidation state of the Mn4CaO5 cluster (S1) leads to formation of two distinct states, the open-cubane S2 conformation [Mn1(III)Mn2(IV)Mn3(IV)Mn4(IV)] with low spin and the closed-cubane S2 conformation [Mn1(IV)Mn2(IV)Mn3(IV)Mn4(III)] with high spin. In electron paramagnetic resonance (EPR) spectroscopy, the open-cubane S2 conformation exhibits a g = 2 multiline signal. However, its protonation state remains unclear. Here, we investigated the protonation state of the open-cubane S2 conformation by calculating exchange couplings in the presence of the PSII protein environment and simulating the pulsed electron–electron double resonance (PELDOR). When a ligand water molecule, which forms an H-bond with D1-Asp61 (W1), is deprotonated at dangling Mn4(IV), the first-exited energy (34 cm−1) in manifold spin excited states aligns with the observed value in temperature-dependent pulsed EPR analyses, and the PELDOR signal is best reproduced. Consequently, the g = 2 multiline signal observed in EPR corresponds to the open-cubane S2 conformation with the deprotonated W1 (OH−).
Significance Statement.
Photosystem II (PSII) is a protein complex that catalyzes the light-driven oxidation of water to molecular oxygen. We investigated the protonation state of the oxygen-evolving Mn4CaO5 cluster in PSII using a quantum mechanical/molecular mechanical approach that fully considers the protein environment, including the H-bond network. By combining with pulsed electron–electron double resonance simulations, we identified the open-cubane S2 conformation with the ligand water molecule (W1) deprotonated at the dangling Mn4(IV) site as the source of the g = 2 multiline signal observed in electron paramagnetic resonance spectroscopy. The results demonstrate the importance of considering the protein environment in interpreting spectroscopic data and suggest alternative methods to investigate the protonation state and spin structure of the metal complex.
Introduction
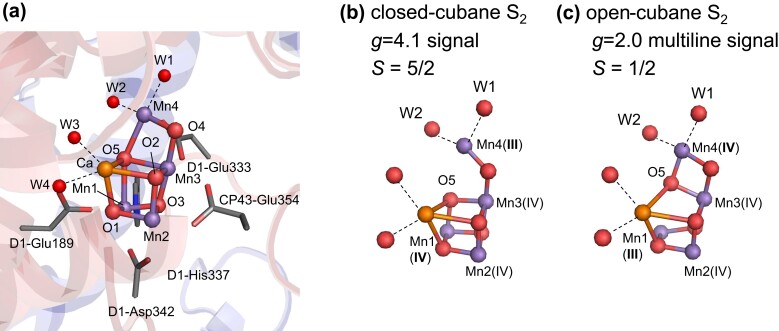
The Mn4CaO5 cluster in photosystem II (PSII) plays a vital role as the catalytic center for oxidizing substrate water molecules (1, 2). The oxidation state of the Mn4CaO5 cluster, denoted as Sn (n = 0, 1, 2, or 3), increases with electron transfer (Fig. 1), leading to O2 evolution during the S3 to S0 transition. As the reaction progresses, protons are released in the S0 → S1 → S2 → S3 → S0 transitions with a stoichiometry of 1:0:1:2. The Mn4CaO5 cluster consists of three Mn and one Ca sites in the cubane region (Mn1, Mn2, Mn3, and Ca) and a dangling Mn site (Mn4) (Fig. 1). Two ligand water molecules, W1 and W2, are present at the Mn4 site, while two additional water molecules, W3 and W4, are located at the Ca site. In the high oxidation state model for S1 (3), the Mn valence state is Mn(III)2Mn(IV)2 and Mn2 and Mn3 are already oxidized to Mn(IV) based on the redox potential (4). Thus, either Mn1(III) or Mn4(III) serves as the oxidation site in the S1 to S2 transition.
Fig. 1.
Mn4CaO5 cluster in PSII. (A) Protein environment of the Mn4CaO5 cluster. (B) Closed-cubane S2 conformation (Mn1(IV) and Mn4(III)) with W1 = OH− and W2 = H2O (3). (C) Open-cubane S2 conformation (Mn1(III) and Mn4(IV)). Dotted lines indicate ligand interactions.
The closed-cubane S2 conformation [Mn1(IV)Mn2(IV)Mn3(IV)Mn4(III)] forms (Fig. 1A), as the Mn1(IV)–O5 bond shortens and the Mn4(III)–O5 bond lengthens upon the oxidation of Mn1(III) to Mn1(IV) during the S1 to S2 transition (5, 6). Conversely, the open-cubane S2 conformation [Mn1(III)Mn2(IV)Mn3(IV)Mn4(IV)] forms (Fig. 1C), as the Mn1(III)–O5 bond lengthens and the Mn4(IV)–O5 bond shortens upon the oxidation of Mn4(III) to Mn4(IV) during the S1 to S2 transition (5, 6). The open-cubane S2 conformation has been observed in the X-ray free electron laser (XFEL) structures, whereas the closed-cubane S2 conformation has not been identified (7–10). This observation suggests that the open-cubane S2 conformation is more energetically favorable than the closed-cubane structure in cyanobacterial PSII (11–14).
In the S2 to S3 transition, a water molecule is incorporated into the Mn4CaO5 cluster according to the XFEL structures (7–10). This transition also involves a two-step proton transfer process: the release of the proton from the Mn4CaO5 cluster and the transient protonation of D1-Asp61 (15–18), followed by subsequent proton transfer via D1-Glu65/D2-Glu312 toward the lumenal bulk surface (19). The experimentally observed small (∼1) and large (∼2) kinetic isotope effects (20) likely correspond to the first and second processes, respectively.
Electron paramagnetic resonance (EPR) spectroscopy is a method to determine the spin structure and the protonation state of the Mn4CaO5 cluster and W1–W4. In EPR spectroscopy, two signals are observed as follows: the g = 2 multiline signal and the g ≥ 4.1 signals (e.g. (21–25)). The g ≥ 4.1 signals can be categorized into two groups as follows: the g = 4.1 signal and the g ∼ 5 signal (26, 27). The g = 4.1 signal corresponds to the high-spin closed-cubane S2 conformation (5, 6, 28), while the g ∼ 5 signal geometry has not been identified yet. To determine the protonation state of the Mn4CaO5 cluster and the ligand water molecules (W1–W4), results were usually interpreted using quantum chemical calculations of the high-spin S2 conformation conducted mostly in the absence of the PSII protein environment for simplicity (5, 6, 29, 30). These theoretical models with the isolated Mn4CaO5 cluster proposed that W1 = H2O and W2 = OH− (5, 6, 30). In contrast, recent theoretical studies conducted in the presence of the PSII protein environment indicated that W1 = OH− and W2 = H2O for the g = 4.1 signal, as the g = 4.1 EPR signal was reproduced only when the high-spin closed-cubane S2 conformation (total spin S = 5/2) had W1 = OH− and W2 = H2O, not W1 = H2O and W2 = OH− (Fig. 1B) (28). The g = 4.1 signal was observed in plant PSII, but not in cyanobacterial PSII under physiological conditions (31, 32). This observation aligns with the energetically unstable nature of the closed-cubane S2 conformation in cyanobacterial PSII (28). Thus, it is a prerequisite to consider the protein environment in theoretical calculations when interpreting EPR spectroscopy (28).
On the other hand, the g = 2 multiline signal corresponds to the open-cubane S2 conformation with low spin (S = 1/2) (5, 6). T1 (electron spin-lattice relaxation time) measurements indicated that an excited spin state manifold exists 22–37 cm−1 above the ground state manifold corresponding to the g = 2 multiline signal (33, 34). The 55Mn electron nuclear double resonance (ENDOR) analysis was used to probe the hyperfine interaction (HFI) constants (e.g. the isotropic part of the effective HFI constant Aiso) of Mn sites in the S2 low-spin state (35, 36). In ENDOR experiments, the HFI constants of the four Mn sites were obtained as the set of four values for Aiso of −245, 217, −297, and 200 MHz (37) or 312, 251, 208, and 191 MHz (29) for the four Mn sites.
Pantazis et al. converted spin densities into HFI constants using the following equation:
| (1) |
where Ai,iso is the isotopic part of the HFI constant for the i-th Mn site (Mn(i), where i = 1, 2, 3, and 4), ai,iso is the intrinsic HFI constant, and ρi is the spin projection (36). Importantly, the equation is guaranteed only in the absence of the zero-field splitting (ZFS), i.e. the anisotropy of the spin projection matrices ρi can be neglected and ρi are proportional to the identity matrix (36). Although Eq. 1 is applicable to the model compounds of a two-spin system (38), it remains unclear whether the Mn4CaO5 cluster is the case.
Using Eq. 1, the Aiso values in the low-spin S2 state were calculated in the absence of the PSII protein environment with density functional theory (DFT) methods, e.g. (−276, 170, 165, and −228 MHz) (5) and (342, 245, 207, and 195 MHz) (34) for the four Mn sites. However, the assignment of Aiso to Mn sites did not fit quantitatively to the other experimental results, e.g. (−245, 217, −297, and 200 MHz) for the four Mn sites (37). Therefore, the inconsistency in the HFI constants suggests that the proposed methodology based on the comparison between calculated and experimentally measured HFI constants is not conclusive enough to determine the protonation state of the Mn4CaO5 cluster.
The spin structure of the low-spin S2 state has also been studied using pulsed electron–electron double resonance (PELDOR)/double electron–electron resonance (DEER) (39, 40). PELDOR can provide direct measurement of spin densities, by detecting a dipole interaction between tyrosine D radical (TyrD•) and the spin densities on each Mn site of the Mn4CaO5 cluster. Thus, PELDOR can directly obtain the spin densities, enabling a straightforward comparison with the spin densities calculated using the PSII structure.
PELDOR studies indicated a spin configuration of (↑↓↑↓) for (Mn1, Mn2, Mn3, and Mn4), with Mn1 having a large positive spin projection (ρ1 = 1.97), Mn3 having a small positive spin projection (ρ3 = 1.19), and Mn2 and Mn4 having negative spin projections (ρ2 = −1.2 and ρ4 = −0.96) (39). Consistently, Stich et al. (41) also reported a large spin projection for Mn1 with the D1-His332 ligand (ρ1 = 1.77) using the electron spin-echo envelope modulation (ESEEM). The large spin on Mn1 suggested in PELDOR (39) and ESEEM (41) studies was consistent with the ENDOR (37) results, but not with the previous calculations of HFI constants in the absence of the PSII protein environment (34, 36). As calculations of the HFI constants suffer from the uncertainty (29, 35, 37), the comparison between the spin projection distribution suggested in PELDOR and ESEEM studies and that calculated in theoretical models is more likely to provide further insights into the relevant spin structure of the Mn4CaO5 cluster in the PSII protein environment. Thus, the protonation state of the Mn4CaO5 cluster in the open-cubane S2 conformation corresponding to the g = 2 multiline signal has not been identified unambiguously, despite the extensive EPR studies including ENDOR, PELDOR, and ESEEM. Moreover, most theoretical calculations used to interpret spectroscopic results were conducted in the absence of the PSII protein environment (5, 29, 34, 37), which may be a reason for the uncertainty in the protonation state of the Mn4CaO5 cluster.
Here, we investigate the origin of the g = 2 multiline signal, using a quantum mechanical/molecular mechanical (QM/MM) approach and considering interactions between the open-cubane S2 conformation and the PSII protein environment.
Methods
Atomic coordinates
The X-ray diffraction structure of PSII monomer unit “A” (PDB code: 3ARC; 1.9-Å structure) (1) was used in the present study. It is worth noting that the 1.9-Å structure corresponds to S1 (1). Although the X-ray diffraction structure might have experienced over-reduction during data collection, leading to elongated Mn–O bonds (42–48), Suga et al. (2) reported that no significant structural difference exists between the XFEL structure for S1 and the 1.9-Å structure. The S2-state structure, obtained from the single-flash-minus-dark isomorphous difference Fourier map (1F-XFEL structure) at a slightly lower resolution (e.g. PDB code, 6JLK (9)), shows no significant differences compared to the 1.9-Å structure. Notably, the 1.9-Å structure contains more water molecules (1,442 molecules) than the S2-state structure (1,289 molecules). Furthermore, the calculated redox potential values are also essentially the same for the 1F-XFEL and/or 1.9-Å structure (49). Additionally, the g = 4.1 signal for the closed-cubane S2 conformation was also investigated using the 1.9-Å structures (28). To ensure consistency in the protein electrostatic environment for the QM/MM calculations and enable direct comparisons, the 1.9-Å structure was used for the open-cubane S2 conformation in the present study. Water molecules, protonation state of titratable residues, and atomic partial charges were treated as done in previous studies (28).
QM/MM calculations
The unrestricted DFT method employing the B3LYP functional and LACVP* basis sets (Mn and Ca atoms: LANL2DZ [double ζ quality basis set with the Los Alamos effective core potential]; other atoms: and 6-31G*) (50) was used with the QSite (51) program as done in the previous study (28). The QM region was identical to that used for the closed-cubane S2 conformation (28). See Supplementary material for the atomic coordinates of the QM/MM-optimized geometry.
Calculations of spin system
The exchange coupling values, Jij, between Mn(i) and Mn(j) (i, j = 1, 2, 3, 4, and i < j), were determined using the broken symmetry (BS) approach (6, 52, 53). Assuming the classical spin approximation, the total energies for distinct spin configurations can be described by the following equations (53):
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
where SEsc is the total energy of the system for a given total spin S, obtained in QM/MM calculations (Table S1). The spin configuration sc refers to the configuration of spins for (Mn1, Mn2, Mn3, and Mn4), and Jij is the exchange coupling between Mn(i) and Mn(j). The pairwise J values were determined by solving the linear equations (Eqs. 1–8) using singular value decomposition to obtain the best solution in terms of the least-squares sense (52). Using the QM/MM-optimized geometries for all possible spin configurations, the total energy was calculated based on the adiabatic approximation (53).
The effective Hamiltonian describing the spin state of the Mn4CaO5 cluster can be expressed as follows:
| (10) |
where is the operator for electron spin, is the operator for nuclear spin, the gi value is the g-tensor, and Ai is the effective hyperfine tensor in Mn(i). β is the Bohr magneton. In the present study, the gi value was approximated to be isotropic and independent of Mn(i), with a value of 2. is the Hamiltonians of ZFS. is the Hamiltonians of exchange interactions. The term is expressed as
| (11) |
Because the ZFS parameters are unknown, was neglected as done in the previous study (36). Here, Mn2, Mn3, and Mn4 are Mn(IV) (S1 = S2= S3 = 3/2) and Mn1 is Mn(III) (S4 = 2). By diagonalizing , the eigenenergy En(B0) of the n-th state |n(B0)> was determined as a function of B0, excluding the hyperfine splitting term (54). The n-th excited energy En (n = 0 for the ground state) in the manifold spin states is obtained from En(B0 = 0).
The spin projection ρi for Mn(i) was calculated as
| (12) |
where
| (13) |
is the total spin operator and in Eq. 12 represents the expectation value of A.
PELDOR simulations
To simulate PELDOR measurements, the PELDOR result obtained from the previous experiments was used (39). PELDOR simulations were performed as done in the previous study (39). The signal amplitude X(τ′) depends on the time interval τ′ between the first and second pulses and can be expressed as follows:
| (14) |
where p is the fraction of spin affected by the pumping pulse, and D is the dipole interaction between the two spins. The expression for D between the spin density distributions of TyrD• and the Mn4CaO5 cluster is given by:
| (15) |
where ρi is the spin projection at the i-th (i = 1–7) carbon/oxygen atom of the TyrD• molecule and ρj is the spin projection at Mn(j). Rij is the distance between the i-th (i = 1–7) carbon/oxygen atom of the TyrD• and Mn(j). h is the Planck constant, Θij is the angle formed between the external magnetic field H and the distance vector Rij. g1 and g2 are g-factors and were assumed to be 2.00, neglecting ρ anisotropy as a first-order approximation (37).The signal amplitude I(τ′) is calculated by integrating over all angles and can be expressed as:
| (16) |
Results and discussion
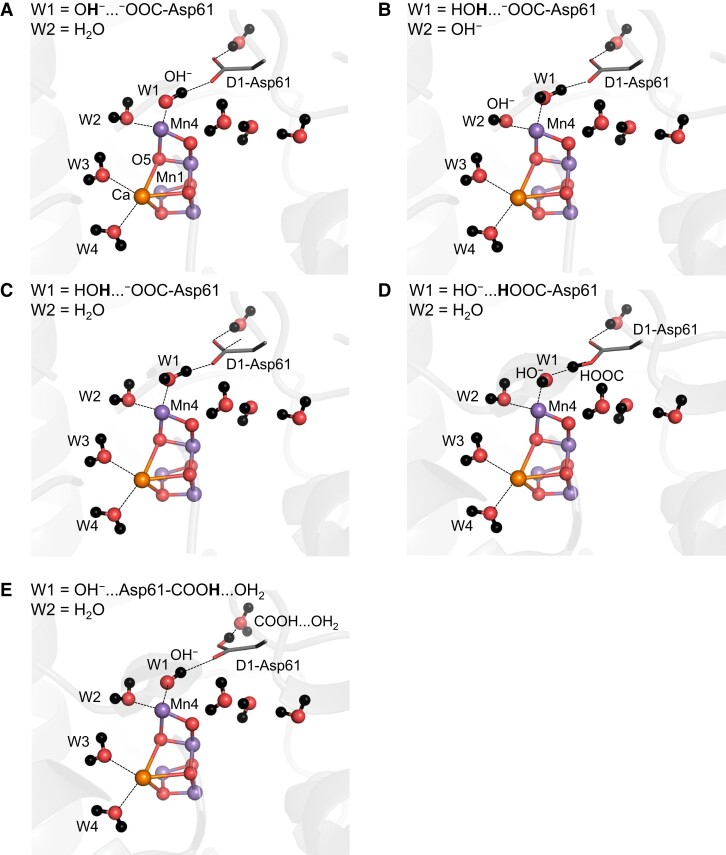
The Mn4 site has two water ligand molecules, W1 and W2. Ames et al. performed DFT calculations without considering the PSII protein environment to interpret the EPR results and proposed that W2 = OH− (5, 6, 30). However, W1 forms a low-barrier H-bond with D1-Asp61 in the open-cubane S2 conformation (15–17, 19), whereas W2 only interacts with water molecules. Thus, the release of W1 toward D1-Asp61 can occur easily with respect to deprotonation of W2. Once the protonated side-chain of D1-Asp61 is reoriented (19, 55), the proton is further transferred toward the lumenal bulk surface. Based on these observations, the following five protonation states are investigated in the open-cubane S2 conformation: (i) W1 = OH− and W2 = H2O; (ii) W1 = H2O and W2 = OH−; (iii) W1 = H2O and W2 = H2O; (iv) W1 = HO−…HOOC-Asp61 and W2 = H2O; and (v) W1 = OH−…Asp61-COOH…OH2 and W2 = H2O (Fig. 2 and Table 1).
Fig. 2.
QM/MM-optimized geometries for the open-cubane S2 conformation. (A) W1 = OH− and W2 = H2O. (B) W1 = H2O and W2 = OH−. (C) W1 = H2O and W2 = H2O. (D) W1 = HO−…HOOC-Asp61 and W2 = H2O. (E) W1 = OH−…Asp61-COOH…OH2 and W2 = H2O.
Table 1.
Calculated values for exchanging coupling Jij (cm−1) and the first excited state energy ΔE01 (i.e. energy difference between the ground and first-excited states) (cm−1) for the open-cubane S2 conformation.
| Conformation/sample | J 12 | J 13 | J 14 | J 23 | J 24 | J 34 | mS total a | ΔE01b |
|---|---|---|---|---|---|---|---|---|
| This study | ||||||||
| W1 = OH− W2 = H2O |
−33.0 | 9.1 | 0.5 | 16.1 | 2.2 | −17.6 | 1/2 | 33.8 |
| W1 = H2O W2 = OH− |
−34.9 | −2.3 | 1.5 | 11.7 | 1.5 | −28.1 | 1/2 | 56.6 |
| W1 = HOH…OOC-Asp61c W2 = H2O |
−28.8 | −1.0 | 0.6 | 12.9 | −0.7 | −30.2 | 1/2 | 53.5 |
| W1 = HO−…HOOC-Asp61d W2 = H2O |
−31.8 | −1.2 | 1.5 | 18.8 | 4.2 | −21.9 | 1/2 | 44.1 |
| W1 = OH−…Asp61-COOH…OH2e W2 = H2O |
−31.8 | 4.4 | 0.6 | 16.7 | 1.8 | −21.6 | 1/2 | 40.8 |
| Experiments | ||||||||
| Thermosynechococcus elongatus PSII | 22.4e | |||||||
| spinach PSII | 24.7e, 36.5f |
The total magnetic spin quantum number mS at the ground state in the QM/MM calculation (see Table S1 for the calculated energies).
Energy difference between the ground and the first-excited states obtained from the diagonalization of the spin Hamiltonian.
The H+ is more populated at the W1 moiety along the low-barrier H-bond between W1 and D1-Asp61.
H+ is more populated at the D1-Asp61 moiety along the low-barrier H-bond between W1 and D1-Asp61.
Protonated D1-Asp61 donates an H-bond to a water molecule in the D1-Glu65/D2-Glu312 channel.
Ref. (34).
Ref. (33).
Exchange couplings
The exchange coupling values Jij were calculated using the five QM/MM-optimized geometries shown in Fig. 2. Regardless of the protonation states of W1 and W2, the exchange couplings between Mn1 and Mn2 (J12) and Mn3 and Mn4 (J34) are consistently negative and have large-magnitude values (−18 to −35 cm−1) in all cases. When W1 = OH− and W2 = H2O, the first excited state energy ΔE01 (34 cm−1) is most consistent with the observed value (22–37 cm−1) (33, 34) (Table 1).
As the negative couplings of J12 and J34 imply that the Mn1/Mn2 and Mn3/Mn4 pairs favor opposite spin directions to each other, the spin configurations of (↑↓↑↓) and (↑↓↓↑) for Mn1(III)Mn2(IV)Mn3(IV)Mn4(IV) [the magnetic spin quantum numbers (mS1, mS2, mS3, mS4) = (4/2, −3/2, −3/2, 3/2), (4/2, −3/2, 3/2, −3/2) and the total magnetic spin quantum number mStotal = 1/2] have the lowest and second-lowest energies, respectively (Table S1). Indeed, in all conformations, the calculated spin projections indicate the spin configuration of (↑↓↑↓) or (↑↓↓↑) in the ground state of the spin Hamiltonian (Table 2). The (↑↓↑↓) configuration exhibits in the ground state only when W1 = OH− and W2 = H2O, which reflects the fact that the difference in the BS energy SEsc between the (4/2, −3/2, −3/2, 3/2) and (4/2, −3/2, 3/2, −3/2) conformations is small (21 cm−1) with respect to the magnitude of the J couplings (Table S1). The (↑↓↑↓) configuration with W1 = OH− and W2 = H2O is consistent with that observed in PELDOR studies (39). Thus, the open-cubane S2 conformation is most likely with W1 = OH− and W2 = H2O. Note that the protonation state with W1 = OH− and W2 = H2O was also reported for the closed-cubane S2 conformation for the g = 4.1 signal (28).
Table 2.
Calculated spin projections ρ1, ρ2, ρ3, and ρ4 for Mn1, Mn2, Mn3, and Mn4 in the ground state of the diagonalized spin Hamiltonian for the open-cubane S2 conformation.
| Conformation | ρ 1 | ρ 2 | ρ 3 | ρ 4 | Spin configuration (Mn1, Mn2, Mn3, Mn4) |
|---|---|---|---|---|---|
| W1 = OH− W2 = H2O |
1.818 | −0.857 | 0.512 | −0.473 | (↑↓↑↓) |
| W1 = H2O W2 = OH− |
1.722 | −0.941 | −0.886 | 1.105 | (↑↓↓↑) |
| W1 = HOH…OOC-Asp61a W2 = H2O |
1.849 | −0.986 | −0.809 | 0.946 | (↑↓↓↑) |
| W1 = HO−…HOOC-Asp61b W2 = H2O |
1.555 | −0.890 | −0.972 | 1.307 | (↑↓↓↑) |
| W1 = OH−…Asp61-COOH…OH2c W2 = H2O |
1.958 | −1.000 | −0.565 | 0.606 | (↑↓↓↑) |
The H+ is more populated at the W1 moiety along the low-barrier H-bond between W1 and D1-Asp61.
The H+ is more populated at the D1-Asp61 moiety along the low-barrier H-bond between W1 and D1-Asp61.
Protonated D1-Asp61 donates an H-bond to a water molecule in the D1-Glu65/D2-Glu312 channel.
PELDOR
The values of the spin projection ρ in the ground state of the spin Hamiltonian of Eq. (12) were calculated based on the five QM/MM-optimized geometries (Fig. 2). Although the calculated ρ values depend on the protonation states of W1 and W2, ρ1 is the largest among the four ρi values for all protonation states (Table 2).
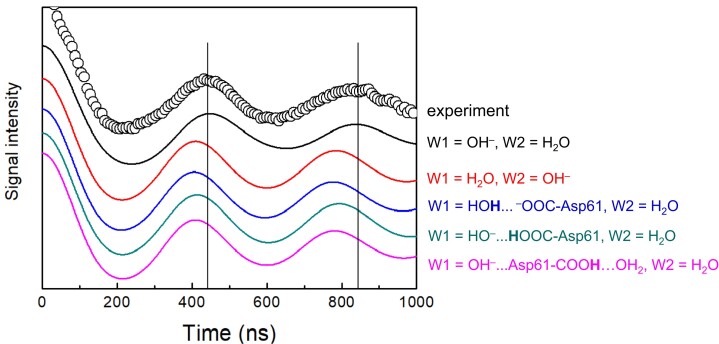
The PELDOR signal was simulated using the calculated ρ values (Fig. 3). The experimentally observed oscillation pattern (39) is best reproduced when W1 = OH− and W2 = H2O in the QM/MM calculation. In contrast, the observed pattern is not reproduced in the other protonation states as the frequencies in the calculated signals are shifted faster (i.e. the peak positions in the calculated signals are shifted). These results suggest that W1 = OH− and W2 = H2O are the protonation state for the low-spin state of the open-cubane S2 conformation.
Fig. 3.
Simulated PELDOR signals arising from the interaction between TyrD• and the Mn4CaO5 cluster in the high-spin S2 state. The experimental signals for spinach PSII (39) are shown by circles. The vertical lines indicate the peak positions in the experimental signal.
When W1 = OH− and W2 = H2O, the calculated ρ1 value for Mn1(III) is 1.82 (Table 2), which is consistent with ρ1 ≈ 2 suggested in previous PELDOR studies (39) and ρ1 = 1.7 suggested in ENDOR and ESEEM studies (37, 41). All of these studies show that ρ1 has the largest magnitude among the four ρi values (Table 2), including DFT calculations of the Mn4CaO5 cluster performed by Ames et al. (5) in the absence of the PSII protein environment.
Uncertainty in the calculated Ai,iso values
Ames et al. (5) performed DFT calculations without considering the PSII protein environment and found that the magnitude of the calculated ρ1 value for Mn1(III) was the largest among those for the four Mn sites in the open-cubane S2 conformation. This result is consistent with ESEEM (41), PELDOR (39), and the present calculation (Table 2).
While the ρi value is already known and the ai,iso value can be calculated using the BS approach (52), if Eq. 1 was relevant to the Mn4CaO5 cluster, all these studies would indicate that Ai,iso was largest at Mn1(III) among the four Mn sites. However, in the same study, Ames et al. (5) controversially reported that the calculated Ai,iso value was the largest at Mn4(IV). This inconsistency between experimentally measured Ai,iso values (29, 37) and calculated Ai,iso values (5) suggests that Eq. 1 is unlikely to be applicable to the Mn4CaO5 cluster.
The source of the inconsistency may be due to insufficient consideration of anisotropy in Eq. 1. Eq. 1 is guaranteed only in the absence of ZFS (36) and may be applicable to the two-spin system in a model compound with the ai,iso values obtained using the BS calculation (38). However, it seems unlikely that Eq. 1 is directly applicable to the multi-coupled system due to its anisotropy. In particular, inter-dipole interactions cause the anisotropy in the Mn4CaO5 cluster, because the total ZFS consists of ZFSs on the four Mn sites (56, 57). Therefore, a direct comparison between Ai,iso converted using Eq. 1 from calculated ρi values and those measured experimentally has not been established in the Mn4CaO5 cluster (e.g. (29, 37)).
Formation of OH− at W1 in EPR-detected S2 in EPR experiments
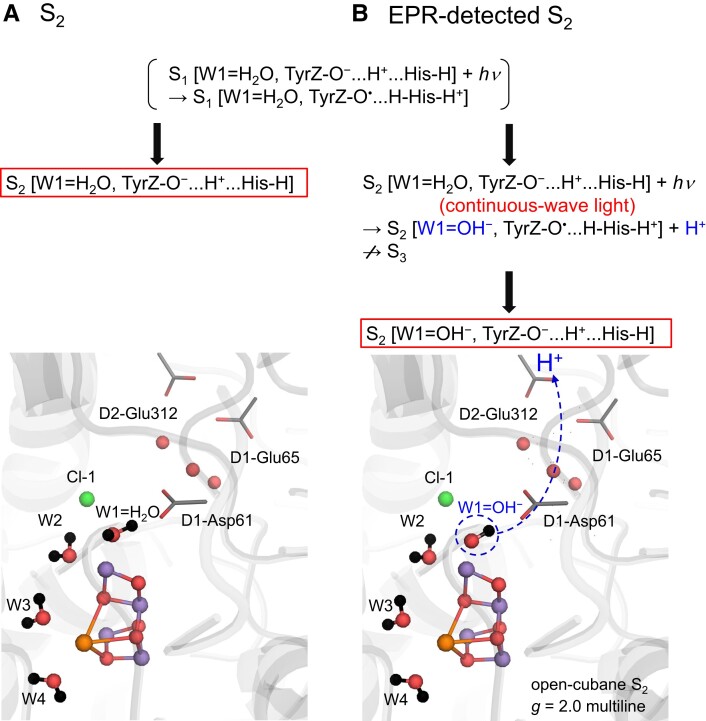
H2O at W1 releases the proton during the S2 to S3 transition (19, 55). In the actual S2 state, the proton migrates along the low-barrier H-bond between W1 and D1-Asp61, as demonstrated in Fourier transform infrared spectroscopy (16) and theoretical (19, 55) studies. However, at this stage, the proton is not yet released toward the lumenal bulk surface (e.g. (15, 58)) (Fig. 4A). In contrast, the present results show that the open-cubane S2 conformation with W1 = OH− and W2 = H2O is most consistent with the observed first excited energy ΔE01 in T1 measurements (33, 34, 59) (Table 1) and the observed PELDOR signal (39) (Fig. 3) for the low-spin S2 state. That is, OH− already exists at W1 in the EPR-detected S2 samples.
Fig. 4.
Comparison of the protonation states of the open-cubane S2 structure in (A) S2 (W1 = H2O) and (B) EPR-detected S2 (W1 = OH−) exposed to continuous-wave light for ∼5 minutes at low temperature (200 K). While the S2 to S3 transition is blocked, proton release from W1 can still occur, leading to the formation of OH− at W1 in the EPR-detected S2 sample. Boxed states indicate resulting states.
The difference in the protonation state between S2 and EPR-detected S2 could be due to the difference in the precursor. Although charge separation occurs in S2, S2 does not proceed to S3 at low temperature (∼200 K) in EPR measurements (60, 61). However, the sample is under continuous-wave light conditions, which still allows P680 to be photoexcited, oxidizing [TyrZ-O−…H + …N-His190-NH] to [TyrZ-O•…HN-His190-NH]+ and deprotonating the lowest-pKa site at the Mn4CaO5 moiety in S2 (e.g. (18, 62)). As QM/MM calculations performed in the presence of the PSII protein environment have suggested that W1 is the lowest-pKa site among all titratable sites at the Mn4CaO5 moiety in S2 (63), it seems possible that W1 releases the proton, forming OH− under continuous-wave light conditions in EPR measurements (Fig. 4B). This may explain the discrepancy between S2 and EPR-detected S2.
Conclusions
The exchange coupling Jij calculated in the presence of the PSII protein environment indicates that the spin configuration of the open-cubane S2 conformation is (↑↓↑↓) or (↑↓↓↑) for Mn1(III)Mn2(IV)Mn3(IV)Mn4(IV) (Table 1). Diagonalization of the spin Hamiltonian obtained using the J couplings shows that when W1 = OH− and W2 = H2O, the first excited energy (ΔE01 = 34 cm−1) in the manifold spin states is consistent with the experimentally observed value (27–37 cm−1) (Table 1). The magnitude of the calculated ρ1 value for Mn1(III) is the largest among those for the four Mn sites in the open-cubane S2 conformation (Table 2), which is consistent with ESEEM (41) and PELDOR (39) studies and previous DFT calculations conducted without considering the PSII protein environment (5). The PELDOR signal observed for the low-spin S2 state (39) is reproduced only when W1 = OH− and W2 = H2O in the open-cubane S2 conformation (Fig. 3). These results obtained from the present QM/MM calculations conducted in the presence of the PSII protein environment consistently suggest that the g = 2 multiline signal in EPR corresponds to the open-cubane S2 conformation with W1 = OH− and W2 = H2O (Fig. 4B).
Supplementary Material
Contributor Information
Keisuke Saito, Department of Applied Chemistry, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8654, Japan; Research Center for Advanced Science and Technology, The University of Tokyo, 4-6-1 Komaba, Meguro-ku, Tokyo 153-8904, Japan.
Shunya Nishio, Department of Applied Chemistry, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8654, Japan.
Mizue Asada, Instrument Center, Institute for Molecular Science, 38 Nishigo-Naka, Myodaiji, Okazaki 444-8585, Japan.
Hiroyuki Mino, Division of Material Science, Graduate School of Science, Nagoya University, Furo-cho, Chikusa-ku, 464-8602 Nagoya, Aichi, Japan.
Hiroshi Ishikita, Department of Applied Chemistry, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8654, Japan; Research Center for Advanced Science and Technology, The University of Tokyo, 4-6-1 Komaba, Meguro-ku, Tokyo 153-8904, Japan.
Supplementary Material
Supplementary material is available at PNAS Nexus online.
Funding
This research was supported by (JP23H04963 to K.S.; JP22K06160 to H.M.; JP20H03217 and JP23H02444 to H.I.), the Interdisciplinary Computational Science Program in CCS, University of Tsukuba (K.S.), and Advanced Research Infrastructure for Materials and Nanotechnology in Japan (ARIM) of MEXT, Institute for Molecular Science (JPMXP1223MS1007 to H.M.).
Author Contributions
H.I. designed research; K.S., S.N., M.A., H.M., and H.I. performed research; K.S. and H.I. analyzed data; and K.S. and H.I. wrote the paper.
Data availability
All data are included in the manuscript and/or supporting information.
References
- 1. Umena Y, Kawakami K, Shen J-R, Kamiya N. 2011. Crystal structure of oxygen-evolving photosystem II at a resolution of 1.9 Å. Nature. 473:55–60. [DOI] [PubMed] [Google Scholar]
- 2. Suga M, et al. 2015. Native structure of photosystem II at 1.95 Å resolution viewed by femtosecond X-ray pulses. Nature. 517:99–103. [DOI] [PubMed] [Google Scholar]
- 3. Cheah MH, et al. 2020. Assessment of the manganese cluster's oxidation state via photoactivation of photosystem II microcrystals. Proc Natl Acad Sci U S A. 117:141–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Mandal M, Kawashima K, Saito K, Ishikita H. 2020. Redox potential of the oxygen-evolving complex in the electron transfer cascade of photosystem II. J Phys Chem Lett. 11:249–255. [DOI] [PubMed] [Google Scholar]
- 5. Ames W, et al. 2011. Theoretical evaluation of structural models of the S2 state in the oxygen evolving complex of photosystem II: protonation states and magnetic interactions. J Am Chem Soc. 133:19743–19757. [DOI] [PubMed] [Google Scholar]
- 6. Pantazis DA, Ames W, Cox N, Lubitz W, Neese F. 2012. Two interconvertible structures that explain the spectroscopic properties of the oxygen-evolving complex of photosystem II in the S2 state. Angew Chem Int Ed. 51:9935–9940. [DOI] [PubMed] [Google Scholar]
- 7. Suga M, et al. 2017. Light-induced structural changes and the site of O=O bond formation in PSII caught by XFEL. Nature. 543:131–135. [DOI] [PubMed] [Google Scholar]
- 8. Kern J, et al. 2018. Structures of the intermediates of Kok’s photosynthetic water oxidation clock. Nature. 563:421–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Suga M, et al. 2019. An oxyl/oxo mechanism for oxygen–oxygen coupling in PSII revealed by an X-ray free-electron laser. Science. 366:334–338. [DOI] [PubMed] [Google Scholar]
- 10. Ibrahim M, et al. 2020. Untangling the sequence of events during the S2 → S3 transition in photosystem II and implications for the water oxidation mechanism. Proc Natl Acad Sci U S A. 117:12624–12635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Isobe H, et al. 2012. Theoretical illumination of water-inserted structures of the CaMn4O5 cluster in the S2 and S3 states of oxygen-evolving complex of photosystem II: full geometry optimizations by B3LYP hybrid density functional. Dalton Trans. 41:13727–13740. [DOI] [PubMed] [Google Scholar]
- 12. Saito K, Ishikita H. 2014. Influence of the Ca2+ ion on the Mn4Ca conformation and the H-bond network arrangement in photosystem II. Biochim Biophys Acta. 1837:159–166. [DOI] [PubMed] [Google Scholar]
- 13. Yang J, Hatakeyama M, Ogata K, Nakamura S, Li C. 2014. Theoretical study on the role of Ca2+ at the S2 state in photosystem II. J Phys Chem B. 118:14215–14222. [DOI] [PubMed] [Google Scholar]
- 14. Amin M, Pokhrel R, Brudvig GW, Badawi A, Obayya SS. 2016. Effect of chloride depletion on the magnetic properties and the redox leveling of the oxygen-evolving complex in photosystem II. J Phys Chem B. 120:4243–4248. [DOI] [PubMed] [Google Scholar]
- 15. Narzi D, Bovi D, Guidoni L. 2014. Pathway for Mn-cluster oxidation by tyrosine-Z in the S2 state of photosystem II. Proc Natl Acad Sci U S A. 111:8723–8728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Debus RJ. 2014. Evidence from FTIR difference spectroscopy that D1-Asp61 influences the water reactions of the oxygen-evolving Mn4CaO5 cluster of photosystem II. Biochemistry. 53:2941–2955. [DOI] [PubMed] [Google Scholar]
- 17. Kawashima K, Ishikita H. 2018. Energetic insights into two electron transfer pathways in light-driven energy-converting enzymes. Chem Sci. 9:4083–4092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Allgöwer F, Gamiz-Hernandez AP, Rutherford AW, Kaila VRI. 2022. Molecular principles of redox-coupled protonation dynamics in photosystem II. J Am Chem Soc. 144:7171–7180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Kuroda H, et al. 2021. Proton transfer pathway from the oxygen-evolving complex in photosystem II substantiated by extensive mutagenesis. Biochim Biophys Acta. 1862:148329 . [DOI] [PubMed] [Google Scholar]
- 20. Shimizu T, Sugiura M, Noguchi T. 2018. Mechanism of proton-coupled electron transfer in the S0-to-S1 transition of photosynthetic water oxidation as revealed by time-resolved infrared spectroscopy. J Phys Chem B. 122:9460–9470. [DOI] [PubMed] [Google Scholar]
- 21. Rutherford AW. 1985. Orientation of EPR signals arising from components in photosystem II membranes. Biochim Biophys Acta. 807:189–201. [Google Scholar]
- 22. Casey JL, Sauer K. 1984. EPR detection of a cryogenically photogenerated intermediate in photosynthetic oxygen evolution. Biochim Biophys Acta. 767:21–28. [Google Scholar]
- 23. Zimmermann JL, Rutherford AW. 1984. EPR studies of the oxygen-evolving enzyme of photosystem-II. Biochim Biophys Acta. 767:160–167. [Google Scholar]
- 24. de Paula JC, Beck WF, Miller A-F, Wilson RB, Brudvig GW. 1987. Studies of the manganese site of photosystem II by electron spin resonance spectroscopy. J Chem Soc Faraday Trans 1. 83:3635–3651. [Google Scholar]
- 25. Boussac A, Un S, Horner O, Rutherford AW. 1998. High-spin states (S ≥ 5/2) of the photosystem II manganese complex. Biochemistry. 37:4001–4007. [DOI] [PubMed] [Google Scholar]
- 26. Taguchi S, Noguchi T, Mino H. 2020. Molecular structure of the S2 state with a g = 5 signal in the oxygen evolving complex of photosystem II. J Phys Chem B. 124:5531–5537. [DOI] [PubMed] [Google Scholar]
- 27. Taguchi S, et al. 2020. Formation of the high-spin S2 state related to the extrinsic proteins in the oxygen evolving complex of photosystem II. J Phys Chem Lett. 11:8908–8913. [DOI] [PubMed] [Google Scholar]
- 28. Saito K, Mino H, Nishio S, Ishikita H. 2022. Protonation structure of the closed-cubane conformation of the O2-evolving complex in photosystem II. PNAS Nexus. 1:pgac221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Cox N, et al. 2011. Effect of Ca2+/Sr2+ substitution on the electronic structure of the oxygen-evolving complex of photosystem II: a combined multifrequency EPR, 55Mn-ENDOR, and DFT study of the S2 state. J Am Chem Soc. 133:3635–3648 . [DOI] [PubMed] [Google Scholar]
- 30. Corry TA, O’Malley PJ. 2020. Molecular identification of a high-spin deprotonated intermediate during the S2 to S3 transition of nature's water-oxidizing complex. J Am Chem Soc. 142:10240–10243. [DOI] [PubMed] [Google Scholar]
- 31. Boussac A, et al. 2018. The low spin–high spin equilibrium in the S2-state of the water oxidizing enzyme. Biochim Biophys Acta. 1859:342–356. [DOI] [PubMed] [Google Scholar]
- 32. Boussac A, Etienne AL. 1982. Oxido-reduction kinetics of signal II slow in tris-washed chloroplasts. Biochem Biophys Res Commun. 109:1200–1205. [DOI] [PubMed] [Google Scholar]
- 33. Lorigan GA, Britt RD. 1994. Temperature-dependent pulsed electron paramagnetic resonance studies of the S2 state multiline signal of the photosynthetic oxygen-evolving complex. Biochemistry. 33:12072–12076. [DOI] [PubMed] [Google Scholar]
- 34. Su JH, et al. 2011. The electronic structures of the S2 states of the oxygen-evolving complexes of photosystem II in plants and cyanobacteria in the presence and absence of methanol. Biochim Biophys Acta. 1807:829–840. [DOI] [PubMed] [Google Scholar]
- 35. Kulik LV, Epel B, Lubitz W, Messinger J. 2005. 55Mn Pulse ENDOR at 34 GHz of the S0 and S2 states of the oxygen-evolving complex in photosystem II. J Am Chem Soc. 127:2392–2393. [DOI] [PubMed] [Google Scholar]
- 36. Kulik LV, Epel B, Lubitz W, Messinger J. 2007. Electronic structure of the Mn4OxCa cluster in the S0 and S2 states of the oxygen-evolving complex of photosystem II based on pulse 55Mn-ENDOR and EPR spectroscopy. J Am Chem Soc. 129:13421–13435. [DOI] [PubMed] [Google Scholar]
- 37. Peloquin JM, et al. 2000. 55Mn ENDOR of the S2-state multiline EPR signal of photosystem II: implications on the structure of the tetranuclear Mn cluster. J Am Chem Soc. 122:10926–10942. [Google Scholar]
- 38. Cox N, et al. 2011. Electronic structure of a weakly antiferromagnetically coupled Mn(II)Mn(III) model relevant to manganese proteins: a combined EPR, 55Mn-ENDOR, and DFT study. Inorg Chem. 50:8238–8251 . [DOI] [PubMed] [Google Scholar]
- 39. Asada M, et al. 2013. Electronic structure of S2 state of the oxygen-evolving complex of photosystem II studied by PELDOR. Biochim Biophys Acta. 1827:438–445. [DOI] [PubMed] [Google Scholar]
- 40. Banham JE, et al. 2008. Distance measurements in the borderline region of applicability of CW EPR and DEER: a model study on a homologous series of spin-labelled peptides. J Magn Reson. 191:202–218. [DOI] [PubMed] [Google Scholar]
- 41. Stich TA, Yeagle GJ, Service RJ, Debus RJ, Britt RD. 2011. Ligation of D1-His332 and D1-Asp170 to the manganese cluster of photosystem II from Synechocystis assessed by multifrequency pulse EPR spectroscopy. Biochemistry. 50:7390–7404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Yano J, et al. 2005. X-ray damage to the Mn4Ca complex in single crystals of photosystem II: a case study for metalloprotein crystallography. Proc Natl Acad Sci U S A. 102:12047–12052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Yano J, Yachandra V. 2014. Mn4Ca cluster in photosynthesis: where and how water is oxidized to dioxygen. Chem Rev. 114:4175–4205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Grabolle M, Haumann M, Muller C, Liebisch P, Dau H. 2006. Rapid loss of structural motifs in the manganese complex of oxygenic photosynthesis by X-ray irradiation at 10–300 K. J Biol Chem. 281:4580–4588. [DOI] [PubMed] [Google Scholar]
- 45. Dau H, Zaharieva I, Haumann M. 2012. Recent developments in research on water oxidation by photosystem II. Curr Opin Chem Biol. 16:3–10. [DOI] [PubMed] [Google Scholar]
- 46. Galstyan A, Robertazzi A, Knapp EW. 2012. Oxygen-evolving Mn cluster in photosystem II: the protonation pattern and oxidation state in the high-resolution crystal structure. J Am Chem Soc. 134:7442–7449. [DOI] [PubMed] [Google Scholar]
- 47. Askerka M, Vinyard DJ, Wang J, Brudvig GW, Batista VS. 2015. Analysis of the radiation-damage-free X-ray structure of photosystem II in light of EXAFS and QM/MM data. Biochemistry. 54:1713–1716. [DOI] [PubMed] [Google Scholar]
- 48. Li Y, et al. 2020. Mimicking the catalytic center for the water-splitting reaction in photosystem II. Catalysts. 10:185. [Google Scholar]
- 49. Mandal M, Saito K, Ishikita H. 2022. Requirement of chloride for the downhill electron transfer pathway from the water-splitting center in natural photosynthesis. J Phys Chem B. 126:123–131. [DOI] [PubMed] [Google Scholar]
- 50. Hay PJ, Wadt WR. 1985. Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitals. J Chem Phys. 82:299–310. [Google Scholar]
- 51. QSite, version 5.8, Schrödinger, LLC, New York, NY. 2012.
- 52. Pantazis DA, et al. 2009. A new quantum chemical approach to the magnetic properties of oligonuclear transition-metal complexes: application to a model for the tetranuclear manganese cluster of photosystem II. Chem Eur J. 15:5108–5123. [DOI] [PubMed] [Google Scholar]
- 53. Yamaguchi K, Isobe H, Shoji M, Yamanaka S, Okumura M. 2016. Theory of chemical bonds in metalloenzymes XX: magneto-structural correlations in the CaMn4O5 cluster in oxygen-evolving complex of photosystem II. Mol Phys. 114:519–546. [Google Scholar]
- 54. Mino H, Nagashima H. 2020. Orientation of ligand field for dangling manganese in photosynthetic oxygen-evolving complex of photosystem II. J Phys Chem B. 124:128–133. [DOI] [PubMed] [Google Scholar]
- 55. Kawashima K, Takaoka T, Kimura H, Saito K, Ishikita H. 2018. O2 evolution and recovery of the water-oxidizing enzyme. Nat Commun. 9:1247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Zheng M, Dismukes GC. 1996. Orbital configuration of the valence electrons, ligand field symmetry, and manganese oxidation states of the photosynthetic water oxidizing complex: analysis of the S2 state multiline EPR signals. Inorg Chem. 35:3307–3319. [DOI] [PubMed] [Google Scholar]
- 57. Schäfer K-O, et al. 1998. Electronic structure of antiferromagnetically coupled dinuclear manganese (MnIIIMnIV) complexes studied by magnetic resonance techniques. J Am Chem Soc. 120:13104–13120. [Google Scholar]
- 58. Dau H, Haumann M. 2008. The manganese complex of photosystem II in its reaction cycle—basic framework and possible realization at the atomic level. Coord Chem Rev. 252:273–295. [Google Scholar]
- 59. Pace RJ, Smith P, Bramley R, Stehlik D. 1991. EPR saturation and temperature-dependence studies on signals from the oxygen-evolving center of photosystem-II. Biochim Biophys Acta. 1058:161–170. [Google Scholar]
- 60. Inoue Y, Shibata K. 1978. Oscillation of thermoluminescence at medium-low temperature. FEBS Lett. 85:193–197. [DOI] [PubMed] [Google Scholar]
- 61. Styring S, Rutherford AW. 1988. Deactivation kinetics and temperature-dependence of the S-state transitions in the oxygen-evolving system of photosystem-II measured by EPR spectroscopy. Biochim Biophys Acta. 933:378–387. [Google Scholar]
- 62. Capone M, Narzi D, Bovi D, Guidoni L. 2016. Mechanism of water delivery to the active site of photosystem II along the S2 to S3 transition. J Phys Chem Lett. 7:592–596. [DOI] [PubMed] [Google Scholar]
- 63. Saito K, Nakagawa M, Ishikita H. 2020. pKa of the ligand water molecules in the oxygen-evolving Mn4CaO5 cluster in photosystem II. Commun Chem. 3:89. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data are included in the manuscript and/or supporting information.