Abstract
The discovery of circulating tumor cells (CTCs) has envisioned an excellent outlook for cancer diagnosis and prognosis. Among numerous efforts proposed for CTCs isolation, vortex separation is a well-known method for capturing CTCs from blood due to its applicability, low sample volume requirement, and ability to retain cell viability. It is a label-free, passive, low-cost, and automated method, making it an ideal solution for lab-on-a-chip applications. The previous designs that employed vortex technology have shown reaching high throughput and 70% separation efficiency although it was after three processing cycles which are not desired. Inspired by our earlier design, in this work, we redesigned the chip geometry by elevating the columned reservoir height to capture more particles and consequently reduce particle–particle collision, eventually improving efficiency. So, a height-variable chip with fewer elevated columned reservoirs (ECRs) was employed to isolate 20 μm microparticles representing CTCs from 8 μm microparticles. Also, numerical simulations were conducted to investigate the third axis contribution to the separation mechanism. The new design with ECRs resulted in a 14% increase in average efficiency, reaching ∼80% ± 8.3% in microparticle separation and 61% purity. Moreover, the proposed chip geometry demonstrated more than three times higher capacity in retaining orbiting particles up to 1300 in peak performance without sacrificing efficiency compared to earlier single-layer designs. We came up with an upgraded injection system to facilitate this chip characterization. We also presented an effortless and straightforward approach for purging air bubbles trapped inside the reservoirs to preserve regular chip operation, especially where there is a mismatch between channel and reservoir heights.
1. Introduction
Circulating tumor cells (CTCs) are known as early indicators for cancer metastasis in patients.1 They are shed from the primary tumor, enter the blood circulation system, and result in a metastatic outbreak.2 Recent investigations have shown that not all CTCs contribute to forming new tumors.3 While new biomarkers such as circulating tumor DNA, circulating RNA, and exosomes are more precise in cancer diagnosis,4 CTCs have demonstrated multiple advantages for patient monitoring, drug testing, and investigating tumor spread.3,5 Liquid biopsy has emerged as a promising alternative method for patient monitoring and offers reduced pain and invasiveness compared to conventional tumor biopsies.6 Besides, CTC molecular analysis is a new approach to gene investigation and acquiring real-time information on a patient’s cancer situation.7 It can be further utilized for next-generation sequencing and mass cytometry to characterize single-cell genome, transcriptome, methylome, and proteome.3,8
The deficient number of CTCs in patient blood, approximately 1 per mL in the early stage9 and up to 1000 per mL in the late stages,10 poses a significant challenge for separation.11 CTCs are heterogeneous and usually larger than normal blood cells,9 and their scarcity is directly related to the effectiveness of the treatment and the patient’s overall survival.12 Hence, numerous methods in microfluidics have been introduced to achieve a more effective CTC separation and quantification.12−17 Microfluidics technology offers numerous advantages, including but not limited to minimal sample volume requirements and the potential for integrating multiple experiments on a single chip, thereby reducing time and cost.18 Microfluidics has further facilitated straightforward testing methodologies, thereby enabling point-of-care diagnostics, and has been employed for various purposes such as sample preparation, biomarker separation, fluid mixing, droplet generation, and single-cell analysis.19−22
CellSearch is the unique FDA-approved CTC counting method, using magnetic immune fluorescent nanoparticles labeling and an image analyzer,23 which does not provide viable cells after detection.24 Label-free techniques are more desired because of their high cell viability after separation and the ability to recover distinct CTC/cluster subpopulations with important information for predicting patient outcomes by eliminating the bias of using molecular markers.25 Viable CTCs can allow for further research in personal therapy and precision oncology. Some separation methods reported better performance than CellSearch.26,27
Vortex technology is a passive, high-throughput, and label-free method that relies solely on particle size and physical parameters.28,29 Separated CTCs in this method are intact, pure, and viable for downstream clinical examination.30−32 The processing time for whole blood is short due to optimizing the flow rate and establishing a high-throughput separation mechanism. Additionally, it is cost-effective and automated, requiring no need for a laboratory expert. It was first introduced in 201133,34 and has been ultimately commercialized for research-based viable CTCs separation.
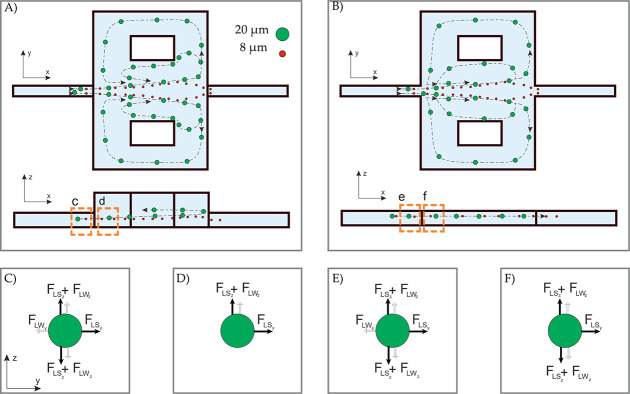
Within the vortex system, the balance of forces is pivotal for efficiently focusing and expulsing particles. As the fluid flows through tiny microchannels at a high rate, it generates a velocity profile known as Poiseuille flow, forming micro-vortices in expanded regions. These micro-vortices play a critical role in the separation mechanism, exerting inertial forces that can trap larger particles than a specific threshold within the vortex streamlines (Figure 1A,B).35 In this process, the lift force plays a crucial role. It depends on the flow rate and is responsible for achieving maximum efficiency. This is known as the critical Reynolds number (Recr). As the flow rate decreases, the vortex disappears and releases the cells. The lift force primarily affects particles larger than 0.07 of the channel’s hydraulic diameter. It is composed of the shear-induced and the wall-induced lift forces. These forces are in equilibrium at the balance point, where the flow focuses the particles across the channel (Figure 1C,E). Upon reaching the reservoir entrance, the abrupt removal of the wall eliminates the wall-induced force. In contrast, the shear-induced force propels the particles perpendicular to the main flow, expelling them into the reservoir space (Figure 1D,F). The interaction between drag and lift forces establishes a new equilibrium for the particles, causing them to orbit around the vortex core and remain within the reservoir.36 Briefly, Figure 1 illustrates the fundamental separation mechanism in the vortex technique, distinguishing between the constant height chip (CHC) and the elevated columned reservoir (ECR).
Figure 1.
Fundamental of the vortex separation mechanism in (A) the ECR and (B) the CHC for the same Re. It can be observed that the ECR reaches the whole-cell vortex at a lower flow rate compared to CHC. The predominant forces acting on the particle are depicted before and after entering the reservoir. (C) The balance of wall and shear-induced lift forces across the y and z-axis. (D) The remaining forces cause imbalance and alter the velocity direction. (E) The balance of active forces in CHC. (F) The imbalance of dynamic forces leads to changes in velocity direction.
One challenge of CTCs separation using vortex technology is the low efficiency, which requires more than three times reprocessing the sample to achieve a high separation efficiency. Furthermore, vortex technology-based devices showed a highly dependent capture efficiency to the sample concentration.33,37 Researchers have endeavored to enhance vortex efficiency since its introduction38,39 by modifying various parameters, including channel width,34,37,40 channel height,37,40 reservoir aspect ratio,41 primary channel length,27,42 reservoir spacing,27 the number of reservoirs along the channel,27,40 the number of parallel channels,27,42 side outlets for the reservoirs,43−45 different fabrication methods and chip materials,46 and ultimately the novel geometry of the reservoirs.47,48 Although upstream channel deformation was seen in the early report of vortex separation,34 the effect of chip deformability was not evaluated until 2018.46 Finally, for commercialization, VTX-1, i.e., the Vortex-HT (high-throughput) design introduced in ref (27), was fabricated on a rigid substrate and demonstrated higher efficiency due to lower deformability.46
Among the reported designs, columned reservoirs demonstrated higher efficiency, with the CHC vortex achieving 67% separation in a single step.49 Placing columns inside the reservoir was to make duplicate vortices in each reservoir to increase the capacity and reduce particle–particle collision. The inner vortex, which is smaller, looks similar to Vortex-HT, and the outer vortex, which is greater, encompasses the reservoir around the column. Multiple vortices in a reservoir provide more space for the particles to orbit and reduce the chance of particle–particle collision.49
Our previous work demonstrated the first three-dimensional (3D) vortex chip reservoir employing the third axis for separation.48 Based on numerical simulations and laboratory experiments, it was demonstrated that raising the height of the reservoir allows the system to apply conventional forces beside new imbalanced forces in a new direction simultaneously. Also, elevating the reservoir’s elevation increased the chip volume to trap more particles in each reservoir and reduce particle collisions. In the conventional vortex reservoir, which we call the two-dimensional (2D) vortex, particles orbit at a specific height,33 whereas in the elevated height reservoir, the 3D vortex enabled the particles to rise into a parallel plane upper from the inertial focusing position within the main flow. In other words, particles are no longer limited to a specific height in the reservoir and may elevate up or down. Hence, they have fewer common paths for orbiting and have a lower collision chance. Employing the 3D vortex resulted in 1.5 times higher efficiencies than the 2D vortex.48
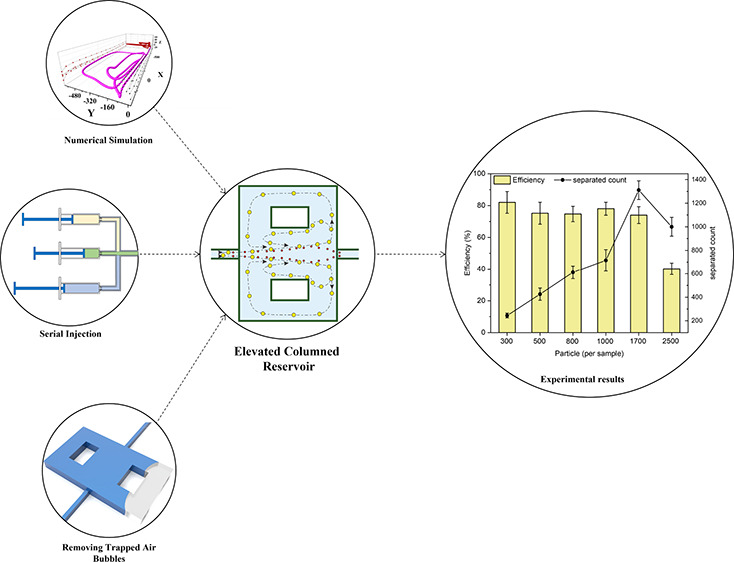
In this study, we extended our previous research48 by introducing the ECR design to take advantage of the 3D vortex and further enhance the separation efficiency. We took inspiration from the efficiency improvement for the columned reservoir that Paiè introduced.49 Her design consisted of a CHC with rectangular columns in each reservoir, dividing the vortex path into two.
2. Materials and Methods
The Sylgard 184 polydimethylsiloxane (PDMS) was acquired from Dow Corning, and the SU-82050 photoresist and propylene-glycol-methyl-ether-acetate (PGMEA) were obtained from Microchem. Also, polystyrene microbeads measuring 8 and 20 μm, coated with red and green fluorescent dyes, respectively, were purchased from Phosphorex. The experimental procedures also involved using TWEEN 20, ethanol, and phosphate buffer saline (PBS).
2.1. Numerical Simulations
Fluid flow was simulated using COMSOL Multiphysics 6.0 to solve the momentum and continuity equations for a single-phase Newtonian fluid. The fluid’s density (ρ) and dynamic viscosity (μ) were set at 1000 kg/m3 and 8 × 10–4 Pa·s, respectively. We performed a mesh independence analysis, the results of which are presented in Figure S1A,B. Additionally, we simulated the particle trapping behavior by utilizing the Lagrangian particle tracing module, coupled with the fluid flow, and solving Newton’s second law.50Supplementary Information provides further details regarding the simulations.
2.2. Chip Design
The chip design was inspired by architectural concepts in the literature.27,37,48,49 It consists of 16 parallel microchannels with a 40 × 70 μm cross-section, where six reservoirs are arranged along each channel in a row (see Figure S2). The channels connect columned reservoirs, drawing inspiration from the work by Paiè,49 with dimensions of 1290 μm in length and 720 μm in width. These columns, measuring 200 × 320 μm, are positioned at a distance of 200 μm from the side channel. The selection for the number of reservoirs was based on our previous study, which revealed that reducing the number of reservoirs enhances the trapping mechanism in the last four reservoirs, owing to the lower pressure drop experienced within the chip. As previously discussed, we incorporated a double-layer chip design for the reservoirs, providing ample space for orbiting particles and facilitating the utilization of out-of-plane forces.48
2.3. Device Fabrication
The device mold was fabricated following a two-step process described in our previous work.48 Initially, a two-inch silicon wafer was meticulously cleaned with acetone and isopropyl alcohol, and then rinsed with deionized (DI) water. For the first layer, a 70 μm thick coating of SU-8 was spin-coated onto the wafer, subsequently baked, and exposed to ultraviolet (UV) light using a mask that defined the inlet/outlets and parallel channels. The structure was then developed in PGMEA. Then, a second layer consisting of a 40 μm thick coating of SU-8 was spin-coated onto the prepared structure. A mask containing the layout of reservoirs, comprising 96 reservoirs, was precisely aligned with the bottom structure and exposed to UV light, following the exact baking and development procedure.
The PDMS chip was fabricated using the soft-lithography method. The PDMS elastomer was blended with its curing agent at a 10:1 ratio and cast onto the prepared mold. Before baking, the mixture was thoroughly degassed and maintained for an hour at 80 °C in an oven. The chip was carefully peeled off from the mold, and inlet and outlet holes were punched using a 1 mm biopsy punch. The glass slide and the PDMS component were subjected to 25 W oxygen plasma for 1 min, and then bonded and baked at 80 °C in the oven for 30 min. Lastly, polytetrafluoroethylene tubes were affixed to the chip holes and connected to the test setup.
2.4. Test Setup
Sample flow during each injection was monitored using an optical microscope (Olympus CX22). Fluorescent images were captured using an upright fluorescent microscope (Optika) equipped with a CCD camera (Optika). A ‘three-way stopcock’ facilitated the injection process, connecting multiple syringes to a single chip inlet. A local provider’s syringe pump (Zistrad 4SP94-1) was utilized for controlled sequential injections of specific solutions. To optimize the process of serial injection, we reprogrammed the pump controller (Mega 2560) using Arduino software. This involved establishing a novel connection approach that allowed the controller to seamlessly switch between different solutions with minimal delay, mitigating any potential pressure drop during the testing procedure. Moreover, the program was designed to enable the independent operation of the individual syringes, receiving real-time commands from a PC to ensure accurate and comprehensive testing. A photograph of the actual test setup is provided in Figure S3.
2.5. Preparing Solutions
To prevent particle aggregation, 0.1% TWEEN 20 was added to a specific concentration of microparticles at a 0.1% ratio in PBS. In order to ensure a homogeneous solution during the injection process, a small stainless-steel sphere with a diameter of 2 mm was embedded in the syringe. The solution underwent continuous agitation by utilizing an external magnet to shake the stainless-steel ball, resulting in thorough mixing and dispersion of the particles.
2.6. Experiments
The chip underwent testing under various conditions. A mixture of 20 μm fluorescent microbeads, totaling approximately 300 particles in 5 mL, was injected into the chip to assess its efficiency at different flow rates. The samples were injected following our procedure, and the output was collected in a 96-well plate and categorized into two separate groups. The first category, ‘waste,’ consisted of the flow exiting the chip during the sample injection, which contained non-trapped particles exiting from the chip. The second category, referred to as ‘main,’ encompassed an approximately 200 μL volume of fluid released from the chip when the flow rate was decreased. Trapped particles were easily flushed from the reservoirs by lowering the flow rate and gathering them in the main outlet. The fluorescent microscope was used to count the particles in the waste and main outlets. The reservoir’s capacity was also measured by injecting different quantities of 20 μm microbeads, ranging from 300 to 2500 particles, in a solution. The microbeads in each outlet were counted separately. The efficiency was calculated by dividing the number of microbeads in the main outlet by the total number in both outlets (main + waste).
Moreover, some mixtures of 8 and 20 μm microbeads were introduced into the chip to specify the selectivity of the device. The mixture consists of a constant number of 20 μm microbeads, approximately 300, besides different concentrations of 8 μm microparticles, including 1000, 3000, and 5000 in each sample. Ultimately, efficiency was calculated as mentioned earlier, and the purity was calculated by counting the number of 20 and 8 μm within the main outlet and calculating the ratio of 20 μm in the main outlet. The rejection rate was calculated by dividing the number of 8 μm particles passed from the chip by the total number of injected 8 μm microbeads.
The injection procedure consisted of the following steps:
Step 1: air removal—Ethanol injection for 3 min at a 6 mL/min flow rate to eliminate air bubbles from the reservoirs. Finally, changing the three-way stopcock prevented alcohol diffusion in the subsequent steps.
Step 2: primary vortex—PBS injection at the test flow rate for 30 s creates the primary vortex and removes the remnant alcohol from the chip.
Step 3: sample injection—Injection of the sample at the test flow rate while agitating the metal sphere. During this step, the output particles were collected in a Petri dish to count the untrapped particles (waste outlet).
Step 4: channel wash—PBS injection at the same flow rate for channel cleaning without delay. This step was necessary to eliminate the error for particles which were not reached the chip yet. Moreover, any unstable orbiting particles, such as 8 μm, were washed through the reservoirs.
Step 5: particle collection—Reduction of the flow rate to 0.5 mL/min to release the trapped particles and collect them in a 96-well plate (main outlet).
3. Results and Discussion
Our previous study48 emphasized the importance of elevated reservoirs. This work aims to present the simulation results of the redesigned reservoir and explore the impact of varying reservoir height on the chip performance. Moreover, we conducted experimental characterizations of the ECR chip and supplemented them with in-depth technical discussions.
3.1. Design Considerations and Simulations
In order to investigate the impact of reservoir height on microparticle trapping, we conducted simulations using vortex chambers with varying heights (H2) ranging from 70 to 140 μm, connected to a 70 μm height channel (H1). The fluid flow field and particle tracing were solved using COMSOL Multiphysics 6.0. We analyzed velocity profiles and streamlines to examine the hydrodynamic changes resulting from variations in H2. Additionally, particle trapping was simulated using the Lagrangian particle tracing module. Further details on the numerical modeling can be found in the Supplementary Information dedicated to numerical simulations.
3.1.1. Velocity Profiles
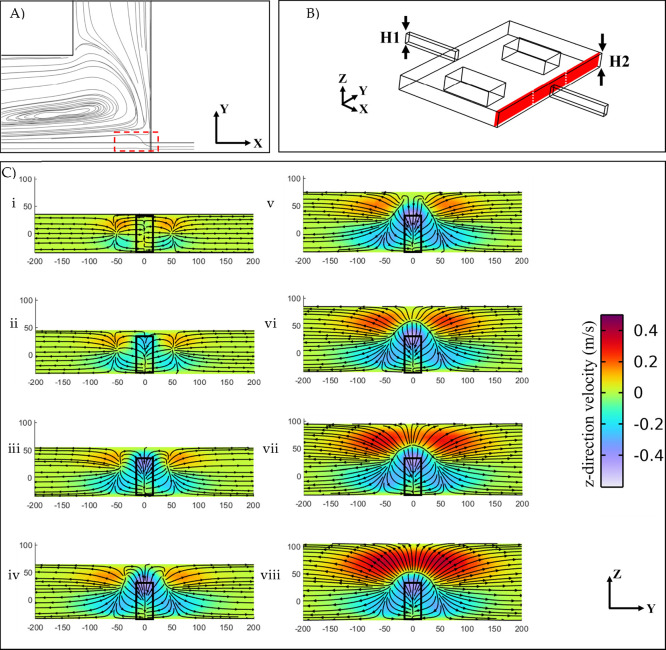
The term “Separatrix” refers to the region located at the end of a reservoir, where the main flow streamlines gradually expand and move outward (Figure 2A). The width of the separatrix serves as a threshold for the minimum lateral movement required for a particle to be trapped. This region holds significant importance as it directly influences the balance of forces acting on a particle and its stability within the reservoir. In Figure 2B, cross-sectional velocity profiles and streamlines near the end of the vortex chamber are depicted, highlighting the intensification of the separatrix. According to Figure 2C-i–viii, these profiles are related to differences in reservoir height with the same flow rate of 525 μL/min. When the inlet channel and the vortex chamber have equal heights (Figure 2C-i), the fluid passing through the chamber can directly exit, resulting in a balanced horizontal flow.
Figure 2.
(A), The separatrix region at the end of the reservoir, indicated by the red rectangle. (B) Schematic representation of the reservoir with a channel height of H1 = 70 μm and a vortex chamber height of H2. The cut-plane is positioned at a 20 μm distance from the end of the vortex chamber. (C) Velocity profiles and streamlines in the cut-plane for different geometries with H1 = 70 μm and varying H2 values: (i) 70 μm, (ii) 80 μm, (iii) 90 μm, (iv) 100 μm, (v) 110 μm, (vi) 120 μm, (vii) 130 μm, (viii) 140 μm. A constant flow rate of 525 μL/min was injected in all cases. The color bar represents the magnitude of the vertical velocity, with positive and negative velocities indicating the direction of fluid flow along the z-direction. The black rectangular window highlights the channel outlet at the end of the chamber.
When the height of the vortex chamber is increased from 70 to 140 μm, the fluid flow pattern changes notably. Specifically, the z-component of fluid velocity (uz > 0) increases along the reservoir. Toward the end of the reservoir, the streamlines of the main flow tend to move downward (uz < 0), rejoining the mainstream to exit from the chamber. As the chamber height increases, the cross-sectional shape of the separatrix at the end of the reservoir undergoes a transition: from a rectangle to a trapezoid (70–110 μm) as depicted in Figure 2C-i–iv, and then to a semicircle when the upward and downward horizontal flows are balanced (H > 120 μm), as shown in Figure 2C-v–viii. These changes in the flow pattern play a crucial role in understanding the stability of particles within the reservoir.
The reservoir height is crucial in achieving optimal separation efficiency, as measured by Recr.(48) When the reservoir height exceeds the channel height, the chamber reaches a state of whole-cell vortex at lower flow rates. For instance, CHC achieves this at Re = 180, while a reservoir height of 110 μm can achieve a similar state at approximately Re = 120. Both the whole-cell vortex and Recr represent maximum efficiency although the former is determined through numerical simulations, and the latter is derived from experimental data. Reducing Recr in chip design can help to compensate for PDMS deformation.37,46 Therefore, investigating the characteristics of the whole-cell vortex is vital for predicting the performance of the PDMS chip under pressure and deformation. Increasing the reservoir height can also result in vortex formation at lower flow rates.48
Another reason for Recr is because of changes in the boundary layer neighboring the top and bottom surfaces of the reservoir. In the case of CHC, where there is no extra distance between the main flow and the reservoir’s edge surfaces, the boundary layer appears in a narrower region and experiences a higher shear rate along the z-axis. This leads to forming a stable vortex in a limited space and height. Larger elevated reservoirs result in the formation of the whole-cell vortex at lower Re numbers. However, this comes at the cost of a lower shear rate, which should be considered a trade-off. Consequently, Recr occurs at a higher flow rate in the experiment, while the vortex core approaches the end of the reservoir to meet the requirement for higher separation flow rates. A significant difference in flow rates between the whole-cell vortex and Recr disrupts the streamlines and disturbs the stability of particles. Our observations indicate that the vortex core forms a symmetrical orbit in Recr. Meanwhile, by increasing the Re number, the deformation of vortex streamlines intensifies until the vortex core becomes too close to the end of the reservoir, which is significantly probable to miss trapped particles.
In addition to the hydrodynamic advantages of elevating the chamber reservoir, this modification also improves the reservoir capacity and saturation level. Increasing the reservoir height, such as from 70 to 110 μm, expands the chamber size by 60%, allowing for capturing more particles within the larger chamber. Furthermore, the shear rate, which represents the relative movement of adjacent fluid layers, is a crucial factor that influences the efficiency and peak performance of the separation mechanism.27,37 Specifically, surpassing the Reynolds critical number (Recr), which serves as a fluid instability threshold, can compromise trapped particles’ stability by increasing the flow rate. This instability can disrupt the particle orbiting within the chamber,36 potentially leading to particle escape and reducing the effectiveness of the separation process.
In conclusion, reservoir height is critical in achieving efficient particle separation. Based on the experiments and simulations presented in this study, setting the reservoir height around 110 μm is recommended for optimal performance, as previously reported. At this height, vortex formation occurs at lower flow rates while maintaining a sufficiently high shear rate to ensure the stability of trapped particles. Furthermore, increasing the reservoir height can enhance the chamber capacity and saturation level.
3.1.2. Particle Tracing
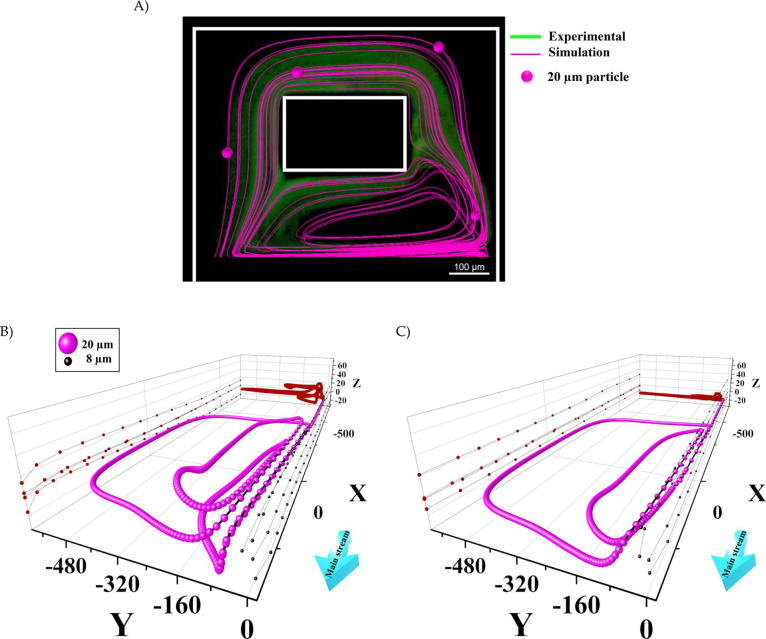
The motion of particles in vortex chambers with heights of 70 and 110 μm was visualized using a Lagrangian particle tracing module coupled with the fluid flow field, as described in the Supplementary Information. To validate the simulation results, we compared the fluorescent image of the vortices carrying several 20 μm fluorescent beads in the 110 μm height ECR at a flow rate of 375 μL/min with the numerical simulation results (Figure 3A). The particle trajectory was plotted from the moment it entered the vortex chamber for a period of 0.4 s (the whole 3D particle trajectory of a single particle after this period is shown in Figure S4). Figure 3A demonstrates that the predicted particle trajectory aligns with the experimental data, providing validation for the simulation results.
Figure 3.
(A) Validation of particle tracing using numerical simulation (pink lines) compared with the green fluorescent image of vortices carrying 20 μm fluorescent beads at a flow rate of 375 μL/min (0.4 s into simulation). (B) The 3D trajectories of a single 20 μm trapped particle after multiple rounds of orbiting in the vortices (depicted in pink) and those of four represented 8 μm microparticles passing straight through the chamber (depicted in black) are shown for ECR versus (C) CHC. The yz projections of 20 μm particle trajectories (highlighted in red) were plotted to compare vortex formation between the two chips. The flow rates for the constant and elevated height chips are 525 and 375 μL/min, respectively.
The movement of a single 20 μm particle and several 8 μm particles along the z-direction was investigated in vortex chambers with heights of 70 μm (CHC) and 110 μm (ECR). Figure 3B,C compare the predicted particle trajectories in the vortex chambers with heights of 110 μm (Recr = 142) and 70 μm (Recr = 200), respectively. Notably, elevating the chamber height alters the vortex shape.
As it is clear from Figure 3B, 8 μm particles passed the vortex chambers while 20 μm particle was trapped. The simulation results for 20 μm for CHC align with the findings of the confocal microscope tests presented in ref (33), where the most stable orbits were observed at the lower reservoir height. Additionally, as depicted in Figure 3C, the selected particle in CHC primarily orbits in a parallel plane with the xy-plane and predominantly within a limited height range. Conversely, as shown in Figure 3B, the particle moves at different heights along the z-direction while orbiting in the vortices in ECR (the z-axis trajectories are plotted on the back yz-plane for comparison). In summary, in the ECR chip, the height of the particles changes gradually during motion, whereas it remains fixed in the CHC.
Moreover, the simulation results for 8 μm particles reveal that while particles pass through the chamber in the ECR chip, they experience a z-direction movement. The projection of 8 μm microparticles is plotted in the xz-plane for both Figure 3B,C. The particle paths in the ECR elevate slightly in the z-direction from the entrance to almost the end of the reservoir while rapidly declining in the separatrix to exit the reservoir. These particles were not trapped in the vortex in both simulations. Notably, this minor particle elevation can increase the probability of 8 μm particles becoming trapped in the vortex, reducing the purity in the main outlet.
The change in 20 μm particle height during its orbit can be attributed to the modulation of lift and drag forces caused by the elevation of the chamber. As discussed earlier, elevating the vortex chamber facilitates the formation of a three-dimensional vortex. In CHC, where the vortex is generated in two dimensions (xy-plane as shown in Figure 3C), the drag force acts on the particle in both the x and y directions, causing the trapped particles to orbit horizontally without vertical movement (uz ≈ 0). In CHC, no z-direction force affects the particle due to the symmetrical flow pattern along the z-direction resulting from the constant height geometry. However, when the chamber is elevated (Figure 3B), the asymmetrical flow pattern along the z-direction introduces a z-direction component to the fluid flow velocity. Consequently, the z-direction component of the drag force (Fdrag) generates a vertical flow along the z-axis. This explains why particles trapped in an orbit move toward the top of the chamber outlet, where the z-direction velocity increases.
Furthermore, the velocity profile of the vertical flow generated in the chamber results in a shear-rate gradient, affecting the lift force acting on the trapped particles. In the vicinity of the chamber inlet, the shear rate increases due to the higher velocity, causing the trapped particles to be pushed toward the chamber bottom near the inlet. As shown in Figure 3B, the particles become trapped in an undulating vortex and exhibit a non-constant height trajectory (as depicted in the figure’s yz projection of particle positions). This indicates that in addition to their movement in the xy-plane, the particles also undergo vertical movement along the z-axis. This contributes to enhancing the stability of the trapped particles within the vortex.
In the subsequent analysis, we opted for the 110 μm height reservoir due to its similarity in geometry to our previous successful study. It possesses three fundamental properties that provide advantages over CHC:
-
1.
Lowering Recr reduces the deformation of the PDMS channel and increases efficiency.
-
2.
The larger reservoir volume enhances the capacity for trapping more particles.
-
3.
The presence of 3D streamlines allows particles to orbit out of the plane, unlike the predominantly in-plane orbit observed in CHC. This lowers the likelihood of particle collision.
3.2. Chip Characterization
3.2.1. Separation Efficiency
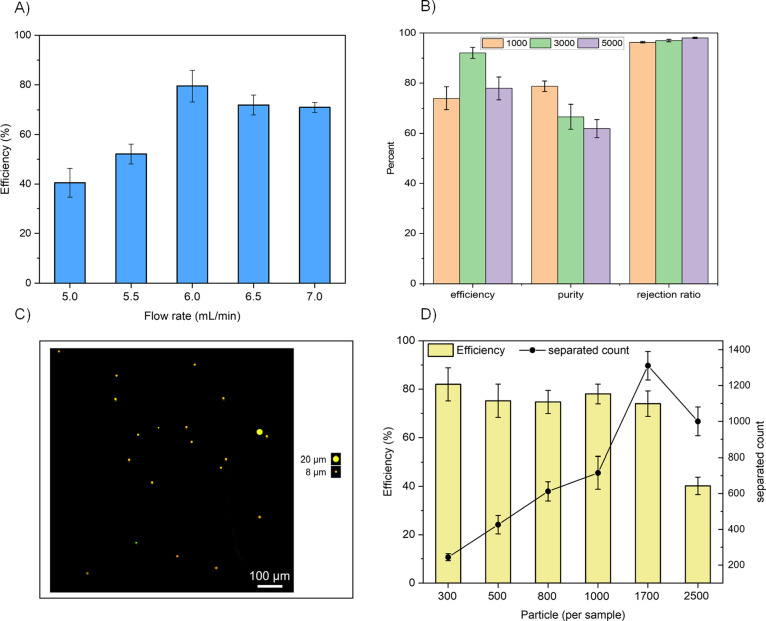
We conducted experiments with different flow parameters to characterize the chip and evaluate the separation efficiency and purity for 20 μm microbeads. The results of these tests are presented in Figure 4. Our results demonstrate that the proposed ECR chip operates effectively at a lower flow rate (Re = 140) compared to the previous vortex chip (Re = 175–190).27,49 To determine the optimal condition for particle trapping, we also measured the chip’s efficiency for a low-concentration sample at various Reynolds numbers (between 120 and 170). Figure 4A illustrates the introduction of 300 microparticles per sample into the chip at flow rates ranging from 4 to 7 mL/min. The device’s performance at different flow rates aligns well with other relevant studies.37,48
Figure 4.
(A) The trapping efficiency of the proposed ECR chip versus different flow rates for a sample volume containing particles measuring 20 μm in size. (B) Characterization of the chip for a mixed solution of 8 and 20 μm particles with approximately 1000, 3000, and 5000 number of 8 μm particles and roughly a constant 300 number of 20 μm particles in each test (n = 3). (C) A picture of the waste outlet representing a 20 μm particle among a series of 8 μm particles. (D) The chip’s efficiency is a function of the number of particles in the sample volume. The chip exhibits a saturation limit of approximately 1300 particles (n = 3).
The highest separation performance was observed at a flow rate of 6 mL/min (Re = 140) for 20 μm particles, resulting in an average efficiency of 80.6 ± 8.3%. The efficiency slightly decreased at higher flow rates than 6 mL/min. This decrease can be attributed to the displacement of the vortex core toward the end of the reservoir, where particles need to navigate through a narrower region and experience more significant changes in velocity and direction abruptly. As a result, there is a greater chance for particles to deviate from their intended orbit and potentially escape the vortex. Based on these observations, we conclude that the Recr for achieving optimal separation efficiency is 140 at the 6 mL/min flow rate.
We observed that injecting lower flow rates than 6 mL/min (Re = 140) cannot provide complete stability. In this range, while the trapping mechanism functions effectively, the orbiting beads are not sufficiently stable and can suddenly escape from the reservoir. This indicates that the microparticles become trapped and begin orbiting along the vortices. However, they eventually escape from the vortex after a short period. This behavior can be attributed to the low shear rate in the orbit, as discussed in detail earlier.51
Figure 4B shows the efficiency, purity, and rejection ratio of the proposed ECR chip for different test conditions. The tests consisted of three concentrations of 8 μm microbeads with around 1000, 3000, and 5000 particles mixed with a constant concentration of 20 μm microbeads with approximately 300 particles. The purpose of using 8 μm microparticles was to emulate red blood cells. The results show that the device maintains an average efficiency of over 81.3% ± 7.6 for trapping 20 μm microparticles. Although a small number of 8 μm microbeads were also trapped and detected in the main outlet, the number did not exceed 105 ± 5 particles in the highest concentration tests.
Increasing the concentration of smaller particles by fivefold (from 1000 to 5000) resulted in a 17% decrease in purity from 78.7 to 61.9%. However, the rejection ratio, representing the percentage of untrapped smaller particles from the total number of injected particles, remained extremely high, above 97.1 ± 0.7%. Figure 4B demonstrates the excellent selectivity of the device in removing smaller particles at high concentrations from the injected mixture solution. In summary, the device exhibited high efficiency for trapping 20 μm particles, a high rejection rate for 8 μm particles, and an acceptable purity for size-selective separation.
These experimental results are consistent with the simulation results visualizing the behavior of 8 μm microparticles through the ECR chip, as shown in Figure 3B. Furthermore, Figure 4C provides a visual representation of the waste, which contains a more significant number of 8 μm microbeads and a smaller number of 20 μm microbeads.
3.2.2. Chip Saturation
The previous design of the vortex chip was reported to trap a maximum of approximately 300 particles.49 Conventional chips face challenges in trapping a large number of particles in each reservoir, particularly for highly concentrated solutions. In our proposed design, the increased capacity of the chamber enables 3D streamlines that carry particles with a reduced risk of collision. To investigate reservoir saturation, we conducted tests with different sample concentrations. We used 300, 500, 800, and 1000 microparticles in a constant sample volume of 5 mL to examine chip efficiency at different concentrations. As depicted in Figure 4D, the proposed chip maintains an efficiency of 75% for up to 1700 injected particles in a sample. Additionally, we tested higher concentrated solutions of up to 2500 particles in the same volume, reaching the chip’s saturation level.
Although the chip exhibited the ability to retain 1300 particles when injecting 1700 particles, this number declined to around 1000 ± 80 for 2500 particles per sample injection, resulting in an efficiency drop to approximately 39%, as depicted in Figure 4D. The main reason for this reduction can be attributed to the extensive particle–particle collisions at higher concentrations. Since each reservoir can only trap a certain number of particles, the chip becomes saturated, and particles collide with each other while orbiting within the reservoir, reducing the total number of trapped particles. The decrease in efficiency directly results from the limited space available for the vortex space within the entire reservoir. Figure 4D illustrates that the capacity of our chip is 4× higher than that of Paiè’s design.49 This significant improvement is due to the formation of 3D particle orbits within the elevated reservoir, as shown in Figure 3. The benefit of a higher saturation number lies in its ability to retain the maximum number of introduced cells within a sample from a late-stage cancer patient.
The increase in saturation in high-concentration solutions can be primarily attributed to the larger reservoir volume and the presence of 3D streamlines. These factors enhance the separation mechanism by promoting the formation of more stable particle orbits. However, we also observed that not all reservoirs trapped a significant number of particles. This discrepancy may be due to variations in pressure between the channels, as described by Sollier.37 As a result, we believe that ECR’s higher saturation limit is caused by particle orbits at different heights within the chambers.
Previous reports have suggested that increasing the number of serialized reservoirs in a channel can improve efficiency.27 However, in our work, we opted for only six reservoirs along the channel, similar to our previous design.48 Adding more reservoirs would increase the back-pressure of the chip and result in higher deformation of the channels. This deformation would significantly impair the initial reservoirs and make them ineffective. Instead, we focused on leveraging the 3D vortex separation mechanism to achieve an efficiency of approximately 80% in a PDMS chip. This mechanism, coupled with the increased reservoir volume and lower flow rate, helped minimize PDMS deformation. Additionally, we used a customized syringe pump for sequential injection, facilitating a stable and reliable separation setup during the experimental tests described in the following sections.
3.2.3. Trapped Air Bubbles in the Reservoirs
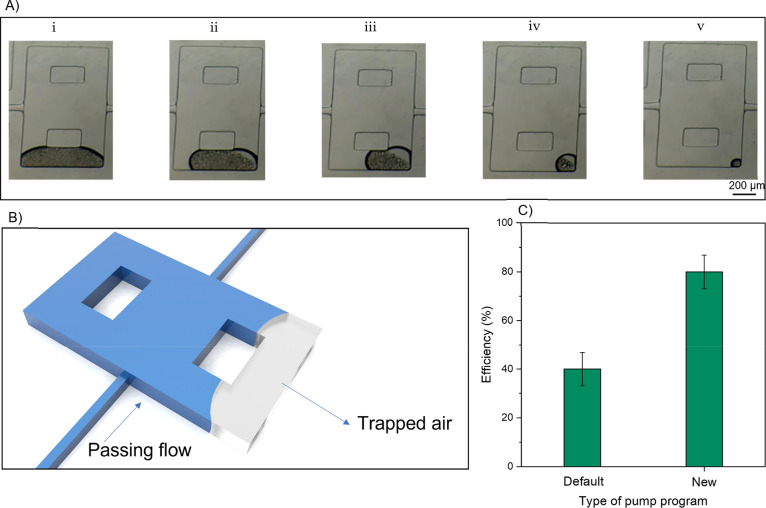
The existence of air bubbles posed a significant challenge in ECR chip design. In this reservoir type, the outlet channel is positioned in the bottom half of the chamber, which has a lower height than the reservoir. Initially, the entire volume of the chambers and channels is filled with ambient air before operation. When fluid flow is introduced into the chamber, air bubbles become trapped in the upper space of the reservoir, particularly behind the columns, which acts as a dead zone with no path to exit. The trapped bubbles can be observed in Supplementary Video 1 during the injection of PBS. As the fluid flow stabilizes in the channel and pushes the trapped air toward the chamber’s top, the bubbles cannot exit the chamber. Consequently, they move behind the columns and shrink away from the stream, as depicted in Figure 5A-i,B. Trapped bubbles reduce the reservoir volume and capacity and disrupt the formation of vortices, leading to a deficiency in particle trapping. Previous studies have proposed various geometric solutions to address this issue.52−54
Figure 5.
(A) Sequential steps for removing air bubbles from the reservoir using ethanol saturates the bubbles’ atmosphere, causing them to reach the dew point rapidly. Ethanol droplets penetrate the bubble from both sides of the chip and gradually join the flow after 3 min. (B) Schematic illustration of air bubble trapping inside the reservoir due to the height difference. (C) Comparison of separation efficiency using the default pump operation and the pump reprogrammed for serial injection strategy (n = 3).
To investigate the process of bubble removal, we conducted injections of various solutions. While the injection of ethanol at a low flow rate (0.14 μL/min) did not yield significant results in bubble removal,55 the most effective outcome was achieved by injecting pure ethanol (99.5%) at a high flow rate (6 mL/min or approximately 375 μL/min in each channel). The following paragraph will discuss the mechanism behind removing trapped air bubbles from the vortex chamber by injecting ethanol solution.
The evaporation characteristics of ethanol differ significantly from those of DI water or PBS. It is worth noting that as ethanol flows through the same channel, it experiences different shear rates and pressures due to its higher viscosity (11.2% higher) and lower density (21.1% lower) compared to water. The flow pressure enhances the evaporation of ethanol due to its higher vapor pressure and lower boiling point. The higher vapor pressure of ethanol facilitates its rapid evaporation into the surrounding air, leading to a higher evaporation rate. Additionally, the lower boiling point of ethanol means that it requires less thermal energy to evaporate, further contributing to its increased evaporation rate. Consequently, when ethanol is injected into the chip, it evaporates quickly into the bubbles, penetrating the bubble’s atmosphere and saturating it through continuous evaporation (the flow rate of ethanol remains constant during the air bubble removal process). Eventually, the atmosphere inside the bubble reaches the dew point, causing ethanol droplets to form on the surfaces within the bubble, as depicted in Figure 5A-i–v and Supplementary Video 2. These ethanol droplets can wet the inner boundaries of the bubble within the reservoir. Over a short period, the fluid flows through the bubble, and the ethanol droplets eventually evaporate, leaving no trapped air behind. Our observations indicate that passing ethanol through the chip for 3 min eliminates remnant bubbles in the chambers and fills the chip with fluid.
In our study, we have discovered a correlation between pressure and the removal of trapped air in the reservoirs, highlighting the significance of pressure in eliminating air bubbles. We observed that the first reservoirs in the channel became bubble-free sooner than the reservoirs further down the channel, indicating the influence of pressure on the reservoirs. This observation aligns with the hypothesis discussed in Section 3.2.2 regarding the impact of pressure on the reservoirs. Therefore, the pressure within the reservoirs is critical in effectively removing trapped air. This approach could be applied to other microfluidic chips to remove trapped air by adjusting the flow rate to an appropriate level.
3.2.4. Serial Injection Setup
To ensure smooth and uninterrupted vortex separation, a specific injection system is necessary to minimize injection delays and maintain stable flow while switching injection steps. In our experiments, we explored various strategies to assess the impact of shock-free injection. We observed that slight delays between two injection phases could significantly disrupt the orbiting particles, particularly during the washing step. To overcome this challenge, we reprogrammed a four-syringe pump controller that was initially not optimized for delay-free sequential injection. This modification allowed us to achieve precise and synchronized injections, ensuring the stability of the vortex separation process.
The developed program employs a novel protocol for real-time communication between the syringe pump and PC, allowing each syringe to be controlled independently. This need for a new controlling method in managing the change of solutions was crucial and inevitable, as its impact is illustrated in Figure 5C. Any delay or overlap between injection steps can disrupt the primary flow’s pressure, leading to a drop in the velocity of the microparticles. Such disruptions can result in particle loss and decreased efficiency due to shear-rate decline. For instance, without using a synchronized flow control unit, especially when changing solutions, any mismatch in flow rates can negatively affect the process. Developing an automated program to address this issue was imperative, ensuring no overlap or delays occurred during the injection process. This optimization helped achieve the high separation efficiency demonstrated in this study, as also highlighted by Lemaire et al.46Figure 5C clearly shows that the new injection program resulted in a twofold increase in efficiency. Additionally, it demonstrates the sensitivity of the proposed chip to pressure due to its lower Reynolds number. The injection program ensures reliable orbit stability during solution changes, as observed in Supplementary Video 3.
4. Conclusions
The primary objective of this study was to explore and validate the effectiveness of the vortex separation mechanism using ECRs. To achieve this, we initially conducted simulations using COMSOL Multiphysics to analyze the proposed reservoir geometry. The simulations confirmed our hypothesis of non-planar vortex streamlines. Subsequently, we fabricated a double-layer mold. The performance of fabricated chips was assessed by injecting 20 μm microparticles to study the efficiency and 8 μm to observe the size selectivity of the chip. The results demonstrated a significant improvement in separation efficiency compared to previous designs. Through experimental characterization and numerical simulations, we discovered that reducing the required flow rate slightly enhanced the chip’s performance, reducing the deformation of the PDMS channels and mitigating any adverse effects caused by the deformation.
Elevating the reservoir in the chip design increases its volume, allowing more particles or cells to be trapped within each chamber. The experimental results revealed that the chip has a capacity of approximately 1300 microparticles, which does not significantly affect the efficiency of the separation process. Notably, the chip has fewer reservoirs arranged in a row compared to a similar CHC design reported in a previous study.49 However, the complex design of the reservoirs introduced a challenge of trapped air bubbles within the chamber. Utilizing a modified syringe pump capable of injecting different types of fluids, we addressed the challenge of trapped air by introducing pure ethanol, a highly evaporating fluid. This modification was also necessary as we observed the orbiting particles within the reservoir, which could escape if no automated solution changed during the injection process. With the enhanced reservoir design and automated solution switching, the chip achieved an efficiency of 80% for 20 μm particles and higher than 61% purity for separation from 8 μm microparticles when utilizing a continuous injection system.
Acknowledgments
The authors would like to acknowledge Mohammadjavad Bouloorchi from MEMS Lab, University of Tehran, for assistance with the chip fabrication.
Glossary
Abbreviations
- CHC
constant height chip, chips fabricated in a single layer with constant height
- EHC
elevated height chip, chips fabricated in the double layer where the height of reservoirs is larger
- ECR
elevated columned reservoir, a subset of EHC with an elevated column embedded in each reservoir (the new design proposed in this report)
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.3c03136.
Numerical simulation descriptions, pictures of chip and test setup, long-time simulation of orbiting particle in an ECR reservoir, and effect of pump overlap on the pressure in chip (PDF)
Supplementary Video S1: trapped air bubbles while injecting PBS (MP4)
Supplementary Video S2: disappearing bubbles while injecting ethanol (MP4)
Supplementary Video S3: stable orbits by employing the new pump program (MP4)
Author Contributions
The contributions of the authors for this paper are as follows: A.M. was responsible for designing the chip, leading the experimental characterization, preparing test samples, and writing the original and revised draft. H.H. supervised the project, provided financial support, and revised the manuscript. M.K. assisted with the experimental characterization. A.K. performed numerical simulations, assisted with the experimental characterization, and contributed to the original draft. M.T.A. programmed the Arduino controller and provided laboratory assistance. S.M.H. provided laboratory assistance and revised the manuscript. M.B. served as the co-advisor, supported the chip fabrication, helped design experiments, contributed to the original draft, and frequently revised the manuscript.
The authors declare no competing financial interest.
Supplementary Material
References
- Gao R.; et al. Efficient separation of tumor cells from untreated whole blood using a novel multistage hydrodynamic focusing microfluidics. Talanta 2020, 207, 120261 10.1016/j.talanta.2019.120261. [DOI] [PubMed] [Google Scholar]
- Habli Z.; et al. Circulating tumor cell detection technologies and clinical utility: Challenges and opportunities. Cancers 2020, 12, 1930. 10.3390/cancers12071930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castro-Giner F.; Aceto N. J. G. M. Tracking cancer progression: From circulating tumor cells to metastasis. Gen. Med. 2020, 12, 31. 10.1186/s13073-020-00728-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H.; et al. Aptamer-Functionalized Barcodes in Herringbone Microfluidics for Multiple Detection of Exosomes. Small Methods 2022, 6, 2200236 10.1002/smtd.202200236. [DOI] [PubMed] [Google Scholar]
- Pantel K.; Alix-Panabières C. Liquid biopsy and minimal residual disease—latest advances and implications for cure. Nat. Rev. Clin. Oncol. 2019, 16, 409–424. 10.1038/s41571-019-0187-3. [DOI] [PubMed] [Google Scholar]
- Cho H.; et al. Microfluidic technologies for circulating tumor cell isolation. Analyst 2018, 143, 2936–2970. 10.1039/C7AN01979C. [DOI] [PubMed] [Google Scholar]
- Macaraniag C.; et al. Microfluidic techniques for isolation, formation, and characterization of circulating tumor cells and clusters. APL Bioeng. 2022, 6, 031501 10.1063/5.0093806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin D.; et al. Circulating tumor cells: biology and clinical significance. Signal Transduction Targeted Ther. 2021, 6, 404. 10.1038/s41392-021-00817-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Z.; et al. Recent Advances in Microfluidic Platforms Applied in Cancer Metastasis: Circulating Tumor Cells’(CTCs) Isolation and Tumor-On-A-Chip. Small 2020, 16, 1903899 10.1002/smll.201903899. [DOI] [PubMed] [Google Scholar]
- Cheng S.-B.; et al. Current techniques and future advance of microfluidic devices for circulating tumor cells. TrAC, Trends Anal. Chem. 2019, 117, 116. 10.1016/j.trac.2019.06.018. [DOI] [Google Scholar]
- Chelakkot C.; Yang H.; Shin Y. K. Relevance of Circulating Tumor Cells as Predictive Markers for Cancer Incidence and Relapse. Pharmaceuticals 2022, 15, 75. 10.3390/ph15010075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riethdorf S.; et al. Detection of circulating tumor cells in peripheral blood of patients with metastatic breast cancer: a validation study of the CellSearch system. Clin. Cancer Res. 2007, 13, 920–928. 10.1158/1078-0432.CCR-06-1695. [DOI] [PubMed] [Google Scholar]
- Vona G.; et al. Isolation by size of epithelial tumor cells: a new method for the immunomorphological and molecular characterization of circulating tumor cells. Am. J. Pathol. 2000, 156, 57–63. 10.1016/S0002-9440(10)64706-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desitter I.; et al. A new device for rapid isolation by size and characterization of rare circulating tumor cells. Anticancer Res. 2011, 31, 427–441. [PubMed] [Google Scholar]
- Miller M. C.; et al. The ParsortixTM cell separation system—A versatile liquid biopsy platform. Cytometry A 2018, 93, 1234–1239. 10.1002/cyto.a.23571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagrath S.; et al. Isolation of rare circulating tumour cells in cancer patients by microchip technology. Nature 2007, 450, 1235–1239. 10.1038/nature06385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ozkumur E.; et al. Inertial focusing for tumor antigen–dependent and–independent sorting of rare circulating tumor cells. Sci. Transl. Med. 2013, 5, 179ra47. 10.1126/scitranslmed.3005616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pattanayak P.; et al. Microfluidic chips: recent advances, critical strategies in design, applications and future perspectives. Microfluid. Nanofluid. 2021, 25, 99. 10.1007/s10404-021-02502-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gale B. K.; et al. A review of current methods in microfluidic device fabrication and future commercialization prospects. Inventions 2018, 3, 60. 10.3390/inventions3030060. [DOI] [Google Scholar]
- Chen H.; et al. Microfluidic technologies for cell deformability cytometry. Smart Med. 2022, 1, e20220001 10.1002/SMMD.20220001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu D.; et al. Integrated microfluidic devices for in vitro diagnostics at point of care. Aggregate 2022, 3, e184 10.1002/agt2.184. [DOI] [Google Scholar]
- Shamsi A.; et al. High throughput blood plasma separation using a passive PMMA microfluidic device. Microsyst. Technol. 2016, 22, 2447–2454. 10.1007/s00542-015-2664-7. [DOI] [Google Scholar]
- Yap K.; et al. Circulating tumor cells: State-of-the-art update on technologies and clinical applications. Curr. Hematol. Malign. Rep. 2019, 14, 353–357. 10.1007/s11899-019-00531-x. [DOI] [PubMed] [Google Scholar]
- Rushton A. J.; et al. A review of circulating tumour cell enrichment technologies. Cancers 2021, 13, 970. 10.3390/cancers13050970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeinali M.; et al. High-Throughput Label-Free Isolation of Heterogeneous Circulating Tumor Cells and CTC Clusters from Non-Small-Cell Lung Cancer Patients. Cancers 2020, 12, 127. 10.3390/cancers12010127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antfolk M.; Laurell T. Continuous flow microfluidic separation and processing of rare cells and bioparticles found in blood–A review. Anal. Chim. Acta 2017, 965, 9–35. 10.1016/j.aca.2017.02.017. [DOI] [PubMed] [Google Scholar]
- Che J.; et al. Classification of large circulating tumor cells isolated with ultra-high throughput microfluidic Vortex technology. Oncotarget 2016, 7, 12748. 10.18632/oncotarget.7220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raillon C.; et al. Toward Microfluidic Label-Free Isolation and Enumeration of Circulating Tumor Cells from Blood Samples. Cytometry, Part A 2019, 95, 1085. 10.1002/cyto.a.23868. [DOI] [PubMed] [Google Scholar]
- Cha H.; et al. Effects of obstacles on inertial focusing and separation in sinusoidal channels: An experimental and numerical study. Chem. Eng. Sci. 2023, 276, 118826 10.1016/j.ces.2023.118826. [DOI] [Google Scholar]
- Ju J. A.; et al. Partial thermal imidization of polyelectrolyte multilayer cell tethering surfaces (TetherChip) enables efficient cell capture and microtentacle fixation for circulating tumor cell analysis. Lab Chip 2020, 20, 2872–2888. 10.1039/D0LC00207K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailey P. C.; Martin S. S. Insights on CTC biology and clinical impact emerging from advances in capture technology. Cell 2019, 8, 553. 10.3390/cells8060553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson K. N.; et al. Microtubule disruption reduces metastasis more effectively than primary tumor growth. Breast Cancer Res. 2022, 24, 13. 10.1186/s13058-022-01506-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hur S. C.; Mach A. J.; Di Carlo D. High-throughput size-based rare cell enrichment using microscale vortices. Biomicrofluidics 2011, 5, 022206 10.1063/1.3576780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mach A. J.; et al. Automated cellular sample preparation using a Centrifuge-on-a-Chip. Lab Chip 2011, 11, 2827–2834. 10.1039/c1lc20330d. [DOI] [PubMed] [Google Scholar]
- Jiang D.; et al. Numerical simulation of particle migration in different contraction–expansion ratio microchannels. Microfluid. Nanofluid. 2019, 23, 7. 10.1007/s10404-018-2176-8. [DOI] [Google Scholar]
- Jiang M.; Qian S.; Liu Z. Fully resolved simulation of single-particle dynamics in a microcavity. Microfluid. Nanofluid. 2018, 22, 144. 10.1007/s10404-018-2166-x. [DOI] [Google Scholar]
- Sollier E.; et al. Size-selective collection of circulating tumor cells using Vortex technology. Lab Chip 2014, 14, 63–77. 10.1039/C3LC50689D. [DOI] [PubMed] [Google Scholar]
- Volpe A.; Gaudiuso C.; Ancona A. Sorting of Particles Using Inertial Focusing and Laminar Vortex Technology: A Review. Micromachines 2019, 10, 594. 10.3390/mi10090594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang D.; et al. Inertial microfluidics in contraction–expansion microchannels: A review. Biomicrofluidics 2021, 15, 041501 10.1063/5.0058732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhar M.; et al. High efficiency vortex trapping of circulating tumor cells. Biomicrofluidics 2015, 9, 064116 10.1063/1.4937895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haddadi H.; Di Carlo D. Inertial flow of a dilute suspension over cavities in a microchannel. J. Fluid Mech. 2017, 811, 436–467. 10.1017/jfm.2016.709. [DOI] [Google Scholar]
- Che J.; et al. Microfluidic purification and concentration of malignant pleural effusions for improved molecular and cytomorphological diagnostics. PLoS One 2013, 8, e78194 10.1371/journal.pone.0078194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volpe A.; et al. Polymeric fully inertial lab-on-a-chip with enhanced-throughput sorting capabilities. Microfluid. Nanofluid. 2019, 23, 37. 10.1007/s10404-019-2206-1. [DOI] [Google Scholar]
- Wang X.; Zhou J.; Papautsky I. Vortex-aided inertial microfluidic device for continuous particle separation with high size-selectivity, efficiency, and purity. Biomicrofluidics 2013, 7, 044119 10.1063/1.4818906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X.; Yang X.; Papautsky I. An integrated inertial microfluidic vortex sorter for tunable sorting and purification of cells. Technology 2016, 4, 88–97. 10.1142/S2339547816400112. [DOI] [Google Scholar]
- Lemaire C. A.; et al. Fast and label-free isolation of circulating tumor cells from blood: from a research microfluidic platform to an automated fluidic instrument, VTX-1 liquid biopsy system. SLAS Technol.: Transl. Life Sci. Innov. 2018, 23, 16–29. 10.1177/2472630317738698. [DOI] [PubMed] [Google Scholar]
- Shen F.; et al. Round cavity-based vortex sorting of particles with enhanced holding capacity. Phys. Fluids 2021, 33, 082002 10.1063/5.0061481. [DOI] [Google Scholar]
- Amini A.; et al. Efficient label-free CTC enrichment using novel elevated height chip chamber by vortex technology. Microfluid. Nanofluid. 2022, 26, 48. 10.1007/s10404-022-02553-z. [DOI] [Google Scholar]
- Paiè P.; Che J.; Di Carlo D. Effect of reservoir geometry on vortex trapping of cancer cells. Microfluid. Nanofluid. 2017, 21, 104. 10.1007/s10404-017-1942-3. [DOI] [Google Scholar]
- Karabacak N. M.; et al. Microfluidic, marker-free isolation of circulating tumor cells from blood samples. Nat. Protoc. 2014, 9, 694–710. 10.1038/nprot.2014.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen F.; et al. Evolution of single-particle recirculating orbits within a hydrodynamic microvortex. J. Micromech. Microeng. 2018, 28, 085018 10.1088/1361-6439/aac02d. [DOI] [Google Scholar]
- Cho H.; Kim J.; Han K.-H. An assembly disposable degassing microfluidic device using a gas-permeable hydrophobic membrane and a reusable microsupport array. Sens. Actuators, B 2019, 286, 353–361. 10.1016/j.snb.2019.01.118. [DOI] [Google Scholar]
- Huang C.; et al. Eliminating air bubble in microfluidic systems utilizing integrated in-line sloped microstructures. Biomed. Microdevices 2020, 22, 76. 10.1007/s10544-020-00529-w. [DOI] [PubMed] [Google Scholar]
- Kang J. H.; Kim Y. C.; Park J.-K. Analysis of pressure-driven air bubble elimination in a microfluidic device. Lab Chip 2008, 8, 176–178. 10.1039/B712672G. [DOI] [PubMed] [Google Scholar]
- Lochovsky C.; Yasotharan S.; Günther A. Bubbles no more: in-plane trapping and removal of bubbles in microfluidic devices. Lab Chip 2012, 12, 595–601. 10.1039/C1LC20817A. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.