Gradient nanostructured steel with superior tensile plasticity

Abstract

Nanostructured metallic materials with abundant high-angle grain boundaries exhibit high strength and good radiation resistance. While the nanoscale grains induce high strength, they also degrade tensile ductility. We show that a gradient nanostructured ferritic steel exhibits simultaneous improvement in yield strength by 36% and uniform elongation by 50% compared to the homogenously structured counterpart. In situ tension studies coupled with electron backscattered diffraction analyses reveal intricate coordinated deformation mechanisms in the gradient structures. The outermost nanolaminate grains sustain a substantial plastic strain via a profound deformation mechanism involving prominent grain reorientation. This synergistic plastic co-deformation process alters the rupture mode in the post-necking regime, thus delaying the onset of fracture. The present discovery highlights the intrinsic plasticity of nanolaminate grains and their significance in simultaneous improvement of strength and tensile ductility of structural metallic materials.

Heterogenous deformation enables exceptional plasticity in a strong and ductile gradient nanostructured steel.

INTRODUCTION

Nanocrystalline (NC) metallic materials have unique properties such as ultrahigh strength, distinct fatigue resistance, and radiation tolerance and thus are appealing structural materials for various industrial applications (1–3). However, the refined microstructure with a significant volume fraction of grain boundaries (GBs) often alters the deformation behaviors markedly, leading to an inherent brittleness with limited tensile elongation and fracture toughness (4–6). Tremendous efforts have been made to improve the ductility and work hardening rate of NC metallic materials under room temperature tension, such as introducing bimodal distribution of grain sizes, twin boundaries, or dispersive nanoprecipitates (7–12).

Recent studies show that certain metallic materials with gradient microstructures produced by surface severe plastic deformation (SSPD) techniques exhibit a combination of high strength and ductility compared with their homogeneously structured counterparts (13–19). Several mechanisms have been identified to account for the improved ductility. The high tensile plasticity of a gradient Cu was ascribed to the prominent grain coarsening in the surface NC layers during deformation, and the extent of grain coarsening depends on initial grain size (17, 20, 21). Heterodeformation-induced (HDI) hardening generated by the pileup of geometrically necessary dislocations (GNDs) and a multiaxial stress state can also boost work hardening rate in gradient materials (18, 19, 22). In addition to improved ductility, the gradient microstructures may also enhance the fracture toughness, thermal stability, radiation, oxidation, and fatigue resistance of the materials (15, 23–27).

Despite the promising findings in certain gradient metallic materials, most studies are still limited to pure metals (such as copper and nickel) (17, 28–30), low stacking fault energy alloys (such as nickel alloys and high entropy alloys) (31, 32), and face-centered cubic (FCC) steels [such as austenitic stainless steels, twinning-induced plasticity (TWIP) steels, and transformation-induced plasticity steels] (15, 33–35). The generation of gradient layer in these materials is often facilitated by deformation twinning or phase transformation. In contrast, tensile deformation behavior of gradient structures is much less well understood in body-centered cubic (BCC) steel systems, such as ferritic/martensitic (F/M) steels. A correlation between the evolution of gradient microstructures and their co-deformation processes remains elusive. Furthermore, it is critical to understand how NC grains in gradient materials sustain large tensile plasticity during deformation.

In the present study, we used a modified ferritic 9Cr-1Mo steel, also known as T91 steel, as a model system, which has been widely used as a structural material in nuclear and petrochemical industries because of its good phase stability and resistance to stress corrosion cracking (36–40). A gradient nanostructured T91 (G-T91) steel with 20 volume percent (%) gradient microstructure was fabricated by surface mechanical grinding treatment (SMGT). Uniaxial tensile tests were performed on the G-T91 coupled with interrupted in situ electron backscattered diffraction (EBSD) analyses to interrogate the intragranular strain evolution in the gradient structures. The G-T91 exhibits a combination of high yield strength (690 MPa) and large uniform elongation (10%), much greater than homogeneous T91 (H-T91), surpassing a majority of the current F/M steels. The unique nanolaminate (NL) grains in the gradient alloys accommodated more than 100% true strain via a distinct deformation mechanism. The present study highlights the intrinsic plasticity of the NL grains and the significance of the gradient microstructures in achieving high strength and high tensile ductility and thus largely advances our understanding on the design of strong and ductile structural alloys.

RESULTS

Microstructures of G-T91

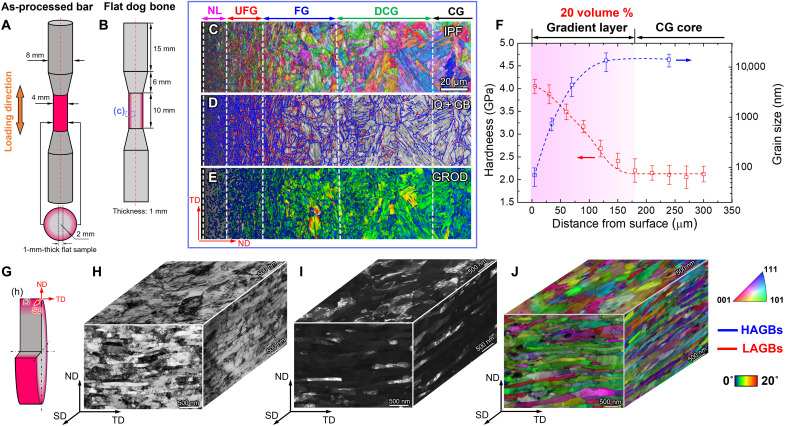
Inverse pole figure (IPF) in Fig. 1C depicts the grain morphology and crystal orientations in the gradient structures spanning from the processed surface to the interior of the bar. Image quality (IQ) plus grain boundary (GB) maps in Fig. 1D provide the GB morphology in each region of the gradient layer. The grain reference orientation deviation (GROD) map plotted in Fig. 1E indicates the intragranular strain distribution in each grain. A brighter color indicates a greater orientation deviation from the reference value, which is defined as the average orientation of the grain. From the IPF and GROD maps, five regions were identified in the gradient structures: NL layer, ultrafine grain (UFG) layer, fine grain (FG) layer, deformed coarse grain (DCG) layer, and CG core. On the basis of the GROD map in Fig. 1E, the estimated gradient layer thickness is 200 μm in the G-T91 steel. The grain size in the DCG region remained comparable to that in the CG region, but dislocations may have already accumulated and piled up in the grain interior, leading to an evident strain gradient (Fig. 1E). Figure S1 displays the magnified IPFs, kernel average misorientation, and corresponding GROD maps in the UFG, FG, and CG regions. The microstructural gradient gives rise to a hardness gradient, varying from 2.2 GPa in the CG core to 4.1 GPa in the NL surface region (Fig. 1F). The smallest grain size of 70 nm was achieved in NL region with an average hardness of 4.1 GPa, followed by the UFG region with an average grain size of 750 nm. The average grain size in the FG region is 4.4 μm, resulting in a hardness of 3.2 to 3.5 GPa. The grain size in DCG (13.6 μm) and CG (14.1 μm) regions are very close, while the hardness of the DCG region is slightly higher than that of the CG region due to the deformed microstructures.

Fig. 1. Microstructure overview of the as-processed G-T91 steel bar.

Schematic diagrams show the dimension of (A) surface-treated tensile bar sample and (B) the corresponding sectioned flat tensile specimen. (C) Inverse pole figure (IPF) from the gauge area in (B) shows the crystal orientation and grain size variation from the treated surface to the coarse-grained (CG) core. (D) Image quality (IQ) overlapped with grain boundary (GB) maps display the boundary types in the gradient layers. (E) Grain reference orientation deviation (GROD) map illustrates the intragranular strain distribution. The gradient microstructure consists of nanolaminate (NL) layer, ultrafine grain (UFG) layer, fine grain (FG) region, deformed coarse grain (DCG) region, and a CG core. (F) The variations of the average grain size and hardness with depth from the surface. The microstructure gradient induced a hardness gradient from the surface to the interior of the bar probed by Vickers hardness. The highest hardness (~4 GPa) was achieved in the NL layer. volume %, volume percent. (G) The schematics of a sliced disk from the gauge area illustrates a three-dimensional cube sectioned from the NL layer. Three directions were identified: normal direction (ND), transverse direction (TD), and shear direction (SD). (H) Transmission electron microscopy (TEM) bright-field (BF), (I) dark-field (DF), and (J) IPF taken along the three directions depict the three dimensional grain size, morphology, and crystal orientation in the NL layer. LAGBs, low-angle GBs; HAGBs, high-angle GBs.

In Fig. 1G, a sliced disk from the gauge section of the tensile bar sample shows a sectioned cube from the NL region selected for in-depth microstructure analyses. Three axes were defined on the basis of the severe plastic deformation characteristics of the surface NL layer. Normal direction (ND) is the radial direction of the treated bar. Transverse direction (TD) is parallel to the long axis of the bar, and shear direction (SD) is the rotation direction of the bar during the SMGT. Three-dimensional transmission electron microscopy (TEM) bright-field (BF) and dark-field (DF) images and IPFs in Fig. 1 (H to J) display the internal microstructures, including the grain size and crystal orientation of the NL cube. Figure S2 summarizes the length and thickness distribution of the as-processed NL grains along the three different directions, and the average values are t_ND = 70 nm, l_SD = 460 nm, and l_TD = 230 nm.

Tensile properties of G-T91

Representative engineering stress-strain curves in Fig. 2A compare the tensile properties of the G-T91 steel with the H-T91 control sample. The yield strength of the G-T91 steel reached 690 MPa, 40% higher than that of the H-T91 specimen. The uniform elongation of the gradient sample is 10% compared with 7% of the H-T91 sample. Note that the elongation to fracture of the G-T91 reached 45%, more than double that of the H-T91 sample (20%). The inserted optical image in Fig. 2A shows the fractured G-T91 tensile bar with a cup-and-cone ductile fracture morphology. Figure 2B plots the true stress-strain curves and the strain hardening rate curves of the G-T91 and the H-T91 samples. The G-T91 exhibits a prominently higher work hardening rate than the homogeneous sample. Figure 2C compares the yield strength versus uniform strain for various F/M steels and the present ferritic G-T91 steel. The ferritic G-T91 steel in our study has an improved yield strength and a greater uniform elongation than conventional ferritic (α) F/M steels. In addition, data points from dual-phase (α + α′) F/M steels within the orange region were also added for comparison. The uniform strain of the G-T91 reaches 10%, much greater than those F/M steels, with comparable yield strength.

Fig. 2. Uniaxial tensile properties of the G-T91 dog-bone bar samples.

(A) Representative engineering stress-strain curves of the homogeneously structured T91 (H-T91) and the gradient T91 (G-T91) dog-bone bar samples. (B) The corresponding true stress-strain curves and strain hardening rate curves of the two types of specimens. (C) Plot of yield strength versus uniform strain compares the strength-ductility tradeoff of various commercial ferritic/martensitic (F/M) steels from literatures and the current ferritic G-T91 steel (77–86).

In situ EBSD of gradient structures

To reveal the deformation mechanisms of G-T91, interrupted in situ EBSD analyses were performed in CG, FG, and UFG regions at 0, 3, 6, and 9% plastic strains (fig. S3). Figure 3 shows representative IPFs and magnified GROD maps from the CG and FG regions at 0, 3, and 6% tensile strains. No obvious grain morphology and orientation variation are discernable up to 6% strain in the two regions. A line scan within the strain localization region shows an increasing rate of point-to-origin misorientation angle from 1.5° to 5°/μm in the CG alloy as the tensile strain reaches 6% (Fig. 3G). However, similar analyses in the FG region indicate far less variation of the misorientation angle (from 2°/μm at 0% to 2.1°/μm at 6% strain).

Fig. 3. Quasi–in situ EBSD analyses on the G-T91 under uniaxial tensile tests.

IPFs and GROD maps from the (A to F) CG and (H to M) FG regions of the G-T91 at 0, 3, and 6% plastic strain. The IPFs taken along the SD display the grain morphology and crystal orientation evolution with the tensile strain in the two regions. Locally magnified GROD maps indicate the corresponding intragranular strain distribution. (G and N) Representative line scans were drawn in grain interior to quantify the point-to-origin misorientation variation at 0, 3, and 6% tensile strain in the two regions.

Figure 4 (A to C) summarizes the variation of average orientation deviation with tensile strain from 0 to 9% in the CG, FG, and UFG regions. Multiple EBSD scans were performed at the same depth from the sample surface in each gradient layer (CG, FG, and UFG) to obtain the error bars of each data point. The orientation deviation elevates in CG and UFG regions at a rate of 0.19°/% and 0.06°/%, respectively. GROD maps in Fig. 4 (D and E) illustrate that intragranular strain gradients were often initiated from GBs in the CG region marked by the white arrows. However, strain accumulation in the UFG region is much less (Fig. 4, H and I). The intragranular strain evolution in the FG region is intriguing, since the orientation deviation first increases at a rate of 0.24°/% up to 3% plastic strain followed by a reduction at −0.3°/% (Fig. 4B). FGs (labeled by white arrows) with much less intragranular strain concentration were frequently observed in the FG region at the plastic strain of 3% (Fig. 4G).

Fig. 4. Deformation mechanisms in each layer of the G-T91 steel.

A summary plot shows the variation of average orientation deviation as a function of tensile plastic strain derived from the GROD maps in the (A) CG, (B) FG, and (C) UFG regions. The average orientation deviation increases with the plastic strain in the CG and UFG regions. In the FG region, orientation deviation increases in the first 3% strain followed by a subsequent drop to 9% strain. Representative GROD maps taken along the SD depict the intragranular strain distribution in the (D and E) CG, (F and G) FG, and (H and I) UFG regions at 0 and 3% tensile strain. (Several locations at the same depth were investigated.)

In addition, the variation of maximum orientation deviations in the CG, FG, and UFG regions with the plastic strain were plotted in fig. S4. In the CG region (fig. S4D), the variation of maximum orientation deviation is consistent with the trend of the average orientation deviation. In the FG region, although the maximum orientation deviation keeps increasing, the slope of the increment after 3% strain is much less than that in the CG region (fig. S4E), suggesting an obvious strain relaxation. In fig. S5 (A to C), the intragranular strain variation during the in situ deformation of the FG region suggests the formation of a small subgrain. The corresponding point-to-point misorientation profiles were plotted in fig. S5 (D to F) with the peak misorientation increasing from 3° to 6.5° at about 700 nm. However, in the UFG region, the maximum orientation deviation gradually increases followed by a subsequent reduction after 6% strain (fig. S4F), indicating a more prominent strain relaxation process.

Microstructure evolution of deformed NL grains

It is unexpected to see that the NL grains can plastically deform together with the CG core to 45% overall engineering strain. In the present study, three representative locations (L1, L2, and L3) were selected on the fractured sample surface (Fig. 5A). TEM foils were lifted out within 10 μm from the sample edge in the three locations with the lamellae perpendicular to the ND, ensuring that the TEM lamella correspond to the original NL region in the sample. Using a method similar to that in (17, 20), we estimated that the corresponding true strains of the surface NL layer in the necking region were 10, 21, and 120% in L1, L2, and L3, respectively. Coarsened NL grains were frequently observed in L1 region. A representative grain highlighted with blue dash lines in Fig. 5B has a grain size of 800 nm with few dislocations in the grain interior. The deformed NL grains tend to rotate parallel to TD in L2 region with 21% strain. Dislocations were frequently observed in the interior of the NL grains and in the region close to GBs, as shown in the TEM BF and corresponding DF images in Fig. 5 (C and D). When the true strain reaches 120% in L3, most NL grains are elongated along TD instead of SD in the undeformed state (Fig. 5E). Magnified TEM images in Fig. 5 (F and G) depict an array of screw dislocations parallel to the $(01\overline{1})$ direction.

Fig. 5. TEM characterization on the deformed NL grains at various strain levels.

(A) Combined scanning electron microscopy (SEM) images show a sliced gauge section from a fractured G-T91 dog-bone bar. Transmission electron microscopy (TEM) lamellae were prepared by focused ion beam (FIB) lift-out on the outmost NL layer at various locations along the treated surface. The NL grains at different surface locations experienced different tensile strain levels. (B) A TEM BF image captured a coarsened grain in the sample with 10% strain. The image was taken close to <111> zone axis with g₀₁₁ spot strongly excited. (C and D) BF and corresponding DF TEM images illustrate dislocation structures in the 21% strained specimen. (E) BF TEM image shows the grain morphology in the sample experiencing 120% local plastic strain. (F and G) Magnified TEM BF and DF images from (E) depict dislocation arrays within a deformed grain. (H to J) The corresponding IPF, IQ + GB, and GROD maps of the grain in (F) show the orientation, GB types, and intragranular strain distribution. (K) The point-to-point and point-to-origin misorientation angle variation along the line drawn in (I). All the images were taken along the ND.

An overview of the morphological evolution of the deformed NL grains was revealed along ND in the IPFs (Fig. 6, A to D) and TEM micrographs (fig. S6). The variations of average lamella lengths along SD (l_SD) and TD (l_TD) with true strains are summarized in Fig. 6 (E to G). Deformation of most NL grains is accompanied by prominent grain coarsening along TD up to 10% applied strain (corresponding to the uniform elongation). Thereafter, most coarsened grains underwent gradual yet notable rotation along TD, and a subsequent refinement when external strain varies from 21 to 120% (Fig. 6, C and D). Consequently, the NL grains experienced a prominent reorientation along TD with a marked change in aspect ratio (L_SD/L_TD) from 3.6 to 0.4. Figure S7 shows the TEM microstructures observed from the ND of the NL grains from a G-T91 tensile dog-bone sample deformed to different engineering strains (8, 16, and 40%). At 8% strain in the uniform deformation region, the NL grains such as G1 and G2 obviously coarsened along the TD, which is also the tensile direction (fig. S7, D and G). At 16% strain, a few percent after the initiation of necking, NL grains such as G3 became elongated along TD by a gradual grain rotation process. The irregular shape of G3 indicated that the grain rotation process needs substantial accommodations from the neighboring NL grains. During this process, the microstructure of the NL layer is rather nonuniform. At 40% strain after fracture, NL grains such as G4 and G5 rotated further and appeared elongated along the TD due to the large plastic strain in the necking region. Meanwhile, the laminate thickness of G4 and G5 along the SD reduced prominently. The dimensions of the NL grains along ND, SD, and TD before and after fracture are summarized in fig. S2.

Fig. 6. Deformation mechanisms of the surface NL grains under uniaxial tension.

(A to D) IPFs visualize the grain morphology and crystal orientation evolution in the outmost NL layer at 0, 10, 21, and 120% local plastic strains along the ND. (E and F) The variation of the grain size along the SD and TD and the (G) corresponding grain aspect ratios were plotted as a function of the true plastic strain. (H to K) A series of schematic illustration shows the grain rotation procedures in the NL layer from the ND, which consists of three steps: l_TD coarsening, grain rotation, and l_SD refinement.

DISCUSSION

Unique NL grains in G-T91

The grain refinement mechanism in the current T91 steel processed by the SMGT process has been discussed in our previous study (27). Grain rotations between adjacent blocks or laths and dislocation activities are involved in the grain refinement process, resulting in a higher fraction of low-angle GBs (LAGBs) in the UFG and FG regions. The surface NL layer is of particular interest, since it sustains an overall engineering strain up to 45%. Different from other SSPD treatments, SMGT introduces elongated NL grains on the sample surface, and the three-dimensional morphology of the NL grains is visualized in Fig. 1 (H to J). Previous studies show that nanograins introduced by ultrasonic shot peening or surface mechanical attrition treatment are often equiaxed grains instead of elongated lamellae due to a lack of shear strain (14, 19, 41). Liu et al. (30) ascribed the formation of NL to shear deformation with large plastic strain (24 to 58), high strain rates (10³ to 10⁴ s⁻¹), and strain gradients (0.26 to 0.63 μm⁻¹) in a gradient Ni.

In the present study, the G-T91 bars were processed with comparable shear strain and strain rate. However, the smallest lamella thickness is 70 nm in the G-T91 steel, greater than those in the gradient Ni (20 nm) (30). In addition, different from the elongated strips in the gradient Ni (30), the NL layer in the G-T91 consists of numerous elliptical disk-like grains within the SD-TD plane and elongated along SD. When examined from the ND, the grains are generally 460 nm in length and 250 nm in width, and an average laminate thickness is 70 nm. No obvious texture along the three directions formed in the NL layers of the G-T91 in contrast to the prominent shear texture in gradient Ni (30). It is well known that screw dislocations in BCC metals are easier to cross slip leading to a suppressed strain hardening rate and a shortened stage II strain hardening regime compared with FCC metals, thus influencing the dislocation accumulation and annihilation during the SMGT process (42).

Deformation mechanisms of gradient layers

HDI hardening in G-T91

High strain gradient generated during the deformation of gradient structured materials is often accommodated by long-range GNDs near the region boundaries throughout the entire gradient layer (43, 44). The pileup of GNDs often generates HDI hardening, which further enhances the work hardening capability of the materials (43). Cyclic loading-unloading tests of the G-T91 specimen show that HDI hardening increases (from 436 to 486 MPa) during the first 10% tensile strain (corresponding to the uniform strain of the sample) followed by a subsequent reduction to 468 MPa (fig. S8).

The increase and decrease of the back stress due to HDI hardening often indicates the magnitude of GND pileups and GND density (43). The increase of HDI hardening during the first 10% strain indicates the accumulation of long-range GNDs at the region boundaries to accommodate co-deformation of each region in the gradient layer. Upon further deformation, the density of GNDs at the region boundaries tends to decrease, suggesting other deformation mechanisms such as grain reorientations dominate the rest of the plastic deformation. Therefore, HDI hardening induced by high strain gradient should contribute to the work hardening of the G-T91 in the early stage of the tensile deformation. Note that HDI hardening used to explain the well-known Bauschinger effect and the improved strain hardening is actually not limited to gradient structured materials (18, 31, 45, 46). Instead, HDI hardening has been widely observed in polycrystalline and heterogeneous materials, such as laminates, dual-phase materials, bimodal structure, and metal matrix composites (47–51).

Intragranular strain evolution in gradient layers

The distinct trends of average orientation deviation with plastic strain in CG, FG, and UFG regions imply different yet coordinated co-deformation mechanisms involved in each layer of the gradient structure. The GROD maps in Fig. 3 (D to F) show that intragranular strain builds up quickly with tensile strain in the vicinity of GBs in the CG regions, forming strain localization (“hot spots”) that can act as nucleation sites for cracks or voids (52). A more rapid increase in misorientation due to dislocation accumulation in the CG region indicates a global event of hot spot formation that introduces plastic instability (Fig. 4, A, D, and E). A lower increment rate in UFG layers in Fig. 4C suggests that the UFGs can accommodate plastic strain more readily, thus generating fewer hot spots. It is likely that other deformation mechanisms are involved in the UFG region in addition to dislocation activities. A recent finite element simulation work on a gradient Cu shows that CG core accommodates a majority of plastic strains, while the surface nanograins provide most of the tensile strength at a small strain level (44). Thus, stress and strain gradients build up across the gradient microstructures, resulting in multiaxial stress state and a gradient spatial distribution of GNDs (19, 44).

Compared with the CG region, grains in the FG region were predeformed during the surface treatment with large plastic strain manifested by GND pileups (fig. S1, F and K). The reduction of orientation deviation in the FG layer after 3% plastic strain in Fig. 4B indicates strain relief manifested by a reduction of dislocation density, probably resulting from grain refinement by forming sub-GBs or dynamic recrystallization. This interpretation is supported by the formation of new grains with less intragranular strain labeled by white arrows in the FG region at a strain of 3% in Fig. 4G. The distinct deformation mechanisms in each layer can generate elastic and plastic constraint among adjacent regions, thus facilitating the nucleation of homogeneously dispersed shear bands (23, 53). In the G-T91, dispersive shear localization zones nucleated from the NL layer at the surface and then propagated toward the CG core before fracture. The distance between two neighboring shear zones is 200 μm with an angle of ~90° (fig. S9). The propagation of adjacent stable shear zones can be blocked by each other thus introducing a sluggish shear propagation rate and delaying the localized plastic deformation in the G-T91, lastly resulting in an enhanced tensile elongation (53, 54).

Intrinsic plasticity of NL grains

Reorientation of NL grains

High plasticity of NL grains by substantial grain reorientation event at room temperature is rarely reported in literature. High intrinsic plasticity of NC grains was reported in a gradient Cu where the surface nanograins can be tensile deformed to a total true strain of 127% via prominent grain coarsening (17). Deformation-induced grain coarsening in NC pure metals has been frequently observed even at room temperature (55–58). The high density of metastable GBs in a nonequilibrium state in NC materials primarily contributes to the grain growth (55, 59). The critical grain size below which prominent grain growth occurs is often correlated with the saturated grain size induced by severe plastic deformation (20). Factors such as deformation temperature, strain rate, strain gradient, and chemical composition of the materials can affect the critical grain size (28, 47, 60–63). Fang et al. (20) found a critical grain size of 165 nm for grain coarsening in gradient Cu during the uniaxial tension. Song et al. (5, 6) performed a series of thermomechanical treatments (TMTs) on T91 steel and reported a minimum grain size of 320 nm. Different from gradient Cu, we found that the grain reorientation plays a critical role in achieving high intrinsic plasticity (more than 100%) of the NL grains in the current G-T91. As shown in fig. S2A, the average dimension along ND (t_ND) increased by 66% from 70 to 118 nm during deformation, while the size along SD (l_SD) shown in fig. S2B decreased by 70% from 460 to 138 nm. In addition, the length along TD (l_TD) shown in fig. S2C increased by 88% from 230 to 433 nm. This finding indicates that the surface NL grains have experienced a significant amount of plastic strain during the uniaxial tensile test of the G-T91.

Our study reveals that the grain reorientation process is governed by coarsening of l_TD (from 0 to 10% true strain), gradual yet substantial grain rotation (from 10 to 21%), and subsequent refinement of l_SD (above 21% true strain) in the NL grains of G-T91. Grain rotation–dominated plasticity at low temperature has been extensively studied in NC metallic materials with a grain size of tens of nanometer (64, 65). In the present study, note that the deformation process alters the aspect ratio (l_SD/l_TD) of the NL grains from 3.6 to 0.4, suggesting a prominent grain reorientation process. This phenomenon is rarely reported in other NC and gradient materials under uniaxial tensile test. Grain rotation of NL with such a high aspect ratio often requires substantial accommodation from the neighboring NL grains. Instead, the NL grains first coarsen along the TD and reduce their aspect ratios during the uniform deformation. Upon further deformation with the initiation of necking, the coarsened NL grains gradually rotate and elongate along the TD to fracture. The eventual uniform and fine NL grains along TD are the results of extremely large plastic strain (more than 100% strain in the NL) within the necking region.

Emission of dislocation lines from metastable NL GBs was frequently captured by the representative TEM BF and corresponding DF images (Fig. 5, F and G). At least two sets of dislocations glided along $[1\overline{1}0]$ and $[0\overline{1}1]$ directions from a projected view. These dislocations are likely GNDs, since they share the same Burgers vector and morphology (see the Supplementary Materials on GND analyses). Automated Crystal Orientation Mapping (ACOM) analyses on the same grain reveal that these dislocations tend to pile up and form two short LAGBs marked in Fig. 5 (H and I). The formation of LAGBs helps release the intragranular strain accumulation induced by the dislocation pileup indicated by the corresponding GROD map in Fig. 5J. A misorientation line profile in Fig. 5K confirms that a 22.5° misorientation gradient was accommodated by introducing 6.3° and 13° LAGBs. The dislocation emission events were frequently observed in the NL grains with 21 and 120% strain (fig. S10) and contributed to the plastic flow of NL grains in the G-T91. Dislocation emissions from GBs have been observed during in situ TEM straining experiments and modeled by simulations (66–71). In addition, it has been simulated that dislocation emission from defective and nonequilibrium metastable GBs is significantly enhanced compared with their structurally equilibrium counterparts (72). Furthermore, in 9 to 12% Cr F/M steel with a low carbon concentration, dislocation density in the martensitic lath remains relatively high in the range of 1 × 10¹⁴ to 10 × 10¹⁴ m⁻² (73). Most of these dislocations in tempered martensite are in form of dense dislocation arrays, forming sub-GBs (lath and block boundaries) that can readily transform into defective metastable GBs with a high GB dislocation density during SMGT process (fig. S11).

Deformation mechanism of NL grains

On the basis of the forgoing discussion, Fig. 6 (H to K) illustrates the hypothetical grain reorientation mechanism of the NL grains in three steps. (i) At low strain level, coarsening of l_TD dominates the plastic deformation. (ii) At intermediate strain, NL grains gradually rotate along TD. (iii) A gradual refinement of l_SD takes over during the subsequent tensile deformation of the rotated grains. In the current NL T91 grains, coordinated deformation among the grain network is critical for the high intrinsic plasticity of the NL grains, which involves substantial grain rotation. Grain rotation–dominated plasticity at low temperature often requires very small grain size (less than 10 nm) (74). In the current NL grains with the shortest grain size of 70 nm, the grain rotation process should be assisted by frequent dislocation activities.

The TEM images of the deformed NL T91 grains in Fig. 5 evidenced that the deformation process was accompanied by emitting and absorbing high-density short-range GNDs from highly defective metastable GBs to accommodate the plastic strain gradient. The formation of GNDs accommodates both lattice rotation in the grain interior and misorientation variation across the GBs, thus enhancing the rotation of grains and crystal lattice to ensure the continuity and compatibility of plastic deformation (75). The density of short-range GNDs (ρ_G) for a single slip system in each grain can be expressed as (47, 76)

$${\mathrm{\rho }}_{\mathrm{G}}=\frac{1}{b}\frac{\mathrm{\partial }\mathrm{\gamma }}{\mathrm{\partial }x}$$ (1)

where, b is the magnitude of the Burgers vector. γ is the macroscopic plastic shear strain across the distance x. Considering the crystal discontinuity across GBs, x is often limited by the grain size of the materials. Therefore, at the same strain level, a smaller grain size leads to a higher density of short-range GND required for compatible deformation and correspondingly a larger degree of lattice rotation. The formation of short-range GNDs also facilitates grain rotation process in the NL, UFG, and FG regions, making a coordinated deformation of the GB networks possible. Similar GND-facilitated grain rotation processes have been reported in a gradient TWIP steel where the outermost FGs show a more remarkable grain rotation than center CGs in the gradient tensile specimen (75). Such a prominent grain reorientation phenomenon in the deformed NL grains has not been reported previously and may widely exist in gradient materials. The deformation mechanism may contain the key answer to numerous scientific questions regarding ductility and co-deformation mechanisms of various microstructures in gradient materials.

Strength-ductility trade-off

In the present work, the T91 bar was annealed at 800°C before SMGT, yielding a fully tempered martensite microstructure (α) in the ferritic matrix. In the blue region in Fig. 2C, all the other F/M steels with various chemical compositions are in fully tempered state as well, thus making a consistent comparison (77–86). It is noted that introducing 20 volume % gradient structures in T91 steel overcomes the strength-ductility trade-off in F/M steels. A dual-phase microstructure with both ferrite and martensite (α + α′) can be achieved in T91 steel via TMTs in a previous study (86), and the strength of the steel can reach 850 MPa, but the uniform strain is mostly limited below 6%, as labeled in the orange region at the top left corner.

The current G-T91 steel also fractured in a relatively ductile mode compared with H-T91. In situ scanning electron microscopy (SEM) tension snapshots in Fig. 7 (A to H) show the fracture behaviors of H-T91 and G-T91. Figure 7 (I to J) quantitatively compare the total number and size distribution of voids generated during the deformation of H-T91 and G-T91. Larger voids (9 μm) with a higher density nucleated on both specimen surface and fracture surface of H-T91 throughout the entire necking region, suggestive of a nucleation-growth-coalescence process. Intervoid necking mechanism might contribute to the failure of H-T91, and in this mechanism intervoid ligaments often lead to void growth and coalescence, thus triggering fracture of the materials (87, 88). Fewer voids with much smaller size (3.8 μm) in G-T91 are confined only to the shear localization zone (marked by red dash lines in Fig. 7F) within the necked region, suggesting a possible void sheeting mechanism that is often considered as a ductile fracture mode (87, 89).

Fig. 7. A comparison on the fracture mechanisms in the H-T91 and G-T91 specimens.

In situ SEM snapshots capture the sample surface morphology and void nucleation in the flat (A and B) H-T91 and (E and F) G-T91 dog-bone specimens under uniaxial tension at 15 and 35% strain and after fracture. The SEM images were taken along the SD. The red arrows label the formation of voids and microcracks. Magnified SEM images from (B) and (F) depict void formation on the specimen surface away from or close to the fracture surface in the (C and D) H-T91 and (G and H) G-T91. (I and J) Statistical distribution indicates average void sizes of 9 and 3.8 μm in the two types of fractured specimens.

By introducing a gradient microstructure, a strong and ductile T91 steel was fabricated. Intragranular strain analyses indicate distinct co-deformation mechanisms in the gradient structures. Notably, the NL layer was deformed to 45% fracture strain by a complex grain reorientation mechanism consisting of initial grain coarsening, gradual rotation, and subsequent refinement processes. High-density GNDs emitted from defective GBs were found to facilitate the substantial grain reorientation without fracture. The highly deformable NL and the gradient layers in the G-T91 specimen enable a ductile void sheeting mechanism, delaying catastrophic tensile fracture. Such a previously undiscovered deformation mechanism warrants future investigations by integrating various plasticity modeling techniques at various length scales. The current work provides valuable insights into understanding the deformation behaviors of gradient structural materials.

MATERIALS AND METHODS

Material fabrication

The chemical composition (in weight %) of as-received (AR) T91 steel is shown in table S1. The AR T91 steel was normalized at 1038°C for 0.5 hours followed by air cooling and a subsequent tempering at 760°C for 0.5 hours with air cooling. Bar samples with a length of 52 and 10 mm in diameter were cut from the AR T91 steel billet using electro-discharge machining (EDM) for SMGT. Before SMGT, the bar samples were annealed at 800°C for 1 hour to reach a fully tempered microstructure, and the as-annealed (AA) specimens were machined into tensile dog-bone bar shape. The tensile dog-bone bars had a gauge length of 10 mm and a diameter of 4 mm as illustrated in Fig. 1A. Specimens with the same dimension were fabricated from AA T91 steel for comparison, specified here as H-T91. The basic setup and configuration of SMGT processing can be found in the literature (13). During the SMGT processing, the AA T91 steel bar rotated at a speed of 600 rounds per minute, while a tungsten carbide tip penetrated into the sample surface and moved along the axial direction at a velocity of 10 mm/min. The sample was grinding treated by eight passes with a penetration depth of 25 μm for each pass. Cooling oil was applied to avoid temperature rise during the processing. For in situ tension and EBSD analyses, flat tensile dog-bone samples with a thickness of 1 mm were cut from the as-processed bars by EDM as indicated in Fig. 1B. The flat surfaces for EBSD analyses were prepared according to standard mechanical grinding and polishing procedures, followed by a vibratory polishing for 5 hours using colloidal silica to remove the surface scratches.

Microstructure characterization

TEM analyses were carried out on an FEI Talos 200X TEM microscope operated at 200 kV equipped with a high-angle annular dark field (HAADF) detector. IPF and GB characterization were obtained by the precession electron diffraction (PED) technique using the NanoMEGAS ASTAR (ACOM and phase mapping hardware/software package for TEM) system (90). A precession angle of 0.6° and a step size of 8 nm were used. For GND characterization, a step size of 3 nm was used. The cross-section TEM specimens from the NL layer in the as-processed G-T91 before and after deformation were prepared by focused ion beam (FIB) using an FEI Helios G4 dual beam SEM. Before FIB milling, a platinum layer was deposited to protect the surface from ion damage. To remove FIB induced damage, the TEM samples were ion polished using a low current (27 pA) at a low voltage (2 keV) multiple times as the final steps. The average size of NL grains was estimated from the TEM images and IPFs using the intercept method (91).

In situ and ex situ mechanical testing

Uniaxial tensile tests were performed on an MTS tensile frame with a load cell of 30 kN at a constant strain rate of 1 × 10⁻³ s⁻¹. An Epsilon axial extensometer was used to precisely measure the strain of the samples during tensile tests. The yield strengths of all samples were identified using the stress corresponding to 0.2% offset strain. At least three samples were tested for each condition to ensure the reproducibility of the tensile results. Vickers hardness was measured on the cross section of the round tensile bar samples using a LECO LM247 microhardness indenter with an applied load of 10 g holding for 13 s. Interrupted in situ EBSD measurements of the strained G-T91 specimens were performed in a JEOL JSM-IT300HRLV field emission gun (FEG) SEM at I³SEM Facility at Sandia National Laboratories. The SEM microscope was equipped with EDAX Velocity fast-scan EBSD camera (92). An acquisition rate of 150 to 200 frames per second and a step size of 0.05 μm were used for the EBSD scan in the present study. An MTI SEMtester 1000 EBSD tensile stage with a maximum load capacity of 4500 N was used for straining the flat G-T91 specimens in the SEM chamber at the same strain rate used for the ex situ testing. Detailed analyses on the EBSD and PED results were performed using the orientation imaging microscopy software. The acquired data points with a confidence index value greater than 0.1 are used for the quantitative analyses. Detailed descriptions of the intragranular strain and GND analyses can be found in the Supplementary Materials.

Supplementary Materials

This PDF file includes:

Intragranular strain analyses

GND analyses

True strain calculation in necking region

HDI hardening calculation

Figs. S1 to S14

Tables S1 and S2

References