Volumetric versus distortional deformation in rat lungs

Abstract

There are several lung diseases that lead to alterations in regional lung mechanics, including acute respiratory distress syndrome. Such alterations can lead to localized underventilation of the affected areas resulting in the overdistension of the surrounding healthy regions. They can also lead to the surrounding alveoli expanding unevenly or distorting. Therefore, the quantification of the regional deformation in the lungs offers insights into identifying the regions at risk of lung injury. Although few recent studies have developed image processing techniques to quantify the regional volumetric deformation in the lung from dynamic imaging, the presence and extent of distortional deformation in the lung, and its correlation with volumetric deformation, remain poorly understood. In this study, we present a method that uses the four-dimensional displacement field obtained from image registration to quantify both regional volumetric and distortional deformation in the lung. We used dynamic computed tomography scans in a healthy rat over the course of one respiratory cycle in free breathing. Non-rigid image registration was performed to quantify voxel displacement during respiration. The deformation gradient was calculated using the displacement field and its determinant was used to quantify regional volumetric deformation. Regional distortion was calculated as the ratio of maximum to minimum principal stretches using the isochoric part of the Cauchy green tensor. We found an inverse correlation between volumetric strains and distortion indicating that poorly expanding alveoli tend to experience larger distortion. The combination of regional volumetric strains and distortion may serve as high-fidelity biomarkers to identify the regions at risk of most adverse lung injuries.

1. INTRODUCTION

There are several lung diseases that lead to regional and global alterations in the mechanical behavior of the lungs, such as acute respiratory distress syndrome (ARDS). ¹ Such alterations can lead to localized under-ventilation, which affects the surrounding regions due to parenchymal interdependence.² Localized under-ventilation leads to overdistension, and, consequently, volutrauma of the surrounding healthy regions when the lungs are mechanically ventilated.³ Thus, it proves important to quantify regional lung kinematics to predict the regions at risk for volutrauma.

Using micromechanics-based models to investigate the deformation behavior of the alveolar septal walls, prior studies have estimated that alveolar wall stress can be 12 to 27 times greater than the applied alveolar pressure during mechanical ventilation.⁴ Hence, overventilation can lead to high regional alveolar pressures causing an increased risk of damage to the alveolar septal walls. To estimate elevations of the stress at the alveolar septa walls during respiration, it is necessary to estimate the regional deformation behavior of lung parenchyma. Medical imaging,^{5, 6} combined with image registration,^7–9 has proven to be a powerful and non-invasive tool that can be used to quantify and assess in-vivo deformation.

Regional variations in the mechanical behavior of the lungs can also lead to the surrounding alveoli expanding unevenly⁷ or distorting. In this study, we define distortion as the deviation from sphericity. It is expected that such an uneven expansion and/or distortion can lead to an increased risk of adhesive/compressive atelectasis due to the increased proximity of alveolar septal walls. Hence, it is important to study lung regional distortion in addition to under- and over-ventilated regions to prioritize regions for treatment and minimize injury to healthy tissues. In this study, we investigate the distortion experienced by lung parenchyma in a healthy rat during natural respiration and its correlation with regional alveolar volumetric expansion.

2. METHODS

2.1. Image acquisition

Four-dimensional (4D) computed tomography (CT) scans were obtained for a healthy Sprague-Dawley (SD) rat under isoflurane anesthesia. Sixteen equally-spaced image stacks were collected over the course of one respiratory cycle and used for image registration.

2.2. Image registration

We used an open-source image registration algorithm (Nifty-reg)^{10, 11} to perform non-linear non-rigid image registration to obtain voxel-based displacement. We quantified the deformation field via two methods (described below) to verify the displacements calculated by the image registration algorithm. The lungs were segmented from the reference image stack using Slicer, and the segmentation was propagated through image registration to track the region of interest throughout the respiratory cycle.

2.3. Displacement propagation method

In this method, we obtained the total displacement between the current time point and the reference time point (at the start of inspiration) through the summation of the voxel displacement between consecutive time points. Let $\mathbf{U}=\left[\begin{array}{lll}{U}_x& U_y& U_z\end{array}\right]=\left[\begin{array}{lll}\mathrm{\Sigma }{u}_x& \mathrm{\Sigma }{u}_y& \mathrm{\Sigma }{u}_z\end{array}\right]$ be the total displacement from the reference image obtained using image registration. The deformation gradient tensor $\mathbf{F}$ is calculated through the following equation:

$$\mathbf{F}=\mathbf{I}+\left[\begin{array}{lll}\frac{\partial U_x}{\partial x}& \frac{\partial U_y}{\partial x}& \frac{\partial U_z}{\partial x}\\ \frac{\partial U_x}{\partial y}& \frac{\partial U_y}{\partial y}& \frac{\partial U_z}{\partial y}\\ \frac{\partial U_x}{\partial z}& \frac{\partial U_y}{\partial z}& \frac{\partial U_z}{\partial z}\end{array}\right],$$ (1)

where $\mathbf{I}$ is the identity matrix. The volumetric deformation $J$ is obtained as the third invariant (determinant) of $\mathbf{F}$. Following the calculation of $J$, the deformation gradient is decomposed into volumetric and isochoric deformation parts where the isochoric deformation gradient $\overline{\mathbf{F}}$ is given by

$$\mathbf{F}=(J^{1/3}\mathbf{I})\overline{\mathbf{F}},\text{where}J=det(\mathbf{F}).$$ (2)

The distortion $\left(D\right)$ is calculated as the ratio between the largest and smallest principal stretch values, given by

$$D=\frac{max\left({\bar{\lambda }}_1,{\bar{\lambda }}_2,{\bar{\lambda }}_3\right)}{min\left({\bar{\lambda }}_1,{\bar{\lambda }}_2,{\bar{\lambda }}_3\right)},$$ (3)

where the principal stretches ${\bar{\lambda }}_1^2,{\bar{\lambda }}_2^2,{\bar{\lambda }}_3^2$ are the eigenvalues of the symmetric and isochoric Cauchy green tensor $\overline{\mathbf{C}}$ defined by

$$\mathbf{C}=(J^{2/3}\mathbf{I})\overline{\mathbf{C}},\text{where}\mathbf{C}={\mathbf{F}}^T\mathbf{F}.$$ (4)

Here $J>0$ and $D\ge 1$ are independent of the frame of reference. $J>1$ indicates volumetric dilation of the voxels while $J<1$ indicates volumetric compression. $D=1$ indicates no distortion while $D>1$ indicates the presence of distortion.

2.4. Deformation gradient propagation method

In this method, we calculated the deformation gradient $\mathbf{F}$ from the displacement between two consecutive time points and propagated $\mathbf{F}$ between consecutive pairs of time points to obtain the total deformation gradient. The procedure is summarized as

$${\mathbf{F}}_i=\mathbf{I}+\left[\begin{array}{lll}\frac{\partial u_x}{\partial x}\hfill & \frac{\partial u_y}{\partial x}\hfill & \frac{\partial u_z}{\partial x}\hfill \\ \frac{\partial u_x}{\partial y}\hfill & \frac{\partial u_y}{\partial y}\hfill & \frac{\partial u_z}{\partial y}\hfill \\ \frac{\partial u_x}{\partial z}\hfill & \frac{\partial u_y}{\partial z}\hfill & \frac{\partial u_z}{\partial z}\hfill \end{array}\right],$$ (5)

$$\mathbf{F}=\prod {\mathbf{F}}_i.$$ (6)

Next, $J$ and $D$ are calculated from $\mathbf{F}$ at the point of interest. Comparing $J$ and $D$ values obtained from both methods allowed us to verify the calculation of the deformation gradient at large parenchymal deformation. Next, the relationship between $J$ and $D$ was determined using the Pearson correlation coefficient $\left(PCC\right)$ incorporating the spatial distribution of $J$ and $D$ across the lungs as

$$PCC=\frac{Cov(J,D)}{{\sigma }_J{\sigma }_D},$$ (7)

where $Cov(J,D)$ is the covariance of $J$ and $D$, and ${\sigma }_J$ and ${\sigma }_D$ are the standard deviations for $J$ and $D$, respectively.

3. RESULTS

The segmentation from the reference image stack was successfully propagated and followed the shape of the lungs through the remaining image stacks indicating that the chosen image registration algorithm was capable of tracking the motion of the lungs throughout the respiratory cycle. In addition, both the displacement and deformation gradient tensor propagation methods resulted in the same regional strains (results not shown). Volumetric strain results indicated that regions in the lung could experience a maximum volumetric strain of $J=4$, which implies a four-fold increase in local volume (Figs. 1c,f). Further, our calculations indicated that, at the end of inspiration, 67% of the lungs experience volume expansion ($J>1$), and 33% of the lungs experience volume reduction ($J<1$). The average volume expansion and volume reduction were $J=1.56$ and $J=0.75$, corresponding to a 56% increase and a 25% reduction in volume, respectively. The results for $J$ also indicated that highly-expanded regions are localized with a sharp transiting to regions with a moderate volumetric expansion (Fig. 1).

Figure 1.

Reconstruction of rat lungs from segmentation showing frontal plane (a) and transverse plane (b) with directions marked. Volumetric strain (in log scale) at the start of inspiration in the frontal (c) and transverse (d) view. Volumetric strain at the end of inspiration in the frontal (e) and transverse view (f).

The distortion contour at end-inspiration indicates that the regions with high distortion tend to lie in regions with minimal volumetric strains and near the surface of the lungs (Figs. 2b,d). Distortion values reached up to 20, indicating that the maximum principal stretch is 20 times the minimum. High distortion implies that alveoli in such regions tend to deform into ellipsoidal shapes, i.e., they do not expand/contract spherically. Plotting the distortion versus volumetric strain of each voxel indicated that regions that experience compressive volumetric strains ($J<1$) tend to exhibit higher distortion (Fig. 3) and this is in agreement with a negative $PCC$, which was found to be −0.42.

Figure 2.

Distortion at the start of inspiration in the frontal (a) and transverse (b) view. Distortion at the end of inspiration in the frontal (c) and transverse (d) view.

Figure 3.

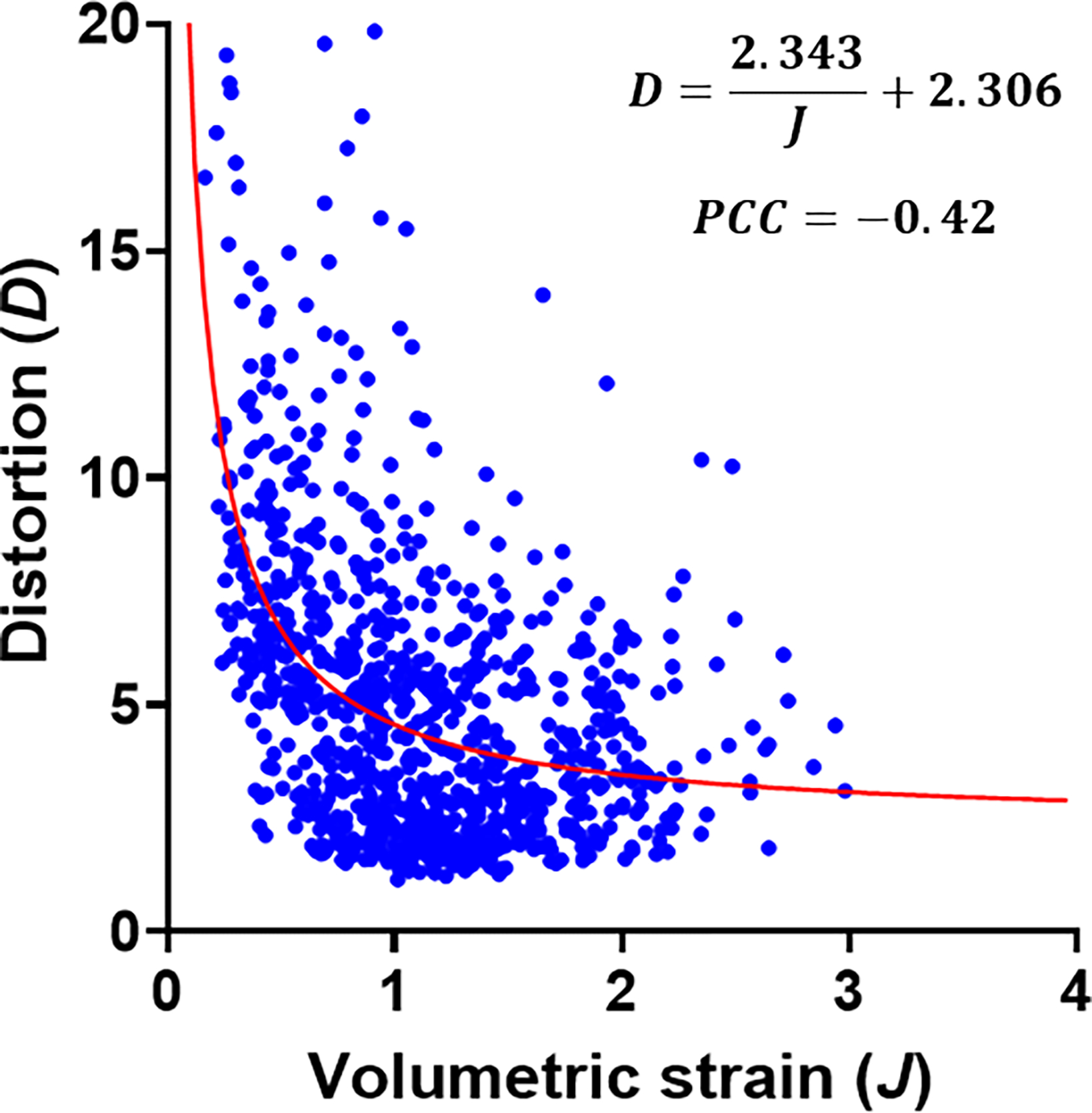
The correlation between volumetric strain $J$ and distortion $D$ with subsampled data (every 10th voxel). The equation of the fitted curve $D=2.343/J+2.306$. PCC is the Pearson correlation coefficient.

4. DISCUSSION

In this study, we have presented a method to quantify the regional volumetric and distortional deformation in the lungs. Although volumetric strain has been used to determine regional inflation levels of alveoli, lung regional distortion and its relationship to inflation remain understudied. Our results for distortion indicated that regions that are volumetrically compressed ($J<1$) are at the highest risk for large distortions. The combination of volumetric compression and high distortion could imply that these regions experience atelectasis, and regions with sustained atelectasis could be at higher risk for damage due to repeated opening and collapse. In addition, kinematic parameters such as volumetric strain and distortion can be used as early markers for regional lung injury leading to global lung dysfunction. Indeed, regional changes in lung mechanical function due to injury are often accompanied or preceded by changes to the local kinematic behavior of lung parenchyma. Thus, distortion and volumetric strains presented in this work can serve as additional diagnostic metrics to complement existing markers obtainable from functional magnetic resonance imaging¹² to improve diagnosis and prognosis in lung injuries.

Information regarding volumetric strain and distortion can be used to develop, validate and parameterize in-silico models to improve their predictive capabilities.¹³ The displacements and deformations can also be used as inputs to such in-silico models, in combination with pressure measurements, to predict the patient-specific regional material behavior of the lung parenchyma. Volumetric strains and distortion values are also applicable to micromechanical models^{4, 14–16} where kinematic metrics can be used to create physiologically realistic loads and deformations for in-silico experiments.

Finally, in this study, we assumed a continuum and compressible solid representation of lung parenchyma. The continuum assumption is, in part, a limitation of imaging resolution in vivo, which does not reach the fidelity needed to capture details of alveolar septal wall motion. The volumetric strain was presented on a logarithmic scale since $J=1$ is the deformation-free state. We performed our analysis for one SD rat $(\mathrm{n}=1)$. Further investigation and validation of our results are warranted in a larger sample cohort undergoing 4D-CT scans to be conducted in the future.

5. CONCLUSION

In this study, we have used 4D-CT scans of rat lungs to characterize the regional kinematics of lung parenchyma. We have used volumetric strain as a metric to investigate regional ventilation and introduced a complementary metric, distortion, measuring uneven (distorted) deformation of alveoli. Our results indicated that regions with low levels of ventilation exhibit higher levels of distortion. We expect that the combination of regional volumetric strain and distortion can improve the identification of lung regions susceptible to the most injury in acute and chronic lung disease.