Light-controlled growth of DNA organelles in synthetic cells

Abstract

Living cells regulate many of their vital functions through dynamic, membraneless compartments that phase separate (condense) in response to different types of stimuli. In synthetic cells, responsive condensates could similarly play a crucial role in sustaining their operations. Here we use DNA nanotechnology to design and characterize artificial condensates that respond to light. These condensates form via the programmable interactions of star-shaped DNA subunits (nanostars), which are engineered to include photo-responsive protection domains. In the absence of UV irradiation, the nanostar interactions are not conducive to the formation of condensates. UV irradiation cleaves the protection domains, increases the nanostar valency and enables condensation. We demonstrate that this approach makes it possible to tune precisely the kinetics of condensate formation by dosing UV exposure time. Our experimental observations are complemented by a computational model that characterizes phase transitions of mixtures of particles of different valency, under changes in the mixture composition and bond interaction energy. In addition, we illustrate how UV activation is a useful tool to control the formation and size of DNA condensates in emulsion droplets, as a prototype organelle in a synthetic cell. This research expands our capacity to remotely control the dynamics of DNA-based components via physical stimuli and is particularly relevant to the development of minimal artificial cells and responsive biomaterials.

1. Introduction

Phase separation of engineered biomolecules has become a versatile approach to build artificial mimics of membraneless organelles observed in living cells [1] and is emerging as a key method in synthetic cell research [2]. Recent in vitro studies have demonstrated artificial phase-separated condensates with specific properties by taking advantage of DNA nanotechnology, which allows for on-demand assembly of DNA nanostructures [3,4]. An elegant approach is the spontaneous formation of DNA-rich condensates through the self-assembly of star-shaped DNA motifs known as DNA nanostars [5–7]. A DNA nanostar is composed of multiple hybridized single strands of DNA, whose sequence is designed according to Watson–Crick–Franklin base pairing. A functional nanostar has three or more arms each including single-stranded palindromic domains at the tip of the arms (sticky ends) that enable the formation of bonds among nanostars and their condensation [5]. The phase transitions of DNA nanostars depend on typical factors like nanostar concentration, temperature and ionic strength of the solvent [6–9]. Their phase diagram can be shaped by the nanostar design parameters, including sticky end length, sequence and number of arms [10,11]. Unpaired bases near the sticky end or at the core of the nanostar can facilitate condensation by enhancing the bond mobility [6].

For DNA condensates to operate as mimics of dynamic cellular organelles, it is necessary to understand and harness the kinetics of their formation and dissolution. The ‘constitutive’ growth rate of DNA condensates is determined by certain structural parameters of the nanostars: for example, longer arms speed up both coarsening and fusion of condensates [9], while longer sticky ends reduce the speed of fusion, as the bond mobility is reduced [11]. To modify condensate formation/dissolution rates over time (without altering the nanostar structural parameters or the environment), a simple approach is to change the amount of particles available for phase separation: this can be done via biochemical reactions that convert nanostars between an active and an inactive form. A change in concentration in the appropriate range can enable a phase transition. Dissolution can be achieved by deactivating nanostar bonds, for example via restriction enzymes [12], or via the introduction of DNA inhibiting strands that hybridize to the sticky ends [13] or to nanostar connectors [14]. Formation of condensates can be similarly achieved by activating DNA nanostars through strand displacement of inhibitors [13]. The transition kinetics can be controlled by changing the reaction rate parameters (via optimization of hybridization domain length and sequence content) or the concentrations of activating/inhibiting reactants [13].

Building on these results, here we demonstrate a method to trigger DNA condensate formation by controlling the active/inactive state of DNA nanostars via UV irradiation. We design a modified three-arm nanostar in which one arm is occluded by a ‘protector’ domain, reducing the effective nanostar valency to 2 and preventing condensation. By including a photocleavable (PC) linker [15,16], the protector domain can be cleaved upon UV irradiation, thereby increasing the nanostar valency to 3, enabling a phase transition. Through a computational model, we first set up an expectation for the phase transitions of a mixture that includes fully active nanostars (valency 3) and deactivated nanostars (valency 2 plus 1 deactivated arm). We find that the critical concentration for condensation depends on both the fraction of deactivated nanostars and the efficiency of arm deactivation. Next, we experimentally demonstrate our design and identify a PC hairpin protector that allows for triggering condensate formation upon UV exposure, while suppressing condensation in the absence of UV exposure. We then show that it is possible to control condensation kinetics by the UV irradiation time, which determines the fraction of activated nanostars. Finally, we illustrate the usefulness of a ‘remote’ nanostar activation mechanism by forming DNA condensates in water-in-oil (w/o) droplets, which can be viewed as synthetic organelles forming inside elementary protocells. We show that the UV irradiation time dosage not only controls the kinetics of DNA organelle formation, but also their final size, providing means to program the internal organization of synthetic cell populations with light patterns.

2. Methods

2.1. Oligonucleotides

Custom oligonucleotides were purchased from Integrated DNA Technologies, Inc. Fluorophore-labelled strands and PC-modified strands were purified to the high-performance liquid chromatography grade. Oligonucleotide sequences and modifications are provided in §1 of the electronic supplementary material.

2.2. Sample preparation

Nanostars were formed by mixing the target concentration of each oligomer in a buffer consisting of 20 mM Tris–HCl (pH 8.0) and 350 mM NaCl. One of the strands was modified using a fluorescently labelled dye without sticky ends, which was mixed at a 5% molar ratio in the solution. To prepare the nanostars containing the PC modification, we annealed only the two non-modified strands, and later added the modified strand at room temperature. Annealing was done using a thermocycler, held at 95°C for 5 min and then cooled to room temperature at a rate of −1°C min⁻¹. After annealing, samples were incubated at 27°C. For consistency, the same protocol was followed for the control experiments using non-modified strands (one strand was added isothermally after annealing) [17]. Samples containing nanostars were irradiated with an 8 W 320 nm UV lamp (115 V, 60 Hz), with a distance of 4 cm between the lamp and the test tube containing the sample. Fluorescence microscopy images taken over time were processed via in-house scripts that measure the condensate size (area, radius). For triplicate experiments, mean values reported are the average over the mean values of all replicas, and error bars report the standard deviation of the mean. For non-triplicate experiments, the mean values and error bars were obtained via bootstrapping (see electronic supplementary material, §2.4).

2.3. Fluorescence microscopy

Samples were imaged using an inverted microscope (Nikon Eclipse TI-E) with Nikon CFI Plan Apo Lambda 60X Oil (MRD01605) objective. The Cy3 signal was measured using the Eclipse Cy3 filter cube, using an excitation wavelength of 559 nm. Details on the slide preparation are in the electronic supplementary material, §2.1; briefly, samples were imaged using coverslips (Fisherbrand™, cat. 12-545-JP) measuring 60 mm × 22 mm, with a thickness between 0.13 and 0.17 mm were soaked in 5% (w/v) bovine serum albumin and dissolved in 20 mM Tris–HCl (pH 8.0) for over 30 min to prevent non-specific interactions of the DNA on the glass surface and avoid wetting and surface-induced nucleation of condensates.

2.4. Image processing

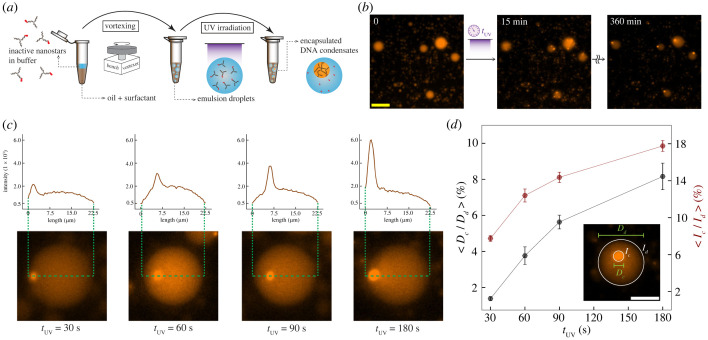
We analysed all the microscopy raw data obtained from the experiments by means of a custom image processing tool developed in our group. For each experimental condition, we measured the average condensate area and the condensate number from a consistent number of images. The image processing tool is available on Github: https://github.com/klockemel/Condensate-Detection. A detailed description, elaborating on the condensate detection criteria can be found in electronic supplementary material, §2.2. The normalized intensity of condensates encapsulated in w/o droplets (figure 4d) was computed as follows: the condensate intensity I_c is measured by the sum of all the pixel intensities within the condensate region (circle with diameter D_c). The droplet intensity I_d is the sum of intensities within the droplet region (circle with diameter D_d) outside of D_c. We used the I_c/I_d ratio (akin to a partition coefficient) as the normalized fluorescence intensity of a condensate.

Figure 4.

Light-triggered formation of condensates of controllable size in synthetic protocells. (a) Schematic of the encapsulation process of DNA nanostars in w/o droplets. The oil–surfactant phase stabilizes the encapsulation after the vortexing step. After UV irradiation of the sample, condensation begins. (b) Representative fluorescence microscopy images of the photoactivated condensates within the w/o droplets, wherein the exposure duration is 180 s. Snapshots from left to right represent before exposure, 15 min and 360 min after exposure, respectively. Scale bar: 50 µm. (c) Intensity analysis of an example droplet image taken 6 h from UV irradiation, considering t_UV equal to 30 s, 60 s, 90 s and 180 s, respectively, from left to right. The plots show the fluorescent intensity variation across the droplets, and clearly the peak intensity increases with longer irradiation time. Droplet images were rotated and aligned to facilitate comparison of the line intensities. (d) Normalized diameter and intensity of condensates in w/o droplets, plotted against the UV irradiation time. Intensity is integrated over the entire condensate or droplet. In each case, 12 droplets of similar size are chosen to be analysed, and each data point represents the value of the computed quantities averaged over all the droplets considered. The error bars represent the standard error. Scale bar: 15 µm.

2.5. Preparation of emulsion droplets

We generated emulsion droplets encapsulating DNA nanostars following the protocols in [18,19]. The oil–surfactant mix includes FC-40 fluorinated oil and 2% (w/v) perfluoropolyether–polyethylene glycol block copolymer fluorosurfactant with Krytox-FSH via an amide group (Ran Biotechnologies). Fluorinert™ FC-40 was purchased from Sigma-Aldrich™ (CAS Number 86508-42-1; MDL number MFCD00131095). Inactive nanostar solution was added on top of the oil–surfactant phase within an Eppendorf tube and mixed on a benchtop vortexer for 50 s to generate a large number of droplets in the oil phase. The average droplet size is affected by both time and vortexing speed. After vortexing, the w/o droplets were incubated at room temperature for a few minutes to allow droplets to cream at the surface. To avoid overcrowded fields of view, aliquots for imaging were harvested below the dense droplet layer at the top of the sample. Aliquots were transferred into the well of an Ibidi chamber slide (µ-Slide VI 0.4, hydrophobic coating) prior to UV irradiation and imaging after appropriate incubation time. To prevent contamination and evaporation of the sample, the wells were sealed by covering the top edge of each input with vacuum grease (Dow Corning®) and covered with a glass coverslip.

2.6. Computational simulations

We performed our computational simulations through scripts developed in house. We modelled nanostars as particles of finite valency via a patchy particle model. Particles are modelled as spherically symmetric, with an excluded volume interaction and an angular interaction depending on the orientation of the particles. Two particles i and j interact through the following potential:

$$\varphi ({\mathbf{r}}_i,{\mathbf{r}}_j)={\varphi }_{HS}({\mathbf{r}}_i,{\mathbf{r}}_j)+{\varphi }_{\mathrm{Patch}}({\mathbf{r}}_i,{\mathbf{r}}_j),$$

where ${\varphi }_{HS}({\mathbf{r}}_i,{\mathbf{r}}_j)$ corresponds to a hard sphere repulsion given by the Weeks–Chandler–Andersen (WCA) potential:

$$\begin{array}{ccc}{U}_{WCA}(r)=4\epsilon \left[{\left({\displaystyle \frac{\sigma }{r}}\right)}^{12}-{\left({\displaystyle \frac{\sigma }{r}}\right)}^6+{\displaystyle \frac{1}{4}}\right]& \mathrm{if}& r<2^{1/6}\sigma ,\\ U_{WCA}(r)=0& \mathrm{if}& r\ge 2^{1/6}\sigma .\end{array}$$

Two patches interact via a modified Kern–Frenkel [20] potential given by

$${\varphi }_{KFM}(r_{ij},{\theta }_i,{\theta }_j)=-{\epsilon }_{\mathrm{att}}\exp \left(-{\displaystyle \frac{1}{2}{\left({\displaystyle \frac{r_{ij}}{d}}\right)}^{10}}\right)\cos \left({\displaystyle \frac{\pi {\theta }_i}{2{\theta }_m}}\right)\cos \left({\displaystyle \frac{\pi {\theta }_j}{2{\theta }_m}}\right),$$

where ε_att is the attractive interaction strength, which can be chosen separately for each of the interactions between the patches. As we are examining the case in which nanostars have 1 arm that is fully or partially inhibited when compared to the other 2 arms, we consider a class of ‘2 + 1’ particles for which the energy of one of the patches (${\epsilon }_{\mathrm{att}}^I$) is chosen to be a fraction of the energy of the other patches (${\epsilon }_{\mathrm{att}}^A$). Each patch is positioned on the vertices of the triangle encompassing a plane of the sphere. θ_i is the angle to the centre of the patch on particle i to the vector joining the centres of particles i and j, r_ij, and θ_m is the total angular aperture of the patch.

We integrate this potential using the algorithm given in [21] under a Langevin thermostat which gives a random force f(t) with the following property:

$$⟨\hspace{0.17em}f\hspace{0.17em}(t)f\hspace{0.17em}(t^{\mathrm{\prime }})⟩=2k_{b}T\gamma \delta (t-t^{\mathrm{\prime }}),$$

where δ is the Dirac delta function. The thermostat has both a rotational and translational friction coefficient, which is given by 6πησ and 6πησ³. For our simulations, we set η = 0.1, k_bT = 1, and we choose a wide patch angle, cos(θ_m) = 0.927, with a range d = 1.4. These parameters ensure that condensation, when it occurs, leads to more liquid-like states than solid-like states, as very small patch angles require larger energies in order to form condensates, which leads to bonds that are effectively irreversible on the timescale of simulations. The simulations were performed with periodic boundary conditions for a given volume fraction of valency 3 particles.

3. Results

3.1. Simulations indicate that mixtures of particles of different valency have competitive phase behaviour

Our idea for controlling the phase transition of DNA nanostars is to selectively control the state (active/inactive) of only one of the three arms via a light-activatable domain (figure 2a). Under appropriate conditions, a population of nanostars (particles) with valency 3 should form a condensed phase as previously shown through experiments and modelling [7,8]. Our expectation is that under the same conditions, nanostars with valency 2 cannot condense into condensates: intuition suggests that the lowest energy state (the one that satisfies the condition that every subunit has both of its binding sites occupied) would correspond to a chain of particles, i.e. a polymer. The inability of valency 2 particles to form condensates, but the possibility that valency 3 particles could, would mean that mixtures of valency 2 and valency 3 particles may have more complex phase behaviour than valency 2 or valency 3 particles alone [8]. In particular, as the ground state of valency 2 particles is a chain, and the ground state of valency 3 particles could be a condensate, how might we expect mixtures of valency 2 and 3 particles to look as we go towards lower temperatures? How would this picture change if valency 2 particles were to include an additional binding site whose interaction energy is a fraction of the others (valency 2 + 1)? To address these questions, we built a model for mixtures of nanostars of given valency in which nanostars are treated as colloidal particles (figure 1a), assuming spherical symmetric potentials to treat attractive interactions between particles [22] (see Methods; and electronic supplementary material, §4).

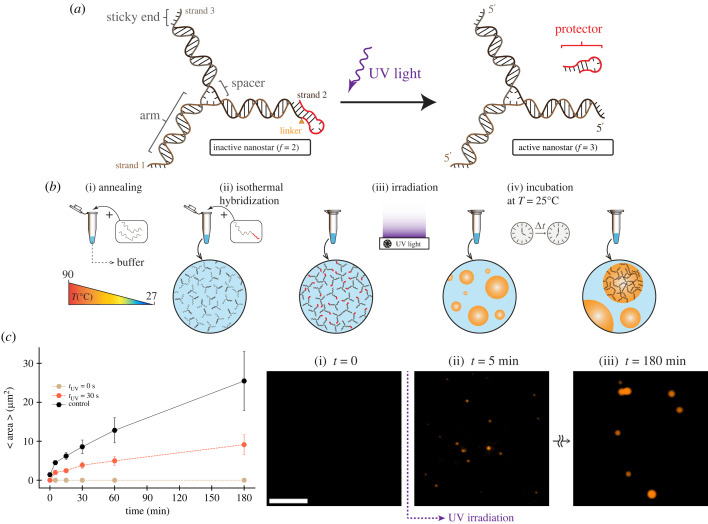
Figure 2.

Photo-activatable DNA nanostar motif. (a) Schematic of three-arm DNA nanostar. One of the nanostar sticky ends was modified to include a single-stranded overhang, or toehold (red domain on the 5′ end of one arm), separated by a PC linker. This overhang when cleaved releases the protected sticky end and enables nanostar to form condensates. (b) Single-stranded DNA oligomers are annealed to form three-armed DNA nanostructure (nanostars). Nanostars form isothermally and interact through their sticky ends and phase separate into condensates. (c) Plots of the increase in average area of condensates when incubated at room temperature (27°C) over 3 h. Time equal to 0 shows the average area of condensates at the end of the anneal process. The sample was irradiated for 30 s given a total nanostar concentration of 2.5 µM. The plot includes a positive control (no PC linker, no UV irradiation) as well as a negative control (no UV irradiation). Dots show the mean of one experimental replicate; error bars are obtained by bootstrapping. Right: representative fluorescence microscopy images for activated nanostars phase separating into condensates after 30 s UV exposure. Scale bar: 15 µm.

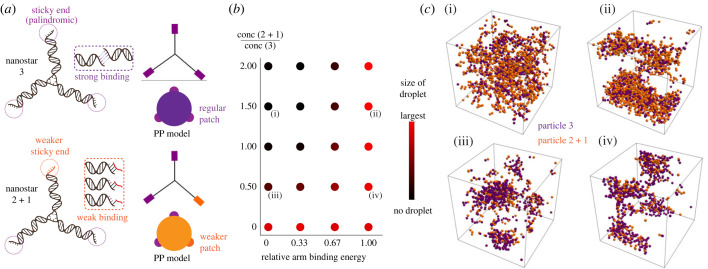
Figure 1.

Phase diagram of a binary mixture of nanostars with mixed valency. Using a patchy particle model, we simulated the phase behaviour of a mixture of nanostars having valency 3 (three sticky ends with the same interaction strength) and valency 2 + 1 (one sticky end allows for weaker interactions). (a) Schematic representation of 2 + 1 nanostars and a coarse-grained representation of them as a patchy particle. The nanostar is modelled as a hard sphere with attractive patches on the surface. (b) Representation of the behaviour of a mixture of 3 and 2 + 1 particles at varying concentrations of 2 + 1 relative to 3 and interaction energy of the +1 compared to the other arms. In this case, the interaction between the patches on valency 3 particles is 12 k_bT (with k_bT = 1) and the volume fraction is 0.01. Dots coloured by size of the condensate, normalized by the size of the largest observed condensate over all parameters. Adding 2 + 1 valency particles disrupts phase separation when the energy of the +1 arm is too low and promotes it when it is higher. All simulations were performed at a fixed volume fraction of valency 3 particles. (c) Snapshots of condensates formed from mixtures of valency 3 and valency 2 + 1 particles, indicated at points on the phase diagram in (b). Large interaction energies of +1 lead to participation of the 2 + 1 particles in phase separation; however, low interaction energies lead to disruption of phase separation.

From our simulations, we sought to quantify the equilibrium effect of adding valency 2 + 1 particles to a collection of valency 3 particles that undergo phase separation. For this purpose, we measured the size of condensates normalized by the size of the largest observed condensate over all parameters. We examine the system under changes in the relative attraction energy ${\epsilon }_{\mathrm{att}}^I$ of the +1 bond (with respect to the attraction energy of the other bonds ${\epsilon }_{\mathrm{att}}^A$) and in the ratio of concentration of particles of valency 2 + 1 and of valency 3. The simulation results are reported in figure 1b and allow us to make the following observations:

• (1) Valency 3 particles can undergo phase separation, in line with intuition, as illustrated by the bottom left red dot of figure 1b. This is true over a range of values of ρ (the packing fraction) and ${\epsilon }_{\mathrm{att}}^A$, as illustrated in the electronic supplementary material, figures S8–S10.
• (2) Adding valency 2 particles disrupts phase separation: going up the left-hand side sequence of dots in figure 1b shows that the size of condensates decreases as larger numbers of valency 2 particles are added. This somewhat counterintuitive result arises from adding a large number of attractive subunits to the system yielding less phase separation. Such an effect could only be explained through accurate accounting of the valency of the particles involved. The precise mechanism of this effect is not immediately apparent through simulation but can be understood through the fact that the valency 2 particles bind to each of the valency 3 binding sites. While one may expect that this would just correspond to extending the size of the valency 3 particles, in practice additional valency 2 particles can bind to the combined structure. Careful study of the simulation data shows a plethora of partially self-assembled structures, which are not amenable to condensation into large spherical droplets due to the distributions of their available binding sites (see electronic supplementary material, figure S11, for examples of such structures). Mixing valency 2 and valency 3 particles therefore produces a competition between self-assembly and liquid–liquid phase separation, analogous to reentrant phase transitions [23]. However, at very large interaction strengths, it is still possible for these small partially assembled structures to phase separate into a disordered gel-like phase.
• (3) Competition between self-assembly into small structures that cannot phase separate, and phase separation of the entire system can be altered: modulating the energy of an additional binding site ${\epsilon }_{\mathrm{att}}^I$ of the valency 2 particles (leading to valency 2 + 1 particles) eventually reverses this phenomenon, leading to all particles participating in phase separation. This parameter therefore tunes the competition between self-assembly and phase separation. As expected, when the energy of the +1 bond is equal to the valency 3 bonds, the particles are indistinguishable and participate in phase separation (as seen in the snapshots of figure 1); note that the snapshots are with periodic boundary conditions, therefore droplets extend across the boundaries. Periodic boundary conditions can also lead to cylindrical phases being favoured, but this is due to the boundary conditions rather than any feature of particles themselves. The choice of boundary conditions does not materially affect our conclusions.

In conclusion, these computational simulations corroborate our intuition that the effectiveness of our approach to activate/deactivate nanostars depends both on how tightly the arm is deactivated as well as on the fraction of particles with a deactivated arm. Electronic supplementary material, figures S8–S10, extend our computational analysis to a range of densities ρ and attractivity ${\epsilon }_{\mathrm{att}}^A$, obtaining consistent results. The proposed model can be used in various methods of sticky end modification of a valency 3 particle, including our current strategy, which introduce DNA particles of different valency present in the solution.

3.2. Building light-activated DNA condensates

We adopted the three-arm DNA nanostars proposed by Sato et al. [7] that interact via palindromic, four-nucleotide (nt) long sticky ends present at the end of each arm. To monitor the condensates via fluorescence microscopy, we doped the mixture with 5% of Cy3 labelled strand 1. After assembly, these nanostars can be considered subunits that spontaneously yield DNA-rich condensed droplets, which in our case are expected to remain liquid at room temperature (27°C) while ripening and fusing into larger condensates (electronic supplementary material, figure S7, shows example images of droplets after 48 h of incubation).

To make a DNA nanostar that can condense upon photoactivation, we modified one of the three arms to include a UV-controlled interaction domain. We elongated one of the sticky end domains to fold into a hairpin that should prevent interactions with other sticky ends (figure 2a) and block condensation, as predicted by our theory (figure 1b). The stem of the hairpin includes a PC spacer, a photolabile functional group (2-nitrobenzyl linker) available as a custom modification in commercial DNA synthesis [24]. The PC spacer is cleavable by UV light of specific wavelength (300–350 nm) and nicks the DNA backbone. Once the stem is cleaved, it is expected to become an unstable complex that disassembles thereby ‘reactivating’ the third nanostar arm, leading to condensate formation.

We began to characterize this idea by testing hairpin designs that vary by stem length. Our goal was to find the appropriate hairpin stem length to block condensate formation prior to UV irradiation, while rapidly disassembling post UV irradiation and enabling the formation of condensates. Because the PC modification is unstable at high temperature, our tests were conducted by annealing the two non-modified DNA strands composing the nanostars, and adding the PC-modified strand isothermally, so that the PC linker is intact at the time of nanostar formation (figure 2b). We verified the correct formation of this nanostar complex via native polyacrylamide gel electrophoresis (PAGE) (electronic supplementary material, figure S1A). In these experiments, we found a 5 nt stem to be insufficient to completely suppress the formation of condensates in the absence of UV stimulation, presumably because it only partially hinders interactions of the protected arm (electronic supplementary material, table S2 and figure S1B). A longer 6 nt stem fully suppresses formation of condensates. Once irradiated with UV light (320 nm) for 30 s, visible condensates form within minutes, as shown in figure 2c. The average condensate area measured over time (image processing methods are described in the electronic supplementary material, §2) shows that condensates grow by ripening and fusion at a rate comparable to that observed in previous experiments by us and others [9,13]; however, at 30 s irradiation condensates grow at less than half the speed of the control (no hairpin). These experiments validate our hypothesis that condensation of a three-arm DNA nanostar can be controlled by modulating the conformation of one of the arms through a UV-responsive hairpin.

3.3. The condensate growth rate is controlled by the irradiation dose

Our model predicts that in a mixture of nanostars of different valency, phase transitions depend on the relative abundance of the active/inactive species (figure 1b). Further, the growth rate of DNA condensates, like other phase-separating systems, depends on the concentration of subunits. Thus, we reasoned that by changing the irradiation time we could control the fraction of activated nanostars in solution (given a fixed total amount of inactive nanostars) and thus both determine whether condensation occurs as well as change the rate at which condensates form.

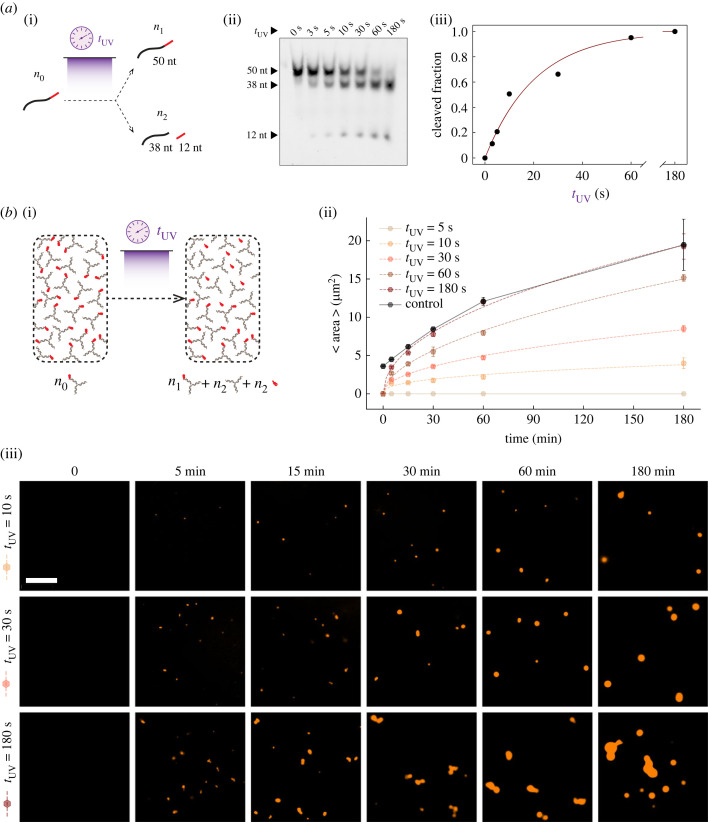
To identify the appropriate range of irradiation time for cleaving a controllable fraction of the DNA sample, we used gel electrophoresis to characterize the cleavage efficiency of the 50 nt nanostar strand that includes the PC modification. Upon UV irradiation, the cleaved linker should split the strand into two portions of 12 and 38 nts, shown in figure 3a(i). We irradiated the sample for different amounts of time, from 3 to 180 s, and we quantified the fraction of cleaved DNA using denaturing PAGE shown in figure 2a(ii), obtaining a dose–response shown in figure 3a(iii). The data are well fitted by an exponential curve that can be derived as the solution of the differential equation describing the kinetics of the chemical reaction $x\stackrel{k}{⟶}{x}_1+x_2$, where x is the uncleaved DNA and x₁ and x₂ are the cleaved fractions:

$$x_1(t_{UV})=(1-e^{-k\cdot t_{UV}}),$$

with fitted k = 0.048 s⁻¹. Given the power of the lamp and the irradiation working distance we adopted, we found that all the DNA is cleaved within 3 min of irradiation.

Figure 3.

Controlling condensate growth rate by dosing UV irradiation. (a) (i) Schematic illustration of the cleaved fraction (i.e. n₂/n₀) dependence of the modified strands on the exposure duration when they get exposed to the UV light. (ii) PAGE gel electrophoresis image, depicting the change in the population of cleaved and uncleaved strands in the solution with respect to the exposure duration. (iii) Plotting the cleaved fractions with respect to the exposure time (data points), as well as the exponential fitted curve (solid line) to the experimental data. (b) (i) A schematic summarizing our experiment in which we varied the UV exposure time to modulate the fraction of activated nanostars. (ii) Average area of the condensates over time, after UV irradiation of different duration (t_UV of 5 s, 10 s, 30 s, 60 s and 180 s). The reference time (t = 0) on the horizontal axis is the moment the UV exposure starts. For the positive control (nanostars have no protector hairpin), t = 0 is the beginning of the incubation process right after annealing. The control sample is given by three-arm nanostars without the protector hairpin. Dots represent averages over three experimental replicates; error bars represent the standard deviation of the mean. All the experiments are done at a total nanostar concentration of 2.5 µM. Dashed lines correspond to the fitted curve based on our growth rate model (electronic supplementary material, §3.1). Solid lines simply connect the data points as a guide to the eye. (iii) Representative snapshots of the fluorescence microscopy images for three experiments (t_UV = 10 s, 30 s and 180 s), taken at the incubation times of 0 min, 5 min, 15 min, 30 min, 60 min and 180 min. Scale bar: 15 µm.

The irradiation time/cleavage fraction dose–response makes it possible to estimate the irradiation time needed to activate a particular fraction of DNA nanostars. We produced inactive DNA nanostars at a concentration of 2.5 µM and irradiated the samples for 5–180 s, which should activate 20% to 100% of the nanostar population (figure 3b(i)). We then took fluorescence microscopy images of the samples for up to 3 h, extracting the average condensate area versus time, shown in figure 3b(ii). Box plots reporting the area statistics are in the electronic supplementary material, figure S3. Example images are provided in figure 3b(iii), and additional representative microscopy images are in the electronic supplementary material, figure S4. These data show that the condensate growth rate is determined by the irradiation time, which is a user-controllable input parameter. We repeated the same experiment using a lower total concentration of nanostars, 1.25 µM, confirming that the condensate growth rate is controlled by the irradiation time (electronic supplementary material, figure S5).

The condensate growth rate should follow a power law with respect to time, as we showed in previous work [9] (electronic supplementary material, §3.1). This model considers particles that are large with respect to the solvent and assumes that condensate growth is mainly driven by fusion. (Indeed, we observe frequent coalescence events in our experiments, visible in some of the reported images as non-spherical droplet aggregates in the process of fusing.) Such a mode of growth would have a prefactor that scales as the active fraction of nanostars squared. We verified whether this model captures the data by fitting the measured condensate radius with a simple model $g{x}_1^2{t}^{\alpha }$, with $x_1(t_{UV})=(1-e^{-k\cdot t_{UV}})$, that combines the power law growth rate model with the previous expression estimating the level of active nanostars as a function of irradiation time. The fit yielded an average exponent α = 0.236 and a prefactor g that is roughly constant across the different irradiation conditions, with the 10 UV irradiation time experiments being an outlier. The model trajectories (converted to condensate area) are the dashed lines in figure 3b(iii). All the fitted parameters are reported in electronic supplementary material, table S3. It is worth noting that DNA condensates exhibit gravitational sedimentation down to the surface of the imaging chambers over time, so condensate size distribution near the surface may slightly differ from the actual size distribution within the sample.

The fraction of activated nanostars necessary to enable condensation appears lower than expected. An irradiation time of at least 10 s (the minimum required for both 2.5 µM and 1.25 µM total nanostar concentration) corresponds to approximately 50% activated nanostars, as we found from the cleavage control experiments in figure 3a(iii). This low fraction is comparable to previous work in which one of the arms is deactivated by hybridization with an inhibitor strand [13]: also in that case, at least 50% active nanostars are required for condensation. Here, this is likely due to the fact that the inactive arm still weakly interacts with other arms via one unprotected base in the sticky end, an interaction that may be enhanced in a dense phase. As illustrated by our computational model (figure 1), weak interactions of one arm can have a dramatic effect on the phase transition.

We also find UV irradiation to be less efficient at promoting growth than one would predict based on the protector cleavage dose–response (figure 3a(iii)). We compared the growth rate of UV-irradiated samples with that of non-UV-irradiated control samples including a mix of active and inactive nanostars (one protected arm) (electronic supplementary material, figure S2). A sample including 30% active nanostars grows at a rate comparable to 30 s irradiation, which is expected to activate 70% of the nanostars. Similarly, a sample including 70% active nanostars grows like the 60 s UV irradiation sample, which is expected to activate 90% of the nanostars. The sample with 100% active nanostars grows comparably to the 180 s irradiation time. We hypothesize that the cleaved protector, which is partially complementary to the nanostar sticky ends, might slow down condensate growth by competing for sticky ends and reducing the effective concentration of active nanostars. This phenomenon seems to be more significant at low activated nanostar levels, presumably when concentrations are close to the boundary of the phase diagram.

To summarize, the formation of these condensates depends on UV irradiation time, it follows a power law as expected, and it appears to be influenced by two phenomena: the potential interactions of the protected arm with other sticky ends allow condensation to begin with a low fraction of activated nanostars, but cleaved protector weakly competes for sticky ends, reducing the effective level of activated nanostars and reducing the growth rate of condensates.

Overall, the irradiation time determines not only the growth rate but also the total mass of activated subunits, and therefore it should also control the equilibrium volume of condensed matter. In the next section, we evaluated this in additional experiments that track condensates in confinement.

3.4. Light-based control of DNA organelle growth in synthetic cells

Like condensates in living cells, which adapt to stimuli by assembling and disassembling dynamically, a triggerable synthetic condensate system could make it possible for artificial cells to form organelles on demand. To achieve this potential, it is important to identify methods to control the kinetics and equilibrium properties of condensates within a compartment. Here we demonstrate that the UV activation is an ideal ‘remote control’ mechanism for this purpose, as it does not require changes in the sample temperature or in the biochemical inputs.

As a mimic of synthetic cells we used w/o emulsion droplets to generate isolated compartments with high throughput and with size that ranges from a few micrometres to tens of micrometres in diameter [18]. Each droplet is an isolated environment that remains stable and can be stored for days at room temperature. While these w/o droplets are far from having the capacity to reproduce functions and properties of living cells, which can freely exchange resources with the surrounding aqueous media, they make it possible to monitor and characterize synthetically engineered systems in confined, cell-size compartments for extended periods of time.

We encapsulated inactive nanostars inside w/o droplet ‘protocells’ made through a ‘shaken’ protocol employing a bench vortexer (figure 4a) [18,19]. Like in the non-encapsulated experiments (figures 2 and 3), we observed that inactive nanostars remain in the dispersed phase after encapsulation. Condensation begins only after UV irradiation that cleaves the PC linker and activates the third arm. Right after irradiation, we observe the formation of several small condensates that fuse over time, eventually producing a single condensate in each protocell, consistent with expectation [25] (figure 4b; refer to electronic supplementary material, figure S6, for additional microscopy images). By exposing the sample to increasing irradiation times we qualitatively note that condensates form at higher speed, as one would expect based on the non-encapsulated experiments (figure 3b). It should be noted that encapsulation in the emulsion droplets might reduce the efficiency of UV irradiation of the nanostar solution; thus we had to increase the minimum irradiation time needed to activate the formation of condensates.

As different irradiation times activate a different fraction of nanostars, the total condensed mass should differ. We assessed this by measuring the diameter of the single condensate present in each protocell 6 h after irradiation, normalized relative to the protocell diameter. Figure 4d shows that the normalized condensate diameter grows with the irradiation time of the sample. Similarly, the normalized condensate fluorescence intensity (which has to be proportional to the number of fluorescent particles in the dense phase) shows an increasing trend with the irradiation time, confirming that a longer irradiation time induces the condensation of a larger amount of fluorescent particles.

Collectively, these experiments show that UV irradiation time can be used as an easy-to-tune experimental parameter to control the size of artificial DNA organelles inside protocells without direct influx of chemical signals, and without having to change the total concentration or the structure of the condensing particles to calibrate the organelle size.

4. Discussion and conclusion

We have developed methods to use UV irradiation to regulate the kinetics of DNA nanostar phase separation. Our design relies on the idea of controlling phase transitions by changing the valency of nanostars between the values of 2 and 3. Through a patchy particle computational model, we illustrated how the phase transitions depend on the relative abundance of nanostars of different valency, as well as on the strength of the deactivated bond. We then demonstrated that condensation of three-arm DNA nanostars can be suppressed by protecting one of the arms through a hairpin; by introducing a PC linker, the hairpin can be removed through UV irradiation, which increases the nanostar valency and enables condensation. By dosing the UV irradiation time, it is possible to modulate the fraction of active nanostars and thereby tune their growth rate. We finally highlighted the versatility of this method to control the size of DNA organelles in synthetic protocells.

The use of UV PC linkers has several advantages. (i) The DNA cleaving dose response versus irradiation time curve can be tuned by changing the irradiation intensity and distance. Previous work has shown that the UV-cleavage dose responses can be modulated in the range of tens of minutes rather than seconds [15,26]. (ii) This is a ‘remote’ mechanism to control condensation that does not require alteration of the sample ionic conditions, temperature and components. (iii) The strategy works at room temperature and does not require thermal treatment. (iv) This approach is agnostic to sequence design, and protectors could be easily adapted to a variety of nanostar sticky end sequences. (v) The presence of short photo-cleaved DNA domains does not appear to affect the morphology of condensates, but appears to slow down their kinetics; these effects could be systematically explored through a rigorous characterization of their phase diagram [25]. Overall, we believe our approach is a versatile enabling method to characterize phase separation of DNA-based motifs, as well as self-assembly of a broad class of DNA motifs interacting through a finite number of domains.

Our results build on previous studies highlighting the potential of light irradiation to control condensation [27,28]. Reversible coacervation and shuttling of molecules upon sequential exposure to UV–visible light were demonstrated in mixtures of double-stranded DNA and a light-responsive azobenzene cation [29]. Photoswitchable molecular communication among DNA nanostar-based coacervates was also demonstrated within w/o droplet protocells, by introducing azobenzene-tethered DNA molecules that capture and release their complement [30]. PC linkers like the ones we adopted were also used to break DNA nanostar links and dissolve condensates, providing an opportunity to photopattern hydrogels formed within w/o droplet protocells [31].

Overall, our work adds to the library of molecular tools that allow control of programmable DNA nanostructures with potential use in a variety of applications. With such a versatile control toolbox, our system is not limited to the biomimicry of cellular condensates but can be used as an engineerable model system for studying physical properties of phase separation and oligonucleotide interactions in natural and synthetic cells.

Ethics

This work did not require ethical approval from a human subject or animal welfare committee.

Data accessibility

Data are available on request from the authors.

Additional experiments are provided in the electronic supplementary material [32].

Authors' contributions

S.A.: conceptualization, data curation, methodology, project administration, supervision, writing—original draft and writing—review and editing; M.D.: data curation, investigation, methodology, writing—original draft and writing—review and editing; D.O.: conceptualization, formal analysis, software, writing—original draft and writing—review and editing; E.F.: conceptualization, formal analysis, funding acquisition, methodology, project administration, resources, supervision, visualization, writing—original draft and writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

We declare we have no competing interests.

Funding

This research was supported by NSF CAREER award 1938194 and FMRG:BIO award 2134772 to E.F., and by the Sloan Foundation through award G-2021-16831.